Octave: Guia de Estudo
|
|
|
- Stella Camelo Machado
- 8 Há anos
- Visualizações:
Transcrição
1 Octave: Guia de Estudo Nuno Cavalheiro Marques e Carmen Morgado 1 Breve Introdução O Octave é uma linguagem de programação de alto nível, destinada ao tratamento de problemas para computação numérica. O interface com o programador é efectuado através de uma linha de comando. O Octave pode efectuar cálculos aritméticos com reais, escalares complexos e matrizes; resolver sistemas de equações algébricas; integrar funções sobre intervalos finitos e infinitos e integrar sistemas de equações diferenciais ordinárias e diferenciais algébricas. Permite gerar para o ecrã e para a impressora gráficos 2D e 3D, utilizando o Gnuplot. O Octave é em grande parte compatível com o MatLab. Este documento constitui um breve resumo do manual do Octave que pode ser consultado em ou localmente em 2 Utilização do sistema Nesta secção apresentar-se-á o Octave como uma ferramenta de cálculo para problemas de computação numérica. O seu objectivo é descrever o funcionamento geral da aplicação, enquanto linguagem de linha de comando. O Octave ( é uma aplicação desenvolvida utilizando uma filosofia OpenSource. A principal vantagem deste tipo de aplicações relativamente aos seus equivalentes comerciais (nomeadamente do MatLab, é o custo: as ferramentas OpenSource são de utilização livre, estando inclusive o seu código fonte disponível para o público em geral. Assim aplicações com este tipo de licença, podem ser livremente distribuídas e instaladas em qualquer computador. O código fonte da aplicação está igualmente disponível, o que fornece uma garantia de qualidade e robustez, sendo ainda possível adaptar ou estender a própria aplicação para a solução de determinados problemas. Podem ser obtidos mais detalhes sobre as ferramentas desenvolvidas com este tipo de licença, consultando O Octave é uma ferramenta desenvolvida para o Sistema Operativo Linux 1 de :51
2 ( sendo actualmente distribuída com as principais versões deste sistema operativo. A sua utilização no ambiente Windows é igualmente possível através da utilização da ferramenta Cygwin ( a qual fornece um ambiente de emulação da plataforma Linux sobre Microsoft Windows. Pode efectuar-se o download do Octave para MS-Windows quer da página da cadeira ( quer directamente, do site A instalação do Octave num computador equipado com sistema operativo Windows XP, NT ou 2000, deverá ser relativamente simples. A instalação é igualmente possível nos sistemas MS-Windows 95/98 e Me, no entanto nestes últimos por vezes ocorrem problemas. Após efectuar o Download do programa de instalação, bastará executar este programa e o Octave será instalado no seu computador. Em caso de dificuldades, o site indicado para obter mais informação para resolução de problemas relativamente à instalação do Octave sobre plataformas Windows é Linha de Comandos O primeiro passo para trabalhar com o Octave é obviamente o inicio desta aplicação. Para tal bastará seleccionar o programa no menu iniciar, conforme a figura abaixo. De seguida deverá ser apresentada a linha de comandos do Octave com uma aparência semelhante à seguinte figura: 2 de :51
3 Contrariamente aos ambientes gráficos normalmente disponíveis no Windows, o Octave caracteriza-se por receber os seus comandos directamente da linha de comandos (ou Prompt). Na linha de comando, o sistema indica que aguarda um comando apresentando (por omissão) o texto "octave:1>" seguido de um cursor a piscar. Após este prompt é possível escrever os comandos que controlam a aplicação. Deverá introduzir cada comando separadamente e seguido pela tecla [Return]. Num ambiente gráfico os comandos são especificados ao computador através de acções do rato sobre símbolos (ou ícones) visuais. Numa linha de comandos os comandos devem ser especificados através do teclado. No exemplo anterior foi introduzido (pelo utilizador) um comando simples: 5+5 Tendo o computador dado a resposta (resultado): 10 Seguida do prompt pedindo novo comando: octave:2> É fácil utilizar o Octave como calculadora. Eis alguns exemplos auto-explicativos: octave:9> octave:10> octave:11> 2*2 4 3 de :51
4 octave:12> 2/ octave:13> 5*5*5 125 octave:14> 5^3 125 octave:15> 5^ octave:16> 8\ octave:17> 2\4 2 octave:18> 3*( /6)/ octave:19> 5^ O único comando menos usual é a divisão à esquerda, a qual pode ser facilmente compreendida com a igualdade x/y y\x. De igual forma podem ser utilizados comandos um pouco mais complexos, envolvendo funções. As seguintes funções elementares de cálculo poderão ser utilizadas: octave:20> sqrt(5) raíz quadrada octave:21> log10(1000) 3 logaritmo base 10 octave:22> log(e^10) 10 octave:23> pi pi = logaritmo neperiano constante pi octave:24> sin(pi/6) octave:25> cos(0) 1 octave:26> tan(pi/4) octave:27> sin(pi) e-16 seno coseno tangente seno de pi não é 0, por causa de erros de aproximanção 4 de :51
5 octave:28> 30*pi/ octave:29> sin(ans)^2+cos(ans)^2 1 utilização de valor anterior em cálculo Repare-se que sin(pi) não é calculado como zero! Tal deve-se a um erro de cálculo do próprio computador. O número apresentado é no entanto muito próximo de zero: Trata-se de um erro de aproximação do algoritmo de cálculo do seno. Normalmente este número varia de computador para computador, mas está sempre presente quando se efectuam cálculos reais. Note-se aliás que é possível calcular a precisão de um resultado, para tal utiliza-se o comando format: octave:61> pi pi = octave:62> format long octave:63> pi pi = octave:64> format short octave:65> pi pi = 3.14 octave:66> sin(pi) 1.22e-16 octave:67> format bank octave:68> sin(pi) 0.00 octave:69> format octave:70> pi pi = contante pi formatação long, a partir deste ponto a precisão dos resultados passa a ser de 15 algarismos significativos (máx de 24 caracteres) formatação short, precisão passa a ser de 3 algarismos significativos formatação bank, precisão passa a ser de 2 casas decimais formatação standard, precisão de 5 algarismos significativos (é o default) Em geral os interfaces por linha de comandos são menos intuitivos que os interfaces gráficos, pois exigem do seu utilizador a memorização de um conjunto de palavras chave. No entanto, após o período inicial de adaptação os interfaces de linha de comandos revelam-se bastante mais fiáveis e fáceis de descrever: o número de formas distintas de entrar um mesmo comando é muito menor, sendo o número de acções de gestão de interface reduzidas ao mínimo. Compreende-se pois que seja muito mais fácil descrever a interacção com uma ferramenta deste tipo que a interacção com uma ferramenta visual. Por ser igualmente mais difícil entrar comandos não intencionais, é igualmente muito mais claro qual foi a acção que deu origem a um determinado erro. 5 de :51
6 A maior vantagem desta forma de interacção é no entanto a de permitir ao utilizador especificar sequências não elementares de comandos simples. É assim possível a definição de comandos extremamente complexos. Este tipo de utilização será descrito no próximo capítulo. Neste capítulo vamos centrar-nos na aprendizagem dos comandos elementares. Durante o estudo deste texto, é muito importante testar cada um dos comandos isoladamente, para melhor se compreender a que se deve cada erro. Basta escrever mal uma letra, ou esquecer um dos espaços necessários num comando para que este não seja entendido pelo computador e dê origem a um erro. Tal como na generalidade dos interfaces com prompt de comando, é possível navegar pelo histórico de comandos, bem como pesquisar comandos antigos. De seguida são apresentadas algumas das teclas utilizadas no Octave para facilitar (e tornar mais rápida) a entrada e alteração de comandos: Teclas cursoras (cima e baixo): comando anterior/seguinte no histórico de comandos. Teclas cursoras (esquerda e direita): letra anterior/seguinte no comando corrente. Em alguns terminais onde as teclas cursoras não funcionem, pode ser necessário utilizar as teclas CTRL-b (de backward) e CTRL-f (de forward). CTRL-a : o cursor desloca-se para o inicio do texto. CTRL-e : o cursor desloca-se para o fim do texto. CTRL-r/CTRL-s : pesquisa incremental de um comando anterior/seguinte no histórico de comandos. CTRL-_ : desfazer o último comando. TAB : Terminar o comando. CTRL-k : Mover todo o texto até ao fim da linha na área de transferência do Octave. CTRL-y : Mover o texto na área de transferencia do Octave para a linha de comandos. Convém igualmente referir a possibilidade de o computador começar a executar cálculos muito longos ou mesmo que não terminem. Nesse caso há um conjunto de teclas destinado a indicar ao computador que deve interromper os seus cálculos e voltar a apresentar a linha de entrada de comandos. Para interromper qualquer calculo no Octave, bastará manter pressionadas em simultâneo a tecla Ctrl e a tecla c (i.e. CTRL-c). Há igualmente alguns comandos de controle do próprio Octave que pode ser útil conhecer: o comando help, o comando history, o comando run_history e o 6 de :51
7 comando exit. O comando help, apresenta um manual on-line referindo todos os possíveis comandos do Octave. Pode ser seguido do texto de outro comando, como por exemplo: octave:1> help exit O comando history possibilita ao utilizador visualizar os comandos que entrou até ao momento. O comando run_history <numero_inicial> <numero_final> possibilita ao utilizador repetir comandos anteriores. Veja-se o exemplo: octave:100> history * ; octave:101> run_history O comando exit termina a execução do Octave e retorna ao MS-Windows. Resumo Como iniciar o Octave. Linha de comandos. Operações básicas de cálculo. Formatação. Vantagens da linha de comando face aos interfaces gráficos. Teclas de edição. Comandos de controlo do Octave. 2.2 Variáveis e Matrizes 7 de :51
8 A principal vocação do Octave é, como tem sido referido, o calculo numérico e matricial. Comecemos pois por definir a matriz a: octave:3> a=[ 1,1,2 ; 3,5,8 ; 13,21,34 ] a = variável a passa a representar a matriz: Como se pode observar, representando novas colunas e os ; representando novas linhas. Podemos igualmente definir uma matriz como o retorno de uma função, neste caso uma função que retorna uma matriz com 3 linhas e 2 colunas com valores aleatórios entre 0 e 1: octave:4> b=rand(3,2) ; Desta vez, no entanto, o Octave não imprime o resultado após o comando. Tal deve-se ao Ponto e Vírgula no final da linha de comando. Este ponto e vírgula indica que não estamos para já interessados na avaliação do valor definido (que pode ser bastante pesada). Assim que pretendermos ver um valor anteriormente definido, bastará pedir o seu valor, p.ex: octave:4> b b = octave:5> a*b o valor de a e b utilizado no produto de matrizes, é o da matriz a e b já definidas Os exemplos anteriores introduzem igualmente o conceito de variável no Octave. Em Octave uma variável é um nome que se atribui (através da utilização do operador =) a um valor (seja ele escalar ou matriz), por forma a que este valor possa ser repetidamente consultado mais tarde. Os nomes das variáveis podem conter qualquer sequência de letras, números ou underscore (i.e. o carácter _ ) que não seja iniciada por número. Não é aconselhável utilizar nomes de variáveis com mais de 30 caracteres. 8 de :51
9 A utilização de letras minúsculas ou maiúsculas é relevante e tem significados distintos. Assim a variável a pode conter um valor e a variável A outro, i.e. a e A são distintos. Há dois comandos essenciais para gerir as variáveis definidas até determinado momento: who e clear. who lista as variáveis já definidas e clear remove variáveis. octave:41> i = 10; octave:42> id = [1,0;0,1] id= octave:43> who *** local user variables: i id octave:44>clear i octave:45>who *** local user variables: id As variáveis iniciadas por dois sinais de underscore seguidos estão reservadas para utilização do sistema. Não devem pois ser utilizadas, excepto se se souber exactamente o que se quer fazer. Há igualmente um conjunto de variáveis de sistema que disponibilizam informações relevantes sobre o sistema. Por agora apenas necessitaremos de utilizar a variável ans - último valor calculado. 2.3 Matrizes e Séries A principal vantagem do Octave é a sua capacidade para tratamento de Matrizes. Vamos utilizar a matriz a da secção anterior: octave:3> a = [ 1,1,2; 3,5,8; 13,21,34 ] Podemos igualmente criar novas matrizes contendo esta. O único cuidado a ter é manter o número de linhas e colunas constante. Será fácil definir as matrizes: 9 de :51
10 Correcto octave:4> [ a, a ] ans= octave:5> [ a; a ] ans= Errado octave:4> [ a, a; a] error: number of columns must match (3!= 6) Podemos consultar uma dada posição ou submatriz numa matriz especificando os índices das respectivas dimensões num tuplo. Como pode observar nos seguintes exemplos (assumindo a matriz a anteriormente definida) octave:14> a(1,2) 1 octave:15> a(1,[1,2,3]) octave:16> a([1,2,3],2) Repare-se, nos 2º e 3º exemplos, na utilização dum vector para indicar, respectivamente, as colunas e linhas a seleccionar. A necessidade de especificar séries enquanto vectores é tão grande, que existe um operador especifico para o fazer: octave:1> 1: octave:2> 1:3: A sintaxe geral de uma série é pois: 10 de :51
11 LIMITE_INFERIOR:PASSO:LIMITE_SUPERIOR O valor de PASSO pode ser omitido (será considerado a 1 por omissão). Há ainda outra simplificação às séries, quando utilizados como índices de matrizes. Neste caso, como sabemos o limite inferior e superior podemos utilizar apenas o sinal : para especificar toda uma linha ou toda uma coluna da matriz original: octave:23> [a(1:2,2:3); a(:,2:3)] O tamanho da matriz pode igualmente ser obtido com a função size (retorna o número de linhas e colunas): octave:24> size(a) 3 3 octave:25> size(ans) 1 2 octave:26> ans(1) 1 Por fim resta referir que o operador de atribuição permite alterar posições numa matriz, podendo ser utilizada a matriz vazia ([]) para apagar linhas ou colunas: octave:51> a(:,1) = [ 1; 2; 0 ] a = octave:52> a(1,:) = 1:10:30 a = octave:53> size(a) 3 3 octave:54> a(1,:) = [] a = 11 de :51
12 octave:55> size(a) 2 3 octave:56> a(:,1)= [] a = octave:57> size(a) 2 2 Com pares de valores, podemos igualmente atribuir variáveis dentro de uma matriz: octave:58> [la,ca] = size(a) la = 2 ca = 2 Resumo Definição de matrizes. Variáveis. Comandos who e clear sobre variáveis. Construção de matrizes compostas. Selecção de submatrizes. Tamanho de uma matriz. Séries. Atribuição de submatrizes Remoção de linhas e colunas 2.4 Strings Uma constante do tipo String é uma sequência de caracteres entre " ou '. Em Octave uma string pode ter qualquer tamanho. Eis um exemplo: octave:1> a= "uma cadeia de caracteres" a = uma cadeia de caracteres 12 de :51
13 Se tentarmos definir uma matriz com várias strings numa mesma linha acabamos por obter uma string com a junção das várias strings base: octave:2> ["Uma string e",a] Uma string euma cadeia de caracteres De facto as strings são vistas internamente como vectores linha contendo caracteres. As linhas de uma matriz de strings têm forçosamente a mesma dimensão. É assim possível utilizar os operadores: octave:3> ["123";"3"] octave:4> a(1:7) uma cad Vejamos algumas funções pré-definidas para o tratamento de strings: Descrição findstr(s,t) : Encontra todas as posições de t em s split(s,t) : Divide uma string num vector (coluna) de strings separados por t Exemplo octave:5> findstr("abcabcabdad","ab") octave:6> split("abcabcabdad","ab") c c dad strrep(s, x, y) : substitui todas as ocorrências de x por y na string s str2num(s) : converte um número representado numa string para um número tolower(s) / toupper(s) : converte uma string para minúsculas/maiúsculas octave:6> strrep("abcabcabdad","ab","ab") ABcABcABdad octave:7> str2num("555") octave:8> toupper("atencao - aviso") ATENCAO - AVISO 13 de :51
14 strcmp(s1,s2) : compara as strings s1 com s2, se forem iguais retorna 1, se diferentes retorna 0 octave:9> strcmp("teste 1", "teste 1") 1 octave:10> strcmp("teste 1", " test") 0 Na página 40 (capítulo 5) do manual de Octave poderá obter mais informação sobre outras funções para a manipulação de Strings. 2.5 Principais Operadores e Funções Até agora vimos as principais características essenciais ao funcionamento do Octave. Resta no entanto enumerar as principais funções e operadores. A lista que se segue é complementada com exemplos ilustrativos do tipo de cálculos que podem ser obtidos com os diversos operadores. Eye, Ones e Zeros As matrizes Identidade, ou contendo apenas zeros ou uns são tão frequentes que foram criados três operadores específicos para as gerar: octave:37> eye(3) octave:38> eye(3,2) octave:39> ones(3,2) octave:40> zeros(2,4) Matriz transposta Para converter linhas em colunas bastará aplicar o operador ' a uma matriz: 14 de :51
15 octave:41> ones(3,2)' Operadores Soma e subtracção Para além de efectuarem a adição básica, efectuam também a adição e subtracção de matrizes. O número de linhas/colunas tem de ser igual. octave:1> analitico = [0.0314, , ]; octave:2> numerico = [0.0389, , ]; octave:3> erro = analitico - numerico erro = Operadores para Produto e Potenciação em Matrizes O operador produto é dos mais poderosos no Octave/Matlab. De facto pode ser aplicado a pares de números, a um número e matriz ou a duas matrizes n-por-m e m-por-p, em todos os casos o significado é o usual da álgebra. Considere-se o exemplo: octave:4> tudo = [1,0,0;0,1,0;-1,1,0]*[analitico;numerico;zeros(1,3)] tudo = octave:5> errototal=(([0,0,0; 0,0,0; 0,0,1]* tudo)'*ones(3,1))'*ones(3,1) errototal = octave:6> [1,0,0;0,1,0;0,0,1/erroTotal*100]*tudo Neste exemplo, na linha 4 (2º termo), construímos uma matriz contendo na primeira linha um conjunto de resultados analíticos, na segunda dados observados (numéricos) e na terceira zeros. Devido à primeira matriz, 15 de :51
16 construiu-se uma matriz tudo, contendo as primeiras 2 linhas da matriz do 2º termo e no fim a subtracção da 1ª linha pela 2ª linha. A linha 5 é um pouco mais sofisticada. A ideia base é obter apenas a última linha da variável tudo num vector linha. Para tal, primeiro anulam-se todos os elementos das duas primeiras linhas, e depois com uma matriz de uns, retira-se apenas a última linha. Depois multiplica-se o resultado por um vector linha contendo uns, para obter o somatório de todos os elementos. Obviamente trata-se de um simples exercício para ilustrar as potencialidades do produto de matrizes. A solução Octave seria bem mais simples: tudo(3,:) A linha 6 limita-se a transformar a última linha da matriz tudo num valor percentual. Tal como o produto, a potenciação de matrizes (que só pode ser aplicada a matrizes quadradas), limita-se a efectuar o produto de uma matriz por ela própria n vezes. Extensão das funções simples a matrizes: produto e potenciação pontual Podemos aplicar qualquer das funções elementares a uma matriz: a função é simplesmente aplicada elemento a elemento. Veja-se o seguinte exemplo: octave:60> A=[1,2,3;4,5,6;7,8,9] A = octave:61> L=log10(A) L = octave:62> (10*ones(size(A))).^L-A e e e e e e e e e+00 Note-se o operador.^ que eleva todos os elementos da matriz (individualmente) a L. Comandos semelhantes são o produto pontual e a divisão pontual: 16 de :51
17 octave:66> A.*[zeros(1,3) ; ones(2,3)] octave:67> A./(ones(size(A))/2) Solução de sistemas de equações lineares e determinantes O cálculo de um determinante em Octave é realizado com o auxílio da função det(a). Vejamos um exemplo para solução de um sistema de equações: Pode ser representado por duas matrizes A e B, se considerarmos AX=B: octave:71> A=[1, 2, 3; 2, 3, 4; 4, 2, 5] A = octave:72> B=[4;5;1] B = A aplicação da regra de Cramer (onde se substitui as colunas de A, correspondentes a cada x i, por B de modo a obter 3 matrizes, dividindo-se o determinante de cada matriz obtida pelo determinante de A), pode ser feita da seguinte forma: octave:84> D1=A; D1(:,1) = B D1 = de :51
18 1 2 5 octave:85> D2=A; D2(:,2) = B D2 = octave:86> D3=A; D3(:,3) = B D3 = octave:87> X=[det(D1); det(d2); det(d3)] / det(a) X = octave:88> A*X-B e e e-16 Eliminação Gaussiana: Podemos obter o mesmo resultado utilizando o operador \ (eliminação Gaussiana): octave:89> X =A \ B X = Inversão de Matrizes A inversão de uma matriz é feita com o comando inv(m). octave:90> inv( A ) octave:90> A * inv( A ) de :51
19 Gráficos Os gráficos em Octave utilizam uma ferramenta OpenSource especialmente dedicada à geração de gráficos: o GnuPlot. O Octave comunica com o gnuplot com duas funções base (sobre as quais as restantes são implementadas), estas funções são descritas nas páginas 125 (gplot) e 131 (gsplot). Na prática iremos apenas utilizar funções de mais alto nível (desenvolvidas com recurso às funções elementares apresentadas). Gráficos simples Na sua forma mais simples, a função plot apresenta um gráfico dos valores de dois vectores linha, correspondendo ao eixo dos X e Y: octave:19> x = 0:pi/90:4*pi; octave:20> y = sin(x); octave:21> plot(x,y) Neste momento deverá ser aberta uma nova janela contendo o gráfico. Poderá ter que utilizar o sistema operativo para ver esta janela (bastará carregar conjuntamente em ALT-TAB). Poderá alterar os parâmetros do gráfico com funções adicionais. Para visualizar as alterações terá que executar o comando replot: octave:29> xlabel('x,radianos'); octave:30> ylabel('sin(x)'); octave:31> grid; octave:32> replot 19 de :51
20 De facto, a função plot pode ter diversos comportamentos distintos, consoante o tipo de argumentos utilizados. Para mais detalhes consultar o manual do Octave página 127. Duas funções gráficas também bastante utilizadas são: bar e hist : octave:34> clearplot; octave:35> bar([20,10,30,15,30,30,40]) 20 de :51
21 octave:36> clearplot octave:37> a = [10,10,10,20,20,30]; octave:38> hist(a,[1,10,20,30]) O primeiro argumento da função contém a amostra de valores. O segundo, o centro de distribuição. Pode igualmente utilizar gráficos em coordenadas polares: octave:61> clearplot octave:62> m = 0.1; octave:63> phi = 0:pi/60:4*pi; octave:64> r = exp(m*phi) octave:65> polar(phi,r) 21 de :51
22 Gráficos Sobrepostos Antes de cada comando, o Octave, por omissão, limpa a janela de gráfico. Caso se pretendam comparar diversos gráficos pode ser utilizado o comando hold on para sobrepor gráficos: octave:71> clearplot octave:72> hold on octave:73> x = -5*pi:pi/90:5*pi; octave:74> y1 = sin(x); octave:75> y2 = cos(x); octave:76> y3 = sin(x)+2*cos(x); octave:77> plot(x,y1) octave:78> plot(x,y2) octave:79> plot(x,y3) 22 de :51
23 Note igualmente que pode utilizar directamente os menus na janela do GnuPlot para alterar o seu gráfico. Se quiser apresentar vários gráficos numa mesma janela poderá utilizar as funções multiplot e subwindow: octave:93> multiplot(2,2) octave:94> subwindow(1,1) octave:95> xlabel("x, radianos") octave:96> ylabel("sin(x)") octave:97> title("g1") octave:98> plot(x,y1) octave:99> subwindow(2,2) octave:100> ylabel("cos(x)") octave:101> title("g2") octave:102> plot(x,y2) octave:103> subwindow(1,2) octave:104> plot(x,x.*x) octave:105> subwindow(2,1) octave:106> plot(x,sqrt(x)) 23 de :51
24 Para voltar ao modo normal: octave:108> oneplot octave:109> clearplot Gráficos 3D A criação de um gráfico 3D necessita da definição de uma matriz de valores sobre os quais a função vai ser avaliada. Tal pode ser conseguido com a função meshdom: octave:30> clearplot octave:31> x = -10:0.5:10; octave:32> [X,Y]=meshdom(x,x); Resta apresentar o gráfico: octave:33> hold on octave:34> grid octave:35> mesh(x,y,-sqrt(x.^2+y.^2)*5+40) octave:36> mesh(x,y,x.^2+y.^2) 24 de :51
25 2.6 Exercícios I 1- Escrever numa matriz de 15 colunas e 1 linha, os quadrados dos primeiros 15 naturais (1, 4, 9...). octave:1> (1:15).^2 2- Escrever numa matriz de 15 linhas e 1 coluna, os cubos dos primeiros 15 naturais (1, 8, 27...) octave:2> [(1:15).^3]' 3- Escrever numa tabela de 15 linhas por 3 colunas, os primeiros 15 naturais na 1ª coluna; os quadrados dos primeiros 15 naturais na 2ª e os cubos dos primeiros 15 naturais na 3ª coluna. octave:3> seq=(1:15) octave:4> [seq; seq.^2; seq. ^3]' 4- Dado que a conversão de graus Fahrenheit para graus Célcios se faz com a seguinte fórmula C= (5/9). (F - 32). Coloque em tabela as conversões para as temperaturas de 0ºF, 25ºF,..., 250ºF. octave:5> faixa = 0:25:250 octave:6> [faixa;(5/9)*(faixa-32)]' 5- Faça uma tabela que traduza graus Célcios em graus Fahrenheit. Coloque em tabela as conversões para as temperaturas de -200ºC, -175ºC,..., 200ºC. 25 de :51
26 octave:7> faixa= -200:25:200 octave:8> [faixa; faixa * (9/5) + 32]' 6- Considere o problema "Quem quer ser milionário?" já conhecido. Resolva o seguinte utilizando Octave: 6.1- Qual o valor do saldo ao longo dos anos? octave:9> limite=10 octave:10> cap_inicial= octave:11> periodo=0:10 octave:12> taxa=1.05 octave:13> [periodo; cap_inicial * (taxa.^periodo)]' 6.2- Junte uma coluna que indique o ganho (relativo ao ano aterior) ao longo dos anos. octave:14>acumulado = cap_inicial * taxa.^ periodo octave:15>ant_acumulado = [cap_inicial,acumulado(1:limite)] octave:16>evolução=[periodo; acumulado; acumulado - ant_acumulado]' 6.3- Indique o ganho médio e ao longo dos anos. octave:17>ganho_médio= sum(evolução(3,1:11))/limite 6.4- Indique o ganho total octave:18>ganho_total=sum(evolução(3,:)) Ou octave:18>ganho_total = evolução(2,limite+1) - cap_inicial 3 Programação Como já foi visto anteriormente, o Octave permite ao utilizador especificar instruções através de uma linha de comando. Nesta secção vamos elaborar um pouco mais o tipo de instruções que podem ser executadas e introduzir algumas noções básicas de programação. Assim, os objectivos desta secção são os seguintes: Compreender os conceitos básicos de programação, e saber quais os comandos Matlab/Octave que os implementam; Dado um problema de engenharia concreto, conseguir determinar qual a sequência de comandos da linguagem MatLab/Octave a utilizar; 26 de :51
27 3. 4. Implementar essa sequência de comandos sobre a forma de um Script; Conseguir depurar os erros desse Script, e adaptar o código desenvolvido a novos problemas de Engenharia. 3.1 Alguns conceitos básicos Ao programar está-se de um modo geral a expressar acções ou comportamentos que simulem uma determinada actividade do mundo real. Assim, será primeiro necessário compreender a actividade que se quer simular. Depois, saber quais são os dados ou parâmetros que condicionam a actividade no mundo real (i.e. quais os elementos que contêm a informação necessária para o problema). Por fim é necessário identificar quais as acções e comportamentos que permitem simular esse processo. No fundo é necessário modelar o problema ou, se tal já tiver sido feito, utilizar um modelo (normalmente matemático) que já alguém elaborou. Como já foi estudado nas aulas teóricas, um computador é uma máquina que funciona com base num conjunto de acções elementares bastante simples e pode ser descrito matematicamente por um máquina de Turing Universal. Tal como na máquina de Turing, as acções e comportamentos estão associados ao controlo da sequência de instruções que constituem o programa. Normalmente este processo é designado como controlo de fluxo de execução do programa. No desenvolvimento de um programa é igualmente usual especificar primeiro acções mais complexas. Cada acção complexa deverá ser decomposta em acções mais simples, as quais por sua vez serão mais uma vez decompostas, até termos por fim todas as acções expressas através de pequenas acções elementares. No caso de comandos matlab este paradigma pode ser chamado de programação de Cima para Baixo. Alguns autores propõe também a abordagem inversa: começar por conjugar acções elementares até se resolver o problema final (esta abordagem pode também ser designada por da programação de Baixo para Cima). Na prática é usual conjugar ambos os métodos: constroem-se de baixo para cima acções relativamente simples que sabemos serem necessárias e depois tenta-se decompor o problema de acordo com essas e outras instruções. No meio de tudo o que é necessário reter é que qualquer sequência de acções, por mais complexa que seja, pode ser expressa numa linguagem de programação desde que essa linguagem possua: um mecanismo sequencial; um mecanismo condicional; e um mecanismo de repetição. Fica como exercício compreender de que forma estes mecanismos são implementados e implementam a máquina de Turing (i.e. na prática são igualmente expressivos!). 27 de :51
OPERADORES E ESTRUTURAS DE CONTROLE
 OPERADORES E ESTRUTURAS DE CONTROLE 3.1 Operadores Os operadores indicam o tipo de operação matemática que será executada gerando novos valores a partir de um ou mais operadores. São muito utilizados em
OPERADORES E ESTRUTURAS DE CONTROLE 3.1 Operadores Os operadores indicam o tipo de operação matemática que será executada gerando novos valores a partir de um ou mais operadores. São muito utilizados em
Algoritmos e Programação (Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br
 (Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br Introdução O computador como ferramenta indispensável: Faz parte das nossas vidas; Por si só não faz nada de útil; Grande capacidade de resolução
(Prática) Profa. Andreza Leite andreza.leite@univasf.edu.br Introdução O computador como ferramenta indispensável: Faz parte das nossas vidas; Por si só não faz nada de útil; Grande capacidade de resolução
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
Múltiplos Estágios processo com três estágios Inquérito de Satisfação Fase II
 O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
O seguinte exercício contempla um processo com três estágios. Baseia-se no Inquérito de Satisfação Fase II, sendo, por isso, essencial compreender primeiro o problema antes de começar o tutorial. 1 1.
Programação 2ºSemestre MEEC - 2010/2011. Programação 2º Semestre 2010/2011 Enunciado do projecto
 Mestrado Integrado em Engenharia Electrotécnica e de Computadores Programação 2º Semestre 2010/2011 Enunciado do projecto O projecto a desenvolver pelos alunos consistirá numa sistema de monitorização,
Mestrado Integrado em Engenharia Electrotécnica e de Computadores Programação 2º Semestre 2010/2011 Enunciado do projecto O projecto a desenvolver pelos alunos consistirá numa sistema de monitorização,
PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012
 Departamento de Engenharia Electrotécnica PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012 Mestrado Integrado em Engenharia Electrotécnica e de Computadores 1º ano 2º semestre Trabalho Final Reservas de viagens
Departamento de Engenharia Electrotécnica PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012 Mestrado Integrado em Engenharia Electrotécnica e de Computadores 1º ano 2º semestre Trabalho Final Reservas de viagens
AMBIENTE DE PROGRAMAÇÃO PYTHON
 Computadores e Programação Engª Biomédica Departamento de Física Faculdade de Ciências e Tecnologia da Universidade de Coimbra Ano Lectivo 2003/2004 FICHA 1 AMBIENTE DE PROGRAMAÇÃO PYTHON 1.1. Objectivos
Computadores e Programação Engª Biomédica Departamento de Física Faculdade de Ciências e Tecnologia da Universidade de Coimbra Ano Lectivo 2003/2004 FICHA 1 AMBIENTE DE PROGRAMAÇÃO PYTHON 1.1. Objectivos
MANUAL DO UTILIZADOR
 MANUAL DO UTILIZADOR Versão 1.6 PÁGINA DE PESQUISA A página principal do PacWeb permite a realização de um número muito variado de pesquisas, simples, ou pelo contrário extremamente complexas, dependendo
MANUAL DO UTILIZADOR Versão 1.6 PÁGINA DE PESQUISA A página principal do PacWeb permite a realização de um número muito variado de pesquisas, simples, ou pelo contrário extremamente complexas, dependendo
O AMBIENTE DE TRABALHO DO WINDOWS
 O AMBIENTE DE TRABALHO DO WINDOWS O Windows funciona como um Sistema Operativo, responsável pelo arranque do computador. Um computador que tenha o Windows instalado, quando arranca, entra directamente
O AMBIENTE DE TRABALHO DO WINDOWS O Windows funciona como um Sistema Operativo, responsável pelo arranque do computador. Um computador que tenha o Windows instalado, quando arranca, entra directamente
Tutorial de Matlab Francesco Franco
 Tutorial de Matlab Francesco Franco Matlab é um pacote de software que facilita a inserção de matrizes e vetores, além de facilitar a manipulação deles. A interface segue uma linguagem que é projetada
Tutorial de Matlab Francesco Franco Matlab é um pacote de software que facilita a inserção de matrizes e vetores, além de facilitar a manipulação deles. A interface segue uma linguagem que é projetada
PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012
 Departamento de Engenharia Electrotécnica PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012 Mestrado Integrado em Engenharia Electrotécnica e Computadores 1º ano 2º semestre Trabalho nº 0 Instalação dos programas
Departamento de Engenharia Electrotécnica PROGRAMAÇÃO DE MICROPROCESSADORES 2011 / 2012 Mestrado Integrado em Engenharia Electrotécnica e Computadores 1º ano 2º semestre Trabalho nº 0 Instalação dos programas
Departamento: Matemática Curso: Eng a Madeiras Ano: 1 o Semestre: 2 o Ano Lectivo: 2006/2007. Aula prática n o 1 - Introdução ao MATLAB
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Métodos Numéricos Curso: Eng a Madeiras Ano: 1 o Semestre: 2 o Ano Lectivo: 2006/2007 Aula prática n o 1 - Introdução
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Métodos Numéricos Curso: Eng a Madeiras Ano: 1 o Semestre: 2 o Ano Lectivo: 2006/2007 Aula prática n o 1 - Introdução
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Manipulação de Células, linhas e Colunas
 Manipulação de Células, linhas e Colunas Seleccionar células Uma vez introduzidos os dados numa folha de cálculo, podemos querer efectuar alterações em relação a esses dados, como, por exemplo: apagar,
Manipulação de Células, linhas e Colunas Seleccionar células Uma vez introduzidos os dados numa folha de cálculo, podemos querer efectuar alterações em relação a esses dados, como, por exemplo: apagar,
e à Linguagem de Programação Python
 Introdução a Algoritmos, Computação Algébrica e à Linguagem de Programação Python Curso de Números Inteiros e Criptografia Prof. Luis Menasché Schechter Departamento de Ciência da Computação UFRJ Agosto
Introdução a Algoritmos, Computação Algébrica e à Linguagem de Programação Python Curso de Números Inteiros e Criptografia Prof. Luis Menasché Schechter Departamento de Ciência da Computação UFRJ Agosto
No final desta sessão o formando deverá ser capaz de aceder ao Word e iniciar um novo documento.
 Sessão nº 2 Iniciar um novo documento Objectivos: No final desta sessão o formando deverá ser capaz de aceder ao Word e iniciar um novo documento. Iniciar um novo documento Ao iniciar-se o Word, este apresenta
Sessão nº 2 Iniciar um novo documento Objectivos: No final desta sessão o formando deverá ser capaz de aceder ao Word e iniciar um novo documento. Iniciar um novo documento Ao iniciar-se o Word, este apresenta
Neste tutorial irá criar uma animação simples com base num desenho do Mechanical Desktop.
 Neste tutorial irá criar uma animação simples com base num desenho do Mechanical Desktop. Inicialize o 3D Studio VIZ. Faça duplo clique no ícone de 3D Studio VIZ Abre-se a janela da figura seguinte. Esta
Neste tutorial irá criar uma animação simples com base num desenho do Mechanical Desktop. Inicialize o 3D Studio VIZ. Faça duplo clique no ícone de 3D Studio VIZ Abre-se a janela da figura seguinte. Esta
ZS Rest. Manual Profissional. BackOffice Mapa de Mesas. v2011
 Manual Profissional BackOffice Mapa de Mesas v2011 1 1. Índice 2. Introdução... 2 3. Iniciar ZSRest Backoffice... 3 4. Confirmar desenho de mesas... 4 b) Activar mapa de mesas... 4 c) Zonas... 4 5. Desenhar
Manual Profissional BackOffice Mapa de Mesas v2011 1 1. Índice 2. Introdução... 2 3. Iniciar ZSRest Backoffice... 3 4. Confirmar desenho de mesas... 4 b) Activar mapa de mesas... 4 c) Zonas... 4 5. Desenhar
Os objetivos indicados aplicam-se a duas linguagens de programação: C e PHP
 AGRUPAMENTO DE ESCOLAS DE SANTA COMBA DÃO CURSO PROFISSIONAL DE TÉCNICO DE GESTÃO E PROGRAMAÇÃO DE SISTEMAS INFORMÁTICOS 2012-2015 PROGRAMAÇÃO E SISTEMAS DE INFORMAÇÃO MÓDULO 2 Mecanismos de Controlo de
AGRUPAMENTO DE ESCOLAS DE SANTA COMBA DÃO CURSO PROFISSIONAL DE TÉCNICO DE GESTÃO E PROGRAMAÇÃO DE SISTEMAS INFORMÁTICOS 2012-2015 PROGRAMAÇÃO E SISTEMAS DE INFORMAÇÃO MÓDULO 2 Mecanismos de Controlo de
Curso: Ciência da Computação Disciplina: Construção de Compiladores Período: 2010-1 Prof. Dr. Raimundo Moura
 UFPI CCN DIE Curso: Ciência da Computação Disciplina: Construção de Compiladores Período: 2010-1 Prof. Dr. Raimundo Moura O projeto Desenvolver um compilador de um subconjunto básico da linguagem PORTUGOL.
UFPI CCN DIE Curso: Ciência da Computação Disciplina: Construção de Compiladores Período: 2010-1 Prof. Dr. Raimundo Moura O projeto Desenvolver um compilador de um subconjunto básico da linguagem PORTUGOL.
Curso de Programação Computadores
 3 O Primeiro Programa em C Unesp Campus de Guaratinguetá Curso de Programação Computadores Prof. Aníbal Tavares Profa. Cassilda Ribeiro 3 O Primeiro Programa em C 3.1 - Introdução Depois dos conceitos
3 O Primeiro Programa em C Unesp Campus de Guaratinguetá Curso de Programação Computadores Prof. Aníbal Tavares Profa. Cassilda Ribeiro 3 O Primeiro Programa em C 3.1 - Introdução Depois dos conceitos
Dicas para usar melhor o Word 2007
 Dicas para usar melhor o Word 2007 Quem está acostumado (ou não) a trabalhar com o Word, não costuma ter todo o tempo do mundo disponível para descobrir as funcionalidades de versões recentemente lançadas.
Dicas para usar melhor o Word 2007 Quem está acostumado (ou não) a trabalhar com o Word, não costuma ter todo o tempo do mundo disponível para descobrir as funcionalidades de versões recentemente lançadas.
Aplicações de Escritório Electrónico
 Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Resumo da Matéria de Linguagem de Programação. Linguagem C
 Resumo da Matéria de Linguagem de Programação Linguagem C Vitor H. Migoto de Gouvêa 2011 Sumário Como instalar um programa para executar o C...3 Sintaxe inicial da Linguagem de Programação C...4 Variáveis
Resumo da Matéria de Linguagem de Programação Linguagem C Vitor H. Migoto de Gouvêa 2011 Sumário Como instalar um programa para executar o C...3 Sintaxe inicial da Linguagem de Programação C...4 Variáveis
Programação WEB I Estruturas de controle e repetição
 Programação WEB I Estruturas de controle e repetição Operadores de Incremento Operadores de incremento servem como expressões de atalho para realizar incrementos em variáveis Operadores de Incremento Vamos
Programação WEB I Estruturas de controle e repetição Operadores de Incremento Operadores de incremento servem como expressões de atalho para realizar incrementos em variáveis Operadores de Incremento Vamos
1. Ambiente de Trabalho
 1 Ambiente de Trabalho 1. Ambiente de Trabalho Ao nível do ambiente de trabalho, depois de o Excel 2007 ter introduzido novos componentes (e.g., Botão Office e Friso) e eliminado alguns dos componentes
1 Ambiente de Trabalho 1. Ambiente de Trabalho Ao nível do ambiente de trabalho, depois de o Excel 2007 ter introduzido novos componentes (e.g., Botão Office e Friso) e eliminado alguns dos componentes
Guia de Estudo Folha de Cálculo Microsoft Excel
 Tecnologias da Informação e Comunicação Guia de Estudo Folha de Cálculo Microsoft Excel Estrutura geral de uma folha de cálculo: colunas, linhas, células, endereços Uma folha de cálculo electrónica ( electronic
Tecnologias da Informação e Comunicação Guia de Estudo Folha de Cálculo Microsoft Excel Estrutura geral de uma folha de cálculo: colunas, linhas, células, endereços Uma folha de cálculo electrónica ( electronic
A VISTA BACKSTAGE PRINCIPAIS OPÇÕES NO ECRÃ DE ACESSO
 DOMINE A 110% ACCESS 2010 A VISTA BACKSTAGE Assim que é activado o Access, é visualizado o ecrã principal de acesso na nova vista Backstage. Após aceder ao Access 2010, no canto superior esquerdo do Friso,
DOMINE A 110% ACCESS 2010 A VISTA BACKSTAGE Assim que é activado o Access, é visualizado o ecrã principal de acesso na nova vista Backstage. Após aceder ao Access 2010, no canto superior esquerdo do Friso,
Registos em Ficheiros - Estruturas. Pedro Barahona DI/FCT/UNL Introdução aos Computadores e à Programação 2º Semestre 2009/2010
 Registos em Ficheiros - Estruturas Pedro Barahona DI/FCT/UNL Introdução aos Computadores e à Programação 2º Semestre 2009/2010 4 Maio 2011 Registos em Ficheiros - Estruturas 1 Leitura de Ficheiros Texto
Registos em Ficheiros - Estruturas Pedro Barahona DI/FCT/UNL Introdução aos Computadores e à Programação 2º Semestre 2009/2010 4 Maio 2011 Registos em Ficheiros - Estruturas 1 Leitura de Ficheiros Texto
Algoritmos com VisuAlg
 Algoritmos com VisuAlg Prof Gerson Volney Lagemann Depto Eng de Produção e Sistemas UDESC - CCT Algoritmos com VisuAlg Introdução A linguagem VisuAlg é simples, seu objetivo é disponibilizar um ambiente
Algoritmos com VisuAlg Prof Gerson Volney Lagemann Depto Eng de Produção e Sistemas UDESC - CCT Algoritmos com VisuAlg Introdução A linguagem VisuAlg é simples, seu objetivo é disponibilizar um ambiente
A lógica de programação ajuda a facilitar o desenvolvimento dos futuros programas que você desenvolverá.
 INTRODUÇÃO A lógica de programação é extremamente necessária para as pessoas que queiram trabalhar na área de programação, seja em qualquer linguagem de programação, como por exemplo: Pascal, Visual Basic,
INTRODUÇÃO A lógica de programação é extremamente necessária para as pessoas que queiram trabalhar na área de programação, seja em qualquer linguagem de programação, como por exemplo: Pascal, Visual Basic,
Hugo Pedro Proença, 2007
 Stored Procedures À medida que a complexidade dos sistemas aumenta, torna-se cada vez mais difícil a tarefa de integrar o SQL com as aplicações cliente. Além disto, é necessário que todas as aplicações
Stored Procedures À medida que a complexidade dos sistemas aumenta, torna-se cada vez mais difícil a tarefa de integrar o SQL com as aplicações cliente. Além disto, é necessário que todas as aplicações
FICHA ORIENTADA Nº1. Barra de fórmulas. Área de trabalho T E C N O L O G I A S D E I N F O R M A Ç Ã O E C O M U N I C A Ç Ã O
 T E C N O L O G I A S D E I N F O R M A Ç Ã O E C O M U N I C A Ç Ã O FICHA ORIENTADA Nº1 INTRODUÇÃO À FOLHA DE CÁLCULO CRIAÇÃO DE UMA FOLHA DE CÁLCULO O Microsoft Excel é um programa que faz parte das
T E C N O L O G I A S D E I N F O R M A Ç Ã O E C O M U N I C A Ç Ã O FICHA ORIENTADA Nº1 INTRODUÇÃO À FOLHA DE CÁLCULO CRIAÇÃO DE UMA FOLHA DE CÁLCULO O Microsoft Excel é um programa que faz parte das
Introdução aos cálculos de datas
 Page 1 of 7 Windows SharePoint Services Introdução aos cálculos de datas Aplica-se a: Microsoft Office SharePoint Server 2007 Ocultar tudo Você pode usar fórmulas e funções em listas ou bibliotecas para
Page 1 of 7 Windows SharePoint Services Introdução aos cálculos de datas Aplica-se a: Microsoft Office SharePoint Server 2007 Ocultar tudo Você pode usar fórmulas e funções em listas ou bibliotecas para
Tarefa Orientada 2 Criar uma base de dados
 Tarefa Orientada 2 Criar uma base de dados Objectivos: Criar uma base de dados vazia. O Sistema de Gestão de Bases de Dados MS Access Criar uma base dados vazia O Access é um Sistema de Gestão de Bases
Tarefa Orientada 2 Criar uma base de dados Objectivos: Criar uma base de dados vazia. O Sistema de Gestão de Bases de Dados MS Access Criar uma base dados vazia O Access é um Sistema de Gestão de Bases
Módulo III. Folhas de Cálculo
 Módulo III Ferramentas do Office Folhas de Cálculo Ferramentas de produtividade 1 Folhas de Cálculo O que é: Uma Folha de Cálculo é, por tradição, um conjunto de células que formam uma grelha ou tabela
Módulo III Ferramentas do Office Folhas de Cálculo Ferramentas de produtividade 1 Folhas de Cálculo O que é: Uma Folha de Cálculo é, por tradição, um conjunto de células que formam uma grelha ou tabela
Nesta aula serão apresentados alguns comandos de condição, repetição e gráficos.
 3 COMANDOS CONDICIONAIS E DE LAÇO Nesta aula serão apresentados alguns comandos de condição, repetição e gráficos. 3.1 COMANDOS CONDICIONAIS 3.1.1 Comando IF Como o próprio nome já indica, estes comandos
3 COMANDOS CONDICIONAIS E DE LAÇO Nesta aula serão apresentados alguns comandos de condição, repetição e gráficos. 3.1 COMANDOS CONDICIONAIS 3.1.1 Comando IF Como o próprio nome já indica, estes comandos
Usando o Excel ESTATÍSTICA. A Janela do Excel 2007. Barra de título. Barra de menus. Barra de ferramentas padrão e de formatação.
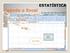 Barra de deslocamento ESTATÍSTICA Barra de menus Barra de título Barra de ferramentas padrão e de formatação Barra de fórmulas Conjuntos e Células (Intervalos) Área de trabalho Separador de folhas Barra
Barra de deslocamento ESTATÍSTICA Barra de menus Barra de título Barra de ferramentas padrão e de formatação Barra de fórmulas Conjuntos e Células (Intervalos) Área de trabalho Separador de folhas Barra
Algoritmos e Estrutura de Dados. Introdução a Linguagem Python (Parte I) Prof. Tiago A. E. Ferreira
 Algoritmos e Estrutura de Dados Aula 1 Introdução a Linguagem Python (Parte I) Prof. Tiago A. E. Ferreira Linguagem a ser Utilizada? Nossa disciplina é de Algoritmos e Estrutura de Dados, e não de linguagem
Algoritmos e Estrutura de Dados Aula 1 Introdução a Linguagem Python (Parte I) Prof. Tiago A. E. Ferreira Linguagem a ser Utilizada? Nossa disciplina é de Algoritmos e Estrutura de Dados, e não de linguagem
Resolução de problemas e desenvolvimento de algoritmos
 SSC0101 - ICC1 Teórica Introdução à Ciência da Computação I Resolução de problemas e desenvolvimento de algoritmos Prof. Vanderlei Bonato Prof. Cláudio Fabiano Motta Toledo Sumário Análise e solução de
SSC0101 - ICC1 Teórica Introdução à Ciência da Computação I Resolução de problemas e desenvolvimento de algoritmos Prof. Vanderlei Bonato Prof. Cláudio Fabiano Motta Toledo Sumário Análise e solução de
COMPETÊNCIAS BÁSICAS EM TIC NAS EB1
 COMPETÊNCIAS BÁSICAS EM TIC NAS EB1 Oficina do Correio Para saber mais sobre Correio electrónico 1. Dicas para melhor gerir e organizar o Correio Electrónico utilizando o Outlook Express Criar Pastas Escrever
COMPETÊNCIAS BÁSICAS EM TIC NAS EB1 Oficina do Correio Para saber mais sobre Correio electrónico 1. Dicas para melhor gerir e organizar o Correio Electrónico utilizando o Outlook Express Criar Pastas Escrever
Microsoft Access 2010. Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento
 Microsoft Access 2010 Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento 1 Principais objetos do Access Tabelas Guardam a informação da BD (Base de Dados)
Microsoft Access 2010 Para conhecermos o Access, vamos construir uma BD e apresentar os conceitos necessários a cada momento 1 Principais objetos do Access Tabelas Guardam a informação da BD (Base de Dados)
Faculdade de Ciências Universidade Agostinho Neto Departamento de Matemática e Engenharia Geográfica Ciências da Computação
 FaculdadedeCiências UniversidadeAgostinhoNeto DepartamentodeMatemáticaeEngenhariaGeográfica CiênciasdaComputação ProgramaçãoII SegundaParte Adaptado de um original dos docentes de ISCTE Objectivos Os alunos
FaculdadedeCiências UniversidadeAgostinhoNeto DepartamentodeMatemáticaeEngenhariaGeográfica CiênciasdaComputação ProgramaçãoII SegundaParte Adaptado de um original dos docentes de ISCTE Objectivos Os alunos
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
Utilização do SOLVER do EXCEL
 Utilização do SOLVER do EXCEL 1 Utilização do SOLVER do EXCEL José Fernando Oliveira DEEC FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO MAIO 1998 Para ilustrar a utilização do Solver na resolução de
Utilização do SOLVER do EXCEL 1 Utilização do SOLVER do EXCEL José Fernando Oliveira DEEC FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO MAIO 1998 Para ilustrar a utilização do Solver na resolução de
Barra de ferramentas padrão. Barra de formatação. Barra de desenho Painel de Tarefas
 Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
Aluísio Eustáquio da Silva
 1 Aluísio Eustáquio da Silva SciLab Programável Material didático usado em aulas de Programação de Computadores, Algoritmos e Lógica de Programação Betim Maio de 2012 2 PROGRAMAÇÃO O SciLab permite que
1 Aluísio Eustáquio da Silva SciLab Programável Material didático usado em aulas de Programação de Computadores, Algoritmos e Lógica de Programação Betim Maio de 2012 2 PROGRAMAÇÃO O SciLab permite que
Seu manual do usuário EPSON LQ-630 http://pt.yourpdfguides.com/dref/1120693
 Você pode ler as recomendações contidas no guia do usuário, no guia de técnico ou no guia de instalação para. Você vai encontrar as respostas a todas suas perguntas sobre a no manual do usuário (informação,
Você pode ler as recomendações contidas no guia do usuário, no guia de técnico ou no guia de instalação para. Você vai encontrar as respostas a todas suas perguntas sobre a no manual do usuário (informação,
Arquitetura de Computadores. Tipos de Instruções
 Arquitetura de Computadores Tipos de Instruções Tipos de instruções Instruções de movimento de dados Operações diádicas Operações monádicas Instruções de comparação e desvio condicional Instruções de chamada
Arquitetura de Computadores Tipos de Instruções Tipos de instruções Instruções de movimento de dados Operações diádicas Operações monádicas Instruções de comparação e desvio condicional Instruções de chamada
Configuração do Ambiente de Trabalho
 pag. 1 Configuração do Ambiente de Trabalho 1. Utilização da Área de Trabalho Criação de Atalhos: O Windows NT apresenta um Ambiente de Trabalho flexível, adaptável às necessidades e preferências do utilizador.
pag. 1 Configuração do Ambiente de Trabalho 1. Utilização da Área de Trabalho Criação de Atalhos: O Windows NT apresenta um Ambiente de Trabalho flexível, adaptável às necessidades e preferências do utilizador.
Linguagem algorítmica: Portugol
 Programação de Computadores I Aula 03 Linguagem algorítmica: Portugol José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/34 Introdução I Lógica A lógica é usada
Programação de Computadores I Aula 03 Linguagem algorítmica: Portugol José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/34 Introdução I Lógica A lógica é usada
Manual de Utilizador. Disciplina de Projecto de Sistemas Industriais. Escola Superior de Tecnologia. Instituto Politécnico de Castelo Branco
 Escola Superior de Tecnologia Instituto Politécnico de Castelo Branco Departamento de Informática Curso de Engenharia Informática Disciplina de Projecto de Sistemas Industriais Ano Lectivo de 2005/2006
Escola Superior de Tecnologia Instituto Politécnico de Castelo Branco Departamento de Informática Curso de Engenharia Informática Disciplina de Projecto de Sistemas Industriais Ano Lectivo de 2005/2006
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
CURSO DE PROGRAMAÇÃO EM JAVA
 CURSO DE PROGRAMAÇÃO EM JAVA Introdução para Iniciantes Prof. M.Sc. Daniel Calife Índice 1 - A programação e a Linguagem Java. 1.1 1.2 1.3 1.4 Linguagens de Programação Java JDK IDE 2 - Criando o primeiro
CURSO DE PROGRAMAÇÃO EM JAVA Introdução para Iniciantes Prof. M.Sc. Daniel Calife Índice 1 - A programação e a Linguagem Java. 1.1 1.2 1.3 1.4 Linguagens de Programação Java JDK IDE 2 - Criando o primeiro
MICROSOFT ACCESS MICROSOFT ACCESS. Professor Rafael Vieira Professor Rafael Vieira
 MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
O que é o JavaScript?
 JavaScript Introdução O JavaScript é utilizado por milhões de páginas na web para melhorar o design, validar forms, e muito mais O JavaScript foi inicialmente desenvolvido pela Netscape e é a linguagem
JavaScript Introdução O JavaScript é utilizado por milhões de páginas na web para melhorar o design, validar forms, e muito mais O JavaScript foi inicialmente desenvolvido pela Netscape e é a linguagem
ALGORITMOS PARTE 01. Fabricio de Sousa Pinto
 ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
Aplicações de Escritório Electrónico
 Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Algoritmo e Programação
 Algoritmo e Programação Professor: José Valentim dos Santos Filho Colegiado: Engenharia da Computação Prof.: José Valentim dos Santos Filho 1 Ementa Noções básicas de algoritmo; Construções básicas: operadores,
Algoritmo e Programação Professor: José Valentim dos Santos Filho Colegiado: Engenharia da Computação Prof.: José Valentim dos Santos Filho 1 Ementa Noções básicas de algoritmo; Construções básicas: operadores,
UNIDADE 2: Sistema Operativo em Ambiente Gráfico
 Ambiente Gráfico Configurações Acessórios O Sistema Operativo (SO) é o conjunto de programas fundamentais que permitem que o computador funcione e que comunique com o exterior. Actualmente o Windows é
Ambiente Gráfico Configurações Acessórios O Sistema Operativo (SO) é o conjunto de programas fundamentais que permitem que o computador funcione e que comunique com o exterior. Actualmente o Windows é
2. OPERADORES... 6 3. ALGORITMOS, FLUXOGRAMAS E PROGRAMAS... 8 4. FUNÇÕES... 10
 1. TIPOS DE DADOS... 3 1.1 DEFINIÇÃO DE DADOS... 3 1.2 - DEFINIÇÃO DE VARIÁVEIS... 3 1.3 - VARIÁVEIS EM C... 3 1.3.1. NOME DAS VARIÁVEIS... 3 1.3.2 - TIPOS BÁSICOS... 3 1.3.3 DECLARAÇÃO DE VARIÁVEIS...
1. TIPOS DE DADOS... 3 1.1 DEFINIÇÃO DE DADOS... 3 1.2 - DEFINIÇÃO DE VARIÁVEIS... 3 1.3 - VARIÁVEIS EM C... 3 1.3.1. NOME DAS VARIÁVEIS... 3 1.3.2 - TIPOS BÁSICOS... 3 1.3.3 DECLARAÇÃO DE VARIÁVEIS...
Modelo Cascata ou Clássico
 Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
Curso de Iniciação ao Access Basic (I) CONTEÚDOS
 Curso de Iniciação ao Access Basic (I) CONTEÚDOS 1. A Linguagem Access Basic. 2. Módulos e Procedimentos. 3. Usar o Access: 3.1. Criar uma Base de Dados: 3.1.1. Criar uma nova Base de Dados. 3.1.2. Criar
Curso de Iniciação ao Access Basic (I) CONTEÚDOS 1. A Linguagem Access Basic. 2. Módulos e Procedimentos. 3. Usar o Access: 3.1. Criar uma Base de Dados: 3.1.1. Criar uma nova Base de Dados. 3.1.2. Criar
Novo Formato de Logins Manual de Consulta
 Gestão Integrada de Acessos Novo Formato de Logins Manual de Consulta Gestão Integrada de Acessos Histórico de Alterações Versão Descrição Autor Data 1.0 Versão inicial DSI/PPQ 2014-07-11 Controlo do documento
Gestão Integrada de Acessos Novo Formato de Logins Manual de Consulta Gestão Integrada de Acessos Histórico de Alterações Versão Descrição Autor Data 1.0 Versão inicial DSI/PPQ 2014-07-11 Controlo do documento
Aplicações de Escritório Electrónico
 Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
AMBIENTE PARA AUXILIAR O DESENVOLVIMENTO DE PROGRAMAS MONOLÍTICOS
 UNIVERSIDADE REGIONAL DE BLUMENAU CENTRO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE CIÊNCIAS DA COMPUTAÇÃO BACHARELADO AMBIENTE PARA AUXILIAR O DESENVOLVIMENTO DE PROGRAMAS MONOLÍTICOS Orientando: Oliver Mário
UNIVERSIDADE REGIONAL DE BLUMENAU CENTRO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE CIÊNCIAS DA COMPUTAÇÃO BACHARELADO AMBIENTE PARA AUXILIAR O DESENVOLVIMENTO DE PROGRAMAS MONOLÍTICOS Orientando: Oliver Mário
Algoritmos em Javascript
 Algoritmos em Javascript Sumário Algoritmos 1 O que é um programa? 1 Entrada e Saída de Dados 3 Programando 4 O que é necessário para programar 4 em JavaScript? Variáveis 5 Tipos de Variáveis 6 Arrays
Algoritmos em Javascript Sumário Algoritmos 1 O que é um programa? 1 Entrada e Saída de Dados 3 Programando 4 O que é necessário para programar 4 em JavaScript? Variáveis 5 Tipos de Variáveis 6 Arrays
Folha de cálculo. Excel. Agrupamento de Escolas de Amares
 Folha de cálculo Excel Agrupamento de Escolas de Amares Índice 1. Funcionalidades básicas... 3 1.1. Iniciar o Excel... 3 1.2. Criar um livro novo... 3 1.3. Abrir um livro existente... 3 1.4. Inserir uma
Folha de cálculo Excel Agrupamento de Escolas de Amares Índice 1. Funcionalidades básicas... 3 1.1. Iniciar o Excel... 3 1.2. Criar um livro novo... 3 1.3. Abrir um livro existente... 3 1.4. Inserir uma
TUTORIAL MATLAB MATEMÁTICA COMPUTACIONAL Aula 20-Novembro-2013
 TUTORIAL MATLAB MATEMÁTICA COMPUTACIONAL Aula 20-Novembro-2013 MATLAB (MATrix LABoratory) é um software de alta performance direccionado para o cálculo numérico. O MATLAB integra áreas como análise numérica,
TUTORIAL MATLAB MATEMÁTICA COMPUTACIONAL Aula 20-Novembro-2013 MATLAB (MATrix LABoratory) é um software de alta performance direccionado para o cálculo numérico. O MATLAB integra áreas como análise numérica,
GeoMafra Portal Geográfico
 GeoMafra Portal Geográfico Nova versão do site GeoMafra Toda a informação municipal... à distância de um clique! O projecto GeoMafra constitui uma ferramenta de trabalho que visa melhorar e homogeneizar
GeoMafra Portal Geográfico Nova versão do site GeoMafra Toda a informação municipal... à distância de um clique! O projecto GeoMafra constitui uma ferramenta de trabalho que visa melhorar e homogeneizar
APROG - Civil. Excel. Técnicas de pesquisa de informação em tabelas. Instituto Superior de Engenharia do Porto 2000-2007
 APROG - Civil Excel Técnicas de pesquisa de informação em tabelas Instituto Superior de Engenharia do Porto 2000-2007 Elaborado por: António Silva (DEI-ISEP) Pesquisa de Informação em Tabelas O Excel
APROG - Civil Excel Técnicas de pesquisa de informação em tabelas Instituto Superior de Engenharia do Porto 2000-2007 Elaborado por: António Silva (DEI-ISEP) Pesquisa de Informação em Tabelas O Excel
Orientação a Objetos
 1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB
 NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
3 Sistemas de Numeração:
 3 Sistemas de Numeração: Os computadores eletrônicos têm como base para seu funcionamento a utilização de eletricidade. Diferente de outras máquinas que a presença ou ausência de eletricidade apenas significam
3 Sistemas de Numeração: Os computadores eletrônicos têm como base para seu funcionamento a utilização de eletricidade. Diferente de outras máquinas que a presença ou ausência de eletricidade apenas significam
CONCEITOS BÁSICOS DE UM SISTEMA OPERATIVO
 4 CONCEITOS BÁSICOS DE UM SISTEMA OPERATIVO CONCEITOS BÁSICOS MS-DOS MICROSOFT DISK OPERATION SYSTEM INSTALAÇÃO E CONFIGURAÇÃO DE UM SISTEMA OPERATIVO LIGAÇÕES À INTERNET O que é um sistema operativo?
4 CONCEITOS BÁSICOS DE UM SISTEMA OPERATIVO CONCEITOS BÁSICOS MS-DOS MICROSOFT DISK OPERATION SYSTEM INSTALAÇÃO E CONFIGURAÇÃO DE UM SISTEMA OPERATIVO LIGAÇÕES À INTERNET O que é um sistema operativo?
Relatório SHST - 2003
 Relatório da Actividade dos Serviços de Segurança, Higiene e Saúde no Trabalho Relatório SHST - 2003 Programa de Validação e Encriptação Manual de Operação Versão 1.1 DEEP Departamento de Estudos, Estatística
Relatório da Actividade dos Serviços de Segurança, Higiene e Saúde no Trabalho Relatório SHST - 2003 Programa de Validação e Encriptação Manual de Operação Versão 1.1 DEEP Departamento de Estudos, Estatística
Module Introduction. Programação. Cap. 4 Algoritmos e Programação Estruturada
 5374 : Engenharia Informática 6638 : Tecnologias e Sistemas de Informação 9099 : Bioengenharia 10135 : Ciências Biomédicas Cap. 4 Algoritmos e Estruturada Module Introduction Algoritmos e Estruturada Objectivos:
5374 : Engenharia Informática 6638 : Tecnologias e Sistemas de Informação 9099 : Bioengenharia 10135 : Ciências Biomédicas Cap. 4 Algoritmos e Estruturada Module Introduction Algoritmos e Estruturada Objectivos:
Engenharia de Software e Sistemas Distribuídos. Enunciado Geral do Projecto
 LEIC-A, LEIC-T, LETI, MEIC-T, MEIC-A Engenharia de Software e Sistemas Distribuídos 2 o Semestre 2014/2015 Enunciado Geral do Projecto O que se segue é uma descrição geral do domínio do projecto a desenvolver
LEIC-A, LEIC-T, LETI, MEIC-T, MEIC-A Engenharia de Software e Sistemas Distribuídos 2 o Semestre 2014/2015 Enunciado Geral do Projecto O que se segue é uma descrição geral do domínio do projecto a desenvolver
Introdução ao MATLAB
 Introdução ao MATLAB O MATLAB é um programa cálculo numérico que pode ser usado interactivamente. A sua estrutura de dados fundamental é a matriz, que pode ter elementos reais ou complexos. Embora na sua
Introdução ao MATLAB O MATLAB é um programa cálculo numérico que pode ser usado interactivamente. A sua estrutura de dados fundamental é a matriz, que pode ter elementos reais ou complexos. Embora na sua
SAFT para siscom. Manual do Utilizador. Data última versão: 07.11.2008 Versão: 1.01. Data criação: 21.12.2007
 Manual do Utilizador SAFT para siscom Data última versão: 07.11.2008 Versão: 1.01 Data criação: 21.12.2007 Faro R. Dr. José Filipe Alvares, 31 8005-220 FARO Telf. +351 289 899 620 Fax. +351 289 899 629
Manual do Utilizador SAFT para siscom Data última versão: 07.11.2008 Versão: 1.01 Data criação: 21.12.2007 Faro R. Dr. José Filipe Alvares, 31 8005-220 FARO Telf. +351 289 899 620 Fax. +351 289 899 629
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES
 CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
ZS Rest. Manual Avançado. Menus. v2011 - Certificado
 Manual Avançado Menus v2011 - Certificado 1 1. Índice 2. Introdução... 2 3. Iniciar o ZSRest... 3 4. Menus... 4 b) Novo Produto:... 5 i. Separador Geral.... 5 ii. Separador Preços e Impostos... 7 iii.
Manual Avançado Menus v2011 - Certificado 1 1. Índice 2. Introdução... 2 3. Iniciar o ZSRest... 3 4. Menus... 4 b) Novo Produto:... 5 i. Separador Geral.... 5 ii. Separador Preços e Impostos... 7 iii.
Criando um script simples
 Criando um script simples As ferramentas de script Diferente de muitas linguagens de programação, você não precisará de quaisquer softwares especiais para criar scripts de JavaScript. A primeira coisa
Criando um script simples As ferramentas de script Diferente de muitas linguagens de programação, você não precisará de quaisquer softwares especiais para criar scripts de JavaScript. A primeira coisa
O código JavaScript deve ser colocado entre tags de comentário para ficar escondido no caso de navegadores antigos que não reconhecem a linguagem.
 1 - O que é JAVASCRIPT? É uma linguagem de script orientada a objetos, usada para aumentar a interatividade de páginas Web. O JavaScript foi introduzido pela Netscape em seu navegador 2.0 e posteriormente
1 - O que é JAVASCRIPT? É uma linguagem de script orientada a objetos, usada para aumentar a interatividade de páginas Web. O JavaScript foi introduzido pela Netscape em seu navegador 2.0 e posteriormente
Representação de Dados
 Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Representação de Dados Introdução Todos sabemos que existem diferentes tipos de números: fraccionários, inteiros positivos e negativos, etc. Torna-se necessária a representação destes dados em sistema
Alteração do POC (Decreto de Lei nº. 35/2005) no sispoc
 DOSPrinter Manual do Utilizador Alteração do POC (Decreto de Lei nº. 35/2005) no sispoc Data última versão: 20.03.2006 Versão : 1.1 Data criação: 01.03.2006 Faro R. Dr. José Filipe Alvares, 31 8005-220
DOSPrinter Manual do Utilizador Alteração do POC (Decreto de Lei nº. 35/2005) no sispoc Data última versão: 20.03.2006 Versão : 1.1 Data criação: 01.03.2006 Faro R. Dr. José Filipe Alvares, 31 8005-220
1. Introdução ao uso da calculadora
 1. Introdução ao uso da calculadora O uso da calculadora científica no curso de Estatística é fundamental pois será necessário o cálculo de diversas fórmulas com operações que uma calculadora com apenas
1. Introdução ao uso da calculadora O uso da calculadora científica no curso de Estatística é fundamental pois será necessário o cálculo de diversas fórmulas com operações que uma calculadora com apenas
Para além das funções (comandos) pré-definidas no matlab, o utilizador pode também criar as suas próprias funções
 Funções em Matlab Para além das funções (comandos) pré-definidas no matlab, o utilizador pode também criar as suas próprias funções O comando function permite criá-las. Uma função deve ser definida da
Funções em Matlab Para além das funções (comandos) pré-definidas no matlab, o utilizador pode também criar as suas próprias funções O comando function permite criá-las. Uma função deve ser definida da
MICROSOFT OFFICE EXCEL 2007
 LEIAME Nenhuma informação da APOSTILA - MICROSOFT OFFICE EXCEL 2007 poderá ser copiada, movida ou modificada sem autorização prévia e escrita do autor. MICROSOFT OFFICE EXCEL 2007 Efetue cálculos, analise
LEIAME Nenhuma informação da APOSTILA - MICROSOFT OFFICE EXCEL 2007 poderá ser copiada, movida ou modificada sem autorização prévia e escrita do autor. MICROSOFT OFFICE EXCEL 2007 Efetue cálculos, analise
Pesquisa e organização de informação
 Pesquisa e organização de informação Capítulo 3 A capacidade e a variedade de dispositivos de armazenamento que qualquer computador atual possui, tornam a pesquisa de informação um desafio cada vez maior
Pesquisa e organização de informação Capítulo 3 A capacidade e a variedade de dispositivos de armazenamento que qualquer computador atual possui, tornam a pesquisa de informação um desafio cada vez maior
Instalação do Sistema Operativo Windows XP
 Curso Profissional - Técnico de Informática de Gestão 10ºB Prof. Pedro Lopes Ficha de Trabalho nº1 S i s t e m a s d e I n f o r m a ç ã o Instalação do Sistema Operativo Windows XP A instalação de um
Curso Profissional - Técnico de Informática de Gestão 10ºB Prof. Pedro Lopes Ficha de Trabalho nº1 S i s t e m a s d e I n f o r m a ç ã o Instalação do Sistema Operativo Windows XP A instalação de um
PACWEB Módulo de Pesquisa MANUAL DO UTILIZADOR
 MANUAL DO UTILIZADOR Versão 1.3 ÍNDICE 1. INTRODUÇÃO 2 2. INSTALAÇÃO E CONFIGURAÇÃO 3 2.1 INSTALAÇÃO 3 Instalar o Pacweb 3 Alterar o Ficheiro Default.htm 3 Criar um Virtual Directory 3 2.2 CONFIGURAÇÃO
MANUAL DO UTILIZADOR Versão 1.3 ÍNDICE 1. INTRODUÇÃO 2 2. INSTALAÇÃO E CONFIGURAÇÃO 3 2.1 INSTALAÇÃO 3 Instalar o Pacweb 3 Alterar o Ficheiro Default.htm 3 Criar um Virtual Directory 3 2.2 CONFIGURAÇÃO
Linguagem e Técnicas de Programação I Operadores, expressões e funções. Prof. MSc. Hugo Souza Material desenvolvido por: Profa.
 Linguagem e Técnicas de Programação I Operadores, expressões e funções Prof. MSc. Hugo Souza Material desenvolvido por: Profa. Ameliara Freire Operadores básicos Toda linguagem de programação, existem
Linguagem e Técnicas de Programação I Operadores, expressões e funções Prof. MSc. Hugo Souza Material desenvolvido por: Profa. Ameliara Freire Operadores básicos Toda linguagem de programação, existem
Organização e Arquitetura de Computadores I
 Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Oficina de Construção de Páginas Web
 COMPETÊNCIAS BÁSICAS EM TIC NAS EB1 Oficina de Construção de Páginas Web Criação e Publicação Guião Páginas WWW com o editor do Microsoft Office Word 2003 1. Introdução. 2. Abrir uma página Web. 3. Guardar
COMPETÊNCIAS BÁSICAS EM TIC NAS EB1 Oficina de Construção de Páginas Web Criação e Publicação Guião Páginas WWW com o editor do Microsoft Office Word 2003 1. Introdução. 2. Abrir uma página Web. 3. Guardar
Capacidade = 512 x 300 x 20000 x 2 x 5 = 30.720.000.000 30,72 GB
 Calculando a capacidade de disco: Capacidade = (# bytes/setor) x (méd. # setores/trilha) x (# trilhas/superfície) x (# superfícies/prato) x (# pratos/disco) Exemplo 01: 512 bytes/setor 300 setores/trilha
Calculando a capacidade de disco: Capacidade = (# bytes/setor) x (méd. # setores/trilha) x (# trilhas/superfície) x (# superfícies/prato) x (# pratos/disco) Exemplo 01: 512 bytes/setor 300 setores/trilha
Associação Educacional Dom Bosco Curso de Engenharia 1º ano
 Formatação condicional utilizando o valor da célula O que é? Algumas vezes é preciso destacar os valores, ou seja, como colocar em vermelho ou entre parênteses, os negativos, e de outra cor os positivos,
Formatação condicional utilizando o valor da célula O que é? Algumas vezes é preciso destacar os valores, ou seja, como colocar em vermelho ou entre parênteses, os negativos, e de outra cor os positivos,
Bases de Dados. Lab 1: Introdução ao ambiente
 Departamento de Engenharia Informática 2010/2011 Bases de Dados Lab 1: Introdução ao ambiente 1º semestre O ficheiro bank.sql contém um conjunto de instruções SQL para criar a base de dados de exemplo
Departamento de Engenharia Informática 2010/2011 Bases de Dados Lab 1: Introdução ao ambiente 1º semestre O ficheiro bank.sql contém um conjunto de instruções SQL para criar a base de dados de exemplo
Manual de Utilização. Site Manager. Tecnologia ao serviço do Mundo Rural
 Manual de Utilização Site Manager Tecnologia ao serviço do Mundo Rural Índice 1. Acesso ao Site Manager...3 2. Construção/Alteração do Menu Principal...4 3. Inserção/ Alteração de Conteúdos...7 4. Upload
Manual de Utilização Site Manager Tecnologia ao serviço do Mundo Rural Índice 1. Acesso ao Site Manager...3 2. Construção/Alteração do Menu Principal...4 3. Inserção/ Alteração de Conteúdos...7 4. Upload
