8.1 Partículas Idênticas
|
|
|
- Salvador Molinari
- 5 Há anos
- Visualizações:
Transcrição
1 Capítulo 8 Estatística Quântica 8. Partículas Idênticas Classicamente, partículas são sempre distinguíveis: podemos seguir suas trajetórias e sempre dizer qual é qual. Quanticamente, duas partículas idênticas, e.g. dois elétrons, são indistinguíveis: se trocarmos dois elétrons de posição, o sistema continua idêntico a antes da troca. Suponha que a partícula está no estado ψ a (x ) e a partícula no estado ψ b (x ): ψ a (x ) : partícula com número quântico a, na posição x (8.) ψ b (x ) : partícula com número quântico b, na posição x (8.) Se essas partículas não interagem, classicamente o estado do sistema de partículas seria: ψ(x,x ) = ψ a (x )ψ b (x ) (Partículas Distinguíveis) (8.3) Neste caso, quando trocamos as partículas de posição, i.e. x x, obtemos um novo estado distinguível do anterior: ψ(x,x ) = ψ a (x )ψ b (x ) ψ(x,x ) (8.4) Mascomoaspartículassãoidênticas,amudançax x deveproduzirumestadoindistinguível do estado inicial ψ(x,x ), ou seja o novo estado ψ(x,x ) é dado por ψ(x,x ) = c ψ(x,x ), c = const. (8.5) pois a constante muda apenas a fase, ou a normalização, da função de onda. Por outro lado, se mudarmos as posições novamente x x, obtemos: ou seja ψ(x,x ) = c ψ(x,x ) = c ψ(x,x ), (8.6) c = ± (8.7) Portanto, quando mudamos as partículas de posição, a função de onda tem apenas duas opções: ) permanecer exatamente igual ou ) mudar de sinal. 09
2 0 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA Obviamente, a função de onda expressa na Eq. 8.3 não se encaixa em nenhum desses casos, já que lá a troca de partículas produz um novo estado, distinguível daquele antes da troca. Portanto, para partículas idênticas, a função de onda do sistema de partículas deve ter uma das duas formas: ψ S (x,x ) = [ψ a (x )ψ b (x )+ψ a (x )ψ b (x )] (Simétrica) (8.8) ψ A (x,x ) = [ψ a (x )ψ b (x ) ψ a (x )ψ b (x )] (Anti-simétrica) (8.9) Essas duas possibilidades tem as propriedades de que: ψ S (x,x ) = ψ S (x,x ) (8.0) ψ A (x,x ) = ψ A (x,x ) (8.) Uma partícula deve escolher de uma vez por todas se terá função de onda simétrica ou antisimétrica. Suponhaqueumadadapartícula(e.g. umelétron)tivessefunçõesdeondatantoψ S como ψ A. Nestecaso, elateriatambémcombinaçõeslinearesαψ S +βψ A, quenãosãonemsimétricas, nem anti-simétricas, gerando uma contradição. Portanto, se medirmos que uma partícula tem função de onda simétrica, sabemos que esta é uma propriedade intrínsica dela. 8.. Estatística de Spin: Bósons e Férmions As partículas elementares possuem propriedades intrínsecas, e.g. massa, carga. Uma dessas propriedades é o spin, que é uma espécie de momento angular intrínseco. Verifica-se na natureza que as partículas possuem sempre spin inteiro (0,,...) ou semi-inteiro (/, 3/,...) em unidades de. Por outro lado, partículas com funções de onda simétricas ψ S são chamadas bósons, e partículas com funções de onda anti-simétricas ψ A são chamadas férmions. Exemplos de bósons incluem o fóton (spin 0), os mésons (spin 0, ) e os glúons (spin ). Exemplos de férmions incluem bárions, como prótons e nêutrons e tambem elétrons (spin /). Um fato da natureza é que todos os bósons tem spin inteiro, enquanto todos os férmions tem spin semi-inteiro. Esse fato pode ser demonstrado no contexto da Teoria Quântica de Campos, que unifica a Teoria Quântica e a Relatividade Especial. Portanto: Férmions : Função de onda anti-simétrica ψ A, spin semi-inteiro n /, e.g. eletron (8.) Bósons : Função de onda simétrica ψ S, spin inteiro n, e.g. foton (8.3) 8.. Princípio de Exclusão de Pauli Suponha que temos férmions, e.g. dois elétrons, com uma função de onda anti-simétrica: ψ A (x,x ) ψ a (x )ψ b (x ) ψ a (x )ψ b (x ) (8.4) Suponha agora que os férmions estão no mesmo estado quântico, i.e. a = b. Neste caso, teríamos: ψ A (x,x ) ψ a (x )ψ a (x ) ψ a (x )ψ a (x ) = 0 (8.5) ou seja, é impossível ter dois férmions com o mesmo estado quântico. Similarmente, suponha que os férmions tem estados quânticos diferentes, mas ocupam posições espaciais muito próximas, i.e. x x. Neste caso: ψ A (x,x ) ψ a (x )ψ b (x ) ψ a (x )ψ b (x ) = 0 (8.6) ou seja, dois férmions não podem ocupar o mesmo lugar no espaço. Isso determina a posições e os estados de elétrons nos átomos, já que eles não podem ter o mesmo estado quântico.
3 8.. PARTÍCULAS IDÊNTICAS 8..3 Spin e Tabela Periódica A função de onda total é a função de onda espacial vezes a função de onda do spin da partícula. Portanto, se elétrons têm os mesmos números quânticos n l e m, eles necessariamente devem ter spins diferentes, e.g. + / ou /. A tabela periódica de elementos químicos é explicada com elétrons ocupando os níveis energéticos disponíveis, respeitando o Princípio de Pauli Partículas Clássicas e Quânticas Considere um gás com apenas partículas A e B, que podem existir em 3 estados,,3. Estatística Clássica: Neste caso, temos particulas são distinguíveis e qualquer número de partículas pode estar em qualquer estado. As 9 configurações possíveis são mostradas na Tab. 8. As partículas satisfazem a Estatística de Maxwell-Boltzmann (MB) 3 AB AB AB A B B A A B B A A B B A Tabela 8.: Configurações de partículas A,B em 3 estados, na estatística clássica de Maxwell-Boltzmann. Estatística de Bósons: Neste caso, as partículas sõ idênticas (A=B) e qualquer número de partículas pode estar em qualquer estado. As 6 configurações possíveis são mostradas na Tab. 8. As partículas satisfazem a Estatístitica de Bose-Einstein (BE). 3 AA AA AA A A A A A A Tabela 8.: Configurações de partículas idênticas em 3 estados, na estatística de Bose-Einstein. Estatística de Férmions: Neste caso, as partículas são idênticas (A=B) e pode haver no máximo partícula em cada estado (Princípio de Exclusão). As 3 configurações possíveis sao mostradas na Tab. 8.3 As partículas satisfazem a Estatístitica de Fermi-Dirac (FD).
4 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA 3 A A A A A A Tabela 8.3: Configurações de partículas idênticas em 3 estados, na estatística de Fermi-Dirac. Para cada uma destas estatísticas, podemos calcular a razão P, definida: P = Número de configurações com partículas no mesmo estado Número de configurações com partículas em estados diferentes (8.7) Temos: P MB = 3 6 = (8.8) P BE = 3 3 = (8.9) P FD = 0 3 = 0 (8.0) Portanto, relativamente à estatística clássica de Maxwell-Boltzmann, podemos concluir: Bose-Einstein: Tendência das partículas se aglomerarem no mesmo estado (e.g. condensado de Bose-Einstein a baixas temperaturas). Fermi-Dirac: Tendência das partículas se repelirem no mesmo estado, ou ocuparem estados diferentes: princípio de exclusão (e.g. átomos, anãs brancas). 8. Estatística Quântica: Ensemble Grand-Canônico No caso quântico, uma configuração pode ser representada por (N,N,...,N r,...) : configuração (8.) onde temos N r partículas no estado r, com energia ǫ r cada uma. Gostaríamos de saber o número médio N r de partículas no estado r. No caso clássico de um gás ideal, os estados eram contínuos e vimos que N(v) e βmv / ou N(E) e βe (8.) No caso quântico, precisamos retornar às medias calculadas usando a distribuição grand-canônica: P(E r,n r ) = Ce β(er µnr) (8.3) Com N r partículas no estado r, cada uma com energia ǫ r, temos que a energia total E r no estado r é dada por: E r = N r ǫ r (8.4)
5 8.. ESTATÍSTICA QUÂNTICA: ENSEMBLE GRAND-CANÔNICO 3 Assim, P(E r,n r ) = Ce β(ǫr µ)nr = Ce βǫ r Nr (8.5) ǫ r = ǫ r µ (8.6) e o número médio no estado r fica N r = s N re βǫ sn s s e βǫ sn s (8.7) onde a soma é feita sobre todas as configurações possíveis do sistema. Temos então N r = β onde a função de grand-partição Z g é ǫ r s= e βǫ sn s s= e βǫ sn s = β Z g Z g ǫ r = β lnz g ǫ r (8.8) Z g = e βǫ s Ns. (8.9) s= Com as energias ǫ s fixadas pelos estados quânticos, as diferentes configurações são obtidas variando os números (N,N,...,N r,...) de 0 a e temos, equivalentemente: N r = N,N,...N N r,... re β(ǫ N +ǫ N +...ǫ rn r+...) N N,N,...N r,... e β(ǫ N +ǫ N +...ǫ r Nr+...) = r N r e βǫ rn r N s N r e β(ǫ N +ǫ N +...) N r e βǫ r Nr N s N r e β(ǫ N +ǫ N +...) (8.30) O somatório em N s N r se cancela, e obtemos N r = N r= N re βǫ rn r N r= e βǫ r Nr = β ǫ r N r= e βǫ r Nr N r= e βǫ r Nr = β lns r ǫ r (8.3) onde a soma S r é feita apenas no estado r: S r = N r= ( e βǫ r) Nr (8.3) enquanto a função de partição é feita em todas as configurações: Z g = e β(ǫ N +ǫ N +...ǫ r Nr+...) (8.33) N,N,...N r, Distribuição de Fermi-Dirac No caso de férmions, N r = 0, apenas e S r = N r=0, ( e βǫ r) Nr = +e βǫ r (8.34)
6 4 Portanto ou seja, N r = β ǫ r N r = ln(+e βǫ r) = β e β(ǫr µ) + CAPÍTULO 8. ESTATÍSTICA QUÂNTICA βe βǫ r +e βǫ r = e βǫ r + (8.35) Fermi-Dirac (8.36) Figura 8.: Distribuicao de Fermi-Dirac para diferentes temperaturas. A energia de Fermi neste caso é ǫ F = ev. No zero absoluto, todos os estados com ǫ < ǫ F estão ocupados, enquanto os estados ǫ > ǫ F estão vazios. Vejamos o que ocorre quando a temperatura de um sistema de Férmions abaixa. Neste caso, T 0, i.e. β e temos { e β(ǫ µ) 0 se ǫ < µ(t = 0) = (8.37) se ǫ > µ(t = 0) Definimos a Energia de Fermi ǫ F = µ(t = 0), e temos entao que { se ǫ < N(ǫ) = e β(ǫ ǫf) + = ǫf (8.38) 0 se ǫ > ǫ F ou seja, em T = 0, todos os estados com ǫ < ǫ F são ocupados, e os estados com ǫ > ǫ F ficam vazios. À medida que T aumenta, os estados com ǫ > ǫ F também vão sendo ocupados. 8.. Distribuição de Bose-Einstein No caso de bósons, N r = 0,,..., e devemos calcular o somatório: ( Nr S r = e r) βǫ = +e βǫ r +e βǫ r +e 3βǫ r +... (8.39) Portanto N r=0 e βǫ rs r = e βǫ r +e βǫ r +e 3βǫ r +... (8.40) e subtraindo as duas equações, após cancelamentos, obtemos Assim ou seja, N r = β S r e βǫ rs r = S r = ǫ r N r = ln( e βǫ r) = β e β(ǫr µ) e βǫ r βe βǫ r e βǫ r = e βǫ r (8.4) (8.4) Bose-Einstein (8.43)
7 8.. ESTATÍSTICA QUÂNTICA: ENSEMBLE GRAND-CANÔNICO 5 Fótons No caso particular de fótons, a energia pode variar independente do número de partículas, já que fótons podem ser criados/destruídos sem restrição. Isso implica µ = 0, ou seja obtemos novamente a distribuição de Planck: N r = e βǫr 8..3 Distribuição de Maxwell-Boltzmann Distribuição de Planck (Fótons) (8.44) No caso de partículas distinguíveis, a troca de partículas entre estados distintos gera novas configurações. Entretanto a troca de partículas no mesmo estado não gera uma nova configuração. Assim, para cada configuração (N,N,...) do caso de bósons, temos N! N!N!... (8.45) configurações no caso clássico, onde N = r N r é o numero total de partículas do sistema. Portanto, a função de grand-partição fica N! Z g = N!N!... e β(ǫ N +ǫ N +...ǫ rn r+...) = Usando a expansão binomial: temos então Portanto e temos (a+b+c+...) N = N,N,...N r,... N,N,...N r,... N,N,...,N r,... N! N!N!... (e βǫ ) N (e βǫ ) N... (8.46) N! N!N!... an b N c N 3..., onde r N r = N (8.47) ( N Z g = (e βǫ +e βǫ +...) N = e r) βǫ (8.48) N r = β lnz g = N ln lnz g ǫ r = N β ( r e βǫ r βe βǫ r r e βǫ r r ) = N e βǫ r r e βǫ r Inserindo ǫ r = ǫ r µ e cancelando e βµ no numerador e denominador, temos e obviamente (8.49) (8.50) N r = N e βǫr r e βǫr Maxwell-Boltzmann (8.5) r N r = N (8.5) Ou seja, reobtemos o resultado da estatística clássica, mesmo com estados quânticos.
8 6 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA 8..4 Limite Clássico Somando as partículas nos vários estados, obtemos o número total N de partículas N = r N r = r e β(ǫr µ) ± (8.53) Mesmo no caso de fótons, em que este número não é fixo, ainda assim ele deve se manter finito. No limite de baixas densidades, temos N o que implica que cada N r, e e βǫ r. Já no limite de altas temperaturas, β 0, e os termos de energias ǫ r mais altas, i.e. Nr com r mais alto, tendem a contribuir para a somatória. Para que N continue sendo finito novamente é preciso que N r, o que ocorre com µ(t) negativo o suficiente e implica e βǫ r. Portanto em baixas densidades e/ou altas temperaturas, ambas as distribuições quânticas (BE e FD) se aproximam de N r = e βǫ r ± e βǫ r (MB) (8.54) i.e. as distribuições de BE e de FD se reduzem a distribuição clássica de MB Comparação Figura 8.: Comparação entre as distribuições de Maxwell-Boltzmann (clássica), Bose-Einstein (bósons) e Fermi-Dirac (férmions). Para βǫ, as três distribuições coincidem. Para βǫ 0, bosons tendem a se aglomerar no estado fundamental, enquanto fermions devem respeitar o principio de Exclusao. Comparamos as 3 distribuições na Fig. 8.. Relativamente à distribuição de Maxwell- Boltzmann, a distribuiç!ao de Bose-Einstein esta sempre acima, enquanto a distribuiçao de Fermi-Dirac esta sempre abaixo. Como vimos, em altas energias (ǫ ) ou altas temperaturas (β ) as distribuições de FD e BE se reduzem à de MB, ou seja, as 3 distribuições coincidem. Já em baixas temperaturas as distribuições se diferenciam muito. A distribuição de BE (e também a de MB) faz com que todas as partículas tendam a ocupar o estado fundamental de mais baixa energia do sistema, fazendo com que N(ǫ = 0). Já a distribuição de FD deve respeitar o princípio de Exclusão e portanto N(ǫ), fazendo com que os estados sejam mais homogeneamente ocupados.
9 8.3. ESTATÍSTICA QUÂNTICA: ENSEMBLE MICRO-CANÔNICO Estatística Quântica: Ensemble Micro-Canônico Vamos agora re-obter as distribuições de MB, FD e BE usando o ensemble microcanônico, i.e. explicitamente contando todas as configurações possíveis em cada caso. O estado de equilibrio é aquele que maximiza o número de configurações (estado mais provável), ou similarmente, que maximiza a entropia do sistema Configurações Suponha que tenhamos estados degenerados, i.e. estados distintintos mas com a mesma energia. Vimos que isso ocorre, por exemplo, no átomo de Hidrogênio, onde os estados eram caracterizados por 4 números quânticos (n,l,m,m z ), mas a energia dependia apenas de n. Portanto, havia vários estados do elétron com a mesma energia. Vamos supor então que temos d i estados com energia ǫ i e que vamos distribuir N i partículas nesses d i estados: ǫ {}}{... }{{} d estados N partículas ǫ {}}{... }{{} d estados N partículas... ǫ i {}}{... }{{} d i estados N i partículas... O caso não-degenerado corresponde a d i =. Os números de estados d i são fixos e determinados pela mecânica quântica do sistema específico que estamos considerando. O número de partículas N i ocupando estes estados no entanto pode variar e definir diferentes configurações do sistema. Estamos interessados em saber o número de configurações Ω possíveis com N partículas com energia ǫ cada, N partículas com energia ǫ e assim por diante, mas com energia total e número total de partículas fixados, i.e. Ω(N,N,...,N i,...) com N i = N e N i ǫ i = E (8.55) Vamos considerar as várias estatísticas para calcular o número de configurações acima. Distinguíveis Vamos considerar primeiro o caso da estatística clássica, em que as partículas sao distinguíveis e pode haver qualquer número de partículas em qualquer estado. Uma configuração típica nos níveis de energia ǫ i é mostrada abaixo: i i ǫ i {}}{... }{{} d i estados N i partículas - Para preencher os estados de energia ǫ, devemos i) Escolher N partículas entre as N possiveis. O número de maneiras de fazer isso é ( N N ) = N! N! (N N )! (8.56)
10 8 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA ii) Distribuir as N partículas entre os d estados. Cada uma das N partículas terá d escolhas, já que elas podem inclusive ocupar os mesmos estados. Portanto o número de maneiras de fazer isso é (d ) N (8.57) Portanto, o número de maneiras de ter N partículas nos d estados de ǫ é: ǫ : Ω(N ) = N! d N N! (N N )! (8.58) Por exemplo, se d = 3 estados e N = partículas, as configurações possíveis para ǫ são as 9 já mostradas na Tab 8., ou similarmente: : (AB,0,0) : (0,AB,0) : (0,0,AB) : (A,B,0) : (B,A,0) : (A,0,B) : (B,0,A) : (0,A,B) : (0,B,A) De fato, com N =, N = e d = 3, temos Ω(N ) =!3 /!(0)! = 9. -Paraosestadosdeenergiaǫ, procedemosdamesmaforma, mascomojáusamosn partículas, somente (N N ) estão disponíveis. Portanto, fazendo N N, temos: ǫ : Ω(N ) = (N N )! d N N! (N N N )! (8.59) - Procedemos similarmente para todas as energias ǫ i. O número total de configurações possíveis é obtido então multiplicando: Ω(N,N,...) = Ω(N )Ω(N )... = N! d N N! (N N )! (N N )! d N N! (N N N )!... = dn... N!dN N!N!... (8.60) ou seja Ω(N,N,...) = N! n= d Nn n N n! (8.6)
11 8.3. ESTATÍSTICA QUÂNTICA: ENSEMBLE MICRO-CANÔNICO 9 Bósons Para bósons a tarefa é mais facil, já que as partículas são idênticas. Portanto, não precisamos escolher N i partículas dentre as N disponíveis, já que todas produzirão uma mesma configuração. Isso elimina o passo i) do caso anterior. A única coisa a se determinar é o numero de maneiras de distribuir as N i partículas idênticas em d i estados. Podemos pensar que temos N i bolas representando partículas identicas e d i partições que limitam os d i estados: ǫ i {}}{... }{{}... }{{} N i particulas d i particoes Por exemplo, uma configuração típica para bósons é mostrada abaixo: ǫ i {}}{... }{{} d i estados N i partículas (8.6) - O número de configuraçoes possíveis para a energia ǫ é o número de permutações do conjunto de N +d objetos, sendo N idênticos e d idênticos, ou seja: ǫ : Ω(N ) = (N +d )! N! (d )! (8.63) Por exemplo, se d = 3 estados (d = particoes) e N = partículas, as configurações possíveis para ǫ são as 6 já mostradas na Tab 8., ou similarmente:: : (AA,0,0) : (0,AA,0) : (0,0,AA) De fato Ω(N ) = (+3 )!/!(3 )! = 4!/!! = 6. : (A,A,0) : (A,0,A) : (0,A,A) - O mesmo se aplica para os estados de energia ǫ e todas as outras, e o número total de configurações fica: Ω(N,N,...) = n= (N n +d n )! N n!(d n )! (8.64)
12 0 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA Férmions Para férmions a situação é parecida com a de bósons, mas as partículas devem satisfazer o princípio de exclusão, i.e. pode haver no máximo uma partícula por estado. Uma configuração típica para férmions é mostrada abaixo: ǫ i {}}{... }{{} d i estados N i partículas (8.65) - O número de maneiras de preencher os estados de energia ǫ é igual ao número de combinações dos d estados disponíveis em grupos de N estados completos, ou seja: ( ) d d! ǫ : Ω(N ) = = (8.66) N! (d N )! N Por exemplo, se d = 3 estados (d = partiçoes) e N = partículas, as configurações possíveis para ǫ são as 3 já mostradas na Tab 8.3, ou similarmente: : (A,A,0) : (A,0,A) : (0,A,A) De fato Ω(N ) = 3!/!(3 )! = 3. -Paraosestadosdeenergiaǫ, procedemosdamesmaforma, mascomojáusamosn partículas, somente (N N ) estão disponíveis. Portanto, fazendo N N N, temos: ǫ : Ω(N ) = (N N )! d N N! (N N N )! (8.67) - O mesmo se aplica para os estados de energia ǫ e todas as outras, e o número total de configurações fica: Ω(N,N,...) = n= d n! N n!(d n N n )! (8.68) 8.3. Distribuição de Equilibrio A distribuição de estados mais provável é aquela que contem o maior número de configurações, ou seja é aquela que maximiza a função Ω(N,N,...), ou similarmente seu logaritmo lnω(n,n,...) (a entropia do sistema), sujeitos a vínculos de energia e número total de partículas: N n = N, N n ǫ n = E (8.69) n n EstamaximizaçãopodeserfeitapelométododemultiplicadoresdeLagrange. MaximizarlnΩ(N,N,...) sujeito aos vínculos acima é equivalente a maximizar a função G(N,N,...,α,β): [ [ ] G(N,N,...) = lnω(n,n,...)+α N N n ]+β E N n ǫ n (8.70) n= n=
13 8.3. ESTATÍSTICA QUÂNTICA: ENSEMBLE MICRO-CANÔNICO onde α e β são multiplicadores de Lagrange. De fato, o máximo de G ocorre quando: G N n = 0 e G α = G β = 0 (8.7) A primeira condicão garante que lnω é máxima e determina a distribuição N n em que isso ocorre. As outras duas condições garantem que os vínculos são satisfeitos Distribuição Maxwell-Boltzmann No caso de partículas distinguíveis, temos [ [ ] G = lnn!+ (N n lnd n lnn n!)+α N N n ]+β E N n ǫ n n= n= n= (8.7) Para N n podemos usar a approximação de Stirling: obtendo Portanto o que implica G = lnn!+αn +βe + lnn n! N n lnn n N n (N n, Stirling) (8.73) [N n lnd n N n lnn n +N n αn n +βǫ n N n ] (8.74) n= G N n = lnd n lnn n + α βǫ n = 0 (8.75) N n = d n e (α+βǫn) (Maxwell-Boltzmann) (8.76) ou seja, re-obtemos a distribuição de Maxwell-Boltzmann Distribuição de Bose-Einstein No caso de bósons, temos [ [ ] G = [ln(n n +d n ) lnn n! ln(d n )!]+α N N n ]+β E N n ǫ n ou seja n= n= n= G [(N n +d n )ln(n n +d n ) (N n +d n ) N n lnn n N n αn n βǫ n N n ] n= [ln(d n )!]+αn +βe n=
14 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA Portanto G N n = ln(n n +d n ) lnn n α βǫ n = 0 (8.77) o que implica ou seja ( ln + d ) n = α+βǫ n N n d n N n = e α+βǫn (8.78) N n = d n e α+βǫn (Bose-Einstein) (8.79) ou seja, re-obtemos a distribuiçao de Bose-Einstein. Note que a constante d n pode ser absorvida na normalização da distribuição. Distribuição de Fótons alpha=0 No caso de fótons, não existe o vinculo no numero de particulas. Portanto, tudo é igual ao caso geral de bosons, mas com α = 0: N n d n e βǫn (Bose-Einstein) (8.80) ou seja, re-obtemos a distribuicao de Bose-Einstein. Note que a constante d n pode ser absorvida na normalizacao da distribuicão Distribuição de Fermi-Dirac No caso de férmions, temos [ [ ] G = [lnd n! lnn n! ln(d n N n )!]+α N N n ]+β E N n ǫ n n= Assumindo N n e também d n N n, temos n= n= Portanto G [ N n lnn n (d n N n )ln(d n N n )+(d n N n ) N n αn n βǫ n N n ] n= + [lnd n!]+αn +βe n= G N n = lnn n +ln(d n N n ) α βǫ n = 0 (8.8)
15 8.4. APLICAÇÕES 3 o que implica ou seja ( ) dn ln = α+βǫ n N n d n N n = e α+βǫn + (8.8) N n = d n e α+βǫn + (Fermi-Dirac) (8.83) ou seja, re-obtemos a distribuição de Fermi-Dirac. Novamente a constante d n pode ser absorvida na normalização da distribuição. 8.4 Aplicações 8.4. Gás de Bósons Considere um gás de bósons, e.g. um gás de fótons, mas vamos manter µ 0 para generalidade. Temos e o número total de partículas é N r = e β(ǫr µ) (8.84) N = r N r = n N(ǫ n )Ω(ǫ n ) n (8.85) onde Ω(ǫ n ) é o número de estados com energia ǫ n e n. Supondo bósons em uma caixa quadrada de comprimento L, os estados de energia são: ǫ n = h n 8mL, onde n = n x +n y +n z (8.86) O número de estados é contado por n, e em um intervalo n dn fica: Como Portanto Ω(ǫ n )dn = 4πn 8 dn = πn ǫ = h n 8mL ou n = dǫ = h 8mLndn ou ndn = πn dn = (ndn) (8.87) ( ) 8mL / ǫ / h ( 8mL h ) dǫ Ω(n)dn = π ( ) 8mL / ( ) 8mL h ǫ / dǫ h = π 4 ( 8mL h ) 3/ ǫ / dǫ = 4πL3 h 3 (m3 ) / ǫ / dǫ e com V = L 3, temos Ω(ǫ)dǫ = 4πV h 3 (m3 ) / ǫ / dǫ (8.88)
16 4 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA Assim, o número de partículas fica A integral dá N = N(ǫ n )Ω(ǫ n ) n N(ǫ)Ω(ǫ)dǫ n 0 = 4πV h 3 (m3 ) / ǫ / e β(ǫ µ) dǫ (8.89) N = (πmk BT) 3/ ( h 3 Ve βµ + 3/eβµ + ) 3 3/eβµ (8.90) Para m,t grande, devemos ter e βµ 0, pois N é fixo. Isso ocorre se µ. Neste caso, temos N (πmk BT) 3/ h 3 Ve βµ ou e βµ Nh 3 (πmk B T) 3/ V (8.9) Ja a energia total é dada por E = 0 N(ǫ)Ω(ǫ) ǫ dǫ = 4πV h 3 (m3 ) / ( 3 k BT (πmk BT) 3/ h 3 V Para m,t grandes, temos entao ou E N 3 ( k BT + )( 5/eβµ ) 3/eβµ = 3 k BT 0 ǫ 3/ e β(ǫ µ) dǫ )e βµ ( + 5/eβµ + 3 5/eβµ +... E N 3 k BT }{{} Nh 3 5/ V(πmk B T) }{{ 3/ } Clássico correção quântica de a ordem 3/ }{{} / /5 ) 5/ eβµ (8.9) (8.93) (8.94) Portanto a energia média de um gás de bósons a altas temperaturas é menor do que a de um gas clássico, já que os bósons tendem a se aglomerar em energias mais baixas, diminuindo a energia média. Condensado de Bose-Einstein Para que N(ǫ r ) 0 para todos os estados, devemos ter Se ǫ min = ǫ 0 0, então e β(ǫr µ) µ ǫ (8.95) µ 0 (8.96)
17 8.4. APLICAÇÕES 5 Mas µ = µ(t), e existe uma temperatura crítica T c na qual µ = 0. Ela é determinada por N = (πmk BT c ) 3/ ( h 3 V + 3/ + 3 ) / (8.97) Pode-se mostrar que para T < T c, a partículas tendem a se aglomerar no estado fundamental ǫ 0 : condensado de Bose-Einstein. Esse efeito foi verificado experimentalmente em 995 por Cornell, Ketterle e Wieman, que ganharam o prêmio Nobel em Gás de Férmions Considere agora um gás de férmions, e.g. um gás de elétrons livres. De fato, em um condutor metálico, os elétrons nas camadas exteriores (banda de condução) estão fracamente ligados ao núcleo e são approximadamente livres (elétrons de condução). Como elétrons tem possibilidades de spin (± /), o número de estados é multiplicado por relativamente ao de bósons: Assim, o número de partículas fica Para T 0, β e Portanto N = Ω(ǫ)dǫ = 8πV h 3 (m3 ) / ǫ / dǫ (8.98) 0 N(ǫ)Ω(ǫ)dǫ = 8πV h 3 (m3 ) / N(ǫ) = 0 ǫ / e β(ǫ ǫf) dǫ (8.99) + { se ǫ < ǫf 0 se ǫ > ǫ F (8.00) ou N = 8πV ǫf h 3 (m3 ) / 0 ǫ / dǫ = 6πV(m3 ) / 3h 3 ǫ 3/ F (8.0) ǫ F = h 8m ( ) 3N /3 (Energia de Fermi) (8.0) πv Para a energia, temos Portanto, E = 0 N(ǫ)Ω(ǫ) ǫ dǫ = 8πV h 3 (m3 ) / ǫf 0 ǫ 3/ dǫ = 6πV(m3 ) / 5h 3 ǫ 5/ F (8.03) E N = 3 5 ǫ F (8.04)
18 6 CAPÍTULO 8. ESTATÍSTICA QUÂNTICA ou E = 3 5 N [ h 8m ( ) ] 3N /3 πv (8.05) O gás de férmions exerce uma pressão nas paredes de um recipiente, quando se expande de dv: de = E dv = P dv = dw (8.06) }{{ 3V} P ou seja P = E 3 V = 3 3N 5 V [ h ( ) ] 3N /3 8m πv Anãs Brancas h P = 58m ( 3 π ) /3 ( N V ) 5/3 (Pressão de Degenerescência) (8.07) Estrelas passam a primeira parte de sua existência usando a energia liberada nas reações nucleares no seu interior. Essas reações de fusão nuclear liberam uma quantidade enorme de energia e produzem uma pressão sobre o material estelar para fora da estrela. Esta pressão balanceia a atração gravitacional que tende a fazer o material estelar colapsar para o centro. À medida que os combustíveis usuais das reações nucleares (hidrogênio, hélio,...) se esgotam, a estrela passa a fundir e produzir elementos mais pesados. Eventualmente a fusão não é mais favorável energeticamente, pois a energia de ligação por nucleon passa a diminuir nos produtos. Neste ponto, se a estrela não for muito massiva, ela se expande e perde suas camadas externas, restandoapenasumnúcleoestelarmuitodenso. Aestrelapassaasechamarumaanãbranca. Como não há mais reações nucleares, a anã branca balanceia a gravidade com a pressão de degenerescência dos elétrons, que é muito alta devido à alta densidade. A estrela pode co-existir desta forma por um período indefinido. Quanto maior a massa da estrela, maior a sua densidade e maior a sua pressão de degenerescência. Entretanto, o aumento da massa também implica aumento da gravidade, e existe uma massa limite (limite de Chandrasekhar) que a pressão de degenerescência consegue suportar. Eventualmente, a anã branca pode ganhar massa de uma estrela companheira (e.g. um sistema binário), e ultrapassar o limite de Chandrasekhar. Se isso ocorrer, a gravidade ganha da pressão de degenerescência e a estrela começa a colapsar. A sua temperatura então começa a aumentar muito, o que acaba dando início a reações nucleares, que até então eram improváveis. Essas reações são muito violentas e, de fato, fazem a estrela explodir e expelir seu material para o meio inter-estelar proximo à estrela. Essa explosão é chamada supernova do tipo IA. Em 998, os astrônomos Riess, Schmidt e Perlmutter usaram medidas de luminosidade e redshift de supernovas IA para mostrar que a expansão do universo está ocorrendo de forma acelerada. Estas importantes medidas deram origem à chamada era da cosmologia de prescisão, que busca entender as causas desta aceleração cósmica via medidas astronômicas precisas. Por esse trabalho, Riess, Schmidt e Perlmutter ganharam o prêmio Nobel em 0.
Física Estatística ??? Representação macroscópica. Representação microscópica. sistema U (S, V, N) S (U, V, N)
 Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física estatística MEFT, IST. Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
 Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
Representação grande
 Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 12 ESTATÍSTICA QUÂNTICA Primeira Edição junho de 2005 CAPÍTULO 12 ESTATÍSTICA QUÂNTICA ÍNDICE 12-1- Introdução 12.2- Indistinguibilidade
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 12 ESTATÍSTICA QUÂNTICA Primeira Edição junho de 2005 CAPÍTULO 12 ESTATÍSTICA QUÂNTICA ÍNDICE 12-1- Introdução 12.2- Indistinguibilidade
n, l, m l, ms (1) quando estes quatro números quânticos são dados, o estado físico do sistema (no caso, um elétron) é então especificado.
 Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
Formalismo microcanônico ( ensemble microcanônico) Formalismo canônico ( ensemble canônico)
 Formalismo microcanônico ( ensemble microcanônico) sist(j) estado j f j = Ω j Ω Formalismo canônico ( ensemble canônico) reservatório de temperatura tot res sistema f j = Ω res+sist(j) Ω tot sist(j) Física
Formalismo microcanônico ( ensemble microcanônico) sist(j) estado j f j = Ω j Ω Formalismo canônico ( ensemble canônico) reservatório de temperatura tot res sistema f j = Ω res+sist(j) Ω tot sist(j) Física
Física estatística. A distribuição de equiĺıbrio de um gás rarefeito: conjunto microcanónico e o método da distribuição mais provável MEFT, IST
 Física estatística A distribuição de equiĺıbrio de um gás rarefeito: conjunto microcanónico e o método da distribuição mais provável MEFT, IST A realidade nem sempre é provável Jorge Luis Borges Equiĺıbrio
Física estatística A distribuição de equiĺıbrio de um gás rarefeito: conjunto microcanónico e o método da distribuição mais provável MEFT, IST A realidade nem sempre é provável Jorge Luis Borges Equiĺıbrio
Mecânica Quântica e Indiscernibilidade
 Mecânica Quântica e Indiscernibilidade t ou ou?? Mecânica clássica Partículas discerníveis ( A, A ) ψ ( A A ) ψ =, Mecânica quântica Partículas indiscerníveis ( A, A ) ψ ( A A ) ψ = ψ, ou = ( A, A ) ψ
Mecânica Quântica e Indiscernibilidade t ou ou?? Mecânica clássica Partículas discerníveis ( A, A ) ψ ( A A ) ψ =, Mecânica quântica Partículas indiscerníveis ( A, A ) ψ ( A A ) ψ = ψ, ou = ( A, A ) ψ
INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN
 Introdução à Astrofísica Lição 18 A Distribuição de Maxwell INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN Um estado de um gás é especificado por suas coordenadas, de modo que representemos
Introdução à Astrofísica Lição 18 A Distribuição de Maxwell INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN Um estado de um gás é especificado por suas coordenadas, de modo que representemos
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
Aula 22. Gás de Fermi. Sumário CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA DEPARTAMENTO DE FÍSICA PROGRAMA DE PÓS-GRADUAÇÃO
 FIS 75 Mecânica Estatística - 26. - Notas de Aulas - 27 CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA DEPARTAMENTO DE FÍSICA PROGRAMA DE PÓS-GRADUAÇÃO Aula 22 Gás de Fermi Sumário Dedução a partir do ensemble
FIS 75 Mecânica Estatística - 26. - Notas de Aulas - 27 CENTRO DE CIÊNCIAS EXATAS E DA NATUREZA DEPARTAMENTO DE FÍSICA PROGRAMA DE PÓS-GRADUAÇÃO Aula 22 Gás de Fermi Sumário Dedução a partir do ensemble
Física Quântica. Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli. Pieter Westera
 Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Instituto de Física - UFF Profissional - 11 de Dezembro de 2009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das
 Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 11 de Dezembro de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3
Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 11 de Dezembro de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3
Física Moderna II Aula 08. Marcelo G Munhoz Edifício HEPIC, sala 202, ramal
 Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 munhoz@if.usp.br 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 munhoz@if.usp.br 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Cap. 10. Interiores Estelares. Fontes de energia. Transporte de energia: radiação. AGA 0293, Astro?sica Estelar Jorge Meléndez
 Cap. 10. Interiores Estelares. Fontes de energia. Transporte de energia: radiação AGA 0293, Astro?sica Estelar Jorge Meléndez Equação de Conservação de Massa dm r = ρ dv dr Equilíbrio hidrostálco P+dP
Cap. 10. Interiores Estelares. Fontes de energia. Transporte de energia: radiação AGA 0293, Astro?sica Estelar Jorge Meléndez Equação de Conservação de Massa dm r = ρ dv dr Equilíbrio hidrostálco P+dP
Física estatística. Fotões e a radiação do corpo negro MEFT, IST
 Física estatística Fotões e a radiação do corpo negro MEFT, IST A scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually
Física estatística Fotões e a radiação do corpo negro MEFT, IST A scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
AULA 01 TEORIA ATÔMICA COMPLETA
 AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. Estrutura Eletrônica
AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. Estrutura Eletrônica
Descoberta do Núcleo
 Unidade 3 Núcleo Atômico Descoberta do Núcleo Propriedades dos Núcleos Forças Nucleares Estabilidade Nuclear Ressonância Magnética Nuclear Consultas http://hyperphysics.phy-astr.gsu.edu/hbase/nuccon.html#nuccon
Unidade 3 Núcleo Atômico Descoberta do Núcleo Propriedades dos Núcleos Forças Nucleares Estabilidade Nuclear Ressonância Magnética Nuclear Consultas http://hyperphysics.phy-astr.gsu.edu/hbase/nuccon.html#nuccon
CONDENSADO DE BOSE-EINSTEIN Andrés Rodriguez Salas Instituto de Fisica de São Carlos Junio 20 de 2011
 Resumo CONDENSADO DE BOSE-EINSTEIN Andrés Rodriguez Salas Instituto de Fisica de São Carlos Junio 20 de 20 O tratamento estadistico dado por Bose ao problema da radiação do corpo negro, tratando a luz
Resumo CONDENSADO DE BOSE-EINSTEIN Andrés Rodriguez Salas Instituto de Fisica de São Carlos Junio 20 de 20 O tratamento estadistico dado por Bose ao problema da radiação do corpo negro, tratando a luz
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi
 Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
Introdução à Astrofísica. Lição 21 Fontes de Energia Estelar
 Introdução à Astrofísica Lição 21 Fontes de Energia Estelar A taxa de energia que sai de uma estrela é extremamente grande, contudo ainda não tratamos da questão que relaciona à fonte de toda essa energia.
Introdução à Astrofísica Lição 21 Fontes de Energia Estelar A taxa de energia que sai de uma estrela é extremamente grande, contudo ainda não tratamos da questão que relaciona à fonte de toda essa energia.
INTRODUÇÃO À ASTROFÍSICA
 Introdução à Astrofísica INTRODUÇÃO À ASTROFÍSICA LIÇÃO 21 O EQUILÍBRIO HIDROSTÁTICO Lição 20 O Equilíbrio Hidrostático As estrelas se formam a partir de regiões densas e frias, chamadas de nebulosas.
Introdução à Astrofísica INTRODUÇÃO À ASTROFÍSICA LIÇÃO 21 O EQUILÍBRIO HIDROSTÁTICO Lição 20 O Equilíbrio Hidrostático As estrelas se formam a partir de regiões densas e frias, chamadas de nebulosas.
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
AULA 01 TEORIA ATÔMICA COMPLETA
 AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
Átomos polieletrónicos
 Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
Os Ensembles Caps. 4, 5, 7 do Salinas
 Os Ensembles Caps. 4, 5, 7 do Salinas ensemble = conjunto, coleção de sistemas em condições idênticas ao sistema que queremos estudar FFI319 - Física Estatística 20 27 de Setembro p. 1 Microcanônico Micro-estados
Os Ensembles Caps. 4, 5, 7 do Salinas ensemble = conjunto, coleção de sistemas em condições idênticas ao sistema que queremos estudar FFI319 - Física Estatística 20 27 de Setembro p. 1 Microcanônico Micro-estados
Aula 17 Tudo sobre os Átomos
 Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Aula-11. (quase) Tudo sobre os átomos
 Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Átomos e Moléculas. Ligações moleculares. Energia do ion. A molécula de hidrogênio H 2
 Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Problemas de Física Estatística e Termodinâmica
 1 Problemas de Física Estatística e Termodinâmica Todas as grandezas físicas se supõem expressas no Sistema Internacional de Unidades. 1. Uma variável aleatória y pode tomar valores no conjunto {1,2,3,4,5}
1 Problemas de Física Estatística e Termodinâmica Todas as grandezas físicas se supõem expressas no Sistema Internacional de Unidades. 1. Uma variável aleatória y pode tomar valores no conjunto {1,2,3,4,5}
A teoria de Hartree. r r. r r
 A teoria de Hartree Vimos, na aula 4, a proposta de Hartree: tratamento autoconsistente Ou seja, V(r) obtido a posteriori, a partir das distribuições de carga dos e -, deve concordar com o V(r) usado para
A teoria de Hartree Vimos, na aula 4, a proposta de Hartree: tratamento autoconsistente Ou seja, V(r) obtido a posteriori, a partir das distribuições de carga dos e -, deve concordar com o V(r) usado para
Teoria de Bandas 1 Elétrons Livres. CF086 - Introdução a Física do Estado Sólido 1
 Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
Gases quânticos sem interação
 UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
Prof. Rodrigo Negreiros UFF XI Escola do CBPF
 Prof. Rodrigo Negreiros UFF XI Escola do CBPF I. Introdução. Aula I II. Visão geral de estrelas compactas. III. Física nuclear relativística. Aula II IV. Estrelas de Nêutrons no contexto da física nuclear.
Prof. Rodrigo Negreiros UFF XI Escola do CBPF I. Introdução. Aula I II. Visão geral de estrelas compactas. III. Física nuclear relativística. Aula II IV. Estrelas de Nêutrons no contexto da física nuclear.
Física Quântica. Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões. Pieter Westera
 Física Quântica Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html
Física Quântica Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html
Átomo de Hélio. Tiago Santiago. 2 de novembro de Resumo
 Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
ESTRUTURA ELETRÔNICA DOS ÁTOMOS
 ESTRUTURA ELETRÔNICA DOS ÁTOMOS 2 Natureza ondulatória da luz 3 Natureza ondulatória da luz 4 Natureza ondulatória da luz 5 Natureza ondulatória da luz 6 Energia quantizada e fótons Planck quantum h é
ESTRUTURA ELETRÔNICA DOS ÁTOMOS 2 Natureza ondulatória da luz 3 Natureza ondulatória da luz 4 Natureza ondulatória da luz 5 Natureza ondulatória da luz 6 Energia quantizada e fótons Planck quantum h é
ESTRUTURA ATÔMICA. Prof. Dr. Cristiano Torres Miranda Disciplina: Química Geral I QM81B Turmas Q13 e Q14
 ESTRUTURA ATÔMICA Prof. Dr. Cristiano Torres Miranda Disciplina: Química Geral I QM81B Turmas Q13 e Q14 TEORIA ATÔMICA DA MATÉRIA Demócrito e Leucipo (discípulo) (460 370 a.c.) Aristóteles (384 a.c. 322
ESTRUTURA ATÔMICA Prof. Dr. Cristiano Torres Miranda Disciplina: Química Geral I QM81B Turmas Q13 e Q14 TEORIA ATÔMICA DA MATÉRIA Demócrito e Leucipo (discípulo) (460 370 a.c.) Aristóteles (384 a.c. 322
Mecânica I (FIS-14) Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 Mecânica I (FIS-14) Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Mecânica Mecânica: estuda o estado de movimento (ou repouso) de corpos sujeitos à ação
Mecânica I (FIS-14) Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Mecânica Mecânica: estuda o estado de movimento (ou repouso) de corpos sujeitos à ação
Aula 01 Estrutura eletrônica
 Universidade Tecnológica Federal do Paraná Departamento Acadêmico de Química e Biologia Aula 01 Estrutura eletrônica Dr. Tiago P. Camargo Átomos - Estrutura Núcleo (prótons e nêutrons) Eletrosfera (elétrons)
Universidade Tecnológica Federal do Paraná Departamento Acadêmico de Química e Biologia Aula 01 Estrutura eletrônica Dr. Tiago P. Camargo Átomos - Estrutura Núcleo (prótons e nêutrons) Eletrosfera (elétrons)
Elétrons como ondas? Um bom modelo deve ser capaz de explicar propriedades atômicas, propriedades periódicas, ligação química
 OS ELÉTRONS O MODELO DA MECÂNICA QUÂNTICA E AS ENERGIAS ELETRÔNICAS Modelo atual se baseia na MECÂNICA QUÂNTICA Considera os conceitos da quantização da energia eletrônica (Bohr), fornecendo uma explicação
OS ELÉTRONS O MODELO DA MECÂNICA QUÂNTICA E AS ENERGIAS ELETRÔNICAS Modelo atual se baseia na MECÂNICA QUÂNTICA Considera os conceitos da quantização da energia eletrônica (Bohr), fornecendo uma explicação
CF100 - Física Moderna II. 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018
 CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
4.1 Estados de Energia
 Capítulo 4 Mecânica Estatística O objetivo principal da mecânica estatística é relacionar as propriedades microscópicas de sistemas físicos (seus estados quânticos) com suas propriedades macroscópicas
Capítulo 4 Mecânica Estatística O objetivo principal da mecânica estatística é relacionar as propriedades microscópicas de sistemas físicos (seus estados quânticos) com suas propriedades macroscópicas
FIS-14 Mecânica I. Ronaldo Rodrigues Pela
 FIS-14 Mecânica I Ronaldo Rodrigues Pela Objetivos Visão geral: Termodinâmica e Mecânica Velocidade rms Equipartição da Energia e calor específico Origem microscópica da distribuição de Maxwell-Boltzmann
FIS-14 Mecânica I Ronaldo Rodrigues Pela Objetivos Visão geral: Termodinâmica e Mecânica Velocidade rms Equipartição da Energia e calor específico Origem microscópica da distribuição de Maxwell-Boltzmann
Gás de elétrons livres. Introdução à Mecânica Estatística 29/10/2009
 Gás de elétrons livres Introdução à Mecânica Estatística 9/10/009 1 Distribuição de Fermi-Dirac Distribuição de Fermi-Dirac ou f ( ) 1 ( ) e 1 também chamada função de Fermi 1 kt B Exemplo: elétrons em
Gás de elétrons livres Introdução à Mecânica Estatística 9/10/009 1 Distribuição de Fermi-Dirac Distribuição de Fermi-Dirac ou f ( ) 1 ( ) e 1 também chamada função de Fermi 1 kt B Exemplo: elétrons em
Gás de elétrons livres
 Capítulo 6 Gás de elétrons livres 8 de dezembro de 29 1 Estados eletrônicos Metais Os metais possuem propriedades singulares quando comparados com outros tipos de sólidos. Possuem ductibilidade, maleabilidade
Capítulo 6 Gás de elétrons livres 8 de dezembro de 29 1 Estados eletrônicos Metais Os metais possuem propriedades singulares quando comparados com outros tipos de sólidos. Possuem ductibilidade, maleabilidade
8 de dezembro de 2009
 Capítulo 3 Gás de fótons 8 de dezembro de 29 1 Lei de Planck Fótons Neste capítulo examinamos as propriedades térmicas da radiação eletromagnética em uma cavidade. A análise das equações de Maxwell nos
Capítulo 3 Gás de fótons 8 de dezembro de 29 1 Lei de Planck Fótons Neste capítulo examinamos as propriedades térmicas da radiação eletromagnética em uma cavidade. A análise das equações de Maxwell nos
1 Ψ S. bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A. férmions estatística de Fermi: n(e) = e α e E/kT +1
 Estatística Quântica Boltzmann: n(e) = 1 e α e E/kT Indistinguibilidade Ψ S ou Ψ A 1 Ψ S bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A férmions estatística de Fermi: n(e) = e α e E/kT +1 1 Distribuição
Estatística Quântica Boltzmann: n(e) = 1 e α e E/kT Indistinguibilidade Ψ S ou Ψ A 1 Ψ S bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A férmions estatística de Fermi: n(e) = e α e E/kT +1 1 Distribuição
Ensemble Grande Canônico
 UFABC - NANHT3036-15SA - Mecânica Estatística Curso 017. Prof. Germán Lugones CAPÍTULO 5 Ensemble Grande Canônico 1 Sistema em contato com um reservatório Vamos procurar um ensemble que seja apropriado
UFABC - NANHT3036-15SA - Mecânica Estatística Curso 017. Prof. Germán Lugones CAPÍTULO 5 Ensemble Grande Canônico 1 Sistema em contato com um reservatório Vamos procurar um ensemble que seja apropriado
Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein
 Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein Edigles Guedes e-mail: edigles.guedes@gmail.com 24 de junho de 2012. RESUMO Nós construímos a Teoria da Relatividade
Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein Edigles Guedes e-mail: edigles.guedes@gmail.com 24 de junho de 2012. RESUMO Nós construímos a Teoria da Relatividade
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
O Ensemble Grande Canônico
 Capítulo 6 O Ensemble Grande Canônico Vimos nos capítulos anteriores que sistemas ergódicos isolados pertencem ao ensemble microcanônico. Quando tais sistemas trocam energia com um reservatório térmico
Capítulo 6 O Ensemble Grande Canônico Vimos nos capítulos anteriores que sistemas ergódicos isolados pertencem ao ensemble microcanônico. Quando tais sistemas trocam energia com um reservatório térmico
Apresentar os conceitos fundamentais da termodinâmica estatística e como aplicá-los as propriedades termodinâmicas vista até então.
 Introdução À Termodinâmica Estatística Aula 15 Meta Apresentar os conceitos fundamentais da termodinâmica estatística e como aplicá-los as propriedades termodinâmicas vista até então. Objetivos Ao final
Introdução À Termodinâmica Estatística Aula 15 Meta Apresentar os conceitos fundamentais da termodinâmica estatística e como aplicá-los as propriedades termodinâmicas vista até então. Objetivos Ao final
Física da Matéria Condensada - GFI 04129
 Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
Energia de Fermi de 2N electrões
 Energia de Fermi de 2N electrões Ângelo Dias N.º 65087 Mariana Branco N.º 65112 Física Quântica da Matéria Mestrado Integrado em Engenharia Biomédica 29 de Março de 2011 I. Resumo Neste trabalho é discutida
Energia de Fermi de 2N electrões Ângelo Dias N.º 65087 Mariana Branco N.º 65112 Física Quântica da Matéria Mestrado Integrado em Engenharia Biomédica 29 de Março de 2011 I. Resumo Neste trabalho é discutida
Prof. Rodrigo Negreiros UFF XI Escola do CBPF
 Prof. Rodrigo Negreiros UFF XI Escola do CBPF I. Introdução. Aula I II. Visão geral de estrelas compactas. III. Física nuclear relativística. Aula II IV. Estrelas de Nêutrons no contexto da física nuclear.
Prof. Rodrigo Negreiros UFF XI Escola do CBPF I. Introdução. Aula I II. Visão geral de estrelas compactas. III. Física nuclear relativística. Aula II IV. Estrelas de Nêutrons no contexto da física nuclear.
Aula 12. (quase) Tudo sobre os átomos. Física Geral F-428
 Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
TEORIAS ATÔMICAS. Menor partícula possível de um elemento (Grécia antiga) John Dalton (1807)
 TEORIAS ATÔMICAS Átomo Menor partícula possível de um elemento (Grécia antiga) John Dalton (1807) 1. Os elementos são constituídos por partículas extremamente pequenas chamadas átomos; 2. Todos os átomos
TEORIAS ATÔMICAS Átomo Menor partícula possível de um elemento (Grécia antiga) John Dalton (1807) 1. Os elementos são constituídos por partículas extremamente pequenas chamadas átomos; 2. Todos os átomos
Átomos multi-eletrônicos. Indistinguibilidade
 Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Gás de elétrons livres
 Capítulo 6 Gás de elétrons livres 6.1 Estados eletrônicos Metais Os metais possuem propriedades singulares quando comparados com outros tipos de sólidos. Possuem ductibilidade, maleabilidade e apresentam
Capítulo 6 Gás de elétrons livres 6.1 Estados eletrônicos Metais Os metais possuem propriedades singulares quando comparados com outros tipos de sólidos. Possuem ductibilidade, maleabilidade e apresentam
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Astrofísica Geral. Tema 12: A morte das estrelas
 ma 12: A morte das estrelas Outline 1 Evolução e morte estelar 2 Cadáveres estelares 3 Supernovas 4 Bibliografia 2 / 22 Outline 1 Evolução e morte estelar 2 Cadáveres estelares 3 Supernovas 4 Bibliografia
ma 12: A morte das estrelas Outline 1 Evolução e morte estelar 2 Cadáveres estelares 3 Supernovas 4 Bibliografia 2 / 22 Outline 1 Evolução e morte estelar 2 Cadáveres estelares 3 Supernovas 4 Bibliografia
A Equação de Onda de Schröedinger. O Princípio da Incerteza de Heisenberg. λ =
 O Modelo Mecânico-Quântico Louis de Broglie apresentou a idéia de que, se as ondas luminosas exibiam características de partícula, então talvez as partículas de matéria pudessem mostrar propriedades ondulatórias.
O Modelo Mecânico-Quântico Louis de Broglie apresentou a idéia de que, se as ondas luminosas exibiam características de partícula, então talvez as partículas de matéria pudessem mostrar propriedades ondulatórias.
LCE0143 Química Geral. Estrutura Atômica. Wanessa Melchert Mattos.
 LCE0143 Química Geral Estrutura Atômica Wanessa Melchert Mattos wanemelc@usp.br Princípio da Incerteza Elétron dualidade onda-partícula W. Heisenberg: impossível fixar a posição de um elétron em um átomo
LCE0143 Química Geral Estrutura Atômica Wanessa Melchert Mattos wanemelc@usp.br Princípio da Incerteza Elétron dualidade onda-partícula W. Heisenberg: impossível fixar a posição de um elétron em um átomo
Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149):
 Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149): (Mink.) na pg 149 escolhemos ε real, que é útil para polariz. transversa. Para polarizações
Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149): (Mink.) na pg 149 escolhemos ε real, que é útil para polariz. transversa. Para polarizações
Os fundamentos da Física Volume 3 1. Resumo do capítulo
 Os fundamentos da Física Volume 1 Capítulo 0 Física Nuclear AS FORÇAS FUNDAMENTAIS DA NATUREZA Força nuclear forte Mantém a coesão do núcleo atômico. Intensidade 10 8 vezes maior do que a força gravitacional.
Os fundamentos da Física Volume 1 Capítulo 0 Física Nuclear AS FORÇAS FUNDAMENTAIS DA NATUREZA Força nuclear forte Mantém a coesão do núcleo atômico. Intensidade 10 8 vezes maior do que a força gravitacional.
ÁTOMOS DE MUITOS ELÉTRONS E MOLÉCULAS
 FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville ÁTOMOS DE MUITOS ELÉTRONS E MOLÉCULAS É errado pensar que a tarefa da física é descobrir como a natureza é.
FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville ÁTOMOS DE MUITOS ELÉTRONS E MOLÉCULAS É errado pensar que a tarefa da física é descobrir como a natureza é.
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos Teorema de Hohenberg-Kohn Equações de Kohn-Sham Problema de N elétrons Aproximação de Born-Oppenheimer: os núcleos estão totalmente
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos Teorema de Hohenberg-Kohn Equações de Kohn-Sham Problema de N elétrons Aproximação de Born-Oppenheimer: os núcleos estão totalmente
O spin do elétron. Vimos, na aula 2, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com 2 valores, com propriedades de momento angular.
 O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
Revisão de conceitos de mecânica quântica
 Revisão de conceitos de mecânica quântica Quantização de energia A Radiação de corpo negro Estudos de Planck (1900) sobre a radiação de corpo negro, levaram a ideia de que a energia é dependente da frequência
Revisão de conceitos de mecânica quântica Quantização de energia A Radiação de corpo negro Estudos de Planck (1900) sobre a radiação de corpo negro, levaram a ideia de que a energia é dependente da frequência
Regras de Feynman no espaço dos momentos (Euclideano): Regras de Feynman para a matriz S (Minkowski / Momentos):
 Regras de Feynman no espaço dos momentos (Euclideano): Teoria Quântica de Campos I 193 propagador do férmion: (Euclid.) índices espinoriais (α,β=1...4) ( eq. 193.1 ) o sentido do momento não importa (Euclid.)
Regras de Feynman no espaço dos momentos (Euclideano): Teoria Quântica de Campos I 193 propagador do férmion: (Euclid.) índices espinoriais (α,β=1...4) ( eq. 193.1 ) o sentido do momento não importa (Euclid.)
Estrutura de Helicidade em um referencial específico
 Teoria Quântica de Campos I 82 Logo podemos fazer o crossing direto nas variáveis de Mandelstam e obter: Estrutura de Helicidade em um referencial específico Façamos novamente o cálculo da seção de choque
Teoria Quântica de Campos I 82 Logo podemos fazer o crossing direto nas variáveis de Mandelstam e obter: Estrutura de Helicidade em um referencial específico Façamos novamente o cálculo da seção de choque
Introdução ao Método de Hartree-Fock
 Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
Sistemas de Bose ideais MEFT, IST
 Física estatística Sistemas de Bose ideais MEFT, IST It is a miracle that curiosity survives formal education. Albert Einstein (1879 1955) Gás de Bose ideal Já sabemos que PV kt = log (z, V, T )= X p log
Física estatística Sistemas de Bose ideais MEFT, IST It is a miracle that curiosity survives formal education. Albert Einstein (1879 1955) Gás de Bose ideal Já sabemos que PV kt = log (z, V, T )= X p log
-> Foi laureado com o Nobel de Física e um dos fundadores da Mecânica Quântica.
 Werner Karl Heisenberg (5 de Dezembro de 1901, Würzburg 1 de Fevereiro de 1976, Munique, Alemanha). -> foi um físico alemão. -> Foi laureado com o Nobel de Física e um dos fundadores da Mecânica Quântica.
Werner Karl Heisenberg (5 de Dezembro de 1901, Würzburg 1 de Fevereiro de 1976, Munique, Alemanha). -> foi um físico alemão. -> Foi laureado com o Nobel de Física e um dos fundadores da Mecânica Quântica.
Partículas Elementares
 Partículas Elementares Átomos consistem de elétrons que formam as camadas eletrônicas, e núcleos, compostos por prótons e nêutrons que, por sua vez,consistem de quarks ( dos tipos u e d, ou seja,up e down).
Partículas Elementares Átomos consistem de elétrons que formam as camadas eletrônicas, e núcleos, compostos por prótons e nêutrons que, por sua vez,consistem de quarks ( dos tipos u e d, ou seja,up e down).
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White
 QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
Quantização de um campo fermiônico
 Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Átomo de Hidrogênio 1
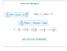 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Anãs Brancas: As Sobras Degeneradas de Estrelas. Elvis Soares. Coloquinho dos Estudantes - 09/05/14
 Anãs Brancas: As Sobras Degeneradas de Estrelas Elvis Soares Coloquinho dos Estudantes - 09/05/14 1 Sumário Fatos Históricos e um pouco de Astronomia Elétrons e Degenerescência Limite de Chandrasekhar
Anãs Brancas: As Sobras Degeneradas de Estrelas Elvis Soares Coloquinho dos Estudantes - 09/05/14 1 Sumário Fatos Históricos e um pouco de Astronomia Elétrons e Degenerescência Limite de Chandrasekhar
ESTRUTURA ATÔMICA. Modelos Atômicos
 ESTRUTURA ATÔMICA Modelos Atômicos 1.Modelo atômico de Dalton 2.Modelo atômico de Thomson 3.Modelo atômico de Rutherford 4.Modelo atômico de Rutherford-Bohr 5.Modelo atômico atual MODELOS ATÔMICOS 1808
ESTRUTURA ATÔMICA Modelos Atômicos 1.Modelo atômico de Dalton 2.Modelo atômico de Thomson 3.Modelo atômico de Rutherford 4.Modelo atômico de Rutherford-Bohr 5.Modelo atômico atual MODELOS ATÔMICOS 1808
No limite. é livre. é livre. Note que a equação 78.1 está na forma:
 Teoria Quântica de Campos I 78 (aqui está a vantagem dos estados coerentes, se tentássemos fazer o mesmo no espaço de Fock apareceriam problemas pois o termo com fontes mistura níveis de Fock diferentes)
Teoria Quântica de Campos I 78 (aqui está a vantagem dos estados coerentes, se tentássemos fazer o mesmo no espaço de Fock apareceriam problemas pois o termo com fontes mistura níveis de Fock diferentes)
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Introdução à Física Computacional
 7600017 Introdução à Física Computacional Sexto Projeto (prazo até 26/06/18) Instruções Crie um diretório PROJ6 #usp em /home/public/fiscomp18/proj6 Proteja seu diretório para não ser lido por g e o Deixe
7600017 Introdução à Física Computacional Sexto Projeto (prazo até 26/06/18) Instruções Crie um diretório PROJ6 #usp em /home/public/fiscomp18/proj6 Proteja seu diretório para não ser lido por g e o Deixe
Física IV Poli Engenharia Elétrica: 20ª Aula (04/11/2014)
 Física IV Poli Engenharia Elétrica: ª Aula (4/11/14) Prof. Alvaro Vannucci a última aula vimos: Átomos multi-eletrônicos: as energias dos estados quânticos podem ser avaliadas através da expressão: 13,6
Física IV Poli Engenharia Elétrica: ª Aula (4/11/14) Prof. Alvaro Vannucci a última aula vimos: Átomos multi-eletrônicos: as energias dos estados quânticos podem ser avaliadas através da expressão: 13,6
O Método de Hartree-Fock
 O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
Física. B) Determine a distância x entre o ponto em que o bloco foi posicionado e a extremidade em que a reação é maior.
 Física 01. Uma haste de comprimento L e massa m uniformemente distribuída repousa sobre dois apoios localizados em suas extremidades. Um bloco de massa m uniformemente distribuída encontra-se sobre a barra
Física 01. Uma haste de comprimento L e massa m uniformemente distribuída repousa sobre dois apoios localizados em suas extremidades. Um bloco de massa m uniformemente distribuída encontra-se sobre a barra
Aula anterior. Equação de Schrödinger a 3 dimensões. d x 2m - E -U. 2m - E -U x, y, z. x y z x py pz cin cin. E E ( x, y,z ) - 2m 2m x y z
 6/Maio/2013 Aula 21 Efeito de túnel quântico: decaimento alfa. Aplicações: nanotecnologias; microscópio por efeito de túnel. Equação de Schrödinger a 3 dimensões. Átomo de hidrogénio Modelo de Bohr 8/Maio/2013
6/Maio/2013 Aula 21 Efeito de túnel quântico: decaimento alfa. Aplicações: nanotecnologias; microscópio por efeito de túnel. Equação de Schrödinger a 3 dimensões. Átomo de hidrogénio Modelo de Bohr 8/Maio/2013
n Camadas K L M N...
 Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
Capacidade térmica de sólidos
 Capítulo 5 Capacidade térmica de sólidos 1 Relação de dispersão As excitações elementares num sólido correspondem a ondas elásticas. Para exemplificar, considere uma cadeia de N átomos ligados por molas
Capítulo 5 Capacidade térmica de sólidos 1 Relação de dispersão As excitações elementares num sólido correspondem a ondas elásticas. Para exemplificar, considere uma cadeia de N átomos ligados por molas
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das
 Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
SUPERNOVAS E NUCLEOSSÍNTESE
 SUPERNOVAS E NUCLEOSSÍNTESE UMA SUPERNOVA ATINGE UM BRILHO DE CERCA DE CERCA DE 10 9-10 10 L POR ALGUMAS HORAS DEPOIS DA EXPLOSÃO Existem dois tipos básicos de supernova : 1. Tipo II 2. Tipo Ia TIPO II
SUPERNOVAS E NUCLEOSSÍNTESE UMA SUPERNOVA ATINGE UM BRILHO DE CERCA DE CERCA DE 10 9-10 10 L POR ALGUMAS HORAS DEPOIS DA EXPLOSÃO Existem dois tipos básicos de supernova : 1. Tipo II 2. Tipo Ia TIPO II
Teoria de bandas nos sólidos
 Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
N P P N. Ciências de Materiais I Prof. Nilson C. Cruz. Aula 2 Ligação Química. Átomos. Diferença entre materiais = Diferença entre arranjos atômicos e
 Ciências de Materiais I Prof. Nilson C. Cruz Aula 2 Ligação Química Átomos Diferença entre materiais = Diferença entre arranjos atômicos e N P P N e N P e Carga (x 1,6x10-19 C) 0 1-1 Massa (x 1,673x10-24
Ciências de Materiais I Prof. Nilson C. Cruz Aula 2 Ligação Química Átomos Diferença entre materiais = Diferença entre arranjos atômicos e N P P N e N P e Carga (x 1,6x10-19 C) 0 1-1 Massa (x 1,673x10-24
Física IV Escola Politécnica P3 7 de dezembro de 2017
 Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 Tabela Periódica dos elementos 2 8 8 Alcalinos, um elétron livre na camada
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 Tabela Periódica dos elementos 2 8 8 Alcalinos, um elétron livre na camada
