a) 256 b) 360 c) 450 d) 648 e) 1 296

Transcrição

1 Chama-se palíndromo qualquer número, palavra ou frase que se pode ler da esquerda para a direita ou da direita para a esquerda, sem que o seu sentido seja alterado. Por exemplo, são palíndromos: o número e a palavra ROTOR. Certo dia, um funcionário de uma Agência do Banco do Brasil, contabilizando as cédulas que havia em caixa, verificou que elas totalizavam X reais, < X< Sabendo que o número X é um palíndromo em que os algarismos das unidades, das dezenas e das centenas são distintos entre si, os possíveis valores de X são a) 256 b) 360 c) 450 d) 648 e) 1 296

2 Considerando que as equipes A, B, C, D e E disputem um torneio que premie as três primeiras colocadas, julgue os itens a seguir. O total de possibilidades distintas para as três primeiras colocações é 58. Certo Errado

3 Considerando que as equipes A, B, C, D e E disputem um torneio que premie as três primeiras colocadas, julgue os itens a seguir. O total de possibilidades distintas para as três primeiras colocações com a equipe A em primeiro lugar é 15. Certo Errado

4 Considerando que as equipes A, B, C, D e E disputem um torneio que premie as três primeiras colocadas, julgue os itens a seguir. Se a equipe A for desclassificada, então o total de possibilidades distintas para as três primeiras colocações será 24. Certo Errado

5 Considerando que uma empresa tenha 5 setores, cada setor seja dividido em 4 subsetores, cada subsetor tenha 6 empregados e que um mesmo empregado não pertença a subsetores distintos, julgue os itens subsequentes. O número de subsetores dessa empresa é superior a 24. Certo Errado

6 Considerando que uma empresa tenha 5 setores, cada setor seja dividido em 4 subsetores, cada subsetor tenha 6 empregados e que um mesmo empregado não pertença a subsetores distintos, julgue os itens subsequentes. O número de empregados dessa empresa é inferior a 125. Certo Errado

7 Supondo que André, Bruna, Cláudio, Leila e Roberto sejam, não necessariamente nesta ordem, os cinco primeiros classificados em um concurso, julgue os itens seguintes. O número de possibilidades distintas para a classificação com um homem em último lugar é 144. Certo Errado

8 Usamos FATORIAL toda vez que pensamos em troca. 5!= 5x4x3x2x1 = 120 4!= 4x3x2x1 = 24 3!= 3x2x1 = 6 2!= 2x1 = 2 1!= 1 (Por definição) 0!= 1 (Por convenção)

9

10 João, Pedro, Celso, Raul e Marcos foram aprovados em um concurso. Cada um trabalhará em uma unidade diferente da empresa: P, Q, R, S ou T. Considerando que João já foi designado para trabalhar na unidade P, de quantos modos distintos é possível distribuir os demais aprovados pelas unidades restantes? a) 12 b) 24 c) 48 d) 90 e) 120

11

12 Supondo que André, Bruna, Cláudio, Leila e Roberto sejam, não necessariamente nesta ordem, os cinco primeiros classificados em um concurso, julgue os itens seguintes. Existem 120 possibilidades distintas para essa classificação. Certo Errado

13 Supondo que André, Bruna, Cláudio, Leila e Roberto sejam, não necessariamente nesta ordem, os cinco primeiros classificados em um concurso, julgue os itens seguintes. Com André em primeiro lugar, existem 20 possibilidades distintas para a classificação. Certo Errado

14 Supondo que André, Bruna, Cláudio, Leila e Roberto sejam, não necessariamente nesta ordem, os cinco primeiros classificados em um concurso, julgue os itens seguintes. Com Bruna, Leila e Roberto classificados em posições consecutivas, existem 36 possibilidades distintas para classificação. Certo Errado

15 Na sala de reuniões de uma empresa há uma mesa de formato retangular com 8 cadeiras dispostas da forma como é mostrado na figura abaixo. Sabe-se que, certo dia, seis pessoas reuniram-se nessa sala: o Presidente, o Vice-Presidente e 4 Membros da Diretoria. Considerando que o Presidente e o Vice- Presidente sentaram-se nas cabeceiras da mesa, de quantos modos podem ter se acomodado nas cadeiras todas as pessoas que participaram da reunião?

16 a) 720 b) 360 c) 120 d) 72 e) 36

17 Marcelo vai passar quatro dias na praia e leva em sua bagagem sete camisetas (três camisetas brancas diferentes, uma preta, uma amarela, uma vermelha e uma laranja) e quatro bermudas (uma preta, uma cinza, uma branca e uma azul). De quantos modos distintos Marcelo poderá escolher uma camiseta e uma bermuda para vestirse, de modo que as peças escolhidas sejam de cores diferentes? a) 14 b) 17 c) 24 d) 26 e) 28

18 Caso as senhas de acesso dos clientes aos caixas eletrônicos de certa instituição bancária contenham 3 letras das 26 do alfabeto, admitindose repetição, nesse caso, a quantidade dessas senhas que têm letras repetidas é superior a Certo Errado

19 Anagramas ou anágramas são letras que trocam de lugar, sem necessitar que haja formação de palavra inteligível. Tomando por base as letras da palavra CERTO, responda os itens: * Quantos anagramas podemos formar?

20 Palavra CERTO * Quantos anagramas podemos formar, começando por C? * Quantos anagramas podemos formar, começando por vogal e terminando por consoante?

21 Se todos os anagramas da palavra BRASIL forem dispostos em ordem alfabética, o primeiro anagrama cuja última letra é B ocupará que posição? a) 5ª b) 25ª c) 34ª d) 49ª e) 121ª

22 Julgue os itens que se seguem, a respeito de contagem. Ao se listar todas as possíveis permutações das 13 letras da palavra PROVAVELMENTE, incluindo-se as repetições, a quantidade de vezes que esta palavra aparece é igual a 6. Certo Errado

23 Quando há letras repetidas... Exemplo: Quantos anagramas podemos formar com as letras da palavra ALA Como pensar, para poder calcular? São três letras que TROCAM de lugar, mas tanto faz a TROCA de duas letras A

24 Quantos anagramas distintos podemos formar com as letras da palavra ARARA?

25 A quantidade de permutações distintas que podem ser formadas com as 7 letras da palavra REPETIR, que começam e terminam com R, é igual a 60. Certo Errado

26 Com as letras da palavra TROCAS é possível construir mais de 300 pares distintos de letras. Certo Errado

27 Uma reunião possui 40 participantes. Ao final todos se cumprimentam com um aperto de mão. Quantos apertos de mão foram dados no final dessa reunião?

28 Com relação a lógica sentencial, contagem e combinação, julgue os itens a seguir. Em um torneio em que 5 equipes joguem uma vez entre si em turno único, o número de jogos será superior a 12. Certo Errado

29 Em um tribunal, os julgamentos dos processos são feitos em comissões compostas por 3 desembargadores de uma turma de 5 desembargadores. Nessa situação, a quantidade de maneiras diferentes de se constituírem essas comissões é superior a 12.

30 Num grupo de 7 mulheres e 5 homens deseja-se formar uma comissão representativa com 3 mulheres e 2 homens. Quantas comissões distintas podem ser formadas?

31 7 mulheres e 5 homens Quantas comissões distintas de 4 pessoas poderemos formar com, no mínimo, 3 mulheres?

32 Considere que 7 tarefas devam ser distribuídas entre 3 funcionários de uma repartição de modo que o funcionário mais recentemente contratado receba 3 tarefas, e os demais, 2 tarefas cada um. Nessa situação, sabendo-se que a mesma tarefa não será atribuída a mais de um funcionário, é correto concluir que o chefe da repartição dispõe de menos de 120 maneiras diferentes para distribuir essas tarefas.

33 7 tarefas. O funcionário mais recentemente contratado receba 3 tarefas, e os demais, 2 tarefas cada um. Menos de 120 maneiras diferentes para distribuir essas tarefas. 7 x 6 x 5 x 4 x 3 x 2 x 1 3! 2! 2! 7 x 5 x 3 x 2 = 210 maneiras

34 O número de países representados nos Jogos Pan-Americanos realizados no Rio de Janeiro foi 42, sendo 8 países da América Central, 3 da América do Norte, 12 da América do Sul e 19 do Caribe. Com base nessas informações, julgue os itens que se seguem.

35 Países: 42 ACentral: 8 ANorte: 3 ASul: 12 Caribe: 19 * Considerando-se apenas os países da América do Norte e da América Central participantes dos Jogos Pan-Americanos, a quantidade de comitês de 5 países que poderiam ser constituídos contendo pelo menos 3 países da América Central é inferior a 180. ACentral: 8 ANorte: 3

36 ACentral: 8 ANorte: 3 * Comitês de 5 países com pelo menos 3 países da América Central é inferior a x 7 x 6 x 3 x 2 3! 2! 8 x 7 x 6 x 5 x 3 4! = 168 = x 7 x 6 x 5 x 4 = 56 5! Total = 434

37 * Considerando-se que, em determinada modalidade esportiva, havia exatamente 1 atleta de cada país da América do Sul participante dos Jogos Pan-Americanos, então o número de possibilidades distintas de dois atletas desse continente competirem entre si é igual a 66. ASul: x 11 2! = 66

38 COMBINAÇÃO COM REPETIÇÃO Teoria

39 Uma loja vende barras de chocolate de diversos sabores. Em uma promoção, era possível comprar três barras de chocolate com desconto, desde que estas fossem dos sabores ao leite, amargo, branco ou com amêndoas, repetidos ou não. Assim, um cliente que comprar as três barras na promoção poderá escolher os sabores de n modos distintos, sendo n igual a a) 20 b) 16 c) 12 d) 10 e) 4

40

41 Com 3 marcas diferentes de cadernos, a quantidade de maneiras distintas de se formar um pacote contendo 5 cadernos será...

42 Como identificar ARRANJO, COMBINAÇÃO e PERMUTAÇÃO.

43

44 Teoria Permutação Circular

45 Uma mesa circular tem seus 6 lugares que serão ocupados pelos 6 participantes de uma reunião. Nessa situação, o número de formas diferentes para se ocupar esses lugares com os participantes da reunião é superior a 10 2.

46 Para o policiamento ostensivo e ininterrupto de uma cidade, o comando local estabeleceu a escala de 24 horas de plantão por 48 horas de folga para cada policial local e, em cada plantão, por razões de segurança, determinou que nenhum policial poderá trabalhar sozinho. Com base nas informações da situação hipotética acima apresentada, julgue os itens que se seguem.

47 Escala de 24 por 48 horas, nenhum policial poderá trabalhar sozinho. Caso o comando local disponha de 12 policiais e 4 deles devam estar de plantão a cada dia, então, nesse caso, haverá mais de 500 maneiras distintas de se escolher a equipe que trabalhará no primeiro dia. ERRADO

48 Escala de 24 por 48 horas, nenhum policial poderá trabalhar sozinho. Considere que, entre os 12 policiais do comando local, sejam sorteados dois prêmios distintos e que um mesmo policial não receba os dois prêmios. Nesse caso, existem mais de 100 maneiras distintas de se distribuírem esses prêmios. CERTO

49 A Associação dos Correspondentes de Imprensa Estrangeira no Brasil (ACIE) organiza, pelo quinto ano consecutivo, o Prêmio e Mostra ACIE de Cinema. Os filmes indicados serão seguidos pela votação de aproximadamente 250 correspondentes afiliados às associações de correspondentes do Rio de Janeiro, de São Paulo e de Brasília. Os vencedores serão escolhidos nas categorias Melhor Filme (ficção), Melhor Documentário, Melhor Diretor, Melhor Roteiro, Melhor Ator, Melhor Atriz, Melhor Fotografia e Melhor Filme Júri Popular. A partir da organização do texto acima e considerando os princípios de contagem, julgue os itens subseqüentes.

50 250 filmes indicados. Correspondentes do Rio de Janeiro, de São Paulo e de Brasília. Categorias Melhor Filme (ficção), Melhor Documentário, Melhor Diretor, Melhor Roteiro, Melhor Ator, Melhor Atriz, Melhor Fotografia e Melhor Filme Júri Popular. Caso se deseje escolher, entre os 50 correspondentes mais antigos, 3 para constituírem uma comissão consultiva especial, haverá menos de 20 mil maneiras possíveis para se formar essa comissão. Certo Errado

51 PROBABILIDADE OPERAÇÃO CONJUNTOS

52

53 Uma urna contém 10 bolas, sendo 4 brancas, 3 azuis, 2 amarelas e 1 vermelha. Baseando-se nesses dados, responda as questões que seguem.

54 Retirando-se apenas uma bola da urna, qual a probabilidade de que ela seja branca?

55 Retirando-se apenas uma bola da urna, qual a probabilidade de que ela seja vermelha?

56

57 Retirando-se apenas uma bola da urna, qual a probabilidade de que ela seja branca ou azul?

58 Retirando-se duas bolas, com reposição, qual a probabilidade que elas sejam branca e azul, nesta ordem?

59 Retirando-se duas bolas, sem reposição, qual a probabilidade que elas sejam branca e azul, nesta ordem?

60

61 Retirando-se duas bolas, com reposição, qual a probabilidade que elas sejam branca e azul, independentemente da ordem?

62 Retirando-se apenas uma bola da urna, qual a probabilidade de se retirar uma bola azul, sabendo que a bola retirada não é branca?

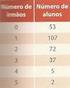
63 Suponha que certa Agência do Banco do Brasil tenha 25 funcionários, cujas idades, em anos, são as seguintes: A probabilidade de que, ao escolher-se aleatoriamente um desses funcionários, a sua idade seja superior a 48 anos é de a) 28%. b) 27,4%. c) 27%. d) 25,8%. e) 24%.

64 Tendo como referência a figura acima, que mostra os valores das taxas de juros anuais, em dois anos consecutivos, denominados anterior e atual, em 10 países, julgue os itens seguintes.

65 Se um dos dez países considerados for selecionado ao acaso, então a probabilidade de que a taxa de juros atual desse país encontre-se entre 5,5% e 10% será igual a 0,2. Certo Errado

66 Na Agência dos Correios de uma certa cidade trabalham 20 funcionários. Sabe-se que 12 desses funcionários jogam futebol, 8 jogam vôlei e 5 jogam futebol e vôlei. Escolhendo ao acaso um dos funcionários, qual a probabilidade dele não praticar nenhum desses esportes? a) 12% b) 5% c) 25% d) 50% e) 75%

67 José sabe que a probabilidade de encontrar Ana no shopping é de 68%, a probabilidade de encontrar Paulo no shopping é de 54%. Mas José também sabe que a probabilidade de encontrar ambos no shopping é de 52%. Então qual a probabilidade de José não encontrar nem Ana nem Paulo no shopping?

68 Ana é de 68%, Paulo é de 54%. Ambos é de 52%. Então qual a probabilidade de José não encontrar nem Ana nem Paulo no shopping?

69 Saul e Fred poderão ser contratados por uma empresa. A probabilidade de Fred não ser contratado é igual a 0,75; a probabilidade de Saul ser contratado é igual a 0,5; e a probabilidade de os dois serem contratados é igual a 0,2. Nesse caso, é correto afirmar que a probabilidade de

70 a) pelo menos um dos dois ser contratado é igual a 0,75. b) Fred ser contratado é igual a 0,5. c) Saul ser contratado e Fred não ser contratado é igual a 0,3. d) Fred ser contratado e Saul não ser contratado é igual a 0,1. e) Saul não ser contratado é igual a 0,25.

71 Os bilhetes de uma rifa são numerados de 1 a 100. A probabilidade do bilhete sorteado ser um número maior que 40 ou número par é: A) 60% B) 70% C) 80% D) 90% E) 50%

72

73 OBSERVANDO OS TERMOS Quando constarem termos como SABENDO QUE, CONSIDERANDO QUE, TENDO EM VISTA QUE, etc... pode ser que o total esteja sendo reduzido.

74 Em uma sala com 50 alunos há 7 alunos com camiseta preta e 10 com camiseta azul escura. Os outros estão vestindo camisetas com cores claras. As cores claras são amarelo (12 alunos), branco ( 8 alunos) e azul claro ( 13 alunos). CORES CLARAS CORES ESCURAS Amarelo: 12 Preto: 7 Branco:8 Azul escuro: 10 Azul Claro: 13

75 CORES CLARAS CORES ESCURAS Amarelo: 12 Preto: 7 Branco:8 Azul escuro: 10 Azul Claro: 13 Sendo escolhido aleatoriamente um aluno dessa turma, qual a probabilidade do aluno escolhido estar vestindo camisa amarela, sabendo que o escolhido possui camiseta de cor clara?

76 Considerando como valor aproximado para e -5, julgue os próximos itens, relativos à movimentação de clientes acima descrita.

77 A probabilidade de que, em determinado minuto, cheguem dois ou mais clientes é inferior a 95%.

78 A probabilidade de que, em determinado minuto, chegue exatamente um cliente é inferior a 4%.

79 Em um setor de uma fábrica trabalham 10 pessoas que serão divididas em 2 grupos de 5 pessoas cada para realizar determinadas tarefas. João e Pedro são duas dessas pessoas. Nesse caso, a probabilidade de João e Pedro ficarem no mesmo grupo é: a) inferior a 0,36 b) superior a 0,36 e inferior a 0,40 c) superior a 0,40 e inferior a 0,42 d) superior a 0,42 e inferior a 0,46 e) superior a 0,46

80

81

82 a) inferior a 0,36 b) superior a 0,36 e inferior a 0,40 c) superior a 0,40 e inferior a 0,42 d) superior a 0,42 e inferior a 0,46 e) superior a 0,46

83 Considere-se que, das 82 varas do trabalho relacionadas no sítio do TRT da 9.ª Região, 20 ficam em Curitiba, 6 em Londrina e 2 em Jacarezinho. Considere-se, ainda, que, para o presente concurso, haja vagas em todas as varas, e um candidato aprovado tenha igual chance de ser alocado em qualquer uma delas. Nessas condições, a probabilidade de um candidato aprovado no concurso ser alocado em uma das varas de Curitiba, ou de Londrina, ou de Jacarezinho é superior a 1/3

84 Total: 82 varas Curitiba: 20 Londrina: 6 Jacarezinho: 2 A probabilidade de um candidato aprovado no concurso ser alocado em uma das varas de Curitiba, ou de Londrina, ou de Jacarezinho é superior a 1/3

85 De 100 processos guardados em um armário, verificou-se que 10 correspondiam a processos com sentenças anuladas, 20 estavam solucionados sem mérito e 30 estavam pendentes, aguardando a decisão de juiz, mas dentro do prazo vigente. Nessa situação, a probabilidade de se retirar desse armário um processo que esteja com sentença anulada, ou que seja um processo solucionado sem mérito, ou que seja um processo pendente, aguardando a decisão de juiz, mas dentro do prazo vigente, é igual a 3/5

86 Total: 100 processos Sentenças anuladas: 10 Solução sem mérito: 20 Pendentes: 30 A probabilidade de se retirar um processo que esteja com sentença anulada, ou que seja um processo solucionado sem mérito, ou que seja um processo pendente é igual a 3/5

87 Um juiz deve analisar 12 processos de reclamações trabalhistas, sendo 4 de médicos, 5 de professores e 3 de bancários. Considere que, inicialmente, o juiz selecione aleatoriamente um grupo de 3 processos para serem analisados. Com base nessas informações, a probabilidade de que, nesse grupo, todos os processos sejam de bancários é inferior a 0,005.

88 Em 2005, a ANCINE coordenou a mostra de filmes brasileiros no Ano do Brasil na França. No 17.º Encontro de Cinematografia da América Latina, que ocorreu entre 11 e 20 de março de 2005, em Toulouse, foi programada a exibição de um lote de 16 filmes de longa metragem brasileiros. Considerando essas informações, julgue os itens que se seguem.

89 Suponha que as cópias de 4 desses 16 filmes estivessem com defeito. Nesse caso, a probabilidade de que 3 outras cópias, retiradas aleatória e sucessivamente desse lote de filmes, não estivessem com defeito é superior a 0,36. CERTO

90 Um investigador, ao chegar ao local de um crime, tem de executar 10 tarefas, entre as quais se incluem: "procurar a arma do crime", "buscar por impressões digitais" e "verificar se houve arrombamento de portas e janelas". O investigador tem autonomia para decidir em que ordem as 10 tarefas serão executadas. Com base nessa situação, julgue os itens seguintes.

91 * A probabilidade de a tarefa "procurar a arma do crime" ser executada em terceiro lugar é inferior a 3!/10!

92 * A probabilidade de a tarefa "verificar se houve arrombamento de portas e janelas" ser executada imediatamente após a tarefa "buscar por impressões digitais" é inferior a 1/12

93 Considere que a tabela a seguir mostra o número de vítimas fatais em acidentes de trânsito ocorridos em quatro estados brasileiros. Estado em que Total de vítimas fatais ocorreu o acidente Sexo masculino Sexo feminino Maranhão Paraíba Paraná Santa Catarina

94 A fim de fazer um estudo de causas, a PRF elaborou relatórios, um para cada uma das vítimas fatais mencionadas na tabela acima, contendo o perfil da vítima e as condições em que ocorreu o acidente. Com base nessas informações, julgue os itens que se seguem, acerca de um relatório escolhido aleatoriamente entre os citados acima.

95 * A probabilidade de que esse relatório corresponda a uma vítima de um acidente ocorrido no estado do Maranhão é superior a 0,2. Estado Total de vítimas fatais masculino feminino Maranhão Total: relatórios

96 * A chance de que esse relatório corresponda a uma vítima do sexo feminino é superior a 23% Estado vítimas masc fem Maranhão Paraíba Paraná Sta Catarina

97 * Considerando que o relatório escolhido corresponda a uma vítima do sexo masculino, a probabilidade de que o acidente nele mencionado tenha ocorrido no estado do Paraná é superior a 0,5. Estado vítimas masc fem Maranhão Paraíba Paraná Sta Catarina Total homens= 1098

98 * Considerando que o relatório escolhido corresponda a uma vítima de um acidente que não ocorreu no Paraná, a probabilidade de que ela seja do sexo masculino e de que o acidente tenha ocorrido no estado do Maranhão é superior a 0,27. Estado vítimas masc fem Maranhão Paraíba Paraná Sta Catarina Não Paraná: = 731

99 * A chance de que o relatório escolhido corresponda a uma vítima do sexo feminino ou a um acidente ocorrido em um dos estados da região Sul do Brasil listados na tabela é inferior a 70%. Estado vítimas masc fem Maranhão Paraíba Paraná Sta Catarina

100 Três pessoas, X, Y e Z, terminaram empatadas em uma competição de um programa de auditório. A produção do programa decide, então, premiar os três ou nenhum deles, dependendo exclusivamente da sorte. Para cada pessoa, é oferecida uma urna com bolinhas idênticas, numeradas de 1 a 5. A pessoa X tira de sua urna uma bolinha com número x, a pessoa Y tira de sua urna uma bolinha com o número y, e a pessoa Z tira de sua urna uma bolinha com o número z. As três pessoas ganham o prêmio se xy + z for par, e todos perdem caso contrário.

101

102 Para cada pessoa, é oferecida uma urna com bolinhas idênticas, numeradas de 1 a 5. A pessoa X tira bolinha com número x, a pessoa Y tira bolinha com o número y, e a pessoa Z tira bolinha com o número z. As três pessoas ganham o prêmio se xy + z for par, e todos perdem caso contrário. Sabendo que x = 3, qual a probabilidade de eles ganharem o prêmio?

103 a) 16% b) 36% c) 48% d) 50% e) 52%

104 Para disputar a final de um torneio internacional de natação, classificaram-se 8 atletas: 3 norteamericanos, 1 australiano, 1 japonês, 1 francês e 2 brasileiros. Considerando que todos os atletas classificados são ótimos e têm iguais condições de receber uma medalha (de ouro, prata ou bronze), a probabilidade de que pelo menos um brasileiro esteja entre os três primeiros colocados é igual a: a) 5/14 b) 3/7 c) 4/7 d) 9/14 e) 5/7

105 PROBABILIDADE EM DADOS DE JOGO

106

107

108 Um dado não viciado, com a forma de um cubo e com as faces numeradas de 1 até 6, foi lançado por 3 vezes. Sabendo-se que a soma dos resultados obtidos foi igual a 5, qual é a probabilidade de o resultado do segundo lançamento do dado ter sido igual a 2? a) 1 18 b) 1 6 c) 1 5 d) 1 3 e) 1 2

109

110 Ao se jogar um determinado dado viciado, a probabilidade de sair o número 6 é de 20%, enquanto as probabilidades de sair qualquer outro número são iguais entre si. Ao se jogar este dado duas vezes, qual o valor mais próximo da probabilidade de um número par sair duas vezes?

111 Ao se jogar este dado duas vezes, qual o valor mais próximo da probabilidade de um número par sair duas vezes? a) 20% b) 27% c) 25% d) 23% e) 50%

112 Ao se jogar um dado honesto três vezes, qual o valor mais próximo da probabilidade de o número 1 sair exatamente uma vez? a) 35% b) 17% c) 7% d) 42% e) 58%

113 PROBABILIDADE EM MOEDAS

114 Uma moeda não tendenciosa é lançada até que sejam obtidos dois resultados consecutivos iguais. Qual a probabilidade de a moeda ser lançada exatamente três vezes? a) 1/8 b) 1/4 c) 1/3 d) 1/2 e) 3/4

115 Um jogador aposta que, em três lançamentos de uma moeda honesta, obterá duas caras e uma coroa. A probabilidade de que ele ganhe a aposta é: A) 1/3 B) 2/3 C) 1/8 D) 3/8 E) 5/8

116 Uma moeda é viciada, de forma que as caras são três vezes mais prováveis de aparecer do que as coroas. Determine a probabilidade de num lançamento sair coroa. A) 25% B) 50% C) 35% D) 70% E) 20%

117 PROBABILIDADE EM CARTAS

118 Paulo e Raul pegaram 10 cartas de baralho para brincar: A, 2, 3, 4, 5, 8, 9, 10, J e Q, todas de copas. Paulo embaralhou as 10 cartas, colocou-as aleatoriamente sobre a mesa, todas voltadas para baixo, e pediu a Raul que escolhesse duas. Considerando-se que todas as cartas têm a mesma chance de serem escolhidas, qual a probabilidade de que, nas duas cartas escolhidas por Raul, estejam escrita as letras A, J ou Q?

119 * 10 cartas de copas : A, 2, 3, 4, 5, 8, 9, 10, J e Q, * Qual a probabilidade de que, nas duas cartas escolhidas por Raul, estejam escrita as letras A, J ou Q? a)1/10 b)3/10 c)1/15 d)2/15 e)1/45

120 Uma carta é retirada de um baralho comum, de 52 cartas, e, sem saber qual é a carta, é misturada com as cartas de um outro baralho idêntico ao primeiro. Retirando, em seguida, uma carta do segundo baralho, a probabilidade de se obter uma dama é: A) 3/51 B) 5/53 C) 5/676 D) 1/13 E) 5/689

121 As cartas de um baralho são amontoadas aleatoriamente. Qual é a probabilidade de a carta de cima ser de copas e a de baixo também? O baralho é formado por 52 cartas de 4 naipes diferentes (13 de cada naipe). A) 1/17 B) 1/25 C) 1/27 D) 1/36 E) 9/45

122