Introdução à Física Quântica
|
|
|
- Marcelo Zagalo Olivares
- 9 Há anos
- Visualizações:
Transcrição
1 Itrodução à Física Quâtica A icapacidade da Física clássica em eplicar certos feómeos levou ao desevolvimeto de duas teorias que revolucioaram a Física o iício do século XX: A Teoria da Relatividade de Eistei A Física Quâtica Em particular, foi a impossibilidade de se coseguir eplicar classicamete as seguites eperiêcias radiação do corpo egro efeito foto-eléctrico que levou ao desevolvimeto da Física Quâtica.
2 Radiação do corpo egro Qualquer objecto a uma temperatura superior ao zero absoluto (T > 0K) emite radiação. Essa radiação é produzida pelas suas cargas eléctricas em movimeto acelerado Quado a temperatura é elevada (~ 500 ºC), o objecto emite radiação a zoa do vermelho e, à medida que a temperatura aumeta, a radiação vai mudado para comprimetos de oda meores (maiores frequêcias) O espectro de eergia radiada por uidade de tempo é cotíuo e depede da temperatura T e do comprimeto de oda λ da radiação emitida 2
3 Radiação do corpo egro (cot.) Itesidade da radiação em fução do comprimeto de oda, para 4 temperaturas. A quatidade de radiação emitida (a área defiida por cada curva) aumeta quado a temperatura aumeta 3
4 Radiação do corpo egro (cot.) Como a radiação também depede das propriedades da superfície do objecto (emissividade), a melhor maeira de simular um corpo egro é usar um objecto cuja superfície ão ifluecie a radiação, ou seja, um sistema que se aproime do corpo egro ideal Uma boa aproimação é uma cavidade com uma abertura muito pequea: a radiação emitida vai depeder apeas da temperatura o iterior da cavidade Aproimação do corpo egro ideal: a luz (radiação) que etra pela abertura é reflectida pelas paredes iteriores. Em cada refleão, parte dessa luz é também absorvida. Ao fim de algumas refleões, toda a luz icidete foi absorvida. Etão, toda a radiação que for emitida e sair pela abertura é apeas fução da temperatura o iterior da cavidade. 4
5 Radiação do corpo egro (cot.) Depedêcia de λ MAX com a temperatura: Lei de Wie λ MAX B T Eergia radiada por uidade de tempo pela superfície de um corpo: Lei de Stefa W rad e. σ. A. T 4 W(λ) B m.k σ Wm -2 K e e 0 e Emissividade Corpo egro λ 5
6 Justificação clássica para esta radiação: Radiação do corpo egro (cot.) -os átomos e moléculas à superfície do objecto vibram mais quado a temperatura aumeta; esta vibração implica a emissão de radiação. W ( ) λ A descrição clássica coduz à lei de Rayleigh-Jeas: W 2 ( ν ) dν ~ ν dν 2 ( ν ) dν ~ ktν dν λ ( λ) dλ ~ ( kt ) dλ W 4 Nº de osciladores com frequêcias etre ν e ν+dν Espectro de potêcia tedo em cota que E(oscilador)kT Comparação dos resultados eperimetais com a curva prevista pelo modelo clássico de Rayleigh-Jeas para a distribuição da radiação emitida por um corpo egro 6
7 Radiação do corpo egro (cot.) Problema com a descrição clássica : para os λ grades, a teoria clássica está de acordo com os resultados eperimetais mas quado λ 0, a itesidade da radiação ( catástrofe do ultra-violeta ) 900, Ma Plack E E E 6 E 5 E 4 E 3 E 2 hν E E 0 Descrição Clássica Espectro cotíuo Depede da amplitude Descrição Quâtica Espectro discreto Depede da frequêcia 7
8 Radiação do corpo egro (cot.) Cosiderações acerca das moléculas à superfície do corpo egro (Plack): As moléculas só podem radiar (emitir radiação) em íveis discretos de eergia E, com E h ν sedo um iteiro positivo (úmero quâtico) e ν a frequêcia de vibração das moléculas As moléculas emitem (e absorvem) eergia em pacotes discretos chamados fotões, cuja eergia é igual a h ν Represetação pictórica dos fotões ( pacotes de luz). Cada fotão possui uma eergia discreta dada por h ν. 8
9 Níveis discretos de eergia As moléculas têm eergias quatizadas. Uma molécula o estado 3 terá uma eergia E 3 3 h ν. Se essa molécula emitir um fotão, a molécula passa para o estado 2, que tem uma eergia E 2 2 h ν a eergia de um fotão correspodete a difereças eergéticas etre estados quâticos adjacetes é igual a E h ν. A molécula emite (ou absorve) eergia apeas quado muda de estado quâtico. Se permaecer um dado estado, ão eiste trasferêcia de eergia. Níveis de eergia possíveis para uma molécula (eemplo). As trasições permitidas com estão idicadas. 9
10 Radiação do corpo egro cálculo da eergia média de oscilador E E 6 E 5 E 4 P ε hν C ep C ep KT KT hν E 3 E 2 E E 0 Descrição Quâtica Espectro discreto Depede da frequêcia 0 P C 0 ep C ep 0 hν Z KT hν KT P ep Z ε KT E ε P hν.ep Z hν KT 0
11 KT h h Z KT h h E ν ν ν ν ep ;.ep ( ) 2 0 d d d d d d h h E ν ν ( ) h h E ν ν ep kt h h E ν ν Radiação do corpo egro cálculo da eergia média de oscilador
12 Radiação do corpo egro espectro de potêcia E hν hν ep kt Limite clássico hν << kt E kt 2 ( ν ) dν ~ ν dν Nº de osciladores com frequêcias etre ν e ν+dν u 8π hν c hν ep kt ( ν ) dν 2 ν dν ( ) 3 8 λ d u λ dλ π 4 Desidade de eergia hc hc ep λkt λ λ 2
13 Espectro de potêcia emitida por uidade de área, cosiderado a lei de Plack (900) (em perfeito acordo com os W resultados eperimetais). w E hν hν ep kt hc λ hc ep λkt ( λ) dλ 2πc 4 dλ λ ( ) λ Espectro de potêcia emitida por uidade de área cosiderado <E>KT modelo clássico de Rayleigh-Jeas (físicamete impossível!) 3
14 Radiação do corpo egro Lei de Wie má [ w( λ) ] w Solução (umérica) hc y 4,96 λ k T MAX ( λ) dλ 2πc 4 hc mí ep λkt hc λ hc ep λkt 5. λ Lei de Wie λ MAX B T B dν λ y [( ) ] y 5 e y y hc 4,96. k hc λkt m.k 4
15 Radiação do corpo egro Lei de Stefa w 2π hν 2 c hν ep kt 2 ( ν ) dν ν dν w ( T ) 4 2π. k 3 2 h c 0 y ep 3 ( y) dy. T 4 hν y ; dν kt kt h dy Lei de Stefa W rad σ. A. T 4 σ Wm -2 K -4 Eergia radiada por uidade de tempo pela superfície de um corpo egro de área A 5
16 A temperatura da pele humaa é aproimadamete igual a 35 ºC. Qual é o comprimeto de oda para o qual se verifica o máimo da radiação emitida? A partir da lei de Wie : λ má. T 0, m K λ má 0, m K / 308 K 9, m 960 m O máimo da radiação é emitida para um comprimeto de oda a região dos ifra-vermelhos: Espectro visível 6
17 Admitido que o filameto de tugstéio de uma lâmpada de icadescêcia se comporta como um corpo egro, determie o comprimeto de oda para o qual se verifica o máimo de itesidade da radiação emitida se a temperatura do filameto for igual a 2900 K A partir da lei de Wie : λ má. T 0, m K λ má 0, m K / 2900 K. 0-6 m 000 m Embora a lâmpada de icadescêcia emita luz braca (frequêcias a bada visível do espectro), o máimo de itesidade emitida acotece para a região dos ifra-vermelhos a maior parte da radiação é emitida sob a forma de calor Espectro visível 7
18 Efeito foto-eléctrico No fim do séc. XIX, algumas eperiêcias (Heirich Hertz, 887) demostraram que quado se fazia icidir luz a superfície de algus metais, estes emitiam electrões (efeito foto-eléctrico ) Luz Quado ão icide luz a célula, ão se regista emissão de electrões a partir da superfície E e, portato, a idicação o amperímetro é A 0 Quado luz moocromática com um comprimeto de oda adequado icide a placa E, verifica-se emissão de electrões que vão icidir a placa C. A correte (fotoelectróica) é medida o amperímetro + - 8
19 Efeito foto-eléctrico (cot.) Os foto-electrões saem da placa E com uma certa quatidade de eergia. Se a tesão aplicada V aumetar (ote-se que a polarização é iversa), etão quado V for igual à eergia dos fotoelectrões, a correte (foto)eléctrica será igual a zero: os foto-electrões ão terão eergia (ciética) suficiete para atigir a placa C Luz A tesão aplicada V (multiplicada pela carga do electrão) é igual à eergia com que os electrões deiam a superfície E. Eperimetalmete, é possível verificar que o potecial de paragem V 0 (que multiplicado pela carga eléctrica é igual à eergia dos electrões emitidos) é idepedete da itesidade da radiação icidete. + - Dispositivo para observação do efeito foto-eléctrico 9
20 Efeito foto-eléctrico - Eperiêcia vs. Teoria clássica Luz Eistêcia de Correte eléctrica Eperiêcia Teoria clássica Depede da itesidade da luz? NÃO SIM Depede da frequêcia da luz? SIM NÃO
21 Efeito foto-eléctrico Iterpretação quâtica (Eistei 905). A luz é costituída por fotões de Eergia: Ehν 2. A itesidade lumiosa é determiada pelo úmero de fotões W 0 Eergia míima para libertar os electrões Frequêcia míima para libertar os electrões dada por hν 0 W 0 Eergia ciética de um electrão libertado por um fotão de frequêcia ν > ν 0 declive h E C hν - W 0 h.(ν ν 0 ) Eperimetalmete, a E cimá varia liearmete com a frequêcia da luz icidete 2
22 Efeito foto-eléctrico (cot.) Diferetes metais w 0 Diferetes metais diferetes limiares (fução de trabalho) 22
23 Uma superfície de sódio é ilumiada com radiação com um comprimeto de oda de 300 m. A fução de trabalho para o sódio é de 2,64 ev. Calcule: a) a eergia ciética dos foto-electrões emitidos b) o comprimeto de oda crítico ( λ c ) para o sódio a) A eergia dos fotões icidetes é igual a E hν hc/ λ E (6, Js) (3,0. 08 m/s) / m 6, J 6, J /, J/eV 4,4 ev Usado Emá h ν - ϕ temos Emá 4,4 2,46,68 ev 23
24 b) O comprimeto de oda crítico pode ser calculado a partir de λ c hc/ ϕ Como ϕ 2,46 ev (2,46eV) (, J/eV) 3, J vem λ c h c/ ϕ (6, Js) (3,0.0 8 m/s) / 3, J 5, m 505 m Este comprimeto de oda correspode a uma radiação a região verde do espectro visível: Espectro visível 24
Introdução à Física Quântica
 17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 1 Introdução
17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 1 Introdução
FÍSICA MODERNA I AULA 05
 Uiversiae e São Paulo Istituto e Física FÍSICA MODERNA I AULA 05 Profa. Márcia e Almeia Rizzutto Pelletro sala 220 [email protected] 1o. Semestre e 2015 Moitor: Gabriel M. e Souza Satos Págia o curso:
Uiversiae e São Paulo Istituto e Física FÍSICA MODERNA I AULA 05 Profa. Márcia e Almeia Rizzutto Pelletro sala 220 [email protected] 1o. Semestre e 2015 Moitor: Gabriel M. e Souza Satos Págia o curso:
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
INTRODUÇÃO À ASTROFÍSICA
 Introdução à Astrofísica Lição 9 O Espectro da Luz INTRODUÇÃO À ASTROFÍSICA LIÇÃO 10 O ESPECTRO CONTÍNUO DA LUZ A medição do brilho das estrelas está diretamente ligada à medida de distância. A medida
Introdução à Astrofísica Lição 9 O Espectro da Luz INTRODUÇÃO À ASTROFÍSICA LIÇÃO 10 O ESPECTRO CONTÍNUO DA LUZ A medição do brilho das estrelas está diretamente ligada à medida de distância. A medida
Química 5 aula 1. aula 2 COMENTÁRIOS ATIVIDADES PARA SALA COMENTÁRIOS ATIVIDADES PROPOSTAS. 7. ( F ) Raios x são prejudiciais aos pacientes.
 Química 5 aula 1 1. A alterativa icorreta ecotra-se em a, pois para a ideia de átomo idivisível, o que é por todo errado.. Atualmete, sabe-se que átomos do mesmo elemeto químico podem apresetar diferetes
Química 5 aula 1 1. A alterativa icorreta ecotra-se em a, pois para a ideia de átomo idivisível, o que é por todo errado.. Atualmete, sabe-se que átomos do mesmo elemeto químico podem apresetar diferetes
Prof. Dr. Lucas Barboza Sarno da Silva
 Prof. Dr. Lucas Barboza Sarno da Silva A radiação do corpo negro e as hipóteses de Planck Um corpo, em qualquer temperatura emite radiação, algumas vezes denominada radiação térmica. O estudo minucioso
Prof. Dr. Lucas Barboza Sarno da Silva A radiação do corpo negro e as hipóteses de Planck Um corpo, em qualquer temperatura emite radiação, algumas vezes denominada radiação térmica. O estudo minucioso
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
Radiação térmica e a constante de Planck
 Material complementar de física 4 Professores: Márcia e Fabris Radiação térmica e a constante de Planck Em 14 de dezembro de 19, Max Planck apresentou a Sociedade Alemã de Física o seu artigo sobre a eoria
Material complementar de física 4 Professores: Márcia e Fabris Radiação térmica e a constante de Planck Em 14 de dezembro de 19, Max Planck apresentou a Sociedade Alemã de Física o seu artigo sobre a eoria
CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA
 Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Itrodução CINÉTICA QUÍMICA FATORES DE INFLUÊNCIA - TEORIA A Ciética Química estuda a velocidade com a qual as reações acotecem e os fatores que são capazes de realizar ifluêcia sobre ela. A medida mais
Virgílio A. F. Almeida DCC-UFMG 1/2005
 Virgílio A. F. Almeida DCC-UFMG 1/005 !" # Comparado quatitativamete sistemas eperimetais: Algoritmos, protótipos, modelos, etc Sigificado de uma amostra Itervalos de cofiaça Tomado decisões e comparado
Virgílio A. F. Almeida DCC-UFMG 1/005 !" # Comparado quatitativamete sistemas eperimetais: Algoritmos, protótipos, modelos, etc Sigificado de uma amostra Itervalos de cofiaça Tomado decisões e comparado
INTRODUÇÃO À ASTROFÍSICA LIÇÃO 9 O PROBLEMA DO CORPO NEGRO
 Introdução à Astrofísica INTRODUÇÃO À ASTROFÍSICA LIÇÃO 9 O PROBLEMA DO CORPO NEGRO Lição 8 O Problema do Corpo Negro A maior parte de toda a física do século XIX estava bem descrita através da mecânica
Introdução à Astrofísica INTRODUÇÃO À ASTROFÍSICA LIÇÃO 9 O PROBLEMA DO CORPO NEGRO Lição 8 O Problema do Corpo Negro A maior parte de toda a física do século XIX estava bem descrita através da mecânica
) E X. ) = 0 2 ( 1 p ) p = p. ) E 2 ( X ) = p p 2 = p ( 1 p ) ( ) = i 1 n. ( ) 2 n E( X) = ( ) = 1 p ( ) = p V ( X ) = E ( X 2 E X
 3.5 A distribuição uiforme discreta Defiição: X tem distribuição uiforme discreta se cada um dos valores possíveis,,,, tiver fução de probabilidade P( X = i ) = e represeta-se por, i =,, 0, c.c. X ~ Uif
3.5 A distribuição uiforme discreta Defiição: X tem distribuição uiforme discreta se cada um dos valores possíveis,,,, tiver fução de probabilidade P( X = i ) = e represeta-se por, i =,, 0, c.c. X ~ Uif
Novo Espaço Matemática A 12.º ano Proposta de Teste [março ]
![Novo Espaço Matemática A 12.º ano Proposta de Teste [março ] Novo Espaço Matemática A 12.º ano Proposta de Teste [março ]](/thumbs/100/145898345.jpg) Proposta de Teste [março - 08] Nome: Ao / Turma: N.º: Data: / / Não é permitido o uso de corretor. Deves riscar aquilo que pretedes que ão seja classificado. A prova iclui um formulário. As cotações dos
Proposta de Teste [março - 08] Nome: Ao / Turma: N.º: Data: / / Não é permitido o uso de corretor. Deves riscar aquilo que pretedes que ão seja classificado. A prova iclui um formulário. As cotações dos
A = Amplitude (altura máxima da onda) c = velocidade da luz = 2,998 x 10 8 m.s -1 3,00 x 10 8 m.s -1. 10 14 Hz. Verde: λ = = Amarela: λ =
 RADIAÇÃO ELETROMAGNÉ QUÍMICA BÁSICAB ESTRUTURA ATÔMICA II PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DAQBI Prof. Luiz Alberto RADIAÇÃO ELETROMAGNÉ RADIAÇÃO ELETROMAGNÉ λ comprimeto de oda Uidade: metro
RADIAÇÃO ELETROMAGNÉ QUÍMICA BÁSICAB ESTRUTURA ATÔMICA II PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DAQBI Prof. Luiz Alberto RADIAÇÃO ELETROMAGNÉ RADIAÇÃO ELETROMAGNÉ λ comprimeto de oda Uidade: metro
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
EMISSÃO e ABSORÇÃO de radiação
 EMISSÃO e ABSORÇÃO de radiação a EMISSÃO ocorre quando um elétron de um átomo salta de uma órbita superior para uma inferior (fundamentalização): um fóton é emitido (produzido). e - e - + n 2, E 2 n 1,
EMISSÃO e ABSORÇÃO de radiação a EMISSÃO ocorre quando um elétron de um átomo salta de uma órbita superior para uma inferior (fundamentalização): um fóton é emitido (produzido). e - e - + n 2, E 2 n 1,
O Átomo de Hidrogênio
 Física IV Poli geharia létrica: 11ª Aula (3/08/014) Pro. Alvaro Vaucci Na última aula vimos: h eito Compto: ' 0 (1 cos ) ( Lei decompto) mc e Ou seja, um óto (comportameto corpuscular), além de possuir
Física IV Poli geharia létrica: 11ª Aula (3/08/014) Pro. Alvaro Vaucci Na última aula vimos: h eito Compto: ' 0 (1 cos ) ( Lei decompto) mc e Ou seja, um óto (comportameto corpuscular), além de possuir
Prova-Modelo de Matemática
 Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS.
 TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
UNIDADES, ERROS E GRÁFICOS
 UNIDADES ERROS E GRÁFICOS. Gradeas Físicas e Uidades SI: Sstème Iteratioal d Uités Sèvres Fraça http://www.bipm.r http://phsics.ist.gov/cuu As gradeas e uidades de base do SI Gradea Uidade Nome Símbolo
UNIDADES ERROS E GRÁFICOS. Gradeas Físicas e Uidades SI: Sstème Iteratioal d Uités Sèvres Fraça http://www.bipm.r http://phsics.ist.gov/cuu As gradeas e uidades de base do SI Gradea Uidade Nome Símbolo
Propriedades das Ondas
 Propriedades das Odas Reflexão, Refração da Luz e Difração da Luz Reflexão, Absorção e Trasmissão de uma oda E icidete = E reflectida + E absorvida + E trasmitida Reflexão Regular e Difusa da Luz Quado
Propriedades das Odas Reflexão, Refração da Luz e Difração da Luz Reflexão, Absorção e Trasmissão de uma oda E icidete = E reflectida + E absorvida + E trasmitida Reflexão Regular e Difusa da Luz Quado
ESCOLA BÁSICA DE ALFORNELOS
 ESCOLA BÁSICA DE ALFORNELOS FICHA DE TRABALHO DE MATEMÁTICA 9.º ANO VALORES APROXIMADOS DE NÚMEROS REAIS Dado um úmero xe um úmero positivo r, um úmero x como uma aproximação de x com erro iferior a r
ESCOLA BÁSICA DE ALFORNELOS FICHA DE TRABALHO DE MATEMÁTICA 9.º ANO VALORES APROXIMADOS DE NÚMEROS REAIS Dado um úmero xe um úmero positivo r, um úmero x como uma aproximação de x com erro iferior a r
4Parte OBJETIVO GERAL. Parte I Preparação da atividade laboratorial
 Relatórios das atividades laboratoriais AL 3.1 ONDAS: ABSORÇÃO, REFLEXÃO, REFRAÇÃO E REFLEXÃO TOTAL OBJETIVO GERAL Ivestig os feómeos de absorção, reflexão, refração e reflexão total, determi o ídice de
Relatórios das atividades laboratoriais AL 3.1 ONDAS: ABSORÇÃO, REFLEXÃO, REFRAÇÃO E REFLEXÃO TOTAL OBJETIVO GERAL Ivestig os feómeos de absorção, reflexão, refração e reflexão total, determi o ídice de
étodos uméricos MÉTODO DOS MOMENTOS - MOM Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
b) Fabrico de peças cilíndricas Capítulo 5 - Distribuições conjuntas de probabilidades e complementos X - comprimento da peça Y - diâmetro da peça
 Capítulo 5 - Distribuições cojutas de probabilidades e complemetos 5.1 Duas variáveis aleatórias discretas. Distribuições cojutas, margiais e codicioais. Idepedêcia Em relação a uma mesma eperiêcia podem
Capítulo 5 - Distribuições cojutas de probabilidades e complemetos 5.1 Duas variáveis aleatórias discretas. Distribuições cojutas, margiais e codicioais. Idepedêcia Em relação a uma mesma eperiêcia podem
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
6. Radiação. , a. = é a constante de Planck. energia. , onde
 39 6. Radiação Radiação diferetemete da codução e covecção é o mecaismo de troca de eergia etre sistemas à distâcia, sem fazer cotato direto. Uma trasferêcia líquida de calor por radiação pode ocorrer
39 6. Radiação Radiação diferetemete da codução e covecção é o mecaismo de troca de eergia etre sistemas à distâcia, sem fazer cotato direto. Uma trasferêcia líquida de calor por radiação pode ocorrer
Determinação da constante de Planck: o efeito fotoeléctrico
 Determinação da constante de Planck: o efeito fotoeléctrico Objectivos: - Verificação experimental do efeito fotoeléctrico - Determinação da energia cinética dos fotoelectrões em função da frequência da
Determinação da constante de Planck: o efeito fotoeléctrico Objectivos: - Verificação experimental do efeito fotoeléctrico - Determinação da energia cinética dos fotoelectrões em função da frequência da
O ESPECTRO ELETROMAGNÉTICO
 O ESPECTRO ELETROMAGNÉTICO ONDAS: Interferência construtiva e destrutiva Onda 1 Onda 2 Onda composta a b c d e A luz apresenta interferência: natureza ondulatória: O experimento de Young (~1800) Efeito
O ESPECTRO ELETROMAGNÉTICO ONDAS: Interferência construtiva e destrutiva Onda 1 Onda 2 Onda composta a b c d e A luz apresenta interferência: natureza ondulatória: O experimento de Young (~1800) Efeito
CORDAS E TUBOS SONOROS TEORIA
 CORDAS E TUBOS SONOROS TEORIA Já vimos a formação de odas estacioárias de maeira geral. Agora, vamos estudar este assuto de forma mais específica. Primeiramete, vamos os cocetrar em uma corda, que pode
CORDAS E TUBOS SONOROS TEORIA Já vimos a formação de odas estacioárias de maeira geral. Agora, vamos estudar este assuto de forma mais específica. Primeiramete, vamos os cocetrar em uma corda, que pode
EFEITO FOTOELÉCTRICO
 EFEITO FOTOELÉCTRICO 1. Resumo Neste trabalho pretende se efectuar a verificação experimental do efeito fotoeléctrico e, partindo daí, determinar o valor de uma das constantes fundamentais da natureza,
EFEITO FOTOELÉCTRICO 1. Resumo Neste trabalho pretende se efectuar a verificação experimental do efeito fotoeléctrico e, partindo daí, determinar o valor de uma das constantes fundamentais da natureza,
A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos
 Universidade de São Paulo Instituto de Física de São Carlos A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos Nome: Mirian Denise Stringasci Disciplina: Mecânica Quântica Aplicada
Universidade de São Paulo Instituto de Física de São Carlos A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos Nome: Mirian Denise Stringasci Disciplina: Mecânica Quântica Aplicada
Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3.
![Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3. Gabarito: Resposta da questão 1: [D] Observando a figura, temos que: Do meio 3 para o 2, o raio se aproxima da normal, logo: n2 n 3.](/thumbs/99/140792776.jpg) Gabarito: Resposta da questão : [D] Observado a figura, temos que: Do meio 3 para o, o raio se aproxima da ormal, logo: 3. Do meio para o, o raio sofre reflexão total, logo:. Aplicado a lei de Sell do
Gabarito: Resposta da questão : [D] Observado a figura, temos que: Do meio 3 para o, o raio se aproxima da ormal, logo: 3. Do meio para o, o raio sofre reflexão total, logo:. Aplicado a lei de Sell do
Mestrado Integrado em Engenharia Civil. Disciplina: TRANSPORTES. Sessão Prática 4: Amostragem
 Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
O teste de McNemar. A tabela 2x2. Depois - Antes
 Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ [email protected] O teste de McNemar O teste de McNemar para a sigificâcia de mudaças é particularmete aplicável aos experimetos do tipo "ates e depois"
Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ [email protected] O teste de McNemar O teste de McNemar para a sigificâcia de mudaças é particularmete aplicável aos experimetos do tipo "ates e depois"
2 - PRINCÍPIO DE FUNCIONAMENTO DO GERADOR DE CORRENTE CONTINUA
 2 - PRICÍPIO D FUCIOAMTO DO GRADOR D CORRT COTIUA 2.1 - A FORÇA LTROMOTRIZ IDUZIDA O pricípio de fucioameto do gerador de correte cotíua tem por base a Lei de Faraday que estabelece que, se o fluxo magético
2 - PRICÍPIO D FUCIOAMTO DO GRADOR D CORRT COTIUA 2.1 - A FORÇA LTROMOTRIZ IDUZIDA O pricípio de fucioameto do gerador de correte cotíua tem por base a Lei de Faraday que estabelece que, se o fluxo magético
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
1 Distribuições Amostrais
 1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
1 Distribuições Amostrais Ao retirarmos uma amostra aleatória de uma população e calcularmos a partir desta amostra qualquer quatidade, ecotramos a estatística, ou seja, chamaremos os valores calculados
CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA
 1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
Aula 21 Fótons e ondas de matéria I. Física Geral IV FIS503
 Aula 21 Fótons e ondas de matéria I Física Geral IV FIS503 1 Correção da aula passada: Energia relativística: uma nova interpretação m p = 1, 007276 u m 4 He = 4, 002603 u ΔE = (mhe 4m p )c 2 = 0, 026501
Aula 21 Fótons e ondas de matéria I Física Geral IV FIS503 1 Correção da aula passada: Energia relativística: uma nova interpretação m p = 1, 007276 u m 4 He = 4, 002603 u ΔE = (mhe 4m p )c 2 = 0, 026501
Ótica geométrica. Descrição dos fenómenos óticos que ocorrem em sistemas com componentes de dimensões superiores aos comprimentos de onda da radiação
 Ramos da Ótica Ótica Geométrica Ótica geométrica Descrição dos feómeos óticos que ocorrem em sistemas com compoetes de dimesões superiores aos comprimetos de oda da radiação Ótica Física Em sistemas com
Ramos da Ótica Ótica Geométrica Ótica geométrica Descrição dos feómeos óticos que ocorrem em sistemas com compoetes de dimesões superiores aos comprimetos de oda da radiação Ótica Física Em sistemas com
4.1 Optoelectrónica Aplicada Capítulo 4
 4.1 Optoelectróica Aplicada Capítulo 4 CAPÍTULO 4. EMISSORES DE LUZ Os emissores de luz fazem parte de uma família de dispositivos que geericamete se desigam por coversores electro-ópticos. Nestes dispositivos
4.1 Optoelectróica Aplicada Capítulo 4 CAPÍTULO 4. EMISSORES DE LUZ Os emissores de luz fazem parte de uma família de dispositivos que geericamete se desigam por coversores electro-ópticos. Nestes dispositivos
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 2 RADIAÇÃO TÉRMICA E CORPO NEGRO Primeira Edição junho de 2005 CAPÍTULO 2 RADIAÇÃO TÉRMICA E CORPO NEGRO ÍNDICE 2.1- Introdução 2.2- Corpo
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 2 RADIAÇÃO TÉRMICA E CORPO NEGRO Primeira Edição junho de 2005 CAPÍTULO 2 RADIAÇÃO TÉRMICA E CORPO NEGRO ÍNDICE 2.1- Introdução 2.2- Corpo
Tópicos: Análise e Processamento de BioSinais. Mestrado Integrado em Engenharia Biomédica. Faculdade de Ciências e Tecnologia. Universidade de Coimbra
 Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
Prova Escrita de MATEMÁTICA A - o Ao 08 - a Fase Proposta de resolução Cadero... Como P µ σ < X < µ + σ 0,94, logo como P X < µ σ P X > µ + σ, temos que: P X < µ σ 0,94 E assim, vem que: P X > µ σ P X
Termodinâmica e Estrutura da Matéria
 Termodinâmica e Estrutura da Matéria Laboratório 2 (Grupos A, B e C) Efeito fotoeléctrico OBJECTIVOS Estudar o efeito fotoeléctrico. Determinar a constante de Planck. 1. INTRODUÇÃO O efeito fotoeléctrico
Termodinâmica e Estrutura da Matéria Laboratório 2 (Grupos A, B e C) Efeito fotoeléctrico OBJECTIVOS Estudar o efeito fotoeléctrico. Determinar a constante de Planck. 1. INTRODUÇÃO O efeito fotoeléctrico
GABARITO AULA DE VÉSPERA USP/UNICAMP
 GABARITO AULA DE VÉSPERA USP/UNICAMP João Paulo 1 4 5 6 7 8 9 10 C B C C C 11 1 1 14 15 16 17 18 19 0 C C C E B E E D A 1 4 5 6 7 8 9 0 E A C D D D C A C 1 4 5 6 7 8 9 40 C E B A A B E B B D COMENTÁRIOS
GABARITO AULA DE VÉSPERA USP/UNICAMP João Paulo 1 4 5 6 7 8 9 10 C B C C C 11 1 1 14 15 16 17 18 19 0 C C C E B E E D A 1 4 5 6 7 8 9 0 E A C D D D C A C 1 4 5 6 7 8 9 40 C E B A A B E B B D COMENTÁRIOS
CPV O cursinho que mais aprova na fgv
 CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
Universidade São Judas Tadeu Faculdade de Tecnologia e Ciências Exatas Laboratório de Física e Química
 Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
2. Propriedades Corpusculares das Ondas
 2. Propriedades Corpusculares das Ondas Sumário Revisão sobre ondas eletromagnéticas Radiação térmica Hipótese dos quanta de Planck Efeito Fotoelétrico Geração de raios-x Absorção de raios-x Ondas eletromagnéticas
2. Propriedades Corpusculares das Ondas Sumário Revisão sobre ondas eletromagnéticas Radiação térmica Hipótese dos quanta de Planck Efeito Fotoelétrico Geração de raios-x Absorção de raios-x Ondas eletromagnéticas
A letra x representa números reais, portanto
 Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
GABARITO DO GE5 ONDAS ESTACIONÁRIAS, BATIMENTOS E EFEITO DOPPLER
 GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
Processamento Digital de Sinais Lista de Exercícios Suplementares 3-1 quad. 2012
 Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
Probabilidade II Aula 9
 Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Transporte Iônico e o Potencial de Membrana
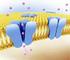 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
Les 201 Matemática Aplicada à Economia. Relações entre CMg e CMe. Aulas Relações entre CMg e CMe. dct. dcme. CMe = = = =
 Les 0 Matemática Aplicada à Ecoomia Aulas -4 Derivadas Aplicação em Ecoomia Derivadas de Ordem Superiores Derivadas Parciais Determiate Jacobiao 9 e 0/09/06 Aplicações da a. Derivada em Ecoomia Dada a
Les 0 Matemática Aplicada à Ecoomia Aulas -4 Derivadas Aplicação em Ecoomia Derivadas de Ordem Superiores Derivadas Parciais Determiate Jacobiao 9 e 0/09/06 Aplicações da a. Derivada em Ecoomia Dada a
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
