Momento Angular. 8.1 Álgebra do Momento Angular
|
|
|
- Mario Aldeia Brandt
- 6 Há anos
- Visualizações:
Transcrição
1 Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira parte deste capítulo. Por outro lado, também é muito instrutivo estudar o problema de autovalores para o momento angular orbital já que isto não só fornece maiores informações sobre a solução obtida pelo método de operadores, mas também prepara o terreno para o estudo de problemas tridimensionais. 8. Álgebra do Momento Angular O momento angular orbital é uma quantidade importante para a análise de problemas clássicos e quânticos que contém potenciais centrais, dado que ele é uma quantidade conservada. O momento angular orbital é definido por L x p, (8.) sendo que esta expressão não apresenta problema de ordenamento em Mecânica Quântica. As componentes do momento angular orbital são dadas por L x = yp z zp y, (8.2) L y = zp x xp z, (8.3) L z = xp y yp x. (8.4) 35
2 36 Capítulo 8. Momento Angular Daqui podemos obter as seguintes relações de comutação: L x, L y ] = i hl z, (8.5) L y, L z ] = i hl x, (8.6) L z, L x ] = i hl y, (8.7) as quais podem ser resumidas usando-se o tensor de Levi-Civita (ɛ kjn ), L k, L j ] = i hɛ kjn L n, (8.8) onde as componentes, 2 e 3 representam x, y e z respectivamente. Também é útil definir o quadrado do momento angular orbital L 2 L L = L 2 x + L2 y + L2 z. (8.9) Utilizando as relações (8.5) a (8.7) temos que L 2 comuta com todas as componentes do momento angular orbital, i.e. L 2, L i ] = 0. (8.0) Como veremos logo abaixo, é conveniente definir as seguintes combinações dos operadores L x e L y L + = L x + il y, (8.) L = L x il y, (8.2) as quais estão ligadas através de L + = L. Mais ainda, podemos expressar L 2 em termos dos operadores L ± utilizando as seguintes relações: L + L = L 2 L 2 z + hl z, (8.3) L L + = L 2 L 2 z hl z, (8.4) onde o útil termo destas equações origina-se do comutador de L x com L y. É também fácil mostrar, usando as relações de comutação (8.5) a (8.7), que L 2, L ± ] = 0, (8.5) L z, L ± ] = ± hl ±. (8.6)
3 8.2. Solução Algébrica Solução Algébrica Vamos agora determinar os autovalores do momento angular orbital utilizando apenas as relações obtidas na seção anterior, em analogia com a solução do oscilador harmônico apresentada no capítulo 6. Tendo em vista as relações de comutação (8.8) e (8.0), podemos encontrar autovetores simultâneos apenas de L 2 e uma componente de L a qual escolhemos ser L z. Em princípio podemos encontrar os autovetores de L 2 (ou L z ) apenas. Ao fazermos isto, em geral, podemos obter autovetores de L 2 que não são autovetores de L z uma vez que os autovetores escolhidos podem ser uma superposição linear de autoestados de L z associados a autovalores distintos. Uma vantagem de encontrar-se o conjunto de autovetores comuns a L 2 e L z é que estes autovetores estão completamente determinados, a menos de fases, uma vez que saibamos a que autovalores eles estão associados. Resolvamos o seguinte problema de autovalores: L 2 Φ lm = h 2 l(l + ) Φ lm, (8.7) L z Φ lm = hm Φ lm, (8.8) onde explicitamos fatores de h para que l e m sejam adimensionais e escrevemos de forma conveniente os autovalores de L 2. Visando simplificar as expressões, admitiremos que as autofunções Φ lm estão propriamente normalizadas, i.e. Φ lm Φ lm =. Para esta análise, utilizaremos os seguintes fatos:. Visto que o módulo do vetor L Φ lm é positivo ou nulo, temos que L Φ lm L Φ lm = h 2 (l(l + ) m 2 + m) 0, (8.9) onde utilizamos que L + = L e a relação (8.3). 2. Analogamente, considerando o vetor L + Φ lm temos que L + Φ lm L + Φ lm = h 2 (l(l + ) m 2 m) 0. (8.20) Se utilizássemos a notação de Dirac os autovalores de L 2 e L z seriam denotados por lm Φ lm.
4 38 Capítulo 8. Momento Angular 3. O operador L + aplicado a Φ lm é um autoestado de L z com autovalor h(m + ), ou seja o operador L + é análogo ao operador de criação a do oscilador harmônico. De fato, L z (L + Φ lm ) = (L + L z + hl + )Φ lm = h(m+)(l + Φ lm ), (8.2) onde utilizamos a equação (8.6) para obter a primeira igualdade. 4. Analogamente, o operador L aplicado a Φ lm é autovetor de L z com autovalor h(m ), mostrando que L é análogo ao operador de aniquilação a do oscilador harmônico. L z (L Φ lm ) = (L L z hl )Φ lm = h(m )(L Φ lm ), (8.22) 5. Uma vez que L ± e L 2 comutam os vetores L ± Φ lm são autoestados de L 2 com autovalor h 2 l(l + ), i.e. L 2 (L ± Φ lm ) = h 2 l(l + )(L ± Φ lm ). (8.23) Autovalores Obtenhamos os possíveis valores de l e m a partir destes fatos. As desigualdades (8.9) e (8.20) permitem-nos concluir que m l. (8.24) Visto que a ação de L + aumenta de uma unidade o autovalor m, vide (8.2), e que m l, temos que deve existir um m max tal que L + Φ lmmax = 0, (8.25) para que o vínculo (8.24) não seja violado. Dado que o vetor L + Φ lmmax tem módulo nulo, usando (8.20) para este vetor segue que l(l + ) m max (m max + ) = 0 = m max = l. (8.26) Logo, temos que L + Φ ll = 0. (8.27)
5 8.2. Solução Algébrica 39 Analogamente, o fato de L abaixar de uma unidade o autovalor m juntamente com l m de (8.24) conduzem a conclusão de que deve existir um valor mínimo para m (m min ) tal que L Φ lmmin = 0. Pode-se mostrar utilizando (8.9) que m min = l. Logo, L Φ l l = 0. (8.28) Uma vez que ações sucessivas de L + devem eventualmente levar ao vetor nulo para que (8.24) não seja violada, sucessivas aplicações L + a Φ l l devem produzir a um estado proporcional a Φ ll. Portanto, 2l deve ser um número inteiro: o de aplicações de L + que conduzem de Φ l l a Φ ll. Com isso, temos que os valores possíveis de l são inteiros e semi-inteiros. l = 0, 2,, 3 2, 2, (8.29) enquanto que m é inteiro ou semi-inteiro conforme l o seja e satisfaz l m l. Autovetores Analogamente à solução por operadores do oscilador harmônico do capítulo 6, podemos determinar os autoestados do momento angular partindo da equação (8.27) ou de (8.28), substituindo a forma explícita do operador L + ou L respectivamente. Este procedimento conduz a uma equação simples que fornece como resultado Φ ll ou Φ l l. De posse de um destes vetores, sucessivas aplicações de L + ou L permitem-nos construir todos os autoestados com m l dado um valor de l. Uma vez que assumimos que os autovetores Φ lm estão normalizados e que L ± Φ lm é um autoestado de L z com autovalor h(m±), as relações (8.9) e (8.20) permitem-nos escrever que Φ lm± = h l(l + ) m(m ± ) L ±Φ lm. (8.30) A seguir obteremos os autoestados do momento angular orbital resolvendo explicitamente as equações de autovalores em vez de utilizar o método descrito acima. Todavia, recomendamos fortemente ao leitor que obtenha alguns autoestados do momento angular orbital utilizando o método acima.
6 40 Capítulo 8. Momento Angular 8.3 Solução Expĺıcita A solução explícita do problema de autovalores e autovetores do momento angular orbital é mais direta quando escolhemos coordenadas esféricas (r, θ, ϕ). Neste sistema de coordenadas o operador momento angular orbital é dado por L = h i r, (8.3) onde = e r r + e ϕ r sin θ ϕ + e θ r θ. (8.32) Os versores do sistema de coordenadas esféricas estão relacionados com os versores cartesianos usuais (i,j,k) através de Portanto, temos que e r = sin θ cosϕ i + sin θ sin ϕ j + cos θ k, (8.33) e θ = cosθ cosϕ i + cos θ sin ϕ j sin θ k, (8.34) e ϕ = sin ϕ i + cosϕ j. (8.35) L = h i ( e ϕ θ e θ sin θ ) ϕ, (8.36) o que nos permite obter as seguintes expressões explícitas: L 2 = h 2 2 sin 2 θ ϕ + ( sin θ )], (8.37) 2 sin θ θ θ L z = h i ϕ, (8.38) ( L ± = he ±iϕ θ ± i cotan θ ). (8.39) ϕ Substituindo as expressões acima no problema de autovetores simultâneos de L 2 e L z (8.7) e (8.8) obtemos as seguintes equações diferenciais acopladas sin 2 θ 2 ϕ 2 + sin θ ( sin θ )] θ θ Y lm = l(l + ) Y lm,(8.40) ϕ Y lm = imy lm, (8.4)
7 8.3. Solução Expĺıcita 4 onde os autoestados Φ lm são dados pelas funções Y lm (θ, ϕ). Para facilitar a análise, usaremos o resultado da seção anterior que m l variando em passos de uma unidade. Para especificarmos completamente o problema devemos adotar uma condição de contorno. Neste problema é natural impor que o valor de Y lm seja o mesmo para (θ, ϕ = 0) e (θ, ϕ = 2π), uma vez que estas duas escolhas representam o mesmo ponto do espaço. Y lm (θ, 0) = Y lm (θ, 2π) (8.42) A solução de (8.4) pode ser facilmente obtida, sendo dada por Y lm = H(θ) e imϕ, (8.43) onde H é um função apenas de θ. Impondo a condição de contorno (8.42) temos que m deve ser um inteiro, ou seja, a condição de contorno não é compatível com valores semi-inteiros para m. Com isso, temos que m e l podem apenas ser inteiros no caso do momento angular orbital. Para maiores informações, veja a próxima seção. Para determinarmos H(θ) substituímos (8.43) em (8.40), resultando em sin θ ( d sin θ dh ) dθ dθ m2 sin 2 H + l(l + )H = 0. (8.44) θ É conveniente neste ponto fazer a substituição de variáveis ξ = cosθ, que nos permite escrever d ( ξ 2 ) dh ] dξ dξ m2 ξ2h + l(l + )H = 0. (8.45) Esta é a equação diferencial de Legendre cujas soluções bem comportadas (não divergentes) no intervalo ξ são as funções associadas de Legendre P m l (ξ). P m l (ξ) = ( )m (l + m)! 2 l l!(l m)! ( ξ 2 ) m 2 d l m dξ l m( ξ2 ) l (8.46) Portanto, a solução do problema de autovetores é dada por Y lm (θ, ϕ) = C lm e imϕ P m l (cosθ), (8.47)
8 42 Capítulo 8. Momento Angular onde a constante C lm deve ser escolhida para que o estado esteja propriamente normalizado. Tendo em vista que os estados que estamos tratando dependem apenas de θ e ϕ, é natural definir o produto escalar através de 2π π Ψ Φ dϕ dθ sin θ Ψ (θ, ϕ)φ(θ, ϕ), (8.48) 0 0 onde a integral é feita apenas sobre a parte angular do elemento de volume em coordenadas esféricas. Requerendo que Y lm Y l m = δ ll δ mm (8.49) as constantes C lm ficam determinadas a mesmos de uma fase, sendo que na convenção que adotamos os harmônicos esféricos Y lm são dados por Y lm (θ, ϕ) = ( ) m 2l + 4π (l m)! (l + m)! eimϕ P m l (cosθ). (8.50) Os harmônicos esféricos com l mais baixos são Y 00 = 4π, (8.5) 3 Y 0 = cosθ, (8.52) 4π 3 Y ± = 8π e±iϕ sin θ, (8.53) 5 ( Y 20 = 3 cos 2 θ ), (8.54) 6π 5 Y 2± = 8π e±iϕ cosθ sin θ, (8.55) 5 Y 2±2 = 32π e±2iϕ sin 2 θ. (8.56) 8.4 Discussão A solução formal do problema de autovetores de L 2 e L z, obtida pelo método de operadores, permite que l e m assumam valores semi-inteiros.
9 8.4. Discussão 43 Por outro lado, a solução explícita através da resolução de equações diferenciais conduz apenas a valores inteiros de l e m. Há alguma contradição nestes dois fatos? A resposta é simplesmente não. A solução explícita levou apenas a valores inteiros de m devido a condição de contorno (8.42) que aplicamos. No caso da solução pelo método de operadores, a qual é compatível com valores inteiros e semi-inteiros, usamos apenas as propriedades do operador momento angular orbital. Caso tivéssemos calculado as autofunções Φ ll que são soluções de (8.27) veríamos que estas satisfazem as condições de contorno apenas se l for inteiro. Logo, não existe conflito entre os dois métodos. Apesar dos valores semi-inteiros de l não ocorrerem para o momento angular orbital, aprendemos da solução formal que operadores que satisfazem as relações de comutação (8.5) a (8.7) podem, em princípio, exibir valores de l semi-inteiro. Obviamente, isto vai depender da forma explícita do operador, assim como ocorreu no caso do momento angular orbital. Veremos mais adiante que as partículas podem apresentar um momento angular intrínseco (spin) associado a valores semi-inteiros de l. Visto que esta nova contribuição para o momento angular total não tem análogo clássico, utilizaremos as relações de comutação (8.5) a (8.7) como guia na definição dos operadores hermitianos associados a este novo grau de liberdade.
Lista Considere um oscilador harmonico tridimencional com o potencial, resolve a Equação de Schrödinger independente no tempo
 Lista 8. Considere um oscilador harmonico tridimencional com o potencial, V = m 2 ( ω 2 x x 2 + ω 2 yy 2 + ω 2 zz 2), onde ω x, ω y e ω z representam as frequências deste oscilador (clássico) nas direções,
Lista 8. Considere um oscilador harmonico tridimencional com o potencial, V = m 2 ( ω 2 x x 2 + ω 2 yy 2 + ω 2 zz 2), onde ω x, ω y e ω z representam as frequências deste oscilador (clássico) nas direções,
Lista Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor.
 Lista 4 1. Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor. = ( ) (a) Mostre que a rotação própria (o que não envolve inversão dos eixos,
Lista 4 1. Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor. = ( ) (a) Mostre que a rotação própria (o que não envolve inversão dos eixos,
Mecânica Quântica. Spin 1/2 e a formulação da M. Q. Parte II. A C Tort 1. Instituto Física Universidade Federal do Rio de Janeiro
 Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
pelo sistema de coordenadas Cartesianas. Podemos utilizar também o sistema de coordenadas
 A. Coordenadas Curvilineares. Teorema de Gauss em coordenadas curvilineares Para especificar a posição, utilizamos a base e x, e y, e z e x r = y z pelo sistema de coordenadas Cartesianas. Podemos utilizar
A. Coordenadas Curvilineares. Teorema de Gauss em coordenadas curvilineares Para especificar a posição, utilizamos a base e x, e y, e z e x r = y z pelo sistema de coordenadas Cartesianas. Podemos utilizar
Momento Angular. Química Teórica e Estrutural. P.J.S.B. Caridade & U. Miranda. 18/11/ /11/2013, Aula 6
 Momento Angular Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 18/11/2013 21/11/2013, Aula 6 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Momento angular orbital Em mecânica clássica
Momento Angular Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 18/11/2013 21/11/2013, Aula 6 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Momento angular orbital Em mecânica clássica
1 O Átomo de Hidrogênio
 O modelo de Bohr para o átomo de hidrogênio, embora forneça valores corretos para as energias dos estados atômicos e do espectro da radiação emitida, não pode ser correto do ponto de vista da mecânica
O modelo de Bohr para o átomo de hidrogênio, embora forneça valores corretos para as energias dos estados atômicos e do espectro da radiação emitida, não pode ser correto do ponto de vista da mecânica
FNC376N: Lista de março de ψ r ψ = Eψ. sin θ Y )
 FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/2 e de Dois Níveis
 Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento angular bem definido
 ÁTOMO DE HIDROGÊNIO Primeiro sistema tratado quanticamente por Schrödinger Modelo de Bohr Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento
ÁTOMO DE HIDROGÊNIO Primeiro sistema tratado quanticamente por Schrödinger Modelo de Bohr Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento
Problemas de Duas Partículas
 Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II. q exp( q 2 ) ( 2 π. 2 (2q 2 1) exp( q 2 )
 CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
Aula de Física Atômica e molecular. Operadores em Mecânica Quântica Prof. Vicente
 Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
SEGUNDA PROVA - F789. angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) =
 SEGUNDA PROVA - F789 NOME: RA:. Considere uma partícula de spin. Seja S seu spin e L seu momento angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) = r, ± Ψ na base r, ± de autoestados
SEGUNDA PROVA - F789 NOME: RA:. Considere uma partícula de spin. Seja S seu spin e L seu momento angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) = r, ± Ψ na base r, ± de autoestados
O ÁTOMO DE HIDROGÊNIO
 O ÁTOMO DE HIDROGÊNIO Alessandra de Souza Barbosa 04 de dezembro de 013 O átomo de hidrogênio Alessandra de Souza Barbosa CF37 - Mecânica Quântica I /36 Sistema de duas particulas um elétron e um próton;
O ÁTOMO DE HIDROGÊNIO Alessandra de Souza Barbosa 04 de dezembro de 013 O átomo de hidrogênio Alessandra de Souza Barbosa CF37 - Mecânica Quântica I /36 Sistema de duas particulas um elétron e um próton;
A Experiência de Stern-Gerlach e o Spin do Elétron
 UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
Mecânica Quântica:
 Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Rotor quântico. Quanticamente o rotor é descrito por uma função de onda, tal que: l A função de onda do estado estacionário é dada por:
 Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever:
 Temos então a corrente conservada: Teoria Quântica de Campos I 12 ( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever: De forma que : ( eq. 12.2)
Temos então a corrente conservada: Teoria Quântica de Campos I 12 ( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever: De forma que : ( eq. 12.2)
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Funções ortogonais e problemas de Sturm-Liouville. Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE
 Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Os Postulados da Mecânica Quântica
 Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Desenvolvimento. Em coordenadas esféricas:
 Desenvolvimento Para que possamos resolver a equação da onda em coordenadas esféricas, antes é necessária a dedução do operador Laplaciano nessas coordenadas, portanto temos: Em coordenadas esféricas:
Desenvolvimento Para que possamos resolver a equação da onda em coordenadas esféricas, antes é necessária a dedução do operador Laplaciano nessas coordenadas, portanto temos: Em coordenadas esféricas:
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Fases de Berry. David A. Ruiz Tijerina. November 11, Evolução temporal de um autoestado e a fase de Berry
 Fases de Berry David A. Ruiz Tijerina November 11, 15 1 Evolução temporal de um autoestado e a fase de Berry Vamos supor que temos um Hamiltoniano H(R) que depende de um conjunto de parámetros R = {R i
Fases de Berry David A. Ruiz Tijerina November 11, 15 1 Evolução temporal de um autoestado e a fase de Berry Vamos supor que temos um Hamiltoniano H(R) que depende de um conjunto de parámetros R = {R i
Representação grande
 Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Princípios Gerais da Mecânica Quântica
 Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas
 Campo Escalar e Gradiente Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas Prof. Alex G. Dias (alex.dias@ufabc.edu.br) Prof. Alysson F. Ferrari (alysson.ferrari@ufabc.edu.br) Um campo escalar
Campo Escalar e Gradiente Fundamentos da Eletrostática Aula 02 Cálculo Vetorial: derivadas Prof. Alex G. Dias (alex.dias@ufabc.edu.br) Prof. Alysson F. Ferrari (alysson.ferrari@ufabc.edu.br) Um campo escalar
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi
 Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Teoria Clássica de Campos
 Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
Operadores Tensoriais
 Operadores Tensoriais Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br CF70 Física Quântica I Operadores Tensoriais Operadores Vetoriais Como os operadores
Operadores Tensoriais Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br CF70 Física Quântica I Operadores Tensoriais Operadores Vetoriais Como os operadores
O ÁTOMO DE HIDROGÊNIO
 FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville O ÁTOMO DE HIDROGÊNIO A elegância, a riqueza, a complexidade e a diversidade dos fenômenos naturais que decorrem
FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville O ÁTOMO DE HIDROGÊNIO A elegância, a riqueza, a complexidade e a diversidade dos fenômenos naturais que decorrem
Equações Parciais Em Coordenadas Esféricas
 Equações Parciais Em Coordenadas Esféricas Lucas Nobrega Natã Gomes David de Mattos Pereira João Paulo Carvalho Corrêa Ricardo Wertes Motta UFF Depto. de Matemática Aplicada Métodos Matemáticos Aplicados
Equações Parciais Em Coordenadas Esféricas Lucas Nobrega Natã Gomes David de Mattos Pereira João Paulo Carvalho Corrêa Ricardo Wertes Motta UFF Depto. de Matemática Aplicada Métodos Matemáticos Aplicados
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
PGF Mecânica Clássica
 PGF 5005 - Mecânica Clássica Prof. Iberê L. Caldas Segunda Lista de Exercícios o semestre de 018 1. Considere, inicialmente, a seguinte Hamiltoniana integrável: H 0 = I 1 + I I 1 3I 1 I + I, a qual está
PGF 5005 - Mecânica Clássica Prof. Iberê L. Caldas Segunda Lista de Exercícios o semestre de 018 1. Considere, inicialmente, a seguinte Hamiltoniana integrável: H 0 = I 1 + I I 1 3I 1 I + I, a qual está
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Breve Revisão de Mecânica
 Capítulo 1 Breve Revisão de Mecânica Quântica Seguimos as secções 5.1 a 5.3 do Griffiths [1] e a secção 1.1 do meu texto de Introdução à Teoria de Campo []. É assumido como pré-requisito o conhecimento
Capítulo 1 Breve Revisão de Mecânica Quântica Seguimos as secções 5.1 a 5.3 do Griffiths [1] e a secção 1.1 do meu texto de Introdução à Teoria de Campo []. É assumido como pré-requisito o conhecimento
P1 de Álgebra Linear I
 P1 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Para
P1 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Para
Universidade de São Paulo em São Carlos Mecânica Quântica Aplicada Prova 1
 Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
- identificar operadores ortogonais e unitários e conhecer as suas propriedades;
 DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
Átomo de Hidrogênio 1
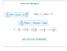 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica
 CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3 Equações de Poisson e Laplace Vimos na aula passada o método de separação de
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3 Equações de Poisson e Laplace Vimos na aula passada o método de separação de
Aula 6 Produto interno
 MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Não serão aceitas respostas sem justificativa:
 Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Álgebra Linear I - Aula 3. Roteiro
 Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Álgebra Linear I - Aula 3 1. Produto escalar. Ângulos. 2. Desigualdade triangular. Roteiro 1 Produto escalar Considere dois vetores ū = (u 1, u 2, u 3 ) e v = (v 1, v 2, v 3 ) de R 3. O produto escalar
Partícula em 3 dimensões
 Part I Partícula em 3 dimensões Neste Catítulo, estudamos a dinâmica de uma partícula numa situação mais realistica, ou seja, o movimento no espaço tridimensional sob a força derivada de um potencial V
Part I Partícula em 3 dimensões Neste Catítulo, estudamos a dinâmica de uma partícula numa situação mais realistica, ou seja, o movimento no espaço tridimensional sob a força derivada de um potencial V
2, ao medirmos um observável deste estado que possui autovetores 0 e 1, obtemos o resultado 0 com probabilidade α 2, e 1 com probabilidade β 2.
 4 Informação Quântica A teoria da Informação Quântica foi basicamente desenvolvida na última década (3, 10, 16). Nosso objetivo neste capítulo é apresentar sua estrutura fundamental, o bit quântico, e
4 Informação Quântica A teoria da Informação Quântica foi basicamente desenvolvida na última década (3, 10, 16). Nosso objetivo neste capítulo é apresentar sua estrutura fundamental, o bit quântico, e
Quantização de um campo fermiônico
 Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Lista de Exercícios 5
 FFI5 Física-Matemática II Lista de Eercícios 5 Seja Φ a distribuição definida por Φ[f] := f (n) (a), n N, a R, onde f representa uma função teste qualquer e f (n) (a) sua n-ésima derivada calculada em
FFI5 Física-Matemática II Lista de Eercícios 5 Seja Φ a distribuição definida por Φ[f] := f (n) (a), n N, a R, onde f representa uma função teste qualquer e f (n) (a) sua n-ésima derivada calculada em
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
Adição de dois spins1/2
 Adição de dois spins/ a c tort de julho de O momento angular é um dos pontos mais importantes da mecânica quântica. Saber somar dois ou três momentos angulares é crucial para o entendimento da estrutura
Adição de dois spins/ a c tort de julho de O momento angular é um dos pontos mais importantes da mecânica quântica. Saber somar dois ou três momentos angulares é crucial para o entendimento da estrutura
Ney Lemke. Departamento de Física e Biofísica
 Revisão Matemática Ney Lemke Departamento de Física e Biofísica 2010 Vetores Sistemas de Coordenadas Outline 1 Vetores Escalares e Vetores Operações Fundamentais 2 Sistemas de Coordenadas Coordenadas Cartesianas
Revisão Matemática Ney Lemke Departamento de Física e Biofísica 2010 Vetores Sistemas de Coordenadas Outline 1 Vetores Escalares e Vetores Operações Fundamentais 2 Sistemas de Coordenadas Coordenadas Cartesianas
Quantização por Integrais de Trajetória:
 Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
MOMENTO DIPOLAR ELÉCTRICO. Resumo O objectivo deste trabalho é a resolução do problema 9 da série de exercícios n o 1 de Física Quântica da Matéria.
 MESTRADO EM ENGENHARIA FÍSICA TECNOLÓGICA - FÍSICA QUÂNTICA DA MATÉRIA Preprint typeset using LATEX style emulateapj v. 8// MOMENTO DIPOLAR ELÉCTRICO ALEXANDRE FREITAS, N o 5255 RAQUEL PINTO, N o 57 Mestrado
MESTRADO EM ENGENHARIA FÍSICA TECNOLÓGICA - FÍSICA QUÂNTICA DA MATÉRIA Preprint typeset using LATEX style emulateapj v. 8// MOMENTO DIPOLAR ELÉCTRICO ALEXANDRE FREITAS, N o 5255 RAQUEL PINTO, N o 57 Mestrado
Exame de Ingresso na Pós-graduação
 Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 09 de Junho de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3 (três)
Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 09 de Junho de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3 (três)
Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico
 Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico André Juan Ferreira Martins de Moraes Resumo Estas notas se baseiam na Seção 1.1 do artigo 1, na qual as equações
Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico André Juan Ferreira Martins de Moraes Resumo Estas notas se baseiam na Seção 1.1 do artigo 1, na qual as equações
Análise Vetorial. Capítulo Sejam os dois segmentos de reta AB e CD, com AB = B A tal que:
 Capítulo 1 Análise etorial 1.1 ejam os dois segmentos de reta AB e CD, com AB = B A e CD = D C, tal que: AB = î 2ĵ ˆk CD = 3î 6ĵ 3ˆk Para verificar que AB e CD são paralelos basta verificar que AB CD =
Capítulo 1 Análise etorial 1.1 ejam os dois segmentos de reta AB e CD, com AB = B A e CD = D C, tal que: AB = î 2ĵ ˆk CD = 3î 6ĵ 3ˆk Para verificar que AB e CD são paralelos basta verificar que AB CD =
Tensores (Parte 1) 15 de abril de Primeira aula sobre tensores para a disciplina de CVT 2019Q1
 Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
G3 de Álgebra Linear I
 G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
Conjugação de Carga: deve fazer o mesmo para o spin invertido, trocando ξ s por ξ -s na função de onda, defini- mos: Para os espinores temos:
 Teoria Quântica de Campos I 142 deve fazer o mesmo para o spin invertido, trocando ξ s por ξ -s na função de onda, defini- e que mos: ( eq. 142.1 ) Para os espinores temos: (basta expandir a raiz em p)
Teoria Quântica de Campos I 142 deve fazer o mesmo para o spin invertido, trocando ξ s por ξ -s na função de onda, defini- e que mos: ( eq. 142.1 ) Para os espinores temos: (basta expandir a raiz em p)
O spin do elétron. Vimos, na aula 2, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com 2 valores, com propriedades de momento angular.
 O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica. Sistemas com três variáveis - Parte 1. Terceiro Ano do Ensino Médio
 Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
Postulados da Mecânica Quântica
 Postulados da Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin Operadores Propriedades Princípio da Incerteza Princípios da Mecânica Quântica A função de onda contém toda a informação que
Postulados da Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin Operadores Propriedades Princípio da Incerteza Princípios da Mecânica Quântica A função de onda contém toda a informação que
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
CAPÍTULO 9 CINEMÁTICA DO MOVIMENTO ESPACIAL DE CORPOS RÍGIDOS
 82 CPÍTULO 9 CINEMÁTIC DO MOVIMENTO ESPCIL DE CORPOS RÍGIDOS O estudo da dinâmica do corpo rígido requer o conhecimento da aceleração do centro de massa e das características cinemáticas do corpo denominadas
82 CPÍTULO 9 CINEMÁTIC DO MOVIMENTO ESPCIL DE CORPOS RÍGIDOS O estudo da dinâmica do corpo rígido requer o conhecimento da aceleração do centro de massa e das características cinemáticas do corpo denominadas
Gases quânticos sem interação
 UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
Mecânica Analítica. Dinâmica Hamiltoniana. Licenciatura em Física. Prof. Nelson Luiz Reyes Marques MECÂNICA ANALÍTICA PARTE 2
 Mecânica Analítica Dinâmica Hamiltoniana Licenciatura em Física Prof. Nelson Luiz Reyes Marques Princípio de Hamilton O caminho real que uma partícula percorre entre dois pontos 1 e 2 em um dado intervalo
Mecânica Analítica Dinâmica Hamiltoniana Licenciatura em Física Prof. Nelson Luiz Reyes Marques Princípio de Hamilton O caminho real que uma partícula percorre entre dois pontos 1 e 2 em um dado intervalo
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
 Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Aula 19 Operadores ortogonais
 Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Uma pequena introdução à álgebra para mecânica
 Technical Report Uma pequena introdução à álgebra para mecânica quântica Prof. Dr. João Cândido Lima Dovicchi 1 Florianópolis SC 2014 1 Prof. Associado do Departamento de Informática e Estatística da Universidade
Technical Report Uma pequena introdução à álgebra para mecânica quântica Prof. Dr. João Cândido Lima Dovicchi 1 Florianópolis SC 2014 1 Prof. Associado do Departamento de Informática e Estatística da Universidade
Equação de Dirac e o Átomo de Hidrogênio
 Equação de Dirac e o Átomo de Hidrogênio Rodrigo Andrade e Silva Mecânica Quântica 2 Introdução A equação de Dirac fornece o análogo da equação de Schrodinger para uma mecânica quantica relativistica,
Equação de Dirac e o Átomo de Hidrogênio Rodrigo Andrade e Silva Mecânica Quântica 2 Introdução A equação de Dirac fornece o análogo da equação de Schrodinger para uma mecânica quantica relativistica,
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
4.4 Autovalores e Autovetores
 4.4-1 4.4 Autovalores e Autovetores 4.4.1 A Equação de Euler O vetor do momento angular pode ser representado como onde os e i o são os vetores unitários ao longo dos eixos principais, denominados com
4.4-1 4.4 Autovalores e Autovetores 4.4.1 A Equação de Euler O vetor do momento angular pode ser representado como onde os e i o são os vetores unitários ao longo dos eixos principais, denominados com
JOSÉ ROBERTO RIBEIRO JÚNIOR. 9 de Outubro de 2017
 9 de Outubro de 2017 Vetores Ferramenta matemática que é utilizada nas seguintes disciplinas dos cursos de Engenharia: Física; Mecânica Resistência dos materiais Fenômenos do transporte Consideremos um
9 de Outubro de 2017 Vetores Ferramenta matemática que é utilizada nas seguintes disciplinas dos cursos de Engenharia: Física; Mecânica Resistência dos materiais Fenômenos do transporte Consideremos um
O Método de Hartree-Fock
 O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
Fundamentos da Eletrostática Aula 19 Problemas Energia num Dielétrico
 Fundamentos da Eletrostática Aula 19 Problemas Energia num Dielétrico Problema 1: Capacitor preenchido com dielétrico Prof. Alex G. Dias Prof. Alysson F. Ferrari Considere um capacitor de placas paralelas,
Fundamentos da Eletrostática Aula 19 Problemas Energia num Dielétrico Problema 1: Capacitor preenchido com dielétrico Prof. Alex G. Dias Prof. Alysson F. Ferrari Considere um capacitor de placas paralelas,
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.1 Vibrações de uma membrana Como mencionado na aula passada, pode-se deduzir
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.1 Vibrações de uma membrana Como mencionado na aula passada, pode-se deduzir
Física III IQ 2014 ( )
 Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
OBSERVÁVEIS COMPATÍVEIS Mecânica Quântica I ( ) - Capítulo 04
 SUPERPOSIÇÃO E OBSERVÁVEIS COMPATÍVEIS Mecânica Quântica I (1108045) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2014.2 1 / 59 Sumário Superposição Princípio da superposição Interpretação do espaço
SUPERPOSIÇÃO E OBSERVÁVEIS COMPATÍVEIS Mecânica Quântica I (1108045) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2014.2 1 / 59 Sumário Superposição Princípio da superposição Interpretação do espaço
Linear. 5.1 Espaços vetoriais
 Capítulo 5 Mecânica Quântica e a Álgebra Linear Neste capítulo faremos uma recordação de alguns fatos básicos de Álgebra Linear, sem preocuparmos com o rigor matemático. Também formularemos os postulados
Capítulo 5 Mecânica Quântica e a Álgebra Linear Neste capítulo faremos uma recordação de alguns fatos básicos de Álgebra Linear, sem preocuparmos com o rigor matemático. Também formularemos os postulados
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC
 Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Equação de Schrödinger
 Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0)
 este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
Bilineares do Campo de Dirac. Analogamente:
 Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
F 789 A - MECÂNICA QUÂNTICA II -Prof. Eduardo Granado - PROVA 1 (01/04/2015) (θ,ϕ), em que u k,l. (r). Nesta equação, E k,l e l (l+1)ħ 2 são os
 F 789 A - MECÂNICA QUÂNTICA II -Prof. Eduardo Granado - PROVA 1 (01/04/2015) 1) Considere um sistema de duas partículas de massa m 1 e m 2 que interagem através de um potencial central V(r), onde r é a
F 789 A - MECÂNICA QUÂNTICA II -Prof. Eduardo Granado - PROVA 1 (01/04/2015) 1) Considere um sistema de duas partículas de massa m 1 e m 2 que interagem através de um potencial central V(r), onde r é a
Spin e Adição de Momento Angular
 96 Capítulo Spin e Adição de Momento Angular Até este momento consideramos que o estado de um elétron encontrase completamente especificado pela sua função de onda Ψ(x). Neste capítulo mostraremos que
96 Capítulo Spin e Adição de Momento Angular Até este momento consideramos que o estado de um elétron encontrase completamente especificado pela sua função de onda Ψ(x). Neste capítulo mostraremos que
Translação e Rotação Energia cinética de rotação Momentum de Inércia Torque. Física Geral I ( ) - Capítulo 07. I. Paulino*
 ROTAÇÃO Física Geral I (1108030) - Capítulo 07 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 25 Translação e Rotação Sumário Definições, variáveis da rotação e notação vetorial Rotação com aceleração angular
ROTAÇÃO Física Geral I (1108030) - Capítulo 07 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 25 Translação e Rotação Sumário Definições, variáveis da rotação e notação vetorial Rotação com aceleração angular
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
Simetrias na Mecânica Quântica
 Simetrias na Mecânica Quântica Prof. 7 de junho de 2011 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, G(a) M.Q. ˆT(G(a)), ˆT(G(a)) operador unitário.
Simetrias na Mecânica Quântica Prof. 7 de junho de 2011 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, G(a) M.Q. ˆT(G(a)), ˆT(G(a)) operador unitário.
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
Simetrias na Mecânica Quântica
 Simetrias na Mecânica Quântica Prof. 26 de maio de 2010 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, ˆT(G(a)) operador unitário. G(a) M.Q. ˆT(G(a)),
Simetrias na Mecânica Quântica Prof. 26 de maio de 2010 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, ˆT(G(a)) operador unitário. G(a) M.Q. ˆT(G(a)),
