Spin e Adição de Momento Angular
|
|
|
- Júlio César Cerveira Pais
- 6 Há anos
- Visualizações:
Transcrição
1 96
2 Capítulo Spin e Adição de Momento Angular Até este momento consideramos que o estado de um elétron encontrase completamente especificado pela sua função de onda Ψ(x). Neste capítulo mostraremos que o elétron possui um momento angular intrínseco (spin), o qual requer a introdução de um grau de liberdade adicional para descrevê-lo. Também estudaremos como compor dois momentos angulares em Mecânica Quântica. Isto permitirá que analisemos o momento angular total de um sistema contendo várias partículas, as quais podem apresentar momento angular orbital e spin.. Experimento de Stern Gerlach Historicamente, a primeira evidência para a existência de um momento angular intrínseco foi dada por Stern e Gerlach em 920. Estes estudaram o movimento de feixes atômicos na presença de um campo magnético, obtendo resultados não esperados, os quais levaram a introdução do conceito de spin. Para compreendermos este experimento devemos saber como uma partícula comporta-se na presença de um campo magnético externo. 97
3 98 Capítulo. Spin e Adição de Momento Angular.. Momento de dipolo magnético Vamos agora obter a relação clássica entre o momento de dipolo magnético de uma partícula pontual e seu momento angular orbital. Para tanto devemos lembrar que, no eletromagnetismo clássico, o momento de dipolo magnético (m) associado a uma distribuição de correntes J(x) é dado por m = d 3 x x J(x), (.) 2c onde adotamos o sistema gaussiano de unidades. A densidade de corrente elétrica de uma partícula pontual é J(x) = qvδ(x x p ), (.2) onde q é a carga elétrica da partícula, x p sua posição e v sua velocidade. Logo, utilizando (.) e (.2) temos que o momento de dipolo magnético de uma partícula satisfaz m = q 2c x p v = q 2µc L, (.3) com µ sendo a sua massa e L seu momento angular orbital. No caso de um elétron escrevemos q = e, onde e é a carga do próton, o que resulta em m = e L 2µc, (.4) onde podemos verificar o aparecimento do magneton de Bohr µ B = e 2µc = 9, erg/gauss. (.5) Um fato interessante sobre a relação (.4) é que ela nos permite medir o momento angular do sistema L através da análise do comportamento do sistema na presença de um campo magnético. No que segue, utilizaremos que o momento de dipolo magnético de uma partícula e seu momento angular (em geral!) são proporcionais, sendo que a constante de proporcionalidade depende do inverso da massa.
4 .. Experimento de Stern Gerlach 99 Figura.: Esquema do experimento de Stern e Gerlach...2 Descrição do experimento Consideremos um feixe de átomos passando por uma região de campo magnético cujo módulo varia rapidamente, enquanto sua direção é aproximadamente constante como mostra a figura.. Assumindo que as dimensões características do problema são muito maiores que a escala natural do sistema quântico, podemos utilizar a Mecânica Clássica para analisar a evolução do pacote de ondas até o anteparo onde os átomos são observados. A interação entre o campo magnético e o momento de dipolo magnético do sistema dá origem a uma força F = ( m B), = (m z B z ) m z B z, (.6) = q 2µc L z B z. Classicamente, a componente z do momento angular do sistema pode ser qualquer e conseqüentemente m z e F também. Logo, deveríamos observar átomos em todos os pontos do anteparo como mostra Exercício: Explique o porquê deste experimento ser extremamente difícil de realizar com feixes de elétrons livres.
5 200 Capítulo. Spin e Adição de Momento Angular (a) (b) Figura.2: (a) Resultado esperado classicamente. (b) Resultado experimental. a figura.2a. Por outro lado, a Mecânica Quântica prevê apenas um conjunto finito de valores para L z, o que implica que F pode assumir apenas 2l + valores discretos. Portanto, devemos observar apenas 2l + linhas no anteparo, as quais correspondem a átomos com valores diferentes de m. Num experimento com átomos de alumínio, Stern e Gerlach observaram apenas duas linhas no anteparo; vide figura.2b. A explicação para este fato é que o átomo de alumínio possui momento angular total /2. Uma vez que o momento angular orbital dos elétrons pode assumir apenas valores inteiros, devemos interpretar este resultado como um sinal de que os elétrons possuem um momento angular intrínseco, o qual é semi-inteiro e igual a /2. 2 Este resultado surpreendente cai como uma luva para a teoria do momento angular que desenvolvemos no capítulo 8, uma vez que a álgebra obedecida pelo momento angular conduz-nos naturalmente a valores inteiros, como os do momento angular orbital, bem como a valores semi-inteiros, como o apresentado pelos elétrons. Logo, é natural 2 Exercício: Argumente que o momento angular semi-inteiro do sistema está relacionado aos elétrons em vez do núcleo atômico.
6 .. Experimento de Stern Gerlach 20 associar ao spin operadores hermitianos S i, os quais obedecem a [S i, S j ] = i ǫ ijk S k. (.7) Antes de estudarmos como podemos representar explicitamente estes operadores para partículas de spin /2 é interessante discutirmos um pouco mais o conceito de spin...3 Origem do spin Dado que o elétron exibe um momento angular intrínseco, além do seu momento angular orbital, somos tentados a interpretá-lo como sendo devido à rotação do elétron em torno de seu eixo, a exemplo do que ocorre com a Terra. Todavia, isto não pode ser verdade, já que se o fosse, este seria um momento angular orbital e forçosamente deveria ser inteiro! Portanto, a única conclusão que podemos tirar é que o elétron possui um novo grau de liberdade, o qual está associado ao spin. Esta novidade não pode ser explicada pela Mecânica Quântica não relativística, sendo necessário para sua melhor compreensão o uso da teoria relativística de Dirac, a qual foge ao escopo destas notas. É interessante notar que o momento angular intrínseco de uma partícula pode ser inteiro ou semi-inteiro, dependo da partícula considerada. Por exemplo, elétrons, prótons e nêutrons possuem spin /2, enquanto que os pions (π 0, π ± ) e os kaons (K 0, K ± ) possuem spin zero. São também conhecidas partículas com spin, tais como o fóton, Z 0, W ±, e o ρ, e com spin 3/2, tais como Momento magnético intrínseco Vimos anteriormente que existe um momento de dipolo magnético associado ao momento angular orbital de partículas carregadas através de (.3). Analogamente, existe um momento de dipolo magnético associado ao spin. Assumiremos que estes são proporcionais, como em (.3), m = g q 2µc S, (.8)
7 202 Capítulo. Spin e Adição de Momento Angular onde o fator q/2µc foi introduzido por análise dimensional e g deve ser determinado experimentalmente. O fator g é chamado de constante giro-magnética. Para um elétron m = g 2 µ B σ, (.9) onde a constante µ B é o magneton de Bohr dado por (.5). O valor de g para o elétron é uma das quantidades medidas com maior precisão em Física, sendo o seu valor numérico g = 2 (, ± 0, ). (.0) No caso dos prótons, que também são partículas de spin /2, temos que (.9) continua válida com a óbvia troca da massa do elétron pela massa do nucleon em (.5). Experimentos revelam que para o próton g P = 2, 79. Mais ainda, nêutrons também são partículas de spin /2 mas de carga nula. É interessante definir neste caso que m N = g N 2 e σ, (.) 2µ N c sendo que g N =, 9. Intuitivamente, é natural supor que m N fosse nulo já que carga elétrica do nêutron é nula. O fato de g N ser diferente de zero indica que o nêutron é um objeto composto cujos constituintes possuem carga elétrica não nula. Passemos agora ao estudo de como podemos representar as partículas com momento angular intrínseco /2, o que requer a introdução um grau de liberdade extra..2 Spin /2 As conseqüências das relações de comutação (.7) já foram estudadas anteriormente, e o que nos resta fazer é obter uma representação explícita dos operadores S i para spin /2. Sabemos que podemos diagonalizar S 2 e S z simultaneamente S 2 ϕ sms = 2 s (s + ) ϕ sms (.2) S z ϕ sms = m s ϕ sms (.3)
8 .2. Spin /2 203 onde s = /2 e m s = ±/2. Note que os autovetores do problema acima geram um espaço com 2s + (= 2) dimensões. Entretanto, nós já estudamos sistemas com apenas dois estados! Logo, somos naturalmente levados a considerar o espaço vetorial cujos elementos são matrizes coluna da forma ( ) a Ψ =, b adotando o produto escalar onde Ψ Φ = a c + b d, Φ = ( c d Observando o que foi feito anteriormente para sistemas de dois níveis, operadores são dados por matrizes 2 2, sendo fácil notar que uma representação para os S i é dada por S = 2 σ x = ( ) 0, (.4) 2 0 S 2 = 2 σ y = ( ) 0 i, (.5) 2 i 0 S 3 = 2 σ z = ( ) 0, (.6) 2 0 onde esta pode ser verificada através da substituição em (.7). Portanto, todo o tratamento de sistema de dois níveis, desenvolvido anteriormente, pode ser aplicado diretamente a sistemas envolvendo partículas com spin /2! Por exemplo, nesta representação para os operadores de spin S i, temos que os estados satisfazendo (.2) e (.3) são dados por ( ) ϕ =, (.7) ( ) 0 ϕ =. (.8) 2 2 ).
9 204 Capítulo. Spin e Adição de Momento Angular Mais ainda, toda a estrutura desenvolvida previamente para a evolução temporal de sistemas de dois níveis pode ser também utilizada diretamente sem problema algum..2. Precessão do spin num campo magnético O spin de uma partícula pode manifestar-se através de sua interação com um campo magnético. Por esta razão, vamos discutir rapidamente a precessão que o spin de um elétron sofre quando colocado sob a ação de um campo magnético constante B = Be z. A hamiltoniana que governa a evolução temporal do sistema é dada por ( ) 0 H = m B = µ B B, (.9) 0 onde usamos (.9) e tomamos g = 2. A equação de Schrödinger dependente do tempo escreve-se como i ( ) ( ) α(t) α(t) = m B, (.20) t β(t) β(t) onde o estado do sistema é Ψ(t) = ( α(t) β(t) ). A nossa experiência anterior com sistema de dois níveis mostra que para obtermos a solução deste problema devemos resolver o problema de autovalores de H. É fácil verificar que os autovetores e respectivos autovalores de (.9) são dados por ( ) E + = µ B B u + =, (.2) 0 ( ) 0 E = µ B B u =. (.22) Escrevendo o estado inicial em função de u ± ( ) α(0) Ψ(0) = = α(0) u β(0) + + β(0) u, (.23)
10 .2. Spin /2 205 a solução deste problema de valor inicial é dada por ( ) α(t) Ψ(t) = = α(0) u β(t) + e ie +t/ + β(0) u e ie t/. (.24) Para compreendermos o significado físico de (.24) consideremos um sistema cujo estado inicial seja autovetor de σ x com autovalor +. Neste caso α(0) = β(0) = / 2 e conseqüentemente Ψ(t) = 2 ( e iωt/2 e iωt/2 ), (.25) onde Ω = 2µ B B/ é a freqüência de Larmor. A interpretação deste estado é imediata se calcularmos os seguintes valores esperados. S x = cos Ωt (.26) 2 S y = sin Ωt 2 (.27) S z = 0 (.28) Destas expressões podemos ver claramente que o valor esperado do spin esta precessando ao redor do eixo determinado pelo campo magnético 3. Note que este é o mesmo comportamento previsto classicamente para um dipolo magnético sob a ação de uma campo magnético B, o qual dá origem a um torque m B..2.2 Ressonância Magnética Vamos agora descrever uma técnica para a medida do fator giro-magnético do próton g P, ou seja de seu momento de dipolo magnético intrínseco. Conforme vimos na seção anterior, um momento magnético associado a uma partícula de spin /2 imerso em um campo uniforme B na direção z apresenta dois estados de energia bem definida. Consideraremos um dipolo magnético que se encontra inicialmente no estado de energia mais baixa, isto é alinhado com o campo magnético externo, 3 Exercício: Mostre que este fato ocorre para um estado inicial genérico. Qual é o efeito da precessão de spin na análise do experimento de Stern-Gerlach?
11 206 Capítulo. Spin e Adição de Momento Angular e então aplicaremos um campo magnético perpendicular ao original o qual oscila com freqüência ω. Mostraremos que a probabilidade do estado do sistema passar para o estado de energia mais alta é maximizada para ω g P, o que nos permite a determinação deste parâmetro. Mais ainda, várias aplicações como relógio atômico e tomografia por ressonância magnética nuclear estão baseadas no conteúdo desta seção. Consideremos um próton cujo momento de dipolo magnético é dado por e S m = g p 2M P c g S p µ P. (.29) Consideremos que este próton está na presença do campo magnético B = B T cos(ωt)i B T sin(ωt)j + B L k. (.30) De (.20), temos que a equação de movimento para o spin deste próton é dada então por i ( ) a = g ( ) ( ) Pµ P BL B T e iωt a t b 2 B T e iωt (.3) B L b Definindo as freqüências Ω L = g pµ p B L 2 e Ω T = g pµ p B T 2 (.32) podemos reescrever (.3) como um par de equações diferenciais acopladas a t b t = i ( Ω T e iωt b + Ω L a ), = i ( Ω T e iωt a Ω L b ). Agora, procuremos soluções de (.33) da forma (.33) a = a 0 e iωat e b = b 0 e iω bt, (.34) onde a 0, b 0, ω a e ω b são constantes. Substituindo este ansatz em (.33) temos que ( ) ( ) (ωa Ω L ) Ω T e iϕt a0 Ω T e iϕt = 0, (.35) (ω b + Ω L ) b 0
12 .2. Spin /2 207 onde ϕ = ω a ω b ω. Tendo em vista que supusemos que a 0 e b 0 são constantes, devemos ter que ϕ = 0, isto é ω a = ω b + ω. (.36) Mais ainda, para que obtenhamos uma solução não trivial o determinante da matriz em (.35) deve anular-se, o que nos conduz a com ω a = ω 2 ± ω e ω b = ω 2 ω 2 = ± ω, (.37) ( Ω L ω ) 2 + Ω 2 T 2. (.38) Agora podemos escrever a solução geral de (.3) a(t) = a e i( ω 2 ω)t + a 2 e i( ω 2 + ω)t, (.39) b(t) = b e i( ω 2 + ω)t + b 2 e i( ω 2 ω)t. (.40) Para especificarmos completamente o problema assumiremos que o sistema encontra-se no instante t = 0 no estado de energia mais baixa, a saber, a(0) = e b(0) = 0. Utilizando estas condições iniciais, bem como (.33) para obter as derivadas em t = 0, segue que a(t) = [ i b(t) = Ω T ω ( ω 2 + Ω L ) ] sin( ωt) + ω cotan( ωt) e i ω 2 t, (.4) ω ω sin( ωt) e i 2 t. (.42) Logo a probabilidade de transição para o estado de energia mais alta é dada por Ω 2 T b(t) 2 = ( ) ΩL ω 2 sin 2 ( ωt). (.43) + Ω 2 2 T Note que esta probabilidade é máxima para ω res = 2Ω L, i.e. para ω res = g pµ p B L. (.44) Mais ainda, para aplicar este cálculo para elétrons trocamos os parâmetros do próton pelos do elétron. Com isso é fácil ver que a freqüência de ressonância dos elétrons é muito diferente da do próton, permitindo assim a separação dos efeitos devidos aos prótons e aos elétrons.
13 208 Capítulo. Spin e Adição de Momento Angular B Campo oscilante Stern Gerlach /2 /2 Stern Gerlach /2 B detector Figura.3: Esquema do experimento de Rabi. Experimento de Rabi O experimento de Rabi 4 consiste de dois aparatos de Stern-Gerlach com campos magnéticos opostos separados por uma região contendo um campo estático e um oscilante como em (.30); vide a figura.3. Na ausência do campo oscilante o feixe gerado com autovalor /2 de S Z no primeiro aparato de Stern-Gerlach é detectado integralmente após o segundo desses aparatos. Quando o campo oscilante é ligado o número de átomos detectados é menor, sendo que o número de átomos que chegam ao detector depende da freqüência do campo oscilante. Quando esta freqüência é a de ressonância dada por (.44) o número de átomos detectados é mínimo. Isso permite-nos medir com precisão ω res, e conseqüentemente g p ; vide a figura.4..3 Funções de onda incluindo spin Na descrição que fizemos nos capítulos anteriores dos elétrons ignoramos por completo o fato destes possuírem spin /2. A fim de incluir o grau de liberdade extra associado ao momento angular intrínseco, devemos notar que os operadores de spin (S 2 e S z ) comutam tanto com x, bem como com p e L. Isto significa que S 2 e S z podem ser 4 Para maiores detalhes vide, Rabi XXXX.
14 .3. Funções de onda incluindo spin 209 Figura.4: Número de átomos detectados em função do freqüência do campo magnético B L num experimento de Rabi. O campo transversal utilizado foi B T = 0 4 T e ω = 4 MHz. diagonalizados simultaneamente com qualquer um destes operadores. Por simplicidade, consideremos uma partícula livre de spin /2 cuja hamiltoniana é dada por H = p2. Neste caso H comuta com os operadores de spin e podemos diagonalizar simultaneamente 5 H, P, S 2 e S z. 2µ Logo, escrevemos H φ ksms = 2 k 2 2µ φ ksm s, (.45) P φ ksms = k φ ksms, (.46) S 2 φ ksms = 2 s(s + ) φ ksms, (.47) S z φ ksms = m s φ ksms. (.48) A partir destas equações é fácil notar que os estados φ ksms podem ser escritos como uma função das coordenadas vezes uma parte devida ao 5 Cuidado! Nem sempre os operadores de spin comutam com a hamiltoniana do sistema. Por exemplo, forças nucleares exibem termos dependentes do spin.
15 20 Capítulo. Spin e Adição de Momento Angular spin. Mais explicitamente, estes estados são ( ) e ik x, 0 ( ) 0 e ik x. Note que o número de estados foi duplicado em relação a uma partícula sem spin. Na verdade, este é um fato geral: se a hamiltoniana de um sistema de partículas de spin s comuta com os operadores de spin, então a degenerescência dos estados é multiplicada por 2s +. Por exemplo para um átomo de hidrogênio, a degenerescência do nível n passa de n 2 para 2n 2 devido ao fato do elétron ter spin /2. Um outro ponto interessante a respeito das soluções acima é que o estado do sistema passou a ser dado por uma matriz coluna ( ) Ψ (x) Ψ =, (.49) Ψ 2 (x) cujos elementos são funções da posição. Uma vez que modificamos o estado do sistema devemos redefinir o produto escalar associado ao espaço vetorial dos estados. Tendo em vista as propriedades exigidas do produto escalar e a forma dos estados é natural definir Ψ Φ = = d 3 x Ψ Φ, d 3 x (Ψ (x) Ψ 2(x)) ( Φ (x) Φ 2 (x) ) d 3 x (Ψ (x)φ (x) + Ψ 2(x)Φ 2 (x)),, (.50) onde denota a operação de obter o hermitiano conjugado da matriz, i.e. tomar o complexo conjugado e transpor 6. É interessante notar que para estados que são o produto de uma função de spin por uma função 6 Exercício: Mostre que esta definição de produto escalar obedece a todas as propriedades esperadas.
16 .4. Composição de momentos angulares 2 onda, o produto escalar é obtido multiplicando-se o produto escalar da função de onda pelo produto escalar de spin 7. O significado probabilístico dos estados (.49) também deve ser redefinido: Agora a densidade de probabilidade do elétron estar em x é dada por Ψ (x) 2 + Ψ 2 (x) 2. Por outro lado, a probabilidade do elétron ter m s = /2 ( /2) é dada por d 3 x Ψ (2) (x) 2..4 Composição de momentos angulares Usualmente somos levados a tratar sistemas cujo momento angular total é a soma de diversas contribuições. Por exemplo, átomos com muitos elétrons ou uma partícula com spin. Vamos agora estudar a adição de momento angular em Mecânica Quântica. Consideremos um sistema cujo momento angular total é dado pela soma de duas parcelas J = L + 2 L, (.5) onde L e 2 L obedecem à álgebra de momento angular (.7). Mais ainda, L e 2 L comutam já que estes operadores referem-se a partículas diferentes ou ao spin e ao momento angular orbital de uma mesma partícula. O operador J, que descreve a soma de dois momentos angulares, também satisfaz a álgebra de momento angular [J i,j j ] = i ǫ ijk J k, (.52) [ J 2,J j ] = 0, (.53) com J 2 ( L + 2 L) 2 = ( L) 2 + ( 2 L) L 2L, (.54) onde utilizamos que [ L, 2 L] = 0. Para prosseguir devemos verificar quais operadores podem ser diagonalizados simultaneamente. Portanto, devemos obter as relações de comutação entre os operadores L, 2 L e J. É fácil demonstrar que as 7 Exercício: Mostre este fato.
17 22 Capítulo. Spin e Adição de Momento Angular seguintes relações são satisfeitas 8 [ ] Ji, (2) L j = i ǫ ijk (2) L k, (.55) [ ] J 2, (2) L i = i2 ǫ lik 2() L l (2) L k, (.56) [ Ji, (2) L 2] = 0, (.57) [ J 2, (2) L 2] = 0. (.58) Estas relações implicam que J 2 não pode ser diagonalizado simultaneamente com a componente z de L ou 2 L. É tradicional diagonalizar ( L 2, L z, 2 L 2, 2 L z ) ou o conjunto (J 2, J z, L 2, 2 L 2 ). No primeiro caso chamamos a base gerada pelos autovetores de base desacoplada, enquanto no segundo chamamos de base acoplada. Estudemos com maior detalhe estas duas bases, bem como a relação entre elas..4. Base desacoplada Esta escolha é mais simples, no sentido que a obtenção dos autoestados é trivial uma vez que já conhecemos os autovetores e autovalores de (2)L 2 e (2) L z. De fato, o problema de autovalores que define essa base é L 2 Φ l l 2 m m 2 = 2 l (l + )Φ l l 2 m m 2, (.59) L z Φ l l 2 m m 2 = m Φ l l 2 m m 2, (.60) 2L 2 Φ l l 2 m m 2 = 2 l 2 (l 2 + )Φ l l 2 m m 2, (.6) 2L z Φ l l 2 m m 2 = m 2 Φ l l 2 m m 2, (.62) cuja solução é Φ l l 2 m m 2 = ϕ l m ϕ l2 m 2, (.63) onde ϕ li m i são os autoestados conhecidos de i L 2 e i L z (i =, 2). Por exemplo, se L é o momento angular orbital de um elétron no átomo 8 Exercício: Demonstre estas relações.
18 .4. Composição de momentos angulares 23 de hidrogênio e 2 L é seu spin, então a base desacoplada é dada por ( ) Φ l = Y 2 m lm (θ, φ), (.64) 2 0 ( ) 0 Φ l = Y 2 m lm (θ, φ). (.65) 2 Ou ainda, se (2) L forem os momentos angulares orbitais dos elétrons num átomo de hélio, então Φ l l 2 m m 2 = Y l m (θ, φ ) Y l2 m 2 (θ 2, φ 2 ), (.66) onde (θ (2), φ (2) ) são as coordenadas angulares dos elétrons. Apesar de sua simplicidade de obtenção, a base desacoplada possui o grave defeito de não ser autoestado de J 2! Logo, em muitas aplicações devemos trabalhar com a base acoplada..4.2 Base acoplada Podemos também escolher diagonalizar simultaneamente os operadores (J 2, J z, L 2, 2 L 2 ), i.e. J 2 Φ jml l 2 = 2 j(j + )Φ jml l 2, (.67) J z Φ jml l 2 = mφ jml l 2, (.68) L 2 Φ jml l 2 = 2 l (l + )Φ jml l 2, (.69) 2L 2 Φ jml l 2 = 2 l 2 (l 2 + )Φ jml l 2. (.70) Este conjunto de equações define os estados Φ jml l 2, i.e. podemos em princípio resolver estas equações. Todavia, é mais simples e geral obter estes estados como combinações lineares dos vetores da base desacoplada. Isto é possível pois estes dois conjuntos de vetores (acoplados e dasacoplados) formam bases do mesmo espaço vetorial e conseqüentemente um pode ser expresso como combinação linear do outro. Logo, podemos escrever, sem perda de generalidade, que Φ jml l 2 = m m 2 C m m 2 Φ l l 2 m m 2. (.7)
19 24 Capítulo. Spin e Adição de Momento Angular Note que esta soma é apenas sobre m e m 2 já que l e l 2 estão fixos pois as duas bases são formadas de autovetores de (2) L 2. Mais ainda, sabemos que C m m 2 = Φ l l 2 m m 2 Φ jml l 2. (.72) Os coeficientes C m m 2 da expansão (.7) são chamados de coeficientes de Clebsch Gordan. Apesar de não estar explicitado, os coeficientes C m m 2 dependem de j, m, l e l 2. Nosso objetivo agora é mostrar que a relação (.7) pode ser usada para determinar quais os possíveis valores que j pode assumir. Posteriormente, mostraremos um método para o cálculo dos coeficientes de Clebsch Gordan. Relação fundamental Em primeiro lugar devemos notar que a soma sobre m e m 2 em (.7) não é arbitrária, sendo que ela deve satisfazer ao vínculo m +m 2 = m. De fato, consideremos o elemento de matriz Φ jml l 2 J z Φ l l 2 m m 2 = (m + m 2 ) Φ jml l 2 Φ l l 2 m m 2 (.73) = m Φ jml l 2 Φ l l 2 m m 2. (.74) A primeira igualdade é obtida escrevendo que J z = L z + 2 L z, enquanto que a segunda decorre do fato de J z ser hermitiano e de Φ jml l 2 ser seu autovetor. Logo, podemos inferir que C m m 2 é não nulo somente se Exemplo m = m + m 2. (.75) Neste ponto é instrutivo verificar quais são os possíveis valores que m pode assumir, bem como sua degenerescência, para o caso da soma de dois momentos angulares com l =. Utilizando (.75) podemos obter a tabela. abaixo. A partir desta tabela podemos verificar os seguintes fatos (gerais): O maior m possível não é degenerado. O segundo maior valor de m é duplamente degenerado.
20 .4. Composição de momentos angulares 25 m m 2 m Tabela.: Valores possíveis de m e sua multiplicidade no caso da adição de dois momentos angulares com l = A degenerescência de m aumenta em passos de até atingir um valor máximo, então vindo a diminuir. Neste exemplo é fácil ver que os valores possíveis de j são 2, e 0. De fato, o maior j deve ser 2 já que temos um estado com m = 2. Retirados os 5 estados com j = 2, sobram 4 possibilidades com valor máximo de m igual a. Logo, temos j =, o qual explica três dos estados, restando apenas um estado com m = 0 associado a j = 0. O fato de j variar em passos de é um fato geral que o leitor deve verificar utilizando as observações ( ) acima. Relação triangular A partir de (.75) podemos deduzir que o máximo valor para m é dado por l + l 2, o qual corresponde aos máximos valores possíveis para m e m 2. Uma vez que J i obedece à álgebra de momento angular devemos ter que o máximo valor de j é dado por j max = l + l 2. (.76) Mais ainda, a relação (.75) implica que os possíveis m diferem entre si por inteiros, já que isto ocorre para m e m 2. Logo, os valores
21 26 Capítulo. Spin e Adição de Momento Angular admissíveis para j devem diferir de j max por um inteiro. Para obtermos os valores possíveis de j compatíveis com l e l 2 dados, basta impor que a dimensão do espaço gerado pela base desacoplada seja igual a do espaço gerado pela base acoplada. A partir da base desacoplada sabemos que a dimensão deste espaço é dada por (2l + )(2l 2 + ). Lembrando que para cada valor de j temos 2j + estados segue que j max j min (2j + ) = (2l + )(2l 2 + ), (.77) o que nos permite concluir que j min = l l 2. Portanto, temos que l l 2 j l + l 2. (.78) Por exemplo, quando compomos um momento angular com l = com um segundo com l 2 = 3 podemos obter j = 2, 3 e 4. Ou ainda, a adição de dois spins /2 resulta em j = 0 ou j =. Coeficientes de Clebsch-Gordan Vamos agora apenas delinear o procedimento para a obtenção dos coeficientes de mudança da base desacoplada para a acoplada. Via de regra a obtenção dos coeficientes de Clebsch-Gordan é direta mas entediante! Os passos a serem seguidos são os seguintes:. Para j = j max e m = j max é trivial ver que pois esta é a única combinação possível. Φ jmaxj maxl l 2 = Φ l l 2 l l 2, (.79) 2. Agora aplicando J = L + 2 L a (.79) obtemos todos os estados Φ jmaxml l 2 em função da base desacoplada. 3. O próximo passo é obter Φ jjl l 2, onde j é o maior valor de j ainda não determinado. Isto é feito exigindo-se que este estado seja ortogonal a Φ j jl l 2, com j > j, i.e. este estado deve ser ortogonal a todos os estados com o mesmo autovalor de J z mas
22 .4. Composição de momentos angulares 27 com autovalores de J 2 maiores. Além disso exigimos que o estado Φ jjl l 2 esteja normalizado Os estados Φ jml l 2 com m < j são obtidos usando o operador J, como no segundo passo. 5. Voltamos agora para o terceiro passo até ter obtidos todos os coeficientes. Para exemplificar este procedimento consideremos a adição de um momento angular orbital l = com um spin /2. Denotamos por α e β os autovetores de spin /2 com componente S z igual a /2 e /2 respectivamente. α = ( 0 ) Para j = m = 3/2 temos que Φ Aplicando J resulta que ( ) ( ) 2 + e β = ( 0 ) = Y (θ, φ) α. (.80) Φ ( + )( + ) Y 0 α + = ( ) ( 2 ) 2 + Y β. Para obter os estados com m = /2 e m = 3/2 aplicamos J mais duas vezes. Com isso temos que Φ Φ Φ = 3 Y 0α + 3 Y β, (.8) 2 = 3 Y α + 3 Y 0β, (.82) = Y β. (.83) 9 Existe uma fase arbitrária que deve ser fixada.
23 28 Capítulo. Spin e Adição de Momento Angular Agora escrevemos que e impomos que Φ = ay 0 α + by β, (.84) Φ3 Φ Φ Φ o que nos permite obter a e b. Φ = Y 0α + Atuando com J chegamos a 2 Φ = Y α + = 0, (.85) =, (.86) 2 3 Y β (.87) 3 Y 0β (.88) Exercício Obtenha a base acoplada para a adição de dois spins /2.
24 .5. Apêndice: produto tensorial de espaços vetoriais 29.5 Apêndice: produto tensorial de espaços vetoriais Muitos dos resultados deste capítulo podem ser expressos utilizando o produto tensorial de espaços vetoriais. Tendo em vista a sua utilidade, faremos uma rápida revisão das principais propriedades deste produto..5. Espaço produto Consideremos três espaços vetoriais V, V 2 e V. Dizemos que V é o produto tensorial de V por V 2, denotado por V V 2, se. Existir uma função função bilinear V V 2 V v v 2 v v 2, onde v i V i (i =, 2) e v v 2 V. Lembre-se que uma função bilinear deve obedecer a (a) (α v ) v 2 = α ( v v 2 ) = v (α v 2 ) (b) ( u + v ) v 2 = u v 2 + v v 2 (c) v ( u 2 + v 2 ) = v u 2 + v v 2 onde u i, v i V i para i =, 2 e α é uma constante. 2. Dadas as bases de { u i } de V e { v j } de V 2, então o conjunto { u i v j } é uma base de V. Exemplo Consideremos uma partícula de spin /2 movendo-se ao longo de uma reta. O espaço de Hilbert associado ao spin /2 é, conforme vimos, V = C, enquanto que o seu movimento unidimensional está associado ao espaço das funções de quadrado integrável V 2 = L. Por outro lado o espaço de Hilbert associado a este sistema, vide (.49), é V = { Ψ = ( Ψ (x) Ψ 2 (x) ) } dx Ψ i (x) 2 < (.89)
25 220 Capítulo. Spin e Adição de Momento Angular.5.2 Vetores de V V 2 Consideremos bases arbitrárias { u i (2) } de V (2). Dois vetores genéricos ϕ e ϕ 2 pertencentes a V e V 2, respectivamente, podem ser escritos como ϕ = a i u i e ϕ 2 = b j u j. (.90) i j Logo, o produto tensorial destes vetores é dado por ϕ ϕ 2 = ij a i b j u i uj 2, (.9) ou seja, as componente do vetor ϕ ϕ 2 na base { u i u j 2 } são a i b j. Por outro lado, um vetor ψ arbitrário de V V 2 pode ser escrito como ψ = c ij u i u j 2, (.92) ij onde c ij são constantes. Todavia, nem sempre é possível encontrar a i e b j tais que c ij = a i b j, isto é, não são todos os vetores de V V 2 que podem ser escritos como u produto tensorial de vetores de V por outro de V 2. Exemplo Considere o espaço vetorial V definido por (.89).
Momento Angular. 8.1 Álgebra do Momento Angular
 Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/2 e de Dois Níveis
 Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Lista Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor.
 Lista 4 1. Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor. = ( ) (a) Mostre que a rotação própria (o que não envolve inversão dos eixos,
Lista 4 1. Definimos uma rotação em termos de um vetor unitário que difine o plano da rotação e o ângulo em torno deste vetor. = ( ) (a) Mostre que a rotação própria (o que não envolve inversão dos eixos,
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Mecânica Quântica. Spin 1/2 e a formulação da M. Q. Parte II. A C Tort 1. Instituto Física Universidade Federal do Rio de Janeiro
 Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
SEGUNDA PROVA - F789. angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) =
 SEGUNDA PROVA - F789 NOME: RA:. Considere uma partícula de spin. Seja S seu spin e L seu momento angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) = r, ± Ψ na base r, ± de autoestados
SEGUNDA PROVA - F789 NOME: RA:. Considere uma partícula de spin. Seja S seu spin e L seu momento angular orbital. O estado da partícula, Ψ, tem componentes Ψ ± (r) = r, ± Ψ na base r, ± de autoestados
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
A Experiência de Stern-Gerlach e o Spin do Elétron
 UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Lista Considere um oscilador harmonico tridimencional com o potencial, resolve a Equação de Schrödinger independente no tempo
 Lista 8. Considere um oscilador harmonico tridimencional com o potencial, V = m 2 ( ω 2 x x 2 + ω 2 yy 2 + ω 2 zz 2), onde ω x, ω y e ω z representam as frequências deste oscilador (clássico) nas direções,
Lista 8. Considere um oscilador harmonico tridimencional com o potencial, V = m 2 ( ω 2 x x 2 + ω 2 yy 2 + ω 2 zz 2), onde ω x, ω y e ω z representam as frequências deste oscilador (clássico) nas direções,
- identificar operadores ortogonais e unitários e conhecer as suas propriedades;
 DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
O spin do elétron. Vimos, na aula 2, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com 2 valores, com propriedades de momento angular.
 O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
Os Postulados da Mecânica Quântica
 Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Física Quântica. Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli. Pieter Westera
 Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FNC376N: Lista de março de ψ r ψ = Eψ. sin θ Y )
 FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
O Método de Hartree-Fock
 O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
Adição de dois spins1/2
 Adição de dois spins/ a c tort de julho de O momento angular é um dos pontos mais importantes da mecânica quântica. Saber somar dois ou três momentos angulares é crucial para o entendimento da estrutura
Adição de dois spins/ a c tort de julho de O momento angular é um dos pontos mais importantes da mecânica quântica. Saber somar dois ou três momentos angulares é crucial para o entendimento da estrutura
Aula de Física Atômica e molecular. Operadores em Mecânica Quântica Prof. Vicente
 Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica
 CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
O ÁTOMO DE HIDROGÊNIO
 FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville O ÁTOMO DE HIDROGÊNIO A elegância, a riqueza, a complexidade e a diversidade dos fenômenos naturais que decorrem
FÍSICA PARA ENGENHARIA ELÉTRICA José Fernando Fragalli Departamento de Física Udesc/Joinville O ÁTOMO DE HIDROGÊNIO A elegância, a riqueza, a complexidade e a diversidade dos fenômenos naturais que decorrem
Rotor quântico. Quanticamente o rotor é descrito por uma função de onda, tal que: l A função de onda do estado estacionário é dada por:
 Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Aula 17 Tudo sobre os Átomos
 Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Mecânica Quântica:
 Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
O ÁTOMO DE HIDROGÊNIO
 O ÁTOMO DE HIDROGÊNIO Alessandra de Souza Barbosa 04 de dezembro de 013 O átomo de hidrogênio Alessandra de Souza Barbosa CF37 - Mecânica Quântica I /36 Sistema de duas particulas um elétron e um próton;
O ÁTOMO DE HIDROGÊNIO Alessandra de Souza Barbosa 04 de dezembro de 013 O átomo de hidrogênio Alessandra de Souza Barbosa CF37 - Mecânica Quântica I /36 Sistema de duas particulas um elétron e um próton;
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 8. A equação de Schrödinger
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
i : V W V W é o produto tensorial de V e W se, ao considerarmos um outro espaço vetorial U sobre o mesmo corpo K e B também uma aplicação bilinear:
 3 Produto Tensorial Sistemas quânticos individuais podem interagir para formarem sistemas quânticos compostos. Existe um postulado em Mecânica Quântica que descreve como o espaço de estados do sistema
3 Produto Tensorial Sistemas quânticos individuais podem interagir para formarem sistemas quânticos compostos. Existe um postulado em Mecânica Quântica que descreve como o espaço de estados do sistema
Universidade de São Paulo em São Carlos Mecânica Quântica Aplicada Prova 1
 Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Valores esperados. ψ (x)xψ(x)dx. ψ ψ dx. xp(x)dx P(x)dx. Vimos que: x = = ψ xψ dx. No caso geral de uma função de x: f (x) = f (x) =
 Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
Física Moderna II Aula 03. Marcelo G Munhoz Pelletron, sala 245, ramal 6940
 Física Moderna II Aula 03 Marcelo G Munhoz Pelletron, sala 245, ramal 6940 munhoz@if.usp.br Schroedinger X Bohr Qual a vantagem da teoria de Schroedinger sobre a teoria de Bohr do ponto de vista da observação
Física Moderna II Aula 03 Marcelo G Munhoz Pelletron, sala 245, ramal 6940 munhoz@if.usp.br Schroedinger X Bohr Qual a vantagem da teoria de Schroedinger sobre a teoria de Bohr do ponto de vista da observação
Aula 12. (quase) Tudo sobre os átomos. Física Geral F-428
 Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
Introdução ao Método de Hartree-Fock
 Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
QFL 2144 Parte 3A: Ressonância magnética nuclear
 QFL 2144 Parte 3A: Ressonância magnética nuclear Espectroscopia de RMN: espectroscopia associada com a mudança de estado energético de núcleos atômicos na presença de um campo magnético. Elementos básicos
QFL 2144 Parte 3A: Ressonância magnética nuclear Espectroscopia de RMN: espectroscopia associada com a mudança de estado energético de núcleos atômicos na presença de um campo magnético. Elementos básicos
Princípios Gerais da Mecânica Quântica
 Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Introdução. O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico.
 Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Raios atômicos Física Moderna 2 Aula 6
 Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
O poço quadrado finito
 O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
1 O Átomo de Hidrogênio
 O modelo de Bohr para o átomo de hidrogênio, embora forneça valores corretos para as energias dos estados atômicos e do espectro da radiação emitida, não pode ser correto do ponto de vista da mecânica
O modelo de Bohr para o átomo de hidrogênio, embora forneça valores corretos para as energias dos estados atômicos e do espectro da radiação emitida, não pode ser correto do ponto de vista da mecânica
Átomo de Hidrogênio 1
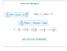 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Quantização. Quantização da energia (Planck, 1900) hc h. Efeito fotoelétrico (Einstein, 1905) Espectros atômicos (linhas discretas) v 2
 Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II. q exp( q 2 ) ( 2 π. 2 (2q 2 1) exp( q 2 )
 CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
Funções ortogonais e problemas de Sturm-Liouville. Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE
 Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Teoria Escalar da Difração
 Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Física IV Escola Politécnica P3 7 de dezembro de 2017
 Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
SPI5814 Física atômica e molecular - Equações de Bloch ópticas
 SPI5814 Física atômica e molecular - Equações de Bloch ópticas Rafael Bruno Barbosa Lima Instituto de Física de São Carlos, Universidade de São Paulo, São Carlos, Brasil (Dated: Novembro de 2015) 1 I.
SPI5814 Física atômica e molecular - Equações de Bloch ópticas Rafael Bruno Barbosa Lima Instituto de Física de São Carlos, Universidade de São Paulo, São Carlos, Brasil (Dated: Novembro de 2015) 1 I.
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
Exame Unificado EUF. 1º Semestre/2013 Parte 1 16/10/2012
 Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
1 Matrizes Ortogonais
 Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
Notas de Aula da Disciplina
 Notas de Aula da Disciplina Mecânica Quântica Alexandre Souto Martinez Universidade de São Paulo - USP Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto - FFCLRP Departamento de Física - DF tel:
Notas de Aula da Disciplina Mecânica Quântica Alexandre Souto Martinez Universidade de São Paulo - USP Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto - FFCLRP Departamento de Física - DF tel:
7.1 Representação de Heisenberg
 Capítulo 7 Representação de Heisenberg e Simetrias Quando apresentamos os postulados da Mecânica Quântica definimos de forma arbitrária que os estados evoluem no tempo ao passo que os observáveis são constantes.
Capítulo 7 Representação de Heisenberg e Simetrias Quando apresentamos os postulados da Mecânica Quântica definimos de forma arbitrária que os estados evoluem no tempo ao passo que os observáveis são constantes.
Física IV Poli Engenharia Elétrica: 20ª Aula (04/11/2014)
 Física IV Poli Engenharia Elétrica: ª Aula (4/11/14) Prof. Alvaro Vannucci a última aula vimos: Átomos multi-eletrônicos: as energias dos estados quânticos podem ser avaliadas através da expressão: 13,6
Física IV Poli Engenharia Elétrica: ª Aula (4/11/14) Prof. Alvaro Vannucci a última aula vimos: Átomos multi-eletrônicos: as energias dos estados quânticos podem ser avaliadas através da expressão: 13,6
Eletromagnetismo I. Preparo: Diego Oliveira. Aula c 2 2 A i
 Eletromagnetismo I Prof. Dr. R.M.O Galvão - 2 Semestre 214 Preparo: Diego Oliveira Aula 26 Transformada de Fourier da Equação de Onda Nós vimos que, em uma dimensão, a equação de onda é dada por 2 A i
Eletromagnetismo I Prof. Dr. R.M.O Galvão - 2 Semestre 214 Preparo: Diego Oliveira Aula 26 Transformada de Fourier da Equação de Onda Nós vimos que, em uma dimensão, a equação de onda é dada por 2 A i
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0)
 este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
Bilineares do Campo de Dirac. Analogamente:
 Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
Eletromagnetismo II. 5 a Aula. Professor Alvaro Vannucci. nucci
 Eletromagnetismo II 5 a Aula Professor Alvaro Vannucci nucci Na aula passada, das Equações de Maxwell,, vimos: 1 o ) Conservação de Energia n da = S S ( E H ) ˆ (Vetor de Poynting) 1 + + H B E D V dv t
Eletromagnetismo II 5 a Aula Professor Alvaro Vannucci nucci Na aula passada, das Equações de Maxwell,, vimos: 1 o ) Conservação de Energia n da = S S ( E H ) ˆ (Vetor de Poynting) 1 + + H B E D V dv t
Não serão aceitas respostas sem justificativa:
 Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
2, ao medirmos um observável deste estado que possui autovetores 0 e 1, obtemos o resultado 0 com probabilidade α 2, e 1 com probabilidade β 2.
 4 Informação Quântica A teoria da Informação Quântica foi basicamente desenvolvida na última década (3, 10, 16). Nosso objetivo neste capítulo é apresentar sua estrutura fundamental, o bit quântico, e
4 Informação Quântica A teoria da Informação Quântica foi basicamente desenvolvida na última década (3, 10, 16). Nosso objetivo neste capítulo é apresentar sua estrutura fundamental, o bit quântico, e
Teoria Clássica de Campos
 Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Mecânica Quântica. Química Quântica Prof a. Dr a. Carla Dalmolin. A Equação de Schrödinger Postulados da Mecânica Quântica
 Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
Simetrias C, P e T para férmions
 Teoria Quântica de Campos I 152 ( eq. 152.1 ) No entanto a corrente axial: só é conservada se o férmion em questão não tiver massa: Simetrias C, P e T para férmions ( eq. 152.2 ) Além da simetria de Lorentz
Teoria Quântica de Campos I 152 ( eq. 152.1 ) No entanto a corrente axial: só é conservada se o férmion em questão não tiver massa: Simetrias C, P e T para férmions ( eq. 152.2 ) Além da simetria de Lorentz
Universidade de São Paulo Instituto de Física. Física Moderna II. Profa. Márcia de Almeida Rizzutto 2 o Semestre de Física Moderna 2 Aula 5
 Universidade de São Paulo Instituto de Física Física Moderna II Profa. Márcia de Almeida Rizzutto o Semestre de 014 1 19: experiência de Stern&Gerlach Proposta: Medir os valores possíveis do momento de
Universidade de São Paulo Instituto de Física Física Moderna II Profa. Márcia de Almeida Rizzutto o Semestre de 014 1 19: experiência de Stern&Gerlach Proposta: Medir os valores possíveis do momento de
Equação de Schrödinger
 Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
CONTEÚDO PROGRAMÁTICO EMENTA
 UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
n, l, m l, ms (1) quando estes quatro números quânticos são dados, o estado físico do sistema (no caso, um elétron) é então especificado.
 Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
Representação grande
 Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Correlação Eletrônica - CI e MP2
 Correlação Eletrônica - CI e MP2 CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do
Correlação Eletrônica - CI e MP2 CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
OPERADORES HERMITIANOS Mecânica Quântica I ( ) - Capítulo 03
 ESPAÇO DE FUNÇÕES E OPERADORES HERMITIANOS Mecânica Quântica I (1108045) - Capítulo 03 I. Paulino* *UAF/CCT/UFCG - Brasil 2015.2 1 / 47 Sumário Conceitos Preparatórios Partícula numa caixa Princípio da
ESPAÇO DE FUNÇÕES E OPERADORES HERMITIANOS Mecânica Quântica I (1108045) - Capítulo 03 I. Paulino* *UAF/CCT/UFCG - Brasil 2015.2 1 / 47 Sumário Conceitos Preparatórios Partícula numa caixa Princípio da
Simetrias na Mecânica Quântica
 Simetrias na Mecânica Quântica Prof. 26 de maio de 2010 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, ˆT(G(a)) operador unitário. G(a) M.Q. ˆT(G(a)),
Simetrias na Mecânica Quântica Prof. 26 de maio de 2010 Definição de Simetria na Mecânica Quântica G(a) elemento de um grupo G de transformações contínuas, ˆT(G(a)) operador unitário. G(a) M.Q. ˆT(G(a)),
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Física Computacional 18 matrizes: inversão, valores próprios e sol. da eq. De Schrödinger
 Física Computacional 18 matrizes: inversão, valores próprios e sol. da eq. De Schrödinger 1. Trabalhar com matrizes, e aplicá-las a um problema físico a. Inversão da matriz, eliminação de Gauss b. Determinante
Física Computacional 18 matrizes: inversão, valores próprios e sol. da eq. De Schrödinger 1. Trabalhar com matrizes, e aplicá-las a um problema físico a. Inversão da matriz, eliminação de Gauss b. Determinante
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
JORNADA DE FÍSICA TEÓRICA INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a
 JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
Exame Unificado das Pós-graduações em Física EUF
 Exame Unificado das Pós-graduações em Física EUF 1º Semestre/01 Parte 1 04/10/011 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
Exame Unificado das Pós-graduações em Física EUF 1º Semestre/01 Parte 1 04/10/011 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS
 EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
h (1 cos θ) onde, m e é a massa do elétron, θ é o ângulo pelo qual a direção do fóton muda λ 1 é o comprimento de onda do fóton antes do espalhamento,
 Universidade Federal do Pará Instituto de Ciências Exatas e Naturais Programa de Pós-Graduação em Física Exame de Seleção - Data: 09/06/2014 Nome do Candidato: Nível: Mestrado Doutorado 1. A função de
Universidade Federal do Pará Instituto de Ciências Exatas e Naturais Programa de Pós-Graduação em Física Exame de Seleção - Data: 09/06/2014 Nome do Candidato: Nível: Mestrado Doutorado 1. A função de
ONDULATÓRIA: EQUAÇÃO DE ONDAS E CONCEITOS
 TE053-Ondas Eletromagnéticas ONDULATÓRIA: EQUAÇÃO DE ONDAS E CONCEITOS BÁSICOS PROF. CÉSAR AUGUSTO DARTORA - UFPR E-MAIL: CADARTORA@ELETRICA.UFPR.BR CURITIBA-PR Roteiro da Aula: Conceitos básicos sobre
TE053-Ondas Eletromagnéticas ONDULATÓRIA: EQUAÇÃO DE ONDAS E CONCEITOS BÁSICOS PROF. CÉSAR AUGUSTO DARTORA - UFPR E-MAIL: CADARTORA@ELETRICA.UFPR.BR CURITIBA-PR Roteiro da Aula: Conceitos básicos sobre
PGF Mecânica Clássica Prof. Iberê L. Caldas
 PGF 55 - Mecânica Clássica Prof. Iberê L. Caldas Terceiro Estudo Dirigido o semestre de 18 Os estudos dirigidos podem ser realizados em duplas. Apenas os exercícios marcados com asteriscos precisam ser
PGF 55 - Mecânica Clássica Prof. Iberê L. Caldas Terceiro Estudo Dirigido o semestre de 18 Os estudos dirigidos podem ser realizados em duplas. Apenas os exercícios marcados com asteriscos precisam ser
Física III IQ 2014 ( )
 Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
Atividade de treinamento - Introdução: Esta atividade tem dois objetivos: 1) Apresentar os conceitos de distribuições contínuas de carga e momento de dipolo ) Revisar técnicas de cálculo e sistemas de
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.1 Vibrações de uma membrana Como mencionado na aula passada, pode-se deduzir
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 5 Ref. Butkov, caps. 8 e 9, seções 8.8 e 9.1 Vibrações de uma membrana Como mencionado na aula passada, pode-se deduzir
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
A Equação de Onda de Schröedinger. O Princípio da Incerteza de Heisenberg. λ =
 O Modelo Mecânico-Quântico Louis de Broglie apresentou a idéia de que, se as ondas luminosas exibiam características de partícula, então talvez as partículas de matéria pudessem mostrar propriedades ondulatórias.
O Modelo Mecânico-Quântico Louis de Broglie apresentou a idéia de que, se as ondas luminosas exibiam características de partícula, então talvez as partículas de matéria pudessem mostrar propriedades ondulatórias.
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi
 Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II ONDAS. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II ONDAS Prof. Bruno Farias Ondas Uma onda surge quando um sistema é deslocado de sua posição
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA II ONDAS Prof. Bruno Farias Ondas Uma onda surge quando um sistema é deslocado de sua posição
