dy dt d 2 y dt 2 d n y dt n y dy y= F t a= f t, v, x dv dt = f t, a dx = f t, v
|
|
|
- Aparecida Gorjão Franco
- 7 Há anos
- Visualizações:
Transcrição
1 Cap. 9.- Integração de Equações Diferenciais Ordinárias (ODE's) 9.1. Definições ODE ou EDO Equações diferenciais ordinárias são aquelas que relacionam derivadas totais de variáveis dependentes com uma única variável independente. A ordem da equação depende da ordem da maior derivada envolvida na expressão. Primeira ordem Segunda ordem dt d 2 y dt 2 = f t, y = f t, y, dt Ordem n d n y dt n = f t, y, dt,, d n 1 y dt n 1 As ODE's podem ser lineares ou não-lineares em função da sua função da variável dependente ser linear ou não. Linear Não-linear dt y=f t y y= F t dt Onde F(t) é chamado de termo fonte e quando é diferente de zero a equação é chamada de não-homogênea. Homogênea e não-linear Se o termo fonte é nulo a equação é chamada de homogênea. y y=0 dt Um sistema de ODE's envolve mais de uma variável dependente. Sistema de ODE's a= f t, v, x dv dt = f t, a dx = f t, v dt José Eduardo Mautone Barros 21/01/13 1/12
2 9.1. Definições(cont.) PDE ou EDP Primeira ordem Equações diferenciais parciais são aquelas que relacionam derivadas parciais de variáveis dependentes com duas ou mais variáveis independentes. y t y = f t, x, y x As equações diferenciais podem ser classificadas quanto ao problema físico representado, ou seja, suas condições iniciais e de contorno. Problema de valor inicial (IVP ou PIV) A solução é encontrada resolvendo a equação a partir de valores iniciais conhecidos. ex: sistema massamola-amortecedor x= x 0 parat=t 0 x Problema de valor de contorno (BVP ou PVC) A solução é encontrada resolvendo a equação a partir de valores iniciais conhecidos e condições especificadas em pontos determinados do domínio. ex: viga com engastamento duplo y 0 =0 para x=0 y L =0 para x= L x y 9.2. Solução Numérica de ODE's FDE ou EDF O processo de solução consiste em transformar as ODE's em equações algébricas através da discretização do domínio e aproximar as derivadas por diferenças finitas. As equações obtidas são chamadas de equações de diferenças finitas (FDE's) e constituem uma aproximação das ODE's originais. Exemplo de Métodos de Solução de ODE's O passo varia com o erro estimado. Euler explícito Preditor-Corretor Runge-Kutta (várias ordens) Adams-Bashforth-Moulton Gear (equações tipo stiff) Métodos de passo adaptativo José Eduardo Mautone Barros 21/01/13 2/12
3 Referências Cap. 6 do livro do Barroso et al., 1987 Cap. 12 do livro do Al-Khafaji et Tooley, 1986 Part II e Cap. 7 do livro do Hoffman, Método da Série de Taylor Seja a equação diferencial expressa por uma função e uma condição inicial (CI): y' = f t, y yt 0 = y 0 Equação Diferencial Condição Inicial Expandindo y(t) em uma série de Taylor em torno do ponto t = t 0, têm-se, ou, yt= yt 0 y' t 0 t t y ' ' t 0 t t y' ' ' t 0 t t n! y n t 0 t t 0 n yt= y t 0 y ' t 0 t 1 2 y ' ' t 0 t y ' ' ' t 0 t 3 onde, Leonhard Euler ( ) t=t t 0 é chamado de passo de integração A solução pelo método da Série de Taylor envolve a avaliação de várias derivadas de diferentes ordens, o que pode ser bastante complexo e trabalhoso Método de Euler Explícito Seja, y' = f t, y yt 0 = y 0 Equação Diferencial Condição Inicial O( ) = ordem do erro detruncamento da série O método explícito usa valores de derivadas em um ponto anterior ao ponto em cálculo Aproximando a derivada pela série de Taylor e usando somente os dois primeiros termos, têm-se, yt= y t 0 y ' t 0 t t 0 O t 2 Assim, pode-se escrever, para o método de Euler Explícito: y n1 = y n t f t n, y n José Eduardo Mautone Barros 21/01/13 3/12
4 9.5. Método de Runge-Kutta A idéia do método é assumir que a variação da variável dependente Δy = y n+1 -y n pode ser obtida por uma média ponderada de m estimativas Δy i (i = 1..m) calculadas usando diferentes valores de derivadas f(t,y) ao longo do intervalo de integração Δt. O método pode ser descrito por: Carl Dave Tolme Runge y n1 y n = c 1 y 1 c 2 y 2 c 3 y 3 y 1, y n y 2 2, y n 2 y 3 3, y n 3 y 4 4, y n 4 Os parâmetros c i, α i e β i são constantes do método escolhidas para ajustar a série de Taylor para y(t) até uma certa ordem. Runge-Kutta de 2 a ordem (ver dedução no livro texto) y n1 = y n y 2 y 1, y n y 2 t 2, y n y 1 2 Runge-Kutta de 4 a ordem y n1 = y n 1 6 y 12 y 2 2 y 3 y 4 y 1, y n y 2 t 2, y n y 1 2 y 3 t 2, y y 2 n 2 y 4 t, y n y 3 Notar que o primeiro termo é a estimativa do método de Euler Explícito e os outros termos são pontos a meia distância do ponto final t+δt e consistem em um procedimento de correção da estimativa inicial. Martin Wilhelm Kutta O método ainda é explícito e exige a avaliação de quatro derivadas em cada passo de integração (4 a ordem). José Eduardo Mautone Barros 21/01/13 4/12
5 9.6. Interpretação Geométrica Y Solução ODE Função Euler 0,4 Runge-Kutta 0,4 Runge-Kutta Y1 Runge-Kutta Y2 Runge-Kutta Y3 Runge-Kutta Y X 9.7. Erros Convergente Divergente A integração é dita convergente se a solução numérica se aproxima da solução exata. A integração é dita divergente se a solução numérica se afasta rapidamente da solução exata Solução ODE Função Euler 0,05 Euler 0,1 Euler 0,4 Runge-Kutta 0,4 Y X José Eduardo Mautone Barros 21/01/13 5/12
6 Observação Equações duras (Stiff) (Stiffness) Exemplo São equações que apresentam termos da derivada que variam muito rapidamente em diferentes faixas de integração. Os métodos tradicionais de integração divergem rapidamente para estas equações. y x= e 1000x x2 y' x= 1000[ y x2] y=-exp(-1000x)+(x+2) Y X /dx=-1000(y-x-2) dy/dx X José Eduardo Mautone Barros 21/01/13 6/12
7 Exemplos OFFICE CI = condição inicial CC =condição de contorno Euler Explícito h = passo de integração ODE Solução dt = y 2, CI y(0)=1 y=e t / 2 A B C 1 t y y' B2/2 3 A2+h B2+h*C2... Runge-Kutta 2a ordem Y n+1 =Y n +J2 A B C D E F 1 t y t1 y1 y'1 delta y A2 B2 B2/2 h*e2 3 A2+h Y n G H I J 1 t2 y2 y'2 delta y2 2 A2+h/2 B2+F2/2 H2/2 h*i Runge-Kutta 4a ordem h = passo de integração Y n+1 =Y n +1/6*(F2+ 2*J2+2*N2+R2) A B C D E F 1 t y t1 y1 y'1 delta y A2 B2 B2/2 h*e2 3 A2+h Y n G H I J 1 t2 y2 y'2 delta y2 2 A2+h/2 B2+F2/2 H2/2 h*i K L M N 1 t3 y3 y'3 delta y3 2 A2+h/2 B2+J2/2 L2/2 h*m O P Q R 1 t4 y4 y'4 delta y4 2 A2+h B2+N2 P2/2 h*q José Eduardo Mautone Barros 21/01/13 7/12
8 Exemplos (cont.) ODE dt = y 2, CI y 0=1 Solução y=e t / 2 Euler Explícito delta t = 0,4 t y y' y exato Erro(%) 0,00 1, , , ,0000 0,40 1, , , ,7523 0,80 1, , , ,4739 1,20 1, , , ,1653 1,60 2, , , ,8271 delta t = 0,1 t y y' y exato Erro(%) 0,00 1, , , ,0000 0,10 1, , , ,1209 0,20 1, , , ,2417 0,30 1, , , ,3623 0,40 1, , , ,4828 0,50 1, , , ,6031 0,60 1, , , ,7233 0,70 1, , , ,8433 0,80 1, , , ,9632 0,90 1, , , ,0829 1,00 1, , , ,2025 1,10 1, , , ,3220 1,20 1, , , ,4413 1,30 1, , , ,5605 1,40 1, , , ,6795 1,50 2, , , ,7984 1,60 2, , , ,9171 delta t = 0,05 t y y' y exato Erro(%) 0,00 1, , , ,0000 0,05 1, , , ,0307 0,10 1, , , ,0615 0,15 1, , , ,0922 0,20 1, , , ,1229 0,25 1, , , ,1536 0,30 1, , , ,1843 0,35 1, , , ,2149 0,40 1, , , ,2456 0,45 1, , , ,2763 0,50 1, , , ,3069 1,55 2, , , ,9484 1,60 2, , , ,9788 José Eduardo Mautone Barros 21/01/13 8/12
9 Exemplos (cont.) ODE dt = y 2, CI y 0=1 Solução y=e t / 2 Runge-Kutta 2 a ordem delta t = 0,2 t y t1=t y1=y y'1 delta y1=deltat*y'1 0,00 1, , , , , ,20 1, , , , , ,40 1, , , , , ,60 1, , , , , ,80 1, , , , , ,00 1, , , , , ,20 1, , , , , ,40 2, , , , , ,60 2, , , , ,22228 t2=t+deltat/2 y2=y+deltay1/2 y'2 deltay2=deltat*y'2 y exato Erro(%) 0, , , , , ,0000 0, , , , , ,0155 0, , , , , ,0309 0, , , , , ,0464 0, , , , , ,0618 1, , , , , ,0773 1, , , , , ,0928 1, , , , , ,1082 1, , , , , ,1237 José Eduardo Mautone Barros 21/01/13 9/12
10 Exemplos (cont.) ODE dt = y 2, CI y 0=1 Solução y=e t / 2 Runge-Kutta 4 a ordem delta t = 0,4 t y t1=t y1=y y'1 delta y1=deltat*y'1 0,00 1, , , , , ,40 1, , , , , ,80 1, , , , , ,20 1, , , , , ,60 2, , , , ,44510 t2=t+deltat/2 y2=y+deltay1/2 y'2 deltay2=deltat*y'2 0, , , , , , , , , , , , , , , , , , , ,48961 t3=t+deltat/2 y3=y+deltay2/2 y'3 delta y3=deltat*y'3 0, , , , , , , , , , , , , , , , , , , ,49407 t4=t+deltat y4=y+deltay3 y'4 delta y4=deltat*y'4 0, , , , , , , , , , , , , , , , , , , ,54392 y exato Erro(%) 1, ,0000 1, ,0002 1, ,0005 1, ,0007 2, ,0009 2,5 2,0 1,5 Y 1,0 F(t) Euler explícito 0,5 Runge-Kutta 2a Runge-Kutta 4a 0,0 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 t José Eduardo Mautone Barros 21/01/13 10/12
11 Exemplos (cont.) SCILAB ODE dt = y2 y sent cost CI y 0=0 rk = método de Runge- Kutta de quarta ordem adaptativo function ydot=f(t,y), ydot=y^2-y*sin(t)+cos(t),endfunction y0=0; t0=0; t=0:0.1:2*%pi; y=ode('rk',y0,t0,t,f) plot(t,y) plot = comando para apresentar um gráfico 2D José Eduardo Mautone Barros 21/01/13 11/12
12 Exercício Aeronave da equipe do CEFET-MG em 2002 Obs: Resolver separadamente o movimento em x (posição) e em y (altitude)! Peso da aeronave: 3 kg Carga útil: 10 kg Peso na decolagem (M): 13 kg Empuxo do motor a plena carga (E): 35 N Massa específica do ar (ρ): 1,22 kg/m 3 Coeficiente de arrasto (C d ): 0,1 Área de referência do arrasto (área transversal da fuselage) (A d ): 0,0176 m 2 Coeficiente de resistência ao rolamento (μ): 0,01 A competição SAE Aerodesign consiste no projeto de uma aeronave radiocontrolada conforme limitações impostas pela organização da prova, visando a maior carga útil possível ( O recorde atual é de 12,5 kg. O avião pesa em média 3 kg contando com o combustível. Calcular usando as informações abaixo, a velocidade da aeronave a 61 m da partida e a distância de decolagem. Deve-se usar dois métodos de integração de ODE s (Euler Explícito e Runge-Kutta de 2ª ordem) e comparar os resultados por meio de gráficos. As duas equações diferenciais que modelam o movimento do avião são definidas a seguir: dv dt = 1 M [ E 1 2 C d v 2 A d] dv dt = 1 M [ E 1 2 C d v 2 A d P L] dx dt =v dt =0 se L P dt = 1 M L Pt se LP onde, L= 1 2 C s v 2 A s e P=M g Coeficiente de sustentação (C s ): 2,0 Área de referência da sustentação (projeção horizontal da asa) (A s ): 0,3750 m 2 Distância máxima de decolagem (x max ): 61 m Altitude inicial (y): 0 m Posição inicial (x): 0 m Velocidade inicial (v): 0 m/s se PL se P L José Eduardo Mautone Barros 21/01/13 12/12
Solução Numérica de EDOs
 Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Solução Numérica de EDOs Maria Luísa Bambozzi de Oliveira SME0300 Cálculo Numérico 10 de Novembro, 2010 Introdução Equação Diferencial de 1a. Ordem y = f (x, y) f : função real dada, de duas variáveis
Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma:
 Edgard Jamhour Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma: n f x, x 0 = n=0 a n x x 0 f(x,x 0 ) = a 0 + a 1 (x-x 0 ) + a 2 (x-x
Edgard Jamhour Funções podem ser representadas como série de potências Uma série de potências centrada em x 0 tem a seguinte forma: n f x, x 0 = n=0 a n x x 0 f(x,x 0 ) = a 0 + a 1 (x-x 0 ) + a 2 (x-x
Métodos de Runge-Kutta
 Solução numérica de Equações Diferenciais Ordinárias: Métodos de Runge-Kutta Marina Andretta/Franklina Toledo ICMC-USP 31 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D.
Solução numérica de Equações Diferenciais Ordinárias: Métodos de Runge-Kutta Marina Andretta/Franklina Toledo ICMC-USP 31 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D.
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
Equações Diferenciais Métodos Adaptativos e Rigidez. Computação 2º Semestre 2016/2017
 Equações Diferenciais Métodos Adaptativos e Rigidez Computação 2º Semestre 2016/2017 Métodos Adaptativos Por vezes as soluções das EDOs têm diferentes escalas temporais: Em alguns intervalos de tempo a
Equações Diferenciais Métodos Adaptativos e Rigidez Computação 2º Semestre 2016/2017 Métodos Adaptativos Por vezes as soluções das EDOs têm diferentes escalas temporais: Em alguns intervalos de tempo a
10 Estabilidade de Métodos de Passo Simples
 MAP 2310 - Análise Numérica e Equações Diferenciais I 1 o Semestre de 2008 Análise Numérica NÃO REVISADO! 10 Estabilidade de Métodos de Passo Simples Continuamos interessados em estudar Métodos de Discretização
MAP 2310 - Análise Numérica e Equações Diferenciais I 1 o Semestre de 2008 Análise Numérica NÃO REVISADO! 10 Estabilidade de Métodos de Passo Simples Continuamos interessados em estudar Métodos de Discretização
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EDOs de primeira ordem Problema de Valor Inicial (PVI) dy dx = f x, y y x 0 = y 0 Método de passo simples valor novo = valor antigo + inclinação passo Método de Euler y
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EDOs de primeira ordem Problema de Valor Inicial (PVI) dy dx = f x, y y x 0 = y 0 Método de passo simples valor novo = valor antigo + inclinação passo Método de Euler y
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno
 étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
Cap. 4- Interpolação Numérica Definições. Censos de BH. Qual o número de habitantes na cidade de Belo Horizonte em 1975?
 Cap. 4- Interpolação Numérica 4.1. Definições Censos de BH População em BH (Habitantes,5,,, 1,5, 1,, 5, 194 196 198 Ano Ano 195 196 197 198 1991 1996 1 No. habitantes 5.74 68.98 1.5. 1.78.855..161.91.71.8.56.75.444
Cap. 4- Interpolação Numérica 4.1. Definições Censos de BH População em BH (Habitantes,5,,, 1,5, 1,, 5, 194 196 198 Ano Ano 195 196 197 198 1991 1996 1 No. habitantes 5.74 68.98 1.5. 1.78.855..161.91.71.8.56.75.444
Equações Diferenciais Problemas de Valor Inicial. Computação 2º Semestre 2016/2017
 Equações Diferenciais Problemas de Valor Inicial Computação 2º Semestre 2016/2017 Equações Diferenciais Uma equação diferencial é uma equação cuja incógnita é uma função que aparece na equação sob a forma
Equações Diferenciais Problemas de Valor Inicial Computação 2º Semestre 2016/2017 Equações Diferenciais Uma equação diferencial é uma equação cuja incógnita é uma função que aparece na equação sob a forma
Modelagem Computacional. Aula 5 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 5 2 Prof. Thiago Alves de Queiroz 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 5 2 Prof. Thiago Alves de Queiroz 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Algoritmos Numéricos 2 a edição
 Algoritmos Numéricos 2 a edição Capítulo 7: Equaç~oes diferenciais ordinárias c 2009 FFCf 2 Capítulo 7: Equações diferenciais ordinárias 7.1 Solução numérica de EDO 7.2 Métodos de Runge-Kutta 7.3 Métodos
Algoritmos Numéricos 2 a edição Capítulo 7: Equaç~oes diferenciais ordinárias c 2009 FFCf 2 Capítulo 7: Equações diferenciais ordinárias 7.1 Solução numérica de EDO 7.2 Métodos de Runge-Kutta 7.3 Métodos
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Profa. Simone Aparecida Miloca UNIOESTE 2017 Sumario EQUAÇÕES DIFERENCIAIS ORDINÁRIAS MÉTODO DE EULER MÉTODOS DE SÉRIES DE TAYLOR MÉTODOS DE RUNGE KUTTA EQUAÇÕES DIFERENCIAIS
Equações Diferenciais Ordinárias Profa. Simone Aparecida Miloca UNIOESTE 2017 Sumario EQUAÇÕES DIFERENCIAIS ORDINÁRIAS MÉTODO DE EULER MÉTODOS DE SÉRIES DE TAYLOR MÉTODOS DE RUNGE KUTTA EQUAÇÕES DIFERENCIAIS
Cálculo Numérico P2 EM33D
 Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
Erros nas aproximações numéricas
 Erros nas aproximações numéricas Prof. Emílio Graciliano Ferreira Mercuri Departamento de Engenharia Ambiental - DEA, Universidade Federal do Paraná - UFPR emilio@ufpr.br 4 de março de 2013 Resumo: O objetivo
Erros nas aproximações numéricas Prof. Emílio Graciliano Ferreira Mercuri Departamento de Engenharia Ambiental - DEA, Universidade Federal do Paraná - UFPR emilio@ufpr.br 4 de março de 2013 Resumo: O objetivo
Capítulo 7 - Equações Diferenciais Ordinárias
 Capítulo 7 - Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Química e Gestão Industrial Carlos
Capítulo 7 - Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil, Química e Gestão Industrial Carlos
Queremos resolver uma equação diferencial da forma. dy dx. = f(x, y), (1)
 Resolução Numérica de Equações Diferenciais Método de Runge Kutta Queremos resolver uma equação diferencial da forma dy dx = f(x, y), (1) Isto é: queremos obter a função y(x) sabendo sua derivada. Numericamente:
Resolução Numérica de Equações Diferenciais Método de Runge Kutta Queremos resolver uma equação diferencial da forma dy dx = f(x, y), (1) Isto é: queremos obter a função y(x) sabendo sua derivada. Numericamente:
Métodos Numéricos em Engenharia Química
 Universidade Federal do Paraná UFPR Programa de Pós-Graduação em Engenharia Química PPGEQ Métodos Numéricos em Engenharia Química Prof. Éliton Fontana 2018/1 Conteúdo 1. Introdução 3 1.1. Classicação das
Universidade Federal do Paraná UFPR Programa de Pós-Graduação em Engenharia Química PPGEQ Métodos Numéricos em Engenharia Química Prof. Éliton Fontana 2018/1 Conteúdo 1. Introdução 3 1.1. Classicação das
Métodos Numéricos em Equações Diferenciais Aula 02 - Método de Euler
 Métodos Numéricos em Equações Diferenciais Aula 02 - Método de Euler Profa. Vanessa Rolnik curso: Matemática Aplicada a Negócios Introdução Método de Diferenças: { w0 = α w i+1 = w i + h φ(t i, w i ),
Métodos Numéricos em Equações Diferenciais Aula 02 - Método de Euler Profa. Vanessa Rolnik curso: Matemática Aplicada a Negócios Introdução Método de Diferenças: { w0 = α w i+1 = w i + h φ(t i, w i ),
dn dt = kn mudança de variável dn N = kdt dn N = k dt Solução: ln (N)=-kt + C N 0 =e k 0 e C t=0 resolvendo a equação diferencial tem-se N t =N 0 e kt
 1 CAPITULO 6 6.0 SOLUÇÕES NUMÉRICAS DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Conforme VILATTE ( 2001, p.1), Equação diferencial é qualquer relação entre uma função e suas derivadas. As equações diferenciais
1 CAPITULO 6 6.0 SOLUÇÕES NUMÉRICAS DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Conforme VILATTE ( 2001, p.1), Equação diferencial é qualquer relação entre uma função e suas derivadas. As equações diferenciais
Equações diferenciais ordinárias
 Departamento de Física Universidade Federal da Paraíba 24 de Junho de 2009 Motivação Problemas envolvendo equações diferenciais são muito comuns em física Exceto pelos mais simples, que podemos resolver
Departamento de Física Universidade Federal da Paraíba 24 de Junho de 2009 Motivação Problemas envolvendo equações diferenciais são muito comuns em física Exceto pelos mais simples, que podemos resolver
MÉTODOS NUMÉRICOS. ENGENHARIA e GESTÃO INDUSTRIAL
 UNIVERSIDADE DO MINHO MÉTODOS NUMÉRICOS ENGENHARIA e GESTÃO INDUSTRIAL EXERCÍCIOS PRÁTICOS Ano lectivo de 2005/2006 Métodos Numéricos - L.E.G.I. Exercícios práticos - CONUM Solução de uma equação não linear
UNIVERSIDADE DO MINHO MÉTODOS NUMÉRICOS ENGENHARIA e GESTÃO INDUSTRIAL EXERCÍCIOS PRÁTICOS Ano lectivo de 2005/2006 Métodos Numéricos - L.E.G.I. Exercícios práticos - CONUM Solução de uma equação não linear
Waldemar Celes. 2 de Setembro de 2014
 Simulação Física Métodos Numéricos de Integração Waldemar Celes celes@inf.puc-rio.br Tecgraf, DI/PUC-Rio 2 de Setembro de 2014 W. Celes, DI/PUC-Rio Simulação Física 1 Sumário Método de Euler Método de
Simulação Física Métodos Numéricos de Integração Waldemar Celes celes@inf.puc-rio.br Tecgraf, DI/PUC-Rio 2 de Setembro de 2014 W. Celes, DI/PUC-Rio Simulação Física 1 Sumário Método de Euler Método de
Lançamento Balístico
 Lançamento Balístico O estudo de sistemas, principalmente, sistemas naturais, trouxe grandes desafios para a ciência. Em um primeiro momento, o desafio era a representação desses sistemas por meio de modelagem.
Lançamento Balístico O estudo de sistemas, principalmente, sistemas naturais, trouxe grandes desafios para a ciência. Em um primeiro momento, o desafio era a representação desses sistemas por meio de modelagem.
4 Modelagem Numérica. 4.1 Método das Diferenças Finitas
 4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
Equações Diferenciais Ordinárias
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 2004/2005 Equações Diferenciais Ordinárias PROBLEMAS 1 Considere a equação diferencial dy dx = y(x2 1) com y(0) = 1 e x [0,
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 2004/2005 Equações Diferenciais Ordinárias PROBLEMAS 1 Considere a equação diferencial dy dx = y(x2 1) com y(0) = 1 e x [0,
Lista de Exercícios 3 e soluções
 Lista de Exercícios 3 e soluções MAT 069 - Cálculo Numérico Prof Dagoberto Adriano Rizzotto Justo 2 de Dezembro de 2006 Calcule a integral (a) A f dx = 0 (0) = = (b) A f 0 dx = 0 (0) = = 0 (c) A ( 2 f
Lista de Exercícios 3 e soluções MAT 069 - Cálculo Numérico Prof Dagoberto Adriano Rizzotto Justo 2 de Dezembro de 2006 Calcule a integral (a) A f dx = 0 (0) = = (b) A f 0 dx = 0 (0) = = 0 (c) A ( 2 f
Andréa Maria Pedrosa Valli
 1-24 Equações Diferenciais Ordinárias Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória,
1-24 Equações Diferenciais Ordinárias Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória,
Métodos Previsor-Corretor
 Solução numérica de Equações Diferenciais Ordinárias: Métodos Previsor-Corretor Marina Andretta/Franklina Toledo ICMC-USP 7 de novembro de 2013 Baseado no livro Cálculo Numérico, de S. Arenales e A. Darezzo.
Solução numérica de Equações Diferenciais Ordinárias: Métodos Previsor-Corretor Marina Andretta/Franklina Toledo ICMC-USP 7 de novembro de 2013 Baseado no livro Cálculo Numérico, de S. Arenales e A. Darezzo.
Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias
 Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
MAP CÁLCULO NUMÉRICO (POLI) Lista de Exercícios sobre Interpolação e Integração. φ(x k ) ψ(x k ).
 MAP 22 - CÁLCULO NUMÉRICO (POLI) Lista de Exercícios sobre Interpolação e Integração : Sejam x =, x =, x 2 = 2 e x 3 = 3. (a) Determine os polinômios de Lagrange L i (x) correspondentes a estes pontos
MAP 22 - CÁLCULO NUMÉRICO (POLI) Lista de Exercícios sobre Interpolação e Integração : Sejam x =, x =, x 2 = 2 e x 3 = 3. (a) Determine os polinômios de Lagrange L i (x) correspondentes a estes pontos
Cálculo Numérico. Resumo e Exercícios P2
 Cálculo Numérico Resumo e Exercícios P2 Fórmulas e Resumo Teórico P2 Interpolação Em um conjunto de n pontos (x #, y # ), consiste em encontrar uma função f tal que f x # = y # para todo i = 1,2,, n. Na
Cálculo Numérico Resumo e Exercícios P2 Fórmulas e Resumo Teórico P2 Interpolação Em um conjunto de n pontos (x #, y # ), consiste em encontrar uma função f tal que f x # = y # para todo i = 1,2,, n. Na
Lista de Exercícios 2 Cálculo Numérico - Professor Daniel
 Lista de Exercícios 2 Cálculo Numérico - Professor Daniel Observação: Esta lista abrange integração numérica e resolução numérica de EDO s. Em outras palavras, ela abrange toda a matéria da terceira prova.
Lista de Exercícios 2 Cálculo Numérico - Professor Daniel Observação: Esta lista abrange integração numérica e resolução numérica de EDO s. Em outras palavras, ela abrange toda a matéria da terceira prova.
Introdução ao Projeto de Aeronaves. Aula 10 Características do Estol e Utilização de Flapes na Aeronave
 Introdução ao Projeto de Aeronaves Aula 10 Características do Estol e Utilização de Flapes na Aeronave Tópicos Abordados O Estol e suas Características. Influência da Forma Geométrica da Asa na Propagação
Introdução ao Projeto de Aeronaves Aula 10 Características do Estol e Utilização de Flapes na Aeronave Tópicos Abordados O Estol e suas Características. Influência da Forma Geométrica da Asa na Propagação
Universidade de Coimbra Departamento de Engenharia Electrotecnica e Computadores Matemática Computacional
 Ano Lectivo: 2007/2008 Sumários da turma Teórico-Prática [TP1]: Aula: 1 Data: 2008-02-12 Hora de Início: 15:00 Duração: 1h30m Apresentação da Unidade Curricular. Discussão de aspectos relacionados com
Ano Lectivo: 2007/2008 Sumários da turma Teórico-Prática [TP1]: Aula: 1 Data: 2008-02-12 Hora de Início: 15:00 Duração: 1h30m Apresentação da Unidade Curricular. Discussão de aspectos relacionados com
Trajetórias de objetos: fundamentos
 Trajetórias de objetos: fundamentos Moussa Reda Mansour Por que Física????? Por que Física????? A física está presente no mundo real; A física pode tornar os jogos mais próximos do mundo real; Jogos que
Trajetórias de objetos: fundamentos Moussa Reda Mansour Por que Física????? Por que Física????? A física está presente no mundo real; A física pode tornar os jogos mais próximos do mundo real; Jogos que
A solução deste modelos pode ser analítica ou numérica.
 Cap. 8.- Derivação Numérica 8.1. Introdução Praticamente todos os modelos matemáticos dos problemas de engenharia podem ser escritos no formato de equações diferenciais ordinárias ou parciais. A solução
Cap. 8.- Derivação Numérica 8.1. Introdução Praticamente todos os modelos matemáticos dos problemas de engenharia podem ser escritos no formato de equações diferenciais ordinárias ou parciais. A solução
Testes Formativos de Computação Numérica e Simbólica
 Testes Formativos de Computação Numérica e Simbólica Os testes formativos e 2 consistem em exercícios de aplicação dos vários algoritmos que compõem a matéria da disciplina. O teste formativo 3 consiste
Testes Formativos de Computação Numérica e Simbólica Os testes formativos e 2 consistem em exercícios de aplicação dos vários algoritmos que compõem a matéria da disciplina. O teste formativo 3 consiste
Na Física (em módulo) é uma Lei
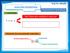 1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
7 Equações Diferenciais. 7.1 Classificação As equações são classificadas de acordo como tipo, a ordem e a linearidade.
 7 Equações Diferenciais Definição: Uma equação diferencial é uma equação em que as incógnitas são funções e a equação envolve derivadas dessas funções. : = 5x + 3 4 d3 3 + (sen x) d2 2 + 5x = 0 2 t 2 4
7 Equações Diferenciais Definição: Uma equação diferencial é uma equação em que as incógnitas são funções e a equação envolve derivadas dessas funções. : = 5x + 3 4 d3 3 + (sen x) d2 2 + 5x = 0 2 t 2 4
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V
 Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
Exercícios de MATEMÁTICA COMPUTACIONAL Capítulo V Integração Numérica 1. Considere o integral: 1 0 e x2 dx a) Determine o seu valor aproximado, considerando 4 subintervalos e utilizando: i. A regra dos
Métodos tipo quadratura de Gauss-Radau
 COQ-8 Métodos Numéricos para Sistemas Algébricos e Diferenciais Métodos tipo quadratura de Gauss-Radau Introdução Método de quadratura de Gauss com pontos internos+ extremidade superior Considerando a
COQ-8 Métodos Numéricos para Sistemas Algébricos e Diferenciais Métodos tipo quadratura de Gauss-Radau Introdução Método de quadratura de Gauss com pontos internos+ extremidade superior Considerando a
Solução Numérica do Problema de Blasius da Camada Limite Laminar
 Universidade de Brasília Departamento de Engenharia Mecânica Mecânica dos Fluidos II 0) Prof. Francisco Ricardo da Cunha e Prof. Gustavo Coelho Abade Monitor: Nuno Jorge Sousa Dias Solução Numérica do
Universidade de Brasília Departamento de Engenharia Mecânica Mecânica dos Fluidos II 0) Prof. Francisco Ricardo da Cunha e Prof. Gustavo Coelho Abade Monitor: Nuno Jorge Sousa Dias Solução Numérica do
Modelagem Computacional. Parte 8 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Para temos : que é a ideia de um polinômio. A série pode convergir para alguns valores de mas pode divergir para outros valores de.
 MATERIAL DIDÁTICO Professora Sílvia Victer CÁLCULO 2 SÉRIES DE POTÊNCIAS Definição: Séries de Potências é uma série infinita de termos variáveis. Elas podem ser usadas em várias aplicações, como por exemplo,
MATERIAL DIDÁTICO Professora Sílvia Victer CÁLCULO 2 SÉRIES DE POTÊNCIAS Definição: Séries de Potências é uma série infinita de termos variáveis. Elas podem ser usadas em várias aplicações, como por exemplo,
Método de Diferenças Finitas
 Método de Diferenças Finitas Câmpus Francisco Beltrão Disciplina: Professor: Jonas Joacir Radtke Aplicações Quase todos os problemas em ciências físicas e engenharia podem ser reduzidos a uma equação diferencial.
Método de Diferenças Finitas Câmpus Francisco Beltrão Disciplina: Professor: Jonas Joacir Radtke Aplicações Quase todos os problemas em ciências físicas e engenharia podem ser reduzidos a uma equação diferencial.
Introdução ao Projeto de Aeronaves. Aula 18 Tempo para a Missão e Metodologia para o Gráfico de Carga Útil
 Introdução ao Projeto de Aeronaves Aula 18 Tempo para a Missão e Metodologia para o Gráfico de Carga Útil Tópicos Abordados Tempo Estimado para a Missão. Traçado do Gráfico de Carga Útil. Dicas para Análise
Introdução ao Projeto de Aeronaves Aula 18 Tempo para a Missão e Metodologia para o Gráfico de Carga Útil Tópicos Abordados Tempo Estimado para a Missão. Traçado do Gráfico de Carga Útil. Dicas para Análise
Resolução do Exame Tipo
 Departamento de Matemática e Engenharias Análise e Computação Numérica Resolução do Exame Tipo 1. O computador IBM 3090 possuía um sistema de vírgula flutuante F F(16, 5, 65, 62) (em precisão simples),
Departamento de Matemática e Engenharias Análise e Computação Numérica Resolução do Exame Tipo 1. O computador IBM 3090 possuía um sistema de vírgula flutuante F F(16, 5, 65, 62) (em precisão simples),
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Métodos Numéricos para EDO S
 Métodos Numéricos para EDO S 9.1 Introdução O estudo das equações diferenciais foi motivado inicialmente por problemas da física, ou seja problemas de mecânica, eletricidade termodinâmica, magnetismo etc.
Métodos Numéricos para EDO S 9.1 Introdução O estudo das equações diferenciais foi motivado inicialmente por problemas da física, ou seja problemas de mecânica, eletricidade termodinâmica, magnetismo etc.
Palavras-chave Desempenho, Decolagem, AeroDesign.
 1 Modelo analítico para se estimar o comprimento de pista necessário para a decolagem de uma aeronave destinada a participar da competição SAE-Aerodesign. uiz Eduardo Miranda José Rodrigues Professor MSc.
1 Modelo analítico para se estimar o comprimento de pista necessário para a decolagem de uma aeronave destinada a participar da competição SAE-Aerodesign. uiz Eduardo Miranda José Rodrigues Professor MSc.
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Subida e Descida. Subida e Descida
 Mecânica de oo I Mecânica de oo I 763 º Ano da Licenciatura em Engenharia Aeronáutica Mecânica de oo I. Equações de Movimento linha de referência do avião α ε T, linha de tracção γ L γ, trajectória de
Mecânica de oo I Mecânica de oo I 763 º Ano da Licenciatura em Engenharia Aeronáutica Mecânica de oo I. Equações de Movimento linha de referência do avião α ε T, linha de tracção γ L γ, trajectória de
Capítulo 3 - Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias
 Capítulo 3 - Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática
Capítulo 3 - Problemas com Valores de Fronteira para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática
Aula 4 Otimização e Discretização
 Universidade Federal do ABC Aula 4 Otimização e Discretização EN3224 Dinâmica de Fluidos Computacional Forma adimensional das equações Motivação: às vezes, as equações são normalizadas para: facilitar
Universidade Federal do ABC Aula 4 Otimização e Discretização EN3224 Dinâmica de Fluidos Computacional Forma adimensional das equações Motivação: às vezes, as equações são normalizadas para: facilitar
MOVIMENTO EM UMA LINHA RETA
 MOVIMENTO EM UMA LINHA RETA MOVIMENTO EM UMA LINHA RETA Objetivos de aprendizagem: Descrever o movimento em uma linha reta em termos de velocidade média, velocidade instantânea, aceleração média e aceleração
MOVIMENTO EM UMA LINHA RETA MOVIMENTO EM UMA LINHA RETA Objetivos de aprendizagem: Descrever o movimento em uma linha reta em termos de velocidade média, velocidade instantânea, aceleração média e aceleração
Introdução aos Métodos Numéricos
 Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Métodos de passo simples para equações diferenciais ordinárias. Nelson Kuhl
 Métodos de passo simples para equações diferenciais ordinárias Nelson Kuhl 1. Solução Numérica de Equações Diferencias Ordinárias Métodos de Passo Simples Explícitos 1.1 Introdução Para a maioria das equações
Métodos de passo simples para equações diferenciais ordinárias Nelson Kuhl 1. Solução Numérica de Equações Diferencias Ordinárias Métodos de Passo Simples Explícitos 1.1 Introdução Para a maioria das equações
CURSO DE RESOLUÇÃO DE PROVAS de MATEMÁTICA da ANPEC Tudo passo a passo com Teoria e em sequência a resolução da questão! Prof.
 Prof. Chico Vieira MATEMÁTICA da ANPEC Tudo Passo a Passo Teoria e Questões FICHA com LIMITES, DERIVADAS, INTEGRAIS, EDO, SÉRIES Integrais Dupla e Tripla LIMITES ANPEC QUESTÕES JÁ GRAVADAS DERIVADAS ANPEC
Prof. Chico Vieira MATEMÁTICA da ANPEC Tudo Passo a Passo Teoria e Questões FICHA com LIMITES, DERIVADAS, INTEGRAIS, EDO, SÉRIES Integrais Dupla e Tripla LIMITES ANPEC QUESTÕES JÁ GRAVADAS DERIVADAS ANPEC
Métodos Numéricos. Turma CI-202-X. Josiney de Souza.
 Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 20 (09/11/15) Interpolação: Introdução Características Interpolação Linear: Introdução Características Exercícios
Métodos Numéricos Turma CI-202-X Josiney de Souza josineys@inf.ufpr.br Agenda do Dia Aula 20 (09/11/15) Interpolação: Introdução Características Interpolação Linear: Introdução Características Exercícios
AERODESIGN AULA 1 MATLAB
 AERODESIGN AULA 1 MATLAB INTERFAE (Apontar "espaços" na janela inicial do MATLAB) Diretório (riar uma pasta no desktop e usá-la) Browser ommand Window Variable Editor OMANDOS BÁSIOS Soma ( + 3) Subtração
AERODESIGN AULA 1 MATLAB INTERFAE (Apontar "espaços" na janela inicial do MATLAB) Diretório (riar uma pasta no desktop e usá-la) Browser ommand Window Variable Editor OMANDOS BÁSIOS Soma ( + 3) Subtração
y(x n+1 ) = y(x n ) + hy (x n ) + h2 q! y (q) (x n )
 2. Método de Taylor de ordem q Seja y(x) a solução exata do p.v.i., contínua e suficientemente derivável em [a, b]. A expansão em série de Taylor para y(x n + h) em torno do ponto x n é dada por: y(x n+1
2. Método de Taylor de ordem q Seja y(x) a solução exata do p.v.i., contínua e suficientemente derivável em [a, b]. A expansão em série de Taylor para y(x n + h) em torno do ponto x n é dada por: y(x n+1
MVO-31: Desempenho de Aeronaves
 Planeio Departamento de Mecânica do Voo Divisão de Engenharia Aeroespacial Instituto Tecnológico de Aeronáutica 2019 PARTE III Planeio Permanente g: ângulo de trajetória L D velocidade peso: mg Decompondo-se
Planeio Departamento de Mecânica do Voo Divisão de Engenharia Aeroespacial Instituto Tecnológico de Aeronáutica 2019 PARTE III Planeio Permanente g: ângulo de trajetória L D velocidade peso: mg Decompondo-se
3 Métodos Numéricos Análise das Equações de Movimento
 3 Métodos Numéricos A dinâmica de sistemas mecânicos normalmente é modelada como um sistema de equações diferenciais. Estas equações diferenciais devem ser resolvidas a fim de relacionar as variáveis entre
3 Métodos Numéricos A dinâmica de sistemas mecânicos normalmente é modelada como um sistema de equações diferenciais. Estas equações diferenciais devem ser resolvidas a fim de relacionar as variáveis entre
Equações diferenciais ordinárias EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 1 Sumário 1 Equações diferenciais ordinárias Métodos de Euler Exemplo de EDO linear: Método implícito Métodos multi-passo lineares Fórmulas de Adams-Bashforth Fórmulas de Adams-Moulton Fórmulas do tipo
1 Sumário 1 Equações diferenciais ordinárias Métodos de Euler Exemplo de EDO linear: Método implícito Métodos multi-passo lineares Fórmulas de Adams-Bashforth Fórmulas de Adams-Moulton Fórmulas do tipo
Adérito Araújo. Gonçalo Pena. Adérito Araújo. Adérito Araújo. Gonçalo Pena. Método da Bissecção. Resolução dos exercícios 2.14, 2.15, 2.16 e 2.17.
 1 2011-02-08 13:00 2h Capítulo 1 Aritmética computacional 1.1 Erros absolutos e relativos 1.2 O polinómio de Taylor Resolução do exercício 1.3 2 2011-02-08 15:00 1h30m As aulas laboratoriais só começam
1 2011-02-08 13:00 2h Capítulo 1 Aritmética computacional 1.1 Erros absolutos e relativos 1.2 O polinómio de Taylor Resolução do exercício 1.3 2 2011-02-08 15:00 1h30m As aulas laboratoriais só começam
1 o Exame de Estabilidade de Voo O exame tem a duração de 3h00m. Justifique convenientemente todas as respostas.
 Instituto Superior Técnico Ano Lectivo de 2014/2015 Mestrado Integrado em Engenharia Aeroespacial 5 de Janeiro de 2015 1 o Exame de Estabilidade de Voo O exame tem a duração de 3h00m. Justifique convenientemente
Instituto Superior Técnico Ano Lectivo de 2014/2015 Mestrado Integrado em Engenharia Aeroespacial 5 de Janeiro de 2015 1 o Exame de Estabilidade de Voo O exame tem a duração de 3h00m. Justifique convenientemente
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3 Equações de Poisson e Laplace Vimos na aula passada o método de separação de
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aulas 3 e 4 Ref. Butkov, cap. 8, seção 8.3 Equações de Poisson e Laplace Vimos na aula passada o método de separação de
Método de Euler. Marina Andretta/Franklina Toledo ICMC-USP. 29 de outubro de 2013
 Solução numérica de Equações Diferenciais Ordinárias: Método de Euler Marina Andretta/Franklina Toledo ICMC-USP 29 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D. Faires;
Solução numérica de Equações Diferenciais Ordinárias: Método de Euler Marina Andretta/Franklina Toledo ICMC-USP 29 de outubro de 2013 Baseado nos livros: Análise Numérica, de R. L. Burden e J. D. Faires;
Sabendo que f(x) é um polinômio de grau 2, utilize a formula do trapézio e calcule exatamente
 MÉTODOS NUMÉRICOS E COMPUTACIONAIS II EXERCICIOS EXTRAIDOS DE PROVAS ANTERIORES EXERCICIOS RESOLVIDOS - INTEGRACAO-NUMERICA - EDO. Considere a seguinte tabela de valores de uma função f x i..5.7..5 f(x
MÉTODOS NUMÉRICOS E COMPUTACIONAIS II EXERCICIOS EXTRAIDOS DE PROVAS ANTERIORES EXERCICIOS RESOLVIDOS - INTEGRACAO-NUMERICA - EDO. Considere a seguinte tabela de valores de uma função f x i..5.7..5 f(x
1 [30] A figura ao lado mostra o zoom da discretização de uma função
![1 [30] A figura ao lado mostra o zoom da discretização de uma função 1 [30] A figura ao lado mostra o zoom da discretização de uma função](/thumbs/92/110361962.jpg) TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
Aula Prática 1: Movimento Longitudinal
 Aula Prática 1: Movimento Longitudinal AB-722 Flávio Luiz Cardoso Ribeiro http://flavioluiz.github.io flaviocr@ita.br Departamento de Mecânica do Voo Divisão de Engenharia Aeronáutica e Aeroespacial Instituto
Aula Prática 1: Movimento Longitudinal AB-722 Flávio Luiz Cardoso Ribeiro http://flavioluiz.github.io flaviocr@ita.br Departamento de Mecânica do Voo Divisão de Engenharia Aeronáutica e Aeroespacial Instituto
Capítulo 10 Solução de Equações Diferenciais Ordinárias
 Capítulo 10 Solução de Equações Diferenciais Ordinárias As equações diferenciais ordinárias são do tipo: Exemplo 10.1 Seja a equação diferencial ordinária para a posição y de um automóvel, com a condição
Capítulo 10 Solução de Equações Diferenciais Ordinárias As equações diferenciais ordinárias são do tipo: Exemplo 10.1 Seja a equação diferencial ordinária para a posição y de um automóvel, com a condição
EXERCICIOS RESOLVIDOS - INT-POLIN - MMQ - INT-NUMERICA - EDO
 Cálculo Numérico EXERCICIOS EXTRAIDOS DE PROVAS ANTERIORES o sem/08 EXERCICIOS RESOLVIDOS - INT-POLIN - MMQ - INT-NUMERICA - EDO x. Considere a seguinte tabela de valores de uma função f: i 0 f(x i ).50
Cálculo Numérico EXERCICIOS EXTRAIDOS DE PROVAS ANTERIORES o sem/08 EXERCICIOS RESOLVIDOS - INT-POLIN - MMQ - INT-NUMERICA - EDO x. Considere a seguinte tabela de valores de uma função f: i 0 f(x i ).50
Métodos Numéricos. Professor Tenani - 9 de Agosto de 2015
 Métodos Numéricos Professor Tenani - www.professortenani.com.br 9 de Agosto de 2015 Métodos Numéricos Professor Tenani - www.professortenani.com.br 1 / 51 Índice Métodos Numéricos Professor Tenani - www.professortenani.com.br
Métodos Numéricos Professor Tenani - www.professortenani.com.br 9 de Agosto de 2015 Métodos Numéricos Professor Tenani - www.professortenani.com.br 1 / 51 Índice Métodos Numéricos Professor Tenani - www.professortenani.com.br
SME Cálculo Numérico. Lista de Exercícios: Gabarito
 Exercícios de prova SME0300 - Cálculo Numérico Segundo semestre de 2012 Lista de Exercícios: Gabarito 1. Dentre os métodos que você estudou no curso para resolver sistemas lineares, qual é o mais adequado
Exercícios de prova SME0300 - Cálculo Numérico Segundo semestre de 2012 Lista de Exercícios: Gabarito 1. Dentre os métodos que você estudou no curso para resolver sistemas lineares, qual é o mais adequado
Modelagem Computacional. Parte 4 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 4 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 4 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 5] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Cap. 10. Resolução Numérica de Equações Diferenciais Ordinárias: Problemas de Valor Inicial. Filipe J. Romeiras
 MATEMÁTICA COMPUTACIONAL Cap.. Resolução Numérica de Equações Diferenciais Ordinárias: Problemas de Valor Inicial Filipe J. Romeiras Departamento de Matemática Instituto Superior Técnico Apontamentos das
MATEMÁTICA COMPUTACIONAL Cap.. Resolução Numérica de Equações Diferenciais Ordinárias: Problemas de Valor Inicial Filipe J. Romeiras Departamento de Matemática Instituto Superior Técnico Apontamentos das
AA-220 AERODINÂMICA NÃO ESTACIONÁRIA
 AA-22 AERODINÂMICA NÃO ESTACIONÁRIA Aerodinâmica Linearizada Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Linearização da Equação do Potencial Completo - proposta ( φ φ) 2 2 1 φ φ ( φ φ) φ 2 + + =
AA-22 AERODINÂMICA NÃO ESTACIONÁRIA Aerodinâmica Linearizada Prof. Roberto GIL Email: gil@ita.br Ramal: 6482 1 Linearização da Equação do Potencial Completo - proposta ( φ φ) 2 2 1 φ φ ( φ φ) φ 2 + + =
CÁLCULO NUMÉRICO UFRJ Lista 0: revisão de cálculo e álgebra linear
 CÁLCULO NUMÉRICO UFRJ 2016 LISTAS DE EXERCÍCIOS Lista 0: revisão de cálculo e álgebra linear 1. Ao longo desta curso usaremos frequentemente as seguintes propriedades de uma função contínua g definida
CÁLCULO NUMÉRICO UFRJ 2016 LISTAS DE EXERCÍCIOS Lista 0: revisão de cálculo e álgebra linear 1. Ao longo desta curso usaremos frequentemente as seguintes propriedades de uma função contínua g definida
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Introdução aos Métodos Numéricos
 Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Introdução à Resolução de Equações Diferenciais Ordinárias
Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Introdução à Resolução de Equações Diferenciais Ordinárias
Prof.: Roberto F. Ausas. Semestre
 Cálculo Numérico Resolução numérica de EDO s Prof.: Roberto F. Ausas Cálculo Numérico e-mail: rfausas@icmc.usp.br ICMC-USP - São Carlos Instituto de Ciências Matemáticas e de Computação Semestre 2-2017
Cálculo Numérico Resolução numérica de EDO s Prof.: Roberto F. Ausas Cálculo Numérico e-mail: rfausas@icmc.usp.br ICMC-USP - São Carlos Instituto de Ciências Matemáticas e de Computação Semestre 2-2017
Cálculo Numérico IPRJ/UERJ. Sílvia Mara da Costa Campos Victer ÍNDICE. Aula 4- Diferenciação numérica: - Fórmulas de diferença avançada e recuada
 Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer ÍNDICE Aula 4- Diferenciação numérica: - Fórmulas de diferença avançada e recuada - Fórmula de três pontos - Fórmula de cinco pontos Aula 4
Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer ÍNDICE Aula 4- Diferenciação numérica: - Fórmulas de diferença avançada e recuada - Fórmula de três pontos - Fórmula de cinco pontos Aula 4
Mestrado Integrado em Engenharia Mecânica Aerodinâmica 1º Semestre 2014/15
 Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 4/5 Exame de ª época, 3 de Janeiro de 5 Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
Mestrado Integrado em Engenharia Mecânica Aerodinâmica º Semestre 4/5 Exame de ª época, 3 de Janeiro de 5 Nome : Hora : 8: Número: Duração : 3 horas ª Parte : Sem consulta ª Parte : onsulta limitada a
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
3ª LISTA DE EXERCÍCIOS CÁLCULO NUMÉRICO Prof.: Magnus Melo
 ª LISTA DE EXERCÍCIOS CÁLCULO NUMÉRICO Prof.: Magnus Melo Os eercícios a 4 se referem a interpolação polinomial. Resolva-os com os dois polinômios interpoladores estudados. 4 ) Dada a função f ( ), determine:
ª LISTA DE EXERCÍCIOS CÁLCULO NUMÉRICO Prof.: Magnus Melo Os eercícios a 4 se referem a interpolação polinomial. Resolva-os com os dois polinômios interpoladores estudados. 4 ) Dada a função f ( ), determine:
3 Equações diferenciais
 3 Equações diferenciais 3. Forma geral das equações diferenciais Uma equação diferencial ordinária ou de forma abreviada, EDO de ordem n é uma relação entre uma função y(x) e as suas derivadas y, y,...,
3 Equações diferenciais 3. Forma geral das equações diferenciais Uma equação diferencial ordinária ou de forma abreviada, EDO de ordem n é uma relação entre uma função y(x) e as suas derivadas y, y,...,
Introdução à Física Computacional
 7600017 Introdução à Física Computacional Terceiro Projeto (prazo até 04/05/18) Instruções Crie um diretório PROJ3 #usp em /home/public/fiscomp18/proj3 Proteja seu diretório para nao ser lido por g e o
7600017 Introdução à Física Computacional Terceiro Projeto (prazo até 04/05/18) Instruções Crie um diretório PROJ3 #usp em /home/public/fiscomp18/proj3 Proteja seu diretório para nao ser lido por g e o
Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções
 Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções As Equações Diferenciais são equações que contêm derivadas. Os seguintes exemplos são fenômenos físicos que envolvem taxas de variação: Movimento
Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções As Equações Diferenciais são equações que contêm derivadas. Os seguintes exemplos são fenômenos físicos que envolvem taxas de variação: Movimento
Capítulo 2 - Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valor Inicial para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o Semestre
Capítulo 2 - Problemas de Valor Inicial para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o Semestre
Cálculo Numérico Lista 03
 Cálculo Numérico Lista 03 Professor: Daniel Henrique Silva Essa lista abrange integração numérica, e resolução numérica de EDO s, e abrange toda a matéria da 3ª prova. Instruções gerais para entrega Nem
Cálculo Numérico Lista 03 Professor: Daniel Henrique Silva Essa lista abrange integração numérica, e resolução numérica de EDO s, e abrange toda a matéria da 3ª prova. Instruções gerais para entrega Nem
Física Computacional 5
 Física Computacional 5 1. Derivadas com diferenças finitas a. O conceito de derivada, menos simples que o de integral b. Cálculo numérico da derivada com diferenças finitas c. Um outro conceito, Equação
Física Computacional 5 1. Derivadas com diferenças finitas a. O conceito de derivada, menos simples que o de integral b. Cálculo numérico da derivada com diferenças finitas c. Um outro conceito, Equação
Questão 1: (2.0 pontos) (a) (1.0 ponto) Obtenha os cinco primeiros termos da série de Taylor da função f(x) = cos x em.
 Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
MAT EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17
 MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
II. REVISÃO DE FUNDAMENTOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
Diferenciais Ordinárias
 Capítulo 1 Solução Numérica de Equações Diferenciais Ordinárias 1.1 Introdução Muitos problemas encontrados em engenharia e outras ciências podem ser formulados em termos de equações diferenciais. Por
Capítulo 1 Solução Numérica de Equações Diferenciais Ordinárias 1.1 Introdução Muitos problemas encontrados em engenharia e outras ciências podem ser formulados em termos de equações diferenciais. Por
