0, OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel
|
|
|
- Sônia Abreu Vidal
- 8 Há anos
- Visualizações:
Transcrição
1 Nível Intermediário 0, OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel Quando um jovem estudante de matemática começa a estudar os números reais, é difícil não sentir certo desconforto e estranhamento. De repente, algumas coisas que faziam sentido param de funcionar tão bem assim. Com certeza, uma das mais estranhas pode ser resumida na igualdade 0, = 1, Como assim? No mundo dos números inteiros (com a exceção muito razoável de 0 = 0), qualquer número tem uma única representação decimal (os zeros à esquerda não são um problema sério, ou definimos que nunca podemos começar com 0 o que deixa o próprio zero em uma situação meio desconfortável de ter uma representação decimal vazia ou definimos que sempre vamos completar com infinitos zeros à esquerda), e esta se comporta bem i.e. qualquer número da forma 8xxxxxxx é menor que qualquer número da forma 9yyyyyyy com o mesmo número de dígitos. Como pode haver um número começado por 0,9 que não seja menor que um número começado por 1,0 e, pior, que seja igual!? A resposta explica, mas não convence: se definirmos as seqüências: a n = (n dígitos 9) e b n = (n dígitos 0) temos que a n < < b n. No entanto, como b n a n = 1/10 n, que converge para 0, a diferença entre e , que é menor que qualquer das diferenças b n a n só pode ser 0, logo os números são iguais. OK, entendido, mas ainda tem caroço neste angu. Por que a representação decimal, que se comporta tão bem para números inteiros tem este tipo de esquisitice para números reais? A verdade é que usar a representação decimal para números reais é enfiar um bloco quadrado em um buraco redondo. Em primeiro lugar, até agora estamos usando a representação decimal (base 10) apenas porque é a representação com que estamos mais acostumados. Será que o problema está com o número 10? Infelizmente não. Mesmo que usemos outras bases, o problema continua: = 1, em base 2 0, = 1, em base 3 e o mesmo problema acontece em qualquer base que escolhamos (e a demonstração é exatamente a mesma, mutatis mutandis, que fizemos lá em cima). Antes de entrarmos a fundo em por que a representação decimal (ou em qualquer base N) tem estes problemas, é bom ver que outras opções nós temos para representar os números reais. Em primeiro lugar, nossas notações foram feitas para trabalhar com números inteiros, que é o que nos é familiar (a ponto de Pitágoras afirmar que os números inteiros são a fundação do universo). Dos números inteiros conseguimos de forma natural derivar os números racionais (os números da forma a/b, onde a e b são inteiros). O pulo para os números reais irracionais, no entanto, é menos natural, e as únicas maneiras que temos para tentar nomear os números irracionais são através das aproximações por números racionais. A própria representação decimal é a aproximação por números racionais da
2 forma A/10 n (ou A/N n, em base N). Duas outras formas de representar os números reais são as frações contínuas e os cortes de Dedekind. A representação por frações contínuas tem a forma N N N O algoritmo para construir a representação por frações contínuas de um número x é bastante simples. Em primeiro lugar, N 1 é a parte inteira de x (i.e. o maior número inteiro que é menor ou igual a x). Se x N 1 = 0, acabou, senão, x N 1 é maior que 0 e menor que 1, portanto y = 1/(x N 1 ) é um número maior que 1. Seja N 2 então a parte inteira deste número, o que equivale a dizer que 1/(N 2 + 1) < x N 1 1/N 2. Agora repita o processo com y no lugar de x (i.e. N 3 é o número tal que 1/(N 3 + 1) < y N 2 1/N 3 ), e assim por diante até chegar a um número inteiro ou continuando para sempre. A representação por frações contínuas não tem o mesmo problema da representação decimal (cada número real tem uma e somente uma representação por frações contínuas), mas tem outros inconvenientes. O primeiro, que não é tão sério assim, é que os números N i, que seriam equivalentes aos dígitos, podem ser arbitrariamente grandes, ao contrário dos dígitos decimais que só podem ser de 0 a 9. O segundo, muito mais sério, é que é terrivelmente difícil fazer contas com frações contínuas. Este foi o principal motivo de a representação decimal ter substituído a numeração romana na Europa no século XV era imensamente mais simples fazer contas com a representação decimal do que com a representação romana. (E este também é o principal motivo de a representação binária ter tomado espaço da representação decimal no século XX, é ainda mais fácil fazer contas em binário). Outra representação dos números reais é através dos cortes de Dedekind. A diferença do corte de Dedekind para a representação decimal ou de frações contínuas é que, enquanto as últimas usam uma seqüência convergente de números racionais, os cortes usam conjuntos sem uma seqüência definida. Um corte de Dedekind é um conjunto de números racionais limitado, que não possui um maior elemento e fechado inferiormente. Ou seja, um conjunto de racionais A tal que: 1) existe um racional X tal que X > a para todo a pertencente a A 2) para todo a pertencente a A, existe um b pertencente a A tal que b > a. 3) Se a pertence a A, e um racional c < a, então c pertence a A. Em outras palavras, cada um destes conjuntos é o conjunto de todos os números racionais menores que um número real determinado. Esta representação é útil teoricamente para provar algumas propriedades dos números reais, mas é praticamente impossível de ser utilizada na prática para as tarefas corriqueiras do dia-a-dia. A conclusão é que, apesar dos seus defeitos, a representação de base N é a representação mais prática que temos para os números reais. Então vamos entendê-la mais a fundo.
3 Em primeiro lugar, a parte antes da vírgula (ou ponto decimal, dependendo de em qual lugar do mundo você vive) é apenas a parte inteira do número, com a nossa velha e bem comportada representação decimal de números inteiros. Vamos nos concentrar então na parte à direita da vírgula, os números entre 0 e 1. 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 O primeiro dígito decimal diz em qual dos dez intervalos acima o número está. Para descobrir o segundo dígito, basta subdividir cada intervalo novamente em 10 pedaços, ou, equivalentemente, multiplicar o número por 10 e ver em qual dos intervalos a parte fracionária deste novo número (10x) cai, de acordo com o gráfico abaixo: 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Os pontos onde nasce o nosso problema são justamente estes pontos marcados na nossa linha (0; ; 0,2;...; 1). Repare que o gráfico acima é descontínuo nestes pontos por exemplo, as imagens dos pontos se aproximando de 0,2 pela esquerda tendem a 1, enquanto pela direita tendem a 0. Dito de outra forma, os números se aproximando pela esquerda de 0,2 vão ter uma seqüência longa de 9 s depois do e pela direita uma seqüência longa de 0 s depois do 0,2. Antes de prosseguir com a análise, já vimos que não existe nada de especial no número 10, portanto, por pura preguiça, a partir de agora vou mudar para base 2, mas deixo ao leitor desconfiado a tarefa de reescrever tudo o que se segue em base 10. Apenas para começar do ponto onde paramos, o gráfico acima para base 2 fica assim:
4 Relembrando, o problema está no ponto da descontinuidade, neste caso o (também conhecido como ½). A origem do problema é o fato de haver números começados por arbitrariamente próximos de, quando, naturalmente, números começados por deveriam ser distintamente menores do que. Vamos tentar corrigir este problema dando um pequeno espaço entre os intervalos no nosso desenho. Vamos passar agora para o segundo dígito O espaço que demos entre os intervalos do primeiro dígito naturalmente se propaga para o segundo dígito (senão teríamos o mesmo problema nos números 1 ¼ - e 1 ¾). [Em base 10 seriam 9 buracos na primeira rodada e 90 na segunda, entenderam a minha preguiça?] Neste ponto, já não é difícil imaginar o processo para o terceiro dígito criar mais um buraco no meio de cada um dos 4 intervalos restantes, e assim por diante. O conjunto dos números que sobram depois de fazermos este processo infinitas vezes é um conjunto em que podemos usar a nossa representação de base 2 (ou base 10, se fizermos o processo no desenho original lá de cima) sem medo cada número tem apenas uma representação, e elas respeitam a ordem e as distâncias que esperaríamos: por exemplo, se um número começa por 1010 ele é estritamente menor que qualquer número que comece por O único problema é que o conjunto que temos no final deste processo é tão esfarelado que ele não contém nem um intervalinho que seja. Se escolhêssemos um número entre 0 e 1 aleatoriamente, ele teria 0% de chance de estar no nosso conjunto repare que eu disse 0% não uma em um quaquilhão elevado a um googleplex, não a chance de ganhar na megasena todas as semanas pelo resto da vida, mas zero! Este conjunto é tão importante que tem um nome conjunto de Cantor, em homenagem ao matemático Georg Cantor que, entre outras coisas criou a teoria dos conjuntos (todos os conjuntos então são um pouquinho conjuntos de Cantor) e provou que existiam mais números irracionais do que números racionais. Dado que acabamos de ver que o próprio sistema de representação decimal
5 que usamos todos os dias na verdade é um conjunto de Cantor, é de se admirar que apenas no final do século XIX tenhamos passado a conhecê-lo. Pelo que acabamos de ver, o nosso sistema de numeração é um mapeamento entre um conjunto de Cantor e o intervalo []. O cerne da nossa questão é que esta função não é injetiva, ou seja, existem elementos distintos a e b no conjunto de Cantor que são mapeados para o mesmo número real (a diferente de b, f(a) = f(b)), por exemplo, e 0,2. [Parênteses: outra forma de ver isto é afirmar que o intervalo [] é o espaço quociente do conjunto de Cantor pela relação de equivalência entre os números terminados por e os seus correspondentes terminados por , ver o artigo Egalité] no endereço: Vamos tentar desenhar o gráfico desta função: Os dois extremos do buraco do meio são os pontos e que representam o mesmo número ½, portanto a função é constante igual a ½ neste intervalo. Da mesma forma cada um dos buracos de gerações maiores corresponde a diferentes platôs no gráfico. O mais surpreendente é que, depois de criarmos os infinitos platôs, o gráfico final é um gráfico contínuo, que é chamado de função de Cantor, ou de escada do diabo (porque sempre existem infinitos degraus entre quaisquer dois degraus da escada, você nunca conseguiria sair do lugar assim como Aquiles correndo atrás da tartaruga). Infelizmente, é o que se tem quando se tenta botar um bloco quadrado em um buraco redondo, ou neste caso, botar um intervalo dentro de um conjunto de Cantor.
Aula 4 Estatística Conceitos básicos
 Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIAS
 MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto
 Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO
 RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO Caro aluno, Disponibilizo abaixo a resolução resumida das questões de Raciocínio Lógico-Matemático da prova de Técnico de Atividade Judiciária do
RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO Caro aluno, Disponibilizo abaixo a resolução resumida das questões de Raciocínio Lógico-Matemático da prova de Técnico de Atividade Judiciária do
MD Sequências e Indução Matemática 1
 Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Objetivo principal: aprender como definir e chamar funções.
 12 NOME DA AULA: Escrevendo músicas Duração da aula: 45 60 minutos de músicas durante vários dias) Preparação: 5 minutos (se possível com introduções Objetivo principal: aprender como definir e chamar
12 NOME DA AULA: Escrevendo músicas Duração da aula: 45 60 minutos de músicas durante vários dias) Preparação: 5 minutos (se possível com introduções Objetivo principal: aprender como definir e chamar
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
3 - CONJUNTO DOS NÚMEROS RACIONAIS
 3 - CONJUNTO DOS NÚMEROS RACIONAIS Introdução É o conjunto de todos os números que estão ou podem ser colocados em forma de fração. Fração Quando dividimos um todo em partes iguais e queremos representar
3 - CONJUNTO DOS NÚMEROS RACIONAIS Introdução É o conjunto de todos os números que estão ou podem ser colocados em forma de fração. Fração Quando dividimos um todo em partes iguais e queremos representar
Universidade Federal de São Carlos Departamento de Matemática 083020 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/04/2008
 Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade
 REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
Computadores XII: Aprendendo a Somar A4 Texto 3
 Computadores XII: Aprendendo a Somar A4 Texto 3 http://www.bpiropo.com.br/fpc20051017.htm Sítio Fórum PCs /Colunas Coluna: B. Piropo Publicada em 17/10/2005 Autor: B.Piropo Na coluna anterior, < http://www.forumpcs.com.br/viewtopic.php?t=131250
Computadores XII: Aprendendo a Somar A4 Texto 3 http://www.bpiropo.com.br/fpc20051017.htm Sítio Fórum PCs /Colunas Coluna: B. Piropo Publicada em 17/10/2005 Autor: B.Piropo Na coluna anterior, < http://www.forumpcs.com.br/viewtopic.php?t=131250
Faculdade de Computação
 UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE. Prof. Dr. Daniel Caetano 2012-1
 ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
NA LOJA DE CHAPÉUS. Karl Valentin. Personagens. Vendedora. Valentin ATO ÚNICO
 NA LOJA DE CHAPÉUS De Karl Valentin Personagens Vendedora Valentin ATO ÚNICO Bom dia, senhor. O que deseja? Um chapéu. Que tipo de chapéu? Um chapéu pra botar na cabeça. Certamente, meu senhor, um chapéu
NA LOJA DE CHAPÉUS De Karl Valentin Personagens Vendedora Valentin ATO ÚNICO Bom dia, senhor. O que deseja? Um chapéu. Que tipo de chapéu? Um chapéu pra botar na cabeça. Certamente, meu senhor, um chapéu
4Distribuição de. freqüência
 4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
Um jogo de preencher casas
 Um jogo de preencher casas 12 de Janeiro de 2015 Resumo Objetivos principais da aula de hoje: resolver um jogo com a ajuda de problemas de divisibilidade. Descrevemos nestas notas um jogo que estudamos
Um jogo de preencher casas 12 de Janeiro de 2015 Resumo Objetivos principais da aula de hoje: resolver um jogo com a ajuda de problemas de divisibilidade. Descrevemos nestas notas um jogo que estudamos
Resolvendo problemas com logaritmos
 A UA UL LA Resolvendo problemas com logaritmos Introdução Na aula anterior descobrimos as propriedades dos logaritmos e tivemos um primeiro contato com a tábua de logarítmos. Agora você deverá aplicar
A UA UL LA Resolvendo problemas com logaritmos Introdução Na aula anterior descobrimos as propriedades dos logaritmos e tivemos um primeiro contato com a tábua de logarítmos. Agora você deverá aplicar
Tabelas vista de estrutura
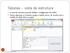 Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
ESTUDO 1 - ESTE É JESUS
 11. Já vimos que Jesus Cristo desceu do céu, habitou entre nós, sofreu, morreu, ressuscitou e foi para a presença de Deus. Leia João 17:13 e responda: Onde está Jesus Cristo agora? Lembremo-nos que: Jesus
11. Já vimos que Jesus Cristo desceu do céu, habitou entre nós, sofreu, morreu, ressuscitou e foi para a presença de Deus. Leia João 17:13 e responda: Onde está Jesus Cristo agora? Lembremo-nos que: Jesus
Potência, uma coisa mais que complicada Parte V
 Potência, uma coisa mais que complicada Parte V Autor: Fernando Antônio Bersan Pinheiro Cálculo de potência necessária em um ambiente fechado No artigo anterior, disponível em http://www.somaovivo.mus.br/artigos.php?id=180,
Potência, uma coisa mais que complicada Parte V Autor: Fernando Antônio Bersan Pinheiro Cálculo de potência necessária em um ambiente fechado No artigo anterior, disponível em http://www.somaovivo.mus.br/artigos.php?id=180,
A Maquina de Vendas Online É Fraude, Reclame AQUI
 A Maquina de Vendas Online É Fraude, Reclame AQUI Muitas pessoas me perguntam se a maquina de vendas online é fraude do Tiago bastos funciona de verdade ou se não é apenas mais uma fraude dessas que encontramos
A Maquina de Vendas Online É Fraude, Reclame AQUI Muitas pessoas me perguntam se a maquina de vendas online é fraude do Tiago bastos funciona de verdade ou se não é apenas mais uma fraude dessas que encontramos
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
1. O que existe por trás do mundo?
 Existem vários caminhos para se chegar à verdade. Os raciocínios que acabamos de discutir são apenas alguns deles e, talvez, não sejam completos nem suficientes para muitas pessoas. No entanto, existem
Existem vários caminhos para se chegar à verdade. Os raciocínios que acabamos de discutir são apenas alguns deles e, talvez, não sejam completos nem suficientes para muitas pessoas. No entanto, existem
Exposição Matemática Viva (piso 0)
 Exposição Matemática Viva (piso 0) Departamento Educativo PNE A Matemática está bem viva e presente em quase todas as actividades do nosso dia-a-dia, ainda que muitas vezes disso não nos dêmos conta. E
Exposição Matemática Viva (piso 0) Departamento Educativo PNE A Matemática está bem viva e presente em quase todas as actividades do nosso dia-a-dia, ainda que muitas vezes disso não nos dêmos conta. E
Sérgio Carvalho Matemática Financeira
 Sérgio Carvalho Matemática Financeira Resolução Matemática Financeira ICMS-RJ/2008 Parte 02 33. Uma rede de lojas, que atua na venda de eletrônicos, anuncia a venda de notebook da seguinte forma: - R$
Sérgio Carvalho Matemática Financeira Resolução Matemática Financeira ICMS-RJ/2008 Parte 02 33. Uma rede de lojas, que atua na venda de eletrônicos, anuncia a venda de notebook da seguinte forma: - R$
9 Comandos condicionais
 9 Comandos condicionais Um comando condicional é uma instrução empregada quando se deseja criar um desvio, isto é, a opção de executar-se ou não um determinado trecho de código, segundo uma condição. Em
9 Comandos condicionais Um comando condicional é uma instrução empregada quando se deseja criar um desvio, isto é, a opção de executar-se ou não um determinado trecho de código, segundo uma condição. Em
Análise de Arredondamento em Ponto Flutuante
 Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Ambos têm os algarismos 7854 seguidos, a potência de dez apenas moverá a vírgula, que não afeta a quantidade de algarismos significativos.
 ALGARISMOS SIGNIFICATIVOS Os algarismos significativos são os algarismos que têm importância na exatidão de um número, por exemplo, o número 2,67 tem três algarismos significativos. Se expressarmos o número
ALGARISMOS SIGNIFICATIVOS Os algarismos significativos são os algarismos que têm importância na exatidão de um número, por exemplo, o número 2,67 tem três algarismos significativos. Se expressarmos o número
1. A corrida de vetores numa folha de papel.
 1. A corrida de vetores numa folha de papel. desenhando a pista. o movimento dos carros. o início da corrida. as regras do jogo. 2. A corrida no computador. o número de jogadores. o teclado numérico. escolhendo
1. A corrida de vetores numa folha de papel. desenhando a pista. o movimento dos carros. o início da corrida. as regras do jogo. 2. A corrida no computador. o número de jogadores. o teclado numérico. escolhendo
Estruturas de Repetição
 Estruturas de Repetição Lista de Exercícios - 04 Algoritmos e Linguagens de Programação Professor: Edwar Saliba Júnior Estruturas de Repetição O que são e para que servem? São comandos que são utilizados
Estruturas de Repetição Lista de Exercícios - 04 Algoritmos e Linguagens de Programação Professor: Edwar Saliba Júnior Estruturas de Repetição O que são e para que servem? São comandos que são utilizados
Sistemas Lineares. Módulo 3 Unidade 10. Para início de conversa... Matemática e suas Tecnologias Matemática
 Módulo 3 Unidade 10 Sistemas Lineares Para início de conversa... Diversos problemas interessantes em matemática são resolvidos utilizando sistemas lineares. A seguir, encontraremos exemplos de alguns desses
Módulo 3 Unidade 10 Sistemas Lineares Para início de conversa... Diversos problemas interessantes em matemática são resolvidos utilizando sistemas lineares. A seguir, encontraremos exemplos de alguns desses
Configurando a emissão de boletos no sistema
 Configurando a emissão de boletos no sistema Entre nossos sistemas, o GIM, o GECOB, o GEM, o TRA-FRETAMENTO e os 15 sistemas da linha 4U (GE-COMERCIO 4U, GEPAD 4U, GE-INFO 4U, etc ) possuem funções para
Configurando a emissão de boletos no sistema Entre nossos sistemas, o GIM, o GECOB, o GEM, o TRA-FRETAMENTO e os 15 sistemas da linha 4U (GE-COMERCIO 4U, GEPAD 4U, GE-INFO 4U, etc ) possuem funções para
3 Dicas Infalíveis Para Ganhar Dinheiro Online. Por Tiago Bastos, Criador da Máquina de Vendas Online
 Por Tiago Bastos 1 Se não pode subir a montanha, torne-se uma. Por Tiago Bastos 2 3 Dicas Infalíveis Para Ganhar Dinheiro Online! Por Tiago Bastos Declaração De Ganhos Com O Uso De Nossos Produtos A empresa
Por Tiago Bastos 1 Se não pode subir a montanha, torne-se uma. Por Tiago Bastos 2 3 Dicas Infalíveis Para Ganhar Dinheiro Online! Por Tiago Bastos Declaração De Ganhos Com O Uso De Nossos Produtos A empresa
A Matemática do ENEM em Bizus
 A Matemática do ENEM em Bizus Neste primeiro artigo sobre a Matemática do ENEM, eu quero abordar a estratégia do conteúdo, tendo por base as provas anteriores e as tendências de abordagem. Quando confrontamos
A Matemática do ENEM em Bizus Neste primeiro artigo sobre a Matemática do ENEM, eu quero abordar a estratégia do conteúdo, tendo por base as provas anteriores e as tendências de abordagem. Quando confrontamos
Morfologia Matemática Binária
 Morfologia Matemática Binária Conceitos fundamentais: (Você precisa entender bem esses Pontos básicos para dominar a área! Esse será nosso game do dia!!! E nossa nota 2!!) Morfologia Matemática Binária
Morfologia Matemática Binária Conceitos fundamentais: (Você precisa entender bem esses Pontos básicos para dominar a área! Esse será nosso game do dia!!! E nossa nota 2!!) Morfologia Matemática Binária
Propriedades das Funções Deriváveis. Prof. Doherty Andrade
 Propriedades das Funções Deriváveis Prof Doerty Andrade 2005 Sumário Funções Deriváveis 2 Introdução 2 2 Propriedades 3 3 Teste da derivada segunda para máimos e mínimos 7 2 Formas indeterminadas 8 2 Introdução
Propriedades das Funções Deriváveis Prof Doerty Andrade 2005 Sumário Funções Deriváveis 2 Introdução 2 2 Propriedades 3 3 Teste da derivada segunda para máimos e mínimos 7 2 Formas indeterminadas 8 2 Introdução
CURSO E COLÉGIO APOIO. Professor: Ronaldo Correa
 CURSO E COLÉGIO APOIO Professor: Ronaldo Correa Holiday - Christmas.mpg medidas 1-Medidas Grandeza tudo aquilo que pode ser medido. Medir comparar com um padrão. No Brasil e na maioria dos países as unidades
CURSO E COLÉGIO APOIO Professor: Ronaldo Correa Holiday - Christmas.mpg medidas 1-Medidas Grandeza tudo aquilo que pode ser medido. Medir comparar com um padrão. No Brasil e na maioria dos países as unidades
Variáveis aleatórias contínuas e distribuiçao Normal. Henrique Dantas Neder
 Variáveis aleatórias contínuas e distribuiçao Normal Henrique Dantas Neder Definições gerais Até o momento discutimos o caso das variáveis aleatórias discretas. Agora vamos tratar das variáveis aleatórias
Variáveis aleatórias contínuas e distribuiçao Normal Henrique Dantas Neder Definições gerais Até o momento discutimos o caso das variáveis aleatórias discretas. Agora vamos tratar das variáveis aleatórias
Imagens Mentais Por Alexandre Afonso
 2 Imagens Mentais Por Alexandre Afonso 1ª Edição, 08/04/2016 As novas edições serão sempre disponibilizadas no link: http://alexandreafonso.com.br/e book imagens mentais 2016 alexandreafonso.com.br. Todos
2 Imagens Mentais Por Alexandre Afonso 1ª Edição, 08/04/2016 As novas edições serão sempre disponibilizadas no link: http://alexandreafonso.com.br/e book imagens mentais 2016 alexandreafonso.com.br. Todos
Sistemas de Numeração
 Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Sistemas de Numeração Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Sistemas de Numeração Prover símbolos e convenções
Teorema de Taylor. Prof. Doherty Andrade. 1 Fórmula de Taylor com Resto de Lagrange. 2 Exemplos 2. 3 Exercícios 3. 4 A Fórmula de Taylor 4
 Teorema de Taylor Prof. Doherty Andrade Sumário 1 Fórmula de Taylor com Resto de Lagrange 1 2 Exemplos 2 3 Exercícios 3 4 A Fórmula de Taylor 4 5 Observação 5 1 Fórmula de Taylor com Resto de Lagrange
Teorema de Taylor Prof. Doherty Andrade Sumário 1 Fórmula de Taylor com Resto de Lagrange 1 2 Exemplos 2 3 Exercícios 3 4 A Fórmula de Taylor 4 5 Observação 5 1 Fórmula de Taylor com Resto de Lagrange
Frações. Números Racionais
 Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
Frações Números Racionais Consideremos a operação 4:5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números porque não há
Usando o do-file editor Automatizando o Stata
 Usando o do-file editor Automatizando o Stata 1 O QUE É O EDITOR DE DO-FILE O Stata vem com um editor de texto integrado, o do-file editor (editor de do-files, em português), que pode ser usado para executar
Usando o do-file editor Automatizando o Stata 1 O QUE É O EDITOR DE DO-FILE O Stata vem com um editor de texto integrado, o do-file editor (editor de do-files, em português), que pode ser usado para executar
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Minicurso Aula 3: Técnicas de Demonstração Matemática. Anliy Natsuyo Nashimoto Sargeant Curso de Verão 2009 DEX - UFLA
 Minicurso Aula 3: Técnicas de Demonstração Matemática Anliy Natsuyo Nashimoto Sargeant Curso de Verão 2009 DEX - UFLA Bibliografia Garbi, Gilberto G., O romance das equações algébricas. Ed Makron Books,
Minicurso Aula 3: Técnicas de Demonstração Matemática Anliy Natsuyo Nashimoto Sargeant Curso de Verão 2009 DEX - UFLA Bibliografia Garbi, Gilberto G., O romance das equações algébricas. Ed Makron Books,
2015 O ANO DE COLHER ABRIL - 1 A RUA E O CAMINHO
 ABRIL - 1 A RUA E O CAMINHO Texto: Apocalipse 22:1-2 Então o anjo me mostrou o rio da água da vida que, claro como cristal, fluía do trono de Deus e do Cordeiro, no meio da RUA principal da cidade. De
ABRIL - 1 A RUA E O CAMINHO Texto: Apocalipse 22:1-2 Então o anjo me mostrou o rio da água da vida que, claro como cristal, fluía do trono de Deus e do Cordeiro, no meio da RUA principal da cidade. De
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
A aposentadoria do serralheiro
 A aposentadoria do serralheiro Roberto Ribeiro Paterlini 1 1 Introdução Há algum tempo estava em casa lendo prazerosamente Um Poeta, um Matemático e um Físico, quando alguém bateu à porta Era o Sr Alcides
A aposentadoria do serralheiro Roberto Ribeiro Paterlini 1 1 Introdução Há algum tempo estava em casa lendo prazerosamente Um Poeta, um Matemático e um Físico, quando alguém bateu à porta Era o Sr Alcides
Sumário. Introdução - O novo hábito... 1. Capítulo 1 - Pra que serve tudo isso?... 3. Sobre o vocabulário... 4. Benefícios... 7
 Sumário Introdução - O novo hábito... 1 Capítulo 1 - Pra que serve tudo isso?... 3 Sobre o vocabulário... 4 Benefícios... 7 Perguntas Frequentes sobre o Orçamento Doméstico... 10 Capítulo 2 - Partindo
Sumário Introdução - O novo hábito... 1 Capítulo 1 - Pra que serve tudo isso?... 3 Sobre o vocabulário... 4 Benefícios... 7 Perguntas Frequentes sobre o Orçamento Doméstico... 10 Capítulo 2 - Partindo
Desmistificando o Programa de Computador
 Desmistificando o Programa de Computador Hoje vou explicar, da maneira mais simples possível, como funciona um programa de computador. Na sua essência um programa de computador nada mais é que uma coletânea
Desmistificando o Programa de Computador Hoje vou explicar, da maneira mais simples possível, como funciona um programa de computador. Na sua essência um programa de computador nada mais é que uma coletânea
Aula 2 Sistemas de Numeração (Revisão)
 Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
Aula 2 Sistemas de Numeração (Revisão) Anderson L. S. Moreira anderson.moreira@recife.ifpe.edu.br http://dase.ifpe.edu.br/~alsm 1 O que fazer com essa apresentação 2 Agenda Breve revisão da aula anterior
Planeamento e Seguimento de Projectos
 Planeamento e Seguimento de Projectos Introdução Uma empresa sem objectivos a atingir é uma empresa desorientada, mas ter objectivos a atingir sem qualquer plano não deixa de ser apenas uma esperança.
Planeamento e Seguimento de Projectos Introdução Uma empresa sem objectivos a atingir é uma empresa desorientada, mas ter objectivos a atingir sem qualquer plano não deixa de ser apenas uma esperança.
Desenvolvido por: Rafael Botelho botelhotech@gmail.com http://rafaelbotelho.com
 Desenvolvido por: Rafael Botelho botelhotech@gmail.com http://rafaelbotelho.com Guia de Instalação do BRlix Como tenho visto no fórum do BRlix que muitas pessoas estão encontrando dificuldades na instalação
Desenvolvido por: Rafael Botelho botelhotech@gmail.com http://rafaelbotelho.com Guia de Instalação do BRlix Como tenho visto no fórum do BRlix que muitas pessoas estão encontrando dificuldades na instalação
SUMÁRIO VOLUME 1 MATEMÁTICA
 SUMÁRIO VOLUME 1 "A Terra é azul!" Yuri Gagarin Capítulo 1 Salve a Terra (Coordenadas, orientação espacial, interpretação de gráficos e tabelas, sólidos geométricos, poliedros, corpos redondos, formas
SUMÁRIO VOLUME 1 "A Terra é azul!" Yuri Gagarin Capítulo 1 Salve a Terra (Coordenadas, orientação espacial, interpretação de gráficos e tabelas, sólidos geométricos, poliedros, corpos redondos, formas
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Apresentação de Dados em Tabelas e Gráficos
 Apresentação de Dados em Tabelas e Gráficos Os dados devem ser apresentados em tabelas construídas de acordo com as normas técnicas ditadas pela Fundação Instituto Brasileiro de Geografia e Estatística
Apresentação de Dados em Tabelas e Gráficos Os dados devem ser apresentados em tabelas construídas de acordo com as normas técnicas ditadas pela Fundação Instituto Brasileiro de Geografia e Estatística
Capítulo II O QUE REALMENTE QUEREMOS
 Capítulo II O QUE REALMENTE QUEREMOS Neste inicio de curso de Formação em Coaching e Mentoring do Sistema ISOR, eu quero fazer a seguinte pergunta: o que vocês mais querem da vida hoje? Alguém pode começar?
Capítulo II O QUE REALMENTE QUEREMOS Neste inicio de curso de Formação em Coaching e Mentoring do Sistema ISOR, eu quero fazer a seguinte pergunta: o que vocês mais querem da vida hoje? Alguém pode começar?
Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/12/2011 pelo CEPERJ
 Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/1/011 pelo CEPERJ 59. O cartão de crédito que João utiliza cobra 10% de juros ao mês,
Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/1/011 pelo CEPERJ 59. O cartão de crédito que João utiliza cobra 10% de juros ao mês,
Programação em papel quadriculado
 4 NOME DA AULA: Programação em papel quadriculado Tempo de aula: 45 60 minutos Tempo de preparação: 10 minutos Objetivo principal: ajudar os alunos a entender como a codificação funciona. RESUMO Ao "programar"
4 NOME DA AULA: Programação em papel quadriculado Tempo de aula: 45 60 minutos Tempo de preparação: 10 minutos Objetivo principal: ajudar os alunos a entender como a codificação funciona. RESUMO Ao "programar"
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Índice. 1. Blocos Lógicos e Material Dourado - Continuação...3. 2. Séries e Sequências...4 3. Espaço e Forma...5. 1.1. Material Dourado...
 GRUPO 5.4 MÓDULO 17 Índice 1. Blocos Lógicos e Material Dourado - Continuação...3 1.1. Material Dourado... 3 2. Séries e Sequências...4 3. Espaço e Forma...5 2 1. BLOCOS LÓGICOS E MATERIAL DOURADO - CONTINUAÇÃO
GRUPO 5.4 MÓDULO 17 Índice 1. Blocos Lógicos e Material Dourado - Continuação...3 1.1. Material Dourado... 3 2. Séries e Sequências...4 3. Espaço e Forma...5 2 1. BLOCOS LÓGICOS E MATERIAL DOURADO - CONTINUAÇÃO
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Aula 4 Conceitos Básicos de Estatística. Aula 4 Conceitos básicos de estatística
 Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
4ª Lista de IP. Questão 1
 4ª Lista de IP Questão 1 Apesar dessa era digital, os jogos de tabuleiros foram jogos que deixaram marcada a infancia de muitos. Assim como Banco Imaboliario e Jogo da Vida por exemplo, esses jogos são
4ª Lista de IP Questão 1 Apesar dessa era digital, os jogos de tabuleiros foram jogos que deixaram marcada a infancia de muitos. Assim como Banco Imaboliario e Jogo da Vida por exemplo, esses jogos são
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
5 Dicas Testadas para Você Produzir Mais na Era da Internet
 5 Dicas Testadas para Você Produzir Mais na Era da Internet Uma das verdades absolutas sobre Produtividade que você precisa saber antes de seguir é entender que se ocupar não é produzir. Não sei se é o
5 Dicas Testadas para Você Produzir Mais na Era da Internet Uma das verdades absolutas sobre Produtividade que você precisa saber antes de seguir é entender que se ocupar não é produzir. Não sei se é o
este ano está igualzinho ao ano passado! viu? eu não falei pra você? o quê? foi você que jogou esta bola de neve em mim?
 viu? eu não falei pra você? o quê? este ano está igualzinho ao ano passado! foi você que jogou esta bola de neve em mim? puxa, acho que não... essa não está parecendo uma das minhas... eu costumo comprimir
viu? eu não falei pra você? o quê? este ano está igualzinho ao ano passado! foi você que jogou esta bola de neve em mim? puxa, acho que não... essa não está parecendo uma das minhas... eu costumo comprimir
VII MARATONA DE PROGRAMAÇÃO UERJ 17/05/2014. Este caderno contém 12 páginas com a descrição de 10 problemas 1 definidos a seguir:
 VII MARATONA DE PROGRAMAÇÃO UERJ 17/05/014 Este caderno contém 1 páginas com a descrição de 10 problemas 1 definidos a seguir: A - Botas B Digito Verificador do passaporte C Jogo da Vida D - A Próxima
VII MARATONA DE PROGRAMAÇÃO UERJ 17/05/014 Este caderno contém 1 páginas com a descrição de 10 problemas 1 definidos a seguir: A - Botas B Digito Verificador do passaporte C Jogo da Vida D - A Próxima
Programa Olímpico de Treinamento. Aula 9. Curso de Combinatória - Nível 2. Tabuleiros. Prof. Bruno Holanda
 Programa Olímpico de Treinamento Curso de Combinatória - Nível Prof. Bruno Holanda Aula 9 Tabuleiros Quem nunca brincou de quebra-cabeça? Temos várias pecinhas e temos que encontrar uma maneira de unir
Programa Olímpico de Treinamento Curso de Combinatória - Nível Prof. Bruno Holanda Aula 9 Tabuleiros Quem nunca brincou de quebra-cabeça? Temos várias pecinhas e temos que encontrar uma maneira de unir
OpenOffice Calc Aula 4
 OpenOffice Calc Aula 4 Objetivos: Apresentar a criação de um gráfico no CALC, a partir dos dados em uma planilha Apresentar os diversos tipos de gráficos e suas aplicações (gráfico de coluna, de linha,
OpenOffice Calc Aula 4 Objetivos: Apresentar a criação de um gráfico no CALC, a partir dos dados em uma planilha Apresentar os diversos tipos de gráficos e suas aplicações (gráfico de coluna, de linha,
Construção dos números racionais, Números fracionários e operações com frações
 Construção dos números racionais, Números fracionários e operações com frações O número racional pode ser definido a partir da aritmética fechamento da operação de divisão entre inteiros ou partir da geometria
Construção dos números racionais, Números fracionários e operações com frações O número racional pode ser definido a partir da aritmética fechamento da operação de divisão entre inteiros ou partir da geometria
SUB12 Campeonato de Resolução de Problemas de Matemática Edição 2009/2010
 SUB12 Campeonato de Resolução de Problemas de Matemática Edição 2009/2010 Problema 2 Bouquets de flores a 6 euros Na florista da Dona Libânia estão à venda ramos de flores por 6 euros. Os vários bouquets
SUB12 Campeonato de Resolução de Problemas de Matemática Edição 2009/2010 Problema 2 Bouquets de flores a 6 euros Na florista da Dona Libânia estão à venda ramos de flores por 6 euros. Os vários bouquets
Desafio para a família
 Desafio para a família Família é ideia de Deus, geradora de personalidade, melhor lugar para a formação do caráter, da ética, da moral e da espiritualidade. O sonho de Deus para a família é que seja um
Desafio para a família Família é ideia de Deus, geradora de personalidade, melhor lugar para a formação do caráter, da ética, da moral e da espiritualidade. O sonho de Deus para a família é que seja um
Redação do Site Inovação Tecnológica - 28/08/2009. Humanos aprimorados versus humanos comuns
 VOCÊ ESTÁ PREPARADO PARA CONVIVER COM OS HUMANOS APRIMORADOS? http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=voce-esta-preparado-conviver-humanosaprimorados&id=010850090828 Redação do
VOCÊ ESTÁ PREPARADO PARA CONVIVER COM OS HUMANOS APRIMORADOS? http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=voce-esta-preparado-conviver-humanosaprimorados&id=010850090828 Redação do
COMO ENSINEI MATEMÁTICA
 COMO ENSINEI MATEMÁTICA Mário Maturo Coutinho COMO ENSINEI MATEMÁTICA.ª edição 511 9 AGRADECIMENTOS À Deus À minha família Aos mestres da matemática do C.E.Visconde de Cairu APRESENTAÇÃO O objetivo deste
COMO ENSINEI MATEMÁTICA Mário Maturo Coutinho COMO ENSINEI MATEMÁTICA.ª edição 511 9 AGRADECIMENTOS À Deus À minha família Aos mestres da matemática do C.E.Visconde de Cairu APRESENTAÇÃO O objetivo deste
Quando vemos o mundo de forma diferente, nosso mundo fica diferente.
 BOLETIM TÉCNICO JULHO 2015 Quando vemos o mundo de forma diferente, nosso mundo fica diferente. Segundo a Psicologia atual ajudada pela compreensão do mundo real que nos trouxe a Física moderna, nós, seres
BOLETIM TÉCNICO JULHO 2015 Quando vemos o mundo de forma diferente, nosso mundo fica diferente. Segundo a Psicologia atual ajudada pela compreensão do mundo real que nos trouxe a Física moderna, nós, seres
O sucesso de hoje não garante o sucesso de amanhã
 Com certeza, esse final de século XX e começo de século XXI mudarão nossas vidas mais do que elas mudaram há 30-40 anos atrás. É muito difícil avaliar como será essa mudança, mas é certo que ela virá e
Com certeza, esse final de século XX e começo de século XXI mudarão nossas vidas mais do que elas mudaram há 30-40 anos atrás. É muito difícil avaliar como será essa mudança, mas é certo que ela virá e
Pontifícia Universidade Católica de Minas Gerais Bacharelado em Sistemas de Informação Trabalho de Diplomação
 Caros alunos e orientadores de conteúdo e acadêmico, Este documento ilustra quais capítulos devemos possuir na monografia de (no mínimo), e o que cada um contempla. O formato deverá ser o utilizado pela
Caros alunos e orientadores de conteúdo e acadêmico, Este documento ilustra quais capítulos devemos possuir na monografia de (no mínimo), e o que cada um contempla. O formato deverá ser o utilizado pela
Manifeste Seus Sonhos
 Manifeste Seus Sonhos Índice Introdução... 2 Isso Funciona?... 3 A Força do Pensamento Positivo... 4 A Lei da Atração... 7 Elimine a Negatividade... 11 Afirmações... 13 Manifeste Seus Sonhos Pág. 1 Introdução
Manifeste Seus Sonhos Índice Introdução... 2 Isso Funciona?... 3 A Força do Pensamento Positivo... 4 A Lei da Atração... 7 Elimine a Negatividade... 11 Afirmações... 13 Manifeste Seus Sonhos Pág. 1 Introdução
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
O QUE É A ESCALA RICHTER? (OU COMO SE MEDE UM TERREMOTO)
 1 O QUE É A ESCALA RICHTER? (OU COMO SE MEDE UM TERREMOTO) Ilydio Pereira de Sá Atualmente, com o crescimento da tecnologia e da informação, tem sido muito comum o noticiário sobre catástrofes, principalmente
1 O QUE É A ESCALA RICHTER? (OU COMO SE MEDE UM TERREMOTO) Ilydio Pereira de Sá Atualmente, com o crescimento da tecnologia e da informação, tem sido muito comum o noticiário sobre catástrofes, principalmente
Meu nome é José Guilherme Monteiro Paixão. Nasci em Campos dos Goytacazes, Norte Fluminense, Estado do Rio de Janeiro, em 24 de agosto de 1957.
 Rio de Janeiro, 5 de junho de 2008 IDENTIFICAÇÃO Meu nome é José Guilherme Monteiro Paixão. Nasci em Campos dos Goytacazes, Norte Fluminense, Estado do Rio de Janeiro, em 24 de agosto de 1957. FORMAÇÃO
Rio de Janeiro, 5 de junho de 2008 IDENTIFICAÇÃO Meu nome é José Guilherme Monteiro Paixão. Nasci em Campos dos Goytacazes, Norte Fluminense, Estado do Rio de Janeiro, em 24 de agosto de 1957. FORMAÇÃO
Unidade 5: Sistemas de Representação
 Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
Arquitetura e Organização de Computadores Atualização: 9/8/ Unidade 5: Sistemas de Representação Números de Ponto Flutuante IEEE 754/8 e Caracteres ASCII Prof. Daniel Caetano Objetivo: Compreender a representação
Discurso do Presidente da República, Luiz Inácio Lula da Silva, no encontro com a delegação de atletas das Paraolimpíadas de Atenas-2004
 , Luiz Inácio Lula da Silva, no encontro com a delegação de atletas das Paraolimpíadas de Atenas-2004 Palácio do Planalto, 14 de outubro de 2004 Meu querido companheiro Agnelo Queiroz, ministro de Estado
, Luiz Inácio Lula da Silva, no encontro com a delegação de atletas das Paraolimpíadas de Atenas-2004 Palácio do Planalto, 14 de outubro de 2004 Meu querido companheiro Agnelo Queiroz, ministro de Estado
OBJETIVO VISÃO GERAL SUAS ANOTAÇÕES
 OBJETIVO Assegurar a satisfação do cliente no pós-venda, desenvolvendo um relacionamento duradouro entre o vendedor e o cliente, além de conseguir indicações através de um sistema de follow-up (acompanhamento).
OBJETIVO Assegurar a satisfação do cliente no pós-venda, desenvolvendo um relacionamento duradouro entre o vendedor e o cliente, além de conseguir indicações através de um sistema de follow-up (acompanhamento).
Gráficos de funções em calculadoras e com lápis e papel (*)
 Rafael Domingos G Luís Universidade da Madeira/Escola Básica /3 São Roque Departamento de Matemática Gráficos de funções em calculadoras e com lápis e papel (*) A difusão de calculadoras gráficas tem levado
Rafael Domingos G Luís Universidade da Madeira/Escola Básica /3 São Roque Departamento de Matemática Gráficos de funções em calculadoras e com lápis e papel (*) A difusão de calculadoras gráficas tem levado
Implementando uma Classe e Criando Objetos a partir dela
 Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 04 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 2 Prof. Cristóvão Cunha Implementando uma Classe
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 04 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 2 Prof. Cristóvão Cunha Implementando uma Classe
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
1. Preconceito e discriminação, 14 Homofobia, 17
 SUMÁRIO Uma breve introdução, 11 PARTE I As principais dúvidas dos pais 1. Preconceito e discriminação, 14 Homofobia, 17 2. O dilema dos pais: um exemplo, 21 Os limites dos pais, 24 Diálogos no consultório,
SUMÁRIO Uma breve introdução, 11 PARTE I As principais dúvidas dos pais 1. Preconceito e discriminação, 14 Homofobia, 17 2. O dilema dos pais: um exemplo, 21 Os limites dos pais, 24 Diálogos no consultório,
Como vender a Gestão por Processos em sua organização?
 Como vender a Gestão por Processos em sua organização? Janeiro de 2012 O presente artigo aborda de forma prática as principais críticas que usualmente são atribuídas a projetos de gestão por processos.
Como vender a Gestão por Processos em sua organização? Janeiro de 2012 O presente artigo aborda de forma prática as principais críticas que usualmente são atribuídas a projetos de gestão por processos.
coleção Conversas #15 - NOVEMBRO 2014 - eg o. m r e é r q Respostas perguntas para algumas que podem estar passando pela sua cabeça.
 o coleção Conversas #15 - NOVEMBRO 2014 - Sou d advoga Será a que e é nã p o r consigo e q u e sou n m pr eg r eg o a?. Respostas perguntas para algumas que podem estar passando pela sua cabeça. A Coleção
o coleção Conversas #15 - NOVEMBRO 2014 - Sou d advoga Será a que e é nã p o r consigo e q u e sou n m pr eg r eg o a?. Respostas perguntas para algumas que podem estar passando pela sua cabeça. A Coleção
Trabalho realizado por: Bento Rosa Nº1 João Matoso Nº9
 Trabalho realizado por: Bento Rosa Nº1 João Matoso Nº9 Introdução Neste trabalho vamos falar sobre o Principio da Hidrostática (Onde surgiu, como surgiu e quem a inventou). Introdução da Hidrostática Hidrostática
Trabalho realizado por: Bento Rosa Nº1 João Matoso Nº9 Introdução Neste trabalho vamos falar sobre o Principio da Hidrostática (Onde surgiu, como surgiu e quem a inventou). Introdução da Hidrostática Hidrostática
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
A menina que queria visitar a tia
 Cenas urbanas A menina que queria visitar a tia A menina, conversando com a jornaleira, na manhã de domingo, tinha o ar desamparado. Revolvia, com nervosismo, um lenço com as pontas amarradas, dentro
Cenas urbanas A menina que queria visitar a tia A menina, conversando com a jornaleira, na manhã de domingo, tinha o ar desamparado. Revolvia, com nervosismo, um lenço com as pontas amarradas, dentro
Piaget diz que os seres humanos passam por uma série de mudanças previsíveis e ordenadas; Ou seja, geralmente todos os indivíduos vivenciam todos os
 Teoria cognitivista Piaget utilizou os princípios conhecidos como o conceito da adaptação biológica para desenvolver esta teoria; Ela diz que o desenvolvimento da inteligência dos indivíduos acontece à
Teoria cognitivista Piaget utilizou os princípios conhecidos como o conceito da adaptação biológica para desenvolver esta teoria; Ela diz que o desenvolvimento da inteligência dos indivíduos acontece à
Mostra Cultural 2015
 Mostra Cultural 2015 Colégio Marista João Paulo II Eu e as redes sociais #embuscadealgumascurtidas Uma reflexão sobre a legitimação do eu através das redes sociais. Iago Faria e Julio César V. Autores:
Mostra Cultural 2015 Colégio Marista João Paulo II Eu e as redes sociais #embuscadealgumascurtidas Uma reflexão sobre a legitimação do eu através das redes sociais. Iago Faria e Julio César V. Autores:
ALEGRIA ALEGRIA:... TATY:...
 ALEGRIA PERSONAGENS: Duas amigas entre idades adolescentes. ALEGRIA:... TATY:... Peça infanto-juvenil, em um só ato com quatro personagens sendo as mesmas atrizes, mostrando a vida de duas meninas, no
ALEGRIA PERSONAGENS: Duas amigas entre idades adolescentes. ALEGRIA:... TATY:... Peça infanto-juvenil, em um só ato com quatro personagens sendo as mesmas atrizes, mostrando a vida de duas meninas, no
