Lista de Exercícios Tratamento de Incerteza baseado em Probabilidade
|
|
|
- Adriano Jardim Vilarinho
- 8 Há anos
- Visualizações:
Transcrição
1 Lista de Exercícios Tratamento de Incerteza baseado em Probabilidade 1) Explique o termo probabilidade subjetiva no contexto de um agente que raciocina sobre incerteza baseando em probabilidade. 2) Explique o que é uma variável randômica e como elas podem ser classificadas de acordo com o domínio. 3) Seja f uma proposição, e x um valor do domínio de f. Seja y um valor real entre 0 e 1. Explique o que significa P(f = x) = y, de acordo com a semântica dos mundos possíveis. 4) Seja h e e proposições. O que é P(h e). O que esta probabilidade significa de acordo com a semântica dos mundos possíveis? 5) Explique por que o Teorema de Bayes é interessante. Por que a probabilidade condicional pode estar disponível em um sentido, mas não em outro? 6) Considere a situação na qual queremos raciocinar sobre o tempo e as viagens. Usaremos três variáveis randômicas booleanas para representar o tempo está ruim (T), os vôos entre Maringá e Curitiba estão canceladas (V) e as viagens de carro na BR369, entre Maringá e Curitiba, estão sendo atrasadas (B). Intuitivamente, sabemos que, para uma dada condição de tempo, os vôos cancelados não afetam atrasos nas BRs, e que atrasos nas BRs não afetam os cancelamento de vôos. Da experiência, sabemos que, se o tempo está ruim, existem 80% de chance que os vôos sejam cancelados. Se o tempo está bom, existem 40% de chances que os vôos sejam cancelados. Além do mais, o tempo ruim causa atrasos nas BRs 30% das vezes, mas com tempo bom as chances de atrasos são de somente 10%. Existem 20% de chance de tempo ruim em Maringá nesta época do ano. a. Crie uma rede Bayseana para este problema, inclua seu grafo e suas tabelas de distribuição condicional. b. Calcule P( V, T, B). 7) Imagine que 99% do tempo à doença RE (DRE) cause olhos vermelhos nas pessoas que a contraem. No entanto, somente 2% de todas as pessoas têm olhos vermelhos no dia-a-dia, e somente 1% contraem a doença DRE. Você tem olhos vermelhos. Qual é a probabilidade de você ter DRE? Lógica Fuzzy 8) Explique a diferença entre o tratamento de incerteza baseado em probabilidade e o tratamento de incerteza baseado em lógica fuzzy. Explique os termos graus de crença e graus de verdade. 9) Enumere as diferenças entre a teoria clássica dos conjuntos (crisp) e a teoria dos conjuntos fuzzy. 10) O que é uma variável lingüística no contexto da lógica fuzzy e como ela pode ser representada? 11) Quais são os principais componentes que formam um sistema especialista fuzzy? Explique rapidamente do que se trata cada um deles. 12) Explique quais são as fases de um sistema fuzzy e do que se trata cada delas.
2 13) O que significa dizer que uma regra é disparada na fase de processamento? Quanto o conseqüente desta regra influenciará na saída do sistema fuzzy? 14) Explique, sucintamente, o processo de construção de um sistema especialista baseado em lógica fuzzy. 15) Supõe que uma universidade moderna resolveu mudar o seu método de avaliação, por pensar que o método em que um aluno com média 6,0 é aprovado e um aluno com média 5,9 é reprovado é um método injusto. A universidade resolveu então, que, além da média anual na disciplina, outros méritos devem ser avaliados para a aprovação ou não de um aluno, como por exemplo, freqüência, e participação em sala de aula. Desta forma, pede-se que você formule um sistema fuzzy que leve em consideração estes méritos, e dê como resposta se o aluno deve ser aprovado, reprovado ou fazer um curso de férias para tentar melhorar seu aproveitamento. Desta forma, defina os itens abaixo, sempre fundamentando sua resposta: a) Os conjuntos fuzzy (no mínimo três) e suas relações de pertinência para as variáveis de entrada média_anual, freqüência e participação. Justifique a sua escolha para a forma da função de pertinência (trapezoidal, triangular, gaussiana...); b) Os conjuntos fuzzy (no mínimo três) e suas relações de pertinência para a variável de saída situação_aluno. Justifique a sua escolha para a forma da função de pertinência (trapezoidal, triangular, gaussiana...); c) As regras de funcionamento do sistema; d) O critério para definir o nível de pertinência do conseqüente quando o antecedente de uma regra com mais de uma variável de entrada disparar; e) O método de defuzzyficação utilizado. Aprendizagem 16) Quais questões afetam o projeto do elemento de aprendizagem de um agente? Explique cada um deles. 17) Os tipos de aprendizagem são classificados de acordo com o tipo de realimentação que o elemento de aprendizagem terá à sua disposição. Quais são estes tipos e dê exemplos de cada um deles. 18) A aprendizagem não supervisionada pode determinar sozinha se uma situação é boa ou ruim para um agente? Por quê? 19) Explique qual é o objetivo da aprendizagem indutiva. Do que precisamos para aprender uma hipótese h? 20) Uma hipótese h induzida por um método de aprendizagem indutiva pode ser facilmente validada? Por quê? 21) O que é o princípio da Navalha de Ockham? e como ele é aplicado no algoritmo de aprendizagem por árvore de decisão? 22) Explique rapidamente como funciona o algoritmo de aprendizagem para árvores de decisão visto em sala de aula. 23) O que significa dizer que um atributo é inútil? E que um atributo é perfeito? 24) De acordo com o conjunto de treinamento abaixo, aplique o algoritmo de aprendizagem em árvores de decisão para derivar uma árvore decisão condizente com os exemplos.
3 Atributos Predicado meta Dia Perspectiva Temperatura Umidade Vento JogarTenis D1 Ensolarado Quente Alta Fraco Não D2 Ensolarado Quente Alta Forte Não D3 Nublado Quente Alta Fraco Sim D4 Chuvoso Moderada Alta Fraco Sim D5 Chuvoso Fresca Normal Fraco Sim D6 Chuvoso Fresca Normal Forte Não D7 Nublado Fresca Normal Forte Sim D8 Ensolarado Moderada Alta Fraco Não D9 Ensolarado Fresca Normal Fraco Sim D10 Chuvoso Moderada Normal Fraco Sim D11 Ensolarado Moderada Normal Forte Sim D12 Nublado Moderada Alta Forte Sim D13 Nublado Quente Normal Fraco Sim D14 Chuvoso Moderada Alta Forte Não 25) Assuma que lhe é dado o conjunto rotulado exemplos de treinamento abaixo, onde cada característica tem três (3) possíveis valores a, b, ou c. Aplique o algoritmo de árvore de decisão a este conjunto. F1 F2 F3 Classificação a a a + b b c - a b c - c b c + c a c + b a a - 26) Assuma que você receba os seguintes atributos com os possíveis valores apresentados: F1 {A, B, C}; F2 {D, E}; F3 {G, H, I}; e F4 {J, K}. Considere os seguintes exemplos de treinamento. ex1 F1 = A F2 = E F3 = H F4 = J categoria = + ex2 F1 = A F2 = E F3 = G F4 = K categoria = - ex3 F1 = A F2 = D F3 = G F4 = J categoria = +
4 ex4 F1 = B F2 = D F3 = G F4 = J categoria = + ex5 F1 = B F2 = E F3 = H F4 = J categoria = + ex6 F1 = B F2 = E F3 = H F4 = K categoria = - ex7 F1 = C F2 = D F3 = H F4 = K categoria = - ex8 F1 = C F2 = D F3 = G F4 = J categoria = - A. Qual escore a formula de ganho de informação atribuí para cada um dos três atributos? (Estes cálculos podem ser úteis: I(x,y)=I(y,x), I(1,0)=0, I(1/2,1/2)=1, I(1/3,2/3)=0.92, I(1/4,3/4)=0.81, I(1/5,4/5)=0.72, I(1/6,5/6)=0.65, I(1/7,6/7)=0.59, I(1/8,7/8)=0.54). Tome cuidado de mostrar todo seu desenvolvimento. B. Que atributo seria escolhido como raiz? (Resolva os empates em favor de F1 sobre F2 sobre F3 sobre F4 e + sobre - ). C. Mostre o próximo nó interior, se existir algum, que o algoritmo de aprendizado de árvore de decisão selecionaria. Note que, para evitar gastar tempo excessivo, está sendo pedido que você crie no máximo os dois (2) primeiros nós interiores. Crie o maior número de nós folhas possíveis, dada a sua escolha de nós interiores. Novamente, tome o cuidado de mostrar todo seu desenvolvimento. 27) Considere coletar dados aonde cada exemplo tem três atributos X1, X2 e X3, e onde X1 possui valores A e B, X2 possui valores C e D, e X3 possui valores E, F, G. Seu objetivo é construir uma árvore de decisão para um conceito booleano dado pelos seguintes exemplos: X1 X2 X3 classificação A C G + A D F + A C F - A D F + B D G - B D G - B C G + B C F - (a) Calcule o ganho de informação para cada um dos três atributos X1, X2 e X3. Mostre seus cálculos. Saiba que: I(1,0)=0, I(0.5,0.5)=1, I(0.75, 0.25)=0.81, e I(0.875, 0.125)=0.54. (b) Qual atributo o algoritmo de aprendizado da árvore de decisão escolherá primeiro para raiz quando se usa o critério de ganho-máximo? E qual serão as próximas raízes. 28) Considere os seguintes exemplos de treinamento onde quatro exemplo de valores booleanos (X1 a X4) são usados para predizer um valor booleano (Y1): X1 X2 X3 X4 Y Desenhe um perceptron para esta tarefa, inicializando todos os pesos e bias em 0,1. Mostre como os pesos e os bias neste perceptron irão ser modificados depois de processar os dois primeiros exemplos acima. Use uma taxa de aprendizagem de 0,5. Mostre todos seus cálculos. 29) Considere um perceptron que tem três unidades de entradas com valores reais e duas unidades de saída com uma função de ativação sigmoidal. Todos os pesos iniciais e os desvios (bias) são iguais a 0,5. Assuma que seu professor tenha dito que a saída deve ser 1 e 0 para os valores de entrada in1 = 0,7; in2 = -0,5 e in3 = 0,3.
5 A) Mostre como a regra de aprendizado do perceptron irá alterar a RNA após processar este exemplo de treinamento. Faça α (a taxa de aprendizagem) ser 0.1, e tenha certeza de ajustar os bias das unidades durante o treinamento. 30) Considere um perceptron que tem duas unidades de entradas com valores reais e uma unidade de saída com uma função de ativação sinal. Suponha os pesos iniciais [0.75; 0.5] e o bias de Assuma o conjunto de exemplos abaixo. Divida o conjunto em dois, um de treinamento de três exemplos e outro de teste de cinco exemplos e aplique o algoritmo de aprendizagem do perceptron até a terceira iteração. Após isto verifique a qualidade do aprendizado obtido. Considere α (a taxa de aprendizagem) igual 0.1, e tenha certeza de ajustar os bias das unidades durante o treinamento. Ex X1 X2 Saída ) Assuma que nós temos uma variável aleatória de diagnóstico (vamos chamá-la de D) e duas variáveis de medida (vamos chamá-las de M1 e M2). Para simplificar, assuma que as variáveis têm três valores possíveis (e.g., low, medium, and high) e que D seja booleana. Nós coletamos dados de 300 episódios e achamos o seguinte: D é true 100 vezes e para estes casos: M1=low 50 vezes, M1=med 30 vezes, and M1 = high 20 vezes M2=low 10 vezes, M2=med 80 vezes, and M2 = high 10 vezes D é false 200 vezes e para estes casos: M1=low 20 vezes, M1=med 80 vezes, and M1 = high 100 vezes M2=low 180 vezes, M2=med 10 vezes, and M2 = high 10 vezes Assuma que M1 e M2 são condicionalmente independentes dado D. i. Mostre como a regra de Bayes pode ser usada para calcular P(D M1, M2) conhecido os dados acima e sobre a hipótese acima definida. [faça isto algebricamente i.e., usando equações.] ii. Em um dos episódios nos achamos M1=low e M2=low. Qual é o diagnóstico mais provável? De uma justificativa numérica. 32) Você recebe alguns documentos, cada um especificado por um vetor de características (X1, X2, X3), no qual cada componente tem um valor binário. Existem duas possíveis classificações para um documento C= 0 ou 1. É 3 vezes mais provável que um documento esteja na classe 1 do que na classe 0. Você também sabe: P(X1 =1 C = 0) = 0.25, P(X2 = 1 C = 0) = 0.5, P(X3 = 1 C = 0) = 0.4, P(X1 = 1 C = 1) = 0.5, P(X2 = 1 C = 1) = 0.25, and P(X3 = 1 C = 1) = 0.3. a) Desenhe uma rede Bayseana (com as TPCs) que representam este problema como um modelo de Bayes ingênuo. b) Dado um novo documento com um vetor característico (X1 = 0, X2 = 1, X3 = 1), determine a classificação deste documento usando o modelo de Bayes ingênuo representado em (a). Mostre seu trabalho.
6 c) Quais das seguintes sentenças expressam a pressuposição de independência condicional usada na definição do modelo de Bayes ingênuo? (i) P(C X1, X2, X3) = [P(X1, X2, X3 C) P(C)] / P(X1, X2, X3) (ii) P(X1, X2, X3 C) = P(X1 C) P(X2 C) P(X3 C) (iii) P(X1, X2, X3) = P(X1) P(X2) P(X3)
Tecnologia da Informação Prof. Mário Henrique de Souza Pardo Resumo Aula 4
 Tecnologia da Informação Prof. Mário Henrique de Souza Pardo Resumo Aula 4 1 MS-Excel Aplicando funções às suas fórmulas de Excel (continuação) Serão vistas, nesta aula as funções de busca e referência
Tecnologia da Informação Prof. Mário Henrique de Souza Pardo Resumo Aula 4 1 MS-Excel Aplicando funções às suas fórmulas de Excel (continuação) Serão vistas, nesta aula as funções de busca e referência
5 Instrução e integração
 SEÇÃO 5 Instrução e integração no meio de trabalho Quando um novo funcionário entra para uma organização, é importante que ele receba um bom apoio para entender sua função e a organização. Instrução é
SEÇÃO 5 Instrução e integração no meio de trabalho Quando um novo funcionário entra para uma organização, é importante que ele receba um bom apoio para entender sua função e a organização. Instrução é
Aprendizagem de Máquina
 Aprendizagem de Máquina Professor: Rosalvo Ferreira de Oliveira Neto Disciplina: Inteligência Artificial Tópicos 1. Definições 2. Tipos de aprendizagem 3. Paradigmas de aprendizagem 4. Modos de aprendizagem
Aprendizagem de Máquina Professor: Rosalvo Ferreira de Oliveira Neto Disciplina: Inteligência Artificial Tópicos 1. Definições 2. Tipos de aprendizagem 3. Paradigmas de aprendizagem 4. Modos de aprendizagem
Engenharia de Software II
 Engenharia de Software II Aula 28 Revisão para a Prova 2 http://www.ic.uff.br/~bianca/engsoft2/ Aula 28-28/07/2006 1 Matéria para a Prova 2 Gestão de projetos de software Conceitos (Cap. 21) Métricas (Cap.
Engenharia de Software II Aula 28 Revisão para a Prova 2 http://www.ic.uff.br/~bianca/engsoft2/ Aula 28-28/07/2006 1 Matéria para a Prova 2 Gestão de projetos de software Conceitos (Cap. 21) Métricas (Cap.
OBJETIVO VISÃO GERAL SUAS ANOTAÇÕES
 OBJETIVO Assegurar a satisfação do cliente no pós-venda, desenvolvendo um relacionamento duradouro entre o vendedor e o cliente, além de conseguir indicações através de um sistema de follow-up (acompanhamento).
OBJETIVO Assegurar a satisfação do cliente no pós-venda, desenvolvendo um relacionamento duradouro entre o vendedor e o cliente, além de conseguir indicações através de um sistema de follow-up (acompanhamento).
Aula 4 Estatística Conceitos básicos
 Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
O Processo de KDD. Data Mining SUMÁRIO - AULA1. O processo de KDD. Interpretação e Avaliação. Seleção e Pré-processamento. Consolidação de dados
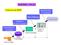 SUMÁRIO - AULA1 O Processo de KDD O processo de KDD Interpretação e Avaliação Consolidação de dados Seleção e Pré-processamento Warehouse Data Mining Dados Preparados p(x)=0.02 Padrões & Modelos Conhecimento
SUMÁRIO - AULA1 O Processo de KDD O processo de KDD Interpretação e Avaliação Consolidação de dados Seleção e Pré-processamento Warehouse Data Mining Dados Preparados p(x)=0.02 Padrões & Modelos Conhecimento
Gerenciamento da Integração (PMBoK 5ª ed.)
 Gerenciamento da Integração (PMBoK 5ª ed.) O PMBoK diz que: O gerenciamento da integração do projeto inclui os processos e as atividades necessárias para identificar, definir, combinar, unificar e coordenar
Gerenciamento da Integração (PMBoK 5ª ed.) O PMBoK diz que: O gerenciamento da integração do projeto inclui os processos e as atividades necessárias para identificar, definir, combinar, unificar e coordenar
Programação em papel quadriculado
 4 NOME DA AULA: Programação em papel quadriculado Tempo de aula: 45 60 minutos Tempo de preparação: 10 minutos Objetivo principal: ajudar os alunos a entender como a codificação funciona. RESUMO Ao "programar"
4 NOME DA AULA: Programação em papel quadriculado Tempo de aula: 45 60 minutos Tempo de preparação: 10 minutos Objetivo principal: ajudar os alunos a entender como a codificação funciona. RESUMO Ao "programar"
planodenegocioapostilaempreendedorismo_exerc.doc Empreendedorismo EXERCÍCIO DE NIVELAMENTO PERGUNTAS E RESPOSTAS
 EXERCÍCIO DE NIVELAMENTO PERGUNTAS E RESPOSTAS 1) Qual o conceito de empreendedor?...empreendedor é um indivíduo que imagina, desenvolve e realiza visões. Ele está sempre buscando novas idéias e criando
EXERCÍCIO DE NIVELAMENTO PERGUNTAS E RESPOSTAS 1) Qual o conceito de empreendedor?...empreendedor é um indivíduo que imagina, desenvolve e realiza visões. Ele está sempre buscando novas idéias e criando
Manual das planilhas de Obras v2.5
 Manual das planilhas de Obras v2.5 Detalhamento dos principais tópicos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Gerando previsão de custos da obra (Módulo
Manual das planilhas de Obras v2.5 Detalhamento dos principais tópicos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Gerando previsão de custos da obra (Módulo
Do neurônio biológico ao neurônio das redes neurais artificiais
 Do neurônio biológico ao neurônio das redes neurais artificiais O objetivo desta aula é procurar justificar o modelo de neurônio usado pelas redes neurais artificiais em termos das propriedades essenciais
Do neurônio biológico ao neurônio das redes neurais artificiais O objetivo desta aula é procurar justificar o modelo de neurônio usado pelas redes neurais artificiais em termos das propriedades essenciais
Empreenda! 9ª Edição Roteiro de Apoio ao Plano de Negócios. Preparamos este roteiro para ajudá-lo (a) a desenvolver o seu Plano de Negócios.
 Empreenda! 9ª Edição Roteiro de Apoio ao Plano de Negócios Caro (a) aluno (a), Preparamos este roteiro para ajudá-lo (a) a desenvolver o seu Plano de Negócios. O Plano de Negócios deverá ter no máximo
Empreenda! 9ª Edição Roteiro de Apoio ao Plano de Negócios Caro (a) aluno (a), Preparamos este roteiro para ajudá-lo (a) a desenvolver o seu Plano de Negócios. O Plano de Negócios deverá ter no máximo
Aula 1: Introdução à Probabilidade
 Aula 1: Introdução à Probabilidade Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 07 de Março de 2012 Experimento Aleatório Um experimento é qualquer processo
Aula 1: Introdução à Probabilidade Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 07 de Março de 2012 Experimento Aleatório Um experimento é qualquer processo
Dois eventos são disjuntos ou mutuamente exclusivos quando não tem elementos em comum. Isto é, A B = Φ
 Probabilidade Vimos anteriormente como caracterizar uma massa de dados, como o objetivo de organizar e resumir informações. Agora, apresentamos a teoria matemática que dá base teórica para o desenvolvimento
Probabilidade Vimos anteriormente como caracterizar uma massa de dados, como o objetivo de organizar e resumir informações. Agora, apresentamos a teoria matemática que dá base teórica para o desenvolvimento
Avaliação da Aprendizagem no Ensino Superior Prof. Dr. Dirceu da Silva
 Avaliação da Aprendizagem no Ensino Superior Prof. Dr. Dirceu da Silva 18 de agosto de 2008 Objetivos deste encontro: 1. Levantar alguns problemas sobre a avaliação da aprendizagem; 2. Refletir sobre o
Avaliação da Aprendizagem no Ensino Superior Prof. Dr. Dirceu da Silva 18 de agosto de 2008 Objetivos deste encontro: 1. Levantar alguns problemas sobre a avaliação da aprendizagem; 2. Refletir sobre o
Estatística II Antonio Roque Aula 9. Testes de Hipóteses
 Testes de Hipóteses Os problemas de inferência estatística tratados nas aulas anteriores podem ser enfocados de um ponto de vista um pouco diferente: ao invés de se construir intervalos de confiança para
Testes de Hipóteses Os problemas de inferência estatística tratados nas aulas anteriores podem ser enfocados de um ponto de vista um pouco diferente: ao invés de se construir intervalos de confiança para
Cotagem de dimensões básicas
 Cotagem de dimensões básicas Introdução Observe as vistas ortográficas a seguir. Com toda certeza, você já sabe interpretar as formas da peça representada neste desenho. E, você já deve ser capaz de imaginar
Cotagem de dimensões básicas Introdução Observe as vistas ortográficas a seguir. Com toda certeza, você já sabe interpretar as formas da peça representada neste desenho. E, você já deve ser capaz de imaginar
Como vender a Gestão por Processos em sua organização?
 Como vender a Gestão por Processos em sua organização? Janeiro de 2012 O presente artigo aborda de forma prática as principais críticas que usualmente são atribuídas a projetos de gestão por processos.
Como vender a Gestão por Processos em sua organização? Janeiro de 2012 O presente artigo aborda de forma prática as principais críticas que usualmente são atribuídas a projetos de gestão por processos.
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
AFETA A SAÚDE DAS PESSOAS
 INTRODUÇÃO Como vai a qualidade de vida dos colaboradores da sua empresa? Existem investimentos para melhorar o clima organizacional e o bem-estar dos seus funcionários? Ações que promovem a qualidade
INTRODUÇÃO Como vai a qualidade de vida dos colaboradores da sua empresa? Existem investimentos para melhorar o clima organizacional e o bem-estar dos seus funcionários? Ações que promovem a qualidade
Prog A B C A e B A e C B e C A,B e C Nenhum Pref 100 150 200 20 30 40 10 130
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
Trata-se do processo de planejamento, identificação, análise e planejamento de respostas e controle de riscos.
 Aula 22 1 2 Trata-se do processo de planejamento, identificação, análise e planejamento de respostas e controle de riscos. O objetivo deste processo é aumentar a possibilidade de eventos positivos e reduzir
Aula 22 1 2 Trata-se do processo de planejamento, identificação, análise e planejamento de respostas e controle de riscos. O objetivo deste processo é aumentar a possibilidade de eventos positivos e reduzir
Faculdade de Computação
 UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
Exercícios Adicionais
 Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Processos Estocásticos
 Processos Estocásticos Terceira Lista de Exercícios 22 de julho de 20 Seja X uma VA contínua com função densidade de probabilidade f dada por Calcule P ( < X < 2. f(x = 2 e x x R. A fdp dada tem o seguinte
Processos Estocásticos Terceira Lista de Exercícios 22 de julho de 20 Seja X uma VA contínua com função densidade de probabilidade f dada por Calcule P ( < X < 2. f(x = 2 e x x R. A fdp dada tem o seguinte
Probabilidade e Estatística I Antonio Roque Aula 11 Probabilidade Elementar: Novos Conceitos
 Probabilidade Elementar: Novos Conceitos Vamos começar com algumas definições: Experimento: Qualquer processo ou ação bem definida que tenha um conjunto de resultados possíveis 1) Lançamento de um dado;
Probabilidade Elementar: Novos Conceitos Vamos começar com algumas definições: Experimento: Qualquer processo ou ação bem definida que tenha um conjunto de resultados possíveis 1) Lançamento de um dado;
Como Passar em Química Geral*
 1 Como Passar em Química Geral* por Dra. Brenna E. Lorenz Division of Natural Sciences University of Guam * traduzido livremente por: Eder João Lenardão; acesse o original em : http://www.heptune.com/passchem.html
1 Como Passar em Química Geral* por Dra. Brenna E. Lorenz Division of Natural Sciences University of Guam * traduzido livremente por: Eder João Lenardão; acesse o original em : http://www.heptune.com/passchem.html
Análise de Risco Valor Monetário Esperado Árvores de Decisão POP II UDESC Prof. Adelmo A. Martins
 Evento E1 O1 Decisão D1 E2 O2 E1 O1 D2 Análise de Risco Valor Monetário Esperado E2 O2 Árvores de Decisão POP II UDESC Prof. Adelmo A. Martins Análise de Riscos O risco é um evento ou condição de incerteza
Evento E1 O1 Decisão D1 E2 O2 E1 O1 D2 Análise de Risco Valor Monetário Esperado E2 O2 Árvores de Decisão POP II UDESC Prof. Adelmo A. Martins Análise de Riscos O risco é um evento ou condição de incerteza
CALEDÁRIO ESCOLAR. Página 1 de 24
 Página 1 de 24 SISTEMA DE CALENDÁRIO ESCOLAR O Sistema de Calendário Escolar é a primeira etapa de uma grande evolução que ocorrerá nos sistemas de informatização da Secretaria de Estado da Educação. As
Página 1 de 24 SISTEMA DE CALENDÁRIO ESCOLAR O Sistema de Calendário Escolar é a primeira etapa de uma grande evolução que ocorrerá nos sistemas de informatização da Secretaria de Estado da Educação. As
Avaliando o que foi Aprendido
 Avaliando o que foi Aprendido Treinamento, teste, validação Predição da performance: Limites de confiança Holdout, cross-validation, bootstrap Comparando algoritmos: o teste-t Predecindo probabilidades:função
Avaliando o que foi Aprendido Treinamento, teste, validação Predição da performance: Limites de confiança Holdout, cross-validation, bootstrap Comparando algoritmos: o teste-t Predecindo probabilidades:função
Início Rápido para o Templo
 Início Rápido para o Templo O FamilySearch.org facilita realizar as ordenanças do templo por seus antepassados. Todo o processo tem apenas alguns passos simples: 1. Descobrir antepassados que precisam
Início Rápido para o Templo O FamilySearch.org facilita realizar as ordenanças do templo por seus antepassados. Todo o processo tem apenas alguns passos simples: 1. Descobrir antepassados que precisam
18/11/2005. Discurso do Presidente da República
 Discurso do presidente da República, Luiz Inácio Lula da Silva, na cerimônia de entrega de certificado para os primeiros participantes do programa Escolas-Irmãs Palácio do Planalto, 18 de novembro de 2005
Discurso do presidente da República, Luiz Inácio Lula da Silva, na cerimônia de entrega de certificado para os primeiros participantes do programa Escolas-Irmãs Palácio do Planalto, 18 de novembro de 2005
MD Sequências e Indução Matemática 1
 Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
0,999... OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel
 Nível Intermediário 0,999... OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel Quando um jovem estudante de matemática começa a estudar os números reais, é difícil não sentir certo desconforto
Nível Intermediário 0,999... OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel Quando um jovem estudante de matemática começa a estudar os números reais, é difícil não sentir certo desconforto
Projeto da Disciplina Parte1: Estudo de Viabilidade. Um Estudo de Viabilidade
 Projeto da Disciplina Parte1: Estudo de Viabilidade ENTREGA: 09/04/09 Professor: Carlos José Maria Olguin Um Estudo de Viabilidade Você deve fazer um estudo de viabilidade para um projeto de sistema de
Projeto da Disciplina Parte1: Estudo de Viabilidade ENTREGA: 09/04/09 Professor: Carlos José Maria Olguin Um Estudo de Viabilidade Você deve fazer um estudo de viabilidade para um projeto de sistema de
Disciplina: Alfabetização
 Título do artigo: As intervenções didáticas no processo de alfabetização inicial Disciplina: Alfabetização Selecionador: Beatriz Gouveia 1 Categoria: Professor 1 Coordenadora de projetos do Instituto Avisa
Título do artigo: As intervenções didáticas no processo de alfabetização inicial Disciplina: Alfabetização Selecionador: Beatriz Gouveia 1 Categoria: Professor 1 Coordenadora de projetos do Instituto Avisa
Roteiro SENAC. Análise de Riscos. Planejamento do Gerenciamento de Riscos. Planejamento do Gerenciamento de Riscos
 SENAC Pós-Graduação em Segurança da Informação: Análise de Riscos Parte 2 Leandro Loss, Dr. Eng. loss@gsigma.ufsc.br http://www.gsigma.ufsc.br/~loss Roteiro Introdução Conceitos básicos Riscos Tipos de
SENAC Pós-Graduação em Segurança da Informação: Análise de Riscos Parte 2 Leandro Loss, Dr. Eng. loss@gsigma.ufsc.br http://www.gsigma.ufsc.br/~loss Roteiro Introdução Conceitos básicos Riscos Tipos de
Módulo 14 Treinamento e Desenvolvimento de Pessoas. 14.1. Treinamento é investimento
 Módulo 14 Treinamento e Desenvolvimento de Pessoas 14.1. Treinamento é investimento O subsistema de desenvolver pessoas é uma das áreas estratégicas do Gerenciamento de Pessoas, entretanto em algumas organizações
Módulo 14 Treinamento e Desenvolvimento de Pessoas 14.1. Treinamento é investimento O subsistema de desenvolver pessoas é uma das áreas estratégicas do Gerenciamento de Pessoas, entretanto em algumas organizações
Algoritmos Indutores de Árvores de
 Algoritmos Indutores de Árvores de Decisão Fabrício J. Barth Sistemas Inteligentes Análise e Desenvolvimento de Sistemas Faculdades de Tecnologia Bandeirantes Abril de 2013 Problema: Diagnóstico para uso
Algoritmos Indutores de Árvores de Decisão Fabrício J. Barth Sistemas Inteligentes Análise e Desenvolvimento de Sistemas Faculdades de Tecnologia Bandeirantes Abril de 2013 Problema: Diagnóstico para uso
Construindo uma aula significativa passo-a-passo.
 Construindo uma aula significativa passo-a-passo. www.juliofurtado.com.br SINOPSE: O As sete etapas da construção de um conceito. O Os três momentos de uma aula significativa. O A mediação de conflitos
Construindo uma aula significativa passo-a-passo. www.juliofurtado.com.br SINOPSE: O As sete etapas da construção de um conceito. O Os três momentos de uma aula significativa. O A mediação de conflitos
BSI Letramento Digital Prof. André Di Thommazo. Organização pessoal
 Organização pessoal Os cursos de graduação exigem que os alunos cursem diversas disciplinas ao mesmo tempo e em alguns semestres a carga horária é grande. Em geral o aluno de ensino a distância tem outras
Organização pessoal Os cursos de graduação exigem que os alunos cursem diversas disciplinas ao mesmo tempo e em alguns semestres a carga horária é grande. Em geral o aluno de ensino a distância tem outras
COMO REDIGIR ARTIGOS CIENTÍFICOS. Profa. EnimarJ. Wendhausen
 COMO REDIGIR ARTIGOS CIENTÍFICOS Profa. EnimarJ. Wendhausen Objetivo do capítulo Contribuir para que o discente, seguindo as etapas apresentadas no texto, tenha condições de redigir um texto em conformidade
COMO REDIGIR ARTIGOS CIENTÍFICOS Profa. EnimarJ. Wendhausen Objetivo do capítulo Contribuir para que o discente, seguindo as etapas apresentadas no texto, tenha condições de redigir um texto em conformidade
3 Qualidade de Software
 3 Qualidade de Software Este capítulo tem como objetivo esclarecer conceitos relacionados à qualidade de software; conceitos estes muito importantes para o entendimento do presente trabalho, cujo objetivo
3 Qualidade de Software Este capítulo tem como objetivo esclarecer conceitos relacionados à qualidade de software; conceitos estes muito importantes para o entendimento do presente trabalho, cujo objetivo
UNIVERSIDADE FEDERAL DE SÃO JOÃO DEL REI
 UNIVERSIDADE FEDERAL DE SÃO JOÃO DEL REI MODELO PARA REDAÇÃO DO PROJETO DE PESQUISA DISCIPLINA: MÉTODO DE PESQUISA QUANTITATIVA PROFA. Dra. MARINA BANDEIRA, Ph.D. MARÇO 2014 1 MODELO PARA REDAÇÃO DOS TRABALHOS
UNIVERSIDADE FEDERAL DE SÃO JOÃO DEL REI MODELO PARA REDAÇÃO DO PROJETO DE PESQUISA DISCIPLINA: MÉTODO DE PESQUISA QUANTITATIVA PROFA. Dra. MARINA BANDEIRA, Ph.D. MARÇO 2014 1 MODELO PARA REDAÇÃO DOS TRABALHOS
Programação Orientada a Objetos e Java - Introdução. Carlos Lopes
 Programação Orientada a Objetos e Java - Introdução Carlos Lopes POO e Java Objetivo: proporcionar uma visão dos conceitos de POO e do seu uso na estruturação dos programas em Java. Classes e objetos em
Programação Orientada a Objetos e Java - Introdução Carlos Lopes POO e Java Objetivo: proporcionar uma visão dos conceitos de POO e do seu uso na estruturação dos programas em Java. Classes e objetos em
Realizando cálculos para o aparelho divisor (I)
 Realizando cálculos para o aparelho divisor (I) A UU L AL A Você já estudou como fazer os cálculos para encontrar as principais medidas para a confecção de uma engrenagem cilíndrica de dentes retos. Vamos
Realizando cálculos para o aparelho divisor (I) A UU L AL A Você já estudou como fazer os cálculos para encontrar as principais medidas para a confecção de uma engrenagem cilíndrica de dentes retos. Vamos
Regras Métodos Identificadores Variáveis Constantes Tipos de dados Comandos de atribuição Operadores aritméticos, relacionais e lógicos
 Lógica Aula 2 Técnicas de Programação Criando algoritmos Regras Métodos Identificadores Variáveis Constantes Tipos de dados Comandos de atribuição Operadores aritméticos, relacionais e lógicos Criando
Lógica Aula 2 Técnicas de Programação Criando algoritmos Regras Métodos Identificadores Variáveis Constantes Tipos de dados Comandos de atribuição Operadores aritméticos, relacionais e lógicos Criando
20 perguntas para descobrir como APRENDER MELHOR
 20 perguntas para descobrir como APRENDER MELHOR Resultados Processo de aprendizagem EXPLORAÇÃO Busco entender como as coisas funcionam e descobrir as relações entre as mesmas. Essa busca por conexões
20 perguntas para descobrir como APRENDER MELHOR Resultados Processo de aprendizagem EXPLORAÇÃO Busco entender como as coisas funcionam e descobrir as relações entre as mesmas. Essa busca por conexões
UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA. Manual do Moodle- Sala virtual
 UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA Manual do Moodle- Sala virtual UNIFAP MACAPÁ-AP 2012 S U M Á R I O 1 Tela de Login...3 2 Tela Meus
UNIVERSIDADE FEDERAL DO AMAPÁ PRÓ REITORIA DE ADMINISTRAÇÃO E PLANEJAMENTO DEPARTAMENTO DE INFORMÁTICA Manual do Moodle- Sala virtual UNIFAP MACAPÁ-AP 2012 S U M Á R I O 1 Tela de Login...3 2 Tela Meus
7 etapas para construir um Projeto Integrado de Negócios Sustentáveis de sucesso
 7 etapas para construir um Projeto Integrado de Negócios Sustentáveis de sucesso Saiba como colocar o PINS em prática no agronegócio e explore suas melhores opções de atuação em rede. Quando uma empresa
7 etapas para construir um Projeto Integrado de Negócios Sustentáveis de sucesso Saiba como colocar o PINS em prática no agronegócio e explore suas melhores opções de atuação em rede. Quando uma empresa
Projeto Matemática 5º ano 4ª série. Objetivos
 Projeto Matemática 5º ano 4ª série Objetivos - Despertar o pensamento, propiciando a troca de experiências e de conhecimentos. - Fazer com que o aluno saiba debater idéias, levantar hipóteses, elaborar
Projeto Matemática 5º ano 4ª série Objetivos - Despertar o pensamento, propiciando a troca de experiências e de conhecimentos. - Fazer com que o aluno saiba debater idéias, levantar hipóteses, elaborar
RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO
 RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO Caro aluno, Disponibilizo abaixo a resolução resumida das questões de Raciocínio Lógico-Matemático da prova de Técnico de Atividade Judiciária do
RESOLUÇÃO DAS QUESTÕES DE RACIOCÍNIO LÓGICO-MATEMÁTICO Caro aluno, Disponibilizo abaixo a resolução resumida das questões de Raciocínio Lógico-Matemático da prova de Técnico de Atividade Judiciária do
Universidade Federal do Paraná. Setor de Ciências Exatas. Departamento de Matemática
 Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática Oficina de Calculadora PIBID Matemática Grupo do Laboratório de Ensino de Matemática Curitiba Agosto de 2013 Duração:
Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática Oficina de Calculadora PIBID Matemática Grupo do Laboratório de Ensino de Matemática Curitiba Agosto de 2013 Duração:
GUIA PRÁTICO PARA PROFESSORES
 GUIA PRÁTICO PARA PROFESSORES (Des)motivação na sala de aula! Sugestões práticas da: Nota introdutória Ser professor é ter o privilégio de deixar em cada aluno algo que este possa levar para a vida, seja
GUIA PRÁTICO PARA PROFESSORES (Des)motivação na sala de aula! Sugestões práticas da: Nota introdutória Ser professor é ter o privilégio de deixar em cada aluno algo que este possa levar para a vida, seja
UnP. fazendo e compartilhando a gente aprende mais
 DIRETRIZES DO ALUNO Olá, você está fazendo parte de um projeto de melhoria acadêmicoaction! Neste material você encontrará todas as pedagógica: o Edu Action informações necessárias para entender como esse
DIRETRIZES DO ALUNO Olá, você está fazendo parte de um projeto de melhoria acadêmicoaction! Neste material você encontrará todas as pedagógica: o Edu Action informações necessárias para entender como esse
Base Nacional Comum Curricular 2016. Lemann Center at Stanford University
 Base Nacional Comum Curricular 2016 Lemann Center at Stanford University Parte II: Base Nacional Comum: Análise e Recomendações da Seção de Matemática Phil Daro Dezembro, 2015 BASE NACIONAL COMUM: ANÁLISE
Base Nacional Comum Curricular 2016 Lemann Center at Stanford University Parte II: Base Nacional Comum: Análise e Recomendações da Seção de Matemática Phil Daro Dezembro, 2015 BASE NACIONAL COMUM: ANÁLISE
Piaget diz que os seres humanos passam por uma série de mudanças previsíveis e ordenadas; Ou seja, geralmente todos os indivíduos vivenciam todos os
 Teoria cognitivista Piaget utilizou os princípios conhecidos como o conceito da adaptação biológica para desenvolver esta teoria; Ela diz que o desenvolvimento da inteligência dos indivíduos acontece à
Teoria cognitivista Piaget utilizou os princípios conhecidos como o conceito da adaptação biológica para desenvolver esta teoria; Ela diz que o desenvolvimento da inteligência dos indivíduos acontece à
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/59 2 - FUNDAMENTOS 2.1) Teoria dos Conjuntos 2.2) Números
Processos Estocásticos
 Processos Estocásticos Segunda Lista de Exercícios 01 de julho de 2013 1 Uma indústria fabrica peças, das quais 1 5 são defeituosas. Dois compradores, A e B, classificam os lotes de peças adquiridos em
Processos Estocásticos Segunda Lista de Exercícios 01 de julho de 2013 1 Uma indústria fabrica peças, das quais 1 5 são defeituosas. Dois compradores, A e B, classificam os lotes de peças adquiridos em
Primeiros passos das Planilhas de Obra v2.6
 Primeiros passos das Planilhas de Obra v2.6 Instalação, configuração e primeiros passos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Preparar inicialização das
Primeiros passos das Planilhas de Obra v2.6 Instalação, configuração e primeiros passos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Preparar inicialização das
Aula 4 Conceitos Básicos de Estatística. Aula 4 Conceitos básicos de estatística
 Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Departamento de Informática. Análise de Decisão. Métodos Quantitativos LEI 2006/2007. Susana Nascimento snt@di.fct.unl.pt.
 Departamento de Informática Análise de Decisão Métodos Quantitativos LEI 26/27 Susana Nascimento snt@di.fct.unl.pt Advertência Autores João Moura Pires (jmp@di.fct.unl.pt) Susana Nascimento (snt@di.fct.unl.pt)
Departamento de Informática Análise de Decisão Métodos Quantitativos LEI 26/27 Susana Nascimento snt@di.fct.unl.pt Advertência Autores João Moura Pires (jmp@di.fct.unl.pt) Susana Nascimento (snt@di.fct.unl.pt)
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa
 1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
MLP (Multi Layer Perceptron)
 MLP (Multi Layer Perceptron) André Tavares da Silva andre.silva@udesc.br Roteiro Rede neural com mais de uma camada Codificação de entradas e saídas Decorar x generalizar Perceptron Multi-Camada (MLP -
MLP (Multi Layer Perceptron) André Tavares da Silva andre.silva@udesc.br Roteiro Rede neural com mais de uma camada Codificação de entradas e saídas Decorar x generalizar Perceptron Multi-Camada (MLP -
Resolução da lista de exercícios de casos de uso
 Resolução da lista de exercícios de casos de uso 1. Explique quando são criados e utilizados os diagramas de casos de uso no processo de desenvolvimento incremental e iterativo. Na fase de concepção se
Resolução da lista de exercícios de casos de uso 1. Explique quando são criados e utilizados os diagramas de casos de uso no processo de desenvolvimento incremental e iterativo. Na fase de concepção se
Lista de Exercícios 3 Estruturas de Controle Profa Susana M Iglesias
 Lista de Exercícios 3 Estruturas de Controle Profa Susana M Iglesias 1. Tendo em vista o alto preço da gasolina, os motoristas estão preocupados com a quilometragem percorrida por seus automóveis. Um motorista
Lista de Exercícios 3 Estruturas de Controle Profa Susana M Iglesias 1. Tendo em vista o alto preço da gasolina, os motoristas estão preocupados com a quilometragem percorrida por seus automóveis. Um motorista
Simulado Banco de Dados I Bimestre 1 Capítulo 1 Projeto Lógico de Banco de Dados
 Simulado Banco de Dados I Bimestre 1 Capítulo 1 Projeto Lógico de Banco de Dados 01) Defina com suas próprias palavras: a) Banco de Dados b) Sistema Gerenciador de Banco de Dados c) Sistema de Banco de
Simulado Banco de Dados I Bimestre 1 Capítulo 1 Projeto Lógico de Banco de Dados 01) Defina com suas próprias palavras: a) Banco de Dados b) Sistema Gerenciador de Banco de Dados c) Sistema de Banco de
5 Um simulador estocástico para o fluxo de caixa
 5 Um simulador estocástico para o fluxo de caixa O objetivo desse capítulo é o de apresentar um simulador estocástico para o fluxo de caixa de um plano de previdência do tipo PGBL de um único indivíduo.
5 Um simulador estocástico para o fluxo de caixa O objetivo desse capítulo é o de apresentar um simulador estocástico para o fluxo de caixa de um plano de previdência do tipo PGBL de um único indivíduo.
Planejamento de Aula - Ferramenta Mar aberto
 Planejamento de Aula - Ferramenta Mar aberto Planejar uma aula é uma arte não uma tarefa. O planejamento de aula através da ferramenta Mar Aberto ajuda e contribui para infinitas possibilidades para seu
Planejamento de Aula - Ferramenta Mar aberto Planejar uma aula é uma arte não uma tarefa. O planejamento de aula através da ferramenta Mar Aberto ajuda e contribui para infinitas possibilidades para seu
Top Guia In.Fra: Perguntas para fazer ao seu fornecedor de CFTV
 Top Guia In.Fra: Perguntas para fazer ao seu fornecedor de CFTV 1ª Edição (v1.4) 1 Um projeto de segurança bem feito Até pouco tempo atrás o mercado de CFTV era dividido entre fabricantes de alto custo
Top Guia In.Fra: Perguntas para fazer ao seu fornecedor de CFTV 1ª Edição (v1.4) 1 Um projeto de segurança bem feito Até pouco tempo atrás o mercado de CFTV era dividido entre fabricantes de alto custo
5 DICAS DE GESTÃO EM TEMPOS DE CRISE. Um guia prático com 5 dicas primordiais de como ser um bom gestor durante um período de crise.
 5 DICAS DE GESTÃO EM TEMPOS DE CRISE Um guia prático com 5 dicas primordiais de como ser um bom gestor durante um período de crise. INTRODUÇÃO Gerir uma empresa não é uma tarefa fácil, mas em tempos de
5 DICAS DE GESTÃO EM TEMPOS DE CRISE Um guia prático com 5 dicas primordiais de como ser um bom gestor durante um período de crise. INTRODUÇÃO Gerir uma empresa não é uma tarefa fácil, mas em tempos de
20 perguntas para descobrir como APRENDER MELHOR
 20 perguntas para descobrir como APRENDER MELHOR Resultados Processo de aprendizagem SENTIDOS (principal) Gosto de informações que eu posso verificar. Não há nada melhor para mim do que aprender junto
20 perguntas para descobrir como APRENDER MELHOR Resultados Processo de aprendizagem SENTIDOS (principal) Gosto de informações que eu posso verificar. Não há nada melhor para mim do que aprender junto
Para o PowerPoint, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides.
 POWERPOINT 1. O QUE É UMA APRESENTAÇÃO Para o PowerPoint, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides. Em cada slide podemos ter vários elementos ou objetos
POWERPOINT 1. O QUE É UMA APRESENTAÇÃO Para o PowerPoint, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides. Em cada slide podemos ter vários elementos ou objetos
Introdução. Introdução. Objetivos da Aula. Bases Computacionais da Ciência(BC-0005)
 1 Bases Computacionais da Ciência(BC-0005) Lógica de Programação: Estruturas Condicionais Maria das Graças Bruno Marietto graca.marietto@ufabc.edu.br Centro de Matemática, Computação e Cognição(CMCC) Universidade
1 Bases Computacionais da Ciência(BC-0005) Lógica de Programação: Estruturas Condicionais Maria das Graças Bruno Marietto graca.marietto@ufabc.edu.br Centro de Matemática, Computação e Cognição(CMCC) Universidade
Estoque. Como controlar o estoque
 Estoque Como controlar o estoque Por que é necessário controlar o estoque? Reduzir custos Se há excesso em estoque A empresa terá custos operacionais para manter o estoque, isto significa capital empatado
Estoque Como controlar o estoque Por que é necessário controlar o estoque? Reduzir custos Se há excesso em estoque A empresa terá custos operacionais para manter o estoque, isto significa capital empatado
Para o OpenOffice Impress, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides.
 OPENOFFICE IMPRESS 1. O QUE É UMA APRESENTAÇÃO Para o OpenOffice Impress, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides. Em cada slide podemos ter vários elementos
OPENOFFICE IMPRESS 1. O QUE É UMA APRESENTAÇÃO Para o OpenOffice Impress, assim como para vários softwares de apresentação, uma apresentação é um conjunto de slides. Em cada slide podemos ter vários elementos
Aula 1 Uma visão geral das comorbidades e a necessidade da equipe multidisciplinar
 Aula 1 Uma visão geral das comorbidades e a necessidade da equipe multidisciplinar Nesta aula, apresentaremos o panorama geral das comorbidades envolvidas na dependência química que serão estudadas ao
Aula 1 Uma visão geral das comorbidades e a necessidade da equipe multidisciplinar Nesta aula, apresentaremos o panorama geral das comorbidades envolvidas na dependência química que serão estudadas ao
UM CAMINHO SIMPLES PARA UMA NUVEM PRIVADA
 UM CAMINHO SIMPLES PARA UMA NUVEM PRIVADA Julho de 2015 Com nuvens privadas de fácil uso concebidas para executar aplicativos corporativos essenciais para os negócios, as principais organizações se beneficiam
UM CAMINHO SIMPLES PARA UMA NUVEM PRIVADA Julho de 2015 Com nuvens privadas de fácil uso concebidas para executar aplicativos corporativos essenciais para os negócios, as principais organizações se beneficiam
PLANO DE GERÊNCIAMENTO DE RISCOS
 1 PLANO DE GERÊNCIAMENTO DE RISCOS Versão 1.1 Rua Pedro Ribeiro, 85 - Matriz, Vitória de Santo Antão - PE, 55612-275 Pernambuco Brasil (81) 3523-0012 www.qualistec.com.br suporte@qualistec.com.br 2 Histórico
1 PLANO DE GERÊNCIAMENTO DE RISCOS Versão 1.1 Rua Pedro Ribeiro, 85 - Matriz, Vitória de Santo Antão - PE, 55612-275 Pernambuco Brasil (81) 3523-0012 www.qualistec.com.br suporte@qualistec.com.br 2 Histórico
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
PESQUISA EM INFORMÁTICA -ESTILOS DE PESQUISA EM COMPUTAÇÃO. Prof. Angelo Augusto Frozza, M.Sc.
 PESQUISA EM INFORMÁTICA -ESTILOS DE PESQUISA EM COMPUTAÇÃO Prof. Angelo Augusto Frozza, M.Sc. O TRABALHO DE CONCLUSÃO Introdução O texto que segue resume os Capítulo 2 e 8, do livro Metodologia de Pesquisa
PESQUISA EM INFORMÁTICA -ESTILOS DE PESQUISA EM COMPUTAÇÃO Prof. Angelo Augusto Frozza, M.Sc. O TRABALHO DE CONCLUSÃO Introdução O texto que segue resume os Capítulo 2 e 8, do livro Metodologia de Pesquisa
Eventos independentes
 Eventos independentes Adaptado do artigo de Flávio Wagner Rodrigues Neste artigo são discutidos alguns aspectos ligados à noção de independência de dois eventos na Teoria das Probabilidades. Os objetivos
Eventos independentes Adaptado do artigo de Flávio Wagner Rodrigues Neste artigo são discutidos alguns aspectos ligados à noção de independência de dois eventos na Teoria das Probabilidades. Os objetivos
Instrumento A. Sistema de valores do instrumento EQ5D de mensuração de qualidade de vida. Número do envelope utilizado SISTEMA DESCRITIVO - EQ-5D
 Instrumento A Questionário nº Sistema de valores do instrumento EQ5D de mensuração de qualidade de vida Instituto Nacional de Cardiologia Universidade Federal do Rio Grande do Sul Universidade Federal
Instrumento A Questionário nº Sistema de valores do instrumento EQ5D de mensuração de qualidade de vida Instituto Nacional de Cardiologia Universidade Federal do Rio Grande do Sul Universidade Federal
Guia Prático ORGANIZAÇÃO FINANCEIRA PARA BANCAR A FACULDADE
 Guia Prático ORGANIZAÇÃO FINANCEIRA PARA BANCAR A FACULDADE ÍNDICE 1 Introdução 2 Qual a importância da educação financeira para estudantes? 3 Comece definindo onde é possível economizar 4 Poupar é muito
Guia Prático ORGANIZAÇÃO FINANCEIRA PARA BANCAR A FACULDADE ÍNDICE 1 Introdução 2 Qual a importância da educação financeira para estudantes? 3 Comece definindo onde é possível economizar 4 Poupar é muito
Módulo 9 A Avaliação de Desempenho faz parte do subsistema de aplicação de recursos humanos.
 Módulo 9 A Avaliação de Desempenho faz parte do subsistema de aplicação de recursos humanos. 9.1 Explicações iniciais A avaliação é algo que faz parte de nossas vidas, mesmo antes de nascermos, se não
Módulo 9 A Avaliação de Desempenho faz parte do subsistema de aplicação de recursos humanos. 9.1 Explicações iniciais A avaliação é algo que faz parte de nossas vidas, mesmo antes de nascermos, se não
Treinamento do Sistema RH1000
 Treinamento do Sistema RH1000 = Bloco Treinamento = Ohl Braga Desenvolvimento Empresarial Atualizado em 25Mai2014 1 Bloco Treinamento Tópico Slide Dinâmica dos treinamentos 4 Áreas de treinamento 5 Treinamentos
Treinamento do Sistema RH1000 = Bloco Treinamento = Ohl Braga Desenvolvimento Empresarial Atualizado em 25Mai2014 1 Bloco Treinamento Tópico Slide Dinâmica dos treinamentos 4 Áreas de treinamento 5 Treinamentos
Perfil Chefe de Transporte
 Manual do Usuário Perfil Chefe de Transporte APRESENTAÇÃO Bem vindos ao manual do usuário do Sistema de Gestão de Frotas. Este Manual proporcionará aos seus usuários, descobrir todas as funcionalidades
Manual do Usuário Perfil Chefe de Transporte APRESENTAÇÃO Bem vindos ao manual do usuário do Sistema de Gestão de Frotas. Este Manual proporcionará aos seus usuários, descobrir todas as funcionalidades
Gerenciamento de Projetos Modulo II Clico de Vida e Organização
 Gerenciamento de Projetos Modulo II Clico de Vida e Organização Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com Bibliografia* Project Management Institute. Conjunto de Conhecimentos
Gerenciamento de Projetos Modulo II Clico de Vida e Organização Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com Bibliografia* Project Management Institute. Conjunto de Conhecimentos
10+10 MINIGUIA... ATITUDES E PALAVRAS ASSERTIVAS. dar FEEDBACK, dizer NÃO, Veronica Z. Herrera Consultora Treinadora Coach Certificada.
 10+10 MINIGUIA... ATITUDES E PALAVRAS Para administrar CONFRONTAÇÃO; dar FEEDBACK, dizer NÃO, expressar DESACORDO ou SATISFAÇÃO Veronica Z. Herrera Consultora Treinadora Coach Certificada CONSTRUINDO MELHORES
10+10 MINIGUIA... ATITUDES E PALAVRAS Para administrar CONFRONTAÇÃO; dar FEEDBACK, dizer NÃO, expressar DESACORDO ou SATISFAÇÃO Veronica Z. Herrera Consultora Treinadora Coach Certificada CONSTRUINDO MELHORES
2aula TEORIA DE ERROS I: ALGARISMOS SIGNIFICATIVOS, ARREDONDAMENTOS E INCERTEZAS. 2.1 Algarismos Corretos e Avaliados
 2aula Janeiro de 2012 TEORIA DE ERROS I: ALGARISMOS SIGNIFICATIVOS, ARREDONDAMENTOS E INCERTEZAS Objetivos: Familiarizar o aluno com os algarismos significativos, com as regras de arredondamento e as incertezas
2aula Janeiro de 2012 TEORIA DE ERROS I: ALGARISMOS SIGNIFICATIVOS, ARREDONDAMENTOS E INCERTEZAS Objetivos: Familiarizar o aluno com os algarismos significativos, com as regras de arredondamento e as incertezas
5 Considerações finais
 5 Considerações finais 5.1. Conclusões A presente dissertação teve o objetivo principal de investigar a visão dos alunos que se formam em Administração sobre RSC e o seu ensino. Para alcançar esse objetivo,
5 Considerações finais 5.1. Conclusões A presente dissertação teve o objetivo principal de investigar a visão dos alunos que se formam em Administração sobre RSC e o seu ensino. Para alcançar esse objetivo,
Programa Olímpico de Treinamento. Aula 9. Curso de Combinatória - Nível 2. Tabuleiros. Prof. Bruno Holanda
 Programa Olímpico de Treinamento Curso de Combinatória - Nível Prof. Bruno Holanda Aula 9 Tabuleiros Quem nunca brincou de quebra-cabeça? Temos várias pecinhas e temos que encontrar uma maneira de unir
Programa Olímpico de Treinamento Curso de Combinatória - Nível Prof. Bruno Holanda Aula 9 Tabuleiros Quem nunca brincou de quebra-cabeça? Temos várias pecinhas e temos que encontrar uma maneira de unir
CAPÍTULO 1 Introduzindo SIG
 CAPÍTULO 1 Introduzindo SIG Por muito tempo, estudou-se o mundo usando modelos como mapas e globos. Aproximadamente nos últimos trinta anos, tornou-se possível colocar estes modelos dentro de computadores
CAPÍTULO 1 Introduzindo SIG Por muito tempo, estudou-se o mundo usando modelos como mapas e globos. Aproximadamente nos últimos trinta anos, tornou-se possível colocar estes modelos dentro de computadores
7 - Análise de redes Pesquisa Operacional CAPÍTULO 7 ANÁLISE DE REDES. 4 c. Figura 7.1 - Exemplo de um grafo linear.
 CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
Programadores e Problemas: Instruções. Introdução. Seu Objetivo. Configuração. Instruções do jogo equipe evolução 5/5/2006 v2.0
 Programadores e Problemas: Instruções Introdução Problemas e Programadores é um jogo educacional na área de engenharia de software. Ele é dirigido a estudantes que já têm conhecimento entre o básico e
Programadores e Problemas: Instruções Introdução Problemas e Programadores é um jogo educacional na área de engenharia de software. Ele é dirigido a estudantes que já têm conhecimento entre o básico e
Matemática em Toda Parte II
 Matemática em Toda Parte II Episódio: Matemática no Transporte Resumo O episódio Matemática no Transporte, da série Matemática em Toda Parte II, vai mostrar como alguns conceitos matemáticos estão presentes
Matemática em Toda Parte II Episódio: Matemática no Transporte Resumo O episódio Matemática no Transporte, da série Matemática em Toda Parte II, vai mostrar como alguns conceitos matemáticos estão presentes
