UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE CIÊNCIAS DEPARTAMENTO DE FÍSICA MÁRCIO DE MELO FREIRE
|
|
|
- Heloísa Paiva Stachinski
- 5 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE CIÊNCIAS DEPARTAMENTO DE FÍSICA PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA MÁRCIO DE MELO FREIRE TEORIA DE FUNÇÕES DE GREEN PARA UMA IMPUREZA ISOLADA LOCALIZADA INTERSTICIALMENTE EM SISTEMAS FERROMAGNÉTICOS FORTALEZA 2017
2 MÁRCIO DE MELO FREIRE TEORIA DE FUNÇÕES DE GREEN PARA UMA IMPUREZA ISOLADA LOCALIZADA INTERSTICIALMENTE EM SISTEMAS FERROMAGNÉTICOS Tese de Doutorado apresentada ao Programa de Pós-Graduação em Física da Universidade Federal do Ceará, como requisito parcial para a obtenção do Título de Doutor em Física. Área de Concentração: Física da Matéria Condensada. Orientador: Prof. Dr. Raimundo Nogueira da Costa Filho Coorientador: Prof. Dr. Raimundo Valmir Leite Filho FORTALEZA 2017
3 Dados Internacionais de Catalogação na Publicação Universidade Federal do Ceará Biblioteca Universitária Gerada automaticamente pelo módulo Catalog, mediante os dados fornecidos pelo(a) autor(a) F934t Freire, Márcio de Melo. Teoria de funções de Green para uma impureza isolada localizada intersticialmente em sistemas ferromagnéticos / Márcio de Melo Freire f. : il. color. Tese (doutorado) Universidade Federal do Ceará, Centro de Ciências, Programa de Pós-Graduação em Física, Fortaleza, Orientação: Prof. Dr. Raimundo Nogueira da Costa Filho. 1. Função de Green. 2. Modelo de Heisenberg-Ising. 3. Ferromagnetos. 4. Ondas de spin. 5. Modos de impureza. I. Título. CDD 530
4 MÁRCIO DE MELO FREIRE TEORIA DE FUNÇÕES DE GREEN PARA UMA IMPUREZA ISOLADA LOCALIZADA INTERSTICIALMENTE EM SISTEMAS FERROMAGNÉTICOS Tese de Doutorado apresentada ao Programa de Pós-Graduação em Física da Universidade Federal do Ceará, como requisito parcial para a obtenção do Título de Doutor em Física. Área de Concentração: Física da Matéria Condensada. Aprovada em 15/02/2017 BANCA EXAMINADORA Prof. Dr. Raimundo Nogueira da Costa Filho Universidade Federal do Ceará (UFC) Prof. Dr. Raimundo Valmir Leite Filho Universidade Estadual Vale do Acaraú (UVA) Prof. Dr. João Milton Pereira Junior Universidade Federal do Ceará (UFC) Prof. Dr. Gil de Aquino Farias Universidade Federal do Ceará (UFC) Prof. Dr. Luiz Ozorio de Oliveira Filho Universidade Estadual Vale do Acaraú (UVA)
5 Aos meus pais, meus filhos e minha esposa
6 AGRADECIMENTOS Ao professor Raimundo Nogueira da Costa Filho, pela orientação. Ao professor Raimundo Valmir Leite Filho, pela coorientação. Aos professores do departamento de física, pelos conhecimentos repassados. Aos professores do curso de física da UVA, em especial ao professor Luiz Ozorio de Oliveira Filho, pelos conhecimentos repassados. Aos amigos Rivânia Maria, Leandro de Oliveira, Francisco Emanuel, Antôio Ribeiro, Naiara Cipriano, Mauricélio Bezerra, Tiago Muniz e Emanuel Wendell, pelo companheirismo. Ao CNPq, pelo apoio financeiro.
7 Resumo Um formalismo da função de Green é usado para calcular o espectro de excitações associadas com uma impureza magnética localizada intersticialmente em diferentes estruturas ferromagnéticas descritas pelo modelo de Ising e de Heisenberg. No capítulo 3, descrevemos um ferromagneto de rede cúbica simples semi-infinita através do modelo de Ising. Neste caso, as excitações não-ressonantes (isto é, os modos de defeito fora da região das ondas de spin de volume e de superfície) e as excitações ressonantes (os modos de defeito dentro da região das ondas de spin de volume) são calculadas numericamente para a fase de alta-temperatura. Duas situações são analisadas, dependendo da posição da impureza em relação a seus vizinhos: a impureza está na superfície (N = 1); a impureza está na região de volume (N 2). Nos demais capítulos, usamos o modelo de Heisenberg/Ising (onde passamos do modelo de Heisenberg para o de Ising através do controle de um parâmetro λ) para descrever os seguintes sistemas: ferromagneto de rede quadrada infinita (capítulo 4), ferromagneto de rede quadrada centrada infinita (capítulo 5), ferromagneto de rede cúbica de corpo centrado infinita (capítulo 6) e rede favo de mel infinita (capítulo 7), todos contendo uma impureza magnética localizada intersticialmente. Nos três primeiros casos, são calculados apenas os modos de defeito acima da banda de volume do material puro (modos ópticos). No capítulo 7, são analisados apenas os modos de defeito abaixo da banda de volume do material puro (modos acústicos). Abstract A Green s function formalism is used to calculate the expectrum of excitations associated with an interstitial magnetic impurity in different ferromagnetic structures described by the Ising and Heisenberg models. In the chapter 3 the non-resonant excitations of the system due to impurity (i.e, the defect modes outside the region of the bulk and surface spin waves) and the resonant excitations (the defect modes inside the region of the bulk and surface spin waves) are calculated numerically for the high-temperature phase. Two situations are analysed, depending on the position of the impurity: the impurity is on the surface (N = 1) and the impurity is in the bulk region (N 2). In the others chapters we use the model Ising/Heisenberg (where we can go from Heisenberg model to Ising model, by controlling the value of a parameter λ) to describe the following systems: ferromagnet with an infinite square lattice (Chap. 4), ferromagnet with an infinite face-centered square lattice (Chap. 5), ferromagnet with an infinite body-centered cubic lattice (Chap. 6) and ferromagnet with an infinite honey-comb lattice (Chap. 7), all the systems with a magnetic interstitial impurity. For the first tree cases, only the optical
8 defect modes are calculated, and for the last one, only the acoustic modes are calculated.
9 LISTA DE FIGURAS Figura 1 Gráfico da função degrau ou função de Heaveside Figura 2 Contorno de integração da Eq.2.36 para valores negativos da variável tempo Figura 3 Contorno de integração da Eq.2.36 para valores positivos da variável tempo. 37 Figura 4 Ferromagneto de rede cúbica simples semi-infinita Figura 5 Ferromagneto de rede cúbica simples semi-infinita contendo uma impureza intersticial na camada n = 1, por exemplo Figura 6 A impureza pode ocupar qualquer posição dentro da região A Figura 7 Frequências dos modos de defeito versus campo aplicado (h /h), no caso de N = 10, para diferentes valores de (p; k): (0,3;0,0) para a linha contínua, (0,3;0,3) para a linha pontilhada, (0,49;0) para a linha tracejada e (0,49;0,49) para a linha traço-pontilhada. Assumimos que J S /J = 1, Figura 8 Frequências dos modos de defeitos versus interação de troca (J /J), no caso de N = 10, para diferentes valores de (p; k): (0,3;0) para a linha contínua, (0,3;0,3) para a linha pontilhada, (0,49;0) para a linha tracejada e (0,49;0,49) para a linha traço-pontilhada. Assumimos que J S /J = 1, 0, h /h = 1, Figura 9 Frequências dos modos de defeito versus interação de troca no caso de N = 10 para diferentes valores de h /h: h /h = 1, 5 para a linha tracejada, h /h = 1, 8 para a linha pontilhada e h /h = 2, 0 para a linha contínua. Assumimos um valor fixo para p e k: (p, k) = (0, 3; 0, 3) Figura 10 Frequências dos modos de defeito versus campo aplicado no caso de N = 10 para diferentes valores de J /J: J /J = 1, 5 para a linha contínua, J /J = 1, 8 para a linha pontilhada e J /J = 2, 0 para a linha tracejada. Assumimos um valor fixo para p e k: (p, k) = (0, 49; 0, 49) Figura 11 Frequências dos modos de defeito versus interação de troca no caso de N = 1 para diferentes valores de h /h: h /h = 1, 5 para a linha tracejada, h /h = 1, 8 para a linha pontilhada e h /h = 2, 0 para a linha contínua. Assumimos um valor fixo para p e k: (p, k) = (0, 3; 0, 3)
10 Figura 12 Frequências dos modos de defeito versus interação de troca para h /h = 1, 0 no caso de N = 1 e para diferentes valores de J S /J: J S /J = 1, 0 para a linha contínua, J S /J = 1, 3 para a linha pontilhada e J S /J = 1, 35 para a linha tracejada Figura 13 Modos associados com uma impureza intersticial na camada da superfície (N = 1). Gráfico da frequência ω (energia) versus interação de troca J, mostrando ambos os modos de defeito e os modos ressonantes. O limite inferior da banda de volume está indicada por uma linha horizontal em ω/j 0, 63, e o limite superior está também indicada por uma linha horizontal, mas em ω/j 1, Figura 14 Modos de impureza mostrados próximos do limite inferior da banda de volume da onda de spin na presença de um modo de superfície (considerando J S /J = 0, 74), assumindo que a impureza está na camada da superfície (N = 1) Figura 15 Modos de impureza mostrados próximos do limite inferior da banda de volume da onda de spin na presença de um modo de superfície acústico (tomando J S /J = 1, 251), assumindo que a impureza está na camada da superfície (N = 1) Figura 16 Ferromagneto de rede quadrada infinita Figura 17 Ferromagneto de rede quadrada infinita contendo uma impureza intersticial. 71 Figura 18 Um sítio qualquer l, num ferromagneto de rede quadrada infinita, e seus quatro primeiro vizinhos Figura 19 Impureza intersticial e seus quatro primeiro vizinhos num ferromagneto de rede quadrada infinita Figura 20 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ Figura 21 Frequências de ondas de spin em função de λ para diferentes valores de q x a/π Figura 22 Gráfico do contorno para os efeitos das componentes q x e q y do vetor de onda q sobre a frequência (energia) ω/j Figura 23 Frequências de ondas de spin como função de J /J, para h /h = 2, 0, S /S = 1, 0 e alguns valores de λ. Modos localizados s, p e d relativos a uma impureza em um ferromagneto de rede quadrada infinita Figura 24 Frequências de ondas de spin como função de h /h, para J /J = 0, 2, S /S = 1, 0 e λ = 1, 0 (modelo de Heisenberg). Modos localizados s relativos a uma impureza em um ferromagneto de rede quadrada infinita. 81
11 Figura 25 Frequências de ondas de spin como funcao de J /J, para h /h = 2, 0 e diferentes valores de S. Modos localizados s, p e d relativos a uma impureza em um ferromagneto de rede quadrada infinita. Tomamos o valor λ = 1, 0 (modelo de Heisenberg) Figura 26 Frequências de ondas de spin como função de λ, para h /h = 2.0, S /S = 1, 0 e J /J = 0, 04. Modos localizados s, p e d relativos a uma impureza em um ferromagneto de rede quadrada infinita Figura 27 Ferromagneto de rede quadrada centrada infinita Figura 28 Ferromagneto de rede quadrada centrada infinita contendo uma impureza intersticial (círculo na cor preta) Figura 29 Um sítio qualquer l, num ferromagneto de rede quadrada centrada infinita, e seus quatro primeiro vizinhos Figura 30 Impureza intersticial e seus cinco primeiro vizinhos, num ferromagneto de rede quadrada centrada infinita Figura 31 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ. Tomamos o valor fixo q y = Figura 32 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ. Tomamos o valor q y = 2π Figura 33 Frequências de ondas de spin como funçãoo de J /J, para h /h = 2, 0, S /S = 2, 5 e alguns valores de λ. Modos localizados p e d relativos a uma impureza em um ferromagneto de rede quadrada centrada infinita.. 92 Figura 34 Frequências de ondas de spin como função de J /J, para h /h = 2, 0, S /S = 2, 5 e alguns valores de λ. Modos localizados s relativos a uma impureza em um ferromagneto de rede quadrada centrada infinita Figura 35 Frequências de ondas de spin como função de J /J, para h /h = 2, 0 e diferentes valores de S. Modos localizados p e d relativos a uma impureza em um ferromagneto de rede quadrada centrada infinita. Tomamos o valor fixo λ = 1, 0 (modelo de Heisenberg) Figura 36 Frequências de ondas de spin como função de J /J, para h /h = 2, 0 e diferentes valores de S. Modos localizados s relativos a uma impureza em um ferromagneto de rede quadrada centrada infinita. Tomamos o valor λ = 1, 0 (modelo de Heisenberg) Figura 37 Frequências de ondas de spin como função de λ, para h /h = 2, 0, S /S = 2, 5 e o valor de J /J = 0, 05. Modos localizados s, p e d relativos a uma impureza em um ferromagneto de rede quadrada centrada infinita Figura 38 Ferromagneto de rede cúbica de corpo centrado infinita
12 Figura 39 Ferromagneto de rede cúbica de corpo centrado infinita contendo uma impureza intersticial (círculo na cor preta) Figura 40 Um sítio qualquer l, num ferromagneto de rede cúbica de corpo centrado infinita, e seus oito primeiro vizinhos Figura 41 Impureza intersticial (círculo na cor preta) e seus nove primeiros vizinhos, num ferromagneto de rede cúbica de corpo centrado infinita Figura 42 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ e os valores fixos de q y = 0 e q z = 2π Figura 43 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ, e os valores fixos q y = q z = 2π Figura 44 As energias dos modos de defeito ópticos associados com uma impureza de S /S = 3, 5 em uma amostra ferromagnética com S = 2 em um campo magnético externo de valor h /h = 3, 55, versus interação de troca. Demais parâmetros encontram-se no texto Figura 45 As energias dos modos de impureza ópticos associados com alguns tipos de impurezas em uma amostra ferromagnética com S = 2 em um campo magnético externo de valor h /h = 3, 55, versus interação de troca. S /S = 2 (linha contínua), S /S = 2, 5 (linha pontilhada) e S /S = 3, 5 (linha tracejada) Figura 46 As energias dos modos de impureza ópticos associados com uma impureza de S /S = 3, 5 em uma amostra ferromagnética de S = 2 para um valor J /J = 0, 038, versus campo aplicado na impureza Figura 47 As energias dos modos de impureza ópticos associados com uma impureza de S /S = 2 em uma amostra ferromagnética de S = 1, 5, em um campo magnético externo de valor h /h = 3, 55, plotados contra J /J Figura 48 As energias dos modos de impureza ópticos associados com alguns tipos de impurezas em uma amostra ferromagnética coms = 1, 5 em um campo magnético externo de valor h /h = 3, 55, versus interação de troca. S /S = 2 (linha contínua), S /S = 2, 5 (linha pontilhada) e S /S = 3, 5 (linha tracejada) Figura 49 As energias dos modos de impureza ópticos associados com uma impureza de S /S = 2 em uma amostra ferromagnética com S = 1, 5, para um valor J /J = 0, 063, versus campo aplicado na impureza. Demais parâmetros são dados no texto
13 Figura 50 Ferromagneto de rede favo de mel infinita pura. Um sítio qualquer l, situado na sub-rede A (círculos em branco), e seus três primeiros vizinhos (1, 2 e 3), situados na sub-rede B (círculos em cinza) Figura 51 Ferromagneto de rede favo de mel infinita impura. Uma impureza intersticial o (círculo em preto), no centro de um dos hexágonos, e seus seis primeiros vizinhos (três na sub-rede A e três na sub-rede B) Figura 52 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ e o valor fixo de q y = 0, para um ferromagneto com S = Figura 53 Frequências de ondas de spin em função de q x a/π para diferentes valores de λ e o valor fixo de q y = 0, para um ferromagneto com S = Figura 54 Gráfico do contorno para os efeitos das componentes q x e q y do vetor de onda q sobre a frequência (energia) ω/j, para um ferromagneto com S = Figura 55 As energias dos modos de impureza acústicos associados a uma impureza intersticial de S /S = 1, 5 em um ferromagneto de rede favo de mel infinita (com número quântico de spin S = 1) em um campo magnético externo de valor h /h = 0, 55, plotados contra J /J Figura 56 As energias dos modos de impureza acústicos associados a diferentes impurezas intersticiais: S /S = 1, 5 (linha tracejada), S /S = 2 (linha contínua), em um ferromagneto de rede favo de mel infinita (com número quântico de spin S = 1) em um campo magnético externo na impureza de valor h /h = 0, 55, plotados contra J /J Figura 57 As energias dos modos de impureza acústicos associados a uma impureza intersticial de S /S = 1, 5 em um ferromagneto de rede favo de mel infinita (outro material com número quântico de spin S = 2) em um campo magnético externo, na impureza, de valor h /h = 0, 55, plotados contra J /J Figura 58 As energias dos modos de impureza acústicos associados a diferentes impurezas intersticiais: S /S = 1, 5 (linha tracejada), S = 2 (linha contínua), em um ferromagneto de rede favo de mel infinita (outro material com número quântico de spin S = 2) em um campo magnético externo, na impureza, de valor h = 0, 55, plotados contra J /J Figura 59 A semi-infinite ferromagnet with a (001) surface and a simple-cubic structure Figura 60 A semi-infinite ferromagnet with a (001) surface and a simple-cubic structure, with an isolated single interstitial magnetic impurity located in the surface layer, for instance
14 Figura 61 The impurity can occupies any position in the region A Figura 62 Calculated values of ω/j for the defect modes in the case of N = 10 plotted against h /h for different values of (p, k) (solid curve, (0.3;0); dotted curve, (0.3;0.3); dashed curve, (0.49;0); dot-dashed curve (0.49;0.49). It has been assumed that J S /J = 1.0, J /J = 1.5 and others parameters are given in the text Figura 63 Calculated values of ω/j for the defect modes in the case of N = 10 plotted against J /J for different values of (p, k) (solid curve, (0.3;0); dotted curve, (0.3;0.3); dashed curve, (0.49;0); dot-dashed curve (0.49;0.49). It has been assumed that J S /J = 1.0, h /h = 1.5 and others parameters are given in the textj /J Figura 64 Calculated values of ω/j for the defect modes in the case of N = 10 plotted against J /J for different values of h /h (dashed curve, h /h = 1.5; dotted curve, h /h = 1.8; solid curve, h /h = 2.0. It has been assumed a fixed value for p and k: (p, k) = (0.3; 0.3) Figura 65 Calculated values of ω/j for the defect modes in the case of N = 10 plotted against h /h for different values of J /J (solid curve, J /J = 1.5; dotted curve, J /J = 1.80; dashed curve, J /J = 2.0. It has been assumed a fixed value for p and k: (p, k) = (0.49; 0.49) Figura 66 As in 64, but for the case of N = Figura 67 Calculated values of ω/j for the defect modes in the case of N = 1 plotted against J /J for h /h = 2.0 and for different values of J S /J (solid curve, J S /J = 1.0; dotted curve, J S /J = 1.3; dashed curve, J S /J = 1.34). 11 Figura 68 Modes associated with an impurity spin in the surface layer (N = 1) plotted for the energy ω and showing both the defect and resonance modes. The lower edge of the bulk band is indicated by the horizontal line at ω/j 0.63, and the upper one, is at ω/j Figura 69 Impurity modes shown near the lower edge of the bulk spin-wave band and below in the presence of an optical surface mode (taking J S /J = 0.74), assuming the impurity to be in the surface layer (N = 1). Others parameters are given in the text Figura 70 Impurity modes shown near the lower edge of the bulk spin-wave band and below in the presence of an acoustic surface mode (taking J S /J = 1.251), assuming the impurity to be in the surface layer (N = 1). Others parameters are given in the text
15 SUMÁRIO Resumo Abstract INTRODUÇÃO O Modelo de Heisenberg O Modelo de Ising FUNÇÕES DE GREEN EM MECÂNICA ESTATÍSTICA Funções de Green Retardada, Avançada e Causal Equações de Evolução para as Funções de Green Funções de Correlação Temporal Representação Espectral Para as Funções de Correlação Temporal Representações Espectrais para G r e G a Representação Espectral para G C IMPUREZA INTERSTICIAL LOCALIZADA NUM FERRO- MAGNETO DE REDE CÚBICA SIMPLES SEMI-INFINITA Introdução Modelo e Formalismo da Função de Green Os modos de Impureza Resultados Numéricos Modos Ressonantes IMPUREZA INTERSTICIAL NUM FERROMAGNETO DE REDE QUADRADA INFINITA Introdução Modelo e Formalismo da função de Green Modos de impureza e resultados numéricos IMPUREZA INTERSTICIAL LOCALIZADA NUM FERRO- MAGNETO DE REDE QUADRADA CENTRADA INFINITA Introdução Modelo e formalismo da função de Green Modos de impureza e resultados numéricos
16 6 IMPUREZA INTERSTICIAL LOCALIZADA NUM FERRO- MAGNETO DE REDE CÚBICA DE CORPO CENTRADO INFINITA Introdução Modelo e formalismo da função de Green Modos de impureza e resultados numéricos IMPUREZA INTERSTICIAL LOCALIZADA NUM FERRO- MAGNETO DE REDE FAVO DE MEL INFINITA Introdução Modelo e formalismo da função de Green Modos de impureza e resultados numéricos CONCLUSÕES REFERÊNCIAS APÊNDICE A -- EQUAÇÃO DE DYSON APÊNDICE B -- OBTENÇÃO DA EQUAÇÃO APÊNDICE C -- OBTENÇÃO DA EQUAÇÃO APÊNDICE D -- OBTENÇÃO DA EQUAÇÃO APÊNDICE E -- OBTENÇÃO DA EQUAÇÃO APÊNDICE F -- GREEN S FUNCTIONS THEORY FOR AN INTERSTITIAL MAGNETIC IMPURITY IN A TRANSVERSE ISING FERROMAGNET ABSTRACT REFERÊNCIAS
17 16 1 INTRODUÇÃO O magnetismo tem sido observado desde a antiguidade,sendo foco de muitas descobertas responsáveis por uma série de conquistas em diversos ramos como na medicina, informática, telecomunicações, etc. Esse grande leque de aplicações se deve aos materiais magnéticos que apresentam propriedades importantes e com finalidades bem definidas. A física do estado sólido é uma vasta área da física que trata da compreensão das propriedades mecânicas, térmicas, ópticas e magnéticas da matéria sólida. Uma descrição teórica dessas propriedades deve levar em consideração o grande número de íons constituintes, da ordem de partículas por centímetro cúbico, o que exige a aplicação de técnicas apropriadas para descrever sistemas de muitos corpos. Porém, desenvolver um modelo teórico capaz de explicar todos os fenômenos que podem ocorrer em um sólido não constitui tarefa simples. Podemos apenas desenvolver modelos simplificados para cada área de interesse. Portanto, qualquer teoria básica do estado sólido deve desenvolver conceitos unificados onde se possa considerar todas as possíveis características individuais de um dado sólido. Uma característica predominante nos sólidos é o arranjo regular de seus íons, onde predomina a interação de um íon com seus vizinhos. Particularmente, um sólido cristalino possui seus átomos arranjados numa configuração periódica denominada rede cristalina. As interações na rede cristalina podem ter um caráter de curto alcance e restrito a um volume limitado em torno do íon. Interações de curto alcance podem enfraquecer com o aumento da distância, como no caso da interação de troca em materiais magnéticos. No entanto, na maioria dos sólidos também podem ocorrer interações de longo alcance, como as de dipolo-dipolo. Na construção de modelos simplificados para sistemas de muitas partículas, deve-se considerar o conceito de excitações elementares, decorrentes das excitações de partículas individuais, as quasi-partículas, ou das correlações do movimento de partículas interagentes, denominados modos coletivos [1, 2, 3, 4]. Como exemplos temos: as vibrações coletivas dos íons na rede cristalina, cujos quanta associados são chamados de fônons; as oscilações coletivas dos elétrons de valência em metais, os plasmons. A interação entre as oscilações coletivas, conhecida como acoplamento, também pode gerar novas excitações elementares, como por exemplo: o acoplamento entre fótons e fônons, denominado polariton de fônon. O estado fundamental de um cristal magneticamente ordenado, tal como um
18 17 ferromagneto ou um antiferromagneto, pode ser excitado de tal maneira que a densidade local de spin eletrônico efetua um movimento de precessão em torno da direção de equilíbrio da magnetização. Os modos normais dessa oscilação são chamados de ondas de spin, cujos quanta associados são chamados mágnons. As ondas de spin foram descobertas por Bloch em 1930 [5]. O estudo da propagação de ondas de spin em sistemas ferromagnéticos a baixas temperaturas é importante sob vários aspectos: por exemplo, elas são responsáveis pelo termo T 3/2 na curva da magnetização em função da temperatura M(T ) [6, 7], elas contribuem na determinação do calor específico, da temperatura de Curie e de outras propriedades termodinâmicas dos sólidos. Como vimos, sólidos são conhecidos como meios que permitem uma variedade de excitações elementares. Para modelar o comportamento dessas excitações, considera-se o meio no qual elas se propagam como um cristal perfeito que se estende infinitamente. Esta consideração em alguns casos, entretanto, não permite uma boa descrição do sistema. Um exemplo é dado quando se trata de um meio de baixa dimensão, tal como um filme fino, no qual a presença de superfícies tem influência no espectro de excitações. A introdução de camadas de impurezas, impurezas localizadas, ou mesmo uma baixa concentração delas, também modifica o espectro de excitações desse meio. Este diferente comportamento ocorre porque a presença de superfícies ou a introdução de impurezas pode modificar as interações microscópicas no material. Também a baixa dimensionalidade do meio, juntamente com a presença de impurezas, provoca uma quebra de simetria translacional no sistema, causando significativas modificações na propagação das excitações e permitindo o surgimento de excitações localizadas. Por impurezas ou defeitos em sólidos cristalinos entende-se uma região onde o arranjo microscópico de íons difere drasticamente do cristal puro [8, 9]. Os defeitos em sólidos podem ser encontrados na forma de superfícies, linhas ou pontos. Os tipos de defeitos mais importantes encontrados em sólidos são: Deslocamentos: linhas de defeitos que, embora provavelmente ausentes num cristal ideal em equilíbrio térmico, são invariavelmente encontradas em um cristal real. Vacâncias: são vazios pontuais causados pela ausência de átomos em algumas posições na rede cristalina. Átomos substitucionais: são defeitos provocados pela presença de átomos estranhos nos próprios vértices da rede cristalina. Átomos intersticiais: são defeitos provocados pela presença de átomos estranhos nos interstícios da rede cristalina. Em cristais iônicos, tais defeitos são inteiramente responsáveis pela condutividade elétrica e podem alterar profundamente suas propriedades ópticas e, em particular, sua cor.
19 18 Os recentes avanços alcançados em técnicas litográficas, os quais permitem a construção de diferentes disposições de átomos nos mais diversos padrões em escala nanométrica, possibilitaram a fabricação de novos sistemas magnéticos que podem ter arranjos de buracos, defeitos ou impurezas. Guedes e colaboradores estudaram a formação de domínios durante a reversão da magnetização devido a um conjunto de furos quadrados em um filme de Fe [10]]. Eles estudaram também as modificações nas propriedades magnéticas devido a um conjunto de furos elípticos em um filme de Fe [11]. Em ambos os casos as medidas foram feitas usando efeito kerr magneto-óptico difratado. Uma área de pesquisas que vem se desenvolvendo rapidamente é a de semicondutores ferromagnéticos diluídos, onde um semicondutor puro é magneticamente dopado por um metal de transição para produzir um semicondutor ferromagnético [12, 13, 14, 15, 16]. Recentemente, foram obtidos avanços significativos na fabricação de dispositivos eletrônicos usados para armazenar dados ou para processar informações, ambos a base de semicondutores ferromagnéticos. Essa tecnologia, conhecida como spintrônica, utiliza simultaneamente os dois graus de liberdade, a carga e o spin dos portadores, para manipulação de dados [17, 18, 19]. Desde o início da década 1960, o efeito da introdução de impurezas em sólidos tem sido tratado em uma grande quantidade de trabalhos. Do ponto de vista teórico, a introdução de impurezas em cristais produz modos com frequências localizadas fora e dentro dos limites da banda de frequências de excitação para um cristal puro. Estes modos são chamados de modos de defeito e modos ressonantes, respectivamente. Izyumov demonstrou que a teoria para estes efeitos para diferentes tipos de excitações elementares é semelhante [20]. Em sistemas magnéticos os modos de impurezas podem ser detectados experimentalmente através de técnicas ópticas ou por espalhamento de nêutrons. As técnicas ópticas mais usadas no estudo de modos de defeitos são a espectroscopia de infravermelho, na qual a absorção de radiação por um cristal é medida em função desta frequência, e espalhamento Raman, na qual o espalhamento inelástico da radiação por uma amostra é observado. Uma revisão das propriedades de defeitos em sólidos magnéticos foi feita por Cowley e Buyers [1]. Recentemente, muitos trabalhos relativos ao estudo de impurezas em sistemas ferromagnéticos e antiferromagnéticos de Heisenberg, usando a técnica de funções de Green (F.G.) para determinar os modos de impurezas, foram publicados [2]-[7]. Estudos experimentais incluem o espalhamento inelástico da luz [8]. Trabalhos relativos ao estudo de impurezas de um sistema ferromagnético descritos pelo modelo de Ising com campo transverso [9]-[19], e pelo modelo Heisenberg/Ising [70],também foram publicados. Neste trabalho estudamos o espectro de ondas de spin relativas a uma impu-
20 19 reza intersticial localizada em sistemas ferromagnéticos, descritos pelos modelos de Ising e de Heisenberg. Para tanto, usamos a técnica de F.G. para estudar a propagação de ondas de spin em regime de troca. No capítulo 2, fazemos uma apresentação da linguagem matemática apropriada para o desenvolvimento deste trabalho. Introduzimos a teoria de F.G. em física da matéria condensada, um método matemático estabelecido por Zubarev [30], cuja aplicação é direcionada para a solução de problemas em sistemas ferromagnéticos. Seguimos, também, a referência [31]. No capítulo 3, fazemos o desenvolvimento do modelo e formalismo da função Green para um sistema ferromagnético de rede cúbica simples semi-infinita, seguindo as referências [11, 18] e aplicamos a técnica de F.G., fundamentada no capítulo 2, para calcular o espectro de excitações para uma impureza intersticial localizada na face que está no plano paralelo à superfície da rede cúbica simples semi-infinita. Faremos com que a posição desta impureza varie, de modo que ela possa ocupar todos os pontos possíveis dentro desta face. Determinamos a equação de movimento para as F.G., onde o sistema é descrito através do modelo de Ising com campo transverso. Como consideramos apenas interações entre primeiros vizinhos, a interação da impureza será com os quatro sítios dos vértices da face em questão. Primeiramente obtemos resultados para as frequências dos modos defeituosos não ressonantes (modos acústicos), como função do parâmetro de troca entre a impureza e seus vizinhos e do campo magnético aplicado. Em seguida empregamos os resultados das funções de Green, aqui encontrados, para estudar os modos ressonantes, ou seja, os modos localizados dentro da banda de volume do material puro. Nos capítulos 4, 5, 6 e 7, utilizamos o modelo de Heisenberg/Ising para descrever estruturas ferromagnéticas de redes: quadrada infinita, quadrada centrada infinita, cúbica de corpo centrado infinita, favo de mel infinita, respectivamente. Neste modelo, podemos passar do modelo de Heisenberg para o modelo de Ising através do controle de um parâmetro λ (para λ = 1, temos o modelo de Heisenberg e para λ = 0, temos o modelo de Ising). Também aplicamos a técnica de F.G. para calcular o espectro de excitações para uma impureza localizada intersticialmente nas estruturas ferromagnéticas apresentadas. 1.1 O Modelo de Heisenberg Para compreender a origem da interação de troca em uma rede de spin vamos inicialmente considerar apenas dois elétrons localizados em sítios vizinhos em uma rede de spin ou, por simplicidade, uma corrente 1D. A função de onda do total de dois elétrons pode ser construída a partir de funções de ondas eletrônicas individuais, que consistem de uma parte devida a função de onda de spin e uma parte devida a função de onda orbital.
21 20 A condição de simetria do princípio de exclusão de Pauli é então satisfeito se a função de onda orbital antissimétrica é multiplicada por uma função de onda de spin simétrica, ou vice-versa. A competição entre a interação coulombiana de repulsão eletrostática para dois elétrons em uma rede de spin e combinações possíveis para o estado fundamental faz a energia de interação entre os dois spins S i e S j depender de sua orientação relativa, que é usualmente expressa em termos do seu produto escalar. O Hamiltoniano do sistema é então dado pelo seguinte termo de troca de Heisenberg: H Heisenberg = 1 J i,j S i S j, (1.1) 2 onde J i,j é conhecida como a constante de troca entre os sítios mais próximos i e j. O valor de J i,j é usualmente obtido experimentalmente. Essencialmente, ele depende do grau de sobreposição das funções de onda eletrônicas. Quando J i,j é maior que zero, os spins na rede estão preferencialmente alinhados paralelamente que é a configuração ferromagnética. Quando J i,j é menor que zero, os spins na rede estão alinhados antiparalelamente, o que caracteriza a configuração antiferromagnética. O Hamiltoniano de Heisenberg é formalmente similar ao Hamiltoniano tight biding, pois ambos são dominados por interações entre primeiros vizinhos [81, 82, 83, 84, 85]. Desde que o elétron tenha um momento magnético dado por µ = gµ B S/ (µ B é o magneto de Bohr, e g é chamado o fator de Landé, sendo igual a 2 para um elétron livre), quando ele é submetido a um campo externo h sua energia potencial U devida ao campo é U = µ h. (1.2) A presença de um campo magnético desloca a energia do elétron por uma quantidade proporcional à componente do momento angular de spin na direção z ao longo do campo magnético. Isto é chamado o efeito Zeeman [86], e sua contribuição ao Hamiltoniano total é H Zeeman = gµ B h Si z. (1.3) i O Hamiltoniano total para a rede de spin, incluindo o termo de troca de Heisenberg e o termo de energia Zeeman pode ser escrito como segue: H T otal = 1 J i,j S i S j gµ B h Si z. (1.4) 2 i,j i i,j
22 O Modelo de Ising Na tentativa de explicar o ferromagnetismo com bases não fenomenológicas, Lenz [61] propôs uma teoria segundo a qual átomos dipolares num cristal seriam livres para girar sobre si próprios numa posição fixa da rede cristalina. Entretanto, critérios energéticos restringiram na prática tais átomos a assumir somente duas orientações espaciais em relação a seus vizinhos. Forças não-magnéticas seriam então responsáveis por diferenças na energia potencial dos átomos nas duas posições relativas, induzindo portanto o alinhamento dos dipolos magnéticos e dando origem a uma magnetização espontânea. Sob a orientação de Lenz, em 1925, Ernst Ising [62] resolveu exatamente em uma dimensão, o modelo que receberia seu nome. O modelo de Ising pode ser representado na forma geral pelo Hamiltoniano de spin H = 1 J ij Si z Sj z h i Si z, (1.5) 2 i,j i onde J é a constante de troca, h é o campo aplicado em todos os sítios e Si z é a componente z do spin nos sítios i = 1, 2, 3,, N de uma rede cristalina em d dimensões. O primeiro termo, onde a soma deve considerar apenas os vizinhos mais próximos, representa as energias de interação que devem ser capazes de produzir um estado ordenado ferromagneticamente (quando J ij > 0), ou, antiferromagneticamente (se J ij < 0). O segundo termo é a energia resultante da interação do campo magnético externo h com o spin localizado no sítio. Embora as variáveis de spin possam assumir diversas interpretações, as primeiras tentativas de solução para o modelo supunham interações uniformes e somente entre primeiros vizinhos, bem como campo e momentos magnéticos também uniformes em redes regulares. O problema unidimensional, resolvido por Ising, não apresentou transição de fase a temperaturas finitas. Contrariamente, as versões bi e tridimensional apresentaram magnetização espontânea para temperaturas suficientemente baixas, como mostrado por Peierls [63]. A temperatura crítica do modelo bidimensional foi determinada exatamente por Kramers e Wannier [64]. Onsager [65] calculou a função de partição do mesmo modelo na ausência de campo magnético. O cálculo da magnetização espontânea correspondente foi apresentado por Yang. Um histórico detalhado dos primeiros desenvolvimentos do modelo de Ising foi feito por Brush [66]. No estudo de excitações magnéticas, o modelo de Ising com campo transverso foi utilizado para descrever materiais magnéticos anisotrópicos reais quando imersos num campo magnético. Isso tem uma ampla aplicabilidade no formalismo da teoria de pseudospin para modelar transições de ordem-desordem em materiais ferroelétricos, como KH 2 PO 4, e alguns sistemas Jahn-Teller, tais como DyVO 4 e TbVO 4 [67]. Um estudo de revisão
23 22 do modelo foi feito por Blinc e Zeks [9], [69] e por Elliott e Young [71]. Aliado à técnica das F.G., o modelo de Ising com campo transverso tem sido amplamente aplicado para estudar a propagação de ondas de spin em sistemas magnéticos.
24 23 2 FUNÇÕES DE GREEN EM MECÂNICA ESTATÍSTICA Na física teórica tem-se diversas classes de funções de Green [21, 22, 23, 24, 25, 26]. A diferença entre elas está na forma de tomarmos os valores médios dos produtos de operadores que aparecem. Se a média for tomada no estado fundamental do sistema, tem-se as funções de Green de teoria de campos [27, 28]. Se a média for tomada sobre um ensemble estatístico, tem-se as funções de Green da mecânica estatística ou termodinâmica. Destacamos que na maioria dos casos basta considerar as funções que dependem de dois tempos, tanto retardadas quanto avançadas. Neste capítulo estabeleceremos as definições e propriedades das funções de Green, obtendo as equações de evolução para as mesmas. Introduziremos as funções de correlação temporal e representações espectrais. 2.1 Funções de Green Retardada, Avançada e Causal Podemos considerar em mecânica estatística, assim como em teoria quântica de campos, diferentes tipos de funções de Green, entre elas a função de Green causal de duplo tempo G c (t, t ), definida em termos do valor médio do produto ˆT de operadores, ou as funções de Green retardada e avançada,g r (t, t ) e G a (t, t ). Definimos as funções de Green retardada G r (t, t ), avançada G a (t, t ) e causal G c (t, t ) da seguinte forma [29, 30, 31]: G r (t, t ) = Â(t); ˆB(t ) r = iθ(t t ) [Â(t), ˆB(t )] ; (2.1a) G a (t, t ) = Â(t); ˆB(t ) a = iθ(t t) [Â(t), ˆB(t )] ; (2.1b) G c (t, t ) = Â(t); ˆB(t ) c = i T {Â(t), ˆB(t )}, (2.1c) onde [Â, ˆB] =  ˆB η ˆB é o comutador ou anticomutador dos operadores  e ˆB. O sinal de η é escolhido positivo ou negativo dependendo do que for mais conveniente para o problema. Usualmente escolhe-se o sinal positivo se  e ˆB são operadores de Bose (para bósons, temos η = 1 e a relação entre os operadores será de comutação) e o negativo, se eles são operadores de Fermi (para férmions, temos η = 1 e a relação entre os operadores será de anticomutação)[32, 31]. Porém, esta não é a única escolha possível. Nestas definições das funções de Green, aparece a relação  ˆB {ou ˆB } que corresponde ao valor médio estatístico do produto de operadores. Esta média é feita sobre o ensemble grão-canônico [33, 34]. Ensemble é definido como sendo uma coleção de sistemas físicos, idênticos entre
25 24 si e preparados nas mesmas condições macroscópicas, que se encontram nos diferentes microestados acessíveis. O ensemble grão-canônico possui um volume definido em contato com uma fonte térmica com a qual também troca partículas. A média feita sobre o ensemble grão-canônico é expressa em termos do traço (soma dos elementos da diagonal principal de uma matriz) deste produto. Assim, o valor médio estatístico de um operador ˆX é dado por [31] ˆX = Tr{e β(ĥ µ ˆN) ˆX}, (2.2) Θ onde Θ = Tr{ e β(ĥ µ ˆN) } é a função de grão-partição, sendo Ĥ o operador Hamiltoniano independente do tempo e ˆN, o operador número total de partículas do sistema. O parâmetro β é dado por β = 1/k B T, onde k B é a constante de Boltzmann e T é a temperatura absoluta. µ é o potencial químico [33, 34]. A aplicação do ensemble grão-canônico é muito conveniente quando o número total de partículas precisa ser levado em consideração e, também, o número de ocupação dos diferentes estados são independentes. A dependência temporal dos operadores fica explicada por trabalharmos na representação de Heisenberg e sua equação de movimento é satisfeita por estes operadores, de modo que Â(t) = e iĥt Âe iĥt = e iĥt Âe iĥt, (2.3) onde usamos uma unidade de medida na qual = 1 e definimos Ĥ como Ĥ = Ĥ µ ˆN. (2.4) As funções de Green contêm, também, a função degrau ou função de Heaveside [35] definida como sendo θ(t) = 1, para t > 0 e θ(t) = 0, para t < 0, conforme mostra a Fig. 1. Derivando esta função no ponto t = 0, sua derivada tende ao infinito, caracterizando a função delta de Dirac. Matematicamente temos dθ(t) dt = δ(t) (2.5) e θ(t) = t δ(t)dt (2.6)
26 25 Figura 1: Gráfico da função degrau ou função de Heaveside. de modo que Na função de Green causal aparece o operador de ordenamento temporal ˆT, ˆT {Â(t), ˆB(t )} = Â(t) ˆB(t ), para t > t e ˆT {Â(t), ˆB(t )} = η ˆB(t )Â(t), para t < t, ou ainda: ˆT {Â(t), ˆB(t )} = θ(t t )Â(t) ˆB(t ) + ηθ(t t) ˆB(t )Â(t). (2.7) Devido a função degrau, as funções de Green (retardada, avançada e causal) não estão definidas em t = t. Podemos verificar que tais funções de Green dependem de t e t através da diferença t t calculando o valor médio estatístico de Â(t) ˆB(t ). Vejamos. Â(t) ˆB(t ) = Tr{e β(ĥ µ ˆN) Â(t) ˆB(t )} Θ = Tr{e βĥe iĥt Âe iĥt e iĥt ˆBe iĥt } Θ = Tr{e βĥe iĥt e iĥt Âe iĥt e iĥt ˆB} Θ = Tr{e βĥe iĥ(t t ) Âe iĥ(t t ) ˆB} Θ = Tr{e βĥâ(t t ) ˆB}, (2.8) Θ onde usamos a propriedade de que os operadores podem ser permutados ciclicamente dentro do traço. Então podemos escrever Â(t) ˆB(t ) F AB (t t ). (2.9)
27 26 Considerando que as funções de Green contêm termos do tipo Â(t) ˆB(t ) e ˆB(t )Â(t) podemos escrever Â(t); ˆB(t ) r,a,c = Â(t t ); ˆB r,a,c = Â; ˆB(t t) r,a,c. (2.10) Assim as funções de Green, em estatística, não dependem somente do tempo mas, também, da temperatura, de modo que, quando esta tende a zero nas Eqs. 2.1, teremos as funções de Green da teoria de campo. Estas funções são as funções de Green causais de tempo múltiplo e são definidas da seguinte maneira: G C ( X 1 t 1,, X n t n, X 1t 1,, X nt n ) 0 ˆT {ψ( X 1 t 1 ) ψ( X n t n )ψ ( X 1t 1)ψ ψ ( X nt n) 0, onde ˆT é o operador de ordenamento temporal, definido como anteriormente, e 0 é o estado fundamental do sistema. ψ( X n t n ) e ψ ( X n t n ) são funções de campo na segunda quantização [26, 27, 32] na representação de Heisenberg ψ( X, t) = k a k (t)ϕ k ( X) e ψ ( X, t) = k a k (t)ϕ k( X). a k e a k são os operadores de aniquilação e destruição (operadores de Fermi ou Bose), ϕ k ( X) é um conjunto ortogonal completo de funções de uma partícula. A função de Green retardada é definida somente para t > t e representa uma informação que foi emitida no tempo t sendo recebida no instante t, posterior a t. Já a função de Green avançada é definida apenas para t < t e representa uma informação que foi emitida num tempo t e que é recebida no instante t, anterior a t, apresentando, assim, dificuldades quanto a uma interpretação física, sendo, portanto, uma ferramenta matemática que eventualmente pode ser utilizada como artifício de cálculo em algum problema específico. E quanto a função de Green causal, ela está definida para qualquer valor não-nulo de t t. Essas funções são muito convenientemente aplicadas em estatística quântica para problemas envolvendo um sistema de muitas partículas interatuantes. Os operadores  e ˆB podem ser de diferentes tipos, tais como os operadores de criação ou de destruição e seus produtos, operador densidade, dentre outros. A escolha dos operadores  e ˆB é determinada pelas condições do problema.
28 Equações de Evolução para as Funções de Green Podemos obter um conjunto de equações para as funções de Green. Como estamos trabalhando na representação de Heisenberg, os operadores satisfazem sua equação de movimento de modo que i dâ(t) dt = [Â(t), Ĥ], (2.11) onde Â(t) é um operador qualquer dependente do tempo e Ĥ é o hamiltoniano do sistema dado pela Eq No lado direito desta equação usamos a forma explícita do Hamiltoniano e as relações de comutação para operadores. Então, para G r (t, t ), teremos: i dg r(t, t ) dt = i d dt Â(t); ˆB(t ) r = i d dt { iθ(t t ) [Â(t), ˆB(t )] } = dθ(t t ) dt )] + θ(t t ) [ dâ(t), dt )] = δ(t t ) [Â(t) ˆB(t )] + θ(t t ) [ i(â(t)ĥ ĤÂ(t)), ˆB(t )] = δ(t t ) [Â(t) ˆB(t )] + { iθ(t t ) [(Â(t)Ĥ ĤA(t)), ˆB(t )] } = δ(t t ) [Â(t) ˆB(t )] + Â(t)Ĥ ĤÂ(t); ˆB(t ) r. (2.12) Podemos fazer o mesmo procedimento para G a (t, t ), o que nos fornece: i dg a(t, t ) dt = i d dt Â(t); ˆB(t ) a = i d dt {iθ(t t) [Â(t), ˆB(t )] } = dθ(t t) dt [Â(t) ˆB(t )] θ(t t) [ dâ(t), dt ˆB(t )] = d[θ(t t) dt [Â(t) ˆB(t )] θ(t t) [ i(â(t)ĥ ĤÂ(t)), ˆB(t )] = { δ(t t ) [Â(t) ˆB(t )] } + iθ(t t) (Â(t)Ĥ ĤÂ(t)), ˆB(t )] = δ(t t ) [Â(t) ˆB(t )] + iθ(t t) [Â(t)Ĥ ĤÂ(t), ˆB(t )] = δ(t t ) [Â(t) ˆB(t )] + Â(t)Ĥ ĤÂ(t); ˆB(t ) a. (2.13) E finalmente podemos fazer o mesmo procedimento para G c (t, t ), o que nos
29 28 dá: i dg c(t, t ) dt = i d dt Â(t); ˆB(t ) c = i d dt ( i ˆT {Â(t), ˆB(t )} ) = d dt θ(t t )Â(t) ˆB(t ) + ηθ(t t)â(t) ˆB(t ) = dθ(t t ) dt Â(t) ˆB(t ) + θ(t t ) dâ(t) ˆB(t ) dt + η dθ(t t) dt ˆB(t )Â(t) + ηθ(t t) ˆB(t ) dâ(t) dt = δ(t t ) Â(t) ˆB(t ) iθ(t t ) [Â(t), Ĥ] ˆB(t ) ηδ(t t ) ˆB(t )Â(t) iηθ(t t ) ˆB(t )[(Â(t), Ĥ] = δ(t t )( Â(t) ˆB(t ) η ˆB(t )Â(t) ) Aqui usamos o fato de que i(θ(t t ) [Â(t), Ĥ] ˆB(t ) iηθ(t t) ˆB(t )[Â(t), Ĥ] ) = δ(t t ) [Â(t), ˆB(t )] i ˆT [Â(t), Ĥ] ˆB(t ) = δ(t t ) [Â(t), ˆB(t )] + Â(t)Ĥ ĤÂ(t); ˆB(t ) c. (2.14) dθ(t t) dt = dθ(t t ). dt As Eqs. 2.12, 2.13 e 2.14 podem ser escritas como uma única, dada por i d dt Â(t); ˆB(t ) k = δ(t t ) [Â(t) ˆB(t )] + Â(t)Ĥ ĤÂ(t); ˆB(t ) k (2.15) onde k = {r, a, c}. As funções de Green do lado direito da Eq são, geralmente falando, de ordem mais alta que as iniciais, ou seja, na equação de movimento para o par de operadores temos uma função de Green de três operadores. As soluções da cadeia de equações contidas na Eq são exatas e são geralmente extremamente complicadas. Pode-se, algumas vezes, por algum método aproximativo, desacoplar esta cadeia, isto é, reduzí-la a um conjunto finito de equações, que pode ser então resolvido. 2.3 Funções de Correlação Temporal Já vimos anteriormente que Â(t) ˆB(t ) = Â(t t ) ˆB(0) = Â(0) ˆB(t t) F AB (t t ).
30 29 Chamamos de função de correlação temporal a média sobre o ensemble grãocanônico do produto de operadores na representação de Heisenberg, ou seja, F AB (t t ) Â(t) ˆB(t ) (2.16) e F BA (t t ) ˆB(t )Â(t). (2.17) Diferentemente das funções de Green (r, a, c), que não estão definidas para t = t devido ao fator θ(t t ), as funções de correlação temporal estão, também, definidas neste caso. Assim, de acordo com a definição, temos F AB (0) = Â(t) ˆB(t) = Â(t t) ˆB(0) = Â(0) ˆB(0). (2.18) Como exemplo vamos considerar o Hamiltoniano para um sistema de partículas idênticas interatuantes[32] dado por Ĥ = T k a k a k + 1 mn V pq a 2 ma na q a p, (2.19) m,n,p,q onde mn V pq = ij V ij l m k i k i l p l n k j k j l q. (2.20) A energia do sistema corresponde ao valor médio termodinâmico do Hamiltoniano Ĥ, que calculado fica: E Ĥ = k = k T k a k a k + 1 mn V pq a 2 ma na q a p m,n,p,q T k ˆη k + 1 mn V pq  2 ˆB, m,n,p,q onde fizemos  = a ma n, ˆB = aq a p e ˆη k = a k a k. ˆη k é o número de ocupação do modo k e a e a são os operadores destruição e criação, respectivamente. Desta forma, concluímos que para obter a energia do sistema, é necessário conhecer as funções de correlação a k a k e a na na q a p, que são bem conhecidas em física estatística. O valor a k a k dá a verdadeira distribuição de momento das partículas e a na na q a p descreve a correlação entre duas partículas. O conhecimento da função distribuição de uma partícula nos permite avaliar, em geral, os valores médios de quantidades dinâmicas aditivas, a função distribuição de pares de caráter binário etc.
31 30 As funções de correlação temporal 2.16 e 2.17 satisfazem as equações i df BA(t t ) dt d ˆB(t )Â(t) = i dt = i ˆB(t ) dâ(t) dt = i ˆB(t ) 1i {Â(t)Ĥ(t) Ĥ(t)Â(t)} = ˆB(t ){Â(t)Ĥ(t) Ĥ(t)Â(t)} e i df AB(t t ) dt = i d Â(t) ˆB(t ) dt = i dâ(t) ˆB(t ) dt = i 1 i {Â(t)Ĥ(t) Ĥ(t)Â(t)} ˆB(t ) = {Â(t)Ĥ(t) Ĥ(t)Â(t)} ˆB(t ), que foram obtidas pela diferenciação com respeito a t e pela utilização da equação de movimento de Heisenberg para os operadores. Notemos que desde que as 2.16 e 2.17 não sejam descontínuas em t = t, as equações acima não têm o termo singular δ(t t ) que ocorre na Eq para as funções de Green. As funções de correlação podem ser avaliadas também pela integração direta destas equações, a qual deve ser adicionada ainda as condições de contorno, ou indiretamente pela avaliação, primeiramente, das equações O segundo método que devemos usar é consideravelmente mais simples, desde que o faça mais fácil para satisfazer as condições de contorno usando teoremas espectrais (Sec. 2.4). 2.4 Representação Espectral Para as Funções de Correlação Temporal Levando em consideração que as funções de Green dependem do tempo através da diferença t t, podemos introduzir expansões em auto-estados que representam um conjunto completo de soluções para as funções de Green, ou seja, podemos através de uma transformada de Fourier [36] passar da dependência temporal para o espaço das frequências e escrever o espectro. Para resolver as equações para as funções de Green é importante ter estas representações espectrais, que suplementam o conjunto de equações, com as condições de
32 31 contorno adequadas. Denotemos o auto estado de Ĥ por ν de modo que Ĥ ν = E ν ν, (2.21) onde a 2.21 é a equação de autovalor, sendo E ν o autovalor (auto energia) do operador Hamiltoniano Ĥ. Assim teremos, para a função de correlação temporal F BA(t t ): F BA (t t ) = ˆB(t )Â(t) = 1 Θ Tr{e βĥ ˆB(t )Â(t)} = 1 Θ Tr{e βĥe iĥt Be iĥt e iĥt Âe iĥt } = 1 ν e βĥeiĥt ˆBe iĥt e iĥt Âe iĥt ν Θ ν = 1 ν e iĥt ˆBe iĥt e iĥt Âe iĥt ν e βeν Θ ν ( ) = 1 ν e iĥt ˆBe iĥt µ µ e iĥt Âe iĥt ν e βeν Θ ν µ = 1 ν e iĥt ˆBe iĥt µ µ e iĥt Âe iĥt ν e βeν Θ ν,µ = 1 e ieνt e ieµt ν Θ ˆB µ µ Â ν eieµt e ieνt e βeν ν,µ = 1 ν Θ ˆB µ µ Â ν e βeν e i(eµ Eν)t e i(eµ Eν)t ν,µ = 1 ν Θ ˆB µ µ Â ν e βeν e i(eµ Eν)(t t ). (2.22) ν,µ Aqui introduzimos o operador unitário µ µ µ que, obviamente, não altera em nada o resultado. Desta forma escrevemos a função de correlação temporal em termos das energias de excitação do sistema.
33 32 Podemos fazer o mesmo para F AB (t t ). Vejamos. F AB (t t ) = Â(t) ˆB(t ) = 1 Θ Tr{e βĥâ(t) ˆB(t )} = 1 Θ Tr{e βĥe iĥt Âe iĥt e iĥt ˆBe iĥt } = 1 ν e βĥeiĥt Âe iĥt e iĥt ˆBe iĥt ν Θ ν = 1 ν e iĥt Âe iĥt e iĥt ˆBe iĥt ν e βeν Θ ν ( ) = 1 ν e iĥt Âe iĥt µ µ e iĥt ˆBe iĥt ν e βeν Θ ν µ = 1 ν e iĥt Âe iĥt µ µ e iĥt Be iĥt ν e βeν Θ ν,µ = 1 e ieνt e ieµt Θ ν Â µ µ ˆB ν e ieµt e ieνt e βeν ν,µ = 1 Θ ν Â µ µ ˆB ν e βeν e i(eν Eµ)t e i(eν Eµ)t ν,µ = 1 Θ ν Â µ µ ˆB ν e βeν e i(eν Eµ)(t t ) ν,µ (2.23) Na equação Eq podemos trocar ν por µ e vice-versa, sem perda de generalidade, o que nos leva à seguinte relação: F BA (t t ) = 1 ν Θ ˆB µ µ Â ν e βeν e i(eµ Eν)(t t ) ν,µ = 1 µ Θ ˆB ν ν Â µ e βeµ e i(eν Eµ)(t t ) µ,ν = 1 Θ ν Â µ µ ˆB ν e βeµ e βeν e βeν e i(eν Eµ)(t t ) µ,ν = 1 Θ ν Â µ µ ˆB ν e βeν e i(eν Eµ)(t t ) e β(eµ Eν). (2.24) µ,ν modo que Assim, encontramos uma relação entre as funções de correlação temporal, de F BA (t t ) = F AB (t t )e β(eµ Eν). (2.25) Vamos introduzir a transformada de Fourier J BA (ω) tal que F BA (t t ) = J BA (ω)e iω(t t ) dω, (2.26)
34 33 com sua transformada inversa dada por A integral que aparece na equação acima pode ser calculada da seguinte maneira: J BA (ω) = J(ω) = 1 2π F BA (t t )e iω(t t ) dt. (2.27) Fazendo τ = t t, de modo que dt = dτ e usando a Eq teremos: J BA (ω) = J(ω) = 1 2π = 1 2π F BA (τ)e iω(τ) dτ [ ] 1 µ Θ ˆB ν ν Â µ e βeµ e i(eν Eµ)(τ) e iω(τ) dτ µ,ν = 1 1 µ Θ 2π ˆB ν ν Â µ e βeµ e iωτ e i(eν Eµ)τ dτ µ,ν = 1 1 µ Θ 2π ˆB ν ν Â µ e βeµ e i[eµ Eν+ω]τ dτ. µ,ν e i[eµ Eν ω]τ dτ = Para ω E µ E ν, teremos: 2π e i[eµ Eν ω]τ dτ = Para ω = E µ E ν, teremos: e i[eµ Eν ω]τ dτ = desta forma podemos concluir que 0 2π cos(e µ E ν ω)τ]dτ i sen[(e µ E ν ω)τ]dτ 0 1 E µ E ν ω ([senφ]2π 0 + i[cos φ] 2π 0 ) = 0. 2π 0 2π cos 0dφ i sen0dφ = [φ] 2π 0 = 2π 0 e i[eµ Eν ω]τ dτ = 2πδ(E µ E ν ω). (2.28) Assim a expressão para J(ω) torna-se: J(ω) = 1 1 µ Θ 2π ˆB ν ν Â µ e βeµ 2πδ(E µ E ν ω) µ,ν = 1 µ Θ ˆB ν ν Â µ e βeµ δ(e µ E ν ω). (2.29) µ,ν
35 34 Analogamente, teremos para a transformada de Fourier de F AB (t t ), F AB (t t ) = com sua transformada inversa dada por (usando a Eq. 2.23): e. J AB (ω) = 1 2π = 1 2π = 1 2π = 1 1 2π Θ F AB (t t )e iω(t t ) dt J AB (ω)e iω(t t ) dω, (2.30) F AB (τ)e iω(τ) dτ [ ] 1 Θ ν  µ µ ˆB ν e βeν e i(eν Eµ)(t t ) e iωτ dτ ν,µ ν  µ µ ˆB ν e βeν e i(eν Eµ+ω) dτ ν,µ = 1 1 2π Θ ν  µ µ ˆB ν e βeµ e βeν e βeµ 2πδ(E ν E µ + ω) ν,µ = 1 Θ ν  µ µ ˆB ν e βeµ δ(e ν E µ + ω)e β(eµ Eν) ν,µ = J BA (ω)e β(eµ Eν) = J(ω)e βω. (2.31) Desta forma podemos escrever as seguintes relações: F BA (t t ) = F AB (t t ) = J(ω)e iωτ dω (2.32) J(ω)e βω e iωτ dω. (2.33) As equações Eqs e 2.33 são as requeridas representações espectrais para as funções de correlação temporal, onde J(ω) é a densidade espectral da função F BA (t, t ). Como exemplo, podemos fazer  a e ˆB a. Desta forma teremos: e F a a(t t ) = J a a(ω)e iωτ dω J a a(ω) = 1 F 2π a a(ω)e iωτ dτ = 1 µ a ν ν a µ e βeµ δ(e µ E ν ω) Θ µ,ν = 1 ν a µ 2 e βeµ δ(e µ E ν ω) Θ µ,ν
36 35 é a seguinte: Assim J a a(ω) é definida positiva. Outra propriedade das funções de correlação Â(t) ˆB(0) = 1 Θ Tr[e βĥe iht Âe iĥt ˆB] = 1 [ ] Θ Tr e βĥ ˆBe βĥe iĥt Âe iĥt e βĥ = 1 [ ] Θ Tr e βĥ ˆBe i(t+iβ)ĥâe i(t+iβ)ĥ = 1 Θ Tr[e βh ˆBÂ(t + iβ)] = ˆB(0)Â(t + iβ). (2.34) Desta forma, a Eq pode ser obtida a partir da Eq através da substituição t t t t + iβ, ou seja, F AB (t t ) = F BA (t t + iβ) = = = J(ω)e iω(t t +iβ) dω J(ω)e iω(t t ) e βω dω J(ω)e βω e iωτ dω. 2.5 Representações Espectrais para G r e G a Consideremos agora as representações espectrais para as funções de Green retardada e avançada. Podemos obtê-las facilmente por meio das representações espectrais para as funções de correlação temporal. Primeiro faremos para G r (t t ). Podemos introduzir a componente de Fourier da mesma através da relação Ou G r (t t ) = G r (τ) = G r (E)e ie(t t ) de (2.35) G r (E)e ieτ de, onde τ = t t e G r (E) é a componente de Fourier da função de Green retardada G r (t t ) que é dada por G r (E) = 1 G r (τ)e ieτ dτ, (2.36) 2π
37 36 cuja equação geral de movimento se obtêm pela substituição da (2.35) na (2.15), ou seja, i d dt Â(t); ˆB(t ) = δ(t t ) [Â(t) ˆB(t )] + [Â(t), Ĥ]; ˆB(t ) i d dt Â(t); ˆB(t ) E e ie(t t ) de = 1 2π + e ie(t t ) de [Â(t), ˆB(t )] [Â(t), Ĥ]; ˆB(t ) E e ie(t t ) de E Â(t); ˆB(t ) E = 1 2π [Â(t), ˆB(t )] + [Â(t), Ĥ]; ˆB(t ) E. (2.37) Utilizando a definição de G r (t t ), teremos a seguinte expressão: G r (E) = 1 2π = 1 2π = i 2π = i 2π G r (τ)e ieτ dτ { iθ(τ) [Â(t t ), ˆB(0)] }e ieτ dτ θ(τ){ Â(t t ) ˆB(0) η ˆB(0)Â(t t ) }e ieτ dτ θ(τ){ Â(τ) ˆB(0) η ˆB(0)Â(τ) }eieτ dτ, que contém as funções de correlação temporal. Como e teremos: G r (E) = i 2π = i 2π = i = i Â(τ) ˆB(0) = J(ω)e βω e iωτ dω ˆB(0)Â(τ) = J(ω)e iωτ dω, [ θ(τ) [ θ(τ) dωj(ω)(e βω η) 1 2π dωj(ω)(e βω η) 1 2π J(ω)e βω e iωτ dω η ] J(ω)e iωτ (e βω η)dω ] J(ω)e iωτ dω e ieτ dτ e ieτ dτ e ieτ e iωτ θ(τ)dτ e i(e ω)τ.θ(τ)dτ Para tornar mais simples esta expressão, faremos uso da representação integral de θ(τ). Como já vimos antes, podemos escrever esta função descontínua em termos da
38 37 função delta de Dirac, δ(τ), ou seja, onde ɛ 0 (ɛ > 0). θ(τ) = τ δ(τ )dτ = τ e ɛτ δ(τ )dτ, Porém uma das representações para a função delta de Dirac é dada por [38] δ(τ) = 1 2π Desta forma, θ(τ) torna-se: θ(τ) = = τ τ = 1 2π = 1 2π = 1 2π = 1 2π = i 2π e ɛτ δ(τ )dτ [ 1 e ɛτ 2π dx dx [ dx e ixτ dx. τ τ ] e ixτ dx dτ e ɛτ e ixτ dτ e (ɛ ix)τ dτ 1 ɛ ix e(ɛ ix)τ e ixτ ɛ ix dx ] τ e ixτ dx. (2.38) X + iɛ Verifica-se que a função definida desta maneira tem, de fato, as propriedades da função descontínua θ(τ). Devemos considerar X como uma variável complexa. Como o integrando contém polo (X = iɛ), a (2.38) será resolvida através do método dos resíduos [37]. Quando τ < 0, o contorno deve ser fechado por cima, não encerrando a singularidade (vide Fig. 2). De acordo com o teorema de Cauchy [37] a integral é nula, ou seja, θ(τ) = i e ixτ dτ = 0. 2π X + ɛ Quando τ > 0, o contorno deve ser fechado por baixo, encerrando a singularidade (vide Fig. 3. Assim, pelo teorema do resíduo, teremos: e ixτ dx = 2πiResf( iɛ), X + iɛ onde o sinal de menos é devido o fato da integração está sendo feita no sentido horário e
39 38 Figura 2: Contorno de integração da Eq.2.36 para valores negativos da variável tempo. Figura 3: Contorno de integração da Eq.2.36 para valores positivos da variável tempo. Resf(a) é o resíduo da função no ponto de singularidade, ou seja, X = a, e é dado por: Assim teremos Resf(a) = lim X a (X a)f(x). e ixτ dx = 2πi lim X + iɛ ɛ 0 + lim X ɛi = 2πi lim ɛ 0 + e i( ɛi)τ = 2πi lim ɛ 0 + e ɛτ = 2πi e ixτ (X + ɛi) X + ɛi
40 39 e θ(τ), será igual a unidade, ou seja, θ(τ) = i 2π e ixτ X + ɛi dx = Teremos, então, a seguinte relação: e i(e ω)τ θ(τ)dτ = = i 2π = i 2π = i 2π = i = e i(e ω)τ dτ i 2π dx X + iɛ dx X + iɛ Desta forma, G r (E) transforma-se em: G r (E) = i = i = 1 2π i ( 2πi) = 1. 2π e ixτ X + iɛ dx e i(e ω)τ e ixτ dτ e i(e ω X)τ dτ dx 2πδ(E ω X) X + iɛ dx δ(e ω X) X + iɛ i E ω + iɛ. (2.39) dωj(ω)(e βω η) 1 2π dωj(ω)(e βω η) 1 e i(e ω)τ θ(τ)dτ i 2π E ω + iɛ J(ω)(e βω dω η) E ω + iɛ. (2.40) Este resultado mostra a relação entre G r (E) e a função de correlação temporal através de J(ω). Analogamente podemos introduzir a componente de Fourier G a (E) para a função de Green avançada, ou seja, G a (t, t ) = G a (E)e ie(t t ) de = G a (E)e ie(τ) de. Utilizando a definição de função de Green avançada a componente de Fourier
41 40 G a (E) torna-se: G a (E) = 1 2π = 1 2π = i 2π = i 2π = i 2π G a (τ)e ieτ dτ iθ( τ) [Â(t t ), ˆB(0)] e ieτ dτ θ( τ) Â(t t ) ˆB(0) η ˆB(0)Â(t t )) e ieτ dτ [ ] dτe ieτ J(ω)e βω e iωτ dω η J(ω)e iωτ dω θ( τ) J(ω)(e βω η)dω dτe i(ω E)τ θ( τ). Porém, Desta forma, G a (E) torna-se: θ( τ) = i e ixτ 2π X + iɛ dx. ou seja, G a (E) = i 2π = 1 (2π) 2 = 1 (2π) 2 = 1 2π J(ω)(e βω η)dω J(ω)(e βω η)dω J(ω)(e βω η)dω dτe i(ω E)τ i e ixτ 2π X + iɛ dx dx e i(e ω+x) dτ X + iɛ dx 2πδ(E ω + X) X + iɛ J(ω)(e βω dω η) E ω iɛ. (2.41) As equações para G r (E) e G a (E) podem ser escritas como uma única equação, G r,a (E) = 1 2π J(ω)(e βω dω η) E ω ± iɛ, (2.42) onde o índice r corresponde ao sinal + e o índice a corresponde ao sinal. Até agora temos considerado E como uma quantidade real. A função G r,a (E) pode ser analiticamente contínua no plano complexo E. Assim, assumindo que E seja complexo, teremos: se Im[E] > 0 e se Im[E] < 0 1 2π 1 2π J(ω)(e βω dω η) E ω = G r(e) J(ω)(e βω dω η) E ω = G r(e) (2.43) Podemos ver que G r (E) pode ser analiticamente estendida ao plano complexo
42 41 Im(E) > 0 da seguinte maneira: onde G r (τ) = 0 para τ < 0. G r (E) = 1 2π G r (τ)e ieτ dτ, Fazendo E = α + βi, com β > 0, teremos: G r (α + iβ) = 1 2π G r (τ)e i(α+iβ)τ dτ = 1 2π G r (τ)e iατ e βτ dτ. Então e βτ desempenha o papel de um fator de corte que faz G r (E) e suas derivadas com respeito a E convergirem sob hipóteses suficientemente gerais sobre a função G r (τ). Podemos, similarmente, ver que que a função G a (E) pode ser analiticamente contínua dentro do plano complexo Im[E] < 0. Vejamos. G a (E) = 1 2π G a (τ)e ieτ dτ. com G a (τ) = 0 para τ > 0. Fazendo E = α + iβ, com β < 0, teremos: G a (E) = 1 0 G a (τ)e i(α+iβ)τ dτ = 1 0 G a (τ)e iατ e βτ dτ. 2π 2π Novamente o termo e βτ faz o papel de um fator de corte. Se conhecermos a função G(E), podemos encontrar também a intensidade espectral J(ω), ou seja, onde E + = E ± iɛ. Desta forma teremos: G(E + ) G(E ) G(E + iɛ) G(E iɛ), G(E + ) G(E ) = 1 2π 1 2π (e βω dω η)j(ω) E + ω (e βω dω η)j(ω) E ω (2.44) Para resolver a Eq usaremos a identidade de Dirac [24] dada por: ( ) 1 1 X ± iɛ = P iπδ(x), (2.45) X onde ɛ 0 + (ɛ > 0, ɛ 0), X é uma variável real e P denota o valor principal na integração sobre X (parte principal da integral)[37]. A parte principal da integral de uma função f(x), num intervalo a x b,
43 42 contínua neste intervalo, exceto no ponto x 0 (a x 0 b), é dada por: P b a [ x0 δ b ] f(x)dx = lim f(x)dx + f(x)dx. (2.46) δ 0 a x 0 δ O significado desta identidade pode ser percebido considerando a seguinte integral, no limite quando ɛ 0: f(x) lim ɛ 0 + X iɛ dx, de modo que f(x) não tem singularidades no eixo real. O resultado desta integral será: lim ɛ 0 + Portanto, lim ɛ 0 f(x) X iɛ f(x) X iɛ dx = P = P r dx = lim lim ɛ 0 r 0 + lim lim ɛ 0 r 0 r f(x) dx + iπ X f(x) dx + iπf(0). X f(x) X iɛ f(x) X iɛ dx. r dx + lim lim ɛ 0 r 0 r Assumimos, sem perda de generalidade, que ɛ r. Então f(x) lim dx = lim ɛ 0 X iɛ r 0 [ r + lim lim ɛ 0 r 0 r f(x) X dx + r δ(x)f(x)dx f(x) X iɛ dx ] dx f(x) X [f(0) + Xf (0) + ] dx. X iɛ As duas primeiras integrais do lado direito correspondem à parte principal da integral e para o último termo fez-se uma expansão em série de Taylor [38] em torno da origem. Uma vez que ɛ é extremamente pequeno, consideraremos apenas o primeiro termo da expansão. Logo, lim ɛ 0 f(x) X iɛ dx = P f(x) X Calculemos a última integral à direita. r r dx X iɛ = ln(x iɛ) r r = ln ( 1 + ir/ɛ = ln 1 ir/ɛ dx + f(0) lim ( r iɛ r iɛ r lim ɛ 0 r 0 r ) ( ) ir + ɛ = ln ir + ɛ dx X iɛ. (2.47) ). (2.48)
44 43 de modo que Agora, podemos utilizar a seguinte relação [39] tanh 1 x = 1 ( ) 1 + x 2 ln, (2.49) 1 x ln ( ) 1 + ir/ɛ = 2 tanh 1 (ir/ɛ). 1 ir/ɛ Porém, se usarmos tanh 1 (ix) = i tan 1 x, teremos ( ) 1 + ir/ɛ ln = 2i tan 1 (r/ɛ). 1 ir/ɛ Assim a Eq torna-se: r ( ) dx 1 + ir/ɛ X iɛ = ln = 2i tan 1 (r/ɛ). (2.50) 1 ir/ɛ r Logo a Eq.2.47 fica f(x) lim ɛ 0 X iɛ dx = P O que mostra a equação Eq torna-se: = P = P f(x) dx + 2if(0) lim X lim ɛ 0 r 0 tan 1 (r/ɛ) f(x) X dx + 2if(0)π 2 f(x) dx + iπf(0). (2.51) X Agora, utilizando tal identidade, com f(x) = (e βω η)j(ω) e X = E ω, a G(E + ) G(E ) = 1 (e βω dω η)j(ω) 2π E ω + iɛ 1 (e βω dω η)j(ω) 2π E ω iɛ = 1 [ (e βω dω ] η)j(ω) 2π E ω iπ dω(e βω η)j(ω)δ(e ω) 1 [ P (e βω dω ] η)j(ω) 2π E ω + iπ dω(e βω η)j(ω)δ(e ω) = 1 2π P (e βω dω η)j(ω) E ω 1 2π P (e βω dω η)j(ω) E ω 1 2π iπ(eβe η)j(e) 1 2π iπ(eβe η)j(e) = i(e βe η)j(e) (2.52) e podemos, então, escrever a seguinte relação para J(ω): J(ω) = i G(E+ ) G(E ) e βω η = i G(ω + iɛ) G(ω iɛ). (2.53) e βω η
45 44 t ) da seguinte forma: Com este resultado, podemos escrever a função de correlação temporal F BA (t F BA (t t ) = i G(E + ) G(E ) e iω(t t ) dω. (2.54) e βω η Desta maneira concluímos que o conhecimento da função de Green permite obter a função de correlação temporal, e a componente de Fourier de G r (t t ) pode ser dada por G r (E) = 1 (e βω dω η)j(ω) 2π E + ω = 1 (e βω dω η)j(ω) 2π E ω + iɛ = 1 [ ] (e βω dω η)j(ω) 2π E ω iπ(eβe η)j(e) = 1 2π P (e βω dω η)j(ω) E ω i 2 (eβe η)j(e), (2.55) de modo que Im[G r (ω)] = 1 2 (eβω η)j(ω) e Re[G r (E)] = 1 2π P = 1 π = 1 π (e βω dω η)j(e) E ω [ 1 ] dω 2 (eβω η)j(ω) ω E Im[G r (ω)] dω, (2.56) ω E que é a relação entre as partes real e imaginária da função de Green retardada. Analogamente, para G a (E), teremos: G a (E) = 1 (e βω dω η)j(ω) 2π E ω = 1 (e βω dω η)j(ω) 2π E ω iɛ = 1 [ ] (e βω dω η)j(ω) 2π E ω + iπ(eβe η)j(e) = 1 2π P (e βω dω η)j(ω) E ω + i 2 (eβe η)j(e), de modo que Im[G a (ω)] = 1 2 (eβω η)j(ω)
46 45 e Re[G a (E)] = 1 2π P = 1 π = 1 π (e βω dω η)j(ω) E ω [ ] 1 dω 2 (eβω η)j(ω) ω E Im[G a (ω)] dω. (2.57) ω E Temos aqui uma conexão entre as partes real e imaginária da função de Green avançada. 2.6 Representação Espectral para G C Trataremos, agora, da representação espectral para a função de Green causal. Consideremos a componente G C (E) de G C (t t ) de modo que e onde E é real. G C (τ) = Temos as seguintes relações: G C (E)e ieτ de G C (E) = 1 G C (τ)e ieτ dτ, 2π G C (t, t ) = i[θ(t t ) Â(t) ˆB(t ) + ηθ(t t) ˆB(t )Â(t) ], que é a definição da função de Green causal; F AB (t t ) Â(t) ˆB(t ) = J(ω)e βω e iωτ dω; F BA (t t ) ˆB(t )Â(t) = J(ω)e iωτ dω. As duas últimas relações são as funções de correlação temporal, já vistas anteriormente. Assim, usando-as, calcularemos a componente de Fourier G C (E). Vejamos. G C (E) = 1 2π = i 2π = i 2π { i[θ(t t ) Â(t) ˆB(t ) + ηθ(t t) ˆB(t )Â(t)] }eieτ dτ ( ) J(ω)e βω e iωτ dωe ieτ θ(τ)dτ + η J(ω)e iωτ dωe ieτ θ( τ)dτ J(ω)e βω dω e i(e ω)τ θ(τ)dτ + η J(ω)dω e i(e ω)τ θ( τ)dτ.
47 46 Fazendo uso da Eq. 2.39, teremos: G C (E) = i [ J(ω)e βω i ] dω 2π E ω + iɛ + η i J(ω)dω ω E iɛ = 1 [ J(ω)e βω dω ] 2π E ω + iɛ η dω J(ω). E ω iɛ Utilizando novamente a Eq. 2.45, teremos: G C (E) = 1 [ ( ) ] 1 J(ω)e βω dω P iπδ(e ω) 2π E ω 1 [ ( ) ] 1 2π η J(ω)dω P + iπδ(e ω) E ω = 1 2π P J(ω)e βω dω E ω 1 2π iπ J(ω)e βω δ(e ω)dω 1 2π ηp dω J(ω) E ω 1 2π iπη J(ω)δ(E ω)dω = 1 2π P J(ω)e βω dω E ω η 2π P dω J(ω) E ω 1 2π iπj(e)eβe η 2π iπj(e) = 1 2π P J(ω)(e βω dω η) E ω i 2 J(E)eβE iη 2 J(E) = 1 2π P de modo que a parte imaginária de G C (E) será e sua parte real será dada por (e βω dω η)j(ω) E ω ij(e) (e β E + η), 2 Im[G C (E)] = 1 2 J(E)(eβE + η) Re[G C (E)] = 1 2π P (e βω dω η)j(ω) E ω = 1 π P [ 1 2 J(ω)(eβω + η)] (eβω η) dω (e βω + η) ω E = 1 π P (e βω η) Im[G C (ω)] dω, (2.58) (e βω + η) ω E que é a relação entre as partes real e imaginária da componente de Fourier G C (E). Pelas definições das funções de Green retardada, avançada e causal, podemos ver que elas dependem não apenas do tempo, mas também da temperatura. Quando a temperatura é diferente de zero os valores esperados do estado fundamental são substituídos pelas médias térmicas sobre um ensemble termodinâmico apropriado. As funções de Green que nos permitem calcular tais médias têm propriedades mais complicadas do
48 47 que as funções de green para temperatura zero, porém existe analogia entre elas. Vamos considerar a função de Green térmica, na qual a variável tempo é substituída pela variável temperatura. Esta tem uma teoria de pertubação análoga à função de Green vista anteriormente, e ela nos permite determinar as propriedades termodinâmicas de equilíbrio do sistema. Para discutir excitações e a resposta do sistema a uma perturbação externa precisamos de uma função de Green dependente do tempo a uma temperatura T. A relação entre os dois tipos de função de Green é discutida na referência [25]. Consideremos, por exemplo, a função de Green térmica G T (σ) = T [A(σ)B(0)] = θ(σ) A(σ)B(0) + θ( σ) B(0)A(σ), (2.59) onde σ é uma variável de temperatura. Pode-se mostrar que ([25]) a função de Green retardada G R (ω) pode ser obtida formalmente a partir de βg T (µ) pela substituição da variável imaginária iµ pela variável complexa ω + iɛ, onde 0 σ β.
49 48 3 IMPUREZA INTERSTICIAL LOCALIZADA NUM FERROMAGNETO DE REDE CÚBICA SIMPLES SEMI-INFINITA 3.1 Introdução Neste capítulo utilizaremos o modelo de Ising com campo transverso para descrever um ferromagneto de rede cúbica simples semi-infinita. Através do formalismo da função de Green, estudaremos os estados localizados associados a uma impureza acrescentada intersticialmente no sistema. Esta impureza se localizará em uma das faces da rede cúbica, paralela à superfície. Tal face pode está na n-ésima camada (n = 1, 2, 3 ) a partir da superfície. No estudo de excitações magnéticas, o modelo de Ising com campo transverso foi utilizado para descrever materiais magnéticos anisotrópicos reais quando imersos num campo magnético. Isso tem uma ampla aplicabilidade no formalismo da teoria de pseudospin para modelar transições de ordem-desordem em materiais ferroelétricos, como KH 2 PO 4, e alguns sistemas Jahn-Teller, tais como DyVO 4 e TbVO 4 [67]. Aliado à técnica das F.G., o modelo de Ising com campo transverso tem sido amplamente aplicado para estudar a propagação de ondas de spin em sistemas magnéticos. 3.2 Modelo e Formalismo da Função de Green O sistema sob estudo é um ferromagneto semi-infinito com uma superfície (001) e uma estrutura cúbica simples (constante de rede a). Qualquer sítio da rede tem um vetor posição r = (x, y, z) = a(l, m, n) com inteiros l, m, n, que assumem os valores < l <, < m <, 1 < n <. Assim, n = 1 denota a camada da superfície (vide Fig. 59). Uma impureza magnética intersticial isolada é introduzida no meio, à distância (N 1)a da superfície (onde N 1) (vide Fig. 60). O Hamiltoniano de Ising na presença de um campo aplicado, usado para descrever o sistema puro, é H 0 = 1 J ij Si z Sj z 2 i,j i h i S x i, (3.1) onde S x i e S z i são as componentes x e z do operador de spin no sítio i, tendo número quântico S = 1 em qualquer lugar. A dupla somatória é feita sobre os pares de sítios de 2 primeiros vizinhos. A interação de troca entre estes primeiros vizinhos J ij, para o material puro, assume o valor J S se ambos os spins estão na camada de superfície e J, se ambos estão dentro do volume. A troca entre a impureza e seus vizinhos é denotada por J se os vizinhos estão dentro do volume e J S, se eles estão na camada da superfície. O campo
50 49 Figura 4: Ferromagneto de rede cúbica simples semi-infinita. magnético transverso h i assume o valor h na impureza, h S, se o sítio está na camada de superfície e h se este sítio está na região de volume. Para obter a relação de dispersão para o sistema de Ising com uma impureza, primeiro avaliamos as funções de Green retardadas da forma S α l ; Sβ m ω, onde α e β são componentes cartesianas, e ω é um índice de frequência. Estas funções de Green devem satisfazer a equação geral de movimento (ver Eq. 2.37) ω S α l ; S β m ω = 1 2π [Sα l, S β m] + [S α l, H 0 ]; S β m ω (3.2) onde o comutador no último termo pode ser avaliado usando aproximação de desacoplamento RPA (Random Phase Approximation) em sua forma generalizada [11]-[52]. Essa aproximação consiste basicamente em desprezar as correlações entre as componentes transversais e longitudinais do operador de spin em pontos distintos da rede. Para o nosso caso
51 50 teremos: S γ i Sα l ; S β m ω = S γ i Sα l ; S β m ω + S α l S γ i ; Sβ m ω. (3.3) É conveniente reescrever o Hamiltoniano como H = H 0 + H, (3.4) onde H 0 é o hamiltoniano do modelo de Ising transverso para o sistema puro e H, é a perturbação devida a impureza intersticial. Para o sistema puro, uma transição de fase de segunda ordem é prevista, a uma temperatura T C que é dada por [11] ( ) h T C = tanh 2k B T C = h 3J. (3.5) Para o sistema com uma impureza pode ser (dependendo de h e J ) que a temperatura crítica T i C total em alguns casos seja maior que T C. Para T < T i C a orientação média de spin em cada sítio pode ter componentes nas direções x e z, enquanto que para T > TC i, ela se concentra ao longo da direção x. Neste trabalho nos concentramos no caso de T > TC i, por simplicidade. Calculemos agora as funções de Green para o sistema puro (isto é, avaliada usando H 0 ) na fase de alta temperatura. componentes de spin na direção z, a (3.2) nos fornece Como o Hamiltoniano de Ising envolve as ω S z l ; S z m ω = 1 2π [Sz l, S z m] + [S z l, H 0 ]; S z m ω. (3.6) Quaisquer que sejam l e m, o primeiro termo se anula na (3.6), pois [S z l, S z m] = 0. (3.7) Usando a (3.1), o comutador do segundo termo da (3.6) fica [Sl z, H 0 ] = 1 J ij (Sl z Si z Sj z Si z Sj z Sl z ) h i (Sl z Si x Si x Sl z ) 2 i,j i = 1 J ij (Sl z Si z Sj z Si z Sl z Sj z + Si z Sl z Sj z Si z Sj z Sl z ) 2 i,j i = 1 J ij ([Sl z, Si z ]Sj z + Si z [Sl z, Sj z ]) h i [Sl z, Si x ] 2 i,j i = i ih i S y l δ li, h i (S z l S x i S x i S z l ) ou [S z l, H 0 ] = ih l S y l, (3.8)
52 51 onde usamos o resultado [S z l, Sx i ] = i S y l δ il, com = 1. Assim a (3.6) torna-se, para i = l, ω S z l ; S z m ω = [S z l, H 0 ]; S z m ω = ih l S y l ; Sz m ω. (3.9) Assim, a evolução da F.G S z l ; Sz m forneceu outra F.G., S y l ; Sz m, cuja evolução temporal é dada por ω S y l ; Sz m ω = 1 2π [Sy l, Sz m] + [S y l, H 0]; S z m ω, (3.10) onde o comutador do segundo termo no segundo membro é dado por, usando a (3.1), [S y l, H 0] = S y l H 0 H 0 S y l = 1 J ij (S y l 2 Sz i Sj z Si z Sj z S y l ) h i (S y l Sx i Si x S y l ) i,j i = 1 J ij (S y l 2 Sz i Sj z Si z S y l Sz j + Si z S y l Sz j Si z Sj z S y l ) h i (Sl z Si x Si x Sl z ) i,j i = 1 J ij ([S y l 2, Sz i ]Sj z + Si z [S y l, Sz j ]) h i [S y l, Sx i ] i,j i = i J ij (Sl x Sj z δ li + Si z Sl x δ lj ) + i h i Sl z δ li 2 i,j i = i J lj Sl x Sj z i J li Si z Sl x + ih l Sl z. (3.11) 2 2 j i Levando este resultado à (3.10), obtemos a expressão ω S y l ; Sz m ω = i 2π Sx l δ lm + ih l Sl z ; Sm z ω i J lj Sl x Sj z ; S z 2 m ω i J li Si z Sl x ; S z 2 m ω. (3.12) j Para resolver esta equação deve-se escrever a equação de movimento para a função de ordem mais alta Sl xsz j ; Sm z ω e Si z Sl x; Sz m ω ). Esta por sua vez conterá uma função de Green de ordem mais alta e se obtem uma cadeia de equações de movimento. Para encontrar a função de interesse é necessário introduzir aproximações que desacoplam as equações. Aqui utilizaremos a aproximação RPA (Eq. 3.3) para desacoplá-la. Assim teremos, fazendo a troca j i (índices mudos), i S x l S z j ; S z m ω S x l S z j ; S z m ω + S z j S x l ; S z m ω = S x l S z j ; S z m ω (3.13)
53 52 e Si z Sl x ; Sm z ω Si z Sl x ; Sm z ω + Sl x Si z ; Sm z ω = Sl x Sj z ; Sm z ω, (3.14) pois o valor médio da componente em z do número quântico de spin se anula para este caso onde a temperatura é superior à temperatura crítica. Levando as (3.14)e (3.13) à (3.12), obtemos a expressão ω S y l ; Sz m ω = i 2π Sx l δ lm + ih l S z l ; S z m ω i j J lj S x l S z j ; S z m ω. (3.15) Voltemos agora à equação (3.9), ou seja, ω S z l ; S z m ω = ih l S y l ; Sz m ω, ou ω 2 S z l ; S z m ω = ih l ω S y l ; Sz m ω. (3.16) Substituindo esta equação (3.16) na (3.15), obtemos a expressão (ω 2 h 2 )G 0 lm(ω) = hrx l 2π δ lm hr x l onde h = h l, R x l = S x l, G0 lm (ω) = Sz l ; Sz m ω e G 0 jm(ω) = S z j ; S z m ω. J lj G 0 lm(ω), (3.17) Vamos considerar, agora, que os spins estão arranjados numa rede cúbica simples semi-infinita (com espaçamento a) e onde os eixos coordenados x, y e z são paralelos as arestas do cubo. Usemos a propriedade da invariância translacional paralela à superfície para escrever as funções de Green G 0 lm(ω) = 1 N j q G 0 q (ω)e iq (R R ), (3.18) G 0 q (ω) = G 0 lm(ω)e iq (R R ), (3.19) R R onde N é o número total de sítios em cada camada, r l = (R, z), r m = (R, z ), com R e R denotando vetores bidimensionais no plano xy, e q = (q x, q y ) é um vetor de onda bidimensional. Os índices das camadas são denotados por n e n (iguais a 1, 2, 3, ), definidos por z = (n 1)a e z = (n 1)a, onde a e o parâmetro de rede.
54 53 É conveniente definir as seguintes somas para as interações de troca: ν (1) n (q ) = δ 1 J lj e iq δ 1 (3.20) e ν (2) n (q ) = δ 2 J lj e iq δ 2, (3.21) onde δ 1 é um vetor conectando qualquer sítio l na camada n com seus primeiros vizinhos, também na camada n, enquanto δ 2 é um vetor conectando qualquer sítio l na camada n com seus primeiros vizinhos nas camadas adjacentes. As séries de equações da função de Green representadas pela (3.17) podem agora ser expressas na forma matricial como AG 0 n,n = δ nn 2πJ, (3.22) onde, no caso de um meio semi-infinito, A e G 0 são matrizes de dimensão infinita, dadas por [11] com e G 0 nn (q, ω) = G 0 nn = G 0 nn (q, ω), (3.23) ( 1 X n n 1 + ) X 1 2πJ(X X 1 ) 1 + X Xn+n d d d 1 0 A = d d (3.24) onde n e n são índices de camada (n, n = 1, 2, 3, ) para sítios r l e r m, e X é uma variável complexa (com X 1) satisfazendo X + X 1 = d = h2 4hJR x γ 2 (q ) ω 2 hjr x, (3.25) com γ 2 (q ) = 1 2 [cos(q xa) + cos(q y a]. (3.26) O parâmetro depende das propriedades da superfície e é dado por = ω2 (h S RS x hrx ) hh S (hrs x h ( ) SR x ) JS 4γ hh S R x RS x 2 (q ) J 1. (3.27) Usamos a notação R x l = Sl x que pode tomar dois valores possíveis para
55 54 o sistema puro: R x l = 1 2 tanh(h S/2k B T ) = R x S R x l = 1 2 tanh(h/2k BT ) = R x, quando o sítio l não está na superfície. quando o sítio l está na superfície ou As funções de Green G 0 nn (q, ω), dadas pela Eq. 3.24, contém uma descrição para os modos de volume e de superfície, juntamente com seus fatores apropriados esperados. De acordo com [11], os modos de volume podem ser obtidos fazendo-se X = e iqza, onde q z é uma componente real do vetor de onda, perpendicular à superfície. Da Eq obtemos a seguinte relação de dispersão para as ondas de spin de volume ω = [h 2 4hR x Jγ(q ) (X + X 1 )hr x J] 1/2. (3.28) Inserindo X = e iqza na equação acima teremos ω B (q ) = {h 2 2hR x J[cos(q x a) + cos(q y a) + cos(q z a)]} 1/2, (3.29) onde q = (q, q z ) é um vetor de onda tridimensional. Esta expressão é reconhecida como um resultado padrão para a relação de dispersão dos modos de volume quando T > T C, num sistema infinito representado por uma rede cúbica simples, descrito pelo Modelo de Ising com Campo Transverso. Vemos, portanto, que a equação de dispersão depende da direção do vetor de onda q, mesmo para um cristal de alta simetria. Os modos de superfície correspondem ao caso no qual X = 1/ na Eq. 3.28, o que nos leva a ω = [h 2 4hR x Jγ(q) ( + 1 )hr x J] 1/2, (3.30) onde é uma função de ω, conforme Eq Dependendo dos parâmetros, os modos de superfície podem ocorrer acima ou abaixo dos limites da banda de volume. São conhecidos como modos ópticos ou acústicos, respectivamente. Por exemplo, no caso especial em que h S = h, o parâmetro de superfície é simplificado a = 4σγ(q ), (3.31) portanto, independente de ω, onde denotamos σ = J S /J 1. Segue então que a relação de dispersão para ondas de spin de superfície corresponde a ω = ω S (q ), onde ω S (q ) = h 2 hr x J[4(1 + σ)γ(q ) + (4σγ(q )) 1 ] 1/2. (3.32) A frequência dos modos de superfície e de volume foi amplamente discutida por Shiwai e Cottam [11]. Consideremos agora o sistema impuro, contendo uma impureza intersticial, que pode ocupar qualquer posição dentro de uma das faces da rede cúbica simples, paralela à superfície (vide Fig.60). Para a perturbação H devida à impureza, há dois casos diferentes
56 55 a considerar. Primeiro quando a impureza está na região de volume (com índice de camada N 2), H é dado simplesmente por Figura 5: Ferromagneto de rede cúbica simples semi-infinita contendo uma impureza intersticial na camada n = 1, por exemplo. H = d J ods z ds z z h S x o, (3.33) onde a soma é feita sobre os quatro primeiros vizinhos da impureza, ou seja, os sítios ocupando os vértices da face onde esta impureza está localizada. Se a impureza está na superfície, o Hamiltoniano será dado por H = d J Sod S z ds z z h S x o. (3.34) A impureza também tem quatro primeiros vizinhos: todos eles (d) na camada de superfície.
57 56 Usando as equações (3.1), (3.2), (3.4), obtemos a expressão: ω Sl z ; Sm z ω = [Sl z, H 0 ]; Sm z z + [Sl z, H ]; Sm z z, (3.35) onde H é dado pela (3.33). O comutador do primeiro termo no segundo membro da (3.35) já foi calculado anteriormente e é dado pela (3.11). Para o comutador do segundo termo, temos: [S z l, H ] = d J od(s z l S z ds z 0 S z ds z 0S z l ) h (S z l S x o S x o S z l ) = h [S z l, S x o ], ou [S z l, H ] = ih S y l δ lo. (3.36) Substituindo as (3.8) e (3.36) na (3.35), obtemos a expressão ω S z l ; S z m ω = ih S y l ; Sz m ω ih S y l ; Sz m ω δ l0 = i(h + h δ l0 ) S y l ; Sz m ω. (3.37) Vemos que a evolução temporal da F.G. S z l ; Sz m ω deu origem a outra F.G., S y l ; Sz m ω, cuja evolução temporal é dada por: ou onde ω S y l ; Sz m ω = 1 2π [Sy l, Sz m] + [S y l, H]; Sz m ω, ω S y l ; Sz m ω = i 2π Sx l + [S y l, H 0]; S z m ω + [S y l, H ]; S z m ω, (3.38) [S y l, H 0] = 1 J ij (S y l 2 Sz i Sj z Si z Sj z S y l ) h i (S y l Sx i Si x S y l ) i,j i = 1 J ij (S y l 2 Sz i Sj z Si z S y l Sz j + Si z S y l Sz j Si z Sj z S y l ) i,j i = 1 J ij ([S y l 2, Sz i ]Sj z + Si z [S y l, Sz j ]) h i [S y l, Sx i ] i,j i = 1 J ij (isl x Sj z δ li + isi z Sl x δ lj ) + i h i Sl z δ li, 2 i,j i ou h i (S y l Sx i S x i S y l ) [S y l, H 0] = i J lj Sl x Sj z i J li Si z Sl x + ihsl z. (3.39) 2 2 j i
58 57 E [S y l, H ] = d J od(s y l Sz ds z o S z ds z os y l ) h (S y l Sx o S x o S y l ) = d J od(s y l Sz ds z o S z os y l Sz d + S z os y l Sz d S z os z ds y l ) h(sy l Sx o S x o S y l ) = d J od([s y l, Sz d]s z o + S z d[s y l, Sz o]) h [S y l, Sx o ], ou [S y l, H ] = i d J od(s x l S z oδ ld + S z ds x l δ lo ) + ih S z l δ lo. (3.40) Substituindo as (3.40) e (3.39) na (3.38), obtemos: ω S y l ; Sz m ω = i 2π Sx l δ lm i J lj Sl x Sj z ; S 2 m z ω j i J li Si z Sl x ; S 2 m z ω i J od S l x So; z Sm z ω δ ld i d i d J od S z ds x l ; S z m ω δ lo + ih S z l ; S z m ω δ lo. (3.41) Novamente, usemos a aproximação RPA para desacoplar as funções de Green, ou seja, S x l S z j ; S z m ω = S x l S z j ; S z m ω + S z j S x l ; S z m ω = S x l S z j ; S z m ω (3.42) S z i S x l ; S z m ω = S z i S x l ; S z m ω + S x l S z i ; S z m ω = S x l S z i ; S z m ω (3.43) S x l S z o; S z m ω = S x l S z o; S z m ω + S z o S x l ; S z m ω = S x l S z o; S z m ω (3.44) S z ds x l ; S z m ω = S z d S x l ; S z m ω + S x l S z d; S z m ω = S x l S z d; S z m ω, (3.45) onde S z i = 0 (a orientação média da componente de spin na direção z é nula) e trocamos
59 58 i por j na (3.42). Assim a (3.41) torna-se: ω S y l ; Sz m ω = i 2π Sx l δ lm i J lj Rl x Sj z ; Sm z ω j J od( S o; z Sm z ω δ ld + Sd; z Sm z ω δ lo ir x l d + ih S z l ; S z m ω δ lo. (3.46) Substituindo este resultado na (3.37), obtemos a expressão ω 2 (h + h δ lo )h δ l0 G h + h lm (ω) = 1 δ lo 2π Sx l δ lm + J lj Rl x G jm (ω) j + Rl x J od(g om (ω)δ ld d + G dm (ω)δ lo ). (3.47) A Eq possui funções de Green que estão acopladas em sítio diferentes na rede. Como não há mais simetria de translação, estas funções não podem mais ser desacopladas através da introdução da transformada de Fourier das funções de Green no espaço. Porém, a Eq. (3.47) pode ser escrita em forma matricial (ver Apêndice A), ou seja, [(G 0 ) 1 V]G = I. (3.48) A vantagem de usar funções de Green é agora evidente, pois a Eq tem a forma de uma equação de Dyson, que pode ser resolvida com métodos similares àqueles usados em problemas de física quântica. Uma análise mais detalhada desta equação tão importante pode ser encontrada na referência [52]. Na Eq. 3.48, G 0 (2π/R x l )G0 lm (ω) e G (2π/Rx l )G lm(ω) são as matrizes função de Green para os sistemas puro e impuro, respectivamente. V é um potencial efetivo relacionado à perturbação H produzida pela impureza. Seus elementos de matriz são são dados por V lj = ω2 (h + h 1) + h (h + h) δ h(h l0 δ lj Rl x + h) J od(δ l0 δ jd + δ j0 δ ld ). (3.49) Para o caso em que a impureza está na superfície, os elementos da matriz V V Slj = ω2 (h + h S 1) + h (h + h S ) δ h S (h lo δ lj Rl x + h S ) d J S od (δ lo δ jd + δ jo δ ld ). (3.50) d
60 Os modos de Impureza Por causa da presença da impureza isolada a simetria translacional não existe mais em nenhuma dimensão. Não é mais possível introduzir um vetor de onda bidimensional paralelo à superfície como no caso do ferromagneto semi-infinito puro. Em vez disso trabalhamos com o espaço real para resolver a equação (3.48) usando as expressões para G 0 e V apropriadas para um sistema semi-infinito. Uma submatriz 5 5 é a única parte diferente de zero da matriz potencial: isto corresponde a impureza numa dada posição o, dentro de uma face paralela à superfície da rede cúbica simples semiinfinita, e seus quatro vizinhos, ocupando os vértices desta face. A equação de Dyson (3.48) relaciona a matriz função de Green G para o sistema impuro à correspondente função de Green G 0 para o sistema puro. As enegias de excitação associadas com o a impureza intersticial são dadas pela condição det[i G 0 V] = 0, (3.51) que representa os polos de G para o sistema impuro. Consideremos, então, a impureza e seus quatro primeiros vizinhos, localizados numa face paralela ao plano xy (n = n ), de modo que a impureza pode ocupar todas as possíveis posições dentro desta face. Admitimos que os eixos coordenados são paralelos às arestas da face e que a origem está no centro da face. Por simetria, vemos que as funções de Green se repetem em cada região (A, B, C, D, E, F, G e H), conforme Fig. 61. Assim, basta considerar a impureza ocupando todas as posições possíveis dentro de uma das regiões (A, por exemplo). A impureza ocupará as posições dadas por r o = kai + paj, onde 0 k < 0, 5, 0 p < 0, 5 e k p. Desta forma o deslocamento relativo entre a impureza e um dos quatro primeiros vizinhos é r o,j = r o r j, e entre vizinhos, é r l,j = r l r j, cujos módulos são d oj = r o r j e d lj = r l r j, respectivamente, com j, l = 1, 2, 3, 4. Quando a impureza se encontra no centro da face, estará a igual distância dos
61 60 Figura 6: A impureza pode ocupar qualquer posição dentro da região A. quatro primeiros vizinhos, tal distância é dada por d = 2 a. (3.52) 2 Para este caso, a interação de troca entre a impureza e cada um de seus quatro primeiros vizinhos assume o valor J. Para uma outra posição qualquer da impureza dentro da face, sua interação de troca com cada vizinho depende da distância entre ela e este vizinho. Vamos considerar que esta interação depende da distância da seguinte forma J oj = d oi d J. (3.53) Assim a interação entre a impureza e os sítios dependem dos parâmentros (p e k) que determinam as posições da impureza dentro da face, ou seja, J o1 = J 1o = d o1 d J = a (0, 5 k)2 + (0, 5 p) 2 2 a J 2 = 2 (0, 5 k) 2 + (0, 5 p) 2 J, (3.54) J o2 = J 2o = d o2 d J = a (0, 5 + k)2 + (0, 5 p) 2 2 a J 2 = 2 (0, 5 + k) 2 + (0, 5 p) 2 J, (3.55)
62 61 J o3 = J 3o = d o3 d J = a (0, 5 k)2 + (0, 5 + p) 2 2 a J 2 = 2 (0, 5 k) 2 + (0, 5 + p) 2 J, (3.56) (3.51), ou seja, J o4 = J 4o = d o4 d J = a (0, 5 + k)2 + (0, 5 + p) 2 2 a J 2 = 2 (0, 5 + k) 2 + (0, 5 + p) 2 J (3.57) Assim os modos de defeito associados com a ipureza são obtidos pela condição [(G 2 o4 G 2 oo)v o4 + (G o3 G o4 G o G 34 )V o3 + (G o2 G o4 G oo G 24 )V o2 + (G o1 G o4 G oo G 14 )V o1 G o4 ]V 4o + [(G o3 G o4 G oo G 34 )V o4 + (G 2 o3 G 2 oo)v o3 + (G o2 G o3 G oo G 23 )V o2 + (G o1 G o3 G oo G 13 )V o1 G o3 ]V 3o + [(G o2 G o4 G oo G 24 )V o4 + (G o2 G o3 G oo G 23 )V o3 + (G 2 o2 G 2 oo)v o2 + (G o1 G o2 G oo G 12 )V o1 G o2 ]V 2o + [(G o1 G o4 G oo G 14 )V o4 + (G o1 G o3 G oo G 13 )V o3 + (G o1 G o2 G oo G 12 )V o2 para N 2 e + G o1 ]V 1o G o4 V o4 G o3 V o3 G o2 V o2 G o1 V o1 G oo V oo + 1 = det[i G 0 V] = 0, (3.58) [(G 2 o4 G 2 oo)v So4 + (G o3 G o4 G o G 34 )V So3 + (G o2 G o4 G oo G 24 )V So2 + (G o1 G o4 G oo G 14 )V So1 G o4 ]V S4o + [(G o3 G o4 G oo G 34 )V So4 + (G 2 o3 G 2 oo)v So3 + (G o2 G o3 G oo G 23 )V So2 + (G o1 G o3 G oo G 13 )V So1 G o3 ]V S3o + [(G o2 G o4 G oo G 24 )V So4 + (G o2 G o3 G oo G 23 )V So3 + (G 2 o2 G 2 oo)v So2 + (G o1 G o2 G oo G 12 )V So1 G o2 ]V S2o + [(G o1 G o4 G oo G 14 )V So4 + (G o1 G o3 G oo G 13 )V So3 + (G o1 G o2 G oo G 12 )V So2 + (G 2 o1 G 2 oo)v So1 G o1 ]V S1o G o4 V So4 G o3 V So3 G o2 V So2 G o1 V So1 G oo V Soo + 1 = det[i G 0 V] = 0, (3.59) para N = 1. As funções G lm = (2π/R x l )G0 l,m (ω), com l e m inteiros assumindo valores de 0 a 4, são os elementos da matriz função de Green G 0 para o sistema puro, sendo obtidos
63 62 pela Os elementos V lj da matriz V são dados por: V oo = ω2 (h + h 1) + h (h + h), (3.60) h(h + h) V o1 = V oo J o1r x o, (3.61) V o2 = V oo J o2r x o, (3.62) V o3 = V oo J o3r x o, (3.63) V o4 = V oo J o4r x o, (3.64) V 1o = V oo J 1oR x 1, (3.65) V 2o = V oo J 2oR x 2, (3.66) V 3o = V oo J 3oR x 3, (3.67) e V 4o = V oo J 4oR x 4 (3.68) V Soo = ω2 (h S + h 1) + h (h + h S ), (3.69) h S (h + h S ) V So1 = V Soo J S o1 R x o, (3.70) V So2 = V Soo J S o2 R x o, (3.71) V So3 = V Soo J S o3 R x o, (3.72) V So4 = V Soo J S o4 R x o, (3.73)
64 63 V S2o = V Soo J S 2o R x o, (3.74) V S3o = V Soo J S 3o R x o, (3.75) V S4o = V Soo J S 4o Ro, x (3.76) com os J oi (J io) dadas pelas ( ). 3.4 Resultados Numéricos É frequentemente útil distinguir entre os modos de ondas de spin se propagando e os modos de ondas de spin localizados. Os primeiros se referem a modos de volume (ou bulk ), e os segundos se referem a modos de superfície e de defeito (associados com a impurezas). Quando os modos de impureza estão fora da banda de volume do material puro, eles são conhecidos como modos não-ressonantes ou modos de defeito. Os modos de impureza dentro da banda de volume são conhecidos como modos ressonantes. Nesta seção, serão discutidos apenas os modos de defeitos. Os modos ressonantes são, experimentalmente, mais difíceis de serem detectados [8] e serão discutidos na próxima seção. No caso de um sistema semi-infinito, pode haver ondas de spin de superfície localizadas, associadas com o material puro [10, 11] e essas podem influenciar os modos de defeito (por analogia com estudos para sistemas magnéticos de Heisenberg [3, 4, 5]). Este efeito deveria ser particularmente evidente quando a impureza está na superfície (N = 1), onde as ondas de spin de superfície tem sua maior amplitude. Agora apresentamos resultados numéricos quando a impureza está localizada na superfície (N = 1) e na região de volume (N = 10). Especificamente, assumimos uma razão fixa J/h = 1, 0 para o material puro e uma temperatura T correspondendo a k B T/h = 2, 5. A temperatura crítica correspondente no material puro satisfaz k B T C /h = 0, 65 para esta escolha de parâmetros. Em todos os casos, plotamos apenas os modos de defeito que estão abaixo da banda de volume do material puro. O limite inferior da banda de volume ocorre em ω/j = 0, 63, a qual está indicada por uma linha horizontal em cada gráfico. Nas Figs. 62 e 63 mostramos resultados para a dependência das frequências dos modos de impureza, em gráficos da quantidade adimensional ω/j versus as razões J /J e h /h, respectivamente, quando a impureza está na camada N = 10. Tomamos h S = h e J S = J, por simplicidade, o que significa que não haverá ondas de spin de superfície
65 64 0,8 0,6 ω/j 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 h /h Figura 7: Frequências dos modos de defeito versus campo aplicado (h /h), no caso de N = 10, para diferentes valores de (p; k): (0,3;0,0) para a linha contínua, (0,3;0,3) para a linha pontilhada, (0,49;0) para a linha tracejada e (0,49;0,49) para a linha traço-pontilhada. Assumimos que J S /J = 1, 0. 0,8 0,6 ω/j 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 J /J Figura 8: Frequências dos modos de defeitos versus interação de troca (J /J), no caso de N = 10, para diferentes valores de (p; k): (0,3;0) para a linha contínua, (0,3;0,3) para a linha pontilhada, (0,49;0) para a linha tracejada e (0,49;0,49) para a linha traço-pontilhada. Assumimos que J S /J = 1, 0, h /h = 1, 5. localizadas para o material puro [10, 11] neste caso. A Fig. 62 mostra um gráfico de ω/j versus h /h para um valor fixo J /J = 1, 5 e a Fig. 63, mostra um gráfico de ω/j versus J /J para um valor fixo h /h = 1, 5. Para ambos os casos, nós consideramos alguns valores de p e k. Estes resultados indicam que ω/j é sensível a mudanças em ambos p and k. Pode ser visto, a partir desses gráficos de ω/j versus h /h e de ω/j versus J /J, que quando os valores de p e k aumentam, as curvas são deslocadas e têm uma mudança na inclinação. Isto se dá devido à dependência da interação de troca na distância entre a impureza e seus vizinhos. A Fig. 64 mostra um gráfico de ω/j versus J /J para alguns valores de h /h (tomando N = 10 e os valores fixos p = 0, 49 e k = 0, 49), enquanto o caso inverso (ω/j
66 65 0,8 0,6 ω/j 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 J /J Figura 9: Frequências dos modos de defeito versus interação de troca no caso de N = 10 para diferentes valores de h /h: h /h = 1, 5 para a linha tracejada, h /h = 1, 8 para a linha pontilhada e h /h = 2, 0 para a linha contínua. Assumimos um valor fixo para p e k: (p, k) = (0, 3; 0, 3). 0,8 0,6 ω/j 0,4 0,2 0,0 0,0 1,0 2,0 3,0 h /h Figura 10: Frequências dos modos de defeito versus campo aplicado no caso de N = 10 para diferentes valores de J /J: J /J = 1, 5 para a linha contínua, J /J = 1, 8 para a linha pontilhada e J /J = 2, 0 para a linha tracejada. Assumimos um valor fixo para p e k: (p, k) = (0, 49; 0, 49). versus h /h) é mostrado na Fig. 65. Estes resultados indicam que ω/j é também sensível a mudanças em ambos h /h e J /J. Alguns resultados análogos para o caso de uma impureza na camada N = 1 são mostrados na Fig. 66, tomando outros parâmetros como antes. Pode ser visto a partir deste gráfico de ω/j versus J /J que, comparado com a Fig. 64, algumas curvas são deslocadas e têm uma mudança na inclinação. Isto se deve ao fato de que a impureza e seus primeiros vizinhos agora estão na superfície, onde suas propriedades são perturbadas. Finalmente, na Fig.67, ilustramos a dependência dos resultados no parâmetro de troca na superfície J S para o meio semi-infinito. Especificamente, plotamos ω/j versus J /J (tomando N = 1 e os valores fixos h /h = 2, 0, k = 0, 49 e p = 0, 49).
67 66 0,8 0,6 ω/j 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 J /J Figura 11: Frequências dos modos de defeito versus interação de troca no caso de N = 1 para diferentes valores de h /h: h /h = 1, 5 para a linha tracejada, h /h = 1, 8 para a linha pontilhada e h /h = 2, 0 para a linha contínua. Assumimos um valor fixo para p e k: (p, k) = (0, 3; 0, 3). Resulatdos são mostrados para alguns valores de J S /J. Quando a razão excede 1, 25, há modos de superfície acústicos (banda de ondas de spin de superfície do material puro abaixo do mínimo da banda de volume [10, 11]). Consequentemente, os modos de defeito nesta região podem decair em um modo de superfície com mesma frequência, e os modos de defeito não são mais excitações bem definidas. Isto explica porque as curvas na Fig. 67 terminam em um valor de ω/j abaixo de 0, 63 quando J S /J aumenta. Em contraste, encontramos que este efeito não ocorre quando J S /J 0, 75. Isto ocorre porque os modos de superfícies ópticos (que podem ocorrer se J S /J 0.75) ocorrem em frequências acima da banda de volume [10, 11], e assim não se torna degenerado com os modos de impureza estudados aqui. 0,8 0,6 ω/j 0,4 0,2 0,0 1,0 2,0 3,0 4,0 5,0 J /J Figura 12: Frequências dos modos de defeito versus interação de troca para h /h = 1, 0 no caso de N = 1 e para diferentes valores de J S /J: J S /J = 1, 0 para a linha contínua, J S /J = 1, 3 para a linha pontilhada e J S /J = 1, 35 para a linha tracejada.
68 Modos Ressonantes Se a energia ω do estado considerado estiver dentro da banda de onda de spin, os elementos de matriz G 0 i,j(ω) são complexos [2]. Não é geralmente possível satisfazer as Eqs e 3.59 para ω real; porém, esta equação pode ser satisfeita pelas partes reais das funções de Green. Então, um estado virtual ou ressonante deve existir quando a parte real do determinante secular se anula. Na Fig. 68 mostramos os modos associados à impureza para um grande intervalo de energias, tomando o caso em que N = 1, com os seguintes parâmetros: h /h = 1, 5, h S /h = J S /J = 1, 0 e (p; k) = (0, 49; 0, 49). Neste caso, não há modos de defeitos acima do topo da banda de volume, a qual corresponde a ω/j 1, 26. Porém, dentro desta banda (0, 63 ω 1, 26), deve existir modos ressonantes associados com a impureza, dependendo do valor de J /J. Em seguida consideramos casos onde a impureza está na superfície e o valor de J S /J é tal que modos de superfície de onda spin estão presentes no espectro do ferromagneto puro. Na Fig. 69, mostramos um exemplo numérico para o caso de J S /J < 0, 75 quando um modo óptico está presente (ramificado para fora, a partir da borda mais alta da banda de volume.) Comparado com a Fig. 68, a curva é deslocada para a esquerda. Este resultado pode ser facilmente compreendido como segue: quando a interação de troca entre os spins na superfície é reduzida, o acoplamente do spin da impureza com seus vizinhos e, então, com o resto do sistema, também é reduzido. É então fácil excitar qualquer modo associado com a impureza comparado com o caso quando ela está fortemente acoplada a todo o sistema. Por outro lado, quando J S > 1, 25J, há um modo de superfície acústico, que se ramifica para fora, a partir da borda mais baixa da banda de energia do material puro. A energia mínima deste ramo acústico está na zona limite do vetor de onda q = (0, 0), e é dada por [11] (vide Eq. 3.31) ω ac min = {h 2 hjr x [4J S /J + (4(J S /J 1)) 1 ]} 1/2. (3.77) Na Fig. 70 mostramos um exemplo com J S /J = 1, 251. É visto que o modo de impureza é dramaticamente perturbado pela presença do modo acústico de superfície. Primeiro, a curva é deslocada para a direita comparada com Fig. 68, segundo, torções são produzidas na curva próximo à energia mínima ω ac min do modo acústico de superfície.
69 68 1,0 0,8 ω/j 0,6 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 6,0 J /J Figura 13: Modos associados com uma impureza intersticial na camada da superfície (N = 1). Gráfico da frequência ω (energia) versus interação de troca J, mostrando ambos os modos de defeito e os modos ressonantes. O limite inferior da banda de volume está indicada por uma linha horizontal em ω/j 0, 63, e o limite superior está também indicada por uma linha horizontal, mas em ω/j 1, 26. 1,0 0,8 ω/j 0,6 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 6,0 J /J Figura 14: Modos de impureza mostrados próximos do limite inferior da banda de volume da onda de spin na presença de um modo de superfície (considerando J S /J = 0, 74), assumindo que a impureza está na camada da superfície (N = 1).
70 69 1,0 0,8 ω/j 0,6 0,4 0,2 0,0 0,0 1,0 2,0 3,0 4,0 5,0 6,0 J /J Figura 15: Modos de impureza mostrados próximos do limite inferior da banda de volume da onda de spin na presença de um modo de superfície acústico (tomando J S /J = 1, 251), assumindo que a impureza está na camada da superfície (N = 1).
71 70 4 IMPUREZA INTERSTICIAL NUM FERROMAGNETO DE REDE QUADRADA INFINITA 4.1 Introdução Neste capítulo (e nos capítulos 5 e 7) estudaremos os estados localizados de ondas de spin, associados a uma impureza intersticial isolada, em sistemas magnéticos bidimensionais. Ondas de spin em sistemas magnéticos 2D são muito interessantes, tanto experimentalmente [87]-[91] como teoricamente [92]-[98]. Por exemplo, estes sistemas são relevantes para a compreensão de supercondutores de alta temperatura [99]-[105], e são a base de muitas aplicações tecnológicas de filmes ferromagnéticos ultrafinos (exemplo, memória magnética, interruptores, magnetorresistência gigante, etc). Em adição, ondas de spin 2D são importantes nos novos campos promissores de spintrônicas. Nos anos recentes, estruturas magnéticas ultrafinas têm sido fabricadas e estudadas extensivamente, por meio da dinâmica de ondas de spin. Tais estruturas podem ter a presença de superfícies, de camadas de impurezas, impurezas localizadas, ou mesmo uma baixa concentração delas. Tudo isso modifica o espectro de excitações desse meio, assim é útil distinguir modos de ondas de spin que se propagam e modos de ondas de spin localizados. Na geometria de um filme, estes modos usualmente se referem a modos de volume (ou bulk) e modos de superfícies e/ou de defeito. Assim, novos estudos teóricos são necessários onde a presença de superfícies e de impurezas são importantes e onde os modos de ondas de spin localizados são considerados em detalhes. Aqui, investigaremos os modos localizados de ondas de spin associados com uma impureza intersticial magnética isolada, em uma rede quadrada simples. Para isto, consideramos o modelo de Heisenberg/Ising, onde podemos passar do modelo de Heisenberg para o de Ising variando um parâmetro explícito λ. Para λ = 1, temos um ferromagneto de Heisenberg e para λ = 0, o ferromagneto de Ising. Este Hamiltoniano abre a possibilidade para uma variedade de espectro de energia de acordo com os valores de λ. Usando a técnica de funções de Green [30], encontramos os modos localizados s, p e d, associados ao sistema impuro. Obtemos resultados numéricos para os modos de defeito localizados como função do parâmetro de troca entre a impureza e sítios vizinhos, assim como o campo aplicado na impureza e o parâmetro λ.
72 Modelo e Formalismo da função de Green O sistema em estudo é uma rede quadrada simples que se estende ao longo do plano xy, onde uma impureza intersticial, que interage ferromagneticamente com seus primeiros vizinhos, é acrescentada. O hamiltoniano usado para descrever o sistema puro (vide Fig.16) pode ser escrito como Figura 16: Ferromagneto de rede quadrada infinita. H = 1 [λ(si x Sj x + S y i 2 Sy j ) + Sz i Sj z ] i,j i h i S z i (4.1) onde Si x, S y i e Si z são as componentes x, y e z, respectivamente, do operador de spin no sítio i, tendo número quântico S em qualquer lugar, exceto na impureza, onde o número quântico spin é denotado por S. A interação de troca entre primeiros vizinhos J ij, para o material puro, assume o valor J. A interação de troca entre a impureza e seus vizinhos é denotada por J. O campo magnético externo é h i = gµ B B 0 = h, exceto na impureza, onde h i = g µ B B 0 = h, com g g. Por conveniência, para descrever o sistema impuro (vide Fig. 17), reescrevemos o Hamiltoniano como H = H 0 + H, onde H 0 é o Hamiltoniano para o sistema puro e H é a perturbação devida à impureza, sendo dado por
73 72 Figura 17: Ferromagneto de rede quadrada infinita contendo uma impureza intersticial. H = J d [λ(s x o S x d + S y o S y d ) + Sz os z d] h S z o, (4.2) onde o índice o rotula a impureza e o índice d, os primeiros vizinhos da impureza. O comutador de dois operadores de spin é um outro operador, e não um simples número complexo. Assim fica muito mais complicado trabalhar diretamente com operadores de spin do que com operadores canônicos bosônicos (fermiônicos) de criação e aniquilação, cujos comutadores (anticomutadores) são simples números complexos. Seria então vantajoso se se pudesse representar os operadores de spin em termos de tais operadores bosônicos ou fermiônicos e trabalhar com estes, ao invés daqueles. Poucas representações são conhecidas. Aqui faremos uso da chamada representação de Holstein- Primakoff (HP) [107]. A transformação Holstein-Primakoff consiste basicamente em obter o Hamiltoniana do sistema na forma diagonal, em função dos operados de criação e aniquilação b i e b i, respectivamente. O operador para o número de desvios do spin no sítio i é n i = S Si z, onde S e S i são o número quântico de spin e sua componente em z. O operador de
74 73 criação de desvio de spin b i é o operador que cria um quantum de desvio de spin, isto é, que reduz Si z de uma unidade. Analogamente o operador de aniquilação de desvio de spin b i aumenta S z i S i de uma unidade. É possível obter relações entre os operadores de escada (S + i = S x i + is y i e = S x i is y i ) e os operadores de criação e aniquilação (b i e b i) [107], estas relações são: S + i = (2S) 1/2 ( 1 b i b i 2S ) 1/2 b i, e S i = (2S) 1/2 b i ( 1 b i b i 2S S z i = S b i b i = S n i ) 1/2 Podemos também expressar as componente x e y do número quântico de spin S em termos dos operadores de escada, ou seja, S x i = 1 2 (S+ i + S i ) (4.3) e S y i = 1 2i (S+ i S i ), (4.4) e, desta forma, escrever o Hamiltoniano em termos estes operadores, ou seja, H = 1 [ ] λ J ij 2 4 (2S+ i S j + 2S i S+ j ) + Sz i Sj z h i Si z ij i = 1 [ J ij λ(s + i 4 S j + S i S+ j ) + ] 2Sz i Sj z h i Si z. (4.5) ij Em temperaturas muito baixas (k B T JS), a aproximação de ondas de spin linearizada pode ser usada para dar S + i = (2S b i b i) 1/2 b i (2S) 1/2 b i, (4.6) i S i = b i (2S b i b i) 1/2 (2S) 1/2 b i, (4.7) S z i = S b i b i. (4.8) Esta aproximação é válida somente se n i /2S 1, isto é, se o valor esperado do número de desvios no spin S i é muito menor do que o valor máximo possível, que é 2S.
75 74 Pela substituição das (4.6), (4.7) e (4.8) na (4.5), obtemos o Hamiltoniano de termos linearizados ( H = S J ij [λ(b i b j 2 + b i b j) b i b i b j b j] + ) h i b i b i i,j i ( + 1 J ij S 2 ) Sh i 2 ij i = H 0 + E 0, (4.9) onde E 0 = 1 J ij S 2 Sh i 2 ij i é a energia do estado fundamental para o sistema ferromagnético e H 0 = [( S ) ] J i,j + h i b i b i S λj i,j b i b j, (4.10) i j i,j é o Hamiltoniano que descreve este sistema. Para o Hamiltoniano devido à impureza, consideramos que S + o = (2S b ob o ) 1/2 (2S ) 1/2 b o, (4.11) S + d = (2S b d b d) 1/2 (2S) 1/2 b d, (4.12) S o = b o(2s b ob o ) 1/2 (2S ) 1/2 b o, (4.13) S d = b d (2S b d b d) 1/2 (2S) 1/2 b d, (4.14) S z o = S b ob o. (4.15) Assim a (4.2) nos fornece: S z d = S b d b d. (4.16) H = JS d [λα(b o b d + b ob d ) βb ob o γb d b d] + h b ob o, (4.17)
76 75 onde definimos as seguintes quantidades α = J S J S, β = J J, γ = J S JS (4.18) Agora, consideremos a função de Green retardada, definida em termos dos operadores dependentes do tempo b l (t) e b m(t ), na representação de Heisenberg, e que satisfaz a equação de movimento ω b l ; b m ω = 1 2π [b l, b m] + [b l, H]; b m ω, (4.19) onde ω é um índice de frequência e H, é o Hamiltoniano do sistema. Substituindo a (4.10) na (4.19) obtemos (vide Apêndice B ): ω b l ; b m ω = 1 2π [b l, b m] [ + i i ( (S j S j J ij + h i ) b i ; b m ω δ li ] J ij + h i ) b j ; b m ω δ li, ou seja, ( ωg 0 lm(ω) = 1 2π δ lm + s j J lj + h ) G 0 lm S j λj lj G 0 jm, (4.20) onde G 0 lm (ω) = b l; b m ω e G 0 jm(ω) = b j ; b m ω Considerando a simetria de translação, introduzamos a transformada de Fourier G q (ω) da função de Green G lm (ω), definida como G 0 lm(ω) = 1 G 0 N q(ω)e iq (r l r m) q G 0 q(ω) = G 0 lm(ω)e iq (rl rm) (4.21) r l r m onde r l e r m são vetores bidimensionais que localizam os sítios na rede quadrada infinita, q = q x î + q y ĵ é um vetor de onda bidimensional ao longo do plano xy e N, é o número
77 76 total de sítios na rede. Assim, pelas (4.20) e (4.21), obtemos ( ωg 0 q(ω) = 1 2π δ lm + s ) J lj + h G 0 q(ω) j ( ) S j λj lj e q (r l r j ) G 0 q(ω), onde (vide Fig.29) Figura 18: Um sítio qualquer l, num ferromagneto de rede quadrada infinita, e seus quatro primeiro vizinhos. 4 J jl e q (r l r j ) j=1 = J l1 e q ( aî) + J l2 e q (aî) + J l3 e q ( aĵ) + J l4 e q (aĵ) = J[e iqxa + e iqxa + e iqya + e iqya ] = 2J[cos(q x a) + cos(q y a)] = 2Jγ 2 (q), onde γ 2 (q) = cos(q x a) + cos(q y a) é o fator de estrutura e consideramos que as interações de troca entre vizinhos são iguais.
78 77 Assim, obtemos a seguinte expressão para G 0 q(ω), ou seja, onde as frequências ω(q, λ) são dadas por G 0 q(ω) = 1 1 2π ω ω(q, λ), (4.22) ω(q, λ) = h + 2JS{2 λγ 2 (q)}. (4.23) Assim, pela (4.21), temos as funções de Green para o sistema puro, ou seja, G 0 lm(ω) = 1 e iq (r l r m) 2πN ω ω(q, λ). (4.24) q Consideremos agora o caso em que o sistema contém uma impureza intersticial, localizada no centro de um dos quadrados da rede quadrada infinita (vide Fig. 17). A função de Green para este caso pode ser construida pela substituição das (4.10) e (4.17) na (4.19), o que nos fornece a seguinte expressão (ver Apêndice C): ( ωg lm = 1 2π δ lm + S ) J lj + h G lm (ω) S λj lj G jm (ω) j j { } JS λα[g om (ω)δ ld + G dm (ω)δ lo ] de Dyson, ou seja, d { } JS [βg om (ω)δ lo + γg dm (ω)δ ld ] d + h G om (ω)δ lo. (4.25) A equação (4.25) pode ser expressa matricialmente na forma de uma equação [I G 0 V]G = G 0, (4.26) onde G 0 é a matriz função de Green para o sistema puro e G, para o sistema impuro, cujos elementos são 2πJSG 0 lm (ω) e 2πJSG lm(ω), respectivamente. A matriz V é o potencial efetivo devido a impureza, cujos elementos são V lj = d [( λα)(δ ld δ jo + δ lo δ jd ) βδ lo δ jo γδ ld δ jd (h /JS)δ lo δ jo ]. (4.27)
79 Modos de impureza e resultados numéricos Nesta seção calculamos o espectro de energia dos modos associados com a impureza. Aqui rotulamos a impureza por índice o e seus quatro primeiros vizinhos por 1 4 (vide Fig.19). A única parte diferente de zero da matriz potencial é uma submatriz 5 5 correspondendo ao spin da impureza e seus vizinhos. O espectro dos modos localizados é, então, encontrado calculando numericamente as frequências que satisfazem a condição Figura 19: Impureza intersticial e seus quatro primeiro vizinhos num ferromagneto de rede quadrada infinita. det[i G 0 V] = 0, (4.28) onde G 0 = G oo G o1 G o1 G o1 G o1 G o1 G oo G 12 G 12 G 14 G o1 G 12 G oo G 14 G 12 G o1 G 12 G 14 G oo G 12 G o1 G 14 G 12 G 12 G oo
80 79 e V = Assim a (4.28) nos fornece ρ λα λα λα λα λα γ λα 0 γ 0 0 λα 0 0 γ 0 λα γ det[i G 0 V] = [D p (ω)] 2 D d (ω)d s (ω) = 0, (4.29) onde D p (ω) = 1 γ(g 00 G 14 ), (4.30) D d (ω) = 1 + γ(2g 12 G oo G 14 ) (4.31) e D s (ω) = [(γρ 4(λα) 2 )G oo γ]g 14 + [(2γρ 8(λα) 2 )G oo 2γ]G 12 + [16(λα) 2 4γρ]G 2 o1 + 8λαG o1 + [γρ 4(λα) 2 ]G 2 oo (ρ + γ)g oo + 1 (4.32) com ρ = β + h /JS. Os modos associados à impureza podem, agora, ser obtidos a partir das Eqs. 4.30, 4.31 e 4.32, encontrando os valores de ω para os quais D p (ω), D d (ω) ou D s (ω) se anulam. Novamente, é útil distinguir entre modos de defeitos (ou não ressonantes), cujas energias podem estar abaixo do limite inferior (modos acústicos) ou acima do limite superior (modos ópticos) da banda de energia da onda de spin do material puro, e modos ressonantes, cujas energias estão dentro destes limites. Os valores desses limites de frequência, para o caso aqui estudado, variam de acordo com a equação ω(λ) = 5±4λ (em unidades de JS), obtida da Eq. 4.23, tomando os cossenos nos limites da primeira zona de Brillouin. Os sinais mais e menos se referem, respectivamente, aos limites superior e inferior da banda da onda de spin. Primeiramente avaliamos as funções de Green G 0 que aparecem nas Eqs. ( ). Estas funções são obtidas através da Eq e somando numericamente sobre o vetor de onda bidimensional q. Aqui analisaremos somente os modos de defeitos (não ressonantes) para cujo caso, as funções de Green são todas quantidades reais. Em todos
81 80 os casos, consideramos os seguintes valores para os parâmetros h (campo aplicado), J (interação de troca) e S (número quântico de spin), referentes ao sistema puro: h = J = S = 1, 0. 7,0 6,0 ω/js 5,0 4,0 λ=0 λ=0,25 λ=0,50 λ=0,75 3,0 λ=1,00 0,0 0,2 0,4 0,6 0,8 1,0 q x a/π Figura 20: Frequências de ondas de spin em função de q x a/π para diferentes valores de λ. 7,0 6,0 q x =1,00π q x =0,75π ω/js 5,0 q x =0,5π 4,0 q x =0,25π q x =0,0π 3,0 0,0 0,2 0,4 0,6 0,8 1,0 λ Figura 21: Frequências de ondas de spin em função de λ para diferentes valores de q x a/π. Na Fig.20, apresentamos a relação de dispersão de ondas de spin com vetor de onda q = q x î+q y ĵ (î e ĵ são vetores unitários nas direções x e y, respectivamente) em uma rede ferromagnética quadrada infinita. Os resultados para as frequências das ondas de spin são obtidos como uma função de q x a/π (constante de rede a) para diferentes valores de λ (veja a Eq. 4.23), onde fixamos o valor de q y em π/2a. Podemos observar a variação nos limites inferior e superior da banda de ondas de spin, bem como sua dependência em λ. Por exemplo, para λ = 0, ou seja, no caso do Hamiltoniano de Ising, os limites inferior e superior da banda coincidem em ω = 5JS. Já no caso em que λ = 1, Hamiltoniano
82 81 Figura 22: Gra fico do contorno para os efeitos das componentes qx e qy do vetor de onda q sobre a freque ncia (energia) ω/j 16,0 modos s modos p modos d 14,0 ω/js 12,0 10,0 λ=1,00 8,0 λ=0,50 6,0 λ=0,00 4,0 0,0 0,1 0,2 0,3 0,4 J /J Figura 23: Freque ncias de ondas de spin como func a o de J 0 /J, para h0 /h = 2, 0, S 0 /S = 1, 0 e alguns valores de λ. Modos localizados s, p e d relativos a uma impureza em um ferromagneto de rede quadrada infinita. de Heisenberg, temos como limite inferior a freque ncia de 1, 0JS e limite superior 9, 0JS, com a freque ncia variando com o cosseno, de acordo com a Eq Na Fig. 21, apresentamos outra relac a o de dispersa o para as ondas de spin. Neste caso, os resultados para as freque ncias dessas ondas sa o apresentados como uma func a o de λ para diferentes valores de qx a/π (valores indicados na figura), com qy fixado em
Ciências Exatas e da Natureza"! IMPUREZAS MAGNÉTICAS ACOPLADAS EM FILMES ULTRA FINOS FERROMAGNÉTICOS
 Ciências Exatas e da Natureza" IMPUREZAS MAGNÉTICAS ACOPLADAS EM FILMES ULTRA FINOS FERROMAGNÉTICOS Raimundo Valmir Leite Filho 1 Raimundo Nogueira da Costa Filho 2 RESUMO O formalismo de funções de Green
Ciências Exatas e da Natureza" IMPUREZAS MAGNÉTICAS ACOPLADAS EM FILMES ULTRA FINOS FERROMAGNÉTICOS Raimundo Valmir Leite Filho 1 Raimundo Nogueira da Costa Filho 2 RESUMO O formalismo de funções de Green
O Modelo de Ising. para sistemas clássicos. Mateus Schmidt. ...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada
 .....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Modelo de Ising para sistemas clássicos Mateus Schmidt Santa Maria - RS, 2012 1 /
.....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Modelo de Ising para sistemas clássicos Mateus Schmidt Santa Maria - RS, 2012 1 /
PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO
 EXATAS E DA TERRA PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO FRANCELINO, Isabella Grinberg. Estudante do Curso de Engenharia Física- ILACVN UNILA; E-mail: isabella.francelino@aluno.unila.edu.br;
EXATAS E DA TERRA PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO FRANCELINO, Isabella Grinberg. Estudante do Curso de Engenharia Física- ILACVN UNILA; E-mail: isabella.francelino@aluno.unila.edu.br;
Impurezas magnéticas em ferromagnetos de Ising com campo transverso
 Universidade Federal do Ceará Centro de Ciências Exatas e da Natureza Departamento de Física Curso de Pós-Graduação em Física Impurezas magnéticas em ferromagnetos de Ising com campo transverso Raimundo
Universidade Federal do Ceará Centro de Ciências Exatas e da Natureza Departamento de Física Curso de Pós-Graduação em Física Impurezas magnéticas em ferromagnetos de Ising com campo transverso Raimundo
A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico
 A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico Ivan de Paula Miranda Nanomagnetismo Redução do tamanho efeitos quânticos individuais Desenvolvimento de técnicas
A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico Ivan de Paula Miranda Nanomagnetismo Redução do tamanho efeitos quânticos individuais Desenvolvimento de técnicas
A Estrutura Eletrônica dos Átomos. Prof. Fernando R. Xavier
 A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
Paramagneto, Ferromagneto e Transições de Fase
 Paramagneto, Ferromagneto e Transições de Fase Estudo a partir da mecânica estatística Mecânica Estatística 014 Sistemas paramagnéticos Sistemas ferromagnéticos Transições de fase Modelo de Ising Sistema
Paramagneto, Ferromagneto e Transições de Fase Estudo a partir da mecânica estatística Mecânica Estatística 014 Sistemas paramagnéticos Sistemas ferromagnéticos Transições de fase Modelo de Ising Sistema
n, l, m l, ms (1) quando estes quatro números quânticos são dados, o estado físico do sistema (no caso, um elétron) é então especificado.
 Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
Introdução. Consideramos nos textos anteriores sistemas quantum mecânicos que possuem vários níveis de energia mas somente um elétron orbital, ou seja, consideramos até o presente momento átomos hidrogenóides.
2.2.1 Efeito Hall e Magnetoresistência Condutividade Elétrica AC Corrente Elétrica em um Campo Magnético
 Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
Representação grande
 Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Átomos e Moléculas. Ligações moleculares. Energia do ion. A molécula de hidrogênio H 2
 Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Gases quânticos sem interação
 UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
UFABC - Mecânica Estatística Curso 2018.1 Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
Ferromagnetismo. 2 Modelo de Ising
 Capítulo 8 Ferromagnetismo 1 Introdução As substâncias ferromagnéticas são caracterizadas por possuírem uma magnetizaçao (espontânea) que pode persistir mesmo na ausência de um campo magnético. Esse comportamento
Capítulo 8 Ferromagnetismo 1 Introdução As substâncias ferromagnéticas são caracterizadas por possuírem uma magnetizaçao (espontânea) que pode persistir mesmo na ausência de um campo magnético. Esse comportamento
Física Quântica. Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli. Pieter Westera
 Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
06 - VIBRAÇÕES DA REDE CRISTALINA: FÔNONS
 06 - VIBRAÇÕES DA REDE CRISTALINA: FÔNONS PROF. CÉSAR AUGUSTO DARTORA - UFPR E-MAIL: CADARTORA@ELETRICA.UFPR.BR CURITIBA-PR Roteiro do Capítulo: Vibrações da Rede Cristalina Modelo Clássico das Vibrações
06 - VIBRAÇÕES DA REDE CRISTALINA: FÔNONS PROF. CÉSAR AUGUSTO DARTORA - UFPR E-MAIL: CADARTORA@ELETRICA.UFPR.BR CURITIBA-PR Roteiro do Capítulo: Vibrações da Rede Cristalina Modelo Clássico das Vibrações
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi
 Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Teoria de Bandas 1 Elétrons Livres. CF086 - Introdução a Física do Estado Sólido 1
 Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
Física de Semicondutores. Sexta aula FÔNONS
 Física de Semicondutores Sexta aula FÔNONS Resumo das aulas anteriores Cálculo dos auto-estados e auto-energias dos elétrons em um semicondutor é complicado, devido ao grande número de átomos. Simetria
Física de Semicondutores Sexta aula FÔNONS Resumo das aulas anteriores Cálculo dos auto-estados e auto-energias dos elétrons em um semicondutor é complicado, devido ao grande número de átomos. Simetria
Física Estatística ??? Representação macroscópica. Representação microscópica. sistema U (S, V, N) S (U, V, N)
 Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física Moderna II Aula 08. Marcelo G Munhoz Edifício HEPIC, sala 202, ramal
 Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 munhoz@if.usp.br 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 munhoz@if.usp.br 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Raios atômicos Física Moderna 2 Aula 6
 Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
Figure 1: Seção transversal de um tubo
 Questão de eletromagnetismo: O Large Hadron Collider (LHC) é o maior acelerador de partículas já construido. Em um túnel circular de 27 km de extensão a aproximadamente 00 metros de profundidade, 2 feixes
Questão de eletromagnetismo: O Large Hadron Collider (LHC) é o maior acelerador de partículas já construido. Em um túnel circular de 27 km de extensão a aproximadamente 00 metros de profundidade, 2 feixes
Disciplinas NMA-207 Magnetismo FIS-601 Tópico de Física III Magnetismo. Prof. Dr. Jose Antonio Souza
 Disciplinas NMA-207 Magnetismo FIS-601 Tópico de Física III Magnetismo Prof. Dr. Jose Antonio Souza 02/2016 Ementa da Disciplina CAMPO MAGNÉTICO; MAGNETIZAÇÃO E MOMENTO MAGNÉTICOS; MEDIDAS MAGNÉTICAS;
Disciplinas NMA-207 Magnetismo FIS-601 Tópico de Física III Magnetismo Prof. Dr. Jose Antonio Souza 02/2016 Ementa da Disciplina CAMPO MAGNÉTICO; MAGNETIZAÇÃO E MOMENTO MAGNÉTICOS; MEDIDAS MAGNÉTICAS;
Átomo de Hidrogênio 1
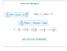 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
= ρ (N.1) A+ 1 c 2 φ. 2 φ 1 2 φ
 Apêndice N Solução Geral da Equação de Ondas Eletromagnéticas No caso geral em que há presença de densidades de cargas ρ e correntes j, vimos que os potenciais eletromagnéticos φ, A satisfazem as Eqs.
Apêndice N Solução Geral da Equação de Ondas Eletromagnéticas No caso geral em que há presença de densidades de cargas ρ e correntes j, vimos que os potenciais eletromagnéticos φ, A satisfazem as Eqs.
Aplicações de Semicondutores em Medicina
 Aplicações de Semicondutores em Medicina A estrutura dos cristais semicondutores Luiz Antonio Pereira dos Santos CNEN-CRCN PRÓ-ENGENHARIAS UFS-IPEN-CRCN Aracaju Março - 010 Como é a estrutura da matéria?
Aplicações de Semicondutores em Medicina A estrutura dos cristais semicondutores Luiz Antonio Pereira dos Santos CNEN-CRCN PRÓ-ENGENHARIAS UFS-IPEN-CRCN Aracaju Março - 010 Como é a estrutura da matéria?
Efeito Hall quântico de vale no grafeno
 Universidade de são paulo Instituto de física Departamento de física de materiais Efeito Hall quântico de vale no grafeno Walace de sousa elias Disciplina: teoria quântica de muitos corpos Prof. Dr. Luis
Universidade de são paulo Instituto de física Departamento de física de materiais Efeito Hall quântico de vale no grafeno Walace de sousa elias Disciplina: teoria quântica de muitos corpos Prof. Dr. Luis
CF100 - Física Moderna II. 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018
 CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
Aula-11. (quase) Tudo sobre os átomos
 Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
O spin do elétron. Vimos, na aula 2, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com 2 valores, com propriedades de momento angular.
 O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
Mecânica Quântica:
 Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Mecânica Quântica: 016-017 6 a Série 1. Considere as matrizes de Pauli, dadas por ( 0 1 0 i 1 0 σ x =, σ 1 0 y =, σ i 0 z = 0 1 ) 1.1. Demonstre que estas matrizes são Hermíticas. Determine os seus valores
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Física de Semicondutores
 Física de Semicondutores Aula 13 Transporte elétrico III Campos elétricos intensos Referência: Fundamentals of Semiconductors, P. Yu & M. Cardona, Springer. Transporte elétrico em semicondutores campos
Física de Semicondutores Aula 13 Transporte elétrico III Campos elétricos intensos Referência: Fundamentals of Semiconductors, P. Yu & M. Cardona, Springer. Transporte elétrico em semicondutores campos
Mecânica Quântica e Indiscernibilidade
 Mecânica Quântica e Indiscernibilidade t ou ou?? Mecânica clássica Partículas discerníveis ( A, A ) ψ ( A A ) ψ =, Mecânica quântica Partículas indiscerníveis ( A, A ) ψ ( A A ) ψ = ψ, ou = ( A, A ) ψ
Mecânica Quântica e Indiscernibilidade t ou ou?? Mecânica clássica Partículas discerníveis ( A, A ) ψ ( A A ) ψ =, Mecânica quântica Partículas indiscerníveis ( A, A ) ψ ( A A ) ψ = ψ, ou = ( A, A ) ψ
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
Física de Semicondutores. Aula 9 DEFEITOS EM SEMICONDUTORES
 Física de Semicondutores Aula 9 DEFEITOS EM SEMICONDUTORES Defeitos permitem controlar o comportamento elétrico e/ou óptico dos materiais e estruturas semicondutoras; tornam possível a imensa variedade
Física de Semicondutores Aula 9 DEFEITOS EM SEMICONDUTORES Defeitos permitem controlar o comportamento elétrico e/ou óptico dos materiais e estruturas semicondutoras; tornam possível a imensa variedade
Física da Matéria Condensada - GFI 04129
 Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
Susceptibilidade Magnética do Modelo de Hubbard Unidimensional em Duas Bandas
 SCIENIA PLENA VOL. 1, NUM. 1 5 www.scientiaplena.org.br Susceptibilidade Magnética do Modelo de Hubbard Unidimensional em Duas Bandas (Magnetic Susceptibility of the One-dimensional wo Bands Hubbard Model)
SCIENIA PLENA VOL. 1, NUM. 1 5 www.scientiaplena.org.br Susceptibilidade Magnética do Modelo de Hubbard Unidimensional em Duas Bandas (Magnetic Susceptibility of the One-dimensional wo Bands Hubbard Model)
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 Tabela Periódica dos elementos 2 8 8 Alcalinos, um elétron livre na camada
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 Tabela Periódica dos elementos 2 8 8 Alcalinos, um elétron livre na camada
denominação de férmions pesados (FP). O que caracteriza estes sistemas não é somente o elevado valor de γ, a susceptibilidade constante χ
 1 Introdução A descoberta de uma nova classe de compostos intermetálicos, denominados sistemas de férmions pesados, tem despertado grande interesse entre físicos da matéria condensada desde sua descoberta.
1 Introdução A descoberta de uma nova classe de compostos intermetálicos, denominados sistemas de férmions pesados, tem despertado grande interesse entre físicos da matéria condensada desde sua descoberta.
Princípios de Magnetoquímica. Prof. Fernando R. Xavier
 Princípios de Magnetoquímica Prof. Fernando R. Xavier UDESC 2015 Parte da física é simples, parte da física é complicada. Magnetismo está na segunda parte. (1921) 2 Conceitos básicos Magnetismo é uma propriedade
Princípios de Magnetoquímica Prof. Fernando R. Xavier UDESC 2015 Parte da física é simples, parte da física é complicada. Magnetismo está na segunda parte. (1921) 2 Conceitos básicos Magnetismo é uma propriedade
Gás de elétrons livres. Introdução à Mecânica Estatística 29/10/2009
 Gás de elétrons livres Introdução à Mecânica Estatística 9/10/009 1 Distribuição de Fermi-Dirac Distribuição de Fermi-Dirac ou f ( ) 1 ( ) e 1 também chamada função de Fermi 1 kt B Exemplo: elétrons em
Gás de elétrons livres Introdução à Mecânica Estatística 9/10/009 1 Distribuição de Fermi-Dirac Distribuição de Fermi-Dirac ou f ( ) 1 ( ) e 1 também chamada função de Fermi 1 kt B Exemplo: elétrons em
O Método de Monte Carlo
 .....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Método de Monte Carlo Aplicações do algoritmo de Metropolis no Modelo de Ising Mateus
.....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Método de Monte Carlo Aplicações do algoritmo de Metropolis no Modelo de Ising Mateus
Física do Estado Sólido: Sólidos Condutores
 Física do Estado Sólido: Sólidos Condutores Trabalho de Física Moderna II Professor Marcelo Gameiro Munhoz 7 de maio de 2012 André E. Zaidan Cristiane Calil Kores Rebeca Bayeh Física do Estado Sólido -
Física do Estado Sólido: Sólidos Condutores Trabalho de Física Moderna II Professor Marcelo Gameiro Munhoz 7 de maio de 2012 André E. Zaidan Cristiane Calil Kores Rebeca Bayeh Física do Estado Sólido -
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 12 ESTATÍSTICA QUÂNTICA Primeira Edição junho de 2005 CAPÍTULO 12 ESTATÍSTICA QUÂNTICA ÍNDICE 12-1- Introdução 12.2- Indistinguibilidade
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 12 ESTATÍSTICA QUÂNTICA Primeira Edição junho de 2005 CAPÍTULO 12 ESTATÍSTICA QUÂNTICA ÍNDICE 12-1- Introdução 12.2- Indistinguibilidade
Átomos polieletrónicos
 Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 2016 14 de outubro de 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do
EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 2016 14 de outubro de 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do
Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change
 Físico-Química 01 Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change, 2nd Ed., Oxford, 2014 Prof. Dr. Anselmo E
Físico-Química 01 Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change, 2nd Ed., Oxford, 2014 Prof. Dr. Anselmo E
Aula 17 Tudo sobre os Átomos
 Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Rafael Cardeal Tavares (Aluno de ICV), Prof. Dr. Paulo Renato Silva de Carvalho(Orientador, Depto de Física UFPI)
 RAZÃO ENTRE AMPLITUDES DA SUSCEPTIBILIDADE PARA O PONTO DE LIFSHITZ Rafael Cardeal Tavares (Aluno de ICV), Prof. Dr. Paulo Renato Silva de Carvalho(Orientador, Depto de Física UFPI) Introdução Muitas ideias
RAZÃO ENTRE AMPLITUDES DA SUSCEPTIBILIDADE PARA O PONTO DE LIFSHITZ Rafael Cardeal Tavares (Aluno de ICV), Prof. Dr. Paulo Renato Silva de Carvalho(Orientador, Depto de Física UFPI) Introdução Muitas ideias
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0)
 este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
este termo já se tornou obsoleto, pois depois das derivadas em φ, qualquer termo que sobrar com J multiplicado vai ser nulo (quando J=0) vetor vetor Teoria Quântica de Campos II 39 estamos generalizando
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White
 QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
Lucas Modesto da Costa orientador Prof. Dr. José Nicodemos Teixeira Rabelo. 20 de abril de 2007
 FEITOS CRISTAIS FEITOS CRISTAIS Lucas Modesto da Costa orientador Prof. Dr. José Nicodemos Teixeira Rabelo Universidade Federal de Goiás Instituto de Física Grupo de Física Estatística 20 de abril de 2007
FEITOS CRISTAIS FEITOS CRISTAIS Lucas Modesto da Costa orientador Prof. Dr. José Nicodemos Teixeira Rabelo Universidade Federal de Goiás Instituto de Física Grupo de Física Estatística 20 de abril de 2007
Introdução à Modelagem Molecular
 Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Átomo de Hélio. Tiago Santiago. 2 de novembro de Resumo
 Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Não é permitido nenhum tipo de consulta!
 INSTRUÇÕES de PRÊMIO IFT-ICTP PARA JOVENS FÍSICOS Não escreva seu nome em nenhum lugar da prova. Em cada das seis folhas de questões, escreva o número do seu RG. Verifique que você tem as seis folhas de
INSTRUÇÕES de PRÊMIO IFT-ICTP PARA JOVENS FÍSICOS Não escreva seu nome em nenhum lugar da prova. Em cada das seis folhas de questões, escreva o número do seu RG. Verifique que você tem as seis folhas de
Atomística. Prof. Fernando R. Xavier
 Atomística Prof. Fernando R. Xavier UDESC 2013 Nem sempre foi tão fácil observar um átomo... Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson 400 a.c. até 1897 d.c. O Modelo de
Atomística Prof. Fernando R. Xavier UDESC 2013 Nem sempre foi tão fácil observar um átomo... Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson 400 a.c. até 1897 d.c. O Modelo de
h mc 2 =hν mc 2 =hc/ λ
 Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
Exame Unificado EUF. para o primeiro semestre de 2014 Parte 1 15/10/2013
 Exame Unificado das Pós-graduações em Física EUF para o primeiro semestre de 2014 Parte 1 15/10/2013 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx).
Exame Unificado das Pós-graduações em Física EUF para o primeiro semestre de 2014 Parte 1 15/10/2013 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx).
ÍNDICE. INTRODUÇÃO À FÍSICA ESTATÍSTICA xiii 1 PASSEIO ALEATÓRIO 1
 ÍNDICE INTRODUÇÃO À FÍSICA ESTATÍSTICA xiii 1 PASSEIO ALEATÓRIO 1 1.1 Probabilidades: definições elementares 3 1.2 Variáveis aleatórias e funções de distribuição 5 1.3 Passeio aleatório simples 9 1.3.1
ÍNDICE INTRODUÇÃO À FÍSICA ESTATÍSTICA xiii 1 PASSEIO ALEATÓRIO 1 1.1 Probabilidades: definições elementares 3 1.2 Variáveis aleatórias e funções de distribuição 5 1.3 Passeio aleatório simples 9 1.3.1
CAPÍTULO V MATERIAIS SEMICONDUTORES
 CAPÍTULO V MATERIAIS SEMICONDUTORES 5.1 - Introdução Vimos no primeiro capítulo desta apostila uma maneira de classificar os materiais sólidos de acordo com sua facilidade de conduzir energia. Desta forma
CAPÍTULO V MATERIAIS SEMICONDUTORES 5.1 - Introdução Vimos no primeiro capítulo desta apostila uma maneira de classificar os materiais sólidos de acordo com sua facilidade de conduzir energia. Desta forma
Representações e Fenomenologia. Soluções (Clássicas) da Equação de Dirac
 Teoria Quântica de Campos I 113 Representações e Fenomenologia Qual destas representações descreve os férmions na natureza? A resposta depende de qual partícula você quer descrever. Para começar note que:
Teoria Quântica de Campos I 113 Representações e Fenomenologia Qual destas representações descreve os férmions na natureza? A resposta depende de qual partícula você quer descrever. Para começar note que:
Além destas duas representações irredutíveis (chamada de Espinores de Weyl), ainda temos uma terceira, definida pela propriedade:
 Esse fator global na ação não parece ter importância, e de fato não afeta a solução clássica, mas quando quantizarmos faz toda diferença ter um fator 2 no operador que estamos invertendo (obtemos um propagador
Esse fator global na ação não parece ter importância, e de fato não afeta a solução clássica, mas quando quantizarmos faz toda diferença ter um fator 2 no operador que estamos invertendo (obtemos um propagador
Campo Escalar Complexo
 Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
b) (4 pt) Escreva a carga conservada em termos da Lagrangiana e a função f j (x).
 Mecânica Clássica ) Considere uma Lagrangiana L(x j, d dt xj ) onde j = a 3 que seja invariante sobre a transformação δx j = f j (x). Esta simetria implica a existência de uma carga conservada. a) ( pt)
Mecânica Clássica ) Considere uma Lagrangiana L(x j, d dt xj ) onde j = a 3 que seja invariante sobre a transformação δx j = f j (x). Esta simetria implica a existência de uma carga conservada. a) ( pt)
Terceira série de exercícios Mecânica Estatística - IFUSP - 13/9/ ensemble canônico -
 Terceira série de exercícios Mecânica Estatística - IFUSP - 3/9/00 - ensemble canônico - We consider especially ensembles of systems in which the index (or logarithm) of probability of phase is a linear
Terceira série de exercícios Mecânica Estatística - IFUSP - 3/9/00 - ensemble canônico - We consider especially ensembles of systems in which the index (or logarithm) of probability of phase is a linear
Spin Ice. Deancarlo Bordin Degregori. 15 de Dezembro de Deancarlo Bordin Degregori () Spin Ice 15 de Dezembro de / 32
 Spin Ice Deancarlo Bordin Degregori 15 de Dezembro de 2011 Deancarlo Bordin Degregori () Spin Ice 15 de Dezembro de 2011 1 / 32 1 Definição 2 História 3 4 Interpretação Monopolar 5 Perspectivas Deancarlo
Spin Ice Deancarlo Bordin Degregori 15 de Dezembro de 2011 Deancarlo Bordin Degregori () Spin Ice 15 de Dezembro de 2011 1 / 32 1 Definição 2 História 3 4 Interpretação Monopolar 5 Perspectivas Deancarlo
Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149):
 Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149): (Mink.) na pg 149 escolhemos ε real, que é útil para polariz. transversa. Para polarizações
Teoria Quântica de Campos I 195 Da mesma forma podemos obter a linha externa do fóton (usando a expansão da pag 149): (Mink.) na pg 149 escolhemos ε real, que é útil para polariz. transversa. Para polarizações
Rotação de Wick para o tempo Euclideano
 Teoria Quântica de Campos I 81 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 75.1. O que ganhamos fazendo de novo este caminho? Para
Teoria Quântica de Campos I 81 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 75.1. O que ganhamos fazendo de novo este caminho? Para
Figura 1.1: Variação de T c em função de vol% Co para nanopartículas de Co, comparado com o caso de átomos de Co e de nanopartículas de Cu [Xing10].
![Figura 1.1: Variação de T c em função de vol% Co para nanopartículas de Co, comparado com o caso de átomos de Co e de nanopartículas de Cu [Xing10]. Figura 1.1: Variação de T c em função de vol% Co para nanopartículas de Co, comparado com o caso de átomos de Co e de nanopartículas de Cu [Xing10].](/thumbs/76/73491639.jpg) 1 Introdução 1.1 Sistemas Híbridos Supercondutor/Ferromagneto Materiais compósitos na escala nanométrica, os chamados nanocompósitos, constituem atualmente um campo muito interessante de pesquisa. Dentro
1 Introdução 1.1 Sistemas Híbridos Supercondutor/Ferromagneto Materiais compósitos na escala nanométrica, os chamados nanocompósitos, constituem atualmente um campo muito interessante de pesquisa. Dentro
Introdução. O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico.
 Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
Física estatística MEFT, IST. Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
 Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
1 Ψ S. bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A. férmions estatística de Fermi: n(e) = e α e E/kT +1
 Estatística Quântica Boltzmann: n(e) = 1 e α e E/kT Indistinguibilidade Ψ S ou Ψ A 1 Ψ S bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A férmions estatística de Fermi: n(e) = e α e E/kT +1 1 Distribuição
Estatística Quântica Boltzmann: n(e) = 1 e α e E/kT Indistinguibilidade Ψ S ou Ψ A 1 Ψ S bósons estatística de Bose: n(e) = e α e E/kT 1 1 Ψ A férmions estatística de Fermi: n(e) = e α e E/kT +1 1 Distribuição
Leis de Biot-Savart e de Ampère
 Leis de Biot-Savart e de Ampère 1 Vimos que uma carga elétrica cria um campo elétrico e que este campo exerce força sobre uma outra carga. Também vimos que um campo magnético exerce força sobre uma carga
Leis de Biot-Savart e de Ampère 1 Vimos que uma carga elétrica cria um campo elétrico e que este campo exerce força sobre uma outra carga. Também vimos que um campo magnético exerce força sobre uma carga
INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN
 Introdução à Astrofísica Lição 18 A Distribuição de Maxwell INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN Um estado de um gás é especificado por suas coordenadas, de modo que representemos
Introdução à Astrofísica Lição 18 A Distribuição de Maxwell INTRODUÇÃO À ASTROFÍSICA LIÇÃO 19 A DISTRIBUIÇÃO DE MAXWELL-BOLZTMANN Um estado de um gás é especificado por suas coordenadas, de modo que representemos
n Camadas K L M N...
 Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
Quantização. Quantização da energia (Planck, 1900) hc h. Efeito fotoelétrico (Einstein, 1905) Espectros atômicos (linhas discretas) v 2
 Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor
 A Equação de Calor Uma das EDP s clássica da FísicaF sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor em um corpo sólido. s E uma aplicação mais recente é a que descreve
A Equação de Calor Uma das EDP s clássica da FísicaF sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor em um corpo sólido. s E uma aplicação mais recente é a que descreve
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO. Prof.
 CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO Prof. Bruno Farias Introdução Neste capítulo vamos aprender: Como descrever a rotação
CENTRO DE CIÊNCIAS E TECNOLOGIA AGROALIMENTAR UNIDADE ACADÊMICA DE TECNOLOGIA DE ALIMENTOS DISCIPLINA: FÍSICA I ROTAÇÃO Prof. Bruno Farias Introdução Neste capítulo vamos aprender: Como descrever a rotação
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
Quantização de um campo fermiônico
 Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/2 e de Dois Níveis
 Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
CONTEÚDO PROGRAMÁTICO EMENTA
 UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
Exame Unificado das Pós-graduações em Física EUF
 Exame Unificado das Pós-graduações em Física EUF º Semestre/01 Parte 1 4/04/01 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
Exame Unificado das Pós-graduações em Física EUF º Semestre/01 Parte 1 4/04/01 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
só temos a parte de aniquilação no futuro Até agora viemos fazendo integrais que tipicamente envolviam exponenciais do tipo:
 Teoria Quântica de Campos I 38 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 32.1. O que ganhamos fazendo de novo este caminho? Para
Teoria Quântica de Campos I 38 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 32.1. O que ganhamos fazendo de novo este caminho? Para
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Momento Angular. 8.1 Álgebra do Momento Angular
 Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
FNC Física Moderna 2 Aula 26
 FNC 0376 - Física Moderna Aula 6 1 Física Nuclear: cronologia do início Descoberta da Radioatividade (Becquerel) 1896 Separação química do Ra (Marie e Pierre Curie) 1898 Modelo atômico de Rutherford 1911
FNC 0376 - Física Moderna Aula 6 1 Física Nuclear: cronologia do início Descoberta da Radioatividade (Becquerel) 1896 Separação química do Ra (Marie e Pierre Curie) 1898 Modelo atômico de Rutherford 1911
Física de Partículas
 matheus@ift.unesp.br http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
matheus@ift.unesp.br http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
Física de Partículas
 matheus@ift.unesp.br http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
matheus@ift.unesp.br http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
Aspectos Quânticos da Óptica Não Linear
 Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
Eletromagnetismo Aplicado
 Eletromagnetismo Aplicado Unidade 3 Prof. Marcos V. T. Heckler 1 Conteúdo Introdução Materiais dielétricos, polarização e permissividade elétrica Materiais magnéticos, magnetização e permeabilidade magnética
Eletromagnetismo Aplicado Unidade 3 Prof. Marcos V. T. Heckler 1 Conteúdo Introdução Materiais dielétricos, polarização e permissividade elétrica Materiais magnéticos, magnetização e permeabilidade magnética
Formalismo de funções de Green em Problemas de Espalhamento
 Formalismo de funções de Green em Problemas de Espalhamento Lucas Medeiros Cornetta Universidade de São Paulo Instituto de física - IFUSP Conteúdo Introdução e Motivações. Formalismo dependente do tempo:
Formalismo de funções de Green em Problemas de Espalhamento Lucas Medeiros Cornetta Universidade de São Paulo Instituto de física - IFUSP Conteúdo Introdução e Motivações. Formalismo dependente do tempo:
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 06 Respostas esperadas Parte Estas são sugestões de possíveis respostas. Outras possibilidades também podem ser consideradas
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 06 Respostas esperadas Parte Estas são sugestões de possíveis respostas. Outras possibilidades também podem ser consideradas
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 015 14 outubro 014 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código (EUFxxx).
EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 015 14 outubro 014 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código (EUFxxx).
