= = 9 6 = 3 2
|
|
|
- Gabriella de Escobar Aranha
- 9 Há anos
- Visualizações:
Transcrição
1 MATEMÁTICA Prof. Rodrigo Pandolfi RESOLUÇÃO DE EXERCÍCIOS CONJUNTOS NUMÉRICOS (PÁG. 162 APOSTILA 2) PRATICANDO (PÁG. 166) 01 (UFF) O número π - 2 pertence ao intervalo: a)[1, 3 2 ] c) [3 2, 2] e) [ 3 2, 0) b) ( 1, 1] d) (-1, 1) 2 GABARITO:C π - 2 = 3,14 1,41 = 1,73 (O número está entre 1,5 e 2) 02 (PUC-RIO) A soma 1, , é igual a: a) 1 2 c) 4 3 e) 3 2 b) 5 2 GABARITO: E 1, = d) 5 3 = 12 9 = = = 9 6 = 3 2 0, = = = (UFSCAR) - Um determinado corpo celeste é visível da Terra a olho nu de 63 em 63 anos, tendo sido visto pela última vez no ano de De acordo com o calendário atualmente em uso, o primeiro ano da Era Cristã em que esse corpo celeste esteve visível a olho nu da Terra foi no ano: a) 15 c) 23 e)31 b) 19 d)27 GABARITO:A Considerando a ordem decrescente dos anos, foram 31 ciclos inteiros de 63 anos mais 15 anos restantes da era Cristã. 1
2 DESENVOLVENDO HABILIDADES (PÁG. 167) 01 (UECE-2015) -) Se a soma e o produto de dois números são, respectivamente, dois e cinco, podemos afirmar corretamente que : a) os dois números são racionais. b) os dois números são complexos não reais. c) os dois números são irracionais. d) um dos números é racional e o outro é irracional. GABARITO: B x + y = 2 x.y = 5 x = 2 - y x.y = 5 (2 y).y =5 2.y y 2 = 5 -y y 5 =0 = b 2 4.a.c = (-1).(-5) = 4 20 = 16 Não existem raízes reais porque o delta é negativo. 02- (Enem 2013 Q162) Em um jogo educativo, o tabuleiro é uma representação da reta numérica e o jogador deve posicionar as fichas contendo números reais corretamente no tabuleiro, cujas linhas pontilhadas equivalem a 1 (uma) unidade de medida. Cada acerto vale 10 pontos. Na sua vez de jogar, Clara recebe as seguintes fichas: Para que Clara atinja 40 pontos nessa rodada, a figura que representa seu jogo, após a colocação das fichas no tabuleiro, é: GABARITO:D 2
3 03 (Enem 2010) Para dificultar o trabalho dos falsificadores, foi lançada uma nova família de cédulas do real. Com tamanho variável - quanto maior o valor, maior a nota - o dinheiro novo terá vários elementos de segurança. A estreia será entre abril e maio, quando começam a circular as notas de RS 50,00 e RS 100,00. As cédulas atuais têm 14 cm de comprimento e 6,5 cm de largura. A maior cédula será a de RS 100,00, com 1,6 cm a mais no comprimento e 0,5 cm maior na largura. Disponivel em Acesso em: 20 abr (adaptado). Quais serão as dimensões da nova nota de R$ 100,00? a) 15,6 cm de comprimento e 6 cm de largura b) 15,6 cm de comprimento e 6,5 cm de largura c) 15,6 cm de comprimento e 7 cm de largura d) 15,9 cm de comprimento e 6,5 cm de largura e) 15,9 cm de comprimento e 7 cm de largura GABARITO:C De acordo com o texto, as dimensões da nova nota de R$100,00 serão ,6 = 15,6cm e 6,5 + 0,5 = 7cm O segmento XY, indicado na reta numérica abaixo, está dividido em dez segmentos congruentes pelos pontos A, B, C, D, E, F, G, H e I. Admita que X e Y representem, respectivamente, os números e. O ponto D representa o seguinte número: a) 1 5 b) 8 15 GABARITO: E c) d) Determinar a amplitude do intervalo = = 8 6 Dividir o intervalo em 10 partes iguais = 8 6 x 1 10 = 8 60 = 2 15 e) = = = =
4 05 (CEFET-2014) Um grupo de alunos cria um jogo de cartas, em que cada uma apresenta uma operação com números racionais. O ganhador é aquele que obtiver um número inteiro como resultado da soma de suas cartas. Quatro jovens ao jogar receberam as cartas indicadas na tabela. O vencedor do jogo foi: a)maria b)selton GABARITO: C c)tadeu d)valentina Fazer pelo método de eliminação das alternativas : Tadeu 1, = = = = = = 360 = ,7 = = = (IFCE-2014) - Considere os seguintes números reais 23, 7, 47, 1, 11, 4, 11. Colocando-se esses números em ordem crescente, o menor e o maior deles são, respectivamente, GABARITO: D O menor número é 7 8 = 0,875 e o maior é 11 8 = 1,375 4
5 07 (UFSJ 2013) Sejam r 1 e r 2 números racionais quaisquer e s 1 e s 2 números irracionais quaisquer, é incorreto afirmar que: a) o produto r 1. r 2 será sempre um número racional. b) o produto s 1. s 2 será sempre um número irracional. c) o produto s 1. r 1 será sempre um número irracional. d) para r2 0, a razão r1 será sempre um número racional. r2 O produto de dois números irracionais = 36 = 6 Número natural 08 (IFAL- 2012) Assinale a alternativa verdadeira a) {1, 2, 4, 6, 7} = [1, 7]. b) Se C = ] 1, 3], então -1 C, mas 3 C. c) Se D = [2, 6], então 2 D, mas 3 D. d) A intersecção de dois intervalos numéricos é sempre um intervalo numérico. e) A união de dois intervalos numéricos pode ser um conjunto vazio. Existem elementos no intervalo [1, 7] que não pertencem ao conjunto {1, 2, 4, 6, 7} como por exemplo o número 5 09 (UFJF-2012) Define-se o comprimento de cada um dos intervalos [a, b], ]a, b[, ]a, b] e [a, b[ como sendo a diferença (b - a). Dados os intervalos M = [3, 10], N = ]6, 14[, e P = [5, 12[, o comprimento do intervalo resultante de (M P) (P N) igual a: a) 1. c)5 e)9 b) 3 d)7 GABARITO : C Como M P [5,10] e P - N = [5, 6], segue que (M P) (P N) [5,10]. Assim, o comprimento desse intervalo é 10 5 = 5 10 (UTFPR 2012) Indique qual dos conjuntos a seguir é constituído somente de números racionais. a){-1, 2, 2, π} c) { -2, 0, π, 2 3 } e){ -1, 0, 3, 1 3 } b){-5, 0, 1, 9} d) { 3, 64, π, 2 } 2 5
6 COMPLEMENTARES (PÁG. 168) 01 (FUVEST-2014) O nu mero real x, que satisfaz 3 < x < 4, tem uma expansa o decimal na qual os primeiros di gitos a direita da vi rgula sa o iguais a 3. Os di gitos seguintes sa o iguais a 2 e os restantes sa o iguais a zero. Considere as seguintes afirmac o es: I. x e irracional. II. x 10 3 III. x e um inteiro par. a)nenhuma das três afirmações é verdadeira b)apenas as afirmações I e II são verdadeiras. c) apenas a afirmação I é verdadeira. d) apenas a afirmação II é verdadeira. e)apenas a afirmação III é verdadeira. GABARITO:E I. Como o número apresenta número finito de algarismos à direita da vírgula (não nulos), ele será um número decimal exato, logo é racional (FALSA). II. Seja y= 10 =3, É fácil observar que 3, , (FALSA) 3 III. X = 3, = que é inteiro par (VERDADEIRO) 02 (CEFET-MG-2013) Considere as afirmações abaixo em que a e b são números reais. I. II. III. IV. a < b Estão corretas as afirmativas: a) I e II. b) I e III. c) II e IV. d) III e IV. GABARITO:D I. Errado pois: II. Errado pois: Mas III. Correto pois = = 25 = 5 IV Correto : média aritmética de dois números 4 e 5 = 4,5 6
7 03 (UFRGS-2012) Sendo a, b e c números reais, considere as seguintes afirmações: 1 1 I - se a 0, b 0 e a b, então. a b a b a b II - se c 0, então. c c c III- se b 0 e c 0, então ( a b) c a ( b c) Quais estão corretas? (A) Apenas I. (C) Apenas I e II. (E) I, II e III. (B) Apenas II. (D) Apenas II e III. 04 (UFF-2010) Segundo o matemático Leopold Kronecker ( ), Deus fez os nu meros inteiros, o resto e trabalho do homem. Os conjuntos nume ricos sa o, como afirma o matemático, uma das grandes invenções humanas. Assim, em relação aos elementos desses conjuntos, é correto afirmar que: a) o produto de dois números irracionais é sempre um número irracional. b) a soma de dois números irracionais é sempre um número irracional. c) entre os números reais 3 e 4 existe apenas um número irracional. d) entre dois números racionais distintos existe pelo menos um número racional. e) a diferença entre dois números inteiros negativos é sempre um número inteiro negativo. GABARITO:D a)falso porque 5. 5 = 5 (natural) b)falso porque 2 + (- 2) = 2-2 = 0 (natural) c) Falso porque entre os números reais 3 e 4 existem infinitos irracionais d) Verdadeiro porque entre a e b tem pelo menos a+b 2 e)falso porque (-5) (-10) = 5 (natural) 7
8 05 (UFMG-2010) Considere a função Então, é correto afirmar que o maior elemento do conjunto abaixo é: a)f( 7 31 ) c)f(3,14) b) f(1) d)f( 24 2 ) GABARITO:C a) 7 31 é um número racional portanto x = ,23 b)1 é um número natural portanto x = 1 c)3,14 é um número decimal exato(racional) portanto x = 3,14 d) 24 2 = 12 é um número irracional portanto = ,3 06 (UFSJ-2012) a charge a seguir, intitulada discussa o Matemática ilustra números pertencentes a dois conjuntos numéricos o conjunto dos números reais (R) e o conjunto dos números complexos (C) Com relação a esses dois números, é correto afirmar que: 07 (IFCE-2014) Considere os conjuntos U = {x Z x < 30}, A = {x N * x 15} e B = { 50, 48, 46, 44,,48,50}. onde N * = N {0}. Seja A C o complementar de A em relação a U e o conjunto vazio. A cardinalidade do conjunto S = (A C ) B é: a)21 c)23 e)25 b)22 d)24 GABARITO: B U = - 30 < x < 30 B = { 50, 48, 46, 44,,48,50} Pares A = 1 x 15 A C = - 30 < x < 1 e 15 < x < elementos + 7 elementos = 22 elementos 8
9 08 (UERJ) Um restaurante self-service cobra pela refeição R$ 6,00 por pessoa, mais uma multa pela comida deixada no prato, de acordo com a tabela. a) Se Júlia pagou R$ 9,00 por uma refeição, indique a quantidade mínima de comida que ela pode ter desperdiçado. 9,00 6,00 = R$ 3,00 (desperdício) Mínimo de 300 gramas b) Y é o valor total pago em reais, por pessoa, e X Æ IR é a quantidade desperdiçada, em gramas. Esboce o gráfico de Y em função de X. 9
CONJUNTOS NUMÉRICOS - LISTA 1
 1. (Acafe 01) Analise as afirmações a seguir e assinale a alternativa correta. l. O número real x não pertence ao intervalo aberto de extremos e. Sabe-se que x 0 ou x 4. Pode-se concluir, então, que x
1. (Acafe 01) Analise as afirmações a seguir e assinale a alternativa correta. l. O número real x não pertence ao intervalo aberto de extremos e. Sabe-se que x 0 ou x 4. Pode-se concluir, então, que x
Interbits SuperPro Web
 . (Ufpr 07) Rafaela e Henrique participaram de uma atividade voluntária que consistiu na pintura da fachada de uma instituição de caridade. No final do dia, restaram duas latas de tinta idênticas (de mesmo
. (Ufpr 07) Rafaela e Henrique participaram de uma atividade voluntária que consistiu na pintura da fachada de uma instituição de caridade. No final do dia, restaram duas latas de tinta idênticas (de mesmo
Simulado 08 / MAI / EXTENSIVO
 Simulado 08 / MAI / EXTENSIVO 1. Assinale a(s) proposição(ões) CORRETA(S). 01. Uma reserva florestal foi dividida em quadrantes de 1 m² de área cada um. Com o objetivo de saber quantas samambaias havia
Simulado 08 / MAI / EXTENSIVO 1. Assinale a(s) proposição(ões) CORRETA(S). 01. Uma reserva florestal foi dividida em quadrantes de 1 m² de área cada um. Com o objetivo de saber quantas samambaias havia
LISTA DE MATEMÁTICA (SETOR A) (Prof. Pinda)
 LISTA DE MATEMÁTICA (SETOR A) (Prof Pinda) 6 (Uece 06) Seja x 0,, 0,760,, 7 7 Se a e b são respectivamente o maior e o menor dos elementos de x, então, a) entre e entre e entre e maior do que a b b um
LISTA DE MATEMÁTICA (SETOR A) (Prof Pinda) 6 (Uece 06) Seja x 0,, 0,760,, 7 7 Se a e b são respectivamente o maior e o menor dos elementos de x, então, a) entre e entre e entre e maior do que a b b um
MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o conjunto A Z tem sete elementos, os sete elemento são três
MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o conjunto A Z tem sete elementos, os sete elemento são três
a) Quantas placas distintas podemos ter sem o algarismo zero na primeira posição reservada aos algarismos?
 1 1. (Fuvest-gv 91) As atuais placas de licenciamento de automóveis constam de sete símbolos sendo três letras, dentre as 26 do alfabeto, seguidas de quatro algarismos. a) Quantas placas distintas podemos
1 1. (Fuvest-gv 91) As atuais placas de licenciamento de automóveis constam de sete símbolos sendo três letras, dentre as 26 do alfabeto, seguidas de quatro algarismos. a) Quantas placas distintas podemos
Matemática. 1
 PROFº Marcelo Jardim www.concursovirtual.com.br 1 CONJUNTOS NUMÉRICOS 1.NÚMEROS NATURAIS O conjunto dos números naturais é representado por IN e IN= {0;1;2;3;4;...} ATENÇÃO!!! O (*) EXCLUI O ZERO. IN*={1;2;3;4;...}
PROFº Marcelo Jardim www.concursovirtual.com.br 1 CONJUNTOS NUMÉRICOS 1.NÚMEROS NATURAIS O conjunto dos números naturais é representado por IN e IN= {0;1;2;3;4;...} ATENÇÃO!!! O (*) EXCLUI O ZERO. IN*={1;2;3;4;...}
3 pode ser associado a letra C.
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - ÁLGEBRA - 8º ANO - ENSINO FUNDAMENTAL ============================================================================ 01- Na figura a seguir foram representados
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - ÁLGEBRA - 8º ANO - ENSINO FUNDAMENTAL ============================================================================ 01- Na figura a seguir foram representados
CANDIDATO: DATA: 20 / 01 / 2010
 UNIVERSIDADE ESTADUAL DO CEARÁ - UECE SECRETARIA DE EDUCAÇÃO A DISTÂNCIA - SEaD Universidade Aberta do Brasil UAB LICENCIATURA PLENA EM MATEMÁTICA SELEÇÃO DE TUTORES PRESENCIAIS CANDIDATO: DATA: 0 / 0
UNIVERSIDADE ESTADUAL DO CEARÁ - UECE SECRETARIA DE EDUCAÇÃO A DISTÂNCIA - SEaD Universidade Aberta do Brasil UAB LICENCIATURA PLENA EM MATEMÁTICA SELEÇÃO DE TUTORES PRESENCIAIS CANDIDATO: DATA: 0 / 0
MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como 2 1, 1414 e 3 1, 7321, representando na reta real o intervalo
MATEMÁTICA - 3o ciclo Intervalos de números Reais (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como 2 1, 1414 e 3 1, 7321, representando na reta real o intervalo
A seguir, estão três afirmativas sobre números reais:
 Questão 01) O conjunto X = {4m + 5n;m,n Z + } contém todos os números inteiros positivos a) pares, a partir de 4. b) ímpares, a partir de 5. c) a partir de 9, inclusive. d) a partir de 12, inclusive. e)
Questão 01) O conjunto X = {4m + 5n;m,n Z + } contém todos os números inteiros positivos a) pares, a partir de 4. b) ímpares, a partir de 5. c) a partir de 9, inclusive. d) a partir de 12, inclusive. e)
EXERCÍCIOS SOBRE CONJUNTOS NUMÉRICOS
 E. M. DR. LEANDRO FRANCESCHINI Rua Geraldo de Souza, nº 157/221 - Jardim Carlos Basso - Sumaré/SP Telefones: (19) 3873-2605/3873-7296/3873-1574 www.leandrofranceschini.com.br EXERCÍCIOS SOBRE CONJUNTOS
E. M. DR. LEANDRO FRANCESCHINI Rua Geraldo de Souza, nº 157/221 - Jardim Carlos Basso - Sumaré/SP Telefones: (19) 3873-2605/3873-7296/3873-1574 www.leandrofranceschini.com.br EXERCÍCIOS SOBRE CONJUNTOS
Interbits SuperPro Web
 Lista ita eponencial e modulo Carlos Peioto. (Ita 07) Esboce o gráfico da função f: dada por f().. (Ita 07) Sejam S {(, y) : y } e área da região S S é S {(, y) : (y ) 5}. A a) 5. 4 π b) 5. 4 π c) 5. 4
Lista ita eponencial e modulo Carlos Peioto. (Ita 07) Esboce o gráfico da função f: dada por f().. (Ita 07) Sejam S {(, y) : y } e área da região S S é S {(, y) : (y ) 5}. A a) 5. 4 π b) 5. 4 π c) 5. 4
Assunto: Conjuntos Numéricos Professor: Daniel Ferretto
 Todas as questões encontram-se comentadas na videoaula do canal maismatemática, disponível para visualização gratuita no seguinte link: https://www.youtube.com/watch?v=tlsqgpe7td8 NÍVEL BÁSICO 1. (G1 -
Todas as questões encontram-se comentadas na videoaula do canal maismatemática, disponível para visualização gratuita no seguinte link: https://www.youtube.com/watch?v=tlsqgpe7td8 NÍVEL BÁSICO 1. (G1 -
2 36) pertence ao. a) { 5, 1, 7, 25} b) { 3, 1, 6, 20} c) { 5, 2, 7, 25} d) { 5, 1, 25} f (1) 9. Calcule f (2). 10. (UFRN) Seja f : D R,
 0. Para que valores de k o ponto eio das abscissas? k 3 b) k k ou k 4 k 0 ou k e) k ou k A (k, 4k 36) pertence ao 06. Seja g a função de domínio A,, 0,,, 3 e contradomínio R tal que de g. {,, 7, } b) {
0. Para que valores de k o ponto eio das abscissas? k 3 b) k k ou k 4 k 0 ou k e) k ou k A (k, 4k 36) pertence ao 06. Seja g a função de domínio A,, 0,,, 3 e contradomínio R tal que de g. {,, 7, } b) {
FUNÇÕES I Exercícios de Revisão 3 a SÉRIE - ENSINO MÉDIO
 MATEMÁTICA I FUNÇÕES I Exercícios de Revisão a SÉRIE - ENSINO MÉDIO NOME :... NÚMERO :... TURMA :... 1) (PUC MG) - A soma dos números naturais que pertencem ao domínio de f(x) = igual a 1 5 - x é a) 5
MATEMÁTICA I FUNÇÕES I Exercícios de Revisão a SÉRIE - ENSINO MÉDIO NOME :... NÚMERO :... TURMA :... 1) (PUC MG) - A soma dos números naturais que pertencem ao domínio de f(x) = igual a 1 5 - x é a) 5
CURSO DE MATEMÁTICA. Conjuntos dos números naturais, inteiros, racionais e irracionais. (propriedades e operações) Josimar Padilha
 CURSO DE MATEMÁTICA Conjuntos dos números naturais, inteiros, racionais e irracionais. (propriedades e operações) Josimar Padilha Qual a importância de conhecer os CONJUNTOS NUMÉRICOS? Meu querido aluno,
CURSO DE MATEMÁTICA Conjuntos dos números naturais, inteiros, racionais e irracionais. (propriedades e operações) Josimar Padilha Qual a importância de conhecer os CONJUNTOS NUMÉRICOS? Meu querido aluno,
A = B, isto é, todo elemento de A é também um elemento de B e todo elemento de B é também um elemento de A, ou usando o item anterior, A B e B A.
 Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Assunto: Conjuntos. 2) Dado o conjunto A = { 4,5,6,7,8 }, diga quais das proposições abaixo são verdadeiras:
 1) Escreva por extensão os conjuntos: Assunto: Conjuntos a) A = { x/ x é divisor inteiro positivo de 18 } b) B = { x Є N / x < 7 } c) C = { x Є N / 2 x 5} resp: a) A = {1,2,3,6,9,18} b) B = { 0,1,2,3,4,5,6}
1) Escreva por extensão os conjuntos: Assunto: Conjuntos a) A = { x/ x é divisor inteiro positivo de 18 } b) B = { x Є N / x < 7 } c) C = { x Є N / 2 x 5} resp: a) A = {1,2,3,6,9,18} b) B = { 0,1,2,3,4,5,6}
Colégio Nossa Senhora de Lourdes. Matemática. Professor: Leonardo Maciel
 Colégio Nossa Senhora de Lourdes Matemática Professor: Leonardo Maciel APOSTILA 2 1. (UFF) A afirmação "Todo jovem que gosta de matemática adora esportes e festas" pode ser representada segundo o diagrama:
Colégio Nossa Senhora de Lourdes Matemática Professor: Leonardo Maciel APOSTILA 2 1. (UFF) A afirmação "Todo jovem que gosta de matemática adora esportes e festas" pode ser representada segundo o diagrama:
FUNÇÕES EXPONENCIAIS
 FUNÇÕES EXPONENCIAIS ) Uma possível lei para a função eponencial do gráfico é (a) = 0,7. (b) =. 0,7 (c) = -. 0,7 (d) = -.,7 (e) = - 0,7. ) Os gráficos de = e = - (a) têm dois pontos em comum. (b) são coincidentes.
FUNÇÕES EXPONENCIAIS ) Uma possível lei para a função eponencial do gráfico é (a) = 0,7. (b) =. 0,7 (c) = -. 0,7 (d) = -.,7 (e) = - 0,7. ) Os gráficos de = e = - (a) têm dois pontos em comum. (b) são coincidentes.
DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: TURNO: NOTURNO
 DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: 2018-2 TURNO: NOTURNO ALUNO a): 1ª Lista de Exercícios - Introdução à Lógica Matemática, Teoria
DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: 2018-2 TURNO: NOTURNO ALUNO a): 1ª Lista de Exercícios - Introdução à Lógica Matemática, Teoria
Existem conjuntos em todas as coisas e todas as coisas são conjuntos de outras coisas.
 MÓDULO 3 CONJUNTOS Saber identificar os conjuntos numéricos em diferentes situações é uma habilidade essencial na vida de qualquer pessoa, seja ela um matemático ou não! Podemos dizer que qualquer coisa
MÓDULO 3 CONJUNTOS Saber identificar os conjuntos numéricos em diferentes situações é uma habilidade essencial na vida de qualquer pessoa, seja ela um matemático ou não! Podemos dizer que qualquer coisa
POTENCIAÇÃO, RADICIAÇÃO, PRODUTOS NOTÁVEIS, FATORAÇÃO, EQUAÇÕES DE 1 o E 2 o GRAUS
 MATEMÁTICA ÁLGEBRA vesti.stockler.com.br Stockler Vesties @StocklerVest Stockler Vesties EXERCÍCIOS DE POTENCIAÇÃO. (FUVEST ª Fase) Qual desses números é igual a 0,064? a) ( 80 ) b) ( 8 ) c) ( ) d) ( 800
MATEMÁTICA ÁLGEBRA vesti.stockler.com.br Stockler Vesties @StocklerVest Stockler Vesties EXERCÍCIOS DE POTENCIAÇÃO. (FUVEST ª Fase) Qual desses números é igual a 0,064? a) ( 80 ) b) ( 8 ) c) ( ) d) ( 800
PROVA DE MATEMÁTICA MÓDULO III DO PISM (triênio )
 QUESTÕES OBJETIVAS PROVA DE MATEMÁTICA MÓDULO III DO PISM (triênio 004-006) 09. Num determinado jogo, cada participante recebe uma ficha circular (tipo uma moeda) com um número impresso em cada uma das
QUESTÕES OBJETIVAS PROVA DE MATEMÁTICA MÓDULO III DO PISM (triênio 004-006) 09. Num determinado jogo, cada participante recebe uma ficha circular (tipo uma moeda) com um número impresso em cada uma das
8º ANO ENSINO FUNDAMENTAL Matemática. 1º Trimestre 45 questões 26 de abril (Sexta-feira)
 8º ANO ENSINO FUNDAMENTAL Matemática S º Trimestre 5 questões 6 de abril (Sexta-feir 09 SIMULADO OBJETIVO 8º ANO º TRIMESTRE. O número, corresponde à fração 0. 00. 000.. 99. MATEMÁTICA COMENTÁRIO/RESOLUÇÃO:
8º ANO ENSINO FUNDAMENTAL Matemática S º Trimestre 5 questões 6 de abril (Sexta-feir 09 SIMULADO OBJETIVO 8º ANO º TRIMESTRE. O número, corresponde à fração 0. 00. 000.. 99. MATEMÁTICA COMENTÁRIO/RESOLUÇÃO:
LISTA DE REVISÃO PROVA MENSAL MATEMÁTICA 1º ANO 2º TRIMESTRE ÁLGEBRA
 LISTA DE REVISÃO PROVA MENSAL MATEMÁTICA 1º ANO º TRIMESTRE ÁLGEBRA 1) Se o preço de um produto aumentou 0% anteontem e 0% hoje, então, de anteontem para hoje, esse preço aumentou: A) 50% B) 54% C) 55%
LISTA DE REVISÃO PROVA MENSAL MATEMÁTICA 1º ANO º TRIMESTRE ÁLGEBRA 1) Se o preço de um produto aumentou 0% anteontem e 0% hoje, então, de anteontem para hoje, esse preço aumentou: A) 50% B) 54% C) 55%
Matemática. 9 o ano. Caderno 1
 Matemática 9 o ano Caderno 1 Módulo 1 1 Leia o texto a seguir e responda ao que se pede. Em janeiro de 21, astrônomos internacionais anunciaram a descoberta da estrela mais antiga conhecida pela ciência,
Matemática 9 o ano Caderno 1 Módulo 1 1 Leia o texto a seguir e responda ao que se pede. Em janeiro de 21, astrônomos internacionais anunciaram a descoberta da estrela mais antiga conhecida pela ciência,
Exercícios de Matemática Produtos Notáveis Fatoração
 Exercícios de Matemática Produtos Notáveis Fatoração TEXTO PARA A PRÓXIMA QUESTÃO (Ufba) Na(s) questão(ões) a seguir escreva nos parênteses a soma dos itens corretos. 1. Sendo m = x + 1, n = x - x, p =
Exercícios de Matemática Produtos Notáveis Fatoração TEXTO PARA A PRÓXIMA QUESTÃO (Ufba) Na(s) questão(ões) a seguir escreva nos parênteses a soma dos itens corretos. 1. Sendo m = x + 1, n = x - x, p =
Prova: MATEMÁTICA GABARITO
 ESCOLA INTERNACIONAL DE JOINVILLE Sociesc PROCESSO SELETIVO DE BOLSA DE ESTUDOS PARA O ANO LETIVO DE 2017 EDITAL 03/2016 Prova: MATEMÁTICA GABARITO 1) (UECE-adaptada) Considere a expressão algébrica x+1
ESCOLA INTERNACIONAL DE JOINVILLE Sociesc PROCESSO SELETIVO DE BOLSA DE ESTUDOS PARA O ANO LETIVO DE 2017 EDITAL 03/2016 Prova: MATEMÁTICA GABARITO 1) (UECE-adaptada) Considere a expressão algébrica x+1
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
BIMESTRAL - MATEMÁTICA - 1ºBIMESTRE
 BIMESTRAL - MATEMÁTICA - 1ºBIMESTRE Série: 3ªEM Gabarito 1- : (PUC-RIO 2010) Sejam x e y números tais que os conjuntos {0, 7, 1} e {x, y, 1} são iguais. Então, podemos afirmar que: x = 0 e y = 5 x + y
BIMESTRAL - MATEMÁTICA - 1ºBIMESTRE Série: 3ªEM Gabarito 1- : (PUC-RIO 2010) Sejam x e y números tais que os conjuntos {0, 7, 1} e {x, y, 1} são iguais. Então, podemos afirmar que: x = 0 e y = 5 x + y
Exercícios de Matemática Funções Função Polinomial
 Exercícios de Matemática Funções Função Polinomial 5. (Unesp) A figura a seguir mostra o gráfico da função polinomial f(x)=ax +x +x,(a 0). 1. (Ufpe) Seja F(x) uma função real, na variável real x, definida
Exercícios de Matemática Funções Função Polinomial 5. (Unesp) A figura a seguir mostra o gráfico da função polinomial f(x)=ax +x +x,(a 0). 1. (Ufpe) Seja F(x) uma função real, na variável real x, definida
NOÇÕES. 04- (F. Santo André-SP) Seja A um conjunto com 7 elementos. O número total de subconjuntos de A é: a) 16 b) 128 c) 56 d) 100 e) 256
 MATQUEST CONJUNTOS PROF.: JOSÉ LUÍS NOÇÕES 01- (CATANDUVA-SP) Dado o conjunto A = {, {a}, b} com {a} b a 0, pode-se afirmar que: a) {, {b}} A b) {, {a}} A c) {, a} A d) {a, b} A e) A 02- (CEFET) Considerando
MATQUEST CONJUNTOS PROF.: JOSÉ LUÍS NOÇÕES 01- (CATANDUVA-SP) Dado o conjunto A = {, {a}, b} com {a} b a 0, pode-se afirmar que: a) {, {b}} A b) {, {a}} A c) {, a} A d) {a, b} A e) A 02- (CEFET) Considerando
III) se deste número n subtrairmos o número 3816, obteremos um número formado pelos mesmos algarismos do número n, mas na ordem contrária.
 1 Projeto Jovem Nota 10 1. (Fuvest 2000) Um número inteiro positivo n de 4 algarismos decimais satisfaz às seguintes condições: I) a soma dos quadrados dos 1 e 4 algarismos é 58; II) a soma dos quadrados
1 Projeto Jovem Nota 10 1. (Fuvest 2000) Um número inteiro positivo n de 4 algarismos decimais satisfaz às seguintes condições: I) a soma dos quadrados dos 1 e 4 algarismos é 58; II) a soma dos quadrados
LISTA DE REVISÃO MENSAL 1º ANO 2º TRIMESTRE PROF. JADIEL
 LISTA DE REVISÃO MENSAL 1º ANO º TRIMESTRE PROF. JADIEL 1) (Unesp 016) Em um terreno retangular ABCD, de 0 m, serão construídos um deque e um lago, ambos de superfícies retangulares de mesma largura, com
LISTA DE REVISÃO MENSAL 1º ANO º TRIMESTRE PROF. JADIEL 1) (Unesp 016) Em um terreno retangular ABCD, de 0 m, serão construídos um deque e um lago, ambos de superfícies retangulares de mesma largura, com
DISCIPLINA: Matemática III PROFESSORA: Juliana Schivani ALUNO(a): Data: / /.
 DISCIPLINA: Matemática III PROFESSORA: Juliana Schivani ALUNO(a): Data: / /. 1. (Ufjf-pism 017) Qual é o polinômio que ao ser multiplicado por g(x) 3 x 2x 5x 4 tem como resultado o polinômio 6 5 4 h(x)
DISCIPLINA: Matemática III PROFESSORA: Juliana Schivani ALUNO(a): Data: / /. 1. (Ufjf-pism 017) Qual é o polinômio que ao ser multiplicado por g(x) 3 x 2x 5x 4 tem como resultado o polinômio 6 5 4 h(x)
Questão 1 (FGV) Sendo A o conjunto solução da inequação (x 2-5x) (x 2-8x + 12) < 0, assinale a alternativa correta: a) ; b) ; c) ;
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (FGV) Sendo A o conjunto solução da inequação (x 2-5x) (x 2-8x + 12) < 0, assinale
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (FGV) Sendo A o conjunto solução da inequação (x 2-5x) (x 2-8x + 12) < 0, assinale
Diagrama de Venn O diagrama de Venn representa conjunto da seguinte maneira:
 Conjuntos Introdução Lembramos que conjunto, elemento e relação de pertinência são considerados conceitos primitivos, isto é, não aceitam definição. Intuitivamente, sabemos que conjunto é uma lista, coleção
Conjuntos Introdução Lembramos que conjunto, elemento e relação de pertinência são considerados conceitos primitivos, isto é, não aceitam definição. Intuitivamente, sabemos que conjunto é uma lista, coleção
2. (Ita 2002) Com base no gráfico da função polinomial y = f(x) esboçado a seguir, responda qual é o resto da divisão de f(x) por (x - 1/2) (x 1).
 1 Projeto Jovem Nota 10 Polinômios Lista B Professor Marco Costa 1. (Fuvest 2002) As raízes do polinômio p(x) = x - 3x + m, onde m é um número real, estão em progressão aritmética. Determine a) o valor
1 Projeto Jovem Nota 10 Polinômios Lista B Professor Marco Costa 1. (Fuvest 2002) As raízes do polinômio p(x) = x - 3x + m, onde m é um número real, estão em progressão aritmética. Determine a) o valor
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
LISTA DE EXERCICIOS 1º TRIMESTRE 1º ANO PROF. JADIEL
 LISTA DE EXERCICIOS 1º TRIMESTRE 1º ANO PROF. JADIEL 1) (G1 - ifsp 016- MODIFICADA) Um pesquisador tem à disposição quatro frascos com a mesma substância. No frasco I, há um quarto de litro dessa substância;
LISTA DE EXERCICIOS 1º TRIMESTRE 1º ANO PROF. JADIEL 1) (G1 - ifsp 016- MODIFICADA) Um pesquisador tem à disposição quatro frascos com a mesma substância. No frasco I, há um quarto de litro dessa substância;
Nome: N.º Turma: Suficiente (50% 69%) Bom (70% 89%)
 Escola E.B.,3 Eng. Nuno Mergulhão Portimão Ano Letivo 01/013 Teste de Avaliação Escrita de Matemática 9.º ano de escolaridade Duração do Teste: 90 minutos 9 de abril de 013 Nome: N.º Turma: Classificação:
Escola E.B.,3 Eng. Nuno Mergulhão Portimão Ano Letivo 01/013 Teste de Avaliação Escrita de Matemática 9.º ano de escolaridade Duração do Teste: 90 minutos 9 de abril de 013 Nome: N.º Turma: Classificação:
Questão 1 (UFMG) Sendo A = 88 o 20', B = 31 o 40' e C = radianos, a expressão A + B - C é igual a: a) radianos b) 116 o 40' ;
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFMG) Sendo A = 88 o 20', B = 31 o 40' e C = radianos, a expressão A + B - C é
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFMG) Sendo A = 88 o 20', B = 31 o 40' e C = radianos, a expressão A + B - C é
DOS REAIS AOS DECIMAIS
 DOS REAIS AOS DECIMAIS Número é a sua representação Na sua origem, número é resultado dos processos de contagem ou de medida. Tais números precisam ter algum tipo de representação, para possibilitar as
DOS REAIS AOS DECIMAIS Número é a sua representação Na sua origem, número é resultado dos processos de contagem ou de medida. Tais números precisam ter algum tipo de representação, para possibilitar as
KmaraDikas da P2. 1) Determine o domínio das funções abaixo:
 KmaraDikas da P. ) Determine o domínio das funções abaio: f ( ) A) B) f ( ) 4 + f ( ) C) ) Determine a soma da(s) proposição(ões) Verdadeira(s). 0 A, tal que a ij i jentão 3 ( A t ) t 0 Se ( a ij ) 0 -
KmaraDikas da P. ) Determine o domínio das funções abaio: f ( ) A) B) f ( ) 4 + f ( ) C) ) Determine a soma da(s) proposição(ões) Verdadeira(s). 0 A, tal que a ij i jentão 3 ( A t ) t 0 Se ( a ij ) 0 -
Circunferências. λ : x y 4x 10y λ : x y 4x 5y 12 0
 Circunferências 1. (Espcex (Aman) 014) Sejam dados a circunferência λ : x y 4x 10y 5 0 e o ponto P, que é simétrico de ( 1, 1) em relação ao eixo das abscissas. Determine a equação da circunferência concêntrica
Circunferências 1. (Espcex (Aman) 014) Sejam dados a circunferência λ : x y 4x 10y 5 0 e o ponto P, que é simétrico de ( 1, 1) em relação ao eixo das abscissas. Determine a equação da circunferência concêntrica
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA Conjuntos. Rafael Carvalho 7º Período Engenharia Civil
 CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2016.2 Conjuntos Rafael Carvalho 7º Período Engenharia Civil Definição Noção intuitiva: São coleções de elementos da mesma espécie. - O conjunto de todos
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2016.2 Conjuntos Rafael Carvalho 7º Período Engenharia Civil Definição Noção intuitiva: São coleções de elementos da mesma espécie. - O conjunto de todos
Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Campus Curitiba Professor Gilmar Bornatto
 Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Campus Curitiba 1. Para fazer uma caixa sem tampa com um único pedaço de papelão, utilizou-se um retângulo de 16 cm de largura por 30 cm
Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Campus Curitiba 1. Para fazer uma caixa sem tampa com um único pedaço de papelão, utilizou-se um retângulo de 16 cm de largura por 30 cm
(UCSAL) Sejam os números reais x e y tais que 12 - x + (4 + y)i = y + xi. O conjugado do número complexo z = x + yi é:
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UCSAL) Sejam os números reais x e y tais que 12 - x + (4 + y)i = y + xi. O conjugado
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UCSAL) Sejam os números reais x e y tais que 12 - x + (4 + y)i = y + xi. O conjugado
Geometria Analítica. Distância entre dois pontos: (d AB ) 2 = (x B x A ) 2 + (y B y A ) 2 A( 7, 5 ) P( 5, 2 ) B( 3, 2 ) Q( 3, 4 ) d = 5.
 Erivaldo UDESC Geometria Analítica Distância entre dois pontos: (d AB ) 2 = (x B x A ) 2 + (y B y A ) 2 A( 7, 5 ) B( 3, 2 ) d 2 = ( 4 ) 2 + ( 3 ) 2 d = 5 P( 5, 2 ) Q( 3, 4 ) d 2 = ( 8 ) 2 + ( 6 ) 2 d =
Erivaldo UDESC Geometria Analítica Distância entre dois pontos: (d AB ) 2 = (x B x A ) 2 + (y B y A ) 2 A( 7, 5 ) B( 3, 2 ) d 2 = ( 4 ) 2 + ( 3 ) 2 d = 5 P( 5, 2 ) Q( 3, 4 ) d 2 = ( 8 ) 2 + ( 6 ) 2 d =
TREINANDO PARA AS AVALIAÇÕES DO 1º BIMESTRE PROF. OSMAR
 TREINANDO PARA AS AVALIAÇÕES DO 1º BIMESTRE PROF. OSMAR 1º ANO ENSINO MÉDIO - QUESTÕES DA APOSTILA 01 1. Considere os dez números abaixo : - 12 ; -0,5 ; 0,111 ; 1,333... ; π ; - 64 ; 12 ; 16 1 ; 5 ; 4
TREINANDO PARA AS AVALIAÇÕES DO 1º BIMESTRE PROF. OSMAR 1º ANO ENSINO MÉDIO - QUESTÕES DA APOSTILA 01 1. Considere os dez números abaixo : - 12 ; -0,5 ; 0,111 ; 1,333... ; π ; - 64 ; 12 ; 16 1 ; 5 ; 4
Atividades de Funções do Primeiro Grau
 Atividades de Funções do Primeiro Grau 1) Numa loja, o salário fio mensal de um vendedor é 500 reais. Além disso, ele recebe de comissão 50 reais por produto vendido. a) Escreva uma equação que epresse
Atividades de Funções do Primeiro Grau 1) Numa loja, o salário fio mensal de um vendedor é 500 reais. Além disso, ele recebe de comissão 50 reais por produto vendido. a) Escreva uma equação que epresse
 Escola Básica de Ribeirão (Sede) ANO LETIVO 0/0 Ficha de Trabalho outubro 0 Nome: N.º: Turma: 9.º Ano Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Números Reais
Escola Básica de Ribeirão (Sede) ANO LETIVO 0/0 Ficha de Trabalho outubro 0 Nome: N.º: Turma: 9.º Ano Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Números Reais
Atividades de Funções do Primeiro Grau
 Atividades de Funções do Primeiro Grau 1) Numa loja, o salário fio mensal de um vendedor é 500 reais. Além disso, ele recebe de comissão 50 reais por produto vendido. a) Escreva uma equação que epresse
Atividades de Funções do Primeiro Grau 1) Numa loja, o salário fio mensal de um vendedor é 500 reais. Além disso, ele recebe de comissão 50 reais por produto vendido. a) Escreva uma equação que epresse
Hewlett-Packard CONJUNTOS NUMÉRICOS. Aulas 01 a 08. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hewlett-Packard CONJUNTOS NUMÉRICOS Aulas 01 a 08 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 2019 Sumário CONJUNTOS NUMÉRICOS... 2 Conjunto dos números Naturais... 2 Conjunto dos números
Hewlett-Packard CONJUNTOS NUMÉRICOS Aulas 01 a 08 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 2019 Sumário CONJUNTOS NUMÉRICOS... 2 Conjunto dos números Naturais... 2 Conjunto dos números
Capítulo 1 Números Reais
 Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 1 Números Reais Conjuntos Numéricos Conjunto dos naturais: N = {1,, 3, 4,... } Conjunto dos inteiros: Z = {..., 3,, 1, 0, 1,, 3,... } {
Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 1 Números Reais Conjuntos Numéricos Conjunto dos naturais: N = {1,, 3, 4,... } Conjunto dos inteiros: Z = {..., 3,, 1, 0, 1,, 3,... } {
Matemática Conjuntos - Teoria
 Matemática Conjuntos - Teoria 1 - Conjunto: Conceito primitivo; não necessita, portanto, de definição. Exemplo: conjunto dos números pares positivos: P = {2,4,6,8,10,12,... }. Esta forma de representar
Matemática Conjuntos - Teoria 1 - Conjunto: Conceito primitivo; não necessita, portanto, de definição. Exemplo: conjunto dos números pares positivos: P = {2,4,6,8,10,12,... }. Esta forma de representar
max(x 2x + 2; 1+ x ) = 50, é igual a:
 . (Ufpr 0) Durante o mês de dezembro, uma loja de cosméticos obteve um total de R$ 900,00 pelas vendas de um certo perfume. Com a chegada do mês de janeiro, a loja decidiu dar um desconto para estimular
. (Ufpr 0) Durante o mês de dezembro, uma loja de cosméticos obteve um total de R$ 900,00 pelas vendas de um certo perfume. Com a chegada do mês de janeiro, a loja decidiu dar um desconto para estimular
// QUESTÃO 01 PROENEM 27/02/2019. A quantidade de números inteiros positivos n, que satisfazem a desigualdade: 3 7 < n 14 < 2 3 é
 MATEMÁTICA PROF. THIAGO LAINETTI // QUESTÃO 01 A quantidade de números inteiros positivos n, que satisfazem a desigualdade: 3 7 < n 14 < 2 3 é a) 2. b) 3. c) 4. d) 5. // QUESTÃO 02 Na bula de um analgésico,
MATEMÁTICA PROF. THIAGO LAINETTI // QUESTÃO 01 A quantidade de números inteiros positivos n, que satisfazem a desigualdade: 3 7 < n 14 < 2 3 é a) 2. b) 3. c) 4. d) 5. // QUESTÃO 02 Na bula de um analgésico,
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
Questão 01 EB EA = EC ED. 6 x = 3. x =
 Questão 0 Seja E um ponto eterno a uma circunferência. Os segmentos EA e ED interceptam essa circunferência nos pontos B e A, e, C e D, respectivamente. A corda AF da circunferência intercepta o segmento
Questão 0 Seja E um ponto eterno a uma circunferência. Os segmentos EA e ED interceptam essa circunferência nos pontos B e A, e, C e D, respectivamente. A corda AF da circunferência intercepta o segmento
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA Conjuntos. Isabelle Araujo 5º período de Engenharia de Produção
 CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2014.1 Conjuntos Isabelle Araujo 5º período de Engenharia de Produção Definição Noção intuitiva: São coleções de elementos da mesma espécie. - O conjunto
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2014.1 Conjuntos Isabelle Araujo 5º período de Engenharia de Produção Definição Noção intuitiva: São coleções de elementos da mesma espécie. - O conjunto
a) 10 b) 7 c) 0 d) 3 e) 4 6. (G1 - cftmg 2013) A soma das raízes da equação a) 7. b) 4. c) 3. d) 5.
 Equações Modulares 1. (Espcex (Aman) 015) O número de soluções da equação 1 x x = x, no conjunto, é a) 1. b). c). d) 4. e) 5.. (Ufsc 014) Assinale a(s) proposição(ões) CORRETA(S). x 1 01) O domínio da
Equações Modulares 1. (Espcex (Aman) 015) O número de soluções da equação 1 x x = x, no conjunto, é a) 1. b). c). d) 4. e) 5.. (Ufsc 014) Assinale a(s) proposição(ões) CORRETA(S). x 1 01) O domínio da
MATRIZ FORMAÇÃO E IGUALDADE
 MATRIZ FORMAÇÃO E IGUALDADE 1. Seja X = (x ij ) uma matriz quadrada de ordem 2, onde i + j para i = j ;1 - j para i > j e 1 se i < j. A soma dos seus elementos é igual a: a. -1 b. 1 c. 6 d. 7 e. 8 2. Se
MATRIZ FORMAÇÃO E IGUALDADE 1. Seja X = (x ij ) uma matriz quadrada de ordem 2, onde i + j para i = j ;1 - j para i > j e 1 se i < j. A soma dos seus elementos é igual a: a. -1 b. 1 c. 6 d. 7 e. 8 2. Se
x é igual a: 07. (Colégio Naval) No conjunto R dos números reais, qual será o 01. (PUC) O valor de m, de modo que a equação
 0. (PUC) O valor de m, de modo que a equação 5 m m 0 b) c) d) 0. Quantos valores de satisfazem a equação a) b) c) d) 5 e) 0 Prof. Paulo Cesar Costa tenha uma das raízes igual a, é: ( ). 07. (Colégio Naval)
0. (PUC) O valor de m, de modo que a equação 5 m m 0 b) c) d) 0. Quantos valores de satisfazem a equação a) b) c) d) 5 e) 0 Prof. Paulo Cesar Costa tenha uma das raízes igual a, é: ( ). 07. (Colégio Naval)
6. Considere. igual a : (A) f (x) + 2x f(x) = 0 (B) f (x) x f(x) = 0 (C) f (x) + f(x) = 0 (D) f (x) f(x) = 0 (E) f (x) 2x f(x) = 0
 QUESTÃO ÚNICA 0,000 pontos distribuídos em 50 itens Marque no cartão de respostas a única alternativa que responde de maneira correta ao pedido de cada item.. O valor da área, em unidades de área, limitada
QUESTÃO ÚNICA 0,000 pontos distribuídos em 50 itens Marque no cartão de respostas a única alternativa que responde de maneira correta ao pedido de cada item.. O valor da área, em unidades de área, limitada
CURSO PRF 2017 MATEMÁTICA
 AULA 001 1 MATEMÁTICA PROFESSOR AULA 001 MATEMÁTICA DAVIDSON VICTOR 2 AULA 01 - CONJUNTOS NUMÉRICOS CONJUNTO DOS NÚMEROS NATURAIS É o primeiro e o mais básico de todos os conjuntos numéricos. Pertencem
AULA 001 1 MATEMÁTICA PROFESSOR AULA 001 MATEMÁTICA DAVIDSON VICTOR 2 AULA 01 - CONJUNTOS NUMÉRICOS CONJUNTO DOS NÚMEROS NATURAIS É o primeiro e o mais básico de todos os conjuntos numéricos. Pertencem
BANCO DE QUESTÕES TURMA PM-PE FUNÇÕES
 01. (ESPCEX-AMAN/016) Considere as funções reais f e g, tais que f(x) x 4 e f(g(x)) x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis valores
01. (ESPCEX-AMAN/016) Considere as funções reais f e g, tais que f(x) x 4 e f(g(x)) x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis valores
SuperPro copyright Colibri Informática Ltda.
 1. (Fuvest-gv) Uma pesquisa de mercado sobre o consumo de três marcas A, B e C de um determinado produto apresentou os seguintes resultados: A - 48% A e B - 18% B - 45% B e C - 25% C - 50% A e C - 15%
1. (Fuvest-gv) Uma pesquisa de mercado sobre o consumo de três marcas A, B e C de um determinado produto apresentou os seguintes resultados: A - 48% A e B - 18% B - 45% B e C - 25% C - 50% A e C - 15%
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos
 Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Conjuntos. Parte I. Página 1. mdc x,y = 33;
 Parte I Conjuntos 1. (Ufsj 2013) O diagrama que representa o conjunto ( A B) C ( C B) A é a) b) c) d) 2. (Cefet MG 2013) Em uma enquete realizada com pessoas de idade superior a 30 anos, pesquisou-se as
Parte I Conjuntos 1. (Ufsj 2013) O diagrama que representa o conjunto ( A B) C ( C B) A é a) b) c) d) 2. (Cefet MG 2013) Em uma enquete realizada com pessoas de idade superior a 30 anos, pesquisou-se as
Matemática Básica. Fração geratriz e Sistema de numeração 1) 0, = ) 2, =
 Erivaldo UDESC Matemática Básica Fração geratriz e Sistema de numeração 1) 0,353535... = 35 99 2) 2,1343434... = 2134 21 99 0 Decimal (Indo-Arábico): 2107 = 2.10 3 + 1.10 2 + 0.10 1 + 7.10 0 Número de
Erivaldo UDESC Matemática Básica Fração geratriz e Sistema de numeração 1) 0,353535... = 35 99 2) 2,1343434... = 2134 21 99 0 Decimal (Indo-Arábico): 2107 = 2.10 3 + 1.10 2 + 0.10 1 + 7.10 0 Número de
ASSUNTO:POLINÔMIOS. a) Do 3º grau resp: m ±6 b) Do 2º grau resp: m=6 c) do 1 º grau m=-6
 ASSUNTO:POLINÔMIOS 1) Identifique as expressões abaixo que são polinômios: a) 3x 3-5x 2 +x-4 b) 5x -4 -x -2 +x-9 c) x 4-16 d)x 2 3 +2x+6 e) x 2 4 resp: a, c,d 2) Dado o polinômio P(x)= 2x 3-5x 2 +x-3.
ASSUNTO:POLINÔMIOS 1) Identifique as expressões abaixo que são polinômios: a) 3x 3-5x 2 +x-4 b) 5x -4 -x -2 +x-9 c) x 4-16 d)x 2 3 +2x+6 e) x 2 4 resp: a, c,d 2) Dado o polinômio P(x)= 2x 3-5x 2 +x-3.
Simulado AFA. 2. Sejam x e y números reais tais que: Então, o número complexo z = x + yi. é tal que z 3 e z valem, respectivamente: (D) i e 1.
 Simulado AFA 1. Uma amostra de estrangeiros, em que 18% são proficientes em inglês, realizou um exame para classificar a sua proficiência nesta língua. Dos estrangeiros que são proficientes em inglês,
Simulado AFA 1. Uma amostra de estrangeiros, em que 18% são proficientes em inglês, realizou um exame para classificar a sua proficiência nesta língua. Dos estrangeiros que são proficientes em inglês,
Aluno(a): Código: 2 Rua T-53 Qd. 92 Lt. 10/11 nº 1356 Setor Bueno
 Aluno(a): Código: Série: 3ª Turma: Data: / / 01. Numa fábrica de bichos de pelúcia, o custo para produção de um determinado modelo é de R$ 12,50 por unidade, mais um custo inicial de R$ 250,00. Determine
Aluno(a): Código: Série: 3ª Turma: Data: / / 01. Numa fábrica de bichos de pelúcia, o custo para produção de um determinado modelo é de R$ 12,50 por unidade, mais um custo inicial de R$ 250,00. Determine
Estudante: Circunferência: Equação reduzida da circunferência: Circunferência: Consideremos uma circunferência de centro C (a, b) e raio r.
 Gênesis Soares Jaboatão, de de 014. Estudante: Circunferência: Circunferência: A circunferência é o conjunto de todos os pontos de plano equidistantes de outro ponto C do mesmo plano chamado centro da
Gênesis Soares Jaboatão, de de 014. Estudante: Circunferência: Circunferência: A circunferência é o conjunto de todos os pontos de plano equidistantes de outro ponto C do mesmo plano chamado centro da
Resposta: f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo 5, 5 5, 5 3, 3. f(g(x) = x 5.
 1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
8º ANO. Lista extra de exercícios
 8º ANO Lista extra de exercícios . Determine os valores de x que tornam as equações a seguir verdadeiras. a) (x + 4)(x ) = 0 b) (x + 6)(x ) = 0 c) (x + )(6x 9) = 0 d) 4x(x ) = 0 e) 7x(x ) = 0. Determine
8º ANO Lista extra de exercícios . Determine os valores de x que tornam as equações a seguir verdadeiras. a) (x + 4)(x ) = 0 b) (x + 6)(x ) = 0 c) (x + )(6x 9) = 0 d) 4x(x ) = 0 e) 7x(x ) = 0. Determine
Questão 1 a) A(0; 0) e B(8; 12) b) A(-4; 8) e B(3; -9) c) A(3; -5) e B(6; -2) d) A(2; 3) e B(1/2; 2/3) e) n.d.a.
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
Matemática 1 INTRODUÇÃO 1 TEOREMA DAS RAÍZES COMPLEXAS 3 TEOREMA DAS RAÍZES RACIONAIS 2 TEOREMA DAS RAÍZES IRRACIONAIS. Exercício Resolvido 2
 Matemática Frente II CAPÍTULO 22 EQUAÇÕES POLINOMIAIS 1 INTRODUÇÃO Nos capítulos anteriores, durante o estudo de polinômios, já estudamos alguns teoremas que nos ajudam a encontrar as raízes de polinômios.
Matemática Frente II CAPÍTULO 22 EQUAÇÕES POLINOMIAIS 1 INTRODUÇÃO Nos capítulos anteriores, durante o estudo de polinômios, já estudamos alguns teoremas que nos ajudam a encontrar as raízes de polinômios.
Problemas do Segundo Grau
 Curso Preparatório Profmat 2013 Universidade Estadual de Santa Cruz Departamento de Ciências Exatas 13/08/2013 Questão 32 Exame de Acesso 2011 Quando Joãozinho tirou 9, 8 em uma prova, sua média subiu
Curso Preparatório Profmat 2013 Universidade Estadual de Santa Cruz Departamento de Ciências Exatas 13/08/2013 Questão 32 Exame de Acesso 2011 Quando Joãozinho tirou 9, 8 em uma prova, sua média subiu
ROTEIRO DE ESTUDOS Recuperação Semestral Turma(s) Professor ADM1, INF1, MET1. Pollyanna Sette Etapa(s) Disciplina 1ª e 2ª
 ROTEIRO DE ESTUDOS Recuperação Semestral Turma(s) Professor ADM, INF, MET Pollyanna Sette Etapa(s) Disciplina ª e 2ª Matemática CONTEÚDOS. CONJUNTOS (LISTAS e 2/ LIVRO: CAP. 2. CONJUNTOS NUMÉRICOS (LISTAS
ROTEIRO DE ESTUDOS Recuperação Semestral Turma(s) Professor ADM, INF, MET Pollyanna Sette Etapa(s) Disciplina ª e 2ª Matemática CONTEÚDOS. CONJUNTOS (LISTAS e 2/ LIVRO: CAP. 2. CONJUNTOS NUMÉRICOS (LISTAS
RLM - PROFESSOR CARLOS EDUARDO AULA 3
 AULA 3 Sucessões = sequências(numéricas) São conjuntos de números reais dispostos numa certa ordem. Uma sequência pode ser FINITA ou INFINITA. Ex: a) (3, 6, 9, 12) sequência finita P.A de razão 3 b) (5,
AULA 3 Sucessões = sequências(numéricas) São conjuntos de números reais dispostos numa certa ordem. Uma sequência pode ser FINITA ou INFINITA. Ex: a) (3, 6, 9, 12) sequência finita P.A de razão 3 b) (5,
Matemática (Prof. Lara) Lista de exercícios recuperação 2 semestre (3Ano) Fazer todos os exercícios e entregar no dia da prova (1 ponto)
 Matemática (Prof. Lara) Lista de exercícios recuperação 2 semestre (3Ano) Fazer todos os exercícios e entregar no dia da prova (1 ponto) 1-)(PUC_MG) Fatorar: (x + y) 2 - (x - y) 2 2-)De acordo com as identidades
Matemática (Prof. Lara) Lista de exercícios recuperação 2 semestre (3Ano) Fazer todos os exercícios e entregar no dia da prova (1 ponto) 1-)(PUC_MG) Fatorar: (x + y) 2 - (x - y) 2 2-)De acordo com as identidades
EXPRESSÕES E FUNÇÕES EXPONENCIAIS E LOGARITMICAS
 EXPRESSÕES E FUNÇÕES EXPONENCIAIS E LOGARITMICAS - 06. (Unicamp 06) Considere a função f() 5, definida para todo número real. a) Esboce o gráfico de y f() no plano cartesiano para. b) Determine os valores
EXPRESSÕES E FUNÇÕES EXPONENCIAIS E LOGARITMICAS - 06. (Unicamp 06) Considere a função f() 5, definida para todo número real. a) Esboce o gráfico de y f() no plano cartesiano para. b) Determine os valores
PROFESSOR FLABER 2ª SÉRIE Circunferência
 PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
EFOMM , sabendo-se que I 1 corresponde ao ruído sonoro de 8 decibéis de uma aproximação de dois. metro quadrado.
 EFOMM 009 (0) Qual é o número inteiro cujo produto por 9 é um número natural composto apenas pelo algarismo? (A) 459 (B) 4569 (C) 45679 (D) 45789 (E) 456789. (0) O logotipo de uma certa Organização Militar
EFOMM 009 (0) Qual é o número inteiro cujo produto por 9 é um número natural composto apenas pelo algarismo? (A) 459 (B) 4569 (C) 45679 (D) 45789 (E) 456789. (0) O logotipo de uma certa Organização Militar
01. D e m o n s t r a r q u e s e. 02. Mostre que se a 1 a2
 Série Professor(a) Aluno(a) Rumo ao ITA Marcelo Mendes Sede Turma Turno Data N / / Ensino Pré-Universitário TC Matemática Revisão de Álgebra OSG.: 85/0 Exercícios de Fixação 0. Encontre os valores das
Série Professor(a) Aluno(a) Rumo ao ITA Marcelo Mendes Sede Turma Turno Data N / / Ensino Pré-Universitário TC Matemática Revisão de Álgebra OSG.: 85/0 Exercícios de Fixação 0. Encontre os valores das
00. Qual o nome do vaso sangüíneo que sai do ventrículo direito do coração humano?
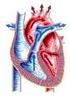 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/889) CONCURSO DE ADMISSÃO À ª SÉRIE DO ENSINO MÉDIO 006/007 DE OUTUBRO DE 006 INSTRUÇÕES AOS CANDIDATOS 0. Duração da prova: 0
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/889) CONCURSO DE ADMISSÃO À ª SÉRIE DO ENSINO MÉDIO 006/007 DE OUTUBRO DE 006 INSTRUÇÕES AOS CANDIDATOS 0. Duração da prova: 0
Unidade I MATEMÁTICA. Prof. Celso Ribeiro Campos
 Unidade I MATEMÁTICA Prof. Celso Ribeiro Campos Números reais Três noções básicas são consideradas primitivas, isto é, são aceitas sem a necessidade de definição. São elas: a) Conjunto. b) Elemento. c)
Unidade I MATEMÁTICA Prof. Celso Ribeiro Campos Números reais Três noções básicas são consideradas primitivas, isto é, são aceitas sem a necessidade de definição. São elas: a) Conjunto. b) Elemento. c)
PROFESSOR: ALEXSANDRO DE SOUSA
 E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO Conjuntos Numéricos PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net MATEMÁTICA, 9º Ano Pontos no plano cartesiano/pares ordenados
E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO Conjuntos Numéricos PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net MATEMÁTICA, 9º Ano Pontos no plano cartesiano/pares ordenados
Conjuntos. Ou ainda por diagrama (diagrama de Venn-Euler):
 Capítulo 1 Conjuntos Conjunto é uma coleção de objetos, não importando a ordem ou quantas vezes algum objeto apareça, exemplos: Conjunto dos meses do ano; Conjunto das letras do nosso alfabeto; Conjunto
Capítulo 1 Conjuntos Conjunto é uma coleção de objetos, não importando a ordem ou quantas vezes algum objeto apareça, exemplos: Conjunto dos meses do ano; Conjunto das letras do nosso alfabeto; Conjunto
Banco de questões. 4 Função quadrática. ) é igual a 60. ( ( )) por g( x) é igual ( ) = 5 ( ) = ( ) e g( f ( 7) funções UNIDADE I I
 UNIDADE I I funções CAPÍTULO Função quadrática Banco de questões 1 (FURG RS) Determine os números reais a e b b para que a função quadrática f x a x x a tenha valor máximo no ponto x = 3 e que esse valor
UNIDADE I I funções CAPÍTULO Função quadrática Banco de questões 1 (FURG RS) Determine os números reais a e b b para que a função quadrática f x a x x a tenha valor máximo no ponto x = 3 e que esse valor
Posição Relativa. 1. Quatro pontos distintos e não coplanares determinam exatamente: (A) 1 plano (B) 2 planos (C) 3 planos (D) 4 planos (E) 5 planos.
 SEI Ensina MILITAR Matemática Posição Relativa 1. Quatro pontos distintos e não coplanares determinam exatamente: (A) 1 plano (B) 2 planos (C) 3 planos (D) 4 planos (E) 5 planos. 2. Considere as seguintes
SEI Ensina MILITAR Matemática Posição Relativa 1. Quatro pontos distintos e não coplanares determinam exatamente: (A) 1 plano (B) 2 planos (C) 3 planos (D) 4 planos (E) 5 planos. 2. Considere as seguintes
