F 01. Coordenadas na reta
|
|
|
- Isaac Lacerda Antunes
- 9 Há anos
- Visualizações:
Transcrição
1 IME IT
2 postila IT F 1 Coordenadas na reta Uma reta diz-se orientada quando sobre ela se escolheu um sentido de percurso, chamada positivo; o sentido inverso chama-se negativo. Numa reta orientada, diz-se que o ponto B está à direita do ponto (portanto que o ponto está à esquerda de B ) quando o sentido de percurso de para B é positivo. Um eio é uma reta orientada na qual se fiou um ponto O, chamado a origem. Todo eio E pode ser posto, de modo natural, em correspondência biunívoca com o conjunto dos números reais. À origem O do eio faz-se corresponder o número zero. cada ponto X de E à direita de O corresponde um número real positivo, a saber, a distância (, ) d O X de X à origem O. os pontos situados à esquerda de O correspondem números reais negativos, cujos valores absolutos medem as distâncias desses pontos à origem. = d O, X se ssim, ao ponto X em E corresponde o número real tal que ( ) X está à direita de O e = d( O, X) se X está à esquerda de O. Se ao ponto X do eio E corresponde, da maneira acima indicada, o número real, diz-se que é a coordenada do ponto X. seta indica o sentido de percurso sobre o eio E, cuja origem é o ponto O, os pontos à direita de O têm coordenadas positivas; os outros, negativa Dados os pontos X e Y sobre o eio E, se suas coordenadas são e respectivamente então a distância do ponto X ao ponto Y é d( X, Y) = =, isto é, tem-se d( X, Y) = se e d( X, Y) = se. Para provar esta afirmação, lembraremos que a distância entre os pontos e B é um número d(, B), que d( B, ) = d( B, ) e que se, B e C são pontos sobre a mesma reta e B está entre e C então (, ) = (, ) + (, ) d C d B d B C Se X = Y, então não há o que provar. Suponhamos, inicialmente, que X esteja à esquerda de Y, ou seja, que <. Há 3 casos a considerar:
3 Matemática 1) X e Y estão à direita da origem, isto é, O< < ; ) X e Y estão à esquerda da origem, ou seja, < < O; 3) X e Y estão em lados opostos da origem, logo < O<. Provando que d( X, Y) =. - No primeiro caso, X está entre O e Y. lém disso, tem-se d( O, X) d( O, Y) =. Segue-se que (, ) (, ) (, ) d O X + d X Y = d O Y, donde (, ) (, ) (, ) d X Y = d O Y d O X = =. - No segundo caso, Y está entre X e O, sendo agora d( O, X) d( O, Y) =. Então (, ) + (, ) = (, ) d O Y d Y X d O X logo d( X, Y) = d( Y, X) = d( O, X) d( O, Y) = + = =. - No terceiro caso, O está entre e, com d( O, X) (, ) (, ) (, ) d X Y = d X O + d O Y = + =. = e = e = e d( O, Y) =. Então Se X estiver à direita de Y a demonstração se faz de modo análogo. Eemplo 1. Sejam, X e Y pontos de coordenadas a e respectivamente, no eio E. Diz-se que Y é o simétrico de X relativamente quando é o ponto médio do segmento cujas etremidades são X e Y. Ou se tem < a < com
4 postila IT a = a, ou < a < com a = a. Em qualquer caso, conclui-se que = a. função s : E E, que associa a cada ponto X do eio E o seu simétrico Y em relação a, chama-se a simetria (ou refleão) em torno do ponto. Se X ' é outro ponto de E com coordenada ' tem-se ( ( ),( ')) = ( ') = ' = (, ') d s X X a a d X X igualdade d( s( X), s( X ')) d( X, X ') =, válida para quaisquer pontos X, X ' se eprime dizendo que a função s : E E preserva as distâncias, ou é uma isometria de E. Eemplo. Outro tipo de isometria de um eio E são as translações. Uma translação t: E E é determinada por um número a. cada ponto X de coordenada em t X, de coordenada + a. Se X ' é outro ponto de E, t faz corresponder o ponto ( ) E, de coordenada ', temos ( ( ), ( ')) ( ' ) ' (, ') d t X t X = + a + a = = d X X. Portanto t preserva distâncias. Um caso particular de translação é a função identidade t( X) = X, que corresponde a tomar a = na definição acima. Uma simetria s e uma translação t do eio E são ambas isometrias mas há duas diferenças cruciais entre elas: a primeira é que s inverte enquanto t preserva orientação. Se X está à esquerda de X ' então s ( X ) está à direita de s( X ') enquanto t( X ) está à esquerda de t( X '). segunda diferença é que s possui um = X se, e somente se X =. Por outro lado, uma translação único ponto fio: s ( X) X ) eceto quando é a função identidade, e neste caso todos os pontos de E são fios. t não possui pontos fios (isto é, tem-se t( X) Coordenadas no Plano o conjunto formado pelos pares ordenados ( ) Indica-se com,, onde e são números reais. Dados (, ) e ( ', ') em, tem-se (, ) = ( ', ' ) se, e somente se, = ' e = '. O número chama-se a primeira coordenada e o número a segunda coordenada do par (, ). Observe, por eemplo, que os pares ordenados ( ) ( 3, ) são diferentes pois a primeira coordenada de ( ), 3 e, 3 é enquanto que a 3
5 Matemática primeira coordenada de ( 3, ) é 3. Por outro lado, os conjuntos {, 3 } e { } 3, são iguais pois um objeto pertence a um deles se, e somente se, pertence ao outro. Portanto, um par ordenado não é a mesma coisa que um conjunto com elementos., pode-se ter, pode-se ter = mas se No par ordenado ( ) = mas se { } {, } é um conjunto com elementos tem-se necessariamente Y. O X Sistema de eios ortogonais Um sistema de eios ortogonais num plano Π é um par de eios OX e OY, tornados em Π, que são perpendiculares e têm a mesma origem O. Diz-se que o eio OX é horizontal e o eio OY é vertical. Um plano Π munido de um sistema de eios ortogonais põe-se, de modo natural, em correspondência biunívoca com. Dado o ponto P do plano, baiamos por ele paralelas ao eios OY e OX. Essas paralelas cortam os eios em pontos cujas coordenadas são e respectivamente. o ponto P do plano Π faz-se então corresponder o par ordenado (, ) R. Reciprocamente, a cada par ordenado (, ) R corresponde o ponto P Π, interseção da paralela a OY traçada pelo ponto de coordenada com a paralela a OX traçada a partir do ponto de OY cuja coordenada é. Os números e chamam-se as coordenadas (cartesianas) do ponto P relativamente ao sistema de eio ortogonais fiado: é a abscissa e a ordenada de P. No que se segue, a menos que seja feita eplicitamente uma menção em contrário, admitiremos que foi fiado um sistema de eios ortogonais no plano, que assim se identificada a P =, do plano passa a ser a mesma. Cada ponto ( ) coisa que um par ordenado de números reais. Os eios ortogonais decompõem o plano em quatro regiões, chamadas quadrantes. Tem-se o primeiro quadrante, formado pelos pontos que têm ambas coordenadas positivas. No segundo quadrante, a abscissa é negativa e a ordenada é positiva. No terceiro, abscissa e ordenada são ambas negativas. No quarto quadrante, os pontos têm abscissa positiva e ordenada negativa. 4
6 postila IT Y º Quadrante 1 P 1 P 1º Quadrante X P 3 3 3º Quadrante 4 4º Quadrante P 4 Coordenadas cartesianas e quadrantes no plano. Evidentemente, os pontos do eio OX das abscissas têm coordenadas (,) e no eio das ordenadas OY os pontos são da forma (, ). O ponto O, origem dos eios, tem coordenadas (, ). Embora utilizemos neste livro eclusivamente sistemas de eios ortogonais, isto não é uma necessidade absoluta da Geometria nalítica. Dados dois eios concorrentes quaisquer, o processo acima descrito permite estabelecer uma correspondência biunívoca entre pontos do plano e pares ordenados de números reais. Na maior parte dos casos não há motivos para se optar por um sistema de eios não-ortogonais mas há algumas situações em que isto pode ser vantajoso. É possível desenvolver a Geometria nalítica usando eios que formam ângulos diferentes de 9. Tal modificação afeta todas as propriedades ligadas ao conceito de distância. Outras propriedades (por eemplo, as relacionadas com colinearidade) não são afetadas por esta mudança. Y P O X Coordenadas cartesianas não-regulares. 5
7 Matemática O uso de um par de eios (ortogonais ou não), não é a única maneira de se estabelecer correspondências entre pontos do plano e pares ordenados de números reais. No sistema de coordenadas polares usa-se um único eio OX. Distância entre dois pontos Dados os pontos P1 = ( 1, 1) e P (, ) distância ( 1, ) novo ponto Q = (, ). =, queremos obter a epressão da d P P em termos das coordenadas de P 1 e P. Para isso, introduzirmos o 1 P P 1 1 Q 1 Como 1 PPQ é retângulo. Sua hipotenusa mede (, ). 1 d P1 P e seus catetos medem 1 e Como P 1 e Q têm a mesma ordenada, o segmento PQ 1 é horizontal (paralelo ao eio OX ). nalogamente, o segmento P Q é vertical (paralelo a OY ). Portanto P 1 P é a hipotenusa do triângulo retângulo PPQ. 1 Pelo visto na seção 1, os catetos deste triângulo medem 1 e 1. Resulta então do Teorema de Pitágoras que 6 (, ) ( ) ( ) d P P = +. Divisão de um segmento O ponto C divide o segmento B em uma razão k, ou seja C k B =, as coordenadas de C são = (1 k) + k c a b
8 postila IT c = (1 k) a + k b, a, a, B( b, b) e C( c, c). 1 Caso k =, chamaremos o ponto C de ponto médio. onde ( ) 1. Determine a distância entre os pontos:,3 B 5,7 a) ( ) e ( ) b) ( 1, ) e B ( 11,5 ) c) ( 1, 3) e B( 4, ) d) ( 3, ) e B( 5, 4) Eercícios. (UnB) No plano cartesiano, os pontos = (, ), B = ( 1, 5) e ( 6, 1) D = são vértices do paralelogramo BCD. Determine a soma das coordenadas do vértice C. C D B 3. Determine as coordenadas dos pontos que dividem o segmento B em três partes 1, 4 B 5,1. iguais, onde ( ) e ( ) 4. Demonstre que as coordenadas do baricentro de um triângulo de vértices a + b + c a + b + c ( a, a), B( b, b) e C( c, c) é dado por G, (UnB) Um triângulo inscrito num círculo tem dois vértices ( 3, 9 ) e ( ) 11, 3 sobre pontos etremos de um dos diâmetros. O terceiro vértice está colocado de tal,, modo que a altura h do triângulo seja a máima possível. Se ( ) e ( ) 1 1 são as possíveis soluções para o 3 o vértice, calcule
9 Matemática 6. (PS-UnB) O diagrama a seguir representa o mapa da região central de uma cidade planejada. Cada quadradinho simboliza uma quadra cujo lado mede 1 m e cada linha representa uma rua. No sistema de coordenadas cartesianas traçado, de origem C, o par ordenado (, ) representa o ponto que está a metros da origem, no sentido do oeste ( O ) para o leste ( L ), e a metros da origem, no sentido de sul ( S ) para o norte ( N ). Os pontos e B simbolizam duas escolas públicas e a origem C representa a estação rodoviária. C B O N S L dmitindo a cidade plana, julgue os itens que se seguem. (1) Considere que um passageiro, ao desembarcar na rodoviária com a intenção de chegar ao fórum, tenha recebido a seguinte orientação: caminhe 5m para leste; depois, 4 m para norte; e 9 m para oeste; em seguida 6 m para sul e, finalmente, 1 m para leste. Nessas condições, é correto concluir que o informante poderia ter indicado um trajeto mais curto para que o passageiro chegasse ao fórum, como, por eemplo, caminhar 5 m para oeste e 4 m para sul. () Se a prefeitura localiza-se em ( 9, 3) e a biblioteca municipal em (3, 9), então a distância, em linha reta, entre esses dois locais públicos é superior a 1.8m. 8
10 postila IT F linhamento de 3 pontos e área de um triângulo Sejam (, ), B(, ) e (, ) Sendo D o determinante obtido por B B C três pontos de um plano cartesiano. C 1 D = B B 1, tem-se que: 1 C C * D =, B e C são colineares; * D, B e C são vértices de um triângulo cuja área S é dada por: S = 1 C D 1. Sendo (, ), ( 3, 4) Eercícios B e C( 5,1), julgue os itens a seguir. (1) O perímetro do triângulo BC é igual a ( 4 ) +. () área do triângulo BC é igual a 56 ua... (3) O ponto (,7 ) pertence ao lado BC.. Calcule a área do pentágono não-conveo BCDE da figura E D B C
11 3. Julgue os itens a seguir. (1) Se os vértices de um triângulo de área 5 ua.. são (5, 3) Matemática, (,) B e C( 1, 3), então é igual a 5/3. () Se o baricentro do triângulo OPQ da figura é o ponto ( 3, ), então o segmento PQ tem medida menor que 1. Q P (3) Se os pontos ( 3, 5), B(1, 1) e C (, 16) pertencem a uma mesma reta, então é um número inteiro. (4) Em um sistema cartesiano ortogonal, a área do quadrilátero de vértices (, ), B (, 5), C ( 4, 6) e D ( 6, ) é igual a 44. 3, C, 1 ; M é (5) Os vértices de um triângulo são os pontos ( 1, ) k, B ( ) e ( ) o ponto médio de B e N é o ponto médio de BC. Se a área do triângulo MCN é igual a, ua.., então k é igual a 18 / Calcule a área do pentágono conveo cujos vértices são (, ), ( 6, 6 ), ( ) ( 1, 6 ) e ( 5, 8 ). 5, 1, 1
12 postila IT F 3 Uma equação da reta é uma equação que relaciona a abscissa ( ) e a ordenada ( ) de tal forma que todo par (, ) que satisfaz a equação pertence à mesma reta. Equação geral da reta equação a + b + c = é conhecida como equação geral da reta. Como dados dois pontos distintos determinam uma única reta, podemos determinar a equação geral da reta que passa pelos pontos e B aplicando a condição de alinhamento, como no eemplo seguinte. Eemplo: Determine a equação geral da reta que passa pelos pontos (,3 ) e ( 1, 4 )? Resolução: Sendo (, ) pontos (,3 ) e ( ) um ponto pertencente a tal reta, este ponto juntamente com os 1, 4 são colineares. plicando a condição de alinhamento temos: = = + 5=. Equação reduzida da reta equação = m + n é conhecida como equação reduzida da reta, onde os coeficientes m e n são conhecidos como coeficiente angular e coeficiente linear, respectivamente. Inclinação inclinação de uma reta é o ângulo formado entre o eio das abscissas no sentido positvo e a reta, medido no sentido anti-horário. 11
13 Matemática r O Observando a figura a seguir temos notamos que m = tg α, pois: P(, ) (, ) O m = tg α= tg ( ) tg = α ( tg ) = tg α + α, ou seja, o coeficiente angular é igual a tangente da inclinação. Outro meio de se obter o coeficiente angular é através de dois pontos distintos pertencentes a reta. Desta forma temos: 1 Δ tg α= = Δ 1 1 b 1 1
14 postila IT Eercícios 1. Determine a equação geral da reta que passa pelos pontos: a) ( 1, ) e ( 3,5 ) 3, 5 b) (,1 ) e ( ). (Unifor CE) Na figura abaio tem-se um triângulo equilátero de lado 6 e cujos vértices, B, C situam-se sobre os eios cartesianos. C B equação da reta suporte do lado BC é 3. (UFPB PB) Determine a equação da reta cujo gráfico está representado no plano cartesiano ao lado (UERJ RJ) área do triângulo formado pela reta = com os eios coordenados vale: a) 6 b) 8 c) 9 d) 1 e) 1 13
15 Matemática 5. (UFF RJ) Determine a equação da reta r, representada na figura abaio, sabendo que O = OB e B = 5.. B r O. 6. (Unifor CE) Considere a reta r, representada na figura abaio. Sua equação é: a) 3 + = 1+ 3 b) 3 = 1 3 c) 3 + = 1 3 d) 3 = 1+ 3 e) 3 + = 3 7. (Unifor CE) nalise a figura abaio r 1 45 s O coeficiente angular da reta r é 14
16 postila IT a) b) 1 1 c) 1 d) e) 3 3 r tem inclinação de 135 e passa pelo ponto P ( 3,5). Determine a equação da reta r que é perpendicular à reta r 1 e passa pelo ponto Q5,3. ( ) 8. (EFEI MG) Uma reta 1 9. (PUC - RG) área do trapézio determinado pelas retas = 3 ; = 4 ; = e = é: a) 7,5 b) 7 c) 6,5 d) 6 e) 5,5 15
17 Matemática F 4 Equação segmentária da reta Sejam p e q os pontos em que a reta r intercepta os eios cartesianos. equação segmentária da reta r é dada por + = 1 p q partir da equação geral da reta podemos chegar a equação segmentárica da seguinte forma a + b + c = 16 a + b = c a b 1 c + c = + = 1 c c a b + = 1 p q Equação paramétrica da reta s equações paramétricas são equações que relacionam as coordenadas através de um parâmetro, ou seja, outra variável nos ajuda a calcular uma abscissa e uma ordenada.
18 postila IT equação paramétrica de uma reta é dada por = a t+ b, = a t + b Onde a, a, b e b são coeficientes e t é o parâmetro. b b pertence a reta e os coeficientes a e a são iguais a a = k cos α e b = k sen α, onde α é inclinação da reta e k depende do parâmetro, ou seja, podemos escolher o parâmetro de tal modo que a = cos α e b = sen α. Deste modo, sendo r uma reta que passa pelo, e possui inclinação α poderá ter a seguinte equação paramétrica Na equação paramétrica da reta o par ordenado (, ) ponto ( ) = cos α t+ = sen α t +. Para se obter a equação reduzida da reta a partir da equação paramétrica basta isolar o parâmetro em uma equação e substituir na outra, como segue: t = cos α = sen α + cos α sen α = ( ) + cos α ( ) = tg α + = m + n. 17
19 Matemática Eercícios 1. (VUNESP) área da região triangular limitada pelas retas: + = 1 e = é igual a: 4 3 a) 9 b) 7 c) 18 d) 1 e) 6 + = 1 ; 3. (USP) equação da reta representada no gráfico cartesiano abaio é: a) = b) = c) = d) = e) = 3. (Unificado RJ) equação da reta mostrada na figura abaio é :
20 postila IT a) = b) = c) = d) 4 3 1= e) = 4. (UFMT MT) Num determinado instante t (em minutos), as posições de duas partículas P e Q são dadas, respectivamente, pelas equações paramétricas das = 1+ t = 4 + t retas e. = 1+ t = 3 + 6t partir das informações dadas, julgue os itens. 5, 3.. s trajetórias se interceptam no ponto ( ) 1. s partículas se chocam no ponto ( 5, 3 ).. partícula Q passa, em ( 5, 3 ), 1 minuto depois que a partícula P. 5. Dadas as equações paramétricas, obtenha a equação geral de cada reta a seguir: a) = 5 t + = 4 t + 3 b) = 6 t + 9 = 7 6. Determine a equação paramétrica da reta que passa pelos pontos (1,) e (5, 5). 7. Determene a equação paramétrica da reta que possui inclinação de 3 e passa pelo ponto (,3 ). 8. Dada a equação geral, obtenha um par de equações paramétrica, usando a substituição sugerida, em cada caso a seguir. a) = ; use = 4 t 1. b) = ; use = 4 t 3. c) = ; use = 3 t 1. 19
21 Matemática
22 IME IT
Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Analítica 3º Ano APROFUNDAMENTO/REFORÇO
 Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Analítica 3º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre 2012 Aluno(a): Número: Turma: 1) Resolva
Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Analítica 3º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre 2012 Aluno(a): Número: Turma: 1) Resolva
1 Geometria Analítica Plana
 UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
Geometria Analítica? Onde usar os conhecimentos. os sobre Geometria Analítica?
 X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
Coordenadas e distância na reta e no plano
 Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Capítulo 1 Coordenadas e distância na reta e no plano 1. Introdução A Geometria Analítica nos permite representar pontos da reta por números reais, pontos do plano por pares ordenados de números reais
Coordenadas Cartesianas
 1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
Matemática Régis Cortes GEOMETRIA ANALÍTICA
 GEOMETRI NLÍTIC 1 GEOMETRI NLÍTIC Foi com o francês René Descartes, filósofo e matemático que surgiu a geometria analítica. issetriz dos quadrantes pares º QUDRNTE ( -, + ) Y ( eio das ORDENDS ) 1º QUDRNTE
GEOMETRI NLÍTIC 1 GEOMETRI NLÍTIC Foi com o francês René Descartes, filósofo e matemático que surgiu a geometria analítica. issetriz dos quadrantes pares º QUDRNTE ( -, + ) Y ( eio das ORDENDS ) 1º QUDRNTE
Exercícios de Matemática Geometria Analítica
 Eercícios de Matemática Geometria Analítica. (UFRGS) Considere um sistema cartesiano ortogonal e o ponto P(. ) de intersecção das duas diagonais de um losango. Se a equação da reta que contém uma das diagonais
Eercícios de Matemática Geometria Analítica. (UFRGS) Considere um sistema cartesiano ortogonal e o ponto P(. ) de intersecção das duas diagonais de um losango. Se a equação da reta que contém uma das diagonais
SERVIÇO PÚBLICO FEDERAL Ministério da Educação
 SERVIÇO PÚLICO FEDERL Ministério da Educação Universidade Federal do Rio Grande Universidade berta do rasil dministração acharelado Matemática para Ciências Sociais plicadas I Rodrigo arbosa Soares Curso
SERVIÇO PÚLICO FEDERL Ministério da Educação Universidade Federal do Rio Grande Universidade berta do rasil dministração acharelado Matemática para Ciências Sociais plicadas I Rodrigo arbosa Soares Curso
Apostila de Geometria Analítica Prof. Luciano Soares Pedroso 1º período de Agronomia e Engenharia Ambiental
 postila de Geometria nalítica º período de gronomia e Engenharia mbiental luno(a): data: / /0 GEOMETRII NLÍÍTIIC.. O PLNO CRTESIINO Y ( eio das ORDENDS ) issetriz dos quadrantes pares issetriz dos quadrantes
postila de Geometria nalítica º período de gronomia e Engenharia mbiental luno(a): data: / /0 GEOMETRII NLÍÍTIIC.. O PLNO CRTESIINO Y ( eio das ORDENDS ) issetriz dos quadrantes pares issetriz dos quadrantes
Geometria Analítica retas equações e inclinações, distância entre dois pontos, área de triângulo e alinhamento de 3 pontos.
 Geometria Analítica retas equações e inclinações, distância entre dois pontos, área de triângulo e alinhamento de pontos. 1. (Ufpr 014) A figura abaixo apresenta o gráfico da reta r: y x + = 0 no plano
Geometria Analítica retas equações e inclinações, distância entre dois pontos, área de triângulo e alinhamento de pontos. 1. (Ufpr 014) A figura abaixo apresenta o gráfico da reta r: y x + = 0 no plano
Ponto 1) Representação do Ponto
 Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
Matemática B Extensivo V. 6
 GRITO Matemática Etensivo V. 6 Eercícios 0) E 0) 0) omo essas retas são perpendiculares, temos que o coeficiente angular de uma das retas é o oposto e inverso da outra, ou seja, m reta. m reta a + a a
GRITO Matemática Etensivo V. 6 Eercícios 0) E 0) 0) omo essas retas são perpendiculares, temos que o coeficiente angular de uma das retas é o oposto e inverso da outra, ou seja, m reta. m reta a + a a
Professor Mascena Cordeiro
 www.mascenacordeiro.com Professor Mascena Cordeiro º Ano Ensino Médio M A T E M Á T I C A. Determine os valores de m pertencentes ao conjunto dos números reais, tal que os pontos (0, -), (, m) e (-, -)
www.mascenacordeiro.com Professor Mascena Cordeiro º Ano Ensino Médio M A T E M Á T I C A. Determine os valores de m pertencentes ao conjunto dos números reais, tal que os pontos (0, -), (, m) e (-, -)
Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b. a) a = 3, b, b R. b) a = 3 e b = 1. c) a = 3 e b 1. d) a 3
 01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
Matemática B Extensivo V. 7
 GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
LISTA DE REVISÃO DE GEOMETRIA 2ºANO PROF. JADIEL
 LISTA DE REVISÃO DE GEOMETRIA ºANO PROF. JADIEL 1. (Eear) Sejam A(, ), B(, 1), C(5, ) e D( 1, ) vértices de um quadrilátero conveo. A medida de uma de suas diagonais é a) 15 b) 1 c) 1 d) 10. (Upe-ssa )
LISTA DE REVISÃO DE GEOMETRIA ºANO PROF. JADIEL 1. (Eear) Sejam A(, ), B(, 1), C(5, ) e D( 1, ) vértices de um quadrilátero conveo. A medida de uma de suas diagonais é a) 15 b) 1 c) 1 d) 10. (Upe-ssa )
Módulo de Geometria Anaĺıtica 1. 3 a série E.M.
 Módulo de Geometria Anaĺıtica 1 Equação da Reta. 3 a série E.M. Geometria Analítica 1 Equação da Reta. 1 Exercícios Introdutórios Exercício 1. Determine a equação da reta cujo gráfico está representado
Módulo de Geometria Anaĺıtica 1 Equação da Reta. 3 a série E.M. Geometria Analítica 1 Equação da Reta. 1 Exercícios Introdutórios Exercício 1. Determine a equação da reta cujo gráfico está representado
Geometria Analítica - AFA
 Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
GEOMETRIA ANALÍTICA. 2) Obtenha o ponto P do eixo das ordenadas que dista 10 unidades do ponto Q (6, -5).
 GEOMETRIA ANALÍTICA Distância entre Dois Pontos Sejam os pontos A(xA, ya) e B(xB, yb) e sendo d(a, B) a distância entre eles, temos: Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem: [d
GEOMETRIA ANALÍTICA Distância entre Dois Pontos Sejam os pontos A(xA, ya) e B(xB, yb) e sendo d(a, B) a distância entre eles, temos: Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem: [d
EXERCÍCIOS DE FIXAÇÃO MATEMÁTICA II 3 a SÉRIE ENSINO MÉDIO INTEGRADO GEOMETRIA ANALÍTICA
 EXERCÍCIOS DE FIXAÇÃO MATEMÁTICA II a SÉRIE ENSINO MÉDIO INTEGRADO GEOMETRIA ANALÍTICA ******************************************************************************** 1) (U.F.PA) Se a distância do ponto
EXERCÍCIOS DE FIXAÇÃO MATEMÁTICA II a SÉRIE ENSINO MÉDIO INTEGRADO GEOMETRIA ANALÍTICA ******************************************************************************** 1) (U.F.PA) Se a distância do ponto
Matemática B Intensivo V. 2
 Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Capítulo 3 - Geometria Analítica
 1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
Matemática B Semi-Extensivo V. 3
 GRITO Matemática Semi-Etensivo V. (, e (, M, Então: M = M = M = M = Eercícios D Substituindo em I, temos: = =. = = Então, = ( = 8 M(, (, (, M = M = 8 M = M = D Sabendo que o eio é o da abcissa e que o
GRITO Matemática Semi-Etensivo V. (, e (, M, Então: M = M = M = M = Eercícios D Substituindo em I, temos: = =. = = Então, = ( = 8 M(, (, (, M = M = 8 M = M = D Sabendo que o eio é o da abcissa e que o
A(500, 500) B( 600, 600) C(715, 715) D( 1002, 1002) E(0, 0) F (711, 0) (c) ao terceiro quadrante? (d) ao quarto quadrante?
 Universidade Federal de Ouro Preto Departamento de Matemática MTM131 - Geometria Analítica e Cálculo Vetorial Professora: Monique Rafaella Anunciação de Oliveira Lista de Exercícios 1 1. Dados os pontos:
Universidade Federal de Ouro Preto Departamento de Matemática MTM131 - Geometria Analítica e Cálculo Vetorial Professora: Monique Rafaella Anunciação de Oliveira Lista de Exercícios 1 1. Dados os pontos:
Matemática capítulo 2
 Matemática capítulo Eercícios propostos. Marque os seguintes pontos no plano cartesiano: (,), (,), (-,), D(-,-), E(,-), F(-,), G(,) θ. Determine os valores de a que satisfazem as condições dadas: a) O
Matemática capítulo Eercícios propostos. Marque os seguintes pontos no plano cartesiano: (,), (,), (-,), D(-,-), E(,-), F(-,), G(,) θ. Determine os valores de a que satisfazem as condições dadas: a) O
PUERI DOMUS ENSINO MÉDIO MATEMÁTICA. Saber fazer saber fazer + MÓDULO
 PUERI DOMUS ENSINO MÉDIO MATEMÁTICA Saber fazer saber fazer + 10 MÓDULO Saber fazer Geometria analítica 1. Determine as coordenadas dos pontos da figura. 2. Sendo A (2, 2), B (4, 6) e C (7, ) vértices
PUERI DOMUS ENSINO MÉDIO MATEMÁTICA Saber fazer saber fazer + 10 MÓDULO Saber fazer Geometria analítica 1. Determine as coordenadas dos pontos da figura. 2. Sendo A (2, 2), B (4, 6) e C (7, ) vértices
(b) { (ρ, θ);1 ρ 2 e π θ } 3π. 5. Representar graficamente
 Universidade Federal de Uberlândia Faculdade de Matemática isciplina : Geometria nalítica (GM003) ssunto: sistemas de coordenadas; vetores: operações com vetores, produto escalar, produto vetorial, produto
Universidade Federal de Uberlândia Faculdade de Matemática isciplina : Geometria nalítica (GM003) ssunto: sistemas de coordenadas; vetores: operações com vetores, produto escalar, produto vetorial, produto
Lista 23 - GEOMETRIA ANALÍTICA - II
 Lista - GEOMETRIA ANALÍTICA - II 1) (UFSM) Sejam o ponto A(, ) e a reta r, bissetriz do 1 o quadrante. A equação da reta que passa pelo ponto A, perpendicular à reta r, é (A) y = + - y = y = - + 8 y +
Lista - GEOMETRIA ANALÍTICA - II 1) (UFSM) Sejam o ponto A(, ) e a reta r, bissetriz do 1 o quadrante. A equação da reta que passa pelo ponto A, perpendicular à reta r, é (A) y = + - y = y = - + 8 y +
Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013
 Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013 Sem limite para crescer Bateria de Exercícios de Matemática II 1) A área do triângulo, cujos vértices são (1, 2),
Nome: nº Professor(a): UBERLAN / CRISTIANA Série: 3ª EM Turmas: 3301 / 3302 Data: / /2013 Sem limite para crescer Bateria de Exercícios de Matemática II 1) A área do triângulo, cujos vértices são (1, 2),
GEOMETRIA ANALI TICA PONTO MEDIANA E BARICENTRO PLANO CARTESIANO DISTÂNCIA ENTRE DOIS PONTOS CONDIÇÃO DE ALINHAMENTO DE TRÊS PONTOS
 GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
GEOMETRIA ANALI TICA PONTO PLANO CARTESIANO Vamos representar os pontos A (-2, 3) e B (4, -3) num plano cartesiano. MEDIANA E BARICENTRO A mediana é o segmento que une o ponto médio de um dos lados do
singular Lista de Exercícios - Ponto e reta Ensino Médio tarde - 2C17/27/37 Profª Liana
 singular Lista de Exercícios - Ponto e reta Ensino Médio tarde - C17/7/7 Profª Liana 01 - (UFJF MG) Dado o triângulo de vértices A = (1,1), B = (,) e C = (4, ). Considere as seguintes afirmações: I. O
singular Lista de Exercícios - Ponto e reta Ensino Médio tarde - C17/7/7 Profª Liana 01 - (UFJF MG) Dado o triângulo de vértices A = (1,1), B = (,) e C = (4, ). Considere as seguintes afirmações: I. O
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano
 Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática [email protected]
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática [email protected]
Média, Mediana e Distância entre dois pontos
 Média, Mediana e Distância entre dois pontos 1. (Pucrj 01) Se os pontos A = ( 1, 0), B = (1, 0) e C = (, ) são vértices de um triângulo equilátero, então a distância entre A e C é a) 1 b) c) 4 d) e). (Ufrgs
Média, Mediana e Distância entre dois pontos 1. (Pucrj 01) Se os pontos A = ( 1, 0), B = (1, 0) e C = (, ) são vértices de um triângulo equilátero, então a distância entre A e C é a) 1 b) c) 4 d) e). (Ufrgs
( ) Assim, de 2013 a 2015 (2 anos) houve um aumento de 40 casos de dengue. Ou seja: = 600 casos em 2015.
 Resposta da questão : [B] É fácil ver que a equação da reta s é = 3. Desse modo, a abscissa do ponto de interseção das retas p e s é tal 8 que 3 = + 3 =. 7 8 7 8 7 Portanto, temos = 3 = e a resposta é,.
Resposta da questão : [B] É fácil ver que a equação da reta s é = 3. Desse modo, a abscissa do ponto de interseção das retas p e s é tal 8 que 3 = + 3 =. 7 8 7 8 7 Portanto, temos = 3 = e a resposta é,.
Exercícios de Aprofundamento Matemática Geometria Analítica
 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0), (t, 0) e no ponto P de abscissa x t pertencente à reta
1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0), (t, 0) e no ponto P de abscissa x t pertencente à reta
Questão 1 a) A(0; 0) e B(8; 12) b) A(-4; 8) e B(3; -9) c) A(3; -5) e B(6; -2) d) A(2; 3) e B(1/2; 2/3) e) n.d.a.
 APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
APOSTILAS (ENEM) VOLUME COMPLETO Exame Nacional de Ensino Médio (ENEM) 4 VOLUMES APOSTILAS IMPRESSAS E DIGITAIS Questão 1 (UFPE) Determine o ponto médio dos segmentos seguintes, que têm medidas inteiras:
GEOMETRIA ANALÍTICA CONTEÚDOS. Distância entre pontos Equação da reta Distância ponto reta Coeficientes Equação da circunferência.
 GEOMETRIA ANALÍTICA CONTEÚDOS Distância entre pontos Equação da reta Distância ponto reta Coeficientes Equação da circunferência. AMPLIANDO SEUS CONHECIMENTOS Neste capítulo, estudaremos a Geometria Analítica.
GEOMETRIA ANALÍTICA CONTEÚDOS Distância entre pontos Equação da reta Distância ponto reta Coeficientes Equação da circunferência. AMPLIANDO SEUS CONHECIMENTOS Neste capítulo, estudaremos a Geometria Analítica.
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA
 EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
Exemplo Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:
 GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
Exercícios de Matemática II
 Nome: nº Professor(a): Série: ª EM. Turma: Data: / /014 Sem limite para crescer Exercícios de Matemática II 1º Trimestre 1. (Uem 011) Um cientista deseja determinar o calor específico de um material. Para
Nome: nº Professor(a): Série: ª EM. Turma: Data: / /014 Sem limite para crescer Exercícios de Matemática II 1º Trimestre 1. (Uem 011) Um cientista deseja determinar o calor específico de um material. Para
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 0. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
2 a Lista de Exercícios de MAT2457 Escola Politécnica 1 o semestre de 2014
 a Lista de Eercícios de MAT4 Escola Politécnica o semestre de 4. Determine u tal que u = e u é ortogonal a v = (,, ) e a w = (, 4, 6). Dos u s encontrados, qual é o que forma um ângulo agudo com o vetor
a Lista de Eercícios de MAT4 Escola Politécnica o semestre de 4. Determine u tal que u = e u é ortogonal a v = (,, ) e a w = (, 4, 6). Dos u s encontrados, qual é o que forma um ângulo agudo com o vetor
MATEMÁTICA 3 ( ) A. 17. Sejam f(x) = sen(x) e g(x) = x/2. Associe cada função abaixo ao gráfico que. 2 e g.f 3. O número pedido é = 75
 MATEMÁTICA 3 17. Sejam f() sen() e g() /2. Associe cada função abaio ao gráfico que melhor a representa. Para cada associação feita, calcule i k, onde i é o número entre parênteses à direita da função,
MATEMÁTICA 3 17. Sejam f() sen() e g() /2. Associe cada função abaio ao gráfico que melhor a representa. Para cada associação feita, calcule i k, onde i é o número entre parênteses à direita da função,
Análise Vetorial na Engenharia Elétrica
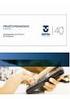 nálise Vetorial na Engenharia Elétrica ula 13/03/09 1.3 - Medida algébrica de um segmento Segmento: um segmento é determinado por um par ordenado d de pontos. figura 1.8 apresenta um segmento Figura 1.8
nálise Vetorial na Engenharia Elétrica ula 13/03/09 1.3 - Medida algébrica de um segmento Segmento: um segmento é determinado por um par ordenado d de pontos. figura 1.8 apresenta um segmento Figura 1.8
Universidade Federal da Bahia
 Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Universidade Federal da Bahia Instituto de Matemática DISCIPLINA: MATA0 - CÁLCULO B UNIDADE I - LISTA DE EXERCÍCIOS Atualizada 00. Áreas de figuras planas em coordenadas cartesianas [] Determine a área
Coordenadas Cartesianas
 GEOMETRIA ANALÍTICA Coordenadas Cartesianas EIXO DAS ORDENADAS OU EIXO DOS Y EIXO DAS ABSCISSAS OU EIXO DOS X EIXO DAS ORDENADAS OU EIXO DOS Y ORIGEM EIXO DAS ABSCISSAS OU EIXO DOS X COORDENADAS DE UM
GEOMETRIA ANALÍTICA Coordenadas Cartesianas EIXO DAS ORDENADAS OU EIXO DOS Y EIXO DAS ABSCISSAS OU EIXO DOS X EIXO DAS ORDENADAS OU EIXO DOS Y ORIGEM EIXO DAS ABSCISSAS OU EIXO DOS X COORDENADAS DE UM
ENSINO PRÉ-UNIVERSITÁRIO PROFESSOR(A) TURNO. 01. Determine a distância entre dois pontos A e B do plano cartesiano.
 SÉRIE ITA/IME ENSINO PRÉ-UNIVERSITÁRIO PROFESSOR(A) ALUNO(A) TURMA MARCELO MENDES TURNO SEDE DATA Nº / / TC MATEMÁTICA Geometria Analítica Exercícios de Fixação Conteúdo: A reta Parte I Exercícios Tópicos
SÉRIE ITA/IME ENSINO PRÉ-UNIVERSITÁRIO PROFESSOR(A) ALUNO(A) TURMA MARCELO MENDES TURNO SEDE DATA Nº / / TC MATEMÁTICA Geometria Analítica Exercícios de Fixação Conteúdo: A reta Parte I Exercícios Tópicos
6. Calcular as equações paramétricas de uma reta s que passa pelo ponto A(1, 1, 1) e é ortogonal x 2
 Lista 2: Retas, Planos e Distâncias - Engenharia Mecânica Professora: Elisandra Bär de Figueiredo x = 2 + 2t 1. Determine os valores de m para que as retas r : y = mt z = 4 + 5t sejam: (a) ortogonais (b)
Lista 2: Retas, Planos e Distâncias - Engenharia Mecânica Professora: Elisandra Bär de Figueiredo x = 2 + 2t 1. Determine os valores de m para que as retas r : y = mt z = 4 + 5t sejam: (a) ortogonais (b)
2. Na gura abaixo, representa-se um cubo. Desenhe a echa de origem H que representa ! DN =! DC
 1 Universidade Estadual de Santa Catarina Centro de Ciências Tecnológicas -DMAT ALG- CCI Professores: Ivanete, Elisandra e Rodrigo I Lista - vetores, retas e planos 1. Dados os vetores ~u e ~v da gura,
1 Universidade Estadual de Santa Catarina Centro de Ciências Tecnológicas -DMAT ALG- CCI Professores: Ivanete, Elisandra e Rodrigo I Lista - vetores, retas e planos 1. Dados os vetores ~u e ~v da gura,
Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105
 Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105 Primeiro período de 2018 Está lista de exercícios contém exercícios de [2], [1] e exercícios de outras referências. Além dos exercícios
Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105 Primeiro período de 2018 Está lista de exercícios contém exercícios de [2], [1] e exercícios de outras referências. Além dos exercícios
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática
 Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GA3X1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Retas e Planos Prof. Lilian
Universidade Tecnológica Federal do Paraná Câmpus Campo Mourão Departamento de Matemática GA3X1 - Geometria Analítica e Álgebra Linear Lista de Exercícios: Estudo Analítico de Retas e Planos Prof. Lilian
PROFESSOR FLABER 2ª SÉRIE Circunferência
 PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Plano Cartesiano e Retas. Vitor Bruno Engenharia Civil
 Plano Cartesiano e Retas Vitor Bruno Engenharia Civil Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é o
Plano Cartesiano e Retas Vitor Bruno Engenharia Civil Sistema cartesiano ortogonal O sistema cartesiano ortogonal é formado por dois eixos ortogonais(eixo x e eixo y). A intersecção dos eixos x e y é o
Banco de questões. Geometria analítica: ponto e reta ( ) ( ) ( )
 UNIDADE X geometria analítica CAPÍTULO 8 Geometria analítica: ponto e reta Banco de questões 1 (Cesgranrio RJ) Observe a figura e considere uma reta r cuja equação é y = x +. A esse respeito, são feitas
UNIDADE X geometria analítica CAPÍTULO 8 Geometria analítica: ponto e reta Banco de questões 1 (Cesgranrio RJ) Observe a figura e considere uma reta r cuja equação é y = x +. A esse respeito, são feitas
UFRJ - Instituto de Matemática
 UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
UFRJ - Instituto de Matemática Programa de Pós-Graduação em Ensino de Matemática www.pg.im.ufrj.br/pemat Mestrado em Ensino de Matemática Seleção 9 Etapa Questão. Determine se as afirmações abaio são verdadeiras
Nenhum obstáculo é tão grande se a sua vontade de vencer for maior.
 COLÉGIO MODELO LUIZ EDUARDO MAGALHÃES LISTA 1: PONTO E RETA MATEMÁTICA 3ª SÉRIE TURMA: II UNIDADE ------ CAMAÇARI - BA PROFESSOR: HENRIQUE PLÍNIO ALUNO (A): DATA: / /2016 Nenhum obstáculo é tão grande
COLÉGIO MODELO LUIZ EDUARDO MAGALHÃES LISTA 1: PONTO E RETA MATEMÁTICA 3ª SÉRIE TURMA: II UNIDADE ------ CAMAÇARI - BA PROFESSOR: HENRIQUE PLÍNIO ALUNO (A): DATA: / /2016 Nenhum obstáculo é tão grande
Matemática - 3ª série Roteiro 04 Caderno do Aluno. Estudo da Reta
 Matemática - 3ª série Roteiro 04 Caderno do Aluno Estudo da Reta I - Inclinação de uma reta () direção É a medida do ângulo que a reta forma com o semieixo das abscissas (positivo) no sentido anti-horário.
Matemática - 3ª série Roteiro 04 Caderno do Aluno Estudo da Reta I - Inclinação de uma reta () direção É a medida do ângulo que a reta forma com o semieixo das abscissas (positivo) no sentido anti-horário.
ÍNDICE: Relações Métricas num Triângulo Retângulo página: 2. Triângulo Retângulo página: 4. Áreas de Polígonos página: 5
 ÍNDICE: Relações Métricas num Triângulo Retângulo página: Triângulo Retângulo página: 4 Áreas de Polígonos página: 5 Área do Círculo e suas partes página: 11 Razão entre áreas de figuras planas semelhantes
ÍNDICE: Relações Métricas num Triângulo Retângulo página: Triângulo Retângulo página: 4 Áreas de Polígonos página: 5 Área do Círculo e suas partes página: 11 Razão entre áreas de figuras planas semelhantes
GEOMETRIA ANALÍTICA 2017
 GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
A x,y e B x,y, as coordenadas do ponto médio desse segmento serão dadas por:
 . Plano Cartesiano: é formado por dois eixos perpendiculares, um horizontal (eixo das abscissas) e outro vertical (eixo das ordenadas), dividido em quatro quadrantes contados no sentido anti-horário como
. Plano Cartesiano: é formado por dois eixos perpendiculares, um horizontal (eixo das abscissas) e outro vertical (eixo das ordenadas), dividido em quatro quadrantes contados no sentido anti-horário como
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Geometria Analítica. Números Reais. Faremos, neste capítulo, uma rápida apresentação dos números reais e suas propriedades, mas no sentido
 Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações
 Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações 1 Sistema Unidimensional de Coordenadas Cartesianas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente
Capítulo 1-Sistemas de Coordenadas, Intervalos e Inequações 1 Sistema Unidimensional de Coordenadas Cartesianas Conceito: Neste sistema, também chamado de Sistema Linear, um ponto pode se mover livremente
PROFª: ROSA G. S. DE GODOY
 ATIVIDADE DE MATEMÁTICA Nome: nº SÉRIE: 3ª E.M. Data: / / 2017 PROFª: ROSA G. S. DE GODOY FICHA DE SISTEMATIZAÇÃO PARA A 3ª AVAL. DO 2º TRIMESTRE BOAS FÉRIAS E APROVEITE PARA ESTUDAR UM POUQUINHO!! BJS
ATIVIDADE DE MATEMÁTICA Nome: nº SÉRIE: 3ª E.M. Data: / / 2017 PROFª: ROSA G. S. DE GODOY FICHA DE SISTEMATIZAÇÃO PARA A 3ª AVAL. DO 2º TRIMESTRE BOAS FÉRIAS E APROVEITE PARA ESTUDAR UM POUQUINHO!! BJS
Matemática B Extensivo v. 8
 Matemática B Etensivo v. 8 Eercícios y = Eio real = a = a = C = A + B ( = ( + B B = a y b = D C y = y = 6 9 Daí, a = 6 e b = 9 c = a + b c = 9 + 6 c = c = c = Portanto, a distância focal é dada por: c
Matemática B Etensivo v. 8 Eercícios y = Eio real = a = a = C = A + B ( = ( + B B = a y b = D C y = y = 6 9 Daí, a = 6 e b = 9 c = a + b c = 9 + 6 c = c = c = Portanto, a distância focal é dada por: c
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
2 LISTA DE MATEMÁTICA
 LISTA DE MATEMÁTICA SÉRIE: º ANO TURMA: º BIMESTRE DATA: / / 011 PROFESSOR: ALUNO(A): Nº: NOTA: POLINÔMIOS I 01. (ITA-1995) A divisão de um polinômio P() por - resulta no quociente 6 + 5 + 3 e resto -7.
LISTA DE MATEMÁTICA SÉRIE: º ANO TURMA: º BIMESTRE DATA: / / 011 PROFESSOR: ALUNO(A): Nº: NOTA: POLINÔMIOS I 01. (ITA-1995) A divisão de um polinômio P() por - resulta no quociente 6 + 5 + 3 e resto -7.
Título do Livro. Capítulo 5
 Capítulo 5 5. Geometria Analítica A Geometria Analítica tornou possível o estudo da Geometria através da Álgebra. Além de proporcionar a interpretação geométrica de diversas equações algébricas. 5.1. Sistema
Capítulo 5 5. Geometria Analítica A Geometria Analítica tornou possível o estudo da Geometria através da Álgebra. Além de proporcionar a interpretação geométrica de diversas equações algébricas. 5.1. Sistema
III CAPÍTULO 21 ÁREAS DE POLÍGONOS
 1 - RECORDANDO Até agora, nós vimos como calcular pontos, retas, ângulos e distâncias, mas não vimos como calcular a área de nenhuma figura. Na aula de hoje nós vamos estudar a área de polígonos: além
1 - RECORDANDO Até agora, nós vimos como calcular pontos, retas, ângulos e distâncias, mas não vimos como calcular a área de nenhuma figura. Na aula de hoje nós vamos estudar a área de polígonos: além
BC Geometria Analítica. Lista 4
 BC0404 - Geometria Analítica Lista 4 Nos exercícios abaixo, deve-se entender que está fixado um sistema de coordenadas cartesianas (O, E) cuja base E = ( i, j, k) é ortonormal (e positiva, caso V esteja
BC0404 - Geometria Analítica Lista 4 Nos exercícios abaixo, deve-se entender que está fixado um sistema de coordenadas cartesianas (O, E) cuja base E = ( i, j, k) é ortonormal (e positiva, caso V esteja
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA
 Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Quantos números pares, formados por algarismos distintos, existem entre 500 e 2000?
 PROVA DE MATEMÁTICA - TURMAS DO 3 O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - AGOSTO DE 011. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 01 Quantos
PROVA DE MATEMÁTICA - TURMAS DO 3 O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - AGOSTO DE 011. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 01 Quantos
3) O ponto P(a, 2) é equidistante dos pontos A(3, 1) e B(2, 4). Calcular a abscissa a do ponto P.
 Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Lista 2: Plano cartesiano, sistema de coordenadas: pontos e retas. 1) Represente no plano cartesiano
Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Lista 2: Plano cartesiano, sistema de coordenadas: pontos e retas. 1) Represente no plano cartesiano
3º. EM Prof a. Valéria Rojas Assunto: Determinante, Área do Triângulo, Equação da reta, Eq. Reduzida da Reta
 1 - O uso do Determinante de terceira ordem na Geometria Analítica 1.1 - Área de um triângulo Seja o triângulo ABC de vértices A(x a, y a ), B(x b, x c ) e C(x c, y c ). A área S desse triângulo é dada
1 - O uso do Determinante de terceira ordem na Geometria Analítica 1.1 - Área de um triângulo Seja o triângulo ABC de vértices A(x a, y a ), B(x b, x c ) e C(x c, y c ). A área S desse triângulo é dada
3º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio 3º ano A, B e C. Prof. Maurício Nome: nº
 º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
º trimestre SALA DE ESTUDOS Data: 11/17 Ensino Médio º ano A, B e C. Prof. Maurício Nome: nº CONTEÚDOS: EQUAÇÃO DA RETA E EQUAÇÃO DA CIRCUNFERÊNCIA. 1. (Eear 017) O triângulo ABC a) escaleno b) isósceles
13. (Uerj) Em cada ponto (x, y) do plano cartesiano, o valor de T é definido pela seguinte equação:
 1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
Preparação para o Cálculo
 Preparação para o Cálculo Referencial cartesiano Representação gráfica Um referencial cartesiano é constituído por duas rectas perpendiculares (fias), com ponto de intersecção O: O diz-se a origem do referencial;
Preparação para o Cálculo Referencial cartesiano Representação gráfica Um referencial cartesiano é constituído por duas rectas perpendiculares (fias), com ponto de intersecção O: O diz-se a origem do referencial;
Lista 22 - GEOMETRIA ANALÍTICA - I
 Lista 22 - GEOMETRIA ANALÍTICA - I 1) Um sistema cartesiano ortogonal é associado à planta de uma cidade plana de modo que o eixo Ox é orientado de oeste para leste, o eixo Oy é orientado de sul para norte
Lista 22 - GEOMETRIA ANALÍTICA - I 1) Um sistema cartesiano ortogonal é associado à planta de uma cidade plana de modo que o eixo Ox é orientado de oeste para leste, o eixo Oy é orientado de sul para norte
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A
 INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A - 009. A LISTA DE EXERCÍCIOS a Questão:. Para cada uma das funções seguintes, determine as derivadas indicadas: a) f(u) = u, u() =,
INSTITUTO DE MATEMÁTICA DA UFBA DEPARTAMENTO DE MATEMÁTICA CÁLCULO A - 009. A LISTA DE EXERCÍCIOS a Questão:. Para cada uma das funções seguintes, determine as derivadas indicadas: a) f(u) = u, u() =,
Capítulo Propriedades das operações com vetores
 Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
Capítulo 6 1. Propriedades das operações com vetores Propriedades da adição de vetores Sejam u, v e w vetores no plano. Valem as seguintes propriedades. Comutatividade: u + v = v + u. Associatividade:
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
(Teste intermédio e exames Nacionais 2012)
 Mais eercícios de 1.º ano: www.prof000.pt/users/roliveira0/ano1.htm (Teste intermédio e eames Nacionais 01) 79. Relativamente à Figura Resolva os itens seguintes, recorrendo a métodos, sabe-se que: eclusivamente
Mais eercícios de 1.º ano: www.prof000.pt/users/roliveira0/ano1.htm (Teste intermédio e eames Nacionais 01) 79. Relativamente à Figura Resolva os itens seguintes, recorrendo a métodos, sabe-se que: eclusivamente
Geometria Analítica. Katia Frensel - Jorge Delgado. NEAD - Núcleo de Educação a Distância. Curso de Licenciatura em Matemática UFMA
 Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Geometria Analítica NEAD - Núcleo de Educação a Distância Curso de Licenciatura em Matemática UFMA Katia Frensel - Jorge Delgado Março, 2011 ii Geometria Analítica Conteúdo Prefácio ix 1 Coordenadas na
Módulo de Plano Cartesiano e Sistemas de Equações. O Plano Cartesiano. Professores: Tiago Miranda e Cleber Assis
 Módulo de Plano artesiano e Sistemas de Equações O Plano artesiano 7 ano E.F. Professores: Tiago Miranda e leber ssis Plano artesiano e Sistemas de Equações O Plano artesiano Eercícios Introdutórios Eercício.
Módulo de Plano artesiano e Sistemas de Equações O Plano artesiano 7 ano E.F. Professores: Tiago Miranda e leber ssis Plano artesiano e Sistemas de Equações O Plano artesiano Eercícios Introdutórios Eercício.
Matemática B Extensivo V. 7
 Matemática Etensivo V. 7 Eercícios ) D ) ) 6 Temos que: 6 e 6 Logo, C (, ) (, ). 6 Completando quadrado, temos: ( ) ( 6) ( ) ( 6 9) 9 ( ) ( ) 9 ( ) ( ) 6 ( ) ( ) 6 ( ) ( ) Logo, C (, ) e r. Portanto, (
Matemática Etensivo V. 7 Eercícios ) D ) ) 6 Temos que: 6 e 6 Logo, C (, ) (, ). 6 Completando quadrado, temos: ( ) ( 6) ( ) ( 6 9) 9 ( ) ( ) 9 ( ) ( ) 6 ( ) ( ) 6 ( ) ( ) Logo, C (, ) e r. Portanto, (
Retas e Funções Lineares
 Capítulo 1 Retas e Funções Lineares 1.1 A equação de uma reta Intuitivamente é fácil perceber que dois pontos distintos denem uma única reta. Na geometria analítica podemos determinar a equação de uma
Capítulo 1 Retas e Funções Lineares 1.1 A equação de uma reta Intuitivamente é fácil perceber que dois pontos distintos denem uma única reta. Na geometria analítica podemos determinar a equação de uma
A B C A 1 B 1 C 1 A 2 B 2 C 2 é zero (exceto o caso em que as tres retas são paralelas).
 MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
Introdução ao Cálculo Vetorial
 Introdução ao Cálculo Vetorial Segmento Orientado É o segmento de reta com um sentido de orientação. Por exemplo AB onde: A : origem e B : extremidade. Pode-se ter ainda o segmento BA onde: B : origem
Introdução ao Cálculo Vetorial Segmento Orientado É o segmento de reta com um sentido de orientação. Por exemplo AB onde: A : origem e B : extremidade. Pode-se ter ainda o segmento BA onde: B : origem
GEOMETRIA ANALÍTICA. Professor Jairo Weber
 GEOMETRIA ANALÍTICA Professor Jairo Weber EXEMPLO. 1. Para que valor(es) de a o ponto P(a+2; -2) está situado sobre o eixo das ordenadas? 2. Seja o ponto T(2s+4; 10) um ponto da primeira bissetriz. Qual
GEOMETRIA ANALÍTICA Professor Jairo Weber EXEMPLO. 1. Para que valor(es) de a o ponto P(a+2; -2) está situado sobre o eixo das ordenadas? 2. Seja o ponto T(2s+4; 10) um ponto da primeira bissetriz. Qual
4 Trigonometria no círculo trigonométrico
 37 4 Trigonometria no círculo trigonométrico Com o surgimento do cálculo infinitesimal e posteriormente da análise matemática as noções básicas da trigonometria ganharam uma nova dimensão. Passaremos a
37 4 Trigonometria no círculo trigonométrico Com o surgimento do cálculo infinitesimal e posteriormente da análise matemática as noções básicas da trigonometria ganharam uma nova dimensão. Passaremos a
Assunto: Estudo do ponto
 Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
com 3 Incógnitas A interseção do plano paralelo ao plano yz, passando por P, com o eixo x determina a coordenada x.
 Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Disciplina: MATEMÁTICA Série: 3º ANO ATIVIDADES DE REVISÃO PARA O REDI (4º BIMESTRE) ENSINO MÉDIO
 Professor (a): Estefânio Franco Maciel Aluno (a): Disciplina: MATEMÁTICA Série: º ANO ATIVIDADES DE REVISÃO PARA O REDI (º BIMESTRE) ENSINO MÉDIO Data: /0/0. x y Questão 0) Dados os sistemas S : e x y
Professor (a): Estefânio Franco Maciel Aluno (a): Disciplina: MATEMÁTICA Série: º ANO ATIVIDADES DE REVISÃO PARA O REDI (º BIMESTRE) ENSINO MÉDIO Data: /0/0. x y Questão 0) Dados os sistemas S : e x y
