Modelos matemáticos para resolução de problemas de afectação de operações a recursos produtivos
|
|
|
- Márcio Taveira Caires
- 5 Há anos
- Visualizações:
Transcrição
1 Métodos de Análise de Sistemas Produtivos Modelos matemáticos para resolução de problemas de afectação de operações a recursos produtivos 17 de Maio de 2002 Alunos: Álvaro Magalhães Bernardo Ribeiro João Bessa José Lúcio Teresa Marques Docentes: Fernando Manuel Ferreira Lobo Pereira Gil Manuel Magalhães de Andrade Gonçalves
2 Índice: Introdução 2 O Grafo 3 Algoritmo de Dijkstra 4 Dijkstra com variável de ocupação da rede 8 Método k shortest path 10 Algoritmo A star Masp grupo 1 1
3 Introdução Este documento pretende enumerar vários modelos matemáticos para resolução de problemas de afectação de operações a recursos produtivos. Os diversos métodos existentes apoiam-se nos algoritmos de caminho mínimo, em especial o algoritmo de dijkstra. Cada método é apresentado pretende demostrar o funcionamento do algoritmo para um dos grafos construídos para o enunciado. Deste documento resultará a escolha de um modelo a seguir de acordo com as vantagens e desvantagens de cada modelo Masp grupo 1 2
4 O Grafo De seguida é apresentado o grafo escolhido como principal e que foi utilizado para demonstração dos vários métodos e para o qual foram calculados os algoritmos matemáticos particulares. Legenda: Tempo, Custo Masp grupo 1 3
5 Algoritmo de Dijkstra Forma Tabelar de resolver o nosso problema especifico: Letra representa recursos e algarismos representam operação; Dentro de ( ) está atribuição a cada recurso de um valor, para que possa ser identificado como um nó; um mesmo recurso pode então estar representado por mais de um nó diferente; I (0) A1 (1) F1 (2) E1 (3) C2 (4) B2 (5) D2 (6) D3 (7) C3 (8) B3 (9) F4 (10) A4 (11) F (12) E E Valor mínimo até ao nó respectivo (cada operação tem apenas um valor mínimo) Valor mínimo dos nós associados às últimas operações possíveis Valor mínimo óptimo final, calculado através do mínimo dos valores a Valor que não o mínimo >>> valor mínimo A solução deste problema é a seguinte sequência: E1 >> D2 >> C3 Esta solução apenas considera um valor fixo para cada arco, considerando para tal que tanto a variável Custo como Tempo têm um peso unitário; Em seguida demonstra-se a resolução do mesmo problema mas considerando o valor de cada ramo em função das duas variáveis já referidas; W = T*x + C*y I (0) A1 (1) F1 (2) E1 (3) C2 (4) B2 (5) D2 (6) 5x + 5y 4x + 3y 3x + 2y 10x + 11y 7x + 8y 6x + 6y E 8x + 5y 6x + 5y 8<10 6=6 5<11 5< Masp grupo 1 4
6 D3 (7) C3 (8) B3 (9) F4 (10) A4 (11) F (12) 11x + 7y 17x + 14y 10x + 7y 13x + 9y 16x + 10y 11x + 7y 11x + 8y 18x + 17y 16x + 10y 11x + 7y 15x + 8y 11<17 10<11 13<18 15<16 11<13<15 7<14 7<8 9<17 8<10 7<8<9 Resolvendo então o nosso problema em função dos pesos das variáveis Tempo e Custo, verifica-se que a solução do problema se mantém a mesma independente dos referidos parâmetros; Em seguida passa-se apresentar um modelo matemático para este problema, em que primeiramente temos uma solução orientada ao nosso problema especifico, e em seguida em função disso se tenta retirar um modelo generalizado que sirva para qualquer outro problema deste tipo; ESPECIFICAÇÕES: W = X*T + Y*C em que... W >> Peso total do arco; T >> Tempo de operação; C >> Custo de operação; X,Y >> pesos das variáveis que estão em jogo; Wi [j] >> Peso do arco com origem em i e destino em j; i,j e [0,12] Ek >> valor mínimo até ao nó k; k e [0,12] E [0] = 0 >> Ponto de partida; E [12] >> solução óptima a encontrar; Pode existir mais de que um nó associado a uma mesmo recurso, por isso convém ter presente quais os nós respectivos para cada recurso, para que depois de encontrada a solução óptima se poder fazer o escalonamento em Masp grupo 1 5
7 termos temporais dos diversos recursos; a identificação através dos nós só serve para resolução do problema, já que um recurso pode aparecer mais de que uma vez na rede, e nessa altura terá que ser tratado como se diferentes recursos se tratassem, 1ª OPERAÇÃO (1) E1 = min { E0 + W0 [1] } E2 = min { E0 + W0 [2] } E3 = min { E0 + W0 [3] } // só entra um arco em cada um destes nós por isso a solução até aqui é imediata; 2ª OPERAÇÃO (2) E4 = min { E1 + W1 [4] ; E2 + W2 [4] } E5 = min { E1 + W1 [5] } E6 = min { E2 + W2 [6] ; E3 + W3 [6] } 3ª OPERAÇÃO (3) E7 = min { E4 + W4 [7] } E8 = min { E5 + W5 [8] ; E6 + W6 [8] } E9 = min { E4 + W4 [9] ; E6 + W6 [9] } 4ª OPERAÇÃO (4) E10 = min { E7 + W7 [10] ; E5 + W5 [10] } E11 = min { E7 + W7 [11] ; E8 + W8 [11] ; E9 + W9 [11] } SOLUÇÃO FINAL: E12 = min { E8 ; E10 ; E11 } >>> solução óptima Masp grupo 1 6
8 Modelo matemático generalizado: Para todas as operações que compõem a rede calcula-se o valor mínimo (E) para todos os nós que lhe estão associados, em que o valor mínimo de cada nó é encontrado da seguinte forma: Sendo h = [0,...,r] o conjunto de nós pertencentes à rede, m o índice do nó para o qual se está a calcular o valor mínimo ( m e h ), e [n,...,t] o intervalo de índices associados aos nós precedentes, que têm arcos a entrar no nó m... Em = min { En + Wn [m] ;... ; Et + Wt [m] }, para m e [0,r-1] Tendo que para inicializar E0 = 0; E que a solução óptima é encontrada quando se encontrar o valor mínimo para Er e que é calculado da seguinte forma: Er = min { Ey ;...; Ex } conjunto de nós que têm arcos com destino ao nó r ; em que [y,...,x] e [0,...,r-1] e que define o De referir que o nó 0 e r não estão associados a recursos mas sim a marcas que representam o início e fim da rede; NOTA: A fim de se entender este raciocínio, é aconselhável ter presente um dos esquemas das redes que foram criadas; Tendo em conta que objectivo é implementar este sistema em MATLAB, é possível que este modelo tenha que ser revisto e completado a fim de se ter toda a rede representada em forma matemática Masp grupo 1 7
9 Dijkstra com variável de ocupação da rede Este método é idêntico ao método de dijktra simples para apenas um grafo. A sua aplicação para apenas um grafo é idêntica à acima mencionado tendo por isso sido decidido apenas apresentar o modelo matemático. Função objectivo: MIN N N i= 1 J= 1 q= 1 N q q [ ( c + ] ij * xij * p1_ ij) ( t ij * xij * p2_ ij) Restrições: N q 1. x ki x k= 1 rede ) N k = 1 q ik ; i=1,...,n q=1,...,n (Assegura a continuidade da 2. p1_ ij td = ; p 2 _ ij td = 1 p td > 1 p td < 1 p 1_ ij 1_ ij 1_ ij = p > p < p 2 _ ij 2 _ ij 2_ ij p p p 1_ ij 1_ ij 1_ ij = 1 p = 1 p = 0 p 2 _ ij 2 _ ij 2_ ij = 1 = 0 = 1 q 3. x ( 0,1) ki Definição de variáveis: c ij -custo de processamento (i,j) q x 1 se (i,j) encontrar-se ocupado no processamento de um produto, ij q caso contrário x = 0 ij p 1_ ij - Peso da decisão em se optar pelo peso do custo p 1 _ ij = 1 p 2_ ij - Peso da decisão em se optar pelo peso do tempo p 2 _ ij = 1 td taxa de decisão Masp grupo 1 8
10 A ideia subjacente a este modelo será a do operador definir à partida um determinado peso para o custo e para o tempo, de forma a permitir uma melhor decisão, tendo sempre em conta a ocupação das máquinas Masp grupo 1 9
11 Método k shortest path Introdução ao k shortest path Este algoritmo é uma generalização do problema de caminho mínimo em que são obtidos não um mas vários caminhos mínimos unindo um nó inicial s e um nó de destino t. O objectivo é listar k caminhos que unem dois pontos de um grafo com o menor comprimento total. A ideia essencial deste algoritmo é calcular vários caminhos mínimos partindo não do nó inicial mas do final. Dessa forma é sempre possível conhecer o valor ao ponto inicial em qualquer ponto da rede. È por isso o contrário do normal algoritmo de Dijkstra. Resolver do problema especifico usando a forma tabular: Letra representa recursos e algarismos representam operação; Dentro de ( ) está atribuição a cada recurso de um valor, para que possa ser identificado como um nó; um mesmo recurso pode então estar representado por mais de um nó diferente; Analisando o grafo e considerando a soma dos diferentes parâmetros tempo e custo, considerando-os unitários ou seja com a mesma importância para o problema, obtêm-se a seguinte tabela : F (12) A4 (11) F4 (10) B3 (9) C3 (8) D3 (7) D2 (6) B2 (5) C2 (4) E1 (3) F1 (2) A1 (1) I (0) E Valor mínimo até ao nó respectivo (cada operação tem apenas um valor mínimo) Valor mínimo óptimo final, calculado através do mínimo dos valores a mínimos Valor que não o mínimo E>>> valor mínimo Masp grupo 1 10
12 A solução deste problema é a seguinte sequência: E1 >> D2 >> C3 Em seguida demonstra-se a resolução do mesmo problema mas considerando o valor de cada ramo em função das duas variáveis já referidas; W = T*x + C*y F (12) A4 (11) F4 (10) B3 (9) C3 (8) D3 (7) D2 (6) 0x + 0y 0x + 0y 5x + 1y 5x + 3y 2x + 2y 10x + 4y E 0x + 0y 5x+ 3y 5x + 2y B2 (5) C2 (4) E1 (3) F1 (2) A1 (1) I (0) 10x + 6y 7x + 3y 8x + 5y 7x + 5y 12x + 9y 11x+ 12y 11x+ 9y 5x + 4y 11x + 5y 12x + 9y 11x + 7y 9x+ 11y 10x + 10y 17x+ 14y 15x+15y Resolvendo então o nosso problema em função dos pesos das variáveis Tempo e Custo, verifica-se que a solução do problema se mantém a mesma independente dos referidos parâmetros. No entanto vê-se que os melhores caminhos alternativos podem variar de acordo com os pesos atribuídos aos diferentes parâmetros. O grande interesse deste método é reconhecer para cada nó qual é o valor mais curto de chegada ao nó final e qual o melhor caminho para o fazer. Caminho óptimo E1 -> 13 D2 ->7 C3 -> 0 Final 18 F1-> 12 D2->7 C3->0 Final 19 A1->20 C2->9 D4->4 F5->0 Final Masp grupo 1 11
13 Grafo do caminho óptimo e caminhos totais alternativos considerando os tempos e custos com pesos iguais Poderemos ver que estes são caminhos directos mas podem ser calculadas as distâncias para caminhos não directos através da inserção de outro caminho da rede. Para o cálculo da perda de distância poder-se-á utilizar a fórmula: δ(e)= l(e) + d(head(e),t)-d(tail(e),t) em que: δ(e) : corresponde à variação no caminho total com a inclusão do novo braço e. l(e) : valor de percorrer o novo braço e d(head(e),t): distância mínima associada ao nó que separa o Início do arco e e o nó final d(tail(e),t): distância mínima associada ao nó que separa o fim do arco de e o nó final por exemplo, se quisermos não passar pelo nó C3 por alguma impossibilidade e em vez disso formos por B3 temos um acrescento ao caminho mínimo de: δ(d2->b3) = -(5+3) +7-6= Masp grupo 1 12
14 Daqui se pode concluir que alterando o percurso para incluir o nó B3 em vez de C3 gastamos mais 7 unidades de distância. De notar que se o nó a incluir já pertencer ao caminho óptimo temos que a variação terá o valor zero. Modelo Matemático Em seguida passa-se apresentar um modelo matemático para este problema: - primeiramente temos uma solução orientada ao nosso problema especifico - em seguida e em função disso tenta-se retirar um modelo generalizado que sirva para qualquer outro problema deste tipo; ESPECIFICAÇÕES: em que... W T C X,Y W = X*T + Y*C Peso total do arco; Tempo de operação; Custo de operação; pesos das variáveis que estão em jogo; Wi [j] Peso do arco com origem em i e destino em j; i,j ε [0,12] Ek Valor mínimo até ao nó k; k e [0,12] E [12] = 0 Ponto de partida; E [0] Solução óptima a encontrar; 1ª OPERAÇÃO (4) E12 = min { E11 + E10 + E8 } E12 = E11 = E10 = E8 // o nó final é único e o valor inicial será neste caso é sempre 0 // devido à forma como estamos a considerar o problema Masp grupo 1 13
15 2ª OPERAÇÃO (3) E9 = min { E11 + W9 [11] } E8 = min { E12 ; E11 + W8 [11] } E7 = min { E10 + W7 [10] ; E11 + W7 [11] } 3ª OPERAÇÃO (2) E6 = min { E9 + W6 [9] ; E8 + W6 [8] } E5 = min { E8 + W5 [8] ; E10 + W5 [10] } E4 = min { E9 + W4 [9] ; E7 + W7 [7] } 4ª OPERAÇÃO (1) E3 = min { E6 + W3 [6] } E2 = min { E6 + W2 [6] ; E4 + W2 [4] } E1 = min { E4 + W1 [4] ; E5 + W1 [5] } SOLUÇÃO FINAL: E0 = min { E1+ W0 [1] ; E2 + W0 [2]; E3 + W0 [3] } >>> solução óptima Modelo matemático generalizado: Para todas as operações que compõem a rede calcula-se o valor mínimo (E) para todos os nós que lhe estão associados, em que o valor mínimo de cada nó é encontrado da seguinte forma: Em = min { En + Wm [n] ;... ; Et + Wm [t] } para m e [0,r-1] e m anterior a n Sendo: h = [0,...,r] o conjunto de nós pertencentes à rede m, o índice do nó para o qual se está a calcular o valor mínimo ( m e h ), Masp grupo 1 14
16 [n,...,t] o intervalo de índices associados aos nós precedentes, que têm arcos a entrar no nó m... A inicialização ocorre para Er = 0; A solução óptima é encontrada quando se encontrar o valor mínimo para Er e que é calculado da seguinte forma: E0 = min { Ey ;...; Ex } em que [y,...,x] e [0,...,r-1] e que define o conjunto de nós que têm arcos com destino ao nó 0 ; De referir que o nó 0 e r não estão associados a recursos mas sim a marcas que representam o início e fim da rede; Um algoritmo de trocas englobado neste modelo foi já referido e é formulado matematicamente através de: δ (em[n])= Wm[n] + Em - En) em que: em[n] : novo braço a incluir no grafo partindo de um nó inicial m e terminando no nó final n δ(em[n]) : corresponde à variação no caminho total com a inclusão do novo braço Em Masp grupo 1 15
17 Algoritmo A star A teoria do A* é relativamente simples. Basicamente, cada nó (posição) no gráfico tem três atributos principais: f, g e h. g é o custo de chegar ao ponto. Este normalmente é o custo de mudar um nó mais o custo do nó pai. h é a distância à meta - não tem que ser a distância real (A * tem muitas aplicação - pathfinder é um). Podemos definir uma classe de heurísticas admissíveis de estratégias de procura usando a função evolução: f(n) =g(n)+h(n). f(n) representa uma estimativa do custo total do caminho desde o início, por n até ao objectivo. Também há duas listas, Aberto e Fechado. Na lista aberta estão todos os nó que não foram explorados. Por explorar, quero dizer todas as posições adjacentes que foram abertas (também passou para a lista Aberta), ou não podem ser aberto. Na lista fechada estão todos os nós que foram explorados. O algoritmo de A* pode ser definido da seguinte forma: 1. Iniciar no primeiro nó; 2. Se o nó actual é o objectivo então, deve-se parar a pesquisa; 3. Se o nó actual não é o nó final, então escolhe-se o caminho com a menor estimativa; 4. Repetir o ponto 2. Desta forma temos que calcular todos os caminhos conhecidos desde o início até ao fim. Com esta informação da estimativa vamos escolher o melhor caminho Masp grupo 1 16
18 Aplicação do método - Atribuição do valores aos nós Resultado final O caminho mínimo está demarcado por uma linha vermelha Masp grupo 1 17
Simulação manual do algoritmo
 Métodos de Análise de Sistemas Produtivos Simulação manual do algoritmo 03 de Junho de 2002 Alunos: Álvaro Magalhães Bernardo Ribeiro João Bessa José Lúcio Elawar Teresa Marques Docentes: Fernando Manuel
Métodos de Análise de Sistemas Produtivos Simulação manual do algoritmo 03 de Junho de 2002 Alunos: Álvaro Magalhães Bernardo Ribeiro João Bessa José Lúcio Elawar Teresa Marques Docentes: Fernando Manuel
Problemas de Fluxo em Redes
 CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
Problemas de Transportes e de Afectação
 CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 21
 Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 21 Três objetivos i. Redução de custos (custos variáveis) ii. iii. Redução de capital (investimento, custos fixos) Melhoria do serviço
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 21 Três objetivos i. Redução de custos (custos variáveis) ii. iii. Redução de capital (investimento, custos fixos) Melhoria do serviço
Problema do Caminho Mínimo
 Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Problemas de Fluxo Máximo
 Investigação Operacional 1 Problemas de Fluxo Máximo Slide 1 Transparências de apoio à leccionação de aulas teóricas Problemas de Fluxo Máximo Definição: Dada uma rede, com um nó de entrada eumnó desaída,
Investigação Operacional 1 Problemas de Fluxo Máximo Slide 1 Transparências de apoio à leccionação de aulas teóricas Problemas de Fluxo Máximo Definição: Dada uma rede, com um nó de entrada eumnó desaída,
Oalgoritmo de Dijkstra
 Dijkstra Oalgoritmo de Dijkstra O algoritmo de Dijkstra, concebido pelo cientista da computação holandês Edsger Dijkstra em 1956 e publicado em 1959, soluciona o problema do caminho mais curto num grafo
Dijkstra Oalgoritmo de Dijkstra O algoritmo de Dijkstra, concebido pelo cientista da computação holandês Edsger Dijkstra em 1956 e publicado em 1959, soluciona o problema do caminho mais curto num grafo
Inteligência Artificial 2008/09 E z D
 /Jan/009 9h-h Inteligência Artificial 008/09 DI/FCT/UNL, Duração: 3h Exame: Época Normal GRUP I I.) Considere o seguinte grafo de estados de um problema de procura. s valores apresentados nos arcos correspondem
/Jan/009 9h-h Inteligência Artificial 008/09 DI/FCT/UNL, Duração: 3h Exame: Época Normal GRUP I I.) Considere o seguinte grafo de estados de um problema de procura. s valores apresentados nos arcos correspondem
Otimização. Otimização em Redes. Paulo Henrique Ribeiro Gabriel Faculdade de Computação Universidade Federal de Uberlândia 2016/2
 Otimização Otimização em Redes Paulo Henrique Ribeiro Gabriel phrg@ufu.br Faculdade de Computação Universidade Federal de Uberlândia 2016/2 Paulo H. R. Gabriel (FACOM/UFU) GSI027 2016/2 1 / 51 Conteúdo
Otimização Otimização em Redes Paulo Henrique Ribeiro Gabriel phrg@ufu.br Faculdade de Computação Universidade Federal de Uberlândia 2016/2 Paulo H. R. Gabriel (FACOM/UFU) GSI027 2016/2 1 / 51 Conteúdo
Selecciona-se dos vértices ainda não seleccionados o vértice v k que está à menor distância de v i,
 V. Problema do caixeiro-viajante Grafos - Problema do caixeiro-viajante onsidere-se um grafo em que os vértices representam cidades e as arestas (ou arcos) representam as estradas de uma dada região (a
V. Problema do caixeiro-viajante Grafos - Problema do caixeiro-viajante onsidere-se um grafo em que os vértices representam cidades e as arestas (ou arcos) representam as estradas de uma dada região (a
W 8. Nas colunas "k =1 a n" executar: Nas linhas "i =1 a m" executar: Em cada linha "i" de "j=1 a n" executar: z = c ik + c kj
 VI. Encaminhamentos de encargo total mínimo Considere-se um grafo (orientado ou não) em que se associa a cada um dos seus arcos (arestas) um dado encargo real (distância, custo, tempo, etc.); admita-se
VI. Encaminhamentos de encargo total mínimo Considere-se um grafo (orientado ou não) em que se associa a cada um dos seus arcos (arestas) um dado encargo real (distância, custo, tempo, etc.); admita-se
Melhor caminho entre duas estações de metro
 Melhor caminho entre duas estações de metro Concepção e Análise de Algoritmos Turma Nuno Machado Matos Tiago Daniel Sá Cunha Data: 11 de Junho de 2010 Introdução No âmbito da realização do projecto da
Melhor caminho entre duas estações de metro Concepção e Análise de Algoritmos Turma Nuno Machado Matos Tiago Daniel Sá Cunha Data: 11 de Junho de 2010 Introdução No âmbito da realização do projecto da
Distâncias Mínimas. Pedro Ribeiro 2014/2015 DCC/FCUP. Pedro Ribeiro (DCC/FCUP) Distâncias Mínimas 2014/ / 27
 Distâncias Mínimas Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Distâncias Mínimas 2014/2015 1 / 27 Distâncias Mínimas Uma das aplicações mais típicas em grafos é o cálculo de distâncias.
Distâncias Mínimas Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Distâncias Mínimas 2014/2015 1 / 27 Distâncias Mínimas Uma das aplicações mais típicas em grafos é o cálculo de distâncias.
Exercícios de Caminho Mínimo Enunciados
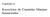 Capítulo Exercícios de Caminho Mínimo Enunciados Enunciados 9 Problema Considere a seguinte rede: 9 7 (a) Usando o algoritmo de Dijkstra, determine a distância mínima do nó aonóe indique o respectivo caminho.
Capítulo Exercícios de Caminho Mínimo Enunciados Enunciados 9 Problema Considere a seguinte rede: 9 7 (a) Usando o algoritmo de Dijkstra, determine a distância mínima do nó aonóe indique o respectivo caminho.
Grafos: caminhos mínimos
 quando o grafo é sem pesos, a determinação de um caminho mais curto pode ser feita através de uma busca em largura caminho mais curto é aquele que apresenta o menor número de arestas quando o grafo tem
quando o grafo é sem pesos, a determinação de um caminho mais curto pode ser feita através de uma busca em largura caminho mais curto é aquele que apresenta o menor número de arestas quando o grafo tem
Teoria dos Grafos AULA
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA Caminho mínimo - Algoritmo de Djskstra Preparado a partir
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA Caminho mínimo - Algoritmo de Djskstra Preparado a partir
Teoria dos Grafos Aula 14
 Teoria dos Grafos Aula 14 Aula passada MST Aula de hoje Construção de algoritmos Paradigma guloso Escalonando tarefas no tempo (interval scheduling) Projetando Algoritmos Dado um problema P, como projetar
Teoria dos Grafos Aula 14 Aula passada MST Aula de hoje Construção de algoritmos Paradigma guloso Escalonando tarefas no tempo (interval scheduling) Projetando Algoritmos Dado um problema P, como projetar
Simplex. Investigação Operacional José António Oliveira Simplex
 18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
Introdução à Lógica de Programação
 Introdução à Lógica de Programação Não estamos aqui para sobreviver e sim para explorar a oportunidade de vencer adquirindo o saber! (Autor Desconhecido) A lógica é a arte de pensar correctamente e, visto
Introdução à Lógica de Programação Não estamos aqui para sobreviver e sim para explorar a oportunidade de vencer adquirindo o saber! (Autor Desconhecido) A lógica é a arte de pensar correctamente e, visto
1. Duma vez por todas, e já que se trata dum novo hotel da Sonhos e Companhia Limitada,
 Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 000.0.7 Duração: horas e 0 minutos Com Consulta. Duma vez por todas, e já que se trata dum novo hotel da Sonhos
Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 000.0.7 Duração: horas e 0 minutos Com Consulta. Duma vez por todas, e já que se trata dum novo hotel da Sonhos
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilceunespbr, socorro@ibilceunespbr Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro
Teoria dos Grafos Valeriano A de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilceunespbr, socorro@ibilceunespbr Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro
GRAFOS Aula 06 Algoritmo de Caminho Mínimo: Dijkstra Max Pereira
 Ciência da Computação GRAFOS Aula 06 Algoritmo de Caminho Mínimo: Dijkstra Max Pereira Publicado em 1959, o algoritmo resolve o problema do caminho mínimo em grafos orientados ou não, sob uma restrição:
Ciência da Computação GRAFOS Aula 06 Algoritmo de Caminho Mínimo: Dijkstra Max Pereira Publicado em 1959, o algoritmo resolve o problema do caminho mínimo em grafos orientados ou não, sob uma restrição:
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A de Oliveira, Socorro Rangel, Silvio A de Araujo Departamento de Matemática Aplicada Capítulo 12: Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro Teoria do
Teoria dos Grafos Valeriano A de Oliveira, Socorro Rangel, Silvio A de Araujo Departamento de Matemática Aplicada Capítulo 12: Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro Teoria do
TABELAS DE DISPERSÃO/HASH
 1/47 TABELAS DE DISPERSÃO/HASH Introdução 2/47 Introdução Motivação - Considerar o problema de pesquisar um determinado valor num vetor: - Se o vetor não está ordenado, a pesquisa requer O(n) de complexidade
1/47 TABELAS DE DISPERSÃO/HASH Introdução 2/47 Introdução Motivação - Considerar o problema de pesquisar um determinado valor num vetor: - Se o vetor não está ordenado, a pesquisa requer O(n) de complexidade
Resolução de problemas difíceis de programação linear através da relaxação Lagrangeana
 problemas difíceis de programação linear através da relaxação Lagrangeana Ana Maria A.C. Rocha Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho arocha@dps.uminho.pt http://www.norg.uminho.pt/arocha
problemas difíceis de programação linear através da relaxação Lagrangeana Ana Maria A.C. Rocha Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho arocha@dps.uminho.pt http://www.norg.uminho.pt/arocha
Optimização em Redes e Não Linear
 Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
MÓDULO 3 - PROBLEMAS DE TRANSPORTE
 UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
Usar a implementação Prolog do A*
 Usar a implementação Prolog do A* 2018/09/16 O algoritmo A* serve para resolver problemas. Basicamente, descobre a sequência de passos necessários para converter um estado inicial num estado final (ou
Usar a implementação Prolog do A* 2018/09/16 O algoritmo A* serve para resolver problemas. Basicamente, descobre a sequência de passos necessários para converter um estado inicial num estado final (ou
Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree
 Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Departamento de Engenharia de Produção UFPR 22
 Departamento de Engenharia de Produção UFPR 22 Geralmente, temos três objetivos i. Redução de custos (custos variáveis) Redução de capital (investimento, custos fixos) i Melhoria do serviço (pode conflitar
Departamento de Engenharia de Produção UFPR 22 Geralmente, temos três objetivos i. Redução de custos (custos variáveis) Redução de capital (investimento, custos fixos) i Melhoria do serviço (pode conflitar
Escola Básica e Secundária Mouzinho da Silveira. MACS 11.º Ano Problema do Caixeiro Viajante
 Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
UNIVERSIDADE FEDERAL DO ABC. 1 Existência e unicidade de zeros; Métodos da bissecção e falsa posição
 UNIVERSIDADE FEDERAL DO ABC BC1419 Cálculo Numérico - LISTA 1 - Zeros de Funções (Profs. André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda) 1 Existência e unicidade de zeros; Métodos
UNIVERSIDADE FEDERAL DO ABC BC1419 Cálculo Numérico - LISTA 1 - Zeros de Funções (Profs. André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda) 1 Existência e unicidade de zeros; Métodos
PERCURSOS. André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré
 PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
Dízimas e intervalos encaixados.
 Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Complementos de Investigação Operacional. Folha nº 1 Programação Inteira 2007/08
 Complementos de Investigação Operacional Folha nº Programação Inteira 2007/08 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Complementos de Investigação Operacional Folha nº Programação Inteira 2007/08 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
C CURSO PROFISSIONAL DE GESTÃO E PROGRAMAÇÃO DE SISTEMAS INFORMÁTICOS CICLO DE FORMACÃO ANO LECTIVO: 2008/2009 ( 3º Ano )
 ESCOLA SECUNDÁRIA c/ 3º CICLO MANUEL DA FONSECA C CURSO PROFISSIONAL DE GESTÃO E PROGRAMAÇÃO DE SISTEMAS INFORMÁTICOS CICLO DE FORMACÃO 2006-2009 ANO LECTIVO: 2008/2009 ( 3º Ano ) CONTEÚDOS Página 1 Módulo
ESCOLA SECUNDÁRIA c/ 3º CICLO MANUEL DA FONSECA C CURSO PROFISSIONAL DE GESTÃO E PROGRAMAÇÃO DE SISTEMAS INFORMÁTICOS CICLO DE FORMACÃO 2006-2009 ANO LECTIVO: 2008/2009 ( 3º Ano ) CONTEÚDOS Página 1 Módulo
Investigação Operacional
 Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Algoritmos de Caminho Mínimo Parte 1
 Algoritmos de Caminho Mínimo Parte 1 A journey of a thousand miles starts with a single step and if that step is the right step, it becomes the last step. Index 1. Introduction 2. Applications 3. Tree
Algoritmos de Caminho Mínimo Parte 1 A journey of a thousand miles starts with a single step and if that step is the right step, it becomes the last step. Index 1. Introduction 2. Applications 3. Tree
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 11: Introdução aos Grafos
 Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 11: Introdução aos Grafos Indução Finita Indução Finita é uma técnica para provar teoremas também usada no projecto de algoritmos. Suponha
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 11: Introdução aos Grafos Indução Finita Indução Finita é uma técnica para provar teoremas também usada no projecto de algoritmos. Suponha
Grafos Hamiltonianos e o Problema do Caixeiro Viajante. Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá
 Grafos Hamiltonianos e o Problema do Caixeiro Viajante Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Grafo Hamiltoniano Definição: Um circuito hamiltoniano em um
Grafos Hamiltonianos e o Problema do Caixeiro Viajante Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Grafo Hamiltoniano Definição: Um circuito hamiltoniano em um
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Função Distribuição Condicional Calculando Probabilidades condicionando Esperança Condicional Aula de hoje Análise de Comandos de Programação
Estatística e Modelos Probabilísticos - COE241 Aula passada Função Distribuição Condicional Calculando Probabilidades condicionando Esperança Condicional Aula de hoje Análise de Comandos de Programação
Teoria da Computação. Unidade 3 Máquinas Universais. Referência Teoria da Computação (Divério, 2000)
 Teoria da Computação Referência Teoria da Computação (Divério, 2000) 1 L={(0,1)*00} de forma que você pode usar uma Máquina de Turing que não altera os símbolos da fita e sempre move a direita. MT_(0,1)*00=({0,1},{q
Teoria da Computação Referência Teoria da Computação (Divério, 2000) 1 L={(0,1)*00} de forma que você pode usar uma Máquina de Turing que não altera os símbolos da fita e sempre move a direita. MT_(0,1)*00=({0,1},{q
Resolução de PL usando o método Simplex
 V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
Introdução à Lógica de Programação. Adaptação de Luis Otavio Alvares
 1 Introdução à Lógica de Programação Adaptação de Luis Otavio Alvares 2 Elaboração de um programa Problema Análise Programa Algoritmo 3 Processo de geração de um programa Análise do problema: Ler atentamente
1 Introdução à Lógica de Programação Adaptação de Luis Otavio Alvares 2 Elaboração de um programa Problema Análise Programa Algoritmo 3 Processo de geração de um programa Análise do problema: Ler atentamente
Ex. 1) Considere que a árvore seguinte corresponde a uma parte do espaço de estados de um jogo de dois agentes: f=7 f=7 f=1 f=2
 LERCI/LEIC Tagus 2005/06 Inteligência Artificial Exercícios sobre Minimax: Ex. 1) Considere que a árvore seguinte corresponde a uma parte do espaço de estados de um jogo de dois agentes: Max Min f=4 f=7
LERCI/LEIC Tagus 2005/06 Inteligência Artificial Exercícios sobre Minimax: Ex. 1) Considere que a árvore seguinte corresponde a uma parte do espaço de estados de um jogo de dois agentes: Max Min f=4 f=7
Método Simplex V 1.1, V.Lobo, EN / ISEGI, 2008
 .,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
.,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
Buscas Informadas ou Heurísticas - Parte II
 Buscas Informadas ou Heurísticas - Parte II Prof. Cedric Luiz de Carvalho Instituto de Informática - UFG Graduação em Ciência da Computação / 2006 FUNÇÕES HEURÍSTICAS - 1/7 FUNÇÕES HEURÍSTICAS - 2/7 Solução
Buscas Informadas ou Heurísticas - Parte II Prof. Cedric Luiz de Carvalho Instituto de Informática - UFG Graduação em Ciência da Computação / 2006 FUNÇÕES HEURÍSTICAS - 1/7 FUNÇÕES HEURÍSTICAS - 2/7 Solução
MÓDULO 2 - OTIMIZAÇÃO DE REDES
 MÓUL - TIMIZÇÃ RS s problemas de otimização de redes podem ocorrer em várias áreas, mas geralmente são encontrados nas áreas de transportes e comunicações. Um problema típico de transporte consiste em
MÓUL - TIMIZÇÃ RS s problemas de otimização de redes podem ocorrer em várias áreas, mas geralmente são encontrados nas áreas de transportes e comunicações. Um problema típico de transporte consiste em
Problemas de Fluxos em Redes
 Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
setor 1102 Aula 20 PRINCÍPIOS BÁSICOS DA CONTAGEM 2 REVISÃO
 setor 1102 1102008 Aula 20 PRINCÍPIOS BÁSICOS DA CONTAGEM 1 PRINCÍPIOS BÁSICOS DA CONTAGEM Seja, por exemplo, uma lanchonete que vende três tipos de refrigerantes e dois tipos de cerveja. Pergunta-se:
setor 1102 1102008 Aula 20 PRINCÍPIOS BÁSICOS DA CONTAGEM 1 PRINCÍPIOS BÁSICOS DA CONTAGEM Seja, por exemplo, uma lanchonete que vende três tipos de refrigerantes e dois tipos de cerveja. Pergunta-se:
Licenciatura em Engenharia Electrotécnica e de Computadores. 1 a chamada Ou seja,
 Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1 a chamada 00-01-08 Resolução da Parte Prática 1 (a) O valor aproximado de w é obtido a partir dos valores aproximados de x,
Licenciatura em Engenharia Electrotécnica e de Computadores Análise Numérica 1 a chamada 00-01-08 Resolução da Parte Prática 1 (a) O valor aproximado de w é obtido a partir dos valores aproximados de x,
Complementos de Investigação Operacional. Folha nº 1 Programação Inteira 2006/07
 Complementos de Investigação Operacional Folha nº Programação Inteira 2006/07 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Complementos de Investigação Operacional Folha nº Programação Inteira 2006/07 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Lista de Exercícios Programação Inteira. x 2 0 e inteiros.
 Lista de Exercícios Programação Inteira ) Resolva os problemas a seguir usando o método B&B a) Max z = 5 x + 2 y s.a x + y 2 x + y 5 x, y 0, x e y inteiros b) Max z = 2 x + y s.a x + 2y 0 x + y 25 x, y
Lista de Exercícios Programação Inteira ) Resolva os problemas a seguir usando o método B&B a) Max z = 5 x + 2 y s.a x + y 2 x + y 5 x, y 0, x e y inteiros b) Max z = 2 x + y s.a x + 2y 0 x + y 25 x, y
Variáveis estatísticas ou variáveis: Os atributos (modalidades) ou magnitudes (valores) que se observam nos indivíduos de uma população.
 CPAR - UFMS A Estatística: é a ciência que estuda, mediante métodos quantitativos, as populações que se obtém com síntese da observação de unidades estatísticas (Ibarrola et. Al, 2006). População: qualquer
CPAR - UFMS A Estatística: é a ciência que estuda, mediante métodos quantitativos, as populações que se obtém com síntese da observação de unidades estatísticas (Ibarrola et. Al, 2006). População: qualquer
Grafos. Fabio Gagliardi Cozman. PMR2300 Escola Politécnica da Universidade de São Paulo
 PMR2300 Escola Politécnica da Universidade de São Paulo Um grafo é uma estrutura que generaliza árvores, sendo formado por nós e arestas. Cada nó em um grafo pode ser conectado a vários outros nós por
PMR2300 Escola Politécnica da Universidade de São Paulo Um grafo é uma estrutura que generaliza árvores, sendo formado por nós e arestas. Cada nó em um grafo pode ser conectado a vários outros nós por
Optimização. Carlos Balsa. Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança
 Optimização Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados Eng. Química e Industrial Carlos Balsa Matemática Aplicada
Optimização Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados Eng. Química e Industrial Carlos Balsa Matemática Aplicada
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford. O problema tem subestrutura óptima
 Caminho mais curto a partir de um nó Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford Fernando Lobo Algoritmos e Estrutura de Dados II Input: Um grafo com pesos nos arcos G =
Caminho mais curto a partir de um nó Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford Fernando Lobo Algoritmos e Estrutura de Dados II Input: Um grafo com pesos nos arcos G =
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford
 Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford Fernando Lobo Algoritmos e Estrutura de Dados II 1 / 28 Caminho mais curto a partir de um nó Input: Um grafo com pesos nos arcos
Caminho mais curto a partir de um nó Algoritmos de Dijkstra e Bellman-Ford Fernando Lobo Algoritmos e Estrutura de Dados II 1 / 28 Caminho mais curto a partir de um nó Input: Um grafo com pesos nos arcos
Otimização em Grafos
 Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
ESTRUTURAS DISCRETAS (INF 1631) GRAFOS. 1. O que é um grafo? Defina um grafo orientado. Defina um grafo não-orientado.
 PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira
 Ciência da Computação GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira Algoritmo de Bellman-Ford Arestas com valores negativos podem parecer inúteis, mas elas podem
Ciência da Computação GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira Algoritmo de Bellman-Ford Arestas com valores negativos podem parecer inúteis, mas elas podem
Problema do Caminho Mais Curto. Problema do Caminho Mais Curto
 Problema do Caminho Mais Curto " Podemos afectar pesos" aos arcos de um grafo, por exemplo, para representar uma distância entre cidades numa rede ferroviária: ria: Chicago 650 600 700 Toronto 200 New
Problema do Caminho Mais Curto " Podemos afectar pesos" aos arcos de um grafo, por exemplo, para representar uma distância entre cidades numa rede ferroviária: ria: Chicago 650 600 700 Toronto 200 New
Módulo 2 OTIMIZAÇÃO DE REDES
 Módulo 2 OTIMIZAÇÃO DE REDES Grafos e Redes Está contida na área de Pesquisa Operacional. Pode ser considerada como uma teoria baseada na interligação de pontos e linhas, utilizada principalmente na solução
Módulo 2 OTIMIZAÇÃO DE REDES Grafos e Redes Está contida na área de Pesquisa Operacional. Pode ser considerada como uma teoria baseada na interligação de pontos e linhas, utilizada principalmente na solução
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Somas aleatórias Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Simulação de Sistemas Discretos É
Estatística e Modelos Probabilísticos - COE241 Aula passada Somas aleatórias Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Simulação de Sistemas Discretos É
Resolução do problema do caixeiro viajante assimétrico (e uma variante) através da relaxação Lagrangeana
 Resolução do problema do caixeiro viajante assimétrico (e uma variante) através da relaxação Ana Maria A.C. Rocha e João Luís C. Soares Departamento de Produção e Sistemas Escola de Engenharia Universidade
Resolução do problema do caixeiro viajante assimétrico (e uma variante) através da relaxação Ana Maria A.C. Rocha e João Luís C. Soares Departamento de Produção e Sistemas Escola de Engenharia Universidade
O Problema do Fluxo de Custos Mínimos Terça-feira 2 de abril. O Problema do Caminho mais Curto. Fórmula. Outra Fórmula
 15.053 Terça-feira 2 de abril O Problema do Caminho mais Curto Algoritmo de Dijkstra para solucionar o Problema do Caminho mais Curto Distribuir: Observações de Aula 1 O Problema do Fluxo de Custos Mínimos
15.053 Terça-feira 2 de abril O Problema do Caminho mais Curto Algoritmo de Dijkstra para solucionar o Problema do Caminho mais Curto Distribuir: Observações de Aula 1 O Problema do Fluxo de Custos Mínimos
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
Grafos: caminhos (matriz adjacência)
 Grafos: caminhos (matriz adjacência) Algoritmos e Estruturas de Dados 2 Graça Nunes 1 O problema do menor caminho Um motorista deseja encontrar o caminho mais curto possível entre duas cidades do Brasil
Grafos: caminhos (matriz adjacência) Algoritmos e Estruturas de Dados 2 Graça Nunes 1 O problema do menor caminho Um motorista deseja encontrar o caminho mais curto possível entre duas cidades do Brasil
Cap. 2 Conceitos Básicos em Teoria dos Grafos
 Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
método de solução aproximada
 método de solução aproximada Definir - Representação - Objectivo - Função de avaliação 73 Representação do problema - Definição das variáveis de decisão do modelo escolhido para o problema real. Importante
método de solução aproximada Definir - Representação - Objectivo - Função de avaliação 73 Representação do problema - Definição das variáveis de decisão do modelo escolhido para o problema real. Importante
Método do Big M. Análise de Sensibilidade
 A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
CRITÉRIOS GERAIS DE CLASSIFICAÇÃO
 Exame Final Nacional de Matemática B Prova 735 2.ª Fase Ensino Secundário 2019 11.º Ano de Escolaridade Decreto-Lei n.º 139/2012, de 5 de julho Decreto-Lei n.º 55/2018, de 6 de julho Critérios de Classificação
Exame Final Nacional de Matemática B Prova 735 2.ª Fase Ensino Secundário 2019 11.º Ano de Escolaridade Decreto-Lei n.º 139/2012, de 5 de julho Decreto-Lei n.º 55/2018, de 6 de julho Critérios de Classificação
Módulo de Elementos básicos de geometria plana. Conceitos Geométricos Básicos. Oitavo Ano
 Módulo de Elementos básicos de geometria plana Conceitos Geométricos Básicos Oitavo Ano Conceitos Geométricos Básicos 1 Exercícios Introdutórios Exercício 1. Dados quatro pontos distintos A, B, C e D,
Módulo de Elementos básicos de geometria plana Conceitos Geométricos Básicos Oitavo Ano Conceitos Geométricos Básicos 1 Exercícios Introdutórios Exercício 1. Dados quatro pontos distintos A, B, C e D,
Investigação Operacional E-FÓLIO A. Ano lectivo 2015/2016. Proposta de Resolução
 Investigação Operacional - 07 E-FÓLIO A Ano lectivo 0/0 Proposta de Resolução. Variáveis: Sejam percentagem de M / Kg de mistura percentagem de M / Kg de mistura percentagem de M / Kg de mistura Tomando
Investigação Operacional - 07 E-FÓLIO A Ano lectivo 0/0 Proposta de Resolução. Variáveis: Sejam percentagem de M / Kg de mistura percentagem de M / Kg de mistura percentagem de M / Kg de mistura Tomando
Equações Diofantinas + = polinómios conhecidos polinómios desconhecidos
 23 Considere-se a equação Equações Diofantinas polinómios conhecidos polinómios desconhecidos Há soluções? Quantas soluções há para uma dada equação? Em geral, a equação pode ser definida num anel (exs.
23 Considere-se a equação Equações Diofantinas polinómios conhecidos polinómios desconhecidos Há soluções? Quantas soluções há para uma dada equação? Em geral, a equação pode ser definida num anel (exs.
Os Problemas de Optimização Combinatória e a Teoria da Complexidade
 Metodologias de Apoio à Decisão Os Problemas de Optimização Combinatória e a Teoria da Complexidade Programação Inteira Mista Programação Linear Programação Binária Mista Programação Inteira Slide Fluxos
Metodologias de Apoio à Decisão Os Problemas de Optimização Combinatória e a Teoria da Complexidade Programação Inteira Mista Programação Linear Programação Binária Mista Programação Inteira Slide Fluxos
a) Defina uma função para obter o máximo entre dois números
 IP, Resoluções comentadas, Semana 2 jrg, vs 002, Out-2012 a) Defina uma função para obter o máximo entre dois números A versão mais imediata talvez seja esta: public static int maior ( int a, int b ) {
IP, Resoluções comentadas, Semana 2 jrg, vs 002, Out-2012 a) Defina uma função para obter o máximo entre dois números A versão mais imediata talvez seja esta: public static int maior ( int a, int b ) {
Algoritmo de Dijkstra
 lgoritmo de Dijkstra Caminhos mínimos em Grafos Considere um grafo orientado ponderado G = (V,E) em que cada aresta possui um rótulo não negativo associado que define o custo da aresta, e um dos vértices
lgoritmo de Dijkstra Caminhos mínimos em Grafos Considere um grafo orientado ponderado G = (V,E) em que cada aresta possui um rótulo não negativo associado que define o custo da aresta, e um dos vértices
apenas os caminhos que passam só por vértices em C, exceto, talvez, o próprio v A Figura 1 a seguir ilustra o significado do conjunto C edovalordist.
 CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
GRAFOS Aula 08 Árvore Geradora Mínima: Algoritmos de Kruskal e Prim-Jarnik Max Pereira
 Ciência da Computação GRAFOS Aula 08 Árvore Geradora Mínima: Algoritmos de Kruskal e Prim-Jarnik Max Pereira Árvore Geradora (spanning tree) É um subconjunto de um grafo G que possui todos os vértices
Ciência da Computação GRAFOS Aula 08 Árvore Geradora Mínima: Algoritmos de Kruskal e Prim-Jarnik Max Pereira Árvore Geradora (spanning tree) É um subconjunto de um grafo G que possui todos os vértices
Teoria dos Grafos Aula 8
 Teoria dos Grafos Aula 8 Aula passada Grafos com pesos, caminhos e distâncias Ideia e algoritmo de Dijkstra Dijkstra o próprio Aula de hoje Corretude de Dijkstra Fila de prioridades e Heap Dijkstra eficiente
Teoria dos Grafos Aula 8 Aula passada Grafos com pesos, caminhos e distâncias Ideia e algoritmo de Dijkstra Dijkstra o próprio Aula de hoje Corretude de Dijkstra Fila de prioridades e Heap Dijkstra eficiente
Otimização em Grafos
 Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 35 Teoria dos Grafos - Relembrando Árvore Um grafo G é uma árvore se é conexo e não possui ciclos (acíclico).
Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 35 Teoria dos Grafos - Relembrando Árvore Um grafo G é uma árvore se é conexo e não possui ciclos (acíclico).
ALGORITMO DE DIJKSTRA
 LGORITMO IJKSTR por runo Miguel Pacheco Saraiva de arvalho epartamento de ngenharia Informática Universidade de oimbra oimbra, Portugal brunomig@student.dei.uc.pt Resumo escreve-se o funcionamento do algoritmo
LGORITMO IJKSTR por runo Miguel Pacheco Saraiva de arvalho epartamento de ngenharia Informática Universidade de oimbra oimbra, Portugal brunomig@student.dei.uc.pt Resumo escreve-se o funcionamento do algoritmo
ª Fase. 16 pontos
 007.ª Fase 16 pontos 007.ª Fase 4 pontos 15 pontos 007.ª Fase 007.ª Fase 0 pontos 5 pontos 007.ª Fase 5 pontos 10 pontos 0 pontos 007.ª Fase 0 pontos 0 pontos 5 pontos TOTAL 00 pontos Prova Escrita de
007.ª Fase 16 pontos 007.ª Fase 4 pontos 15 pontos 007.ª Fase 007.ª Fase 0 pontos 5 pontos 007.ª Fase 5 pontos 10 pontos 0 pontos 007.ª Fase 0 pontos 0 pontos 5 pontos TOTAL 00 pontos Prova Escrita de
CIC 111 Análise e Projeto de Algoritmos II
 CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 19 Paths and circuits Eulerian paths Hamiltonian paths De Bruijn sequences Knight s
CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 19 Paths and circuits Eulerian paths Hamiltonian paths De Bruijn sequences Knight s
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS
 UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS - TEXTO: Torre de Hanói e Triângulo de Sierpinski AUTOR: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR: Prof.
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS - TEXTO: Torre de Hanói e Triângulo de Sierpinski AUTOR: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR: Prof.
Teoria dos Grafos Aula 22
 Teoria dos Grafos Aula 22 Aula passada Caminho mais curto entre todos os pares Algoritmo de Floyd Warshall Programação dinâmica Aula de hoje Caminho mais curto Algoritmo de Bellman Ford Melhorias Caminho
Teoria dos Grafos Aula 22 Aula passada Caminho mais curto entre todos os pares Algoritmo de Floyd Warshall Programação dinâmica Aula de hoje Caminho mais curto Algoritmo de Bellman Ford Melhorias Caminho
Investigação Operacional
 nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
Pesquisa Operacional. Teoria dos Grafos
 Pesquisa Operacional Teoria dos Grafos 1 Sumário Introdução Histórico Aplicações de modelos em grafos Conceitos e Notação Representações de um grafo G Tipos de grafos Algoritmos Algoritmo de Djisktra Algoritmo
Pesquisa Operacional Teoria dos Grafos 1 Sumário Introdução Histórico Aplicações de modelos em grafos Conceitos e Notação Representações de um grafo G Tipos de grafos Algoritmos Algoritmo de Djisktra Algoritmo
= comprimento (distância, valor) da aresta orientada do vértice i ao vértice j,, e:
 8 - Problema do Caminho Mínimo Considere a rede: Dado dois vértices nesta rede, queremos determinar o menor caminho ente eles. Uma primeira questão é como representar os valores associados às arestas neste
8 - Problema do Caminho Mínimo Considere a rede: Dado dois vértices nesta rede, queremos determinar o menor caminho ente eles. Uma primeira questão é como representar os valores associados às arestas neste
Mestrado Integrado em Engenharia Civil. Disciplina: TRANSPORTES Prof. Responsável: José Manuel Viegas
 Mestrado Integrado em Engenharia Civil Disciplina: TRANSPORTES Prof. Responsável: José Manuel Viegas Sessão Prática 12 : Modelos de distribuição e afectação de tráfego 1/27 O MODELO DE 4 PASSOS Passo Objectivo
Mestrado Integrado em Engenharia Civil Disciplina: TRANSPORTES Prof. Responsável: José Manuel Viegas Sessão Prática 12 : Modelos de distribuição e afectação de tráfego 1/27 O MODELO DE 4 PASSOS Passo Objectivo
Busca em Espaço de Estados a
 Busca em Espaço de Estados a Fabrício Jailson Barth BandTec Agosto de 2012 a Slides baseados no material do Prof. Jomi F. Hübner (UFSC) Introdução 2 Agente orientado a meta O projetista não determina um
Busca em Espaço de Estados a Fabrício Jailson Barth BandTec Agosto de 2012 a Slides baseados no material do Prof. Jomi F. Hübner (UFSC) Introdução 2 Agente orientado a meta O projetista não determina um
Podem ser calculados num número finito de operações aritméticas, ao contrário de outras funções (ln x, sin x, cos x, etc.)
 Interpolação polinomial 1 Interpolação Polinomial Slide 1 Definição simples Definição 1 Dados os conjuntos de valores x 0, x 1,..., x n e y 0, y 1,..., y n, determinar uma função f tal que: Slide 2 f(x
Interpolação polinomial 1 Interpolação Polinomial Slide 1 Definição simples Definição 1 Dados os conjuntos de valores x 0, x 1,..., x n e y 0, y 1,..., y n, determinar uma função f tal que: Slide 2 f(x
Estruturas de Dados Grafos
 Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
