Partícula em um Poço de Potencial Infinito e o Método Variacional de Monte Carlo
|
|
|
- Camila Henriques Cortês
- 6 Há anos
- Visualizações:
Transcrição
1 Revista Brasileira de Ensino de Física, vol. 25, no. 1, Março, Partícula em um Poço de Potencial Infinito e o Método Variacional de Monte Carlo (Particle in an infinity potential well and the variational Monte Carlo method) Rodrigo Canabrava rodrigo.canabrava@ic.unicamp.br Silvio A. Vitiello vitiello@ifi.unicamp.br Instituto de Física, Universidade Estadual de Campinas Campinas - SP, Brasil Recebido em 9 de julho, Manuscrito revisado recebido em 16 de dezembro, Aceito em 13 de janeiro, Neste trabalho, apresentamos o método variacional de Monte Carlo, aplicado a um sistema de uma partícula confinada em um poço de potencial infinito. A amostragem da densidade de probabilidade é feita utilizando-se o algoritmo de Metropolis. O objetivo do trabalho é apresentar de forma didática o método e sua implementação em computadores. We apply the variational Monte Carlo method to study a particle in an infinite potential well. The probability density is sampled using the Metropolis algorithm. The aim of this work is to present in a pedagogical way both the method and its computer implementation. I Introdução A simulação de sistemas físicos em computadores vem se tornando essencial para o estudo da física e da ciência dos materiais, pois os modelos teóricos dos sistemas da natureza, cada vez mais realistas, são também cada vez mais complexos. Nessas simulações são avaliadas grandezas de interesse do sistema, sem que as equações que as descrevem sejam explicitamente resolvidas. A idéia desses métodos é obter respostas numéricas sujeitas apenas a incertezas de natureza estatística em situações em que não é possível determinar resultados de forma analítica. Neste artigo, apresentamos o método variacional de Monte Carlo e o aplicamos num problema físico extremamente simples de uma partícula confinada em um poço de potencial infinito. O método de Monte Carlo possibilita o cálculo de diversas grandezas de interesse do sistema, entre elas, a sua energia total. Para tanto, diversas configurações (posições da partícula no espaço), são utilizadas. Cada configuração possui uma probabilidade de ocorrer. Assim, a energia do sistema é dada pela média das energias associadas a cada configuração, e ponderada pela densidade de probabilidade P de esta configuração ocorrer. Essa ponderação é feita escolhendo-se as configurações por essa densidade de probabilidade. Dentre os algoritmos que permitem fazer essa amostragem, está o algoritmo de Metropolis[1]. O algoritmo de Metropolis permite, a cada passo, obter uma nova configuração a partir da anterior, utilizando a densidade de probabilidade P. O algoritmo permite essencialmente que configurações mais prováveis tenham mais chance de ocorrer na média das grandezas de interesse. Na próxima seção, descrevemos o modelo da partícula no poço de potencial. Na seção 3 discutimos o método variacional. Nas duas seções seguintes, apresentamos o método variacional, e o algoritmo de Metropolis, respectivamente. Em seguida, discutimos detalhes da implementação, e apresentamos os resultados obtidos. II Partícula confinada num poço de potencial infinito Para uma partícula em estado estacionário, isto é, em que não há variação na sua energia, a equação de Schrödinger é dada por Hψ n (x) =E n ψ n (x), (1) em que H é a Hamiltoniana, em um problema unidimensional, escrita como H = d2 + V (x). (2) dx2
2 36 Rodrigo Canabrava e Silvio A. Vitiello Para simplificarmos, utilizamos unidades onde = 2m =1. Para uma partícula em um poço de potencial infinito, podemos ter: { 0 se 0 <x<1 V (x) = nos outros casos (3) Assim, as condições de contorno satisfeitas por ψ(x) devem ser: ψ(x) =0se { x 0 x 1. (4) A Eq. (1) é uma equação diferencial de segundo grau homogênea e permite soluções exatas da forma ψ(x) =Asen(kx)+Bcos(kx). (5) Considerando as condições de contorno, soluções obtemos as ψ n (x) =Asen(nπx), (6) com n inteiro e maior que zero. Utilizando este resultado na Eq. (1), obtemos os auto-valores da energia E n : E n =(nπ) 2. (7) Portanto, para o estado fundamental, temos E 0 = π 2 III Método variacional Em situações onde não é possível determinarmos a solução exata da equação de Schrödinger, o método variacional éde grande utilidade. Isso porque, como sabemos[2], ele fornece um limite superior para o valor da energia. Ao construirmos uma função de onda tentativa ψ T,é importante que ela incorpore da melhor maneira possível os conhecimentos que temos do sistema. A energia variacional de um sistema pode ser escrita como: ψt Hψ T dx E T = ψt 2 dx. (8) Se na construção de ψ T utilizamos parâmetros, E T é minimizada com respeito aos mesmos. Para ilustrar a aplicação do método variacional ao problema da partícula no poço de potencial, vamos adotar como função tentativa, para o estado fundamental: ψ T (x) =Nx(1 x), (9) em que N é a constante de normalização. Na Fig. 1 apresentamos uma comparação desta função tentativa com a função de onda exata do problema. Figura 1. Comparação entre a função tentativa utilizada e a função de onda exata do problema (Eq. (6), n=1). No gráfico ambas as curvas foram multiplicadas por constantes de tal forma que em x = 1 2 tenhamos ψ n=1( 1 2 )=ψt( 1 )=1. A linha contínua representa 2 ψ T e a tracejada ψ n=1. Portanto, para esse problema, se substituírmos ψ T dada pela Eq. (9) na Eq. (8), temos que E T =10. Este valor é bem próximo do valor exato da Eq. (7). IV Método variacional de Monte Carlo A integração que acabamos de realizar analiticamente sem dúvida pode ser feita numericamente. Caso estivéssemos tratando um problema de muitas partículas e que envolvessem funções não integráveis analiticamente, provavelmente a única alternativa seria empregarmos o método de Monte Carlo para realizarmos as integrações necessárias. Apesar de nosso problema não justificar a utilização deste método, iremos empregá-lo aqui para ilustrar sua aplicação. Na aplicação do método variacional de Monte Carlo, é útil reescrevermos a Eq. (8) como E T = P (R)E L (R)dR, (10) onde P (R) é uma densidade de probabilidade dada por: e P (R) = ψ T (R) 2 ψt (R) dr E L (R) = Hψ T (R) ψ T (R) (11) (12) é chamada de energia local. Obviamente, para as autofunções da Hamiltoniana (1), E L será uma constante.
3 Revista Brasileira de Ensino de Física, vol. 25, no. 1, Março, A probabilidade de encontrarmos uma partícula numa certa posição, P (x) = ψ 0 (x) 2,é dada, considerando-se a função variacional da Eq. (9), por P (x) =N 2 x 2 (1 x) 2. (13) Note que o método de Metropolis não envolve o conhecimento explícito do valor da constante N. A energia local, neste caso, é dada por 2 E L (x) = x(1 x). (14) A energia variacional, como escrita na Eq. (10), mostra a utilidade dos métodos de Monte Carlo na sua determinação. É necessário amostrarmos a densidade de probabilidade P (x) para obter a seqüência de configurações x 1,x 2,..., x M e compor a média: E T = 1 M E L (x i ) (15) M i=1 com as M configurações x i. No processo de amostragem construimos uma seqüência x i distribuida de acordo com P (x), isto é, teremos mais pontos onde P assume seus maiores valores. Como já mencionamos, os resultados estão sujeitos a incertezas estatísticas, o que torna essencial a estimativa da variância: σ 2 = 1 M 1 M (E L (x i ) E T ) 2 (16) i=1 e conseqüentemente do erro padrão σ/ M. A amostragem de P (x), no caso particular deste trabalho, pode ser feita sem dificuldades utilizando diversos algoritmos. O algoritmo de Metropolis é um dos mais empregados na literatura por ser de aplicação geral. Ele será utilizado aqui e é descrito a seguir. V Algoritmo de Metropolis O algoritmo de Metropolis [1] é muito poderoso porque permite amostrarmos qualquer distribuição de probabilidade P. Uma nova configuração aleatória para o sistema é proposta a partir da anterior. As probabilidades da posição atual e da nova posição proposta são utilizadas para determinar se a nova configuração é aceita. São permitidos movimentos tanto para configurações de maior como de menor probabilidade que a atual. O algoritmo é o seguinte: 1) Escolha uma configuração arbitrária x i onde i =0. 2) Faça x novo = x i +(ɛ 1 2 ), onde ɛ éumnúmero aleatório[3] no intervalo [0,1], e é um parâmetro do qual os resultados são independentes. 3) Se P (xnovo) P (x i) ɛ então x i+1 = x novo senão x i+1 = x i ; ɛ éumnovonúmero aleatório. 4) Faça i = i +1. 5) Se i<mvápara 2, (M éonúmero total de amostras). A nova configuração obtida a cada passo pode, eventualmente, ser igual à anterior. Novas configurações são calculadas e propostas no passo 2. é um parâmetro que determina a amplitude do deslocamento da partícula. Seu valor é ajustado para que cerca de 50% das novas configurações sejam aceitas. No passo 3, temos os testes para aceitar ou não essa configuração. Se o sistema vai para uma nova configuração mais provável, ela é aceita. Mesmo que a probabilidade da nova configuração seja menor, ela ainda pode ser aceita, com uma probabilidade dada pelo número aleatório ɛ. Observa-se que a configuração inicial é arbitrária. Levando em conta esse fato, descartamos os primeiros passos para que o sistema se equilibre. VI Implementação Para realizar a simulação, escrevemos um programa que, a partir de uma configuração inicial arbitrária x 0, com 0 < x 0 < 1, amostrava a distribuição de probabilidade dada pela Eq. (13) utilizando o algoritmo de Metropolis. Com as amostras obtidas, formamos as médias da energia E T,de acordo com a Eq. (15). O algoritmo de Metropolis introduz correlações entre as configurações amostradas. Isso é conseqüência direta do passo 2 do algoritmo. Uma maneira óbvia de resolver esse problema é utilizar no cálculo da energia apenas uma amostragem a cada K posições obtidas. Por exemplo, com K = 200, formaríamos a média da energia apenas com a seqüência X 0,X 200,X 400,... Com isso teríamos eliminado o problema de correlações. Uma maneira mais eficiente de tratar este problema envolve o que chamamos de média por blocos. Utilizamos um valor de K pequeno, obtendo uma seqüência X 0,X K,X 2K,X 3K,... Calculamos as médias parciais das energias a cada grupo de N E dessas posições. Após obtermos as energias de N b blocos, fazemos a média final, com o desvio padrão referente a essa média com N b valores. Assim, por exemplo, para K =5eN E =40, obtemos X 0,X 5,X 10,... E a cada 40 dessas posições, agrupamos numa média parcial E b. A média final E T e o seu erro padrão são calculados assumindo que cada energia de bloco (E b ) seja estatisticamente independente das demais. Esse procedimento resolve o problema de correlação entre as configurações amostradas, com maior eficiência no tempo de uso da máquina.
4 38 Rodrigo Canabrava e Silvio A. Vitiello VII Resultados obtidos O primeiro passo é escolher o valor do parâmetro, que controla a amplitude do movimento da partícula. Para determinarmos o melhor valor para o parâmetro, consideramos a fração de movimentos aceitos como medida, isto é, a razão entre o número de vezes em que uma nova configuração é aceita pelo número total de tentativas. Os resultados podem ser vistos na Tabela 1. Observamos que quanto menor o valor de, maior éa fração de aceitação. Quando é pequeno, a partícula se move muito pouco a cada passo. Para valores maiores de, a razão das probabilidades (passo 3 do algoritmo) pode ser pequena e, além disto, o algoritmo tenta mover a partícula para fora do intervalo com muita freqüência, resultando em rejeitarmos a configuração proposta. Uma regra empírica sugere que a fração de aceitação ideal deve ser aproximadamente 0,5. Note que tanto para o maior como para o menor valor de apresentados na tabela, os cálculos perdem muito de sua eficiência; nestas situações o número de amostras utilizado deixa de ser suficiente. Fato este, que se reflete no valor irrealista do erro padrão. Tabela 1. Resultados do problema da partícula confinada num poço de potencial infinito, para vários valores de. Nestes testes, realizamos 1200 passos, descartando os 200 primeiros. fração de aceitos E T ± ± ± ± ± ± ± Em seguida, realizamos a implementação de média por blocos. Mostramos na Tabela 2 alguns resultados. Esses testes foram realizados sempre com 2000 passos, que eram divididos igualmente num certo número de blocos. Cada um dos testes foi realizado usando-se a mesma sequência de configurações dos outros, de forma que obtivemos o mesmo valor de energia média em todos os casos. Assim, podemos ver mais diretamente a influência do número de blocos no valor do erro. Conforme esperávamos, os valores de desvio padrão apresentam um máximo em função do número de blocos (N b ). Como o número de passos total é sempre o mesmo, quanto maior for o número de blocos, menor será onúmero de passos por bloco (N E ). Por conseqüência, menor será a variância. De fato, estaremos tratando como avaliações independentes da energia resultados que, na realidade, não são independentes. Como já mencionamos, esta é uma decorrência do algoritmo de Metropolis. No outro extremo, a medida que diminuirmos excessivamente o número de blocos, a variância volta a diminuir. A escolha do número de blocos mais adequado nem sempre é fácil[4]. Neste problema, 10 a 20 blocos dão uma boa idéia do erro do valor calculado. Tabela 2. Resultados da implementação de média por blocos para =0.15, utilizando as mesmas 2000 configurações em cada simulação. Um pequeno valor de foi escolhido para por em evidência o comportamento do erro padrão em outras simulações que envolvam sistemas de muitos corpos. VIII Número de blocos E T ± ± ± ± ± ± ± ± ± ± ± ± Conclusão Neste artigo, apresentamos o método variacional de Monte Carlo. Esse método é muito útil em simulações de sistemas físicos em computadores, pois a equação de Schrödinger desses sistemas muitas vezes não permitem soluções analíticas. De forma a exemplificar o uso desse método, utilizamos um modelo muito simples, que tem solução analítica fácil, de forma que podemos comparar o resultado obtido na simulação com a solução da equação de Schrödinger. Além da discussão teórica, também analisamos aspectos de implementação do método variacional de Monte Carlo. Exemplificamos o algoritmo de Metropolis como um dos possíveis algoritmos que fazem a amostragem de configurações neste problema. Analisamos o problema de correlação entre as configurações, e mostramos uma maneira de se resolver esse problema. Os resultados obtidos com a nossa função variacional são muito bons, quando comparados ao resultado exato da Eq. (7). O método variacional de Monte Carlo édefácil implementação e fornece a energia variacional em excelente acordo com o resultado analítico. Este valor está sujeito apenas a incertezas de natureza estatística, as quais podem
5 Revista Brasileira de Ensino de Física, vol. 25, no. 1, Março, ser sistematicamente reduzidas pelo aumento do número de amostras. Agradecimentos Agradecemos ao Centro Nacional de Processamento de Alto Desempenho em São Paulo (CENAPAD-SP) na Unicamp pelo uso de suas facilidades de processamento em paralelo. Agradecemos também à Fundação de Amparo à Pesquisa no Estado de São Paulo (FAPESP) por financiar a pesquisa com bolsa de Iniciação Científica. Referências [1] N. Metropolis et al., J. Chem. Phys. 21, 1087 (1953). [2] D. Griffiths, Introduction to Quantum Mechanics, Prentice Hall, New Jersey, [3] G. Marsaglia e A. Zaman, Comp. Phys. 8, 117 (1994). [4] M. P. Allen e D. J. Tildesley, Computer Simulation of Liquids, Oxford, 1989.
O poço quadrado finito
 O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
6- Probabilidade e amostras: A distribuição das médias amostrais
 6- Probabilidade e amostras: A distribuição das médias amostrais Anteriormente estudamos como atribuir probabilidades a uma observação de alguma variável de interesse (ex: Probabilidade de um escore de
6- Probabilidade e amostras: A distribuição das médias amostrais Anteriormente estudamos como atribuir probabilidades a uma observação de alguma variável de interesse (ex: Probabilidade de um escore de
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
Mecânica Quântica I. Slides 1. Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler. Departamento de Física da Universidade de Évora
 Mecânica Quântica I Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler Slides 1 Departamento de Física da Universidade de Évora A equação de Schrödinger Comparação de descrição clássica e quântica:
Mecânica Quântica I Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler Slides 1 Departamento de Física da Universidade de Évora A equação de Schrödinger Comparação de descrição clássica e quântica:
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2009 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2009 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de agosto de 2011 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de agosto de 2011 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
Partícula na Caixa. Química Quântica Prof a. Dr a. Carla Dalmolin
 Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE DE SCHRÖDINGER Primeira Edição junho de 2005 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE DE SCHRÖDINGER Primeira Edição junho de 2005 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 9. Soluções da equação de Schrödinger: partícula numa caixa infinita
 UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 1 elétron O princípio variacional Função
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 1 elétron O princípio variacional Função
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2010 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2010 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
O oscilador harmônico simples quântico
 1 / 18 O oscilador harmônico simples quântico Prof. Dr. Vicente Pereira de Barros Instituto Federal de Educação Ciência e Tecnologia de São Paulo - Campus Itapetininga 29/05/2014 2 / 18 Introdução Introdução
1 / 18 O oscilador harmônico simples quântico Prof. Dr. Vicente Pereira de Barros Instituto Federal de Educação Ciência e Tecnologia de São Paulo - Campus Itapetininga 29/05/2014 2 / 18 Introdução Introdução
Função de Onda e Equação de Schrödinger
 14/08/013 Função de Onda e Equação de Schrödinger Prof. Alex Fabiano C. Campos, Dr A Função de Onda (ψ) A primeira formulação para esta nova interpretação da Mecânica, a Mecânica Quântica, teoria foi proposta
14/08/013 Função de Onda e Equação de Schrödinger Prof. Alex Fabiano C. Campos, Dr A Função de Onda (ψ) A primeira formulação para esta nova interpretação da Mecânica, a Mecânica Quântica, teoria foi proposta
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenaria de Materiais (DEMAR) Escola de Engenaria de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Variáveis Dinâmicas e Operadores
 Variáveis Dinâmicas e Operadores Variável Dinâmica é qualquer função de x e p: K = p2 2m U = U(x) E = p2 2m + U(x) L = r p Só estudamos sistemas conservativos em MQ. Qual o valor de ω(x, p) (uma VD qualquer)
Variáveis Dinâmicas e Operadores Variável Dinâmica é qualquer função de x e p: K = p2 2m U = U(x) E = p2 2m + U(x) L = r p Só estudamos sistemas conservativos em MQ. Qual o valor de ω(x, p) (uma VD qualquer)
4 e 6/Maio/2016 Aulas 17 e 18
 9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
O Método de Monte Carlo
 .....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Método de Monte Carlo Aplicações do algoritmo de Metropolis no Modelo de Ising Mateus
.....Universidade Federal de Santa Maria...Centro de Ciências Naturais e Exatas Grupo de Teoria da Matéria Condensada O Método de Monte Carlo Aplicações do algoritmo de Metropolis no Modelo de Ising Mateus
Aplicação do Método Variacional na Mecânica Quântica:
 Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
Rotor quântico. Quanticamente o rotor é descrito por uma função de onda, tal que: l A função de onda do estado estacionário é dada por:
 Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB
 MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB Bruno Avila Farenzena 1 Eliete Biasotto Hauser 2 Resumo: Neste trabalho
MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB Bruno Avila Farenzena 1 Eliete Biasotto Hauser 2 Resumo: Neste trabalho
Instituto de Física - UFF Profissional - 11 de Dezembro de 2009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das
 Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 11 de Dezembro de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3
Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 11 de Dezembro de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3
6 Modelo Gamma-Cetuc (GC)
 6 Modelo Gamma-Cetuc (GC) Um modelo de sintetização de séries temporais de atenuação por chuva envolve a geração de dados aleatórios que satisfaçam especificações de estatísticas de primeira e de segunda
6 Modelo Gamma-Cetuc (GC) Um modelo de sintetização de séries temporais de atenuação por chuva envolve a geração de dados aleatórios que satisfaçam especificações de estatísticas de primeira e de segunda
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 12. Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 12 Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico 1 Barreira de potencial Uma barreira de potencial é descrita
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 12 Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico 1 Barreira de potencial Uma barreira de potencial é descrita
Fundamentos de Química Quântica
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Professora: Melissa Soares Caetano Partícula na caixa Sistema ideal
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Professora: Melissa Soares Caetano Partícula na caixa Sistema ideal
Exercícios de programação
 Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Planejamento e Otimização de Experimentos
 Planejamento e Otimização de Experimentos Um Pouco de Estatística Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br anselmo.disciplinas@gmail.com Populações, Amostras e Distribuições População Amostra
Planejamento e Otimização de Experimentos Um Pouco de Estatística Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br anselmo.disciplinas@gmail.com Populações, Amostras e Distribuições População Amostra
Sexta Lista: Geração de Números Pseudo-Aleatórios e Método de Monte Carlo
 Sexta Lista: Geração de Números Pseudo-Aleatórios e Método de Monte Carlo Antônio Carlos Roque da Silva Filho e Cristiano R. F. Granzotti 26 de junho de 2017 Os exercícios desta lista devem ser resolvidos
Sexta Lista: Geração de Números Pseudo-Aleatórios e Método de Monte Carlo Antônio Carlos Roque da Silva Filho e Cristiano R. F. Granzotti 26 de junho de 2017 Os exercícios desta lista devem ser resolvidos
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 11. Soluções da equação de Schrödinger: potencial degrau
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
aula ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES
 ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
Tunelamento em Teoria Quântica de Campos
 Tunelamento em Teoria Quântica de Campos Leonardo Peixoto de Moura Orientador: Prof. Dr Gabriel Flores Hidalgo March 29, 2017 Sumário 1 Introdução 2 N-dimensional 3 T.C. 4 Método de Aproximação 5 Método
Tunelamento em Teoria Quântica de Campos Leonardo Peixoto de Moura Orientador: Prof. Dr Gabriel Flores Hidalgo March 29, 2017 Sumário 1 Introdução 2 N-dimensional 3 T.C. 4 Método de Aproximação 5 Método
Prof. Dr. Lucas Barboza Sarno da Silva
 Prof. Dr. Lucas Barboza Sarno da Silva Uma outra vez a experiência da dupla fenda 18/11/015 Prof. Dr. Lucas Barboza Sarno da Silva Probabilidade de chegada do elétron, com a fenda fechada: * 1 1 1 * Probabilidade
Prof. Dr. Lucas Barboza Sarno da Silva Uma outra vez a experiência da dupla fenda 18/11/015 Prof. Dr. Lucas Barboza Sarno da Silva Probabilidade de chegada do elétron, com a fenda fechada: * 1 1 1 * Probabilidade
A Estrutura Eletrônica dos Átomos. Prof. Fernando R. Xavier
 A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
Distribuição Normal. Prof. Eduardo Bezerra. (CEFET/RJ) - BCC - Inferência Estatística. 25 de agosto de 2017
 padrão - padronização Distribuição Normal Prof. Eduardo Bezerra (CEFET/RJ) - BCC - Inferência Estatística 25 de agosto de 2017 Eduardo Bezerra (CEFET/RJ) Distribuição Normal Março/2017 1 / 32 Roteiro Distribuições
padrão - padronização Distribuição Normal Prof. Eduardo Bezerra (CEFET/RJ) - BCC - Inferência Estatística 25 de agosto de 2017 Eduardo Bezerra (CEFET/RJ) Distribuição Normal Março/2017 1 / 32 Roteiro Distribuições
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Valores esperados. ψ (x)xψ(x)dx. ψ ψ dx. xp(x)dx P(x)dx. Vimos que: x = = ψ xψ dx. No caso geral de uma função de x: f (x) = f (x) =
 Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
Método dos Elementos Finitos
 SEÇÃO DE ENSINO DE ENGENHARIA DE FORTIFICAÇÃO E CONSTRUÇÃO Método dos Elementos Finitos Introdução Prof: Moniz de Aragão Definições Procedimento geral de discretização de problemas da mecânica do contínuo
SEÇÃO DE ENSINO DE ENGENHARIA DE FORTIFICAÇÃO E CONSTRUÇÃO Método dos Elementos Finitos Introdução Prof: Moniz de Aragão Definições Procedimento geral de discretização de problemas da mecânica do contínuo
Física IV Escola Politécnica P3 7 de dezembro de 2017
 Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Instituto de Física USP. Física V - Aula 28. Professora: Mazé Bechara
 nstituto de Física USP Física V - Aula 8 Professora: Mazé Bechara Aula 8 - Estados ligados em movimentos unidimensionais 1. O poço de potencial infinito complementando. Comparação com resultado de de Broglie
nstituto de Física USP Física V - Aula 8 Professora: Mazé Bechara Aula 8 - Estados ligados em movimentos unidimensionais 1. O poço de potencial infinito complementando. Comparação com resultado de de Broglie
( x) = a. f X. = para x I. Algumas Distribuições de Probabilidade Contínuas
 Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
Ref: H.Gould e J. Tobochnik. Para integrais em uma dimensão as regras do trapezóide e de Simpson são
 Método de Monte Carlo Resolução de Integrais Ref: H.Gould e J. Tobochnik Para integrais em uma dimensão as regras do trapezóide e de Simpson são melhores, mais rápidas. A técnica de resolução de integrais
Método de Monte Carlo Resolução de Integrais Ref: H.Gould e J. Tobochnik Para integrais em uma dimensão as regras do trapezóide e de Simpson são melhores, mais rápidas. A técnica de resolução de integrais
Equações diferenciais ordinárias
 Departamento de Física Universidade Federal da Paraíba 24 de Junho de 2009 Motivação Problemas envolvendo equações diferenciais são muito comuns em física Exceto pelos mais simples, que podemos resolver
Departamento de Física Universidade Federal da Paraíba 24 de Junho de 2009 Motivação Problemas envolvendo equações diferenciais são muito comuns em física Exceto pelos mais simples, que podemos resolver
Energia de Fermi de 2N electrões
 Energia de Fermi de 2N electrões Ângelo Dias N.º 65087 Mariana Branco N.º 65112 Física Quântica da Matéria Mestrado Integrado em Engenharia Biomédica 29 de Março de 2011 I. Resumo Neste trabalho é discutida
Energia de Fermi de 2N electrões Ângelo Dias N.º 65087 Mariana Branco N.º 65112 Física Quântica da Matéria Mestrado Integrado em Engenharia Biomédica 29 de Março de 2011 I. Resumo Neste trabalho é discutida
ESTUDO DO COMPORTAMENTO DE UM GÁS POR DINÂMICA MOLECULAR.
 ESTUDO DO COMPORTAMENTO DE UM GÁS POR DINÂMICA MOLECULAR. João Paulo Smykaluk (ICV-UNICENTRO), Eduardo Vicentini (Orientador), e-mail: evicentini@unicentro.br. Universidade Estadual do Centro-Oeste, Setor
ESTUDO DO COMPORTAMENTO DE UM GÁS POR DINÂMICA MOLECULAR. João Paulo Smykaluk (ICV-UNICENTRO), Eduardo Vicentini (Orientador), e-mail: evicentini@unicentro.br. Universidade Estadual do Centro-Oeste, Setor
FÍSICA EXPERIMENTAL C ( )
 FÍSICA EXPERIMENTAL C (4323301) REPRESENTAÇÃO DE INCERTEZAS EM RESULTADOS EXPERIMENTAIS Medida, erro e incerteza Qualquer medida física possui sempre um valor verdadeiro, que é sempre desconhecido, e um
FÍSICA EXPERIMENTAL C (4323301) REPRESENTAÇÃO DE INCERTEZAS EM RESULTADOS EXPERIMENTAIS Medida, erro e incerteza Qualquer medida física possui sempre um valor verdadeiro, que é sempre desconhecido, e um
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 8. A equação de Schrödinger
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
Aula-9 Mais Ondas de Matéria I
 Aula-9 Mais Ondas de Matéria I Estados ligados Vimos, até agora, 3 postulados da Mecânica Quântica: a) Toda partícula possui uma função de onda associada a ela. b) A forma e a evolução temporal desta é
Aula-9 Mais Ondas de Matéria I Estados ligados Vimos, até agora, 3 postulados da Mecânica Quântica: a) Toda partícula possui uma função de onda associada a ela. b) A forma e a evolução temporal desta é
Comparação entre intervalos de confiança calculados com métodos bootstrap e intervalos assintóticos
 Comparação entre intervalos de confiança calculados com métodos strap e intervalos assintóticos Selene Loibel Depto. de Estatística, Matemática Aplicada e Computação, IGCE, UNESP, Rio Claro, SP E-mail:sloibel@rc.unesp.br,
Comparação entre intervalos de confiança calculados com métodos strap e intervalos assintóticos Selene Loibel Depto. de Estatística, Matemática Aplicada e Computação, IGCE, UNESP, Rio Claro, SP E-mail:sloibel@rc.unesp.br,
2 Metodologia. Simulação de defeitos pontuais em um sólido de Lennard-Jones
 Simulação de defeitos pontuais em um sólido de Lennard-Jones SILVA JÚNIOR, Domingos Lopes da 1 ; COSTA, Lucas Modesto da 1 ; RABELO, José Nicodemos Teixeira 2 ; CÂNDIDO, Ladir 3 1 Introdução Apesar de
Simulação de defeitos pontuais em um sólido de Lennard-Jones SILVA JÚNIOR, Domingos Lopes da 1 ; COSTA, Lucas Modesto da 1 ; RABELO, José Nicodemos Teixeira 2 ; CÂNDIDO, Ladir 3 1 Introdução Apesar de
O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana
 Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Física O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana Introdução O Hélio é, depois do Hidrogênio, o átomo mais simples
Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Física O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana Introdução O Hélio é, depois do Hidrogênio, o átomo mais simples
Problemas de Mecânica Quântica Ano lectivo 2007/2008 Engenharia Biomédica, IST
 Problemas de Mecânica Quântica Ano lectivo 2007/2008 Engenharia Biomédica, IST Potenciais unidimensionais, poço de potencial, efeito de túnel, oscilador linear harmónico 1. Gasiorowicz 4.8 Ajudas: (a)
Problemas de Mecânica Quântica Ano lectivo 2007/2008 Engenharia Biomédica, IST Potenciais unidimensionais, poço de potencial, efeito de túnel, oscilador linear harmónico 1. Gasiorowicz 4.8 Ajudas: (a)
Exame Unificado EUF. 1º Semestre/2013 Parte 1 16/10/2012
 Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
As bases da Dinâmica Molecular - 1
 As bases da Dinâmica Molecular - 1 Alexandre Diehl Departamento de Física - UFPel Um pouco de história... IDMSF2017 2 Um pouco de história... A pré-história da Dinâmica Molecular A ideia da Dinâmica Molecular
As bases da Dinâmica Molecular - 1 Alexandre Diehl Departamento de Física - UFPel Um pouco de história... IDMSF2017 2 Um pouco de história... A pré-história da Dinâmica Molecular A ideia da Dinâmica Molecular
2. podemos solucionar problemas não somente probabilisticas, mas tambem qualquer
 Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Física IV Poli Engenharia Elétrica: 14ª Aula (02/10/2014)
 Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
Planejamento e Otimização de Experimentos
 Planejamento e Otimização de Experimentos Um Pouco de Estatística Descritiva Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br elcana@quimica.ufg.br Populações, Amostras e Distribuições População
Planejamento e Otimização de Experimentos Um Pouco de Estatística Descritiva Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br elcana@quimica.ufg.br Populações, Amostras e Distribuições População
Tratamento de dados e representação das incertezas em resultados experimentais
 Tratamento de dados e representação das incertezas em resultados experimentais Medida, erro e incerteza Qualquer medida física sempre possui um valor verdadeiro, que é sempre desconhecido e um valor medido.
Tratamento de dados e representação das incertezas em resultados experimentais Medida, erro e incerteza Qualquer medida física sempre possui um valor verdadeiro, que é sempre desconhecido e um valor medido.
Monte Carlo Method. Peter Frank Perroni. December 1, Monte Carlo Simulation
 Monte Carlo Simulation December 1, 2015 Histórico Técnica muito antiga porém somente recentemente oficializado como método estatístico. Foi muito importante nas simulações da bomba desenvolvida no Projeto
Monte Carlo Simulation December 1, 2015 Histórico Técnica muito antiga porém somente recentemente oficializado como método estatístico. Foi muito importante nas simulações da bomba desenvolvida no Projeto
Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada.
 Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada [alessandro@psr-inc.com] Conteúdo Introdução Estimação não paramétrica (Kernel density) Transformação
Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada [alessandro@psr-inc.com] Conteúdo Introdução Estimação não paramétrica (Kernel density) Transformação
Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional
 Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional Caio Vaz Rímoli Resumo: Partículas Livres não relativísticas estão entre os sistemas mais básicos e mais
Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional Caio Vaz Rímoli Resumo: Partículas Livres não relativísticas estão entre os sistemas mais básicos e mais
6. Mecânica Quântica
 6. Mecânica Quântica Sumário A função de onda A equação de Schrödinger Partícula em uma caixa Poço de potencial Barreira de potencial e o efeito túnel Oscilador harmônico A função de onda Ψ descreve uma
6. Mecânica Quântica Sumário A função de onda A equação de Schrödinger Partícula em uma caixa Poço de potencial Barreira de potencial e o efeito túnel Oscilador harmônico A função de onda Ψ descreve uma
Distribuição Normal. Prof. Herondino
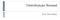 Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Bioestatística INFERÊNCIA ESTATÍSTICA. Silvia Shimakura
 Bioestatística INFERÊNCIA ESTATÍSTICA Silvia Shimakura AMOSTRAS E POPULAÇÕES Inferências sobre populações são geralmente feitas a partir de informações obtidas de amostras. amostras Válido se a amostra
Bioestatística INFERÊNCIA ESTATÍSTICA Silvia Shimakura AMOSTRAS E POPULAÇÕES Inferências sobre populações são geralmente feitas a partir de informações obtidas de amostras. amostras Válido se a amostra
Universidade de São Paulo em São Carlos Mecânica Quântica Aplicada Prova 1
 Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
3 + =. resp: A=5/4 e B=11/4
 ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI-UNITAU EXERCÍCIOS PARA ESTUDO DO EXAME FINAL - 3º ENSINO MÉDIO - PROF. CARLINHOS BONS ESTUDOS! ASSUNTO : POLINÔMIOS 1) Identifique as expressões abaixo que são
ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI-UNITAU EXERCÍCIOS PARA ESTUDO DO EXAME FINAL - 3º ENSINO MÉDIO - PROF. CARLINHOS BONS ESTUDOS! ASSUNTO : POLINÔMIOS 1) Identifique as expressões abaixo que são
Sistemas Aleatórios. Um sistema é aleatório quando seu estado futuro só pode ser conhecido. jogar uma moeda ou um dado. decaimento de uma partícula
 Sistemas Aleatórios Um sistema é aleatório quando seu estado futuro só pode ser conhecido pela realização de uma experiência. jogar uma moeda ou um dado decaimento de uma partícula trajetória de uma partícula
Sistemas Aleatórios Um sistema é aleatório quando seu estado futuro só pode ser conhecido pela realização de uma experiência. jogar uma moeda ou um dado decaimento de uma partícula trajetória de uma partícula
6 Estudo de Casos: Valor da Opção de Investimento em Informação por Aproximação com Números Fuzzy 6.1. Introdução
 6 Estudo de Casos: Valor da Opção de Investimento em Informação por Aproximação com Números Fuzzy 6.1. Introdução Este capítulo apresenta o segundo estudo de casos, no qual também são empregados números
6 Estudo de Casos: Valor da Opção de Investimento em Informação por Aproximação com Números Fuzzy 6.1. Introdução Este capítulo apresenta o segundo estudo de casos, no qual também são empregados números
Cap. 8 - Intervalos Estatísticos para uma Única Amostra
 Intervalos Estatísticos para ESQUEMA DO CAPÍTULO 8.1 INTRODUÇÃO 8.2 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 8.3 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO
Intervalos Estatísticos para ESQUEMA DO CAPÍTULO 8.1 INTRODUÇÃO 8.2 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 8.3 INTERVALO DE CONFIANÇA PARA A MÉDIA DE UMA DISTRIBUIÇÃO
Mais Informações sobre Itens do Relatório
 Mais Informações sobre Itens do Relatório Amostra Tabela contendo os valores amostrados a serem utilizados pelo método comparativo (estatística descritiva ou inferencial) Modelos Pesquisados Tabela contendo
Mais Informações sobre Itens do Relatório Amostra Tabela contendo os valores amostrados a serem utilizados pelo método comparativo (estatística descritiva ou inferencial) Modelos Pesquisados Tabela contendo
Princípios Gerais da Mecânica Quântica
 Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Não serão aceitas respostas sem justificativa:
 Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
FISC TÓPICOS ESPECIAIS DE FÍSICA TEÓRICA (Introdução à Teoria Quântica do Espalhamento)
 FISC-7048 - TÓPICOS ESPECIAIS DE FÍSICA TEÓRICA (Introdução à Teoria Quântica do Espalhamento) Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Ementa:
FISC-7048 - TÓPICOS ESPECIAIS DE FÍSICA TEÓRICA (Introdução à Teoria Quântica do Espalhamento) Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Ementa:
ANÁLISE DA VARIÂNCIA DE DISPERSÃO EM PILHAS DE BLENDAGEM UTILIZANDO SIMULAÇÃO GEOESTATÍSTICA
 ANÁLISE DA VARIÂNCIA DE DISPERSÃO EM PILHAS DE BLENDAGEM UTILIZANDO SIMULAÇÃO GEOESTATÍSTICA Diego Machado Marques, UFRGS, diegommarques@yahoo.com.br João Felipe C. L. Costa, UFRGS, jfelipe@ufrgs.br Introdução
ANÁLISE DA VARIÂNCIA DE DISPERSÃO EM PILHAS DE BLENDAGEM UTILIZANDO SIMULAÇÃO GEOESTATÍSTICA Diego Machado Marques, UFRGS, diegommarques@yahoo.com.br João Felipe C. L. Costa, UFRGS, jfelipe@ufrgs.br Introdução
Funções ortogonais e problemas de Sturm-Liouville. Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE
 Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Funções ortogonais e problemas de Sturm-Liouville Prof. Rodrigo M. S. de Oliveira UFPA / PPGEE Série de Fourier Soma de funções ortogonais entre si Perguntas: -existem outras bases ortogonais que podem
Fis.Rad.I /1 Notas de aula (Prof. Stenio Dore) (Dated: May 28, 2004)
 INTRODUÇÃO À ESTATÍSTICA DE CONTAGEM Fis.Rad.I - 24/1 Notas de aula (Prof. Stenio Dore) (Dated: May 28, 24) I. PROBABILIDADE: E E OU Vimos que, para nossas finalidades podemos definir a probabilidade de
INTRODUÇÃO À ESTATÍSTICA DE CONTAGEM Fis.Rad.I - 24/1 Notas de aula (Prof. Stenio Dore) (Dated: May 28, 24) I. PROBABILIDADE: E E OU Vimos que, para nossas finalidades podemos definir a probabilidade de
CE008 Introdução à Bioestatística INFERÊNCIA ESTATÍSTICA
 CE008 Introdução à Bioestatística INFERÊNCIA ESTATÍSTICA Silvia Shimakura Estimação Amostras são usadas para estimar quantidades desconhecidas de uma população. população Exemplo: prevalência de doenças,
CE008 Introdução à Bioestatística INFERÊNCIA ESTATÍSTICA Silvia Shimakura Estimação Amostras são usadas para estimar quantidades desconhecidas de uma população. população Exemplo: prevalência de doenças,
x exp( t 2 )dt f(x) =
 INTERPOLAÇÃO POLINOMIAL 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia Aproximação
INTERPOLAÇÃO POLINOMIAL 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia Aproximação
Prof. Eduardo Bezerra. 15 de setembro de 2017
 Distribuições Amostrais Prof. Eduardo Bezerra Inferência Estatística 15 de setembro de 2017 Eduardo Bezerra (CEFET/RJ) Distribuições Amostrais 1 / 28 Roteiro Distribuições amostrais 1 Distribuições amostrais
Distribuições Amostrais Prof. Eduardo Bezerra Inferência Estatística 15 de setembro de 2017 Eduardo Bezerra (CEFET/RJ) Distribuições Amostrais 1 / 28 Roteiro Distribuições amostrais 1 Distribuições amostrais
Física IV Escola Politécnica GABARITO DA P3 27 de novembro de 2012
 Física IV - 4320402 Escola Politécnica - 2012 GABARITO DA P3 27 de novembro de 2012 Questão 1 Considere uma partícula de massa m e energia E num potencial unidimensional que é nulo na região 0 < x < d
Física IV - 4320402 Escola Politécnica - 2012 GABARITO DA P3 27 de novembro de 2012 Questão 1 Considere uma partícula de massa m e energia E num potencial unidimensional que é nulo na região 0 < x < d
No limite. é livre. é livre. Note que a equação 78.1 está na forma:
 Teoria Quântica de Campos I 78 (aqui está a vantagem dos estados coerentes, se tentássemos fazer o mesmo no espaço de Fock apareceriam problemas pois o termo com fontes mistura níveis de Fock diferentes)
Teoria Quântica de Campos I 78 (aqui está a vantagem dos estados coerentes, se tentássemos fazer o mesmo no espaço de Fock apareceriam problemas pois o termo com fontes mistura níveis de Fock diferentes)
Universidade Tecnológica Federal do Paraná Câmpus Francisco Beltrão
 Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
Integral de Trajetória de Feynman
 Teoria Quântica de Campos II 7 No estado fundamental, ou vácuo, defindo por a energia é: Energia de ponto zero ou do vácuo Podemos definir um hamiltoniano sem esta energia de ponto zero, definindo o ordenamento
Teoria Quântica de Campos II 7 No estado fundamental, ou vácuo, defindo por a energia é: Energia de ponto zero ou do vácuo Podemos definir um hamiltoniano sem esta energia de ponto zero, definindo o ordenamento
Mecânica Quântica. Química Quântica Prof a. Dr a. Carla Dalmolin. A Equação de Schrödinger Postulados da Mecânica Quântica
 Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
Dois elétrons num bilhar com paredes suaves
 https://eventos.utfpr.edu.br//sicite/sicite2017/index Dois elétrons num bilhar com paredes suaves Pedro Chebenski Júnior pedroj@alunos.utfpr.edu.br Universidade Tecnológica Federal do Paraná, Ponta Grossa,
https://eventos.utfpr.edu.br//sicite/sicite2017/index Dois elétrons num bilhar com paredes suaves Pedro Chebenski Júnior pedroj@alunos.utfpr.edu.br Universidade Tecnológica Federal do Paraná, Ponta Grossa,
Regressão linear simples
 Regressão linear simples Universidade Estadual de Santa Cruz Ivan Bezerra Allaman Introdução Foi visto na aula anterior que o coeficiente de correlação de Pearson é utilizado para mensurar o grau de associação
Regressão linear simples Universidade Estadual de Santa Cruz Ivan Bezerra Allaman Introdução Foi visto na aula anterior que o coeficiente de correlação de Pearson é utilizado para mensurar o grau de associação
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Algoritmo para simular uma fila Medidas de interesse Média amostral Aula de hoje Teorema do Limite Central Intervalo de Confiança Variância amostral
Estatística e Modelos Probabilísticos - COE241 Aula passada Algoritmo para simular uma fila Medidas de interesse Média amostral Aula de hoje Teorema do Limite Central Intervalo de Confiança Variância amostral
Mecânica Quântica para Sistemas Fechados
 1 / 21 Universidade Federal de Santa Maria Centro de Ciências Naturais e Exatas Programa de Pós-Graduação em Física Grupo de Teoria da Matéria Condensada Mecânica Quântica para Sistemas Fechados Jonas
1 / 21 Universidade Federal de Santa Maria Centro de Ciências Naturais e Exatas Programa de Pós-Graduação em Física Grupo de Teoria da Matéria Condensada Mecânica Quântica para Sistemas Fechados Jonas
Índice. AULA 5 Derivação implícita 3. AULA 6 Aplicações de derivadas 4. AULA 7 Aplicações de derivadas 6. AULA 8 Esboço de gráficos 9
 www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
4.1. ESPERANÇA x =, x=1
 4.1. ESPERANÇA 139 4.1 Esperança Certamente um dos conceitos mais conhecidos na teoria das probabilidade é a esperança de uma variável aleatória, mas não com esse nome e sim com os nomes de média ou valor
4.1. ESPERANÇA 139 4.1 Esperança Certamente um dos conceitos mais conhecidos na teoria das probabilidade é a esperança de uma variável aleatória, mas não com esse nome e sim com os nomes de média ou valor
Capítulo 3 Equações Diferenciais. O Wronskiano (de Josef Hoëné-Wronski, polonês, )
 Capítulo 3 Equações Diferenciais O Wronskiano (de Josef Hoëné-Wronski, polonês, 1776 1853) Seja a equação diferencial, ordinária, linear e de 2ª. ordem Podemos dividir por os 2 membros e escrever a equação
Capítulo 3 Equações Diferenciais O Wronskiano (de Josef Hoëné-Wronski, polonês, 1776 1853) Seja a equação diferencial, ordinária, linear e de 2ª. ordem Podemos dividir por os 2 membros e escrever a equação
EXEMPLOS DE APLICAÇÃO
 UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS CURSO DE FÍSICA INTRODUÇÃO AO MÉTODO MONTE CARLO: EXEMPLOS DE APLICAÇÃO TRABALHO DE GRADUAÇÃO Jonas Maziero Santa Maria, RS, Brasil
UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS CURSO DE FÍSICA INTRODUÇÃO AO MÉTODO MONTE CARLO: EXEMPLOS DE APLICAÇÃO TRABALHO DE GRADUAÇÃO Jonas Maziero Santa Maria, RS, Brasil
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística. Curso: Engenharia de Produção
 Considere a função f(x). Para algum x a f (x) pode não existir. Suponha que se queira resolver o seguinte PPNL: Max f(x) s. a a x b Pode ser que f (x) não exista ou que seja difícil resolver a equação
Considere a função f(x). Para algum x a f (x) pode não existir. Suponha que se queira resolver o seguinte PPNL: Max f(x) s. a a x b Pode ser que f (x) não exista ou que seja difícil resolver a equação
, logo, para se obter uma boa precisão seria necessário aumentar, e muito, o número de
 2. Simulação de Monte Carlo A Simulação de Monte Carlo (SMC) é um método numérico que utiliza um gerador de números aleatórios para simular possíveis valores da variável de interesse e assim obter a estimativa
2. Simulação de Monte Carlo A Simulação de Monte Carlo (SMC) é um método numérico que utiliza um gerador de números aleatórios para simular possíveis valores da variável de interesse e assim obter a estimativa
Considere a função f(x). Para algum x a f (x) pode não existir. Suponha que. Max f(x) s. a a x b
 Considere a função f(x). Para algum x a f (x) pode não existir. Suponha que se queira resolver o seguinte PPNL: Max f(x) s. a a x b Pode ser que f (x) não exista ou que seja difícil resolver a equação
Considere a função f(x). Para algum x a f (x) pode não existir. Suponha que se queira resolver o seguinte PPNL: Max f(x) s. a a x b Pode ser que f (x) não exista ou que seja difícil resolver a equação
