Estatística: Aplicação ao Sensoriamento Remoto SER ANO Componentes Principais
|
|
|
- Giovanni Álvares
- 4 Há anos
- Visualizações:
Transcrição
1 Estatística: Aplicação ao Sensoriamento Remoto SER 4 - ANO 9 Componentes Principais Camilo Daleles Rennó camilorenno@inpebr
2 Associação entre Variáveis r = < r < - < r < r = r = - r Cov(, ) Var( ) Var( ) Coeficiente de Correlação (de Pearson) Quanto maior a variância, maior é a variabilidade e portanto maior a informação contida na variável Num caso extremo, se a variância é zero, a variável não apresenta nenhuma informação a respeito do fenômeno por ela representada Por sua vez, a covariância (e a correlação) é interpretada como uma redundância em análises múltiplas ( ou mais variáveis), já que a informação contida numa variável está parcialmente representada em outra Num caso extremo, para que utilizar duas variáveis perfeitamente correlacionadas ( r = ), uma vez que, conhecendo-se o valor de uma, pode-se inferir com precisão o valor da outra?
3 Transformação por Componentes Principais (exemplo D) Como poderíamos eliminar a redundância entre e? W Y W Y Cov(, ) W w Cov( W, W ) Cov(, ) Y W j j j Cov( Y, Y ) rotação com preservação da ortogonalidade dos eixos y w W y Y Y W W Var( Y ) Y W W Var( Y ) a CP a CP são chamados de autovetores são chamados de autovalores ( > ) Var( ) Var( ) informação total é preservada 3
4 mm m m m m α Os autovetores representam as transformações lineares aplicadas em m variáveis correlacionadas de modo a obter m variáveis não correlacionadas e podem ser representados na forma de uma matriz (m m): Autovalores e Autovetores Os autovalores representam a variância de cada componente (variável transformada) e podem ser representadas na forma de uma matriz diagonal (m m): Nesta matriz, os autovetores estão organizados em colunas, ou seja, o o autovetor está na a coluna, o o autovetor está na a coluna e assim por diante ( > > > m ) Mas como são calculados os autovalores e autovetores? m λ 4
5 Matriz de Variância-Covariância Supondo que n amostras sejam avaliadas segundo m variáveis diferentes (atributos), podemos representar o conjunto de valores observados por um matriz, onde cada elemento x ij representa o valor da i-ésima amostra para a j-ésima variável x x xn x x x nm x x x m m m nm A variância de cada variável e as covariâncias entre todos os pares de variáveis podem ser representadas através da matriz de variância-covariância (m m): Σ Cov Cov Cov, Cov, m, Var Cov, Var, Cov, Var m m m m m m Cov(, ) n i i i n Cov(, ) Cov(, ) k l l k Cov(, ) Var( ) k k k 5
6 Cálculo dos Autovalores e Autovetores Os autovalores () e autovetores () são obtidos de modo a satisfazer a seguintes condições: α Σ λα ou λiα Σ sendo αα I (autovetores ortogonais) Como os autovetores são não nulos, então Σ λi gera um polinômio de grau m cujas raízes representam os m autovalores Ordenam-se os autovalores do maior para o menor e para cada autovalor k, calcula-se o autovetor k de modo que: λ Iα Σ k k Assim, os valores transformados para a componente principal k são calculados a partir da matriz : Y k α k 6
7 Exemplo,5,3,3,3 5,,,3, 3,4,5,3,3,3 5,,,3, 3,4 Σ λi 7,659,59 9,,8,39 ) )(,5 8,6 (7,68,8,39 ) )(,5 )(5, (3,4,,65,9,468,9,36,98 ) )(,5 )(5, (3,4,) )( (,5 )(,3) (5,,3) )( (3,4,3)(,3),)( ( ) )(,5 )(5, (3,4 3 Σ λi,46,887, Encontrando as raízes do polinômio, tem-se,5,3,3,3 5,,,3, 3,4 Suponha que Σ I Então Σ λ 7
8 Exemplo Agora, para cada autovalor, calcula-se o autovetor correspondente de modo que Demonstrando para o primeiro autovalor = 5,757 α Σ λα 3, 4,,3, 5,,3 5, 757,3,3,5 3 3,357,,3 3,,557,3 3,3,3 5, , ,84 3 Repetindo para os demais autovalores, chega-se a: 5, α, ,4 7, ,858, Como os autovetores são ortogonais então Assim,76,583, αα I, α, , , ,43497,587338,854569,4385,
9 Análise de Componentes Principais 3 4,596,443 5,8457,7544,46,97 6,9976 4,3787,684,76 5,894,97,54 9,49 6,867,887,733 5,98 4,4443 9,69,7587 7,4789,578 5,574,84 7,464 7,848 5,39,8336 4,5949 4,58 9,457,575,75 4,884,5356,838 7,773,439 5,849,95 4,5368 4,345 8,5466,796 3,739 4,397 8,357,7357,9786 4,347 8,9358,8759 6,595 4, 9,698,394 4,586,9 6,45,5584 4,365 5,595,6657,4849 3,47 3,5743 7,443,369,85 6,346 3,677,5869,9385 4,5867 9,63,794 3,56 3,338 7,47 5 5,,4,6, ,,4,6, Matriz de Variância-Covariância,56,44 -,683 -,37,44 7,3698-3,4-6,36 -,683-3,4,9737 3,886 -,37-6,36 3,886 7, Autovalores 5,765,9,3, Autovetores,34,583,948,38,6485,758 -,67 -,87 -,3437,787 -,837,857 -,6784,5865,7 -, ,,4,6,
10 CP4 CP4 CP4 CP3 CP3 CP Análise de Componentes Principais CP CP CP 3 CP 4-3,444 -,589 -,354,689-5,74,9 -,55,8-3,87,94,4,98-4,944 -,5494,594,8,8577,95 -,36,37 6,7,87 -,94,68-8,993 -,453,486 -,66,589,6859,4 -,35 -,7664,9,4 -,35 6,579,5895,455 -,84,649,4,638,977,3543 -,96 -,344 -,6,6757 -,6745,49,45,9795,35,76 -,6 3,88 -,3335 -,7 -,349 -,7436,786 -,397 -,68,647 -,466 -,65,383-4,393,63 -,669 -,95 -,9 -,76,4,94,3949 -,443,433 -,73,5,5, , ,5 - CP,3,, , -, -,3 -,4 CP,5,,5,, ,5 5 -, -,5 -, -,5 CP,3,, , -, -,3 -,4,5,,5,,5 -, -,5 -, -,5 Matriz de Variância-Covariância 5,765,9,3, CP - - -,5 3 CP A primeira componente guarda 9,% da variação total As primeiras CP, acumulam 99,7% da variação total,5,,5,,5 -,4 -, -,5,,4 -, -,5 -, -,5 CP3
11 Análise de Componentes Principais no R x<-c(596,46,684,54,733,7587,84,8336,575,838,95,796,7357,8759,394, 5584,4849,369,5869,794) x<-c(443,97,76,949,598,74789,7464,45949,75,7773,45368,3739,9786, 6595,4586,4365,347,85,9385,356) x3<-c(58457,69976,5894,6867,44443,578,7848,458,4884,439,4345,4397,4347,4,9, 5595,35743,6346,45867,3338) x4<-c(7544,43787,97,887,969,5574,539,9457,5356,5849,85466,8357,89358,9698, 645,6657,7443,3677,963,747) x<-cbind(x,x,x3,x4) round(cov(x),4) x x x3 x4 x x x x sum(diag(cov(x))) [] pccov<-prcomp(x) pccov Standard deviations: [] Rotation: PC PC PC3 PC4 x x x x λ sum(pccov$sdev^) [] 79458
12 Análise de Componentes Principais no R summary(pccov) Importance of components: PC PC PC3 PC4 Standard deviation Proportion of Variance Cumulative Proportion pc<-pccov$x #Calculando as componentes principais round(cov(pc),4) PC PC PC3 PC4 PC 5764 PC 9 PC3 3 PC4 pairs(x) pairs(pc)
13 Observações A transformação prioriza as variáveis com maior variância Atenção: isso pode ocorrer quando as variáveis possuem diferentes grandezas Para neutralizar o efeito das variâncias de cada variável de modo que todas tenham o mesmo peso, os autovalores e autovetores devem ser calculados a partir da matriz de correlação (que equivale realizar a transformação sobre as variáveis padronizadas) 3
14 ,,,,,, m m m m r r r r r r r Alternativamente, as relações entre as variáveis podem ser expressas através da matriz de correlação: Matriz de Correlação m m,, Var Var Cov r,,, k k k l l k r r r Obs: em R, para computar a transformação por componentes principais utilizando a matriz de correlação, pode-se usar a função pccor<-prcomp(x, scale=true) 4
15 Observações A transformação prioriza as variáveis com maior variância Atenção: isso pode ocorrer quando as variáveis possuem diferentes grandezas Para neutralizar o efeito das variâncias de cada variável de modo que todas tenham o mesmo peso, os autovalores e autovetores devem ser calculados a partir da matriz de correlação (que equivale realizar a transformação sobre as variáveis padronizadas) Por usar covariância (ou correlação), esta transformação pressupõe relações lineares entre variáveis A interpretação dos valores de uma determinada componente principal pode ser bastante difícil, necessitando a avaliação do autovetor correspondente Ex: Y =,34 +,6485,3437 3,
16 Aplicações Diminuição da dimensionalidade do problema Ao invés de se trabalhar com 5 dimensões, escolhem-se as primeiras componentes que guardam a maior parte da informação total Isso melhora o desempenho de classificadores que se baseiam em inversões de matrizes Visualização de Dados A informação contida numa imagem hiperespectral pode ser visualizada usando-se as 3 primeiras componentes numa composição colorida RGB (obs: as cores podem ser de difícil interpretação) 6
17 Visualização de Dados TM/LANDSAT (Bandas a 5 e 7) 7/68 ano 999 B B B3 543/RGB B4 B5 B7 7
18 Visualização de Dados TM/LANDSAT (Bandas a 5 e 7) 7/68 ano 999 (ganho,45 e offset variável) B B B3 543/RGB B4 B5 B7 8
19 Visualização de Dados TM/LANDSAT (Bandas a 5 e 7) 7/68 ano 999 (ganho,45 e offset variável) Média DPadrão B 45,556 9,3 B 8,36,6 B3 5,484,837 B4 3,698 8,8 B5 8,5 44,84 B7 39,7 5,8 Covariância B B B3 B4 B5 B7 B 37,489 95,99 38,969-6,67 493,634 95,37 B 95,99 34,554 8,3-33,44 49,773 45,47 B3 38,969 8,3 434,63-7,4 837,56 499,6 B4-6,67-33,44-7,4 353,868-6,5-6,894 B5 493,634 49, ,56-6,5 95,58 94, B7 95,37 45,47 499,6-6,894 94, 666,57 Autovetor Autovalor B B B3 B4 B5 B7 335,547 CP,3,8,35 -,88,766, ,967 CP,79 -,,55 -,966 -,5,4 7,9 CP3,84,9,4,3 -,38 -,53 35, CP4 -,333,69,549,67 -,487,543 9,45 CP5,3 -,9 -,563,7 -,5,683 4,7 CP6,57 -,877,444,47, -,85 B BB3 B4 B5B7 Importante: Para obtenção das estatísticas é necessário desconsiderar a região sem informação OBS: Em geral, as imagens resultantes não são representadas em bytes ( a 55), tendo valores positivos e negativos 9
20 (mesmo ganho e offset da CP) Visualização de Dados Componentes Principais 8,7% CP 8,8% CP 7,% CP3,9% CP3/RGB CP4 98,5% CP5,5%,% CP6
21 Visualização de Dados Componentes Principais Média DPadrão CP 56,88 CP 8,6 CP3 6,5 CP4 5,934 CP5 4,375 CP6,7 Covariância CP CP CP3 CP4 CP5 CP6 CP 335,55 CP 345,967 CP3 7,9 CP4 35, CP5 9,45 CP6 4,7 CP6 CP5 CP4 CP3 CP CP (ganho e offset arbitrários)
22 Data Aplicações Diminuição da dimensionalidade do problema Ao invés de se trabalhar com 5 dimensões, escolhem-se as primeiras componentes que guardam a maior parte da informação total Isso melhora o desempenho de classificadores que se baseiam em inversões de matrizes Visualização de Dados A informação contida numa imagem hiperespectral pode ser visualizada usando-se as 3 primeiras componentes numa composição colorida RGB (obs: as cores podem ser de difícil interpretação) Detecção de Mudanças Numa comparação de datas (mesma banda), os valores extremos da segunda componente evidenciam onde ocorreu mudança entre datas DesvPad Data
23 Aplicações Diminuição da dimensionalidade do problema Ao invés de se trabalhar com 5 dimensões, escolhem-se as primeiras componentes que guardam a maior parte da informação total Isso melhora o desempenho de classificadores que se baseiam em inversões de matrizes Visualização de Dados A informação contida numa imagem hiperespectral pode ser visualizada usando-se as 3 primeiras componentes numa composição colorida RGB (obs: as cores podem ser de difícil interpretação) Detecção de Mudanças Numa comparação de datas (mesma banda), os valores extremos da segunda componente evidenciam onde ocorreu mudança entre datas Aumento de Contraste por Decorrelação Aplica-se a transformada por componentes principais, faz-se um aumento de contraste das componentes de modo que todas fiquem com a mesma variância e, por fim, faz-se a transformação inversa, restabelecendo-se as variáveis originais PC PC PC PC Cov(, ) > Cov(, ) = 3
24 Aplicações Diminuição da dimensionalidade do problema Ao invés de se trabalhar com 5 dimensões, escolhem-se as primeiras componentes que guardam a maior parte da informação total Isso melhora o desempenho de classificadores que se baseiam em inversões de matrizes Visualização de Dados A informação contida numa imagem hiperespectral pode ser visualizada usando-se as 3 primeiras componentes numa composição colorida RGB (obs: as cores podem ser de difícil interpretação) Detecção de Mudanças Numa comparação de datas (mesma banda), os valores extremos da segunda componente evidenciam onde ocorreu mudança entre datas Aumento de Contraste por Decorrelação Aplica-se a transformada por componentes principais, faz-se um aumento de contraste das componentes de modo que todas fiquem com a mesma variância e, por fim, faz-se a transformação inversa, restabelecendo-se as variáveis originais Simulação de dados correlacionados Calculam-se os autovalores e autovetores da matriz de variância-covariância Simulam-se dados não-correlacionados com variância igual aos autovalores e fazse a transformação inversa 4
25 Exemplo: Simulação de dados correlacionados Simulação de 3 variáveis correlacionadas sendo que 3 ~ N(,3; 3,5) μ,3 35, 7,8 ~ N( 35,; 7,8) 3,5,,5 Σ ~ N( 7,8;,), 7,8,9 3 3,5,9, ~ N μ, Deseja-se simular 5 valores destas 3 variáveis respeitando suas correlações A simulação conjunta, mesmo para uma distribuição gaussiana, não é muito simples Por outro lado, a simulação de variáveis independentes é bastante simples de ser implementada quando se conhece a distribuição destas variáveis Σ 5
26 Exemplo: Simulação de dados correlacionados Σ 3,5,,5, 7,8,9,5,9, TCP λ α 8,869,3867,96,34,589,55,946,8,398,934,77,9886 Por definição, todas as componentes principais tem média zero e a variância de cada componente é dada pelo autovalor correspondente Além disso, no caso de distribuições gaussianas, a forma da distribuição é preservada após a transformação, ou seja, as componentes também têm distribuição gaussiana: PC PC PC 3 ~ N( ; PC ~ N( ; ~ N( ; PC PC 3 8,869),589),55) ' α PC μ ' α μ ' α α αpc μ ' P C ( 5 ) ( 5) 3 ( 5 ) 6
27 Exemplo: Simulação de dados correlacionados Neste exemplo, deseja-se gerar 5 valores para cada variável O processo inicia-se com a geração de números aleatórios de uma distribuição uniforme contínua entre e : U U U
28 Exemplo: Simulação de dados correlacionados A partir de U calcula-se Z através da relação: P( Z z ij ) u ij Exemplo: P ( Z z,),9789 z,,3 U Z U Z U3 Z
29 Exemplo: Simulação de dados correlacionados A partir de Z calcula-se PC multiplicando cada z ij pelo desvio padrão da componente principal i, ou seja, a raiz quadrada do autovalor i: pc Exemplo: pc z,3 8,869 6, 47,, ij z ij i PC Z PC Z PC3 Z
30 x Exemplo: Simulação de dados correlacionados Finalmente, aplica-se a rotação inversa definida pela matriz de autovetores e soma-se a média correspondente a cada uma das variáveis : ij, pc, j, pc, j,3 pc3, j Exemplo: x,, pc,, pc, i onde kw é o k-ésimo elemento do autovetor w,3 pc 3,,3867 6,47,946,778,8,996,3,95 PC Z PC Z PC3 3 Z
31 Exemplo: Simulação de dados correlacionados É importante notar que, por se tratar de uma simulação, os valores de média, variância e covariância estimados a partir dos valores simulados não são exatamente os que se desejava (e variam a cada simulação!): μ,3 35, 7,8,8 35, 7,83 Σ 3,5,,5, 7,8,9,5,9, Σˆ 3,37,6,59,6 8,9,93,59,93,4 3
32 Exemplo: Simulação de dados correlacionados em R m<-c(3,35,78) cov<-cbind(c(35,-,-5),c(-,78,9),c(-5,9,)) auto<-eigen(cov) #gera autovalores e autovetores a partir da matriz de covariância n<-5 Z<-matrix(rnorm(3*n),nrow=n,ncol=3) #as colunas representam amostras de uma normal padrão (independentes) colnames(z)<-c("z","z","z3") pairs(z,upperpanel = NULL) PC<-Z*(matrix(rep(,n))%*%t(sqrt(auto$values))) colnames(pc)<-c("pc", "PC", "PC3") pairs(pc,upperpanel = NULL) 3
33 Exemplo: Simulação de dados correlacionados em R <-t(auto$vectors%*%t(pc)+t(matrix(rep(,n))%*%m)) colnames()<-c("", "", "3") pairs(,upperpanel = NULL) round(colmeans(),) μ,3 35, 7,8 round(cov(),) Σˆ Σ 3,5,,5, 7,8,9,5,9, 33
Sensoriamento Remoto II
 Sensoriamento Remoto II Componentes principais Revisão de matemática Análise de componentes principais em SR UFPR Departamento de Geomática Prof. Jorge Centeno 2016 copyright@ centenet Revisão matemática
Sensoriamento Remoto II Componentes principais Revisão de matemática Análise de componentes principais em SR UFPR Departamento de Geomática Prof. Jorge Centeno 2016 copyright@ centenet Revisão matemática
Mestrado Profissional em Administração. Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 2015
 Mestrado Profissional em Administração Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 015 Decomposição Espectral Autovalores e autovetores MANLY, Cap. Objetivo e Definição
Mestrado Profissional em Administração Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 015 Decomposição Espectral Autovalores e autovetores MANLY, Cap. Objetivo e Definição
ANÁLISE DE COMPONENTES PRINCIPAIS/PCA ou ACP
 Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Função prcomp. 1. Introdução
 Função prcomp 1. Introdução Apresentamos alguns exemplos de utilização da função prcomp do pacote stats em R. Esta função permite realizar uma análise de componentes principais a partir de uma matriz de
Função prcomp 1. Introdução Apresentamos alguns exemplos de utilização da função prcomp do pacote stats em R. Esta função permite realizar uma análise de componentes principais a partir de uma matriz de
Estudo dirigido de Análise Multivariada
 Estudo dirigido de Análise Multivariada Conceitos Iniciais De um modo geral, os métodos estatísticos de análise multivariada são aplicados para analisar múltiplas medidas sobre cada indivíduo ou objeto
Estudo dirigido de Análise Multivariada Conceitos Iniciais De um modo geral, os métodos estatísticos de análise multivariada são aplicados para analisar múltiplas medidas sobre cada indivíduo ou objeto
GPDI Grupo de Profissionais de Dados e Inteligência
 GPDI Grupo de Profissionais de Dados e Inteligência Estatística e sua relação de dados Uma aplicação na redução da dimensionalidade em matrizes de dados Grupo de Profissionais de Dados e Inteligência Quem
GPDI Grupo de Profissionais de Dados e Inteligência Estatística e sua relação de dados Uma aplicação na redução da dimensionalidade em matrizes de dados Grupo de Profissionais de Dados e Inteligência Quem
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
PROCESSAMENTO DIGITAL DE IMAGENS (SERP11) TRANSFORMAÇÕES LINEARES: COMPONENTES PRINCIPAIS, TASSELED CAP, IHS. Daniel C. Zanotta
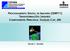 PROCESSAMENTO DIGITAL DE IMAGENS (SERP11) TRANSFORMAÇÕES LINEARES: COMPONENTES PRINCIPAIS, TASSELED CAP, IHS Daniel C. Zanotta ANÁLISE POR PRINCIPAIS COMPONENTES Conceitos básicos Espalhamento bi-dimensional:
PROCESSAMENTO DIGITAL DE IMAGENS (SERP11) TRANSFORMAÇÕES LINEARES: COMPONENTES PRINCIPAIS, TASSELED CAP, IHS Daniel C. Zanotta ANÁLISE POR PRINCIPAIS COMPONENTES Conceitos básicos Espalhamento bi-dimensional:
Análise de Componentes Principais (PCA)
 Análise de Componentes Principais (PCA) Lailson B. Moraes, George D. C. Cavalcanti {lbm4,gdcc}@cin.ufpe.br Roteiro Introdução Características Definição Algoritmo Exemplo Aplicações Vantagens e Desvantagens
Análise de Componentes Principais (PCA) Lailson B. Moraes, George D. C. Cavalcanti {lbm4,gdcc}@cin.ufpe.br Roteiro Introdução Características Definição Algoritmo Exemplo Aplicações Vantagens e Desvantagens
ANÁLISE DE COMPONENTES PRINCIPAIS/PCA ou ACP
 Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Função prcomp em R. 1. Introdução
 Função prcomp em R 1. Introdução Apresentamos alguns exemplos de utilização da função prcomp do pacote stats em R. Esta função permite realizar uma análise de componentes principais a partir de uma matriz
Função prcomp em R 1. Introdução Apresentamos alguns exemplos de utilização da função prcomp do pacote stats em R. Esta função permite realizar uma análise de componentes principais a partir de uma matriz
INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO
 INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS Extração de Informações
INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS Extração de Informações
Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações
 Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações Diogo de Carvalho Bezerra Universidade Federal de Pernambuco Núcleo de Gestão e-mail:dicbezerra@hotmail.com SOBREA Sociedade
Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações Diogo de Carvalho Bezerra Universidade Federal de Pernambuco Núcleo de Gestão e-mail:dicbezerra@hotmail.com SOBREA Sociedade
Aula 5 - Produto Vetorial
 Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Modelo de Regressão Múltipla
 Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Reconhecimento de Padrões. Principal Component Analysis (PCA) Análise dos Componentes Principais
 Universidade Federal de Ouro Preto (UFOP) Programa de Pós-Graduação em Ciência da Computação (PPGCC) Reconhecimento de Padrões Principal Component Analysis (PCA) Análise dos Componentes Principais David
Universidade Federal de Ouro Preto (UFOP) Programa de Pós-Graduação em Ciência da Computação (PPGCC) Reconhecimento de Padrões Principal Component Analysis (PCA) Análise dos Componentes Principais David
Autovalores e Autovetores
 Autovalores e Autovetores Maria Luísa B. de Oliveira SME0300 Cálculo Numérico 24 de novembro de 2010 Introdução Objetivo: Dada matriz A, n n, determinar todos os vetores v que sejam paralelos a Av. Introdução
Autovalores e Autovetores Maria Luísa B. de Oliveira SME0300 Cálculo Numérico 24 de novembro de 2010 Introdução Objetivo: Dada matriz A, n n, determinar todos os vetores v que sejam paralelos a Av. Introdução
Universidade Federal do Paraná Departamento de Informática. Reconhecimento de Padrões PCA. Luiz Eduardo S. Oliveira, Ph.D.
 Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões PCA Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Introduzir os conceitos de PCA e suas aplicações
Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões PCA Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Introduzir os conceitos de PCA e suas aplicações
Ajustamento de Observações
 Ajustamento de Observações Teoria dos Erros Prof. Dr. Marcos Aurélio Basso IFSULDEMINAS Campus Incondentes MG Teoria dos Erros - Introdução Observações e erros de observação; Factores que caracterizam
Ajustamento de Observações Teoria dos Erros Prof. Dr. Marcos Aurélio Basso IFSULDEMINAS Campus Incondentes MG Teoria dos Erros - Introdução Observações e erros de observação; Factores que caracterizam
Estatística Aplicada à Administração II. Tópico. Análise de Componentes Principais
 Estatística Aplicada à Administração II Tópico Análise de Componentes Principais Bibliografia: R.A. Johnson, Applied Multivariate Statistical Analysis, Prentice Hall, 99 Análise de Componentes Principais
Estatística Aplicada à Administração II Tópico Análise de Componentes Principais Bibliografia: R.A. Johnson, Applied Multivariate Statistical Analysis, Prentice Hall, 99 Análise de Componentes Principais
CSE-020 Revisão de Métodos Matemáticos para Engenharia
 CSE-020 Revisão de Métodos Matemáticos para Engenharia Engenharia e Tecnologia Espaciais ETE Engenharia e Gerenciamento de Sistemas Espaciais L.F.Perondi Engenharia e Tecnologia Espaciais ETE Engenharia
CSE-020 Revisão de Métodos Matemáticos para Engenharia Engenharia e Tecnologia Espaciais ETE Engenharia e Gerenciamento de Sistemas Espaciais L.F.Perondi Engenharia e Tecnologia Espaciais ETE Engenharia
Parte 3 - Produto Interno e Diagonalização
 Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Transformação dos dados. Analise de Componentes Principais - PCA
 Transformação dos dados Tratamento nos dados Redução de Dimensionalidade Dados centrados na média e variância xm = /n Σ i=n x i x i = ( x i - xm)/σ (centrados na média) Escalamento ela variância ( quando
Transformação dos dados Tratamento nos dados Redução de Dimensionalidade Dados centrados na média e variância xm = /n Σ i=n x i x i = ( x i - xm)/σ (centrados na média) Escalamento ela variância ( quando
G3 de Álgebra Linear I
 G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
Multicolinariedade e Autocorrelação
 Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
8. Análise em Componentes Principais - ACP
 8. Análise em Componentes Principais - ACP 8.1 Introdução O propósito principal da ACP é substituir as variáveis originais por um número menor de variáveis que são função das variáveis originais. A ACP
8. Análise em Componentes Principais - ACP 8.1 Introdução O propósito principal da ACP é substituir as variáveis originais por um número menor de variáveis que são função das variáveis originais. A ACP
Exemplo 1: Variáveis padronizadas Z t = ( Z 1 (1), Z 2 (1), Z 1 (2), Z 2 Z 1 (1) Z (1) = Z (2) = Z 2. Matriz de correlações:
 Exemplo : Variáveis padronizadas t = (,,, ) = = Matriz de correlações: Ρ Ρ Ρ Ρ Ρ.0 0.4 0.5 0.6 0.4.0 0.3 0.4 0.5 0.3.0 0. 0.6 0.4 0..0 De onde se obtém: /.068 0.9.047 0.083 Ρ Ρ 0.9.068 0.083.047 Ρ / /
Exemplo : Variáveis padronizadas t = (,,, ) = = Matriz de correlações: Ρ Ρ Ρ Ρ Ρ.0 0.4 0.5 0.6 0.4.0 0.3 0.4 0.5 0.3.0 0. 0.6 0.4 0..0 De onde se obtém: /.068 0.9.047 0.083 Ρ Ρ 0.9.068 0.083.047 Ρ / /
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
5. Seja R : R 3 R 3 uma rotação em torno do eixo gerado por (0, 0, 1). Suponha que R mande o vetor
 Universidade Federal do Rio de Janeiro Instituto de Matemática Disciplina: Álgebra Linear II Professor: Bruno Costa, Cesar Niche, Francesco Noseda, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez,
Universidade Federal do Rio de Janeiro Instituto de Matemática Disciplina: Álgebra Linear II Professor: Bruno Costa, Cesar Niche, Francesco Noseda, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez,
Econometria II. Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias.
 Eco 2 monitoria Leandro Anazawa Econometria II Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias. E(a) = a E(aX) = ae(x) E(a + bx) =
Eco 2 monitoria Leandro Anazawa Econometria II Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias. E(a) = a E(aX) = ae(x) E(a + bx) =
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Parte I. Álgebra Linear. Sistemas Dinâmicos Lineares. Autovalores, autovetores. Autovalores, autovetores. Autovalores e Autovetores.
 Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Álgebra Linear I - Aula Matrizes simultaneamente ortogonais e simétricas
 Álgebra Linear I - Aula 22 1. Matrizes 2 2 ortogonais e simétricas. 2. Projeções ortogonais. 3. Matrizes ortogonais e simétricas 3 3. Roteiro 1 Matrizes simultaneamente ortogonais e simétricas 2 2 Propriedade
Álgebra Linear I - Aula 22 1. Matrizes 2 2 ortogonais e simétricas. 2. Projeções ortogonais. 3. Matrizes ortogonais e simétricas 3 3. Roteiro 1 Matrizes simultaneamente ortogonais e simétricas 2 2 Propriedade
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Distância Estatística
 Distância Estatística Renato Assunção 0/05/03 Pressão sistólica A pressão sistólica mede a força do sangue nas artérias, à medida que o coração contrai para impulsionar o sangue através do corpo. Se alta
Distância Estatística Renato Assunção 0/05/03 Pressão sistólica A pressão sistólica mede a força do sangue nas artérias, à medida que o coração contrai para impulsionar o sangue através do corpo. Se alta
Álgebra Linear I - Lista 11. Autovalores e autovetores. Respostas. 1) Calcule os autovalores e autovetores das matrizes abaixo.
 Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
PROCESSAMENTO DE IMAGENS
 PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS- aula de 25/5/10 Introdução Conceitos básicos Pré-processamento Realce Classificação
PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS- aula de 25/5/10 Introdução Conceitos básicos Pré-processamento Realce Classificação
Programa do Curso. Transformação de Dados. Sistemas Inteligentes Aplicados. Carlos Hall. Discretização de Variáveis Contínuas
 Sistemas Inteligentes Aplicados Carlos Hall Programa do Curso Limpeza/Integração de Dados Transformação de Dados Discretização de Variáveis Contínuas Transformação de Variáveis Discretas em Contínuas Transformação
Sistemas Inteligentes Aplicados Carlos Hall Programa do Curso Limpeza/Integração de Dados Transformação de Dados Discretização de Variáveis Contínuas Transformação de Variáveis Discretas em Contínuas Transformação
Álgebra Linear I - Lista 12. Matrizes semelhantes. Diagonalização. Respostas
 Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
TESTE DE MANN-WHITNEY
 TESTE DE MANN-WHITNEY A importância deste teste é ser a alternativa não paramétrica ao teste t para a diferença de médias. Sejam (X,X,...,X n ) e (Y,Y,...,Y m ) duas amostras independentes, de tamanhos
TESTE DE MANN-WHITNEY A importância deste teste é ser a alternativa não paramétrica ao teste t para a diferença de médias. Sejam (X,X,...,X n ) e (Y,Y,...,Y m ) duas amostras independentes, de tamanhos
(b) A não será diagonalizável sobre C e A será diagonalizável sobre R se, e
 Q1. Sejam A M 6 (R) uma matriz real e T : R 6 R 6 o operador linear tal que [T ] can = A, em que can denota a base canônica de R 6. Se o polinômio característico de T for então poderemos afirmar que: p
Q1. Sejam A M 6 (R) uma matriz real e T : R 6 R 6 o operador linear tal que [T ] can = A, em que can denota a base canônica de R 6. Se o polinômio característico de T for então poderemos afirmar que: p
Autovetor e Autovalor de um Operador Linear
 Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Avaliação de Classificação
 Estatística: Aplicação ao Sensoriamento Remoto SER 204 - ANO 2018 Avaliação de Classificação Camilo Daleles Rennó camilo@dpi.inpe.br http://www.dpi.inpe.br/~camilo/estatistica/ Classificação e Incerteza
Estatística: Aplicação ao Sensoriamento Remoto SER 204 - ANO 2018 Avaliação de Classificação Camilo Daleles Rennó camilo@dpi.inpe.br http://www.dpi.inpe.br/~camilo/estatistica/ Classificação e Incerteza
Disciplina: Processamento Estatístico de Sinais (ENGA83) - Aula 05 / Detecção Binária Baseada em
 Disciplina: Processamento Estatístico de Sinais (ENGA83) - Aula 05 / Detecção Binária Baseada em Múltiplas Observações e Detecção com Múltiplas Hipóteses Prof. Eduardo Simas (eduardo.simas@ufba.br) Programa
Disciplina: Processamento Estatístico de Sinais (ENGA83) - Aula 05 / Detecção Binária Baseada em Múltiplas Observações e Detecção com Múltiplas Hipóteses Prof. Eduardo Simas (eduardo.simas@ufba.br) Programa
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
5. Seja A uma matriz qualquer. Assinale a afirmativa
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
P4 de Álgebra Linear I
 P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Variáveis Aleatórias
 Estatística: Aplicação ao Sensoriamento Remoto SER 24 - ANO 218 Variáveis Aleatórias Camilo Daleles Rennó camilo@dpi.inpe.br http://www.dpi.inpe.br/~camilo/estatistica/ Variável atributo Em qualquer tipo
Estatística: Aplicação ao Sensoriamento Remoto SER 24 - ANO 218 Variáveis Aleatórias Camilo Daleles Rennó camilo@dpi.inpe.br http://www.dpi.inpe.br/~camilo/estatistica/ Variável atributo Em qualquer tipo
Medidas de localização (ou de tendência central) Média: definida como o centro de massa (ou ponto de equilíbrio) do conjunto.
 Aula 02 01 de abril Medidas de localização (ou de tendência central) Média: definida como o centro de massa (ou ponto de equilíbrio) do conjunto. No geral, a melhor média é a que mais se aproxima do centro
Aula 02 01 de abril Medidas de localização (ou de tendência central) Média: definida como o centro de massa (ou ponto de equilíbrio) do conjunto. No geral, a melhor média é a que mais se aproxima do centro
NOTAS DE AULA DA DISCIPLINA CE076
 7. ANÁISE DE CORREAÇÃO CANÔNICA 7. INTRODUÇÃO A Análise de Correlação Canônica foi desenvolvida por Hotelling (935) com obetivo de Identificar e quantificar as associações ou relações entre dois conuntos
7. ANÁISE DE CORREAÇÃO CANÔNICA 7. INTRODUÇÃO A Análise de Correlação Canônica foi desenvolvida por Hotelling (935) com obetivo de Identificar e quantificar as associações ou relações entre dois conuntos
1 Matrizes Ortogonais
 Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Redes de Computadores sem Fio
 Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
Autovalores e Autovetores Determinante de. Motivando com Geometria Definição Calculando Diagonalização Teorema Espectral:
 Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
29 e 30 de julho de 2013
 Programa de Pós-Graduação em Estatística e Experimentação Agronômica ESALQ/USP 29 e 30 de julho de 2013 Dia 2 - Conteúdo 1 2 3 Dados multivariados Estrutura: n observações tomadas de p variáveis resposta.
Programa de Pós-Graduação em Estatística e Experimentação Agronômica ESALQ/USP 29 e 30 de julho de 2013 Dia 2 - Conteúdo 1 2 3 Dados multivariados Estrutura: n observações tomadas de p variáveis resposta.
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais
 Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
1 Auto vetores e autovalores
 Auto vetores e autovalores Os autovalores de uma matriz de uma matriz n n são os n números que resumem as propriedades essenciais daquela matriz. Como esses n números realmente caracterizam a matriz sendo
Auto vetores e autovalores Os autovalores de uma matriz de uma matriz n n são os n números que resumem as propriedades essenciais daquela matriz. Como esses n números realmente caracterizam a matriz sendo
Medidas de Dispersão. Introdução Amplitude Variância Desvio Padrão Coeficiente de Variação
 Medidas de Dispersão Introdução Amplitude Variância Desvio Padrão Coeficiente de Variação Introdução Estudo de medidas que mostram a dispersão dos dados em torno da tendência central Analisaremos as seguintes
Medidas de Dispersão Introdução Amplitude Variância Desvio Padrão Coeficiente de Variação Introdução Estudo de medidas que mostram a dispersão dos dados em torno da tendência central Analisaremos as seguintes
Técnicas Multivariadas em Saúde
 Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Modelagem Computacional. Parte 7 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 7 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 7 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Laboratório de Simulação Matemática. Parte 6 2
 Matemática - RC/UFG Laboratório de Simulação Matemática Parte 6 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 6] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Matemática - RC/UFG Laboratório de Simulação Matemática Parte 6 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 6] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Autovalores e Autovetores
 Autovalores e Autovetores INTRODUÇÃO Essa apostila vai explicar um pouco de Auto Valores e Auto Vetores. A primeira coisa que é importante ressaltar é que essa matéria normalmente cai de forma bem simples
Autovalores e Autovetores INTRODUÇÃO Essa apostila vai explicar um pouco de Auto Valores e Auto Vetores. A primeira coisa que é importante ressaltar é que essa matéria normalmente cai de forma bem simples
Técnicas Multivariadas em Saúde. Vetores Aleatórios. Métodos Multivariados em Saúde Roteiro. Definições Principais. Vetores aleatórios:
 Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
MAE Introdução à Probabilidade e Estatística II Resolução Lista 5
 MAE 229 - Introdução à Probabilidade e Estatística II Resolução Lista 5 Professor: Pedro Morettin e Profa. Chang Chian Exercício 1 (a) De uma forma geral, o desvio padrão é usado para medir a dispersão
MAE 229 - Introdução à Probabilidade e Estatística II Resolução Lista 5 Professor: Pedro Morettin e Profa. Chang Chian Exercício 1 (a) De uma forma geral, o desvio padrão é usado para medir a dispersão
Análise Fatorial. Matriz R de coeficientes de correlação: Não confundir análise de componentes principais com análise fatorial!
 Análise Fatorial 1 Na análise fatorial as variáveis y1, y,..., Yp, são combinações lineares de umas poucas variáveis F1, F,..., Fm (m
Análise Fatorial 1 Na análise fatorial as variáveis y1, y,..., Yp, são combinações lineares de umas poucas variáveis F1, F,..., Fm (m
Tratamento estatístico de observações geodésicas
 Tratamento estatístico de observações geodésicas Prof. Dr. Carlos Aurélio Nadal OBJETIVO: parâmetros estatísticos são utilizados para avaliar os métodos empregados ou para o controle de qualidade dos trabalhos.
Tratamento estatístico de observações geodésicas Prof. Dr. Carlos Aurélio Nadal OBJETIVO: parâmetros estatísticos são utilizados para avaliar os métodos empregados ou para o controle de qualidade dos trabalhos.
Autovalores e Autovetores
 Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
Tratamento Estatístico de Dados em Física Experimental
 Tratamento Estatístico de Dados em Física Experimental Prof. Zwinglio Guimarães o semestre de 06 Tópico 7 - Ajuste de parâmetros de funções (Máxima Verossimilhança e Mínimos Quadrados) Método da máxima
Tratamento Estatístico de Dados em Física Experimental Prof. Zwinglio Guimarães o semestre de 06 Tópico 7 - Ajuste de parâmetros de funções (Máxima Verossimilhança e Mínimos Quadrados) Método da máxima
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
Seminário de Análise Multivariada
 Seminário de Análise Multivariada Capítulo 1 - Introdução Conteúdo 1 Introdução 1 11 Aplicações de Técnicas Multivariadas 2 12 Organização de Dados 3 121 Arranjos 3 122 Exemplo 11 - Seleção de recibos
Seminário de Análise Multivariada Capítulo 1 - Introdução Conteúdo 1 Introdução 1 11 Aplicações de Técnicas Multivariadas 2 12 Organização de Dados 3 121 Arranjos 3 122 Exemplo 11 - Seleção de recibos
. Repare que ao multiplicar os vetores (-1,1) e
 Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
Variáveis Aleatórias. Esperança e Variância. Prof. Luiz Medeiros Departamento de Estatística - UFPB
 Variáveis Aleatórias Esperança e Variância Prof. Luiz Medeiros Departamento de Estatística - UFPB ESPERANÇA E VARIÂNCIA Nos modelos matemáticos aleatórios parâmetros podem ser empregados para caracterizar
Variáveis Aleatórias Esperança e Variância Prof. Luiz Medeiros Departamento de Estatística - UFPB ESPERANÇA E VARIÂNCIA Nos modelos matemáticos aleatórios parâmetros podem ser empregados para caracterizar
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina.
 Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina. De forma geral, a prova manteve o padrão das questões da
Caros Alunos, segue a resolução das questões de Estatística aplicadas na prova para o cargo de Auditor Fiscal da Receita Municipal de Teresina. De forma geral, a prova manteve o padrão das questões da
SCC0173 Mineração de Dados Biológicos
 SCC073 Mineração de Dados Biológicos Análise Exploratória de Dados Parte A: Revisão de Estatística Descritiva Elementar Prof. Ricardo J. G. B. Campello SCC / ICMC / USP Tópicos Análise Exploratória de
SCC073 Mineração de Dados Biológicos Análise Exploratória de Dados Parte A: Revisão de Estatística Descritiva Elementar Prof. Ricardo J. G. B. Campello SCC / ICMC / USP Tópicos Análise Exploratória de
Análise de Regressão Linear Simples e
 Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Capitulo 6 Viabilidade Econômica em Situação de Incerteza
 1 Capitulo 6 Viabilidade Econômica em Situação de Incerteza Nos capítulos anteriores, ao construir o fluxo de caixa de um projeto de investimento, supusemos que os valores eram conhecidos com certeza.
1 Capitulo 6 Viabilidade Econômica em Situação de Incerteza Nos capítulos anteriores, ao construir o fluxo de caixa de um projeto de investimento, supusemos que os valores eram conhecidos com certeza.
Exercícios de programação
 Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
AGA Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares
 1 / 0 AGA 0505- Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares Laerte Sodré Jr. 1o. semestre, 018 modelos modelagem dos dados dado um conjunto de dados,
1 / 0 AGA 0505- Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares Laerte Sodré Jr. 1o. semestre, 018 modelos modelagem dos dados dado um conjunto de dados,
Dadas as observações x 1, x 2,..., x n p-variadas, a AF busca responder a seguinte questão.
 Análise Fatorial Métodos de Estimação Dadas as observações x 1, x 2,..., x n p-variadas, a AF busca responder a seguinte questão. O MFO, com um número pequeno de fatores, representa adequadamente os dados?
Análise Fatorial Métodos de Estimação Dadas as observações x 1, x 2,..., x n p-variadas, a AF busca responder a seguinte questão. O MFO, com um número pequeno de fatores, representa adequadamente os dados?
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
CC-226 Aula 05 - Teoria da Decisão Bayesiana
 CC-226 Aula 05 - Teoria da Decisão Bayesiana Carlos Henrique Q. Forster - Instituto Tecnológico de Aeronáutica 2008 Classificador Bayesiano Considerando M classes C 1... C M. N observações x j. L atributos
CC-226 Aula 05 - Teoria da Decisão Bayesiana Carlos Henrique Q. Forster - Instituto Tecnológico de Aeronáutica 2008 Classificador Bayesiano Considerando M classes C 1... C M. N observações x j. L atributos
Estimativas e Erros. Propagação de erros e Ajuste de funções
 Estimativas e Erros Propagação de erros e Ajuste de funções 1 Algumas referências Estimativas e Erros em Experimentos de Física - Vitor Oguri et al (EdUERJ) Fundamentos da Teoria de Erros - José Henrique
Estimativas e Erros Propagação de erros e Ajuste de funções 1 Algumas referências Estimativas e Erros em Experimentos de Física - Vitor Oguri et al (EdUERJ) Fundamentos da Teoria de Erros - José Henrique
CORRELAÇÃO LINEAR. Referência Cap. 7 - Métodos Estatísticos para Geografia
 CORRELAÇÃO LINEAR Referência Cap. 7 - Métodos Estatísticos para Geografia Correlação linear Permite verificar se duas variáveis independentes estão associadas uma com a outra Questionamentos iniciais:
CORRELAÇÃO LINEAR Referência Cap. 7 - Métodos Estatísticos para Geografia Correlação linear Permite verificar se duas variáveis independentes estão associadas uma com a outra Questionamentos iniciais:
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC
 Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Modelagem Computacional. Parte 6 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 6 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 6 e 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 6 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 6 e 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Álgebra Linear e Aplicações - Lista para Primeira Prova
 Álgebra Linear e Aplicações - Lista para Primeira Prova Nestas notas, X, Y,... são espaços vetoriais sobre o mesmo corpo F {R, C}. Você pode supor que todos os espaços têm dimensão finita. Os exercícios
Álgebra Linear e Aplicações - Lista para Primeira Prova Nestas notas, X, Y,... são espaços vetoriais sobre o mesmo corpo F {R, C}. Você pode supor que todos os espaços têm dimensão finita. Os exercícios
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Algebra Linear. 1. Revisitando autovalores e autovetores. 2. Forma Diagonal e Forma de Jordan. 2.1 Autovalores distintos. 2.2 Autovalores complexos
 Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica. Classificação. David Menotti.
 Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica Classificação David Menotti www.inf.ufpr.br/menotti/ci171-182 Hoje Redução de Dimensionalidade Principal Component Analysis (PCA)
Universidade Federal do Paraná (UFPR) Bacharelado em Informática Biomédica Classificação David Menotti www.inf.ufpr.br/menotti/ci171-182 Hoje Redução de Dimensionalidade Principal Component Analysis (PCA)
3 3. Variáveis Aleatórias
 ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
