RESISTÊNCIA DE MATERIAIS
|
|
|
- Maria do Pilar Damásio Braga
- 8 Há anos
- Visualizações:
Transcrição
1 UNVERSDDE DE ÉVOR ESCOL DE CÊNC E TECNOLOG - DEPRTMENTO DE ENGENHR RURL RESSTÊNC DE MTERS ESFORÇO TRNSVERSO (pontamentos para uso dos lunos) JOSÉ OLVER PEÇ ÉVOR 016
2 NDCE Nota do autor Tensões tangenciais em planos paralelos à superfície neutra Esforço de escorregamento em planos longitudinais Problemas resolvidos Problemas não resolvidos Esforço de escorregamento em peças mistas Eemplo resolvido Problemas não resolvidos Tensões tangenciais em secções transversais Em peças abertas de paredes finas Problemas resolvidos Problemas não resolvidos Em peças fechadas de paredes finas Problema resolvido Problemas não resolvidos Centro de corte em peças de paredes finas Problemas resolvidos Problemas não resolvidos Estado de tensão sob momento flector e esforço transverso Problema resolvido Problemas não resolvidos Caderno de problemas Esforço de escorregamento em planos longitudinais Esforço de escorregamento em peças mistas Tensões tangenciais em secções transversais Centro de corte em secções de paredes finas Estado de tensão em fleão simples Referências Teto de apoio aos alunos - 016
3 Nota do autor Tendo sido interrompido, a partir do ano lectivo de 015/016, o 1º Ciclo do Curso de Engenharia Civil, o autor resolveu reunir toda a informação que foi disponibiliada aos alunos da disciplina de Resistência de Materiais, durante os 8 anos em que o curso funcionou na Universidade de Évora. O presente trabalho versa o tema do Esforço transverso da Resistência de Materiais e é uma edição revista e acrescentada das edições que foram publicadas em 013; 009 e 008. No curso, a disciplina de Resistência de Materiais tinha a duração de um único semestre (4º semestre), pelo que foi necessário selecionar os temas mais relevantes a ensinar sobre Esforço transverso. Nos diversos pontos deste trabalho são apresentados os aspectos formais importantes, completados com problemas resolvidos e não resolvidos de aplicação. No último ponto estão incluídos todos os eercícios de aplicação sobre Esforço transverso abordados nas aulas práticas e os que foram alvo de avaliação nas provas de frequência e de eame. Teto de apoio aos alunos
4 1. Tensões tangenciais em planos paralelos à superfície neutra Recorre-se a um eemplo para apresentar as tensões tangenciais em planos paralelos à superfície neutra (shearing stress on longitudinal sections): dmita a seguinte barra sujeita a fleão simples (transverse bending) (M 0; T 0 N=0; Mt=0): q kn/m l Cuja secção transversal está representada na figura seguinte: e.a. h e.n. b figura seguinte mostra os diagramas de esforços na barra (shearing force and bending moment diagrams): T + - M + dmitamos um segmento transversal, infinitesimal, de barra com comprimento d: d Teto de apoio aos alunos
5 d tendendo à variação do esforço transverso e momento flector, acima indicados no diagrama de esforços, podemos admitir a figura seguinte; d M M+dM T+dT T Na figura anterior dm e dt, são as variações do momento flector e do esforço transverso no elemento infinitesimal de comprimento d. dmitamos que a peça é linear, isto é, a barra tem um comprimento muito grande relativamente à altura da secção (l >> h), para que possamos desprear o efeito do esforço transverso na distribuição das tensões normais (normal stresses) nas secções, devido à fleão. distribuição das tensões normais nas secções está representada na figura seguinte: M ( M dm ) d dmitamos o segmento representado na figura, obtido através da intercepção do segmento transversal por um plano, paralelo ao plano, doravante denominado plano longitudinal. Teto de apoio aos alunos
6 Plano longitudinal Ω d figura seguinte mostra a distribuição de tensões normais devido à fleão, no segmento atrás definido e cuja secção transversal é Ω: Ω d s tensões normais integradas na área Ω correspondem às forças aiais representadas na figura seguinte: d ( d ) d Ω e.n. d O equilíbrio de forças do referido segmento pressupõe a eistência de uma força df, tangencialmente ao plano longitudinal: d df ( d ) d Ω d Teto de apoio aos alunos
7 df d d Uma ve que em fleão recta: M dm d df dm dm d dm d S em que S é o momento estático (static moment) da área Ω da secção, relativamente ao eio neutro. Verifica-se que a presença de um momento flector não constante (ou seja esforço transverso diferente de ero) ao longo da barra, provoca o aparecimento de tensões tangenciais τ no plano longitudinal. São essas tensões tangenciais que, no referido plano, induem a força df. dm df bd S Da epressão anterior tira-se o valor da tensão tangencial τ no plano longitudinal: S b dm d tendendo à noção de esforço transverso, obtém-se finalmente: S b T O valor da tensão tangencial τ é máimo no local da peça onde o esforço transverso for máimo e no plano longitudinal da peça correspondente ao valor máimo do momento estático; esse plano longitudinal é a superfície neutra (neutral laer). qkn/m τ T + - Problema resolvido dmita a barra de secção rectangular carregada como mostra a figura seguinte: Teto de apoio aos alunos
8 5kN 5kN D 0cm 0.45m B C 0.45m 5cm a) Determinar as tensões normais máimas; b) Determinar as tensões tangenciais máimas. Resolução T 5kN -5kN M a) 11.5kNm M ma com W W ma m Substituindo: σ ma = 5.4MPa Em qualquer secção transversal da barra situada entre B e C, temos a seguinte distribuição de tensões normais: σ ma = -5.4MPa σ ma = 5.4MPa b) S T b O valor da tensão tangencial τ é máimo na superfície neutra (neutral laer), uma ve que S toma o valor máimo em relação ao eio neutro: Teto de apoio aos alunos
9 0 cm Ω S 1.5cm cm m cm m 3 6 S T kpa 0. 75MPa 8 b Na superfície neutra da peça, entre e B e entre C e D, actuam tensões tangenciais de valor igual a 0.75MPa. figura seguinte mostra a tensão tangencial τ aplicada pela parte superior da barra sobre a parte inferior, ao nível da superfície neutra: B C D τ τ τ 0.75MPa Em outros planos longitudinais da barra (entre e B e entre C e D), paralelas à superfície neutra actuam igualmente tensões tangenciais. O valor dessas tensões diminui com o afastamento à superfície neutra, até que nas faces superior e inferior da barra, o valor é ero. figura seguinte mostra a tensão tangencial τ aplicada pela parte superior da barra sobre a parte inferior, ao nível do plano longitudinal representada. B C -0.75MPa τ τ Teto de apoio aos alunos
10 1.1. Esforço de escorregamento em planos longitudinais dmitamos que temos um comprimento de barra entre 1 e no qual queremos conhecer a força de escorregamento (shearing force) num plano longitudinal (paralela à secção neutra) F 1 b d Td F 1 1 S S 1 T d Na epressão anterior, o integral T d representa a área definida pelo diagrama de esforço transverso entre 1 e : T Problemas resolvidos Problema 1 - Na consola representada na figura, as chapas acompanham o perfil até metade do vão. Determine os esforços para os quais devem ser dimensionadas as ligações entre as chapas e o perfil NP. s chapas têm 1cm de espessura e 1cm de largura; o perfil é NP00 Teto de apoio aos alunos
11 0kN/m B BC B 1.5m 1.5m C Resolução T 60kN M - 90kNm B Plano longitudinal em estudo Dada a simetria do problema, apenas se torna necessário conhecer o esforço de escorregamento no plano indicado, uma ve que no plano simétrico em relação ao plano neutro a força de escorregamento tem a mesma intensidade. tendendo a que: S F T d S cm cm Teto de apoio aos alunos
12 60kN 1.5m 30kN T d kNm Substituindo: 6 S F Td kN Problema - viga B tem 1.m de vão e suporta uma carga concentrada a meio vão de 480kN. viga é construída ligando uma peça de secção rectangular de 1 mm 400mm a quatro cantoneiras de abas iguais (tabela anea). dmitindo que todas as peças são de aço, determine o esforço a que tem de resistir cada uma das ligações. C 1.m 480kN B T 40kN -40kN e.n. M 144kNm S de uma cantoneira em relação ao eio neutro: S cm cm S F Td d kN Teto de apoio aos alunos
13 1.1.. Problemas não resolvidos P1.1) viga B é constituída por 3 peças coladas e está submetida ao carregamento indicado, o qual actua no seu plano de simetria. Determine o esforço a que a colagem terá de resistir entre as secções C, CD e DB. 1.5kN 1.5kN 0.4m C 0.m D 0.4m B 10cm Secção transversal cm cm 8cm cm 6cm Resposta: Ligação entre a aba superior e a alma F C =F DB =5.78kN; F CD =0 Ligação entre a aba inferior e a alma F C =F DB =4.85kN; F CD =0 P1.) viga B tem 100 a de vão e suporta uma carga uniformemente distribuída q. viga é construída ligando uma peça de secção rectangular a 3a a quatro peças de secção quadrada a a. Determine o esforço a que tem de resistir cada uma das ligações. q kn/m C 100a B a Resposta: Ligação entre cada uma das peças quadradas e a peça rectangular: F C =F CB =189.9 q a (kn) 1.. Esforço de escorregamento em peças mistas nalisa-se o caso mais simples de uma peça linear, de largura constante b, constituída por dois materiais de comportamento elástico linear sujeita a uma fleão recta em que é pertinente conhecer o esforço de escorregamento a que tem que resistir a ligação entre os dois materiais ( e B). dmitamos E e E B os módulos de elasticidade dos materiais. Teto de apoio aos alunos
14 Como foi referido anteriormente o eio neutro passa pelo centro de gravidade da secção ponderada com os módulos de elasticidade dos materiais que constituem a peça. dmitamos um segmento infinitesimal de barra com comprimento d: d M M+dM T T+dT O equilíbrio de forças no segmento correspondente ao material, fica: d df d Ω B e.a. b e.n. d ( d ) d Ω o que pressupõe a eistência de uma força df, tangencialmente ao plano longitudinal fronteira entre os dois materiais: df d d Uma ve que em fleão de peças mistas: n M E E B Bn d n dm E E B Bn df n dm E E B Bn d Teto de apoio aos alunos
15 df n dm E E B Bn S n S n é o momento estático da área Ω da secção, relativamente ao eio neutro; n e Bn são os momentos de inércia das secções e B, respectivamente, em relação ao eio neutro. força de corte elementar df é fruto de uma distribuição de tensões de corte τ no plano longitudinal fronteira entre os dois materiais, o qual tem (b d) de área. ssim: dm df bd S n EB n Bn E epressão anterior permite saber a variação, ao longo da peça, do esforço de escorregamento na secção longitudinal fronteira entre os dois materiais: df d n S n E E B Bn dm d tendendo à noção de esforço transverso, obtém-se: df d n S n E E B Bn T dmitindo um comprimento l 1 de barra no qual queremos conhecer a força de escorregamento no plano longitudinal fronteira entre os dois materiais: F n S n E E B Bn l 0 1 T d l Na epressão anterior, o integral 1 T d representa a área definida pelo diagrama de esforço transverso entre 0 e l 1. 0 O mesmo valor de esforço de escorregamento seria obtido recorrendo à epressão seguinte: S l1 Bn F Td E 0 Bn n E S Bn é o momento estático da área Ω B da secção, relativamente ao eio neutro. B Teto de apoio aos alunos
16 1..1. Eemplo resolvido viga representada na figura é constituída por betão e reforçada por duas chapas de aço colocadas como se indica. Calcule o esforço de escorregamento a que têm que resistir cada uma das ligações aço-betão. Considere que o módulo de elasticidade de aço (E a ) é 10 vees o módulo de elasticidade do betão (E b ). qkn/m ço l Betão dmita que as chapas têm largura b e espessura 0.1b. peça de betão tem largura b e altura b. Resolução: qkn/m ço l ql T e.a. e.n. plano em estudo Por raões de simetria da secção da peça, o eio neutro coincide com o eio de simetria. Cálculo do momento de inércia da secção em relação ao eio neutro: n b 3 b b 4 b 10 b b Teto de apoio aos alunos
17 3 b 4 b Bn 0.667b 1 Cálculo do momento estático da secção da chapa de aço inferior, em relação ao eio neutro. tendendo à epressão: S n b b b b 0.105b F n S n E E B Bn l 0 1 T d Obtém-se: F ntegrando entre 0 e l/, obtém-se: l1 b 0 T d l F b Td b ql l ql b 1... Problemas não resolvidos P1.3) Uma barra de alumínio e uma barra de aço, são unidas firmemente para formar uma viga mista. dmita que o módulo de elasticidade do aço é 00GPa e o módulo de elasticidade do alumínio é 70GPa. 6kN e.a. 1m lumínio cm ço 4cm 3cm a) Com a barra submetida à fleão, como se mostra na figura, determine o eio neutro. Teto de apoio aos alunos
18 b) Com a barra submetida à fleão, como se mostra na figura, calcule o maior valor de tensão normal no alumínio. c) Determine o esforço de escorregamento para o qual deve ser dimensionado a ligação entre os dois materiais. Resposta: b) σ al = MPa; c) F = 4.53kN P1.4) Considere a peça mista de betão e aço (E b /E a =0.1). Determine os esforços para os quais devem ser dimensionados os elementos de ligação. 14kN/m 18m 1.4m Material b e.a. 0.16m Material a NP500 Solução: F = 1049kN P1.5) viga representada na figura é constituída por um perfil de alumínio reforçado por duas barras de latão colocadas como se indica. 75kN/m 1m Latão.5cm.5cm 9cm e.a. 1cm 1cm Considere: lumínio 1cm Latão lumínio Latão Módulo de elasticidade 70GPa 105Gpa Valor de cálculo da tensão resistente 100MPa 160MPa 1cm 1cm Teto de apoio aos alunos
19 a) Considerando apenas o momento flector, verifique a segurança da viga, quer no latão quer no alumínio. b) Calcule o valor do esforço de escorregamento a que têm que resistir a ligação de cada uma das barras de latão na ligação com o perfil de alumínio. Resposta: a) σ al = 76.1Mpa, verifica; σ latão = 15.Mpa, verifica; b) F 10kN. Tensões tangenciais em secções transversais tendenda-se à condição de reciprocidade das tensões tangenciais (condition of equalit of shearing stresses) o qual afirma que as componentes das tensões tangenciais que actuam em duas facetas ortogonais e são perpendiculares à aresta comum às duas facetas, são iguais e têm sentidos tais que convergem ambas para a aresta comum ou divergem ambas da mesma. presença de tensões tangenciais τ em planos longitudinais, vai implicar a eistência de tensões tensões tangenciais τ em secções transversais (shearing stress at cross sections) da viga. Numa qualquer secção s: s τ τ s τ τ ssim na secção transversal s haverá uma distribuição de tensões tangenciais, representando-se na figura seguinte: e.a. τ τ e.n. Teto de apoio aos alunos
20 É a integração destas tensões tangenciais nesta secção que constitui o esforço transverso T na secção. NOTR s tensões tangenciais são máimas junto de fibras situadas no centro da peça, local onde são mínimas ou nulas as tensões normais provocadas na fleão. Os valores máimos das tensões tangenciais são normalmente muito inferiores aos das tensões normais..1. Em peças abertas de paredes finas dmita a seguinte barra constituída por uma peça aberta de paredes finas (thin-walled bar) sujeita a fleão simples (transverse bending) (M 0; T 0 N=0; Mt=0): q kn/m l Cuja secção transversal está representada na figura seguinte: M c.g. e e dmitamos um segmento transversal, infinitesimal, de barra com comprimento d. tendendo à variação, ao longo da barra, do esforço transverso e momento flector, podemos admitir a figura seguinte: d M M+dM T+dT T Na figura anterior dm e dt, são as variações do momento flector e do esforço transverso no elemento, transversal, infinitesimal de comprimento d. distribuição das tensões normais nas secções está representada na figura seguinte: Teto de apoio aos alunos
21 M ( M dm ) d dmitamos o segmento representado na figura, obtido através da intercepção do segmento transversal por um plano, paralelo ao plano, doravante denominado plano longitudinal da alma. : d Ω O equilíbrio de forças do referido segmento, fica: d df d ( d ) d Ω e o que pressupõe a eistência de uma força df, tangencialmente ao plano longitudinal: df d d Uma ve que em fleão: M dm d dm dm dm df d d S em que S é o momento estático (static moment) da área Ω da secção, relativamente ao eio neutro. força de corte elementar df é fruto de uma distribuição de tensões tangenciais τ no plano longitudinal. ssim: Teto de apoio aos alunos
22 dm df ed S Da epressão anterior tira-se o valor da tensão de tangencial τ no plano longitudinal da S dm peça: e d tendendo à noção de esforço transverso, obtém-se finalmente: S e O valor da tensão de tangencial τ é máimo no local da peça onde o esforço transverso for máimo e no plano longitudinal da peça correspondente ao valor máimo do momento estático. tendendo à condição de reciprocidade das tensões tangenciais, na secção transversal s haverá uma distribuição de tensões tangenciais τ. T τ τ d e Todo o percurso de raciocínio apresentado será seguidamente repetido nas abas. dmitamos o segmento representado na figura, obtido através da intercepção do segmento transversal por um plano, paralelo ao plano, doravante denominado plano longitudinal da aba. d Ω e Uma ve que a aba está a compressão, o equilíbrio de forças do referido segmento, fica: Teto de apoio aos alunos - 016
23 d df ( d ) d o que pressupõe a eistência de uma força df, tangencialmente ao plano longitudinal da aba: df d d Uma ve que em fleão: M dm d dm dm dm df d d S em que S é o momento estático (static moment) da área Ω da secção, relativamente ao eio neutro. força elementar df é fruto de uma distribuição de tensões tangenciais τ no plano longitudinal da aba. ssim: dm df ed S Da epressão anterior tira-se o valor da tensão tangencial τ no plano longitudinal da aba: S dm e d tendendo à noção de esforço transverso, obtém-se finalmente: S e T O valor da tensão tangencial τ é máimo no local da peça onde o esforço transverso for máimo e no plano longitudinal da aba correspondente ao valor máimo do momento estático. tendendo à condição de reciprocidade das tensões tangenciais, na secção transversal s haverá uma distribuição de tensões tangenciais τ. τ τ e repetição do raciocínio para no segmento longitudinal oposto, condu a tensões tangenciais representadas na figura seguinte: d Teto de apoio aos alunos
24 τ Ω e τ d figura seguinte mostra (setas) as tensões tangenciais em determinado nível da secção transversal da aba. s tensões são nulas em ambas as etremidades da aba, crescendo linearmente para o centro. distribuição triangular representa o valor das tensões em cada nível da secção da aba. τ τ figura seguinte mostra (setas) as tensões tangenciais em determinados níveis da secção transversal da alma. No topo da alma, as tensões são em valor absoluto a soma das tensões no centro da aba. s tensões aumentam, atingindo o máimo no eio neutro e, de seguida vão diminuindo até serem nulas na etremidade inferior da alma. τ figura seguinte mostra as tensões rebatidas lateralmente para se desenhar a distribuição (curva) das tensões ao longo da secção da alma. Teto de apoio aos alunos
25 τ Na figura seguinte mostra-se a distribuição das tangenciais em toda a secção. τ τ τ.1.1. Problemas resolvidos Problema 1 - Determinar a distribuição de tensões tangenciais na secção U (channel) submetida a fleão simples (transverse bending). Determinar a resultante dessas tensões tangenciais Teto de apoio aos alunos
26 Teto de apoio aos alunos Resolução Cálculo do momento de inércia e h e h e e b e e b Desenvolvendo a epressão, fica: e h eh h e be tendendo ao facto de ser uma secção de paredes finas, então: 6 h h e e h e h pelo que a epressão simplifica-se, ficando: b h eh 6 1 Tensões nas abas (flange) h b e e T
27 s τ h/ e b tensão tangencial τ representada na figura é dada pela seguinte epressão: O momento estático S : Substituindo: S S e s e T h 6T ehh 6b s epressão anterior corresponde a uma distribuição linear de tensões tangenciais nas abas (em função de s), figura seguinte mostra (setas) as tensões tangenciais em determinados níveis da secção transversal da aba superior. s tensões são nulas na etremidade da aba, crescendo linearmente para o centro. distribuição triangular representa o valor das tensões em cada nível da secção da aba. Teto de apoio aos alunos
28 τ ma τ ma T h/ e e atingindo o valor máimo para s=b: b ma ma 6T ehh 6b b Rebatendo as tensões para uma posição perpendicular à secção, fica definido o sólido, que é um prisma cuja secção é a distribuição triangular ilustrada na figura anterior. τ ma b e resultante das tensões na aba é a força R aba ilustrada na figura seguinte e corresponde ao volume do prisma triangular; R aba R alma Teto de apoio aos alunos
29 R aba ma Tensões na alma b 6T e eh h 6b b b e 3b h h 6b T s τ h/ tensão tangencial τ representada na figura é dada pela seguinte epressão: área de aba indicada na figura, está submetida a tensões tangenciais τ, dadas pela seguinte epressão: S T e O momento estático S : Substituindo e desenvolvendo: S h s s e e h b e 6T eh h 6b s h s h b epressão anterior corresponde a uma distribuição quadrática de tensões tangenciais na alma (em função de s ), atingindo o valor máimo para s = h/: ma ma 3T h 4b eh h 6b Teto de apoio aos alunos
30 Em toda a secção a distribuição de tensões fica: τ =τ ma τ ma τ ma τ =τ ma τ ma o longo do contorno da secção, não há mudança de sinal do valor das tensões, pelo que na representação abaio indicada as tensões flúem ao longo do contorno da secção sem mudar de sentido, sendo este ditado pelo sentido do vector esforço transverso. τ τ T Resultante das tensões na alma: τ Uma ve que: R alma d eds alma h T 0 0 h S ds S h s s e h e b e e e hs s b h hs s bh e T Ralma h 0 hs s bh ds tendendo a que: R alma e T hs s 3 3 bhs h 0 e T 3 h bh 6 Teto de apoio aos alunos
31 eh h 6b 1 R alma h 6b T h 6b T Portanto a resultante das tensões na alma é o esforço transverso. Resultante das tensões em toda a secção fica como na figura seguinte: R aba R alma R aba Problema - consola da figura está submetida ao carregamento indicado. 10cm e.a. 6.7kN 1cm 30cm 5cm 38cm 1cm a) Determine a máima tensão de compressão na secção..546knm kN d 1 d 6.7kN T 6.7kN 5 1 M -.546kNm Teto de apoio aos alunos
32 T =6.7kN M kNm 10 d1 5 d d d 3cm 1 d 1 1cm d cm e.a. M 1cm cm.01 ma. comp MPa b) Determine a tensão tangencial máima na secção e.a. τ e.n. S e T S cm kNcm MPa Problemas não resolvidos P.1) Considere a secção da viga da figura seguinte e admita que está sujeita a um esforço transverso de 10kN. Determine: a) evolução das tensões tangenciais na alma e nas abas; b) O valor das tensões tangenciais nos pontos e B. Teto de apoio aos alunos
33 1.cm 3cm 10cm T B 10cm 0.6cm 1.cm 15cm Solução: τ = 714.7kPa; τ B = kPa P.) dmita uma barra com a secção indicada na figura sujeita a um esforço transverso T = 50kN: 0.8cm T = 50kN 0.8cm 7.5cm 0.8cm 6cm 5cm a) Determine a epressão geral da distribuição das tensões tangenciais τ no troço vertical do lado direito; b) Utilie a epressão geral obtida na alínea anterior para calcular a tensão τ a meio do troço vertical do lado direito; c) Calcule a resultante da distribuição das tensões tangenciais τ no troço vertical do lado direito; d) Mostre que são nulas as tensões tangenciais τ em qualquer ponto do troço horiontal da secção. (0.5 valor) Solução: b) 5.8MPa; c) R= 16.86kN Teto de apoio aos alunos
34 .. Em peças fechadas de paredes finas Neste ponto serão apresentadas peças fechadas de paredes finas em que o esforço transverso está aplicado segundo um eio de simetria. dmita a seguinte barra constituída por uma peça fechada de paredes finas (thin-walled bar) sujeita a fleão simples (transverse bending) (M 0; T 0 N=0; Mt=0): q kn/m l Cuja secção transversal está representada na figura seguinte: T dmitamos um segmento infinitesimal de barra com comprimento d. tendendo à variação, ao longo da barra, do esforço transverso e momento flector, podemos admitir a figura seguinte: M M+dM T+dT d T Na figura anterior dm e dt, são as variações do momento flector e do esforço transverso no elemento infinitesimal de comprimento d. distribuição das tensões normais nas secções está representada na figura seguinte: M ( M dm ) d dmitamos o segmento longitudinal representado na figura: d Teto de apoio aos alunos
35 O equilíbrio de forças do referido segmento, fica: e d df df d ( d ) d o que pressupõe a eistência de duas forças da peça. df, tangencialmente à secção longitudinal df s forças elementares são fruto de uma distribuição de tensões de tangenciais τ na secção longitudinal da peça e, atendendo à condição de reciprocidade das tensões tangenciais, condu a uma distribuição de tensões tangenciais τ. na secção transversal. τ τ τ τ plicando a mesma dedução matemática efectuada nas secções abertas, obtém-se para as secções fechadas a seguinte epressão geral da tensão tangencial: S e T Teto de apoio aos alunos
36 ..1. Problema resolvido Determine o valor das tensões tangenciais no ponto B da secção indicada na figura: B T 0cm 1cm 15cm 0.8cm Resolução B T S e T S cm cm kNcm 3. 07MPa Problemas não resolvidos P.3) Para T = 10kN, determine o valor das tensões tangenciais no ponto da secção indicada na figura: Teto de apoio aos alunos
37 3cm T 0cm 1cm 15cm 0.8cm Solução τ =.3MPa P.4) consola da figura está submetida ao carregamento indicado. Determine a tensão tangencial máima na secção de encastramento. 0kN Espessura uniforme de 1cm 15cm 10cm Solução: τ ma =8.33MPa.3. Centro de corte em peças de paredes finas Nos pontos anteriores foram deduidas epressões que permitem o cálculo de tensões tangenciais induidas pelo esforço transverso, nomeadamente em secções transversais de vigas em fleão simples (M 0; T 0; N=0; M t =0). Porém, a condição de momento torçor nulo (M t =0) só acontece se a linha de acção do esforço transverso passar por um ponto conhecido por centro de corte (shear centre) ou centro de torção. Caso a linha de acção do esforço transverso não passe pelo centro de corte, então eistirá igualmente um momento torçor o qual induirá na secção tensões tangenciais suplementares. determinação do centro de corte pressupõe o conhecimento da distribuição de tensões tangenciais devidas ao esforço transverso na secção, tarefa que é relativamente simples em secções de paredes finas. Teto de apoio aos alunos
38 .3.1. Problemas resolvidos Retomando a secção e h e b verificámos uma distribuição de tensões devidas ao esforço transverso (T): τ τ T τ o que pressupõe a eistência de resultantes das tensões tangenciais: R aba R alma R aba R 3b T R aba hh 6b alma T Para que o esforço transverso T seja eclusivamente responsável pelo aparecimento das forças resultantes indicadas na figura anterior então, a força T tem de ser uma força equivalente ao sistema de forças formadas pelas forças R aba e R alma, ou seja: Teto de apoio aos alunos
39 R aba T d R alma R aba Centro de corte Faendo momentos em relação ao ponto indicado: T d = R aba (h/) 3b d h 6b O centro de corte (c.c.) está sempre localiado num eio de simetria da secção. Em casos em que a secção seja constituída por troços, cujas linhas médias concorrem num ponto, o c.c. coincide necessariamente com esse ponto. c.c. Determine o centro de corte da secção seguinte, a qual tem espessura uniforme igual a 0.5cm: 0cm.5cm 7.5cm Uma ve que a secção tem um eio de simetria, então o c.c. está sobre ele. Bastará, portanto conhecer a distância (d) do c.c. em relação ao eio da alma da secção. Teto de apoio aos alunos
40 T d Devido ao esforço transverso a secção terá uma distribuição de tensões tangenciais como se indica: T figura seguinte mostra a resultante das tensões tangenciais nas abas e na alma: R 3 R 1 R 5 T d R R 4 Por raões de simetria, R 1 = R e R 3 = R 4. Os sistemas de forças formados pela força T e pelas forças R 1 ; R ; R 3 ; R 4 ; R 5 são equivalentes. determinação da distância d, Teto de apoio aos alunos
41 pode ser feita efectuando os momentos em relação à linha média da alma, o que, por si só, simplifica o problema, uma ve que não se necessita de conhecer a força R 5. figura seguinte mostra o tipo de distribuição das tensões nas abas (distribuição linear). T Tratando-se de uma secção aberta de paredes finas: S e T Cálculo do momento de inércia : cm Cálculo do valor máimo da tensão tangencial na aba superior direita: T S cm 3 Teto de apoio aos alunos
42 36.56 T 0. T Na epressão anterior τ vem em kn/cm. Cálculo da força resultante (R 1 ) na aba superior direita: R T T (kn) Cálculo do valor máimo da tensão tangencial na aba superior esquerda: T S cm 1.19 T 0. T Na epressão anterior τ vem em kn/cm. Cálculo da força resultante (R 3 ) na aba superior esquerda: R T T (kn) Cálculo da distância d: T 0.013T 19.5 T d Da equação anterior conclui-se que d = 1.9cm. ssim o centro de corte da secção em estudo, encontra-se no eio de simetria, 1.9cm para a esquerda da linha média da alma. Teto de apoio aos alunos
43 .3.. Problemas não resolvidos P.5) Determine o centro de corte da secção da figura: cm 1cm 10cm 5cm cm Solução: No eio de simetria, d=.08cm para a esquerda da linha média da alma P.6) Determine o centro de corte da secção da figura: 5cm 5cm 10cm Espessura uniforme de 1cm 1cm 0cm Solução: No eio de simetria, d=5.cm abaio da linha média da aba maior. P.7) Em continuação do problema P., admita que T passa pelo centro de corte. Calcule a distância d. T d Solução: d=1.686cm Teto de apoio aos alunos
44 3. Estado de tensão sob momento flector e esforço transverso verificação do estado de tensão (state of stress), ou seja da segurança, em peças sujeitas a fleão simples (M 0; T 0; N=0; M t =0) compreende, de uma maneira geral, três pontos: 1) Verificação da tensão normal máima nas fibras mais afastadas do eio neutro; σ ma σ Rd sendo σ Rd o valor de cálculo da tensão resistente do material. ) Verificação da tensão tangencial máima que, geralmente ocorre ao nível do eio neutro; ma 3 3) Verificação do estado duplo de tensão nos pontos em que tanto a tensão normal como a tensão tangencial atinjam valores elevados. Nestes pontos a verificação de segurança deverá obedecer a um critério de resistência. Em materiais dúcteis como o aço, usa-se habitualmente o critério de Von Mises. Rd 3 terceira verificação é importante em vigas em ou em U nos pontos de inserção da alma nos banos, em secções em que tanto o momento flector como o esforço transverso atinjam valores máimos, como nas secções próimas do apoio B da figura seguinte: p kn/m Rd B Nos pontos de inserção da alma nos banos a tensão normal aproima-se do máimo e a tensão tangencial é pouco inferir à tensão ao nível do eio neutro: Distribuição de tensões normais σ na secção devido ao momento flector Distribuição de tensões tangenciais τ na alma devido ao esforço transverso Teto de apoio aos alunos
45 3.1. Problema resolvido Utiliando um perfil NP dimensione a seguinte viga em aço, admitindo um valor de cálculo da tensão resistente do material σ Rd =35MPa 30kN/m 50kN m m Resolução Reacções nos apoios 30kN/m 60kNm m m 50kN 110kN Diagrama de esforços 30kN/m 50kN m m T 110kN 50kN M -60kNm -100kNm Dimensionamento da secção à tensão normal: M W m 1106 cm 3 ma W W NP 380 tendendo às Tabelas Técnicas o módulo de fleão do perfil seleccionado é: W = 160cm 3 Teto de apoio aos alunos
46 M kpa MPa ma 6 W MPa 35MPa VERFC Verificação da tensão tangencial máima: Esta tensão ocorre no eio neutro (a meio da alma) S T e S = 741cm 3 (momento estático de meia secção em relação ao eio dos Tabelas Técnicas); = 4010cm 4 (momento de inércia da secção em relação ao eio dos Tabelas Técnicas); e = 13.7mm (espessura da alma Tabelas Técnicas) kncm ma 4. 8MPa MPa << MPa 3 VERFC Verificação do estado de tensão na inserção da alma nos banos: Uma aproimação, por ecesso, é a de utiliar os valores de σ ma e de τ ma das alíneas anteriores, dado que ambos são superiores aos valores que efectivamente se verificam nos pontos de inserção da alma nos banos. Tratando-se de um material dúctil, usa-se habitualmente o critério de Von Mises: 3 Rd MPa 35 MPa VERFC 3.. Problemas não resolvidos P3.1) Para a seguinte viga em aço, admitindo um valor de cálculo da tensão resistente do material σ Rd =35MPa: 50kN/m e.a. B 6m 1.5m C a) Trace os diagramas de esforço transverso e de momento flector para a viga; b) Dimensione a viga à fleão, utiliando um perfil NP; Teto de apoio aos alunos
47 c) De acordo com o diagrama de momento flector ao longo da viga, seleccione, agora, um NP adequado para suportar, não o valor máimo de momento flector do diagrama, mas o pico de momento imediatamente abaio; d) Reforce o NP da resposta anterior, soldando chapa de 15mm de espessura em cada bano, na ona de máimo momento flector do diagrama. Determine qual a largura da chapa a soldar; e) De acordo com o diagrama de esforço transverso, verifique o dimensionamento à tensão tangencial; f) Utiliando o critério de Von Mises, faça a verificação do estado de tensão no final da parte recta da alma, na secção mais desfavorável. Ver nas Tabelas Técnicas a dimensão da parte recta da alma. Solução: b) NP340; c) NP0 d) d = 18cm; e) τ ma =104.MPa; f) 3 17.MPa P3.) Considere a seguinte viga feita de aço (σ Rd =35MPa). 40kN e.a. 3m NP00 a) Verifique a segurança; b) Se a viga não estiver em segurança reforce-a com chapas nos banos onde for necessário. Solução: a) Não verifica; b) chapas com 1.cm de espessura e 13.3cm de largura, em 1.74m. P3.3) Para a seguinte viga em aço, admitindo um valor de cálculo da tensão resistente do material σ Rd =75MPa: e.a. 0kN 60kN 0kN/m 1.5m B m m 1.5m C D UPN a) Trace os diagramas de esforço transverso e de momento flector para a viga; b) Dimensione a viga à fleão, utiliando dois perfi UNP; c) De acordo com o diagrama de esforço transverso, verifique o dimensionamento à tensão tangencial; d) De acordo com os diagramas de esforço transverso e de momento flector, verifique o dimensionamento segundo o critério de Von Mises na secção a meio vão e no ponto de inserção da alma nas abas (use o método epedito); Teto de apoio aos alunos
48 e) De acordo com os diagramas de esforço transverso e de momento flector, verifique o dimensionamento segundo o critério de Von Mises na secção em B e no ponto de inserção da alma nas abas (use o método epedito); f) De acordo com os diagramas de esforço transverso e de momento flector, verifique o dimensionamento segundo o critério de Von Mises na secção em C e no ponto de inserção da alma nas abas (use o método epedito). Solução: b) UNP 160; c) τ ma =37.3MPa; d) 3 e) MPa ; f) MPa 71.MPa 4. Caderno de problemas 4.1. Esforço de escorregamento em planos longitudinais 1) Para a viga representada na figura: 0cm 30kN e.a. 0.6m 1.m 5cm a) Faça a distribuição das tensões tangenciais no plano neutro. b) Determine a força de escorregamento no plano neutro. Solução: b) F=7kN ) figura seguinte mostra uma viga com uma carga concentrada a meio vão: 387kN 3m e.a. viga é um perfil de aço reforçado com chapas de aço de 16mm de espessura e 00mm de largura, conforme a figura anterior. O perfil tem as seguintes características: Teto de apoio aos alunos
49 = 9530cm 4 h = 305mm h b a) Determine a distribuição das tensões normais na secção mais solicitada. b) Determine a força de escorregamento para qual deve ser dimensionada a ligação entre a chapa de reforço e o bano do perfil. c) Optimie o comprimento do reforço tendo em consideração um valor de cálculo de resistência do material de 35MPa. d) Calcule a força de corte na ligação do reforço da alínea anterior. Solução: a) σ ma. comp = MPa; σ ma. trac = MPa, b) F=57.69kN; c) reforço com 1.5m de comprimento, centrado no vão; d) F=86.4kN 3) consola B da figura seguinte, é constituída por um perfil NP 16. No troço C o perfil está reforçado por barra de secção 50mm 0mm, soldada em ambos os banos. Determine os esforços para os quais devem ser dimensionadas as ligações entre as chapas e o perfil NP. 50mm 30kN/m 0mm C B 1m 1m Solução: F=105.4kN Teto de apoio aos alunos
50 4) figura seguinte mostra uma viga com uma carga concentrada a meio vão: QkN m viga é constituída por dois perfi de aço soldados pelos banos, conforme a figura anterior. Cada perfil tem as seguintes características: 1 h 1 = 887cm 4 1 = 313cm 4 Ω=30.4cm h = 1.7cm b = 1.7cm 1 b dmitindo que a força de escorregamento na ligação dos dois não deve ultrapassar o valor de 960kN, determine o máimo valor da carga Q. Solução: Q 40kN 5) figura seguinte mostra uma viga com uma carga uniforme q: qknm m viga é constituída por dois perfi de aço soldados pelos banos, conforme a figura anterior. Cada perfil tem as seguintes características: Teto de apoio aos alunos
51 1 h = 887cm 4 = 313cm 4 Ω=30.4cm h = 1.7cm b = 1.7cm 1 b dmitindo que a força de escorregamento na ligação dos dois não deve ultrapassar o valor de 960kN, determine o máimo valor da carga q. Solução: q=40kn/m 6) viga B suporta uma carga uniformemente distribuída q. viga é construída ligando 3 peças de secção rectangular, todas do mesmo material, como se mostra na figura: q kn/m 0.8m B Secção transversal 60mm 60mm 60mm 00mm 10mm e.a. dmitindo que o esforço de escorregamento admissível na ligação das peças é de.13kn, calcule o valor máimo admissível para a carga q. Solução: q=3.69kn/m 7) figura seguinte mostra uma viga com uma carga distribuída e uniforme. viga é constituída por perfi UNP 80 de aço reforçado com chapas de aço de 16mm de espessura e 400mm de largura, conforma a figura anterior. Determine a força de escorregamento para qual deve ser dimensionada a ligação entre chapas de reforço e o bano de cada perfil. Teto de apoio aos alunos
52 500kN/m 3m e.a. Solução: F=655.76kN, em cada bano 8) viga tem aplicada acções cujos valores de cálculo estão indicados na figura: 17kN 17kN/m 17kN 0.7m m 0.7m viga é constituída por um perfil NP 1 reforçado no troço entre os apoios com duas chapas de aço, iguais, ligadas aos banos. e.a. Chapa 40mm 10mm Determine o esforço de escorregamento na ligação dos dois materiais. Solução: F=33.15kN 9) viga é um perfil NP14 de aço reforçado com chapas de aço de 5mm de espessura e 80mm de largura, conforme a figura seguinte: e.a. viga está solicitada como indicado na figura seguinte: Teto de apoio aos alunos
53 15kN/m m Determine a força de escorregamento para qual deve ser dimensionada a ligação entre chapas de reforço e os banos do perfil. Solução: F=87.55kN 10) Quatro barras de latão estão unidas firmemente, formando a secção composta ilustrada: 10 mm 10 mm Latão 10 mm Latão 40 mm 10 mm 40 mm qual está solicitada como indicado na figura seguinte: 1.5kN/m m a) Determine o esforço de escorregamento nos primeiros 50cm de viga, a contar do encastramento, para o qual tem de estar dimensionada cada ligação; b) Determine o esforço de escorregamento nos segundos 50cm de viga, a contar do encastramento, para o qual tem de estar dimensionada cada ligação; c) Determine o esforço de escorregamento nos últimos 100cm de viga até à etremidade livre, para o qual tem de estar dimensionada cada ligação. Solução:a) F=1.4kN, b) F=15.9kN, c) F=1.3kN Teto de apoio aos alunos
54 4.1.1 Esforço de escorregamento em peças mistas 11) Para a viga mista de madeira reforçada com uma placa de aço, determine o esforço de escorregamento na ligação dos dois materiais. dmita que o módulo de elasticidade do aço é 0 vees o módulo de elasticidade da madeira 5kN 3m Madeira 15cm ço 1.5cm.5cm 10cm Solução: F=3.44kN 1) viga de madeira reforçada com duas placas de aço está sujeita a cargas cujos valores de cálculo estão indicados na figura. Determine o esforço de escorregamento na ligação dos dois materiais. dmita: E madeira =13Gpa; E aço =00Gpa. 35kN/m 40kN 1.5m 3m ço 1.0cm Madeira 5cm ço 15cm 1.0cm Solução: F=13.31kN 13) Duas barras de latão estão unidas firmemente a duas barras de alumínio, formando a secção composta ilustrada: Teto de apoio aos alunos
55 10 mm 10 mm Latão 10 mm lumínio 40 mm 10 mm 40 mm qual está solicitada como indicado na figura seguinte: 1.5kN/m m dmitindo: Latão - módulo de elasticidade de 105 GPa; - valor de cálculo para a tensão resistente de 160 MPa. lumínio - módulo de elasticidade de 70 GPa; - valor de cálculo para a tensão resistente de 100 MPa. Determine o esforço de escorregamento na ligação dos dois materiais. Solução: F=51.9kN 4.. Tensões tangenciais em secções transversais 14) Para a viga representada na figura: 0cm 30kN e.a. 0.6m 1.m 5cm a) Faça a representação da distribuição das tensões normais na secção mais solicitada. b) Faça a distribuição das tensões tangenciais na secção mais solicitada. Solução: a) σ ma. comp = -5.76MPa; σ ma. trac = 5.76MPa, b) τ ma = 600kPa Teto de apoio aos alunos
56 15) Na secção indicada na figura, sujeita a um esforço transverso de 50kN, determine: cm 16cm T=50kN cm 16cm e) Determine a epressão geral da distribuição das tensões tangenciais na alma; f) Calcule a resultante da distribuição das tensões na alma; g) Determine a epressão geral da distribuição das tensões tangenciais na aba; h) Calcule a resultante da distribuição das tensões na aba. Solução: a) τ ma = 19.64MPa; b) R alma 50kN; c) τ ma = 9.05MPa; d) R aba = 7.4kN 16) Determine o valor das tensões tangenciais devido a esforço transverso: a) Máima; b) No ponto mais afastado da parte recta da alma. T =50kN UPN00 Solução: a) τ ma = 17.55MPa; b) τ = 13.8MPa 17) Considere a seguinte secção sujeita a um esforço transverso de 0kN: cm 0cm T=0kN cm 0cm Teto de apoio aos alunos
57 a) Determine a epressão geral da distribuição das tensões tangenciais no troço vertical da secção (alma); b) Calcule a resultante da distribuição das tensões na alma. Solução: b) R=19.88kN 18) dmita que a secção representada na figura seguinte está sujeita a um esforço transverso de T = 0.8 kn, o qual não indu qualquer torção na peça. T =0.8 kn 0.3 cm 0.3 cm 15 cm 0.3 cm 10 cm a) Faça a representação do diagrama rebatido das tensões tangenciais devido ao esforço transverso nas abas e na alma; b) Calcule a tensão máima devido a esforço transverso na alma; c) Calcule a tensão máima devido a esforço transverso na aba; d) Calcule a resultante da distribuição das tensões numa das abas; e) Calcule a resultante da distribuição das tensões na alma. Solução: b) τ ma =1.955MPa; c) τ ma =1.4MPa; d)0.13kn; e)0.8kn 19) dmita uma barra com a secção indicada na figura, sujeita a uma fleão simples e recta segundo o eio da acção igualmente indicado na figura. Na secção o valor do esforço transverso é 6.5kN. cm 4cm cm T=6.5kN 0cm cm e.a. a) Determine a epressão geral da distribuição das tensões tangenciais no troço vertical superior do lado esquerdo; Teto de apoio aos alunos
58 b) Qual o valor máimo da tensão tangencial no troço vertical superior do lado esquerdo; c) Calcule a resultante da distribuição das tensões tangenciais no troço vertical superior do lado esquerdo; Solução: b) τ ma =1.1MPa; c) R=1.615kN 0) dmita uma barra com a secção indicada na figura, sujeita a uma fleão simples e recta segundo o eio da acção igualmente indicado na figura. Na secção o valor do esforço transverso é 10kN. barra é feita de aço e constituída por dois perfi U e duas chapas soldadas nas abas. 1cm 5.4cm 1cm 40cm 7cm T=10kN 5cm e.a. Cada perfil U tem as seguintes características: 1 d 1 h 1 = 810cm 4 1 = 94.9cm 4 Ω=8.97cm h = 5.4cm b = 6.5cm d = 1.61cm b Calcule, no ponto, o valor da tensão tangencial devido ao esforço transverso. Solução: τ =0.5MPa Teto de apoio aos alunos
59 4.3. Centro de corte em secções de paredes finas 1) Determine o centro de corte da seguinte secção de espessura uniforme igual a 1cm. 5cm 5cm 5cm 5cm 5cm Solução: d=15.9mm à esquerda da linha média de alma ) Para o perfil indicado na figura seguinte determine a distância d do Centro de Corte à linha média da alma. 0.3 cm 0.3 cm 15 cm 0.3 cm 10 cm Solução: d=40mm à esquerda da linha média de alma Teto de apoio aos alunos
60 3) Para o perfil indicado na figura seguinte localie o Centro de Corte. O fluo das tensões tangenciais na secção estão igualmente representados na figura: E C G 3cm D H 3cm B 3cm F 3cm Espessuras (cm) B E BF CG DH Solução: d=9.176mm à esquerda da linha média de B 4) Para o perfil indicado na figura seguinte determine a distância d ao Centro de Corte. dmita que a secção tem espessura uniforme de 5mm. d 15mm c.c. 100mm 75mm 50mm Solução: d=55.3mm Teto de apoio aos alunos
61 5) Determine o Centro de Corte da secção seguinte a qual tem espessura uniforme de 3mm. dmita que o fluo das tensões tangenciais na secção são os apresentados na figura. 100mm 50mm 150mm 50mm Solução: d=3.3mm à esquerda da linha média da alma 6) Para o perfil indicado na figura seguinte determine a distância d ao Centro de Corte. 0cm C.C. d 0cm 5cm 60cm 15cm 60cm 70cm 0cm Solução: d=0.57cm à esquerda da linha média da alma Teto de apoio aos alunos
62 7) dmita uma barra com a secção indicada na figura, com espessura uniforme e igual a 0.8cm, sujeita a um esforço transverso T = 50kN: T = 50kN 7.5cm 6cm d 5cm a) Calcule a tensão τ a meio do troço vertical do lado direito; b) Mostre que são nulas as tensões tangenciais τ em qualquer ponto do troço horiontal da secção. c) dmita que T passa pelo centro de corte. Calcule a distância d. Solução: a) τ =5.7MPa; c) d=1.69cm 8) Determine o centro de corte da secção seguinte de espessura uniforme igual a 0.5cm. dmita que =136.6cm 4 0cm.5cm 7.5cm Solução: d=19.mm à esquerda da linha média da alma Teto de apoio aos alunos
63 9) Para o perfil indicado na figura seguinte determine a distância b de forma a que o Centro de Corte fique situado no ponto O. dmita que a secção tem espessura uniforme de 1cm. 1cm b cm 4 6cm 6cm 1cm O 4.5cm 4.5cm 3cm bcm Solução: b=4cm Teto de apoio aos alunos
64 4.4. Estado de tensão em fleão simples 30) Considere a viga sujeita às acções cujos valores de cálculo estão indicados na figura: seguinte: 60kN 60kN 10kN 0.4m 0.8m 1.4m 0.8m dmita que a viga tem a secção indicada na figura seguinte: 7.4mm 47mm 11mm 0mm a) Trace os diagramas de esforços (T; M); b) dmitindo um valor de cálculo da tensão resistente do material σ Rd = 35MPa, verifique a viga quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação utiliando o método epedito. Solução: b) 198.9MPa<35MPa, Verifica. 31) Considere a viga sujeita às acções cujos valores de cálculo estão indicados na figura: seguinte: 100kN/m 10kN 1.m 1.0m 0.8m dmita que a viga tem a secção indicada na figura seguinte: Teto de apoio aos alunos
65 7.4mm 47mm 11mm 0mm a) Trace os diagramas de esforços (T; M); b) dmitindo um valor de cálculo da tensão resistente do material σ Rd = 35MPa, verifique a viga quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação utiliando o método simplificado por ecesso. Solução: b) 198.9MPa<35MPa, Verifica. 3) Considere a viga ilustrada na figura seguinte: 5 kn/m 40 kn 40 kn 0.6 m 1.8 m 0.6 m a) Trace os diagramas de esforços (T; M); b) Dimensione a viga apenas em relação ao momento flector, assumindo um perfil NP (tabela anea) e um valor de cálculo da tensão resistente do material, σ Rd = 35 MPa; c) No ponto assinalado da secção, utilie o critério de Von Mises para verificar se o perfil seleccionado na alínea anterior garante a segurança quando se combina esforço transverso e momento flector. Para os fins eclusivos de cálculo de momento estático, assuma que os banos do perfil são rectangulares com a espessura média indicada na tabela anea. d) Verifique de novo a viga nà mesma secção utiliando o método simplificado por ecesso. Solução: b) NP 0 c) MPa<35MPa, Verifica; d) MPa<35MPa, Verifica Teto de apoio aos alunos
66 150kN C 150kN 0.8m 0.8m 0.8m 90kN/m B D Universidade de Évora Escola de Ciência e Tecnologia - Departamento de Engenharia Rural 33) Considere a viga sujeita a acções cujo valor de cálculo se ilustram na figura seguinte: 30kN/m B C D 30kN 30kN 0.6m 1.8m 0.6m a) Trace os diagramas de esforços (T; M); b) Para a viga foi utiliado um perfil NP 180 (tabela anea) reforçado entre B e C. O reforço é constituído por barra rectangular de aço, soldada em cada um dos banos. Cada barra rectangular tem espessura de 0.5cm e a largura de b. Dimensione a largura b do reforço, tendo em consideração apenas o momento flector e um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; c) Verifique a viga à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação utiliando o método simplificado por ecesso. Solução: b) b 4.95cm, c) 31.4MPa<35MPa, Verifica. 34) Considere a viga sujeita a acções cujos valores de cálculo se ilustram na figura seguinte: 45kN/m 18kN e.a. C 1.4m B 1.6m a) Trace os diagramas de esforços; b) Eclusivamente com base nas tensões normais, dimensione a viga como um perfil NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa. c) Verifique a viga à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação utiliando o método simplificado por ecesso. Solução: b) NP 6 c) 10.06MPa<35MPa, Verifica. 35) viga simplesmente apoiada, sujeita a uma fleão simples e recta, tem aplicadas acções cujos valores de cálculo estão indicados na figura: 150kN 150kN 90kN/m C D E B 0.8m 0.8m 0.8m.4m Teto de apoio aos alunos
67 a) Trace os diagramas de esforços; b) Eclusivamente com base nas tensões normais, dimensione a viga como um perfil NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; c) Verifique a inserção da alma com os banos quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação de forma aproimada, usando valores de tensões obtidos por ecesso. Solução: b) NP 40 c) 8.15MPa<35MPa Verifica. 36) dmita a barra indicada na figura, sujeita a uma fleão simples e recta: 60kN 10kN/m 0kN/m B m m m a) Trace os diagramas de esforços; b) Eclusivamente com base nas tensões normais, dimensione a viga como um perfil NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; c) Verifique a inserção da alma com os banos quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação de forma aproimada, usando valores obtidos por ecesso. Solução: b) NP 8 c).65mpa<35mpa Verifica. 37) Considere a viga sujeita a acções cujo valor de cálculo se ilustram na figura seguinte: 1kN/m kn/m e.a. B C m D 4m 4m a) Trace os diagramas de esforços (T; M); b) Dimensione a viga à fleão, utiliando um perfil NP e considerando um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; c) Em C, verifique a viga à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação utiliando o método simplificado por ecesso. Solução: b) NP 1 c) 18.9MPa<35MPa Verifica. Teto de apoio aos alunos
68 38) Uma viga constituída por um perfil NP está submetida a cargas cujo valor da acção se encontra na figura seguinte 0kN/m 30kN/m e.a. C D B 3.m 0.8m 0.8m dmita um valor de cálculo da tensão resistente do material, σ Rd =140MPa a) Trace os diagramas de esforço transverso e de momento flector; b)verifique o dimensionamento unicamente à tensão normal; c)verifique o dimensionamento unicamente à tensão tangencial; d) Na secção C faça a verificação do estado de tensão utiliando o critério de Von Mises. Sugere-se que efectue esta verificação utiliando o método simplificado por ecesso. Solução: b) 13.59MPa<140MPa Verifica; c) 3.4MPa<140/ 3MPa Verifica; d) 79.16MPa<140MPa Verifica. 39) Em cada uma das quatro vigas de 4.5m está aplicada uma carga cujo valor de cálculo é 36kN/m. Estas vigas estão suportadas pela viga D e em paredes de betão. a) Eclusivamente com base nas tensões normais, dimensione todas as vigas como perfis NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; b) Na viga D verifique a inserção da alma com os banos quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação de forma aproimada, usando valores de tensões obtidos por ecesso. c) Verifique as vigas de 4.5m quanto à tensão tangencial máima. Solução: a) Viga D: NP55; restantes vigas: NP6; b) 6.59MPa<35MPa, Verifica; c) 38.6MPa<135.68MPa, Verifica. Teto de apoio aos alunos
69 40) Considere a viga sujeita às acções cujos valores de cálculo estão indicados na figura seguinte: 10kN/m 0kN 1.5m 1.5m a) Eclusivamente com base nas tensões normais, dimensione a viga como perfis NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; b) Verifique a inserção da alma com os banos quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação de forma aproimada, usando valores de tensões obtidos por ecesso. Solução: a) NP 4 b) 17.9MPa<35MPa Verifica. 41) viga da figura seguinte tem aplicada acções cujos valores de cálculo estão indicados na figura: a) Trace os diagramas de esforços; b) Eclusivamente com base nas tensões normais, dimensione a viga como um perfil NP (ver dados na tabela anea), admitindo um valor de cálculo da tensão resistente do material, σ Rd = 35MPa; c) Verifique a inserção da alma com os banos quanto à combinação das tensões normais e tangenciais (critério de Von Mises). Sugere-se que efectue esta verificação de forma aproimada, usando valores de tensões obtidos por ecesso 30kN/m 50kN m m Solução: b) NP 38 c) 10.78MPa<35MPa Verifica. 4) viga em consola tem aplicada acções cujos valores de cálculo estão indicados na figura. É um perfil NP 60 reforçado ao longo de m, a partir do encastramento, com chapa de aço, soldada em cada um dos banos. Cada chapa tem espessura de 1cm e a largura de 8cm. Teto de apoio aos alunos
70 30kN/m 50kN m m a) tendendo eclusivamente à solicitação devida a momento flector, verifique se o dimensionamento satisfa a segurança ao longo de toda a barra. dmita um valor de cálculo da tensão resistente do material, σ Rd = 35MPa. b) dmitindo a simplificação geométrica para a secção NP 60 indicada na figura seguinte, verifique a segurança no ponto (indicado) de inserção da alma nos bano do perfil, utiliando o critério de Von Mises. 1.41cm NP 60 6cm 0.94cm = 5740cm cm 1.41cm c) Repita a verificação usando o método aproimado por ecesso. Solução: a) Troço c/ reforço 8.MPa<35MPa, verifica; troço s/ reforço 6.5MPa<35MPa, verifica. b) Troço c/ reforço 1.6MPa<35MPa, verifica; troço s/ reforço 16.1MPa<35MPa, verifica. c) Troço c/ reforço 16.1MPa<35MPa, verifica; troço s/ reforço 18.1MPa<35MPa, verifica. 43) viga de aço tem aplicada acções cujos valores de cálculo estão indicados na figura. a) Utiliando um perfil NP, dimensione a viga eclusivamente à fleão, admitindo um valor de cálculo da tensão resistente do material σ Rd =35 MPa; b) Verifique a viga de acordo com o critério de Von Mises. 50kN 30kN/m e.a. 1.5m B 4m C Solução: a) NP 80; b) 11.9MPa<35MPa, verifica Teto de apoio aos alunos
71 Referências Dias da Silva, V. Mecânica e Resistência dos Materiais, capítulo V Esforço Transverso. ª Edição. Edição: ZUR Edição de Livros Técnicos, Lda SBN: X. William Nash Resistência de Materiais. Edição: McGraw-Hill SBN: Teto de apoio aos alunos
Várias formas da seção transversal
 Várias formas da seção transversal Seções simétricas ou assimétricas em relação à LN Com o objetivo de obter maior eficiência (na avaliação) ou maior economia (no dimensionamento) devemos projetar com
Várias formas da seção transversal Seções simétricas ou assimétricas em relação à LN Com o objetivo de obter maior eficiência (na avaliação) ou maior economia (no dimensionamento) devemos projetar com
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil 2º ANO EXERCICIOS PRÁTICOS Ano lectivo 2004/2005 MECÂNICA APLICADA II I - Teoria do estado de tensão I.1 - Uma barra, com a
RESISTÊNCIA DE MATERIAIS II
 RESISTÊNCIA DE MATERIAIS II - 014-015 Problema 1 PROBLEMAS DE TORÇÃO A viga em consola representada na figura tem secção em T e está submetida a uma carga distribuída e a uma carga concentrada, ambas aplicadas
RESISTÊNCIA DE MATERIAIS II - 014-015 Problema 1 PROBLEMAS DE TORÇÃO A viga em consola representada na figura tem secção em T e está submetida a uma carga distribuída e a uma carga concentrada, ambas aplicadas
Elementos Finitos 2014/2015 Colectânea de trabalhos, exames e resoluções
 Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
Curso de Mestrado em Engenharia de Estruturas 1. a Edição (014/015) Elementos Finitos 014/015 Colectânea de trabalhos, exames e resoluções Lista dos trabalhos e exames incluídos: Ano lectivo 014/015 Trabalho
CAPÍTULO 3: DIMENSIONAMENTO DE VIGAS
 Curso de Engenharia Civil Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CPÍTULO 3: DIMENSIONMENTO DE VIGS 3.1 - Introdução Escolher o material e as dimensões da
Curso de Engenharia Civil Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CPÍTULO 3: DIMENSIONMENTO DE VIGS 3.1 - Introdução Escolher o material e as dimensões da
Curso de Engenharia Civil. Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CAPÍTULO 3: FLEXÃO
 Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURAS DE BETÃO 2. 1ª Parte (SEM CONSULTA)
 Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE ETÃO 2 1ª Parte (SEM CONSULT) 13 de Junho de 2002 1ª Chamada Duração: 1h 1) (4 valores) Figura 1a representa
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE ETÃO 2 1ª Parte (SEM CONSULT) 13 de Junho de 2002 1ª Chamada Duração: 1h 1) (4 valores) Figura 1a representa
Disciplina de Estruturas Metálicas
 Disciplina de Estruturas Metálicas Aulas de Problemas Francisco Virtuoso, Eduardo Pereira e Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 4 versão de 2009/2010 Capítulo
Disciplina de Estruturas Metálicas Aulas de Problemas Francisco Virtuoso, Eduardo Pereira e Ricardo Vieira 2013/2014 Versão actualizada a partir de Aulas de problemas capítulo 4 versão de 2009/2010 Capítulo
RESISTÊNCIA DE MATERIAIS II
 RESISTÊNCIA DE MATERIAIS II - 2014-2015 PROBLEMAS DE VERIFICAÇÃO DA SEGURANÇA Problema 1 (Problema 100 da colectânea, modificado) Considere a estrutura representada na figura, a qual está contida no plano
RESISTÊNCIA DE MATERIAIS II - 2014-2015 PROBLEMAS DE VERIFICAÇÃO DA SEGURANÇA Problema 1 (Problema 100 da colectânea, modificado) Considere a estrutura representada na figura, a qual está contida no plano
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais II. Capítulo 3 Flexão
 Capítulo 3 Flexão 3.1 Revisão Flexão provoca uma tensão de tração de um lado da viga e uma tensão de compressão do outro lado. 3.2 A fórmula da flexão O momento resultante na seção transversal é igual
Capítulo 3 Flexão 3.1 Revisão Flexão provoca uma tensão de tração de um lado da viga e uma tensão de compressão do outro lado. 3.2 A fórmula da flexão O momento resultante na seção transversal é igual
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
MECÂNICA APLICADA II
 Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil º ANO EXERCICIOS PRÁTICOS Ano lectivo 005/006 Ano lectivo: 005/006.º semestre MECÂNICA APLICADA II I - Teoria do estado de
Escola Superior de Tecnologia e Gestão MECÂNICA APLICADA II Engenharia Civil º ANO EXERCICIOS PRÁTICOS Ano lectivo 005/006 Ano lectivo: 005/006.º semestre MECÂNICA APLICADA II I - Teoria do estado de
RESISTÊNCIA DOS MATERIAIS II
 SEÇÃO DE ESTRUTURS DERTMENTO DE ENGENHRI IVI FUDDE DE IÊNIS E TENOOGI UNIVERSIDDE NOV DE ISO RESISTÊNI DOS MTERIIS II roblemas 1. Flexão lástica 2. orte 3. Torção 4. Solicitações ompostas e Verificação
SEÇÃO DE ESTRUTURS DERTMENTO DE ENGENHRI IVI FUDDE DE IÊNIS E TENOOGI UNIVERSIDDE NOV DE ISO RESISTÊNI DOS MTERIIS II roblemas 1. Flexão lástica 2. orte 3. Torção 4. Solicitações ompostas e Verificação
RESISTÊNCIA DE MATERIAIS II
 RESISTÊNCIA DE MATERIAIS II - 2014-2015 PROBLEMAS DE CORTE Problema 1 (problema 50(b) da colectânea) Considere a viga em consola submetida a uma carga concentrada e constituída por duas peças de madeira,
RESISTÊNCIA DE MATERIAIS II - 2014-2015 PROBLEMAS DE CORTE Problema 1 (problema 50(b) da colectânea) Considere a viga em consola submetida a uma carga concentrada e constituída por duas peças de madeira,
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/11 Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial 13ª Aula Duração - 2 Horas Data - 12 de Novemro de 2003 Sumário: Tensões Axiais e Deformações Axiais numa viga com Secção
1/11 Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial 13ª Aula Duração - 2 Horas Data - 12 de Novemro de 2003 Sumário: Tensões Axiais e Deformações Axiais numa viga com Secção
TENSÕES DE FLEXÃO e de CISALHAMENTO EM VIGAS
 DIRETORIA ACADÊMICA DE CONSTRUÇÃO CIVIL Tecnologia em Construção de Edifícios Disciplina: Construções em Concreto Armado TENSÕES DE FLEXÃO e de CISALHAMENTO EM VIGAS Notas de Aula: Edilberto Vitorino de
DIRETORIA ACADÊMICA DE CONSTRUÇÃO CIVIL Tecnologia em Construção de Edifícios Disciplina: Construções em Concreto Armado TENSÕES DE FLEXÃO e de CISALHAMENTO EM VIGAS Notas de Aula: Edilberto Vitorino de
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I. Capítulo 6 Flexão
 Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos.
 EME311 Mecânica dos Sólidos Objetivo do Curso: ornecer ao aluno os fundamentos teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos. 1-1 EME311
EME311 Mecânica dos Sólidos Objetivo do Curso: ornecer ao aluno os fundamentos teóricos necessários para se calcular as tensões e as deformações em elementos estruturais de projetos mecânicos. 1-1 EME311
Sumário: Tensões Tangenciais Resultantes do Esforço Transverso em Secções Rectangulares, em I e em T.
 Sumário e Objectivos Sumário: Tensões Tangenciais Resultantes do Esforço Transverso em Secções Rectangulares, em I e em T. Objectivos da Aula: Ser capaz de determinar a forma como se distribuem as tensões
Sumário e Objectivos Sumário: Tensões Tangenciais Resultantes do Esforço Transverso em Secções Rectangulares, em I e em T. Objectivos da Aula: Ser capaz de determinar a forma como se distribuem as tensões
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/8 Resistência dos ateriais 003/004 urso de Gestão e Engenharia Industrial 10ª ula e 11ª ula Duração - Horas Data - 3 de Novembro de 003 Sumário: onceito de viga. Vigas Isostáticas. Equações de Equilíbrio
1/8 Resistência dos ateriais 003/004 urso de Gestão e Engenharia Industrial 10ª ula e 11ª ula Duração - Horas Data - 3 de Novembro de 003 Sumário: onceito de viga. Vigas Isostáticas. Equações de Equilíbrio
PME Mecânica dos Sólidos I 4 a Lista de Exercícios
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal.
 CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
ENG285 4ª Unidade 1. Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais.
 ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Maio, 2016. 5 Análise e projeto de vigas em flexão Conteúdo Introdução Diagramas de Força Cortante e Momento Fletor Problema
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Maio, 2016. 5 Análise e projeto de vigas em flexão Conteúdo Introdução Diagramas de Força Cortante e Momento Fletor Problema
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
São as vigas que são fabricadas com mais de um material.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
PROBLEMA 1. Considere a estrutura plana representada na figura submetida ao carregamento indicado.
 PROBLEMA 1 Considere a estrutura plana representada na figura submetida ao carregamento indicado. E=00GPa a) Determine os esforços instalados na estrutura, indicando todos os valores necessários à sua
PROBLEMA 1 Considere a estrutura plana representada na figura submetida ao carregamento indicado. E=00GPa a) Determine os esforços instalados na estrutura, indicando todos os valores necessários à sua
Seção 7 (Flexão) - Exemplos dados em aula
 UFPR - MECÂNICA DOS SÓLIDOS I Seção 7 (Flexão) - Exemplos dados em aula Prof. Marcos S. Lenzi May 24, 2016 Exemplo 7.1 - Considere uma barra de aço com seção tranversal retangular conforme mostrado abaixo
UFPR - MECÂNICA DOS SÓLIDOS I Seção 7 (Flexão) - Exemplos dados em aula Prof. Marcos S. Lenzi May 24, 2016 Exemplo 7.1 - Considere uma barra de aço com seção tranversal retangular conforme mostrado abaixo
Universidade Politécnica
 Universidade Politécnica A POLITÉCNICA ESCOLA SUPERIOR DE GESTÃO CIÊNCIA E TECNOLOGIA Curso Semestre / Ano Ano Lectivo Tempo Disponível Variante Laboral ou Pós - Laboral Data Licenciatura em Engenharia
Universidade Politécnica A POLITÉCNICA ESCOLA SUPERIOR DE GESTÃO CIÊNCIA E TECNOLOGIA Curso Semestre / Ano Ano Lectivo Tempo Disponível Variante Laboral ou Pós - Laboral Data Licenciatura em Engenharia
CAPÍTULO VII FLEXÃO PURA
 1 CAPÍTULO VII FLEXÃO PURA I. VIGAS CARREGADAS TRANSVERSALMENTE Uma viga é um elemento linear de estrutura que apresenta a característica de possuir uma das dimensões (comprimento) muito maior do que as
1 CAPÍTULO VII FLEXÃO PURA I. VIGAS CARREGADAS TRANSVERSALMENTE Uma viga é um elemento linear de estrutura que apresenta a característica de possuir uma das dimensões (comprimento) muito maior do que as
UNIVERSIDADE POLITÉCNICA
 UNIVERSIDADE POITÉCNICA ANÁISE E DIMENSIONAMENTO DE VIGAS PAREDE. VERIFICACAO DA SEGURANÇA Índice Temático 1. Definição de vigas parede (REBAP - Artº 128º)... 1 2. Definição do Vão Teórico e Espessura
UNIVERSIDADE POITÉCNICA ANÁISE E DIMENSIONAMENTO DE VIGAS PAREDE. VERIFICACAO DA SEGURANÇA Índice Temático 1. Definição de vigas parede (REBAP - Artº 128º)... 1 2. Definição do Vão Teórico e Espessura
Mecânica dos Sólidos I Parte 3 Estado Plano de Tensão
 Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
(atualizado em 12/07/2014)
 ENG285 4ª Unidade 1 (atualizado em 12/07/2014) Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para
ENG285 4ª Unidade 1 (atualizado em 12/07/2014) Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para
Resistência dos Materiais, MA, IST,
 11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
11ª Aula Flexão Flexão elástica recta Define-se barra ou peça linear como todo o corpo cujo material se confina à vizinhança de uma linha do espaço a que se chama eixo. Segundo o Vocabulário de Teoria
ESTRUTURAS DE BETÃO ARMADO II
 ESTRUTURAS DE BETÃO ARMADO II ENUNCIADOS DOS EXERCÍCIOS DAS AULAS PRÁTICAS PROBLEMA 1.1 Considere o pavimento representado na figura e constituído por dois painéis de laje aligeirada de vigotas. O pavimento
ESTRUTURAS DE BETÃO ARMADO II ENUNCIADOS DOS EXERCÍCIOS DAS AULAS PRÁTICAS PROBLEMA 1.1 Considere o pavimento representado na figura e constituído por dois painéis de laje aligeirada de vigotas. O pavimento
para a = 110 cm, o momento torçor e a tensão no trecho A-B é dada por:
 Lista de torção livre Circular Fechada - Valério SA. - 2015 1 1) a. Determinar a dimensão a de modo a se ter a mesma tensão de cisalhamento máxima nos trechos B-C e C-D. b. Com tal dimensão pede-se a máxima
Lista de torção livre Circular Fechada - Valério SA. - 2015 1 1) a. Determinar a dimensão a de modo a se ter a mesma tensão de cisalhamento máxima nos trechos B-C e C-D. b. Com tal dimensão pede-se a máxima
CAPÍTULO VII FLEXÃO PURA
 59 CAPÍTULO VII FLEXÃO PURA I. ELEMENTOS DE VIGA São elementos lineares, isto é, que apresentam uma das dimensões (comprimento) muito maior do que as outras duas (dimensões da seção transversal) e que
59 CAPÍTULO VII FLEXÃO PURA I. ELEMENTOS DE VIGA São elementos lineares, isto é, que apresentam uma das dimensões (comprimento) muito maior do que as outras duas (dimensões da seção transversal) e que
Tensões de Cisalhamento em Vigas sob Flexão
 31 de outubro de 2016 (a) Peças sem acoplamento. (b) Peças com acoplamento. (a) Peças sem acoplamento. (b) Peças com acoplamento. Na primeira situação, mostrada na Figura (a), as peças trabalham de forma
31 de outubro de 2016 (a) Peças sem acoplamento. (b) Peças com acoplamento. (a) Peças sem acoplamento. (b) Peças com acoplamento. Na primeira situação, mostrada na Figura (a), as peças trabalham de forma
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano 2º Semestre 6 de Junho de 2011 Responsável: Prof. José Oliveira Pedro
 ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano º Semestre 6 de Junho de 0 Responsável: Prof. José Oliveira Pedro Identifique todas as folhas com o número e nome. Justifique adequadamente todas
ESTRUTURAS ESPECIAIS Mestrado em Engenharia Civil 5º Ano º Semestre 6 de Junho de 0 Responsável: Prof. José Oliveira Pedro Identifique todas as folhas com o número e nome. Justifique adequadamente todas
Disciplina de Estruturas Metálicas
 DECivil Departamento de Engenharia Civil e Arquitectura Disciplina de Estruturas Metálicas Aulas de Problemas Prof. Francisco Virtuoso Prof. Eduardo Pereira 2009/2010 Capítulo 7 Ligações em estruturas
DECivil Departamento de Engenharia Civil e Arquitectura Disciplina de Estruturas Metálicas Aulas de Problemas Prof. Francisco Virtuoso Prof. Eduardo Pereira 2009/2010 Capítulo 7 Ligações em estruturas
Exercícios de Resistência dos Materiais A - Área 3
 1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RETÊNCA DO MATERA Ferdinand P. Beer E. Russell Johnston, Jr. Carregamento Transversal Capítulo 5 Carregamento Transversal 5.1 ntrodução 5.2 Carregamento Transversal 5.3 Distribuição
Terceira Edição CAPÍTULO RETÊNCA DO MATERA Ferdinand P. Beer E. Russell Johnston, Jr. Carregamento Transversal Capítulo 5 Carregamento Transversal 5.1 ntrodução 5.2 Carregamento Transversal 5.3 Distribuição
NL AE. 9,72x10 m. Logo, os cabos atendem com folga o limite máximo estabelecido pois: 1,17x10 m. CD 9,72x10 1,17x10 8,55x10 m = 0,0855 cm
 Q1) Para os cálculos deste eercício serão usadas as seguintes unidades: força [kn], comprimento [m], tensão [kpa=kn/m ]. Os comparativos com os deslocamentos permissíveis serão feitos em [cm]. A equação
Q1) Para os cálculos deste eercício serão usadas as seguintes unidades: força [kn], comprimento [m], tensão [kpa=kn/m ]. Os comparativos com os deslocamentos permissíveis serão feitos em [cm]. A equação
Tensões associadas a esforços internos
 Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 00. Esforços axiais e tensões
Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 00. Esforços axiais e tensões
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CÍTULO RESISTÊNCI DOS MTERIIS erdinand. Beer E. Russell Johnston Jr. Conceito de Tensão Capítulo 1 Conceito de Tensão 1.1 Introdução 1.2 orças e Tensões; 1.3 orças iais: Tensões Normais;
Terceira Edição CÍTULO RESISTÊNCI DOS MTERIIS erdinand. Beer E. Russell Johnston Jr. Conceito de Tensão Capítulo 1 Conceito de Tensão 1.1 Introdução 1.2 orças e Tensões; 1.3 orças iais: Tensões Normais;
Sumário e Objectivos. Mecânica dos Sólidos 10ª Aula. Lúcia M.J.S. Dinis 2007/2008
 Sumário e Objectivos Sumário: onceito de viga. Vigas Isostáticas. Equações de Equilíbrio de Forças e Momentos. Reacções de poio. Esforços Transversos e Momentos Flectores. Esforço ial. Diagramas de Esforços.
Sumário e Objectivos Sumário: onceito de viga. Vigas Isostáticas. Equações de Equilíbrio de Forças e Momentos. Reacções de poio. Esforços Transversos e Momentos Flectores. Esforço ial. Diagramas de Esforços.
Programa de Pós-graduação em Engenharia Mecânica da UFABC. Disciplina: Fundamentos de Mecânica dos Sólidos II. Lista 2
 Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Programa de Pós-graduação em Engenharia Mecânica da UFABC Disciplina: Fundamentos de Mecânica dos Sólidos II Quadrimestre: 019- Prof. Juan Avila Lista 1) Para as duas estruturas mostradas abaixo, forneça
Mecânica dos Sólidos II Parte 1 (Revisão)
 Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: [email protected] Tel:
Departamento de Engenharia Mecânica Parte 1 (Revisão) Prof. Arthur M. B. Braga 214.2 ENG 174 Prof. Arthur M. B. Braga Secretaria do DEM ou Lab de Sensores a Fibra Óptica E-Mail: [email protected] Tel:
UNIVERSIDADE NOVA DE LISBOA FACULDADE DE CIÊNCIAS E TECNOLOGIA CURSO DE LICENCIATURA EM ENGENHARIA GEOLÓGICA
 UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
UNIVERSIAE NOVA E LISBOA FACULAE E CIÊNCIAS E TECNOLOGIA CURSO E LICENCIATURA EM ENGENHARIA GEOLÓGICA Resistência de Materiais (LEG): Exame de época normal Semestre par 005/006, 6 de Julho 006, duração
Estruturas de Aço e Madeira Aula 07 Vigas de Alma Cheia (2)
 Estruturas de Aço e Madeira Aula 07 Vigas de Alma Cheia (2) - Flexão em Vigas de Alma Não-Esbelta com Contenção Lateral - Tabela G.1 da NBR 8800 / 2008 ( FLA e FLM em vigas de alma não-esbelta ) - Esforço
Estruturas de Aço e Madeira Aula 07 Vigas de Alma Cheia (2) - Flexão em Vigas de Alma Não-Esbelta com Contenção Lateral - Tabela G.1 da NBR 8800 / 2008 ( FLA e FLM em vigas de alma não-esbelta ) - Esforço
Sumário: Flexão Combinada com Esforço Axial. Flexão combinada com torção.
 Sumário e Objectivos Sumário: Flexão Combinada com Esforço Axial. Flexão combinada com torção. Objectivos da Aula: Ser Capaz de calcular as Tensões tangenciais e normais quando existem combinação de esforços.
Sumário e Objectivos Sumário: Flexão Combinada com Esforço Axial. Flexão combinada com torção. Objectivos da Aula: Ser Capaz de calcular as Tensões tangenciais e normais quando existem combinação de esforços.
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil
 Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURAS DE BETÃO 2 11 de Julho de 2005 Recurso Duração: 3 h 1) (5.0 valores) A figura representa em corte transversal
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURAS DE BETÃO 2 11 de Julho de 2005 Recurso Duração: 3 h 1) (5.0 valores) A figura representa em corte transversal
Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial.
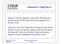 Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário: Flexão Combinada com Torção
 Sumário e Objectivos Sumário: Flexão Combinada com Torção Objectivos da Aula: Apreensão da Sobreposição de Efeitos nas vigas, no caso vertente apreensão da combinação de Flexão com Torção 1 Estruturas
Sumário e Objectivos Sumário: Flexão Combinada com Torção Objectivos da Aula: Apreensão da Sobreposição de Efeitos nas vigas, no caso vertente apreensão da combinação de Flexão com Torção 1 Estruturas
23.(UNIFESPA/UFPA/2016) A viga de madeira de seção I composta da Figura 5 é constituída por três peças de madeira de 6 x 16 centímetros.
 .(UNIFESPA/UFPA/016) A viga de madeira de seção I composta da Figura 5 é constituída por três peças de madeira de 6 x 16 centímetros. Figura 5 Viga de madeira de seção composta pregada. Dimensões em centímetros.
.(UNIFESPA/UFPA/016) A viga de madeira de seção I composta da Figura 5 é constituída por três peças de madeira de 6 x 16 centímetros. Figura 5 Viga de madeira de seção composta pregada. Dimensões em centímetros.
ESTRUTURAS DE BETÃO 2. 9 de Julho de 2007 Época de Recurso Duração: 3h
 Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE BETÃO 2 9 de Julho de 2007 Época de Recurso Duração: 3h Notas importantes: Responda com precisão e de forma
Faculdade de Engenharia da Universidade do Porto Departamento de Engenharia Civil ESTRUTURS DE BETÃO 2 9 de Julho de 2007 Época de Recurso Duração: 3h Notas importantes: Responda com precisão e de forma
ANÁLISE DE ESTRUTURAS I Ano lectivo de 2018/2019 1º Semestre L/2 L/2 L. E, h, ν uniformes. Figura 1 Figura 2
 Eercício 1 - Introdução à análise de lajes ANÁISE DE ESTRUTURAS I Ano lectivo de 018/019 1º Semestre Problema 1 (4 de Fevereiro de 003) Considere as lajes finas representadas nas figuras 1 e. / / E, h,
Eercício 1 - Introdução à análise de lajes ANÁISE DE ESTRUTURAS I Ano lectivo de 018/019 1º Semestre Problema 1 (4 de Fevereiro de 003) Considere as lajes finas representadas nas figuras 1 e. / / E, h,
Elementos de Engenharia Civil 2009/2010. Enunciados dos problemas *
 DEPARTAMENTO DE ENGENHARIA CIVIL E ARQUITECTURA SECÇÁO DE HIDRÁULICA E RECURSOS HÍDRICOS E AMBIENTAIS Elementos de Engenharia Civil 2009/2010 2 SEMESTRE Enunciados dos problemas * (módulo de Hidráulica)
DEPARTAMENTO DE ENGENHARIA CIVIL E ARQUITECTURA SECÇÁO DE HIDRÁULICA E RECURSOS HÍDRICOS E AMBIENTAIS Elementos de Engenharia Civil 2009/2010 2 SEMESTRE Enunciados dos problemas * (módulo de Hidráulica)
4ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO ANÁLISE DE TENSÕES
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
RESISTÊNCIA DE MATERIAIS
 UNIVERSIDDE DE ÉVOR ESOL DE IÊNI E TENOLOGI - DEPRTMENTO DE ENGENHRI RURL RESISTÊNI DE MTERIIS DEFORMÇÃO DEVID MOMENTO FLETOR INSTILIDDE EM OMPRESSÃO XIL (pontamentos para uso dos lunos) JOSÉ OLIVEIR PEÇ
UNIVERSIDDE DE ÉVOR ESOL DE IÊNI E TENOLOGI - DEPRTMENTO DE ENGENHRI RURL RESISTÊNI DE MTERIIS DEFORMÇÃO DEVID MOMENTO FLETOR INSTILIDDE EM OMPRESSÃO XIL (pontamentos para uso dos lunos) JOSÉ OLIVEIR PEÇ
5 CISALHAMENTO SIMPLES
 5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
Estruturas de Aço e Madeira Aula 15 Peças de Madeira em Flexão
 Estruturas de Aço e Madeira Aula 15 Peças de Madeira em Flexão - Flexão Simples Reta; - Flambagem Lateral; - Flexão Simples Oblíqua; Prof. Juliano J. Scremin 1 Aula 15 - Seção 1: Flexão Simples Reta 2
Estruturas de Aço e Madeira Aula 15 Peças de Madeira em Flexão - Flexão Simples Reta; - Flambagem Lateral; - Flexão Simples Oblíqua; Prof. Juliano J. Scremin 1 Aula 15 - Seção 1: Flexão Simples Reta 2
Aula 2 - Tensão Normal e de Cisalhamento.
 Aula 2 - Tensão Normal e de Cisalhamento. A - TENSÃO NORMAL MÉDIA 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a figura 1.17a. Se AB tiver diâmetro de 10 mm
Aula 2 - Tensão Normal e de Cisalhamento. A - TENSÃO NORMAL MÉDIA 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a figura 1.17a. Se AB tiver diâmetro de 10 mm
Enunciados Exames 2002/2003 Enunciados Exames 2003/2004 Enunciados Trabalhos 2003/2004
 INSTITUTO POLITÉCNICO E BRAGANÇA MECÂNICA APLICAA I Escola Superior de Tecnologia e de Gestão Curso: Engenharia Civil epartamento de Mecânica Aplicada Ano lectivo: 200/2005 Enunciados Eames 2002/2003 Enunciados
INSTITUTO POLITÉCNICO E BRAGANÇA MECÂNICA APLICAA I Escola Superior de Tecnologia e de Gestão Curso: Engenharia Civil epartamento de Mecânica Aplicada Ano lectivo: 200/2005 Enunciados Eames 2002/2003 Enunciados
DEPEC. Departamento de Engenharia Civil do CEFET/RJ ESTRUTURAS 4 ESTRUTURAS METÁLICAS. Aula 07 CORTANTE. Professor Ricardo Rodrigues de Araujo
 DEPEC Departamento de Engenharia Civil do CEFET/RJ ESTRUTURAS 4 ESTRUTURAS METÁLICAS Aula 07 CORTANTE Barras Prismáticas Submetidas ao Esforço Cortante No dimensionamento, deve ser atendida a seguinte
DEPEC Departamento de Engenharia Civil do CEFET/RJ ESTRUTURAS 4 ESTRUTURAS METÁLICAS Aula 07 CORTANTE Barras Prismáticas Submetidas ao Esforço Cortante No dimensionamento, deve ser atendida a seguinte
Sumário e Objectivos. Mecânica dos Sólidos 18ªAula. Lúcia M.J. S. Dinis 2007/2008
 Sumário e Objectivos Sumário: Método da Viga Conjugada. Objectivos da Aula: Ser capaz de determinar a flecha e a inclinação num ponto fazendo uso do Método da Viga Conjugada 1 Viga Flectida Estrutura de
Sumário e Objectivos Sumário: Método da Viga Conjugada. Objectivos da Aula: Ser capaz de determinar a flecha e a inclinação num ponto fazendo uso do Método da Viga Conjugada 1 Viga Flectida Estrutura de
Ministério da Educação UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Campus Pato Branco. Lista de Exercícios - Sapatas
 Lista de Exercícios - Sapatas 1 Dimensione uma sapata rígida para um pilar de dimensões 30 x 40, sendo dados: N k = 1020 kn; M k = 80 kn.m (em torno do eixo de maior inércia); A s,pilar = 10φ12,5 σ adm
Lista de Exercícios - Sapatas 1 Dimensione uma sapata rígida para um pilar de dimensões 30 x 40, sendo dados: N k = 1020 kn; M k = 80 kn.m (em torno do eixo de maior inércia); A s,pilar = 10φ12,5 σ adm
Flexão. Tensões na Flexão. e seu sentido é anti-horário. Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras.
 Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/16 Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial 3ª Aula Duração - 2 Horas Data - 29 de Setembro de 2003 Sumário: Equações de Equilíbrio de Forças. Equações de Equilíbrio
1/16 Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial 3ª Aula Duração - 2 Horas Data - 29 de Setembro de 2003 Sumário: Equações de Equilíbrio de Forças. Equações de Equilíbrio
Resistência dos Materiais Teoria 2ª Parte
 Condições de Equilíbrio Estático Interno Equilíbrio Estático Interno Analogamente ao estudado anteriormente para o Equilíbrio Estático Externo, o Interno tem um objetivo geral e comum de cada peça estrutural:
Condições de Equilíbrio Estático Interno Equilíbrio Estático Interno Analogamente ao estudado anteriormente para o Equilíbrio Estático Externo, o Interno tem um objetivo geral e comum de cada peça estrutural:
Exercícios de linha elástica - prof. Valério SA Universidade de São Paulo - USP
 São Paulo, dezembro de 2015. 1. Um pequeno veículo de peso P se move ao longo de uma viga de seção retangular de largura e altura de, respectivamente, 2 e 12 cm. Determinar a máxima distância s, conforme
São Paulo, dezembro de 2015. 1. Um pequeno veículo de peso P se move ao longo de uma viga de seção retangular de largura e altura de, respectivamente, 2 e 12 cm. Determinar a máxima distância s, conforme
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
LISTA DE EXERCÍCIOS ÁREA 1. Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02
 LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
Conceito de tensões Exercícios O Tensor de tensões Exercício. Tensões. 24 de agosto de Profa. Patrícia Habib Hallak Prof Afonso Lemonge.
 24 de agosto de 2016 Profa. Patrícia Habib Hallak Prof Afonso Lemonge Conceito de tensão Conceito de tensões 2 F 2 Com os conceitos da física a pressão P no interior do duto é constante e tem valor: P=
24 de agosto de 2016 Profa. Patrícia Habib Hallak Prof Afonso Lemonge Conceito de tensão Conceito de tensões 2 F 2 Com os conceitos da física a pressão P no interior do duto é constante e tem valor: P=
Professor: José Junio Lopes
 Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Problema resolvido 4.2
 Problema resolvido 4.2 A peça de máquina de ferro fundido é atendida por um momento M = 3 kn m. Sabendo-se que o módulo de elasticidade E = 165 GPa e desprezando os efeitos dos adoçamentos, determine (a)
Problema resolvido 4.2 A peça de máquina de ferro fundido é atendida por um momento M = 3 kn m. Sabendo-se que o módulo de elasticidade E = 165 GPa e desprezando os efeitos dos adoçamentos, determine (a)
ENG01140 Turma C (Prof. Alexandre Pacheco)
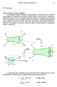 ENG01140 Turma C (rof. leandre acheco) 32 11 TENSÃO Tensão Normal e Tensão Cisalhante: Na ilustração a seguir, considera-se, primeiramente, a mesma parte seccionada do corpo rígido de forma genérica ilustrado
ENG01140 Turma C (rof. leandre acheco) 32 11 TENSÃO Tensão Normal e Tensão Cisalhante: Na ilustração a seguir, considera-se, primeiramente, a mesma parte seccionada do corpo rígido de forma genérica ilustrado
Resistência dos Materiais
 - Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
- Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I
 LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas
 RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas Prof. José Junio Lopes BIBLIOGRAFIA BÁSICA HIBBELER, Russell Charles. Resistência dos Materiais ed. São Paulo: Pearson Prentice Hall, 2009. 1 - CONCEITOS FUNDAMENTAIS
RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas Prof. José Junio Lopes BIBLIOGRAFIA BÁSICA HIBBELER, Russell Charles. Resistência dos Materiais ed. São Paulo: Pearson Prentice Hall, 2009. 1 - CONCEITOS FUNDAMENTAIS
1ª Lista de exercícios Resistência dos Materiais IV Prof. Luciano Lima (Retirada do livro Resistência dos materiais, Beer & Russel, 3ª edição)
 11.3 Duas barras rígidas AC e BC são conectadas a uma mola de constante k, como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica P cr para o sistema.
11.3 Duas barras rígidas AC e BC são conectadas a uma mola de constante k, como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica P cr para o sistema.
6.00 m. z (y) 3.00 m. 920 kn. 15 kn/m. Secção transversal do pilar A-B. (x) SHS 200x150x8 mm 1/29
 VIGA-OLUA Exemo : onsidere a viga-coluna A-B de suporte de um balanço B- representado na Figura abaixo A coluna é engastada na seção da base sendo a seção do topo (seção B) livre de rodar mas impedida
VIGA-OLUA Exemo : onsidere a viga-coluna A-B de suporte de um balanço B- representado na Figura abaixo A coluna é engastada na seção da base sendo a seção do topo (seção B) livre de rodar mas impedida
Conteúdo. Resistência dos Materiais. Prof. Peterson Jaeger. 3. Concentração de tensões de tração. APOSTILA Versão 2013
 Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
