Controle Ótimo - Aula 1 (Prova do Algoritmo da PD e Exemplo 1)
|
|
|
- Lúcia Caires Raminhos
- 6 Há anos
- Visualizações:
Transcrição
1 1 Controle Ótimo - Aula 1 (Prova do Algoritmo da PD e Exemplo 1) Adriano Almeida Gonçalves Siqueira e Marco H. Terra Algoritmo da Programação Dinâmica: Para cada condição inicial x 0, o custo ótimo J (x 0 ) do problema básico é igual a J 0 (x 0 ), o último passo do seguinte algoritmo que evolui de modo reverso no tempo de N 1 até 0 : Passo N: J N (x N ) := g N (x N ) para todo x N S k Passo k: J k (x k ) = min uk U k (x k ){E wk {g k (x k, u k, w k ) + J k+1 (f k (x k, u k, w k ))}}, k = N 1,..., 0 Passo 0: J (x 0 ) = J 0 (x 0 ) Se u k = µ k (x k) minimiza o lado direito da equação do passo k, a política π = {µ 0, µ 1,..., µ } é ótima Prova: (I) Notação: Para qualquer política admissível π = {µ 0, µ 1,..., µ } e para cada k = 0, 1,..., N 1 denote: Políticas de controle admissíveis do instante k ao instante final N: Distúrbios do instante k ao instante final N: π k := {µ k, µ k+1,..., µ } d k := {w k, w k+1,..., w } Custo ótimo para o problema que começa no estado x k =x k no instante k e termina no instante N: { } J k (x k) := min π ke d k g N (x N ) + i=k Custo ótimo para o problema que começa no estado x N no instante final N: J N (x N) := g N (x N ) (II) As funções de custo ótimas J k são exatamente as funções J k computadas pelo Algoritmo da Programação Dinâmica para todo k. Prova por indução: A hipótese de indução vale para N:
2 2 Segue pelas definições que J N = g N = J N. Suponha que a hipótese de indução valha para k + 1, ou seja, suponha que a função custo ótima J k+1 seja dada exatamente pela função J k+1 computada pelo Algoritmo da Programação Dinâmica, ou seja, temos J k+1 (x k+1) = J k+1 (x k+1 ), para todo x k+1 S k+1 Vamos mostrar que a hipótese é válida para k: Fixe x k S k e note que π k = {µ k, π k+1 } e d k = {w k, d k+1 }. Temos por definição: J k (x k ) :=min π ke dk {g N (x N ) + =min {µk,π k+1 }E {wk,d k+1 } { i=k } g k (x k, µ k (x k ), w k ) + g N (x N ) + i=k+1 Sendo a distribuição de w k independente da distribuição de d k+1 := {w k+1,..., w }, J k (x k) = min {µk,π k+1 }E wk {g k (x k, µ k (x k ), w k ) + E d k+1 [ g N (x N ) + i=k+1 Como o termo g k (x k, µ k (x k ), w k ) não depende da política de controle futura π k+1 J k (x k ) = min µk E wk {g k (x k, µ k (x k ), w k ) + min π k+1e d k+1 Segue da definição do custo ótimo a partir do instante k + 1 que [ g N (x N ) + i=k+1 J k (x k ) = min µk E wk { gk (x k, µ k (x k ), w k ) + J k+1 (f k (x k, µ k (x k ), w k )) } Sendo válida a hipótese para k + 1 J k (x k) = min µk E wk {g k (x k, µ k (x k ), w k ) + J k+1 (f k (x k, µ k (x k ), w k ))} } Sendo x k fixo, variar a função: µ k : S k U k (x k ), x k u k é o mesmo que variar u k, assim, ]} ]} J k (x k ) =min uk U k (x k )E wk {g k (x k, u k, w k ) + J k+1 (f k (x k, u k, w k ))} =J k (x k ) Exemplo1: Problema de Rota de Avião com gasto mínimo de combustível [Lewis p.294, ex 4.1-1] Um avião pode voar da esquerda para a direita ao longo dos caminhos mostrados na figura 1. As intercecções a,b,c,... representam cidades. Os números representam o combustível requerido para completar cada caminho (custo para cada instante g k (x k, u k )). A cada instante k pode-se decidir movimentarse para o próximo estágio k + 1 indo para cima (u k = +1), ou indo para baixo (u k = 1).
3 3 Fig. 1. Problema de Rota Ótima. O problema é determinar o caminho que o avião deve percorrer partindo de a e chegando a i com gasto mínimo de combustível. Vamos colocar o problema na forma padrão ([B95]p.10) 1) O estado corrente é o nó onde estamos fazendo a decisão corrente. Assim, o estado inicial é x 0 = a. No instante k = 1, o estado pode ser x 1 = b ou x 1 = d. Pela figura, o espaço de estados para cada instante k é dado por S 0 = {a}, S 1 = {b, d}, S 2 = {c, e, g}, S 3 = {f, h}, S 4 = {i} 2) A variável de decisão (controle) u k a ser selecionada no instante k pertence ao espaço C k = {+1, 1}. Note que o controle u k é retringido a tomar valores em um sub-conjunto U k (x k ) C k que depende do instante k e do valor corrente do estado x k. Por exemplo, para k = 2, x 2 = c e assim, temos U 2 (x 2 = c) = { 1} C 1 = {+1, 1}. 3) O sistema dinâmico x k+1 = f k (x k, u k ) pode ser dado de forma tabular pelos dados contidos na figura (por exemplo, é evidente que x 2 = c quando x 1 = b e u 1 = +1). 4) O custo a cada instante g k (x k, u k ) pode ser dado de forma tabular pelos dados contidos na figura (por exemplo, é evidente que g 2 (x 2 = b, u 2 = 1) = 2). Podemos determinar a rota ótima de x 0 = a para x N = i fazendo-se comparações com todos os possíveis caminhos u = (u 0,..., u ) de x 0 = a para x N = i conforme a expressão: J (x 0 = a) = min u=(u0,...,u ){g N (x N ) + A solução por este procedimento requer um grande número de cálculos. k=0 g k (x k, u k )} Baseados no princípio de otimalidade de Bellman, vamos aplicar o algorítmo da Programação Dinâmica para reduzir o número de cálculos necessários (por restringir o número de decisões a serem tomadas).
4 4 Comece com k = N = 4. Nenhuma decisão é necessária aqui. Assim, J 4 (x 4 = i) = g 4 (x 4 = i) = 0. k = N 1 = 3 O espaço de estados é S 3 = {f, h}. Se x 3 = f o custo ótimo é e a lei de controle ótimo é J 3 (x 3 = f) =min u3 U 3 (x 3 =f){g 3 (x 3 = f, u 3 ) + J 4 (f 3 (x 3 = f, u 3 ))} =g 3 (x 3 = f, u 3 = 1) = 4 µ 3 (x 3 = f) =arg{min u3 U 3 (x 3 =f){g 3 (x 3 = f, u 3 ) + J 4 (f 3 (x 3 = f, u 3 ))}} = 1 Se x 3 = h o custo ótimo é J 3 (x 3 = h) =min u3 U 3 (x 3 =h){g 3 (x 3 = h, u 3 ) + J 4 (f 3 (x 3 = h, u 3 ))} =g 3 (x 3 = h, u 3 = 1) = 4 e a lei de controle ótimo é µ 3 (x 3 = h) = 1. Assim, a função J 3 : S 3 R + e a lei de controle admissível µ 3 : S 3 C 3 são dados pela tabela x 3 J 3 (x 3 ) µ 3 (x 3 ) f 4 1 h 2 +1 k = 2 O espaço de estados é S 2 = {c, e, g}. Se x 2 = c o custo ótimo é J 2 (x 2 = c) =min u2 U 2 (x 2 =c){g 2 (x 2 = c, u 2 ) + J 3 (f 2 (x 2 = c, u 2 ))} e a lei de controle ótimo é µ 2 (x 2 = c) = 1. Se x 2 = e o custo ótimo é =g 2 (x 2 = c, u 2 = 1) + J 3 (f) = = 7
5 5 J 2 (x 2 = e) =min u2 U 2 (x 2 =e){g 2 (x 2 = e, u 2 ) + J 3 (f 2 (x 2 = e, u 2 ))} =min{g 2 (x 2 = e, u 2 = 1) + J 3 (f 2 (x 2 = e, u 2 = 1)), g 2 (x 2 = e, u 2 = 1) + J 3 (f 2 (x 2 = e, u 2 = 1))} =min{g 2 (x 2 = e, u 2 = 1) + J 3 (f), g 2 (x 2 = e, u 2 = 1) + J 3 (h)} =min{3 + 4, 2 + 2} = 4 e a lei de controle ótimo é µ 2 (x 2 = e) = 1. Se x 2 = g o custo ótimo é J 2 (x 2 = g) =min u2 U 2 (x 2 =g){g 2 (x 2 = g, u 2 ) + J 3 (f 2 (x 2 = g, u 2 ))} e a lei de controle ótimo é µ 2 (x 2 = g) = +1. =g 2 (x 2 = g, u 2 = 1) + J 3 (h) = = 6 Assim, a função J 2 : S 2 R + e a lei de controle admissível µ 2 : S 2 C 2 são dados pela tabela x 2 J 2 (x 2 ) µ 2 (x 2) c 7 1 e 4 1 g 6 +1 k = 1 O espaço de estados é S 1 = {b, d}. Se x 1 = b o custo ótimo é J 1 (x 1 = b) =min u1 U 1 (x 1 =b){g 1 (x 1 = b, u 1 ) + J 2 (f 1 (x 1 = b, u 1 ))} =min{g 1 (x 1 = b, u 1 = 1) + J 2 (f 1 (x 1 = b, u 1 = 1)), g 1 (x 1 = b, u 1 = 1) + J 2 (f 1 (x 1 = b, u 1 = 1))} =min{g 1 (x 1 = b, u 1 = 1) + J 2 (c), g 1 (x 1 = b, u 1 = 1) + J 2 (e)} =min{2 + 7, 1 + 4} = 5 e a lei de controle ótimo é µ 1 (x 1 = b) = 1. Se x 1 = d o custo ótimo é J 1 (x 1 = d) =min u1 U 1 (x 1 =d){g 1 (x 1 = d, u 1 ) + J 2 (f 1 (x 1 = d, u 1 ))} =min{g 1 (x 1 = d, u 1 = 1) + J 2 (e), g 1 (x 1 = d, u 1 = 1) + J 2 (g)} =min{3 + 4, 2 + 6} = 7 e a lei de controle ótimo é µ 1 (x 1 = d) = +1. Assim, a função J 1 : S 1 R + e a lei de controle admissível µ 1 : S 1 C 1 são dados pela tabela
6 6 x 1 J 1 (x 1 ) µ 1 (x 1) b 5 1 d 7 +1 k = 0 O espaço de estados é S 0 = {a}. O custo ótimo é J 0 (x 0 = a) =min u0 U 0 (x 0 =a){g 0 (x 0 = a, u 0 ) + J 1 (f 0 (x 0 = a, u 0 ))} =min{g 0 (x 0 = a, u 0 = 1) + J 1 (b), g 0 (x 0 = a, u 0 = 1) + J 1 (d)} =min{3 + 5, 1 + 7} = 8 e a lei de controle ótimo não é única e podemos fazer µ 1 0 (x 0 = a) = +1 ou µ 2 0 (x 0 = a) = 1. Assim, pelo algoritmo da programação dinâmica chegamos à solução ótima do problema original J (x 0 = a) = J 0 (x 0 = a) = 8 e temos duas políticas (leis de realimentação) ótimas π i = {µ i 0, µ 1, µ 2, µ 3 } Em particular, percorrendo a partir de x 0 = a pela política ótima obtemos um sinal de controle ótimo em malha aberta e a correspondente trajetória ótima u = ( u 0,..., u ) = (u 0, u 1, u 2, u 3) = (+1, 1, 1, +1) x = (a, b, e, h, i) Para o outro sinal de controle ótimo em malha aberta e a correspondente trajetória ótima u = (u 0, u 1, u 2, u 3 ) = ( 1, +1, 1, +1) x = (a, d, e, h, i)
Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4)
 Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4) Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Sistemas dinâmicos discretos no tempo O Problema
Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4) Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Sistemas dinâmicos discretos no tempo O Problema
Controle Ótimo - Aula 10 Princípio do Mínimo de Pontryagin
 Controle Ótimo - Aula 10 Princípio do Mínimo de Pontryagin Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos O problema de controle ótimo
Controle Ótimo - Aula 10 Princípio do Mínimo de Pontryagin Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos O problema de controle ótimo
Controle Ótimo - Aula 8 Equação de Hamilton-Jacobi
 Controle Ótimo - Aula 8 Equação de Hamilton-Jacobi Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos O problema de controle ótimo Considere
Controle Ótimo - Aula 8 Equação de Hamilton-Jacobi Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos O problema de controle ótimo Considere
Controle Ótimo - Aula 6 Exemplos e Exercícios
 Controle Ótimo - Aula 6 Exemplos e Exercícios Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Probabilidades Probabilidade: número entre
Controle Ótimo - Aula 6 Exemplos e Exercícios Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Probabilidades Probabilidade: número entre
GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira
 Ciência da Computação GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira Algoritmo de Bellman-Ford Arestas com valores negativos podem parecer inúteis, mas elas podem
Ciência da Computação GRAFOS Aula 07 Algoritmos de Caminho Mínimo: Bellman-Ford / Floyd-Warshall Max Pereira Algoritmo de Bellman-Ford Arestas com valores negativos podem parecer inúteis, mas elas podem
No circuito abaixo determinar as correntes nos ramos e seus verdadeiros sentidos.
 No circuito abaixo determinar as correntes nos ramos e seus verdadeiros sentidos. Dados do problema Resistores R 1 = Ω; R = Ω R = Ω; R 4 = Ω R = Ω; R 6 = Ω; R 7 = Ω; R 8 = Ω. f.e.m. das pilhas E 1 = V;
No circuito abaixo determinar as correntes nos ramos e seus verdadeiros sentidos. Dados do problema Resistores R 1 = Ω; R = Ω R = Ω; R 4 = Ω R = Ω; R 6 = Ω; R 7 = Ω; R 8 = Ω. f.e.m. das pilhas E 1 = V;
Programação Dinâmica: Modelos Determinísticos
 Programação Dinâmica: Modelos Determinísticos Prof. Fernando Augusto Silva Marins Departamento de Produção Faculdade de Engenharia Campus de Guaratinguetá UNESP www.feg.unesp.br/~fmarins fmarins@feg.unesp.br
Programação Dinâmica: Modelos Determinísticos Prof. Fernando Augusto Silva Marins Departamento de Produção Faculdade de Engenharia Campus de Guaratinguetá UNESP www.feg.unesp.br/~fmarins fmarins@feg.unesp.br
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
5 Análise de Sensibilidade
 MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
apenas os caminhos que passam só por vértices em C, exceto, talvez, o próprio v A Figura 1 a seguir ilustra o significado do conjunto C edovalordist.
 CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Em 1970, Bellman e Zadeh (Bellman, 1970) apresentaram a otimização IX]]\, que é um conjunto de técnicas utilizadas em problemas de otimização com
![Em 1970, Bellman e Zadeh (Bellman, 1970) apresentaram a otimização IX]]\, que é um conjunto de técnicas utilizadas em problemas de otimização com Em 1970, Bellman e Zadeh (Bellman, 1970) apresentaram a otimização IX]]\, que é um conjunto de técnicas utilizadas em problemas de otimização com](/thumbs/88/116982484.jpg) 4 ±0('/$ 5'd Muito já foi feito no desenvolvimento de metodologias para a resolução de problemas de programação linear IX]]\. Entretanto a grande parte dos trabalhos apresentados procurou obter uma solução
4 ±0('/$ 5'd Muito já foi feito no desenvolvimento de metodologias para a resolução de problemas de programação linear IX]]\. Entretanto a grande parte dos trabalhos apresentados procurou obter uma solução
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
Eletromagnetismo - Instituto de Pesquisas Científicas AULA 09 CIRCUITO RC
 ELETROMAGNETISMO AULA 09 CIRCUITO RC A PONTE DE WHITESTONE Antes de inserirmos um novo elemento em nosso circuito vamos estudar um caso especial de montagem (de circuito) que nos auxilia na determinação
ELETROMAGNETISMO AULA 09 CIRCUITO RC A PONTE DE WHITESTONE Antes de inserirmos um novo elemento em nosso circuito vamos estudar um caso especial de montagem (de circuito) que nos auxilia na determinação
ˆLψ(x) = f(x), (1) Se for possível encontrar a função de Green G(x, x ) que satisfaz a equação acima, então a solução da Eq.
 Notas sobre Funções de Green FMA 43 Prof. Luís Raul Weber Abramo Departamento de Física Matemática Instituto de Física USP Introdução geral às funções de Green A função de Green (G. Green, c. 828) é uma
Notas sobre Funções de Green FMA 43 Prof. Luís Raul Weber Abramo Departamento de Física Matemática Instituto de Física USP Introdução geral às funções de Green A função de Green (G. Green, c. 828) é uma
AULA 08 CIRCUITOS E LEIS DE KIRCHHOFF. Eletromagnetismo - Instituto de Pesquisas Científicas
 ELETROMAGNETISMO AULA 08 CIRCUITOS E LEIS DE KIRCHHOFF OS ELEMENTOS DO CIRCUITO Sabemos que o circuito é o caminho percorrido pela corrente elétrica. Nessa aula iremos analisar esses circuitos. Mas antes
ELETROMAGNETISMO AULA 08 CIRCUITOS E LEIS DE KIRCHHOFF OS ELEMENTOS DO CIRCUITO Sabemos que o circuito é o caminho percorrido pela corrente elétrica. Nessa aula iremos analisar esses circuitos. Mas antes
CÁLCULO I. Apresentar e aplicar a Regra de L'Hospital.
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o : Limites Innitos e no Innito. Assíntotas. Regra de L'Hospital Objetivos da Aula Denir ite no innito e ites innitos; Apresentar alguns tipos
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o : Limites Innitos e no Innito. Assíntotas. Regra de L'Hospital Objetivos da Aula Denir ite no innito e ites innitos; Apresentar alguns tipos
Método Simplex. Marina Andretta ICMC-USP. 19 de outubro de 2016
 Método Simplex Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização linear
Método Simplex Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização linear
Árvore Binária de Busca Ótima
 MAC 5710 - Estruturas de Dados - 2008 Referência bibliográfica Os slides sobre este assunto são parcialmente baseados nas seções sobre árvore binária de busca ótima do capítulo 4 do livro N. Wirth. Algorithms
MAC 5710 - Estruturas de Dados - 2008 Referência bibliográfica Os slides sobre este assunto são parcialmente baseados nas seções sobre árvore binária de busca ótima do capítulo 4 do livro N. Wirth. Algorithms
Programação Linear/Inteira - Aula 5
 Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
Jogos de Anti-Coordenação e Colorações Estáveis em Grafos. Renato Lui Geh NUSP:
 Jogos de Anti-Coordenação e Colorações Estáveis em Grafos Renato Lui Geh NUSP:8536030 Introdução Jogos de coordenação: Classe de jogos em que jogadores jogam cooperativamente. Jogador i fazer a mesma ação
Jogos de Anti-Coordenação e Colorações Estáveis em Grafos Renato Lui Geh NUSP:8536030 Introdução Jogos de coordenação: Classe de jogos em que jogadores jogam cooperativamente. Jogador i fazer a mesma ação
AULA 13 PROJETO E ANÁLISE DE ALGORITMOS. Problema do caminho mais curto de uma única origem em grafos Karina Valdivia Delgado
 AULA 13 PROJETO E ANÁLISE DE ALGORITMOS Problema do caminho mais curto de uma única origem em grafos Karina Valdivia Delgado Roteiro Motivação Relaxamento Algoritmo de Dijkstra Motivação Suponha que você
AULA 13 PROJETO E ANÁLISE DE ALGORITMOS Problema do caminho mais curto de uma única origem em grafos Karina Valdivia Delgado Roteiro Motivação Relaxamento Algoritmo de Dijkstra Motivação Suponha que você
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
2.1. Construção da Pista
 2 Malha de Controle Para que se possa controlar um dado sistema é necessário observar e medir suas variáveis de saída para determinar o sinal de controle, que deve ser aplicado ao sistema a cada instante.
2 Malha de Controle Para que se possa controlar um dado sistema é necessário observar e medir suas variáveis de saída para determinar o sinal de controle, que deve ser aplicado ao sistema a cada instante.
Programação Dinâmica. Prof. Anderson Almeida Ferreira. Adaptado do material elaborado por Andrea Iabrudi Tavares
 Programação Dinâmica Prof. Anderson Almeida Ferreira Adaptado do material elaborado por Andrea Iabrudi Tavares Programação Dinâmica 1950, Bellman Evitar recálculos dos subproblemas em comum Menor para
Programação Dinâmica Prof. Anderson Almeida Ferreira Adaptado do material elaborado por Andrea Iabrudi Tavares Programação Dinâmica 1950, Bellman Evitar recálculos dos subproblemas em comum Menor para
CÁLCULO I. Efetuar transformações no gráco de uma função. Aplicando esse teste às seguintes funções, notamos que
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 03: Funções Inversas e Compostas.Transformações no Gráco de uma Função. Objetivos da Aula Denir função bijetora e função
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 03: Funções Inversas e Compostas.Transformações no Gráco de uma Função. Objetivos da Aula Denir função bijetora e função
Álgebra Linear I - Aula 6. Roteiro
 Álgebra Linear I - Aula 6 1. Equação cartesiana do plano. 2. Equação cartesiana da reta. 3. Posições relativas: de duas retas, de uma reta e um plano, de dois planos. Roteiro 1 Equação cartesiana do plano
Álgebra Linear I - Aula 6 1. Equação cartesiana do plano. 2. Equação cartesiana da reta. 3. Posições relativas: de duas retas, de uma reta e um plano, de dois planos. Roteiro 1 Equação cartesiana do plano
Exemplo: Maximização de lucros em uma chocolateria que produz os seguintes produtos: (1) Chocolate Pyramide (2) Chocolate Pyramide Nuit
 Universidade Tecnológica Federal do Paraná Professor Murilo V. G. da Silva Notas de aula Estrutura de Dados 2 (Aula 09) Conteúdos da Aula: [DPV06 7.1, 7.2, 7.3] [Observação: Estas notas de aula são apenas
Universidade Tecnológica Federal do Paraná Professor Murilo V. G. da Silva Notas de aula Estrutura de Dados 2 (Aula 09) Conteúdos da Aula: [DPV06 7.1, 7.2, 7.3] [Observação: Estas notas de aula são apenas
Formulação de Programação Linear Inteira para o Problema de Particionamento em Conjuntos Convexos
 Formulação de Programação Linear Inteira para o Problema de Particionamento em Conjuntos Convexos Teobaldo L. Bulhões Júnior a a Instituto de Computação, Universidade Federal Fluminense, Niterói, RJ, Brazil
Formulação de Programação Linear Inteira para o Problema de Particionamento em Conjuntos Convexos Teobaldo L. Bulhões Júnior a a Instituto de Computação, Universidade Federal Fluminense, Niterói, RJ, Brazil
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 20 DE JULHO 2018 CADERNO 1
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 0 DE JULHO 08 CADERNO... P00/00 Como se trata de uma distribuição normal temos que: ( ) 0,9545. P µ σ
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 0 DE JULHO 08 CADERNO... P00/00 Como se trata de uma distribuição normal temos que: ( ) 0,9545. P µ σ
Programação Dinâmica. Prof. Anderson Almeida Ferreira
 Programação Dinâmica Prof. Anderson Almeida Ferreira Programação Dinâmica 1950, Bellman Evitar recálculos dos subproblemas em comum Menor para maior (bottom-up) Tabelas ou memorização É uma técnica de
Programação Dinâmica Prof. Anderson Almeida Ferreira Programação Dinâmica 1950, Bellman Evitar recálculos dos subproblemas em comum Menor para maior (bottom-up) Tabelas ou memorização É uma técnica de
Distribuição Normal. Prof. Herondino
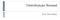 Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
No circuito abaixo determinar as correntes nos ramos, seus verdadeiros sentidos e quais elementos são geradores e receptores.
 No circuito abaixo determinar as correntes nos ramos, seus verdadeiros sentidos e quais elementos são geradores e receptores. Dados do problema Resistores: R 1 = 0, Ω; R = 0, Ω; R 3 = 1 Ω; R 4 = 0, Ω;
No circuito abaixo determinar as correntes nos ramos, seus verdadeiros sentidos e quais elementos são geradores e receptores. Dados do problema Resistores: R 1 = 0, Ω; R = 0, Ω; R 3 = 1 Ω; R 4 = 0, Ω;
Escalonamento em uma máquina
 Capítulo 4 Escalonamento em uma máquina Veremos neste capítulo vários problemas relacionados ao escalonamento em uma máquina. Estes problemas são importantes, pois além de fornecerem idéias para problemas
Capítulo 4 Escalonamento em uma máquina Veremos neste capítulo vários problemas relacionados ao escalonamento em uma máquina. Estes problemas são importantes, pois além de fornecerem idéias para problemas
lnteligência Artificial Introdução ao Processo Decisório de Markov
 lnteligência Artificial Introdução ao Processo Decisório de Markov Aprendizado - paradigmas Aprendizado supervisionado O crítico comunica a EA o erro relativo entre a ação que deve ser tomada idealmente
lnteligência Artificial Introdução ao Processo Decisório de Markov Aprendizado - paradigmas Aprendizado supervisionado O crítico comunica a EA o erro relativo entre a ação que deve ser tomada idealmente
Programação Dinâmica (incompleto!!!!!)
 Departamento de Engenharia de Produção UFPR 108 Programação Dinâmica (incompleto!!!!!) A programação dinâmica-pd (incluindo o nome) foi introduzida por Richard Bellman na década de 1950. A PD é uma abordagem
Departamento de Engenharia de Produção UFPR 108 Programação Dinâmica (incompleto!!!!!) A programação dinâmica-pd (incluindo o nome) foi introduzida por Richard Bellman na década de 1950. A PD é uma abordagem
RESOLUÇÃO DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA Considere a soma. S n = n 2 n 1
 DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA 1 1. Considere a soma S n = 1 2 0 + 2 2 1 + 3 2 2 + + n 2 n 1. Mostre, por indução finita, que S n = (n 1)2 n + 1. Indique claramente a base da indução, a
DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA 1 1. Considere a soma S n = 1 2 0 + 2 2 1 + 3 2 2 + + n 2 n 1. Mostre, por indução finita, que S n = (n 1)2 n + 1. Indique claramente a base da indução, a
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 20 DE JULHO 2018 CADERNO 1
 Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 500-36 Lisboa Tel.: +35 76 36 90 / 7 03 77 Fax: +35 76 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 7-A 500-36 Lisboa Tel.: +35 76 36 90 / 7 03 77 Fax: +35 76 64 4 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA
Aula Exemplos e aplicações - continuação. Exemplo 8. Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos.
 Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Aula 1 Nesta aula continuamos com mais exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações - continuação Exemplo 8 Considere o plano π : x + y + z = 3 e a reta r paralela ao vetor v =
Aprendizado por Reforço
 Aprendizado por Reforço Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aprendizado por Reforço 2. Q-Learning 3. SARSA 4. Outras ideias 1 Aprendizado por Reforço Problemas de decisão
Aprendizado por Reforço Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aprendizado por Reforço 2. Q-Learning 3. SARSA 4. Outras ideias 1 Aprendizado por Reforço Problemas de decisão
Aula 11. Cristiano Quevedo Andrea 1. Curitiba, Outubro de DAELT - Departamento Acadêmico de Eletrotécnica
 Aula 11 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro de 2011. Resumo 1 Introdução - Lugar das Raízes
Aula 11 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro de 2011. Resumo 1 Introdução - Lugar das Raízes
Projeto e Análise de Algoritmos Projeto de Algoritmos Programação Dinâmica (continuação) Prof. Humberto Brandão
 Projeto e Análise de Algoritmos Projeto de Algoritmos (continuação) Prof. Humberto Brandão humberto@dcc.ufmg.br aula disponível no site: http://www.bcc.unifal-mg.edu.br/~humberto/ Universidade Federal
Projeto e Análise de Algoritmos Projeto de Algoritmos (continuação) Prof. Humberto Brandão humberto@dcc.ufmg.br aula disponível no site: http://www.bcc.unifal-mg.edu.br/~humberto/ Universidade Federal
CINEMÁTICA. Introdução
 CINEMÁTICA Introdução Cinemática Parte da Física que estuda o movimento sem preocupar-se com as causas que deram origem ou interferem no movimento. Ponto material ou partícula Dizemos que um corpo é uma
CINEMÁTICA Introdução Cinemática Parte da Física que estuda o movimento sem preocupar-se com as causas que deram origem ou interferem no movimento. Ponto material ou partícula Dizemos que um corpo é uma
Aula 22: Formulações com número exponencial de variáveis
 Aula 22: Formulações com número exponencial de variáveis Otimização Linear e Inteira Túlio Toffolo http://www.toffolo.com.br BCC464 / PCC174 2018/2 Departamento de Computação UFOP Aula de Hoje 1 Correção
Aula 22: Formulações com número exponencial de variáveis Otimização Linear e Inteira Túlio Toffolo http://www.toffolo.com.br BCC464 / PCC174 2018/2 Departamento de Computação UFOP Aula de Hoje 1 Correção
LISTA EXTRA DE EXERCÍCIOS MAT /I
 LISTA EXTRA DE EXERCÍCIOS MAT 008/I. Dados os vetores v = (0,, 3), v = (-, 0, 4) e v 3 = (, -, 0), efetuar as operações indicadas: (a) v 3-4v R.: (4,-,-6) (b) v -3v +v 3 R.: (3,0,-6). Determine: (a) x,
LISTA EXTRA DE EXERCÍCIOS MAT 008/I. Dados os vetores v = (0,, 3), v = (-, 0, 4) e v 3 = (, -, 0), efetuar as operações indicadas: (a) v 3-4v R.: (4,-,-6) (b) v -3v +v 3 R.: (3,0,-6). Determine: (a) x,
Pesquisa Operacional
 Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
SEM561 - SISTEMAS DE CONTROLE
 SEM561 - SISTEMAS DE CONTROLE Adriano Almeida Gonçalves Siqueira Aula 1 - Introdução a Sistemas de Controle Índice O que é controle? Exemplo 1: componentes de um sistema de controle Exemplo 2: malha aberta
SEM561 - SISTEMAS DE CONTROLE Adriano Almeida Gonçalves Siqueira Aula 1 - Introdução a Sistemas de Controle Índice O que é controle? Exemplo 1: componentes de um sistema de controle Exemplo 2: malha aberta
SEM561 - SISTEMAS DE CONTROLE
 SEM561 - SISTEMAS DE CONTROLE Adriano Almeida Gonçalves Siqueira Aula 1 - Introdução a Sistemas de Controle Índice O que é controle? Exemplo 1: componentes de um sistema de controle Exemplo 2: malha aberta
SEM561 - SISTEMAS DE CONTROLE Adriano Almeida Gonçalves Siqueira Aula 1 - Introdução a Sistemas de Controle Índice O que é controle? Exemplo 1: componentes de um sistema de controle Exemplo 2: malha aberta
Estratégias informadas de Busca. February 19, 2018
 Estratégias informadas de Busca February 19, 2018 Busca de Soluções: Métodos Informados ˆ Utilizam conhecimento específico do problema para encontrar a solução ˆ algoritmo geral de busca somente permite
Estratégias informadas de Busca February 19, 2018 Busca de Soluções: Métodos Informados ˆ Utilizam conhecimento específico do problema para encontrar a solução ˆ algoritmo geral de busca somente permite
Teoria de dualidade. Marina Andretta ICMC-USP. 19 de outubro de 2016
 Teoria de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Teoria de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Redes de Computadores III / /
 Redes de Computadores III / / Aula : Algoritmo Vetor de Distância Professor: Eraldo Silveira e Silva eraldo@ifsc.edu.br 1 Objetivos da Aula Apresentar o algoritmo vetor de distâncias; Discutir algumas
Redes de Computadores III / / Aula : Algoritmo Vetor de Distância Professor: Eraldo Silveira e Silva eraldo@ifsc.edu.br 1 Objetivos da Aula Apresentar o algoritmo vetor de distâncias; Discutir algumas
CÁLCULO I. 1 Velocidade Instantânea. Objetivos da Aula. Aula n o 04: Limites e Continuidade. Denir limite de funções; Calcular o limite de uma função;
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 04: Limites e Continuidade Objetivos da Aula Denir ite de funções; Calcular o ite de uma função; Utilizar as propriedades operatórias do
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 04: Limites e Continuidade Objetivos da Aula Denir ite de funções; Calcular o ite de uma função; Utilizar as propriedades operatórias do
1. Operações com vetores no espaço
 Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
Capítulo 10 1. Operações com vetores no espaço Vamos definir agora as operações de adição de vetores no espaço e multiplicação de um vetor espacial por um número real. O processo é análogo ao efetuado
Resolução de problemas difíceis de programação linear através da relaxação Lagrangeana
 problemas difíceis de programação linear através da relaxação Lagrangeana Ana Maria A.C. Rocha Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho arocha@dps.uminho.pt http://www.norg.uminho.pt/arocha
problemas difíceis de programação linear através da relaxação Lagrangeana Ana Maria A.C. Rocha Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho arocha@dps.uminho.pt http://www.norg.uminho.pt/arocha
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Capítulo Regra da cadeia
 Cálculo 2 - Capítulo 28 - Regra da cadeia 1 Capítulo 28 - Regra da cadeia 281 - Introdução 283 - Generalização 282 - Regra da cadeia Este capítulo trata da chamada regra da cadeia para funções de duas
Cálculo 2 - Capítulo 28 - Regra da cadeia 1 Capítulo 28 - Regra da cadeia 281 - Introdução 283 - Generalização 282 - Regra da cadeia Este capítulo trata da chamada regra da cadeia para funções de duas
Estruturas Condicionais
 Estruturas Condicionais Prof. rapchan@terra.com.br Introdução Um algoritmo deve ter alguma forma de poder escolher entre diversos caminhos, aquele que irá seguir. A estrutura condicional permite esta escolha.
Estruturas Condicionais Prof. rapchan@terra.com.br Introdução Um algoritmo deve ter alguma forma de poder escolher entre diversos caminhos, aquele que irá seguir. A estrutura condicional permite esta escolha.
CÁLCULO I. 1 A Função Logarítmica Natural. Objetivos da Aula. Aula n o 22: A Função Logaritmo Natural. Denir a função f(x) = ln x;
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 22: A Função Logaritmo Natural Objetivos da Aula Denir a função f(x) = ln x; Calcular limites, derivadas e integral envolvendo a função
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 22: A Função Logaritmo Natural Objetivos da Aula Denir a função f(x) = ln x; Calcular limites, derivadas e integral envolvendo a função
Algoritmos e Estruturas de Dados II
 Algoritmos e Estruturas de Dados II Grafos VI: Grafos Ponderados & Caminhos Mínimos (Bellman-Ford) Ricardo J. G. B. Campello Parte deste material é baseado em adaptações e extensões de slides disponíveis
Algoritmos e Estruturas de Dados II Grafos VI: Grafos Ponderados & Caminhos Mínimos (Bellman-Ford) Ricardo J. G. B. Campello Parte deste material é baseado em adaptações e extensões de slides disponíveis
1 Trajeto Euleriano. > Trajeto Euleriano 0/20
 Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
CÁLCULO I. Calcular o limite de uma função composta;
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 06: Limites Laterais. Limite da Função Composta. Objetivos da Aula Denir ites laterais de uma função em um ponto de seu
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 06: Limites Laterais. Limite da Função Composta. Objetivos da Aula Denir ites laterais de uma função em um ponto de seu
Nyquist, Função de Sensibilidade e Desempenho Nominal
 Nyquist, Função de Sensibilidade e Desempenho Nominal 1. Revisitando o critério de estabilidade de Nyquist 1.1. Margens de ganho e de fase 2. Erro de rastreamento e função de sensibilidade 2.1. Vetor de
Nyquist, Função de Sensibilidade e Desempenho Nominal 1. Revisitando o critério de estabilidade de Nyquist 1.1. Margens de ganho e de fase 2. Erro de rastreamento e função de sensibilidade 2.1. Vetor de
MAP Cálculo Numérico e Aplicações
 MAP151 - Cálculo Numérico e Aplicações Lista 6 Correção Neste ponto, todos já sabemos que todas as questões têm o mesmo valor, totalizando 1. pontos. Questão 1 Comecei escrevendo uma função ajusta reta.sci
MAP151 - Cálculo Numérico e Aplicações Lista 6 Correção Neste ponto, todos já sabemos que todas as questões têm o mesmo valor, totalizando 1. pontos. Questão 1 Comecei escrevendo uma função ajusta reta.sci
Para identificar intervalos de crescimento e decrescimento de uma função analisamos o comportamento de sua primeira derivada.
 O CONCEITO DE DERIVADA (continuação) Funções Crescentes e Decrescentes Existe uma relação direta entre a derivada de uma função e o crescimento desta função. Em geral, temos: Se, para todo x ]a, b[ tivermos
O CONCEITO DE DERIVADA (continuação) Funções Crescentes e Decrescentes Existe uma relação direta entre a derivada de uma função e o crescimento desta função. Em geral, temos: Se, para todo x ]a, b[ tivermos
Inteligência Artificial
 Inteligência Artificial Fabrício Olivetti de França 07 de Junho de 2018 1 Busca Informada 2 Recapitulando Definição de um problema: Conjunto de estados Conjunto de ações Função de transição Função de custo
Inteligência Artificial Fabrício Olivetti de França 07 de Junho de 2018 1 Busca Informada 2 Recapitulando Definição de um problema: Conjunto de estados Conjunto de ações Função de transição Função de custo
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA DÉCIMA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos o Teorema do Valor Médio e algumas de suas conseqüências como: determinar os intervalos de
CÁLCULO L1 NOTAS DA DÉCIMA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos o Teorema do Valor Médio e algumas de suas conseqüências como: determinar os intervalos de
Otimização Combinatória - Parte 4
 Graduação em Matemática Industrial Otimização Combinatória - Parte 4 Prof. Thiago Alves de Queiroz Departamento de Matemática - CAC/UFG 2/2014 Thiago Queiroz (DM) Parte 4 2/2014 1 / 33 Complexidade Computacional
Graduação em Matemática Industrial Otimização Combinatória - Parte 4 Prof. Thiago Alves de Queiroz Departamento de Matemática - CAC/UFG 2/2014 Thiago Queiroz (DM) Parte 4 2/2014 1 / 33 Complexidade Computacional
MAT VETORES E GEOMETRIA - IF/IME 1 o SEMESTRE 2015
 MAT 112 - VETORES E GEOMETRIA - IF/IME 1 o SEMESTRE 2015 LISTA 1 1. Ache a soma dos vetores indicados na figura, nos casos: 2. Ache a soma dos vetores indicados em cada caso, sabendo-se que (a) ABCDEFGH
MAT 112 - VETORES E GEOMETRIA - IF/IME 1 o SEMESTRE 2015 LISTA 1 1. Ache a soma dos vetores indicados na figura, nos casos: 2. Ache a soma dos vetores indicados em cada caso, sabendo-se que (a) ABCDEFGH
Programação II Aula 07
 Engenharias de Produção e Petróleo Programação II Aula 07 Adan Lucio P. Rodovia BR 101 Norte, Km. 60, Bairro Litorâneo, CEP 29932-540, São Mateus ES, Tel.: +55 (27) 3312-1511 - CEUNES Métodos de Ordenação
Engenharias de Produção e Petróleo Programação II Aula 07 Adan Lucio P. Rodovia BR 101 Norte, Km. 60, Bairro Litorâneo, CEP 29932-540, São Mateus ES, Tel.: +55 (27) 3312-1511 - CEUNES Métodos de Ordenação
Aula 1: Revisando o Conjunto dos Números Reais
 Aula 1: Revisando o Conjunto dos Números Reais Caro aluno, nesta aula iremos retomar um importante assunto, já estudado em anos anteriores: o conjunto dos números reais. Frequentemente, encontramo-nos
Aula 1: Revisando o Conjunto dos Números Reais Caro aluno, nesta aula iremos retomar um importante assunto, já estudado em anos anteriores: o conjunto dos números reais. Frequentemente, encontramo-nos
Arranjo Físico (Layout) Arranjo Físico 1
 Arranjo Físico (Layout) Arranjo Físico 1 Projeto do Arranjo Físico (Layout) Projetar um arranjo físico é decidir onde colocar todas as instalações, máquinas, equipamentos e pessoal de produção. O arranjo
Arranjo Físico (Layout) Arranjo Físico 1 Projeto do Arranjo Físico (Layout) Projetar um arranjo físico é decidir onde colocar todas as instalações, máquinas, equipamentos e pessoal de produção. O arranjo
FÍSICA 1ºTA REPOSICAÇÃO 2015 CINEMÁTICA ESCALAR DEFINIÇÕES E CONCEITOS
 FÍSICA ºTA REPOSICAÇÃO 205 CINEMÁTICA ESCALAR DEFINIÇÕES E CONCEITOS O QUE É A CINEMÁTICA A Cinemática estuda o movimento dos corpos, independentemente das causas desse movimento. Seu objetivo é descrever
FÍSICA ºTA REPOSICAÇÃO 205 CINEMÁTICA ESCALAR DEFINIÇÕES E CONCEITOS O QUE É A CINEMÁTICA A Cinemática estuda o movimento dos corpos, independentemente das causas desse movimento. Seu objetivo é descrever
O Teorema do Valor Intermediário
 Universidade de Brasília Departamento de Matemática Cálculo 1 O Teorema do Valor Intermediário Suponha que f é uma função contínua em todo o intervalo fechado [a,b]. Isto significa que, para todo c (a,b),
Universidade de Brasília Departamento de Matemática Cálculo 1 O Teorema do Valor Intermediário Suponha que f é uma função contínua em todo o intervalo fechado [a,b]. Isto significa que, para todo c (a,b),
MAT 112 Vetores e Geometria. Prova SUB C
 MAT 112 Vetores e Geometria Prof. Paolo Piccione 02 de julho de 2019 Prova SUB C Turmas: 2019146 e 2019134 Nome: Número USP: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos.
MAT 112 Vetores e Geometria Prof. Paolo Piccione 02 de julho de 2019 Prova SUB C Turmas: 2019146 e 2019134 Nome: Número USP: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos.
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 06: Continuidade de Funções Objetivos da Aula Definir função contínua; Reconhecer uma função contínua através do seu gráfico; Utilizar as
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 06: Continuidade de Funções Objetivos da Aula Definir função contínua; Reconhecer uma função contínua através do seu gráfico; Utilizar as
CEFET/RJ Inteligência Artificial (2017.2) Professor: Eduardo Bezerra Lista de exercícios 03
 . CEFET/RJ Inteligência Artificial (2017.2) Professor: Eduardo Bezerra (ebezerra@cefet-rj.br) Lista de exercícios 03 Créditos: essa lista de exercícios contém a tradução dos exercícios disponibilizados
. CEFET/RJ Inteligência Artificial (2017.2) Professor: Eduardo Bezerra (ebezerra@cefet-rj.br) Lista de exercícios 03 Créditos: essa lista de exercícios contém a tradução dos exercícios disponibilizados
4.1 posição relativas entre retas
 4 P O S I Ç Õ E S R E L AT I VA S Nosso objetivo nesta seção é entender a posição relativa entre duas retas, dois planos e ou uma reta e um plano, isto é, se estes se interseccionam, se são paralelos,
4 P O S I Ç Õ E S R E L AT I VA S Nosso objetivo nesta seção é entender a posição relativa entre duas retas, dois planos e ou uma reta e um plano, isto é, se estes se interseccionam, se são paralelos,
Sessão 03: Introduzindo os conceitos de Máximos e Mínimos.
 7.6.3. Sessão 03: Introduzindo os conceitos de Máximos e Mínimos. Data: 26/04/2010, horário: 07h30min.. Turma: T14 do curso de Engenharia Elétrica, Cálculo A MTM 1019. 7.6.3.1. Atividade 03: Situação Problema
7.6.3. Sessão 03: Introduzindo os conceitos de Máximos e Mínimos. Data: 26/04/2010, horário: 07h30min.. Turma: T14 do curso de Engenharia Elétrica, Cálculo A MTM 1019. 7.6.3.1. Atividade 03: Situação Problema
Teoria dos Grafos Aula 22
 Teoria dos Grafos Aula 22 Aula passada Caminho mais curto entre todos os pares Algoritmo de Floyd Warshall Programação dinâmica Aula de hoje Caminho mais curto Algoritmo de Bellman Ford Melhorias Caminho
Teoria dos Grafos Aula 22 Aula passada Caminho mais curto entre todos os pares Algoritmo de Floyd Warshall Programação dinâmica Aula de hoje Caminho mais curto Algoritmo de Bellman Ford Melhorias Caminho
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/30 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/30 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
Método Simplex dual. Marina Andretta ICMC-USP. 24 de outubro de 2016
 Método Simplex dual Marina Andretta ICMC-USP 24 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Método Simplex dual Marina Andretta ICMC-USP 24 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
DANIEL V. TAUSK. se A é um subconjunto de X, denotamos por A c o complementar de
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
Técnicas Inteligência Artificial
 Universidade do Sul de Santa Catarina Ciência da Computação Técnicas Inteligência Artificial Aula 03 Métodos de Busca Parte 1 Prof. Max Pereira Solução de Problemas como Busca Um problema pode ser considerado
Universidade do Sul de Santa Catarina Ciência da Computação Técnicas Inteligência Artificial Aula 03 Métodos de Busca Parte 1 Prof. Max Pereira Solução de Problemas como Busca Um problema pode ser considerado
Problema de Designação. Fernando Nogueira Problema de Designação 1
 Problema de Designação Fernando Nogueira Problema de Designação 1 O Problema de Designação é um caso específico de um Problema de Transporte, que por sua vez é um caso específico de um Problema de Programação
Problema de Designação Fernando Nogueira Problema de Designação 1 O Problema de Designação é um caso específico de um Problema de Transporte, que por sua vez é um caso específico de um Problema de Programação
Conjuntos Numéricos Aula 6. Conjuntos Numéricos. Armando Caputi
 Conjuntos Numéricos Aula 6 Conjuntos Numéricos E-mail: armando.caputi@ufabc.edu.br Página: http://professor.ufabc.edu.br/~armando.caputi Sala 549-2 - Bloco A - Campus Santo André Conjuntos Numéricos Aula
Conjuntos Numéricos Aula 6 Conjuntos Numéricos E-mail: armando.caputi@ufabc.edu.br Página: http://professor.ufabc.edu.br/~armando.caputi Sala 549-2 - Bloco A - Campus Santo André Conjuntos Numéricos Aula
Aula 19: Lifting e matrizes ideais
 Aula 19: Lifting e matrizes ideais Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously... Branch-and-bound Formulações
Aula 19: Lifting e matrizes ideais Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously... Branch-and-bound Formulações
Codificação de Huffman
 Codificação de Huffman Bruna Gregory Palm 11 de setembro de 2017 A codificação de Huffman é um método de compressão que considera as probabilidades de ocorrência de cada símbolo no conjunto de dados a
Codificação de Huffman Bruna Gregory Palm 11 de setembro de 2017 A codificação de Huffman é um método de compressão que considera as probabilidades de ocorrência de cada símbolo no conjunto de dados a
7 Definição da Trajetória via Controle Ótimo
 7 Definição da Trajetória via Controle Ótimo O objetivo desse trabalho é avaliar a metodologia de projeto e os controladores não só em percursos que representem o centro da pista, mas trajetórias ótimas
7 Definição da Trajetória via Controle Ótimo O objetivo desse trabalho é avaliar a metodologia de projeto e os controladores não só em percursos que representem o centro da pista, mas trajetórias ótimas
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
Capítulo 1. Aula Conectividade Caminhos
 Capítulo 1 Aula 7 1.1 Conectividade Muitos problemas podem ser modelados com caminhos formados ao percorrer as arestas dos grafos. Por exemplo, o problema de determinar se uma mensagem pode ser enviada
Capítulo 1 Aula 7 1.1 Conectividade Muitos problemas podem ser modelados com caminhos formados ao percorrer as arestas dos grafos. Por exemplo, o problema de determinar se uma mensagem pode ser enviada
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
MEDIÇÃO DE GRANDEZAS. Ana Maria Torres da Silva Engenharia Civil Rafael Santos Carvalho- Engenharia Civil
 CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2015.2 MEDIÇÃO DE GRANDEZAS Ana Maria Torres da Silva Engenharia Civil Rafael Santos Carvalho- Engenharia Civil Medindo Grandezas Medimos cada grandeza
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 2015.2 MEDIÇÃO DE GRANDEZAS Ana Maria Torres da Silva Engenharia Civil Rafael Santos Carvalho- Engenharia Civil Medindo Grandezas Medimos cada grandeza
AULA 4 -Probabilidade Condicional e Regra de Bayes
 AULA 4 - e Regra de Bayes Susan Schommer Introdução à Estatística Econômica - IE/UFRJ : exemplos A soma dos resultados de dois lançamentos de um dado é 9. Qual a probabilidade do primeiro resultado ter
AULA 4 - e Regra de Bayes Susan Schommer Introdução à Estatística Econômica - IE/UFRJ : exemplos A soma dos resultados de dois lançamentos de um dado é 9. Qual a probabilidade do primeiro resultado ter
Otimização em Grafos
 Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Álgebra Linear I - Aula 10. Roteiro
 Álgebra Linear I - Aula 10 1. Distância entre duas retas. 2. A perpendicular comum a duas retas. 3. Posições relativas. Roteiro 1 Distância entre duas retas r e s Calcularemos a distância entre duas retas
Álgebra Linear I - Aula 10 1. Distância entre duas retas. 2. A perpendicular comum a duas retas. 3. Posições relativas. Roteiro 1 Distância entre duas retas r e s Calcularemos a distância entre duas retas
Modelização do Sistema Produtivo Teoria das Filas de Espera
 Modelização do Sistema Produtivo Teoria das Filas de Espera http://www.fe.up.pt/maspwww Licenciatura em Engenharia Electrotécnica e de Computadores Gil M. Gonçalves Gil.Goncalves@fe.up.pt 2004/2005 Outline
Modelização do Sistema Produtivo Teoria das Filas de Espera http://www.fe.up.pt/maspwww Licenciatura em Engenharia Electrotécnica e de Computadores Gil M. Gonçalves Gil.Goncalves@fe.up.pt 2004/2005 Outline
Cones e raios extremos
 Cones e raios extremos Marina Andretta ICMC-USP 7 de novembro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Cones e raios extremos Marina Andretta ICMC-USP 7 de novembro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Aula 10 Produto interno, vetorial e misto -
 MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
