Aprendizado, minimização do arrependimento e equilíbrio (Learning, Regret Minimization, and Equilibria)
|
|
|
- Paulo Fonseca Estrada
- 6 Há anos
- Visualizações:
Transcrição
1 Aprendizado, minimização do arrependimento e equilíbrio (Learning, Regret Minimization, and Equilibria) Victor Alberto Romero Instituto de Matemática e Estatística Universidade de São Paulo Teoria dos Jogos e Algorítmica
2 Introdução O problema principal é tomar decisões em ambientes desconhecidos. A aproximação usada neste capítulo é desenhar algoritmos adaptativos que podem aprender entendendo a dinâmica do sistema. A estratégia usada é a análise do arrependimento (Regret), ou seja, o cálculo da diferença entre a melhor utilidade que poderia ter sido e a utilidade real obtida. Temos três análises possíveis do arrependimento
3 Introdução O problema principal é tomar decisões em ambientes desconhecidos. A aproximação usada neste capítulo é desenhar algoritmos adaptativos que podem aprender entendendo a dinâmica do sistema. A estratégia usada é a análise do arrependimento (Regret), ou seja, o cálculo da diferença entre a melhor utilidade que poderia ter sido e a utilidade real obtida. Temos três análises possíveis do arrependimento
4 Introdução O problema principal é tomar decisões em ambientes desconhecidos. A aproximação usada neste capítulo é desenhar algoritmos adaptativos que podem aprender entendendo a dinâmica do sistema. A estratégia usada é a análise do arrependimento (Regret), ou seja, o cálculo da diferença entre a melhor utilidade que poderia ter sido e a utilidade real obtida. Temos três análises possíveis do arrependimento
5 Introdução Arrependimento Externo (External Regret) Também conhecido como Combining expert advice Compara com a melhor opção individual que poderia ter sido (a melhor em retrospectiva) Dá uma metodologia geral para o desenvolvimento de algoritmos online.
6 Introdução Arrependimento Externo (External Regret) Também conhecido como Combining expert advice Compara com a melhor opção individual que poderia ter sido (a melhor em retrospectiva) Dá uma metodologia geral para o desenvolvimento de algoritmos online.
7 Introdução Arrependimento Externo (External Regret) Também conhecido como Combining expert advice Compara com a melhor opção individual que poderia ter sido (a melhor em retrospectiva) Dá uma metodologia geral para o desenvolvimento de algoritmos online.
8 Introdução Arrependimento Externo (External Regret) No capítulo, o autor faz um desenvolvimento muito interessante: começa como um algoritmo guloso simples, e sobre ele vai construindo até chegar num algoritmo no qual a ( ) perda é, no máximo, O TlogN a mais do que a melhor escolha, onde T é o número de passos dados até o momento. Ou seja, o máximo afastamento do ótimo por lance é: ( ) logn O T
9 Introdução Arrependimento Externo (External Regret) No capítulo, o autor faz um desenvolvimento muito interessante: começa como um algoritmo guloso simples, e sobre ele vai construindo até chegar num algoritmo no qual a ( ) perda é, no máximo, O TlogN a mais do que a melhor escolha, onde T é o número de passos dados até o momento. Ou seja, o máximo afastamento do ótimo por lance é: ( ) logn O T
10 Introdução Arrependimento interno e de troca (Internal Regret and Swap Regret) Arrependimento interno (Internal Regret) Considera a historia Permite que uma ação passada seja substituída por outra Arrependimento de troca (Swap Regret) Considera a historia Permite qualquer mapeamento de {1,..., N} para {1,..., N} e pode ser aumentado num fator de N
11 Introdução Arrependimento interno e de troca (Internal Regret and Swap Regret) Arrependimento interno (Internal Regret) Considera a historia Permite que uma ação passada seja substituída por outra Arrependimento de troca (Swap Regret) Considera a historia Permite qualquer mapeamento de {1,..., N} para {1,..., N} e pode ser aumentado num fator de N
12 Introdução Modelo de informação parcial (partial information model) Também conhecido como Multiarmed bandit - MAB Só pode ver as perdas de sua escolha atual, não as perdas das outras escolhas (e por isso, não pode saber diretamente se é a melhor escolha ou não!!) O autor deixa claro que os resultados obtidos nesse capítulo não são os melhores que se conhecem. Nas notas do capítulo tem uma lista de trabalhos que apresentam melhores algoritmos para este problema.
13 Introdução Modelo de informação parcial (partial information model) Também conhecido como Multiarmed bandit - MAB Só pode ver as perdas de sua escolha atual, não as perdas das outras escolhas (e por isso, não pode saber diretamente se é a melhor escolha ou não!!) O autor deixa claro que os resultados obtidos nesse capítulo não são os melhores que se conhecem. Nas notas do capítulo tem uma lista de trabalhos que apresentam melhores algoritmos para este problema.
14 Introdução Modelo de informação parcial (partial information model) Também conhecido como Multiarmed bandit - MAB Só pode ver as perdas de sua escolha atual, não as perdas das outras escolhas (e por isso, não pode saber diretamente se é a melhor escolha ou não!!) O autor deixa claro que os resultados obtidos nesse capítulo não são os melhores que se conhecem. Nas notas do capítulo tem uma lista de trabalhos que apresentam melhores algoritmos para este problema.
15 Modelo e preliminares Jogos de adversários online (processa só a entrada, sem memória de estados anteriores) como X ={1,...,N} opções para cada jogador Em cada passo t o algoritmo H escolhe uma distribuição p t sobre o conjunto de N ações. Depois disso o adversário escolhe um vetor de perdas l t [0,1] N (um valor de perda para cada escolha), onde l t i [0,1] é a perda se o jogador escolhe a opção i no momento t
16 Modelo e preliminares Jogos de adversários online (processa só a entrada, sem memória de estados anteriores) como X ={1,...,N} opções para cada jogador Em cada passo t o algoritmo H escolhe uma distribuição p t sobre o conjunto de N ações. Depois disso o adversário escolhe um vetor de perdas l t [0,1] N (um valor de perda para cada escolha), onde l t i [0,1] é a perda se o jogador escolhe a opção i no momento t
17 Modelo e preliminares Jogos de adversários online (processa só a entrada, sem memória de estados anteriores) como X ={1,...,N} opções para cada jogador Em cada passo t o algoritmo H escolhe uma distribuição p t sobre o conjunto de N ações. Depois disso o adversário escolhe um vetor de perdas l t [0,1] N (um valor de perda para cada escolha), onde l t i [0,1] é a perda se o jogador escolhe a opção i no momento t
18 Modelo e preliminares Modelo com informação completa (full information model) No modelo com informação completa (full information model) o algoritmo H recebe o vetor de perdas l t e tem um valor de perda: l t H = N i=1 p t il t i que é a perda esperada quando o algoritmo escolhe a opção i X com probabilidade p t i.
19 Modelo e preliminares Modelo de informação parcial (partial information model) No modelo de informação parcial (partial information model) o algoritmo H recebe (l t k,k t ), onde k t segue a distribuição p t, e t l t H =lt k é sua perda. A perda da i-ésima ação durante os primeiros t T passos é: e a perda de H é: L T i = T l t i t=1 L T H = T t=1l t H
20 Modelo e preliminares Arrependimento externo (external regret) A razão para calcular o arrependimento externo (external regret) é poder criar um algoritmo online que possa se aproximar ao melhor algoritmo de uma classe específica de algoritmos G. Isto quer dizer, que queremos uma perda próxima a: L T G,min = min g G L T g Formalmente nós queremos minimizar o arrependimento externo: R G = L T H L T G,min
21 Modelo e preliminares Classe de comparação Aqui G é chamada a classe de comparação. Em geral, usa-se uma classe de comparação G = X (ou seja, todas as possíveis escolhas) e procura-se um algoritmo online com uma perda perto de L T min = min il T i sendo o arrependimento externo: R=L T H L T min
22 Modelo e preliminares Regras de modificação Normalmente o arrependimento externo usa uma classe de comparação fixa G, mas poderia ter-se uma classe que dependa das ações escolhidas pelo algoritmo online. Neste caso podemos considerar regras de modificação que mudem as ações escolhidas pelo algoritmo online e produzam uma estratégia alternativa. Uma regra de modificação F recebe na entrada o histórico de ações e a ação atual escolhidas por H, e devolve uma ação (que pode ser diferente ou não). Chama-se F t à função F no momento t
23 Modelo e preliminares Regras de modificação Normalmente o arrependimento externo usa uma classe de comparação fixa G, mas poderia ter-se uma classe que dependa das ações escolhidas pelo algoritmo online. Neste caso podemos considerar regras de modificação que mudem as ações escolhidas pelo algoritmo online e produzam uma estratégia alternativa. Uma regra de modificação F recebe na entrada o histórico de ações e a ação atual escolhidas por H, e devolve uma ação (que pode ser diferente ou não). Chama-se F t à função F no momento t
24 Modelo e preliminares Regras de modificação Dada uma sequência de distribuições de probabilidade p t usada pelo algoritmo H e uma regra de modificação F, pode-se definir uma nova sequência de distribuições de probabilidade f t = F t (p t ), onde A perda desta nova sequência é: fi t = p t j j:f t (j)=i L T H,F = t fil t t i i no livro é: L H,F = t fil t t i i Nota-se que no momento t, F muda a probabilidade de H associando a ação j a ação F t (j). Isto implica que a regra de modificação F gera uma distribuição diferente, que é função da distribuição de H, p t.
25 Modelo e preliminares Regras de modificação Dada uma sequência de distribuições de probabilidade p t usada pelo algoritmo H e uma regra de modificação F, pode-se definir uma nova sequência de distribuições de probabilidade f t = F t (p t ), onde A perda desta nova sequência é: fi t = p t j j:f t (j)=i L T H,F = t fil t t i i no livro é: L H,F = t fil t t i i Nota-se que no momento t, F muda a probabilidade de H associando a ação j a ação F t (j). Isto implica que a regra de modificação F gera uma distribuição diferente, que é função da distribuição de H, p t.
26 Modelo e preliminares Regras de modificação Dada uma sequência de distribuições de probabilidade p t usada pelo algoritmo H e uma regra de modificação F, pode-se definir uma nova sequência de distribuições de probabilidade f t = F t (p t ), onde A perda desta nova sequência é: fi t = p t j j:f t (j)=i L T H,F = t fil t t i i no livro é: L H,F = t fil t t i i Nota-se que no momento t, F muda a probabilidade de H associando a ação j a ação F t (j). Isto implica que a regra de modificação F gera uma distribuição diferente, que é função da distribuição de H, p t.
27 Modelo e preliminares Regras de modificação Dada uma sequência de distribuições de probabilidade p t usada pelo algoritmo H e uma regra de modificação F, pode-se definir uma nova sequência de distribuições de probabilidade f t = F t (p t ), onde A perda desta nova sequência é: fi t = p t j j:f t (j)=i L T H,F = t fil t t i i no livro é: L H,F = t fil t t i i Nota-se que no momento t, F muda a probabilidade de H associando a ação j a ação F t (j). Isto implica que a regra de modificação F gera uma distribuição diferente, que é função da distribuição de H, p t.
28 Modelo e preliminares Regras de modificação O artigo foca-se num conjunto finito F de regras de modificação que não requer memória. Dada uma sequência de vetores de perda, o arrependimento de usar o algoritmo online H com relação às regras de modificação F é: { R F = max L T H L T H,F} F F
29 Modelo e preliminares Regras de modificação O artigo foca-se num conjunto finito F de regras de modificação que não requer memória. Dada uma sequência de vetores de perda, o arrependimento de usar o algoritmo online H com relação às regras de modificação F é: { R F = max L T H L T H,F} F F
30 Modelo e preliminares Arrependimento interno (internal regret) Pode-se ver que o arrependimento externo é equivalente a ter um conjunto de F ex de N regras de modificação F i, onde cada F i tem como saída a ação i. Para o arrependimento interno (internal regret), o conjunto F in consiste em N(N 1) regras de modificação F i,j, onde F i,j (i)=j e F i,j (i )=i, para i i. Então o arrependimento interno de H é: { max L T H L T } T F F in H,F = max i,j X{ t=1p t i( l t i l t ) } j
31 Modelo e preliminares Arrependimento de troca (swap regret) Um caso mais geral das regras de modificação sem memória é o arrependimento de troca (swap regret), definido pela classe F sw. F sw inclui as N N funções F :{1,...,N} {1,...,N}, onde a função F troca a ação atual de H, de i para F(i). O arrependimento de troca para H é: { max L T H L T N H,F} = F F max sw j X i=1 { T p t i( l t i l t ) } j t=1 É importante notar que: F ex F in F sw F sw
32 Modelo e preliminares Arrependimento de troca (swap regret) Um caso mais geral das regras de modificação sem memória é o arrependimento de troca (swap regret), definido pela classe F sw. F sw inclui as N N funções F :{1,...,N} {1,...,N}, onde a função F troca a ação atual de H, de i para F(i). O arrependimento de troca para H é: { max L T H L T N H,F} = F F max sw j X i=1 { T p t i( l t i l t ) } j t=1 É importante notar que: F ex F in F sw F sw
33 Minimização do arrependimento externo Más noticias: Não é possível garantir um baixo arrependimento em relação à sequência ótima de decisões em retrospetiva. (Borodin e El-Yaniv, 1998; Sleator e Tarjan, 1985) Como alternativa, o autor propõe focar em classes de comparação mais restritas. Vamos usar a classe G all, que é o conjunto de funções que fazem o mapeamento de instantes de tempo {1,...,T} para escolhas X ={1,...,N}
34 Minimização do arrependimento externo Más noticias: Não é possível garantir um baixo arrependimento em relação à sequência ótima de decisões em retrospetiva. (Borodin e El-Yaniv, 1998; Sleator e Tarjan, 1985) Como alternativa, o autor propõe focar em classes de comparação mais restritas. Vamos usar a classe G all, que é o conjunto de funções que fazem o mapeamento de instantes de tempo {1,...,T} para escolhas X ={1,...,N}
35 Minimização do arrependimento externo Teorema Teorema Para todo algoritmo online H existe uma sequência de vetores de perda T como a qual o arrependimento R G é pelo menos all T ( 1 1 N). Demonstração. Para cada instante t, a escolha i t de mais baixa probabilidade p t i toma um valor de perda de 0 e todas as outras escolhas tomam o valor de 1. Como: min i {p t i } 1 N Então, a perda de H ao longo de T passos é pelo menos T ( 1 1 N). Também pode-se definir um g G all, tal que g(t)=i t e tem um perda total de 0.
36 Minimização do arrependimento externo Teorema Teorema Para todo algoritmo online H existe uma sequência de vetores de perda T como a qual o arrependimento R G é pelo menos all T ( 1 1 N). Demonstração. Para cada instante t, a escolha i t de mais baixa probabilidade p t i toma um valor de perda de 0 e todas as outras escolhas tomam o valor de 1. Como: min i {p t i } 1 N Então, a perda de H ao longo de T passos é pelo menos T ( 1 1 N). Também pode-se definir um g G all, tal que g(t)=i t e tem um perda total de 0.
37 Minimização do arrependimento externo Para simplificar, vamos supôr que todas as perdas são ou 0 ou 1. Vamos chamar L t i = t τ=1 lτ i a perda acumulada até o momento t da ação i Um algoritmo guloso vai escolher para cada momento t uma ação: x t = arg min i X L t 1 i
38 Minimização do arrependimento externo Para simplificar, vamos supôr que todas as perdas são ou 0 ou 1. Vamos chamar L t i = t τ=1 lτ i a perda acumulada até o momento t da ação i Um algoritmo guloso vai escolher para cada momento t uma ação: x t = arg min i X L t 1 i
39 Minimização do arrependimento externo Para simplificar, vamos supôr que todas as perdas são ou 0 ou 1. Vamos chamar L t i = t τ=1 lτ i a perda acumulada até o momento t da ação i Um algoritmo guloso vai escolher para cada momento t uma ação: x t = arg min i X L t 1 i
40 Minimização do arrependimento externo Algoritmo Guloso Algoritmo Guloso Inicializa: x 1 = 1 Em cada momento t: L min t 1 = min i XL t 1 i { } S t 1 = i : L t 1 i = L min t 1 x t = min S t 1 Teorema O algoritmo guloso tem uma perda acumulada L T G N LT min +(N 1) para qualquer sequência de perdas
41 Minimização do arrependimento externo Algoritmo Guloso Algoritmo Guloso Inicializa: x 1 = 1 Em cada momento t: L min t 1 = min i XL t 1 i { } S t 1 = i : L t 1 i = L min t 1 x t = min S t 1 Teorema O algoritmo guloso tem uma perda acumulada L T G N LT min +(N 1) para qualquer sequência de perdas
42 Minimização do arrependimento externo Algoritmo Guloso Demonstração. Em cada momento t no qual o algortimo perda 1 e o L t min não mude, pelo menos uma ação e removida do S t. Isto ocorre no máximo N vezes até que L t min incremente em 1. Ou seja, o algoritmo tem uma perda de máximo N entre incrementos de L t min : L t G N St +N L t min Pode-se ver que o algoritmo é O(N) vezes pior que o ótimo. Vamos ver que qualquer algoritmo determinístico tem pelo menos o mesmo fator.
43 Minimização do arrependimento externo Algoritmo Guloso Demonstração. Em cada momento t no qual o algortimo perda 1 e o L t min não mude, pelo menos uma ação e removida do S t. Isto ocorre no máximo N vezes até que L t min incremente em 1. Ou seja, o algoritmo tem uma perda de máximo N entre incrementos de L t min : L t G N St +N L t min Pode-se ver que o algoritmo é O(N) vezes pior que o ótimo. Vamos ver que qualquer algoritmo determinístico tem pelo menos o mesmo fator.
44 Minimização do arrependimento externo Algoritmo Guloso Teorema Para qualquer algoritmo determinístico D existe uma sequência de perdas para a qual L T D = T e LT min = T N Nota-se que este teorema implica que L T D N LT min +(T mod N) o que é um limite superior para o algoritmo guloso.
45 Minimização do arrependimento externo Algoritmo Guloso Teorema Para qualquer algoritmo determinístico D existe uma sequência de perdas para a qual L T D = T e LT min = T N Nota-se que este teorema implica que L T D N LT min +(T mod N) o que é um limite superior para o algoritmo guloso.
46 Minimização do arrependimento externo Algoritmo Guloso Demonstração. Para a prova, vamos fixar um algoritmo online D e vamos dizer que x t é sua saída no momento t. Vamos então a gerar uma sequência assim: No momento t vamos definir a perda para x t de 1 e para qualquer outra ação de 0. Isto garante que o algoritmo D tem uma perda de 1 em cada passo, então L T D = T. Como existem N ações diferentes, tem que existir uma ação que o algoritmo D tenha escolhido pelo menos T N vezes. Então, por construção, como só as ações escolhidas por D tem perdas, implica que L T min T N
47 Minimização do arrependimento externo Algoritmo Guloso Aleatório Dá para pensar então que pode acontecer se o algoritmo guloso tem como saída uma distribuição de probabilidade. Vamos chamar esse algoritmo Gusloso Aleatório Algoritmo Guloso Aleátorio Inicializa: p 1 i = 1/N para i X Em cada momento t: L min t 1 = min i XL t 1 i { } S t 1 = i : L t 1 i = L min t 1 p t i = 1 para i S t 1 e p t S t 1 i = 0 em outro contrario
48 Minimização do arrependimento externo Algoritmo Guloso Aleatório Dá para pensar então que pode acontecer se o algoritmo guloso tem como saída uma distribuição de probabilidade. Vamos chamar esse algoritmo Gusloso Aleatório Algoritmo Guloso Aleátorio Inicializa: p 1 i = 1/N para i X Em cada momento t: L min t 1 = min i XL t 1 i { } S t 1 = i : L t 1 i = L min t 1 p t i = 1 para i S t 1 e p t S t 1 i = 0 em outro contrario
49 Minimização do arrependimento externo Algoritmo Guloso Aleatório Teorema O algoritmo guloso aleatório tem, para qualquer sequência de perdas, uma perda de L T RG (ln N)+(1+ln N)LT min Demonstração. Como no caso anterior, vai se provar que entre incrementos sucessivos de L T min o algoritmo incorre numa perda pelo menos 1+ln N. Seja t j o momento onde L t min atinge por primeira vez uma perda j. Vamos ver que acontece entre os instantes t j e t j+1. Para qualquer instante de tempo t temos que 1 S t N. (continua)
50 Minimização do arrependimento externo Algoritmo Guloso Aleatório Teorema O algoritmo guloso aleatório tem, para qualquer sequência de perdas, uma perda de L T RG (ln N)+(1+ln N)LT min Demonstração. Como no caso anterior, vai se provar que entre incrementos sucessivos de L T min o algoritmo incorre numa perda pelo menos 1+ln N. Seja t j o momento onde L t min atinge por primeira vez uma perda j. Vamos ver que acontece entre os instantes t j e t j+1. Para qualquer instante de tempo t temos que 1 S t N. (continua)
51 Minimização do arrependimento externo Algoritmo Guloso Aleatório Demonstração. (continuação) Agora, se num instante t (t j,t j+1 ] o comprimento de S t encolhe de n para n k, a perda do algoritmo vai ser k n (dado que toda ação tem peso de 1 n. Por último, pode-se ver que podemos fazer uma aproximação de k n por 1 n + 1 (n 1) (n k+1). Isto gera uma perda para o intervalo (t j,t j+1 ] de pelo menos: 1 N + 1 (N 1) + 1 (N 2) ln N Por indução ( pode-se ver que ) L t RG 1 N + 1 (N 1) + 1 (N 2) ( S t +1) +(1+ln N)L t min
52 Minimização do arrependimento externo Algoritmo aleatório de peso maioritário Uma ideia que surge naturalmente quando se pensa no algoritmo guloso aleatório é mudar as probabilidades para que não todas sejam iguais. Vamos associar para cada escolha i, como uma perda total L i, um peso w i =(i η) L i, e uma probabilidade p i = w i N j=1 w j Aqui η é uma constante pequena e ajustável. No capítulo usam η = 0.01 Algoritmo aleatório de peso maioritário Inicializa: w 1 i = 1 p 1 i = 1 N para i X Em cada momento t: se l t 1 i = 1 então w t i = wt 1 i (1 η); se no então w t i = wt 1 i p t i = wt i W t, onde W t = i X w t i.
53 Minimização do arrependimento externo Algoritmo aleatório de peso maioritário Uma ideia que surge naturalmente quando se pensa no algoritmo guloso aleatório é mudar as probabilidades para que não todas sejam iguais. Vamos associar para cada escolha i, como uma perda total L i, um peso w i =(i η) L i, e uma probabilidade p i = w i N j=1 w j Aqui η é uma constante pequena e ajustável. No capítulo usam η = 0.01 Algoritmo aleatório de peso maioritário Inicializa: w 1 i = 1 p 1 i = 1 N para i X Em cada momento t: se l t 1 i = 1 então w t i = wt 1 i (1 η); se no então w t i = wt 1 i p t i = wt i W t, onde W t = i X w t i.
54 Minimização do arrependimento externo Algoritmo aleatório de peso maioritário Teorema Para qualquer η 1 2, a perda do algoritmo aleatório de peso maioritário como uma sequência binária {0, 1} de perdas é: L T RWM (1+η)LT min + ln N η Definindo η = min{ (ln N) T, 1 2 }, temos que L T RWM L T min + 2 T ln N
55 Limite Inferior Mas, quanto podemos baixar? Teorema Vamos assumir T < log 2 N. Então existe uma geração aleatória de perdas que, para qualquer algoritmo R1, gera uma perda esperada E[L T R1 ]= T 2, e ainda assim LT min = 0
56 Limite Inferior Mas, quanto podemos baixar? Teorema Vamos assumir T < log 2 N. Então existe uma geração aleatória de perdas que, para qualquer algoritmo R1, gera uma perda esperada E[L T R1 ]= T 2, e ainda assim LT min = 0
57 Limite Inferior Demonstração. Vamos considerar a seguinte sequência de perdas. No instante t= 1, vamos ter um subconjunto de N/2 ações como uma perda de 0, e o resto vai ter uma perda de 1. No instante t=2, vamos escolher um subconjunto aleatório de N/4 ações (dos que no t=1 tiveram uma perda de 0), que vão ter uma perda de 0 no instante t=2 e ao resto damos uma perda de 1. Se repetimos o proceso, em cada passo qualquer algoritmo online vai ter uma perda esperada de 1/2. Mas ainda assim, pode-se ver que pelo menos para T < log 2 N, sempre existe uma ação como uma perda total de 0.
58 Rota para pesquisas futuras O limite imposto para o arrependimento que foi presentado depende únicamente do número de passos dados T, e não depende do resultado da melhor ação. Isto é conhecido como limite de ordem zero. Pode-se encontrar outros limites: Primeiro Ordem: Depende da perda da melhor escolha Segundo Ordem: Depende da soma dos quadrados das perdas. Ter um arrependimento externo que seja proporcional à variança da melhor escolha. Problemas como um número de ações possíveis muito grande. Por exemplo, um problema onde as escolhas possíveis sejam todos os caminhos simples entre dois nós (combinatório) Analizar a dinâmica dos algoritmos de minimização de arrependimento.
Medida do Tempo de Execução de um Programa. Bruno Hott Algoritmos e Estruturas de Dados I DECSI UFOP
 Medida do Tempo de Execução de um Programa Bruno Hott Algoritmos e Estruturas de Dados I DECSI UFOP Medida do Tempo de Execução de um Programa O projeto de algoritmos é fortemente influenciado pelo estudo
Medida do Tempo de Execução de um Programa Bruno Hott Algoritmos e Estruturas de Dados I DECSI UFOP Medida do Tempo de Execução de um Programa O projeto de algoritmos é fortemente influenciado pelo estudo
Medida do Tempo de Execução de um Programa. David Menotti Algoritmos e Estruturas de Dados II DInf UFPR
 Medida do Tempo de Execução de um Programa David Menotti Algoritmos e Estruturas de Dados II DInf UFPR Medida do Tempo de Execução de um Programa O projeto de algoritmos é fortemente influenciado pelo
Medida do Tempo de Execução de um Programa David Menotti Algoritmos e Estruturas de Dados II DInf UFPR Medida do Tempo de Execução de um Programa O projeto de algoritmos é fortemente influenciado pelo
3. Resolução de problemas por meio de busca
 Inteligência Artificial - IBM1024 3. Resolução de problemas por meio de busca Prof. Renato Tinós Local: Depto. de Computação e Matemática (FFCLRP/USP) 1 Principais Tópicos 3. Resolução de problemas por
Inteligência Artificial - IBM1024 3. Resolução de problemas por meio de busca Prof. Renato Tinós Local: Depto. de Computação e Matemática (FFCLRP/USP) 1 Principais Tópicos 3. Resolução de problemas por
Complexidade de Algoritmos. Edson Prestes
 Edson Prestes Existem famílias de problemas cuja solução é alcançada de forma semelhante. O relacionamento entre problemas: caso especial; versão abstração; similar. Exemplos: A inserção de um elemento
Edson Prestes Existem famílias de problemas cuja solução é alcançada de forma semelhante. O relacionamento entre problemas: caso especial; versão abstração; similar. Exemplos: A inserção de um elemento
3 Aprendizado por reforço
 3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
Teoria dos Jogos Algorítmica Maximização de Lucros no Design de Mecanismos
 Teoria dos Jogos Algorítmica Maximização de Lucros no Design de Mecanismos Luis Gustavo Rocha Vianna. Instituto de Matemática e Estatística IME Universidade de São Paulo USP Maximização de Lucros Design
Teoria dos Jogos Algorítmica Maximização de Lucros no Design de Mecanismos Luis Gustavo Rocha Vianna. Instituto de Matemática e Estatística IME Universidade de São Paulo USP Maximização de Lucros Design
RESOLUÇÃO DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA Considere a soma. S n = n 2 n 1
 DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA 1 1. Considere a soma S n = 1 2 0 + 2 2 1 + 3 2 2 + + n 2 n 1. Mostre, por indução finita, que S n = (n 1)2 n + 1. Indique claramente a base da indução, a
DCC-UFRJ MATEMÁTICA COMBINATÓRIA 2006/2 PROVA 1 1. Considere a soma S n = 1 2 0 + 2 2 1 + 3 2 2 + + n 2 n 1. Mostre, por indução finita, que S n = (n 1)2 n + 1. Indique claramente a base da indução, a
Aula 14. Aula de hoje. Aula passada
 Aula 14 Aula passada Autovalores, autovetores, decomposição Convergência para estacionaridade Tempo de mistura Spectral gap Tempo de mistura de passeios aleatórios Aula de hoje Caminho amostral Teorema
Aula 14 Aula passada Autovalores, autovetores, decomposição Convergência para estacionaridade Tempo de mistura Spectral gap Tempo de mistura de passeios aleatórios Aula de hoje Caminho amostral Teorema
4. Algoritmos de Busca em Vetores
 Introdução à Computação II 5952011 4. Algoritmos de Busca em Vetores Prof. Renato Tinós Local: Depto. de Computação e Matemática (FFCLRP/USP) 1 Principais Tópicos 4.1. Introdução 4.2. Busca Linear 4.2.1.
Introdução à Computação II 5952011 4. Algoritmos de Busca em Vetores Prof. Renato Tinós Local: Depto. de Computação e Matemática (FFCLRP/USP) 1 Principais Tópicos 4.1. Introdução 4.2. Busca Linear 4.2.1.
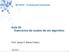
Espaço amostral Ω: Conjunto enumerável de todos os possíveis resultados de um experimento aleatório. um evento elementar. E = E[X j ] X j.
![Espaço amostral Ω: Conjunto enumerável de todos os possíveis resultados de um experimento aleatório. um evento elementar. E = E[X j ] X j. Espaço amostral Ω: Conjunto enumerável de todos os possíveis resultados de um experimento aleatório. um evento elementar. E = E[X j ] X j.](/thumbs/97/133173938.jpg) Universidade Tecnológica Federal do Paraná Professor Murilo V G da Silva Notas de aula Algoritmos Avançados I (Aula 04 Conteúdos da aula: [CLR09: cap 7 e 9][MIE05 4, 5] Vamos estudar nesta aula três algoritmos
Universidade Tecnológica Federal do Paraná Professor Murilo V G da Silva Notas de aula Algoritmos Avançados I (Aula 04 Conteúdos da aula: [CLR09: cap 7 e 9][MIE05 4, 5] Vamos estudar nesta aula três algoritmos
MAP Métodos Numéricos e Aplicações Escola Politécnica 1 Semestre de 2017 EPREC - Entrega em 27 de julho de 2017
 1 Preliminares MAP3121 - Métodos Numéricos e Aplicações Escola Politécnica 1 Semestre de 2017 EPREC - Entrega em 27 de julho de 2017 A decomposição de Cholesky aplicada a Finanças O exercício-programa
1 Preliminares MAP3121 - Métodos Numéricos e Aplicações Escola Politécnica 1 Semestre de 2017 EPREC - Entrega em 27 de julho de 2017 A decomposição de Cholesky aplicada a Finanças O exercício-programa
apenas os caminhos que passam só por vértices em C, exceto, talvez, o próprio v A Figura 1 a seguir ilustra o significado do conjunto C edovalordist.
 CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
CAMINHO DE CUSTO MÍNIMO Dados dois pontos A e B, em muitos problemas práticos fazemos 2 perguntas: 1. existe um caminho de A para B? ou 2. se existe mais de um caminho de A para B, qual deles é o mais
Análise de Algoritmos
 Análise de Algoritmos Parte 1 Prof. Túlio Toffolo http://www.toffolo.com.br BCC202 Aula 04 Algoritmos e Estruturas de Dados I Qual a diferença entre um algoritmo e um programa? Como escolher o algoritmo
Análise de Algoritmos Parte 1 Prof. Túlio Toffolo http://www.toffolo.com.br BCC202 Aula 04 Algoritmos e Estruturas de Dados I Qual a diferença entre um algoritmo e um programa? Como escolher o algoritmo
Teoria e Algoritmos em Grafos
 Teoria e Algoritmos em Grafos 2018.2 Conjunto Independente Conjuntos Independentes são subconjuntos de vértices de um grafo no qual nenhum vértice é adjacente entre si. Conjunto Independente Conjuntos
Teoria e Algoritmos em Grafos 2018.2 Conjunto Independente Conjuntos Independentes são subconjuntos de vértices de um grafo no qual nenhum vértice é adjacente entre si. Conjunto Independente Conjuntos
Dízimas e intervalos encaixados.
 Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Dízimas e intervalos encaixados. Recorde que uma dízima com n casas decimais é um número racional da forma a 0.a a 2...a n = a 0 + a 0 + a 2 0 2 + + a n n 0 n = a j 0 j em que a 0,a,...,a n são inteiros
Sistemas discretos sem memória e codificação da fonte
 Sistemas discretos sem memória e codificação da fonte Luis Henrique Assumpção Lolis 10 de setembro de 2013 Luis Henrique Assumpção Lolis Sistemas discretos sem memória e codificação da fonte 1 Conteúdo
Sistemas discretos sem memória e codificação da fonte Luis Henrique Assumpção Lolis 10 de setembro de 2013 Luis Henrique Assumpção Lolis Sistemas discretos sem memória e codificação da fonte 1 Conteúdo
Interpolação polinomial: Polinômio de Lagrange
 Interpolação polinomial: Polinômio de Lagrange Marina Andretta ICMC-USP 09 de maio de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo
Interpolação polinomial: Polinômio de Lagrange Marina Andretta ICMC-USP 09 de maio de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo
Problemas de otimização
 Problemas de otimização Problemas de decisão: Existe uma solução satisfazendo certa propriedade? Resultado: sim ou não Problemas de otimização: Entre todas as soluções satisfazendo determinada propriedade,
Problemas de otimização Problemas de decisão: Existe uma solução satisfazendo certa propriedade? Resultado: sim ou não Problemas de otimização: Entre todas as soluções satisfazendo determinada propriedade,
Jogos de soma zero com dois jogadores
 Jogos de soma zero com dois jogadores Problema: Dada uma matriz A m n, encontrar um equilíbrio de Nash (de estratégias mistas). Jogador 1 quer encontrar p que maximize v sujeito a i p i = 1 sujeito a (pa)
Jogos de soma zero com dois jogadores Problema: Dada uma matriz A m n, encontrar um equilíbrio de Nash (de estratégias mistas). Jogador 1 quer encontrar p que maximize v sujeito a i p i = 1 sujeito a (pa)
Os números inteiros. Álgebra (Curso de CC) Ano lectivo 2005/ / 51
 Os números inteiros Abordaremos algumas propriedades dos números inteiros, sendo de destacar o Algoritmo da Divisão e o Teorema Fundamental da Aritmética. Falaremos de algumas aplicações como sejam a detecção
Os números inteiros Abordaremos algumas propriedades dos números inteiros, sendo de destacar o Algoritmo da Divisão e o Teorema Fundamental da Aritmética. Falaremos de algumas aplicações como sejam a detecção
Modelagem e Análise de Sistemas - COS767
 Modelagem e Análise de Sistemas - COS767 Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Geração de variáveis aleatórias: método da transformada inversa Simulação
Modelagem e Análise de Sistemas - COS767 Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Geração de variáveis aleatórias: método da transformada inversa Simulação
Otimização por Colônia de Formigas (Ant Colony Optimization - ACO)
 Otimização por Colônia de Formigas (Ant Colony Optimization - ACO) Eros Moreira de Carvalho Gabriel Silva Ramos CI209 - Inteligência Artificial BCC - Bacharelado em Ciência da Computação DInf - Departamento
Otimização por Colônia de Formigas (Ant Colony Optimization - ACO) Eros Moreira de Carvalho Gabriel Silva Ramos CI209 - Inteligência Artificial BCC - Bacharelado em Ciência da Computação DInf - Departamento
MA21: Resolução de Problemas - segunda prova - gabarito. Problema 1 (Olimpíada turca de 1996; 2 pontos) Considere o polinomio:
 MA21: Resolução de Problemas - segunda prova - gabarito Problema 1 (Olimpíada turca de 1996; 2 pontos) Considere o polinomio: p(x) (1 + x 3 ) (1 + 2x 9 ) (1 + 3x 27 )... (1 + nx 3n )... (1 + 1996 x 31996
MA21: Resolução de Problemas - segunda prova - gabarito Problema 1 (Olimpíada turca de 1996; 2 pontos) Considere o polinomio: p(x) (1 + x 3 ) (1 + 2x 9 ) (1 + 3x 27 )... (1 + nx 3n )... (1 + 1996 x 31996
Amostragem e distribuições por amostragem
 Amostragem e distribuições por amostragem Carla Henriques e Nuno Bastos Departamento de Matemática Escola Superior de Tecnologia de Viseu Contabilidade e Administração População, amostra e inferência estatística
Amostragem e distribuições por amostragem Carla Henriques e Nuno Bastos Departamento de Matemática Escola Superior de Tecnologia de Viseu Contabilidade e Administração População, amostra e inferência estatística
MCTA028 Programação Estruturada Aula 20 Exercícios de custos de um algoritmo
 MCTA028 Programação Estruturada Aula 20 Exercícios de custos de um algoritmo Prof. Jesús P. Mena-Chalco Q-2017 1 Estudo de algoritmos O projeto de algoritmos é influenciado pelo estudo de seus comportamentos.
MCTA028 Programação Estruturada Aula 20 Exercícios de custos de um algoritmo Prof. Jesús P. Mena-Chalco Q-2017 1 Estudo de algoritmos O projeto de algoritmos é influenciado pelo estudo de seus comportamentos.
Teoria dos Jogos. Ivan Sendin. 12 de novembro de FACOM - Universidade Federal de Uberlândia
 Otimização FACOM - Universidade Federal de Uberlândia ivansendin@yahoo.com,sendin@ufu.br 12 de novembro de 2018 Otimização Decisões dado um cenário Modalegem Matemática Solução Gráfica/Simplex O mundo
Otimização FACOM - Universidade Federal de Uberlândia ivansendin@yahoo.com,sendin@ufu.br 12 de novembro de 2018 Otimização Decisões dado um cenário Modalegem Matemática Solução Gráfica/Simplex O mundo
Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4)
 Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4) Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Sistemas dinâmicos discretos no tempo O Problema
Controle Ótimo - Aula 2 (Exemplos 2, 3 e 4) Adriano A. G. Siqueira e Marco H. Terra Departamento de Engenharia Elétrica Universidade de São Paulo - São Carlos Sistemas dinâmicos discretos no tempo O Problema
15/03/2018. Professor Ariel da Silva Dias Algoritmo e Contagem de Instruções. Prof. Ariel da Silva Dias -
 Professor Ariel da Silva Dias Algoritmo e Contagem de Instruções 1 Um algoritmo pode ser visto como uma sequência de ações executáveis para a obtenção de uma solução para um determinado tipo de problema.
Professor Ariel da Silva Dias Algoritmo e Contagem de Instruções 1 Um algoritmo pode ser visto como uma sequência de ações executáveis para a obtenção de uma solução para um determinado tipo de problema.
Inteligência Artificial. Resolução de problemas por meio de algoritmos de busca. Aula VI Busca Competitiva
 Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação http://www.inf.unioeste.br/~claudia/ia2017.html Inteligência Artificial Resolução de problemas por meio de algoritmos
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação http://www.inf.unioeste.br/~claudia/ia2017.html Inteligência Artificial Resolução de problemas por meio de algoritmos
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Somas aleatórias Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Simulação de Sistemas Discretos É
Estatística e Modelos Probabilísticos - COE241 Aula passada Somas aleatórias Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes Números Simulação de Sistemas Discretos É
Codificação de Huffman
 Codificação de Huffman Bruna Gregory Palm 11 de setembro de 2017 A codificação de Huffman é um método de compressão que considera as probabilidades de ocorrência de cada símbolo no conjunto de dados a
Codificação de Huffman Bruna Gregory Palm 11 de setembro de 2017 A codificação de Huffman é um método de compressão que considera as probabilidades de ocorrência de cada símbolo no conjunto de dados a
Unidade VII Amostragem
 Unidade VII Amostragem Na última aula... Saber os motivos que levam o pesquisador a trabalhar com amostra e entender a importância da inferência. Saber identificar população, amostra e variável aleatória.
Unidade VII Amostragem Na última aula... Saber os motivos que levam o pesquisador a trabalhar com amostra e entender a importância da inferência. Saber identificar população, amostra e variável aleatória.
Non-clairvoyant Scheduling Games
 1/35 Non-clairvoyant Scheduling Games Mijail Gamarra Holguin 9 de novembro de 2012 /35 Agenda 1 Introdução Definições Preliminares 2 Equiĺıbrio de Nash Random em máquinas uniformes Random em máquinas não
1/35 Non-clairvoyant Scheduling Games Mijail Gamarra Holguin 9 de novembro de 2012 /35 Agenda 1 Introdução Definições Preliminares 2 Equiĺıbrio de Nash Random em máquinas uniformes Random em máquinas não
Hashing: conceitos. Hashing
 Hashing: conceitos hashing é uma técnica conhecida como espalhamento, mapeamento ou randomização que tenta distribuir dados em posições aleatórias de uma tabela (array) associa cada objeto (de um determinado
Hashing: conceitos hashing é uma técnica conhecida como espalhamento, mapeamento ou randomização que tenta distribuir dados em posições aleatórias de uma tabela (array) associa cada objeto (de um determinado
Redes Neurais e Sistemas Fuzzy
 Redes Neurais e Sistemas Fuzzy O ADALINE e o algoritmo LMS O ADALINE No contexto de classificação, o ADALINE [B. Widrow 1960] pode ser visto como um perceptron com algoritmo de treinamento baseado em minimização
Redes Neurais e Sistemas Fuzzy O ADALINE e o algoritmo LMS O ADALINE No contexto de classificação, o ADALINE [B. Widrow 1960] pode ser visto como um perceptron com algoritmo de treinamento baseado em minimização
Jogos Estratégias Mistas
 Jogos Estratégias Mistas Redes Sociais e Econômicas Prof. André Vignatti Aula Passada Equilíbrio de Nash ninguém tem incentivo de desviar da estratégia Vários equilíbrios qual será a saída? Jogos de Coordenação
Jogos Estratégias Mistas Redes Sociais e Econômicas Prof. André Vignatti Aula Passada Equilíbrio de Nash ninguém tem incentivo de desviar da estratégia Vários equilíbrios qual será a saída? Jogos de Coordenação
Algoritmos de Aproximação Segundo Semestre de 2012
 Algoritmos de Aproximação Segundo Semestre de 2012 Aproximação p. 1 Problema dos k-centros Dados: um grafo completo G = (V,E), um inteiro k > 0 e distâncias d ij para cada i e j em V tais que d ii = 0
Algoritmos de Aproximação Segundo Semestre de 2012 Aproximação p. 1 Problema dos k-centros Dados: um grafo completo G = (V,E), um inteiro k > 0 e distâncias d ij para cada i e j em V tais que d ii = 0
Noções de Simulação. Ciências Contábeis - FEA - Noturno. 2 o Semestre MAE0219 (IME-USP) Noções de Simulação 2 o Semestre / 23
 Noções de Simulação Ciências Contábeis - FEA - Noturno 2 o Semestre 2013 MAE0219 (IME-USP) Noções de Simulação 2 o Semestre 2013 1 / 23 Objetivos da Aula Sumário 1 Objetivos da Aula 2 Motivação 3 Geração
Noções de Simulação Ciências Contábeis - FEA - Noturno 2 o Semestre 2013 MAE0219 (IME-USP) Noções de Simulação 2 o Semestre 2013 1 / 23 Objetivos da Aula Sumário 1 Objetivos da Aula 2 Motivação 3 Geração
Aula 7. Aula de hoje. Aula passada
 Aula 7 Aula passada Método de Monte Carlo Estimando somatórios Calculando erro Estimando Erro de Integração de Monte Carlo Monte Carlo Ray Tracing Aula de hoje Gerando amostras de v.a. discretas Gerando
Aula 7 Aula passada Método de Monte Carlo Estimando somatórios Calculando erro Estimando Erro de Integração de Monte Carlo Monte Carlo Ray Tracing Aula de hoje Gerando amostras de v.a. discretas Gerando
Cadeias de Markov em Tempo Continuo
 Cadeias de Markov em Tempo Continuo Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Capitulos 6 Taylor & Karlin 1 / 44 Análogo ao processo
Cadeias de Markov em Tempo Continuo Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Capitulos 6 Taylor & Karlin 1 / 44 Análogo ao processo
Problema do Caminho Mínimo
 Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Distribuições por Amostragem
 Distribuições por Amostragem Departamento de Matemática Escola Superior de Tecnologia de Viseu (DepMAT ESTV) Distribuições por Amostragem 2007/2008 1 / 27 Introdução: População, amostra e inferência estatística
Distribuições por Amostragem Departamento de Matemática Escola Superior de Tecnologia de Viseu (DepMAT ESTV) Distribuições por Amostragem 2007/2008 1 / 27 Introdução: População, amostra e inferência estatística
2. podemos solucionar problemas não somente probabilisticas, mas tambem qualquer
 Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Aula 3 (21/3/211, 23/3/211). Métodos de Monte Carlo I. Introdução. 1 Teoria ão temos no momento a definição exata de metodos de Monte Carlo. o nosso curso metodos de Monte Carlo vamos chamar metodos computacionais
Otimização em Grafos
 Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
Otimização em Grafos Luidi G. Simonetti PESC/COPPE 2017 Luidi Simonetti (PESC) EEL857 2017 1 / 33 Definição do Problema Dado: um grafo ponderado G = (V, E), orientado ou não, onde d : E R + define as distâncias
Projeto e Análise de Algoritmos
 Projeto e Análise de Algoritmos Aula 01 Complexidade de Algoritmos Edirlei Soares de Lima O que é um algoritmo? Um conjunto de instruções executáveis para resolver um problema (são
Projeto e Análise de Algoritmos Aula 01 Complexidade de Algoritmos Edirlei Soares de Lima O que é um algoritmo? Um conjunto de instruções executáveis para resolver um problema (são
Introdução a Redes Complexas
 Introdução a Redes Complexas Jornadas de Atualização em Informática (JAI) CSBC 2011 Encontro 3/3 Daniel R. Figueiredo LAND PESC/COPPE/UFRJ Organização do Mini-curso Três encontros (Qui 17h, Sex 11h, Sex
Introdução a Redes Complexas Jornadas de Atualização em Informática (JAI) CSBC 2011 Encontro 3/3 Daniel R. Figueiredo LAND PESC/COPPE/UFRJ Organização do Mini-curso Três encontros (Qui 17h, Sex 11h, Sex
SME Roberto F. Ausas / Gustavo C. Buscaglia
 SME0305-2016 Roberto F. Ausas / Gustavo C. Buscaglia ICMC - Ramal 736628, rfausas@gmail.com ICMC - Ramal 738176, gustavo.buscaglia@gmail.com Métodos iterativos Vamos considerar o problema: Achar x R n
SME0305-2016 Roberto F. Ausas / Gustavo C. Buscaglia ICMC - Ramal 736628, rfausas@gmail.com ICMC - Ramal 738176, gustavo.buscaglia@gmail.com Métodos iterativos Vamos considerar o problema: Achar x R n
Algoritmos Evolutivos Canônicos
 Algoritmos Evolutivos Canônicos Como representar os indivíduos Vetor de comprimento fixo com L características escolhidas previamente. Ex.: Definição
Algoritmos Evolutivos Canônicos Como representar os indivíduos Vetor de comprimento fixo com L características escolhidas previamente. Ex.: Definição
Busca Competitiva. Inteligência Artificial. Até aqui... Jogos vs. busca. Decisões ótimas em jogos 9/22/2010
 Inteligência Artificial Busca Competitiva Aula 5 Profª Bianca Zadrozny http://www.ic.uff.br/~bianca/ia-pos Capítulo 6 Russell & Norvig Seção 6.1 a 6.5 2 Até aqui... Problemas sem interação com outro agente.
Inteligência Artificial Busca Competitiva Aula 5 Profª Bianca Zadrozny http://www.ic.uff.br/~bianca/ia-pos Capítulo 6 Russell & Norvig Seção 6.1 a 6.5 2 Até aqui... Problemas sem interação com outro agente.
Problema de seleção de atividades. Aula 14. Exemplo. Algoritmos Gulosos. Algoritmos Gulosos. Intervalo: par ordenado de números
 Problema de seleção de atividades Aula 14 Algoritmos Gulosos Prof. Marco Aurélio Stefanes marco em dct.ufms.br www.dct.ufms.br/ marco Intervalo: par ordenado de números [s[i],f[i]): início e fim do intervalo
Problema de seleção de atividades Aula 14 Algoritmos Gulosos Prof. Marco Aurélio Stefanes marco em dct.ufms.br www.dct.ufms.br/ marco Intervalo: par ordenado de números [s[i],f[i]): início e fim do intervalo
Alternativamente pode ser pensado como uma forma de maximizar o minimo ganho possível.
 Inteligência Artificial Algoritmo i com cortes Alfa-Beta Ana Saraiva 050509087 Ana Barbosa 050509089 Marco Cunha 050509048 Tiago Fernandes 050509081 FEUP - MIEIC 3ºAno/ºSemestre 1 Introdução O algoritmo
Inteligência Artificial Algoritmo i com cortes Alfa-Beta Ana Saraiva 050509087 Ana Barbosa 050509089 Marco Cunha 050509048 Tiago Fernandes 050509081 FEUP - MIEIC 3ºAno/ºSemestre 1 Introdução O algoritmo
Elementos de Matemática Finita ( ) Exercícios resolvidos
 Elementos de Matemática Finita (016-017 Exercícios resolvidos Ficha 7-1. ( ( 30 10 0 10. Ficha 7 -. 4 10 ( 4 10. Ficha 7-3. A resposta à primeira pergunta é (5 3 ( 5 6. A probabilidade de acertar exactamente
Elementos de Matemática Finita (016-017 Exercícios resolvidos Ficha 7-1. ( ( 30 10 0 10. Ficha 7 -. 4 10 ( 4 10. Ficha 7-3. A resposta à primeira pergunta é (5 3 ( 5 6. A probabilidade de acertar exactamente
Buscas Informadas ou Heurísticas - Parte II
 Buscas Informadas ou Heurísticas - Parte II Prof. Cedric Luiz de Carvalho Instituto de Informática - UFG Graduação em Ciência da Computação / 2006 FUNÇÕES HEURÍSTICAS - 1/7 FUNÇÕES HEURÍSTICAS - 2/7 Solução
Buscas Informadas ou Heurísticas - Parte II Prof. Cedric Luiz de Carvalho Instituto de Informática - UFG Graduação em Ciência da Computação / 2006 FUNÇÕES HEURÍSTICAS - 1/7 FUNÇÕES HEURÍSTICAS - 2/7 Solução
Aprendizado por Reforço
 Aprendizado por Reforço Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aprendizado por Reforço 2. Q-Learning 3. SARSA 4. Outras ideias 1 Aprendizado por Reforço Problemas de decisão
Aprendizado por Reforço Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aprendizado por Reforço 2. Q-Learning 3. SARSA 4. Outras ideias 1 Aprendizado por Reforço Problemas de decisão
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
SISTEMAS LINEARES PROF. EDÉZIO
 SOLUÇÕES NUMÉRICAS DE SISTEMAS LINEARES PROF. EDÉZIO Considere o sistema de n equações e n incógnitas: onde E : a x + a x +... + a n x n = b E : a x + a x +... + a n x n = b. =. () E n : a n x + a n x
SOLUÇÕES NUMÉRICAS DE SISTEMAS LINEARES PROF. EDÉZIO Considere o sistema de n equações e n incógnitas: onde E : a x + a x +... + a n x n = b E : a x + a x +... + a n x n = b. =. () E n : a n x + a n x
Estatística e Modelos Probabilísticos - COE241
 Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
Estatística e Modelos Probabilísticos - COE241 Aula passada Análise da dados através de gráficos Introdução a Simulação Aula de hoje Introdução à simulação Geração de números aleatórios Lei dos Grandes
1 Conjuntos enumeráveis
 Medida e Integração. Departamento de Física e Matemática. USP-RP. Prof. Rafael A. Rosales de maio de 007. Conjuntos enumeráveis Denotamos por Q os numeros racionais, logo [0, ] Q, são os números racionais
Medida e Integração. Departamento de Física e Matemática. USP-RP. Prof. Rafael A. Rosales de maio de 007. Conjuntos enumeráveis Denotamos por Q os numeros racionais, logo [0, ] Q, são os números racionais
INF 1771 Inteligência Artificial
 Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 24 Aprendizado Por Reforço Formas de Aprendizado Aprendizado Supervisionado Árvores de Decisão. K-Nearest Neighbor (KNN).
Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 24 Aprendizado Por Reforço Formas de Aprendizado Aprendizado Supervisionado Árvores de Decisão. K-Nearest Neighbor (KNN).
MAC Aula 7. Walter Mascarenhas 13/04/2011
 MAC 5796. Aula 7 Walter Mascarenhas 13/04/011 Resumo Resolução da lista de exercícios 1 Resolução da lista de exercícios 3 4 A figura fundamental do cálculo f (x + δ) o ( δ ) δ f (x) + f (x)δ + 1 f (x)δ
MAC 5796. Aula 7 Walter Mascarenhas 13/04/011 Resumo Resolução da lista de exercícios 1 Resolução da lista de exercícios 3 4 A figura fundamental do cálculo f (x + δ) o ( δ ) δ f (x) + f (x)δ + 1 f (x)δ
Estruturas de Dados Tabelas de Espalhamento
 Estruturas de Dados Tabelas de Espalhamento Prof. Eduardo Alchieri (introdução) Uma estrutura como, as árvores binárias de busca, que trabalhe na ordem de log n é muito eficiente, mas em algumas situações
Estruturas de Dados Tabelas de Espalhamento Prof. Eduardo Alchieri (introdução) Uma estrutura como, as árvores binárias de busca, que trabalhe na ordem de log n é muito eficiente, mas em algumas situações
Aprendizado de Máquina (Machine Learning)
 Ciência da Computação (Machine Learning) Aula 07 Classificação com o algoritmo knn Max Pereira Classificação com o algoritmo k-nearest Neighbors (knn) Como os filmes são categorizados em gêneros? O que
Ciência da Computação (Machine Learning) Aula 07 Classificação com o algoritmo knn Max Pereira Classificação com o algoritmo k-nearest Neighbors (knn) Como os filmes são categorizados em gêneros? O que
Modelagem e Análise de Sistemas de Computação Aula 20
 Modelagem e Análise de Sistemas de Computação Aula 20 Aula passada Lei dos grandes números Calculando integrais Gerando outras distribuições Método da transformada inversa Aula de hoje Simulando uma fila
Modelagem e Análise de Sistemas de Computação Aula 20 Aula passada Lei dos grandes números Calculando integrais Gerando outras distribuições Método da transformada inversa Aula de hoje Simulando uma fila
Algoritmos de Aprendizado. Formas de Aprendizado. Aprendizado Batch x Incremental. Aprendizado Batch x Incremental
 Algoritmos de Aprendizado Regra de Hebb Perceptron Delta Rule (Least Mean Square Back Propagation Formas de Aprendizado Existe dois métodos básicos de aplicação do algoritmo Back Propagation: Aprendizado
Algoritmos de Aprendizado Regra de Hebb Perceptron Delta Rule (Least Mean Square Back Propagation Formas de Aprendizado Existe dois métodos básicos de aplicação do algoritmo Back Propagation: Aprendizado
Aprendizado por Reforço usando Aproximação
 Aprendizado por Reforço usando Aproximação de Funções Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aproximação de Funções 2. Do the evolution 1 Aproximação de Funções Função Utilidade
Aprendizado por Reforço usando Aproximação de Funções Fabrício Olivetti de França Universidade Federal do ABC Tópicos 1. Aproximação de Funções 2. Do the evolution 1 Aproximação de Funções Função Utilidade
Marina Andretta. 10 de outubro de Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis.
 Solução básica viável inicial Marina Andretta ICMC-USP 10 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
Solução básica viável inicial Marina Andretta ICMC-USP 10 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
lnteligência Artificial Introdução ao Processo Decisório de Markov
 lnteligência Artificial Introdução ao Processo Decisório de Markov Aprendizado - paradigmas Aprendizado supervisionado O crítico comunica a EA o erro relativo entre a ação que deve ser tomada idealmente
lnteligência Artificial Introdução ao Processo Decisório de Markov Aprendizado - paradigmas Aprendizado supervisionado O crítico comunica a EA o erro relativo entre a ação que deve ser tomada idealmente
Método Guloso. Troco mínimo. Paulo Eustáquio Duarte Pinto (pauloedp arroba ime.uerj.br) junho/2012. Troco mínimo. Troco mínimo
 Notas de aula da disciplina IME - ALGORITMOS E ESTRUTURAS DE DADOS II Paulo Eustáquio Duarte Pinto (pauloedp arroba ime.uerj.br) Troco mínimo Dados os tipos de moedas de um país, determinar o número mínimo
Notas de aula da disciplina IME - ALGORITMOS E ESTRUTURAS DE DADOS II Paulo Eustáquio Duarte Pinto (pauloedp arroba ime.uerj.br) Troco mínimo Dados os tipos de moedas de um país, determinar o número mínimo
Profa. Lidia Rodella UFPE-CAA
 Profa. Lidia Rodella UFPE-CAA O que é estatística? É conjunto de técnicas que permite, de forma sistemática, coletar, organizar, descrever, analisar e interpretar dados oriundos de estudos ou experimentos,
Profa. Lidia Rodella UFPE-CAA O que é estatística? É conjunto de técnicas que permite, de forma sistemática, coletar, organizar, descrever, analisar e interpretar dados oriundos de estudos ou experimentos,
> Princípios de Contagem e Enumeração Computacional 0/19
 Conteúdo 1 Princípios de Contagem e Enumeração Computacional Permutações Combinações > Princípios de Contagem e Enumeração Computacional 0/19 Permutações Utilizamos P(n, r) para denotar o número de sequências
Conteúdo 1 Princípios de Contagem e Enumeração Computacional Permutações Combinações > Princípios de Contagem e Enumeração Computacional 0/19 Permutações Utilizamos P(n, r) para denotar o número de sequências
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
INF 1771 Inteligência Artificial
 INF 1771 Inteligência Artificial Aula 18 Aprendizado Por Reforço Edirlei Soares de Lima Formas de Aprendizado Aprendizado Supervisionado Árvores de Decisão. K-Nearest Neighbor (KNN).
INF 1771 Inteligência Artificial Aula 18 Aprendizado Por Reforço Edirlei Soares de Lima Formas de Aprendizado Aprendizado Supervisionado Árvores de Decisão. K-Nearest Neighbor (KNN).
Matemática Discreta 12
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta 12 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti 1 Introdução
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta 12 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br - www.univasf.edu.br/~jorge.cavalcanti 1 Introdução
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/26 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/26 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
Aula 1: k-nearest Neighbors
 Aula 1: k-nearest Neighbors Paulo C. Marques F. Aula ministrada no Insper 29 de Janeiro de 2016 Insper Aula 1: k-nearest Neighbors 29 de Janeiro de 2016 1 / 14 O problema geral de classificação Insper
Aula 1: k-nearest Neighbors Paulo C. Marques F. Aula ministrada no Insper 29 de Janeiro de 2016 Insper Aula 1: k-nearest Neighbors 29 de Janeiro de 2016 1 / 14 O problema geral de classificação Insper
= comprimento (distância, valor) da aresta orientada do vértice i ao vértice j,, e:
 8 - Problema do Caminho Mínimo Considere a rede: Dado dois vértices nesta rede, queremos determinar o menor caminho ente eles. Uma primeira questão é como representar os valores associados às arestas neste
8 - Problema do Caminho Mínimo Considere a rede: Dado dois vértices nesta rede, queremos determinar o menor caminho ente eles. Uma primeira questão é como representar os valores associados às arestas neste
Análise de Complexidade de Algoritmos. mario alexandre gazziro
 Análise de Complexidade de Algoritmos mario alexandre gazziro Definição A complexidade de um algoritmo consiste na quantidade de esforço computacional necessária para sua execução. Esse esforço é expresso
Análise de Complexidade de Algoritmos mario alexandre gazziro Definição A complexidade de um algoritmo consiste na quantidade de esforço computacional necessária para sua execução. Esse esforço é expresso
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS
 EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
Análise e Complexidade de Algoritmos
 Análise e Complexidade de Algoritmos Principais paradigmas do projeto de algoritmos - Recursividade - Tentativa e erro - Divisão e Conquista - Programação dinâmica - Algoritmos Gulosos e de Aproximação
Análise e Complexidade de Algoritmos Principais paradigmas do projeto de algoritmos - Recursividade - Tentativa e erro - Divisão e Conquista - Programação dinâmica - Algoritmos Gulosos e de Aproximação
Avaliação e Desempenho Aula 18
 Avaliação e Desempenho Aula 18 Aula passada Fila com buffer finito Fila com buffer infinito Medidas de interesse: vazão, número médio de clientes na fila, taxa de perda. Aula de hoje Parâmetros de uma
Avaliação e Desempenho Aula 18 Aula passada Fila com buffer finito Fila com buffer infinito Medidas de interesse: vazão, número médio de clientes na fila, taxa de perda. Aula de hoje Parâmetros de uma
Teoria dos Grafos AULA
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA Caminho mínimo - Algoritmo de Djskstra Preparado a partir
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA Caminho mínimo - Algoritmo de Djskstra Preparado a partir
MC102 Aula 26. Instituto de Computação Unicamp. 17 de Novembro de 2016
 MC102 Aula 26 Recursão Instituto de Computação Unicamp 17 de Novembro de 2016 Roteiro 1 Recursão Indução 2 Recursão 3 Fatorial 4 O que acontece na memória 5 Recursão Iteração 6 Soma em um Vetor 7 Números
MC102 Aula 26 Recursão Instituto de Computação Unicamp 17 de Novembro de 2016 Roteiro 1 Recursão Indução 2 Recursão 3 Fatorial 4 O que acontece na memória 5 Recursão Iteração 6 Soma em um Vetor 7 Números
Introdução Paradigmas
 Introdução Paradigmas Recursividade Algoritmos tentativa e erro Divisão e conquista Programação dinâmica Algoritmos gulosos Algoritmos aproximados 1 Introdução O projeto de algoritmos requer abordagens
Introdução Paradigmas Recursividade Algoritmos tentativa e erro Divisão e conquista Programação dinâmica Algoritmos gulosos Algoritmos aproximados 1 Introdução O projeto de algoritmos requer abordagens
Técnicas de Projeto de Algoritmos
 UNIVERSIDADE NOVE DE JULHO - UNINOVE Pesquisa e Ordenação Técnicas de Projeto de Algoritmos Material disponível para download em: www.profvaniacristina.com Profa. Vânia Cristina de Souza Pereira 03 _ Material
UNIVERSIDADE NOVE DE JULHO - UNINOVE Pesquisa e Ordenação Técnicas de Projeto de Algoritmos Material disponível para download em: www.profvaniacristina.com Profa. Vânia Cristina de Souza Pereira 03 _ Material
Estruturas de Dados Algoritmos de Ordenação
 Estruturas de Dados Prof. Eduardo Alchieri (introdução) Considere uma sequência arbitrária S = {s1, s2, s3,...sn} composta por n 0 elementos retirados do conjunto universo U O objetivo da ordenação é arrumar
Estruturas de Dados Prof. Eduardo Alchieri (introdução) Considere uma sequência arbitrária S = {s1, s2, s3,...sn} composta por n 0 elementos retirados do conjunto universo U O objetivo da ordenação é arrumar
1.3 Outras definições de probabilidade
 14 CHAPTER 1. INTRODUÇÃO 1.3 Outras definições de probabilidade Até agora definimos probabilidade de um evento segundo a definição clássica, supondo sempre resultados equiprováveis. Outros métodos de definir
14 CHAPTER 1. INTRODUÇÃO 1.3 Outras definições de probabilidade Até agora definimos probabilidade de um evento segundo a definição clássica, supondo sempre resultados equiprováveis. Outros métodos de definir
Aula 5: k-means. Paulo C. Marques F. 1 de Abril de Aula ministrada no Insper. Insper Aula 5: k-means 1 de Abril de / 19
 Aula 5: k-means Paulo C. Marques F. Aula ministrada no Insper 1 de Abril de 2016 Insper Aula 5: k-means 1 de Abril de 2016 1 / 19 Aprendizagem não supervisionada Encerramos, por hora, o capítulo sobre
Aula 5: k-means Paulo C. Marques F. Aula ministrada no Insper 1 de Abril de 2016 Insper Aula 5: k-means 1 de Abril de 2016 1 / 19 Aprendizagem não supervisionada Encerramos, por hora, o capítulo sobre
Cap. 8 - Variáveis Aleatórias
 Variáveis Aleatórias Discretas: A de Poisson e Outras ESQUEMA DO CAPÍTULO 8.1 A DISTRIBUIÇÃO DE POISSON 8.2 A DISTRIBUIÇÃO DE POISSON COMO APROXIMAÇÃO DA DISTRIBUIÇÃO BINOMIAL 8.3 O PROCESSO DE POISSON
Variáveis Aleatórias Discretas: A de Poisson e Outras ESQUEMA DO CAPÍTULO 8.1 A DISTRIBUIÇÃO DE POISSON 8.2 A DISTRIBUIÇÃO DE POISSON COMO APROXIMAÇÃO DA DISTRIBUIÇÃO BINOMIAL 8.3 O PROCESSO DE POISSON
Canais discretos sem memória e capacidade do canal
 Canais discretos sem memória e capacidade do canal Luis Henrique Assumpção Lolis 17 de outubro de 2013 Luis Henrique Assumpção Lolis Canais discretos sem memória e capacidade do canal 1 Conteúdo 1 Canais
Canais discretos sem memória e capacidade do canal Luis Henrique Assumpção Lolis 17 de outubro de 2013 Luis Henrique Assumpção Lolis Canais discretos sem memória e capacidade do canal 1 Conteúdo 1 Canais
Módulo Tópicos Adicionais. Recorrências
 Módulo Tópicos Adicionais Recorrências Módulo Tópico Adicionais Recorrências 1 Exercícios Introdutórios Exercício 1 Considere a sequência definida por x 1 d e x n r + x n 1, para n > 1 Trata-se de uma
Módulo Tópicos Adicionais Recorrências Módulo Tópico Adicionais Recorrências 1 Exercícios Introdutórios Exercício 1 Considere a sequência definida por x 1 d e x n r + x n 1, para n > 1 Trata-se de uma
Análise de Dados e Simulação
 Universidade de São Paulo Instituto de Matemática e Estatística http:www.ime.usp.br/ mbranco Simulação de Variáveis Aleatórias Contínuas. O método da Transformada Inversa Teorema Seja U U (0,1). Para qualquer
Universidade de São Paulo Instituto de Matemática e Estatística http:www.ime.usp.br/ mbranco Simulação de Variáveis Aleatórias Contínuas. O método da Transformada Inversa Teorema Seja U U (0,1). Para qualquer
Aprendizado Bayesiano
 Aprendizado Bayesiano Marcelo K. Albertini 26 de Junho de 2014 2/20 Conteúdo Teorema de Bayes Aprendizado MAP Classificador ótimo de Bayes 3/20 Dois papéis para métodos bayesianos Algoritmos de aprendizado
Aprendizado Bayesiano Marcelo K. Albertini 26 de Junho de 2014 2/20 Conteúdo Teorema de Bayes Aprendizado MAP Classificador ótimo de Bayes 3/20 Dois papéis para métodos bayesianos Algoritmos de aprendizado
Minera c ao de Dados Aula 6: Finaliza c ao de Regress ao e Classifica c ao Rafael Izbicki 1 / 33
 Mineração de Dados Aula 6: Finalização de Regressão e Classificação Rafael Izbicki 1 / 33 Como fazer um IC para o risco estimado? Vamos assumir que ( X 1, Ỹ1),..., ( X s, Ỹs) são elementos de um conjunto
Mineração de Dados Aula 6: Finalização de Regressão e Classificação Rafael Izbicki 1 / 33 Como fazer um IC para o risco estimado? Vamos assumir que ( X 1, Ỹ1),..., ( X s, Ỹs) são elementos de um conjunto
Refinamentos de Equilíbrios de Nash
 Refinamentos de Equilíbrios de Nash Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Estatística - UFPE Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 06 de Outubro de 2014 Equilíbrio
Refinamentos de Equilíbrios de Nash Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Estatística - UFPE Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 06 de Outubro de 2014 Equilíbrio
4 Métodos Existentes. 4.1 Algoritmo Genético
 61 4 Métodos Existentes A hibridização de diferentes métodos é em geral utilizada para resolver problemas de escalonamento, por fornecer empiricamente maior eficiência na busca de soluções. Ela pode ser
61 4 Métodos Existentes A hibridização de diferentes métodos é em geral utilizada para resolver problemas de escalonamento, por fornecer empiricamente maior eficiência na busca de soluções. Ela pode ser
Primeiro Exercício programa: Como o Google ordena páginas. MAP-2121 para EPUSP
 Primeiro Exercício programa: Como o Google ordena páginas MAP-2121 para EPUSP 1 Instruções gerais Os exercícios computacionais pedidos na disciplina Cálculo Numérico têm por objetivo fundamental familiarizar
Primeiro Exercício programa: Como o Google ordena páginas MAP-2121 para EPUSP 1 Instruções gerais Os exercícios computacionais pedidos na disciplina Cálculo Numérico têm por objetivo fundamental familiarizar
5 TORIA ELEMENTAR DA AMOSTRAGEM
 5 TORIA ELEMENTAR DA AMOSTRAGEM É errôneo pensar que, caso tivéssemos acesso a todos os elementos da população, seríamos mais precisos. Os erros de coleta e manuseio de um grande número de dados são maiores
5 TORIA ELEMENTAR DA AMOSTRAGEM É errôneo pensar que, caso tivéssemos acesso a todos os elementos da população, seríamos mais precisos. Os erros de coleta e manuseio de um grande número de dados são maiores
Continuidade de processos gaussianos
 Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
Continuidade de processos gaussianos Roberto Imbuzeiro Oliveira April, 008 Abstract 1 Intrudução Suponha que T é um certo conjunto de índices e c : T T R é uma função dada. Pergunta 1. Existe uma coleção
