Observabilidade, Decomposição Canônica
|
|
|
- Carlos Eduardo Henrique Estrela
- 5 Há anos
- Visualizações:
Transcrição
1 Observabilidade, Decomposição Canônica 1. Observabilidade de Sistemas LIT 2. Dualidade 3. Índices de Observabilidade 4. Decomposição Canônica pag.1 Teoria de Sistemas Lineares Aula 16
2 Observabilidade Sistemas LIT Um estado pode ser observado (acessado) a partir saída? R 1 R 2 u + C 1 R 3 C 2 y Definem-se as variáveis de estado como v C1 e v C2 Note que a corrente através de R 3 iguala-se a entrada u (o circuito está aberto em y), portanto a resposta gerada pelo estado inicial v C1 (0) não aparece na saída y. Então o estado inicial v C1 (0) não pode ser observado a partir da saída pag.2 Teoria de Sistemas Lineares Aula 16
3 Observabilidade Sistemas LIT Conceito dual à controlabilidade Considere a equação dinâmica de dimensão n, p entradas e q saídas ẋ = Ax + Bu y = Cx + Du com A R n n, B R n p, C R q n e D R q p A equação de estado acima ou o par (A, C) é observável se, para qualquer estado inicial x(0), existir um tempo finito t 1 tal que o conhecimento da entrada u e da saída y no intervalo [0, t 1 ] seja suficiente para se determinar de maneira única o estado inicial x(0) pag.3 Teoria de Sistemas Lineares Aula 16
4 Observabilidade Sistemas LIT Exemplo i + u + 1 Ω x + 1 Ω y C 1 Ω 1 Ω Se a entrada é nula, a saída y é sempre nula independentemente da tensão inicial no capacitor (simetria do circuito). Conhece-se a entrada e a saída, porém não pode-se determinar unicamente o estado inicial O sistema é não observável... pag.4 Teoria de Sistemas Lineares Aula 16
5 Observabilidade Sistemas LIT Exemplo L x 1 + u R 1 R 2 C + x 2 y Variáveis de estado: corrente no indutor x 1 e tensão no capacitor x 2 Se u = 0, x 1 (0) = x 10 0 e x 2 (0) = 0, a saída y = x 2 é igual a zero. Qualquer condição inicial x(0) = [ a 0 ] com u = 0 produz a mesma saída y = 0 Não é possível determinar o estado inicial (não observável) pag.5 Teoria de Sistemas Lineares Aula 16
6 Observabilidade Sistemas LIT A saída do sistema para uma condição inicial x(0) e uma entrada u(t) é dada por y(t) = Ce At x(0) + C t 0 e A(t τ) Bu(τ)dτ + Du(t) Assumindo y e u conhecidos, a única incógnita é x(0). Então Ce At x(0) = ȳ ȳ y(t) C t t 0 e A(t τ) Bu(τ)dτ Du(t) pag.6 Teoria de Sistemas Lineares Aula 16
7 Observabilidade Sistemas LIT Estudar a observabilidade se reduz a obter x(0) a partir de u(t) e y(t). Se u 0, a saída ȳ(t) reduz-se a resposta à entrada nula y(t) = Ce At x(0) Um sistema é observável se e somente se o estado inicial x(0) pode ser determinado de maneira única a partir da resposta à entrada nula durante um intervalo de tempo Note que para um t fixo, com q < n, a matriz Ce At tem posto no máximo igual a q e, conseqüentemente, nulidade n q ou maior, e as soluções não são únicas pag.7 Teoria de Sistemas Lineares Aula 16
8 Observabilidade Sistemas LIT Teorema O sistema é observável se e somente se a matriz n n W o (t) = for não singular para qualquer t > 0 t 0 e A τ C Ce Aτ dτ Demonstração Pré-multiplicando Ce At x(0) = ȳ(t) por e A t C e integrando no intervalo [0, t 1 ] tem-se ( t1 ) t1 e A t C Ce At dt x(0) = e A t C ȳ(t)dt 0 Se W o (t 1 ) é não singular, x(0) é único e dado por x(0) = W 1 o (t 1) t1 0 0 e A t C ȳ(t)dt Isso mostra que se W o (t) é não singular para qualquer t > 0 então o sistema é observável pag.8 Teoria de Sistemas Lineares Aula 16
9 Observabilidade Sistemas LIT Agora, mostra-se que se W o (t 1 ) é singular (ou, equivalentemente, semidefinda positiva) para todo t 1 > 0, então o sistema é não observável Se W o (t 1 ) é semidefinda positiva, existe v R n 1 não nulo tal que v W o (t 1 )v = = t1 0 t1 0 v e A t C Ce At vdt Ce At v 2 dt = 0 o que implica Ce At v 0 para todo t [0, t 1 ]. Se u 0, as condições iniciais x 1 (0) = v 0 e x 2 (0) = 0 produzem a mesma saída e portanto o sistema é não observável y(t) = Ce At x 1 (0) = Ce At x 2 (0) 0 pag.9 Teoria de Sistemas Lineares Aula 16
10 Observabilidade Sistemas LIT Teorema (Dualidade) O par (A, B) é controlável se e somente se o par (A, B ) for observável Demonstração (A, B) controlável se e somente se W c (t) = t 0 e Aτ BB e A τ dτ for não singular para qualquer t > 0. O par (A, B ) é observável se e somente se, trocando A por A e C por B W o (t) = t 0 e Aτ BB e A τ dτ for não singular para qualquer t > 0 pag.10 Teoria de Sistemas Lineares Aula 16
11 Observabilidade Sistemas LIT Observabilidade: depende apenas de (A, C) Teorema As afirmações abaixo são equivalentes: 1. O par (A, C) é observável 2. A matriz n n é não-singular t > 0 W o (t) = t 0 e A τ C Ce Aτ dτ 3. A matriz de observabilidade nq n (comando obsv no Matlab) C CA O =. CA n 1 tem posto n (posto completo de colunas) pag.11 Teoria de Sistemas Lineares Aula 16
12 Observabilidade Sistemas LIT 4. A matriz (n + q) n λi A C tem posto n (posto completo de colunas) para todo autovalor λ de A 5. Se todos os autovalores de A têm parte real negativa, a solução única de A W o + W o A = C C é definida positiva. Essa solução é chamada de Gramiano de observabilidade e pode ser expressa como W o = 0 e A τ C Ce Aτ dτ pag.12 Teoria de Sistemas Lineares Aula 16
13 Índices de Observabilidade Considere A R n n e C R q n com C de posto completo de linhas (se não for o caso, alguma linha redundante pode ser eliminada) Se (A, C) for observável, a matriz de observabilidade O tem rank n e, conseqüentemente, n linhas linearmente independentes (de um total de nq linhas) Seja c i a i-ésima linha de C. De maneira dual à controlabilidade, se uma linha associada a c m torna-se LD, todas as demais linhas subseqüentes também o serão. Seja ν m o número de linhas LI associadas a c m. Se O tem rank n, ν 1 + ν ν q = n {ν 1, ν 2,..., ν p } são índices de observabilidade e é o índice de observabilidade de (A, C) ν = max {ν 1, ν 2,..., ν p } pag.13 Teoria de Sistemas Lineares Aula 16
14 Índices de Observabilidade Se (A, C) é observável, o índice de observabilidade ν é o menor inteiro tal que ρ(o ν ) = ρ O intervalo para ν é dado por C CA = n. CA ν 1 n/q ν min ( n, n q + 1) q = rank (C) sendo n o grau do polinômio mínimo de A pag.14 Teoria de Sistemas Lineares Aula 16
15 Índices de Observabilidade Corolário O par (A, C) com A R n n e ρ(c) = q é observável se e somente se a matriz C CA O n q+1 =. tiver posto n CA n q Teorema A observabilidade é invariante sob qualquer transformação de equivalência Teorema O conjunto de índices de observabilidade do par (A, C) é invariante sob qualquer transformação de equivalência e para qualquer re-ordenamento das linhas de C pag.15 Teoria de Sistemas Lineares Aula 16
16 Índices de Observabilidade Diferenciando Ce At x(0) = ȳ(t) e tomando t = 0, tem-se C ȳ(0) CA ȳ(0) x(0) = O ν x(0) = ỹ(0).. CA ν 1 ȳ (ν 1) (0) Uma solução x(0) existe se ỹ(0) estiver no range de O ν. Se (A, C) é observável, O ν tem rank completo de colunas e a solução é única x(0) = [O O] 1 O ỹ(0) Note que para a determinação do vetor ỹ(0) (contendo as derivadas) é necessário o conhecimento de ȳ(t) na vizinhança de t = 0 pag.16 Teoria de Sistemas Lineares Aula 16
17 Sistemas Equivalentes Considere o sistema ẋ y = Ax + Bu = Cx + Du Seja x = P x com P não singular. Então x = Ā x + Bu y = C x + Du Ā = PAP 1 ; B = PB ; C = CP 1 ; D = D é um sistema equivalente (A, B) controlável (Ā, B) controlável (A, C) observável (Ā, C) observável pag.17 Teoria de Sistemas Lineares Aula 16
18 Sistemas Equivalentes Todas as propriedades (estabilidade, controlabilidade e observabilidade) são preservadas pela transformação de equivalência. As matrizes de controlabilidade e de observabilidade se relacionam da seguinte forma C = PC ; Ō = OP 1 pag.18 Teoria de Sistemas Lineares Aula 16
19 Decomposição Canônica Teorema Considere um sistema de dimensão n com ([ ]) ρ(c) = ρ B AB A n 1 B = n 1 < n [ e forme a matriz n n, P 1 q 1 q n1 q n ], cujas primeiras n 1 colunas são quaisquer n 1 colunas LI de C e as demais são escolhidas arbitrariamente de modo que P seja não singular A transformação de equivalência x = Px transforma o sistema em x c x c = y = Āc Ā 12 0 Ā c x c [ C c C c ] x c com Ā c R n 1 n 1 e Ā c R (n n 1) (n n 1 ) x c x c + + Du B c 0 u pag.19 Teoria de Sistemas Lineares Aula 16
20 Decomposição Canônica A sub-equação de dimensão n 1 x c = Ā c x c + B c u ȳ = C c x c + Du é controlável e tem a mesma matriz de transferência do sistema original pag.20 Teoria de Sistemas Lineares Aula 16
21 Decomposição Canônica Demonstração A transformação x = P 1 x realiza uma mudança de representação do estado da base ortonormal para a base Q P 1 = {q 1,..., q n1,..., q n }. A i-ésima coluna de Ā é a representação de Aq i na base {q 1,..., q n1,..., q n }. Para i = 1,..., n 1, os vetores Aq i são LD no conjunto {q 1,..., q n1 } e são LI em {q n1 +1,..., q n }, o que explica a forma da matriz Ā As colunas de B são a representação das colunas de B em relação à base {q 1,..., q n1,..., q n }. Mas as colunas de B dependem apenas de {q 1,..., q n1 }, o que explica a forma de B. Note que se B R n p tem rank p e se suas colunas são escolhidas como as primeiras p colunas de P 1, então a parte superior de B será a matriz identidade de ordem p pag.21 Teoria de Sistemas Lineares Aula 16
22 Decomposição Canônica Seja C a matriz de controlabilidade de (A, B). Então, tem-se ρ(c) = ρ( C) = n 1 e pode-se verificar que C = B c Ā c B c Ā n 1 c B c Ā n 1 c B c } = C c Ā n 1 c B c Ā n 1 c B c n 1 linhas } n n 1 linhas sendo C c a matriz de controlabilidade do par (Ā c, B c ). Como as colunas de Ā k c B c, para k n 1, são LD das colunas de C c, a condição ρ(c) = n 1 implica ρ( C) = n 1 e portanto a equação de dimensão n 1 é controlável Resta mostrar que a equação de dimensão n 1 tem a mesma função de transferência do sistema original? pag.22 Teoria de Sistemas Lineares Aula 16
23 Decomposição Canônica A equação de dimensão n 1 tem a mesma FT do sistema original? Como a transformação de equivalência não altera a FT, basta mostrar que a FT do sistema de dimensão n 1 é igual à do sistema transformado Note que no sistema transformado tem-se: 1 si Ā ( ) 1 c Ā 12 si Āc M = ( ) 1 0 si Ā c 0 si Ā c com M = ( si Ā c ) 1 Ā 12 ( si Ā c ) 1 e portanto a matriz de transferência do sistema transformado é... pag.23 Teoria de Sistemas Lineares Aula 16
24 Decomposição Canônica Matriz de transferência: [ C c C c ] si Ā c Ā 12 0 si Ā c 1 B c 0 + D = [ C c C c ] ( ) 1 si Āc M ( ) 1 0 si Ā c B c 0 + D = C c ( si Āc ) 1 B c + D i.e., têm a mesma FT... pag.24 Teoria de Sistemas Lineares Aula 16
25 Decomposição Canônica Na transformação de equivalência x = Px, o espaço de estados é dividio em dois subespaços: um controlável e outro não controlável Decomposição do espaço de estados não-controlável; dimensão n n 1 x c x c = x c x c controlável; dimensão n 1 pag.25 Teoria de Sistemas Lineares Aula 16
26 Decomposição Canônica Exemplo ẋ = x [ u ; y = ] x rank(b) é 2 C 2 = [ B AB ] ρ(c 2 ) = ρ o sistema é não controlável = 2 < 3 pag.26 Teoria de Sistemas Lineares Aula 16
27 Decomposição Canônica Escolha: P 1 = Q = ; x = Px as duas primeiras colunas de Q são as duas primeiras colunas LI de C 2. Note Ā = PAP 1 = ; B = PB = C = CP 1 = [ ] pag.27 Teoria de Sistemas Lineares Aula 16
28 Decomposição Canônica Sistema de dimensão n 1 = 2 x c = 1 0 x c u ; y = [ 1 2 ] x MATLAB A função ctrbf transforma o sistema para a forma canônica controlável, mas com as colunas de P 1 na ordem inversa, resultando Ā c 0 ; 0 B Ā 21 Ā c c pag.28 Teoria de Sistemas Lineares Aula 16
29 Decomposição Canônica Teorema (Decomposição Canônica Forma Dual) Considere um sistema de dimensão n com C CA ρ(o) = ρ. = n 2 < n. CA n 1 [ ] e forme a matriz n n P p 1... p n2... p n cujas primeiras n 2 linhas são quaisquer n 2 linhas LI de O e as demais são escolhidas arbitrariamente de modo que P seja não singular. Então... pag.29 Teoria de Sistemas Lineares Aula 16
30 Decomposição Canônica Então, x = Px transforma o sistema em x o = Āo 0 xō Ā 21 Āō y = [ C o 0 x o ] x o xō xō + + Du B o Bō u Ā o R n 2 n 2 e Āō R (n n 2) (n n 2 ). A sub-equação de dimensão n 2 x o = Ā o x o + B o u ȳ = C o x o + Du é observável e tem a mesma matriz de transferência MATLAB obsvf pag.30 Teoria de Sistemas Lineares Aula 16
31 Decomposição Canônica Teorema (Decomposição de Kalman) Toda equação de estado pode ser transformada na forma canônica equivalente x co Ā co 0 Ā 13 0 x co B co x cō Ā 21 Ā cō Ā 23 Ā 24 x cō B cō = + u x co 0 0 Ā co 0 x co 0 x cō 0 0 Ā 43 Ā cō 0 x cō y = [ C co 0 C co 0 ] x + Du sendo, x co controlável e observável; x cō controlável e não observável; x co não controlável e observável e x cō não controlável e não observável pag.31 Teoria de Sistemas Lineares Aula 16
32 Decomposição Canônica O sistema é equivalente (para estado inicial nulo) à equação de estado controlável e observável x co = Ā co x co + B co u y = C co x co + Du com a matriz de transferência dada por: G(s) = C co (si Ā co ) 1 B co + D pag.32 Teoria de Sistemas Lineares Aula 16
33 Decomposição de Kalman Decomposição Canônica CŌ u CO y CO C CŌ Descrição por FT não é necessariamente equivalente à descrição por equações de estado MATLAB minreal (realização mínima, cancelando pólos e zeros) pag.33 Teoria de Sistemas Lineares Aula 16
34 Decomposição Canônica Exemplo 2 F 1 Ω + x 1 u x 2 1 H 1 H 1 Ω 1 Ω 2 F x 4 + y + x 3 1 Ω 1 Ω Eliminando as variáveis de estado que são não controláveis e/ou não observáveis... pag.34 Teoria de Sistemas Lineares Aula 16
35 Decomposição Canônica Eliminando as variáveis de estado que não são controláveis (circuito com o R+L do lado aberto em y) e e/ou não são observáveis (C+L em paralelo na malha da fonte de corrente u) (note ainda que devido a simetria x 3 é não controlável e não observável...): u 1 Ω 1 Ω 1 Ω 1 Ω + y Corrente em cada ramo: u/2 e saída y = u/2 + u/2 = u. Portanto FT: y = u, i.e., G(s) = 1 pag.35 Teoria de Sistemas Lineares Aula 16
36 Decomposição Canônica Equação de estado do circuito original (forma canônica controlável) ẋ = x + u [ ] y = x + u Parte controlável ẋ c = y = x c u [ ] 0 0 x c + u y = u pag.36 Teoria de Sistemas Lineares Aula 16
Teoria de Sistemas Lineares I
 Teoria de Sistemas Lineares I Prof. Aguinaldo S.e Silva, Universidade Federal de Santa Catarina Observabilidade Conceito dual à controlabilidade. Considere a equação dinâmica de dimensão n, p entradas
Teoria de Sistemas Lineares I Prof. Aguinaldo S.e Silva, Universidade Federal de Santa Catarina Observabilidade Conceito dual à controlabilidade. Considere a equação dinâmica de dimensão n, p entradas
Teoria de Sistemas Lineares I
 Prof. Aguinaldo S.e Silva Universidade Federal de Santa Catarina Controlabilidade e Observabilidade Considere a equação dinâmica de dimensão n e p entradas ẋ = Ax + Bu com A R n n e B R n p. Definição:
Prof. Aguinaldo S.e Silva Universidade Federal de Santa Catarina Controlabilidade e Observabilidade Considere a equação dinâmica de dimensão n e p entradas ẋ = Ax + Bu com A R n n e B R n p. Definição:
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2
 FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
Sistemas Dinâmicos Lineares
 Sistemas Dinâmicos Lineares 1. Descrição de sistemas dinâmicos 1.1. Sinais? 1.2. Sistemas? 1.3. Espaço de estados. Resposta do sistema dinâmico 2. Estabilidade de sistemas dinâmicos 2.1. Análise de estabilidade
Sistemas Dinâmicos Lineares 1. Descrição de sistemas dinâmicos 1.1. Sinais? 1.2. Sistemas? 1.3. Espaço de estados. Resposta do sistema dinâmico 2. Estabilidade de sistemas dinâmicos 2.1. Análise de estabilidade
Realimentação de Estado Sistemas SISO
 1. Realimentação de Estado para Sistemas SISO pag.1 Teoria de Sistemas Lineares Aula 18 Considere o sistema n dimensional, SISO: ẋ = Ax + bu y = cx Na realimentação de estados, a entrada u é dada por u
1. Realimentação de Estado para Sistemas SISO pag.1 Teoria de Sistemas Lineares Aula 18 Considere o sistema n dimensional, SISO: ẋ = Ax + bu y = cx Na realimentação de estados, a entrada u é dada por u
EES-20: Sistemas de Controle II. 06 Setembro 2017
 EES-2: Sistemas de Controle II 6 Setembro 217 1 / 56 Recapitulando: Observador de Estado Modelo da planta: Observador de estado: ẋ = Ax + Bu y = Cx ˆx = Aˆx + Bu + L(y ŷ) ŷ = C ˆx Erro de estimação do
EES-2: Sistemas de Controle II 6 Setembro 217 1 / 56 Recapitulando: Observador de Estado Modelo da planta: Observador de estado: ẋ = Ax + Bu y = Cx ˆx = Aˆx + Bu + L(y ŷ) ŷ = C ˆx Erro de estimação do
Cap. 3 - Observabilidade e desacoplamento da Saída
 Cap. 3 - Observabilidade e desacoplamento da Saída Visão geral do capítulo No capítulo 2 mostramos que a controlabilidade está relacionada com o menor subespaço A-invariante que contém a imagem de B. Mostramos
Cap. 3 - Observabilidade e desacoplamento da Saída Visão geral do capítulo No capítulo 2 mostramos que a controlabilidade está relacionada com o menor subespaço A-invariante que contém a imagem de B. Mostramos
SISTEMAS REALIMENTADOS
 SISTEMAS REALIMENTADOS Prof.: Helder Roberto de O. Rocha Engenheiro Eletricista Doutorado em Computação Representação no Espaço de Estados É apropriada para sistemas que possuem várias entradas e várias
SISTEMAS REALIMENTADOS Prof.: Helder Roberto de O. Rocha Engenheiro Eletricista Doutorado em Computação Representação no Espaço de Estados É apropriada para sistemas que possuem várias entradas e várias
X. MÉTODOS DE ESPAÇO DE ESTADOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE X. MÉTODOS DE ESPAÇO DE ESTADOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE X. MÉTODOS DE ESPAÇO DE ESTADOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
Estimadores ou Observadores de Estado
 Estimadores ou Observadores de Estado 1. Estimadores ou Observadores de Estado: sistemas SISO 1. Extensões para Sistemas a Tempo Discreto pag.1 Teoria de Sistemas Lineares Aula 19 Estimadores ou Observadores
Estimadores ou Observadores de Estado 1. Estimadores ou Observadores de Estado: sistemas SISO 1. Extensões para Sistemas a Tempo Discreto pag.1 Teoria de Sistemas Lineares Aula 19 Estimadores ou Observadores
EES-20: Sistemas de Controle II. 21 Agosto 2017
 EES-2: Sistemas de Controle II 21 Agosto 217 1 / 52 Recapitulando: Realimentação de estado r t u t y t x t Modelo da planta: Lei de controle: ẋ = Ax + Bu y = Cx u = Kx + Fr Representação para o sistema
EES-2: Sistemas de Controle II 21 Agosto 217 1 / 52 Recapitulando: Realimentação de estado r t u t y t x t Modelo da planta: Lei de controle: ẋ = Ax + Bu y = Cx u = Kx + Fr Representação para o sistema
Estabilidade Interna. 1. Estabilidade Interna. 2. Análise de Estabilidade Segundo Lyapunov. 3. Teorema de Lyapunov
 Estabilidade Interna 1. Estabilidade Interna 2. Análise de Estabilidade Segundo Lyapunov 3. Teorema de Lyapunov 4. Teorema de Lyapunov Caso Discreto pag.1 Teoria de Sistemas Lineares Aula 13 Estabilidade
Estabilidade Interna 1. Estabilidade Interna 2. Análise de Estabilidade Segundo Lyapunov 3. Teorema de Lyapunov 4. Teorema de Lyapunov Caso Discreto pag.1 Teoria de Sistemas Lineares Aula 13 Estabilidade
Revisão - Controlabilidade e observabilidade - SLIT.
 Revisão - Controlabilidade e observabilidade - SLIT. ENGC65: Sistemas de Controle III Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 12 de maio de 2014 Prof. Tito Luís Maia
Revisão - Controlabilidade e observabilidade - SLIT. ENGC65: Sistemas de Controle III Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 12 de maio de 2014 Prof. Tito Luís Maia
1. Realimentação de Estado: sistemas MIMO
 Realimentação de Estado: sistemas MIMO 1. Realimentação de Estado: sistemas MIMO 2. Estimadores de Estado: sistemas MIMO pag.1 Teoria de Sistemas Lineares Aula 20 Realimentação de Estado: sistemas MIMO
Realimentação de Estado: sistemas MIMO 1. Realimentação de Estado: sistemas MIMO 2. Estimadores de Estado: sistemas MIMO pag.1 Teoria de Sistemas Lineares Aula 20 Realimentação de Estado: sistemas MIMO
Algebra Linear. 1. Ortonormalização. 2. Sistema de Equações Lineares. pag.1 Teoria de Sistemas Lineares Aula 6. c Reinaldo M.
 Algebra Linear 1. Ortonormalização 2. Sistema de Equações Lineares pag.1 Teoria de Sistemas Lineares Aula 6 Ortonormalização Um vetor x é dito estar normalizado se sua norma Euclidiana é igual a 1, ie,
Algebra Linear 1. Ortonormalização 2. Sistema de Equações Lineares pag.1 Teoria de Sistemas Lineares Aula 6 Ortonormalização Um vetor x é dito estar normalizado se sua norma Euclidiana é igual a 1, ie,
Algebra Linear. 1. Revisitando autovalores e autovetores. 2. Forma Diagonal e Forma de Jordan. 2.1 Autovalores distintos. 2.2 Autovalores complexos
 Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Controlabilidade. Uma representação (ou realização) de um sistema dinâmico no espaço de estados:
 Controlabilidade Uma representação (ou realização) de um sistema dinâmico no espaço de estados: x = Ax + Bu ou equivalentemente o par (A, B), é dito controlável (completamente controlável, de estado controlável)
Controlabilidade Uma representação (ou realização) de um sistema dinâmico no espaço de estados: x = Ax + Bu ou equivalentemente o par (A, B), é dito controlável (completamente controlável, de estado controlável)
Cap.2. Representação de Estado e Controlabilidade
 Cap.2. Representação de Estado e Controlabilidade Visão geral do capítulo Neste capítulo trataremos o problema da controlabilidade de sistemas lineares invariantes no tempo. Faremos antes uma breve revisão
Cap.2. Representação de Estado e Controlabilidade Visão geral do capítulo Neste capítulo trataremos o problema da controlabilidade de sistemas lineares invariantes no tempo. Faremos antes uma breve revisão
Matrizes e Linearidade
 Matrizes e Linearidade 1. Revisitando Matrizes 1.1. Traço, Simetria, Determinante 1.. Inversa. Sistema de Equações Lineares. Equação Característica.1. Autovalor & Autovetor 4. Polinômios Coprimos 5. Função
Matrizes e Linearidade 1. Revisitando Matrizes 1.1. Traço, Simetria, Determinante 1.. Inversa. Sistema de Equações Lineares. Equação Característica.1. Autovalor & Autovetor 4. Polinômios Coprimos 5. Função
SEM Sistemas de Controle. Aula 4 - Controladores PID, Avanço, Atraso, Esp. Estados
 SEM 5928 - Sistemas de Controle Aula 4 - Controladores PID, Avanço, Atraso e no Espaço de Estados Universidade de São Paulo Controlador PID Controlador Proporcional Controlador Integral Controlador PID
SEM 5928 - Sistemas de Controle Aula 4 - Controladores PID, Avanço, Atraso e no Espaço de Estados Universidade de São Paulo Controlador PID Controlador Proporcional Controlador Integral Controlador PID
Estabilidade para Sistemas LVT
 Estabilidade para Sistemas LVT 1. Estabilidade de Sistemas Variante no Tempo 2. Estabilidade da Resposta à Entrada Nula pag.1 Teoria de Sistemas Lineares Aula 14 Estabilidade de Sistemas Variante no Tempo
Estabilidade para Sistemas LVT 1. Estabilidade de Sistemas Variante no Tempo 2. Estabilidade da Resposta à Entrada Nula pag.1 Teoria de Sistemas Lineares Aula 14 Estabilidade de Sistemas Variante no Tempo
Encontro 5: Soluções no Espaço de Estados Parte I
 Encontro 5: Soluções no Espaço de Estados Parte I Samir A. M. Martins 1 2 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET MG e UFSJ
Encontro 5: Soluções no Espaço de Estados Parte I Samir A. M. Martins 1 2 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET MG e UFSJ
Estabilidade. 1. Estabilidade Entrada-Saída Sistemas LIT. 2. Estabilidade BIBO Sistemas LIT. 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT
 Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1
 FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Revisão O que é um corpo (campo)? O que é um espaço
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Revisão O que é um corpo (campo)? O que é um espaço
Modelagem Matemática de Sistemas
 Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
LISTAS DE EXERCÍCIOS PTC Controle Linear Multivariável (Pós-Graduação) Prof. Paulo Sérgio Pereira da Silva
 LISTAS DE EXERCÍCIOS PTC - 5746 Controle Linear Multivariável Pós-Graduação Prof. Paulo Sérgio Pereira da Silva 27 ạ Lista de Exercícios Algebra Linear Controle Multivariável PTC 5746 Prof. Paulo Sérgio
LISTAS DE EXERCÍCIOS PTC - 5746 Controle Linear Multivariável Pós-Graduação Prof. Paulo Sérgio Pereira da Silva 27 ạ Lista de Exercícios Algebra Linear Controle Multivariável PTC 5746 Prof. Paulo Sérgio
Álgebra Linear Teoria de Matrizes
 Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
Controlabilidade. Uma representação (ou realização) de um sistema dinâmico no espaço de estados:
 Controlabilidade Uma representação (ou realização) de um sistema dinâmico no espaço de estados: x Ax Bu ou equivalentemente o par (A, B), é dito controlável (completamente controlável, de estado controlável)
Controlabilidade Uma representação (ou realização) de um sistema dinâmico no espaço de estados: x Ax Bu ou equivalentemente o par (A, B), é dito controlável (completamente controlável, de estado controlável)
-GNE219 - Controle em Espaço de Estados
 Universidade Federal de Lavras Departamento de Engenharia -GNE219 - Controle em Espaço de Estados Prof. Daniel Leite E-mail: daniel.leite@deg.ufla.br 2/2017 1/29 Sumário Controlabilidade Observabilidade
Universidade Federal de Lavras Departamento de Engenharia -GNE219 - Controle em Espaço de Estados Prof. Daniel Leite E-mail: daniel.leite@deg.ufla.br 2/2017 1/29 Sumário Controlabilidade Observabilidade
ANÁLISE DE SISTEMAS LINEARES NO ESPAÇO DE ESTADOS
 AE- ANÁLISE DE SISTEMAS LINEARES NO ESPAÇO DE ESTADOS AE- Determine os valores e vectores próprios de a) A= -.5.5 -.5 b) B= - - AE- Forma canónica controlável. a) Mostre que a equação diferencial homogénea
AE- ANÁLISE DE SISTEMAS LINEARES NO ESPAÇO DE ESTADOS AE- Determine os valores e vectores próprios de a) A= -.5.5 -.5 b) B= - - AE- Forma canónica controlável. a) Mostre que a equação diferencial homogénea
Estabilidade de sistemas de controle lineares invariantes no tempo
 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
Teoria de Controle (sinopse) 8 Controlabilidade. J. A. M. Felippe de Souza
 Teoria de Controle (sinopse) 8 Controlabilidade J. A. M. Felippe de Souza Primeiramente introduziremos o conceito de controlabilidade e alcançabilidade. Definição U ou U [t,t ] espaço das funções contínuas
Teoria de Controle (sinopse) 8 Controlabilidade J. A. M. Felippe de Souza Primeiramente introduziremos o conceito de controlabilidade e alcançabilidade. Definição U ou U [t,t ] espaço das funções contínuas
Estabilidade. Samir A. M. Martins 1. Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG
 Interna Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG O que nos espera? Interna 1 em sistemas multivariáveis
Interna Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG O que nos espera? Interna 1 em sistemas multivariáveis
Modelagem Matemática de Sistemas
 Modelagem Matemática de Sistemas 1. de modelagem com Circuitos Elétricos 2. Sistemática para Obtenção de Equações de Estado pag.1 Teoria de Sistemas Lineares Aula 4 Descrição Matemática de Sistemas Exemplo
Modelagem Matemática de Sistemas 1. de modelagem com Circuitos Elétricos 2. Sistemática para Obtenção de Equações de Estado pag.1 Teoria de Sistemas Lineares Aula 4 Descrição Matemática de Sistemas Exemplo
Parte I. Álgebra Linear. Sistemas Dinâmicos Lineares. Autovalores, autovetores. Autovalores, autovetores. Autovalores e Autovetores.
 Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Sistemas Dinâmicos Lineares Romeu Reginatto Programa de Pós-Graduação em Engenharia de Sistemas Dinâmicos e Energéticos Universidade Estadual do Oeste do Paraná Parte I Álgebra Linear Adaptado das notas
Modelagem de Sistemas de Controle por Espaço de Estados
 Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
Noções de Álgebra Linear
 Noções de Álgebra Linear 1. Espaços vetoriais lineares 1.1. Coordenadas 2. Operadores lineares 3. Subespaços fundamentais 4. Espaços normados 5. Espaços métricos 6. Espaços de Banach 7. Espaços de Hilbert
Noções de Álgebra Linear 1. Espaços vetoriais lineares 1.1. Coordenadas 2. Operadores lineares 3. Subespaços fundamentais 4. Espaços normados 5. Espaços métricos 6. Espaços de Banach 7. Espaços de Hilbert
Redução de Múltiplos Subsistemas. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Redução de Múltiplos Subsistemas Carlos Alexandre Mello 1 Introdução Sistemas mais complexos são compostos por diversos subsistemas Queremos representar múltiplos subsistemas com apenas uma função de transferência
Redução de Múltiplos Subsistemas Carlos Alexandre Mello 1 Introdução Sistemas mais complexos são compostos por diversos subsistemas Queremos representar múltiplos subsistemas com apenas uma função de transferência
(b) A não será diagonalizável sobre C e A será diagonalizável sobre R se, e
 Q1. Sejam A M 6 (R) uma matriz real e T : R 6 R 6 o operador linear tal que [T ] can = A, em que can denota a base canônica de R 6. Se o polinômio característico de T for então poderemos afirmar que: p
Q1. Sejam A M 6 (R) uma matriz real e T : R 6 R 6 o operador linear tal que [T ] can = A, em que can denota a base canônica de R 6. Se o polinômio característico de T for então poderemos afirmar que: p
14 Estimador assintótico
 Teoria de Controle (sinopse) 4 J. A. M. Felippe de Souza Neste capítulo continuaremos no estudo de que foi iniciado no capítulo anterior. Estimadores de Estado, A exemplo dos capítulos anteriores será
Teoria de Controle (sinopse) 4 J. A. M. Felippe de Souza Neste capítulo continuaremos no estudo de que foi iniciado no capítulo anterior. Estimadores de Estado, A exemplo dos capítulos anteriores será
Trabalho para ser realizado no MATLAB Controle Multivariável PTC-2513 Prof. Paulo Sérgio
 Trabalho para ser realizado no MATLAB Controle Multivariável PTC-253 Prof. Paulo Sérgio Parte I - A ser entregue na primeira aula após a primeira prova. Considere o modelo linearizado do sistema de pêndulo
Trabalho para ser realizado no MATLAB Controle Multivariável PTC-253 Prof. Paulo Sérgio Parte I - A ser entregue na primeira aula após a primeira prova. Considere o modelo linearizado do sistema de pêndulo
Algebra Linear. 1. Espaços Vetoriais Lineares. 2. Coordenadas em Espaços Lineares. 3. Operadores Lineares. 4. Transformação de Similaridade
 Algebra Linear 1 Espaços Vetoriais Lineares Coordenadas em Espaços Lineares 3 Operadores Lineares 4 Transformação de Similaridade Matriz como Operador Norma de Vetores e Produto Interno pag1 Teoria de
Algebra Linear 1 Espaços Vetoriais Lineares Coordenadas em Espaços Lineares 3 Operadores Lineares 4 Transformação de Similaridade Matriz como Operador Norma de Vetores e Produto Interno pag1 Teoria de
Estabilidade de sistemas de controle lineares invariantes no tempo
 Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
Samir A. M. Martins 1
 Realizações Mínimas Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET MG e UFSJ O que nos espera? 1 Realização
Realizações Mínimas Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET MG e UFSJ O que nos espera? 1 Realização
Tópicos de Álgebra Linear Verão 2019 Lista 2: Transformações Lineares
 Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 2: Transformações Lineares Exercício 1. Prove que cada uma das transformações
Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 2: Transformações Lineares Exercício 1. Prove que cada uma das transformações
Análise Dinâmica de Sistemas Mecânicos e Controle
 Análise Dinâmica de Sistemas Mecânicos e Controle Unidade 3 Espaço de Estados: álgebra e resolução das equações dinâmicas Prof. Thiago da Silva Castro thiago.castro@ifsudestemg.edu.br Para trabalhar no
Análise Dinâmica de Sistemas Mecânicos e Controle Unidade 3 Espaço de Estados: álgebra e resolução das equações dinâmicas Prof. Thiago da Silva Castro thiago.castro@ifsudestemg.edu.br Para trabalhar no
Controle utilizando variáveis de estado - v1.1
 2 ontrole utilizando variáveis de estado - v. 2. Objetivo O objetivo desta experiência é, utilizando o enfoque de espaço de estados, projetar e implementar um controlador digital para uma planta simples
2 ontrole utilizando variáveis de estado - v. 2. Objetivo O objetivo desta experiência é, utilizando o enfoque de espaço de estados, projetar e implementar um controlador digital para uma planta simples
Diagonalização de Operadores. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes.
 Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Capítulo 8: Estado. Samir A. M. Martins 1. Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET MG e UFSJ
 Capítulo 8: Realimentação de Estados e Estimadores de Estado Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET
Capítulo 8: Realimentação de Estados e Estimadores de Estado Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre CEFET
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Teoria de Sistemas Lineares I
 Teoria de Sistemas Lineares I Prof. Aguinaldo S.e Silva Universidade Federal de Santa Catarina Estabilidade Entrada-Saída BIBO Estabilidade Considere o sistema linear SISO invariante no tempo, causal e
Teoria de Sistemas Lineares I Prof. Aguinaldo S.e Silva Universidade Federal de Santa Catarina Estabilidade Entrada-Saída BIBO Estabilidade Considere o sistema linear SISO invariante no tempo, causal e
EES-20: Sistemas de Controle II. 31 Julho 2017
 EES-20: Sistemas de Controle II 31 Julho 2017 1 / 41 Folha de informações sobre o curso 2 / 41 O que é Controle? Controlar: Atuar sobre um sistema físico de modo a obter um comportamento desejado. 3 /
EES-20: Sistemas de Controle II 31 Julho 2017 1 / 41 Folha de informações sobre o curso 2 / 41 O que é Controle? Controlar: Atuar sobre um sistema físico de modo a obter um comportamento desejado. 3 /
EES-20: Sistemas de Controle II
 EES-: Sistemas de Controle II 14 Agosto 17 1 / 49 Recapitulando: Estabilidade interna assintótica Modelo no espaço de estados: Equação de estado: ẋ = Ax + Bu Equação de saída: y = Cx + Du Diz-se que o
EES-: Sistemas de Controle II 14 Agosto 17 1 / 49 Recapitulando: Estabilidade interna assintótica Modelo no espaço de estados: Equação de estado: ẋ = Ax + Bu Equação de saída: y = Cx + Du Diz-se que o
DAS 5142 Sistemas Dinâmicos
 DAS 5142 Sistemas Dinâmicos Prof. Hector Bessa Silveira Universidade Federal de Santa Catarina UFSC Centro Tecnológico CTC Departamento de Automação e Sistemas DAS Sala 208 E-mail: hector.silveira@ufsc.br
DAS 5142 Sistemas Dinâmicos Prof. Hector Bessa Silveira Universidade Federal de Santa Catarina UFSC Centro Tecnológico CTC Departamento de Automação e Sistemas DAS Sala 208 E-mail: hector.silveira@ufsc.br
Autovetor e Autovalor de um Operador Linear
 Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
IV. ESTABILIDADE DE SISTEMAS LIT
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE IV. ESTABILIDADE DE SISTEMAS LIT Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE IV. ESTABILIDADE DE SISTEMAS LIT Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
Realimentação e Observador no Espaço de Estados Revisão
 Realimentação e Observador no Espaço de Estados Revisão 1. Realimentação de estados 1.1. Um tour por alocação de pólos 2. Observador ou Estimador 2.1. Observador? Por quê? 3. Princípio da separação 4.
Realimentação e Observador no Espaço de Estados Revisão 1. Realimentação de estados 1.1. Um tour por alocação de pólos 2. Observador ou Estimador 2.1. Observador? Por quê? 3. Princípio da separação 4.
1 a Lista de Exercícios de MAT3458 Escola Politécnica 2 o semestre de 2016
 1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
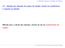 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
SISTEMAS LINEARES E INVARIANTES NO TEMPO
 SISTEMAS LINEARES E INVARIANTES NO TEMPO Paulo Lopes dos Santos Departamento de Engenharia Electrotécnica e Computadores Faculdade de Engenharia da Universidade do Porto Rua Dr Roberto Frias, s/n 4200-464
SISTEMAS LINEARES E INVARIANTES NO TEMPO Paulo Lopes dos Santos Departamento de Engenharia Electrotécnica e Computadores Faculdade de Engenharia da Universidade do Porto Rua Dr Roberto Frias, s/n 4200-464
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00
 Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00 [ ] 4 2 Questão 1. Seja T : R 2 R 2 o operador linear cuja matriz, com respeito à base canônica de R 2, é. 1 3 [ ] 2 0 Seja B uma base de R 2 tal que
Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00 [ ] 4 2 Questão 1. Seja T : R 2 R 2 o operador linear cuja matriz, com respeito à base canônica de R 2, é. 1 3 [ ] 2 0 Seja B uma base de R 2 tal que
1 Controlabilidade, observabilidade e estabilidade de sistemas em tempo contínuo
 Rio de Janeiro, 24 de março de 2006. 1 a Lista de Exercícios de Controle e Servomecanismos II Tópicos: autovalores, estabilidade, controlabilidade, observabilidade, realimentação de estado e observadores
Rio de Janeiro, 24 de março de 2006. 1 a Lista de Exercícios de Controle e Servomecanismos II Tópicos: autovalores, estabilidade, controlabilidade, observabilidade, realimentação de estado e observadores
Funções suaves e Variedades
 a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
DESCRIÇÃO MATEMÁTICA DE SISTEMAS PARTE 1
 DESRIÇÃO MATEMÁTIA DE SISTEMAS PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Modelagem de sistemas dinâmicos Descrição Entrada-Saída
DESRIÇÃO MATEMÁTIA DE SISTEMAS PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Modelagem de sistemas dinâmicos Descrição Entrada-Saída
-GNE219 - Controle em Espaço de Estados
 Universidade Federal de Lavras Departamento de Engenharia -GNE219 - Controle em Espaço de Estados Prof. Daniel Leite E-mail: daniel.leite@deg.ufla.br 2/2017 1/35 Sumário Conceitos básicos de modelos em
Universidade Federal de Lavras Departamento de Engenharia -GNE219 - Controle em Espaço de Estados Prof. Daniel Leite E-mail: daniel.leite@deg.ufla.br 2/2017 1/35 Sumário Conceitos básicos de modelos em
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
ÁLGEBRA LINEAR - MAT0024
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
5 Descrição entrada-saída
 Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Teorema 2.3: (Identidade de Bezout Generalizada) Sejam G(s) = N(s)D 1 1
 Teorema 2.3: (Identidade de Bezout Generalizada) ejam G(s) D (s) D (s)ñ(s) DFMs irredutíveis, então existem matrizes polinomiais X (s), Y (s), X(s) e Y(s) tais que Y(s) X(s) X (s) D(s) Ñ(s) D(s) Y (s)
Teorema 2.3: (Identidade de Bezout Generalizada) ejam G(s) D (s) D (s)ñ(s) DFMs irredutíveis, então existem matrizes polinomiais X (s), Y (s), X(s) e Y(s) tais que Y(s) X(s) X (s) D(s) Ñ(s) D(s) Y (s)
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA. Sistemas
 INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Ferramentas Matemáticas para Sistemas Lineares: Álgebra Linear
 Ferramentas Matemáticas para Sistemas Lineares: Álgebra Linear Samir Angelo Milani Martins 1 1 UFSJ-MG / Campus Santo Antônio, MG Brasil Mestrado em Engenharia Elétrica UFSJ/CEFET-MG S. A. M. Martins (UFSJ
Ferramentas Matemáticas para Sistemas Lineares: Álgebra Linear Samir Angelo Milani Martins 1 1 UFSJ-MG / Campus Santo Antônio, MG Brasil Mestrado em Engenharia Elétrica UFSJ/CEFET-MG S. A. M. Martins (UFSJ
III) Os vetores (m, 1, m) e (1, m, 1) são L.D. se, somente se, m = 1
 Lista de Exercícios de SMA000 - Geometria Analítica 1) Indique qual das seguintes afirmações é falsa: a) Os vetores (m, 0, 0); (1, m, 0); (1, m, m 2 ) são L.I. se, somente se, m 0. b) Se u, v 0, então
Lista de Exercícios de SMA000 - Geometria Analítica 1) Indique qual das seguintes afirmações é falsa: a) Os vetores (m, 0, 0); (1, m, 0); (1, m, m 2 ) são L.I. se, somente se, m 0. b) Se u, v 0, então
Algebra Linear. 1. Funções de Matriz Quadrada 1.1. Teorema de Cayley-Hamilton. pag.1 Teoria de Sistemas Lineares Aula 8. c Reinaldo M.
 Algebra Linear 1. 1.1. Teorema de Cayley-Hamilton pag.1 Teoria de Sistemas Lineares Aula 8 Considere A R n n associada a transformação linear f : R n R n Polinômios de matriz quadrada Para k positivo e
Algebra Linear 1. 1.1. Teorema de Cayley-Hamilton pag.1 Teoria de Sistemas Lineares Aula 8 Considere A R n n associada a transformação linear f : R n R n Polinômios de matriz quadrada Para k positivo e
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC
 Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
Cap. 4 - Formas Canônicas e
 Cap. 4 - Formas Canônicas e Teoria da Realização Visão geral do capítulo Dada uma matriz de transferência G(s), uma realização de G(s) é um sistema linear: x(t) = Ax(t) + Bu(t) (1a) y(t) = Cx(t) + Du(t)
Cap. 4 - Formas Canônicas e Teoria da Realização Visão geral do capítulo Dada uma matriz de transferência G(s), uma realização de G(s) é um sistema linear: x(t) = Ax(t) + Bu(t) (1a) y(t) = Cx(t) + Du(t)
Aula 6 - Desempenho e Estabilidade MIMO, Ganho Pequeno
 Aula 6 - Desempenho e Estabilidade MIMO, Teorema do Ganho Pequeno Universidade de São Paulo Sistemas Multivariáveis Espaço de Estados ẋ =Ax + Bu y =Cx + Du Exemplo [ 1 4 A = 2 3 [ 1 2 C = 0 1 ] [ 1 0,
Aula 6 - Desempenho e Estabilidade MIMO, Teorema do Ganho Pequeno Universidade de São Paulo Sistemas Multivariáveis Espaço de Estados ẋ =Ax + Bu y =Cx + Du Exemplo [ 1 4 A = 2 3 [ 1 2 C = 0 1 ] [ 1 0,
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
1 a Lista de Exercícios MAT 3211 Álgebra Linear Prof. Vyacheslav Futorny
 1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
Estabilização de Sistemas a Excitação Persistente
 13 de janeiro de 2014 CMAP, École Polytechnique França Tópicos 1 Introdução Problema de interesse Sistemas a excitação persistente 2 (T, µ)-estabilizador Estabilização com hipóteses espectrais sobre A
13 de janeiro de 2014 CMAP, École Polytechnique França Tópicos 1 Introdução Problema de interesse Sistemas a excitação persistente 2 (T, µ)-estabilizador Estabilização com hipóteses espectrais sobre A
1. Não temos um espaço vetorial, pois a seguinte propriedade (a + b) v = a v + b v não vale. De fato:
 Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
Sumário No que se segue, C, R, Q, Z, N denotam respectivamente, o conjunto dos números complexos, reais, racionais, inteiros e naturais. Denotaremos por I (ou id) End(V ) a função identidade do espaço
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Exponencial de uma matriz
 Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
Comecemos escrevendo a forma geral de uma equação diferencial de ordem n, 1 inear e invariante no tempo, , b i
 3 6 ADL aula 2 Função de Transferência Comecemos escrevendo a forma geral de uma equação diferencial de ordem n, 1 inear e invariante no tempo, onde c(t) é a saída, r(t) é a entrada e os a i, b i e a forma
3 6 ADL aula 2 Função de Transferência Comecemos escrevendo a forma geral de uma equação diferencial de ordem n, 1 inear e invariante no tempo, onde c(t) é a saída, r(t) é a entrada e os a i, b i e a forma
1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0
![1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0 1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0](/thumbs/77/76694592.jpg) 1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
MAT-27 Lista-07 Setembro/2011
 MAT-27 Lista-07 Setembro/2011 1. Seja F L(R 3, R 2 ) definida por F (x, y, z) = (x + z, y 2z). Determinar (F ) B,C, sendo B = {(1, 2, 1), (0, 1, 1), (0, 3, 1)} e C = {(1, 5), (2, 1)}. 2. Determinar as
MAT-27 Lista-07 Setembro/2011 1. Seja F L(R 3, R 2 ) definida por F (x, y, z) = (x + z, y 2z). Determinar (F ) B,C, sendo B = {(1, 2, 1), (0, 1, 1), (0, 3, 1)} e C = {(1, 5), (2, 1)}. 2. Determinar as
CONTROLO LINEAR. Mestrado em Matemática e Aplicações. Universidade de Aveiro
 CONTROLO LINEAR Mestrado em Matemática e Aplicações Universidade de Aveiro Sistemas dinâmicos de controlo u - entrada y - saída x - estado - memória do sistema (condições iniciais) x(t ) u(t), t t y(t),
CONTROLO LINEAR Mestrado em Matemática e Aplicações Universidade de Aveiro Sistemas dinâmicos de controlo u - entrada y - saída x - estado - memória do sistema (condições iniciais) x(t ) u(t), t t y(t),
P3 de Álgebra Linear I
 P3 de Álgebra Linear I 2008.2 Data: 14 de Novembro de 2008. Gabarito. 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Considere uma transformação linear T : R 3 R 3 tal que existem vetores
P3 de Álgebra Linear I 2008.2 Data: 14 de Novembro de 2008. Gabarito. 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Considere uma transformação linear T : R 3 R 3 tal que existem vetores
