Matheus Soares da Silva

Transcrição

1 MÉTODO FDTD INCONDICIONALMENTE ESTÁVEL BASEADO EM POLINÔMIOS DE LAGUERRE PARA SIMULAÇÕES ELETROMAGNÉTICAS EM REGIME TRANSITÓRIO Matheus Soares da Silva Projeto de Graduação apresentado ao Curso de Engenharia Elétrica da Escola Politécnica, Universidade Federal do Rio de Janeiro, como parte dos requisitos necessários à obtenção do título de Engenheiro. Orientadores: Wescley Tiago Batista de Sousa Rubens de Andrade Júnior Rio de Janeiro Setembro de 217

2 MÉTODO FDTD INCONDICIONALMENTE ESTÁVEL BASEADO EM POLINÔMIOS DE LAGUERRE PARA SIMULAÇÕES ELETROMAGNÉTICAS EM REGIME TRANSITÓRIO Matheus Soares da Silva PROJETO DE GRADUAÇÃO SUBMETIDO AO CORPO DOCENTE DO CURSO DE ENGENHARIA ELÉTRICA DA ESCOLA POLITÉCNICA DA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO COMO PARTE DOS REQUISITOS NECESSÁRIOS PARA A OBTENÇÃO DO GRAU DE ENGENHEIRO ELETRICISTA. Examinado por: Prof. Rubens de Andrade Júnior, D.Sc. Prof. Antonio Carlos Siqueira de Lima, D.Sc. Eng. Bárbara Maria Oliveira Santos, RIO DE JANEIRO, RJ BRASIL SETEMBRO DE 217

3 Soares da Silva, Matheus Método FDTD Incondicionalmente Estável Baseado em Polinômios de Laguerre para Simulações Eletromagnéticas em Regime Transitório/Matheus Soares da Silva. Rio de Janeiro: UFRJ/ Escola Politécnica, 217. XV, 81 p.: il.; 29, 7cm. Orientadores: Wescley Tiago Batista de Sousa Rubens de Andrade Júnior Projeto de Graduação UFRJ/ Escola Politécnica/ Curso de Engenharia Elétrica, 217. Referências Bibliográcas: p WLP-FDTD. 2. FDTD. 3. Eletromagnetismo Computacional. I. Tiago Batista de Sousa, Wescley et al. II. Universidade Federal do Rio de Janeiro, Escola Politécnica, Curso de Engenharia Elétrica. III. Título. iii

4 Agradecimentos Gostaria de agradecer: ˆ Ao meu orientador, Wescley, por ter me dado um tema desaador e interessante para pesquisar enquanto Aluno de Iniciação Cientíca. Creio que esta foi uma das melhores IC's que eu poderia ter feito e a experiência me ajudou a decidir pela carreira acadêmica. Agradeço também pelos conselhos variados que me deu e pelo bom humor que sempre teve. Obrigado, te desejo sucesso e felicidades pra toda a família. ˆ Ao Professor Rubens, primeiro pela excelente disciplina de Eletromagnetismo II, uma das que mais gostei durante a graduação e o motivo pelo qual, em última análise, estou escrevendo este Projeto Final. Em seguida, pela paciência que teve comigo nestes últimos meses enquanto escrevia este trabalho, além das sugestões e dicas. Te levo como exemplo de acadêmico para o futuro. ˆ A todos os professores do departamento que eventualmente me orientaram e deram dicas prossionais: Antônio Lopes, Antônio Carlos Ferreira, Helói Moreira, Maurício Aredes, Robson Dias, Sérgio Hazan e Walter Suemitsu. ˆ Aos colegas de LASUP por terem sempre criado um ambiente agradável de trabalho, devo agradecer dentre eles especialmente à Bárbara pelas diversas dicas sobre como navegar esse período de m de curso e por ter me cedido momentaneamente o seu computador, muito obrigado! Também devo agradecer ao Felipe Costa por ter me recomendado muito material sobre diferenças nitas e ao Professor Elkin por estar sempre me dando incentivo e perguntando como estava andando o trabalho. ˆ A Felipe Cabral por ter disponibilizado o padrão LaTeX que utilizei pra escrever este trabalho. ˆ A minha mãe, Teresa Cristina, pelo suporte e pela conança que depositou em mim. ˆ Aos meus amigos de faculdade pelo companheirismo, especialmente ao Felipe iv

5 Dicler pelas diversas conversas sobre os mais variados assuntos, dicas acadêmicas que me deu em diversos momentos e por ter me apresentado o Inkscape! Também devo agradecer especialmente a Mike Mattos por ter sido meu bom amigo desde os tempos de CEFET e a Erick Gama, meu amigo desde o primeiro período. Desejo sucesso e felicidades a todos vocês! ˆ Ao meu amigo, Fred Guimarães, pelas dicas que me deu relativas a este trabalho. v

6 Resumo do Projeto de Graduação apresentado à Escola Politécnica/ UFRJ como parte dos requisitos necessários para a obtenção do grau de Engenheiro Eletricista. MÉTODO FDTD INCONDICIONALMENTE ESTÁVEL BASEADO EM POLINÔMIOS DE LAGUERRE PARA SIMULAÇÕES ELETROMAGNÉTICAS EM REGIME TRANSITÓRIO Matheus Soares da Silva Setembro/217 Orientadores: Wescley Tiago Batista de Sousa Curso: Engenharia Elétrica Rubens de Andrade Júnior O método das Diferenças Finitas no Domínio do Tempo (FDTD, do inglês: Finite Dierence Time Domain), desenvolvido por K. Yee em 1966, é uma forma largamente utilizada e relativamente simples de, numericamente, resolver as Equações de Maxwell. O algoritmo encontra um vasto ramo de aplicações em engenharia elétrica, do projeto de antenas à análise de transitórios eletromagnéticos. No entanto, esta técnica pode se tornar instável na análise de alguns sistemas físicos devido a condição de Courant-Friedrichs-Lewy, que exige que tempo e espaço estejam discretizados de forma acoplada. Trabalhos tem sido desenvolvidos desde os anos 2 no sentido de desenvolver versões incondicionalmente estáveis do algoritmo. Uma destas versões se baseia nas propriedades dos polinômios de Laguerre. Este trabalho contém o desenvolvimento do algoritmo FDTD baseado em polinômios de Laguerre e sua aplicação a dois casos de eletrodinâmica; um deles unidimensional e o outro bidimensional. Ambos os casos são validados por comparação com resultados presentes na literatura. vi

7 Abstract of Undergraduate Project presented to POLI/UFRJ as a partial fulllment of the requirements for the degree of Engineer. UNCONDITIONALLY STABLE FDTD SCHEME BASED ON LAGUERRE POLYNOMIALS FOR SIMULATIONS OF ELECTROMAGNETIC TRANSIENTS Matheus Soares da Silva September/217 Advisors: Wescley Tiago Batista de Sousa Rubens de Andrade Júnior Course: Electrical Engineering The Finite-Dierence Time-Domain method based on the Yee Algorithm is a traditional and relatively simple numerical technique to solve the Maxwell Equations. This algorithm nds many applications throughout electrical engineering, from antenna design to electromagnetic transients analysis. However, this technique becomes unstable in the analysis of some physical systems because of the Courant- Friedrichs-Lewy Condition, that introduces a coupling requirement between the discretization of time and space. Work on the development of unconditionally stable versions of the algorithm is ongoing since the 2's. One of these versions is based on the Laguerre polynomials properties. The present work presents the development of the Laguerre Polynomials based FDTD algorithm and application to two eletrodynamics problems. The results are validated by comparison with those available in the scientic literature. vii

8 Sumário Lista de Figuras Lista de Tabelas Lista de Símbolos Lista de Abreviaturas x xii xiii xv 1 Introdução Motivação Objetivos Organização O Método FDTD Introdução Diferenças Finitas Equações de Maxwell Modos Transversais Eletromagnéticos (Modos TEM) Modo Transversal Elétrico (Modo TE) Modo Transversal Magnético (Modo TM) Algoritmo de Yee Condições de Fronteira Estabilidade e a Condição Courant-Friedrichs-Lewy O Método FDTD baseado em Polinômios de Laguerre Introdução Polinômios de Laguerre Ortogonalidade O Método FDTD Baseado em Polinômios de Laguerre Modo TE Modo TEM Condições de Fronteira viii

9 4 Simulações e Resultados Metodologia Estrutura do Algoritmo Simulação Bidimensional: Sistema Físico Apresentado por Chung et al Resultados Simulação Unidimensional: Propagação de Onda Transversal Eletromagnética Resultados Conclusão e Trabalhos Futuros Conclusão Trabalhos Futuros Referências Bibliográcas 56 A Critério de Von Neumann para Estabilidade Numérica 59 B Correlação Linear 62 C Código Desenvolvido para o Caso Bidimensional utilizando WLP- FDTD 63 D Código Desenvolvido para o Caso Unidimensional utilizando WLP- FDTD 77 ix

10 Lista de Figuras 2.1 Aumento no número de artigos publicados em IEEE Transactions on Microwaves utilizando FDTD a partir dos anos Diferenças centradas (DC), regressivas (DR) e progressivas (DP) Malha de Yee para o modo TE z Malha de Yee para o modo TEM em relação a x polarizado em y Visualização da Malha de Yee no espaço-tempo, o círculo vermelho mostra o ponto onde o operador diferencial é discretizado para que se obtenha a Equação de Atualização para Campos Elétricos (Equação 2.43) Visualização da Malha de Yee no espaço-tempo, o círculo vermelho mostra o ponto onde o operador diferencial é discretizado para que se obtenha a Equação de Atualização para Campos Magnéticos (Equação 2.44) Simulação de Campo Elétrico E y utilizando método FDTD com S c = Simulação de Campo Elétrico E y utilizando método FDTD com S c = Simulação de Campo Elétrico E y utilizando método FDTD com S c = Polinômios de Laguerre de ordem a Bases de Laguerre até ordem 4, escala temporal s = Síntese de um sinal utilizando diferentes números de bases de Laguerre Síntese de um sinal utilizando 1 bases de Laguerre Fluxograma do Algoritmo Implementado para o Método WLP-FDTD Simulação bidimensional para validação do método Forma da densidade de corrente elétrica inserida no problema bidimensional Resultado da simulação bidimensional mostrada na Figura x

11 4.5 Resultados para a simulação bidimensional utilizando o método WLP- FDTD Resultados para a simulação bidimensional utilizando o método WLP- FDTD Estrutura do problema unidimensional Forma de Onda da Densidade Supercial de Corrente K y Sobreposição dos resultados da simulação unidimensional utilizando o método WLP-FDTD e dos apresentados por Feynman et al. [1] Sobreposição dos resultados da simulação unidimensional utilizando o método WLP-FDTD e dos apresentados por Feynman et al. [1] Sobreposição dos resultados da simulação unidimensional utilizando o método WLP-FDTD e dos apresentados por Feynman et al.[1] xi

12 Lista de Tabelas 2.1 Algumas das Grandezas Físicas Eletromagnéticas Comparação entre os valores obtidos por Chung et al. e os obtidos por algoritmo próprio, para os pontos a, b, c e d Comparação entre os valores analíticos e os obtidos pelo método WLP-FDTD para campo elétrico no sistema físico unidimensional xii

13 Lista de Símbolos A Matriz de coecientes utilizada no método WLP-FDTD, p. 33 B f Máxima frequência, em Hertz, presente em uma forma de onda., p. 28 C H x,y, C E x,y Constantes utilizadas no método WLP-FDTD, p. 32 L n Polinômio de Laguerre de ordem n, p. 22 N L O(h n ) Número necessário de bases de Laguerre para sintetizar uma certa função., p. 28 Notação Big-Oh denotando a ordem n de um certo método de diferenças nitas., p. 5 R P earson Coeciente de Correlação de Pearson, p. 38 T f Duração, em segundos, de uma forma de onda., p. 28 U Função qualquer descrita como uma série., p. 29 t Discretização Temporal, p. 13 x Discretização Espacial, coordenada x, p. 13 y Discretização Espacial, coordenada y, p. 13 Φ,1,2... Conjunto ortogonal innito de funções, p. 24 β q 1 Vetor coluna contendo os somatórios dos termos de campos elétricos e magnéticos de todas as iterações anteriores do método WLP-FDTD, p. 33 δ mn Delta de Kronecker, p. 24 ɛ Permissividade Elétrica, Unidade SI: F/m, p. 7 µ Permeabilidade Magnética, Unidade SI: H/m, p. 7 xiii

14 φ p,q Base de Laguerre de ordem p ou q, p. 25 σ Condutividade Elétrica, Unidade SI: S/m, p. 7 B Densidade de Fluxo Magnético, Unidade SI: W b/m 2, p. 7 D Densidade de Fluxo Elétrico, Unidade SI: C/m 2, p. 7 E Intensidade de Campo Elétrico, Unidade SI: V/m, p. 7 H Intensidade de Campo Magnético, Unidade SI: A/m, p. 7 J Densidade de Corrente, Unidade SI: A/m 2, p. 7 K Densidade Supercial de Corrente, p. 46 c,1,2... Coecientes a serem determinados., p. 24 f Função qualquer., p. 4 h Raio de um certo intervalo., p. 4 i Índice horizontal de um certo ponto na malha de Yee, p. 14 j Índice vertical de um certo ponto na malha de Yee, p. 14 k Um número natural qualquer., p. 22 p 1 Ponto de medição de campo elétrico., p. 41 s Fator de escala temporal, p. 26 t Tempo, p. 12 u, v, w Vetores quaisquer., p. 23 v Velocidade qualquer de propagação de uma onda eletromagnética, dada em m/s, p. 16 w(t) Função peso., p. 25 x x N L max Ponto central de um intervalo, ponto este no qual se deseja avaliar o operador diferencial., p. 4 Maior zero dentre os polinômios de Laguerre utilizados para sintetizar uma certa função., p. 28 xiv

15 Lista de Abreviaturas ABC Absorbing Boundary Conditions, p. 15 CAE Computer Assisted Engineering, p. 1 CFL Courant-Friedrichs-Lewy, p. 1 FDTD Finite Dierence Time Domain, p. vi IEEE Institute of Electrical and Electronic Engineers, p. 3 LASUP Laboratório de Aplicações de Supercondutores, p. 2 PEC Perfect Electric Conductor, p. 15 PML Perfectly Matched Layer, p. 16 TE Transversal Elétrica(o), p. 9 TM Transversal Magnética(o), p. 9 WLP-FDTD Weighted Laguerre Polynomials Finite Dierence Time Domain, p. 2 xv

16 Capítulo 1 Introdução 1.1 Motivação Métodos computacionais encontram vasta aplicação na solução de problemas em engenharia. A utilização destes nas últimas décadas permitiu o crescimento de uma área conhecida como CAE (do inglês: Computer Assisted Engineering ). Esta popularidade advém da possibilidade de se fazer análise física de sistemas complexos de maneira mais rápida e simples, sem necessidade de se criar um modelo analítico para cada novo problema, além de se conseguir tratar problemas para os quais não existe modelo analítico. Com estes programas, em muitos casos, só se torna necessário representar corretamente o problema em termos geométricos, de materiais e de condições de contorno. No entanto, a utilização de softwares comerciais na simulação de materiais supercondutores do tipo II se revela um problema em aberto. Estes materiais apresentam acoplamento entre temperatura, densidade de corrente e campo magnético, além de um comportamento não-linear na relação entre campo elétrico e densidade de corrente. Tais diculdades motivam a criação de novos modelos de simulação, utilizando códigos próprios [2] [3] [4] [5] [6]. Em eletrodinâmica, o método das Diferenças Finitas no Domínio do Tempo (ou FDTD, do inglês Finite-Dierence Time Domain) é largamente empregado e possui diversas implementações na forma de softwares, comerciais e gratuitos. Este método se baseia na discretização tanto do espaço quanto do tempo em termos de diferenças nitas. No entanto, para que o método mantenha sua estabilidade, a discretização do espaço e do tempo deve estar acoplada. Este acoplamento é dado pela condição de Courant-Friedrichs-Lewy (ou condição CFL) [7] [8] [9]. Com isso, o método se torna impróprio para as chamadas simulações multiescala, onde se deseja observar o comportamento de um sistema em escalas diferentes em uma mesma simulação, ou seja, em casos onde a discretização do espaço de 1

17 simulação é bastante na em relação ao espaço, ou tempo, total de simulação. Nestas situações o método se torna muito dispendioso computacionalmente [1]. Este se revela o caso em aplicações de supercondutores em sistemas de potência, onde a malha de discretização do espaço deve ser na e, ao mesmo tempo, as frequências são relativamente baixas e um tempo relativamente longo de simulação se faz necessário [5]. O método das Diferenças Finitas no Domínio do Tempo usando Polinômios de Laguerre (também conhecido como Laguerre-FDTD ou WLP-FDTD, do inglês Weighted Laguerre Polynomials - Finite-Dierence Time Domain ) utiliza as propriedades dos polinômios de Laguerre para modicar o método FDTD tradicional e torná-lo incondicionalmente estável, permitindo que tempo e espaço possam ser discretizados de maneira desacoplada e que as simulações sejam mais ecientes [11] [1]. Utilizando o método WLP-FDTD, este trabalho foi desenvolvido no Laboratório de Aplicações de Supercondutores da UFRJ (LASUP) com o objetivo de dar uma contribuição inicial a uma linha de pesquisa que busca avançar simulações multifísicas de supercondutores, adicionando a descrição das contribuições da parcela eletromagnética a métodos baseados em diferenças nitas que já realizam, com sucesso, simulações eletrotérmicas [5] [12]. 1.2 Objetivos O objetivo é apresentar as bases teóricas do método FDTD baseado em polinômios de Laguerre, desenvolver um algoritmo próprio e, por comparação com resultados da literatura, demonstrar que, utilizando o domínio das bases de Laguerre é possível construir um método preciso e incondicionalmente estável de solução numérica das Equações de Maxwell para regimes transitórios. 1.3 Organização A organização deste trabalho é feita da seguinte forma: O Capítulo 1 contém a motivação, os objetivos e esta organização. O Capítulo 2 trata do Método FDTD baseado no Algoritmo de Yee, passando pelas Equações de Maxwell e por alguns conceitos de métodos numéricos. O Capítulo 3 trata dos Polinômios de Laguerre e do Método das Diferenças Finitas no Domínio do Tempo utilizando estes Polinômios. O Capítulo 4 traz a metodologia, a estrutura geral dos algoritmos desenvolvidos, a descrição das simulações feitas e os resultados e análise destes. Por m, o Capítulo 5 traz a conclusão e sugestões para trabalhos futuros. 2

18 Capítulo 2 O Método FDTD 2.1 Introdução Desenvolvidas no século XIX, as Equações de Maxwell são de fundamental importância em todas as áreas da ciência que utilizam teoria eletromagnética. Até meados do século XX, a modelagem de sistemas eletromagnéticos era feita, principalmente, utilizando o domínio da frequência em estado estacionário com soluções normalmente encontradas analiticamente, utilizando séries innitas ou formas fechadas. Tais abordagens possuem algumas limitações no tratamento de materiais com geometrias complexas, ou que possuam não linearidades. Em 1966, K. Yee desenvolve um método numérico no domínio do tempo que, embora simples conceitualmente, é capaz de resolver as Equações de Maxwell [7]. A popularidade de soluções diretamente no domínio do tempo, discretizando o espaço-tempo em forma de malha, aumenta durante as décadas de 8 e 9, impulsionada pelo desenvolvimento dos computadores modernos. Também durante as décadas de 8 e 9 o método de Yee é renado por outros pesquisadores como Taove, Mur, Berenger e Sullivan, adicionando funcionalidades ao método e estudando seus critérios de estabilidade. O gráco da Figura 2.1 mostra o crescimento na quantidade de artigos publicados no periódico IEEE Transactions on Microwaves tratando do assunto entre os anos 8 e 9 [13]. 3

19 5 Publicações Utilizando FDTD Número de Publicações Ano Figura 2.1: Aumento no número de artigos publicados em IEEE Transactions on Microwaves utilizando FDTD a partir dos anos Diferenças Finitas Métodos numéricos de Diferenças Finitas para solução de Equações Diferenciais se baseiam fundamentalmente na discretização das variáveis de interesse. Isso é feito aplicando-se aproximações por diferenças nitas para operadores diferenciais. O método FDTD utiliza, especicamente, a chamada aproximação por diferenças centradas tanto para o espaço quanto para o tempo, fazendo deste um dos métodos conhecidos como métodos leapfrog [14]. Tomamos uma função f e um intervalo de raio h ao redor do ponto x, usar expansão por Série de Taylor para representar a função no extremo positivo do intervalo resulta na Equação (2.1) [9] [14] [15]: f(x + h) = f(x ) + h f(x) x + h2 x=x 2! 2 f(x) x 2 + h3 x=x 3! 3 f(x) x 3 + (2.1) x=x Rearranjando termos e dividindo por h os dois lados da Equação (2.1) obtemos: f(x + h) f(x ) h = f(x) x + h x=x 2! 2 f(x) x 2 + h2 x=x 3! 3 f(x) x 3 + (2.2) x=x Truncando o lado direito desta equação no segundo termo conseguimos uma aproximação pra derivada conhecida como aproximação por diferenças progressivas (Equação (2.3)): 4

20 f(x) x = f(x + h) f(x ) + O(h) (2.3) x=x h O termo O(h) está representado na notação Big Oh e simboliza o erro devido ao truncamento. Como neste caso o primeiro termo do truncamento é proporcional a h, o erro de truncamento cresce linearmente com o passo de discretização h. Aproximações que apresentam esta relação linear entre erro e discretização são ditas aproximações de primeira ordem. Por outro lado, realizar a expansão por Séries de Taylor para representar a função no extremo inferior do intervalo [x h, x + h] resulta na Equação (2.4): f(x h) = f(x ) h f(x) x + h2 x=x 2! 2 f(x) x 2 h3 x=x 3! 3 f(x) x 3 + (2.4) x=x Seguindo o mesmo procedimento anterior chegamos na chamada aproximação por diferenças regressivas, apresentada na Equação (2.5). Este tipo de aproximação é, assim como a aproximação por diferenças progressivas, de primeira ordem. f(x) x = f(x) f(x h) + O(h) (2.5) x=x h É possível, a partir das Equações (2.1) e (2.4), chegar em mais um tipo de aproximação, conhecida como aproximação por diferenças centradas (ou centrais). Começamos subtraindo as duas equações: f(x + h) f(x h) = h f(x) x + 2 h3 x=x 3! Dividindo por h nos dois lados da equação obtemos: 3 f(x) x 3 + (2.6) x=x f(x + h) f(x h) h = f(x) x + 2 h2 x=x 3! 3 f(x) x 3 + (2.7) x=x Importante notar que, neste caso, o termo a ser truncado depende de h 2 e, portanto, o erro de truncamento cai com o quadrado da discretização. A aproximação por diferenças centradas (Equação (2.8)) é dita de segunda ordem e, como já dito anteriormente, é a base do método FDTD. 5

21 f(x + h) f(x h) h = f(x) x + O(h 2 ) (2.8) x=x A aproximação por diferenças centradas também é aplicável, naturalmente, às funções de mais de uma variável e suas derivadas parciais, como mostrado na Equação (2.9) [15]. f((x + h), y) f((x h), y) h = f(x, y) x + O(h 2 ) (2.9) x=x A Figura 2.2 ilustra os três tipos de aproximação apresentados. É notável que, para uma aproximação razoável da derivada da função f(x) no ponto x, as aproximações por diferenças regressivas e progressivas necessitam de um intervalo h de discretização consideravelmente menor do que a aproximação por diferenças centradas. DC DR DP Figura 2.2: Diferenças centradas (DC), regressivas (DR) e progressivas (DP). 6

22 2.3 Equações de Maxwell As Equações de Maxwell na forma diferencial mostradas nas Equações (2.1), (2.11), (2.12) e (2.13) governam fenômenos eletromagnéticos em um meio sem cargas livres descrito por coordenadas cartesianas [1] [7] [16] [17] : H = J + D t E = B t (2.1) (2.11) D = (2.12) B = (2.13) Supondo a presença exclusiva de materiais lineares, isotrópicos e não dispersivos, podemos usar as relações constitutivas (2.14) e (2.15). D = ɛ E (2.14) B = µ H (2.15) Na presença de materiais condutores é preciso adicionar também a Equação (2.16). J = J independente + σ E (2.16) A Tabela 2.1 descreve as grandezas físicas utilizadas até agora. Tabela 2.1: Algumas das Grandezas Físicas Eletromagnéticas. Representação Grandeza Física Unidade SI V E Campo Elétrico m C D Densidade de Fluxo Elétrico m 2 A H Campo Magnético m W b B Densidade de Fluxo Magnético m 2 A J Densidade de Corrente Elétrica m 2 F ɛ Permissividade Elétrica m H µ Permeabilidade Magnética m σ Condutividade Elétrica S 7

23 Utilizando as equações constitutivas (2.14) e (2.15), podemos reescrever as Equações de Maxwell em função somente dos campos E e H. E t = 1 ɛ ( H J) (2.17) H t = 1 µ ( E) (2.18) ɛ E = (2.19) µ B = (2.2) Escrevendo os rotacionais de maneira explícita em termos de derivadas espaciais nas Equações (2.17) e (2.18) obtemos as seguintes seis equações acopladas: E x t E y t E z t H x t H y t H z t = 1 µ = 1 µ = 1 µ ( Ey z E ) z y ( Ez x E ) x z ( Ex y E ) y x = 1 ( Hz ɛ y H ) y z J x = 1 ( Hx ɛ z H ) z x J y = 1 ɛ ( Hy x H ) x y J z (2.21) (2.22) (2.23) (2.24) (2.25) (2.26) É possível modicar as Equações (2.21), (2.22), (2.23), (2.24), (2.25) e (2.26) de modo a reduzir a ordem do espaço de simulação e descrever o comportamento de sistemas eletromagnéticos bidimensionais e unidimensionais Modos Transversais Eletromagnéticos (Modos TEM) Considerando que a geometria estudada, os campos e eventuais excitações de corrente se estendem innitamente sem sofrer qualquer variação na direção de duas das três coordenadas espaciais, é possível anular duas das três derivadas espaciais presentes nas Equações (2.21), (2.22), (2.23), (2.24), (2.25) e (2.26). O desenvolvimento neste trabalho é feito anulando as derivadas em relação a y e z. Este procedimento 8

24 resulta nas Equações (2.31), (2.32), (2.33) e (2.34): E z t E y t H y t H z t = 1 ɛ = 1 ɛ ( ) Hy x J z = 1 µ ( = 1 µ ( ) Ez t H ) z x J y ( E ) y x (2.27) (2.28) (2.29) (2.3) Estas quatro equações podem ser organizadas em dois conjuntos compostos de duas equações e independentes entre si. Estes conjuntos são denominados modos. O conjunto formado pelas Equações (2.31) e (2.32) é chamado de modo transversal eletromagnético polarizado em z [7] ou de modo transversal magnético unidimensional (1D TM) [18]. Neste trabalho é feita a opção de utilizar a nomenclatura usada por Taove em [7]. Este modo será mencionado como modo TEM x polar. z. E z t H y t = 1 ɛ ( ) Hy x J z = 1 µ ( ) Ez t (2.31) (2.32) O conjunto formado pelas Equações (2.33) e (2.34) é chamado de modo transversal eletromagnético polarizado em y [7] ou de modo transversal elétrico unidimensional (1D TE) [18]. Neste trabalho é feita a opção de utilizar a nomenclatura usada por Taove em [7]. Este modo será mencionado como modo TEM x polar. y. E y t H z t = 1 ɛ ( = 1 µ H ) z x J y ( E ) y x (2.33) (2.34) Os dois modos apresentados, TEM x polar. z e TEM x polar. y, constituem duas formas possíveis de se realizar simulações unidimensionais no eixo x. É evidente que estes modos somente podem ser usados para se obter resultados precisos quando o problema é composto de geometrias e grandezas físicas que possam ser aproximadas 9

25 como invariantes em duas das três coordenadas cartesianas Modo Transversal Elétrico (Modo TE) Considerando que a geometria estudada, os campos e eventuais excitações de corrente se estendem innitamente em apenas uma das direções sem sofrer qualquer variação, as derivadas em relação a esta direção se tornam nulas e podemos construir equações bidimensionais. Como exemplo, é suposto que não há qualquer variação na direção z e que, portanto, as derivadas em relação a z se tornam nulas e as Equações (2.21), (2.21), (2.22), (2.23), (2.24), (2.25) e (2.26) podem ser um pouco simplicadas e resultam em outro conjunto de seis equações: E z t H z t H x t E x t E y t H y t = 1 ɛ = 1 µ = 1 µ ( = 1 µ E ) z y ( ) Ez x ( Ex y E ) y x = 1 ( ) Hz ɛ y J x = 1 ( H ) z ɛ x J y ( Hy x H ) x y J z (2.35) (2.36) (2.37) (2.38) (2.39) (2.4) As Equações (2.35), (2.36), (2.37), (2.38), (2.39) e (2.4) podem dar origem a dois conjuntos de equações independentes entre si, denominados modos, de acordo com a orientação dos campos elétricos e magnéticos no espaço [18]. No modo transversal elétrico o campo magnético somente possui componente não-nula na direção na qual não há qualquer variação (no caso, a direção z), enquanto os campos elétricos só possuem componentes não-nulas nas direções perpendiculares a esta, no caso, no plano xy. Para denir este modo, basta agrupar as Equações (2.37), (2.38) e (2.39). Como é na direção z que não há qualquer variação, este modo é dito modo transversal elétrico em relação a z, ou modo TE z [7]. E x t E y t = 1 ( ) Hz ɛ y J x = 1 ( H ) z ɛ x J y (2.41) (2.42) 1

26 H z t = 1 µ ( Ex y E ) y x (2.43) Modo Transversal Magnético (Modo TM) Já no modo transversal magnético, o campo elétrico somente possui componente não-nula na direção na qual não há variação (no caso, a direção z), enquanto os campos magnéticos só possuem componentes não-nulas nas direções perpendiculares (no caso, o plano xy). Para denir este modo basta agrupar as Equações (2.35), (2.36) e (2.4). Este modo é dito modo transversal magnético em relação a z, ou Modo TM z : E z t H x t H y t = 1 ɛ = 1 µ ( = 1 µ E ) z y ( ) Ez x ( Hy x H ) x y J z (2.44) (2.45) (2.46) Os dois modos apresentados,tm z e TE z constituem as duas formas possíveis de se realizar simulações bidimensionais no plano xy. É evidente que estes modos somente podem ser usados para se obter resultados precisos quando o problema é composto de geometrias e grandezas físicas que possam ser aproximadas como invariantes na direção z. 11

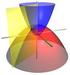
27 2.4 Algoritmo de Yee O método FDTD discretiza o tempo (t) e o espaço em diferenças centrais e desloca as grandezas eletromagnéticas no espaço, fazendo com que cada componente de campo elétrico E esteja cercada por quatro componentes de campo magnético H, e vice-versa [9]. A Figura 2.3 mostra como exemplo a malha de Yee para estudos bidimensionais (modo TE z ) e a Figura 2.4 para estudos unidimensionais, modo TEM em relação a x, polarizado em y. Figura 2.3: Malha de Yee para o modo TE z. 12

28 Figura 2.4: Malha de Yee para o modo TEM em relação a x polarizado em y. Os índices i e j são os índices de discretização horizontal e vertical, respectivamente. Estes índices são números inteiros denidos tais que, sendo x e y os passos de discretização espacial, um ponto no espaço localizado na malha de Yee e com coordenadas cartesianas da forma (x, y) possa ter sua posição descrita com uma expressão da forma (i x, j y) [7]. É importante observar que campos elétricos e magnéticos estão deslocados também no tempo. Como exemplo trataremos do caso unidimensional. Após aplicar a aproximação por diferenças centradas para as derivadas temporais e espaciais das Equações (2.33) e (2.34) do modo transversal eletromagnético polarizado na direção y, existirão duas equações conhecidas como Equações de Atualização. Uma destas equações, (2.47), atualizará os valores para os campos elétricos E z e a outra (Equação (2.48)) atualizará os valores para os campos magnéticos H y. Estas equações serão aplicadas de maneira intermitente de forma a avançar a simulação no tempo. As Figuras 2.5 e 2.6 ilustram o processo. E y t+1 i = E y t i t ( Hz t ɛ x i H z i 1) t H z t+1 i = H z t i t ( Ey t µ x i+1 E y i) t (2.47) (2.48) 13

29 Figura 2.5: Visualização da Malha de Yee no espaço-tempo, o círculo vermelho mostra o ponto onde o operador diferencial é discretizado para que se obtenha a Equação de Atualização para Campos Elétricos (Equação 2.43). Figura 2.6: Visualização da Malha de Yee no espaço-tempo, o círculo vermelho mostra o ponto onde o operador diferencial é discretizado para que se obtenha a Equação de Atualização para Campos Magnéticos (Equação 2.44). 14

30 Adicionando J y (t) como função forçante obtemos: E y t+1 i = E y t i t ( Hz t i H z t t ɛ x i 1) + ɛ J y t+1 i (2.49) ( Ey t i+1 E y i) t H z t+1 i = H z t i t µ x (2.5) As Equações (2.49) e (2.5) são as Equações de Atualização do método FDTD para excitação com densidade de corrente. A adição de corrente não modica a lógica demonstrada nas Figuras 2.5 e 2.6, em cada iteração temporal do método, campos elétricos e magnéticos são recalculados utilizando estas equações e atualizados antes de avançar para a próxima iteração, este processo é conhecido como processo de marcha no tempo ou esquema leapfrog Condições de Fronteira O espaço discretizado pela simulação é, assim como a memória disponível para descrevê-lo, nito. Portanto, é fundamental determinar o comportamento das fronteiras da simulação. Condições do tipo PEC Em alguns casos deseja-se determinar um espaço de simulação cercado por condutores perfeitos. Com isso, haverá reexão de ondas eletromagnéticas que atinjam seus limites. Este tipo de condição é útil no caso de, por exemplo, câmaras ressonantes. Fronteiras deste tipo são conhecidas como fronteiras PEC (do inglês: Perfect Electric Conductor ). Denir uma condição deste tipo é bem simples, só é necessário determinar os campos elétricos tangentes às fronteiras como zero [9]. Condições Absorventes Em alguns casos se deseja simular uma malha de simulação innita, isto é, deseja-se que ondas que atinjam a fronteira do espaço de simulação o abandonem denitivamente, sem qualquer tipo de reexão. Criar um espaço de simulação muito maior do que o necessário em geral não é uma opção, pois exigiria uma quantidade não disponível de memória. A solução é, portanto, encerrar o espaço de simulação articialmente, usando condições que simulem uma absorção perfeita de energia. Em 1981, Gerrit Mur [19] deniu uma formulação para condições de fronteira que absorvem energia. Muitas outras formas se seguiram mas trataremos neste trabalho exclusivamente das chamadas condições de Mur de Primeira Ordem, que tem como base a Equação (2.51) [18]. Este tipo de condição de fronteira é conhecida como condição ABC (do inglês: Absorbing Boundary Conditions ). 15

31 ( x ± 1 v ) E y (x, y, t) = (2.51) t sendo v a velocidade de propagação da onda eletromagnética no meio estudado. A Equação (2.51) pode ter duas soluções, a saber: ( x + 1 v ( x 1 v ) E y (x, t) = E y (x, t) = f(x vt) (2.52) t ) E y (x, t) = E y (x, t) = f(x + vt) (2.53) t Note que as soluções descrevem ondas que se propagam em somente uma direção, a Equação (2.51) é a chamada Equação da Onda Unidirecional e pode ser discretizada utilizando diferenças centrais. O desenvolvimento é feito, como exemplo, para uma fronteira vertical presente em x =, equivalente a i = 1. O ponto de discretização espacial utilizado é normalmente i = 1, de modo a caracterizar o início 2 da fronteira no ponto médio entre dois campos elétricos, o ponto de discretização temporal é t = 1, ou seja, também no ponto médio entre dois campos elétricos, 2 mas no tempo. Estas escolhas para realizar a aproximação por diferenças centrais resultam na Equação (2.54) [18]: E y t+1 i=1+1/2 E y t i=1+1/2 v t = E y t+1/2 i=2 E y t+1/2 i=1 x (2.54) Como o campo elétrico não está efetivamente denido para os pontos intermediários de tempo e espaço que foram escolhidos, uma interpolação linear é feita, resultando em: ( Ey t+1 i=1 +E y t+1 i=2) (Ey t i=1+e y t i=2) 2v t = ( Ey t+1 i=2 +E ) ( y t i=2 Ey t+1 i=1 +E ) y t i=1 2 x (2.55) Finalmente, rearranjando para o campo elétrico na fronteira, conseguimos chegar à Equação de Atualização (2.56): E y t+1 i=1 = E y t i=2 + ( ) v t x (Ey t+1 i=2 v t + x E ) y t i=1 (2.56) Esta é uma formulação que funciona bem para situações onde se espera que qualquer incidência de onda eletromagnética ocorra de forma aproximadamente perpendicular às fronteiras da simulação. Caso este não seja o caso, outros métodos posteriores tais como o Perfectly-Matched Layer (PML) são recomendados [8]. 16

32 2.5 Estabilidade e a Condição Courant-Friedrichs- Lewy Estabilidade é denida como a característica de métodos numéricos que não possuem crescimento ilimitado de erro, sendo uma condição necessária mas não suciente para que as simulações entreguem resultados precisos [2]. O método FDTD, como dito anteriormente, é um método explícito e está sujeito a instabilidade de acordo com os passos de discretização espaço-temporais. Métodos numéricos explícitos de resolução de alguns tipos de Equações Diferenciais Parciais (nas quais se encaixam as Equações de Maxwell) estão sujeitos à condição Courant- Friedrichs-Lewy (ou condição CFL) para que se mantenham estáveis. Para o caso do método FDTD bidimensional descrito no plano xy, a condição CFL se traduz na Inequação (2.57) [7] [18]. t v x 2 y 2 (2.57) Esta condição para a relação entre discretização espacial e temporal pode ser deduzida utilizando o chamado Critério de Von Neumann, apresentado no Anexo A. Mais informação sobre esta linha de análise de estabilidade também pode ser encontrada nas referências [18] e [21]. Esta relação também pode ser justicada por um argumento físico: a discretização da malha não pode ser feita de forma a violar a causalidade. Como em cada passo temporal informações sobre grandezas físicas passam de um ponto da malha para outro, a discretização tem que ser feita de tal forma que esta transmissão de informação ocorra em uma velocidade próxima da prevista analiticamente para ondas eletromagnéticas, v = 1 µɛ [14] [22]. Em outras palavras, a denição do valor assumido por um grandeza física qualquer em um ponto no espaço-tempo deve ser em função somente de pontos dos quais a própria solução analítica dependa. Ou seja, é natural esperar que a condição CFL especique claramente que a máxima discretização espacial não pode ser superior a propagação da luz em um passo temporal, caso contrário o método FDTD estaria fazendo uso de informação ainda não disponível, de acordo com o modelo analítico. Em simulações unidimensionais a razão mostrada na Equação (2.58) é útil, esta é conhecida como Número de Courant. S c = v t x (2.58) A Figura 2.7 mostra resultados para campo elétrico E y de uma simulação unidimensional da propagação de uma onda transversal eletromagnética utilizando o 17

33 método FDTD com S c = 1. (valor considerado ideal para este tipo de simulação [9]). Note que, utilizando Número de Courant unitário, a onda eletromagnética percorre a geometria sem sofrer distorções Distribuição de E y ao longo da geometria em diferentes instantes t =.93 ns t = 1.6 ns t = 1.19 ns t = 1.33 ns.4.2 E y (V/m) Eixo x (cm) Figura 2.7: Simulação de Campo Elétrico E y utilizando método FDTD com S c = 1.. A mesma simulação é agora apresentada para o caso onde a condição de Courant foi desrespeitada, ou seja: S c > 1.. Mais especicamente: S c = 1.5. A Figura 2.8 mostra a intensidade do campo elétrico E y para diferentes tempos de simulação, de forma a ressaltar a instabilidade na simulação. Note que, com o passar do tempo de simulação, o erro cresce sem limite. Este comportamento, como já dito anteriormente, caracteriza a instabilidade numérica. 18

34 1 Distribuição de E y ao longo da geometria em um certo instante. 1 Distribuição de E y ao longo da geometria em um certo instante E y (V/m) E y (V/m) Eixo x (cm) Eixo x (cm) (a) t =.134 ns (b) t =.335 ns 1 Distribuição de E y ao longo da geometria em um certo instante. 2 Distribuição de E y ao longo da geometria em um certo instante E y (V/m) E y (V/m) Eixo x (cm) Eixo x (cm) (c) t =.469 ns (d) t =.536 ns 2 Distribuição de E y ao longo da geometria em um certo instante. 2 Distribuição de E y ao longo da geometria em um certo instante E y (V/m) E y (V/m) Eixo x (cm) Eixo x (cm) (e) t =.63 ns (f) t =.67 ns Figura 2.8: Simulação de Campo Elétrico E y utilizando método FDTD com S c =

35 1 Distribuição de E y ao longo da geometria em um certo instante. 5 Distribuição de E y ao longo da geometria em um certo instante E y (V/m) E y (V/m) Eixo x (cm) Eixo x (cm) (g) t =.84 ns (h) t =.938 ns Figura 2.8: Simulação de Campo Elétrico E y utilizando método FDTD com S c =

36 Capítulo 3 O Método FDTD baseado em Polinômios de Laguerre 3.1 Introdução A partir dos anos 2 surgiram novas formulações do método FDTD com o objetivo de eliminar, ou reduzir, a limitação imposta pela condição CFL. A primeira destas versões foi o método FDTD Alternado-Direto Implícito, ou ADI- FDTD (do inglês:alternate-direct Implicit FDTD ). Embora o método ADI seja incondicionalmente estável, ou seja, não dependa da condição CFL para que o erro não cresça monotonicamente, ele ainda não garante precisão para qualquer razão entre a discretização espacial e temporal [11]. Em outras palavras, ainda haverá erro numérico para razões de discretização que se distanciem da condição CFL, tudo que o método ADI-FDTD garante é que este erro não crescerá sem limites. Outras tentativas surgiram na última década (tais como o método Cole's Non-Standard FDTD) mas um tratamento destas está além do objetivo deste trabalho. Em um artigo publicado em 23 por Chung, Sarkar, Jung e Salazar-Palma [11], uma versão incondicionalmente estável utilizando polinômios de Laguerre é sugerida. A ideia fundamental é abandonar o esquema de marcha no domínio do tempo mostrado no Capítulo 2 e adotar um outro domínio, que tem como bases os polinômios de Laguerre. Este método é abreviado na literatura como Laguerre- FDTD ou WLP-FDTD (do inglês: Weighted Laguerre Polinomials-FDTD) 21

37 3.2 Polinômios de Laguerre A Equação Diferencial (3.1) é chamada a Equação de Laguerre. x 2 y + (1 x) y + ky = (3.1) x2 x sendo x e k um número natural, a solução em termos de séries innitas desta equação diferencial é descrita pela Equação (3.2). ( k(k 1) y k (x) = a 1 kx + x 2 k(k 1)(k 2) x ) k(k 1)(k 2)(k 3) + x 4 ( 1) n (3.2) k! (n! ) 2 (k n)! xn Aplicar k =, 1, 2, 3... e a = k! na Equação (3.2) resulta na família de polinômios mostrada na Equação (3.3) L (x) = 1 L 1 (x) = 1 x L 2 (x) = 2 4x + x 2 L 3 (x) = 6 18x + 9x 2 x 3... L k (x) = (k! ) 2 k n= ( 1) n (n! ) 2 (k n)! xn (3.3) Estes polinômios são denominados Polinômios de Laguerre e podem ser escritos de uma forma recursiva, ou seja, o polinômio L n, se n > 2, pode ser escrito em função dos dois polinômios anteriores, como mostrado na Equação (3.4) [23]. L (x) = 1 L 1 (x) = 1 x L k (x) = (2k 1 x) L k 1(x) (k 1) L k 2 (x) k para k 2 (3.4) 22

38 A Figura 3.1 mostra os cinco primeiros polinômios de Laguerre Ordem Ordem 1 Ordem 2 Ordem 3 Ordem 4 1 L(x) x Figura 3.1: Polinômios de Laguerre de ordem a 4. A partir daqui passaremos a tratar a variável da qual dependem os polinômios de Laguerre como a variável tempo, t. 3.3 Ortogonalidade Os conceitos vetoriais de produto interno escalar e ortogonalidade podem ser generalizados para funções. Consideremos dois vetores u e v, denidos, por exemplo, no espaço vetorial IR 2. O produto interno entre esses dois vetores, representado u v, é denido pelas seguintes propriedades [24]: i. u v = v u ii. ku v = k(u v), sendo k escalar. iii. u u = se u = e u u > se u iv. u + v w = u w + v w, sendo w vetor no IR 2. Uma integral denida do produto entre duas funções f 1 e f 2 no intervalo [a, b] apresenta as propriedades (i-iv) apresentadas. Com isso, é possível denir o produto interno entre funções como (3.5): 23

39 f 1 f 2 = b a f 1 (t)f 2 (t)dt (3.5) As duas funções f 1 e f 2 serão ditas ortogonais se o resultado da integral em (3.5) for zero. Prosseguindo com a analogia entre vetores e funções: um conjunto formado por vetores mutualmente ortogonais forma uma base do espaço de vetores. Isso signica dizer que qualquer outro vetor neste mesmo espaço pode ser representando como uma combinação linear destes. Por exemplo, se u e v formam base no espaço bidimensional IR 2, qualquer vetor w também contido neste espaço pode ser representado pela combinação linear (3.6). w = c 1 u + c 2 v (3.6) É possível fazer mais uma vez um paralelo com funções: um conjunto ortogonal innito de funções Φ n denido no intervalo t = [a, b], ou seja, um conjunto da forma [Φ, Φ 1, Φ 2...] que respeita a condição (3.7). b a Φ m (t) Φ n (t) dt = δ mn (3.7) sendo δ mn o delta de Kronecker, denido por: 1, se m = n, δ mn =, se m n. (3.8) constitui uma base do chamado espaço de funções e, portanto, pode representar funções f(t) denidas no intervalo [a, b] como mostrado na Equação (3.9): onde c n são coecientes a serem determinados. f(t) = c Φ + c 1 Φ 1 + c 2 Φ c n Φ n (3.9) Alguns conjuntos de funções são ditos ortogonais em relação a uma função peso w(t) > : 24

40 b a w(t) Φ m (t) Φ n (t) dt = δ mn (3.1) O conjunto de polinômios de Laguerre se encaixa no caso (3.1). Estas tem uma relação de ortogonalidade para uma função peso igual a e t. Observando também que o intervalo anteriormente representado por t = [a, b] está denido para este caso como t = [, ]. O conceito de ortogonalidade pode ser descrito, para o caso especíco dos polinômios de Laguerre, pela Equação (3.11). É interessante observar que enquanto em análise vetorial é possível dar um sentido geométrico de perpendicularidade à palavra ortogonal, o mesmo não ocorre no presente caso, sendo esta uma simples denição advinda da generalização do produto interno entre vetores. e t L p L q dt = δ pq (3.11) Isto signica dizer que é possível denir bases do espaço de funções utilizando polinômios de Laguerre, como mostrado na Equação (3.12). A Figura 3.2 mostra as cinco primeiras bases de Laguerre. φ p (t, s) = e s.t 2 Lp (s.t) (3.12) 25

41 1 Ordem Ordem 1 Ordem 2 Ordem 3 Ordem 4.5 φp(t) t Figura 3.2: Bases de Laguerre até ordem 4, escala temporal s = 1. Importante notar que na Equação (3.12) zemos uso de um fator de escala temporal s >. Isso é justicável ao observar a Figura 3.2, note que as bases de Laguerre decaem a zero após a passagem de um tempo t sucientemente grande, na ordem de segundos. Mas o comportamento das grandezas físicas em simulações não é xo e muito menos xo na escala de segundos. Em algumas simulações as variáveis de interessem podem tender a zero em escalas de tempo muito inferiores e, neste caso, os polinômios de Laguerre não seriam capazes de sintetizá-las. Isso signica que, para sintetizar sinais em escalas temporais diferentes, é necessário utilizar uma escala de modo a ajustar as bases ao problema especíco a ser estudado [1]. Em termos práticos, dado um número sucientemente grande de bases de Laguerre, é possível representar (ou sintetizar) qualquer função transitória como um somatório ponderado dessas bases, um conceito similar ao da Série de Fourier. t 15 ( ) A Figura 3.3 mostra a síntese do pulso e 5 2 fazendo uso de 5, 8 e 12 bases de Laguerre. Fica evidente que com o número crescente de bases a descrição da função ca cada vez mais próxima da função original. 26

42 1.5 Sinal, f(t) Sinal Original Sintese com 5 bases de Laguerre Sintese com 8 bases de Laguerre Sintese com 12 bases de Laguerre t Figura 3.3: Síntese de um sinal utilizando diferentes números de bases de Laguerre. A Figura 3.4 mostra, por m, a síntese deste mesmo sinal utilizando 1 bases de Laguerre. 1.5 Sinal, f(t) Sinal Original Sintese com 1 bases de Laguerre t Figura 3.4: Síntese de um sinal utilizando 1 bases de Laguerre. 27

43 As escolhas para o número N L de bases de Laguerre e para o valor da escala temporal s a serem utilizados variam e se baseiam, respectivamente, nas Equações (3.13) e (3.14) [25]. sendo: N L = 2B f T f + 1 (3.13) N L o número necessário de bases de Laguerre. B f a máxima frequência, em Hertz, presente na forma de onda a ser descrita. T f a duração em segundos da forma de onda. sendo: s = xn L max T f (3.14) x N L max o maior zero dentre os polinômios de Laguerre utilizados. Uma pergunta razoável é: Por que utilizar especicamente polinômios de Laguerre? Existem diversas outras classes de funções que apresentam ortogonalidade. Além dos já citados senos e cossenos poderíamos citar os polinômios de Chebyshev e Legendre. Alguns dos motivos estão apresentados a seguir [1]: ˆ Os polinômios de Laguerre formam uma classe de funções ortogonais denidas de a (os polinômios de Chebyshev, por exemplo, estão denidos de -1 a 1). Isto faz com que polinômios de Laguerre sejam uma boa escolha para simulação de sistemas físicos em função do tempo, pois é neste mesmo intervalo que o tempo está denido. ˆ Como a função peso dos polinômios de Laguerre é uma exponencial decrescente, todas as bases de Laguerre eventualmente decaem a zero. Para simulações transitórias, isto é ideal, pois garante estabilidade incondicional, ou seja, o método numérico jamais retornará um sinal que cresça sem limite e, portanto, jamais resultará em um erro que cresça sem limite. ˆ A relação de recursividade entre os polinômios de Laguerre faz com que seja simples computacionalmente obtê-los em tempo de execução, sem necessidade de ocupar memória armazenando as bases a priori. 28

44 3.4 O Método FDTD Baseado em Polinômios de Laguerre Utilizando as propriedades dos polinômios de Laguerre se torna possível representar grandezas físicas de comportamento transitório em termos de somas de bases de Laguerre ponderadas por coecientes. A Equação (3.15) mostra, como exemplo, o caso do campo elétrico. A mesma equação se aplica para campos magnéticos e correntes elétricas. sendo: E x (r, t) = Ex(r) p φ p ( t) (3.15) p= E x (r, t) o campo elétrico na direção x em um determinado ponto r, função da variável tempo t. t = s.t simplesmente uma representação para o tempo escalado pelo fator s. r a variável posição no espaço. φ p a base de Laguerre de ordem p. Ex(r) p o coeciente de ponderação da base Laguerre de ordem p para a representação do campo elétrico E x em uma posição especíca r. É possível demonstrar que a derivada temporal de uma função U qualquer escrita na forma da Equação (3.15), será escrita como na Equação (3.16) [11]: U(r, t) t = s (.5 U p (r) + p= p 1 k=,p> ) U k (r) φ p ( t) (3.16) Partindo das Equações (3.15) e (3.16) é possível desenvolver o método para os diferentes modos já apresentados (TE e TEM) Modo TE Primeiro, reapresentamos as equações que representam o Modo TE z : E x t E y t = 1 ( ) Hz ɛ y J x = 1 ( H ) z ɛ x J y (3.17) (3.18) 29

45 H z t = 1 µ ( Ex y E ) y x (3.19) O primeiro passo é utilizar as Equações (3.15) e (3.16) para reescrever as grandezas desconhecidas (campos elétricos e magnéticos) e suas derivadas temporais presentes em (3.17), (3.18) e (3.19) utilizando formulações em termos de polinômios de Laguerre. s ( p 1 ).5Ex(x, p y) + Ex(x, k y) φ p ( t) p= = 1 ɛ p= k= Hz p y (x, y) φ p( t) J x(x, y, t) ɛ (3.2) s ( p 1 ).5Ey(x, p y) + Ey k (x, y) φ p ( t) p= = 1 ɛ p= k= Hz p y (x, y) φ p( t) J y(x, y, t) ɛ (3.21) s ( p 1 ).5Hz p (x, y) + Hz k (x, y) φ p ( t) p= = 1 µ k= ( ) E p x y (x, y) Ep y (x, y) φ p ( t) x p= (3.22) É importante lembrar que o objetivo do método é abandonar o domínio do tempo e, no entanto, as bases φ p ( t) e as densidades de corrente ainda apresentam termos com dependência em relação ao tempo. Para eliminar esta dependência utilizamos um procedimento conhecido como Procedimento de Teste Temporal de Galerkin [11] que consiste em, fazendo uso das propriedades ortogonais das bases de Laguerre, multiplicar os dois lados da Equação (3.2) por uma base especíca φ q e integrar em função de t no intervalo [, T f ), sendo T f um período de tempo sucientemente grande, de modo a garantir que todas as formas de onda já tenham decaído a praticamente zero. Aplicar este procedimento elimina a dependência explicita em relação ao tempo das seguintes formas: ˆ Como as bases são ortogonais entre si e o procedimento consiste em realizar o produto φ p φ q dentro de uma integral, todos os termos dos somatórios presentes 3

46 nas Equações (3.2), (3.21) e (3.22) com q p desaparecem, e quando q = p, o termo resulta simplesmente em 1. ˆ Os termos relativos a densidade de corrente passam a ser: Jx(x, q y) = Jy(x, q y) = TF TF J (x) (x, y, t) φ q ( t) d t J (y) (x, y, t) φ q ( t) d t (3.23) ou seja, determinam-se assim os termos do somatório de bases de Laguerre que sintetizam a densidade de corrente (que já é conhecida para todo o tempo de simulação). Aplicando estes dois resultados do procedimento às Equações (3.2), (3.21) e (3.22) temos: ( q 1 ) s.5ex(x, q y) + Ex(x, k y) = 1 Hz q ɛ y (x, y) J x(x, q y) ɛ k= ( q 1 ) s.5ey(x, q y) + Ey k (x, y) = 1 ɛ k= k= Hz q y (x, y) J y(x, q y) ɛ ( q 1 ) s.5hz q (x, y) + Hz k (x, y) = 1 ( ) E q x µ y (x, y) Eq y (x, y) x (3.24) (3.25) (3.26) Feito o procedimento de passagem do domínio do tempo para o domínio das bases de Laguerre, faz-se necessário discretizar o espaço, o método WLP-FDTD não difere do método FDTD neste sentido e utiliza a mesma malha deslocada de Yee, ou seja, campos elétricos e magnéticos são avaliados em pontos diferentes, como já mostrado para o caso bidimensional na Figura 2.3. Aplicando a discretização espacial em diferenças centrais, seguida de alguma manipulação algébrica, nas Equações (3.24), (3.25) e (3.26) obtemos (3.27), (3.28) e (3.29). Ex q i,j = Cy E [Hz q i,j Hz q i,j 1 ] 2 q 1 sɛ J x q i,j 2 Ex k i,j (3.27) Ey q i,j = Cx E [Hz q i,j Hz q i 1,j ] 2 q 1 sɛ J y q i,j 2 Ey k i,j (3.28) k= k= 31

47 H q z i,j = C H x q 1 [ ] [ ] E q y i+1,j Ey q i,j + C H y E q x i,j+1 Ey q i,j 2 Hz k i,j (3.29) k= sendo: C E x = 2 sɛ x. C E y = 2 sɛ y. C H x = 2 sµ x. C H y = 2 sµ y. Observando as Equações (3.27), (3.28) e (3.29) é possível notar que existe uma relação implícita entre campos elétricos e magnéticos. Em outras palavras, é possível substituir a Equação (3.29) nas Equações (3.27) e (3.28), o que resultará no conjunto composto pelas Equações (3.3) e (3.31), apresentado a seguir: [ ] 1 [ ] [ ] Ex q i,j + C H Cy E y + Cy H + Ex q i,j 1 C H y + E q x i,j+1 C H y + [ ] [ ] [ ] [ ] Ey q i,j C H x + E q y i,j 1 C H x + E q y i+1,j C H x + E q y i+1,j 1 C H x = y J q x i,j 2 C E y q 1 q 1 q 1 Ex k i,j + 2 Hz k i,j 1 2 Hz k i,j k= k= k= (3.3) [ ] 1 [ ] [ ] Ey q i,j + C H Cx E x + Cx H + Ey q i 1,j C H x + E q y i+1,j C H x + [ ] [ ] [ ] [ ] Ex q i,j C H y + E q x i 1,j C H y + E q x i 1,j+1 C H y + E q x i,j+1 C H y = x J q y i,j 2 C E x q 1 q 1 q 1 Ey k i,j 2 Hz k i 1,j + 2 Hz k i,j k= k= k= (3.31) O método se baseia em descobrir os termos da série que denem o campo elétrico na Equação (3.15) utilizando as Equações (3.3) e (3.31). Para isso, são necessárias tantas iterações quanto termos da série. Em outras palavras, serão necessárias tantas iterações quanto bases de Laguerre utilizadas para sintetizar as grandezas físicas. A relação descrita pelas Equações (3.3) e (3.31) valerá para todos os pontos da geometria, exceto os pontos nas fronteiras, como será mostrado adiante. Isto dá 32

48 origem a um sistema linear como o mostrado na Equação (3.32). Este sistema será resolvido em cada uma das iterações. Cada uma das linhas da matriz descreve a equação para os campo elétricos de cada ponto da geometria. No caso do modo TE, existem dois campos elétricos a serem determinados para cada ponto da geometria, por isso, a matriz terá como número de linhas o dobro do número de pontos utilizados para discretizar a geometria. [A] 2m 2m [E q ] 2m 1 = [J q ] 2m 1 + [β q 1 ] 2m 1 para q = 1, 2... (3.32) sendo: m, o número de pontos utilizados para discretizar a geometria. [A] 2m 2m, a matriz dos coecientes que multiplicam os termos de campo elétrico. [E q ] 2m 1 o vetor coluna contendo todos os termos de Laguerre para os campos elétricos. [J q ] 2m 1 o vetor coluna contendo os termos de Laguerre para todas as correntes. [β q 1 ] 2m 1 o vetor coluna contendo os somatórios dos termos de campos elétricos e magnéticos de todas as iterações anteriores. Portanto, este vetor não existe para q =. É importante observar que os termos do campo elétrico da iteração atual q cam dependendo somente de termos já descobertos dos campos magnéticos. Descobrir os próprios campos magnéticos da iteração atual não é um problema, isto pode ser feito em termos de campos elétricos através da Equação (3.29). Também não há problema no fato dos termos do campo elétrico da iteração atual E q terem dependência em relação aos termos de densidade de corrente de mesma iteração J q, pois, no método WLP-FDTD, a densidade de corrente atua como conhecida a priori e, obviamente, todos os seus termos já são também conhecidos. Como não existem termos anteriores na primeira iteração, [β q 1 ] é inexistente e a Equação (3.32) se torna simplesmente [A] [E ] = [J ]. Uma observação nal é que a matriz A só precisa ser calculada uma vez no início do problema, a partir daí ela se mantém a mesma para todas as iterações. Isto permite a utilização de métodos de aceleração de resolução do sistema linear, tais quais fatoração LU [11]. 33

49 3.4.2 Modo TEM O modo transversal eletromagnético tem um desenvolvimento similar ao do modo transversal elétrico mostrado anteriormente, começamos reapresentando o modo TEM x polar. y e suas Equações, (3.33) e (3.34). E y t H z t = 1 ɛ ( ) Hz x J y = 1 µ ( ) Ey x Aplicando as Equações (3.15) e (3.16) obtemos as Equações (3.35) e (3.36): (3.33) (3.34) s ( q 1 ).5Ey(x) p + Ey k (x) φ p ( t) = 1 ɛ p= k= p= Hz p x (x) φ p( t) J y(x, t) ɛ (3.35) s ( q 1 ).5Hz p (x) + Hz k (x) φ p ( t) = 1 µ p= k= p= Aplicando o Procedimento de Teste Temporal de Galerkin: s ( q 1 ).5Ey(x) q + Ey k (x) = 1 Hz q ɛ x (x) J y(x) q ɛ s k= ( q 1 ).5Hz q (x) + Hz k (x) k= = 1 µ E p y x (x) φ p( t) (3.36) (3.37) Ey q (x) (3.38) x Aplicando a discretização espacial por diferenças centradas e rearranjando termos camos com as Equações (3.39) e (3.4): Ey q i = Cx E (Hz q i Hz q i 1 ) 2 q 1 sɛ J y q i 2 Ey k i (3.39) k= sendo: C E x = 2 sɛ x. C H x = 2 sµ x. H q z i = C H x q 1 ( ) E q y i+1 Ey q i 2 Hz k i (3.4) k= 34

50 Assim como no caso do modo TE, existe uma relação implícita entre campos elétricos e magnéticos. Substituindo a Equação (3.4) em (3.39) se torna possível escrever: E q y i [ 1 C E x ] [ ] [ ] + Cx H + Cx H + Ey q i 1 C H x + E q y i+1 C H x = x J q y i 2 C E x q 1 q 1 q 1 (3.41) Ey k i 2 Hz k i Hz k i,j k= k= k= Assim como no caso anterior, chega-se a um sistema linear. O sistema para o modo TEM x polar. y é da forma mostrada na Equação (3.42). [A] m m [E q ] m 1 = [J q ] m 1 + [β q 1 ] m 1 para q = 1, 2... (3.42) sendo: m, o número de pontos utilizados para discretizar a geometria. [A] m m, a matriz dos coecientes que multiplicam os termos de campo elétrico. [E q ] m 1 o vetor coluna contendo todos os termos de Laguerre para os campos elétricos. [J q ] m 1 o vetor coluna contendo os termos de Laguerre para todas as correntes. [β q 1 ] m 1 o vetor coluna contendo os somatórios dos termos de campos elétricos e magnéticos de todas as iterações anteriores. Este vetor não existe para q =. Observe que nesse caso, ao contrário do modo TE, só existe um campo elétrico a ser determinado para cada ponto da geometria. Com isso, enquanto o sistema de um problema bidimensional tem tantas linhas quanto o dobro de pontos usados pra discretizar a geometria, o sistema linear de um problema unidimensional terá simplesmente tantas linhas quanto pontos usados pra discretizar a geometria. Todas as observações feitas anteriormente sobre a relação entre iterações e ordens dos polinômios, além da estrutura do algoritmo, se mantém Condições de Fronteira As condições de fronteira apresentadas na Seção também podem ser implementadas no método WLP-FDTD. Estas condições são adicionadas exatamente da mesma forma tanto para problemas bidimensionais (modos TE e TM) quanto para unidimensionais (modo TEM). 35

51 Condição PEC (Perfect Electric Conductor ) A condição do tipo PEC é adicionada de maneira razoavelmente simples modicando o sistema linear (3.32) em dois passos : ˆ As linhas da matriz [A] 2m 2m correspondentes aos pontos presentes no limite da geometria devem ter, excetuando-se a diagonal principal, somente elementos nulos. ˆ As linhas dos vetores [β q 1 ] 2m 1 e [J q ] 2m 1 devem ser zeradas. Condição Absorvente de Mur (ABC) A condição de Mur de primeira ordem para limites laterais (por exemplo, x = ou x = L para uma geometria denida no intervalo [, L]) é dada pela Equação (2.51), apresentada na Seção [11]. Note que somente a componente do campo elétrico tangente à fronteira é tratada (no caso, E y ). Para inserir esta condição no algoritmo do método WLP-FDTD é necessário escrevê-la em termos das bases de Laguerre e, para isso, as Equações (3.15) e (3.16) são utilizadas. Substituindo estas em (2.51) obtemos a Equação (3.43): ( ) Ey(x, q y) + s E q q 1 y (x, y) + Ey k (x, y) = (3.43) x v 2 Aplicando a discretização espacial por diferenças centrais no ponto x = (Equação (3.44)) e, fazendo alguma manipulação algébrica, obtém-se a condição de Mur de primeira ordem aplicada ao WLP-FDTD para o ponto x =, mostrada na Equação (3.45): k= E y x Eq y 2,j Ey q 1,j 1+ 1,j= 2 2 (3.44) [ s Ey q 1,j 4v + 1 ] [ s + E q x y 2,j 4v 1 ] x = s 2v q 1 ( ) E k y 2,j + Ey k 1,j k= (3.45) Aplicando o mesmo procedimento no outro extremo da geometria (x = L), obtemos a relação dada pela Equação (3.46), semelhante à Equação (3.45). [ s Ey q L,j 4v + 1 ] [ s + E q x y L 1,j 4v 1 ] x = s 2v q 1 ( ) E k y L,j + Ey k L 1,j k= (3.46) As Equações (3.45) e (3.46) podem ser inseridas nas linhas referentes às fron- 36

52 teiras do sistema linear da Equação (3.32). O sistema linear terá sua matriz A e seu vetor coluna β modicados nas linhas referentes aos extremos da geometria. O desenvolvimento para fronteiras verticais se dá da mesma forma, apenas se faz necessária a substituição da coordenada utilizada na derivada espacial da condição de Mur (x por y), além da utilização da componente tangente de campo elétrico correspondente. 37

53 Capítulo 4 Simulações e Resultados 4.1 Metodologia Este trabalho tem, como dito anteriormente, o objetivo de validar as características de estabilidade incondicional e precisão do método WLP-FDTD. Para isso, foram desenvolvidos algoritmos próprios utilizando linguagem MATLAB para os casos TEM x polar. y e TE z. Utilizando estes algoritmos, foram realizadas simulações de dois sistemas físicos, ambos com respostas eletromagnéticas presentes na literatura. A validação é feita, para o caso TE z, por comparação entre o gráco obtido pelo algoritmo próprio e o presente na referência [11]. Para o caso TEM x polar. y, a validação é feita por comparação com o resultado analítico disponível na referência [1]. Grácos baseados na solução analítica foram gerados para comparação com os grácos obtidos pelo algoritmo próprio. Além disso, o coeciente de correção linear R P earson entre as duas respostas é obtido. Este coeciente está limitado entre -1 e 1, inclusive. R P earson = 1 denota correlação positiva completa entre as grandezas, R P earson = 1 denota correlação negativa completa e R P earson = denota a completa ausência de correlação [26]. O Anexo B trata brevemente deste conceito. 4.2 Estrutura do Algoritmo Tanto o algoritmo unidimensional quanto o bidimensional se baseiam, fundamentalmente, em quatro loops: ˆ Loop de denição das bases de Laguerre (N L iterações): Neste loop, as equações 3.4 e 3.12 são utilizadas para gerar as bases de Laguerre. Neste mesmo loop já são obtidos os coecientes de Laguerre Jx q e Jy q para a densidade de corrente escolhida, utilizando a Equação (3.23). 38

54 ˆ Loop de denição da matriz A (2m iterações para casos bidimensionais, m iterações para casos unidimensionais. Sendo m o número de pontos escolhido para discretizar a geometria): Durante estas iterações, as equações (3.3) e (3.31) (para o caso TE z ) ou a Equação (3.41) (para o caso TEM x polar. y ) são utilizadas para construir a matriz A do sistema linear apresentado na Equação (3.32) (para o caso TE z ) ou na Equação (3.42) (para o caso TEM x polar. y ). Existem loops internos para tratar os extremos do espaço de simulação e aplicar as condições de fronteira. ˆ Loop principal (N L iterações): Neste loop, três processos ocorrem; Primeiro, o vetor β, dependente do somatório dos termos já descobertos, é atualizado com os coecientes da última iteração, se esta é a primeira iteração, este vetor simplesmente não existe. Em seguida, utilizando o vetor β, os termos Jx q e Jy q descobertos no primeiro Loop, e a matriz A construída no segundo Loop, o sistema linear ((3.32) ou (3.42)) é resolvido. Em seguida, utilizando os coecientes E q e a Equação (3.29) (bidimensional), ou a Equação (3.4) (unidimensional), os coecientes H q são descobertos. Estes termos são utilizados na próxima iteração, de modo a atualizar o vetor β. ˆ Loop de retorno ao domínio do tempo (2m iterações para o caso bidimensional, m iterações para o caso unidimensional): Neste loop nal, os termos descobertos no Loop principal são aplicados na Equação (3.15) para todos os pontos da geometria, de modo a fazer com que as grandezas físicas retornem ao domínio do tempo. A Figura 4.1 mostra um uxograma com a visão geral do algoritmo implementado neste trabalho para o algoritmo WLP-FDTD. 39

55 Loop de definição das bases de Laguerre Loop de retorno ao domínio do tempo Gerador de Gráficos Loop de definição da Matriz A Loop principal Dados de Geometria e Discretização Figura 4.1: Fluxograma do Algoritmo Implementado para o Método WLP-FDTD. 4.3 Simulação Bidimensional: Sistema Físico Apresentado por Chung et al. Para validação do algoritmo próprio para o caso bidimensional, decidiu-se replicar os resultados apresentados na referência [11]. A conguração simulada é a mostrada na Figura