LISTA DE EXERCÍCIOS 1 ESTATÍSTICA E PROBABILIDADES

Transcrição

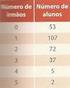
1 LISTA DE EXERCÍCIOS 1 ESTATÍSTICA E PROBABILIDADES 1- Ordene os dados indicando o 1º, 2º e 3º quartil 45, 56, 62, 67, 48, 51, 64, 71, 66, 52, 44, 58, 55, 61, 48, 50, 62, 51, 61, Faça a análise da distribuição de altura obtida a partir de uma amostra de 40 alunos de uma escola. Altura Frequência 3- Qual a reta ajustada que melhor representa a correlação entre a grandeza X e Y representada abaixo? Xi Yi Calcule a média, a mediana e a moda dos dados apresentados a seguir: 82, 86, 88, 84, 85, 85, 91, 93

2 5- Um professor está interessado em demonstrar que as notas de algumas disciplinas têm relação direta com as notas de outras. No caso foram analisados um conjunto de 12 alunos em duas disciplinas: Estatística e Cálculo. Analise se há uma correlação entre as notas das duas áreas. Aluno Nota em Matemática Nota em Estatística A 5 6 B 8 9 C 7 8 D E 6 5 F 7 7 G 9 8 H 3 4 I 8 6 J 5 3 K 4 7 L O quadro seguinte representa as alturas (em cm) de 40 alunos de uma classe. a) Construir uma tabela de freqüência das alturas dos alunos. b) Construir o histograma.

3 7- Meça os colegas de sua turma e pergunte a massa em kg. Construa uma correlação relacionando a altura e o peso dos colegas somente dos colegas. 8- Um fabricante pretende avaliar a correlação existente entre a temperatura do dia e o consumo de cerveja. Os dados foram inseridos na tabela a seguir. Avalie qual a correlação é mais adequada. 9- Calcule a correlação que relaciona a idade e a altura de uma criança.

4 10- Construa o histograma que represente a distribuição do peso dos estudantes de uma determinada escola.

5 Lista de Exercícios 2 Estatística e Probabilidades 1- Uma empresa precisa selecionar 1 novo colaborador entre 50 que realizaram 6 tipos de provas. 3 deles obtiveram as melhores notas: A, B e C, conforme a tabela. Considerando-se o critério de escolha o candidato com menor variância, qual deles deve ser escolhido? Candidato Prova 1 Prova 2 Prova 3 Prova 4 Prova 5 Prova 6 A 7 7, ,5 9 B C 7, ,5 σ 2 = ( Xi x) 2 ( n 1 ) 2- Cinco empregados coletados aleatoriamente de 3 empresas (A, B e C). Perguntou-se o salário deles (em salários mínimos) Em qual você trabalharia a partir dessa pesquisa? A B C 5, ,5 9 7

6 3- No exercício de correlação entre temperatura do dia ( o C) e consumo de cerveja (litros), calcule qual é o coeficiente R. T C Uma pesquisa com 100 pessoas mediu o tempo de reação para frear um carro em milisegundos. O valor médio obtido foi de 180ms com um desvio padrão de 50ms. Considerando que o tempo de reação obedece a lei da distribuição normal, qual é a probabilidade de encontrar uma pessoa com tempo de reação menor que 100ms? 5- Uma fabrica de cimentos necessita encher sacos com peso médio de 50kg. Mas em alguns casos o peso varia de acordo com a distribuição normal. Uma amostra de 20 sacos de cimento apresentou massa média de 50kg e desvio padrão de 2 kg. Se um saco de cimento for selecionado aleatoriamente no depósito para análise, qual a probabilidade de que ele tenha menos de 48kg?

7 Lista de exercícios 3 Estatística e probabilidades 1- Em um lançamento de duas moedas não viciadas (ao mesmo tempo), qual é a probabilidade de sair 2 coroas? 2- Uma caixa tem 3 bolas brancas e 2 bolas pretas. Selecionando-se aleatoriamente (por sorteio) 2 bolas sem reposição, qual a probabilidade de sair 2 bolas pretas? E se houvesse reposição? 3- Considere 3 lançamentos seguidos de uma moeda honesta. Qual a probabilidade de sair apenas 1 cara nesses 3 lançamentos? 4- Considere que dois dados honestos sejam lançados juntos. Em cada jogada, calcula-se a soma dos resultados. Qual a probabilidade de que a soma seja 6 ou 7? 5- Um piloto tem probabilidade de vencer uma corrida calculada em 1/5. Qual a probabilidade do piloto não vencer a corrida? 6- De um baralho de 52 cartas extraem-se 2 cartas sucessivamente e sem reposição. Qual a probabilidade de se obter um ás e um valete nessa ordem? 7- Lança-se dois dados não viciados. Se a soma dos pontos nos dois lados foi 8, calcule a probabilidade de ocorrer a face 5 em um deles? 8- Uma caixa tem 9 bolas, sendo 2 brancas, 3 vermelhas e 4 pretas. Qual a probabilidade de ser retirar uma bola que não seja preta? 9- Escolhe-se ao acaso um dos anagramas da palavra XADREZ. Qual a probabilidade da palavra escolhida começar por XA? 10- Uma urna contém bolas numeradas de 1 a 25. Uma bola é extraída ao acaso dessa urna. Qual a probabilidade de o número da bola sorteada ser múltiplo de 2 ou de 3?

8 Lista de exercícios número 4 1- Uma caixa contém 11 bolas numeradas de 1 a 11. Retirando-se uma delas ao acaso, observa-se que a mesma traz um número ímpar. Determinar a probabilidade de que esse número seja menor que Dois dados, um azul e um verde são lançados e cada uma das seis faces são equiprováveis nos dois dados. Qual a probabilidade do dado verde ter resultado 6 dado que a soma dos resultados foi 8? 3- Em uma comunidade, 15% das pessoas lêem o jornal A, 12% lêem o jornal B e 3% lêem ambos os jornais. Sorteando-se uma pessoa e sabendo que ela lê o jornal B, qual a probabilidade de que ela leia também o jornal A? 4- Em uma pesquisa realizada com consumidores sobre a preferência da marca de sabão em pó, verificou-se que utilizam a marca X, utilizam a marca Y, utilizam as duas marcas. Foi sorteada uma pessoa desse grupo e verificou-se que ela utiliza a marca X, Qual a probabilidade dessa pessoa também ser usuária da marca Y? 5- Uma caixa tem bolas numeradas de 1 a 10. Sorteamos 1 bola ao acaso. Qual a probabilidade da bola sorteada ser múltiplo de 2? E qual a probabilidade da bola ser múltiplo de 3?

9 Lista de exercícios 5- Estatística e Probabilidades 1-Qual a probabilidade de uma caixa de leite, escolhida aleatoriamente seja do tipo U, sabendo que ele está fora das especificações? Tipo B Tipo C Tipo U Total Dentro das especificações Fora das especificações Total Em uma rede de computadores, em 60% dos dias ocorre alguma falha. Construir a distribuição de probabilidades para a variável aleatória X = número de dias com falha na rede, considerando o período de observação de 3 dias. Suponha que os eventos são independentes. 3- Uma caixa tem 9 bolas, sendo 2 brancas, 3 vermelhas e 4 pretas. Qual a probabilidade de ser retirar uma bola que não seja preta? 4- Um casal pretende ter 3 filhos. Qual a probabilidade de nascerem dois meninos? 5- Dois aparelhos de alarme funcionam de forma independente, detectando presença com probabilidades de 0,95 e 0,90. Qual a probabilidade de que um dado problema seja detectado por apenas um dos aparelhos? 6- Em um lote de 12 peças, 4 são defeituosas. 2 peças são retiradas uma após a outra sem reposição e de forma aleatória. Qual a probabilidade de que ambas sejam boas? 7- Uma fábrica tem 3 máquinas A, B e C responsáveis por 40%, 50% e 10% da produção. Os percentuais de peças defeituosas produzidas pelas respectivas máquinas são: 3%, 5% e 2%. Uma peça é sorteada ao acaso e verifica-se que ela é defeituosa. Qual a probabilidade de que ela tenha vindo da máquina B?

10 8- Uma moeda viciada é lançada 8 vezes. A probabilidade de se obter cara em cada jogada é de 0,60. No total de lançamentos, qual a probabilidade de se obter 5 caras? 9- Uma central telefônica PABX recebe uma média de 5 chamadas por minuto. Qual a probabilidade de que a central não receber nenhuma chamada durante um intervalo de 1 minuto? 10- Um servidor HTTP recebe uma média de 3,5 acessos por minuto. Qual a probabilidade de observarmos apenas 2 acessos por minuto? 11- Considerando X como sendo uma variável aleatória discreta igual ao número de vezes em que ocorre a face CARA em 5 lançamentos de uma moeda honesta. Qual a probabilidade de ocorrer duas caras? Qual a probabilidade de ocorrer no máximo 2 caras? 12- Um banco de sangue catalogou doadores durante 5 dias. Os dados foram organizados na tabela. Analisando estas informações, calcule qual a probabilidade de um doador ter o sangue do tipo O ou do tipo A. Calcule também a probabilidade de um doador selecionado aleatoriamente ter o sangue tipo B ou que seu Rh seja negativo. Sangue tipo Sangue tipo Sangue tipo Sangue tipo Total O A B AB Fator Rh Fator Rh Total

11 13- Em uma amostra de 150 estudantes, 70 disseram que somente têm um aparelho de CD, 50 disseram que somente têm uma TV e 25 disseram que têm ambos. O Diagrama de Venn a seguir descreve esta situação. Se um estudante e selecionado ao acaso, qual e a probabilidade de que ele tenha somente um aparelho de CD? De que ele tenha somente uma TV? De que ele tenha tanto uma TV como um aparelho de CD? 14- Considerando um lote de peças. Admitamos que 10% delas sejam defeituosas. Duas peças são selecionadas aleatoriamente. Qual a probabilidade de que ambas sejam perfeitas? 15- Considere o circuito da figura. A probabilidade de que cada relé esteja fechado é de 12%. Todos os relés funcionam independentemente. Qual é a probabilidade de que o circuito permita a passagem de corrente entre A e B? 16 Uma multinacional produz circuitos integrados em 3 fábricas F1, F2 e F3 na proporção de 30%, 45% e 25% respectivamente. As probabilidades de que um circuito integrado produzido por essas fábricas não funcione são 1%, 2% e 3%. Escolhido ao acaso um circuito com defeito, qual a probabilidade de que ele seja fabricado na F1?

12 17- Um professor importante, residente no Rio de Janeiro, preocupado com um possível sequestro, adota a seguinte estratégia para se deslocar da sua casa até o escritório onde trabalha: duas vezes por semana usa um carro branco, duas vezes por semana usa um carro azul e uma vez por semana um carro cinza prateado; duas vezes por semana usa a rota A, duas vezes por semana a rota B e uma vez por semana a rota C; A decisão sobre qual rota e qual carro utilizar em uma dada semana é independente e é escolhida ao acaso no domingo à noite, porém sempre é mantida a proporção acima. Determine a probabilidade deste professor estar usando o carro azul na rota B em uma terça-feira durante uma semana sem feriados. 18- Suponha que numa linha de produção a probabilidade de se obter uma peça defeituosa (sucesso) é p=0,1. Toma-se uma amostra de 10 peças para serem inspecionadas. Qual a probabilidade de se obter: a) Uma peça defeituosa? b) Nenhuma peça defeituosa? c) Duas peças defeituosas? D) No mínimo duas peças defeituosas? E) No máximo duas peças defeituosas? 19- Um módulo eletrônico é formado por peças do tipo A, B e C. A taxa de defeitos em cada peça é de 50 por milhão, 80 por milhão e 120 por milhão respectivamente. Somente montando é possível perceber o defeito. Qual o número de módulos por milhão que darão o defeito? 20- Na Páscoa uma avó compra ovos para seus 8 netos. Ela comprou 1 chocolate Lacta e 2 chocolates Garotos para cada neto. Dentro do chocolate há brindes, sendo que a probabilidade de se encontrar um brinde no chocolate Lacta é de 1/8. Já para o chocolate Garoto a chance é de 1/16. Nesse caso, qual é a probabilidade do neto mais velho ser o único a ganhar um brinde no chocolate Lacta?