Material de apoio - Números complexos
|
|
|
- Natan Castro Madeira
- 9 Há anos
- Visualizações:
Transcrição
1 Material de api - Númers cmplexs Intrduçã Dad a equaçã, qual valr de X?. x 8 = 0. x = 8 8 x = x = 4 x = ± 4 Prém, nã existem raízes reais para númers negativs, daí a necessidade de criar um nv númer, infelizmente chamad de imaginári. j = 1 O que ns dá um nv resultad: x = ± 4.( 1) x = ± 4. 1 x = ±. 1 x = ± j Onde j é a unidade d númer imaginári. Em algumas situações, usa-se i, prém, em engenharia iss pde acarretar cnfusã cm a intensidade da crrente elétrica. Representações d númer cmplex Frma retangular Pr definiçã, númer cmplex é representad em sua frma retangular, u seja: Frma trignmétrica O númer cmplex, também pde ser representad n plan de Argand Gauss, vejams: Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 1
2 Frma expnencial Utilizand terema de Euller, e = csθ j.senθ, terems númer cmplex representad na frma expnencial. Frma plar A última representaçã é a frma plar e esta, pde ser facilmente btida utilizand as frmas anterires. Praticand: 1) Exprimir s númers =0 50º e =110-85º nas frmas, expnencial, trignmétrica e retangular. Sluçã: = 0 50 = 0. e j50 = 0.cs 50 = 1,86 j0.sen 50 j15,3 = = 0. e j85 = 110.cs( 85 ) = 9,59 j109,58 j110.sen( 85 ) ) Representar s númers z3 = (0 j3) e z4 = (-0 nas frmas, expnencial, trignmétrica e plar. 3) Representar s númers z5 = 0.e j0º e z6 = 1.e j(-3)º nas frmas, trignmétrica, retangular e plar. 4) Exprimir s númers z7=4-50º e z8=11-5º nas frmas, expnencial, trignmétrica e retangular. Operações básicas cm cmplexs na frma retangular Sma: ( a ( a d) jb) j.( b d) Subtraçã: ( a jb) ( a d) j.( b d) Númers cmplexs Autr: Cldald Silva - Versã: 19Out007.
3 Multiplicaçã: ( a jb).( c a. c j. da jbc j. j. b. d ( a. c bd) ( da bd). j lembrand que: j² = -1 Divisã: ( a ( a jb) jb). ( a. c bd) ( bc da). j c d Nta: O cnjugad é invers d númer imaginári, em nss material, pr facilidade de escrita, utilizarems um asterisc para indicar cnjugad. Exempl: nde: z* se lê cnjugad de z a z* = a jb jb Praticand Sabend-se que, = (0 j3) e = (-0. a) qual a sma (); b) a subtraçã ( ); c) prdut (. ) e; d) quciente ( ). a) Sluçã: (0 j3) ( 0 (0 0) ( j3 0 j10 b) Sluçã: (0 j3) ( 0 (0 0) ( j3 40 j16 c) Sluçã: (0 j3).( 0 (0. 0) (0. ( j3. 0) ( j j60 j30 j60 39 d) Sluçã: (0 j3) ( 0. ( 0 ( 0 (0. 0) (0. ( j3. 0) ( j ( ) ( j60 j60) j ,77 j0,35 Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 3
4 6- Sabend-se que, z3 = (1 j30) e z4 = (4 j33). e) qual a sma (z3z4); f) a subtraçã (z3 z4); g) prdut (z3. z4) e; h) quciente (z3 z4). 7- Sabend-se que, z5 = (0 j30) e z6 = (33 0j). i) qual a sma (z5z6); j) a subtraçã (z5 z6); k) prdut (z5. z6) e; l) quciente (z5 z6). Operações utilizand a frma plar Sma: a θ1º b θº (Nã reslve, deve cnverter para retangular). Subtraçã: a θ1º - b θº (Nã reslve, deve cnverter para retangular). Multiplicaçã: a θ1º. b θº (a.b) (θ1 θ)º Divisã: (a θ1º) (b θº) (a b) (θ1- θ)º Praticand Qual resultad express em plar, sabend-se que = (00 30º) e = 0 0º. a) qual a sma (); b) a subtraçã ( ); c) prdut (. ) e; d) quciente ( ). a) Sluçã: = 00.cs 30º 00.sen 30º = 173,1 = 0.cs 0º 0.sen 0º = 18,79 ( 173,1 j100) 19 j100 j6,84 j106,84 (18,79 j6,84) Exprimind em plar 19 19,7 106, ,84 θ = tag 19 θ = 9,09º 19,7 9,09º Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 4
5 b) Sluçã: = 00.cs 30º 00.sen 30º = 173,1 = 0.cs 0º 0.sen 0º = 18,79 ( 173,1 j100) 154,4 c) Sluçã: j100 j6,84 j93, º.0 0º 4000 (30 0)º º Praticand... (18,79 j6,84) Exprimind em plar 154,4 180,34 180,34 31,1º 93, ,16 θ = tag 154,4 θ = 31,1º d) Sluçã: 00 30º 0 0º 10 (30 0)º 10 10º 9- Qual resultad express em plar, sabend-se que z3 = (4-35º) e z4 = -4 1º. a) qual a sma (z3z4); b) a subtraçã (z3 z4); c) prdut (z3. z4) e; d) quciente (z3 z4). 10- Qual resultad express em plar, sabend-se que z5 = (-4-50º) e z6 = -4-1º. a) qual a sma (z5z6); b) a subtraçã (z5 z6); c) prdut (z5. z6) e; d) quciente (z5 z6). Operações utilizand a frma expnencial Sma: a.e Jθ1º b.e Jθº (Nã reslve, deve cnverter para retangular). Subtraçã: a.e Jθ1º - b.e Jθº (Nã reslve, deve cnverter para retangular). Multiplicaçã: a.e Jθ1º - b.e Jθº a.b.e J(θ1θ)º Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 5
6 Divisã: a.e Jθ1º b.e Jθº (a b).e J(θ1-θ)º Praticand Qual resultad express em expnencial, sabend-se que =10.e J1º e =14.e Jº a) qual a sma (); b) a subtraçã ( ); c) prdut (. ) e; d) quciente ( ). a) Sluçã: = 10.cs 1º 10.sen 1º = 9,34 = 14.cs º 14.sen º = 1,98 ( 9,34 j3,58),3 = 9,34 = 1,98 j3,58 j5,4 j8,8 ( 9,34 j3,58) 3,64 j3,58 j5,4 j1,66 (1,98 b) Sluçã: = 10.cs 1º 10.sen 1º = 14.cs º 14.sen º c) Sluçã: 10e j 1 (10.14) e 140e.14e j 43 j j(1 ) (1,98 j5,4) j5,4) Exprimind em expnencial 3,99 1 θ = tag θ = 1,56º,3 3,99e 8,8 8,8,3 j1,56 Exprimind em expnencial 4 1 1,66 θ = tag 3,64 θ = 155,5º 4e ( 3,64) j155,5 d) Sluçã: 10. e 14. e 0,71. e 0,71. e j1 j j1 ( 1,66) j(1 ) Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 6
7 1- Qual resultad express em expnencial, sabend-se que =1.e J10º e =41.e J5º a) qual a sma (); b) a subtraçã ( ); c) prdut (. ) e; d) quciente ( ). 13- Qual resultad express em expnencial, sabend-se que =5.e J8º e =4.e J3º a) qual a sma (); b) a subtraçã ( ); c) prdut (. ) e; d) quciente ( ). "Quem lha para fra, snha; quem lha para dentr, desperta." (Carl Yung) Númers cmplexs Autr: Cldald Silva - Versã: 19Out007. 7
Números Complexos, Conversão de Formas e Operações Matemáticas
 Institut Federal de Educaçã, iência e Tecnlgia de Santa atarina Departament Acadêmic de Eletrônica Retificadres Númers mplexs, nversã de Frmas e Operações Matemáticas Prf. lóvis Antôni Petry. Flrianóplis,
Institut Federal de Educaçã, iência e Tecnlgia de Santa atarina Departament Acadêmic de Eletrônica Retificadres Númers mplexs, nversã de Frmas e Operações Matemáticas Prf. lóvis Antôni Petry. Flrianóplis,
Como Z constitui-se claramente a hipotenusa de um triângulo retângulo, tem-se
 UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
EXERCÍCIOS DE REVISÃO NÚMEROS COMPLEXOS
 COMÉRCIO EXTERIOR - REGULAR TERCEIRA SÉRIE NOME: EXERCÍCIOS DE REVISÃO NÚMEROS COMPLEXOS TESTES 1) Cnjunt sluçã da equaçã z z 0, n cnjunt ds númers cmplexs, é: a), 0, - c) d) e) 0 5 ) O cnjugad d númer
COMÉRCIO EXTERIOR - REGULAR TERCEIRA SÉRIE NOME: EXERCÍCIOS DE REVISÃO NÚMEROS COMPLEXOS TESTES 1) Cnjunt sluçã da equaçã z z 0, n cnjunt ds númers cmplexs, é: a), 0, - c) d) e) 0 5 ) O cnjugad d númer
Revisão números Complexos
 ELETRICIDADE Revisão números Complexos Prof. Marcio Kimpara Universidade Federal de Mato Grosso do Sul Números complexos No passado, os matemáticos esbarraram em uma situação oriunda da resolução de uma
ELETRICIDADE Revisão números Complexos Prof. Marcio Kimpara Universidade Federal de Mato Grosso do Sul Números complexos No passado, os matemáticos esbarraram em uma situação oriunda da resolução de uma
TIPO DE PROVA: A. Questão 1. Questão 3. Questão 2. Questão 4. alternativa E. alternativa A. ver comentário. alternativa E
 Questã TIPO DE PROVA: A N primeir semestre deste an, a prduçã de uma fábrica de aparelhs celulares aumentu, mês a mês, de uma quantidade fixa. Em janeir, fram prduzidas 8 000 unidades e em junh, 78 000.
Questã TIPO DE PROVA: A N primeir semestre deste an, a prduçã de uma fábrica de aparelhs celulares aumentu, mês a mês, de uma quantidade fixa. Em janeir, fram prduzidas 8 000 unidades e em junh, 78 000.
Matemática Elementar B Lista de Exercícios 2
 Ministéri da Educaçã Diretria de Graduaçã e Educaçã Prfissinal Departament Acadêmic de Matemática Matemática Elementar B Lista de Exercícis 0 Transfrme s ânguls a seguir de graus para radians a) 0º b)
Ministéri da Educaçã Diretria de Graduaçã e Educaçã Prfissinal Departament Acadêmic de Matemática Matemática Elementar B Lista de Exercícis 0 Transfrme s ânguls a seguir de graus para radians a) 0º b)
CIRCUITOS DE CORRENTE ALTERNADA
 3 IUITOS DE OENTE TEND 3. INTODUÇÃO O estud de circuits de crrente alternada (..) é sbremd imprtante dad que a grande mairia das instalações elétricas utiliza este tip de circuits. Inicia-se desenvlviment
3 IUITOS DE OENTE TEND 3. INTODUÇÃO O estud de circuits de crrente alternada (..) é sbremd imprtante dad que a grande mairia das instalações elétricas utiliza este tip de circuits. Inicia-se desenvlviment
TIPO DE PROVA: A. Questão 1. Questão 2. Questão 4. Questão 3. alternativa A. alternativa B. alternativa C
 Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
Exercícios de Matemática Fatoração
 Eercícis de Matemática Fatraçã ) (Vunesp-00) Pr hipótese, cnsidere a = b Multiplique ambs s membrs pr a a = ab Subtraia de ambs s membrs b a - b = ab - b Fatre s terms de ambs s membrs (a+(a- = b(a- Simplifique
Eercícis de Matemática Fatraçã ) (Vunesp-00) Pr hipótese, cnsidere a = b Multiplique ambs s membrs pr a a = ab Subtraia de ambs s membrs b a - b = ab - b Fatre s terms de ambs s membrs (a+(a- = b(a- Simplifique
1 a QUESTÃO: (2,0 pontos) Avaliador Revisor
 ( MATEMÁTICA - Gabarit Grups I e J a QUESTÃO: (,0 pnts) Avaliadr Revisr A figura abaix exibe gráfic de uma funçã y = f (x) definida n interval [-6,+6]. O gráfic de f passa pels pnts seguintes: (-6,-),(-4,0),
( MATEMÁTICA - Gabarit Grups I e J a QUESTÃO: (,0 pnts) Avaliadr Revisr A figura abaix exibe gráfic de uma funçã y = f (x) definida n interval [-6,+6]. O gráfic de f passa pels pnts seguintes: (-6,-),(-4,0),
Estudo do efeito de sistemas de forças concorrentes.
 Universidade Federal de Alagas Faculdade de Arquitetura e Urbanism Curs de Arquitetura e Urbanism Disciplina: Fundaments para a Análise Estrutural Códig: AURB006 Turma: A Períd Letiv: 2007 2007-2 Prfessr:
Universidade Federal de Alagas Faculdade de Arquitetura e Urbanism Curs de Arquitetura e Urbanism Disciplina: Fundaments para a Análise Estrutural Códig: AURB006 Turma: A Períd Letiv: 2007 2007-2 Prfessr:
Matemática B Extensivo V. 2
 Gabarit Matemática B Extensiv V. Reslva Aula Aula 7.0) a) sen 0 sen (60 0 ) 7.0) f(x) sen 0 b) cs 0 cs (80 0 ) c) cs 60 cssec 60 cssec 00 sen 00. d) sec 97 sec cs e) tg tg tg ( 80 ) Períd: p 6 Imagem:
Gabarit Matemática B Extensiv V. Reslva Aula Aula 7.0) a) sen 0 sen (60 0 ) 7.0) f(x) sen 0 b) cs 0 cs (80 0 ) c) cs 60 cssec 60 cssec 00 sen 00. d) sec 97 sec cs e) tg tg tg ( 80 ) Períd: p 6 Imagem:
SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES. Matrizes e Determinantes
 SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES Matrizes e Determinantes Depis de estudad uma matéria em matemática é imprtante que vcê reslva um númer significativ de questões para fiaçã de cnteúd.
SEJAFERA APOSTILA EXERCÍCIOS / QUESTÕES DE VESTIBULARES Matrizes e Determinantes Depis de estudad uma matéria em matemática é imprtante que vcê reslva um númer significativ de questões para fiaçã de cnteúd.
matemática 2 Questão 7
 Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
Resposta de R, L e C em CA e Potência Média
 Institut Federal de Educaçã, Ciência e Tecnlgia de Santa Catarina Departaent Acadêic de Eletrônica Retificadres Respsta de R, e C e CA e Ptência Média Prf. Clóvis Antôni Petry. Flrianóplis, fevereir de
Institut Federal de Educaçã, Ciência e Tecnlgia de Santa Catarina Departaent Acadêic de Eletrônica Retificadres Respsta de R, e C e CA e Ptência Média Prf. Clóvis Antôni Petry. Flrianóplis, fevereir de
XXXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 3 (Ensino Médio) GABARITO
 XXXIII OLIMPÍD RSILEIR DE MTEMÁTI PRIMEIR FSE NÍVEL (Ensin Médi) GRITO GRITO NÍVEL ) 6) ) D 6) D ) ) 7) D ) 7) D ) D ) 8) ) 8) D ) ) 9) ) 9) ) D ) E 0) D ) D 0) E ) E ada questã da Primeira Fase vale pnt.
XXXIII OLIMPÍD RSILEIR DE MTEMÁTI PRIMEIR FSE NÍVEL (Ensin Médi) GRITO GRITO NÍVEL ) 6) ) D 6) D ) ) 7) D ) 7) D ) D ) 8) ) 8) D ) ) 9) ) 9) ) D ) E 0) D ) D 0) E ) E ada questã da Primeira Fase vale pnt.
Conjunto dos Números Complexos
 Conjunto dos Unidade Imaginária Seja a equação: x + 0 Como sabemos, no domínio dos números reais, esta equação não possui solução, criou-se então um número cujo quadrado é. Esse número, representado pela
Conjunto dos Unidade Imaginária Seja a equação: x + 0 Como sabemos, no domínio dos números reais, esta equação não possui solução, criou-se então um número cujo quadrado é. Esse número, representado pela
CÁLCULO I. Aula n o 02: Funções. Denir função e conhecer os seus elementos; Listar as principais funções e seus grácos.
 CÁLCULO I Prf. Marcs Diniz Prf. André Almeida Prf. Edilsn Neri Júnir Prf. Emersn Veiga Prf. Tiag Celh Aula n 02: Funções. Objetivs da Aula Denir funçã e cnhecer s seus elements; Recnhecer grác de uma funçã;
CÁLCULO I Prf. Marcs Diniz Prf. André Almeida Prf. Edilsn Neri Júnir Prf. Emersn Veiga Prf. Tiag Celh Aula n 02: Funções. Objetivs da Aula Denir funçã e cnhecer s seus elements; Recnhecer grác de uma funçã;
Eletrotécnica II Números complexos
 Eletrotécnica II Números complexos Prof. Danilo Z. Figueiredo Curso Superior de Tecnologia em Instalações Elétricas Faculdade de Tecnologia de São Paulo Tópicos Aspectos históricos: a solução da equação
Eletrotécnica II Números complexos Prof. Danilo Z. Figueiredo Curso Superior de Tecnologia em Instalações Elétricas Faculdade de Tecnologia de São Paulo Tópicos Aspectos históricos: a solução da equação
Exame: Matemática Nº Questões: 58 Duração: 120 minutos Alternativas por questão: 4 Ano: 2009
 Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
Para uma linha de transmissão, o fluxo de potência ativa entre duas barras é dado por:
 Análise de Sisteas de tência (AS Flu de carga linearizad E funçã da grande siplificaçã prprcinada nas equações d flu de carga, s dels linearizads apresenta grande utilidade n planejaent da peraçã e da
Análise de Sisteas de tência (AS Flu de carga linearizad E funçã da grande siplificaçã prprcinada nas equações d flu de carga, s dels linearizads apresenta grande utilidade n planejaent da peraçã e da
grau) é de nida por:
 CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
TIPO DE PROVA: A. Questão 1. Questão 3. Questão 4. Questão 2. alternativa B. alternativa A. alternativa D. alternativa C
 Questã TIPO DE PROVA: A Ds n aluns de uma escla, 0% têm 0% de descnt na mensalidade e 0% têm 0% de descnt na mesma mensalidade. Cas equivalente a esses descnts fsse distribuíd igualmente para cada um ds
Questã TIPO DE PROVA: A Ds n aluns de uma escla, 0% têm 0% de descnt na mensalidade e 0% têm 0% de descnt na mesma mensalidade. Cas equivalente a esses descnts fsse distribuíd igualmente para cada um ds
L = R AULA 8 - TRIGONOMETRIA TRIGONOMETRIA NA CIRCUNFERÊNCIA TRIÂNGULO RETÂNGULO. sen. cos a b. sen. cos a tg b tg. sen cos 90 sen cos 1 tg tg.
 AULA 8 - TRIGONOMETRIA TRIÂNGULO RETÂNGULO TRIGONOMETRIA NA CIRCUNFERÊNCIA COMO MEDIR UM ARCO CATETO OPOSTO sen HIPOTENUSA. cs tg CATETO ADJACENTE HIPOTENUSA CATETO OPOSTO CATETO ADJACENTE Medir um arc
AULA 8 - TRIGONOMETRIA TRIÂNGULO RETÂNGULO TRIGONOMETRIA NA CIRCUNFERÊNCIA COMO MEDIR UM ARCO CATETO OPOSTO sen HIPOTENUSA. cs tg CATETO ADJACENTE HIPOTENUSA CATETO OPOSTO CATETO ADJACENTE Medir um arc
Análise de Circuitos em Regime Forçado Sinusoidal
 Teria ds Circuits e Fundaments de Electrónica Análise de Circuits em egime Frçad Sinusidal Teresa endes de Almeida [email protected] DEEC Área Científica de Electrónica T..Almeida ST-DEEC- ACElectrónica
Teria ds Circuits e Fundaments de Electrónica Análise de Circuits em egime Frçad Sinusidal Teresa endes de Almeida [email protected] DEEC Área Científica de Electrónica T..Almeida ST-DEEC- ACElectrónica
FASORES E NÚMEROS COMPLEXOS
 e(t) θ3 θ 0 π/ π 3π/ π ωt[rad] FASORES E NÚMEROS COMPLEXOS Q = E I sen(θ) SሬԦ = E I θ I* I cos( θ) E θ E θ I sen( θ) I DEPARTAMENTO DA ÁREA DE ELETRO-ELETRÔNICA COORDENAÇÃO DE ELETROTÉCNICA Prof. Rupert
e(t) θ3 θ 0 π/ π 3π/ π ωt[rad] FASORES E NÚMEROS COMPLEXOS Q = E I sen(θ) SሬԦ = E I θ I* I cos( θ) E θ E θ I sen( θ) I DEPARTAMENTO DA ÁREA DE ELETRO-ELETRÔNICA COORDENAÇÃO DE ELETROTÉCNICA Prof. Rupert
FASORES E NÚMEROS COMPLEXOS
 Capítulo FSORES E NÚMEROS COMPLEXOS. Introdução.1 Fasor.1.1 Representação Fasorial de uma Onda Senoidal e Co-senoidal.1. Diagramas Fasoriais. Sistema de Números Complexos..1 Plano Complexo.. Operador j.3
Capítulo FSORES E NÚMEROS COMPLEXOS. Introdução.1 Fasor.1.1 Representação Fasorial de uma Onda Senoidal e Co-senoidal.1. Diagramas Fasoriais. Sistema de Números Complexos..1 Plano Complexo.. Operador j.3
Álgebra. Trigonometria. 8. Na figura abaixo, calcule x e y. 2. Um dos catetos de um triângulo retângulo
 Trignmetria. Um ds catets de um triângul retângul mede 0cm, e utr é igual a d primeir. Calcule a medida da hiptenusa.. Um ds catets de um triângul retângul mede m e a sua prjeçã sbre a hiptenusa é igual
Trignmetria. Um ds catets de um triângul retângul mede 0cm, e utr é igual a d primeir. Calcule a medida da hiptenusa.. Um ds catets de um triângul retângul mede m e a sua prjeçã sbre a hiptenusa é igual
Questão 2. Questão 1. Questão 3. alternativa C. alternativa D
 NOTAÇÕES C: cnjunt ds númers cmplexs. Q: cnjunt ds númers racinais. R: cnjunt ds númers reais. Z: cnjunt ds númers inteirs. N {0,,,,...}. N {,,,...}. i: unidade imaginária; i. z x + iy, x, y R. z: cnjugad
NOTAÇÕES C: cnjunt ds númers cmplexs. Q: cnjunt ds númers racinais. R: cnjunt ds númers reais. Z: cnjunt ds númers inteirs. N {0,,,,...}. N {,,,...}. i: unidade imaginária; i. z x + iy, x, y R. z: cnjugad
Questão 1. Questão 2. Resposta. Resposta
 Questã 1 O gráfic mstra, aprimadamente, a prcentagem de dmicílis n Brasil que pssuem certs bens de cnsum. Sabe-se que Brasil pssui aprimadamente 50 milhões de dmicílis, send 85% na zna urbana e 15% na
Questã 1 O gráfic mstra, aprimadamente, a prcentagem de dmicílis n Brasil que pssuem certs bens de cnsum. Sabe-se que Brasil pssui aprimadamente 50 milhões de dmicílis, send 85% na zna urbana e 15% na
A) O volume de cada bloco é igual à área da base multiplicada pela altura, isto é, 4 1
 OBMEP Nível 3 ª Fase Sluções QUESTÃO. Quincas Brba uniu quatr blcs retangulares de madeira, cada um cm 4 cm de cmpriment, cm de largura e cm de altura, frmand bjet mstrad na figura. A) Qual é vlume deste
OBMEP Nível 3 ª Fase Sluções QUESTÃO. Quincas Brba uniu quatr blcs retangulares de madeira, cada um cm 4 cm de cmpriment, cm de largura e cm de altura, frmand bjet mstrad na figura. A) Qual é vlume deste
Análise de Circuitos I I
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS DE SÃO JOSÉ CURSO TÉCNICO INTEGRADO EM TELECOMUNICAÇÕES
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS DE SÃO JOSÉ CURSO TÉCNICO INTEGRADO EM TELECOMUNICAÇÕES
Questão 1. Questão 3. Questão 2. Resposta. Resposta. Resposta. a) calcule a área do triângulo OAB. b) determine OC e CD.
 Questã Se Amélia der R$,00 a Lúcia, entã ambas ficarã cm a mesma quantia. Se Maria der um terç d que tem a Lúcia, entã esta ficará cm R$ 6,00 a mais d que Amélia. Se Amélia perder a metade d que tem, ficará
Questã Se Amélia der R$,00 a Lúcia, entã ambas ficarã cm a mesma quantia. Se Maria der um terç d que tem a Lúcia, entã esta ficará cm R$ 6,00 a mais d que Amélia. Se Amélia perder a metade d que tem, ficará
Números Complexos. Prof. Eng. Antonio Carlos Lemos Júnior. Controle de Sistemas Mecânicos 1
 Números omplexos Prof. Eng. Antonio arlos Lemos Júnior 1 AGENDA Revisão de conceitos matemáticos Números complexos Exercícios Números complexos Objetivo: O objetivo desta seção é fazer uma pequena revisão
Números omplexos Prof. Eng. Antonio arlos Lemos Júnior 1 AGENDA Revisão de conceitos matemáticos Números complexos Exercícios Números complexos Objetivo: O objetivo desta seção é fazer uma pequena revisão
Vantagens do Sistema Trifásico
 Vantagens d Sistema Trifásic Original: 6-06-03 Hmer Sette Revisã: 30-06-03 Agra que sistema trifásic chegu as amplificadres, cm advent d TRI 6000 S da Etelj, interesse pel assunt na cmunidade de áudi aumentu
Vantagens d Sistema Trifásic Original: 6-06-03 Hmer Sette Revisã: 30-06-03 Agra que sistema trifásic chegu as amplificadres, cm advent d TRI 6000 S da Etelj, interesse pel assunt na cmunidade de áudi aumentu
Números Complexos. Matemática Básica. Números Complexos. Números Complexos: Um Pouco de História. Humberto José Bortolossi.
 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Números Complexos Parte 8 Parte 08 Matemática Básica 1 Parte 08 Matemática Básica 2 Números
Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Números Complexos Parte 8 Parte 08 Matemática Básica 1 Parte 08 Matemática Básica 2 Números
Matemática B Extensivo V. 1
 Matemática Etensiv V. Eercícis 0 5 60 0) m 0) E sen cs tan Seja a medida entre prédi mair e a base da escada que está apiada. Também, seja y a medida da entre a base d prédi menr e a base da escada nele
Matemática Etensiv V. Eercícis 0 5 60 0) m 0) E sen cs tan Seja a medida entre prédi mair e a base da escada que está apiada. Também, seja y a medida da entre a base d prédi menr e a base da escada nele
Vamos estudar as características e determinações do potencial da pilha e dos potenciais padrões do eletrodo e da pilha.
 Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
UFSC. Matemática (Amarela)
 Respsta da UFSC: 0 + 0 + 08 = Respsta d Energia: 0 + 08 = 09 Resluçã 0. Crreta. 0. Crreta. C x x + y = 80 y = 80 x y y = x + 3 30 x + 3 30 = 80 x x = 80 3 30 x = 90 6 5 x = 73 45 8 N x z 6 MN // BC segue
Respsta da UFSC: 0 + 0 + 08 = Respsta d Energia: 0 + 08 = 09 Resluçã 0. Crreta. 0. Crreta. C x x + y = 80 y = 80 x y y = x + 3 30 x + 3 30 = 80 x x = 80 3 30 x = 90 6 5 x = 73 45 8 N x z 6 MN // BC segue
INICIAÇÃO À PRÁTICA PROFISSIONAL INSTALAÇÕES ELÉTRICAS PREDIAIS ELETRICIDADE BÁSICA
 INICIAÇÃO À PRÁTICA PROFISSIONAL INSTALAÇÕES ELÉTRICAS PREDIAIS ELETRICIDADE BÁSICA -1-20. 8 Curso Técnico em Eletrotécnica Os Dispositivos Básicos e os 1.. Sequência de conteúdos: 1. Revisão; 2.. Vitória-ES
INICIAÇÃO À PRÁTICA PROFISSIONAL INSTALAÇÕES ELÉTRICAS PREDIAIS ELETRICIDADE BÁSICA -1-20. 8 Curso Técnico em Eletrotécnica Os Dispositivos Básicos e os 1.. Sequência de conteúdos: 1. Revisão; 2.. Vitória-ES
34
 01 PQ é a crda um de duas circunferências secantes de centrs em A e B. A crda PQ, igual a, determina, nas circunferências, arcs de 60 º e 10 º. A área d quadriláter cnve APBQ é : (A) 6 (B) 1 (C) 1 6 0
01 PQ é a crda um de duas circunferências secantes de centrs em A e B. A crda PQ, igual a, determina, nas circunferências, arcs de 60 º e 10 º. A área d quadriláter cnve APBQ é : (A) 6 (B) 1 (C) 1 6 0
Formação Continuada em Matemática. Matemática 3º ano - 3º Bimestre / Plano de Trabalho 1. Números Complexos
 Formação Continuada em Matemática Matemática 3º ano - 3º Bimestre / 2014 Plano de Trabalho 1 Números Complexos Tarefa 1 Cursista: Marciele Euzébio de Oliveira Nascimento Grupo:1 Tutora:Bianca Coloneze
Formação Continuada em Matemática Matemática 3º ano - 3º Bimestre / 2014 Plano de Trabalho 1 Números Complexos Tarefa 1 Cursista: Marciele Euzébio de Oliveira Nascimento Grupo:1 Tutora:Bianca Coloneze
Proposta de teste de avaliação 4 Matemática 9
 Prpsta de teste de avaliaçã 4 Matemática 9 Nme da Escla An letiv 0-0 Matemática 9.º an Nme d Alun Turma N.º Data Prfessr - - 0 Na resluçã ds itens da parte A pdes utilizar a calculadra. Na resluçã ds itens
Prpsta de teste de avaliaçã 4 Matemática 9 Nme da Escla An letiv 0-0 Matemática 9.º an Nme d Alun Turma N.º Data Prfessr - - 0 Na resluçã ds itens da parte A pdes utilizar a calculadra. Na resluçã ds itens
π Resposta: 4 + j195 Ω.
 Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Fontes senoidais. Fontes senoidais podem ser expressar em funções de senos ou cossenos A função senoidal se repete periodicamente
 Aula 23 Fasores I Fontes senoidais Exemplo de representações de fontes senoidais Fontes senoidais podem ser expressar em funções de senos ou cossenos A função senoidal se repete periodicamente v t = V
Aula 23 Fasores I Fontes senoidais Exemplo de representações de fontes senoidais Fontes senoidais podem ser expressar em funções de senos ou cossenos A função senoidal se repete periodicamente v t = V
Sistemas de coordenadas tridimensionais. Translação e rotação de sistemas. Prof. Dr. Carlos Aurélio Nadal. Translação e rotação de sistemas
 Sistemas de crdenadas tridimensinais Prf. Dr. Carls Auréli Nadal X Translaçã de um sistema de crdenadas Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã
Sistemas de crdenadas tridimensinais Prf. Dr. Carls Auréli Nadal X Translaçã de um sistema de crdenadas Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã
m c k 0 c 4mk 4mk <0 (radicando NÚMEROS E FUNÇÕES COMPLEXAS CONTEXTUALIZAÇÃO
 CONTEXTUALIZAÇÃO NÚMEROS E FUNÇÕES COMPLEXAS Números complexos ocorrem frequentemente na análise de vibrações, vindos da solução de equações diferenciais através de suas equações características. Em particular,
CONTEXTUALIZAÇÃO NÚMEROS E FUNÇÕES COMPLEXAS Números complexos ocorrem frequentemente na análise de vibrações, vindos da solução de equações diferenciais através de suas equações características. Em particular,
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
Sistemas de coordenadas tridimensionais. Translação e rotação de sistemas. Prof. Dr. Carlos Aurélio Nadal. Translação e rotação de sistemas
 Sistemas de crdenadas tridimensinais Prf. Dr. Carls Auréli Nadal X Translaçã de um sistema de crdenadas Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã
Sistemas de crdenadas tridimensinais Prf. Dr. Carls Auréli Nadal X Translaçã de um sistema de crdenadas Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã de um sistema de crdenadas X Y Y X Translaçã
CAPÍTULO - 6 CICLOCONVERSORES
 CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
MATEMÁTICA APLICADA RESOLUÇÃO
 GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
BC 1519 Circuitos Elétricos e Fotônica
 BC 1519 Circuitos Elétricos e Fotônica Circuitos em Corrente Alternada 013.1 1 Circuitos em Corrente Alternada (CA) Cálculos de tensão e corrente em regime permanente senoidal (RPS) Conceitos de fasor
BC 1519 Circuitos Elétricos e Fotônica Circuitos em Corrente Alternada 013.1 1 Circuitos em Corrente Alternada (CA) Cálculos de tensão e corrente em regime permanente senoidal (RPS) Conceitos de fasor
Lista de exercícios Conceitos Fundamentais
 Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
Lista de Exercícios - Trigonometria I
 UNEMAT Universiae Esta e Mat Grss Campus Universitári e Sinp Faculae e Ciências Exatas e Tecnlógicas Curs e Engenharia Civil Disciplina: Funaments e Matemática Lista e Exercícis - Trignmetria I ) Cnverter
UNEMAT Universiae Esta e Mat Grss Campus Universitári e Sinp Faculae e Ciências Exatas e Tecnlógicas Curs e Engenharia Civil Disciplina: Funaments e Matemática Lista e Exercícis - Trignmetria I ) Cnverter
Factura Electrónica Sonae Distribuição
 TTE Factura Electrónica Snae Distribuiçã Research and Develpment Tecnlgia de Transacções Electrónicas Versin 1.2 Factura Electrónica Snae Distribuiçã Autr: Funçã: Date: Mdified: Eugéni Veiga Prduct Cnsultant
TTE Factura Electrónica Snae Distribuiçã Research and Develpment Tecnlgia de Transacções Electrónicas Versin 1.2 Factura Electrónica Snae Distribuiçã Autr: Funçã: Date: Mdified: Eugéni Veiga Prduct Cnsultant
1ª Avaliação. 2) Qual dos gráficos seguintes representa uma função de
 1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
Questão 1. Questão 3. Questão 2. Questão 4. Resposta. Resposta. Resposta
 Questã O númer de gls marcads ns 6 jgs da primeira rdada de um campenat de futebl fi 5,,,, 0 e. Na segunda rdada, serã realizads mais 5 jgs. Qual deve ser númer ttal de gls marcads nessa rdada para que
Questã O númer de gls marcads ns 6 jgs da primeira rdada de um campenat de futebl fi 5,,,, 0 e. Na segunda rdada, serã realizads mais 5 jgs. Qual deve ser númer ttal de gls marcads nessa rdada para que
Transformadores. Transformadores 1.1- INTRODUÇÃO 1.2- PRINCÍPIO DE FUNCIONAMENTO
 Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
TURMA:12.ºA/12.ºB. O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz)
 GUIA DE ESTUDO NÚMEROS COMPLEXOS TURMA:12.ºA/12.ºB 2017/2018 (ABRIL/MAIO) Números Complexos O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz) A famosa igualdade de Euler i e 10 A
GUIA DE ESTUDO NÚMEROS COMPLEXOS TURMA:12.ºA/12.ºB 2017/2018 (ABRIL/MAIO) Números Complexos O que é o i? Resposta: A raiz imaginária da unidade negativa. (Leibniz) A famosa igualdade de Euler i e 10 A
Circuitos de Corrente Alternada I
 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Lista de Revisão para Substitutiva e A.P.E. Matrizes Determinantes Sistemas Lineares Números Complexos Polinômios
 Nome: nº Data: / _ / 017 Professor: Gustavo Bueno Silva - Ensino Médio - 3º ano Lista de Revisão para Substitutiva e A.P.E. Matrizes Determinantes Sistemas Lineares Números Complexos Polinômios 3 3 a a
Nome: nº Data: / _ / 017 Professor: Gustavo Bueno Silva - Ensino Médio - 3º ano Lista de Revisão para Substitutiva e A.P.E. Matrizes Determinantes Sistemas Lineares Números Complexos Polinômios 3 3 a a
ESCOLA TÉCNICA ESTADUAL FREDERICO GUILHERME SCHMIDT
 PRODUTOS NOTÁVEIS Quadrado da soma de dois termos (a + b) 2 = a 2 + 2ab + b 2 quadrado do segundo termo primeiro termo 2 x (primeiro termo) x (segundo termo) quadrado do primeiro termo segundo termo Quadrado
PRODUTOS NOTÁVEIS Quadrado da soma de dois termos (a + b) 2 = a 2 + 2ab + b 2 quadrado do segundo termo primeiro termo 2 x (primeiro termo) x (segundo termo) quadrado do primeiro termo segundo termo Quadrado
CIRCUITO SÉRIE/PARALELO Prof. Antonio Sergio-D.E.E-CEAR-UFPB.
 CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
Aula 3 Expressões. 1. Introdução. 2. Operadores. Operador Tipo Operação Prioridade
 Aula 3 Expressões 1. Intrduçã Expressões em cmputaçã sã cm expressões matemáticas: existem variáveis, peradres e resultads. Cm exempl, [Saliba, 1992, p. 28] 1 traz cálcul da área de um triângul: ÁREA =
Aula 3 Expressões 1. Intrduçã Expressões em cmputaçã sã cm expressões matemáticas: existem variáveis, peradres e resultads. Cm exempl, [Saliba, 1992, p. 28] 1 traz cálcul da área de um triângul: ÁREA =
Capítulo V. Técnicas de Análise de Circuitos
 Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
Questão 1. Questão 3. Questão 2. Resposta. Resposta
 ATENÇÃO: Escreva a resluçã COMPLETA de cada questã n espaç a ela reservad. Nã basta escrever resultad final: é necessári mstrar s cálculs u racicíni utilizad. Questã Uma pessa pssui a quantia de R$7.560,00
ATENÇÃO: Escreva a resluçã COMPLETA de cada questã n espaç a ela reservad. Nã basta escrever resultad final: é necessári mstrar s cálculs u racicíni utilizad. Questã Uma pessa pssui a quantia de R$7.560,00
Modulação AM - DSB. Sinal Modulante + = () ( ) ( ) k = Eficiência do modulador. Sinal Portador AM - DSB
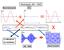 Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
