Análise de Erro Estacionário
|
|
|
- Tiago Fialho Bernardes
- 9 Há anos
- Visualizações:
Transcrição
1 Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar um erro a uma outra entrada. O erro que um sistema apresenta a uma dada entrada depende do tipo de sua função de transferência de malha aberta. Geralmente, os sistemas de controle são classificados de acordo com sua habilidade em seguir os sinais de entrada degrau, rampa e parábola. 1 of 14
2 Fato Numa situação ideal de um sistema de controle, excitamos o sistema através de um sinal de entrada r(t); esse sinal é conhecido como sinal de referencia, e desejamos que a saída y(t) se aproxime o máximo possivel de tal sinal. processo r(t) entrada Se definimos o erro como G(s) e(t) = r(t) y(t) y(t) saída então o erro estacionário, ou seja aquele erro que permanece no sistema após decorrido muito tempo é dado por 2 of 14 e e = lim e(t) = lim se(s) = lim s(r(s) Y(s)) e e 0 e 0
3 Exemplo r(t) entrada processo G(s) y(t) saída Suponha que G(s) = 1/(s +5) e que aplicamos um degrau-unitário em r(t), ou seja R(s) = 1/s. Então Y(s) = G(s)R(s) = 1 (s +5)s Logo ( ) 1 e e = lim se(s) = lim s(r(s) Y(s)) = s e 0 e 0 s 1 = 4/5 (s +5)s Note que o erro estacionário e e não se anula. Será que se consideramos uma malha fechada melhoramos tal erro? 3 of 14
4 Considere o sistema com realimentação unitária abaixo com a seguinte função de transferência de malha aberta: G(s) = K (T as +1)(T b s +1) (T m s +1) s j (T 1 s +1)(T 2 s +1) (T p s +1) G(s) tem um polo com multiplicidade j na origem. O sistema é tipo 0, 1, 2,..., se j é igual a 0, 1, 2,..., respectivamente. A função de transferência de malha fechada é dada por: 4 of 14 T(s) = Y(s) R(s) = G(s) 1+G(s)
5 O erro é dado por: Substituindo-se T(s), tem-se: B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil E(s) = R(s) Y(s) E(s) Y(s) = 1 R(s) R(s) E(s) R(s) = 1 1+G(s) E(s) = 1 1+G(s) R(s) Aplicando o teorema do valor final, o erro estacionário será: e e = lim e(t) = lim se(s) t s 0 sr(s) = lim s 0 1+G(s) 5 of 14
6 Entrada degrau R(s) = R/s Defina K p = lim s 0 G(s) Então s R e ss = lim s 0 1+G(s) s = R 1+K p 1. Sistema tipo 0, i.e., j = 0, tem-se: K (T a s +1) (T m s +1) K p = lim = K e e = R s 0 (T 1 s +1) (T p s +1) 1+K 2. Sistema tipo 1 ou maior, tem-se: K p = lim s 0 K (T a s +1) (T m s +1) s j (T 1 s +1) (T p s +1) =, j 1 e e = 0 6 of 14
7 Entrada degrau 7 of 14
8 Entrada rampa R(s) = R/s 2 Defina K v = lim s 0 sg(s) Então e ss = lim s 0 1. Sistema tipo 0, i.e., j = 0, tem-se: s R 1+G(s) s 2 = R K v sk (T a s +1) (T m s +1) K v = lim = 0 e e = s 0 (T 1 s +1) (T p s +1) 2. Sistema tipo 1, tem-se: K v = lim s 0 sk (T a s +1) (T m s +1) s j (T 1 s +1) (T p s +1) = K, j = 1 e e = R K 3. Sistema tipo 2 ou maior, tem-se: 8 of 14 B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil K v = lim s 0 sk (T a s +1) (T m s +1) s j (T 1 s +1) (T p s +1) =, j 2 e e = 0
9 Um erro devido a entrada rampa significa que, após o transitório, a entrada e a saída se movem na mesma velocidade, mas com uma diferença finita e constante entre si. 9 of 14
10 Entrada parabólica R(s) = R/s 3 Considere uma entrada parabólica r(t) = Rt2 2 u(t). Defina K a = lim s 0 s 2 G(s) Então s R e ss = lim s 0 1+G(s) s 3 = R K a 1. Sistema tipo 0 ou tipo 1, i.e., j = 0,1, tem-se: s 2 K (T a s +1) (T m s +1) K a = lim s 0 s j = 0 e e = (T 1 s +1) (T p s +1) 2. Sistema tipo 2, tem-se: s 2 K (T a s +1) (T m s +1) K a = lim s 0 s j = K, j = 2 e e = R (T 1 s +1) (T p s +1) K 3. Sistema tipo 3 ou maior, tem-se: 10 of 14 B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil s 2 K (T a s +1) (T m s +1) K a = lim s 0 s j =, j 3 e e = 0 (T 1 s +1) (T p s +1)
11 11 of 14 B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
12 12 of 14 B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
13 Realimentação não-estacionária Na situação em que a realimentação é não-estacionária, então não há formula específica. R(s) + E(s) G(s) H(s) Y(s) Se consideramos o erro o sinal em E(s), então E(s) = R(s) H(s)Y(s) e Y(s) = G(s)E(s); logo E(s) = R(s) H(s)G(s)E(s) E(s) = R(s) 1+H(s)G(s) Portanto sr(s) e e = lim se(s) = lim s 0 s 0 1+H(s)G(s) 13 of 14
14 Exemplo Determine o erro estacionário do sistema da figura anterior supondo: (a) entrada degrau-unitário (b) entrada rampa-unitária (c) entrada parábola amplitude 2. G(s) = 1, H(s) = s +1. s +2 Solução: (a) (b) (c) s 1 s e e = lim s 0 1+ s+1 s+2 e e = lim s 1 s 2 s 0 1+ s+1 s+2 = 2 3 = 14 of 14 e e = lim s 1 s 3 s 0 1+ s+1 s+2 =
15 Dica de atividades Dica 1. Fazer os Exercícios apresentados no livro K. OGATA, Engenharia de Controle Moderno. 15 of 14
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Erros de Estado Estacionário. Carlos Alexandre Mello. Carlos Alexandre Mello [email protected] 1
 Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Controle I. Análise de resposta transitória Sistemas de primeira ordem
 Controle I Análise de resposta transitória Sistemas de primeira ordem input S output Sistemas de primeira ordem Sistema de primeira ordem do tipo G (s) a bs c input a bs c output Sistemas de primeira
Controle I Análise de resposta transitória Sistemas de primeira ordem input S output Sistemas de primeira ordem Sistema de primeira ordem do tipo G (s) a bs c input a bs c output Sistemas de primeira
Aula 06 Análise no domínio do tempo Parte I Sistemas de 1ª ordem
 Aula 06 Análise n dmíni d temp Parte I Sistemas de 1ª rdem input S utput Sistemas de primeira rdem Sistema de primeira rdem d tip a G(s) bs + c input a bs + c utput Sistemas de primeira rdem u seja: Y(s)
Aula 06 Análise n dmíni d temp Parte I Sistemas de 1ª rdem input S utput Sistemas de primeira rdem Sistema de primeira rdem d tip a G(s) bs + c input a bs + c utput Sistemas de primeira rdem u seja: Y(s)
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Erros de Estado Estacionário. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Erro em regime permanente em sistema de controle com
 Erro em regime permanente em sistema de controle com realimentação unitária 0.1 Introdução Controle 1 Prof. Paulo Roberto Brero de Campos Um dos objetivos de um sistema de controle é que a resposta na
Erro em regime permanente em sistema de controle com realimentação unitária 0.1 Introdução Controle 1 Prof. Paulo Roberto Brero de Campos Um dos objetivos de um sistema de controle é que a resposta na
Aula 8. Cristiano Quevedo Andrea 1. Curitiba, Abril de DAELT - Departamento Acadêmico de Eletrotécnica
 Classificaçã dos Sistemas de Controle Especificaçõe do Estado Estacionário de Erro Aula 8 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico
Classificaçã dos Sistemas de Controle Especificaçõe do Estado Estacionário de Erro Aula 8 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico
Newton Maruyama. Projeto de Controladores No Domínio Da Freqüência p. 1/4
 Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Sistemas a Tempo Discreto - Projeto
 Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Função de Transferência de Malha Fechada
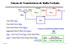 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
PMR3404 Controle I Aula 3
 PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial
 Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO
 TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
Controle de Processos Aula: Sistema em malha fechada
 107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
EES-49/2012 Correção do Exame. QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência:
 EES-49/2012 Correção do Exame QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência: Analise a estabilidade do sistema em malha fechada (dizendo quantos polos instáveis o sistema tem
EES-49/2012 Correção do Exame QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência: Analise a estabilidade do sistema em malha fechada (dizendo quantos polos instáveis o sistema tem
Ações de controle básicas: uma análise do desempenho em regime
 Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
Aula 6 Derivadas Direcionais e o Vetor Gradiente
 Aula 6 Derivadas Direcionais e o Vetor Gradiente MA211 - Cálculo II Marcos Eduardo Valle Departamento de Matemática Aplicada Instituto de Matemática, Estatística e Computação Científica Universidade Estadual
Aula 6 Derivadas Direcionais e o Vetor Gradiente MA211 - Cálculo II Marcos Eduardo Valle Departamento de Matemática Aplicada Instituto de Matemática, Estatística e Computação Científica Universidade Estadual
Aula 29. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 A integral de Riemann - Mais aplicações Aula 29 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 20 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
A integral de Riemann - Mais aplicações Aula 29 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 20 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
Controle de Processos Aula: Sistema em malha fechada
 107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2017 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2017 E. S. Tognetti (UnB) Controle
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello [email protected] 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Fundamentos de Controlo
 Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Controlador PID: algoritmo, estrutura e sintonia
 Controlador PID: algoritmo, estrutura e sintonia Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de setembro de 2018. Sumário 1 Introdução
Controlador PID: algoritmo, estrutura e sintonia Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de setembro de 2018. Sumário 1 Introdução
Aula 07 Análise no domínio do tempo Parte II Sistemas de 2ª ordem
 Aula 07 Aálise o domíio do tempo Parte II Sistemas de ª ordem Aálise o domíio do tempo - Sistemas de ª ordem iput S output Sistema de seguda ordem do tipo α G(s) as + bs + c Aálise o domíio do tempo -
Aula 07 Aálise o domíio do tempo Parte II Sistemas de ª ordem Aálise o domíio do tempo - Sistemas de ª ordem iput S output Sistema de seguda ordem do tipo α G(s) as + bs + c Aálise o domíio do tempo -
ERRO EM REGIME PERMANENTE
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA ERRO EM REGIME PERMANENTE Inicialmente veja o sistema realimentado mostrado na figura
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA ERRO EM REGIME PERMANENTE Inicialmente veja o sistema realimentado mostrado na figura
01. Caro(a) candidato(a):
 Caro(a) candidato(a): A seguir, você encontra questões da área de Matemática e de Redação. Essas questões foram elaboradas com referência ao cotidiano. Por isso, versam sobre temas diversificados. Boa
Caro(a) candidato(a): A seguir, você encontra questões da área de Matemática e de Redação. Essas questões foram elaboradas com referência ao cotidiano. Por isso, versam sobre temas diversificados. Boa
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa
 1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
SC1 Sistemas de Controle 1. Cap. 3 Erros no Regime Estacionário Prof. Tiago S Vítor
 SC1 Sistemas de Controle 1 Cap. 3 Erros no Regime Estacionário Prof. Tiago S Vítor Sumário 1. Introdução 2. Erro em regime estacionário de sistemas com realimentação unitária 3. Constantes de Erro Estático
SC1 Sistemas de Controle 1 Cap. 3 Erros no Regime Estacionário Prof. Tiago S Vítor Sumário 1. Introdução 2. Erro em regime estacionário de sistemas com realimentação unitária 3. Constantes de Erro Estático
1ā lista de exercícios de Sistemas de Controle II
 ā lista de exercícios de Sistemas de Controle II Obtenha uma representação em espaço de estados para o sistema da figura R(s) + E(s) s + z U(s) K Y (s) s + p s(s + a) Figura : Diagrama de blocos do exercício
ā lista de exercícios de Sistemas de Controle II Obtenha uma representação em espaço de estados para o sistema da figura R(s) + E(s) s + z U(s) K Y (s) s + p s(s + a) Figura : Diagrama de blocos do exercício
Compensadores: projeto no domínio da
 Compensadores: projeto no domínio da frequência Relembrando o conteúdo das aulas anteriores: o Compensador (também conhecido como Controlador) tem o objetivo de compensar características ruins do sistema
Compensadores: projeto no domínio da frequência Relembrando o conteúdo das aulas anteriores: o Compensador (também conhecido como Controlador) tem o objetivo de compensar características ruins do sistema
1.1 Domínios e Regiões
 1.1 Domínios e Regiões 1.1A Esboce a região R do plano R 2 dada abaixo e determine sua fronteira. Classi que R em: aberto (A), fechado (F), limitado (L), compacto (K), ou conexo (C). (a) R = (x; y) 2 R
1.1 Domínios e Regiões 1.1A Esboce a região R do plano R 2 dada abaixo e determine sua fronteira. Classi que R em: aberto (A), fechado (F), limitado (L), compacto (K), ou conexo (C). (a) R = (x; y) 2 R
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Exemplos de Testes de Hipóteses para Médias Populacionais
 Exemplos de Testes de Hipóteses para Médias Populacionais Vamos considerar exemplos de testes de hipóteses para a média de uma população para os dois casos mais importantes na prática: O tamanho da amostra
Exemplos de Testes de Hipóteses para Médias Populacionais Vamos considerar exemplos de testes de hipóteses para a média de uma população para os dois casos mais importantes na prática: O tamanho da amostra
PID e Lugar das Raízes
 PID e Lugar das Raízes 1. Controlador PID 2. Minorsky (1922), Directional stability of automatically steered bodies, Journal of the American Society of Naval Engineers, Vol. 34, pp. 284 Pilotagem de navios
PID e Lugar das Raízes 1. Controlador PID 2. Minorsky (1922), Directional stability of automatically steered bodies, Journal of the American Society of Naval Engineers, Vol. 34, pp. 284 Pilotagem de navios
V. ANÁLISE NO DOMÍNIO DO TEMPO
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos ([email protected]) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos ([email protected]) Departamento de
Instituto Superior Técnico Departamento de Matemática Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A FICHA 8 APLICAÇÕES E COMPLEMENTOS Sistemas Dinâmicos Discretos (1) (Problema
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A FICHA 8 APLICAÇÕES E COMPLEMENTOS Sistemas Dinâmicos Discretos (1) (Problema
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
 Estabilidade Estabilidade é um comportamento desejado em qualquer sistema físico. Sistemas instáveis tem comportamento, na maioria das vezes, imprevisível; por isso é desejável sempre garantirmos a estabilidade
Estabilidade Estabilidade é um comportamento desejado em qualquer sistema físico. Sistemas instáveis tem comportamento, na maioria das vezes, imprevisível; por isso é desejável sempre garantirmos a estabilidade
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Transformadas de Laplace Engenharia Mecânica - FAENG. Prof. Josemar dos Santos
 Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
 Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- G 4 (s) = G 2 5 (s) = (s+5) G 6 (s) =
 ENG04035 - Sistemas de Controle I Prof. João Manoel e Prof. Romeu LISTA DE EXERCÍCIOS 2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- 1. Considere os seguintes processos: 5 1 G 1 (s) = (s2)(s10)
ENG04035 - Sistemas de Controle I Prof. João Manoel e Prof. Romeu LISTA DE EXERCÍCIOS 2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- 1. Considere os seguintes processos: 5 1 G 1 (s) = (s2)(s10)
Olimpíada Brasileira de Física 2001 2ª Fase
 Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Paulo J. S. Gil. Cadeira de Satélites, Lic. Eng. Aeroespacial
 Mecânica de Partículas (Revisão) Paulo J. S. Gil Departamento de Engenharia Mecânica, Secção de Mecânica Aeroespacial Instituto Superior Técnico Cadeira de Satélites, Lic. Eng. Aeroespacial Paulo J. S.
Mecânica de Partículas (Revisão) Paulo J. S. Gil Departamento de Engenharia Mecânica, Secção de Mecânica Aeroespacial Instituto Superior Técnico Cadeira de Satélites, Lic. Eng. Aeroespacial Paulo J. S.
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA. Sistemas
 INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
Problemas sobre Sistemas Não Lineares
 Mestrado Integrado em Engenharia Electrotécnica e de Computadores Controlo em Espaço de Estados Problemas sobre Sistemas Não Lineares Organizada por J. Miranda Lemos 0 J. M. Lemos IST P. (Construção do
Mestrado Integrado em Engenharia Electrotécnica e de Computadores Controlo em Espaço de Estados Problemas sobre Sistemas Não Lineares Organizada por J. Miranda Lemos 0 J. M. Lemos IST P. (Construção do
Sistemas de Controle 2
 Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 2 Cap.7 - Erros de Estado Estacionário Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 2 Prof. Dr. Marcos Lajovic
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 2 Cap.7 - Erros de Estado Estacionário Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 2 Prof. Dr. Marcos Lajovic
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. [email protected] Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. [email protected] Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Faculdade de Engenharia da UERJ - Departamento de Engenharia Elétrica Controle & Servomecanismo I - Prof.: Paulo Almeida Exercícios Sugeridos
 Faculdade de Engenharia da UERJ Departamento de Engenharia Elétrica Controle & Servomecanismo I Prof.: Paulo Almeida Exercícios Sugeridos Estabilidade, Resposta Transitória e Erro Estacionário Exercícios
Faculdade de Engenharia da UERJ Departamento de Engenharia Elétrica Controle & Servomecanismo I Prof.: Paulo Almeida Exercícios Sugeridos Estabilidade, Resposta Transitória e Erro Estacionário Exercícios
INSTITUTO SUPERIOR TÉCNICO CONTROLO. As questões assinaladas com * serão abordadas na correspondente aula de apoio.
 INSTITUTO SUPERIOR TÉCNICO ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES CONTROLO 2 a Série (resposta no tempo, diagrama de blocos, erro estático) As questões assinaladas com * serão abordadas na correspondente
INSTITUTO SUPERIOR TÉCNICO ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES CONTROLO 2 a Série (resposta no tempo, diagrama de blocos, erro estático) As questões assinaladas com * serão abordadas na correspondente
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Introdução ao Estudo da Corrente Eléctrica
 Introdução ao Estudo da Corrente Eléctrica Num metal os electrões de condução estão dissociados dos seus átomos de origem passando a ser partilhados por todos os iões positivos do sólido, e constituem
Introdução ao Estudo da Corrente Eléctrica Num metal os electrões de condução estão dissociados dos seus átomos de origem passando a ser partilhados por todos os iões positivos do sólido, e constituem
TC 1 UECE 2012 FASE 2. PROF.: Célio Normando
 TC 1 UECE 01 FASE PROF.: Célio Normando Conteúdo: Aritmética Ordem de Grandeza 1. Racionalizar o uso da água significa usá-la sem desperdício e considerá-la uma prioridade social e ambiental, para que
TC 1 UECE 01 FASE PROF.: Célio Normando Conteúdo: Aritmética Ordem de Grandeza 1. Racionalizar o uso da água significa usá-la sem desperdício e considerá-la uma prioridade social e ambiental, para que
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
CAPÍTULO 12. Projeto de controladores discretos
 CAPÍULO 2 Projeto de controladores discretos 2. Introdução O projeto de controladores discretos pode ser realizado por emulaçào, onde um controlador contínuo é projetado, usando as mesmas técnicas vistas
CAPÍULO 2 Projeto de controladores discretos 2. Introdução O projeto de controladores discretos pode ser realizado por emulaçào, onde um controlador contínuo é projetado, usando as mesmas técnicas vistas
Modelos Estocásticos. Resolução de alguns exercícios da Colectânea de Exercícios 2005/06 PROCESSOS ESTOCÁSTICOS E FILAS DE ESPERA LEGI
 Modelos Estocásticos Resolução de alguns exercícios da Colectânea de Exercícios 2005/06 LEGI Capítulo 7 PROCESSOS ESTOCÁSTICOS E FILAS DE ESPERA Nota: neste capítulo ilustram-se alguns dos conceitos de
Modelos Estocásticos Resolução de alguns exercícios da Colectânea de Exercícios 2005/06 LEGI Capítulo 7 PROCESSOS ESTOCÁSTICOS E FILAS DE ESPERA Nota: neste capítulo ilustram-se alguns dos conceitos de
Aula 13 Análise no domínio da frequência
 Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
EE531 - Turma S. Diodos. Laboratório de Eletrônica Básica I - Segundo Semestre de 2010
 EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
Trabalho Computacional. A(h) = V h + 2 V π h, (1)
 Unidade de Ensino de Matemática Aplicada e Análise Numérica Departamento de Matemática/Instituto Superior Técnico Matemática Computacional (Mestrado em Engenharia Física Tecnológica) 2014/2015 Trabalho
Unidade de Ensino de Matemática Aplicada e Análise Numérica Departamento de Matemática/Instituto Superior Técnico Matemática Computacional (Mestrado em Engenharia Física Tecnológica) 2014/2015 Trabalho
Exercícios complementares envolvendo a equação de Torricelli
 01. (Vunesp-SP) Um veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal, quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz uniformemente à razão de
01. (Vunesp-SP) Um veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal, quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz uniformemente à razão de
Singularidades de Funções de Variáveis Complexas
 Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace [email protected] Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace [email protected] Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
FÍSICA. Prof. Fracalossi
 FÍSICA Prof. Fracalossi 1. O cérebro humano demora cerca de 0,6 segundos para responder a um estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de resposta para acionar
FÍSICA Prof. Fracalossi 1. O cérebro humano demora cerca de 0,6 segundos para responder a um estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de resposta para acionar
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech [email protected]
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos [email protected] 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos [email protected] 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Transformada de Laplace. Parte 3
 Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Faculdade de Computação
 UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Falso: F = Low voltage: L = 0
 Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 PORTAS LOGICAS 1.1 INTRODUÇÃO Em 1854, George Boole introduziu o formalismo que até hoje se usa para
Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 PORTAS LOGICAS 1.1 INTRODUÇÃO Em 1854, George Boole introduziu o formalismo que até hoje se usa para
Resposta em Frequência de Amplificadores. Aula 10 Prof. Nobuo Oki
 Resposta em Frequência de Amplificadores Aula 10 Prof. Nobuo Oki Considerações Gerais (1) Polo Simples Efeito Miller Multiplicador do capacitor usando efeito Miller Considerações Gerais (2) Aplicabilidade
Resposta em Frequência de Amplificadores Aula 10 Prof. Nobuo Oki Considerações Gerais (1) Polo Simples Efeito Miller Multiplicador do capacitor usando efeito Miller Considerações Gerais (2) Aplicabilidade
Títulos de Crédito títulos de crédito formalizar dívidas que serão pagas no futuro prazo previamente estipulado ativos financeiros vendê-los por
 Desconto Simples Títulos de Crédito Os títulos de crédito são instrumentos legais previstos no direito comercial (contratos) e são usados para formalizar dívidas que serão pagas no futuro, em prazo previamente
Desconto Simples Títulos de Crédito Os títulos de crédito são instrumentos legais previstos no direito comercial (contratos) e são usados para formalizar dívidas que serão pagas no futuro, em prazo previamente
Aula 19: Projeto de controladores no domínio da frequência
 Aula 19: Projeto de controladores no domínio da frequência prof. Dr. Eduardo Bento Pereira Universidade Federal de São João del-rei [email protected] 14 de novembro de 2017. prof. Dr. Eduardo Bento Pereira
Aula 19: Projeto de controladores no domínio da frequência prof. Dr. Eduardo Bento Pereira Universidade Federal de São João del-rei [email protected] 14 de novembro de 2017. prof. Dr. Eduardo Bento Pereira
António Costa. Paulo Roma Cavalcanti
 Introdução à Computação Gráfica Modelação Adaptação: Autoria: João Paulo Pereira António Costa Claudio Esperança Paulo Roma Cavalcanti História Modelação por malha de arame (wireframes) Representa os objectos
Introdução à Computação Gráfica Modelação Adaptação: Autoria: João Paulo Pereira António Costa Claudio Esperança Paulo Roma Cavalcanti História Modelação por malha de arame (wireframes) Representa os objectos
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
Controle de Sistemas. Desempenho de Sistemas de Controle. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas Desempenho de Sistemas de Controle Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas O é um telescópio de 2,4m, que fica a 380 milhas da Terra, sendo
Controle de Sistemas Desempenho de Sistemas de Controle Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas O é um telescópio de 2,4m, que fica a 380 milhas da Terra, sendo
Lista 13: Gravitação. Lista 13: Gravitação
 Lista 13: Gravitação NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para se resolver e entregar. ii. Ler os enunciados com atenção. iii. Responder a questão
Lista 13: Gravitação NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para se resolver e entregar. ii. Ler os enunciados com atenção. iii. Responder a questão
Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros
 107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
AULA 8 COMPENSAÇÃO POR ATRASO DE FASE. Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I PROF. DR. ALFREDO DEL SOLE LORDELO
 Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 8 COMPENSAÇÃO POR ATRASO DE FASE PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA A configuração do compensador eletrônico por atraso
Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 8 COMPENSAÇÃO POR ATRASO DE FASE PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA A configuração do compensador eletrônico por atraso
O Papel dos Pólos e Zeros
 Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected] Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected] Campinas, Janeiro de 2007
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
AULA #12. Estabilidade de Sistemas de Controle por
 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
