CAPÍTULO 12. Projeto de controladores discretos
|
|
|
- Maria Fernanda Abreu Amarante
- 8 Há anos
- Visualizações:
Transcrição
1 CAPÍULO 2 Projeto de controladores discretos 2. Introdução O projeto de controladores discretos pode ser realizado por emulaçào, onde um controlador contínuo é projetado, usando as mesmas técnicas vistas nos capitulos 6 e 7, e então discretizados, ou diretamente no plano Z. A primeira abordagem apresenta a vantagem de utlizar os resultados de projeto para controladores analógicos e dispensar a necessidade de um estudo mais detalhado de técnicas discretas. A desvantagem desta abordagem é o fato de que o sustentador de ordem zero não é considerado no projeto e portanto, deve-se esperar uma degradação do desempenho. As técnicas baseadas no projeto do controlador usando diretamente o plano Z são mais precisas, mas ao custo de uma maior complexidade. Na seqüência apresentaremos as estruturas básicas dos controladores discretos e então algumas técnicas de projeto. Duas abordagens para o projeto serão consideradas: o projeto por emulação e o projeto diretamente do controlador discreto. 2.2 Estruturas de controladores As estruturas dos controladores discretos são os equivalentes discretos das estruturas de controladores analógicos apresentados no Capítulo 5. Assim, podemos ter controladores do tipo proporcional, proporcional-integral, proporcional-derivativo, proporcional-integral-derivativo e de avanço e atraso de fase. A abela abaixo resume as estruturas dos controladores. anto a equação diferença quanto a função de transferência discreta de cada controlador são apresentadas. ipos de Controladores e(k) C(z) u(k)
2 78 Capítulo 2: Projeto de controladores discretos Proporcional u(k) = Ke(k), C(z) = K Derivativo u(k) = K P D (e(k) e(k )) Integral Avanço/Atraso C(z) = K P D ( z ) = K P D z z u(k) = u(k ) + K P I e(k) C(z) = K P I z = K P I z z u(k + ) = βu(k) + k(e(k ) αe(k)) C(z) = K αz βz 2.3 Controle Digital por Emulação Esta abordagem considera que o projeto de um controlador analógico já tenha sido realizado. Este projeto segue exatamente o procedimento estudado em outros capítulos e todo o processo de amostragem e reconstrução do sinal não é, portanto, considerado. O controlador analógico é então discretizado usando-se algum método de discretização. Vários métodos de discretização podem ser usados e aqui abordaremos o método de Euler, o método de ustin, o método da transformação casada de pólos-zeros e o método da transformação casada de pólos-zeros modificado Controle por emulação via Euler Esta técnica consiste em fazer o projeto do controlador analógico, como vimos nos capítulos precedentes, e em seguida aproximar o sinal de controle obtido com C(s) através do método de Euler, usando Ẋ X(k + ) X(k ) = (2.3.) u(t) u(t) u(t) com ZOH u(t) medio com interpolaçao / k Figura 2.: Aproximação de Euler
3 EEL-DAS-UFSC 79 Exemplo 2.3. Encontre a equação recursiva correspondente à digitalização do controlador analógico C(s) = K 0 (s + a). s + b Solução: Seja e(t) o sinal de entrada do controlador e u(t) o sinal de saída. Logo U(s) E(s) = K 0(s + a) s + b : (s + b)u = K 0 (s + a)e : u + bu = K 0 (ė + ae) Aplicando-se o método de Euler temos u = u(k + ) u(k) e ė = e(k + ) e(k) Logo obteremos a seguinte aproximação u(k + ) u(k) que resulta na seguinte equação recursiva e(k + ) e(k) + b u(k) = K 0 ( + a e(k)) e(k + ) e(k) u(k + ) = u(k) + ( bu(k) + K 0 + K 0 a e(k)) = ( b)u(k) + K 0 e(k + ) + ( K 0 a K 0 )e(k) Note que u(k +) é obtido em função de u(k), e(k +) e e(k) de forma recursiva. A representação dessa equação recursiva em termos da função de transferência discreta pode ser obtida com o auxilio da transformada Z: Z[u(k + )] = z U(z) zu(0) Logo para condições iniciais nulas temos Z[e(k + )] = ze(z) ze(0) zu(z) = ( b)u(z) + K 0 z E(z) + ( K 0 a K 0 )E(z) E(z) C(z) U(z) C(z) = K 0 z + K 0 a K 0 z + b = U(z) E(z) e(t) u(t) e(t) e(k) u(k) C(s) C(z) SOZ u(t) Figura 2.2: Control Analógico Control Digital
4 80 Capítulo 2: Projeto de controladores discretos e(k) e(t) e(k ) Area do trapezoide k k Figura 2.3: Integral rapezoidal ( e(k ) + e(k ) Área=. ) 2 t Método de ustin A discretização obtida com o método de Euler pode ser interpretada como a substituição da tangente (derivada) pela secante ( variação da função no intervalo de amostragem ). Ẋ = X(k + ) X(k ) Outra forma de discretização consiste em aproximar a integral pela regra trapezoidal, como ilustrado na Figura 2.3. Desta figura k e(t)dt = k e(t)dt + k e(t)dt 0 0 k Aproximando-se k k e(t)dt pela área do trapézio no intervalo e definindo-se u(k ) como a área acumulada dos sucessivos trapézios até o instante k, temos a seguinte relação recursiva u(k ) = u(k ) + Podemos representar a integração pelo bloco e(k ) + e(k ) (2.3.2) 2 E(s) s U(s) U(s) E(s) = s onde e(t) é o sinal cuja área queremos calcular e u(t) é a área desejada. omando-se a transformada Z da equação recursiva temos U(z) = z U(z) + z E(z) + E(z) 2 E(z) F(z) U(z) U(s) E(s) = F (z) = + z 2 z = 2 z + z
5 EEL-DAS-UFSC 8 Para o sistema abaixo teríamos a relação e(t) a s + a u(t) e(k) a 2 z + a +z C(s) C(z) Nota-se então, dos dois exemplos acima que a relação entre C(s) e C(z) com a aproximação bilinear é dada por C(s) = C(z) com s = 2 z (ustin) + z que expressa uma transformação bilinear de s para z. Exemplo Obtenha um controle digital para que o sistema abaixo tenha em malha fechada uma freqúencia natural ω n = 0, 3 rad/seg e um amortecimento ξ = 0, 7 u(k) r + - e C(s) u s 2 y Figura 2.4: Sistema dp exemplo Solução: Primeiro determinaremos um controlador analógico C(s) que atende as especificações. Em seguida escolhemos um método de emulação para implementar digitalmente o sinal de controle. e(t) u(t) e(t) e(k) u(k) C(s) C(z) SOZ u(t) Figura 2.5: Implementação Analógica Implementação Digital Com os métodos de projeto de controladores de avanço encontramos s + a C(s) = K c a = 0, 2, b = 2, e K c = 0, 8 s + b kc=0,8 2 0,2 Im(s) 0,2 0,2 Re(s) Pólos: s = 0, 2 ± j0, 2 Equação característica: s 2 + 2ξω n s + ω 2 n = 0 :ξ = 0, 7 ω n = 0, 2 2 = 0, 282
6 82 Capítulo 2: Projeto de controladores discretos Para a implementação digital precisamos da freqüência de amostragem. Em sistemas de controle a freqüência de amostragem é geralmente escolhida em torno de 20 vezes a freqüência de banda passante do sistema de malha fechada, que corresponde aproximadamente a ω n. Para o exemplo, adotaremos este fator de 20 vezes. Logo a freqüência de amostragem é ω a = (0, 3).20 = 6 rad/seg = Hz, e o período de amostragem é = seg. Com a aproximação bilinear temos U(z) E(z) = C(z) = K s + a c s + b 2 z s= + z Portanto = K c 2 z + z + a 2 z + z + b = K c 2 2z + a( + z ) 2 2z + b( + z ) = K c 2 + a + (a 2)z 2 + b + (b 2)z U(z)[2 + b + (b 2)z ] = k c [(2 + a) + (a 2)z ]E(z) que por sua vez conduz à seguinte equação recursiva u(k) = 2 b 2 + a u(k ) b 2 + b e(k) + K a 2 c e(k ) 2 + b Note que e(k) = r(k) y(k) e portanto podemos implementar o controlador C(s) através do esquema digital apresentado na Figura 2.6. r(k) y(k) Eq. Recursiva e(k)=r(k) y(k) u(k) u(t) y(t) SOZ s 2 y(k) A/D Figura 2.6: Sistema Discreto Poderíamos ter resolvido o mesmo problema usando um outro método de discretização. Exemplo Refazer o exemplo usando Euler.
7 EEL-DAS-UFSC 83 y(t),4,2,0 t Figura 2.7: Resposta ao Degrau Método da transformação casada de pólos-zeros Neste caso usa-se a relação z = e s para mapear pólos e zeros do controlador contínuo no plano complexo. No caso de funções de transferência com maior número de pólos que zeros, adicionam-se zeros em z =, de modo a igualar o número de zeros e pólos do controlador discreto. Seja uma função de transferência C(s) com um número de pólos maior do que de zeros. Usando-se o mapeamento z = e s, obtem-se C(z). Quando a freqüência ω varia de jω = 0 para jω a /2, que é a máxima freqüência possível no plano Z, tem-se z variando de z = e 0 = a z = e ωa 2 = e jπ =. Como C(s) tem zeros no infinito, que correspondem a ω, segue que C(s) tende para zero quando ω cresce. Para que o mesmo ocorra com H(z), deve-se ter zeros em z =. Exemplo Seja um controlador analógico dado por C(s) = s + s + 2 e seja = 0. seg o período de amostragem. Usando-se o mapeamento z = e s, o zero em e o pólo em 2 são mapeados em e 0. = e e 2 0. = 0.89, respectivamente. A função de transferência amostrada é então C(z) = K d z z onde K d é o valor do ganho a ser determinado. Para que os ganhos em baixa freqüência sejam iguais, deve-se ter C(s = 0) = C(z = ) e portanto K d 0.89 = 2 e segue que K d = A função de transferência amostrada é portanto C(z) = 4.05 z z 0.89 No exemplo anterior a função de transferência do controlador contínuo tinha o mesmo número de pólos e zeros. No exemplo seguinte o controlador contínuo apresenta dois pólos e um zero.
8 84 Capítulo 2: Projeto de controladores discretos Exemplo Seja a função de transferência C(s) = s + s(s + 2) Neste caso tem-se dois pólos e um zero e deve-se então acrescentar um zero em z =. A função de transferência discreta é então C(z) = K d Calculando-se o ganho da função de transferência discreta da mesma forma como anteriormente, tem-se K d = e a função de transferência discreta é (z + )(z 0.905) C(z) = s(z 0.89) Método de transformação casada de pólos-zeros modificada Quando a função de transformação discreta tem o mesmo número de pólos e zeros, a equação diferença correspondente é tal que a saída em um instante de amostragem depende da entrada no mesmo instante. Seja, por exemplo, um controlador dado por Y (z) U(z) = K z + a z + b A equação diferença correspondente é dada por y(k) = by(k ) + Ku(k) + au(k ) e a saída y(k) depende de u(k). Se o tempo de cálculo for tal que a entrada atual não possa ser usada para gerar a saída atual, deve-se manter o número de pólos maior do que o de zeros, modificando-se o método da transformação casada, o qual consiste em introduzir zeros em, de tal modo que se tenha pelo menos um pólo a mais do que um zero. No caso da função de transferência C(s) = s + s(s + 2) por exemplo, não seria acrescentado nenhum zero em z =. 2.4 Projeto por métodos discretos Nos métodos de emulação as operações de derivada e/ou integral executadas pelo controlador são aproximadas por operações algébricas com as amostras dos sinais de entrada/saída do controlador analógico projetado a partir do modelo analógico da planta. Nesta seção veremos como projetar um controlador discreto a partir do modelo discreto da planta. Este modelo inclui o sustentador de ordem zero, e antes da aplicação do método de projeto, deve-se obter a função de transferência da planta. A Figura 2.8 mostra o modelo discreto e a Figura 2.9 mostra o modelo discreto equivalente.
9 EEL-DAS-UFSC 85 r(t) r(k) e(k) u(t) y(t) + C(z) D/A SOZ G(s) y(k) Controle Digital Modelo Analogico Figura 2.8: Modelo Discreto r(k) + - e(k) C(z) u(k) G(z) y(k) Figura 2.9: Modelo Discreto Equivalente Sinal Discreto Z[f(k)] f(k) t=k Amostrador L [F(s)] Ideal F(s) f(t) f(k) * L F(s) * z=e s F(z) sinal amostrado (continuo) f(k)=f(t) * δ(t) rem de impulsos de periodo abelas ou teoremas dos residuos A função de transferência do controlador é C(z) e a função de transferência da planta e do sustentador de ordem zero é calculada por [ ] G(s) G(z) = ( z )Z s Pode-se usar o teorema dos resíduos, para obter esta função, como ilustrado na abela 2.4, usando-se as seguintes fórmulas: F (z) = n R(P i ), P i pólos distintos de F (s). [ ] i= z R(P i ) = (s P i )F (s) (Multiplicidade ) z e s s=p i R(P i ) = [ ] d m (s P (m )! ds m i ) m z F (s) (Multiplicidade m). z e s s=p i Dois métodos de projeto serão estudados nesta seção, o projeto por lugar das raízes e o projeto no domínio da freqüência. Os dois métodos seguem basicamente os mesmos princípios já apresentados para o caso contínuo.
10 86 Capítulo 2: Projeto de controladores discretos 2.4. Projeto pelo lugar das raízes O método de projeto pelo lugar das raízes segue os mesmos princípios usados no caso contínuo. O projeto visa melhorar o desempenho em regime permanente ou o desempenho em regime transitório ou ambos. Projeto por avanço de fase Para melhorar o desempenho em regime transitório usa-se um compensador de avanço de fase, dado por C(z) = z + α z + β As etapas principais do projeto são:. A posição dos pólos dominantes no plano s é determinada a partir dos requisitos de desempenho transitório. Estes pólos são então mapeados no plano Z, usando o mapeamento z = e s. 2. O zero do controlador é fixado, e o pólo é calculado pela condição de pertinência angular. 3. O ganho do controlador é calculado pela condição de pertinência de módulo. 4. As constantes de erro são calculadas e em caso em que a condição de erro for insatisfatória, o projeto é refeito ou um compensador de atraso de fase é acrescentado. Projeto por atraso de fase No caso em que o erro em regime permanente for muito elevado, deve-se acrescentar um compensador de atraso de fase, dado por C(z) = z + α z + β As etapas principais do projeto são:. Determinam-se a constante de erro desejada Kerro desejado, a partir do erro especificado, e a constante atual de erro K erro, onde K erro pode ser o ganho estático, de velocidade ou aceleração. 2. O pólo do compensador é fixado. Usualmente fixa-se este pólo próximo de z =, que corresponde a s = 0 no plano s. 3. Determina-se o zero do compensador fazendo-se K desejado erro K erro = α β Do mesmo modo que no caso contínuo, o aumento de ganho é dado pelo ganho do controlador nas baixas freqüências (s 0 no caso contínuo e z para o caso discreto). A seguir apresentaremos alguns exemplos do projeto pelo lugar das raízes.
11 EEL-DAS-UFSC 87 r(t) r(k) + e(k) C(z) u(k) SOZ u(t) s 2 y(t) y(k) y(t) r(k) + - Figura 2.: Figura para o exemplo e(k) C(z) u(k) G(z) y(k) Figura 2.: Diagrama equivalente Exemplo 2.4. Projete um controlador para que o sistema da Figura 2. em malha fechada apresente um comportamento similar a um sistema analógico com ω n = 0, 3rad/seg. e ξ = 0, 7. Solução: [ ] O diagrama discreto equivalente é apresentado na Figura 2. onde G(z) = ( G(s) z )Z = 2 z + s 2 (z ). 2 Escolhendo-se a freqüência de amostragem como sendo 20 vezes a freqüência da banda passante do sistema de malha fechada temos ω s = (20)(0, 3) = 6rad/seg = Hz. Logo = seg. Assim temos G(z) = z + 2(z ) 2 O lugar das raízes obtido com o controlador proporcional é mostrado na Figura 2.2. Im(z) Re(z) Figura 2.2: Lugar das raízes com controlador proporcional Note que um controlador proporcional não consegue estabilizar o sistema. Com um controlador
12 88 Capítulo 2: Projeto de controladores discretos PD podemos diminuir as oscilações. A função de transferência de um controlador PD é D(z) = K p + K p D ( z ) = K z α z onde α = D e K = K P ( + D ). + D No plano s os pólos desejados são dados por s 2 + 2ξω n s + ω 2 n = 0 : s , 7.0, 3 + (0, 3) 2 = 0 : s d = 0, 2 ± 0, 2j No plano z os pólos desejados são dados por z = e s resulta em: com s sendo os pólos no plano s o que z d = e 0,2±0,2j 0,2(cos ±sen j) = e = 0, 79 ± 0, 7j Com as condições de módulo e fase do lugar das raízes temos C(z 0 d) + G(z d ) = ±π = 0, 7 : = 3, 03:α = 0, 85 0, 79 α = C(z d ) G(z d ) =:K = = 0, 36. 2, 77 Com isso temos z 0, 85 C(z) = 0, 36 z que resulta em la lei de controle = 0, 36( 0, 85z ) u(k) = 0, 36e(k) 0, 348e(k ) que é similar à encontrada num exemplo anterior de projeto via emulação. Normalmente não é necessário que os pólos desejados de malha fechada sejam exatamente aqueles especificados, mas sim estejam dentro de uma região do plano z associada a um fator de amortecimento maior que o especificado (menor oscilações). r(t) + C(z) SOZ u(t) s(s+2) y(t) Figura 2.3: Sistema do Exemplo 2.4.2
13 EEL-DAS-UFSC 89 Exemplo (Ogata, Discrete-time Control Systems, p. 384) Para o sistema mostrado na Figura 2.3 projetar um controlador discreto para atender aos seguintes requisitos de projeto: amortecimentoe ξ = 0, 5 e tempo de resposta t r2% = 2 seg. O período de amostragem é = 0, 2 seg. Pede-se ainda o cálculo da resposta ao degrau e o erro à rampa. Solução: t r2% = 4 = 2 =:ω n = 4 ξω n Os pólos desejados são s d = 2 ± 3, 464j. ipicamente o período de amostragem é escolhido de tal forma que existam pelo menos 9 amostras por ciclo de oscilação amortecida. Conferindo no caso acima temos, Freq. amostragem ω s = 2π = 3, 42 Freq. oscilações amortecidas ω d = 3, 464. Portanto a escolha do período de amostragem é satisfatória. Os pólos dominantes no plano z são z d = e s d = 0, 558 ± 0, 428j = 0, 67 39, 69. O modelo discreto do sistema acima é [ ] e s G(z) = Z[SOZG(s)] = Z G(s) s [ ] G(s) = ( z )Z s [ ] = ( z )Z s 2 (s + 2) 0, 0758(z + 0, 876) = (z )(z 0, 6703) Como o ponto z d deve pertencer ao lugar das raízes, temos K = G(z d)c(z d ): ± 80 = G(z d ) + C(z d ) então C(z d ) = 5, 26. Um controlador que atende a condição de fase acima é um avanço de fase. C(z) = K z α z β Cancelando o pólo em 0, 6703 com a escolha α = 0, 6703 temos z d α z d β = 5, 26 :β = 0, O ganho K é determinado com a condição de módulo Em malha fechada temos então Y (z) R(z) = e a resposta ao degrau unitário G(z d )C(z d ) = =:K = 2, 67 G(z)C(z) + G(z)C(Z) R(z) = = 0, 2227z + 0, 95 z 2, 036z + 0, 4494 = F (z) e Y (z) = F (z) z z
14 90 Capítulo 2: Projeto de controladores discretos A seqüencia y(k ) pode ser obtida pela inversa da transformada Z, tabelas ou mesmo por simulação. O erro de velocidade é dado por e rp = lim z ( z )E(z) = K v onde z K v = lim G(z)C(z) = 2, 80. z Como no caso de sistemas analógicos podemos aumentar o ganho K v, e portanto diminuir o erro de regime, introduzindo um compensador de atraso em cascata como o controlador já projetado. Por exemplo, com C a (z) = z α a z β a e α a = 0, 94, β a = 0, 98 temos o novo ganho de velocidade K v dado por z K v = lim G(z)C(z)C a (z) = (3).(2, 80) (C a () = 3) z que representa um aumento de 3 vezes no ganho K v sem o controlador de atraso. A escolha do zero do controlador de atraso ( α a ) é tipicamente próximo da unidade e deve satisfazer e o valor de β a é escolhido tal que controlador final; C a (z)c(z) = k z α z α a. z β z β a > α a 0, z d (próximo de ) C a () = α a β a = acréscimo desejado Projeto no domínio da freqüência Resposta de um sistema discreto a uma entrada senoidal Vamos considerar um sistema linear, discreto, invariante no tempo, com função de transferência G(z). O sistema é por hipótese, estável, ou seja, todos os pólos de G(z) estão no interior do círculo unitário. A entrada do sistema é um sinal senoidal u(t) = sen ωt, amostrado por um amostrador ideal, resultando em u(k) = sen kω. Então zsen ω U(z) = Z [sen kω ] = (z e jω )(z e jω ) A resposta do sistema é zsen ω Y (z) = G(z)U(z) = G(z) (z e jω )(z e jω ) Fazendo-se a expansão em frações parciais, obtem-se Y (z) = Az z e + Az + termos devidos aos pólos de G(z) jω z e jω
15 EEL-DAS-UFSC 9 onde A indica o conjugado de A. Calculando-se A, usando o procedimento de multiplicar Y (z) por z ejω e fazer z e jω, z obtem-se A = G(ejω 2j Portanto A = G(e jω 2j Denotando G(e jω ) = Me jθ segue que G(e jθ ) = Me jθ A resposta do sistema é então dada por Y (z) = M ( ) e jθ z 2j z e e jθ z + termos devidos aos outros pólos de G(z) jω z e jω No regime permanente, a contribuição dos pólos do sistema para a resposta desaparece, pois por hipótese o sistema é estável. O dois primeiros termos da expansão se combinam para fornecer a resposta em regime permanente no domínio do tempo y rp = M sen(kω + θ) onde M = G(e jω ) e θ = G(e jω ). Esta resposta é também senoidal, com a amplitude multiplicada por G(e jω ) e com um deslocamento de fase dado por θ = G(e jω ), e portanto, é análoga ao caso contínuo. Vimos no caso contínuo que a resposta em freqüência nos permite obter informações sobre o comportamento do sistema, úteis tanto para a análise quanto para a síntese de controladores através de métodos freqüenciais. No caso discreto pode-se usar o mapeamento z = e s, com s = jω, o que permitiria traçar a resposta em freqüência (diagrama de Bode, etc). No entanto tem-se uma dificuldade. No caso discreto, as freqüências estão idealmente limitadas a ωa, onde ω 2 a é a freqüência de amostragem, para que o aliasing seja evitado. Assim, teriamos um diagrama de Bode limitado em freqüência, e a analogia com o caso contínuo seria difícil. Para se manter as vantagens de trabalhar no domínio da freqüência para o caso discreto. tem-se que usar a transformação bilinear. Esta transformação bilinear é dada por z = + 2 w 2 w onde é o período de amostragem. Desta equação obtem-se a transformaçào inversa w = 2 z z + Uma função de transferência pode então se escrita como uma função racional de z e os métodos de resposta em freqüência usados. Com esta transformação, a faixa primária é mapeada no círculo unitário no plano z e por sua vez este é mapeado no lado esquerdo do plano w. No plano w pode-se definir uma freqüência fictícia η, ou seja w = jη. Esta freqüência pode ser relacionada com a freqüência ω do plano s, usando-se os mapeamentos w = 2 z e z = z+ es. w = jη = 2 z z + = 2 e j ω 2 e j ω 2 = 2 z=e jω e j ω 2 + e j ω 2 j tg ω 2
16 92 Capítulo 2: Projeto de controladores discretos ou η = 2 tg ω 2 Desde que ω a = 2π tem-se que η = 2 tg ω π ω a Desta última equação é fácil de ver que quando ω varia de ωa a 0 então η varia de a 0, 2 e quando ω varia de 0 a ωa, então η varia de 0 a. Observa-se então, que com a transformação 2 bilinear tem-se uma freqüência fictícia que varia até, o que retira a restrição para a construção do diagrama de Bode de forma análoga ao caso contínuo. A última equação pode ser escrita como 2 = tg ω ω a π Para valores pequenos de freqüência, pode-se substituir a tangente pelo arco: η ω e portanto a freqüência no plano s e a freqüência fictícia η são aproximadamente iguais. Diagrama de Bode O procedimento para o traçado do diagrama de Bode para G(jη) segue o procedimento para G(jω). Existem no entanto algumas diferenças com relação ao valor da magnitude em altas freqüências. Para uma função da transferência no plano s com maior número de pólos que zeros, a assíntota para altas freqüências tende para, pois lim s = 0. No entanto, quando a freqüência fictícia η, no plano w, a freqüência no plano s tende para ωa. No entanto, lim 2 η G(jη) geralmente é diferente de lim ω ωa 2 G(jω), e o comportamento nas altas freqüências é diferente nos dois casos. Procedimento de projeto O procedimento de projeto consiste nos seguintes passos:. Obter G(z) e então G(w) usando a transformação bilinear z = + 2 w 2 w O período de amostragem deve ser escolhido adequadamente. 2. Faz-se w = jη em G(w) e traça-se o diagrama de Bode de G(jη). 3. Usa-se o diagrama de Bode para fazer o projeto seguindo o mesmo procedimento usado para fazer o projeto no domínio da freqüência para o caso contínuo. 4. Uma vez obtida a função de transferência C(w) do controlador no plano w, transforma-se esta função em C(z), usando-se a transformação bilinear ou seja, w = 2 z z + C(z) = C(w) w= 2 z z+
17 EEL-DAS-UFSC 93 Exemplo Para o sistema representado na Figura 2.4, projete um controlador, no domínio da freqüência, que assegure os seguintes objetivos: margem de fase de 60 ; margem de ganho de pelo menos db; constante de erro de velocidade k v = 2 seg ; período de amostragem = 0, 2seg. O período de amostragem é = 0, 2 seg. R(s) + Σ C e s s K s(s + ) Y (s) Figura 2.4: Sistema para o Exemplo O modelo discreto equivalente é: [ ] e s k K(z + 0, 9356) G(z) = Z = 0, 0873 s s(s + ) (z )(z 0, 887) com a transformaçâo bilinear z = + 2 ω 2 ω :ω = 2 z z + temos G(w) = G(z) + 0, w z= 0, w ( )( w K 300, 6 + w ) = ( ) w w 0, O controlador C(z) = C(w) 2 z deve ser determinado para se atingir os requisitos de w= z + projeto. Como G(w) já possui um ganho a ser determinado, vamos assumir o controlador C(w) com ganho unitário) D(w) = + w/α + w/β (controlador de avanço) O ganho K é determinado para se atingir o requisito K v = 2 de onde tiramos K v = lim w 0 wc(w)g(w) = 2:K = 2.
18 94 Capítulo 2: Projeto de controladores discretos Usando as técnicas de projeto para controlador de avanço no domínio da frequência encontramos + w/0, 997 MF =...0 C(w) = + w/3, 27 MG = 4 db Assim encontramos Em malha fechada ficamos com C(z) = C(w) z w= z + Y (z) R(z) = C(z)G(z) + C(z)G(z) onde os pólos são dados por P, P 2 = 0, 7026 ± 0, 3296j. z 0, 887 = 2, 78 z 0, 507 = 0, 8(z + 0, 9356) (z P )(z P 2 ) 2.5 Questões de Implementação Esta seção discute alguns aspectos da implementação do controle digital. Escolha do período de amostragem Segundo o teorema da amostragem, a freqüência de amostragem deve ser pelo menos 2 vezes a maior freqüência do sinal amostrado. Pode-se então escolher ω a = 2ω m, onde ω m indica a maior freqüência do sinal. No entanto, nas aplicações, uma taxa de amostragem bem superior é usada, para atender requisitos de estabilidade em malha fechada ou outros requisitos de projeto, como seguimento da entrada com baixo erro. Assim usa-se ω a em torno de 8 a vezes ω m. A escolha do período de amostragem é um compromisso entre requisitos de desempenho do sistema em malha fechada, que exigem uma alta taxa de amostragem, e o custo envolvido, já que maiores taxas de amostragem exigem computadores mais rápidos. Em situações práticas, a freqüência de amostragem é selecionada com base na faixa de passagem requerida da resposta e freqüência em malha fechada ou do tempo de resposta ou tempo de subida da resposta transitória. Uma regra prática é amostrar de 8 a vezes durante um ciclo de oscilação, se o sistema é superamortecido. A freqüência de amostragem pode ainda ser escolhida como 8 a vezes a faixa de passagem em malha fechada da resposta em freqüência (algumas vezes 5 é aceitável, outras vezes 20 é necessário).
19 EEL-DAS-UFSC 95 Exercícios. Considere o sistema de controle digital da Figura 4, onde a planta é de primeira ordem e tem um tempo morto de 2 seg. O período de amostragem é = seg. Projete um controlador PI digital, tal que os pólos dominantes de malha fechada tenham um amortecimento ζ = 0.5 e o número de amostras por ciclo de oscilação senoidal amortecida seja. Determine o erro a uma entrada tipo rampa unitária. Obtenha a resposta do sistema a uma entrada do tipo degrau unitário. R(z) + δ D(z) e s s e 2s s + Y (z) Figura 2.5: Exercício 2. Seja o sistema da Figura 5. Projete um controlador digital tal que os pólos dominantes do sistema tenham um amortecimento ζ = 0.5 e o número de amostras por ciclo de oscilação senoidal amortecida seja 8. O período de amostragem é = 0.2 seg. Obtenha a resposta a uma entrada do tipo degrau unitário. Determine a constante de velocidade K v. R(z) + Contr. ZOH Digital s(s + ) δ Y (z) Figura 2.6: Exercício 2 3. Considere o diagrama de blocos de um sistema de controle de uma antena, mostrado na Figura 6. O período é = 0.05 seg. a. Determine a margem de fase com K = e D(z) =. b. Para reduzir o erro em regime permanente, K é aumentado para 5. Projete um controlador de atraso de fase de tal modo que a margem de fase do sistema seja 45 o. c. Projete um controlador de avanço de fase, com K = 5, para que a margem de fase do sistema seja 45 o. d. Use o Scilab para para determinar a resposta no tempo do sistema nos itens b. e c. Compare os tempos de subida e a ultrapassagem para os dois sistemas. Controlador digital amplificador Motor e engrenagens R(z) 20 D(z) ZOH K s 2 + 6s Y (z) Figura 2.7: Exercício 3
20 96 Capítulo 2: Projeto de controladores discretos 4. A função de transferência seguinte é um compensador de avanço projetado para fornecer cerca de 60 O de avanço em ω = 3 rad/s C(s) = s + 0.s + Supondo que o período de amostragem seja = 0.25 seg, calcule e plote no plano z as localizações do pólo e zero da implementação digital de C(s) obtida: a. usando o método de ustin b. método de Euler Para cada caso, calcule o avanço de fase fornecido pelo compensador em z = e jω. 5. A função de transferência de uma planta é G(s) = que deve ser controlada por um controlador digital, com período de amostragem = 0. seg, como mostrado na (s + 0.)(s + 3) Figura 2.8. a. Projete um compensador digital, no plano z, usando o lugar das raízes para que a resposta a um degrau unitário apresente um tempo de subida de seg e um sobressinal de 5%. Sugestão: use o zero do controlador para cancelar o pólo da planta mais próximo da origem. b. Determine o tipo do sistema e o erro correspondente. c. Projete um controlador discreto de atraso de fase, que reduza o erro em regime permanente pela metade. [ Dado: Z s(s + 0.)(s + 3) ] = z( z (z )(z 2.73z ) R(s) + Y (s) D(z) ZOH G(s) Figura 2.8: Exercício 5 6. O sistema de controle de posicionamento de uma antena é mostrado na Figura 2.9 abaixo. O controle deve ser digital com um tempo de amostragem = 0. seg. a. Projete um controlador, usando o lugar das raízes, que asssegure um fator de amortecimento ζ = 0.5. Determine o tempo de resposta a 5%. O lugar das raízes do sistema não compensado, no plano z, assim como o lugar geométrico dos pólos no plano z com amortecimento constante igual a 0.5 são dados na Figura b. Supondo agora que o tempo de resposta a 5% deve ser 2 seg e deseja-se manter o mesmo amortecimento do item anterior, projete um controlador para atingir este objetivo. Sugestão: Use o zero do controlador para cancelar o pólo em [ Dados: Z s 2 (s +.7) ] = z (z ) (z ) 2 (z 0.843) e t r 5% 3 ζω n 7. Para o sistema cujo diagram de Bode no plano w é dado na Figura 2.2: a. Projete um controlador de atraso de fase no domínio da freqüência que garanta uma margem de fase de 50. b. Determine o controlador discreto e a equação recursiva do controlador, supondo que o período de amostragem é = 2 seg. Obs: A freqüência está em Hz. A transformação bilinear é w = 2 z z +
21 EEL-DAS-UFSC 97 R(z) + e s s K s(s +.7) 0. Y (z) Figura 2.9: Exercício Imag. axis Evans root locus ζ = 0.5 Lugar das raizes Real axis open loop zeroes open loop poles Figura 2.20: Lugar das raízes para o Exercício 6 0 db Magnitude Hz 90 degrees Phase Hz Figura 2.2: Diagrama de Bode para o Exercício 7
22
Sistemas a Tempo Discreto - Projeto
 Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Introdução AVALIAÇÃO DE DESEMPENHO. No domínio do tempo. No domínio da freqüência. Função de transferência. Módulo e fase da função de transferência
 AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica
 UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Análise no Domínio do Tempo de Sistemas em Tempo Discreto
 Análise no Domínio do Tempo de Sistemas em Tempo Discreto Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise no Domínio do Tempo de Sistemas em Tempo Discreto Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Newton Maruyama. Projeto de Controladores No Domínio Da Freqüência p. 1/4
 Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Sistemas de Controle Digital
 ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
CONTROLO DE SISTEMAS
 UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
Tipos de malha de Controle
 Tipos de malha de Controle SUMÁRIO 1 - TIPOS DE MALHA DE CONTROLE...60 1.1. CONTROLE CASCATA...60 1.1.1. Regras para Selecionar a Variável Secundária...62 1.1.2. Seleção das Ações do Controle Cascata e
Tipos de malha de Controle SUMÁRIO 1 - TIPOS DE MALHA DE CONTROLE...60 1.1. CONTROLE CASCATA...60 1.1.1. Regras para Selecionar a Variável Secundária...62 1.1.2. Seleção das Ações do Controle Cascata e
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA. Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Função de Transferência de Malha Fechada
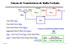 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Equações Diferenciais Ordinárias
 Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
Universidade Presbiteriana Mackenzie. Controle II
 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica Controle II Notas de Aula Prof. Marcio Eisencraft Segundo semestre de 004 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica
Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica Controle II Notas de Aula Prof. Marcio Eisencraft Segundo semestre de 004 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS
 ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
Curso de Instrumentista de Sistemas. Fundamentos de Controle. Prof. Msc. Jean Carlos
 Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Processamento Digital de Sinais
 Processamento Digital de Sinais Capítulo 1 Prof. Rodrigo Varejão Andreão 2010/2 Cap. 1 Introdução PDS: área de rápido desenvolvimento nos últimos 40 anos, resultado do avanço das tecnologias de computação
Processamento Digital de Sinais Capítulo 1 Prof. Rodrigo Varejão Andreão 2010/2 Cap. 1 Introdução PDS: área de rápido desenvolvimento nos últimos 40 anos, resultado do avanço das tecnologias de computação
Aula 19. Conversão AD e DA Técnicas
 Aula 19 Conversão AD e DA Técnicas Introdução As características mais importantes dos conversores AD e DA são o tempo de conversão, a taxa de conversão, que indicam quantas vezes o sinal analógico ou digital
Aula 19 Conversão AD e DA Técnicas Introdução As características mais importantes dos conversores AD e DA são o tempo de conversão, a taxa de conversão, que indicam quantas vezes o sinal analógico ou digital
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
CAP. 3 - EXTENSÔMETROS - "STRAIN GAGES" Exemplo: extensômetro Huggenberger
 CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
CAP. 3 - EXTENSÔMETOS - "STAIN GAGES" 3. - Extensômetros Mecânicos Exemplo: extensômetro Huggenberger Baseia-se na multiplicação do deslocamento através de mecanismos de alavancas. Da figura: l' = (w /
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores. Controlo 2005/2006. Controlo de velocidade de um motor D.C.
 Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
3 Matemática financeira e atuarial
 3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Transformada z. ADL 25 Cap 13. A Transformada z Inversa
 ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
Modulação por Pulsos
 Modulação por Pulsos Propriedades Amostragem de sinais Modulação por amplitude de pulso (PAM) Modulação por pulso codificado (PCM) Modulação por largura de pulso (PWM) Modulação por posição de pulso (PPM)
Modulação por Pulsos Propriedades Amostragem de sinais Modulação por amplitude de pulso (PAM) Modulação por pulso codificado (PCM) Modulação por largura de pulso (PWM) Modulação por posição de pulso (PPM)
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Análise e Processamento de Sinal e Imagem. II - Filtros Analógicos e Digitais. António M. Gonçalves Pinheiro
 II - Filtros Analógicos e Digitais António M. Gonçalves Pinheiro Departamento de Física Covilhã - Portugal pinheiro@ubi.pt Filtros Analógicos e Digitais 1. Filtros de Sinais Contínuos 2. Diagramas de Bode
II - Filtros Analógicos e Digitais António M. Gonçalves Pinheiro Departamento de Física Covilhã - Portugal pinheiro@ubi.pt Filtros Analógicos e Digitais 1. Filtros de Sinais Contínuos 2. Diagramas de Bode
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
AMOSTRAGEM ESTATÍSTICA EM AUDITORIA PARTE ll
 AMOSTRAGEM ESTATÍSTICA EM AUDITORIA PARTE ll! Os parâmetros para decisão do auditor.! Tipos de planos de amostragem estatística em auditoria. Francisco Cavalcante(f_c_a@uol.com.br) Administrador de Empresas
AMOSTRAGEM ESTATÍSTICA EM AUDITORIA PARTE ll! Os parâmetros para decisão do auditor.! Tipos de planos de amostragem estatística em auditoria. Francisco Cavalcante(f_c_a@uol.com.br) Administrador de Empresas
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e Controle
 Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e ontrole EES-5/ ELE/AES Engenharia de ontrole LAB : rojeto e Simulação de ontrolador com ealimentação de
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e ontrole EES-5/ ELE/AES Engenharia de ontrole LAB : rojeto e Simulação de ontrolador com ealimentação de
CDI 20705 Comunicação Digital
 CDI Comunicação Digital DeModulação em Banda Base Digital Communications Fundamentals and Applications Bernard Sklar ª edição Prentice Hall Marcio Doniak www.sj.ifsc.edu.br/~mdoniak mdoniak@ifsc.edu.br
CDI Comunicação Digital DeModulação em Banda Base Digital Communications Fundamentals and Applications Bernard Sklar ª edição Prentice Hall Marcio Doniak www.sj.ifsc.edu.br/~mdoniak mdoniak@ifsc.edu.br
Processamento Digital de Sinais Aula 05 Professor Marcio Eisencraft fevereiro 2012
 Aula 05 - Sistemas de tempo discreto Classificação Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 25-36. HAYKIN, S. S.; VAN VEEN,
Aula 05 - Sistemas de tempo discreto Classificação Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 25-36. HAYKIN, S. S.; VAN VEEN,
Memória cache. Prof. Francisco Adelton
 Memória cache Prof. Francisco Adelton Memória Cache Seu uso visa obter uma velocidade de acesso à memória próxima da velocidade das memórias mais rápidas e, ao mesmo tempo, disponibilizar no sistema uma
Memória cache Prof. Francisco Adelton Memória Cache Seu uso visa obter uma velocidade de acesso à memória próxima da velocidade das memórias mais rápidas e, ao mesmo tempo, disponibilizar no sistema uma
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Karine Nayara F. Valle. Métodos Numéricos de Euler e Runge-Kutta
 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO
 TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
I Controle Contínuo 1
 Sumário I Controle Contínuo 1 1 Introdução 3 11 Sistemas de Controle em Malha Aberta e em Malha Fechada 5 12 Componentes de um sistema de controle 5 13 Comparação de Sistemas de Controle em Malha Aberta
Sumário I Controle Contínuo 1 1 Introdução 3 11 Sistemas de Controle em Malha Aberta e em Malha Fechada 5 12 Componentes de um sistema de controle 5 13 Comparação de Sistemas de Controle em Malha Aberta
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
1 Propagação de Onda Livre ao Longo de um Guia de Ondas Estreito.
 1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
1 I-projeto do campus Programa Sobre Mecânica dos Fluidos Módulos Sobre Ondas em Fluidos T. R. Akylas & C. C. Mei CAPÍTULO SEIS ONDAS DISPERSIVAS FORÇADAS AO LONGO DE UM CANAL ESTREITO As ondas de gravidade
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Análise de Erro Estacionário
 Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Estrutura geral de um sistema com realimentação unitária negativa, com um compensador (G c (s) em série com a planta G p (s).
 2 CONTROLADORES PID Introdução Etrutura geral de um itema com realimentação unitária negativa, com um compenador (G c () em érie com a planta G p (). 2 Controladore PID 2. Acção proporcional (P) G c ()
2 CONTROLADORES PID Introdução Etrutura geral de um itema com realimentação unitária negativa, com um compenador (G c () em érie com a planta G p (). 2 Controladore PID 2. Acção proporcional (P) G c ()
Sistemas a Tempo Discreto
 Sistemas a Tempo Discreto 1. Caracterização de sistemas dinâmicos a tempo discreto 2. Transformada-Z 3. FT discreta, estabilidade e analogia com domínio-s 4. Sistemas amostrados 4.1 Amostragem e retenção
Sistemas a Tempo Discreto 1. Caracterização de sistemas dinâmicos a tempo discreto 2. Transformada-Z 3. FT discreta, estabilidade e analogia com domínio-s 4. Sistemas amostrados 4.1 Amostragem e retenção
Figura 2.1: Carro-mola
 Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Equações Diferenciais
 Equações Diferenciais EQUAÇÕES DIFERENCIAS Em qualquer processo natural, as variáveis envolvidas e suas taxas de variação estão interligadas com uma ou outras por meio de princípios básicos científicos
Equações Diferenciais EQUAÇÕES DIFERENCIAS Em qualquer processo natural, as variáveis envolvidas e suas taxas de variação estão interligadas com uma ou outras por meio de princípios básicos científicos
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
CAPÍTULO 9. y(t). y Medidor. Figura 9.1: Controlador Analógico
 146 CAPÍULO 9 Inrodução ao Conrole Discreo 9.1 Inrodução Os sisemas de conrole esudados aé ese pono envolvem conroladores analógicos, que produzem sinais de conrole conínuos no empo a parir de sinais da
146 CAPÍULO 9 Inrodução ao Conrole Discreo 9.1 Inrodução Os sisemas de conrole esudados aé ese pono envolvem conroladores analógicos, que produzem sinais de conrole conínuos no empo a parir de sinais da
Circuitos de 2 ª ordem: RLC. Parte 1
 Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Introdução ao estudo de equações diferenciais
 Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
Eletrônica Analógica
 UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
Análise de Arredondamento em Ponto Flutuante
 Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
EE531 - Turma S. Diodos. Laboratório de Eletrônica Básica I - Segundo Semestre de 2010
 EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
3.4 O Princípio da Equipartição de Energia e a Capacidade Calorífica Molar
 3.4 O Princípio da Equipartição de Energia e a Capacidade Calorífica Molar Vimos que as previsões sobre as capacidades caloríficas molares baseadas na teoria cinética estão de acordo com o comportamento
3.4 O Princípio da Equipartição de Energia e a Capacidade Calorífica Molar Vimos que as previsões sobre as capacidades caloríficas molares baseadas na teoria cinética estão de acordo com o comportamento
Campos Vetoriais e Integrais de Linha
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Problemas sobre Sistemas Não Lineares
 Mestrado Integrado em Engenharia Electrotécnica e de Computadores Controlo em Espaço de Estados Problemas sobre Sistemas Não Lineares Organizada por J. Miranda Lemos 0 J. M. Lemos IST P. (Construção do
Mestrado Integrado em Engenharia Electrotécnica e de Computadores Controlo em Espaço de Estados Problemas sobre Sistemas Não Lineares Organizada por J. Miranda Lemos 0 J. M. Lemos IST P. (Construção do
3 Metodologia de calibração proposta
 Metodologia de calibração proposta 49 3 Metodologia de calibração proposta A metodologia tradicional de calibração direta, novamente ilustrada na Figura 22, apresenta uma série de dificuldades e limitações,
Metodologia de calibração proposta 49 3 Metodologia de calibração proposta A metodologia tradicional de calibração direta, novamente ilustrada na Figura 22, apresenta uma série de dificuldades e limitações,
Aula 9 ESCALA GRÁFICA. Antônio Carlos Campos
 Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Sinais Senoidais. A unidade de freqüência no SI é o Hertz (Hz) e o tempo é dado em segundos (s).
 Campus Serra COORDENADORIA DE AUTOMAÇÂO INDUSTRIAL Disciplina: ELETRÔNICA BÁSICA Professor: Vinícius Secchin de Melo Sinais Senoidais Os sinais senoidais são utilizados para se representar tensões ou correntes
Campus Serra COORDENADORIA DE AUTOMAÇÂO INDUSTRIAL Disciplina: ELETRÔNICA BÁSICA Professor: Vinícius Secchin de Melo Sinais Senoidais Os sinais senoidais são utilizados para se representar tensões ou correntes
TÉCNICAS DE PLANEJAMENTO E CONTROLE. UNIDADE II - Instrumentos gráficos de planejamento e controle
 TÉCNICAS DE PLANEJAMENTO E CONTROLE UNIDADE II - Instrumentos gráficos de planejamento e controle 2.6. Gráfico de Gantt Para facilitar a visualização e entendimento da programação, a rede PERT pode ser
TÉCNICAS DE PLANEJAMENTO E CONTROLE UNIDADE II - Instrumentos gráficos de planejamento e controle 2.6. Gráfico de Gantt Para facilitar a visualização e entendimento da programação, a rede PERT pode ser
TEORIA UNIDIMENSIONAL DAS
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: O conhecimento das velocidades do fluxo de
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: O conhecimento das velocidades do fluxo de
7 - Análise de redes Pesquisa Operacional CAPÍTULO 7 ANÁLISE DE REDES. 4 c. Figura 7.1 - Exemplo de um grafo linear.
 CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
CAPÍTULO 7 7 ANÁLISE DE REDES 7.1 Conceitos Básicos em Teoria dos Grafos Diversos problemas de programação linear, inclusive os problemas de transporte, podem ser modelados como problemas de fluxo de redes.
3 Transdutores de temperatura
 3 Transdutores de temperatura Segundo o Vocabulário Internacional de Metrologia (VIM 2008), sensores são elementos de sistemas de medição que são diretamente afetados por um fenômeno, corpo ou substância
3 Transdutores de temperatura Segundo o Vocabulário Internacional de Metrologia (VIM 2008), sensores são elementos de sistemas de medição que são diretamente afetados por um fenômeno, corpo ou substância
Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo. Funções Exponenciais e Logarítmicas Progressões Matemáticas
 Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo Funções Exponenciais e Logarítmicas Progressões Matemáticas Funções Exponenciais e Logarítmicas. Progressões Matemáticas Objetivos
Métodos Quantitativos Prof. Ms. Osmar Pastore e Prof. Ms. Francisco Merlo Funções Exponenciais e Logarítmicas Progressões Matemáticas Funções Exponenciais e Logarítmicas. Progressões Matemáticas Objetivos
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A4 (1A) FONTE CHAVEADA PAINEL SOLAR Uma aplicação possível
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A4 (1A) FONTE CHAVEADA PAINEL SOLAR Uma aplicação possível
x d z θ i Figura 2.1: Geometria das placas paralelas (Vista Superior).
 2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
2 Lentes Metálicas Este capítulo destina-se a apresentar os princípios básicos de funcionamento e dimensionamento de lentes metálicas. Apresenta, ainda, comparações com as lentes dielétricas, cujas técnicas
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
APLICAÇÕES DA CURVA s NO GERENCIAMENTO DE PROJETOS
 CONCEITOS GERAIS : A curva S representa graficamente o resultado da acumulação das distribuições percentuais, parciais, relativas à alocação de determinado fator de produção (mão de obra, equipamentos
CONCEITOS GERAIS : A curva S representa graficamente o resultado da acumulação das distribuições percentuais, parciais, relativas à alocação de determinado fator de produção (mão de obra, equipamentos
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Capítulo 3 Modelos Estatísticos
 Capítulo 3 Modelos Estatísticos Slide 1 Resenha Variáveis Aleatórias Distribuição Binomial Distribuição de Poisson Distribuição Normal Distribuição t de Student Distribuição Qui-quadrado Resenha Slide
Capítulo 3 Modelos Estatísticos Slide 1 Resenha Variáveis Aleatórias Distribuição Binomial Distribuição de Poisson Distribuição Normal Distribuição t de Student Distribuição Qui-quadrado Resenha Slide
Capítulo II. Faltas entre fases e entre espiras Por Geraldo Rocha e Paulo Lima* Proteção de geradores
 22 Capítulo II Faltas entre fases e entre espiras Por Geraldo Rocha e Paulo Lima* A proteção do gerador deve ser analisada cuidadosamente, não apenas para faltas, mas também para as diversas condições
22 Capítulo II Faltas entre fases e entre espiras Por Geraldo Rocha e Paulo Lima* A proteção do gerador deve ser analisada cuidadosamente, não apenas para faltas, mas também para as diversas condições
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
Prova 2 - Sistemas de Controle Projetos
 Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
Singularidades de Funções de Variáveis Complexas
 Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Analisador de Espectros
 Analisador de Espectros O analisador de espectros é um instrumento utilizado para a análise de sinais alternados no domínio da freqüência. Possui certa semelhança com um osciloscópio, uma vez que o resultado
Analisador de Espectros O analisador de espectros é um instrumento utilizado para a análise de sinais alternados no domínio da freqüência. Possui certa semelhança com um osciloscópio, uma vez que o resultado
