UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA. Érick Scopel
|
|
|
- Larissa de Oliveira
- 5 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA Érick Scopel CLASSIFICAÇÃO DE SINGULARIDADES SEMI-HIPERBÓLICAS E NILPOTENTES DE CAMPOS PLANARES ANALÍTICOS Santa Maria, RS 2017
2 Érick Scopel CLASSIFCAÇÃO DE SINGULARIDADES SEMI-HIPERBÓLICAS E NILPOTENTES DE CAMPOS PLANARES ANALÍTICOS Dissertação apresentada ao Curso de Mestrado da Pós-Graduação em Matemática, Área de Matemática Pura, da Universidade Federal de Santa Maria (UFSM, RS), como requisito parcial para obtenção do título de Mestre em Matemática. Orientador: Prof o. Dr o. Maurício Fronza da Silva Santa Maria, RS 2017
3 Érick Scopel CLASSIFICAÇÃO DE SINGULARIDADES SEMI-HIPERBÓLICAS E NILPOTENTES DE CAMPOS PLANARES ANALÍTICOS Dissertação apresentada ao Curso de Mestrado da Pós-Graduação em Matemática, Área de Matemática Pura, da Universidade Federal de Santa Maria (UFSM, RS), como requisito parcial para obtenção do título de Mestre em Matemática. Aprovado em 12 de julho de 2017: Maurício Fronza da Silva, Dr. (UFSM) (Presidente/Orientador) Alexandre Tavares Baraviera, Dr. (UFRGS) (Banca 1) Alex Carlucci Rezende Dr. (UNESP) - Videoconferência (Banca 2) Santa Maria, RS 2017
4 DEDICATÓRIA A meu vô e à minha vó, meus exemplos de amor e sabedoria.
5 AGRADECIMENTOS Agradeço, primeiramente, a Deus por oportunizar mais esta chance em minha vida e por me manter integro até o final desta caminhada. Agradeço ao meu pai e à minha mãe por todo o apoio e zelo durante estas idas e vindas. Tenho certeza que sem toda a dedicação e incentivo dedicado a mim, não teria seguido esta área que hoje, faz parte do meu eu. Agradeço, em especial, ao meu amor, Karina Costantin, que me apoiou em todos os momentos e me levantou em todas as quedas que tive neste caminho. Sem seu carinho e determinação, tudo seria muito (e muito) mais difícil. Claro, não posso esquecer de agradecer pelas ajudas no português, inglês e nas ferramentas do word, algo que nunca aprenderia sozinho. Agradeço aos amigos de mestrado que me proporcionaram grandes momentos de estudo, descontração e, principalmente, pelo truco (inesquecível). Em especial, agradeço ao Lucas, colega de graduação, de pós-graduação, de trabalho, de vida... passamos por muitas e outras tantas virão, mas estaremos juntos. Agradeço ao professor Maurício Fronza pela amizade, confiança, dedicação, orientação, pelos ensinamentos e por incentivar em mim o desejo por aprender mais e mais matemática. Ainda, agradeço a todos professores do PPGMat que se mostraram grandes mestres e sempre muito preocupados com a excelência do programa. Em especial, agradeço ao professor Márcio Ferreira pelas excepcionais aulas que são uma inspiração para exercer a profissão docente. Agradeço, também, à CAPES pelo amparo financeiro.
6 RESUMO CLASSIFICAÇÃO DE SINGULARIDADES SEMI-HIPERBÓLICAS E NILPOTENTES DE CAMPOS PLANARES ANALÍTICOS AUTOR: Érick Scopel ORIENTADOR: Maurício Fronza da Silva Neste trabalho, apresentamos resultados clássicos de Teoria Qualitativa das Equações Diferenciais Ordinárias Planares empregadas na investigação do comportamento de soluções na vizinhança de um ponto singular semi-hiperbólico e nilpotente. Palavras Chave: Singularidades Semi-Hiperbólicas. Singularidades Nilpotentes. Comportamento Local. Retrato de Fase.
7 ABSTRACT CLASSIFICATION OF SEMI-HYPERBOLIC AND NILPOTENT SINGULARITIES IN ANALYTIC PLANAR VECTOR FIELDS. AUTHOR: Érick Scopel ADVISOR: Maurício Fronza da Silva In this work, we present some results of Qualitative Theory of Planar Ordinary Differential Equations employed in the investigation of the behavior of solutions in the neighborhood of semi-hyperbolic and nilpotent singularities. Keywords: Semi-Hyperbolic Singularities. Nilpotent Singularities. Local Behavior. Phase Portraits.
8 Lista de Figuras 2.1 Setores Exemplo de blow-up Regiões blow-up direcional Exemplo Possibilidades de retrato de fase no caso semi-hiperbólico Retrato de fase local - singularidade semi-hiperbólica não isolada Possibilidade de retrato de fase - observação item i) Possibilidade de retrato de fase - observação item ii) Interpretação geométrica da conjugação Caso - Nó Interpretação geométrica da conjugação Caso - Sela Possibilidades de retrato de fase no caso nilpotente Caso δ = 1, m ímpar e k 1 par Caso δ = 1, m ímpar e k 1 ímpar Caso m ímpar, δ = 1 e k 1 par Caso m ímpar, δ = 1 e k 1 ímpar Caso m par e δ = Caso m par e δ = Caso m par e δ = Possibilidades de retrato de fase do sistema (6.19) Possibilidades de retrato de fase do sistema (6.18) com n par Possibilidades de retrato de fase do sistema (6.18) com n ímpar Possibilidades de retrato de fase do sistema (6.17) com n par Possibilidades de retrato de fase do sistema (6.17) com n ímpar Caso (4n + 4)a + 1 > 0, a > 0 e n par Caso (4n + 4)a + 1 > 0, a > 0 e n ímpar Caso (4n + 4)a + 1 > 0, a < 0 e n par Caso (4n + 4)a + 1 > 0, a < 0 e n ímpar Caso (4n + 4)a + 1 = 0 e n par
9 6.19 Caso (4n + 4)a + 1 = 0 e n ímpar Caso (4n + 4)a + 1 < 0 e n par Caso (4n + 4)a + 1 < 0 e n ímpar
10 Sumário INTRODUÇÃO 11 1 RESULTADOS PRELIMINARES FÓRMULA DE TAYLOR MULTI-ÍNDICE E FÓRMULA DE TAYLOR NOTAÇÃO O, o E ORDEM DE ANULAMENTO CAMPOS VETORIAIS E FLUXOS EQUIVALÊNCIA E CONJUGAÇÃO DE CAMPOS VETORIAIS FLUXO TUBULAR ESTABILIDADE DE LIAPOUNOV ESTRUTURA LOCAL DE PONTOS SINGULARES PLANARES SETORES FORMAS NORMAIS 32 4 A TÉCNICA BLOW-UP DIRECIONAL BLOW-UP DIRECIONAL BLOW-UP QUASE-HOMOGÊNEO SINGULARIDADE SEMI-HIPERBÓLICA RESULTADOS C RESULTADOS TOPOLÓGICOS PRIMEIRO CASO - NÓ SEGUNDO CASO - SELA TERCEIRO CASO - SELA-NÓ SINGULARIDADES NILPOTENTES RESULTADOS C RESULTADOS TOPOLÓGICOS CASO m < 2n
11 6.2.2 CASO m > 2n CASO m = 2n CONCLUSÃO 112 A 114
12 INTRODUÇÃO As Equações Diferenciais Ordinárias (EDO s) são utilizadas em diversas áreas do conhecimento como Física, Biologia e Engenharias, com a função de modelar fenômenos. Durante muito tempo, a preocupação com as EDO s era obter soluções explícitas. Tal estudo começou a se tornar inviável à medida que as equações ficaram mais complexas. Através da pesquisa de Henri Poincaré ( ), matemático francês (entre outras titulações ), sobre corpos celestes, no final do século XVIII, nasce outra abordagem para analisar EDO s, intitulada Teoria Qualitativa. A Teoria Qualitativa tem por objetivo investigar propriedades e/ou o comportamento de soluções de EDO s sem, de fato, explicitá-las. Com isso, é possível ter informações de como se comportam as soluções no decorrer do tempo. Um dos problemas inerentes à essa teoria é classificar topologicamente os retratos de fase para famílias de sistemas diferenciais planares. Quando um campo tem uma singularidade hiperbólica, o Teorema de Grobman- Hartman, publicado independentemente por D. M. Grobman (1959) e P. Hartman (1960), implica que o retrato de fase local é dado pelo retrato de fase do campo linearizado. Esta dissertação tem como intuito descrever quais são os possíveis retratos de fase para campos de vetores analíticos próximos às singularidades semi-hiperbólicas e nilpotentes. A classificação de singularidades nilpotentes, exceto para o caso do problema centro-foco, foi realizada por A. F. Andreev (1958). Podemos encontrar a classificação de singularidades semi-hiperbólicas e nilpotentes em Andronov et al (1973) e também em Dumortier (1977). Mas buscando seguir uma bibliografia mais moderna, o texto principal utilizado nesse trabalho é Dumortier et al (2006). Assim, a classificação das singularidades semi-hiperbólicas é realizada através de sucessivas mudanças de coordenadas até que sejam encontradas um pequeno número de formas normais. O ingrediente principal para a classificação das singularidades nilpotentes é a técnica de blow-up. Essa dissertação está organizada em seis capítulos da seguinte forma: no Capítulo 1, apresentamos, com a notação de multi-índice, a Fórmula de Taylor com a forma que 12
13 usaremos no restante do texto além das definições e resultados elementares sobre Teoria Qualitativa de EDO s; no Capítulo 2, tratamos especificamente da estrutura do retrato de fase local de campos de vetores planares; no Capítulo 3, trazemos o Teorema das Formas Normais que afirma que, sob determinadas condições, é possível eliminar termos não lineares de um sistema planar, por sucessivas mudanças de coordenadas; no Capítulo 4, tratamos da Técnica Blow-Up, uma mudança de coordenadas, que será amplamente utilizada no decorrer do texto; e nos Capítulos 5 e 6, vamos demonstrar os teoremas que caracterizam localmente o retrato de fase de um campo vetorial próximo a uma singularidade semi-hiperbólica e nilpotente, respectivamente. 13
14 Capítulo 1 RESULTADOS PRELIMINARES Este capítulo introduz os conceitos fundamentais sobre Equações Diferenciais Ordinárias. Por se tratar de uma teoria preliminar para este trabalho, os resultados seguintes são somente enunciados. Baseamos tal capítulo nos livros de Domurtier et al (2006), Sotomayor (1979), Perko (2000) e Lima (2015), onde se encontram as demonstrações. Antes de passar ao estudo das singularidades semi-hiperbólicas e nilpotentes, fixaremos a notação usada no decorrer do texto. Em particular, vamos introduzir a notação de multi-índice e de O e o, além de expressar de forma conveniente a Fórmula de Taylor. 1.1 FÓRMULA DE TAYLOR Neste texto, Ω denota um subconjunto aberto do R R n e um subconjunto aberto de R n. Um ponto de R R n será denotado por (t, x), onde t R e x = (x 1, x 2,, x n ) R n e x denota uma norma de R n. Utilizaremos M n n para representar o espaço das matrizes n n com entradas reais. Dados k, m, n = 1, 2,..., e um aberto de R n, o espaço vetorial das aplicações X : R m que têm todas as derivadas parciais de ordem menor ou igual a k contínuas será denotado por C k (, R m ). Definimos C (, R m ) como o espaço vetorial de todas as aplicações X tais que X C k (, R m ), k {1, 2,...}. Denotamos por C ω (, R m ) o espaço vetorial de todos as aplicações analíticas X : R m. Salvo menção contrária, neste texto k denota um inteiro positivo, + ou ω. Os elementos de C k (, R m ) são chamados de aplicações de classe C k. Quando m = n escrevemos simplesmente C k ( ) para denotar C k (, R n ). Denotamos por Df(x) a matriz jacobiana de f avaliada no ponto x. 14
15 1.1.1 MULTI-ÍNDICE E FÓRMULA DE TAYLOR A notação multi-índice tem por finalidade simplificar a notação de derivadas de ordens altas para funções de várias variáveis. Definição Um n-multi-índice θ é uma n-upla de inteiros não-negativos. O comprimento de θ = (θ 1, θ 2,, θ n ), denotado por θ, é definido por θ = θ 1 + θ θ n. Sendo assim, dado θ = (θ 1, θ 2,, θ n ) e f R θ (, R m ), para cada j = 1, 2, 3,, n, denotaremos θ θ f f =. x θ 1 1 x θ 2 2 x θn n Em palavras, o número θ diz a ordem de derivação de f e cada coordenada θ j explicita o número de derivadas na direção de x j. Se θ = (θ 1, θ 2,, θ n ) e µ = (µ 1, µ 2,, µ n ) são n-multi-índices, então escrevemos θ µ quando θ i µ i, i = 1, 2,. Quando for conveniente diremos apenas multi-índice no lugar de n-multi-índice. Em alguns momentos do texto, estaremos interessados em saber o que acontece com uma certa derivada de um produto de funções. Para tal, vamos fazer uso da Regra de Leibniz com a notação de multi-índice. Dados os multi-índices θ e µ usamos a notação ( ) ( ) ( ) ( ) θ θ1 θ2 θn =. µ µ 1 Teorema (Regra de Leibniz) Sejam θ, µ N n multi-índices. Se f, g C θ (, R p ), p = 1, 2,, então: θ (fg)(x) = µ θ ( θ µ ) µ 2 µ n µ f(x) θ µ g(x), x. Utilizaremos a Fórmula de Taylor com resto integral com o objetivo de obter informações sobre a suavidade e anulamento do resto. Teorema (Fórmula de Taylor com resto integral) Consideremos um aberto de R n, x 0 e f C (, R p ), p = 1, 2,. Para todo x e m = 1, 2,... vale f(x) = θ m θ f(x 0 ) (x x 0 ) θ + r(x), θ! sendo r(x) = (m + 1)! θ =m+1 (x x 0 ) θ θ! 1 0 (1 t) θ θ f(x 0 + t(x x 0 ))dt. 15
16 Quando não for necessário explicitar o resto, vamos utilizar a Fórmula de Taylor como segue abaixo: Corolário Consideremos um aberto de R n, x 0 p = 1, 2 (resp. C ω (, R p )). Para todo x e m = 1, 2,... vale sendo f(x) = θ m r(x) = (m + 1)! e cada f θ é de classe C (resp. C ω ). θ f(x 0 ) (x x 0 ) θ + r(x), θ! θ =m+1 (x x 0 ) θ f θ (x), θ! e f C (, R p ), com Se f C (, R p ), x 0 e p = 1, 2, ou p =, então o símbolo j p f(x 0 ) = 0 significa que θ f(x 0 ) = 0, para todo multi-índice tal que θ p. A expressão f é flat em x 0 é usada quando j f(x 0 ) = NOTAÇÃO O, o E ORDEM DE ANULAMENTO segue: Para simplificar a escrita durante o texto, vamos utilizar as notações de O e o, como Definição Sejam R n aberto contendo o ponto 0 e f, g : R n com g(x) 0, x. Escrevemos se existirem constantes C e δ > 0 tais que f(x) = O(g(x)) 0 < x < δ f(x) g(x) C, e quando f(x) = o(g(x)) f(x) lim x 0 g(x) = 0. Observação Vejamos algumas propriedades de O que decorrem diretamente da definição: 1. Se f 1 (x) = O(g(x)) e f 2 (x) = O(g(x)), então f 1 (x) + f 2 (x) = O(g(x)); 16
17 2. Se f 1 (x) = O(g 1 (x)) e f 2 (x) = O(g 2 (x)), então f 1 (x).f 2 (x) = O(g 1 (x).g 2 (x)); 3. Se f(x) = O( x m ) e 0 n m, então f(x) x n = O( x m n ); 4. Se f(x) = O( x m ), então x n f(x) = O( x m+n ); 5. Se f(x) = O( x m ), então f(x) = O( x n ), para n m; Analogamente, valem propriedades semelhantes para o. Ainda, vale que se f(x) = o( x n ), então f(x) = O( x n ). A fim de simplificar a escrita, vamos usar a definição de ordem de anulamento para dizer quantas derivadas de uma certa função se anulam em um determinado ponto, como segue: Definição Seja f C (, R p ) com p = 1, 2,. Dizemos que f tem ordem de anulamento m em x 0, se temos que θ f(x 0 ) = 0 para todo multi-índice θ tal que θ m 1 mas θ f(x 0 ) 0 para algum θ = m. Assim, um campo de vetores planar X tem ordem de anulamento maior ou igual a dois na origem quando X(0) = 0 e DX(0) = 0. As relações entre O, o e ordem de anulamento são dadas nas observações abaixo, cujas demonstrações seguem da Fórmula de Taylor. Observação Sejam f : R n com 0, f de classe C e j = 1, 2,. Valem então: 1. f(x) = O( x j ) se, e somente se, f se anula de ordem menor ou igual a j em f(x) = o( x j ) se, e somente se, f se anula de ordem menor ou igual a j + 1 em 0. ou É possível verificar então que podemos reescrever a Fórmula de Taylor da forma f(x) = θ f(x 0 ) (x x 0 ) θ + O( x x 0 m+1 ), θ! θ m f(x) = θ m θ f(x 0 ) (x x 0 ) θ + o( x x 0 m ). θ! 1.2 CAMPOS VETORIAIS E FLUXOS da forma A partir de agora, trabalhamos com o estudo de um sistema de equações diferenciais x 1 = X 1 (x 1, x 2,, x n ), x 2 = X 2 (x 1, x 2,, x n ),.. x n = X n (x 1, x 2,, x n ), 17 (1.1)
18 onde cada X i : R é uma aplicação de classe C k, i = 1, 2,..., n. O símbolo ẋ i denota derivação com respeito à variável t. Como as funções X i, i = 1, 2, 3,, n de (1.1) podem ser não lineares, geralmente não é possível encontrar explicitamente suas soluções. A Teoria Qualitativa de EDO s utiliza ferramentas de Álgebra Linear, Análise e Topologia com o intuito de obter informações sobre as soluções de (1.1), mesmo sem conhecê-las explicitamente. Definição Dado um aberto de R n, chamamos de campo de vetores de classe C k a um elemento de C k ( ). Ao campo de vetores X associamos o sistema de equações diferenciais ẋ = X(x). (1.2) Reciprocamente, a todo sistema da forma (1.2), onde X : R n é uma aplicação de classe C k, associamos o campo de vetores X de classe C k. Nas definições a seguir desta seção, salvo menção em contrário, tomamos X como o campo de vetores definido acima. Definição Um ponto x é dito singularidade, ponto de equilíbro, ponto singular ou ponto crítico de X se X(x) = 0. Caso contrário x é ponto regular de X. Definição Um ponto singular p do campo X é dito uma singularidade isolada se existe um aberto V p R n contendo p tal que X(x) 0 para todo x V p \ {p}. Definição Seja I um intervalo da reta. Uma função ϕ : I de classe C k tal que dϕ (t) = X(ϕ(t)), dt para todo t I, é chamada solução, trajetória ou curva integral de X ou da equação diferencial (1.2). O conjunto imagem de uma trajetória chama-se uma órbita de X. Definição Sejam I e J intervalos da reta. Uma curva integral ϕ : I chamase curva integral máxima se para toda curva integral ψ : J tal que I J e ϕ = ψ/i então I = J e, consequentemente, ϕ = ψ. Neste caso, I chama-se intervalo máximo. Definição Uma equação diferencial do tipo (1.2) é chamada de autônoma, pois X independe de t. Teorema Seja X um campo de vetores de classe C k, k 1, definido num aberto de R n. 18
19 i) (Existência e Unicidade de soluções máximas) Para cada x existe um intervalo aberto I x onde está definida a única solução máxima ϕ x : I x, que satisfaz dy dt = X(y), y(0) = x. ii) (Propriedade de grupo) Se y = ϕ(t, x) e t I x, então I y = I x t = {r t; r I x } e ϕ(s, y) = ϕ(t + s, x) para todo s I y. iii) (Diferenciabilidade em relação às condições iniciais) O conjunto D = {(t, x); x, t I x } é aberto em R n+1 e a aplicação ϕ : D R n dada por ϕ(t, x) é de classe C k. Mais ainda, ϕ satisfaz à equação para todo (t, x) D. D 1 D 2 ϕ(t, x) = DX(ϕ(t, x)) D 2 ϕ(t, x), Aqui o símbolo D 2 ϕ(t, x) representa a matriz n n cujas colunas coincidem com as n últimas colunas de Dϕ(t, x). Já o símbolo D 1 D 2 ϕ(t, x) denota a derivação das entradas de D 2 ϕ(t, x) com relação à variável t. Teorema Se ϕ é uma curva integral máxima de (1.2) em I, verifica-se uma única das seguintes alternativas: i) ϕ é uma bijeção; ii) I = R e ϕ é constante; iii) I = R e ϕ é periódica, isto é, existe τ > 0 tal que ϕ(t + τ) = ϕ(t), t R. Definição O conjunto aberto, munido da decomposição em órbitas do campo de vetores X, chama-se retrato de fase de X. As órbitas são orientadas no sentido das curvas integrais do campo X; os pontos singulares são munidos da orientação trivial. Teorema Sejam contendo um ponto x 0, X de classe C 1 e (α, β) o intervalo máximo da solução x(t) para o problema de valor inicial ẋ = X(x), x(0) = x 0. Assuma que β <. Então dado um compacto K, existe t (α, β) tal que x(t) não pertence a K. 19
20 Definição Sejam e X : R n um campo vetorial de classe C k. Seja ϕ(t, p) a curva integral de X passando pelo ponto p, definida no seu intervalo máximo I p = (ω (p), ω + (p)). Se ω + (p) =, define-se o conjunto ω(p) = {q ; (t n ) com t n e ϕ(t n, p) q, quando n }. Analogamente, se ω (p) =, define-se o conjunto α(p) = {q ; (t n ) com t n e ϕ(t n, p) q, quando n }. Os conjuntos ω(p) e α(p) são chamados, respectivamente, de conjunto ω-limite e conjunto α-limite de p. Observação Sejam ϕ(t, p) a curva integral do campo X pelo ponto p e ψ(t, p) a curva integral do campo X pelo ponto p, então ϕ( t, p) = ψ(t, p). Segue daí que o ω-limite de ψ(t, p) é igual ao α-limite de ϕ(t, p) e, reciprocamente, o ω-limite de ϕ(t, p) é igual ao α-limite de ψ(t, p). Segue da Observação que é suficiente nos restringirmos ao estudo do conjunto ω-limite para estudarmos as propriedades gerais dos conjuntos α-limite e ω-limite. Teorema Sejam X : R n um campo vetorial de classe C k e γ + (p) = {ϕ(t, p); t 0} (resp. γ (p) = {ϕ(t, p); t 0}) a semi-órbita positiva (resp. a semiórbita negativa) do campo X pelo ponto p. Se γ + (p) (resp. γ (p)) está contida num subconjunto compacto K, então: i) ω(p) (resp. α(p)); ii) ω(p) é compacto (resp. α(p)); iii) ω(p) é invariante por X (resp. α(p)), isto é, se q ω(p), então a curva integral de X por q está contido em ω(p); iv) ω(p) é conexo (resp. α(p)). Teorema (Poincaré-Bendixson) Sejam Υ um subconjunto aberto de R 2 e X : Υ R 2 um campo vetorial de classe C k. Seja ϕ(t, p) uma curva integral de X definida para todo t 0 tal que γ + (p) = {ϕ(t, p); t 0} esteja contida num compacto K Υ. Suponha que o campo X possua um número finito de singularidades em ω(p). Têm-se as seguintes alternativas: i) Se ω(p) contém somente pontos regulares, então ω(p) é uma órbita periódica; ii) Se ω(p) contém pontos regulares e singulares, então ω(p) consiste de um conjunto de órbitas, cada uma das quais tende a um desses pontos singulares quando t ± ; iii) Se ω(p) não contém pontos regulares, então ω(p) é um ponto singular. 20
21 1.3 EQUIVALÊNCIA E CONJUGAÇÃO DE CAM- POS VETORIAIS Nesta seção, X : 1 R n R n, Y : 2 R n R n são campos de vetores de classe C k definidos nos abertos 1, 2 de R n e ϕ 1, ϕ 2 são seus respectivos fluxos. Definição Diz-se que X é topologicamente equivalente (resp. C k -equivalente) a Y quando existe um homeomorfismo (resp. difeomorfismo de classe C k ) h : 1 2 que leva cada órbita de X em uma órbita de Y preservando a orientação. A aplicação h chama-se equivalência topológica (resp. C k -equivalência) entre X e Y. Mais precisamente, sejam p 1 e γ 1 (p) a órbita orientada de X passando por p. Então h(γ 1 (p)) é a órbita orientada γ 2 (h(p)) de Y passando por h(p). Observe que esta definição estabelece uma relação de equivalência entre campos definidos em abertos de R n. Definição Diz-se que X é topologicamente conjugado (resp. C k -conjugado ou linearmente conjugado) a Y quando existe um homeomorfismo (resp. difeomorfismo de classe C k ou transformação linear) h : 1 2 tal que h(ϕ 1 (t, x)) = ϕ 2 (t, h(x)) para todo (t, x) D 1. Neste caso tem-se I 1 (x) = I 2 (h(x)). O homemorfismo h chama-se conjugação topológica (resp. C k -conjugação ou conjugação linear) entre X e Y. Observação Dizer que X é suavemente conjugado a Y significa dizer que X é C -conjugado a Y. Note que conjugação topológica (resp. C k ) implica em equivalência topológica (resp. C k ), mas não vale a recíproca. Além disso, conjugação linear implica em C k - conjugação e C k -conjugação implica em conjugação topológica, mas não valem as recíprocas. Observação Se X e Y são topologicamente equivalentes com a equivalência h : 1 2, então h leva ponto singular em ponto singular e órbita periódica em órbita periódica. Além disso, se h for uma conjugação topológica entre X e Y então o período das órbitas também é preservado. Proposição Sejam X : 1 R n e Y : 2 R n campos de vetores de classe C k e h : 1 2 um difeomorfismo de classe C k. Então h é uma C k -conjugação entre X e Y se, e somente se, Dh(p)X(p) = Y (h(p)), p 1. Vamos, agora, tratar de conjugação topológica entre campos lineares específicos. 21
22 Definição O campo de vetores linear dado pelo sistema ẋ = Ax, onde A M n n, é dito hiperbólico se todos os valores próprios de A têm parte real diferente de zero. O número s = s(a) de valores próprios, contando suas multiplicidades, que têm parte real negativa, chama-se índice de estabilidade. Para o caso que estamos lidando com campos lineares hiperbólicos, o índice de estabilidade caracteriza a conjugação topológica. Teorema Dois campos de vetores lineares hiperbólicos são topologicamente conjugados se, e somente se, ambos têm o mesmo índice de estabilidade. 1.4 FLUXO TUBULAR Esta seção trata de mostrar que, numa vizinhança de um ponto regular, todo campo de vetores é diferenciavelmente conjugado ao campo constante. Tal resultado é dado pelo Teorema do Fluxo Tubular. Definição Sejam X : R n um campo de vetores de classe C k e A R n 1 um aberto. Uma aplicação diferenciável f : A de classe C k chama-se seção transversal local de X (de classe C k ) quando, para todo a A, Df(a) e X(f(a)) geram o espaço R n. Seja Σ = f(a). Se f : A Σ é um homeomorfismo então dizemos que Σ é uma seção transversal de X. Quando 0 A e escrevemos p = f(0) dizemos ainda que Σ é uma seção transversal de X em p. Observação Sejam p um ponto regular de X e {v 1, v 2,, v n 1, X(p)} uma base de R n. Seja g : R n 1 R n dada por n 1 g(x 1,, x n 1 ) = p + x i v i. Como é aberto existe δ 1 > 0 tal que B δ1 (p). Mas g é contínua e g(0) = p, logo existe δ > 0 tal que g(b δ (0)) B δ1 (p). Fazemos f = g Bδ (0) e obtemos f : B δ (0). Ainda, f é de classe C ω e, como Df(0) e X(f(0)) são linearmente independentes, f é uma seção transversal local de X satisfazendo f(0) = p. Temos ainda que Σ é uma seção transversal de X em p. Teorema (Fluxo Tubular) Seja p um ponto regular de X : R n de classe C k e f : A Σ uma seção transversal local de X de classe C k com f(0) = p. Então existe uma vizinhança V de p em e um difeomorfismo h : V ( ɛ, ɛ) B de classe C k, onde ɛ > 0 e B é uma bola aberta em R n 1 de centro na origem 0 = f 1 (p) tal que: 22 i=1
23 i) h(σ V ) = {0} B; ii) h é uma C r -conjugação entre X V e o campo constante Y : ( ɛ, ɛ) B R n, Y = (1, 0, 0,, 0) R n. 1.5 ESTABILIDADE DE LIAPOUNOV Nesta seção, trataremos do Critério de Liapounov para estabilidade de um ponto singular de um sistema autônomo. Mais geralmente, consideremos o campo dado pelo sistema ẋ = f(t, x), (1.3) onde f : Ω R n é contínua. Definição Um ponto singular p de um campo dado por (1.3) é dito estável quando para toda vizinhança U de p, existe uma vizinhança U 1 de p tal que toda solução ϕ de (1.3) com ϕ(0) U 1, está definida em U para todo t 0. Se além disso lim t ϕ(t) = p, então p é dito assintoticamente estável. Consideremos, um campo f dado pelo sistema autônomo ẋ = f(x), (1.4) onde f : R n de classe C 1. Seja V : R uma função diferenciável. Se ϕ é solução de (1.4) definida no intervalo I, então d dt (V (ϕ(t))) = V (ϕ(t)) ϕ (t) = V (ϕ(t)) f(ϕ(t)), t I, onde denota o produto escalar de R n. Denotando por x = ϕ(0) temos Ponhamos, para cada x, d dt V (ϕ(t)) t=0 = V (x) f(x). V = V (x) f(x). Definição Seja p um ponto singular de (1.4). Uma função de Liapounov para p é uma função V : U R diferenciável definida em um aberto U contendo p, satisfazendo as seguintes condições: i) V (p) = 0 e V (x) > 0; x p; 23
24 ii) V 0 em U. A função de Liapounov V diz-se estrita quando iii) V < 0 em U {p}. O critério de Liapounov para o sistema (1.4) é dado pelo teorema seguinte: Teorema Seja p um ponto singular de (1.4). Se existe uma função de Liapounov para p, então p é estável. Se a função for estrita, p é assintoticamente estável. 24
25 Capítulo 2 ESTRUTURA LOCAL DE PONTOS SINGULARES PLANARES Seja q um ponto regular de um campo de vetores planar X de classe C k. Pelo Teorema do Fluxo Tubular, existe C k -difeomorfismo que conjuga a restrição de X a uma vizinhança de q ao campo constante (1, 0). Portanto, não há nada a investigar quanto ao retrato de fase numa vizinhança de pontos regulares. Passamos, assim, a investigar a estrutura local de pontos singulares planares. Tal capítulo é baseado em Dumortier et al (2006). Seja p = (x 0, y 0 ) um ponto singular do campo planar X = (P (x, y), Q(x, y)) de classe C k onde P (x, y) e Q(x, y) são funções de classe C k em R 2. Definição O ponto singular p é dito não degenerado se zero não é um autovalor de DX(p), hiperbólico se os dois autovalores de DX(p) têm parte real não nula, semi-hiperbólico se exatamente um autovalor de DX(p) é igual a zero, elementar se for hiperbólico ou semi-hiperbólico, nilpotente se ambos autovalores de DX(p) são nulos mas DX(p) 0, linearmente nulo se DX(p) = 0, centro se existe uma vizinhança aberta de p constituida de órbitas periódicas, centro linear se os autovalores de DX(p) são imaginários puros. 25
26 Definição Seja p um ponto singular de X. Definimos o determinante, o traço e o discriminante de p como det(p) = det DX(p), e tr(p) = trdx(p) = P Q (p) + x y (p), (p) = tr(p) 2 4 det(p), respectivamente. A partir destas definições, observamos que: i) se det(p) 0, então o ponto singular é não-degenerado e este é ou hiperbólico ou um centro linear; ii) se det(p) = 0 mas tr(p) 0, então o ponto singular é semi-hiperbólico; iii) se det(p) = 0 e tr(p) = 0, então o ponto singular é ou linearmente zero ou nilpotente, dependendo se DX(p) é a matriz nula ou não, respectivamente. Ainda, pode-se observar que um ponto singular p pode ser transladado para a origem por meio de uma mudança de coordenadas. Com efeito, se p = (x 0, y 0 ) é um ponto singular do campo X dado pelo sistema ẋ = P (x, y), ẏ = Q(x, y), então o ponto (0, 0) é um ponto singular do sistema x = P ( x, ȳ), ȳ = Q( x, ȳ), (2.1) onde x = x + x 0 e y = ȳ + y 0. Essa translação da singularidade para origem simplificará a escrita do texto daqui para frente. Com isso, utilizando a Fórmula de Taylor, sempre podemos considerar que o sistema (2.1) seja da forma x = a x + bȳ + F ( x, ȳ), (2.2) ȳ = c x + dȳ + G( x, ȳ), onde F (0, 0) = 0, G(0, 0) = 0, DF (0, 0) = 0 e DG(0, 0) = 0. Ainda, a Forma Canônica de Jordan da matriz DX(p) é uma das seguintes: 26
27 se a singularidade é hiperbólica, então a matriz é da forma ( ) ( ) ( λ1 0 λ1 1 α β ou ou 0 λ 2 0 λ 1 β α ), onde λ 1, λ 2 0, α 0 e β > 0, se a singularidade é semi-hiperbólica ou um centro linear, então temos ( ) ( ) λ 0 0 β ou, 0 0 β 0 respectivamente, onde λ 0 e β > 0, se a singularidade é nilpotente ou linearmente nula, então temos ( ) ( ) ou, respectivamente. A seguir, usamos uma mudança linear de coordenadas dada pela forma de Jordan para simplificar a matriz jacobiana de um sistema dado. Proposição Sejam v = ( x, ȳ), v = (x, y), H( v) = (F ( x, ȳ), G( x, ȳ)), A, P M 2 2 com P inversível. Então a mudança de coordenadas v = P 1 v (2.3) conjuga linearmente o sistema (2.2) com o sistema v = Jv + H(v), onde J = P 1 AP, H(0) = 0 e D H(0) = 0. Prova: Note, primeiramente, que o sistema (2.2) é da forma v = A v + H( v), onde H( v) = 0 e DH( v) = 0. Da mudança de coordenadas (2.3), segue que v = P 1 v = P 1 (A v + H( v)) = P 1 (A(P v) + H(P v)) = P 1 A(P v) + P 1 H(P v) = (P 1 AP )v + P 1 H(P v) = Jv + P 1 H(P v), 27
28 isto é, v = Jv + H(v), (2.4) onde H(v) = P 1 H(P v). Concluímos a proposição observando que H(0) = P 1 H(0) = 0 e D H(0) = P 1 DH(0) = 0. Da Proposição 2.0.3, vemos que um campo de vetores planar de classe C k com um ponto singular semi-hiperbólico na origem é linearmente conjugado ao campo definido pelo sistema ẋ = λx + F (x, y), ẏ = G(x, y), onde F (0, 0) = 0, G(0, 0) = 0, DF (0, 0) = 0, DG(0, 0) = 0 e λ 0. Analogamente, um campo de vetores planar de classe C k com a origem como singularidade nilpotente é linearmente conjugado ao campo definido pelo sistema ẋ = y + F (x, y), ẏ = G(x, y), onde F (0, 0) = 0, G(0, 0) = 0, DF (0, 0) = 0 e DG(0, 0) = 0. Os dois próximos resultados serão amplamente utilizados na sequência do texto. O lema abaixo afirma que ao multiplicar um campo de vetores planar por uma função não nula em um aberto de R 2, as órbitas permanecem as mesmas mudando a escala de tempo e, aonde a função é negativa, a orientação. Lema Sejam f, g, u C k (, R 2 ) com u(x, y) 0,. Nestas condições, o campo definido por ẋ = f(x, y)u(x, y), (2.5) ẏ = g(x, y)u(x, y), é C k -equivalente ao campo dado por ẋ = f(x, y), ẏ = g(x, y). (2.6) Prova: Para cada (x 0, y 0 ), tome a solução (x(t), y(t)) de (2.5), tal que x(0) = x 0 e y(0) = y 0. Definimos τ tal que dτ dt = u(x(t), y(t)), 28
29 para t I(x 0, y 0 ). Pelo Teorema da Função Inversa, podemos escrever t em função de τ e, logo, o que implica que µ(τ) = x(t(τ)), dµ dτ = dx dt dt dτ = dx dt 1 dτ dt 1 = f(x, y)u(x, y) u(x, y) = f(x, y), para τ J, onde J é a imagem do intervalo I(x 0, y 0 ) por τ. Ainda, escrevemos o que implica que ϑ(τ) = y(t(τ)), dϑ dτ = dϑ dt dt dτ = dy dt 1 dτ dt = g(x, y), para τ J. Conclui-se, assim, que as soluções de (2.6) são obtidas a partir das soluções de (2.5) por uma mudança de escala de tempo. Logo, as órbitas dos sitemas (2.5) são iguais as do sistemas (2.6). Então, tomando h : dado por h(x, y) = (x, y), segue a conclusão do lema. 2.1 SETORES Os pontos singulares separam o retrato de fase de um campo de vetores em setores. Em especial, veremos os setores elípticos, onde todos os caminhos começam e terminam no ponto crítico; setores parabólicos, onde apenas um extremo do caminho está no ponto crítico e setores hiperbólicos, onde nenhum dos caminhos alcança o ponto crítico. Definição Seja p um ponto singular. é uma órbita tendendo a p para tempo positivo (resp. inclinação bem definida, isto é, γ(t) p para t (resp. (γ(t) p) lim (resp. t γ(t) p lim (γ(t) p) ) existe. t γ(t) p Uma órbita característica γ(t) em p para tempo negativo) com um t ) e o limite 29
30 Definição Seja ρ : S 1 R 2 e 2πit ρ(e 2πit ) com ρ de classe C 1, ρ 0 em todo ponto e ρ injetiva. Chamamos ρ de parametrização permissível do círculo. Seja X um campo de vetores de classe C 1 definido numa vizinhança compacta V de p, da qual V é a imagem de uma parametrização permissível do cículo ρ : S 1 V de classe C 2, e suponha que X(p) = 0 e X(q) 0 para todo q V \ {p}. i) Dizemos que X V é um centro se V é uma órbita periódica e todas as órbitas em V \ {p} são periódicas; ii) Dizemos que X V é um nó ou foco atrator se em todos os pontos de V o campo de vetores aponta para dentro e para todos q \V \{p}, ω(q) = {p} e γ (q) V ; iii) Dizemos que X V é um nó ou foco repulsor se em todos os pontos de V o campo de vetores aponta para fora e para todos q \ V \ {p}, α(q) = {p} e γ + (q) V ; iv) Diremos que X V tem uma decomposição setorial finita não trivial se não estamos nos casos (i), (ii) ou (iii) e se existe um número finito de órbitas características c 0, c 1,, c n 1, cada uma cortanto V transversalmente em um ponto p i, no sentido de que V é uma seção transversal próximo a p i, e com a propriedade que entre c i e c i+1 (com c n = c 0 e ordenada de tal modo que p 0,, p n 1 siga a ordem cíclica de ρ), temos um dos seguintes casos com respeito ao setor S i, definido como a região compacta limitada por {p}, c i, c i+1 e o segmento de V limitada por p i e p i+1 : 1. Setor parabólico atrator: em todos os pontos de [p i, p i+1 ] V o campo de vetores aponta para dentro, e para todo q S i \ {p}, ω(q) = {p} e γ (q) V ; 2. Setor parabólico repulsor: em todos os pontos de [p i, p i+1 ] V o campo de vetores aponta para fora, e para todo q S i \ {p}, α(q) = {p} e γ + (q) V ; 3. Setor hiperbólico: existe um ponto q i [p i, p i+1 ) V com a propriedade de que em todos os pontos de [p i, q i ) (resp. (q i, p i+1 )) o campo de vetores aponta para fora (resp. para dentro); no ponto q i o campo de vetores é tangente a V e a tangência é externa no sentido de que a x-órbita de q i permanece fora de V ; e para todo q S i \ c i c i+1 q i temos que γ + (q) V e γ (q) V ; 4. Setor elíptico: existe um ponto q i (p i, p i+1 ) V com a propriedade de que γ(q i ) V com ω(q i ) = α(q i ) = {p}; em todos os pontos q [p i, q i ) o campo de 30
31 vetores aponta para dentro, γ + (q) V e ω(q) = {p}. Denotamos por S [pi,q i ] = q [pi,q i ]γ + (q); em todos os pontos q (q i, p i+1 ] o campo de vetores aponta para fora, γ (q) V e α(q) = {p}. Denotamos por S [qi,p i+1 ] = q [qi,p i+1 ]γ (q); em todos os pontos q S \ (S [qi,p i+1 ] S [pi,q i ] {p}) temos que γ(q) V com ω(q) = α(q) = p. O mesmo ocorre para [q i, p i+1 ] ao invés de [p i, q i ]. A Figura 2.1 retrata os setores. Figura 2.1: (a) Setor hiperbólico (b) Setor elíptico (c) Setor parabólico atrator (d) Setor parabólico repulsor (a) (b) (c) (d) Definição Uma órbita γ(p) é dita separatriz se é homeomorfa à R e para a qual não existe uma vizinhança V de γ(p) tal que: i) para todo q V, α(q) = α(p) e ω(q) = ω(p); ii) a fronteira V de V é formada por α(p), ω(p) e duas órbitas γ(q 1 ) e γ(q 2 ) tais que α(p) = α(q 1 ) = α(q 2 ) e ω(p) = ω(q 1 ) = ω(q 2 ). Neste texto, as separatrizes são denotadas por linhas com espessura mais grossa, enquanto que linhas de singularidades são representadas por linhas potilhadas. 31
32 Capítulo 3 FORMAS NORMAIS Neste capítulo, abordaremos um teorema de Formas Normais de campo de vetores. Tal teorema afirma que, por sucessivas mudanças de coordenadas que dependem apenas da matriz jacobiana do campo, é possível eliminar determinados termos não-lineares de um campo de vetores X. Tal capítulo é baseado nos livros de Guckenheimer (1983) e de Dummortier et al (2006). Agora, seja X(x) = Ax + f(x) um campo de vetores em R n com a origem como singularidade, sendo A = DX(0) e f uma função C tal que f(0) = 0 e Df(0) = 0. A ideia da teoria das formas normais é determinar uma classe restrita de funções F n tais que, após uma mudança de coordenadas, o campo X mantenha sua parte linear e seja o mais simples possível podendo, assim, ser escrito da forma X(x) = Ax + f(x), x R n, com f F n. Desse modo, o espaço F n contém os termos que não podem ser eliminados pela mudança de variáveis estudada neste capítulo que se caracteriza por depender somente da parte linear do campo X. Para enunciar o resultado que determina tal mudança de coordenadas, começamos denotando por H q (R n ) o conjunto dos campos vetoriais polinomiais homogêneos em R n com grau q. Para cada q N definimos a aplicação ad q A : H q (R n ) H q (R n ) X [A, X], onde o campo [A, X] é definido por [A, X](x) = A X(x) DX Ax, x R n. Seja B q = ad q A(H q (R n )) e seja G q um complemento de B q, isto é, um subespaço vetorial tal que H q = B q G q. A demonstração do Teorema 2.1 de Dumortier et al (2006) prova o seguinte resultado: 32
33 Teorema Seja X : R n um campo de vetores de classe C definido no aberto R n com 0. Suponha que X pode ser escrito da forma s 1 X(x) = Ax + g r (x) + O( x s ), r=2 onde A M n n, s = 3,, g r G r, com r = 2, 3,, s 1. Então existe um polinômio homogêneo P s : R n R n de grau s, tal que a aplicação h s : R n R n dada por h s (y) = y + P s (y), é uma C ω conjugação entre X e um campo da forma s X(y) = Ay + g r (y) + o( y s ), com g s G s. Além disso sempre podemos escolher G r = Ker(ad r A T ), r = 1, 2,...s. r=2 Observação Observe que a mudança de coordenadas h s altera os termos de ordem menores ou iguais a s 1. do Teorema não No próximo exemplo aplicamos o Teorema (3.0.1) a um campo com uma singularidade semi-hiperbólica. Exemplo Considere o sistema ẋ = xg(x, y), ẏ = λy + F (x, y), (3.1) onde λ 0, F e G são funções reais de classe C em uma vizinhança da origem de R 2, com F (0, 0) = G(0, 0) = 0 e DF (0, 0) = 0. Nesse caso, [ ] 0 0 A T =. 0 λ Para descobrirmos os termos que não são removíveis pelas conjugações dadas no Teorema 3.0.1, vamos calcular Ker(ad q A T ) para cada q N. A fim de ilustrar o procedimento, vamos considerar q = 2. De modo a conhecer quais polinômios de H 2 (R n ) estão em Ker(ad 2 A T ), tomemos a base de H 2 (R n ) dada por β = {x 2 x, xy x, y2 x, x2 y, xy y, y2 y }. 33
34 Assim, calculamos: [ λy y, ] x2 = x ( λ ) ( x 2 0 ) ( 2x ) ( 0 λy ) ( 0 = 0 ) ; [ λy y, xy ] ( 0 0 = x 0 λ ) ( xy 0 ) ( y x 0 0 ) ( 0 λy ) ( λxy = 0 ) ; [ λy y, ] ( 0 0 y2 = x 0 λ ) ( y 2 0 ) ( 0 2y 0 0 ) ( 0 λy ) ( 2λy 2 = 0 ) ; [ λy y, ] ( 0 0 x2 = y 0 λ ) ( 0 x 2 ) ( 0 0 2x 0 ) ( 0 λy ) ( 0 = λx 2 ) ; [ λy y, xy ] ( 0 0 = y 0 λ ) ( 0 xy ) ( 0 0 y x ) ( 0 λy ) ( 0 = 0 ) ; [ λy y, ] ( 0 0 y2 = y 0 λ ) ( 0 y 2 ) ( y ) ( 0 λy ) ( 0 = λy 2 ). Disso, é possível mostrar que Ker(ad 2 A T ) é gerado pelos polinômios x 2 x e xy y. Logo, pelo Teorema 3.0.1, existe uma mudança de coordenadas tal que o campo dado pelo sistema (3.1) é C ω -conjugado ao campo dado por ẋ = a 2 x 2 + Ā(x, y), ẏ = λy + b 2 xy + B(x, y), com Ā(x, y) = o( (x, y) 2 ) e B(x, y) = o( (x, y) 2 ). De uma maneira geral, para q N qualquer, uma base de H q (R n ) é o conjunto β = {x q 1 y q 2 x ; q 1 + q 2 = q} {x q 1 y q 2 y ; q 1 + q 2 = q}. (3.2) Daí, para cada (q 1, q 2 ) N 2 tais que q 1 + q 2 = q, temos: [ λy y, xq 1 y q ] ( ) ( ) ( x q 1 y q 2 q1 x q 1 1 q 2 x q 1 y q 2 1 = x 0 λ ( ) λq2 x q 1 y q 2 = 0 34 ) ( 0 λy )
35 e [ λy y, xq 1 y q 2 ] ( ) ( ) ( = y 0 λ x q 1 y q 2 ( ) 0 =. λx q 1 y q 2 λq 2 x q 1 y q q 1 x q 1 1 y q 2 q 2 x q 1 y q 2 1 ) ( 0 y ) Note que a igualdade q 2 x q 1 y q 2 = 0 se verifica quando q 2 = 0 e, logo, q 1 = q. Ainda, a igualdade se verifica quando q 2 = 1 e, logo, q 1 = q 1. λx q 1 y q 2 q 2 λx q 1 y q 2 = 0 Com isso é possível mostrar que Ker(ad q A T ) é gerado pelos polinômios x q e x x q 1 y. Portanto, do Teorema 3.0.1, temos que existem sucessivas mudanças de coordenadas tais que o campo dado pelo sistema (3.1) é C ω -conjugado ao campo dado y pelo sistema ẋ = ẏ = λy + q a i x i + Ā(x, y), i=2 q b i x i 1 y + B(x, y), i=2 com Ā(x, y) = o( (x, y) q ) e B(x, y) = o( (x, y) q ). (3.3) A seguir aplicamos o Teorema (3.0.1) a um campo com uma singularidade nilpotente. Veremos que, nesse caso, a escolha de G q como Ker(ad q A T ) não é o mais conveniente. Exemplo Considere agora o campo dado pelo sistema ẋ = y + F (x, y), ẏ = G(x, y), (3.4) com F (x, y) e G(x, y) funções reais de classe C em uma vizinhança da origem de R 2, com F (0, 0) = G(0, 0) = 0 e DF (0, 0) = DG(0, 0) = 0. Nesse caso, [ ] 0 0 A T =
36 Assim como no exemplo anterior, temos o objetivo de encontar uma base para o Ker(ad q A T ), onde q N. De maneira geral, tomemos a base de H q (R n ) dada por (3.2). Daí, para cada (q 1, q 2 ) N 2 tal que q 1 + q 2 = q temos [ x y, xq 1 y q ] ( ) q2 x q1+1 y q = x x q 1 y q 2 e [ x y, xq 1 y q ] ( ) 0 2 =. y q 2 x q1+1 y q 2 1 ( ) Disso, é possível demonstrar que Ker(ad q A T ) é gerado por x q e x ( q y x) + ( ) x q 1 y. No entanto, para o estudo das singularidades nilpotentes a ser desenvolvido y nesse texto é conveniente outra escolha para o subespaço G q que satisfaça ad q A(H q ) G q = H q. Com argumentos análogos aos utilizados acima, verifica-se que é possível escolher G q como o subespaço gerado por { x q y, xq 1 y }. y Assim, segue do Teorema que existem sucessivas mudanças de coordenadas tais que o campo dado pelo sistema (3.4) é C ω -conjugado ao campo dado pelo sistema ẋ = y + C(x, y), q q ẏ = b i x i y a i x i 1 + D(x, (3.5) y), i=2 i=2 com C(x, y) = o( (x, y) q ) e D(x, y) = o( (x, y) q ). Os termos que podem ser eliminados pelas mudanças de variáveis dadas pelo Teorema são usualmente chamados de não-ressonantes. Nosso próximo objetivo é produzir uma única mundaça de coordenadas que elimine todos os termos não-ressonantes. Para tal, vamos combinar o Teorema com o próximo teorema, chamado Teorema de Borel cuja prova se encontra em Kahn (1980). Dada uma função f C (, R m ), onde R n é aberto, o símbolo f(x) a µ x µ µ N n significa que, para cada s = 0, 1, 2,..., o Polinômio de Taylor de f de grau s no ponto 0 é dado por a µ x µ. µ s 36
37 Teorema (Teorema de Borel) Para qualquer coleção de números reais {a µ ; µ Z n +} indexada por multi-índices, existe uma função f : R, onde R n contendo a origem, de classe C tal que f(x) c α x α. α 0 Para a prova do próximo lema vamos utilizar, como argumento principal, o Teorema de Borel. Logo, mesmo que o campo X seja analítico, a conjugação obtida através do lema é de classe C. Aliado ao teorema, vamos utilizar os resultados presentes no Apêndice A. Teorema Seja X : R n um campo de vetores de classe C, onde é uma vizinhança da origem com X(0) = 0 e denote A = DX(0). Então existe h : 1 definida numa vizinhança 1 da origem que é uma conjugação de classe C entre X e um campo de vetores X : 1 R n de classe C tal que X(y) Ay + e g r G r, r = 2, 3,. g r (y), Prova. Pelo Teorema de Borel, existe P : R n R n de classe C tal que r=2 P (y) P r (y), r=2 onde cada P r é dado pelo Teorema (3.0.1). Defina h : R n R n por h(y) = y + P (y). Note que Dh(0) = I logo, pelo Teorema da Função Inversa, h é um difeomorfismo local de classe C. Podemos supor que h : 1 é um difeomorfismo de classe C, onde 1 é uma vizinhança apropriada da origem. Então, pela Proposição (1.3.5), o campo de vetores X dado por X(y) = Dh 1 (h(y))x(h(y)), y, (3.6) é C -conjugado a X. Mostraremos que para cada s = 0, 1, 2, 3, temos s X(y) [Ay + g r (y)] = o( y s ). (3.7) r=2 Para s = 0 basta mostrarmos que X(0) = 0 e A.0 = 0. A primeira igualdade decorre diretamente do fato da origem ser uma singularidade do campo X junto com (3.6) e a segunda decorre do fato de A ser linear. 37
38 Note, ainda, que para s = 1 vale (3.7) visto que, de (3.6), temos D X(0) = A. Suponha agora s = 2, 3,. Definamos h 1, Q 1, Q 2 : R n R n pelas identidades abaixo: e s+1 h 1 (y) = y + P r (y) = y + Q 1 (y) (3.8) r=2 s+1 Q 2 (y) = P (y) P r (y). A estratégia da demonstração consiste em observar que, pelo Teorema 3.0.1, o campo Y que é C -conjugado a X por h 1 difere de Ay + s r=2 g r(y) apenas por termos o( y s ). Então, utilizamos estimativas do Apêndice A para mostrar que as parcelas de h h 1 não provocam alterações de ordem inferior a o( y s ) em Y. r=2 Da definição de h 1 e do Teorema 3.0.1, segue que Dh 1 1 (h 1 (y))x(h 1 (y)) [Ay + logo, para demonstrar (3.7), basta mostrar que s g r (y)] = o( y s ), r=2 Dh 1 1 (h 1 (y))x(h 1 (y)) X(y) = o( y s ). (3.9) Para isso, observe que Q 2 (y) = o( y s+1 ), logo DQ 2 (y) = o( y s ). (3.10) Note que h = h 1 + Q 2. (3.11) Usando a Regra da Cadeia temos D(h 1 (h(y)) = [Dh(y))] 1, y 1. (3.12) Então, de (3.6), (3.8), (3.10), (3.11) e do Lema A.0.6 resulta X(y) = [Dh(y)] 1 X(h(y)) = [I + DQ 1 (y) + DQ 2 (y)] 1 X(h(y)) = {[I + DQ 1 (y)] 1 + o( y s )}X(h(y)) = [Dh 1 (y)] 1 X(h(y)) + o( y s ). Observe que h 1 também é um difeomorfismo de classe C e vale identidade análoga à (3.12), logo X(y) = Dh 1 1 (h 1 (y))x(h(y)) + o( y s ). (3.13) Mas da Desigualdade do Valor Médio e de (3.11) resulta X(h(y)) X(h 1 (y)) A h(y) h 1 (y) = A Q 2 (y), 38
39 logo X(h(y)) = X(h 1 (y)) + o( y s+1 ). (3.14) De (3.13), (3.14) e (3.9), segue o resultado. Aplicaremos a seguir o Teorema aos campos com singularidades semi-hiperbólica e nilpontente já estudados neste capítulo. Exemplo Existe uma vizinhança da origem tal que o campo dado pelo sistema (3.1) é C -conjugado ao campo definido por ẋ = x m f(x) + xα(x, y), ẏ = λy + yg(x) + xβ(x, y), (3.15) com f, g, α e β funções de classe C, m 2, λ 0, g(0) = 0, j α(0, 0) = (0, 0) e j β(0, 0) = (0, 0). De fato, pelo Teorema 3.0.6, temos vizinhança da origem V tal que o campo dado pelo sistema (3.1) é C -conjugado a um campo X tal que ( i=2 X(x, y) a ) ix i λy + i=2 b. ix i 1 y Escrevendo X = ( X 1, X 2 ), temos que X 1 (x, y) a i x i (3.16) e, portanto, X1 (0, y) = 0, para todo y V. Pelo Teorema de Borel, existe f C (I), onde I R é uma vizinhança da origem, tal que f(x) a i x i (3.17) e, logo, f(0) = 0. i=2 i=2 Diminuindo V se necessário e fixando y V qualquer, ao aplicar a Fórmula de Taylor à função A, definida por A(x, y) = X 1 (x, y) f(x), no ponto (0, y) temos que A(x, y) = A(0, y) + xα(x, y), sendo α uma função de classe C em uma vizinhança da origem. Mas, A(0, y) = X 1 (0, y) f(0) = 0 e, logo, A(x, y) = xα(x, y). Note que, por (3.16) e (5.76), j A(0, 0) = 0 e, portanto, j α(0, 0) = 0. Argumentando de modo análogo para X 2 obtemos a conclusão do Exemplo
40 Capítulo 4 A TÉCNICA BLOW-UP DIRECIONAL O objetivo desse capítulo é apresentar uma mudança de coordendas, chamada de blow-up, que não é um difeomorfismo, mas consiste na principal ferramenta para o estudo de singularidades não elementares de campos de vetores planares. Essa técnica foi introduzida por Bendixson em 1901 sem prova-lá. Em 1968, Seidenberg deu uma primeira prova rigorosa para o caso analítico. Tal técnica foi estendida para campos de vetores C do tipo Lojasiewicz em 1977 por Dumortier. Já em 1979, Van den Essen utilizou uma técnica alternativa para campos de vetores analíticos. A grosso modo, a ideia do blow-up é explodir a singularidade, através de mudança de coordenadas, que não é difeomorfismo, para uma linha ou para um círculo. Os pontos que aparecerão nesta linha ou círculo serão, provavelmente, mais simples de serem estudados. Nesse texto ficaremos restritos ao blow-up direcional e não apresentaremos o blowup em coordenadas polares. Essas notas estão baseadas em Andronov (1973), Dumortier (1977), Dumortier et al (2006) e Álvarez et al (2011). Considere o sistema ẋ = P (x, y), (4.1) ẏ = Q(x, y), onde P e Q são funções analíticas definidas em uma vizinhança da origem de R 2. Suponha que (0, 0) é uma singularidade isolada de (4.1). Estamos interessados em estudar a decomposição setorial do sistema (4.1) na origem. 40
41 4.1 BLOW-UP DIRECIONAL Consideramos a mudança de coordendas dada por x = u, y = uv, (4.2) chamada de blow-up na direção x. Intuitivamente, a singularidade do sistema (4.1) localizada na origem explode no eixo vertical u = 0. Observe que o blow-up na direção x é um difeomorfismo entre as regiões {(x, y) R 2 ; x 0} e {(u, v) R 2 ; u 0} mas não possui inversa definida sobre os pontos da reta u = 0. Tal mudança de coordenadas troca os pontos (x, y) do segundo quadrante por pontos (u, v) do terceiro quadrante e os pontos (x, y) do terceiro quadrante por pontos (u, v) do segundo quadrante, mais precisamente, x < 0, y > 0 u < 0, v < 0, x < 0, y < 0 u < 0, v > 0. (4.3) Os demais quadrantes são invariantes pelo blow-up na direção x. Antes da formalização, apresentamos um exemplo ilustrativo. Exemplo Determine a decomposição setorial do sistema ẋ = ax 2 2xy, ẏ = y 2 axy, (4.4) na origem, sendo a > 0 constante. Observe que (0, 0) é uma singularidade do sistema (4.4) do tipo linearmente zero. Fazendo a mudança de coordenadas dada por (4.2) o sistema (4.4) torna-se u = u(au 2uv), v = vu(3v 2a). (4.5) Aplicando o Lema 2.0.4, temos que o campo dado pelo sistema (4.5) é C - equivalente, na região u 0, ao campo dado por ū = aū 2ū v, v = 3 v 2 2a v. (4.6) As singularidades (ū, v) do sistema (4.6) com ū = 0 são (0, 0) e (0, 2a/3). Note que a Jacobiana do sistema (4.6) em (0, 0) é [ a 0 0 2a 41 ],
Modelagem em Sistemas Complexos
 Modelagem em Sistemas Complexos Bifurcação local de campos vetoriais Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Abril de 2012 Nesta aula discutiremos
Modelagem em Sistemas Complexos Bifurcação local de campos vetoriais Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Abril de 2012 Nesta aula discutiremos
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
Apostila Minicurso SEMAT XXVII
 Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
1 Equações Diferenciais Ordinárias: Sistemas de Equações
 Equações Diferenciais Ordinárias: Sistemas de Equações O sistema geral de duas equações diferenciais pode ser escrito como: ẋ = F x,y,t ẏ = Gx,y,t Uma Solução de é um par x t e y t de funções de t tais
Equações Diferenciais Ordinárias: Sistemas de Equações O sistema geral de duas equações diferenciais pode ser escrito como: ẋ = F x,y,t ẏ = Gx,y,t Uma Solução de é um par x t e y t de funções de t tais
1 Álgebra linear matricial
 MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
3.3 Retrato de fase de sistemas lineares de 1 a ordem
 MAP 2310 - Análise Numérica e Equações Diferenciais I Continuação - 25/05/2006 1 o Semestre de 2006 3.3 Retrato de fase de sistemas lineares de 1 a ordem O espaço de fase de um sistema da forma ẏ = Ay,
MAP 2310 - Análise Numérica e Equações Diferenciais I Continuação - 25/05/2006 1 o Semestre de 2006 3.3 Retrato de fase de sistemas lineares de 1 a ordem O espaço de fase de um sistema da forma ẏ = Ay,
O Teorema de Peano. f : D R n. uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e uma função ϕ : I R n tais que
 O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
O Teorema de Peano Equações de primeira ordem Seja D um conjunto aberto de R R n, e seja f : D R n (t, x) f(t, x) uma função contínua. Vamos considerar o seguinte problema: Encontrar um intervalo I R e
Introdução à Teoria de Poincaré-Bendixson para campos de vetores planares
 Introdução à Teoria de Poincaré-Bendixson para campos de vetores planares Otávio Henrique Perez e Tiago de Carvalho 7 de julho de 2014 Resumo O Teorema de Poincaré-Bendixson é um resultado muito importante
Introdução à Teoria de Poincaré-Bendixson para campos de vetores planares Otávio Henrique Perez e Tiago de Carvalho 7 de julho de 2014 Resumo O Teorema de Poincaré-Bendixson é um resultado muito importante
DANIEL V. TAUSK. se A é um subconjunto de X, denotamos por A c o complementar de
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK Ao longo do texto, denotará sempre um espaço topológico fixado. Além do mais, as seguintes notações serão utilizadas: supp f denota o suporte
Cálculo Diferencial e Integral II Resolução do Exame/Teste de Recuperação 02 de Julho de 2018, 15:00h - versão 2 Duração: Exame (3h), Teste (1h30)
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
O Teorema de Poincaré Bendixson e o Teorema de Hartman Grobman
 Aline de Melo Machado O Teorema de Poincaré Bendixson e o Teorema de Hartman Grobman Volta Redonda RJ 13 de maio de 2016 Aline de Melo Machado O Teorema de Poincaré Bendixson e o Teorema de Hartman Grobman
Aline de Melo Machado O Teorema de Poincaré Bendixson e o Teorema de Hartman Grobman Volta Redonda RJ 13 de maio de 2016 Aline de Melo Machado O Teorema de Poincaré Bendixson e o Teorema de Hartman Grobman
A (u + iv) = (a + ib) (u + iv) = (au bv) + i (av + bu).
 DICAS E RESPOSTAS DA LISTA DE EXERCÍCIOS 4 EDO II - MAP 036 PROF: PEDRO T P LOPES WWWIMEUSPBR/ PPLOPES/EDO Os exercícios a seguir foram selecionados dos livros dos autores Claus Doering-Artur Lopes e Jorge
DICAS E RESPOSTAS DA LISTA DE EXERCÍCIOS 4 EDO II - MAP 036 PROF: PEDRO T P LOPES WWWIMEUSPBR/ PPLOPES/EDO Os exercícios a seguir foram selecionados dos livros dos autores Claus Doering-Artur Lopes e Jorge
Estudo de Campos Vetoriais Descontínuos dados na forma de Jordan com autovalores complexos
 Estudo de Campos Vetoriais Descontínuos dados na forma de Jordan com autovalores complexos Lucyjane de Almeida Silva 1, João Carlos da Rocha Medrado 2 2 Instituto de Matemática e Estatística, Universidade
Estudo de Campos Vetoriais Descontínuos dados na forma de Jordan com autovalores complexos Lucyjane de Almeida Silva 1, João Carlos da Rocha Medrado 2 2 Instituto de Matemática e Estatística, Universidade
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham.
 Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
Variedades diferenciáveis e grupos de Lie
 LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
LISTA DE EXERCÍCIOS Variedades diferenciáveis e grupos de Lie 1 VARIEDADES TOPOLÓGICAS 1. Seja M uma n-variedade topológica. Mostre que qualquer aberto N M é também uma n-variedade topológica. 2. Mostre
1 Diferenciabilidade e derivadas direcionais
 UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
DERIVADAS PARCIAIS. y = lim
 DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Estudo dos retratos de fase dos campos de vetores polinomiais quadráticos com integral primeira racional de grau 2.
 Estudo dos retratos de fase dos campos de vetores polinomiais quadráticos com integral primeira racional de grau 2 Daniela Peruzzi SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP Dada de Depósito: Assinatura: Estudo
Estudo dos retratos de fase dos campos de vetores polinomiais quadráticos com integral primeira racional de grau 2 Daniela Peruzzi SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP Dada de Depósito: Assinatura: Estudo
Cap. 5 Estabilidade de Lyapunov
 Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
Funções suaves e Variedades
 a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
a aula, 5-03-2007 Funções suaves e Variedades Os objectos de estudo da Topologia Diferencial são as variedades e as aplicações suaves, onde suave significa ser de classe C. As variedades consideradas são
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
3 Aplicação do Diffusion Maps a campos de vetores planares
 3 Aplicação do Diffusion Maps a campos de vetores planares É usual que fenômenos relacionados à Física, Química, Biologia e Engenharia sejam modelados com o auxílio de equações diferenciais ordinárias
3 Aplicação do Diffusion Maps a campos de vetores planares É usual que fenômenos relacionados à Física, Química, Biologia e Engenharia sejam modelados com o auxílio de equações diferenciais ordinárias
3 Estabilidade dos Difeomorfismos Morse-Smale
 3 Estabilidade dos Difeomorfismos Morse-Smale No último capítulo foi apresentado o nosso objeto de estudo (os difeomorfismos Morse-Smale) e a propriedade que estamos interessados em observar (Estabilidade
3 Estabilidade dos Difeomorfismos Morse-Smale No último capítulo foi apresentado o nosso objeto de estudo (os difeomorfismos Morse-Smale) e a propriedade que estamos interessados em observar (Estabilidade
SMA 5878 Análise Funcional II
 SMA 5878 Análise Funcional II Alexandre Nolasco de Carvalho Departamento de Matemática Instituto de Ciências Matemáticas e de Computação Universidade de São Paulo 16 de Março de 2017 Objetivos da Disciplina
SMA 5878 Análise Funcional II Alexandre Nolasco de Carvalho Departamento de Matemática Instituto de Ciências Matemáticas e de Computação Universidade de São Paulo 16 de Março de 2017 Objetivos da Disciplina
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Minicurso. Sistemas Dinâmicos: Contínuo e Discreto. Raul Felipe Appis, Wesley de Oliveira Tavares. Novembro de 2015
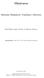 Minicurso Sistemas Dinâmicos: Contínuo e Discreto Raul Felipe Appis, Wesley de Oliveira Tavares Orientadora: Prof. a Dr. a Luci Any Francisco Roberto Novembro de 2015 Departamento de Matemática Pura IBILCE
Minicurso Sistemas Dinâmicos: Contínuo e Discreto Raul Felipe Appis, Wesley de Oliveira Tavares Orientadora: Prof. a Dr. a Luci Any Francisco Roberto Novembro de 2015 Departamento de Matemática Pura IBILCE
A forma canônica de Jordan
 A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
Linearização de Modelos e Teoremas Locais
 Modelos e Teoremas Locais Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de janeiro de 2017. Sumário Introdução => Uma grande parte
Modelos e Teoremas Locais Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de janeiro de 2017. Sumário Introdução => Uma grande parte
Introduzir os conceitos de base e dimensão de um espaço vetorial. distinguir entre espaços vetoriais de dimensão fnita e infinita;
 META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
2 Propriedades geométricas de curvas parametrizadas no R 4
 2 Propriedades geométricas de curvas parametrizadas no R 4 Nesse capítulo trataremos dos conceitos básicos de geometria diferencial referentes à curvas parametrizadas no R 4. 2.1 Curvas Parametrizadas
2 Propriedades geométricas de curvas parametrizadas no R 4 Nesse capítulo trataremos dos conceitos básicos de geometria diferencial referentes à curvas parametrizadas no R 4. 2.1 Curvas Parametrizadas
2 Hiperbolicidade e estabilidade
 2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
EDOs lineares de coeficientes constantes via Álgebra Linear
 EDOs lineares de coeficientes constantes via Álgebra Linear Lucas Seco 26 de Dezembro de 2012 Sempre ouvi falar que a solução de EDOs lineares homogêneas de coeficientes constantes bem como o Método dos
EDOs lineares de coeficientes constantes via Álgebra Linear Lucas Seco 26 de Dezembro de 2012 Sempre ouvi falar que a solução de EDOs lineares homogêneas de coeficientes constantes bem como o Método dos
Dionatan Ricardo Schmidt
 UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA Dionatan Ricardo Schmidt EXISTÊNCIA E CONFIGURAÇÃO DE CICLOS LIMITES EM SISTEMAS DIFERENCIAIS
UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS PROGRAMA DE PÓS-GRADUAÇÃO EM MATEMÁTICA Dionatan Ricardo Schmidt EXISTÊNCIA E CONFIGURAÇÃO DE CICLOS LIMITES EM SISTEMAS DIFERENCIAIS
No que segue, X sempre denota um espaço topológico localmente compacto
 O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK No que segue, sempre denota um espaço topológico localmente compacto Hausdorff. Se f : R é uma função, então supp f denota o{ suporte (relativamente
O TEOREMA DE REPRESENTAÇÃO DE RIESZ PARA MEDIDAS DANIEL V. TAUSK No que segue, sempre denota um espaço topológico localmente compacto Hausdorff. Se f : R é uma função, então supp f denota o{ suporte (relativamente
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
MAT ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS
 MAT 5818 - ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS 1) Mostre que M n (C) munida da norma ((a jk )) 1 j,k n = k=1 2) Defina na álgebra C[X] dos polinômios complexos na variável X a
MAT 5818 - ÁLGEBRAS DE OPERADORES 2 SEMESTRE DE 2017 LISTA DE PROBLEMAS 1) Mostre que M n (C) munida da norma ((a jk )) 1 j,k n = k=1 2) Defina na álgebra C[X] dos polinômios complexos na variável X a
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então
 Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Geometria Diferencial Superfícies no espaço tridimensional
 Geometria Diferencial Superfícies no espaço tridimensional Prof. Ulysses Sodré Londrina-PR, 20 de Setembro de 2007. Conteúdo 1 Topologia de Rn 3 1.1 Bola aberta em Rn................................. 3
Geometria Diferencial Superfícies no espaço tridimensional Prof. Ulysses Sodré Londrina-PR, 20 de Setembro de 2007. Conteúdo 1 Topologia de Rn 3 1.1 Bola aberta em Rn................................. 3
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
y (n) (x) = dn y dx n(x) y (0) (x) = y(x).
 Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Física Matemática II: Notas de aula
 Física Matemática II: Notas de aula Rafael Sussumu Y. Miada Nessas notas, faremos uma introdução à teoria dos espaços métricos e normados, e aos operadores lineares em espaços normados. Os resultados obtidos
Física Matemática II: Notas de aula Rafael Sussumu Y. Miada Nessas notas, faremos uma introdução à teoria dos espaços métricos e normados, e aos operadores lineares em espaços normados. Os resultados obtidos
EXAME DE QUALIFICAÇÃO em Álgebra - Mestrado
 Programa de Pós-Graduação em Matemática Instituto de Matemática e Estatística - IME Universidade Federal de Goiás - UFG EXAME DE QUALIFICAÇÃO em Álgebra - Mestrado Aluno: 1) Seja G um grupo e a, b G tais
Programa de Pós-Graduação em Matemática Instituto de Matemática e Estatística - IME Universidade Federal de Goiás - UFG EXAME DE QUALIFICAÇÃO em Álgebra - Mestrado Aluno: 1) Seja G um grupo e a, b G tais
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
MAT Cálculo Avançado - Notas de Aula
 bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
bola fechada de centro a e raio r: B r [a] = {p X d(p, a) r} MAT5711 - Cálculo Avançado - Notas de Aula 2 de março de 2010 1 ESPAÇOS MÉTRICOS Definição 11 Um espaço métrico é um par (X, d), onde X é um
FUNDAMENTOS DE CONTROLE - EEL 7531
 14 de maio de 2015 Introdução a sistemas não-lineares Embora modelos lineares sejam muito usados, sistemas reais apresentam algum tipo de não-linearidade Em muitos casos a faixa de operação limitada faz
14 de maio de 2015 Introdução a sistemas não-lineares Embora modelos lineares sejam muito usados, sistemas reais apresentam algum tipo de não-linearidade Em muitos casos a faixa de operação limitada faz
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
23 e 24. Forma Quadrática e Equação do Segundo Grau em R 3. Sumário
 23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
CAPÍTULO 13 (G F )(X) = X, X A (F G)(Y ) = Y, Y B. F G = I da e G F = I db,
 CAPÍTULO 3 TEOREMA DA FUNÇÃO INVERSA 3 Introdução A função identidade em R n é a função que a cada elemento de R n associa o próprio elemento ie I d : R n R n X x x n I d X X x x n A função identidade
CAPÍTULO 3 TEOREMA DA FUNÇÃO INVERSA 3 Introdução A função identidade em R n é a função que a cada elemento de R n associa o próprio elemento ie I d : R n R n X x x n I d X X x x n A função identidade
CAPÍTULO 8 REGRA DA CADEIA (UM CASO PARTICULAR)
 CAPÍTULO 8 REGRA DA CADEIA UM CASO PARTICULAR 81 Introdução Em Cálculo 1A, aprendemos que, para derivar a função hx x 2 3x + 2 37, o mais sensato é fazer uso da regra da cadeia A regra da cadeia que é
CAPÍTULO 8 REGRA DA CADEIA UM CASO PARTICULAR 81 Introdução Em Cálculo 1A, aprendemos que, para derivar a função hx x 2 3x + 2 37, o mais sensato é fazer uso da regra da cadeia A regra da cadeia que é
CURVAS REGULARES E EQUAÇÕES DE FRENET. Thiago Mariano Viana ¹, Dr. Fernando Pereira Souza ²
 1 CURVAS REGULARES E EQUAÇÕES DE FRENET Thiago Mariano Viana ¹, Dr. Fernando Pereira Souza ² ¹ Aluno do curso de Matemática CPTL/UFMS, bolsista do grupo PET Matemática CPTL/UFMS; ² Professor do curso de
1 CURVAS REGULARES E EQUAÇÕES DE FRENET Thiago Mariano Viana ¹, Dr. Fernando Pereira Souza ² ¹ Aluno do curso de Matemática CPTL/UFMS, bolsista do grupo PET Matemática CPTL/UFMS; ² Professor do curso de
Unidade 5 - Subespaços vetoriais. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa. 10 de agosto de 2013
 MA33 - Introdução à Álgebra Linear Unidade 5 - Subespaços vetoriais A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Às vezes, é necessário detectar, dentro
MA33 - Introdução à Álgebra Linear Unidade 5 - Subespaços vetoriais A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Às vezes, é necessário detectar, dentro
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
INTEGRABILIDADE LOCAL DE CAMPOS DE VETORES EM R 2 E R 3
 Universidade Federal de Itajubá Programa de Pós Graduação em Matemática INTEGRABILIDADE LOCAL DE CAMPOS DE VETORES EM R 2 E R 3 Willian Pereira Nunes Itajubá, Fevereiro 2015 Universidade Federal de Itajubá
Universidade Federal de Itajubá Programa de Pós Graduação em Matemática INTEGRABILIDADE LOCAL DE CAMPOS DE VETORES EM R 2 E R 3 Willian Pereira Nunes Itajubá, Fevereiro 2015 Universidade Federal de Itajubá
Universidade Estadual Paulista Câmpus de São José do Rio Preto Instituto de Biociências, Letras e Ciências Exatas
 Universidade Estadual Paulista Câmpus de São José do Rio Preto Instituto de Biociências, Letras e Ciências Exatas Ciclos Limites de Sistemas Lineares por Partes Jaime Rezende de Moraes Orientador: Prof.
Universidade Estadual Paulista Câmpus de São José do Rio Preto Instituto de Biociências, Letras e Ciências Exatas Ciclos Limites de Sistemas Lineares por Partes Jaime Rezende de Moraes Orientador: Prof.
7.3 Diferenciabilidade
 CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
Álgebra Linear e suas Aplicações Notas de Aula. Petronio Pulino = Q
 Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino 1 3 4 3 1 0 4 0 1 = Q 4 1 6 Qt Q t Q = 1 1 1 PULINUS Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino Departamento de Matemática
Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino 1 3 4 3 1 0 4 0 1 = Q 4 1 6 Qt Q t Q = 1 1 1 PULINUS Álgebra Linear e suas Aplicações Notas de Aula Petronio Pulino Departamento de Matemática
Análise Matemática III - Turma especial
 Análise Matemática III - Turma especial Fichas 1 a 5 - Solução parcial 1.3 Seja D E k um conjunto fechado. Uma transformação T : D D diz-se uma contracção se existe c < 1 tal que para todos os x, y D se
Análise Matemática III - Turma especial Fichas 1 a 5 - Solução parcial 1.3 Seja D E k um conjunto fechado. Uma transformação T : D D diz-se uma contracção se existe c < 1 tal que para todos os x, y D se
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
3 A estrutura simplética do fluxo geodésico
 3 A estrutura simplética do fluxo geodésico A partir do ponto de vista da mecânica classica, a geodésica é uma solução da equação de Euler-Lagrange considerando-se o lagrangeano L(x v) = 1 v 2 x O objetivo
3 A estrutura simplética do fluxo geodésico A partir do ponto de vista da mecânica classica, a geodésica é uma solução da equação de Euler-Lagrange considerando-se o lagrangeano L(x v) = 1 v 2 x O objetivo
Definimos a soma de seqüências fazendo as operações coordenada-a-coordenada:
 Aula 8 polinômios (Anterior: chinês. ) 8.1 séries formais Fixemos um anel A. Denotaremos por A N o conjunto de todas as funções de N = {, 1, 2,... } a valores em A. Em termos mais concretos, cada elemento
Aula 8 polinômios (Anterior: chinês. ) 8.1 séries formais Fixemos um anel A. Denotaremos por A N o conjunto de todas as funções de N = {, 1, 2,... } a valores em A. Em termos mais concretos, cada elemento
Capítulo 1. f : A B. elementos A com elementos de B ilustradas nos seguintes diagramas.
 Capítulo 1 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Capítulo 1 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Fabio Augusto Camargo
 Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Universidade Federal Fluminense - GAN
 Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
MAE125 Álgebra Linear /1 Turmas EQN/QIN
 MAE25 Álgebra Linear 2 205/ Turmas EQN/QIN Planejamento (última revisão: 0 de junho de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na semana seguinte à aula e valem nota Todas
MAE25 Álgebra Linear 2 205/ Turmas EQN/QIN Planejamento (última revisão: 0 de junho de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na semana seguinte à aula e valem nota Todas
Cálculo Diferencial e Integral II 2012/13 1 o semestre
 Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL
 PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL. Introdução Considere f uma função, não constante, de uma variável real ou complexa, a equação f(x) = 0 será denominada equação de uma incógnita. EXEMPLO e x + senx
PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL. Introdução Considere f uma função, não constante, de uma variável real ou complexa, a equação f(x) = 0 será denominada equação de uma incógnita. EXEMPLO e x + senx
Instituto de Matemática - IM-UFRJ Geometria Riemanniana Lista 2 de exercícios, para entregar na aula de 5/9/2018
 Instituto de Matemática - IM-UFRJ 1. Seja V um espaço vetorial real de dimensão finita, dim R V = n. Para quaisquer bases {e i } e {f i } de V, sabemos que existe uma matriz invertível A = (a ij ) GL(n,R)
Instituto de Matemática - IM-UFRJ 1. Seja V um espaço vetorial real de dimensão finita, dim R V = n. Para quaisquer bases {e i } e {f i } de V, sabemos que existe uma matriz invertível A = (a ij ) GL(n,R)
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
APLICAÇÃO DO TEOREMA DO PONTO FIXO DE BANACH A UM PROBLEMA EM PROBABILIDADE 1
 Disciplinarum Scientia. Série: Ciências Exatas, S. Maria, v.2, n.1, p.59-68, 2001 59 APLICAÇÃO DO TEOREMA DO PONTO FIXO DE BANACH A UM PROBLEMA EM PROBABILIDADE 1 APPLICATION OF BANACH FIXED POINT THEOREM
Disciplinarum Scientia. Série: Ciências Exatas, S. Maria, v.2, n.1, p.59-68, 2001 59 APLICAÇÃO DO TEOREMA DO PONTO FIXO DE BANACH A UM PROBLEMA EM PROBABILIDADE 1 APPLICATION OF BANACH FIXED POINT THEOREM
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
CÁLCULO L1 NOTAS DA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula introduziremos o conceito de derivada e a definição de uma reta tangente ao gráfico de uma função. Também apresentaremos
Teorema das pré-imagens para variedades com bordo
 9 a aula, 17-05-2007 Teorema das pré-imagens para variedades com bordo Teorema das pré-imagens Sejam X, Y variedades orientadas, X com bordo e Y sem bordo tais que dim(x) dim(y ). Se c Y for um valor regular
9 a aula, 17-05-2007 Teorema das pré-imagens para variedades com bordo Teorema das pré-imagens Sejam X, Y variedades orientadas, X com bordo e Y sem bordo tais que dim(x) dim(y ). Se c Y for um valor regular
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA. Medida e Probabilidade
 UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Nome:... Q N Assinatura:... 1 RG:... 2 N o USP:... 3 Turma: Teórica... 4 Professor: Edson Vargas... Total
 1 a Prova de MAT036 - Geometria Diferencial I IME - 9/09/016 Nome:................................................... Q N Assinatura:............................................... 1 RG:......................................................
1 a Prova de MAT036 - Geometria Diferencial I IME - 9/09/016 Nome:................................................... Q N Assinatura:............................................... 1 RG:......................................................
Teoria da Medida e Integração (MAT505)
 Transporte de medidas Teoria da Medida e Integração (MAT505) Transporte de medidas e medidas invariantes. Teorema de Recorrência de Poincaré V. Araújo Instituto de Matemática, Universidade Federal da Bahia
Transporte de medidas Teoria da Medida e Integração (MAT505) Transporte de medidas e medidas invariantes. Teorema de Recorrência de Poincaré V. Araújo Instituto de Matemática, Universidade Federal da Bahia
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Lista de Exercícios Equações Diferenciais Ordinárias I MAT 871
 Lista de Exercícios Equações Diferenciais Ordinárias I MAT 871 1 de abril de 2017 Esta lista contém exercícios de [1], [2], [3] e [4]. separados por aulas em ordem decrescente de aula. Os exercícios estão
Lista de Exercícios Equações Diferenciais Ordinárias I MAT 871 1 de abril de 2017 Esta lista contém exercícios de [1], [2], [3] e [4]. separados por aulas em ordem decrescente de aula. Os exercícios estão
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
25/05/06 MAP Análise Numérica e Equações Diferenciais I 1 o Semestre de EDO linear homogênea a coeficientes constantes - Continução
 25/05/06 MAP 2310 - Análise Numérica e Equações Diferenciais I 1 o Semestre de 2006 Continuação 185 EDO linear homogênea a coeficientes constantes - Continução Exercício 36 Ache a solução geral complexa
25/05/06 MAP 2310 - Análise Numérica e Equações Diferenciais I 1 o Semestre de 2006 Continuação 185 EDO linear homogênea a coeficientes constantes - Continução Exercício 36 Ache a solução geral complexa
A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário
 A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário Renan de Oliveira Pereira, Ouro Preto, MG, Brasil Wenderson Marques Ferreira, Ouro Preto, MG, Brasil Eder Marinho
A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário Renan de Oliveira Pereira, Ouro Preto, MG, Brasil Wenderson Marques Ferreira, Ouro Preto, MG, Brasil Eder Marinho
Singularidades Estáveis de Curvas e Superfícies
 Singularidades Estáveis de Curvas e Superfícies Aluno: Igor Albuquerque Araujo Orientador: Marcos Craizer Introdução Em matemática, a teoria das singularidades estuda e classifica os germes de aplicações
Singularidades Estáveis de Curvas e Superfícies Aluno: Igor Albuquerque Araujo Orientador: Marcos Craizer Introdução Em matemática, a teoria das singularidades estuda e classifica os germes de aplicações
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática. Notas de Aulas de
 Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
 1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
MAT0326 Geometria Diferencial I
 MAT036 Geometria Diferencial I Segunda Prova 06/11/01 Soluções Questão 1 Valor: 3.0 pontos. Considere a superfície S, de Enneper, parametrizada por Xu, v = u u3 3 + uv, v v3 3 + u v, u v. a. Determine
MAT036 Geometria Diferencial I Segunda Prova 06/11/01 Soluções Questão 1 Valor: 3.0 pontos. Considere a superfície S, de Enneper, parametrizada por Xu, v = u u3 3 + uv, v v3 3 + u v, u v. a. Determine
Teoria Escalar da Difração
 Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
14 AULA. Vetor Gradiente e as Derivadas Direcionais LIVRO
 1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
Topologia de Zariski. Jairo Menezes e Souza. 25 de maio de Notas incompletas e não revisadas RASCUNHO
 Topologia de Zariski Jairo Menezes e Souza 25 de maio de 2013 Notas incompletas e não revisadas 1 Resumo Queremos abordar a Topologia de Zariski para o espectro primo de um anel. Antes vamos definir os
Topologia de Zariski Jairo Menezes e Souza 25 de maio de 2013 Notas incompletas e não revisadas 1 Resumo Queremos abordar a Topologia de Zariski para o espectro primo de um anel. Antes vamos definir os
MCTB Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares. Os Exercícios 3 e 4 são os exercícios bônus dessa lista.
 MCTB002-13 Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares Os Exercícios 3 e 4 são os exercícios bônus dessa lista. Definição 1. Dados conjuntos X e Y, uma função ϕ :
MCTB002-13 Álgebra Linear Avançada I Claudia Correa Exercícios sobre transformações lineares Os Exercícios 3 e 4 são os exercícios bônus dessa lista. Definição 1. Dados conjuntos X e Y, uma função ϕ :
Dinâmica e Bifurcações de Campos Vetoriais Polinomiais em R 3 com um Cilindro Invariante
 Dinâmica e Bifurcações de Campos Vetoriais Polinomiais em R 3 com um Cilindro Invariante Naiara Aparecida dos Santos Silva Orientador: Prof. Dr. Marcelo Messias Programa: Matemática Aplicada e Computacional
Dinâmica e Bifurcações de Campos Vetoriais Polinomiais em R 3 com um Cilindro Invariante Naiara Aparecida dos Santos Silva Orientador: Prof. Dr. Marcelo Messias Programa: Matemática Aplicada e Computacional
de modo que γ (t) 2 = 3e t. Pelo Proposição 6.3, γ é retificável no intervalo [0, T], para cada T > 0 e lim γ (t) 2 dt = 3, )) se t 0 0 se t = 0
![de modo que γ (t) 2 = 3e t. Pelo Proposição 6.3, γ é retificável no intervalo [0, T], para cada T > 0 e lim γ (t) 2 dt = 3, )) se t 0 0 se t = 0 de modo que γ (t) 2 = 3e t. Pelo Proposição 6.3, γ é retificável no intervalo [0, T], para cada T > 0 e lim γ (t) 2 dt = 3, )) se t 0 0 se t = 0](/thumbs/83/87991881.jpg) Solução dos Exercícios Capítulo 6 Exercício 6.1: Seja γ: [, + [ R 3 definida por γ(t) = (e t cos t, e t sen t, e t ). Mostre que γ é retificável e calcule seu comprimento. Solução: γ é curva de classe
Solução dos Exercícios Capítulo 6 Exercício 6.1: Seja γ: [, + [ R 3 definida por γ(t) = (e t cos t, e t sen t, e t ). Mostre que γ é retificável e calcule seu comprimento. Solução: γ é curva de classe
Notações e revisão de álgebra linear
 Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
Notações e revisão de álgebra linear Marina Andretta ICMC-USP 17 de agosto de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n
 Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
Universidade Federal de Viçosa Centro de Ciências Exatas - CCE Departamento de Matemática Primeira Lista de MAT641 - Análise no R n 1. Exercícios do livro Análise Real, volume 2, Elon Lages Lima, páginas
Capítulo 2. f : A B. 3. A regra em (3) não define uma função de A em B porque 4 A está associado a mais de um. elemento de B.
 Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
