FENÓMENOS DE TRANSFERÊNCIA I
|
|
|
- Leila Lagos Camilo
- 5 Há anos
- Visualizações:
Transcrição
1 FENÓMENOS DE TRANSFERÊNCIA I Apontamentos Teóricos Helder Teixeira Gomes ESTiG-IPB
2 Nota Introdutória Estes Apontamentos Teóricos foram elaborados com base nos livros Introduction to Heat Transfer (Incropera, DeWitt, Bergman e Lavine) e Transferência de Calor (Çengel). A sua distribuição tem como principal objectivo fornecer aos alunos da unidade curricular de Fenómenos de Transferência I do curso de Licenciatura em Engenharia Química e Biológica da ESTiG-IPB um elemento para o acompanhamento mais eficiente das aulas teóricas, não devendo de forma alguma, constituir o principal elemento do seu estudo. De forma a melhorar futuras versões dos Apontamentos Teóricos, agradeço aos alunos ue me comuniuem possíveis gralhas ue possam encontrar, e incentivo igualmente a colaboração com sugestões ue levem a uma melhoria do funcionamento da unidade curricular. Desejo um bom trabalho a todos ue consultem estes Apontamentos Teóricos. O docente da unidade curricular de Fenómenos de Transferência I, Helder Gomes
3 Capítulo Fundamentos da Transferência de Calor Ao iniciar o estudo da ciência da transferência de calor, a primeira uestão ue se pode colocar é O ue é a transferência de calor?. A sua definição dá-nos a resposta: A transferência de calor é a energia em trânsito devido a uma diferença de temperatura entre dois sistemas. Por exemplo, se retirarmos de uma estufa um objecto com uma temperatura inicial de ºC e o expusermos ao ar ambiente, irá observar-se uma transferência de energia na forma de calor no sentido da temperatura mais elevada para a temperatura mais baixa, isto é, do objecto para o ar circundante. Como conseuência da remoção de calor, a temperatura do objecto irá baixar até atingir um estado de euilíbrio em ue a temperatura do objecto iguala a temperatura do ar circundante e a transferência de calor cessa. A termodinâmica permite determinar a uantidade de calor transferida desde o estado inicial ao estado final de euilíbrio, mas não permite saber uanto tempo demora essa transferência. A ciência da transferência de calor é auela ue permite determinar ual a velocidade de transferência desse calor. A transferência de calor pode ocorrer segundo três mecanismos básicos: a condução, a convecção e a radiação. Nas próximas secções deste capítulo, vamos ver, de uma forma geral, as particularidades de cada um destes mecanismos. Em capítulos posteriores faremos uma abordagem mais detalhada... Condução A condução ocorre sempre ue existe um gradiente de temperatura num meio estacionário (sólido ou fluído), consistindo na transferência de energia das partículas mais energéticas para partículas de menor energia, como resultado de interacções entre essas partículas (colisões e difusão nos líuidos e nos gases, vibrações moleculares e transporte de energia por electrões livres nos sólidos). Como exemplo, vamos considerar uma barra de ferro, inicialmente à temperatura ambiente, usada para remexer as brasas de uma fogueira. A experiência empírica diz-nos ue, se esperarmos tempo suficiente, a temperatura da extremidade em contacto com a mão (oposta à extremidade em contacto com as brasas) começa a aumentar. A explicação reside na condução: como existe um gradiente de temperatura na barra de ferro (a temperatura na extremidade exposta às brasas é superior à temperatura na extremidade em contacto com a mão), vai ocorrer transferência de calor por condução no sentido da temperatura mais elevada,
4 para a temperatura mais baixa. Se esperarmos um tempo suficientemente longo, no euilíbrio, a temperatura da barra irá ficar uniforme, isto é, à temperatura da extremidade da barra exposta às brasas. A velocidade da condução de calor através de um meio depende da configuração geométrica desse meio, da sua espessura, do material de ue é feito e da diferença de temperaturas existente. A evidência empírica mostra ue a velocidade de transferência de calor por condução através de um meio é proporcional à diferença de temperaturas e à área de transferência de calor (perpendicular ao sentido da transferência de calor) e inversamente proporcional à espessura do meio. A constante de proporcionalidade é a condutividade térmica (k) do material, ue é uma medida da capacidade de um material para conduzir calor, e a euação diferencial ue permite determinar a velocidade da transferência de calor por condução é conhecida como a Lei de Fourier: ka dt dx () onde representa a taxa de transferência de calor (J/s ou W), A a área de transferência de calor (m ), T a temperatura (ºC ou K), x a coordenada espacial (m) e k a dt condutividade térmica (W/mºC), característica do material. Notar ue tem sinal dx negativo uando x aumenta no sentido da diminuição da temperatura (Figura ), pelo ue, o sinal negativo na Lei de Fourier garante ue a velocidade de transferência de calor no sentido positivo de x seja uma uantidade positiva. 3
5 T T. T x Figura Condução de calor através de um material. A transferência de calor dá-se no sentido da temperatura mais elevada para a temperatura mais baixa Exemplo: Condução de calor unidimensional em estado estacionário numa placa plana Considere a condução de calor em estado estacionário através da parede de uma casa com espessura Δx L e área de transferência de calor A (Figura ). Considere ainda ue a diferença de temperaturas entre os dois lados da parede é ΔT T T, com T > T. Figura Condução de calor em estado estacionário através de uma parede de espessura Δx e área de transferência de calor A 4
6 A parede da casa pode ser considerada uma placa plana. Como existe um gradiente de temperatura entre os dois lados da parede, então haverá transferência de calor por condução entre a superfície à temperatura T e a superfície à temperatura T. Como iremos deduzir no capítulo, dedicado ao estudo detalhado do mecanismo de condução em estado estacionário, o perfil de temperaturas numa placa plana é linear, o ue implica ue o seu declive seja constante: dt ΔT T T () dx Δx L dt Por substituição de dx na Lei de Fourier, deduz-se a euação ue permite determinar a velocidade de transferência de calor por condução unidimensional em estado estacionário numa placa plana (o termo unidimensional assume ue a transferência de calor se processa apenas numa dimensão, no presente caso na direcção do eixo dos xx, considerando-se ue a placa está isolada nas restantes faces, impedindo a transferência de energia nas direcções yy e zz): T T T T ka ka L L (3) Condutividade térmica A Lei de Fourier para a velocidade de transferência de calor em estado estacionário também pode ser vista como a euação de definição da condutividade térmica (k, em W/mºC). Assim, a condutividade térmica de um material pode-se definir como a velocidade de transferência de calor através de uma espessura unitária de material, por unidade de área e por unidade de diferença de temperatura. A condutividade térmica varia com o tipo de material e serve como medida da capacidade de um material para conduzir calor. Um valor elevado da condutividade térmica indica ue o material é bom condutor de calor e um valor baixo indica ue o material é um mau condutor ou ue é um isolante. Para um mesmo material a condutividade térmica depende da temperatura. Dada a importância da condutividade térmica de um material no estudo da transferência de calor por condução, os valores de k para vários materiais 5
7 em função da temperatura encontram-se compilados em tabelas ue facilmente se encontram em manuais de transferência de calor. Para esta unidade curricular podem-se consultar as Tabelas A3 a A7 disponíveis no material fornecido. Nos capítulos e 3 faremos o estudo detalhado do mecanismo de condução de calor em estado estacionário e em estado transiente. Exercício Considere uma placa plana com faces de 3 m x.5 m e espessura.5 m, constituída por um material com condutividade térmica, k.7 W/mK. Sabendo ue a temperatura em cada uma das faces é, respectivamente, T 4 K e T 5 K e ue a transferência de calor ocorre em regime estacionário, calcule a taxa de transferência de calor observada,. Resolução Assumindo ue a transferência de calor ocorre por condução unidimensional (placa isolada, à excepção das faces, Figura ), podemos utilizar a Lei de Fourier para determinar a velocidade de transferência de calor unidimensional em estado estacionário numa placa plana: T ka T L T ka T L (.5 3) 45 W.5.. Convecção A transferência de calor por convecção ocorre entre uma superfície sólida e um fluído adjacente em movimento, compreendendo os efeitos combinados da condução e do movimento de fluidos, sempre ue se observe uma diferença de temperaturas entre os dois meios. Quanto mais rápido o fluído se movimentar, maior é a transferência de calor por convecção. Note ue, na ausência de ualuer movimento do fluído, a transferência de calor entre a superfície sólida e o fluído adjacente, será por condução pura. A convecção diz-se forçada, se o escoamento do fluído for causado por meios externos. Por exemplo, devido a uma ventoínha, ao vento, etc. (Figura 3(a)). A convecção diz-se natural (ou livre), se o escoamento do fluído for devido a diferenças de densidade causadas por variações na temperatura do fluído (Figura 3(b)). 6
8 Convecção forçada Convecção natural Ar ovo uente Ar ovo uente (a) (b) Figura 3 Arrefecimento de um ovo cozido por (a) convecção forçada; (b) convecção natural A análise detalhada do fenómeno de transferência de calor por convecção pode ser realizada pela teoria da camada limite. Esta teoria considera ue, uando um fluído em movimento contacta uma superfície sólida, se forma uma camada, chamada de camada limite, onde a velocidade e a temperatura do fluído variam. Esta teoria considera ainda ue, à superfície, a velocidade do fluído é nula e a sua temperatura iguala a da superfície. À medida ue nos afastamos da superfície, a velocidade do fluído aumenta e a temperatura varia até chegar ao limite da camada, onde a velocidade do fluído será igual à velocidade e à temperatura no bulk do fluído (Figura 4). Variação da velocidade do ar Fluxo de ar Variação da temperatura do ar Superfície Quente Figura 4 Transferência de calor de uma superfície uente para o ar por convecção. Conceito de camada limite Tendo em atenção estes conceitos, é fácil compreender ue inicialmente a transferência de calor da superfície para o fluído se dê por condução (o fluído à 7
9 superfície está estagnado) e ue depois (ou em simultâneo) haja uma remoção do calor, devido ao movimento do fluído. Apesar da aparente complexidade da convecção, observa-se empiricamente ue a velocidade de transferência de calor por convecção é proporcional à diferença de temperaturas entre a superfície sólida e o fluído, podendo ser determinada pela Lei de Arrefecimento de Newton: conv ha (T T ) (4) s S onde h é o coeficiente de transferência de calor por convecção (W/m ºC), A s a área superficial de transferência de calor (m ), T S a temperatura da superfície do sólido (ºC ou K) e T a temperatura do fluído suficientemente afastado da superfície do sólido (ºC ou K). Ao contrário da condutividade térmica (k) na condução, o coeficiente de transferência de calor por convecção (h) não é uma propriedade do fluído ou do material sólido, mas sim um parâmetro ue se determina experimentalmente, sendo o seu valor dependente da geometria do sólido, da natureza do escoamento do fluído e das suas propriedades termodinâmicas e de transporte. A convecção, e a teoria da camada limite em particular, serão abordadas no capítulo 4 destes Apontamentos Teóricos..3. Radiação A radiação é a energia emitida na forma de ondas electromagnéticas por toda a matéria, devido a alterações nas configurações dos átomos ou das moléculas constituintes. Existem diversos tipos de radiação (raios X, raios gama, microondas, ondas rádio, radiação térmica, ). No estudo dos fenómenos de transferência de calor estamos interessados na radiação térmica, energia emitida por todos os corpos ue se encontrem a uma temperatura não nula (Ex. Radiação Solar). Ao contrário da condução e da convecção, a transferência de energia térmica por radiação não reuer a presença de um meio físico, podendo ocorrer no vácuo. 8
10 A velocidade de emissão de calor por radiação térmica por todos os corpos é proporcional à sua temperatura absoluta, sendo máxima uando se trata de um corpo negro, podendo determinar-se a partir da Lei de Stefan-Boltzmann: 4 σat (5) onde T (K) é a temperatura absoluta da superfície do corpo, A a área da superfície emissora (m ) e σ a constante de Stefan-Boltzmann (σ 5.67x -8 W/m K 4 ). A radiação de um corpo negro representa a uantidade máxima de radiação ue pode ser emitida desde uma superfície ideal a uma temperatura específica. A radiação emitida por todas as superfícies reais é menor ue a emitida por um corpo negro à mesma temperatura e pode ser determinada pela seguinte euação: 4 εσat (6) onde ε é a emissividade da superfície, ue pode tomar valores entre e. Para um corpo negro, ε. Quanto mais próximo de for a emissividade de uma superfície, mais se aproxima à idealização de corpo negro. A radiação será abordada em detalhe no Capítulo 6 deste Apontamentos Teóricos. 9
11 Capítulo Condução de Calor em Estado Estacionário (Unidimensional) No capítulo, definiu-se a condução de calor como a transferência de energia térmica das partículas mais energéticas de um meio estacionário para as partículas adjacentes com menor energia e vimos ue o calor é conduzido no sentido da temperatura decrescente, observando-se um gradiente de temperatura negativo uando o calor é conduzido no sentido positivo do eixo dos xx (Figura ). Foi também referido no capítulo ue a velocidade de transferência de calor através de um meio, numa direcção específica (por exemplo na direcção do eixo dos xx), é proporcional à diferença de temperaturas entre as duas extremidades do meio e à área perpendicular à direcção da transferência de calor, e inversamente proporcional à distância nessa direcção. A euação ue traduz estas dependências é dada pela Lei de Fourier para a condução de calor, uma lei empírica deduzida a partir de observações experimentais, ue na forma unidimensional é traduzida por: x ka dt dx () Neste capítulo, vamos analisar problemas de transferência de calor por condução em estado estacionário, considerando sempre ue essa condução é unidimensional (desprezam-se possíveis transferências de calor noutras direcções). Nas próximas três secções vamos deduzir euações ue nos permitem calcular o perfil de temperaturas e a taxa de transferência de calor em sólidos de diferentes geometrias. Consideremos um elemento de volume infinitesimal de um sólido genérico sujeito a transferência de calor por condução unidimensional, de espessura dx e área superficial A perpendicular à direcção da transferência de calor (Figura 5).
12 Figura 5 Condução unidimensional de calor através de um elemento de volume de um sólido genérico Considerando ue o elemento de volume não gera calor, do balanço de energia em estado estacionário vem ue: x x + dx (7) Atendendo a esta relação, pela definição de derivada obtém-se a seguinte euação, válida para condução de calor em estado estacionário, em meios estacionários não geradores de calor: d x x+ dx lim dx dx dx x (8).. Condução em Placas Planas Seja a condução de calor através de uma parede plana não geradora de calor (a parede de uma casa ou o vidro de uma janela, por exemplo, Figura 6). É razoável considerar a condução de calor neste tipo de geometria como sendo unidimensional, uma vez ue a condução de calor será dominante numa das direcções e desprezável nas outras.
13 Elemento de volume Figura 6 - Condução unidimensional de calor através de um elemento de volume de uma placa plana Fazendo um balanço de energia ao elemento de volume infinitesimal da placa plana indicada na Figura 6, obtém-se a euação (7) e pelo mesmo raciocínio utilizado anteriormente, a euação (8), válida para condução em estado estacionário: d x dx (8) Por sua vez, a taxa de transferência de calor por condução pode ser calculada pela Lei de Fourier, euação (): x ka dt dx () Considerando ue a condutividade térmica (k) na placa é constante (a área de transferência de calor também), por aplicação da euação (8) à euação (), vem ue: d T d T x -ka dx dx d dx (9)
14 Note ue a euação diferencial (9) ue se obteve para a análise da transferência de calor por condução unidimensional em estado estacionário em placas planas, é válida sempre ue a área transversal do meio estacionário em estudo seja constante. Por exemplo, verifiue a validade da euação diferencial (9) na análise da transferência de calor por condução axial na barra cilíndrica apresentada na Figura 7: Figura 7 Condução axial num cilindro A determinação da solução geral do perfil de temperaturas por condução em estado estacionário numa placa plana (ou meio estacionário com área de secção recta constante) não geradora de calor é conseguida resolvendo a euação diferencial (9). Para obtermos a solução particular é necessário conhecer as condições fronteira (consideremos para o efeito ue para x, T T e ue para x L, T T S ). Da integração da euação diferencial (9) obtém-se a solução geral: d T dt C T Cx + C () dx dx Para obter as constantes de integração C e C introduzem-se as condições fronteira. Aplicando a condição para x à solução geral, obtém-se C : x T C T De modo análogo, aplicando a condição para x L: 3
15 x L T C L + T T S TS T L C Substituindo C e C na solução geral, euação (), obtém-se a distribuição de temperaturas, ue é a solução particular do problema: TS T T TS T x + T T T x () L L Do resultado obtido torna-se evidente ue, para condução de calor unidimensional em estado estacionário através de uma placa plana não geradora de calor e condutividade térmica constante, a temperatura varia linearmente com x: T T T S L x Uma vez conhecido o perfil de temperaturas na placa, é possível calcular a taxa de transferência de calor ue a atravessa por condução aplicando a Lei de Fourier, euação (): dt ka x ka x dx L ( T T ) S () Resistência Térmica Por ser um conceito muito importante na análise de problemas de transferência de calor em estado estacionário, vamos introduzir neste ponto a noção de resistência térmica, ue apresenta uma analogia útil com o conceito de resistência eléctrica, como 4
16 iremos abordar mais adiante. Da mesma maneira ue a resistência eléctrica é associada com a condução de electricidade, a resistência térmica pode ser associada com a transferência de calor. Uma resistência é definida como a razão entre uma força motriz e a correspondente taxa de transferência. Da euação (), obtém-se assim a resistência térmica (R T ) para a condução numa placa plana, onde ΔT corresponde à força motriz e x à taxa de transferência: R ΔT L R T (3) ka T x Note ue, uanto maior a resistência térmica, menor a taxa de transferência de calor observada... Condução Radial num Cilindro Um exemplo típico de condução em cilindros ocorre em tubos, cujas superfícies externa e interna estejam em contacto com fluídos a diferentes temperaturas (Figura 8). Fluído frio T,, h Fluído uente T,, h Figura 8 Tubo cilíndrico com superfícies interna e externa em contacto com fluídos a diferentes temperaturas 5
17 Ao contrário do ue acontece numa placa plana, num cilindro sujeito a condução radial, a área de transferência de calor varia com a posição (A r πrl), pelo ue, a taxa de transferência de calor, dada pela Lei de Fourier, é expressa em função de r: r ka r dt dr kπ rl dt dr (4) Por um raciocínio análogo ao realizado uando abordamos placas planas, fazendo um balanço de energia ao elemento de volume infinitesimal do cilindro, obtém-se a euação (8), válida para condução em estado estacionário: d r dr (8) Considerando ue a condutividade térmica (k) no cilindro é constante, por aplicação da euação (8) à euação (4), vem ue: d r d dt d dt - ka r r dr dr dr dr dr (5) A determinação da solução geral do perfil de temperaturas por condução radial em estado estacionário num cilindro não gerador de calor é conseguida resolvendo a euação diferencial (5), sujeita a condições fronteira apropriadas. Da integração da euação diferencial (5) obtém-se a solução geral: d dr dt r dr dt r dr C dr r dt C T Clnr + C (6) Para obter as constantes de integração C e C introduzem-se na euação (6) as condições fronteira. Para o efeito, consideremos as seguintes condições fronteira (CF): CF: r r, T T s, CF: r r, T T s, 6
18 Das condições fronteira: T T s, s, C ln C ln ( r ) ( r ) + C + C C C Ts, T r ln r T s, s, ( T T ) s, s, ln ( r ) r ln r Substituindo C e C na solução geral, obtém-se a distribuição de temperaturas, ue é a solução particular do problema: r ln ( ) r T T s, Ts, Ts, (7) r ln r Note ue, para condução radial de calor em estado estacionário através de um cilindro não gerador de calor e condutividade térmica constante, a temperatura varia com r de uma forma logarítmica, e não linearmente como observado para placas planas nas mesmas condições. O perfil logarítmico descrito, encontra-se esuematizado na imagem interior da Figura 8. Uma vez conhecido o perfil de temperaturas no cilindro, é possível deduzir a euação ue permite calcular a taxa de transferência de calor por condução ue o atravessa, aplicando a Lei de Fourier: r ka r dt dr kπ rl dt dr (4) Como dt dr ( T T ) s, s, r r ln r ( T ) kπ L Ts, s, r (8) r ln r 7
19 Resistência Térmica A partir do resultado anterior torna-se evidente ue a resistência térmica associada à condução radial num cilindro toma a seguinte forma: R T r ln ΔT r R T (9) π.kl r.3. Condução Radial numa Esfera Consideremos agora a condução de calor numa esfera oca (Figura 9). Figura 9 Condução de calor numa casca esférica Tal como num cilindro, numa esfera sujeita a condução radial, a área de transferência de calor varia com a posição (A r 4πr ), pelo ue a taxa de transferência de calor, dada pela Lei de Fourier, é expressa em função de r da seguinte forma: r ka r dt 4kπ r dr dt dr () Realizando um balanço de energia ao elemento de volume infinitesimal da esfera considerado na Figura 9, obtém-se a euação (8), válida para condução em estado estacionário, num sólido sem geração de calor: 8
20 d r dr (8) Considerando ue a condutividade térmica (k) na esfera é constante, por aplicação da euação (8) à euação (), vem ue: d r d dt d dt - ka r r dr dr dr dr dr () A determinação da solução geral do perfil de temperaturas por condução radial em estado estacionário numa esfera não geradora de calor é conseguida resolvendo a euação diferencial (), sujeita a condições fronteira apropriadas. Da integração da euação diferencial () obtém-se a solução geral: d dr r dt r dr dt C dr dr dt C r C T r + C () Para obter as constantes de integração C e C introduzem-se na euação () as condições fronteira. Para o efeito, consideremos as seguintes condições fronteira (CF): CF: r r, T T s, CF: r r, T T s, Das condições fronteira: T T s, s, C r C r + C + C C C Ts, T r r T s, s, ( T T ) s, r r s, r Substituindo C e C na solução geral, obtém-se a distribuição de temperaturas, ue é a solução particular do problema: 9
21 ( T T ) s, s, T Ts, (3) r r r r Note ue, para condução radial de calor em estado estacionário através de uma esfera não geradora de calor e condutividade térmica constante, a temperatura varia com r de uma forma hiperbólica. Uma vez conhecido o perfil de temperaturas na esfera, é possível deduzir a euação ue permite calcular a taxa de transferência de calor por condução ue a atravessa, aplicando a Lei de Fourier: r ka r dt 4kπ r dr dt dr () Como dt dr ( Ts, Ts, ) 4kπ ( T T ) r r r r r r s, s, (4) Resistência Térmica Da definição de resistência térmica, diferença de temperatura dividida pela taxa de transferência de calor, obtém-se: R T ΔT r r R T (5) 4kπ r.4. Condução de Calor em Sólidos com outras Geometrias A metodologia utilizada anteriormente para determinar os perfis de temperatura em placas planas, cilindros e esferas não geradoras de calor sujeitas a condução em estado estacionário, pode ser facilmente generalizada a sólidos com outras geometrias,
22 salvaguardando ue a área de transferência de calor é conhecida em função da coordenada ue caracteriza a direcção da transferência de calor. Seja o exemplo do sólido apresentado na Figura. Isolante Superfície adiabática Figura Condução de calor em estado estacionário num sólido com uma geometria genérica Considerando a área de transferência de calor A x A(x), a taxa de transferência de calor é dada pela Lei de Fourier em função de x: x ka x dt dx ka x dt ( ) dx (6) Realizando um balanço de energia ao elemento de volume infinitesimal da esfera considerado na Figura, obtém-se a euação (8), válida para condução em estado estacionário, num sólido genérico sem geração de calor: d x dx (8) Considerando ue a condutividade térmica (k) no sólido é constante, por aplicação da euação (8) à euação (6), vem ue:
23 d x dx d dx - ka x dt dx d dx dt A x dx ( ) (7) A determinação da solução geral do perfil de temperaturas por condução em estado estacionário no sólido não gerador de calor é depois conseguida resolvendo a euação diferencial (7), sujeita a condições fronteira (CF) apropriadas (por exemplo CF: x x, T T ; CF: x x, T T )..5. Resistência Térmica: Analogia com a Teoria dos Circuitos Eléctricos Referimos anteriormente ue existe uma analogia entre a transferência de calor e a transferência de energia eléctrica. Assim, da mesma maneira ue a resistência eléctrica é associada à transferência de energia eléctrica, a resistência térmica, já definida, pode ser associada à transferência de calor. Uma vez conhecida essa analogia, a aplicação da teoria dos circuitos eléctricos e a representação de circuitos eléctricos análogos em transferência de calor permite de uma forma simples a compreensão e uantificação de problemas de transferência de calor, ue no caso de meios compostos se tornaria mais complexa doutra forma. Vamos de seguida demonstrar a existência dessa analogia. O circuito eléctrico mais simples é composto por uma resistência (R, em Ohms, Ω), ue uando atravessada por uma corrente eléctrica (I, em Ampère, A), provoca uma diferença de potencial (V V A V B, em Volts, V) no circuito: I R V A V B Da teoria dos circuitos eléctricos, pela Lei de Ohm, sabemos ue: V V A V B RI V RI (8) Resistências em Série Consideremos agora duas resistências em série:
24 I R I R I V A V B V C As resistências R e R provocam as seguintes diferenças de potencial no circuito, calculadas pela Lei de Ohm (a corrente eléctrica atravessa as duas resistências com a mesma intensidade I): V V A V B R I V V B V C R I Calculando a diferença de potencial global no circuito, obtém-se uma euação ue nos permite calcular a resistência euivalente do circuito, R e, como a soma das resistências individuais: V V A V C V B V C + V A V B V V R I + R I (R + R )I V (R + R ) I R e I (9) Em resumo, num circuito com duas resistências em série: R e R + R (3) Generalizando para N resistências em série: I R R I I V A V B V V A V B R e I, com R e R + R + + R N R i (3) N i 3
25 Resistências em Paralelo Consideremos agora duas resistências em paralelo: R I I I V A R V B I As resistências R e R provocam as seguintes diferenças de potencial no circuito, calculadas pela lei de Ohm (neste caso, ao contrário do ue sucedia com resistências em série, a corrente eléctrica atravessa as duas resistências com intensidades diferentes, I e I ): V V A V B V R I V V A V B V R I Por outro lado, pelo balanço de cargas aos nós do circuito, obtém-se uma euação ue nos permite calcular a resistência euivalente (R e ) de um circuito com resistências em paralelo: I I + I I V R + V R R + R V V R + R I V R e I Em resumo, num circuito com duas resistências em paralelo: R e (3) + R R 4
26 Generalizando para N resistências em paralelo: I R R I I I V A R N V B I N V V A V B R e I, com R e N (33) R i i Condução de Calor em Placas Planas em Série Vamos estabelecer agora de uma forma clara a analogia entre circuitos eléctricos e circuitos térmicos, começando por considerar um problema de condução de calor através de placas planas em série (Figura ). Fluído uente T,, h Fluído frio T,4, h 4 Figura Análogo eléctrico do circuito térmico de placas planas em série 5
27 R Ti Uma vez conhecidas as resistências térmicas de cada uma das placas L i k A i i, podemos obter pela Lei de Fourier a taxa de transferência de calor ue atravessa a parede composta por uma das seguintes expressões: ( T T ) s, Ts, T R TA R TA ( T T3 ) T T3 R TB R TB ( T T ) 3 s,4 T3 Ts,4 R TC R TC Determinando a diferença de temperaturas global, obtém-se uma euação ue nos permite calcular a resistência térmica euivalente do sistema de placas em série (R Te ) como a soma das resistências térmicas individuais: T s, T s,4 (T s, T s ) + (T T 3 ) + (T 3 T s,4 ) R TA + RTB + RTC (R TA + R TB + R TC ) ΔT T s, T s,4 R Te, com RTe R TA + R TB + R TC Dos resultados obtidos, torna-se evidente a analogia entre um circuito térmico em série e um circuito eléctrico: R TA R TB R TC T s, T s,4 Analogia (N resistências em série): V R e I ΔT R Te R e R + R R N R Te R T + R T + + R TN 6
28 Condução de Calor em Placas Planas em Paralelo Consideremos agora um problema de condução de calor através de placas planas em paralelo (Figura ). T T Figura Circuito térmico de placas planas em paralelo Pela definição de resistência térmica, euação (3), é possível determinar a diferença de temperaturas entre as duas extremidades da parede composta (T T ), usando alternativamente a resistência térmica da placa ou da placa : ΔT T Δ T T T R T T R T Realizando um balanço de energia à parede composta, obtém-se uma euação ue nos permite calcular a resistência térmica euivalente de placas em paralelo (R Te ): + ΔT ΔT + ΔT R T R + T R T R T ΔT + R R Te R R Te T R T T + R T 7
29 Dos resultados obtidos, torna-se evidente a analogia entre um circuito térmico em paralelo e um circuito eléctrico: R T T T R T Analogia (N resistências em paralelo): V R e I ΔT R Te R e R R R N R Te R T + R T R TN Generalização Os conceitos de resistência térmica em série e em paralelo podem facilmente ser generalizados a paredes compostas caracterizadas por uma configuração mista em série e em paralelo, como a apresentada na Figura 3. Figura 3 Parede composta caracterizada por placas planas em série e em paralelo Nesta situação, o análogo eléctrico e a resistência térmica euivalente seriam: 8
30 R Te R TE + + R + R R TF TG TH Uma vez determinada a resistência térmica euivalente do sistema, a taxa de transferência de calor,, pode ser determinada: ΔT R Te Note ue na parede composta do exemplo anterior foi admitida condução de calor unidimensional (foi assumido ue a temperatura na superfície normal ao eixo dos xx é isotérmica), apesar de na prática esta poder ser multi-dimensional (transferência de calor no eixo dos yy entre as placas em paralelo). Esta hipótese é tanto mais razoável uanto menor for a diferença de condutividade térmica dos materiais das placas dispostas em paralelo, k F k G. Resistência Térmica à Convecção É possível determinar também a resistência térmica associada à transferência de calor por convecção numa superfície, Figura 4. Da Lei de Arrefecimento de Newton, has (TS T ), deriva-se a resistência térmica associada à convecção: ΔT R T (34) ha s 9
31 Condução e Convecção em Simultâneo A utilização da analogia entre sistemas térmicos e circuitos eléctricos é particularmente útil em processos de transferência de calor envolvendo mais ue um mecanismo de transferência de calor. O caso mais simples será o da transferência de calor entre dois meios separados por uma placa plana (Figura 4). Fluído uente T,, h Fluído frio T,, h Figura 4 Transferência de calor por convecção e condução em simultâneo. (a) Distribuição de temperaturas; (b) Análogo eléctrico O análogo eléctrico associado ao circuito térmico considerado apresenta-se na Figura 4(b). Do conhecimento de cada resistência térmica envolvida é possível relacionar a diferença de temperaturas com a taxa de transferência de calor ue atravessa o circuito: 3
32 T T R, s, T ha T s, T s, R T L ka T s, T, R T3 ha Por sua vez, a diferença de temperaturas global é relacionada com a resistência térmica euivalente e com a taxa de transferência de calor ue atravessa o circuito: ΔT T, - T, R Te, com RTe R T + R T + R T3 + h A L ka + h A Em sistemas compostos é por vezes conveniente trabalhar com um coeficiente global de transferência de calor (U), definido por uma expressão análoga à Lei de Arrefecimento de Newton: R Te ΔT UA ΔT (35) onde ΔT é a diferença global de temperaturas e A é a área de transferência de calor escolhida como referência. Como é facilmente dedutível da euação anterior, o coeficiente global de transferência de calor relaciona-se com a resistência térmica euivalente do circuito: UA R Te (36) No caso do circuito térmico apresentado na Figura 4, o coeficiente global de transferência de calor calcula-se pela seguinte expressão: 3
33 UA R Te L + + h A ka h A U h L + + k h Determinação do Coeficiente Global de Transferência de Calor num Permutador de Calor de Tubos Concêntricos Consideremos o problema da transferência de calor entre dois fluídos num permutador de calor de tubos concêntricos (Figura 5). Fluído T e T, e T, e Fluído T i T, i r i r e r i r e T e T i T, i Figura 5 Permutador de calor de tubos concêntricos Assumindo ue o fluído se encontra a uma temperatura superior à do fluído, irá ocorrer transferência de calor do fluído para o fluído, havendo três resistências térmicas em série envolvidas: a resistência à transferência de calor por convecção entre o fluído e a superfície interna do tubo, a resistência à transferência de calor por condução no tubo e a resistência à transferência de calor por convecção da superfície externa do tubo e o fluído. Este processo térmico pode ser representado pelo seu análogo eléctrico: R T R T R T3 T, T i T e T, Recorrendo à definição de resistência térmica, é possível relacionar as diferenças de temperaturas envolvidas com a taxa de transferência de calor ue atravessa o sistema: 3
34 T, Ti R T h A i i T T i e R r ln r i T e π kl T T e, R T3 h A e e A resistência térmica euivalente, calcula-se do conhecimento das resistências térmicas individuais: R Te R T + R T + R T3 h i A i + r e ln r i π kl + h e A e Por sua vez, a taxa de transferência de calor pode-se calcular através do conhecimento da resistência térmica euivalente ou do coeficiente global de transferência de calor: UA ΔT R Te ΔT Como referido anteriormente, o coeficiente UA relaciona-se com a resistência térmica euivalente: UA R Te h A i i r e ln r i + π kl + h A e e Note agora ue, ao contrário do observado no sistema térmico da Figura 4, o valor numérico do coeficiente global de transferência de calor depende da área de 33
35 transferência de calor considerada. No caso em estudo A i A e, pelo ue poderemos obter dois valores para U: i) coeficiente global de transferência de calor baseado na área interna (A A i ) U i h i r e Ailn r i + π kl Ai + h A e e ii) coeficiente global de transferência de calor baseado na área externa (A A e ) U e Ae h A i i r e Aeln r i + π kl + h e Resistência Térmica de Contacto Até agora, na análise de paredes compostas, desprezamos a ueda de temperatura ue ocorre na interface entre dois materiais, ueda essa por vezes muito acentuada. Esta diferença de temperatura é atribuída à chamada resistência térmica de contacto, R TC, devida ao efeito da rugosidade das superfícies, ue origina falhas preenchidas com ar (Figura 6). 34
36 contacto T T L A L B falha Figura 6 Queda de temperatura devido à resistência térmica de contacto A taxa de transferência de calor pode ser determinada conhecendo o coeficiente de transferência de calor de contacto, h c, por uma euação similar a Lei de Arrefecimento de Newton, válida para a interface entre os dois materiais: h c ( T ) A T A B (37) Da definição de resistência térmica obtém-se a expressão ue permite calcular a resistência térmica de contacto: T R h A A TB TC R TC c h A c (38) O análogo eléctrico do processo térmico da Figura 6 consiste em três resistências em série: R TA R TC R TB T T A T B T 3 35
37 onde LA R TA, k A A LB R TB e k A B R TC h A c e ΔT T T R Te (R TA + R TC + R TB ) Outro Tipo de Resistências Térmicas Existem outros tipos de resistências térmicas não mencionadas aui, ue poderão ser pertinentes na eficiência de um processo de transferência de calor. Por exemplo, a presença de incrustações em tubagens, como as utilizadas em casas para auecimento. Estas tubagens, normalmente percorridas por água, possuem uma determinada eficiência energética uando novas. Com o tempo vão-se acumulando impurezas e a eficiência (transferência de calor) diminui devido ao aparecimento de uma resistência adicional: T e T i T, i T, e T e T i T T, e deposição de impurezas R Ti R TS R Te R Ti T, i Ti T e T, e T, i T R TI T i R TS T e R Te T, e Exercício Duas barras cilíndricas de aço (k 6.3 W/mK) estão suportadas em duas superfícies a ºC e ºC (Figura 7). O diâmetro das barras é de 3 cm e o seu comprimento é de cm. As duas barras são unidas por compressão à pressão de 5 atm, sendo o coeficiente de transferência de calor de contacto nestas condições de 894 W/m ºC. Calcule o débito axial de calor e a ueda de temperatura na interface das barras. 36
38 ºC 3 cm ºC cm cm Figura 7 Transferência de calor entre duas superfícies através de duas barras cilíndricas comprimidas entre si Resolução A melhor forma de calcular a taxa de transferência de calor,, ue atravessa o sistema, uma vez ue se conhecem as temperaturas nas suas extremidades, é através do cálculo da resistência térmica euivalente, e da sua relação com : R Te ΔT Assim, começamos por considerar o análogo eléctrico do circuito térmico (três resistências em série, à condução em cada uma das barras e de contacto entre as barras): R T R TC R T ºC T T ºC A resistência térmica euivalente é dada por R Te R T + R T + R TC. Calculemos as resistências térmicas envolvidas: 37
39 R T L ka π ( ) K/W R TC h C A π ( ) K/W R T L ka π ( ) K/W R Te K/W A taxa de transferência de calor pode agora ser calculada: R Te ΔT 8.5 ( ) 5.5 W Para obter a ueda de temperatura na interface das barras, usa-se a resistência térmica de contacto: R ( T T ) T T ΔTC R TC º C TC.6. Condução em Sistemas com Geração Interna de Energia Até agora lidamos apenas com problemas em estado estacionário em sistemas sem geração interna de energia. Queremos agora considerar problemas em ue existe geração de energia no interior do sistema. Exemplos típicos são a geração de calor em resistência eléctricas (efeito de Joule) ou uma reacção uímica exotérmica num meio homogéneo. Vamos de seguida analisar algumas situações. 38
40 Placa Plana com Geração Homogénea de Energia Consideremos a placa plana esuematizada na Figura 8, com geração homogénea de energia por unidade de volume, área de transferência de calor A e superfícies mantidas à temperatura T S. dx Figura 8 Condução de calor numa placa plana com geração homogénea de energia e condições fronteira simétricas Devido à geração homogénea de calor e às condições fronteira simétricas, a distribuição de temperaturas apresenta simetria sobre o eixo central da placa ( x) dt( x) dt( x) dt T ( x) T( x) e ; em particular, para x,. Vamos dx dx dx definir V como o débito de energia gerada por unidade de volume (W/m 3 ) e realizar um balanço de energia em estado estacionário a um elemento de volume da placa de espessura dx: v Adx x x + dx dx x x+ dx x dx + x x + dx x + V Adx V A dx 39
41 x dx d + x x uando dx Lim V A V A dx (39) dx dx Aplicando a Lei de Fourier dt x ka à expressão anterior, obtém-se uma dx euação diferencial ordinária de ª ordem ue caracteriza o problema: d T ka dx V d T v A + dx k (4) Esta euação pode ser resolvida em ordem a T de forma a obter a distribuição de temperaturas na placa. Como condições fronteira (CF) podemos considerar as seguintes: dt CF: x, (condição de simetria) dx CF: x L, T T S Por integração da euação (4), obtém-se a solução geral do problema: V T x + Cx + k C (4) Das condições fronteira: C C T V S + L k Substituindo C e C na solução geral, obtém-se a distribuição de temperaturas, ue é a solução particular do problema: 4
42 V T TS + k ( L x ) (4) Obtém-se um perfil parabólico com simetria sobre o eixo x, onde ocorre a temperatura máxima: V TS + L (43) k T Substituindo T S da euação anterior na euação (4), obtém-se uma expressão ue combinada novamente com a euação (4), permite obter a distribuição de temperaturas com a seguinte apresentação alternativa: T T T T S x L (44) A taxa de transferência de calor pode ser calculada em ualuer ponto da placa, substituindo a euação (4) na Lei de Fourier para a condução. Note ue, ao contrário do ue sucede em problemas sem geração interna de energia, a taxa de transferência de calor em problemas com geração de energia não é independente de x. Placa Plana com Geração Não Homogénea de Energia Consideremos agora uma placa plana, exactamente com as mesmas características ue a apresentada na Figura 8, mas com geração não homogénea de energia. Supor ue o débito de energia gerada por unidade de volume varia com a temperatura de acordo com a relação apresentada na Figura 9. 4
43 . V. ( V ) S V V S [ + β( T T )] S T S T Figura 9 Dependência do débito de energia gerada por unidade de volume com a temperatura Do balanço de energia em estado estacionário obtém-se a euação diferencial ordinária de ª ordem, deduzida anteriormente, euação (4): d T v + dx k (4) Esta euação pode ser resolvida em ordem a T de forma a obter a distribuição de temperaturas na placa. Como condições fronteira (CF) podemos considerar novamente as seguintes: dt CF: x, (condição de simetria) dx CF: x L, T T S A diferença deste problema para o da placa plana com geração homogénea de energia, reside no facto de V variar com a temperatura, pelo ue a euação diferencial a resolver toma o seguinte aspecto: 4
44 43 ( ) [ ] T T β k dx T d S S v + + (45) Para resolver esta euação é útil considerar a seguinte mudança de variável: θ T T S > dx T d dx θ d (46) Introduzindo a nova variável na euação (45) obtém-se a seguinte euação: βθ k k dx θ d S V S v + + (47) sujeita às condições fronteira: CF: x, dx dθ CF: x L, θ Para resolver a euação (47), consideremos uma nova mudança de variável: S V S V S V S v dx θ d β k dx φ d dx dθ β k dx dφ βθ k k φ + Introduzindo a nova variável na euação (47) e considerando β k α S V, obtém-se a seguinte euação:
45 d φ + αφ (48) dx sujeita às condições fronteira: dφ CF: x, dx CF: x L, V θ k S A euação (48) é uma euação diferencial ordinária de ª ordem homogénea, ue se pode resolver por determinação das raízes da sua euação característica: λ + α λ ± αi Pelas relações de Euler obtém-se a solução geral do problema: ( αx) C sen( αx) φ C cos + (49) Das condições fronteira, obtém-se C e C : C C cos V S ( αl) Substituindo C e C na solução geral, encontramos a solução para ϕ: 44
46 V φ k S cos cos ( αx) ( αl ) (5) Introduzindo as variáveis originais, obtém-se a solução particular do problema: v φ k S V + k S β V S cos ( ) ( αx) T - TS k cos( αl ) cos( αx) - T β cos( αl ) T S (5) A solução particular apresenta um perfil parabólico com simetria sobre o eixo x, onde ocorre a temperatura máxima: T TS + (5) β cos( αl ) Substituindo T S da euação anterior na euação (5), obtém-se uma expressão ue combinada novamente com a euação (5), permite deduzir a distribuição de temperaturas com a seguinte apresentação alternativa: T T T T S cos cos ( αx) ( αl) (53) Cilindro com Geração Homogénea de Energia Existem várias situações em ue ocorre geração de calor em sistemas de geometria radial. Considerar por exemplo um fio condutor de electricidade (Figura ). 45
47 Fluído frio T, h r + dr r dr r T S Figura Condução num cilindro com geração homogénea de energia Em condições de estado estacionário, a taxa global de geração de calor no cilindro deve igualar a taxa de calor libertada por convecção para um fluído adjacente ao cilindro. Esta condição permite manter a superfície do cilindro a uma temperatura constante T S. Para determinar a distribuição de temperaturas no cilindro, vamos realizar um balanço de energia em estado estacionário ao elemento de volume de espessura dr representado na Figura : r + dr r + V dv onde dv πrdrl r dr + r π rl V dr r dr d + r r uando dr Lim π rl V π rl V dr dr dr dt dt Aplicando a Lei de Fourier r ka r kπ rl à euação anterior, dr dr obtém-se uma euação diferencial ordinária de ª ordem ue caracteriza o problema: 46
48 kπ d L dr dt r dr d dt v π rl V r + r dr dr k (54) Esta euação pode ser integrada de forma a obter a distribuição de temperaturas no cilindro. Como condições fronteira podemos considerar as seguintes: CF: r r, T T S CF: r r, Rs πr L V (o calor gerado é libertado por convecção) A euação (54) pode ser resolvida pelo método de separação de variáveis, obtendo-se a seguinte solução: V r r + k dt dr C Repetindo o procedimento, obtém-se a solução geral do problema: V T r + Cln r + 4k C (55) Das condições fronteira, determina-se C e C : C C T V S + r 4k Substituindo C e C na solução geral, obtém-se a distribuição de temperaturas, ue é a solução particular do problema: 47
49 T T S ( r r ) V + 4k (56) A solução obtida apresenta um perfil parabólico com simetria sobre o eixo r, onde ocorre a temperatura máxima: V TS + r (57) 4k T Substituindo T S da euação anterior na euação (56), obtém-se uma expressão ue, combinada novamente com a euação (56), permite obter a distribuição de temperaturas com a seguinte apresentação alternativa: T T T T S r r (58) A taxa de transferência de calor pode ser calculada em ualuer ponto do cilindro, substituindo a euação (57) na Lei de Fourier para a condução. Condução com Geração de Energia Nuclear por uma Fonte de Forma Esférica A metodologia estudada anteriormente para deduzir as distribuições de temperaturas em placas e cilindros com geração de energia, pode ser estendida a problemas mais complexos. Considerar um sólido esférico com geração de energia revestido por uma camada de isolante (Figura ). isolante geração de energia V T R T S R S Figura Condução com geração de energia nuclear por uma fonte de forma esférica 48
50 Supor ue o débito de energia gerada por unidade de volume na zona de geração de energia não é homogéneo e ue varia com o raio da esfera de acordo com a seguinte relação: r + β R V V Vamos realizar um balanço de energia em estado estacionário a um elemento de volume da esfera de espessura dr: dr r + dr r R T r + dr r + V dv onde dv 4πr dr r dr + r 4π r V dr r dr d + r r uando dr Lim 4π r V 4π r V dr dr dr (59) Na zona isolante não existe geração de calor, pelo ue, como estudado em problemas de condução de calor em esferas em estado estacionário: d r dr (8) 49
51 Para determinar a distribuição de temperaturas na esfera (zona de geração de energia e zona isolante) é necessário resolver as euações (59) e (8), podendo-se considerar as seguintes condições fronteira (CF): Zona de Geração de Energia CF: r, dt é finito dr (caso contrário haveria uma descontinuidade em T) CF: r R, r + r (o calor ue sai da zona de geração de energia entra na zona isolante) Zona Isolante CF3: r R, T T + T (a temperatura na interface zona de geração de energia/zona isolante é T ) CF4: r R S, T T S Na zona de geração de energia: r ka r dt 4kπ r dr dt dr 4kπ d dr r dt 4π r dr V d dr r dt dr + v r k d dr r dt r dr k V + β r R V k r r + β R 4 Integrando a euação anterior obtém-se: V dt dr k r 3 3 r + β 5R C + r 5
52 5 Da condição fronteira CF, para dr dt ser finito, necessariamente C. + 3 V 5R r β 3 r k dr dt (6) Zona de Geração de Energia Na zona isolante: r r C dr dt C dr dt r dr dt r dr d dr d Da condição fronteira CF, como + R R, obtém-se: β 3 k R C R C k 5 R β 3 R dr dt A k dr dt ka I 3 V I V R R I R R I 3 V r k 5 β 3 R dr dt + (6) Zona Isolante Integrando agora esta euação e aplicando a condição fronteira CF4 obtém-se a distribuição de temperaturas na zona isolante: + S I 3 V S R r 5 β 3 3k R T T (6) Zona Isolante
53 5 Integrando a euação (6), obtém-se a solução geral da distribuição de temperaturas na zona de geração de energia: 3 4 V 3 V C R r β 6 r k T 5R r β 3 r k dr dt Por aplicação da condição fronteira CF3 (r R, T T T + ) às euações anteriores, obtém-se a distribuição de temperaturas na zona de geração de energia: S I 3 V S 3 V - R R 5 β 3 3k R T T C R R β 6 R k T V S I 3 V S 3 R R β 6 R k R R 5 β 3 3k R T C V S I 3 V S R r 3β R r 6k R R R 5 3β 3k R T - T Zona de Geração de Energia (63).7. Alhetas Uma alheta é uma extensão de superfície ue tem como objectivo aumentar a área disponível para a transferência de calor por convecção dessa superfície para um fluído adjacente. Considerar a parede plana apresentada na Figura.
54 Figura Utilização de alhetas para aumentar a transferência de calor de uma superfície. (a) superfície não alhetada; (b) superfície alhetada Considerando ue a temperatura da superfície (T S ) e o coeficiente convectivo de transferência de calor (h) se mantém constantes, podemos aumentar a taxa de transferência de calor por convecção da superfície para o fluído adjacente, aumentando a área de superfície através da ual a convecção ocorre. Tal pode ser conseguido, aplicando alhetas à superfície da parede (Figura (b)). Existem inúmeras aplicações práticas da utilização de alhetas no dia-a-dia. Como exemplos, de referir as superfícies alhetadas encontradas em motores, em radiadores e em processadores. Existem também várias configurações possíveis para as alhetas, sendo comum encontrar alhetas rectangulares, circulares, piniformes ou triangulares (Figura 3). Figura 3 Configurações possíveis para alhetas. (a) alheta rectangular de secção recta constante; (b) alheta triangular; (c) alheta circular de espessura constante; (d) alheta piniforme 53
55 Euação Geral das Alhetas Para determinar a taxa de transferência de calor possível obter por aplicação de uma alheta a uma superfície, precisamos primeiro de conhecer a distribuição de temperaturas na alheta. À semelhança da metodologia utilizada nas secções anteriores nas deduções das expressões de distribuição de temperaturas, começamos por realizar um balanço de energia a um elemento de volume diferencial apropriado. Considerar para o efeito a superfície alhetada apresentada na Figura 4. S(x) c A(x) Figura 4 Superfície alhetada e elemento de volume diferencial para a realização de balanços de energia Considerando transferência de calor em estado estacionário, condução unidimensional ao longo do eixo dos xx, condutividade térmica do material (k) e coeficiente convectivo de transferência de calor (h) constantes, o problema fica bastante simplificado. Realizando o balanço de energia ao elemento de volume diferencial considerado obtém-se: x x+ dx + c (64) 54
56 A taxa de transferência de calor por convecção é dada pela seguinte expressão, resultante da aplicação da Lei de Arrefecimento de Newton para a convecção: c ( T T ) hp(x)dx(t T ) hs(x) (65) onde dx representa a espessura do elemento de volume diferencial, S(x) a área disponível para convecção e P(x) o perímetro da alheta, ue podem variar com x. Substituindo (65) em (64) obtém-se: x + dx x + hp(x)dx(t T ) Considerando dx : Lim dx x+ dx x d x + hp(x)(t T ) dx dx + hp(x)(t T ) (66) Por sua vez, da lei de Fourier para a condução sabemos ue: dt x ka(x) dx onde A(x) é a área disponível para a condução. Substituindo na euação (66), obtém-se a euação geral das alhetas, válida para alhetas genéricas: d dx dt ka(x) dx hp(x)(t T ) (67) A solução desta euação para uma alheta com uma geometria específica (sujeita a condições fronteira apropriadas) permite obter a distribuição de temperaturas, ue pode ser usada com a Lei de Fourier para calcular a taxa de transferência de calor por condução em ualuer posição x da alheta. 55
57 .8. Alheta Rectangular com Secção Recta Constante Comecemos por resolver a euação (67) aplicada à geometria de alhetas mais simples: alhetas rectangulares de secção recta constante ou, mais genericamente, alhetas de secção recta constante (Figura 5). Figura 5 Alhetas de secção recta constante Cada alheta encontra-se ligada a uma superfície de base mantida a uma temperatura T T b e estende-se através de um fluído à temperatura T. Note ue a área da(x) de secção recta (A(x) A c A) é constante (logo ), bem como o perímetro dx (P(x) P). A euação geral das alhetas (euação (67)) toma assim a seguinte forma: d dx dt ka(x) dx d T hp hp(x)(t T ) ( T T ) (68) dx ka Para simplificar esta euação consideremos a transformação da variável dependente (T), definindo a variável diferença de temperatura (θ) como: θ T - T 56
58 dθ dt Sendo T uma constante,. Aplicando a mudança de variável definida à dx dx hp euação (68) e considerando β, obtém-se a seguinte euação diferencial de ª ka ordem homogénea, linear e de coeficientes constantes: d θ β θ (69) dx A solução geral desta euação, obtém-se da respectiva euação característica, tomando a seguinte forma: θ C e βx + C e -βx (7) Para obter as constantes C e C é necessário especificar condições fronteira apropriadas. Uma das condições pode ser definida em termos da temperatura na superfície da base da alheta (x ): CF: x, T T θ θ T - T A ª condição pode ser definida na extremidade da alheta (x L). Vamos considerar na análise seguinte três situações físicas diferentes (três casos). CASO : A temperatura na extremidade da alheta é conhecida CF: x L, T T L θ θ L T L - T Substituindo as condições fronteira CF e CF na solução geral do problema, obtém-se o seguinte sistemas de euações: C + C θ βl Ce + Ce βl θ L 57
59 Resolvendo este sistema em ordem a C e C e substituindo na euação (7), após alguma manipulação, obtém-se a solução particular do problema: θ θ θ θ L βx βx β( x L) β( x L) ( e e ) ( e e ) βl βl e e Sabendo ue a seguinte forma: x x x x e e e + e senh(x) e cosh(x) a solução particular toma θ θ L senh(β x) senh[ β(x L) ] θ (7) senh(β L) θ Quando a alheta é muito longa (alheta infinita) obtém-se uma situação particular do CASO (Figura 6): L, θ L θ θ βx e (7) T T T oo x Figura 6 Perfil de temperaturas numa alheta infinita 58
60 CASO : Alheta isolada na extremidade (Figura 7) Fluído T, h Figura 7 Alheta isolada na extremidade dt dθ CF: x L, dx dx x L Substituindo as condições fronteira CF e CF na solução geral do problema, obtém-se o seguinte sistemas de euações: C + C θ βl Cβe Cβe βl Resolvendo este sistema em ordem a C e C e substituindo na euação (7), após alguma manipulação, obtém-se a solução particular do problema: θ θ [ L) ] cosh β(x (73) cosh(β L) CASO 3: Calor dissipado por convecção na extremidade da alheta (Figura 8) Fluído T, h Figura 8 O calor ue chega por condução à extremidade da alheta é dissipado por convecção 59
61 dt dθ h ka - θ dx dx k CF: x L, ha( T - T ) x L Substituindo as condições fronteira CF e CF na solução geral do problema, obtém-se o seguinte sistemas de euações: C + C θ βl Cβe Cβe βl h - k βl βl ( C e + C e ) Resolvendo este sistema em ordem a C e C e substituindo na euação (7), após alguma manipulação, obtém-se a solução particular do problema: θ θ h cosh[ β(l x) ] + senh[ β(l x) ] βk (74) h cosh(β L) + senh(β L) βk O perfil de temperaturas para este caso encontra-se esuematizado na Figura 9. Figura 9 Perfil de temperaturas obtido no CASO 3 6
62 Eficiência da Alheta Para avaliar a performance de uma alheta num determinado sistema térmico, é útil calcular a sua eficiência, η f. A eficiência de uma alheta define-se como a razão entre a taxa de energia dissipada pela alheta e a taxa de energia ue seria dissipada se toda a superfície estivesse à temperatura da base da alheta: η f (75) representa assim a taxa máxima de energia ue a alheta poderia dissipar por convecção numa situação idealizada em ue toda a superfície se encontraria à temperatura da base da alheta: ha T hplθ ( T T ) hpl( T T ) Para saber a eficiência de uma alheta estamos agora particularmente interessados em calcular a taxa de energia dissipada pela alheta. Tal pode ser conseguido de uma forma simples sabendo ue toda a energia dissipada na alheta entra necessariamente por condução na sua base. Assim, aplicando a Lei de Fourier para a condução na base da alheta, obtém-se : dt dθ ka ka () dx dx x x Desta forma, para cada um dos casos abordados anteriormente podemos calcular a taxa de energia dissipada pela alheta e a respectiva eficiência. 6
63 CASO θ kaβ cosh(β L) senh(β L) θ L (76) η f βl θ cosh(β L) θ senh(β L) L (77) Na situação particular do CASO em ue a alheta é muito longa (alheta infinita): kaβ θ (78) f η βl (79) CASO dθ ka dx x kaβ tgh(β L) (8) f η tgh(β L) βl (8) CASO 3 dθ ka kaβ θ dx x h + tgh(β L) βk h + tgh(β L) βk (8) 6
64 η f βl h + tgh(β L) βk h + tgh(β L) βk (83) Chegados ao final desta secção, dedicada a alhetas rectangulares com secção recta constante, recordar o ue foi dito no início de ue todas as expressões deduzidas para alheta rectangular com secção recta constante são válidas para outras geometrias com secção recta constante (A e P constantes). Ver exemplo na Figura Alheta Circular de Espessura Constante A análise do comportamento térmico de alhetas torna-se mais complexa se a alheta for de secção recta não uniforme. Neste caso, A(x), na euação geral das alhetas (euação (67)), é uma função de x, pelo ue a euação diferencial resultante toma uma forma diferente da euação anteriormente deduzida para alhetas de secção recta constante (euação (68)). Consideremos a alheta circular de espessura constante representada na Figura 3, onde a coordenada x é substituída por r (este tipo de alheta é normalmente usado para aumentar a transferência de calor em tubos circulares). L R R Figura 3 Alheta circular de espessura constante Embora a espessura da alheta seja uniforme (L é independente de r), a área de secção recta (A(r) (πr)(l) 4πrL) e o perímetro da superfície da alheta (P(r) (πr) 4πr) variam com r. Substituindo, x r, A(r) e P(r) na euação geral das alhetas, obtém-se uma euação diferencial ordinária de ª ordem: 63
65 d dr dt ka(r) dr d T dt h hp(r)(t T ) r + r( T T ) (84) dr dr kl Considerando as seguintes mudanças de variável: hp h β, z βr, θ T - T ka kl obtém-se a seguinte expressão: z d θ dθ + z z θ (85) dz dz A expressão anterior é uma euação de Bessel modificada de ordem zero. A sua solução geral tem a seguinte forma: θ C I (z) + C K (z) (86) I e K são funções de Bessel modificadas de ordem zero, de ª e ª espécie, respectivamente. Considerando as seguintes condições fronteira: CF: A temperatura na base da alheta é conhecida r R, T T z z βr, θ θ T - T CF : A extremidade da alheta está isolada dt dθ r R, z z βr, dr dz avalia-se C e C e obtém-se a distribuição de temperaturas na alheta: θ θ K(z)I (z) + I(z)K (z) (87) K (z )I (z ) I (z )K (z ) + 64
66 di (z) dk (z) I(z) e K(z) são funções de Bessel modificadas de ordem dz dz um, de ª e ª espécie, respectivamente. Os valores das funções de Bessel modificadas podem ser obtidos em máuinas de calcular programadas para o efeito ou em tabelas. A taxa de transferência de calor dissipada na alheta obtém-se da taxa de energia ue entra na alheta pela base: ka(r ) dt dr r R 4kπk Lβ dθ dz z z 4kπ R Lβ θ I(z)K(z) K(z)I(z) K (z )I (z ) + I (z )K (z ) (88) Finalmente, a partir desta expressão podemos calcular a eficiência da alheta: η f π h R I (z )K (z ) K (z )I (z ) ( R R ) θ β( R R ) K (z )I (z ) + I (z )K (z ) (89) Exercício Considere uma alheta circular de espessura constante (Figura 3) com as seguintes dimensões características: R cm, R 4 cm e L cm. A condutividade térmica da alheta é 9 W/mºC e o coeficiente convectivo de transferência de calor da superfície da alheta para a vizinhança é 4 W/m ºC. Considerando ue a temperatura na base da alheta é de ºC e ue a vizinhança se encontra a 5ºC, calcule: a) A eficiência da alheta b) A potência calorífica dissipada c) A temperatura em r cm, r 3 cm e r 4 cm Resolução a) Para calcular a eficiência da alheta utiliza-se a euação (89): β h kl 4 9 β m 3 65
67 z βr /3 z βr 4/3 I (z ) I (/3).797 K (z ) K (/3).7658 I (z ) I (/3).6899 K (z ) K (/3).785 I (z ) I (4/3).864 K (z ) K (4/3) η f 3 - [( 4 ) ( ) ] b) Para calcular a potência calorífica dissipada utiliza-se a euação (88): 4kπ R Lβ θ I (z )K (z ) K (z )I (z ) K (z )I (z ) + I (z )K (z ) 4π 9 3 ( 5) W c) Para calcular a temperatura numa ualuer posição da alheta utiliza-se a euação (87): r cm z βr. /3 3 I (z).44 K (z) θ θ K(z)I (z) + I(z)K (z) K (z )I (z ) + I (z )K (z ) T (r cm) x( - 5) 76.3ºC 66
68 r 3 cm z βr. 3 3 I (z).667 K (z).44 θ θ K (z )I (z) + I (z )K (z) K (z )I (z ) + I (z )K (z ).567 T (r 3 cm) x( - 5) 67.ºC r 4 cm z βr. 4 4/3 3 I (z) K (z).6637 θ θ K (z )I (z) + I (z )K (z) K (z )I (z ) + I (z )K (z ).5857 T (r cm) x( - 5) 64.6ºC Esboço do perfil de temperaturas na alheta: 67
69 5 T(ºC) r(cm).. Determinação da Eficiência de Alhetas por Métodos Gráficos Uma forma expedita para o cálculo da eficiência de alhetas é através da utilização de gráficos produzidos para o efeito para alhetas de diferentes geometrias (Figura 3 e Figura 3). Figura 3 Eficiência de alhetas rectangulares, triangulares e parabólicas 68
70 Figura 3 Eficiência de alhetas circulares de espessura constante Uma vez conhecida a eficiência de uma alheta, pode-se com facilidade calcular a taxa de transferência de calor dissipada, recorrendo à definição de eficiência: ηf η ha ( T T ) f T (9).. Eficiência Global de Superfícies Alhetadas Enuanto a eficiência de uma alheta, η f, caracteriza a performance de uma única alheta, a eficiência global de uma superfície alhetada, η s, caracteriza a performance de um conjunto de alhetas e da superfície de base à ual estão ligadas. Na Figura 33 mostram-se duas superfícies alhetadas, onde S representa a distância entre alhetas (passo). 69
71 Figura 33 Superfícies alhetadas. (a) alhetas rectangulares; (b) alhetas circulares A eficiência global de uma superfície alhetada define-se pela seguinte expressão: η s T (9) MAX onde T representa a taxa de transferência de calor dissipado pela superfície das alhetas e pela superfície de base (primária) exposta (área total convectiva A T ) e MAX a taxa de transferência de calor ue ocorreria se todo o sistema estivesse à temperatura da superfície primária (T T b MAX ha T ( T T ) ha Tθ ). Considerando uma superfície alhetada com N alhetas, cada uma com uma área superficial convectiva A A, e definindo A B como a área total convectiva da superfície primária, a área total convectiva da superfície alhetada é A T NA A + A B. A taxa total de transferência de calor dissipado por convecção pelas alhetas e pela superfície primária pode então ser expressa da seguinte maneira: T ha B ( T T ) + N A ha Bθ + Nηf ha Aθ onde h é assumido como tendo o mesmo valor para a superfície da alheta e para a superfície de base e η f corresponde à eficiência de uma alheta. Relacionando a área total da superfície alhetada com a área da superfície de base (A T A B + A A ), obtém-se: 7
72 T h A [( A T NA A ) + Nηf A A ] θ h ( ηf ) N A Tθ A A T (9) Substituindo a euação (9) e MAX na euação (9) obtém-se a euação ue permite calcular a eficiência de uma superfície alhetada: η s A A ( ηf )N (93) A T Resistência térmica Recordando a definição de resistência térmica, a euação (9) pode ser usada para deduzir uma expressão para o cálculo da resistência térmica de uma superfície alhetada: R Te θ θ (94) ηsha Tθ ηsha T T onde R Te corresponde à resistência térmica euivalente devido às resistências térmicas em paralelo de condução/convecção nas alhetas e convecção na superfície primária. A Figura 34 ilustra os circuitos térmicos correspondentes numa superfície alhetada. Figura 34 Superfície alhetada e circuito térmico análogo 7
73 Podemos deduzir uma expressão alternativa para o cálculo da resistência térmica euivalente de uma superfície alhetada, recorrendo às resistências térmicas das alhetas e da superfície primária. Consideremos uma superfície alhetada com N alhetas de área superficial A A e N B superfícies primárias, cada uma com uma área superficial A B, de modo ue A B N B A B e A T A B + NA A. A resistência térmica à transferência de calor em cada alheta é obtida da eficiência de alheta: Ai η f R ha A TAi ( T T ) ηf ha A (95) A resistência térmica associada à transferência de calor por convecção em cada superfície primária obtém-se a partir da Lei de Arrefecimento de Newton para a convecção: Bi ha B ( T T ) R TBi ha B (96) Estando as N resistências térmicas devidas às alhetas e as N B resistências térmicas devidas às superfícies primárias em paralelo, calcula-se a resistência térmica euivalente da superfície alhetada da seguinte forma: R Te + R TAi R TBi Nη f ha A + N B A B h R Te h ( A + Nη A ) B f A (97) 7
74 Capítulo 3 Condução de Calor em Estado Transiente No capítulo anterior abordamos problemas de transferência de calor em estado estacionário, deduzindo euações para a determinação do perfil de temperaturas e da taxa de transferência de calor em várias situações. Uma característica comum a todos os casos abordados é ue, para uma dada coordenada espacial, a temperatura e a taxa de transferência de calor são constantes com o tempo, isto é, T e são apenas funções da posição (T f(x) e f(x)). Não consideramos ainda situações nas uais as condições variam com o tempo. Por exemplo, se tivermos um sólido inicialmente a uma temperatura constante T i e subitamente o expusermos a um fluido a uma temperatura T T i, então irá ocorrer um processo de transferência de calor em estado transiente (Figura 35), onde a temperatura em cada ponto do sólido, bem como a taxa de transferência de calor irão variar com o tempo (T f(x, t) e f(x, t)). Estas variações irão continuar até se obter uma nova temperatura no sólido em estado estacionário. Figura 35 Arrefecimento de um sólido considerando diferentes resistências interna e externa à transferência de calor (conceitos a abordar na secção 3..) No exemplo dado, a energia é transferida por convecção e por radiação da superfície do sólido para a vizinhança. Simultaneamente ocorre transferência de calor por condução do interior do sólido para a superfície, diminuindo a temperatura do sólido em cada ponto até se atingir uma nova temperatura de estado estacionário. 73
75 O objectivo deste capítulo é desenvolver procedimentos para a determinação da distribuição de temperaturas num sólido sujeito a um processo de transferência de calor em estado transiente, assim como para a determinação da taxa de transferência de calor da superfície de um sólido para a vizinhança. A natureza do procedimento a adoptar depende de hipóteses possíveis de admitir para o processo em estudo. Antes de avançarmos para a análise dos processos de transferência de calor em estado transiente, vamos ver alguns conceitos fundamentais necessários para a admissão de algumas hipóteses e para o desenvolvimento de procedimentos analíticos: capacidade calorífica, resistências externa e interna e número de Biot. 3.. Capacidade Calorífica Por definição, a capacidade calorífica de uma substância (C) é a uantidade de energia necessária para elevar de ºC a temperatura dessa substância. Assim, se uma substância de capacidade calorífica C sofrer uma variação de temperatura ΔT, é possível determinar a energia transferida a essa substância pela seguinte euação: Q CΔT (98) m A capacidade calorífica (J/ºC, em unidades SI) é uma propriedade extensiva, pois depende da massa da substância. Por isso, é comum apresentar em tabelas o seu valor normalizado pela massa, o designado calor específico (c P ): C c P (J/gºC) (99) m Substituindo (99) em (98), obtém-se outra euação ue permite calcular a energia transferida a uma substância cuja temperatura variou ΔT unidades: Q mc ΔT () P 74
76 Normalmente, como c P depende da temperatura, a energia necessária para elevar a temperatura de uma substância de uma temperatura inicial T a uma temperatura final T obtém-se por integração: T dq mc dt Q m c dt () P T P Voltaremos a esta euação mais adiante. 3.. Resistências Interna e Externa Supor um sólido inicialmente a uma temperatura T, subitamente exposto a um fluído mantido a uma temperatura T < T. Imediatamente após o contacto do sólido com o fluído, como T T, irá observar-se perda de calor por convecção da superfície do sólido para a vizinhança. Simultaneamente, haverá transferência de calor por condução do interior do sólido para a superfície. A taxa de transferência de calor libertado por convecção variará com o tempo, uma vez ue a temperatura da superfície varia, bem como o correspondente gradiente de temperatura entre a superfície e o fluído (T - T ). Estando a condução e a convecção envolvidos no mecanismo de transferência de calor, haverá duas resistências à transferência de calor a considerar: resistência interna devida à condução e resistência externa devida à convecção. Dependendo da ordem de grandeza das resistências envolvidas podemos considerar 3 casos num processo transiente de transferência de calor. CASO A resistência interna à transferência de calor é desprezável Um exemplo deste caso é o arrefecimento de um bloco metálico bom condutor exposto ao ar ambiente (Figura 36). Devido à elevada condutividade dos metais, o calor perdido na superfície do sólido por convecção para o ar é rapidamente reposto do interior, resultando num gradiente de temperatura peueno no interior do sólido (T(x, t) T(t)). Diz-se ue a convecção é dominante. Na prática, pode-se considerar ue todo o sólido está a uma temperatura uniforme em ualuer instante de tempo. A 75
77 diferença de temperaturas a considerar na transferência de calor é apenas entre o sólido e o fluído adjacente. Figura 36 Distribuição de temperaturas em estado transiente num sólido arrefecido por convecção (resistência interna desprezável) CASO A resistência externa à transferência de calor é desprezável Um exemplo deste caso é o arrefecimento de um bloco mau condutor uando inserido em água fria (Figura 37). Devido ao elevado coeficiente convectivo de transferência de calor existente entre a superfície dum sólido e um líuido, uando o bloco é inserido na água, ocorre uma transferência de calor uase instantânea da superfície para o fluído, provocando a diminuição da temperatura da superfície para valores muito próximos de T. Por outro lado, devido à baixa condutividade térmica do material, o calor perdido na superfície do sólido por convecção não consegue ser compensado do interior, resultando na formação de uma distribuição de temperaturas no interior do sólido (T T(x, t)). Diz-se ue a condução é dominante. Figura 37 Distribuição de temperaturas em estado transiente num sólido arrefecido por convecção (resistência externa desprezável) 76
78 CASO 3 A resistência interna e a resistência externa à transferência de calor são ambas significativas Em alguns casos não é possível desprezar nenhuma das resistências (Figura 38). Figura 38 Distribuição de temperaturas em estado transiente num sólido arrefecido por convecção (resistência interna e externa não desprezável) 3.3. Número de Biot O número de Biot, é um parâmetro adimensional definido da seguinte forma: hv Bi () ka onde V representa o volume do sólido e A a área superficial. O número de Biot pode ser interpretado fisicamente como a razão entre as resistências térmicas à condução interna e à convecção externa. Por exemplo, para placas planas, o desenvolvimento da definição do número de Biot confirma o referido significado: Bi hv ka V ka h L ka ha Resistência térmica à condução interna Resistência térmica à convecção externa A avaliação do número de Biot num processo transiente de transferência de calor envolvendo condução e convecção permite tirar conclusões sobre o mecanismo de 77
79 transferência de calor predominante no processo. Assim, pode considerar-se ue, se Bi <., a resistência térmica à condução interna é desprezável. Por outro lado, se Bi >, a resistência térmica à convecção externa é desprezável. Para valores intermédios, ambas as resistências térmicas são importantes na análise do processo. Uma vez ue a análise de processos transientes de transferência de calor onde a resistência interna é desprezável é muito mais simples ue o caso contrário, como iremos ver nas próximas secções, o primeiro passo no estudo destes sistemas é a avaliação do número de Biot Sistemas com Resistência Interna Desprezável Em sistemas com resistência interna desprezável (Bi <.), em cada instante, a temperatura na superfície e no interior do sólido é uniforme e a taxa de transferência de calor entre a superfície e o meio ambiente é calculada pela Lei de Arrefecimento de Newton (euação (4)): t, T T t t, T f(t) f(t) T ha(t T ) (J/s) (4) De notar ue a taxa de transferência de calor varia com o tempo, uma vez ue a temperatura no sólido também varia, diminuindo o seu valor até zero, situação final correspondente a um estado de euilíbrio térmico onde T T. Para conhecer a evolução da temperatura com o tempo, é necessário realizar um balanço de energia ao sólido entre os instantes genéricos t e t + dt, recordando o conceito de capacidade calorífica abordado na secção 3..: dq dt ha(t T )dt mc dt P 78
80 onde dq representa a energia acumulada no sólido durante o período de tempo dt em ue esteve sujeito a uma transferência de calor (perda no exemplo dado) a uma taxa. Considerando um período de tempo dt infinitesimal (dt ), em ue a variação de temperatura será também infinitesimal (dt ), da euação anterior obtém-se uma euação diferencial ue caracteriza o sistema: dt dt ha (T T ) (3) mc P Considerando a mudança de variável: θ T - T dθ dt e reconhecendo ue, se T for constante, obtém-se o seguinte dt dt desenvolvimento da euação diferencial: dθ dt ha dθ ha dθ ha θ dt dt ln mcp θ mcp θ mcp θ θ t θ θ ha mc P t T T T T ha mc t p e (4) A representação gráfica de um processo transiente desde um instante inicial (t, T T ) toma o seguinte aspecto, diminuindo a temperatura do sólido de uma forma exponencial até atingir o euilíbrio térmico: 79
81 T T T oo t Para determinar a energia total transferida (perdida no exemplo apresentado) entre dois instantes de tempo t e t, faz-se a integração da taxa de transferência de calor entre esses dois instantes de tempo: Q P t t dt ha(t T t t t )dt haθ t dt haθ t t e ha mc p t dt mc θ P e ha mc p t t t ha ha ha ha t ( ) t t t t mcp mcp mcp mcp Q P mcpθ e e mcpθe e (5) Vejamos agora o caso de um material condutor com geração interna de energia e dissipação por convecção (a base de um ferro de engomar por exemplo): p t t, T f(t) f(t) t, T T T 8
82 p corresponde à potência gerada no sólido, considerada constante (J/s), e à taxa de transferência de calor entre a superfície e o meio ambiente, ue pode, em cada instante, ser calculada pela Lei de Arrefecimento de Newton: ha(t T ) (J/s) (4) Para conhecer a evolução da temperatura com o tempo, é necessário realizar um balanço de energia ao sólido entre os instantes genéricos t e t + dt: dq p dt mc P dt Considerando um período de tempo dt infinitesimal (dt ), em ue a variação de temperatura será também infinitesimal (dt ), da euação anterior obtém-se uma euação diferencial ue caracteriza o sistema: dt dt p - (6) mc P Considerando as mudanças de variável: θ T - T dθ dt p, α, dt dt mcp ha β mc P obtém-se o seguinte desenvolvimento da euação diferencial: dθ α + βθ dt α β θ t βt [ ln( α + βθ) ] β[ t] θ + + θ e θ α β ha t p p mcp T T + ( T T ) e (7) ha ha 8
83 Notar ue, uando t, se obtém a solução em estado estacionário (T f ), situação na ual a taxa de transferência de calor é obtida pela Lei de Arrefecimento de Newton: ha( T T ) p f (4) De modo análogo ao realizado no exemplo anterior, onde se considerou um sólido sem geração de calor e com resistência interna desprezável, poderia agora obter-se uma euação para calcular a energia transferida para o sólido entre dois instantes de tempo t e t. Fica como sugestão ao leitor para trabalho complementar Sistemas com Resistência Interna não Desprezável Segunda Lei de Fourier No capítulo foi abordado o problema da determinação do perfil de temperaturas no interior de um sólido sujeito a transferência de calor por condução unidimensional em estado estacionário. Nesta situação, a temperatura no sólido varia apenas com a coordenada dimensional, Figura 39(a). Se, partindo da situação em estado estacionário da Figura 39(a), o sólido for arrefecido, então iniciar-se-á um processo de transferência de calor por condução em estado transiente, variando a temperatura no sólido, não apenas com a coordenada espacial, mas também com o tempo (Figura 39(b)). T T f (x) T t, T f (x, t) t, T T t x x Figura 39 Perfil de temperaturas no interior de um sólido sujeito a condução. (a) estado estacionário; (b) estado transiente 8
84 Consideremos agora o caso particular da condução de calor em estado transiente num placa plana com resistência interna não desprezável, inicialmente à temperatura uniforme T i T, sujeita a um processo de arrefecimento: O calor ue a placa perde sai pelas suas faces laterais. Dada a simetria da placa plana, vamos considerar apenas a análise de metade da placa onde o calor sai pela face lateral. Se o problema em análise fosse em regime de estado estacionário, o perfil de temperaturas no interior da placa não dependeria do tempo, pelo ue, T T(x) f (x) e a taxa de transferência de calor em ualuer ponto da placa, x, seria calculado pela Lei de Fourier, sendo igualmente independente do tempo: dt x ka dx g ( x ) () Num problema em estado transiente, a temperatura na placa varia não só com a posição, mas também com o tempo, pelo ue nesta situação, T T(x, t) f (x,t). Como conseuência, x, calculado igualmente pela Lei de Fourier, dependerá também da posição e do tempo: T x ka x g ( x, t ) () Para encontrar a solução transiente do perfil de temperaturas na placa, consideremos um elemento de volume infinitesimal de espessura dx: 83
85 x x + dx dx x x + dx Realizando um balanço de energia entre os instantes de tempo t e t + dt ao elemento de volume considerado obtém-se: Energia Acumulada Energia ue Entra Energia ue Sai dq ( x, t) dt ( x + dx, t)dt Por outro lado, como dq mc P dt e m ρdv ρadx, a euação de balanço de energia toma assim a seguinte forma e desenvolvimento: ( x, t) ( x + dx, t) ( x + dx, t) ( dx, t) P dt c ρadxdt dx ρac P dt dt Considerando dx e dt, obtém-se a seguinte euação diferencial às derivadas parciais: x x ρac P T t (8) Considerando a Lei de Fourier para a condução na euação (8) e definindo k difusividade térmica como α, obtém-se a Segunda Lei de Fourier válida para ρc P placas planas: T ka x x ρac P T t k ρc P x T T t T α x T t (9) 84
86 A resolução da Segunda Lei de Fourier para condições fronteira e inicial particulares, permitirá a obtenção de soluções para uma diversidade de situações de transferência de calor em estado transiente em placas planas. Nas próximas secções irá estudar-se a aplicação da Segunda Lei de Fourier a placas semi-infinitas e a placas finitas Placa Semi-infinita Considera-se ue uma placa plana sujeita a transferência de calor em estado transiente tem comportamento de placa semi-infinita, se possuir uma espessura significativa de tal forma ue uma dada alteração da condição inicial imposta numa das extremidades da placa não afecte a condição inicial na outra extremidade. Como exemplo, vamos supor uma placa de um material isolante, inicialmente a uma temperatura uniforme T (Figura 4). Se, num dado instante, uma das extremidades da placa for auecida de forma a ue a sua temperatura se mantenha constante (T S > T ), a placa será considerada como tendo comportamento de placa semi-infinita se durante o período de análise do processo de transferência de calor, a outra extremidade da placa se mantiver igual (ou aproximadamente igual) a T. Serão analisados de seguida 3 casos de placas semi-infinitas, sujeitas a diferentes condições fronteira. CASO : Extremo mantido a temperatura constante Seja uma placa espessa inicialmente a uma temperatura uniforme T (Figura 4). Num dado instante, a temperatura num dos extremos da placa é alterada para uma temperatura constante T S. T S T L x Figura 4 Placa semi-infinita com extremo mantido a temperatura constante 85
87 Considerando T S > T, a resposta transiente terá um comportamento similar ao apresentado na Figura 4, aumentando a temperatura numa dada posição da placa com o tempo, e mantendo-se inalterada a temperatura numa das extremidades da placa (comportamento de placa semi-infinita). T S t T x L Figura 4 Perfil de temperaturas em função do tempo numa placa semi-infinita com extremo mantido a temperatura constante A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas: T t T α (9) x Condição inicial: t, x, T T Condições fronteira: t >, x, T T S t >, x, T T (placa semi-infinita) O método mais apropriado para resolver a euação (9) sujeita à condição inicial e condições fronteira definidas, consiste na aplicação de Transformadas de Laplace. Antes de avançarmos com a resolução do problema, vamos fazer uma breve revisão de conceitos sobre Transformadas de Laplace. Este método tem como objectivo transformar uma função existente no domínio do tempo (F(t): t < ) para o domínio de Laplace, da seguinte forma e notação: 86
88 L st { F() t } F() s e F()dt t () O problema no domínio de Laplace simplifica-se, envolvendo a resolução de uma euação diferencial ordinária. A solução final no domínio do tempo, obtém-se por aplicação da Transformada Inversa: F - () t L { F( t) } () As Transformadas de Laplace das funções F(t) mais típicas, bem como as correspondentes Transformadas Inversas encontram-se compiladas num conjunto de tabelas, disponíveis no material fornecido em Fenómenos de Transferência I. São apresentadas de seguida as Transformadas da constante e da derivada, ue serão utilizadas na resolução do problema em análise: Transformada de uma constante { constante} L constante s Transformada da derivada df L sl dt { F(t) } F() sf( s) F() Voltando ao problema, vamos considerar a seguinte mudança de variável: θ T T θ(x, t) F(t) A definição de Transformada de Laplace apresentada anteriormente toma a seguinte forma: 87
89 st L{} θ θ e θ(x, t)dt A Segunda Lei de Fourier e as condições inicial e fronteira apresentam-se assim: θ θ α t x () Condição inicial: t, x, θ Condições fronteira: t >, x, θ θ S t >, x, θ (placa semi-infinita) Aplicando Transformadas de Laplace à euação () obtém-se: θ θ d θ L L α sθ θ(x,) α t x dx Da condição inicial, θ(x, ), pelo ue a euação anterior se simplifica, obtendo-se uma Euação Diferencial de ª Ordem Homogénea: d θ d θ s α sθ θ (3) dx dx α A euação (3) resolve-se através do cálculo das raízes da euação característica correspondente: s λ λ ± α s α Como as soluções são reais e diferentes, a solução geral é a seguinte: s x α e + Ce s x α θ C (4) 88
90 As constantes de integração C e C obtém-se da aplicação das condições fronteira do problema no domínio de Laplace: Condição fronteira : t >, x, θ, pelo ue C Condição fronteira : t >, x, θs θ θ, pelo ue C s s s A solução particular do problema em análise no domínio de Laplace é então a seguinte: s x α e θ θs (5) s Para obter a solução no domínio do tempo é necessário inverter a solução do domínio de Laplace, recorrendo à tabela de Transformadas de Laplace: θ(x, t) L s s x x α α Ce θ Ce x {} θ L θ s L erfc s θs s αt Como erfc(φ) erf(φ), a solução pode ser reescrita da seguinte forma: T - T T s T x erf αt (6) erf(φ) designa-se de função erro (erfc(φ) de função erro complementar), e tem a seguinte definição: Φ erf ( Φ) e z dz (7) π 89
91 Os valores da função erro encontram-se também compilados em tabelas, disponíveis no material fornecido na unidade curricular de Fenómenos de Transferência I. Validade da Aproximação a Placa Semi-infinita A solução encontrada só é válida no pressuposto de ue a placa analisada tem comportamento de placa semi-infinita, isto é, se a temperatura na extremidade oposta da placa (em x L) se mantiver constante (ou aproximadamente constante) e igual a T. x Considerando >, podemos ver na tabela da função erro ue αt x erf <.5. Substituindo na solução encontrada, obtém-se ue: αt T - T T s T <.5 L Isto é, se a placa possuir uma espessura L, tal ue >, a temperatura da αt placa em x L durante o período de tempo analisado irá diferir de T no máximo apenas.5%, pelo ue se pode considerar constante e igual a T, e conseuentemente considerar comportamento de placa semi-infinita. Face ao exposto, é possível deduzir euações simples ue nos permitam verificar com facilidade se uma dada placa em estudo pode ser considerada placa semi-inifinita. Pode ser considerada placa semi-infinita se a sua espessura for superior a uma espessura crítica, x c, função do período de tempo considerado na análise (t): x c αt > x > 4 αt (8) c Alternativamente, a placa pode ser considerada placa semi-infinita se o tempo de análise for inferior a um tempo crítico, t c. Para uma placa de espessura L: 9
92 L αt c L > t c < (9) 4α Taxa de Transferência de Calor Uma vez conhecida a solução T(x,t), é possível calcular a taxa de transferência de calor em ualuer ponto da placa, valor ue depende do tempo, (x, t), pela aplicação de lei de Fourier: (x, t) - ka T x x, com ( ) T T + Ts T erf αt Como T x ( ), vem ue: x T s T erf x αt (x, t) ka x ( T T ) erf () s x αt Para calcular x erf, vamos começar por considerar ue φ x αt x αt Deste modo, pela aplicação de definição de função erro, obtém-se ue: x erf erf( φ ) αt π Φ e z dz π [ P( φ) P() ] z e onde P(z) dz, corresponde à primitiva de z e, avaliada em z. Como a derivação é a operação inversa da primitivação, da derivada da primitiva de uma função, obtém-se a própria função, isto é: dp(z) dz e z 9
93 x x αt Voltando agora ao problema do cálculo de erf [ erf ( φ) ] x, tendo em consideração a regra da derivação implícita e o exposto anteriormente, resulta a seguinte dedução: x φ x φ [ erf ( φ) ] [ erf ( φ) ] αt dp( φ) π dφ e φ παt e x 4αt παt () Substituindo () na euação (), obtém-se uma euação para o cálculo da taxa de transferência de calor em função da posição na placa e do tempo: x t ka( Ts T e 4α ) ( x, t) () παt Se considerarmos x, obtemos a euação ue nos permite calcular a taxa de calor ue é transferida para a (ou da) placa em função do tempo: ka(t T ) s παt (3) Quantidade de Energia Recebida (ou Perdida) pela Placa A uantidade de energia acumulada na placa entre o instante inicial e um instante t pode ser calculada pela energia ue entra (ou sai) por condução em x. Realizando um balanço de energia entre os instantes de tempo t e t + dt obtém-se: dq ka(ts T ) ka(ts T ) dt dt Q t dt Q ka(ts T ) παt πα t (4) t πα 9
94 CASO : Placa semi-infinita com extremo sujeito a convecção Consideremos novamente uma placa espessa inicialmente a uma temperatura uniforme T (Figura 4). Num dado instante, um dos extremos da placa é subitamente contactado com um fluído em movimento disponível a uma temperatura T. T T L x Figura 4 Placa semi-infinita com extremo sujeito a convecção A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas, tendo em consideração ue em x, o calor transferido para a placa por convecção é numericamente igual ao calor transferido na placa por condução: T t T α (9) x Condição inicial: t, x, T T T x Condições fronteira: t >, x, ka ha( T T) t >, x, T T (placa semi-infinita) O método de resolução mais apropriado neste caso consiste também na aplicação de Transformadas de Laplace. Os detalhes da resolução não vão ser aui apresentados, fica como sugestão de trabalho complementar, bem como a determinação de euações para o cálculo da taxa de transferência de calor e da energia acumulada na placa. A solução final do problema toma a seguinte forma: 93
95 h h αt x+ T - T k k T T x erfc e αt x.erfc αt h + αt k (5) CASO 3: Placa semi-infinita com taxa de transferência de calor constante num extremo Consideremos novamente uma placa espessa inicialmente a uma temperatura uniforme T (Figura 43). Num dado instante, um dos extremos da placa é subitamente sujeito a uma taxa de transferência de calor constante. T L x Figura 43 Placa semi-infinita com taxa de transferência de calor constante num extremo A solução analítica do problema de condução em estado transiente obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas, tendo em consideração ue em x, o calor transferido para a placa a uma taxa constante é numericamente igual ao calor transferido na placa por condução: T t T α (9) x Condição inicial: t, x, T T Condições fronteira: t >, x, T ka x t >, x, T T (placa semi-infinita) O método de resolução mais apropriado neste caso consiste também na aplicação de Transformadas de Laplace. Os detalhes da resolução não vão ser aui apresentados, 94
96 fica como sugestão de trabalho complementar, bem como a determinação de euações para o cálculo da taxa de transferência de calor e da energia acumulada na placa. A solução final do problema toma a seguinte forma: T - T ka αt π e x x 4α t x.erfc (6) ka αt 3.7. Placa Finita Uma placa plana sujeita a transferência de calor em estado transiente ue não possa ser considerada com comportamento de placa semi-infinita, designa-se placa finita. Como exemplo, vamos supor uma placa de um material isolante, inicialmente a uma temperatura uniforme T (Figura 44). Se, num dado instante, ambas as extremidades da placa forem auecidas de forma a ue as suas temperaturas se mantenham constantes (T S ), a placa será considerada finita, uma vez ue nenhuma das extremidades mantém a condição inicial. Serão analisados de seguida 4 casos envolvendo placas finitas sujeitas a diferentes condições fronteira. T S T S L x Figura 44 Placa finita com extremos mantidos à mesma temperatura CASO : Placa com extremos mantidos à mesma temperatura Seja uma placa com uma distribuição inicial de temperaturas dada por uma função genérica T g(x) (a temperatura pode ser uniforme em toda a placa, ter uma distribuição linear,, como ilustrado na Figura 45). Num dado instante, a temperatura 95
97 em ambos os extremos da placa é subitamente alterada para um valor T S, mantido constante (Figura 44). T g (x) T T g (x) T g 3 (x) x L Figura 45 Exemplos de distribuições iniciais de temperatura numa placa finita A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas da seguinte forma: T t T α (9) x Condição inicial: t, x, T g(x) Condições fronteira: t >, x, T T s t >, x L, T T s Considerando a mudança de variável θ T T s, o problema toma a seguinte forma simplificada: θ θ α t x () Condição inicial: t, x, θ g(x) T s f(x) Condições fronteira: t >, x, θ 96
98 t >, x L, θ Neste tipo de problemas, o método de resolução mais adeuado é o de separação de variáveis, ue consiste em considerar ue a solução do problema, θ(x,t), é dada pelo produto entre uma função dependente apenas da posição e uma função dependente apenas do tempo: θ(x,t) F(x).G(t) (7) Daui resulta ue: θ t dg F dt e θ d F G x dx (8) Substituindo as euações (8) na euação (), obtém-se o seguinte desenvolvimento: θ t θ α x dg F dt d F αg dx dg αg dt F d dx F σ constante Notar ue, sendo G uma função apenas de t, então dg será também uma αg dt d F função de t e ue, sendo F uma função apenas de x, então será também uma F dx função de x. Assim sendo, a única possibilidade para uma função de t ser igual a uma função de x, é essa função ser uma constante. Da conclusão anterior resultam duas euações diferenciais ordinárias, (9) e (3), cuja resolução permite obter as funções F(x) e G(t), respectivamente: d F σf (9) dx dg - ασg (3) dt 97
99 Para obter a solução F(x) por resolução da euação diferencial (9), é necessário adaptar as condições fronteira do problema, tendo em consideração a mudança de variável introduzida, θ(x,t) F(x).G(t): Condição fronteira : t >, x, θ F().G(t) Daui resulta ue, ou F(), ou G(t). Se G(t), então θ(x,t), o ue significa ue a temperatura na placa é uniforme e igual a T s. Este resultado corresponde à solução do problema em estado estacionário, também designada de solução trivial, ue não nos interessa para a análise em estado transiente ue pretendemos efectuar. Assim, conclui-se então ue a condição fronteira ue nos interessa considerar é F(). Condição fronteira : t >, x L, θ F(L).G(t) Daui resulta ue, ou F(L), ou G(t). Se G(t), obtém-se novamente a solução trivial, pelo ue a condição fronteira ue é relevante para o problema em estudo é F(L). Resumindo, o problema a resolver toma a seguinte forma: d F σf (9) dx Condição fronteira : t >, x, F Condição fronteira : t >, x L, F Na resolução da euação diferencial (9) podem ser consideradas três situações, dependendo do valor da constante σ: 98
100 d F Situação : σ F(x) C x + C dx Da aplicação das condições fronteira, obtém-se C C, pelo ue F(x) em ualuer ponto da placa, degenerando a solução de θ(x,t) na solução trivial. Situação : σ λ d F > - λ F F(x) C e λx + C e -λx dx Da aplicação das condições fronteira, obtém-se C C, pelo ue se obtém novamente a solução trivial. Situação 3: σ -λ d F < + λ F dx Nesta situação as raízes da euação característica da euação diferencial ordinária de ª ordem são complexas (± λi), pelo ue a solução geral é a seguinte: F(x) C cos(λx) + C sen(λx) Da condição fronteira, obtém-se C. Da condição fronteira, resulta ue: C sen(λl) C ou sen(λl) Como para C se obtém novamente a solução trivial, a hipótese ue nos interessa analisar para obter a solução transiente de θ(x,t) é sen(λl). Deste modo: sen(λl) λl nπ nπ λ n, com n,, 3, (3) L Existe um conjunto infinito de valores para λ, designados de valores próprios, pelo ue, em conseuência, existe um conjunto infinito de soluções para F(x), designadas de soluções fundamentais ou funções próprias: 99
101 F n (x) sen(λ n x) nπ sen x (3) L Calculemos agora a solução G(t) através da resolução da euação diferencial (3), tendo em consideração ue sabemos de antemão ue a única situação ue interessa analisar é auela em ue a constante σ - λ < e ue existe um conjunto infinito de valores para λ: dg dg - ασg + αλ G dt dt n Daui resulta também um conjunto infinito de soluções para G(t), designadas de funções próprias: G n (t) αλ n t e (33) Como conseuência, θ(x,t) F(x).G(t) possui também um conjunto infinito de soluções, funções próprias de θ(x,t): θ n (x,t) F n (x).g n (t) nπ αλ t sen x e n (34) L A solução geral (completa) para θ(x,t) obtém-se da combinação linear de θ n (x,t): θ(x,t) n C nπ nθ n (x, t) Cnsen x e. n L αλ n t (35) As constantes C n determinam-se a partir da condição inicial: θ(x,) f(x) nπ C nsen x n L
102 f(x) identifica-se como uma série de Fourier de senos, pelo ue C n, se obtém da seguinte euação: C n L nπ f(x)sen x dx L L nπ sen x dx L L nπ f(x)sen x dx L L (36) Considerando uma distribuição inicial de temperatura uniforme: T T x L T T f(x) θ T - T s Obtém-se a seguinte expressão para o cálculo de C n : C n L L θ nπx sen dx θ L [ cos( nπ) ] nπ,se n par 4θ,se n ímpar nπ Da expressão anterior conclui-se ue para n par, se obtém a solução trivial de θ(x,t), pelo ue na solução particular completa consideram-se apenas os valores ímpares de n:
103 θ T Ts θ T T s 4 π n n nπ sen x e. L αλ n t nπ, com λ n e n, 3, 5, 7, L (37) Graficamente, a solução do problema, considerando um processo de auecimento, toma a forma apresentada na Figura 46. T s t t 3 t T t t T x L Figura 46 Solução transiente para o auecimento de uma placa finita com extremos mantidos à mesma temperatura CASO : Placa com extremos mantidos a temperaturas diferentes Seja agora uma placa com uma distribuição inicial de temperaturas dada por uma função genérica T g(x), como ilustrado na Figura 45. Num dado instante, as temperaturas nos extremos da placa sofrem uma alteração súbita de modo ue um dos extremos fica a uma temperatura constante T e o outro a uma temperatura constante T (Figura 47).
104 T T L x Figura 47 Placa finita com extremos mantidos a temperaturas diferentes A solução analítica deste problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas da seguinte forma: T t T α (9) x Condição inicial: t, x, T g(x) Condições fronteira: t >, x, T T t >, x L, T T forma: Considerando a mudança de variável θ T T, o problema toma a seguinte θ θ α t x () Condição inicial: t, x, θ g(x) T s f(x) Condições fronteira: t >, x, θ t >, x L, θ θ Neste caso, ao contrário do caso anterior, como θ, temos de adoptar uma metodologia de resolução diferente. Assim, começa-se por considerar ue a solução do problema, θ(x,t), é a resultante da contribuição da solução em estado estacionário, u(x), com uma componente transitória, v(x,t): 3
105 θ(x,t) u(x) + v(x,t) (38) A solução em estado estacionário obtém-se do conhecimento já aduirido no capítulo anterior de ue o perfil de temperaturas numa placa plana em estado estacionário é linear: θ u(x) x (39) L Para obter a componente transitória, temos necessidade de adaptar a euação diferencial () e as respectivas condições inicial e fronteira ue caracterizam o problema, à nova variável v (notar ue v θ - u): θ t θ α x ( u + v) ( u + v) t α x v t v α x (4) Condição inicial: t, x, v θ(x,) u(x) f(x) u(x) h(x) Condições fronteira: t >, x, v(,t) θ(,t) u() t >, x L, v(l,t) θ(l,t) u(l) θ - θ Notar ue o problema resultante para obter a solução v(x,t) é exactamente igual ao problema formulado no CASO para obter a solução θ(x,t), pelo ue, a solução v(x,t) é igual à solução para θ(x,t) encontrada no CASO pelo método de separação de variáveis: v(x,t) n nπ Cnsen x e. L αλ n t (4) com C n obtidos pela seguinte expressão: C n L nπ h(x)sen x dx L L 4
106 Uma vez conhecidos u(x) e v(x,t) obtém-se a solução θ(x,t) para este problema: θ θ(x,t) u(x) + v(x,t) x + L n nπ Cnsen x e. L αλ nt (4) com C n L x nπ f(x) - θ sen x dx L L L Considerando uma distribuição inicial de temperaturas uniforme, com uma das faces mantida à temperatura inicial (T T ): T T T T x L Como θ T T, vem ue θ f(x) T T T T θ Obtém-se a seguinte solução particular completa após o cálculo de C n : θ T T θ T T x L + π n n nπ sen x e. L αλ n t nπ, com λ n e n, 3, 5, 7, L (43) Graficamente, a solução do problema, considerando um processo de auecimento, toma a forma apresentada na Figura 48. 5
107 T T t t 3 t t T T t x L Figura 48 Solução transiente para o auecimento de uma placa finita com extremos mantidos temperaturas diferentes CASO 3: Placa com uma das faces isolada e outra mantida a temperatura constante Seja uma placa com uma das faces isolada e uma distribuição inicial de temperaturas dada por uma função genérica T g(x), como ilustrado na Figura 45. Num dado instante, a temperatura na face não isolada da placa sofre uma alteração súbita mantendo-se constante e igual a T s (Figura 49). face isolada T s L x Figura 49 - Placa finita com uma das faces isolada e outra mantida a temperatura constante A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas da seguinte forma: 6
108 T t T α (9) x Condição inicial: t, x, T g(x) Condições fronteira: t >, x, T T s T t >, x L, x (face isolada) forma: Considerando a mudança de variável θ T T s, o problema toma a seguinte θ θ α t x () Condição inicial: t, x, θ g(x) T s f(x) Condições fronteira: t >, x, θ θ t >, x L, x Tal como no CASO, o problema deste caso pode ser resolvido pelo método de separação de variáveis para obter θ(x,t): θ(x,t) F(x).G(t) (7) Por uma metodologia de resolução idêntica à utilizada na obtenção da solução no CASO, obtém-se as funções e valores próprios de F(x), G(t) e λ n : F n (x) sen(λ n x) (44) αλ n t G n (t) e (33) 7
109 λ n (n ) π, n,, 3, (45) L Como conseuência, obtém-se a solução geral (completa) para θ(x,t): θ(x,t) n ( n -) π t Cnsen x e. L αλ n (46) As constantes C n determinam-se a partir da condição inicial: θ(x,) f(x) n ( ) n - π C nsen x L f(x) identifica-se como uma série de Fourier de senos, pelo ue C n, se obtém da seguinte euação: C n L L f(x)sen ( ) n - π x dx L (47) Considerando uma distribuição inicial de temperatura uniforme, isto é, T T f(x) θ T - T s Após, o cálculo de C n, obtém-se a seguinte solução particular completa: θ θ π ( n -) π t 4 αλ n n n - sen L x e., com ( n ) π λ n e n,, 3, L (48) Graficamente, a solução do problema, considerando um processo de auecimento, toma a forma apresentada na Figura 5. 8
110 T s t t 3 t T t T t x L Figura 5 Solução transiente para o auecimento de uma placa finita com uma das faces isolada e outra mantida a temperatura constante CASO 4: Placa com convecção em ambas as faces Consideremos agora uma placa de espessura L, inicialmente a uma temperatura uniforme T. Subitamente, ambas as faces da placa são expostas a uma corrente convectiva de um fluído disponível a uma temperatura T (Figura 5). T T - L L Figura 5 - Placa finita com convecção em ambas as faces x A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier, sujeita à condição inicial e condições fronteira definidas da seguinte forma: 9
111 T t T α (9) x Condição inicial: t, x, T T T Condições fronteira: t >, x, x (condição de simetria) T t >, x L, -ka ha(t - T ) x forma: Considerando a mudança de variável θ T T, o problema toma a seguinte θ θ α t x () Condição inicial: t, x, θ θ T - T θ Condições fronteira: t >, x, x t >, x L, k θ + hθ x Tal como no caso anterior, este caso pode também ser resolvido pelo método de separação de variáveis para obter θ(x,t): θ(x,t) F(x).G(t) (7) Por uma metodologia de resolução idêntica à utilizada na obtenção da solução no CASO, obtém-se as funções e valores próprios de F(x), G(t) e λ n : F n (x) cos(λ n x) (49) αλ n t G n (t) e (33)
112 λ n Z n, n,, 3, (5) L onde Z n representam as raízes da euação transcendental (5), ue podem ser também obtidas de tabelas disponíveis no material fornecido em Fenómenos de Transferência I. Z n tg(z n ) Bi hl k (5) Como conseuência, obtém-se a solução geral (completa) para θ(x,t): αλ n n n e. (5) n t θ(x,t) C cos( λ x) As constantes C n determinam-se a partir da condição inicial: n θ(x,) θ C cos( λ x) n n A euação resultante identifica-se como um problema de Sturm-Liouville, pelo ue C n, se obtém da seguinte euação: C n Z 4sen n + ( Zn ) θ sen( Z ) n (53) A solução completa pode também ser escrita da seguinte forma: θ θ T T ' t C ( ) αλ n ncos λ nx e., com λn e n,, 3, (54) T T L n Z n e C n 4sen Z + sen n ( Zn ) ( Z ) n
113 Graficamente, a solução do problema na metade positiva da placa, considerando um processo de auecimento, toma a forma apresentada na Figura 5 (como o problema é simétrico, na metade negativa da placa, entre x -L e, obtém-se as curvas simétricas): T t t 3 t T t T t x L Figura 5 Solução transiente para o auecimento de uma placa finita com convecção em ambas as faces 3.8. Condução em Estado Transiente num Cilindro Exposto à Convecção Consideremos condução radial de calor em estado transiente num cilindro com resistência interna não desprezável, inicialmente à temperatura uniforme T e subitamente sujeito a transferência de calor por convecção (Figura 53). R s T L T Figura 53 Cilindro exposto à convecção
114 Para encontrar a solução transiente do perfil de temperaturas no cilindro, consideremos um elemento de volume infinitesimal de espessura dr: r + dr r r r + dr L Realizando um balanço de energia entre os instantes de tempo t e t + dt ao elemento de volume considerado obtém-se: Energia Acumulada Energia ue Entra Energia ue Sai dq dt r r + dr mc p dt Como m ρdv ρa r dr ρ(πrl)dr, a euação de balanço de energia toma a seguinte forma e desenvolvimento: r + dr r dt ρ(πrl)drc p dt Considerando dr e dt e a Lei de Fourier para a condução obtém-se a seguinte euação diferencial às derivadas parciais: T r ka r, r π rlρc p T t ka r r T r 3
115 Como A r πrl, definindo difusividade térmica como Segunda Lei de Fourier válida para geometria cilíndrica: k α ρc P, obtém-se a T k T T T T ρc P r α + r t (55) t r r r r r A solução analítica do problema de condução em estado transiente, obtém-se aplicando a Segunda Lei de Fourier para geometria cilíndrica, sujeita à condição inicial e condições fronteira definidas da seguinte forma: Condição inicial: t, r, T T T Condições fronteira: t >, r, (ou T é finito em r ) r T t >, r R s, -ka s has (T - T ) r Considerando a mudança de variável θ T T, obtém-se a euação (56): θ t θ α + r r θ r (56) Condição inicial: t, r, θ θ T - T θ Condições fronteira: t >, r, r t >, r R s, k θ + hθ r (ou θ é finito em r ) Tal como no caso da placa plana sujeita a convecção, este problema pode também ser resolvido pelo método de separação de variáveis para obter θ(r,t): θ(r,t) F(r).G(t) (57) 4
116 obtendo-se as seguintes funções e valores próprios de F(r), G(t) e λ n : F n (r) J (λ n r) (58) G n (t) αλ n t e (33) λ n Z n, n,, 3, (59) R s onde Z n representam as raízes da euação transcendental (6), ue podem ser também obtidas de tabelas disponíveis no material fornecido na unidade curricular de Fenómenos de Transferência I. ZnJ(Z J ( Z ) n n ) Bi hr s (6) k Na euações (58) e (6), J e J correspondem às funções de Bessel de ª espécie, de ordem zero e de ordem um, respectivamente. Como conseuência, obtém-se a solução geral (completa) para θ(r,t): αλ C n nj λ nr e. (6) n t θ(r,t) ( ) As constantes C n determinam-se a partir da condição inicial: n θ(r,) θ T - T C J ( λ r) n n A euação resultante identifica-se como a expansão de uma função em série de DINI, pelo ue C n se obtém da seguinte euação: C n J J(Zn ) rf(r)j ( λ nr) dr Cn θ (6) n + n Z n J ( Zn ) + J ( Zn ) ( λ ) J ( λ ) 5
117 A solução completa pode também ser escrita da seguinte forma: θ θ T T ' t C ( ) αλ n nj λ nr e., com T T n Zn λ n e n,, 3, (63) R s e C n Z n J J ( Z ) + J ( Z ) n (Z n ) n 3.9. Condução em Estado Transiente numa Esfera Exposta à Convecção Consideremos agora uma esfera com resistência interna não desprezável sujeita a condução radial de calor em estado transiente, inicialmente à temperatura uniforme T e subitamente sujeita a transferência de calor por convecção (Figura 54). T R s T Figura 54 Esfera exposta à convecção Para encontrar a solução transiente do perfil de temperaturas na esfera, consideremos um elemento de volume infinitesimal de espessura dr: dr r + dr r R s Realizando um balanço de energia entre os instantes de tempo t e t + dt ao elemento de volume considerado obtém-se: 6
118 Energia Acumulada Energia ue Entra Energia ue Sai dq r r + dr dt mc p dt Como m ρdv ρa r dr ρ(4πr )dr, a euação de balanço de energia toma a seguinte forma e desenvolvimento: r + dr r dt ρ(4πr )drc p dt 4 πr ρc Lim p dt dt dt Lim dr r+ dr dr r Considerando a Lei de Fourier para a condução seguinte euação diferencial às derivadas parciais: r ka r T, obtém-se a r 4π r ρc p T t ka r r T r Como A r 4πr, após alguma manipulação algébrica, obtém-se a Segunda Lei de Fourier válida para geometria esférica: r T t k ρc P r r T r T t α r r T T + r r r T t T α + r r T r (64) A solução analítica do problema de condução em estado transiente, obtém-se aplicando a euação (64), sujeita à condição inicial e condições fronteira definidas da seguinte forma: Condição inicial: t, r, T T T Condições fronteira: t >, r, r (ou T é finito em r ) 7
119 T t >, r R s, -ka s has (T - T ) r Considerando a mudança de variável θ T T, obtém-se a euação (65). θ t θ α + r r θ r (65) Condição inicial: t, r, θ θ T - T θ Condições fronteira: t >, r, r t >, r R s, k θ + hθ r (ou θ é finito em r ) Este problema pode também ser resolvido pelo método de separação de variáveis para obter θ(r,t): θ(r,t) F(r).G(t) (57) obtendo-se as seguintes funções e valores próprios de F(r), G(t) e λ n : F n (r) sen λ ( λ r) n r n (66) G n (t) αλ n t e (33) λ n Z n, n,, 3, (59) R s onde Z n representam as raízes da euação transcendental (67), ue podem ser também obtidas de tabelas disponíveis no material fornecido na unidade curricular de Fenómenos de Transferência I. 8
120 Z n cotg(z n ) Bi hr s (67) k Como conseuência, obtém-se a solução geral (completa) para θ(r,t): θ(r,t) sen ( λ r) t n αλ C n n e. (68) n λ nr As constantes C n determinam-se a partir da condição inicial: θ(r,) θ T - T n C n sen λ ( λ r) n r n A euação resultante identifica-se como um problema de Sturm-Liouville, pelo ue C n, se obtém da seguinte euação: sen(zn ) C n 4 θ Z sen(z ) n n (69) A solução completa pode também ser escrita da seguinte forma: θ θ n ( λ r) t T T ' sen n αλ C n n e., com T T λ r n Zn λ n e n,, 3, (7) R s e C n sen(zn )-Zn cos 4 Z sen( Z n ( Z ) n ) n 9
121 Capítulo 4 Transferência de Calor por Convecção Ocorre transferência de calor por convecção sempre ue uma superfície e um fluído em movimento ue a contacte se encontrem a temperaturas diferentes. Por exemplo, a superfície de um sólido mantido à temperatura T s perde calor por convecção para um fluído em movimento com uma velocidade u e temperatura T (considerando T s > T ), Figura 55. Em estado estacionário a taxa de transferência de calor é constante, podendo ser calculada pela Lei de Arrefecimento de Newton, euação (4). T s R s ha(ts T ) u, T Figura 55 Transferência de calor por convecção entre uma superfície mantida à temperatura T s e um fluído em movimento Nos problemas analisados nos capítulos anteriores envolvendo transferência de calor por convecção, foi sempre fornecido um valor para o coeficiente de transferência de calor por convecção (denotado por h). Neste capítulo, pretende-se compreender de ue forma o valor de h é afectado e como proceder ao seu cálculo através de teorias/correlações apropriadas. Foi já referido no capítulo ue o coeficiente convectivo de transferência de calor depende de vários factores, nomeadamente da forma de escoamento do fluído, das propriedades do fluído e da geometria do sólido, pelo ue é fácil de conceber ue o coeficiente convectivo de transferência de calor varia ao longo da superfície de um sólido. Por exemplo, na esfera considerada na Figura 55, o valor do coeficiente de transferência de calor por convecção na zona de impacto do fluído será diferente do valor na zona oposta (e por isso mais resguardada), concluindo-se assim ue existe um coeficiente local de transferência de calor por convecção (denotado por h L ) e ue o coeficiente h utilizado nos cálculos anteriores não é mais do ue um valor médio fornecido para analisar um determinado problema em condições particulares.
122 Uma vez ue o coeficiente de transferência de calor varia ao longo da superfície do sólido, é possível dividir a área do sólido em N elementos de superfície de área da e, em cada elemento, calcular a taxa de transferência de calor por convecção pela aplicação da Lei de Arrefecimento de Newton se o valor de h L (coeficiente local de transferência de calor por convecção) for conhecido: T s R s da d h L (T S T )da u, T A taxa total de transferência de calor por convecção obtém-se pela integração da taxa de transferência de calor por convecção em cada elemento de superfície, ue por sua vez sabemos também ser possível calcular aplicando a Lei de Arrefecimento de Newton se o valor de h (coeficiente médio de transferência de calor por convecção) for conhecido. Assim: A T d (T S T ) A T h L da ha T (T S T ) (T S T ) A T h L da Da euação anterior obtém uma relação entre h e h L : AT h L h (7) A T da Analiticamente, h L pode ser determinado pela teoria da camada limite. Dada a complexidade analítica envolvida nesta teoria, serão aui fornecidas apenas algumas características mais importantes aplicadas à sua análise em placas planas. Para introduzir o conceito de camada limite, considerar o fluxo de um fluído ue se aproxima de uma placa plana a uma velocidade uniforme u (Figura 56).
123 Corrente livre Camada limite fluidodinâmica Figura 56 Desenvolvimento da camada limite fluidodinâmica numa placa plana Quando as partículas do fluído contactam a superfície da placa irão ser retardadas devido a forças de atrito de modo ue a sua velocidade na camada adjacente à placa toma o valor zero. Estas partículas adjacentes à superfície da placa, por sua vez, irão retardar o movimento das partículas da camada adjacente seguinte do fluído, ue por sua vez retardam o movimento das partículas da camada adjacente seguinte, assim sucedendo até ue à distância y δ da superfície da placa, o efeito de retardamento deixa de se notar, e a velocidade das partículas do fluído nessa camada continua a ser igual à velocidade com ue o fluído fez a aproximação à placa. A uantidade δ é denominada de camada limite fluidodinâmica, aumentando o seu valor à medida ue o fluído progride sobre a placa, pelo ue δ δ(x). Da mesma forma ue se desenvolve uma camada limite fluidodinâmica uando um fluído flui sobre uma superfície, observa-se o desenvolvimento de uma camada limite térmica se o fluído estiver a uma temperatura diferente da superfície. Considerar o fluxo de um fluído ue se aproxima de uma placa plana com uma temperatura uniforme T (Figura 57). Corrente livre Camada limite térmica Figura 57 Desenvolvimento da camada limite térmica numa placa plana
124 Quando as partículas do fluído contactam a superfície, devido à transferência de calor entre a superfície e o fluído, a sua temperatura na camada adjacente à placa toma o valor da temperatura da superfície da placa. Por sua vez, estas partículas trocam calor com as partículas da camada de fluído adjacente seguinte, observando-se o desenvolvimento de gradientes de temperatura no fluído. A região do fluído na ual se observam estes gradientes de temperatura é a camada limite, cuja espessura δ t se denomina camada limite térmica. O valor de δ t aumenta à medida ue o fluído progride sobre a placa, pelo ue δ t δ t (x). Notar no entanto ue, enuanto o fluxo de um fluído sobre uma superfície origina sempre uma camada limite fluidodinâmica, uma camada limite térmica é desenvolvida apenas se a temperatura do fluído for diferente da temperatura da superfície (o ue acontece na maioria das situações), pelo ue, numa situação em ue existam as duas camadas limites, estas raramente se desenvolvem com a mesma magnitude e por isso δ e δ t numa dada posição da superfície são normalmente diferentes. Na teoria da camada limite aplicada à transferência de calor pretende-se utilizar o conhecimento dos perfis de velocidade e de temperatura na camada limite para determinar analiticamente o valor do coeficiente local de transferência de calor por convecção, h L, ue permitirá o cálculo do coeficiente médio de transferência de calor, h, pela aplicação da euação (7). No caso particular de uma placa plana com comprimento L e largura W (Figura 58), considerando elementos de superfície de área da Wdx, o coeficiente médio pode ser calculado da seguinte forma: L h LdA h LWdx L A T h h Ldx (7) A WL L T Figura 58 Placa plana sujeita a transferência de calor por convecção 3
125 Pela teoria da camada limite é possível calcular analiticamente as espessuras das camadas limites fluidodinâmica e térmica (solução de Blasius) e h L numa placa plana, obtendo-se os seguintes resultados ue não serão aui demonstrados: δ(x) 5 (73) x Re x T 3 δ(x) Pr (74) δ (x) 3.33k h L (x) Pr Re x x (75) Nas expressões anteriores, Re x e Pr, representam os números de Reynolds local e de Prandtl, respectivamente, definidos da seguinte forma: ρu x Re x (76) μ Pr μc p (77) k De referir ue no caso de escoamento sobre uma placa plana, considera-se escoamento laminar uando Re x < x 5. Pela definição do número de Nusselt local, h x Nu x L, obtém-se a seguinte expressão alternativa para o cálculo de hl numa placa k plana, válida para escoamento em regime laminar, envolvendo apenas números adimensionais: xh k L x 3 x Nu.33Pr Re (78) 4
126 Uma vez conhecido h L, é possível calcular o coeficiente médio de transferência de calor por convecção recorrendo à euação deduzida anteriormente: h h A T L (x)da A T L h L (x)wdx WL L L h (x)dx L L L.33k x Pr 3 ρu x dx μ L.33k ρu.33k ρu x h Pr x dx Pr Pr L x μ L μ L.664k L ρu L μ hl k Nu.664Pr 3 ρu L μ.664pr 3 Re (79) Na euação (79), Nu, representa o número de Nusselt e Re, o número de Reynolds. Comparando Nu com Nu x conclui-se ue o coeficiente médio de transferência de calor por convecção numa placa plana contactada por um fluído em regime laminar é duas vezes superior ao coeficiente convectivo local avaliado em x L, isto é: Nu Nu x (x L) e h h L (x L) (8) De referir ue nos cálculos das propriedades do fluído necessárias nas euações anteriores deve-se utilizar a temperatura média do filme da camada limite: T f Ts + T (8) Correlações para o cálculo de coeficientes médios de transferência de calor por convecção O cálculo analítico de coeficientes convectivos de transferência de calor pela teoria da camada limite para outras geometrias ue não a placa plana, é uma tarefa complexa, ou mesmo impossível em algumas situações, pelo ue na prática são 5
127 utilizadas no seu cálculo correlações empíricas obtidas experimentalmente para uma gama específica de condições. Apresentam-se de seguida algumas dessas correlações. Transferência de calor em tubos cilíndricos Seja um tubo cilíndrico com um fluído em escoamento turbulento no seu interior (Figura 59). u, T D Figura 59 Transferência de calor por convecção entre a parede interna de um tubo cilíndrico e um fluído em movimento Uma correlação adeuada para o cálculo do coeficiente médio de transferência de calor por convecção entre o fluído e a parede interna do tubo é a euação de Dittus- Boelter: Nu D.3Re D.8 Pr.4 (8) onde Nu D e Re D representam os números de Nusselt e de Reynolds calculados usando o diâmetro do tubo: Nu D hd k e Re D ρu D (83) μ A correlação de Dittus-Boelter é válida para regime turbulento (Re >> ) e Pr >.5. As propriedades do fluído devem ser avaliadas à temperatura média do seio do fluído. Convecção forçada em torno de esferas Seja uma esfera sujeita a um escoamento de um fluído (Figura 6). 6
128 Figura 6 Transferência de calor por convecção entre a superfície de uma esfera e um fluído em movimento Uma correlação freuentemente utilizada para o cálculo do coeficiente médio de transferência de calor por convecção entre o fluído e a superfície da esfera é a correlação de Ranz e Marshall, devendo as propriedades do fluído ser avaliadas à temperatura média do filme: Nu D hd +.5.6ReD Pr.333 (84) k Convecção em torno de cilindros Outra situação comum envolve o escoamento de um fluído perpendicularmente ao eixo de um cilindro (Figura 6). D u Figura 6 Transferência de calor por convecção entre a superfície de um cilindro e um fluído em movimento 7
129 Uma correlação adeuada para o cálculo do coeficiente médio de transferência de calor por convecção entre o fluído e a superfície externa do cilindro é a seguinte, devendo as propriedades do fluído ser avaliadas à temperatura média do filme: Nu D hd ( ReD )Pr.3 (85) k Convecção em torno de tubos de secção recta hexagonal Existem disponíveis na literatura muitas outras correlações para geometrias menos convencionais ue as anteriores. Como exemplo último, apresenta-se uma correlação (euação (86)) para o cálculo do coeficiente convectivo em torno de tubos de secção recta hexagonal (Figura 6), devendo as propriedades do fluído ser avaliadas à temperatura média do filme. D Figura 6 Transferência de calor por convecção entre a superfície de um tubo de secção recta hexagonal e um fluído em movimento u Nu D hd red Pr.333 (86) k 8
130 Capítulo 5 Permutadores de Calor O processo de transferência de calor entre dois fluídos a temperaturas diferentes e separados por uma parede sólida é muito freuente em muitas aplicações de engenharia. O euipamento usado para promover essa transferência chama-se permutador de calor. Pretende-se neste capítulo conhecer vários tipos de permutadores de calor disponíveis no mercado e saber como projectar um permutador de calor para aplicações específicas. 5.. Tipos de Permutadores de Calor Tubos concêntricos Os permutadores de calor são tipicamente classificados de acordo com a configuração do escoamento e o tipo de construção. O permutador de calor mais simples é auele no ual os fluídos uente e frio se movimentam no mesmo sentido ou em sentidos opostos num tubo concêntrico (ou tubo de parede dupla). Na configuração em co-corrente (Figura 63(a)), os fluídos uente e frio entram na mesma extremidade, fluem no mesmo sentido e saem na extremidade oposta. Na configuração em contracorrente (Figura 63(b)), os fluídos entram em extremidades opostas, fluem em sentidos opostos e saem em extremidades opostas. Figura 63 Permutadores de calor de tubos concêntricos. (a) configuração em cocorrente; (b) configuração em contra-corrente Escoamento cruzado Alternativamente às configurações de escoamento apresentadas na Figura 63, os fluídos podem mover-se em escoamento cruzado (perpendicularmente um ao outro), como apresentado na Figura 64. 9
131 Escoamento cruzado Escoamento no tubo Figura 64 Permutador de calor de escoamento cruzado Casco e tubos Outro euipamento comum é o permutador de calor de casco e tubos. Existem várias configurações ue diferem no número de passagem dos fluídos no casco e nos tubos. A forma mais simples envolve uma única passagem dos fluídos nos tubos e no casco (Figura 65). Saída do tubo Entrada no casco Saída do casco Entrada no tubo Figura 65 Permutador de calor de casco e tubos com uma passagem nos tubos e uma passagem no casco Permutador de calor de placas Um tipo particular de permutadores de calor é o permutador de placas (Figura 66). 3
132 Figura 66 Permutador de placas Nestes permutadores, a superfície de transferência de calor é composta por uma série de finas placas (até às centenas), possuindo orifícios nos uatro cantos para entrada ou saída dos fluídos, cercados total ou parcialmente por vedantes. As placas são montadas em pacotes, formando cada par adjacente de placas um canal, escoando os dois fluídos em canais alternados no sentido ditado pelos vedantes. Geralmente as placas são enrugadas, o ue permite aumentar a turbulência dos fluídos, provocando um aumento dos coeficientes de transferência de calor, diminuição da deposição de partículas e aumento da área de transferência de calor. A Figura 67 ilustra o princípio de funcionamento de um permutador de placas. Como se pode observar, o fluído (branco) não pode contactar as placas a preto, uma vez ue o vedante do tipo A não o permite, podendo contactar as placas a branco, devido à colocação do vedante tipo B. O fluído (preto) por sua vez, devido à acção do vedantes, pode apenas contactar as placas a preto. Figura 67 Princípio de funcionamento de um permutador de placas 3
133 5.. Balanços Energéticos e Coeficiente Global de Transferência de Calor Para projectar ou prever a performance de um permutador de calor, é essencial relacionar a taxa de calor trocado entre o fluído uente e o fluído frio com as suas temperaturas de entrada e de saída, o coeficiente global de transferência de calor e a área de transferência de calor do permutador. Duas dessas relações podem ser obtidas da aplicação de balanços de energia global ao fluídos uente e frio (Figura 68). m A T A, Fluído A T A, m B Fluído B A, área de transferência de calor T B, T B, Figura 68 Balanços de energia global para os fluídos uente e frio num permutador de calor de tubos concêntricos Considerando desprezável a transferência de calor entre o permutador e a vizinhança, a taxa de calor trocado entre os dois fluídos pode ser calculada pelo balanço de energia ao fluído uente (fluido A) ou ao fluído frio (fluido B): Energia ue entra + Energia acumulada Energia ue sai Energia transferida energia acumulada Ou seja, do balanço ao fluído A: ma cpa (TA, TA, ) (87) Da mesma forma, do balanço ao fluído B: m B cpb (TB, TB,) (88) 3
134 As euações (87) e (88) não consideram mudança de fase e consideram constantes os calores específicos dos fluídos. Relacionando a taxa de calor trocado e a diferença de temperatura entre os dois fluídos, obtemos outra euação útil para a análise de permutadores de calor, euação (89), ue corresponde a uma extensão da Lei de Arrefecimento de Newton, com o coeficiente convectivo de transferência de calor substituído pelo coeficiente global de transferência de calor (U). Como a diferença de temperaturas entre os dois fluídos varia com a posição no permutador de calor, é necessário considerar na euação uma diferença de temperatura média apropriada (ΔT m ). UAΔT m (89) A euação (89), também conhecida como euação geral dos permutadores de calor, pode ser usada com as euações anteriores para analisar permutadores de calor. No entanto, antes de ser possível fazê-lo, convém fazer uma revisão sobre o cálculo do coeficiente global de transferência de calor e especificar de ue forma é calculada a diferença de temperaturas média considerada. Coeficiente Global de Transferência de Calor A determinação do coeficiente global de transferência de calor é um passo essencial (e por vezes o mais incerto) na análise de um permutador de calor. Este coeficiente foi definido no capítulo e relacionado com a resistência térmica à transferência de calor entre dois fluídos. Consideremos o permutador de calor de tubos concêntricos da Figura 69. Fluído T e T, e T, e Fluído T i T, i r i r e r i r e T e T i T, i Figura 69 Permutador de calor de tubos concêntricos 33
135 Na transferência de calor entre os dois fluídos existem três resistências térmicas em série envolvidas: a resistência à transferência de calor por convecção entre o fluído e a superfície interna do tubo (R T ), a resistência à transferência de calor por condução no tubo (R T ) e a resistência à transferência de calor por convecção entre a superfície externa do tubo e o fluído (R T3 ). Este processo térmico pode ser representado pelo seu análogo eléctrico: R T R T R T3 T, R T h i A i T i R T T e r e ln r i π kl R T3 T, h e A e A resistência térmica euivalente, calcula-se do conhecimento das resistências térmicas individuais e relaciona-se com o coeficiente global de transferência de calor, U, podendo-se assim obter este da resolução da euação (9). R Te RT + R T + R T3 UA h i A i + r e ln r i π kl + h e A e (9) De referir ue a euação (9) é válida para um permutador de calor de tubos concêntricos considerando superfícies limpas. Durante a operação normal de um permutador, as superfícies são freuentemente sujeitas a deposições devido a impurezas dos fluídos, formação de ferrugem ou outras reacções entre o fluído e o material ue compõe a parede. Estas deposições levam ao aumento da resistência à transferência de calor entre os dois fluídos, pelo ue, nestes casos, será necessário introduzir na euação uma resistência térmica adicional, denominada de factor de Fouling, R f, cujo valor depende de vários parâmetros, como temperatura de operação, velocidade do fluído e tempo de operação do permutador. 34
136 Determinação de ΔT m Considerar um permutador de calor de tubos concêntricos com um tubo interno de espessura desprezável e onde o fluído uente é vapor saturado em condensação no lado externo do tubo, pelo ue a sua temperatura permanece constante em todo o comprimento do permutador (Figura 7). Vapor saturado em condensação T T m Fluído R T m x Figura 7 Permutador de calor de tubos concêntricos com vapor saturado em condensação como fluído uente Considerando T > T, T, os perfis de temperaturas dos fluídos uente e frio tomam o aspecto apresentado na Figura 7. T Δ T T + ΔT T T x x + Δx L Figura 7 Perfis de temperaturas num permutador de calor de tubos concêntricos com vapor saturado em condensação como fluído uente A diferença de temperaturas (ΔT) entre os dois fluídos é inicialmente alta, decrescendo com o aumento de x, aproximando-se assimptoticamente de zero. É importante recordar ue a temperatura de saída do fluído frio nunca pode exceder a temperatura do fluído uente. Os índices e utilizados para definir as temperaturas de 35
137 entrada e de saída dos fluídos representam respectivamente o lado esuerdo e o lado direito do permutador. Esta convenção será sempre utilizada neste texto. A determinação de ΔT m pode ser conseguida por aplicação de um balanço de energia à secção de tubo considerada na Figura 7, de comprimento Δx e área de transferência de calor ΔA: Δ m c ΔT ou Δ U Δ A( T T) p Onde ΔA πrδx PΔx e ΔT corresponde à diferença de temperaturas local entre o fluído uente e o fluído frio. Igualando as duas euações obtém-se o seguinte desenvolvimento: ΔT UP m c pδt UPΔx Δx m c ( T T) ( T T) p Considerando Δx, obtém-se uma euação diferencial ordinária de variáveis separáveis, euação (9). dt dx UP ( T T) (9) m c p Para integrar esta euação, consideremos a seguinte mudança de variável: θ T T dθ - dt (9) A euação diferencial e respectiva euação fronteira tomam a seguinte forma: dθ dx UP θ (93) m c p Condição Fronteira: x, θ θ T T 36
138 Integrando entre x e x, obtém-se o seguinte desenvolvimento: ln θ θ UP m c T T UP T x ln x T T T T p m c p T e UP x m cp (94) Representando graficamente a solução obtida (T vs. x), obtém-se a Figura 7, onde se pode verificar ue a temperatura de saída do fluído frio aumenta com o aumento do parâmetro UP. m c p T T UP m c p L Figura 7 Variação ualitativa dos perfis de temperatura num permutador de calor de tubos concêntricos com vapor saturado em condensação como fluído uente A temperatura do fluído frio à saída do tubo é calculada pela euação (95), substituindo x por L na euação (94). UP L m cp ( ) T T T e T (95) cálculo de Trabalhando algebricamente a euação (95), obtém-se a euação (96) para o m cp : T ln T T T UP m c p L m cp UP T T ln T T L (96) 37
139 Por outro lado, a energia total transferida entre os dois fluídos pode ser calculada pelo balanço de energia global ao fluído frio, com área total de transferência de calor A PL: m c (T p T ) T T UPL UPL T T ln T T m cp obtido da euação (96) e a ( T - T ) ( T T ) T T ln T T ( ) lm UA ΔT (97) Conclui-se ue diferença média de temperatura a usar na euação geral dos permutadores é a média logarítmica das diferenças de temperaturas do lado esuerdo e direito do permutador Permutadores de Calor em Contra-Corrente Os perfis de temperaturas associados aos fluídos uente e frio de um permutador de calor em contra-corrente apresentam-se na Figura 73. Podemos realizar a mesma análise efectuada na secção anterior à secção de permutador de calor considerada na Figura 73. Assim, a taxa de transferência de calor entre os dois fluídos pode ser calculada por uma das seguintes três euações: Δ m A cpaδta (ΔT A < ) (98) Δ m B cpbδtb (ΔT B < ) (99) Δ UΔA T A T B ( ) (ΔA PΔx) () 38
140 m A T A, m B T B, T A T B + ΔT B Δ ΔA T A + ΔT A Fluído A T B Fluído B T A, área de transferência de calor T B, T A, T A, c pa ΔT A Δ T B, T A, ΔT B T B, c pb T B, Figura 73 Perfis de temperatura num permutador de calor em contra-corrente Manipulando algebricamente as euações (98) e (99), obtém-se a seguinte relação entre ΔT A e ΔT B : ΔT A - ΔT B Δ m A cpa + m Δ B cpb m A cpa m B cpb Δ Definindo w A m A cpa e w B mb cpb, obtém-se o seguinte desenvolvimento algébrico: ΔT Δ w A A ΔT w B B Δ w ( T T ) A A B w B UPΔx ( T T ) A B Δ T ( T T ) A A T B B UP w A w B Δx 39
141 Considerando Δx, obtém-se: ( T T ) d T A A T B B UP w A w B dx Introduzindo a mudança de variável θ T A - T B, obtém-se a seguinte euação diferencial: dθ θ UP dx w A w () B Cuja integração fornece o seguinte resultado: θ TA TB ln ln UA () θ TA TB w A w B Por outro lado, a energia total transferida entre os dois fluídos pode ser calculada pelas euações de balanço de energia global aos fluídos uente e frio: w A (T A T A ) (3) ou w B (T B T B ) (4) Manipulando algebricamente as euações (3) e (4), obtém-se o seguinte desenvolvimento, tendo também em consideração o cálculo do termo euação (): pela w A w B 4
142 ( T T ) ( T T ) A B A B w A w B ( T T ) ( T T ) A A B B ( ) lm A B A B UA UA ΔT T ln T T T (5) Conclui-se novamente ue a diferença de temperaturas média a usar na euação geral dos permutadores é a média logarítmica das diferenças de temperaturas do lado esuerdo e direito do permutador Permutadores de Calor em Co-corrente Os perfis de temperatura associados aos fluídos uente e frio de um permutador de calor em co-corrente apresentam-se na Figura 74. A diferença de temperatura (ΔT) entre os dois fluídos é inicialmente alta, decrescendo com o aumento de x, aproximando-se assimptoticamente de zero. Notar ue a temperatura de saída do fluído frio nunca excede a temperatura de saída do fluído uente. m A T A, m B T B, T A T B Δ T A + ΔT A ΔA T B + ΔT B Fluído A Fluído B T A, área de transferência de calor T B, T A, T A, c pa ΔT A Δ T A, T B, T B, T B, c pb ΔT B Figura 74 Perfis de temperatura num permutador de calor em co-corrente 4
143 Na secção de permutador de calor considerada na Figura 74, a taxa de transferência de calor entre os dois fluídos pode ser calculada por uma das seguintes três euações: Δ w A ΔT A (ΔT A < e w A m A cpa ) (6) Δ w B ΔT B (ΔT B > e m B cpb ) (7) Δ UΔA T A T B ( ) (ΔA PΔx) (8) Manipulando algebricamente as euações (6) e (7), obtém-se a seguinte relação entre ΔT A e ΔT B : ΔT A - ΔT B w A + w B Δ Δ T ( T T ) A A T B B UP w A + w B Δx Considerando Δx, obtém-se: ( T T ) d T A A T B B UP w A + w B dx Considerando a mudança de variável θ T A - T B, obtém-se a seguinte euação diferencial: dθ UP dx θ + w A w (9) B 4
144 Cuja integração fornece o seguinte resultado: θ TA TB ln ln UA + () θ TA TB w A w B Por outro lado, a energia total transferida entre os dois fluídos pode ser calculada pelas euações de balanço de energia global aos fluídos uente e frio: w A (T A T A ) () ou w B (T B T B ) () Manipulando algebricamente as euações () e (), obtém-se o seguinte desenvolvimento, tendo também em consideração o cálculo do termo euação (): + pela w A w B ( T T ) ( T T ) A B A B w A + w B ( T T ) ( T T ) A A B B ( ) lm A B A B ΔT T ln T T T UA UA (3) Conclui-se novamente ue a diferença de temperaturas média a usar na euação geral dos permutadores é a média logarítmica das diferenças de temperaturas do lado esuerdo e direito do permutador, independentemente da configuração do mesmo. 43
145 5.5. Outros Tipos de Permutadores de Calor A euação geral dos permutadores foi deduzida analiticamente considerando permutadores de calor de tubos concêntricos. O tratamento analítico de outro tipo de permutadores (por exemplo: permutadores compactos ou de casco e tubos, Figura 75) é mais complexo, pelo ue, na prática, se definem factores de correcção para uso na euação geral dos permutadores, euação (4). UAF( ΔT) lm (4) ) lm Na euação (4), ( ΔT é calculado considerando fluxo em contra-corrente e F é o factor de correcção, cujo valor depende da configuração do permutador e das temperaturas de entrada e de saída das correntes de fluído uente e de fluído frio. F pode ser obtido em gráficos apropriados, como sejam os da Figura 76, válidos para permutadores de calor de fluxo cruzado e de casco e tubos, em função das razões R e P definidas na Figura. 44
146 Tubo rectangular Tubo circular (a) Alheta em placa Alheta circular Alhetas Placas paralelas Saída do tubo Entrada no casco (b) Saída do casco Entrada no tubo Figura 75 Outros tipos de permutadores de calor diferente de tubos concêntricos. (a) permutadores compactos; (b) permutador de casco e tubos 45
147 Factor de correcção, F Permutador de calor de casco e tubos: passo no casco e, 4, 6, etc. (múltiplos de ) passo nos tubos Factor de correcção, F Factor de correcção, F Factor de correcção, F Permutador de calor de casco e tubos: passos no casco e 4, 8,, etc. (múltiplos de 4) passo nos tubos Permutador de calor de fluxo cruzado de passo e sem mistura promovida nos dois fluídos Permutador de calor de fluxo cruzado de passo e com mistura promovida num dos fluídos Figura 76 Diagramas do factor de correcção F para permutadores de calor de casco e tubos e de fluxo cruzado 46
148 5.6. Cálculo da Eficiência de um Permutador de Calor Da análise realizada na secção 5.3., é possível deduzir a euação (5), válida para um permutador de calor de tubos concêntricos com fluxo em contra-corrente: T T A A T T B B e UA w A wb (5) A euação (5) mostra-nos ue: se w A > w B TA TB > a diferença máxima de T é obtida em T T A B se w A < w B TA TB < a diferença máxima de T é obtida em T T A B Exemplos destas duas situações podem ser visualizados na Figura 77. T A, (a) T A, (b) T A, T B, T B, T B, T A, T B, Figura 77 Perfis de temperatura em permutadores de calor de tubos concêntricos com fluxo em contra-corrente e (a) w A > w B; (b) w A < w B Por outro lado, para um permutador de calor de tubos concêntricos com fluxo em co-corrente, da análise realizada na secção 5.4. é possível deduzir a euação (6). 47
149 T T A A T T B B e UA + wa wb (6) A euação (6) mostra-nos ue: T T A A T T B B >, wa,wb a diferença máxima de T é obtida sempre em A Figura 78 ilustra claramente a relação anterior. T A, T A, c pa ΔT A Δ T A, T B, T B, T B, c pb ΔT B Figura 78 Perfis de temperatura em permutadores de calor de tubos concêntricos com fluxo em co-corrente Para calcular a eficiência de um permutador de calor (η) devemos primeiro conhecer a sua definição: η energia efectivamente trocada energia máxima possível trocar Max (7) No caso de um permutador de calor em contra-corrente, a energia efectivamente trocada pode ser calculada facilmente atendendo às euações analisadas na secção 5.3.: w A (T A T A ) ou w B (TB TB ) 48
150 A energia máxima possível trocar é um valor teórico correspondente à idealização de um permutador de calor de comprimento infinito, onde um dos fluídos teria uma variação de temperatura correspondente à máxima variação possível. Para melhor compreender esta idealização, considerar a situação em ue w A > w B (Figura 77(a)). Neste caso o fluído B seria auele a registar a maior variação de temperatura, e a máxima variação possível corresponderia à situação em ue a temperatura de saída do fluído B (em ) igualaria a temperatura de entrada do fluído A: Max w B (TA TB ) (8) Com um raciocínio análogo, no caso em ue w A < w B (Figura 77(b)), o fluído A seria auele a registar a maior variação de temperatura, e a máxima variação possível corresponderia à situação em ue a temperatura de saída do fluído A (em ) igualaria a temperatura de entrada do fluído B: Max w A (TA TB ) (9) Tendo em consideração o exposto é agora possível calcular a eficiência de um permutador de calor de tubos concêntricos com fluxo em contra-corrente, conhecidas as temperaturas de entrada e de saída dos fluídos e os valores de w A e de w B : B ( TB TB ) TB TB ( TA TB ) TA TB wb η se w A > w B () w A ( TA TA ) TA TA ( TA TB ) TA TB wa η se w A < w B () w No caso de um permutador de calor em co-corrente, a energia efectivamente trocada pode ser calculada atendendo às euações analisadas na secção 5.4.: w A (T A T A ) ou w B (TB TB) 49
151 A energia máxima possível trocar, no caso em ue w A > w B, obtém-se sabendo ue o fluído B seria auele ue registaria a maior variação de temperatura, e a máxima variação possível corresponderia à situação em ue a temperatura de saída do fluído B (em ) igualaria a temperatura de entrada do fluído A: Max w B (TA TB) () Com um raciocínio análogo, no caso em ue w A < w B, o fluído A seria auele a registar a maior variação de temperatura, e a máxima variação possível corresponderia à situação em ue a temperatura de saída do fluido A (em ) igualaria a temperatura de entrada do fluído B: Max w A (TA TB) (3) Assim, é possível calcular a eficiência de um permutador de calor de tubos concêntricos com fluxo em co-corrente, conhecidas as temperaturas de entrada e de saída dos fluídos e os valores de w A e de w B : B ( TB TB ) TB TB ( TA TB ) TA TB wb η se w A > w B (4) w A ( TA TA ) TA TA ( TA TB ) TA TB wa η se w A < w B (5) w 5
152 Capítulo 6 Transferência de Calor por Radiação A radiação térmica é a energia emitida na forma de ondas electromagnéticas por toda a matéria ue se encontra a uma temperatura não nula. Exemplos comuns de fontes de radiação podem ser encontrados no sol, no auecimento doméstico e industrial, em processos de secagem, entre muitos outros. 6.. Natureza da Radiação Nos capítulos anteriores verificou-se ue para ocorrer transferência de calor por mecanismos de condução e convecção é necessária a existência de um gradiente de temperatura num meio físico (um sólido, ar estagnado ou em movimento, etc.). Ao contrário da condução e da convecção, a transferência de calor por radiação térmica não necessita de um meio físico para ocorrer, podendo existir radiação no vácuo, como é o caso da radiação solar ue incide na Terra após percorrer o espaço. Outra característica da radiação está no facto de barreiras físicas impedirem a transferência de calor. Por exemplo, a presença de nuvens na atmosfera impede a transferência de energia por radiação entre a Terra e o Espaço, reduzindo a temperatura máxima no período diurno e elevando a temperatura mínima no período nocturno (Figura 79). ESPAÇO ESPAÇO Radiação Térmica DIA NOITE Radiação Térmica TERRA TERRA Figura 79 As nuvens actuam como barreiras físicas à transferência de calor por radiação entre a Terra e o Espaço 5
153 A intensidade da radiação depende ualitativamente e uantitativamente da temperatura absoluta e da diferença de temperaturas (e não apenas da diferença de temperaturas, como acontece na condução e na convecção). Por exemplo, a cor de objectos incandescentes varia com a temperatura do corpo, devido à variação das suas propriedades ópticas, bem como a taxa de energia radiante. A radiação propaga-se à velocidade da luz e tem propriedades ondulatórias e corpusculares. Sendo caracterizada como uma onda electromagnética, a radiação possui um comprimento de onda (λ) e uma freuência (υ) ue se relacionam pela velocidade da luz (c): c λ (6) υ Para propagação no vácuo, a velocidade da luz toma o valor de 3x 8 m/s. A energia de uma onda electromagnética pode ser calculada pelas seguintes euações, obtidas das teorias ondulatória e corpuscular, respectivamente: E hυ (7) ou E mc (8) onde h representa a constante de Planck (6.65x -34 J.s). Das euações (6) e (7) é fácil constatar ue uanto menor for o comprimento de onda da radiação, maior será a sua freuência e conseuentemente maior será a sua energia. A unidade de comprimento de onda mais utilizada é o micrometro (μm), onde μm -6 m. O espectro completo da radiação electromagnética apresenta-se na Figura 8. 5
154 Visível Violeta Azul Verde Amarelo Vermelho Raios gama Raios X Ultravioleta Infravermelho Radiação térmica Microondas Figura 8 Espectro da radiação electromagnética A radiação de peuenos comprimentos de onda (raios gama, raios X e radiação ultravioleta) é caracterizada por uma elevada energia, sendo útil nas áreas da física e da engenharia nuclear. A radiação de grandes comprimentos de onda (microondas e ondas rádio, λ > 5 μm) é caracterizada por baixa energia, sendo particularmente útil em engenharia electrotécnica. É a gama intermédia do espectro, desde aproximadamente. μm a μm, ue inclui parte da radiação ultravioleta (UV) e toda a radiação visível (λ [ μm]) e infravermelho (IR), ue é denominada radiação térmica, uma vez ue é nesta gama ue a matéria emite radiação ue afecta o estado térmico ou a temperatura da matéria. 6.. Radiação Térmica A radiação térmica incidente sobre uma superfície pode ser reflectida, absorvida ou transmitida (Figura 8). 53
155 Radiação Incidente Radiação Reflectida Radiação Absorvida Radiação Transmitida Figura 8 Absorção, reflexão e transmissão de radiação incidente numa superfície A fracção de radiação incidente ue é reflectida, denomina-se de reflectividade (ρ). A fracção de radiação incidente ue é absorvida, denomina-se de absorptividade (α). A fracção de radiação incidente ue é transmitida, denomina-se de transmitividade (τ). Seja ual for a magnitude de cada uma das fracções envolvidas, as mesmas terão sempre de obedecer à euação (9), resultante do balanço energético à superfície. ρ + α + τ (9) Como definido no início deste capítulo, ualuer superfície a uma temperatura não nula emite radiação. Como exemplo, vamos considerar um sólido no interior de uma cavidade mantida sob vácuo, inicialmente a uma temperatura T S, superior à temperatura T sur da parede da cavidade (Figura 8). Radiação emitida pela parede Sólido Radiação emitida pela superfície Vácuo Parede Figura 8 Arrefecimento por radiação de um sólido auecido 54
156 O facto da cavidade estar sob vácuo impede perdas de energia da superfície do sólido por condução ou convecção. No entanto, a nossa intuição diz-nos ue o sólido irá arrefecer e eventualmente atingir o euilíbrio térmico, onde as temperaturas do sólido e da parede da cavidade se igualam. O arrefecimento do sólido deve-se a emissão de radiação térmica pela sua superfície. Contudo, a superfície do sólido irá também interceptar e absorver radiação emitida pela parede da cavidade. No entanto, como T S > T sur, em termos líuidos ocorre transferência de calor por radiação (a uma taxa rad,net ) da superfície do sólido para a vizinhança, levando ao arrefecimento do sólido até ao euilíbrio térmico. A radiação térmica emitida por uma superfície engloba uma gama de comprimentos de onda e, como exemplificado na Figura 83(a), a intensidade da radiação térmica emitida por uma superfície varia com o comprimento de onda (λ). O termo distribuição espectral é assim usado para realçar a natureza desta dependência. Como iremos ver mais tarde em mais detalhe, uer a intensidade da radiação emitida a um dado comprimento de onda, uer a distribuição espectral, variam com a natureza do material emissor e com a temperatura. A natureza espectral da radiação térmica é uma de duas características ue tornam mais complexa a sua descrição. A segunda característica refere-se à sua direccionalidade. Como observado na Figura 83(b), uma superfície emite preferencialmente em certas direcções, originando uma distribuição direccional da radiação emitida. Se a intensidade da radiação emitida por uma superfície for uniforme em todas as direcções, diz-se ue o emissor é difuso. Emissão de radiação Distribuição espectral (a) Distribuição direccional (b) Comprimento de onda Figura 83 Radiação emitida por uma superfície. (a) Distribuição espectral; (b) Distribuição direccional 55
157 Da mesma forma ue existe uma distribuição direccional para caracterizar a emissão de uma superfície, também existe uma distribuição direccional para caracterizar a reflexão de radiação por uma superfície. Nos casos limites, a reflexão é especular, se o ângulo de incidência da radiação for igual ao ângulo de reflexão (Figura 84(a)). A reflexão será difusa se ocorrer uniformemente em todas as direcções (Figura 84(b)). Radiação Incidente Radiação Reflectida φ φ (a) (b) Figura 84 Radiação reflectida numa superfície. (a) Especular; (b) Difusa Para uantificar os conceitos de emissão, absorção, reflexão e transmissão introduzidos anteriormente, temos necessidade de tratar analiticamente ambos os efeitos espectral e direccional. Este assunto será abordado mais tarde neste capítulo uando fizermos a análise detalhada de superfícies reais. Por enuanto, na próxima secção, iremos concentrar a nossa atenção na análise de superfícies ideais, os designados corpos negros Radiação de um Corpo Negro Um corpo negro é uma superfície ideal ue serve como padrão para a descrição de superfícies reais. Um corpo negro é definido pelas seguintes propriedades: i) Absorve toda a radiação incidente, isto é α, independentemente do comprimento de onda e da direcção; ii) A uma dada temperatura e comprimento de onda, nenhuma superfície emite mais energia ue um corpo negro; iii) A radiação emitida por um corpo negro depende da temperatura e do comprimento de onda, mas é independente da direcção. Por outras palavras, o corpo negro é um emissor difuso. 56
158 Embora existam algumas superfícies ue se aproximem ao comportamento de corpo negro, é importante referir ue não existe nenhuma superfície com as propriedades exactas da definição do conceito de corpo negro. A maior aproximação possível é obtida por uma cavidade acessível por um peueno orifício e com a superfície interna mantida a uma temperatura uniforme (um forno com abertura, por exemplo). Se considerarmos um feixe de radiação a entrar na cavidade pelo orifício (Figura 85(a)), o mais provável é ue ocorram muitas reflexões antes ue a radiação saia novamente da cavidade pelo orifício. Por isso, a radiação incidente na cavidade é uase totalmente absorvida, podendo-se aproximá-la a comportamento de corpo negro. Por um raciocínio análogo, e considerando os princípios da termodinâmica, pode-se concluir ue a radiação ue sai pelo orifício depende apenas da temperatura da superfície, correspondendo à emissão de um corpo negro (Figura 85(b)). Como um corpo negro é um emissor difuso, a intensidade espectral da radiação emitida é independente da direcção. Devido à natureza difusa da radiação na cavidade provocada pelos efeitos cumulativos da emissão e da reflexão, ualuer peuena superfície colocada na cavidade irá receber radiação de uma forma difusa (Figura 85(c)), isto é, com uma intensidade independente da orientação. Emissão difusa Superfície isotérmica, T Figura 85 Características de uma cavidade isotérmica (comportamento de corpo negro). (a) Absorção total; (b) Emissão difusa pelo orifício de acesso à cavidade; (c) Radiação difusa incidente numa peuena superfície no interior da cavidade. 57
159 A energia de radiação emitida por um corpo negro, mais concretamente, o poder emissivo total do corpo negro (em W/m ), é calculado pela lei de Stefan-Boltzmann: b 4 E σt (3) onde T (K) é a temperatura da superfície, A e σ a constante de Stefan-Boltzmann (σ 5.67x -8 W/m K 4 ). A taxa de transferência de calor por radiação emitida pela superfície de área A, obtém-se multiplicando o poder emissivo pela área: 4 σat (5) 6.4. Distribuição de Planck O poder emissivo espectral de um corpo negro pode ser calculado, recorrendo à denominada distribuição de Planck: C E λ, b (W/m.μm) (3) C 5 λ e λt onde C e C são constantes (C 3.74x 8 W.μm 4 /m e C.439x 4 μm.k), λ é o comprimento de onda (em μm) e T é a temperatura absoluta (em K). Na Figura 86 representa-se graficamente a distribuição de Planck para algumas temperaturas seleccionadas. 58
160 Região visível do espectro Radiação solar Poder emissivo espectral Comprimento de onda Figura 86 Poder emissivo espectral de um corpo negro Da análise da Figura 86 obtém-se algumas conclusões importantes: i) A radiação emitida varia continuamente com o comprimento de onda; ii) Para um comprimento de onda fixo, o poder emissivo aumenta com o aumento da temperatura; iii) A região espectral na ual a radiação se concentra depende da temperatura. Comparativamente, a radiação concentra-se a comprimentos de onda mais baixos à medida ue a temperatura aumenta; iv) Parte significativa da radiação solar (o sol pode ser aproximado a um corpo negro a 58 K) é radiação visível. Por outro lado, para temperaturas 59
161 inferiores a 8 K, a emissão é predominantemente na região do infravermelho (radiação não visível ao olho humano) Lei do Deslocamento de Wien Na Figura 86 observa-se ue a distribuição espectral de um corpo negro possui um máximo e ue o comprimento de onda (λ max ) para o ual o poder emissivo é máximo depende da temperatura. A natureza desta dependência pode ser obtida, derivando a distribuição de Planck em ordem a λ e igualando o resultado a zero: λ C λ 5 λ e ( E ) λ, b C λt λ max.t C 3 (3) Obtém-se assim a denominada lei do deslocamento de Wien, onde C 3 é uma constante (897.8 μm.k). O conjunto de pontos dados por esta lei apresentam-se representados na Figura 86 pela linha a traço interrompido. De acordo com este resultado, o poder emissivo espectral máximo desloca-se para comprimentos de onda mais baixos com o aumento da temperatura Lei de Stefan-Boltzmann O poder emissivo total de um corpo negro (E b ) pode ser calculado a partir do poder emissivo espectral, integrando este em ordem ao comprimento de onda: E b E λ,b dλ C 5 λ e C λt dλ 6
162 4 E σt (3) b Obtém-se a lei de Stefan-Boltzmann referida anteriormente. Esta lei simples e importante permite o cálculo da uantidade de radiação emitida em todas as direcções e em todos os comprimentos de onda, bastando apenas conhecer a temperatura do corpo negro. Emissão numa Banda de Comprimentos de Onda Freuentemente, é necessário conhecer a fracção da emissão total de um corpo negro ue se encontra num certo intervalo (banda) de comprimentos de onda. Para uma dada temperatura e um intervalo de comprimentos de onda entre e λ, esta fracção é determinada pela razão entre a área sombreada e a área total sob a curva da Figura 87. Ou seja: λ λ E λ,bdλ E λ,bdλ λt E λ,b F ( λ) d( λt ) (33) 4 5 σt σt E dλ λ,b Eλ,b Como é uma função apenas do produto entre a temperatura e o 5 σt comprimento de onda (λt), o integral pode ser calculado para obter F ( λ) como função apenas de λt. Os resultados obtidos apresentam-se em tabelas disponíveis no material fornecido na unidade curricular de Fenómenos de Transferência I, podendo também ser usados para calcular a fracção de radiação entre uaisuer dois comprimentos de onda λ e λ, uma vez ue: F (λ λ) F ( λ) - F ( λ) (34) 6
163 Figura 87 Radiação emitida por um corpo negro na banda espectral entre e λ Exercício Considere uma cavidade mantida a uma temperatura uniforme de K. Calcule o poder emissivo da radiação ue emerge de uma peuena abertura na superfície da cavidade. Qual é o comprimento de onda, λ, abaixo do ual se concentra % da emissão? Qual é o comprimento de onda, λ, acima do ual se concentra % da emissão? Determine o poder emissivo espectral máximo e o correspondente comprimento de onda ao ual esta emissão ocorre. Resolução A emissão de radiação a partir da abertura de ualuer cavidade isotérmica terá características de radiação de um corpo negro. Assim, pela lei de Stefan-Boltzmann, calcula-se o poder emissivo: E E b σt x -8 x 4 9.7x 5 W/m Na figura 88, visualiza-se ualitativamente o posicionamento dos comprimentos de onda λ e λ, correspondentes, respectivamente, aos limites inferior e superior das bandas espectrais ( λ ) e (λ ) contendo % da radiação emitida. 6
164 Figura 88 Poder emissivo espectral de um corpo negro Para F ( λ)., obtém-se da tabela correspondente ue λ T 95 μm.k, pelo ue λ. μm. Para F (λ ). - F ( λ). F ( λ).9. Da tabela correspondente, obtém-se ue λ T 938 μm.k, pelo ue λ 4.75 μm. Da lei de Wien, λ max.t μm.k λ max.45 μm. O poder emissivo espectral máximo associado a este comprimento de onda pode finalmente ser calculado pela distribuição de Planck: C E W/m.μm 5 λmax, b 4. C 5 λt λ e 6.7. Intensidade de Radiação Após a compreensão das características da radiação em corpos negros, vamos evoluir para a sua análise em superfícies reais. Para tal é necessária a revisão prévia de algumas definições matemáticas fundamentais. Como discutido no início deste capítulo, a radiação emitida por uma superfície real pode propagar-se em todas as direcções possíveis (Figura 83(b)), pelo ue estamos freuentemente interessados em conhecer a sua distribuição espectral. Do mesmo modo, a radiação incidente numa superfície pode ser originária de direcções diferentes e a forma como uma superfície responde a esta reacção pode também depender da direcção. Tais efeitos direccionais podem ser de 63
165 grande importância na determinação da taxa líuida de transferência de calor por radiação e podem ser tratados pela introdução do conceito de intensidade de radiação. Devido à sua natureza, o tratamento matemático da transferência de calor por radiação envolve o uso comum do sistema de coordenadas esféricas (Figura 89(d)), em vez do uso de coordenadas cartesianas. Um ponto P genérico de coordenadas (x, y, z) no sistema cartesiano, em coordenadas esféricas será caracterizado por (r, θ, φ). Os dois sistemas estão relacionados pelas seguintes expressões: x r.senθ.senφ y r.senθ.senφ z r.cosθ Radiação emitida Figura 89 Definições matemáticas. (a) Ângulo plano; (b) Ângulo sólido; (c) Emissão de radiação de uma área diferencial da para um ângulo sólido dw delimitado por da n com origem em da ; (d) Sistemas de coordenadas esféricas 64
166 Da Figura 89(a) recordamos ue o ângulo plano diferencial dα é definido pela região entre os raios de uma circunferência e calculado como a razão entre o arco de circunferência dl e o raio r da circunferência: dl dα (rad - radiano) (35) r Da mesma forma, da Figura 89(b), o ângulo sólido diferencial dw é definido pela região entre os raios de uma esfera e calculado como a razão entre a área da n na esfera e o uadrado do raio da esfera: da n dw (sr - esterorradiano) (36) r Considerar a emissão de radiação numa direcção particular a partir de um elemento de superfície da, como ilustrado na Figura 89(c). A direcção pode ser definida em função dos ângulos θ e φ de um sistema de coordenadas esféricas (Figura 89(d)). A área da n pela ual a radiação atravessa, delimita um ângulo sólido diferencial uando observado desde um ponto em da. Como observado na Figura 9, a área da n corresponde a um rectângulo de dimensão r.dθ x r.senθ.dφ, pelo ue: da n r.senθ.dθ.dφ (37) e da n dw senθ.dθ.dφ (38) r 65
167 Figura 9 Ângulo sólido delimitado por da n com origem num ponto em da no sistema de coordenadas esféricas Regressando à Figura 89(c), vamos agora determinar a taxa de energia radiante emitida por da ue passa por da n. Esta uantidade pode ser expressa em função da intensidade espectral, I λ, definida como a taxa de energia radiante emitida com comprimento de onda λ na direcção caracterizada por (θ, φ), por unidade de área de superfície emissora normal a esta direcção, por unidade de ângulo sólido e por unidade de comprimento de onda. Notar ue a área de superfície emissora usada para definir a intensidade é a componente da perpendicular à direcção da radiação. Da figura 9, verificamos ue a projecção desta área é igual a da.cosθ, o ue na prática corresponde à área da ue seria observada desde da n. Figura 9 Projecção de da no plano normal à direcção da radiação 66
168 A intensidade espectral, com unidades em W/m.sr.μm, toma a seguinte forma: I d λ ( λ, θ, φ) (39) dacosθ.dw.dλ d onde d λ corresponde à taxa de energia radiante com comprimento de onda λ dλ emitida por da ue passa por da n. Rearranjando a euação (39) obtém-se a euação (4). λ d I ( λ, θ, φ) da cosθ. dw λ (W/μm) (4) Esta importante euação permite-nos calcular a taxa à ual a radiação emitida por uma superfície se propaga para uma região do espaço definida pelo ângulo sólido dw na direcção (θ, φ). No entanto, para calcular esta taxa, é necessário conhecer a intensidade espectral da radiação emitida, I λ (λ, θ, φ). A forma sobre como calcular esta uantidade será discutida mais tarde. Se dividirmos a euação (4) pela área da superfície emissora, obtemos o fluxo de radiação espectral associado a da : dq λ d λ da I λ ( λ, θ, φ).cosθ. dw I λ ( λ, θ, φ).cosθ. senθ. dθ. dφ (W/m.μm) (4) 6.8. Poder emissivo espectral Se as distribuições espectral e direccional de I λ forem conhecidas, isto é, se I λ (λ, θ, φ) for conhecida, o fluxo de radiação associado à emissão para ualuer ângulo sólido finito, pode ser calculado por integração da euação (4). Por exemplo, definimos o poder emissivo espectral hemisférico, E λ (em W/m.μm), como a taxa à ual a radiação de comprimento de onda λ é emitida em todas as direcções a partir de uma superfície, por unidade de comprimento de onda e por unidade de área de superfície emissora. Assim, por definição, E λ corresponde ao fluxo de radiação espectral 67
169 associado à emissão para uma superfície hemisférica situada acima de da, como representado na Figura 9. Assim: E λ Q λ d λ da π π I λ ( λ, θ, φ).cosθ. senθ. dθ. dφ (4) e λ E λ A (43) Figura 9 Emissão de radiação de um elemento diferencial de área da para uma superfície hemisférica hipotética centrada num ponto em da Por sua vez, o poder emissivo hemisférico total, E (em W/m ), corresponde à taxa à ual a radiação é emitida por unidade de área em todos os comprimentos de onda possíveis e em todas as direcções possíveis. Assim: E Q E λdλ (44) 68
170 e EA (45) Notar ue, uma vez ue o termo poder emissivo implica sempre emissão em todas as direcções, o termo hemisférico é redundante, sendo freuentemente omitido e comum referir poder emissivo espectral e poder emissivo total para designar E λ e E, respectivamente. Embora a distribuição direccional da emissão de uma superfície varie de acordo com a natureza da superfície, existe um caso especial ue serve como aproximação razoável a muitas superfícies. Diz-se ue uma superfície é um emissor difuso se a intensidade de radiação emitida for independente da direcção. Neste caso especial: I λ (λ, θ, φ) I λ (λ) (46) Como I λ (λ) é uma constante no domínio de θ e de φ, é possível integrar facilmente a euação (4), obtendo-se o resultado apresentado no seguinte desenvolvimento: E λ π. I π π π λ I λ cosθ. senθ. dθ. dφ I cosθ. senθ. dθ π. I λ λ π π cosθ. senθ. dθ. dφ (47) Da mesma forma, obtém-se ue, para um emissor difuso: E Q E λ dλ π.iλdλ π Iλdλ π.i (48) onde I corresponde à intensidade total da radiação emitida. 69
171 6.9. Irradiação Na secção anterior analisamos com detalhe a radiação emitida por uma superfície. No entanto, os conceitos aduiridos podem facilmente ser estendidos à radiação incidente numa superfície Figura 93. Radiação incidente, I iλ Figura 93 Natureza direccional da radiação incidente A radiação incidente numa superfície pode ser originária da emissão e reflexão a ocorrer noutras superfícies e terá distribuições espectral e direccional determinadas pela intensidade espectral incidente I iλ (λ, θ, φ). Esta uantidade é definida como a taxa de energia incidente com comprimento de onda λ a partir da direcção (θ, φ), por unidade de área de superfície receptora normal a esta direcção, por unidade de ângulo sólido e por unidade de comprimento de onda. Tem como unidades W/m.sr.μm. A intensidade da radiação incidente pode ser relacionada com um importante fluxo radiante, denominado irradiação, ue considera a radiação incidente numa superfície a partir de todas as direcções. A irradiação espectral, G λ (em W/m.μm), é definida como a taxa à ual radiação com comprimento de onda λ incide numa superfície, por unidade de área de superfície e por unidade de comprimento de onda. Assim: G λ π π I i λ ( λ, θ, φ).cosθ. senθ. dθ. dφ (49) 7
172 e λ i G λ A (5) Por sua vez, a irradiação total, G (em W/m ), representa a taxa à ual a radiação incide por unidade de área em todos os comprimentos de onda possíveis e de todas as direcções possíveis: G G λ dλ (5) e i GA (5) Se a radiação incidente for difusa, isto é, se a intensidade da radiação incidente for independente da direcção, obtém-se ue: G λ πi iλ (53) G πi i (54) Exercício Considere a seguinte distribuição espectral da irradiação numa superfície: 7
173 Calcule a irradiação total. Resolução A irradiação total pode ser obtida da seguinte euação: G G λ dλ O integral é facilmente calculado dividindo-o em várias partes. Assim: G G λdλ λ.dλ.dλ 5 -.dλ ( 5) + 5. ( 5 ). G W/m 6.. Radiosidade O último fluxo de radiação de interesse para o nosso estudo, denominado radiosidade, considera toda a energia radiante ue deixa uma superfície. Uma vez ue 7
174 esta radiação inclui a parte reflectida da irradiação, bem como a emissão directa (Figura 94), a radiosidade é normalmente diferente do poder emissivo. Radiosidade Emissão Irradiação Parte reflectida da irradiação Figura 94 Radiosidade de uma superfície A radiosidade espectral, J λ (em W/m.μm), representa a taxa à ual radiação de comprimento de onda λ sai de uma superfície, por unidade de área de superfície e por unidade de comprimento de onda. Uma vez ue considera a radiação a sair da superfície em todas as direcções, está relacionada com a intensidade associada a emissão e reflexão, I * λ (λ, θ, φ), através da euação (55). J λ π π * I λ ( λ, θ, φ).cosθ. senθ. dθ. dφ (55) Assim, a radiosidade total, J (em W/m ), calcula-se da seguinte forma: J J λ dλ (56) Se a superfície for simultaneamente um reflector difuso e um emissor difuso, isto é, se I λ * (λ, θ, φ) for independente da direcção, obtém-se as euações (57) e (58). 73
175 J λ πi λ * (57) J πi * (58) 6.. Emissão em Superfícies Reais Uma vez já aduirida a noção de corpo negro para descrever o comportamento de superfícies ideais e de termos estudado as principais características da radiação em superfícies reais, estamos em condições de analisar mais profundamente o comportamento de superfícies reais. Recordar ue o corpo negro é um emissor ideal, no sentido em ue nenhuma superfície pode emitir mais radiação ue um corpo negro à mesma temperatura. Uma propriedade da radiação conhecida como emissividade, ε, pode então ser definida como a razão entre a radiação emitida pela superfície real e a radiação emitida por um corpo negro à mesma temperatura. É importante ter presente ue, normalmente, a radiação espectral emitida por uma superfície real difere ualitativamente da distribuição de Planck (Figura 95(a)) e ue a sua distribuição direccional pode não ser difusa (Figura 95(b)). Por isso, a emissividade pode ter valores diferentes, dependendo se estamos interessados na emissão total (emissividade total, ε), na emissão a um dado comprimento de onda (emissividade espectral, ε λ ), na emissão numa dada direcção (emissividade direccional, ε θ ) ou na emissão a um dado comprimento de onda e numa dada direcção (emissividade espectral direccional, ε λ,θ ). Corpo negro, T Superfície real, T Corpo negro, I λ,b Superfície real Figura 95 Comparação da emissão de um corpo negro com uma superfície real. (a) Distribuição espectral; (b) Distribuição direccional 74
176 Definimos emissividade espectral direccional de uma superfície a uma dada temperatura T, ε λ,θ, como a razão entre a intensidade da radiação emitida por essa superfície a um dado comprimento de onda λ, na direcção (θ, φ) e a intensidade da radiação emitida por um corpo negro considerando os mesmos valores de T e λ: ε λ,θ Iλ ( λ,θ, φ,t) ( λ,θ, φ,t) (59) I ( λ,t) λ,b De modo análogo, a emissividade direccional total hemisférica, ε θ, representa a média espectral de ε λ,θ, sendo definida pela seguinte expressão: ε θ I( θ, φ,t) ( θ, φ,t) (6) I (T) b Na maioria dos cálculos de engenharia é preferível trabalhar com propriedades de superfície ue representem médias direccionais. A emissividade espectral hemisférica, ε λ, é então definida como: ε λ E λ ( λ,t) ( λ,t) (6) E ( λ,t) λ,b A emissividade espectral hemisférica pode ser relacionada com a emissividade espectral direccional, atendendo ao seguinte desenvolvimento da expressão anterior: ε λ ( λ,t) E E λ λ,b ( λ,t) ( λ,t) π π π π I I λ λ, b cosθ. senθ. dθ. dφ cosθ. senθ. dθ. dφ Tendo em consideração a definição de emissividade espectral direccional e ue I λ,b é independente de θ e φ, obtém-se: 75
177 ε λ π π ε λ, θ π π cosθ. senθ. dθ. dφ cosθ. senθ. dθ. dφ Considerando ε λ,θ independente de φ, o ue é uma aproximação razoável para a maioria das superfícies, por avaliação do denominador, obtém-se a seguinte relação: π ε λ ε λ, θ cosθ. sen θ. dθ (6) A emissividade total hemisférica representa uma média de todos os comprimentos de onda e direcções possíveis, sendo definida da seguinte forma: E(T) ε(t) (63) E (T) b Desenvolvendo a expressão anterior obtém-se a euação (64). E ( λ, T ). dλ λ b (T) Eb ( T ) ε E ε(t) E(T) E E (64) λ λ, b b dλ Conhecendo as emissividades de uma superfície, é possível caracterizar facilmente a emissão dessa superfície. Por exemplo, se ε λ for conhecida, pode ser usada para calcular o poder emissivo espectral da superfície a ualuer comprimento de onda e temperatura. Da mesma maneira, se ε for conhecida, pode ser usada para calcular o poder emissivo total da superfície a ualuer temperatura. Actualmente existe uma base de dados muito extensa de propriedades emissivas de vários materiais, resultado de determinações experimentais obtidas por muitos investigadores, pelo ue é possível calcular a emissão real de uma grande uantidade de superfícies de interesse. 76
178 A emissividade direccional de um emissor difuso é uma constante, isto é, independente da direcção. No entanto, embora esta condição seja freuentemente uma boa aproximação, todas as superfícies exibem algum desvio ao comportamento difuso. A emissividade depende da natureza da superfície, sendo normalmente baixa em superfícies metálicas polidas e alta em revestimentos. Variações representativas de ε θ com θ são mostradas esuematicamente na Figura 96 para materiais condutores e não condutores. Para materiais condutores, ε θ é aproximadamente constante até θ 4º, após o ual aumenta com o aumento de θ, decaindo depois para zero. Por outro lado, para materiais não condutores, ε θ é aproximadamente constante até θ 7º, após o ual diminui drasticamente com o aumento de θ. Não condutor Condutor Figura 96 Distribuições direccionais representativas da emissividade direccional total 6.. Absorção, Reflexão e Transmissão em Superfícies Reais Na secção 6.9. definimos irradiação espectral, G λ (em W/m.μm), como a taxa à ual radiação de comprimento de onda λ incide numa superfície, por unidade de área de superfície e por unidade de comprimento de onda. A radiação incidente pode ser originária de todas as direcções possíveis e de fontes diversas. A irradiação total, G (em W/m ), engloba todas as contribuições espectrais. Nesta secção consideraremos os processos resultantes da intercepção desta radiação por uma superfície sólida ou líuida. Na situação mais comum, a irradiação interage com um meio semitransparente, como uma camada de água ou uma lâmina de vidro. Como ilustrado na Figura 97 para uma componente espectral da irradiação, esta radiação pode ser reflectida, absorvida ou transmitida. Do balanço de radiação ao meio obtém-se a euação (65). G λ,i G λ,r + G λ,a + G λ,t (65) 77
179 onde os índices I, R, A e T, identificam, respectivamente, radiação incidente, radiação reflectida, radiação absorvida e radiação transmitida. Reflexão Gλ,R Irradiação G λ G λ,i G λ,r + G λ,a + G λ,t Meio semitransparente Absorção Gλ,A Transmissão Gλ,T Figura 97 Processos de absorção, reflexão e transmissão associados a um meio semitransparente Tal como na emissão de radiação, os processos de absorção, reflexão e transmissão de radiação também têm características espectrais e direccionais. A absorptividade é uma propriedade ue determina a fracção da irradiação absorvida por uma superfície. A absorptividade espectral direccional de uma superfície, α λ,θ (λ, θ, φ), é definida como a fracção da intensidade espectral incidente na direcção (θ, φ) ue é absorvida por essa superfície: α λ, θ I λ, A ( λ, θ, φ) ( λ, θ, φ) (66) I ( λ, θ, φ) λ Na euação (66) foi desprezada a dependência da absorptividade com a temperatura da superfície. Tal dependência é peuena para a maioria das propriedades espectrais da radiação. Está implícito na euação (66) ue as superfícies exibem absorção selectiva em relação ao comprimento de onda e à direcção da radiação incidente. No entanto, na maioria dos cálculos de eengenharia, é desejável trabalhar com propriedades de superfície ue representem médias direccionais. Definimos assim a absorptividade espectral hemisférica, α λ (λ): 78
180 79 ) ( ) ( ) (,, λ λ λ α λ λ λ I A G G (67) A absorptividade total hemisférica, α, representa uma média integrada sobre a direcção e o comprimento de onda. É definida como a fracção da irradiação total absorvida pela superfície:,, λ λ α α λ λ λ d G d G G G I I A (68) De acordo com a euação (68), α depende da distribuição espectral da radiação incidente, bem como da sua distribuição direccional e da natureza da superfície absorvente. Notar no entanto ue, embora α seja aproximadamente independente da temperatura da superfície, o mesmo não acontece com a emissividade total hemisférica, ε. A reflectividade é uma propriedade ue indica a fracção da radiação incidente ue é reflectida por uma superfície. A reflectividade espectral direccional de uma superfície, ρ λ,θ (λ, θ, φ), é definida como a fracção da intensidade espectral incidente na direcção (θ, φ) ue é reflectida por essa superfície: ),, ( ),, ( ),, (,, φ θ λ φ θ λ φ θ λ ρ λ λ θ λ I I R (69) A refectividade espectral hemisférica, ρ λ (λ), é definida como a fracção da irradiação espectral ue é reflectida pela superfície: ) ( ) ( ) (,, λ λ λ ρ λ λ λ I R G G (7) Por sua vez, a reflectividade total hemisférica, ρ, é definida pela euação (7).
181 G ρ G R ρ G λ G λ, I λ, I dλ dλ (7) As superfícies podem ser idealizadas como difusa ou especular, de acordo com a forma como reflectem a radiação (Figura 98). A reflexão difusa ocorre se, independentemente da direcção da radiação incidente, a intensidade da radiação reflectida for independente do ângulo de reflexão (Figura 98(a)). Por outro lado, se toda a radiação for reflectida na direcção θ, igual ao ângulo de incidência θ, diz-se ue ocorre reflexão especular (Figura 98(b)). Embora nenhuma superfície seja perfeitamente difusa ou especular, esta última condição é aproximada por superfícies polidas, tipo espelho, e a primeira condição por superfícies rugosas. A aproximação a reflexão difusa é razoável para a maioria das aplicações de engenharia. Radiação incidente Radiação reflectida com intensidade uniforme Radiação incidente Radiação reflectida (a) (b) Figura 98 Reflexão (a) difusa e (b) especular Tendo em consideração as definições anteriores usadas para caracterizar a absorptividade e a reflectividade, obtemos euações semelhantes para caracterizar a trasmissividade. Assim, a transmissividade espectral direccional tem a seguinte definição: τ λ, θ I λ, T ( λ, θ, φ) ( λ, θ, φ) (7) I ( λ, θ, φ) λ Por sua vez, a transmissividade espectral hemisférica, τ λ (λ), é definida da seguinte forma: 8
182 Gλ, T ( λ) τ λ ( λ) (73) G ( λ) λ, I A transmissividade total hemisférica, τ, é definida pela euação (74). GT τ G τ G λ G λ, I λ, I dλ dλ (74) 6.3. Lei de Kirchhoff Nas secções 6.7. a 6.. consideramos separadamente as propriedades de superfícies reais associadas à emissão e à absorção. Nas próximas secções (6.3. e 6.4.) iremos ver em ue condições essas propriedades são iguais e de ue forma a análise de superfícies reais, obedecendo a essas condições, pode ser simplificada. Seja uma cavidade isotérmica grande com temperatura de superfície T S e vários corpos peuenos confinados no seu interior (Figura 99). Como vimos na secção 6.3., independentemente das suas propriedades de radiação, a superfície de uma cavidade como a descrita terá comportamento de corpo negro. Assim, independentemente da sua orientação, a irradiação experimentada por ualuer corpo na cavidade será difusa e igual à emissão de um corpo negro à temperatura T S : G E b (T S ) σt 4 (75) 8
183 Figura 99 Trocas de radiação numa cavidade isotérmica Em condições de estado estacionário, deverá ocorrer euilíbrio térmico entre os corpos e a cavidade. Assim, T T T S e a taxa líuida de transferência de calor para cada superfície será nula. Realizando um balanço de energia à superfície do corpo A, obtém-se a seguinte relação: α GA E (T S )A (76) Alternativamente, sabendo ue G E b (T S ), vem ue: E(TS ) α E (T ) (77) b S Uma vez ue este resultado se aplica a ualuer corpo confinado, obtém-se a seguinte relação, conhecida como a lei de Kirchhoff: E (T α S ) E (TS )... E b (TS ) (78) α Da definição de emissividade total hemisférica alternativa da lei de Kirchhoff: ε E, obtém-se uma forma E b 8
184 ε α ε... (79) α Assim, para ualuer superfície na cavidade, a sua emissividade total hemisférica é igual à sua absorptividade total hemisférica: ε α (8) Na próxima secção iremos concluir ue os cálculos de transferência de calor por radiação entre superfícies são muito simplificados se pudermos aplicar a lei de Kirchhoff a cada uma das superfícies. No entanto, devemos recordar sempre as condições restritivas usadas na sua derivação. Em particular, recordar ue a irradiação de uma superfície foi considerada ser igual à emissão de um corpo negro à mesma temperatura ue essa superfície. Na próxima secção iremos considerar outras condições menos restritivas ue permitem também aplicar a lei de Kirchhoff se a superfície tiver comportamento de superfície cinzenta (superfície caracterizada por α e ε iguais e constantes numa gama de comprimentos de onda e de temperaturas de interesse). A derivação da lei de Kirchhoff pode ser generalizada e repetida para condições espectrais. Assim, para ualuer superfície no interior da cavidade, obtém-se ue: ε λ α λ (8) As condições associadas ao uso da euação (8) são menos restritivas ue as associadas à lei de Kirchhoff original, euação (8). Em particular, a euação (8) é aplicável se a irradiação for difusa (usual em cálculos de engenharia) ou se a superfície for difusa (razoável para materiais não condutores). Uma forma da lei de Kirchhoff para a ual não existem restrições considera as propriedades espectrais e direccionais da superfície: ε λ,θ α λ,θ (8) Até agora restringimos a nossa atenção aos processos de radiação a ocorrer numa única superfície. Iremos considerar no seguimento problemas de troca de radiação 83
185 entre duas ou mais superfícies. Esta troca depende fortemente da geometria e orientação das superfícies, bem como das suas temperaturas e propriedades de radiação. Inicialmente, iremos considerar ue as superfícies estão separadas por um meio não participativo, isto é, ue não influencia a transferência de calor entre as superfícies (ue não emite, absorve ou refracta radiação). O vácuo cumpre estas condições de uma foram exacta e a maioria dos gases são aproximações excelentes Factores de Forma Para calcular troca de radiação entre uaisuer duas superfícies, temos necessidade de introduzir o conceito de factor de forma. O factor de forma, F ij, é definido como a fracção de radiação ue abandona uma superfície i ue é interceptada por uma superfície j. Para desenvolver uma expressão geral para F ij, vamos considerar as superfícies A i e A j, arbitrariamente orientadas, como mostrado na Figura. As áreas infinitesimais de cada superfície estão ligadas por uma linha de comprimento R, formando ângulos θ i e θ j com a normal às superfícies i e j (n i e n j ), respectivamente. Ter em atenção ue os valores de R, θ i e θ j variam com a posição das áreas infinitesimais consideradas em A i e A j. Figura Factor de forma associado com a troca de radiação entre superfícies infinitesimais de áreas da i e da j. 84
186 Da definição de intensidade de radiação dada na secção 6.7., a taxa à ual a radiação sai de da i e é interceptada por da j pode ser calculada através da seguinte euação: d ij Ii cosθidai dw ji (83) onde Ii corresponde à intensidade de radiação ue abandona a superfície i por emissão e reflexão e dw ji o ângulo sólido delimitado por da j uando observado de da i. Com cosθ jda j dw ji, vem ue: R d cosθi cosθ j ij Ii dai da j (84) R Assumindo ue a superfície i emite e reflecte radiação de uma forma difusa, a sua radiosidade calcula-se da seguinte forma: J i πi i * (85) Pelo ue, substituindo na euação (84), obtém-se a seguinte euação: d ij J i cosθ cosθ i πr j da da i j (86) Por sua vez, a taxa total de radiação ue deixa a superfície i e ue é interceptada por j pode então ser obtida pela integração sobre ambas as superfícies (emissora e receptora): ij Ai Aj J i cosθ cosθ i πr j da da i j (87) 85
187 Da definição de factor de forma (fracção de radiação ue sai de A i e ue é interceptada por A j ) e considerando ue a radiosidade é uniforme sobre a superfície A i, vem ue: F ij ij A J i i J i Ai Aj cosθ cosθ i πr A J i i j da da i j A i Ai Aj cosθ cosθ i πr j da da i j (88) De modo análogo, o factor de forma F ji é definido como a fracção de radiação ue sai de A j e ue é interceptada por A i. O mesmo tipo de raciocínio efectuado anteriormente, conduz à seguinte euação: F ji A j Ai Aj cosθ cosθ i πr j da da i j (89) Recordar ue as euações deduzidas para o cálculo de F ij e de F ji são válidas para uaisuer duas superfícies emissoras e reflectoras difusas e com radiosidade uniforme. Da análise das euações (88) e (89), igualando os integrais, obtém-se uma relação importante dos factores de forma, conhecida como relação de reciprocidade, de grande utilidade, pois permite determinar um factor de forma conhecendo o outro: A i F ij A j F ji (9) Na análise de uma cavidade fechada (Figura ), existe outra relação importante dos factores de forma, derivada do conhecimento de ue a radiação ue deixa a superfície i deve ser toda interceptada pelas superfícies da cavidade: N i i in i + i in Ai J i Fij (9) Ai J i Ai J i Ai J i j 86
188 A relação anterior é conhecida como a regra da soma e pode ser aplicada a cada uma das N superfícies da cavidade. O termo F ii ue aparece neste somatório representa a fracção da radiação ue sai de i e ue é directamente interceptada por i. Se a superfície for côncava, a superfície vê-se a ela própria e F ii é diferente de zero. No entanto, para uma superfície plana ou convexa, F ii. Figura Troca de radiação numa cavidade Para calcular a troca de radiação numa cavidade com N superfícies, é necessário um total de N factores de forma. No entanto, não é preciso determinar directamente todos eles. Para ilustrar o procedimento de determinação dos factores de forma, vamos considerar uma cavidade simples formada por duas esferas (Figura ). Figura Factores de forma para uma cavidade formada por duas esferas 87
189 Embora a cavidade seja caracterizada por N 4 factores de forma (F, F, F e F ), apenas é necessário calcular N(N )/ factor de forma directamente, como iremos ver no seguimento. Neste caso, esse factor de forma pode ser determinado por inspecção. Em particular, uma vez ue toda a radiação ue sai da superfície interna (esfera ) atinge necessariamente a superfície externa (esfera ), obtém-se F : F O mesmo não pode ser dito para a radiação ue sai da superfície externa, uma vez ue esta superfície vê-se a ela própria. No entanto, da relação de reciprocidade, obtém-se F : A F A F A F F F A A A Sabendo ue a radiação ue deixa não atinge, obtém-se F : F Da regra da soma verifica-se F e F, e calcula-se F : F + F F + F F F A A Para determinar F ij para outras geometrias mais complexas, será necessário calcular o integral duplo resultante da sua definição, ou então, utilizar tabelas já compiladas para várias geometrias comuns, como as fornecidas na unidade curricular de Fenómenos de Transferência I. 88
190 6.5. Transferência de Calor por Radiação entre Corpos Negros Da definição de corpo negro sabemos ue toda a energia ue deixa a sua superfície é devida a emissão (não há reflexão num corpo negro) e ue toda a radiação incidente é absorvida. Consideremos as superfícies A i e A j, ambas com comportamento de corpo negro, mantidas às temperaturas T i e T j, respectivamente: n j n i A j, T j A i, T i Do conhecimento dos factores de forma das superfícies, é possível determinar a taxa de energia radiante ue sai da superfície A i e ue é interceptada pela superfície A j : ij ( A i J i ) F ij (9) Como num corpo negro J i E i, obtém-se a seguinte euação: ij A F i ij E i (93) De modo análogo, obtém-se a taxa de energia radiante ue sai da superfície A j e ue é interceptada pela superfície A i : ji A j F ji E j (94) 89
191 A taxa líuida de radiação entre a superfície A i e a superfície A j, i, é dada pela j diferença entre a taxa de energia ue sai de A i e ue é interceptada por A j e a taxa de energia ue é interceptada por A i e ue é proveniente de A j : i j ij ji A F i ij E i A j F ji E j (95) Da relação de reciprocidade, A i F ij A j F ji, vem ue: i j A F i ij ( E E ) i j (96) Como o poder emissivo de um corpo negro é dado pela lei de Stefan-Boltzmann: E σt 4 (3) obtém-se a seguinte euação final para o cálculo da taxa líuida de radiação entre a superfície A i e superfície A j : i j i ij 4 4 ( T T ) A F σ (97) i j Generalizando, para N superfícies no interior de uma cavidade, a taxa global líuida de radiação entre uma superfície A i e as N superfícies da cavidade, i, é obtida da seguinte forma: i i i i N i N i j j N j A F σ ( T i ij 4 i T 4 j ) (98) 9
192 Exercício Considere um forno cilíndrico com a seguinte geometria e condições: T 3 7 ºC T 35 ºC L 5 mm T 65 ºC φ 75 mm Sabendo ue as paredes do forno tem comportamento de corpo negro, calcule a taxa líuida de energia radiante entre as paredes do forno e a sua abertura (superfície 3). Resolução Desprezando transferência de calor por convecção, a taxa de energia radiante entre as paredes do forno e a sua abertura corresponde às contribuições individuais das superfícies e : ( T T ) + A F σ ( T ) A F3σ 3 3 T3 Para calcular F 3 é preciso recorrer à tabela de factores de forma para discos paralelos coaxiais fornecida na documentação da unidade curricular de Fenómenos de Transferência I, uma vez ue as superfícies e 3 correspondem a esta disposição, discos paralelos de raio r.375 m e distância entre discos de L.5 m. Assim, tendo em consideração os parâmetros envolvidos na tabela: R i R j R L r.5 9
193 + R S + 8 R F 3 S [ S 4].6 F3 Pela regra da soma, válida numa cavidade, obtém-se F : F + F 3 F.94 Pela regra da reciprocidade, calcula-se F e F 3 :.75 π A F A F F π.75.5 A F 3 A 3 F 3 A F A F F.8 F3 Uma vez determinados os factores de forma necessários, pode-se calcular : 8 π [ 63 3 ] π [ 93 3 ] 844 W 6.6. Transferência de Calor por Radiação entre Superfícies Cinzentas Em geral, a radiação ue sai de uma superfície opaca e cinzenta é devida a emissão e a reflexão. Por sua vez, essa radiação ao ser interceptada por uma segunda superfície opaca, irá ser também reflectida e absorvida. Numa cavidade, como a apresentada na Figura 3, a radiação pode sofrer múltiplas reflexões em todas as superfícies e absorção parcial em cada uma delas. 9
194 Figura 3 Troca de radiação numa cavidade formada por superfícies cinzentas e difusas. (a) Esuema da cavidade; (b) e (c) Balanços de radiação; (d) Elemento de rede representando a transferência líuida de radiação a partir de uma superfície A análise da troca de radiação numa cavidade pode ser simplificada se considerarmos algumas aproximações, nomeadamente, se considerarmos ue as superfícies da cavidade são isotérmicas, cinzentas, opacas e difusas e caracterizadas por uma radiosidade uniforme e por uma irradiação uniforme. Vamos considerar o termo i como a taxa de energia global líuida ue abandona a superfície i. Este termo representa a taxa de energia ue seria necessária transferir para a superfície para a manter isotérmica, podendo ser calculado pela diferença entre a radiosidade da superfície e a irradiação (Figura 3(b)): 93
195 i A i (J i G i ) (99) Como J i E i + ρ i G i, a taxa líuida de transferência de calor por radiação da superfície pode também ser expressa em termos do poder emissivo da superfície e da irradiação absorvida, considerando uma superfície opaca, pelo ue α i - ρ i : i A i (E i + ρ i G i G i ) A i (E i - α i G i ) (3) A euação obtida encontra-se ilustrada na Figura 3(c). Para uma superfície cinzenta, opaca e difusa, sabendo ue ρ i - α i - ε i, a radiosidade pode também ser expressa da seguinte forma: J i E i + ρ i G i ε i E bi + ( - α i )G i ε i E bi + ( - ε i )G i (3) Resolvendo em ordem a G i, obtém-se a seguinte euação: G i J i ε E i ε i bi (3) Substituindo G i obtido pela euação (3) na euação (99), obtém-se a seguinte dedução: i A i (J i G i ) Ai J i J i ε i E ε i bi A ε i i ( E J ) bi ε i i Aiε i ε i ( E J ) bi (33) i A euação (33) permite uma representação conveniente para a taxa líuida de transferência de calor por radiação de uma superfície. Esta transferência, em analogia com os circuitos eléctricos, pode ser representada pelo elemento de circuito da Figura ε i 3(d), onde (E bi J i ) corresponde à diferença de potencial e R i corresponde à Aiε i resistência superficial da radiação: 94
196 E bi J i ε A ε i i i Ri i i (34) Tendo em consideração a euação (34), verifica-se ue, se o poder emissivo ue a superfície teria se fosse corpo negro exceder a sua radiosidade, então ocorre transferência líuida de calor por radiação da superfície para a vizinhança. Caso contrário, a transferência líuida ocorre da vizinhança para a superfície. Troca de Radiação entre Superfícies Cinzentas Para utilizar a euação (34), é necessário conhecer a radiosidade J i de uma superfície. Para determinar esta uantidade é necessário analisar a troca de radiação entre as superfícies da cavidade (Figura 3(a)). A irradiação da superfície i pode ser obtida a partir das radiosidades de todas as superfícies da cavidade. Em particular, da definição de factor de forma, a taxa total de radiação incidente sobre a superfície i no interior da cavidade, com origem em todas as superfícies, incluindo i, obtém-se da seguinte forma: A i G i F i A J + F i A J + + F Ni A N J N F jia jj j (35) N j ou, da relação de reciprocidade, A j F ji A i F ij : N A i G i A ifijj j (36) j Substituindo a euação (36) em i A i (J i G i ), euação (99), obtém-se ue: J (37) N i A i i F ij J j j 95
197 ou, da regra da soma, como N j N F ij FijJi Ji : j N N N i A ( ) i N F ijji FijJ j A i Fij Ji J j ij j j j j ou i N j ( A ) i N ( Ji J j) ( Ji J j) F ij R j j (38) Estes resultado euaciona a taxa líuida de transferência de calor por radiação da superfície i, i, com a soma das componentes ij relacionadas com a troca de radiação com as outras superfícies. Cada componente pode ser representada por um elemento de circuito no ual (J i J j ) corresponde à diferença de potencial e R j (A i F ij ) - corresponde a uma resistência geométrica (Figura 4). Nó correspondente à superfície i Figura 4 Análogo eléctrico representativo da troca de radiação entre a superfície i e as outras superfícies de uma cavidade 96
198 Combinando as euações (34) e (38), obtém-se a seguinte euação: E J N bi i ( ε ) i j ( A F ) ε A i i i ij ( J J ) i j (39) Como observado na Figura 4, esta euação representa o balanço de radiação ao nó da radiosidade associado com a superfície i, isto é, a taxa de transferência de calor por radiação para i através da sua resistência superficial é igual à taxa líuida de transferência de calor por radiação de i para todas as outras superfícies através das resistências geométricas correspondentes. Para utilizar a metodologia de cálculo de trocas de radiação entre superfícies envolvendo análogos eléctricos, recordar ue: i j A F i J J ij ( i j ) ou J i J j R j i j Exercício Pretende-se fazer a cura de um revestimento de uma superfície curva com área A 5 m. O processo de cura consiste na exposição a um auecedor plano com uma largura W m. O comprimento da superfície e do auecedor é de m, estando separados entre si por uma distância H m. A temperatura do auecedor é T K e a sua emissividade é ε.9. A superfície a curar está a T 6 K e a sua emissividade é ε.5. O sistema está numa sala com as paredes a 3 K. Qual é a taxa efectiva de transferência de calor para a superfície? Paredes da sala Superfície Absorvedora, A, T, ε Auecedor, A, T, ε 97
199 Resolução O sistema pode ser interpretado como uma cavidade composta por três superfícies, sendo a terceira superfície as paredes da sala, ue se podem considerar com comportamento de corpo negro. O esuema do problema toma assim a seguinte forma: Colector, L m 5 m Auecedor, L m Pretende-se obter a taxa líuida de transferência de calor por radiação para a superfície (- ). Para tal iremos usar a abordagem directa. Das expressões deduzidas anteriormente, podemos calcular (note ue representa a taxa líuida de transferência de calor por radiação ue sai da superfície ): Aε b ε ( E J ) Para resolver a euação anterior é necessário determinar primeiro J. Uma vez ue J 3 é conhecido (corpo negro J 3 E b3 σt x -8 x W/m ), obtém-se J e J pela resolução do seguinte sistema de duas euações a duas incógnitas: Aε ε ( E J ) b ( A F ) ( J J ) + ( A F ) 3 ( J J ) 3 Aε ε ( E J ) b ( A F ) ( J J ) + ( A F ) 3 ( J J ) 3 98
200 É necessário determinar os factores de forma envolvidos no sistema de euações. O factor de forma F pode ser obtido, reconhecendo ue F F, isto é, ue a radiação ue abandona A e atinge A é necessariamente a ue atinge A (o rectângulo resultante da projecção de A ). Assim sendo, recorrendo à tabela de factores de forma para rectângulos alinhados paralelamente fornecida na documentação da unidade curricular de Fenómenos de Transferência I: X Y X e X L L F F.39 Da regra da reciprocidade, obtém-se F : 3.9 A F A F x F. 6 5 Aplicando a regra da soma à cavidade e reconhecendo ue F, obtém-se F 3 : F + F 3 F 3.6 Aplicando novamente a regra da reciprocidade, obtém-se F 3 : A F 3 A 3 F 3 F Por outro lado, como a radiação ue se propaga da superfície 3 para a superfície passa obrigatoriamente pela superfície, e como (por simetria) a radiação ue se propaga da superfície 3 para a superfície é igual à radiação ue se propaga da superfície 3 para a superfície, vem ue: 6. F 3 F 3 F 3 A 3 F 3 A F F
201 Substituindo os factores de forma determinados anteriormente no sistema de euações, obtém-se J e J : J +.39J.6J.67J J J 5547 W/m 538 W/m Substituindo na expressão para o cálculo de, obtém-se o resultado procurado: ( ) 77.8 kw Cavidade com Duas Superfícies O caso mais simples na troca de radiação numa cavidade, é uando esta envolve apenas duas superfícies ue trocam radiação entre si (Figura 5). Figura 5 Cavidade com duas superfícies. (a) Esuema; (b) Representação do análogo eléctrico
202 Uma vez ue existem apenas duas superfícies, a taxa líuida de transferência de calor por radiação da superfície,, terá de ser igual à taxa líuida de transferência de calor por radiação para a superfície, -, e ambas as uantidades devem ser iguais à taxa líuida de transferência de calor por radiação entre e : - A taxa de transferência de calor por radiação entre as duas superfícies pode ser calculada pela abordagem directa utilizada no exercício anterior, no entanto, neste caso em estudo, o resultado pretendido pode ser obtido mais facilmente se trabalharmos com o análogo eléctrico da cavidade, apresentado na Figura 5(b), onde se observa ue a resistência total à troca de radiação entre as superfícies e compreende as duas resistências de superfície e a resistência geométrica. Assim sendo, a taxa líuida de transferência de calor por radiação entre as duas superfícies pode ser expressa da seguinte forma: σ( T ) T ε A ε + A F ε + A ε (3) Este resultado pode ser aplicado a uaisuer duas superfícies cinzentas e difusas ue formem uma cavidade. De seguida encontram-se sumarizados alguns caso especiais importantes.
203 Placas Paralelas e Compridas (Infinitas) Cilindros Concêntricos e Compridos (Infinitos) Esferas Concêntricas Peuenos Objectos Convexos numa Cavidade Grande Barreiras de Radiação Com o objectivo de reduzir a transferência líuida de calor por radiação entre duas superfícies, podem-se construir barreiras de radiação com materiais de baixa emissividade (elevada reflectividade). Considere a colocação de uma barreira de radiação (superfície 3) entre duas placas paralelas compridas, como ilustrado na Figura 6.
204 Barreira de radiação Figura 6 Troca de radiação entre duas placas paralelas compridas separadas por uma barreira de radiação. (a) Esuema; (b) Análogo eléctrico Sem a barreira de radiação, a taxa líuida de transferência de calor por radiação entre as superfícies e seria dada pela seguinte euação: 4 4 σ( T ) T ε (3) ε + + A ε A F A ε ou, como A A A e como F, pela euação simplificada correspondente a placas paralelas infinitas: 4 4 Aσ( T T ) (3) + ε ε 3
205 No entanto, com a barreira de radiação, surgem resistências adicionais, como apresentado na Figura 6(b), provocando a diminuição da taxa de transferência de calor, uando comparada à situação sem barreira de radiação. Notar ue a emissividade associada a um dos lados da barreira (ε 3 ) pode ser diferente da emissividade associada ao lado oposto (ε 3 ) e ue as radiosidades serão sempre diferentes. Somando todas as resistências (em série) e tendo em atenção ue F 3 F 3, obtém-se a seguinte resistência térmica euivalente: R T ε ε A + A F 3 ε + ε A ε + ε A A F 3 3 ε + ε A R T A ε ε + + ε 3 3 ε + ε ε (3) R T A ε + ε ε + ε 3 3 ε + ε 3 3 e a seguinte euação para o cálculo da taxa líuida de transferência de calor por radiação entre as superfícies e : 4 4 E ( ) b E b Aσ T T R T ε 3 ε ε ε ε ε (33) Note ue as resistências associadas à barreira de radiação tornam-se muito grandes uando as emissividades ε 3 e ε 3 são muito peuenas. Exercício Um fluído criogénico escoa através de um tubo comprido com mm de diâmetro, cuja superfície externa está a uma temperatura T 77 K e possui uma emissividade ε.. Externamente existe outro tubo concêntrico com diâmetro de 5 mm e com superfície interna à temperatura T 3 K e emissividade ε.5. No espaço entre os tubos foi feito vácuo. Calcule a taxa de calor recebida pelo fluído por unidade de comprimento do tubo. Se for colocada uma barreira de radiação entre os dois 4
206 tubos com 35 mm de diâmetro, possuindo uma emissividade em ambas os lados ε 3., calcule a redução percentual no calor recebido pelo fluido. Resolução O problema descrito para as situações sem barreira e com barreira de radiação apresenta-se no seguinte esuema: Barreira Sem barreira Com barreira O análogo eléctrico do sistema sem a barreira de radiação é auele apresentado na Figura 5(b), sendo a taxa de transferência de calor desejada obtida pela seguinte euação: ε A ε 4 4 ( T ) σ T + A F ε + A ε Tendo em atenção ue F, A πd L e A πd L, obtém-se o seguinte desenvolvimento: ε ( T ) πd Lσ( T T ) Aσ T A + + A ε ε ε D + D ε ε L 3 8 π ( 77 3 ).5 W/m 5
207 O análogo eléctrico do sistema com a barreira de radiação é auele apresentado na Figura 6(b), sendo a taxa de transferência de calor desejada obtida agora pela seguinte euação: E b E R T b 4 4 ( T ) σ T R T onde R T ε ε A + A F 3 ε + ε A A F 3 3 ε + ε A R T A ε ε ε3 + + ε 3 D D 3 D + D 3 ε + ε D D R T 3.6 A L π ( 77 3 ).5 W/m A redução percentual no calor recebido pelo fluído é então de:.5 (.5) Δ 5%.5 Superfícies Reirradiantes Uma superfície reirradiante é uma superfície ideal caracterizada por uma taxa líuida de transferência de calor por radiação nula,. A hipótese de superfície reirradiante é comum em muitas aplicações industriais, podendo o seu comportamento ser aproximado por superfícies reais ue sejam bem isoladas num dos lados e cujos efeitos de convecção possam ser desprezáveis no lado oposto (onde ocorre radiação). Do balanço de energia à superfície obtém-se facilmente ue G i J i E bi : i 6
208 J i A i i Ai (J i G ) J i i G i Aiεi i εi (E bi J ) J i i E bi G i A i G i J i E bi Tendo em atenção o resultado anterior, se a radiosidade de uma superfície reirradiante for conhecida, a sua temperatura é rapidamente determinada. Numa cavidade, a temperatura de euilíbrio de uma superfície reirradiante é determinada pela sua interacção com as outras superfícies, sendo independente da emissividade da superfície reirradiante. Consideremos uma cavidade com três superfícies, sendo uma delas reirradiante (superfície R) e o respectivo análogo eléctrico representados na Figura 7. Figura 7 Um cavidade com três superfícies, sendo uma delas reirradiante. (a) Esuema; (b) Análogo eléctrico Um vez ue em R, R, a transferência líuida de radiação da superfície deve igualar a transferência líuida de radiação para a superfície, isto é,. O análogo eléctrico do problema em estudo é uma combinação de resistências em série e em paralelo, pelo ue da sua análise é fácil de deduzir a seguinte euação: 7
209 b b ε + + εa ε A F E + A F R E + A F R ε A (34) Cavidade com Radiação, Convecção e Condução em Simultâneo Até agora, as trocas de radiação numa cavidade foram consideradas sob condições nas uais a condução e a convecção podiam ser desprezadas. No entanto, em muitas aplicações, a convecção e a condução são comparáveis à radiação e devem ser consideradas na análise da transferência de calor. Considerar a condição geral de uma superfície, como ilustrada na Figura 8. Cavidade Figura 8 Transferência de calor por radiação, convecção e condução numa superfície no interior de uma cavidade. (a) Balanço de energia à superfície; (b) Análogo eléctrico. i,rad Para além da troca de calor por radiação com outras superfícies da cavidade,, pode ocorrer transferência de calor do exterior para a superfície (por auecimento eléctrico, por exemplo, i, ext ) e transferência de calor da superfície por convecção, i,conv, e por condução, i, cond relação:. Do balanço de energia à superfície, obtém-se a seguinte 8
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. Transmissão de calor. 3º ano
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Aula 3 Equação diferencial de condução de calor Condições iniciais e condições de fronteira; Geração de Calor num Sólido;
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Aula 3 Equação diferencial de condução de calor Condições iniciais e condições de fronteira; Geração de Calor num Sólido;
Capitulo 8 Transferência de Calor por Condução
 Fenômenos de Transporte Capitulo 8 Transferência de Calor por Condução Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI TRANSFERÊNCIA DE CALOR POR CONDUÇÃO Quando existe um gradiente de temperatura
Fenômenos de Transporte Capitulo 8 Transferência de Calor por Condução Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI TRANSFERÊNCIA DE CALOR POR CONDUÇÃO Quando existe um gradiente de temperatura
GERAÇÃO DE CALOR UNIFORME EM SÓLIDOS. Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna.
 GEAÇÃO DE CALO UNIFOME EM SÓLIDOS Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna. Se manifesta como um aumento da temperatura do meio. Exemplos:
GEAÇÃO DE CALO UNIFOME EM SÓLIDOS Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna. Se manifesta como um aumento da temperatura do meio. Exemplos:
Transferência de Calor: Origens Físicas F Equações de Taxas de Transferência
 Transferência de Calor: Origens Físicas F e Euações de Taxas de Transferência Transferência de Calor e Energia Térmica O ue é a transferência de calor? A transferência de calor éo trânsito de energia térmica
Transferência de Calor: Origens Físicas F e Euações de Taxas de Transferência Transferência de Calor e Energia Térmica O ue é a transferência de calor? A transferência de calor éo trânsito de energia térmica
FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO
 FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO PROF.: KAIO DUTRA Convecção Térmica O modo de transferência de calor por convecção é composto por dois mecanismos. Além da transferência
FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO PROF.: KAIO DUTRA Convecção Térmica O modo de transferência de calor por convecção é composto por dois mecanismos. Além da transferência
Expansão Térmica de Sólidos e Líquidos. A maior parte dos sólidos e líquidos sofre uma expansão quando a sua temperatura aumenta:
 23/Mar/2018 Aula 8 Expansão Térmica de Sólidos e Líquidos Coeficiente de expansão térmica Expansão Volumétrica Expansão da água Mecanismos de transferência de calor Condução; convecção; radiação 1 Expansão
23/Mar/2018 Aula 8 Expansão Térmica de Sólidos e Líquidos Coeficiente de expansão térmica Expansão Volumétrica Expansão da água Mecanismos de transferência de calor Condução; convecção; radiação 1 Expansão
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br AULA 5 CONDUÇÃO
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br AULA 5 CONDUÇÃO
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br TRANSFERÊNCIA DE
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br TRANSFERÊNCIA DE
OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR. Profa. Dra. Milena Martelli Tosi
 OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR Profa. Dra. Milena Martelli Tosi A IMPORTÂNCIA DA TRANSFERÊNCIA DE CALOR NA INDÚSTRIA DE ALIMENTOS Introdução Revisão: Mecanismos de transferência
OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR Profa. Dra. Milena Martelli Tosi A IMPORTÂNCIA DA TRANSFERÊNCIA DE CALOR NA INDÚSTRIA DE ALIMENTOS Introdução Revisão: Mecanismos de transferência
Aula 6 de FT II. Prof. Gerônimo
 Aula 6 de FT II Prof. Gerônimo Transferência de calor em superfícies estendidas Superfície estendida é comumente usado para descrever um caso especial importante envolvendo a transferência de calor por
Aula 6 de FT II Prof. Gerônimo Transferência de calor em superfícies estendidas Superfície estendida é comumente usado para descrever um caso especial importante envolvendo a transferência de calor por
Condução unidimensional em regime estacionário, Sistemas Radiais
 Com freqüência, em sistemas cilíndricos e esféricos há gradientes de temperatura somente na direção radial, o que permite analisá-los como sistemas unidimensionais. Um exemplo comum é o cilindro oco, cujas
Com freqüência, em sistemas cilíndricos e esféricos há gradientes de temperatura somente na direção radial, o que permite analisá-los como sistemas unidimensionais. Um exemplo comum é o cilindro oco, cujas
Transferência de Calor Condução de Calor
 Transferência de Calor Condução de Calor Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 Lei de Fourier A Lei de Fourier é fenomenológica, ou seja, foi desenvolvida a partir da observação dos
Transferência de Calor Condução de Calor Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 Lei de Fourier A Lei de Fourier é fenomenológica, ou seja, foi desenvolvida a partir da observação dos
TRANSFERÊNCIA DE CALOR POR CONVECÇÃO NATURAL E FORÇADA À VOLTA DE CILINDROS METÁLICOS TP4
 TRANSFERÊNCIA DE CALOR POR CONVECÇÃO NATURAL E FORÇADA À VOLTA DE CILINDROS METÁLICOS TP4 LABORATÓRIOS DE ENGENHARIA QUÍMICA I 2009/2010 1. Objectivo Determinação do coeficiente de convecção natural e
TRANSFERÊNCIA DE CALOR POR CONVECÇÃO NATURAL E FORÇADA À VOLTA DE CILINDROS METÁLICOS TP4 LABORATÓRIOS DE ENGENHARIA QUÍMICA I 2009/2010 1. Objectivo Determinação do coeficiente de convecção natural e
25/Mar/2015 Aula /Mar/2015 Aula 9
 20/Mar/2015 Aula 9 Processos Politrópicos Relações politrópicas num gás ideal Trabalho: aplicação aos gases perfeitos Calor: aplicação aos gases perfeitos Calor específico politrópico Variação de entropia
20/Mar/2015 Aula 9 Processos Politrópicos Relações politrópicas num gás ideal Trabalho: aplicação aos gases perfeitos Calor: aplicação aos gases perfeitos Calor específico politrópico Variação de entropia
EP34D Fenômenos de Transporte
 EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Introdução à Transferência de Calor 2 Introdução à Transferência de Calor O que é Transferência de Calor? Transferência de
EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Introdução à Transferência de Calor 2 Introdução à Transferência de Calor O que é Transferência de Calor? Transferência de
Transferência de Calor
 Transferência de Calor Condução Unidimensional, em Regime Permanente e Sem Geração Interna de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica
Transferência de Calor Condução Unidimensional, em Regime Permanente e Sem Geração Interna de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica
Transferência de calor
 Transferência de calor 1.1 Calor: Forma de energia que se transmite espontaneamente de um corpo para o outro quando entre eles existir uma diferença de temperatura. O calor é uma energia em trânsito provocada
Transferência de calor 1.1 Calor: Forma de energia que se transmite espontaneamente de um corpo para o outro quando entre eles existir uma diferença de temperatura. O calor é uma energia em trânsito provocada
Transferência de Calor
 Transferência de Calor Condução em Superfícies Estendidas Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Condução em Superfícies Estendidas Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor
 Transferência de Calor Aletas e Convecção em Escoamento Interno e Externo Prof. Universidade Federal do Pampa BA000200 Campus Bagé 19 de junho de 2017 Transferência de Calor: Convecção 1 / 30 Convecção
Transferência de Calor Aletas e Convecção em Escoamento Interno e Externo Prof. Universidade Federal do Pampa BA000200 Campus Bagé 19 de junho de 2017 Transferência de Calor: Convecção 1 / 30 Convecção
Transmissão de calor
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS)
 CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS) Prof. Antonio Carlos Foltran EXEMPLOS DE APLICAÇÃO 2 Carregamento de forno LD em aciaria Fonte: Companhia Siderúrgica
CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS) Prof. Antonio Carlos Foltran EXEMPLOS DE APLICAÇÃO 2 Carregamento de forno LD em aciaria Fonte: Companhia Siderúrgica
Mecanismos de Transferência de Calor. Gustavo Dalpian
 Mecanismos de Transferência de Calor Gustavo Dalpian Monitoria Segunda: 14 18hs (Sala 405, disponível a par8r de 26/10) 14 16 hs Luiz Felipe Lopes 16 18 hs Felipe Marcilio Terca: 10 12hs Mariana Barbosa
Mecanismos de Transferência de Calor Gustavo Dalpian Monitoria Segunda: 14 18hs (Sala 405, disponível a par8r de 26/10) 14 16 hs Luiz Felipe Lopes 16 18 hs Felipe Marcilio Terca: 10 12hs Mariana Barbosa
Mecanismos de transferência de calor
 Mecanismos de transferência de calor Condução Potência calor: Q cond A T 1 T x : condutibilidde térmica; A: área de transferência x: espessura ao longo da condução T 1 T : diferença de temperatura ifusividade
Mecanismos de transferência de calor Condução Potência calor: Q cond A T 1 T x : condutibilidde térmica; A: área de transferência x: espessura ao longo da condução T 1 T : diferença de temperatura ifusividade
Lei de Fourier. Considerações sobre a lei de Fourier. A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados.
 Condução de Calor Lei de Fourier A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados Considerações sobre a lei de Fourier q x = ka T x Fazendo Δx 0 q taxa de calor [J/s] ou
Condução de Calor Lei de Fourier A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados Considerações sobre a lei de Fourier q x = ka T x Fazendo Δx 0 q taxa de calor [J/s] ou
ESZO Fenômenos de Transporte
 Universidade Federal do ABC ESZO 001-15 Fenômenos de Transporte Profa. Dra. Ana Maria Pereira Neto ana.neto@ufabc.edu.br Bloco A, torre 1, sala 637 Mecanismos de Transferência de Calor Calor Calor pode
Universidade Federal do ABC ESZO 001-15 Fenômenos de Transporte Profa. Dra. Ana Maria Pereira Neto ana.neto@ufabc.edu.br Bloco A, torre 1, sala 637 Mecanismos de Transferência de Calor Calor Calor pode
CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO
 CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO CONTEÚDO TRANSFERÊNCIA DE CALOR CONDUÇÃO LEI DE FOURIER CONDUTIVIDADE TÉRMICA DIFUSIVIDADE TÉRMICA CONDUÇÃO DE CALOR UNIDIMENSIONAL
CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO CONTEÚDO TRANSFERÊNCIA DE CALOR CONDUÇÃO LEI DE FOURIER CONDUTIVIDADE TÉRMICA DIFUSIVIDADE TÉRMICA CONDUÇÃO DE CALOR UNIDIMENSIONAL
TRANSMISSÃO DE CALOR resumo
 TRANSMISSÃO DE CALOR resumo convecção forçada abordagem experimental ou empírica Lei do arrefecimento de Newton Taxa de Transferência de Calor por Convecção 𝑞"#$ ℎ𝐴 𝑇 𝑇 ℎ 1 𝐴 ℎ - Coeficiente Convectivo
TRANSMISSÃO DE CALOR resumo convecção forçada abordagem experimental ou empírica Lei do arrefecimento de Newton Taxa de Transferência de Calor por Convecção 𝑞"#$ ℎ𝐴 𝑇 𝑇 ℎ 1 𝐴 ℎ - Coeficiente Convectivo
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br AULA 3 REVISÃO E
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br AULA 3 REVISÃO E
Transferência de Calor
 Transferência de Calor Introdução à transferência de calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Introdução à transferência de calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA
 CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA 1) Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e gesso, conforme indicado na figura. Em um dia frio
CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA 1) Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e gesso, conforme indicado na figura. Em um dia frio
Transferência de Energia
 APLICAÇÃO DO FRIO NA CADEIA ALIMENTAR CTeSP em GASTRONOMIA, TURISMO E BEM-ESTAR Definição é a passagem/transmissão de energia, na forma de calor, de um ponto para outro. A transferência de calor efectua-se
APLICAÇÃO DO FRIO NA CADEIA ALIMENTAR CTeSP em GASTRONOMIA, TURISMO E BEM-ESTAR Definição é a passagem/transmissão de energia, na forma de calor, de um ponto para outro. A transferência de calor efectua-se
EP34D Fenômenos de Transporte
 EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Transferência de Calor em Superfícies Estendidas - Aletas 2 É desejável em muitas aplicações industriais aumentar a taxa
EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Transferência de Calor em Superfícies Estendidas - Aletas 2 É desejável em muitas aplicações industriais aumentar a taxa
Aula 3 de FT II. Prof. Geronimo
 Aula 3 de FT II Prof. Geronimo Raio crítico de isolamento O conceito de raio crítico de isolamento, é introduzido para geometrias onde a área de troca de calor varia com uma dimensão especificada. Por
Aula 3 de FT II Prof. Geronimo Raio crítico de isolamento O conceito de raio crítico de isolamento, é introduzido para geometrias onde a área de troca de calor varia com uma dimensão especificada. Por
FICHA DA DISCIPLINA DE TRANSMISSÃO DE CALOR
 FICHA DA DISCIPLINA DE TRANSMISSÃO DE CALOR 3º Ano Regime: 1º Semestre Ano Lectivo: 2006/2007 Carga Horária: 2T+2T/P Docente Responsável: Flávio Chaves Corpo Docente: Flávio Chaves Objectivos Conhecimento
FICHA DA DISCIPLINA DE TRANSMISSÃO DE CALOR 3º Ano Regime: 1º Semestre Ano Lectivo: 2006/2007 Carga Horária: 2T+2T/P Docente Responsável: Flávio Chaves Corpo Docente: Flávio Chaves Objectivos Conhecimento
Condições variam com o tempo. 1 ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar
 Condução de calor em regime transiente Condições variam com o tempo ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar ) Passa-se algum tempo antes
Condução de calor em regime transiente Condições variam com o tempo ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar ) Passa-se algum tempo antes
defi departamento de física
 defi departamento de física aboratórios de Física www.defi.isep.ipp.pt Condutividade térmica Instituto Superior de Engenharia do Porto- Departamento de Física Rua Dr. António Bernardino de Almeida, 431
defi departamento de física aboratórios de Física www.defi.isep.ipp.pt Condutividade térmica Instituto Superior de Engenharia do Porto- Departamento de Física Rua Dr. António Bernardino de Almeida, 431
Automação 2 semestre de 2014
 FENÔMENO DOS TRANSPORTES II Automação 2 semestre de 2014 PROF. Panesi CALOR E TEMPERATURA teoria do calor James Prescott Joule calor poderia ser convertido em trabalho e vice-versa criando dessa forma
FENÔMENO DOS TRANSPORTES II Automação 2 semestre de 2014 PROF. Panesi CALOR E TEMPERATURA teoria do calor James Prescott Joule calor poderia ser convertido em trabalho e vice-versa criando dessa forma
CONDUÇÃO DE CALOR APLICADO AO ESTUDO DE CONCEITOS MATEMÁTICOS DO ENSINO MÉDIO. Douglas Gonçalves Moçato*** Luiz Roberto Walesko*** Sumário
 CONDUÇÃO DE CALOR APLICADO AO ESUDO DE CONCEIOS MAEMÁICOS DO ENSINO MÉDIO Douglas Gonçalves Moçato*** Luiz Roberto Walesko***. Introdução. Conceitos de transmissão de calor. Convecção. Radiação.3 Condução
CONDUÇÃO DE CALOR APLICADO AO ESUDO DE CONCEIOS MAEMÁICOS DO ENSINO MÉDIO Douglas Gonçalves Moçato*** Luiz Roberto Walesko***. Introdução. Conceitos de transmissão de calor. Convecção. Radiação.3 Condução
Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO EM REGIME TRANSIENTE
 Os exercícios e figuras deste texto foram retirados de diversas referências bibliográficas listadas no programa da disciplina 1 FENÔMENOS DE TRANSPORTE Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO
Os exercícios e figuras deste texto foram retirados de diversas referências bibliográficas listadas no programa da disciplina 1 FENÔMENOS DE TRANSPORTE Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO
Transferência de Calor
 Transferência de Calor Introdução e Modos de Transferência Prof. Universidade Federal do Pampa BA000200 Campus Bagé 08 de maio de 2017 Transferência de Calor: Introdução 1 / 29 Introdução à Transferência
Transferência de Calor Introdução e Modos de Transferência Prof. Universidade Federal do Pampa BA000200 Campus Bagé 08 de maio de 2017 Transferência de Calor: Introdução 1 / 29 Introdução à Transferência
FENÔMENOS DE TRANSPORTES
 FENÔMENOS DE TRANSPORTES AULA 11 FUNDAMENTOS DE TRANSFERÊNCIA DE CALOR PROF.: KAIO DUTRA Transferência de Calor Transferência de calor (ou calor) é a energia em trânsito devido a uma diferença de temperatura.
FENÔMENOS DE TRANSPORTES AULA 11 FUNDAMENTOS DE TRANSFERÊNCIA DE CALOR PROF.: KAIO DUTRA Transferência de Calor Transferência de calor (ou calor) é a energia em trânsito devido a uma diferença de temperatura.
Transferência de Calor Condução e Convecção de Calor
 Transferência de Calor Condução e Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 O calor transferido por convecção, na unidade de tempo, entre uma superfície e um fluido, pode ser calculado
Transferência de Calor Condução e Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 O calor transferido por convecção, na unidade de tempo, entre uma superfície e um fluido, pode ser calculado
Termodinâmica e Estrutura da Matéria
 e Estrutura da Matéria A 1ª Lei da Parte 2 J. Seixas 1ª Lei da Processos não Imaginemos um processo que leva do estado 1 ao estado 2 através do caminho C. Nesse caso 0 C 2 1ª Lei da Processos não Imaginemos
e Estrutura da Matéria A 1ª Lei da Parte 2 J. Seixas 1ª Lei da Processos não Imaginemos um processo que leva do estado 1 ao estado 2 através do caminho C. Nesse caso 0 C 2 1ª Lei da Processos não Imaginemos
PNV-2321 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR
 PNV-31 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR TRANSMISSÃO DE CALOR 1) INTRODUÇÃO Sempre que há um gradiente de temperatura no interior de um sistema ou quando há contato de dois sistemas com temperaturas
PNV-31 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR TRANSMISSÃO DE CALOR 1) INTRODUÇÃO Sempre que há um gradiente de temperatura no interior de um sistema ou quando há contato de dois sistemas com temperaturas
ENG 3006 TRANSFERÊNCIA DE CALOR E MASSA 1 o SEMESTRE DE Capítulo 11 Trocadores de Calor
 ENG 3006 TRANSFERÊNCIA DE CALOR E MASSA 1 o SEMESTRE DE 2015 Capítulo 11 Trocadores de Calor Tópicos Tipos de trocadores de calor; O coeficiente global de transferência de calor; Análise térmica de trocadores
ENG 3006 TRANSFERÊNCIA DE CALOR E MASSA 1 o SEMESTRE DE 2015 Capítulo 11 Trocadores de Calor Tópicos Tipos de trocadores de calor; O coeficiente global de transferência de calor; Análise térmica de trocadores
Transmissão de calor
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura e
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura e
Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE
 Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE Parede plana T 1 T s1 T s2! x k T $ # &+! " x % y k T $ # &+! " y % z k T $ T # &+!q ρc p " z % t d " dx k dt % $ ' 0 q # dx & x ka dt dx cte T( x) ax
Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE Parede plana T 1 T s1 T s2! x k T $ # &+! " x % y k T $ # &+! " y % z k T $ T # &+!q ρc p " z % t d " dx k dt % $ ' 0 q # dx & x ka dt dx cte T( x) ax
AULA 4 PAREDES PLANAS COMPOSTAS
 Notas de aula de PME 336 Processos de Transferência de Calor AUA 4 PAEDES PANAS COMPOSTAS Condução unidimensional, regime permanente, sem geração de calor paredes compostas. Para resolver de forma rápida
Notas de aula de PME 336 Processos de Transferência de Calor AUA 4 PAEDES PANAS COMPOSTAS Condução unidimensional, regime permanente, sem geração de calor paredes compostas. Para resolver de forma rápida
Aula 4 de FT II. Prof. Gerônimo
 Aula 4 de FT II Prof. Gerônimo Equação diferencial de Condução Vamos considerar a taxa de geração interna de calor q = E g. Coordenada x, y e z. Regime transiente. Considerando: q = q Volume de controle
Aula 4 de FT II Prof. Gerônimo Equação diferencial de Condução Vamos considerar a taxa de geração interna de calor q = E g. Coordenada x, y e z. Regime transiente. Considerando: q = q Volume de controle
Colégio Técnico de Lorena (COTEL)
 Colégio Técnico de Lorena (COTEL) Operações Unitárias Transferência de Calor Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas destinam-se exclusivamente a
Colégio Técnico de Lorena (COTEL) Operações Unitárias Transferência de Calor Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas destinam-se exclusivamente a
Descrição Macroscópica de um Gás ideal
 Descrição Macroscópica de um Gás ideal O gás não tem volume fixo ou uma pressão fixa O volume do gás é o volume do recipiente A pressão do gás depende do tamanho do recipiente A equação de estado relaciona
Descrição Macroscópica de um Gás ideal O gás não tem volume fixo ou uma pressão fixa O volume do gás é o volume do recipiente A pressão do gás depende do tamanho do recipiente A equação de estado relaciona
Transferência de Calor
 Transferência de Calor Condução Unidimensional, em Regime Permanente com Geração Interna de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica
Transferência de Calor Condução Unidimensional, em Regime Permanente com Geração Interna de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica
Lei de Gauss. O produto escalar entre dois vetores a e b, escrito como a. b, é definido como
 Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
Lei de Gauss REVISÃO DE PRODUTO ESCALAR Antes de iniciarmos o estudo do nosso próximo assunto (lei de Gauss), consideramos importante uma revisão sobre o produto escalar entre dois vetores. O produto escalar
Elementos de Termodinâmica
 TERMODINÂMICA ESCALAS DE TEMPERATURA Estuda as relações entre grandezas como a temperatura, a pressão, o volume, o calor e a energia interna Reparar na necessidade de definir uma escala de temperaturas
TERMODINÂMICA ESCALAS DE TEMPERATURA Estuda as relações entre grandezas como a temperatura, a pressão, o volume, o calor e a energia interna Reparar na necessidade de definir uma escala de temperaturas
superfície que envolve a distribuição de cargas superfície gaussiana
 Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Para a determinação do campo elétrico produzido por um corpo, é possível considerar um elemento de carga dq e assim calcular o campo infinitesimal de gerado. A partir desse princípio, o campo total em
Propagação do calor. Condução térmica
 Propagação do calor A propagação do calor entre dois sistemas pode ocorrer através de três processos diferentes: a condução, a convecção e a irradiação. Condução térmica A condução térmica é um processo
Propagação do calor A propagação do calor entre dois sistemas pode ocorrer através de três processos diferentes: a condução, a convecção e a irradiação. Condução térmica A condução térmica é um processo
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. 3º ano. Prof. Doutor Engº Jorge Nhambiu 1
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
ESTE Aula 1- Introdução à convecção. A camada limite da convecção
 Universidade Federal do ABC ESTE013-13 Aula 1- Introdução à convecção. A camada limite da convecção Convecção Definição: Processo de transferência de calor entre uma superfície e um fluido adjacente, quando
Universidade Federal do ABC ESTE013-13 Aula 1- Introdução à convecção. A camada limite da convecção Convecção Definição: Processo de transferência de calor entre uma superfície e um fluido adjacente, quando
UNIVERSIDADE DE SÃO PAULO
 Calor e trabalho (cont.) Exemplo 1: Conforme mostrado na Fig. o sistema consiste de uma mola e uma força F aplicada na direção do eixo da mola. Assume-se que o produto forçadeslocamento é uma relação linear
Calor e trabalho (cont.) Exemplo 1: Conforme mostrado na Fig. o sistema consiste de uma mola e uma força F aplicada na direção do eixo da mola. Assume-se que o produto forçadeslocamento é uma relação linear
Graça Meireles. Física -10º ano. Física -10º ano 2
 Escola Secundária D. Afonso Sanches Energia do Sol para a Terra Graça Meireles Física -10º ano 1 Variação da Temperatura com a Altitude Física -10º ano 2 1 Sistemas Termodinâmicos Propriedades a ter em
Escola Secundária D. Afonso Sanches Energia do Sol para a Terra Graça Meireles Física -10º ano 1 Variação da Temperatura com a Altitude Física -10º ano 2 1 Sistemas Termodinâmicos Propriedades a ter em
Resistências Térmicas em Paralelo 53 Exercícios 54 Exercícios recomendados 54 III. Transporte por convecção 55 Alguns fatos do cotidiano 55
 SUMÁRIO I. Introdução Portfolio de Fenômenos de Transporte II 1 Algumas palavras introdutórias 2 Senso comum ciência 4 Uma pequena história sobre o nascimento da ciência 4 Das Verdades científicas 6 Tese
SUMÁRIO I. Introdução Portfolio de Fenômenos de Transporte II 1 Algumas palavras introdutórias 2 Senso comum ciência 4 Uma pequena história sobre o nascimento da ciência 4 Das Verdades científicas 6 Tese
CALORIMETRIA E TERMOLOGIA
 CALORIMETRIA E TERMOLOGIA CALORIMETRIA Calor É a transferência de energia de um corpo para outro, decorrente da diferença de temperatura entre eles. quente Fluxo de calor frio BTU = British Thermal Unit
CALORIMETRIA E TERMOLOGIA CALORIMETRIA Calor É a transferência de energia de um corpo para outro, decorrente da diferença de temperatura entre eles. quente Fluxo de calor frio BTU = British Thermal Unit
3ª Lista de Exercícios: TRANSFERÊNCIA DE CALOR (RESOLUCIONÁRIO)
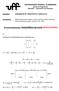 UNIVESIDADE FEDEA FUMINENSE Escola de Engenharia HidroUFF aboratório de Hidráulica Disciplina: FENÔMENOS DE ANSPOE E HIDÁUICA Professores: Gabriel Nascimento (Depto. de Eng. Agrícola e Meio Ambiente) Elson
UNIVESIDADE FEDEA FUMINENSE Escola de Engenharia HidroUFF aboratório de Hidráulica Disciplina: FENÔMENOS DE ANSPOE E HIDÁUICA Professores: Gabriel Nascimento (Depto. de Eng. Agrícola e Meio Ambiente) Elson
MODELAÇÃO NUMÉRICA DA INTERACÇÃO TÉRMICA SOLO-ESTRUTURA: ESTRUTURAS DE FUNDAÇÃO TERMOACTIVAS
 MODELAÇÃO NUMÉRICA DA INTERACÇÃO TÉRMICA SOLO-ESTRUTURA: ESTRUTURAS DE FUNDAÇÃO TERMOACTIVAS Ana Vieira; João R. Maranha Departamento de Geotecnia, LNEC A gestão dos recursos energéticos é um tema central
MODELAÇÃO NUMÉRICA DA INTERACÇÃO TÉRMICA SOLO-ESTRUTURA: ESTRUTURAS DE FUNDAÇÃO TERMOACTIVAS Ana Vieira; João R. Maranha Departamento de Geotecnia, LNEC A gestão dos recursos energéticos é um tema central
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. 3º Ano. Prof. Dr. Engº Jorge Nhambiu & Engº Paxis Roque 1
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Umajanelatémdoisvidrosde5mmdeespessuraeáreade 1,8
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Umajanelatémdoisvidrosde5mmdeespessuraeáreade 1,8
FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA
 FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA FÍSICA (Eletromagnetismo) Nos capítulos anteriores estudamos as propriedades de cargas em repouso, assunto da eletrostática. A partir deste capítulo
FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA FÍSICA (Eletromagnetismo) Nos capítulos anteriores estudamos as propriedades de cargas em repouso, assunto da eletrostática. A partir deste capítulo
Capítulo 4 Condução Bidimensional em Regime Estacionário. Prof. Dr. Santiago del Rio Oliveira
 Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
EM34B Transferência de Calor 2
 EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Trocadores de Calor 2 Trocadores de Calor Introdução Os trocadores de calor são dispositivos que facilitam a transferência
EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Trocadores de Calor 2 Trocadores de Calor Introdução Os trocadores de calor são dispositivos que facilitam a transferência
UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL
 UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL LOM3083 e LOM3213 Fenômenos de Transporte Prof. Luiz T. F. Eleno Lista de exercícios 2 1. Considere uma parede aquecida por convecção de um
UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL LOM3083 e LOM3213 Fenômenos de Transporte Prof. Luiz T. F. Eleno Lista de exercícios 2 1. Considere uma parede aquecida por convecção de um
Transferência de Calor
 Transferência de Calor Trocadores de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de Juiz
Transferência de Calor Trocadores de Calor Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de Juiz
Capítulo 8: Transferência de calor por condução
 Capítulo 8: Transferência de calor por condução Aletas Condução de calor bidimensional Transferência de calor É desejável em muitas aplicações industriais aumentar a taxa de transferência de calor de uma
Capítulo 8: Transferência de calor por condução Aletas Condução de calor bidimensional Transferência de calor É desejável em muitas aplicações industriais aumentar a taxa de transferência de calor de uma
Recursos Energéticos e Meio Ambiente (REMA) Engenharia Ambiental 1º semestre/2018
 Recursos Energéticos e Meio Ambiente (REMA) Engenharia Ambiental 1º semestre/2018 CALOR E TRABALHO Capítulo 4 HINRICHS, R.A. e KLEINBACH, M. Energia e Meio Ambiente. 4ª. Ed. São Paulo: Ed. Thompson, 2011.
Recursos Energéticos e Meio Ambiente (REMA) Engenharia Ambiental 1º semestre/2018 CALOR E TRABALHO Capítulo 4 HINRICHS, R.A. e KLEINBACH, M. Energia e Meio Ambiente. 4ª. Ed. São Paulo: Ed. Thompson, 2011.
Problema 1 R 1 R 2 EO/MEEC-IST -1-11/15/11
 Problema 1 ε L V R 1-a) Para determinar os campos vamos usar a Lei de Gauss para superfícies cilíndricas r de raio r e altura h L, com eixos coincidentes com o do condensador, e em regiões afastadas das
Problema 1 ε L V R 1-a) Para determinar os campos vamos usar a Lei de Gauss para superfícies cilíndricas r de raio r e altura h L, com eixos coincidentes com o do condensador, e em regiões afastadas das
Transmissão de Calor e Permutadores
 CONCURSO PETROBRAS ENGENHEIRO(A) DE PROCESSAMENTO JÚNIOR ENGENHEIRO(A) JÚNIOR - ÁREA: PROCESSAMENTO QUÍMICO(A) DE PETRÓLEO JÚNIOR Transmissão de Calor e Permutadores Questões Resolvidas QUESTÕES RETIRADAS
CONCURSO PETROBRAS ENGENHEIRO(A) DE PROCESSAMENTO JÚNIOR ENGENHEIRO(A) JÚNIOR - ÁREA: PROCESSAMENTO QUÍMICO(A) DE PETRÓLEO JÚNIOR Transmissão de Calor e Permutadores Questões Resolvidas QUESTÕES RETIRADAS
Transferência de Calor
 Transferência de Calor Escoamento Interno - Parte 2 Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Transferência de Calor Escoamento Interno - Parte 2 Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Módulo II Energia, Calor e Trabalho
 Módulo II Energia, Calor e Trabalho Energia A energia pode se manifestar de diversas formas: mecânica, elétrica, térmica, cinética, potencial, magnética, química e nuclear. A energia total de um sistema
Módulo II Energia, Calor e Trabalho Energia A energia pode se manifestar de diversas formas: mecânica, elétrica, térmica, cinética, potencial, magnética, química e nuclear. A energia total de um sistema
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br TRANSFERÊNCIA DE
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro sergio.montoro@usp.br srmontoro@dequi.eel.usp.br TRANSFERÊNCIA DE
Programa Analítico de Disciplina ENG278 Transferência de Calor e Massa
 0 Programa Analítico de Disciplina ENG78 Transferência de Calor e Massa Departamento de Engenharia Agrícola - Centro de Ciências Agrárias Número de créditos: Teóricas Práticas Total Duração em semanas:
0 Programa Analítico de Disciplina ENG78 Transferência de Calor e Massa Departamento de Engenharia Agrícola - Centro de Ciências Agrárias Número de créditos: Teóricas Práticas Total Duração em semanas:
EP34D Fenômenos de Transporte
 EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Transferência de Calor por Condução 2 Transferência de Calor por Condução Análise da Condução A análise da condução diz respeito
EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha arocha@utfpr.edu.br Transferência de Calor por Condução 2 Transferência de Calor por Condução Análise da Condução A análise da condução diz respeito
Escola Politécnica da Universidade de São Paulo. Termodinâmica. Trabalho e calor. v. 1.0
 Termodinâmica Trabalho e calor 1! v. 1.0 Trabalho e calor Energia pode atravessar a fronteira de um sistema fechado apenas através de duas formas distintas: trabalho ou calor. Ambas são interações energéticas
Termodinâmica Trabalho e calor 1! v. 1.0 Trabalho e calor Energia pode atravessar a fronteira de um sistema fechado apenas através de duas formas distintas: trabalho ou calor. Ambas são interações energéticas
4/Abr/2018 Aula 9. Potenciais termodinâmicos Energia interna total Entalpia Energias livres de Helmholtz e de Gibbs Relações de Maxwell
 23/Mar/2018 Aula 8 Expansão Térmica de Sólidos e Líquidos Coeficiente de expansão térmica Expansão Volumétrica Expansão da água Mecanismos de transferência de calor Condução; convecção; radiação 4/Abr/2018
23/Mar/2018 Aula 8 Expansão Térmica de Sólidos e Líquidos Coeficiente de expansão térmica Expansão Volumétrica Expansão da água Mecanismos de transferência de calor Condução; convecção; radiação 4/Abr/2018
Física 3. Resumo e Exercícios P1
 Física 3 Resumo e Exercícios P1 Resuminho Teórico e Fórmulas Parte 1 Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv
Física 3 Resumo e Exercícios P1 Resuminho Teórico e Fórmulas Parte 1 Cargas Elétricas Distribuição Contínua de Cargas 1. Linear Q = dq = λ dl 2. Superficial Q = dq = σ. da 3. Volumétrica Q = dq = ρ. dv
Transferência de Calor
 Transferência de Calor Condução Bidimensional Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Transferência de Calor Condução Bidimensional Filipe Fernandes de Paula filipe.paula@engenharia.ufjf.br Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Transmissão de Calor
 Transmissão de Calor FÍSICA TERMOLOGIA WILD LAGO Condução Térmica Definição: Propagação de calor em que a energia térmica é transmitida de partícula para partícula, mediante as colisões e alterações das
Transmissão de Calor FÍSICA TERMOLOGIA WILD LAGO Condução Térmica Definição: Propagação de calor em que a energia térmica é transmitida de partícula para partícula, mediante as colisões e alterações das
TRANSFERÊNCIA DE CALOR
 UNIVERSIDADE DE SÃO PAULO Faculdade de Ciências Farmacêuticas FBT0530 - Física Industrial TRANSFERÊNCIA DE CALOR A maioria dos processos que acontecem nas indústrias farmacêutica e de alimentos envolve
UNIVERSIDADE DE SÃO PAULO Faculdade de Ciências Farmacêuticas FBT0530 - Física Industrial TRANSFERÊNCIA DE CALOR A maioria dos processos que acontecem nas indústrias farmacêutica e de alimentos envolve
Transferência de Calor
 Transferência de Calor Condução em Paredes Planas e Cilíndricas Prof. Universidade Federal do Pampa BA000200 Campus Bagé 15 de maio de 2017 Transferência de Calor: Condução 1 / 28 Condução: Lei de Fourier
Transferência de Calor Condução em Paredes Planas e Cilíndricas Prof. Universidade Federal do Pampa BA000200 Campus Bagé 15 de maio de 2017 Transferência de Calor: Condução 1 / 28 Condução: Lei de Fourier
Transferência de Calor 1
 Transferência de Calor Guedes, Luiz Carlos Vieira. G94t Transferência de calor : um / Luiz Carlos Vieira Guedes. Varginha, 05. 80 slides; il. Sistema requerido: Adobe Acrobat Reader Modo de Acesso: World
Transferência de Calor Guedes, Luiz Carlos Vieira. G94t Transferência de calor : um / Luiz Carlos Vieira Guedes. Varginha, 05. 80 slides; il. Sistema requerido: Adobe Acrobat Reader Modo de Acesso: World
Fluxos e Conservação Lei de Gauss Isolantes. III - Lei de Gauss. António Amorim, SIM-DF. Electromagnetismo e Óptica. Lei de Gauss /2011
 III - Electromagnetismo e Óptica - 2010/2011 III - Índice 1 Fluxos e Conservação 2 3 III - Outline 1 Fluxos e Conservação 2 3 III - Distribuição Contínua (rev.) Denindo a densidade de carga por unidade
III - Electromagnetismo e Óptica - 2010/2011 III - Índice 1 Fluxos e Conservação 2 3 III - Outline 1 Fluxos e Conservação 2 3 III - Distribuição Contínua (rev.) Denindo a densidade de carga por unidade
Entre sistemas a temperaturas diferentes a energia transfere-se do sistema com temperatura mais elevada para o sistema a temperatura mais baixa.
 Sumário Do Sol ao Aquecimento Unidade temática 1. Mecanismos de transferência de calor: a radiação, a condução e a convecção. O coletor solar e o seu funcionamento. Materiais condutores e isoladores do
Sumário Do Sol ao Aquecimento Unidade temática 1. Mecanismos de transferência de calor: a radiação, a condução e a convecção. O coletor solar e o seu funcionamento. Materiais condutores e isoladores do
TERMODINÂMICA E TEORIA CINÉTICA
 UNIVERSIDADE DA MADEIRA 1. OBJECTIVOS TERMODINÂMICA E TEORIA CINÉTICA T8. Mecanismos de transmissão do calor Estudo do fenómeno de condução térmica. Determinação da condutividade térmica do vidro. Verificar
UNIVERSIDADE DA MADEIRA 1. OBJECTIVOS TERMODINÂMICA E TEORIA CINÉTICA T8. Mecanismos de transmissão do calor Estudo do fenómeno de condução térmica. Determinação da condutividade térmica do vidro. Verificar
EN 2411 Aula 13 Trocadores de calor Método MLDT
 Universidade Federal do ABC EN 24 Aula 3 Trocadores de calor Método MLDT Trocadores de calor São equipamentos utilizados para promover a transferência de calor entre dois fluidos que se encontram sob temperaturas
Universidade Federal do ABC EN 24 Aula 3 Trocadores de calor Método MLDT Trocadores de calor São equipamentos utilizados para promover a transferência de calor entre dois fluidos que se encontram sob temperaturas
Prof. Felipe Corrêa Maio de 2016
 Prof. Felipe Corrêa Maio de 2016 IMPORTÂNCIA Praticamente todos os sistemas envolvidos na engenharia estão direta ou indiretamente ligados com a transferência de calor. Portanto, para que estes sistemas
Prof. Felipe Corrêa Maio de 2016 IMPORTÂNCIA Praticamente todos os sistemas envolvidos na engenharia estão direta ou indiretamente ligados com a transferência de calor. Portanto, para que estes sistemas
Segunda Lista - Lei de Gauss
 Segunda Lista - Lei de Gauss FGE211 - Física III 1 Sumário O fluxo elétrico que atravessa uma superfície infinitesimal caracterizada por um vetor de área A = Aˆn é onde θ é o ângulo entre E e ˆn. Φ e =
Segunda Lista - Lei de Gauss FGE211 - Física III 1 Sumário O fluxo elétrico que atravessa uma superfície infinitesimal caracterizada por um vetor de área A = Aˆn é onde θ é o ângulo entre E e ˆn. Φ e =
(d) E = Eŷ e V = 0. (b) (c) (f) E = Eˆx e V = (f)
 1 Universidade Federal do Rio de Janeiro Instituto de Física Física III 01/ Primeira Prova: 10/1/01 Versão: A F e = q E, E = V, E = k0 q r ˆr Seção 1 Múltipla escolha 10 0,5 = 5,0 pontos) Formulário onde
1 Universidade Federal do Rio de Janeiro Instituto de Física Física III 01/ Primeira Prova: 10/1/01 Versão: A F e = q E, E = V, E = k0 q r ˆr Seção 1 Múltipla escolha 10 0,5 = 5,0 pontos) Formulário onde
Lista de Exercícios para P2
 ENG 1012 Fenômenos de Transporte II Lista de Exercícios para P2 1. Estime o comprimento de onda que corresponde à máxima emissão de cada de cada um dos seguintes casos: luz natural (devido ao sol a 5800
ENG 1012 Fenômenos de Transporte II Lista de Exercícios para P2 1. Estime o comprimento de onda que corresponde à máxima emissão de cada de cada um dos seguintes casos: luz natural (devido ao sol a 5800
Convecção Forçada Interna a Dutos
 Convecção Forçada Interna a Dutos Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Escoamento no interior de dutos Velocidade Média Região de Entrada Hidrodinâmica
Convecção Forçada Interna a Dutos Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Escoamento no interior de dutos Velocidade Média Região de Entrada Hidrodinâmica
Lei de Gauss. Quem foi Gauss? Um dos maiores matemáticos de todos os tempos. Ignez Caracelli 11/17/2016
 Lei de Gauss Ignez Caracelli ignez@ufscar.br Quem foi Gauss? Um dos maiores matemáticos de todos os tempos Um professor mandou ue somassem todos os números de um a cem. Para sua surpresa, em poucos instantes
Lei de Gauss Ignez Caracelli ignez@ufscar.br Quem foi Gauss? Um dos maiores matemáticos de todos os tempos Um professor mandou ue somassem todos os números de um a cem. Para sua surpresa, em poucos instantes
UNIVERSIDADE EDUARDO MONDLANE
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática-2 Condução em regime permanente 2 Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática-2 Condução em regime permanente 2 Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura
Equação Geral da Condução
 Equação Geral da Condução Para um sistema unidimensional demonstrouse: q x = k A T x x Para um sistema multidimensional o fluxo de calor é vetorial: q,, =q x,, i q y,, j q z,, k = k T i k T j k T k =k
Equação Geral da Condução Para um sistema unidimensional demonstrouse: q x = k A T x x Para um sistema multidimensional o fluxo de calor é vetorial: q,, =q x,, i q y,, j q z,, k = k T i k T j k T k =k
