Transmissão de calor
|
|
|
- Osvaldo João Pedro Belmonte de Andrade
- 8 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1
2 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção uniforme Eficiência da alheta Desempenho da alheta Comprimento adequado da alheta Transferência de Calor em Configurações Usuais Prof. Doutor Engº Jorge Nhambiu 2
3 3.6 Superfícies Estendidas O termo superfície estendida é comummente usado em referência a um sólido onde há transferência de energia por condução no interior de suas fronteiras e transferência de energia por convecção (e/ou radiação) entre suas fronteiras e a vizinhança. Em diversas condições de engenharia usam-se superfícies estendidas para aumentar a eficiência de troca de calor, quer na colecta de energia (colectores solares) quer na sua dissipação (motores). Prof Dr. Engº Jorge Nhambiu 3
4 3.6 Superfícies Estendidas Prof. Doutor Engº Jorge Nhambiu 4
5 3.6 Superfícies Estendidas Prof. Doutor Engº Jorge Nhambiu 5
6 3.6 Superfícies Estendidas O principio físico que justifica o uso das alhetas é simples. Baseando-se na Lei de Resfriamento de Newton pode-se escrever: Q ( T ) ha T s s Onde: h é o coeficiente de troca de calor por Convecção; A s é a área superficial; T s é a temperatura superficial; T - é a temperatura do fluído ambiente. Prof. Doutor Engº Jorge Nhambiu 6
7 3.6 Superfícies Estendidas Para aumentar a dissipação de calor pode-se aumentar h, A s e a diferença das temperaturas. O aumento de h pode se conseguir com o aumento da velocidade do fluido (convecção forçada). Aumentar a diferença de temperaturas pode-se conseguir com o abaixamento da temperatura ambiente. A forma mais fácil de se conseguir o aumento da dissipação de calor é aumentando a área superficial. Prof. Doutor Engº Jorge Nhambiu 7
8 3.6 Superfícies Estendidas Condução Estacionária transmissão de calor através de uma alheta Prof. Doutor Engº Jorge Nhambiu 8
9 3.6 Superfícies Estendidas Exemplos de funcionamento de alhetas Prof. Doutor Engº Jorge Nhambiu 9
10 3.6 Superfícies Estendidas Alguns tipos de alhetas Alheta longitudinal de perfil rectangular Alheta longitudinal de perfil triangular Tubo cilíndrico com alheta radial de perfil rectangular Pino cónico truncado Prof. Doutor Engº Jorge Nhambiu 10
11 3.6 Superfícies Estendidas Supondo que a base da alheta esteja a uma temperatura superior à do meio ambiente. Numa secção de comprimento elementar Δx localizada no meio da alheta tem-se energia entrando por condução, no material desse elemento, e por outro lado energia saindo também por condução e não se pode esquecer da parcela que sai para o meio ambiente por convecção. Prof Dr. Engº Jorge Nhambiu 11
12 3.6.1 Balanço de energia para uma face Prof. Doutor Engº Jorge Nhambiu 12
13 3.6.1 Balanço de energia para uma face As hipóteses a serem usadas são: Regime permanente e ausência de fontes internas; Temperatura constante do fluído longe da alheta; As propriedades térmicas do material não variam com a temperatura; As alhetas são finas, assim pode-se modelar a situação como unidimensional; O Coeficiente de transferência de calor por convecção é constante ao longo da alheta; A temperatura da superfície da base da alheta é a mesma que a da superfície primária. Prof. Doutor Engº Jorge Nhambiu 13
14 3.6.1 Balanço de energia para uma face Calor que entra por condução no elemento em x Calor que sai por condução do elemento em x + Δx Calor que sai por convecção do elemento Q!! + Q! cond, x Qcond, x+ dx conv (3.54) Onde: Q! conv ( T ) ha T s Prof. Doutor Engº Jorge Nhambiu 14
15 3.6.1 Balanço de energia para uma face Substituindo e dividindo-se por Δx obtém-se: dq! Δx cond + h As Δx ( T ) 0 T (3.55) Calculando-se o limite quando Δx 0 obtém-se: d da Q! h T T dx dx ( ) s cond + ( ) 0 (3.56) Prof. Doutor Engº Jorge Nhambiu 15
16 3.6.1 Balanço de energia para uma face Da lei de Fourier para a condução obtém-se: Q! cond ka c dt dx Substituindo em 3.56 chega-se a: (3.57) d dx ' % & A c dt dx $ " # h k ou da dx s ( T ) 0 T 2 d T 2 dx ' 1 % & Ac da dx $ dt " # dx ' 1 % & Ac da $ "( T T dx # c s + h k ) 0 (3.58) Prof. Doutor Engº Jorge Nhambiu 16
17 3.6.2 Alhetas com secção uniforme P πd A c πd 2 4 Daqui, depreende-se que: da dx e c da dx s 0 p 2w + 2t Pc A wt Prof. Doutor Engº Jorge Nhambiu 17
18 3.6.2 Alhetas com secção uniforme Então a equação geral transforma-se em: 2 d T 2 dx hp ka c ( T T ) 0 Fazendo: (3.59) θ ( x ) T ( x) T Então: d θ dx dt dx (3.60) (3.61) Prof. Doutor Engº Jorge Nhambiu 18
19 3.6.2 Alhetas com secção uniforme Assumindo que: 2 m hp ka c (3.62) A equação fica: 2 d θ m 2 dx 2 θ 0 A solução geral desta equação de segunda ordem é: (3.63) θ ( x) mx C1e + C2 e mx (3.64) Prof. Doutor Engº Jorge Nhambiu 19
20 3.6.2 Alhetas com secção uniforme Uma das condições é a temperatura na base (x0) θ (0) Tb T θ b Prof. Doutor Engº Jorge Nhambiu 20
21 Alheta que perde calor por convecção pela sua extremidade As alhetas, na prática, são expostas ao ambiente e, portanto, a condição de contorno adequada para a ponta da alheta é a convecção, que também inclui os efeitos da radiação. A equação da alheta pode ainda ser resolvida, neste caso, utilizando a convecção na ponta da alheta como a segunda condição de contorno, mas a análise torna-se complexa e resulta em expressões de distribuição da temperatura e da transferência de calor complicadas. Prof. Doutor Engº Jorge Nhambiu 21
22 Alheta que perde calor por convecção pela sua extremidade Em geral, a área da ponta da alheta é uma pequena fração da área total da superfície da mesma, assim, as complexidades envolvidas na solução da equação, dificilmente podem justificar uma melhora na exactidão. Prof. Doutor Engº Jorge Nhambiu 22
23 Alheta que perde calor por convecção pela sua extremidade Para determinar as constantes C 1 e C 2 na Equação 3.64, é necessário estabelecer as condições de contorno. Q! b Q! f c [ ( ) ] ha T L T Prof. Doutor Engº Jorge Nhambiu 23
24 Alheta que perde calor por convecção pela sua extremidade ha c [ T ( L) T ] hθ ( L) ou ka dθ k dx c x L dt dx x L (3.65) (3.66) θ dai: C 1 C 2 b + e: ( ml ml) ( ml ml C e + C e km C e C e ) h (3.67) (3.68) Prof. Doutor Engº Jorge Nhambiu 24
25 Alheta que perde calor por convecção pela sua extremidade logo, a distribuição da temperatura é dada por: θ θ b cosh m( L x) cosh ml + + ( h ( h mk)sinh mk) sinh m( L ml x) (3.69) O calor perdido pela alheta calcula-se de: Q! f Q! b ka c dt dx ka dθ c x0 dx x0 (3.70) Prof. Doutor Engº Jorge Nhambiu 25
26 Alheta que perde calor por convecção pela sua extremidade Que resulta em: Q! f hpka θ c b sinh ml + ( h cosh ml + ( h mk)cosh ml mk)sinh ml (3.71) Uma outra forma que integra as perdas de calor por convecção é: Q! f A [ ( x) T ] das h T f (3.72) Prof. Doutor Engº Jorge Nhambiu 26
27 Alheta com extremidade isolada As alhetas não são susceptíveis de ser tão longas que a sua temperatura se aproxime da temperatura ambiente na ponta. Uma situação mais realista é a transferência de calor da ponta da alheta ser desprezada dado que a transferência de calor da alheta é proporcional à sua superfície e a superfície da ponta da alheta é geralmente uma fracção insignificante da área total da alheta. A ponta da alheta pode ser considerada como isolada. Prof. Doutor Engº Jorge Nhambiu 27
28 Alheta com extremidade isolada A condição de contorno na ponta da alheta pode ser expressa por: dθ dx xl 0 (3.73) então: C e ml ml 1 C2e O perfil de temperaturas toma o seguinte aspecto: 0 (3.74) θ θ b cosh m( L cosh ml x) (3.75) O calor dissipado pela alheta avalia-se de: Q! f hpka c θ b tanh ml (3.76) Prof. Doutor Engº Jorge Nhambiu 28
29 Alheta com extremidade isolada Quando se refere a uma alheta cuja extremidade se encontra isolada, é muito frequente usar-se o conceito de comprimento corrigido L c que permite usar as expressões relativas à alheta com convecção no seu extremo, com um erro não superior a 8%. Lc L + Ac p (3.77) Usando as relações próprias de A c e p para alhetas de secção rectangular e circular os comprimentos corrigidos ficam respectivamente : L t 2 c,rectangular L + Lc, circular L + D 4 Prof. Doutor Engº Jorge Nhambiu 29
30 Alheta com extremidade isolada O comprimento corrigido L c é definido como o comprimento de uma alheta com o extremo isolado, que transfere o mesmo calor que uma alheta de comprimento L com convecção no extremo. Prof. Doutor Engº Jorge Nhambiu 30
31 Alheta com temperatura prescrita na sua extremidade Se a temperatura da alheta no seu extremo for medida e igual a T L a segunda condição de contorno pode ser dada como: em X L, θ θ L. θ L T L ( ) ( ) Prof. Doutor Engº Jorge Nhambiu 31
32 Alheta com temperatura prescrita na sua extremidade Da condição de contorno resulta: θ ( L) θ L O perfil de temperaturas é dado por: (3.78) θ θ b ( θ L θb)sinh mx + sinh m( L x) sinh ml (3.79) O calor dissipado pela alheta é calculado de: Q! f hpka θ c b cosh ml θ sinh ml L θ b (3.80) Prof. Doutor Engº Jorge Nhambiu 32
33 Alheta com comprimento infinito Para a alhetas suficientemente longas com secção transversal constante (A c constante), a temperatura da alheta no seu extremo tenderá para a temperatura ambiente T e portanto θ tenderá para zero. Isto é: θ ( L) T ( L) T 0 Prof. Doutor Engº Jorge Nhambiu 33
34 Alheta com comprimento infinito Da condição de contorno resulta: θ ( L) 0 (3.81) O perfil de temperaturas é dado por θ θ b e mx (3.82) O calor dissipado pela alheta é calculado de: Q! f hpka c θ b (3.83) Prof. Doutor Engº Jorge Nhambiu 34
35 Alheta com comprimento infinito Variação de temperatura ao longo de uma alheta longa de secção circular constante. Prof. Doutor Engº Jorge Nhambiu 35
36 Eficiência da alheta Transferência de calor real e ideal em uma alheta. Prof. Doutor Engº Jorge Nhambiu 37
37 Eficiência da alheta Eficiência da alheta η a Calor realmente transferido pela alheta Calor que seria transferido se toda alheta estivesse à temperatura da base Para o caso da alheta com extremidade isolada pode-se escrever: ml hp ka hpkaθ b tanh ml hplθ L b h( 2z + 2t) L kzt tanh ml ml (3.84) Se as alhetas forem suficientemente delgadas para o fluxo de calor ser considerado unidimensional pode-se escrever: (3.85) Onde: z é a profundidade da alheta e t - a sua espessura η a Prof. Doutor Engº Jorge Nhambiu 38
38 Eficiência da alheta Partindo do principio que a alheta é suficientemente delgada 2z>>2t, escreve-se: ml 2hz L ktz 2h L kt (3.86) Multiplicando o numerador e denominador por L (1/2) obtém-se: ml 2h L 3 klt 2 Lt é a área do perfil da alheta que define-se como A m Lt, assim: ml 2h L 3 ka m 2 (3.87) Prof. Doutor Engº Jorge Nhambiu 39
39 Eficiência da alheta Para uma situação em que se tem um arranjo de várias alhetas, tem de se tomar em conta as áreas, com e sem alhetas, para se fazer o cálculo da eficiência do arranjo. Prof. Doutor Engº Jorge Nhambiu 40
40 Eficiência da alheta η t t Q! Q! t max a Sendo: A NA + NA Q! t haθ t A b Ou por outra: b ( ) a ηt 1 1 ηa At Onde: N - é o número de alhetas A a A f - área da alheta A b área da superfície primária (3.88) (3.89) (3.90) Prof. Doutor Engº Jorge Nhambiu 41
41 Eficiência da alheta Prof. Doutor Engº Jorge Nhambiu 42
42 Eficiência da alheta Prof. Doutor Engº Jorge Nhambiu 43
43 Desempenho da alheta Prof. Doutor Engº Jorge Nhambiu 44
44 Desempenho da alheta Em alguns casos um método válido de avaliar o desempenho de uma alheta é comparar o calor transferido com a alheta com aquele que seria transferido sem a alheta. A razão entre as quantidades é: Q! Q! com alheta sem alheta ηa Aa hθ ha θ b b b A A Aa pl e Ab Q Q com alheta sem alheta tanh ml ha kp a b A η a (3.91) Onde A a é a área superficial total da alheta A b a área da base da alheta. Para a alheta de extremidade isolada pode-se escrever: (3.92) (3.93) Prof. Doutor Engº Jorge Nhambiu 45
45 Desempenho da alheta A taxa de transferência de calor para uma alheta suficientemente longa consegue-se substituindo na fórmula anterior a de transferência de calor para essa situação dada pela Equação 3.82 ε Q! Q com alheta alheta longa! sem alheta A hpkθ a ha θ b b b kp ha b (3.94) Para determinar a taxa de transferência de calor de uma região alhetada tem de se ter em consideração a parte da superfície que não está alhetada bem como a área das alhetas. Q!! a, tot Qñ alh + Qalh h ha ñ alh ( Añ alh + η alh Aalh ) θ b θ b + η alh ha alh θ b (3.95) Prof. Doutor Engº Jorge Nhambiu 46
46 Desempenho da alheta A eficácia global para uma região alhetada é dada pela seguinte equação: ε alheta,total Q! Q! h total alheta total sem alheta ( A + η A ) ñ alh ha alh sem alheta θ alh b θ b (3.95) Prof. Doutor Engº Jorge Nhambiu 47
47 3.6.5 Comprimento adequado da alheta Devido a perda gradual de temperatura ao longo da alheta, a região perto do extremo da alheta contribui em pouco ou em nada para a transferência de calor. Prof. Doutor Engº Jorge Nhambiu 48
48 3.6.5 Comprimento adequado da alheta Para se ter a sensibilidade do comprimento adequado de uma alheta, compara-se o calor transferido pela alheta de comprimento finito com o de uma de comprimento infinito às mesmas condições, que é dado pela expressão seguinte: ε Q! Q! hpka tanh ml com alheta a b alheta longa sem alheta hpkaa θb θ tanh ml (3.97) Prof. Doutor Engº Jorge Nhambiu 49
49 Exemplo 7.1 Se o valor do coeficiente de convecção for grande a alheta pode originar uma redução na transferência de calor porque a resistência à condução representa então um impedimento maior ao fluxo de calor que a resistência a convecção. Considere-se uma alheta de aço inoxidável em forma de pino com k 16 W/m ºC, L10 cm, d 1 cm exposta a uma situação de transferência de calor por convecção, de água em ebulição onde h 5000 W/m 2 o C Solução ε Q! Q! com alheta sem alheta tanh ml ha kp. (& 5000π tanh-$ (, $ % 16π 2 ( 1 10 )( 4) 2 2 ( 1 10 )!" 2 2 π( 1 10 ) & 5000 $ $ % (4)(16) π (1 10 #! #! )! " 2 ( ) ( * () 1,13 Um pino relativamente grande aumenta a área de transferência de calor em 13% somente. Prof. Doutor Engº Jorge Nhambiu 50
50 3.7 Transferência de Calor em Configurações Usuais Até agora, foi considerada a transferência de calor em geometrias simples, como grandes paredes planas, cilindros longos e esferas. Isso ocorreu porque a transferência de calor em geometrias pode ser aproximada a unidimensional e soluções analíticas simples podem ser facilmente obtidas. Mas muitos problemas na prática, são de duas ou três dimensões e envolvem geometrias bastante complicadas para as quais não há soluções simples disponíveis. Prof Dr. Engº Jorge Nhambiu 51
51 3.7 Transferência de Calor em Configurações Usuais Uma importante classe de problemas de transferência de calor para os quais soluções simples são obtidas, engloba aquelas que envolvem duas superfícies mantidas a temperaturas constantes T 1 e T 2. A taxa constante de transferência de calor entre as duas superfícies é expresso como: ( ) Q Sk T1 T2 (W) (3.96) Onde: S é o factor de forma de condução, que tem a dimensão de comprimento, e k é a condutividade térmica do meio entre as superfícies. O factor de forma de condução depende somente da geometria do sistema. Prof. Doutor Engº Jorge Nhambiu 52
52 3.7.1 Factor de Forma de Condução (1) Cilindro isotérmico de comprimento L, enterrado em um meio semi-infinito (L>> D e z> 1.5D) (2) Cilindro vertical isotérmico, de comprimento L, enterrado em um meio semi-infinito (L>> D) S 2π L ln 4 ( z D) S 2π L ln 4 ( L D) Prof. Doutor Engº Jorge Nhambiu 53
53 3.7.1 Factor de Forma de Condução (3) Dois cilindros isotérmicos paralelos colocados num meio infinito (L>> D (4) Fila de cilindros isotérmicos paralelos equidistantes enterrados num meio semi-infinito (L>> D, Z e W> 1.5D) (por cilindro) S cosh 2π L # 4z D D $ % & 2D D ' 1 2 ( S 2π L " 2w 2π z # ln $ sinh % & π D w ' Prof. Doutor Engº Jorge Nhambiu 54
54 3.7.1 Factor de Forma de Condução (5) Cilindro isotérmico de comprimento L num plano intermédio de uma parede infinita (z> 0,5D) (6) Cilindro isotérmico de comprimento L no centro de uma barra quadrada sólida do mesmo comprimento S 2π L ln 8 ( z π D) S 2π L ln 1,08 ( w D) Prof. Doutor Engº Jorge Nhambiu 55
55 3.7.1 Factor de Forma de Condução (7) Cilindro excêntrico isotérmico de comprimento L em um cilindro do mesmo comprimento (L> D (8) Grande parede plana S cosh 2π L # D D 4z $ % & 2D D ' 1 2 ( S A L Prof. Doutor Engº Jorge Nhambiu 56
56 3.7.1 Factor de Forma de Condução (9) Camada cilíndrica (10) Passagem de fluxo quadrada para a b > 1,4 S 2π L 0,93ln 0,948 ( a b) para a b < 1,41 S ln 2π L ( D D ) 2 1 S 2π L 0, 785ln ( a b) Prof. Doutor Engº Jorge Nhambiu 57
57 3.7.1 Factor de Forma de Condução (11) Camada esférica (12) Disco enterrado num meio infinito paralelamente a superfície (z>>d) S 2π D D D D 1 2 ( S 2 D quando z D) 2 1 S 4D Prof. Doutor Engº Jorge Nhambiu 58
58 3.7.1 Factor de Forma de Condução (13) Canto entre duas paredes adjacentes de espessura igual (14) Canto entre três paredes adjacentes de espessura igual S 0,54w S 0,15L Prof. Doutor Engº Jorge Nhambiu 59
59 3.7.1 Factor de Forma de Condução (15) Esfera isotérmica enterrada num meio semi-infinito (16) Esfera isotérmica enterrada em um meio semi-infinito a T superfície encontra-se isolada S 2π D 2π D 1 0,25D z S 1 + 0,25D z Prof. Doutor Engº Jorge Nhambiu 60
60 Exemplo 7.2 Um tanque cilíndrico 0,6 m de diâmetro e 1,9 m de comprimento, contendo gás natural liquefeito (GNL) a -160 C é colocado no centro de uma barra quadrada sólida de 1,9 m de comprimento, 1,4 m x 1,4 m de secção, feita de um material isolante com k 0,0006 W/m C. Se a temperatura da superfície externa da barra for de 20 C, determinar a taxa de transferência de calor para o tanque. Determinar também a temperatura de GNL após um mês. Considere a massa específica e o calor específico do GNL, 425 kg/m 3 e 3,475 kj / kg C, respectivamente. Prof. Doutor Engº Jorge Nhambiu 61
61 Exemplo 7.2 (Solução I) Um tanque cilíndrico contendo gás natural liquefeito (GNL) é colocado no centro de uma barra quadrada sólida. Devem ser determinadas a taxa de transferência de calor para o tanque e a temperatura do GNL ao fim de um mês. Pressupostos: 1 O regime é permanente. 2 A transferência de calor é bidimensional (sem alteração no sentido axial). 3 A condutividade térmica da barra é constante. 4 A superfície do tanque está a mesma temperatura que o gás natural liquefeito. Propriedades: A condutividade térmica da barra é dada k 0,0006 W /m C. A massa específica e o calor específico do GNL são 425 kg/m 3 e 3,475 kj/kg C, respectivamente, Prof. Doutor Engº Jorge Nhambiu 62
62 Exemplo 7.2 (Solução II) Análise: O factor de forma para esta configuração é dado na Figura (6) 20 C S 2π L 2 π (1,9 m) 12,92 m " 1,08w # " 1,4 m # ln $ % ln 1,08 D $ 0,6 m % & ' & ' C D 0,6 m 1,4 m L 1,9 m O calor transferido determina-se de: 1 2 [ ] Q! Sk( T T ) (12,92 m)(0, 0006 W/m C) 20 ( 160) C 1, 395 W Prof. Doutor Engº Jorge Nhambiu 63
63 Exemplo 7.2 (Solução III) A massa de GNL é dada por: 3 3 D 3 (0,6 m) m ρv ρπ (425 kg/m ) π 48,07 kg 6 6 O calor transferido pelo tanque no período de um mês: Q Q! Δ t (1,395 W)( s) J A temperatura do gás natural ao fim de um mês calcula-se de: Q mc ( T T ) 2 p 1 2 [ T ] J (48,07 kg)(3475 J/kg. C) ( 160) C T -138,4 C 2 Prof. Doutor Engº Jorge Nhambiu 64
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. 3º ano. Prof. Doutor Engº Jorge Nhambiu 1
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 7 * 3.6 Superfícies Estendidas Balanço de energia para uma face Alhetas com secção
Transferência de Calor
 Transferência de Calor Condução em Superfícies Estendidas Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Condução em Superfícies Estendidas Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. Transmissão de calor. 3º ano
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Aula 3 Equação diferencial de condução de calor Condições iniciais e condições de fronteira; Geração de Calor num Sólido;
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Aula 3 Equação diferencial de condução de calor Condições iniciais e condições de fronteira; Geração de Calor num Sólido;
Aula 6 de FT II. Prof. Gerônimo
 Aula 6 de FT II Prof. Gerônimo Transferência de calor em superfícies estendidas Superfície estendida é comumente usado para descrever um caso especial importante envolvendo a transferência de calor por
Aula 6 de FT II Prof. Gerônimo Transferência de calor em superfícies estendidas Superfície estendida é comumente usado para descrever um caso especial importante envolvendo a transferência de calor por
Capítulo 8: Transferência de calor por condução
 Capítulo 8: Transferência de calor por condução Aletas Condução de calor bidimensional Transferência de calor É desejável em muitas aplicações industriais aumentar a taxa de transferência de calor de uma
Capítulo 8: Transferência de calor por condução Aletas Condução de calor bidimensional Transferência de calor É desejável em muitas aplicações industriais aumentar a taxa de transferência de calor de uma
Transmissão de calor
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura e
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura e
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] TRANSFERÊNCIA DE
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] TRANSFERÊNCIA DE
Formulário para Transferência de Calor e Massa I
 Formulário para Transferência de Calor e Massa I Profs. Vicente/Santiago FEB/UNESP-Bauru Balanço de energia Ė Ac = Ėe Ės +ĖG para um corpo a temperatura uniforme: Ė Ac = ρ V c p T t ei de Fourier para
Formulário para Transferência de Calor e Massa I Profs. Vicente/Santiago FEB/UNESP-Bauru Balanço de energia Ė Ac = Ėe Ės +ĖG para um corpo a temperatura uniforme: Ė Ac = ρ V c p T t ei de Fourier para
UNIVERSIDADE EDUARDO MONDLANE
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula Prática 4 Regime transiente 2 Problema -10.1 Placas de latão de 20 mm de espessura são aquecidas durante 15 minutos
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula Prática 4 Regime transiente 2 Problema -10.1 Placas de latão de 20 mm de espessura são aquecidas durante 15 minutos
Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE
 Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE Parede plana T 1 T s1 T s2! x k T $ # &+! " x % y k T $ # &+! " y % z k T $ T # &+!q ρc p " z % t d " dx k dt % $ ' 0 q # dx & x ka dt dx cte T( x) ax
Capítulo 3 CONDUÇÃO DE CALOR 1-D, REGIME PERMANENTE Parede plana T 1 T s1 T s2! x k T $ # &+! " x % y k T $ # &+! " y % z k T $ T # &+!q ρc p " z % t d " dx k dt % $ ' 0 q # dx & x ka dt dx cte T( x) ax
Transferência de Calor
 Transferência de Calor Aletas e Convecção em Escoamento Interno e Externo Prof. Universidade Federal do Pampa BA000200 Campus Bagé 19 de junho de 2017 Transferência de Calor: Convecção 1 / 30 Convecção
Transferência de Calor Aletas e Convecção em Escoamento Interno e Externo Prof. Universidade Federal do Pampa BA000200 Campus Bagé 19 de junho de 2017 Transferência de Calor: Convecção 1 / 30 Convecção
CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA
 CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA 1) Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e gesso, conforme indicado na figura. Em um dia frio
CONDUÇÃO DE CALOR UNIDIMENSIONAL EXERCÍCIOS EM SALA 1) Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e gesso, conforme indicado na figura. Em um dia frio
UNIVERSIDADE EDUARDO MONDLANE
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática-2 Condução em regime permanente 2 Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática-2 Condução em regime permanente 2 Problema -6.1 (I) Uma janela tem dois vidros de 5 mm de espessura
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. 3º Ano. Prof. Dr. Engº Jorge Nhambiu & Engº Paxis Roque 1
 UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Umajanelatémdoisvidrosde5mmdeespessuraeáreade 1,8
UNIVESIDADE EDUADO MONDLANE Faculdade de Engenharia Transmissão de calor 3º Ano 1 Aula 6 Aula Prática- Condução em regime permanente Problema -6.1 (I) Umajanelatémdoisvidrosde5mmdeespessuraeáreade 1,8
Condução de Calor Unidimensional com Geração de Energia
 Condução de Calor Unidimensional com Geração de Energia Equação geral (k constante) E Ac 1 T t E e Ė s = T x T y T z E G q k (.15) Regime Estacionário Fluxo de Calor ocorre em apenas uma direção (unidimensional)
Condução de Calor Unidimensional com Geração de Energia Equação geral (k constante) E Ac 1 T t E e Ė s = T x T y T z E G q k (.15) Regime Estacionário Fluxo de Calor ocorre em apenas uma direção (unidimensional)
EP34D Fenômenos de Transporte
 EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha [email protected] Transferência de Calor em Superfícies Estendidas - Aletas 2 É desejável em muitas aplicações industriais aumentar a taxa
EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha [email protected] Transferência de Calor em Superfícies Estendidas - Aletas 2 É desejável em muitas aplicações industriais aumentar a taxa
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] TRANSFERÊNCIA DE
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] TRANSFERÊNCIA DE
Lei de Fourier. Considerações sobre a lei de Fourier. A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados.
 Condução de Calor Lei de Fourier A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados Considerações sobre a lei de Fourier q x = ka T x Fazendo Δx 0 q taxa de calor [J/s] ou
Condução de Calor Lei de Fourier A lei de Fourier é fenomenológica, isto é, desenvolvida de fenômenos observados Considerações sobre a lei de Fourier q x = ka T x Fazendo Δx 0 q taxa de calor [J/s] ou
Transferência de Calor
 Transferência de Calor Condução Bidimensional Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Transferência de Calor Condução Bidimensional Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de
Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO EM REGIME TRANSIENTE
 Os exercícios e figuras deste texto foram retirados de diversas referências bibliográficas listadas no programa da disciplina 1 FENÔMENOS DE TRANSPORTE Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO
Os exercícios e figuras deste texto foram retirados de diversas referências bibliográficas listadas no programa da disciplina 1 FENÔMENOS DE TRANSPORTE Capítulo 08 - TRANSFERÊNCIA DE CALOR POR CONDUÇÃO
Capitulo 8 Transferência de Calor por Condução
 Fenômenos de Transporte Capitulo 8 Transferência de Calor por Condução Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI TRANSFERÊNCIA DE CALOR POR CONDUÇÃO Quando existe um gradiente de temperatura
Fenômenos de Transporte Capitulo 8 Transferência de Calor por Condução Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI TRANSFERÊNCIA DE CALOR POR CONDUÇÃO Quando existe um gradiente de temperatura
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] AULA 5 CONDUÇÃO
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] AULA 5 CONDUÇÃO
TRANSFERÊNCIA DE CALOR
 UNIVERSIDADE DE SÃO PAULO Faculdade de Ciências Farmacêuticas FBT0530 - Física Industrial TRANSFERÊNCIA DE CALOR A maioria dos processos que acontecem nas indústrias farmacêutica e de alimentos envolve
UNIVERSIDADE DE SÃO PAULO Faculdade de Ciências Farmacêuticas FBT0530 - Física Industrial TRANSFERÊNCIA DE CALOR A maioria dos processos que acontecem nas indústrias farmacêutica e de alimentos envolve
GERAÇÃO DE CALOR UNIFORME EM SÓLIDOS. Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna.
 GEAÇÃO DE CALO UNIFOME EM SÓLIDOS Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna. Se manifesta como um aumento da temperatura do meio. Exemplos:
GEAÇÃO DE CALO UNIFOME EM SÓLIDOS Conversão de uma forma de energia em energia térmica, ou seja, estes meios sólidos têm geração de calor interna. Se manifesta como um aumento da temperatura do meio. Exemplos:
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia. Transmissão de calor. 3º ano
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia ransmissão de calor 3º ano 4. ransmissão de Calor em Regime ransiente Introdução Sistemas Concentrados Condução de Calor em regime ransiente com Efeitos
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia ransmissão de calor 3º ano 4. ransmissão de Calor em Regime ransiente Introdução Sistemas Concentrados Condução de Calor em regime ransiente com Efeitos
Mecanismos de transferência de calor
 Mecanismos de transferência de calor Condução Potência calor: Q cond A T 1 T x : condutibilidde térmica; A: área de transferência x: espessura ao longo da condução T 1 T : diferença de temperatura ifusividade
Mecanismos de transferência de calor Condução Potência calor: Q cond A T 1 T x : condutibilidde térmica; A: área de transferência x: espessura ao longo da condução T 1 T : diferença de temperatura ifusividade
Condução unidimensional em regime estacionário, Sistemas Radiais
 Com freqüência, em sistemas cilíndricos e esféricos há gradientes de temperatura somente na direção radial, o que permite analisá-los como sistemas unidimensionais. Um exemplo comum é o cilindro oco, cujas
Com freqüência, em sistemas cilíndricos e esféricos há gradientes de temperatura somente na direção radial, o que permite analisá-los como sistemas unidimensionais. Um exemplo comum é o cilindro oco, cujas
Capítulo 4 Condução Bidimensional em Regime Estacionário. Prof. Dr. Santiago del Rio Oliveira
 Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
Transferência de Calor
 Transferência de Calor Condução Unidimensional, em Regime Permanente com Geração Interna de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica
Transferência de Calor Condução Unidimensional, em Regime Permanente com Geração Interna de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica
UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL
 UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL LOM3083 e LOM3213 Fenômenos de Transporte Prof. Luiz T. F. Eleno Lista de exercícios 2 1. Considere uma parede aquecida por convecção de um
UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL LOM3083 e LOM3213 Fenômenos de Transporte Prof. Luiz T. F. Eleno Lista de exercícios 2 1. Considere uma parede aquecida por convecção de um
CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS)
 CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS) Prof. Antonio Carlos Foltran EXEMPLOS DE APLICAÇÃO 2 Carregamento de forno LD em aciaria Fonte: Companhia Siderúrgica
CAP 3 CONDUÇÃO UNIDIMENSIONAL EM REGIME PERMANENTE EM PAREDES CILÍNDRICAS (SISTEMAS RADIAIS) Prof. Antonio Carlos Foltran EXEMPLOS DE APLICAÇÃO 2 Carregamento de forno LD em aciaria Fonte: Companhia Siderúrgica
Condições variam com o tempo. 1 ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar
 Condução de calor em regime transiente Condições variam com o tempo ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar ) Passa-se algum tempo antes
Condução de calor em regime transiente Condições variam com o tempo ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar ) Passa-se algum tempo antes
Transferência de Calor
 Transferência de Calor Escoamento Interno - Parte 2 Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Transferência de Calor Escoamento Interno - Parte 2 Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
3ª Lista de Exercícios: TRANSFERÊNCIA DE CALOR (RESOLUCIONÁRIO)
 UNIVESIDADE FEDEA FUMINENSE Escola de Engenharia HidroUFF aboratório de Hidráulica Disciplina: FENÔMENOS DE ANSPOE E HIDÁUICA Professores: Gabriel Nascimento (Depto. de Eng. Agrícola e Meio Ambiente) Elson
UNIVESIDADE FEDEA FUMINENSE Escola de Engenharia HidroUFF aboratório de Hidráulica Disciplina: FENÔMENOS DE ANSPOE E HIDÁUICA Professores: Gabriel Nascimento (Depto. de Eng. Agrícola e Meio Ambiente) Elson
Condução de Calor Bidimensional
 Condução de Calor Bidimensional Soluções analíticas para condução térmica em casos 2D requer um esforço muito maior daquelas para casos 1D. Há no entanto inúmeras soluções baseadas em técnicas da Física-Matemática,
Condução de Calor Bidimensional Soluções analíticas para condução térmica em casos 2D requer um esforço muito maior daquelas para casos 1D. Há no entanto inúmeras soluções baseadas em técnicas da Física-Matemática,
Transferência de Calor Condução e Convecção de Calor
 Transferência de Calor Condução e Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 O calor transferido por convecção, na unidade de tempo, entre uma superfície e um fluido, pode ser calculado
Transferência de Calor Condução e Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 O calor transferido por convecção, na unidade de tempo, entre uma superfície e um fluido, pode ser calculado
CONDUÇÃO DE CALOR APLICADO AO ESTUDO DE CONCEITOS MATEMÁTICOS DO ENSINO MÉDIO. Douglas Gonçalves Moçato*** Luiz Roberto Walesko*** Sumário
 CONDUÇÃO DE CALOR APLICADO AO ESUDO DE CONCEIOS MAEMÁICOS DO ENSINO MÉDIO Douglas Gonçalves Moçato*** Luiz Roberto Walesko***. Introdução. Conceitos de transmissão de calor. Convecção. Radiação.3 Condução
CONDUÇÃO DE CALOR APLICADO AO ESUDO DE CONCEIOS MAEMÁICOS DO ENSINO MÉDIO Douglas Gonçalves Moçato*** Luiz Roberto Walesko***. Introdução. Conceitos de transmissão de calor. Convecção. Radiação.3 Condução
ENGENHARIA DE MATERIAIS. Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa)
 ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] AULA 3 REVISÃO E
ENGENHARIA DE MATERIAIS Fenômenos de Transporte em Engenharia de Materiais (Transferência de Calor e Massa) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] AULA 3 REVISÃO E
EM34F Termodinâmica A
 EM34F Termodinâmica A Prof. Dr. André Damiani Rocha [email protected] Energia 2 Energia Transferência de Energia por Calor Sempre que existir diferença de temperatura haverá transferência de calor. Se
EM34F Termodinâmica A Prof. Dr. André Damiani Rocha [email protected] Energia 2 Energia Transferência de Energia por Calor Sempre que existir diferença de temperatura haverá transferência de calor. Se
Aproximação Unidimensional para Condução de Calor em Superfícies Estendidas
 Aproximação Unidimensional para Condução de Calor em Superfícies Estendidas email: [email protected] Disciplina: DEM/FEB/UNESP/Bauru Aproximação Unidimensional de um Problema Bidimensional Balanço energético:
Aproximação Unidimensional para Condução de Calor em Superfícies Estendidas email: [email protected] Disciplina: DEM/FEB/UNESP/Bauru Aproximação Unidimensional de um Problema Bidimensional Balanço energético:
Transferência de Calor
 Transferência de Calor Condução Unidimensional, em Regime Permanente e Sem Geração Interna de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica
Transferência de Calor Condução Unidimensional, em Regime Permanente e Sem Geração Interna de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica
Transferência de Calor Condução de Calor
 Transferência de Calor Condução de Calor Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 Lei de Fourier A Lei de Fourier é fenomenológica, ou seja, foi desenvolvida a partir da observação dos
Transferência de Calor Condução de Calor Material adaptado da Profª Tânia R. de Souza de 2014/1. 1 Lei de Fourier A Lei de Fourier é fenomenológica, ou seja, foi desenvolvida a partir da observação dos
Transferência de Calor 1
 Transferência de Calor Guedes, Luiz Carlos Vieira. G94t Transferência de calor : um / Luiz Carlos Vieira Guedes. Varginha, 05. 80 slides; il. Sistema requerido: Adobe Acrobat Reader Modo de Acesso: World
Transferência de Calor Guedes, Luiz Carlos Vieira. G94t Transferência de calor : um / Luiz Carlos Vieira Guedes. Varginha, 05. 80 slides; il. Sistema requerido: Adobe Acrobat Reader Modo de Acesso: World
Transferência de Calor: Origens Físicas F Equações de Taxas de Transferência
 Transferência de Calor: Origens Físicas F e Euações de Taxas de Transferência Transferência de Calor e Energia Térmica O ue é a transferência de calor? A transferência de calor éo trânsito de energia térmica
Transferência de Calor: Origens Físicas F e Euações de Taxas de Transferência Transferência de Calor e Energia Térmica O ue é a transferência de calor? A transferência de calor éo trânsito de energia térmica
OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR. Profa. Dra. Milena Martelli Tosi
 OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR Profa. Dra. Milena Martelli Tosi A IMPORTÂNCIA DA TRANSFERÊNCIA DE CALOR NA INDÚSTRIA DE ALIMENTOS Introdução Revisão: Mecanismos de transferência
OPERAÇÕES UNITÁRIAS II AULA 1: REVISÃO TRANSFERÊNCIA DE CALOR Profa. Dra. Milena Martelli Tosi A IMPORTÂNCIA DA TRANSFERÊNCIA DE CALOR NA INDÚSTRIA DE ALIMENTOS Introdução Revisão: Mecanismos de transferência
1 ) Temperatura na superfície de um sólido é alterada e a temperatura no interior do sólido começa a variar
 CONDUÇÃO DE CALOR EM REGIME TRANSIENTE Condições variam com o tempo problema transiente ocorre quando as condições de contorno variam. ) Temperatura na superfície de um sólido é alterada e a temperatura
CONDUÇÃO DE CALOR EM REGIME TRANSIENTE Condições variam com o tempo problema transiente ocorre quando as condições de contorno variam. ) Temperatura na superfície de um sólido é alterada e a temperatura
Aula 4 de FT II. Prof. Gerônimo
 Aula 4 de FT II Prof. Gerônimo Equação diferencial de Condução Vamos considerar a taxa de geração interna de calor q = E g. Coordenada x, y e z. Regime transiente. Considerando: q = q Volume de controle
Aula 4 de FT II Prof. Gerônimo Equação diferencial de Condução Vamos considerar a taxa de geração interna de calor q = E g. Coordenada x, y e z. Regime transiente. Considerando: q = q Volume de controle
Transferência de Calor
 Transferência de Calor Trocadores de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de Juiz
Transferência de Calor Trocadores de Calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal de Juiz
Utilizado quando se necessita rejeitar calor a baixas temperaturas. O uso do AR como meio de resfriamento tem as seguintes vantagens:
 TROCADORES DE CALOR ALETADOS E/OU COMPACTOS Utilizado quando se necessita rejeitar calor a baixas temperaturas. Pode-se utilizar como meios de resfriamento: ÁGUA ou AR O uso do AR como meio de resfriamento
TROCADORES DE CALOR ALETADOS E/OU COMPACTOS Utilizado quando se necessita rejeitar calor a baixas temperaturas. Pode-se utilizar como meios de resfriamento: ÁGUA ou AR O uso do AR como meio de resfriamento
Transferência de Energia
 APLICAÇÃO DO FRIO NA CADEIA ALIMENTAR CTeSP em GASTRONOMIA, TURISMO E BEM-ESTAR Definição é a passagem/transmissão de energia, na forma de calor, de um ponto para outro. A transferência de calor efectua-se
APLICAÇÃO DO FRIO NA CADEIA ALIMENTAR CTeSP em GASTRONOMIA, TURISMO E BEM-ESTAR Definição é a passagem/transmissão de energia, na forma de calor, de um ponto para outro. A transferência de calor efectua-se
5S.1 Representação Gráfica da Condução Unidimensional Transiente na Parede Plana, no Cilindro Longo e na Esfera
 5S.1 Representação Gráfica da Condução Unidimensional Transiente na Parede Plana, no Cilindro Longo e na Esfera Nas Seções 5.5 e 5.6, foram desenvolvidas aproximações pelo primeiro termo para a condução
5S.1 Representação Gráfica da Condução Unidimensional Transiente na Parede Plana, no Cilindro Longo e na Esfera Nas Seções 5.5 e 5.6, foram desenvolvidas aproximações pelo primeiro termo para a condução
INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA. Guia do ensaio de laboratório para a disciplina: Transmissão de Calor
 INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA Guia do ensaio de laoratório para a disciplina: Transmissão de Calor Análise da transferência de calor em superfícies com alhetas ou pinos. João
INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA Guia do ensaio de laoratório para a disciplina: Transmissão de Calor Análise da transferência de calor em superfícies com alhetas ou pinos. João
TRANSMISSÃO DE CALOR resumo
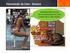 TRANSMISSÃO DE CALOR resumo convecção forçada abordagem experimental ou empírica Lei do arrefecimento de Newton Taxa de Transferência de Calor por Convecção 𝑞"#$ ℎ𝐴 𝑇 𝑇 ℎ 1 𝐴 ℎ - Coeficiente Convectivo
TRANSMISSÃO DE CALOR resumo convecção forçada abordagem experimental ou empírica Lei do arrefecimento de Newton Taxa de Transferência de Calor por Convecção 𝑞"#$ ℎ𝐴 𝑇 𝑇 ℎ 1 𝐴 ℎ - Coeficiente Convectivo
Aula 3 de FT II. Prof. Geronimo
 Aula 3 de FT II Prof. Geronimo Raio crítico de isolamento O conceito de raio crítico de isolamento, é introduzido para geometrias onde a área de troca de calor varia com uma dimensão especificada. Por
Aula 3 de FT II Prof. Geronimo Raio crítico de isolamento O conceito de raio crítico de isolamento, é introduzido para geometrias onde a área de troca de calor varia com uma dimensão especificada. Por
Lista de Exercícios para P2
 ENG 1012 Fenômenos de Transporte II Lista de Exercícios para P2 1. Estime o comprimento de onda que corresponde à máxima emissão de cada de cada um dos seguintes casos: luz natural (devido ao sol a 5800
ENG 1012 Fenômenos de Transporte II Lista de Exercícios para P2 1. Estime o comprimento de onda que corresponde à máxima emissão de cada de cada um dos seguintes casos: luz natural (devido ao sol a 5800
Convecção Forçada Interna a Dutos
 Convecção Forçada Interna a Dutos Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Escoamento no interior de dutos Velocidade Média Região de Entrada Hidrodinâmica
Convecção Forçada Interna a Dutos Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Escoamento no interior de dutos Velocidade Média Região de Entrada Hidrodinâmica
Transferência de Calor
 Transferência de Calor Condução em Paredes Planas e Cilíndricas Prof. Universidade Federal do Pampa BA000200 Campus Bagé 15 de maio de 2017 Transferência de Calor: Condução 1 / 28 Condução: Lei de Fourier
Transferência de Calor Condução em Paredes Planas e Cilíndricas Prof. Universidade Federal do Pampa BA000200 Campus Bagé 15 de maio de 2017 Transferência de Calor: Condução 1 / 28 Condução: Lei de Fourier
Capítulo 8: Transferência de calor por condução
 Capítulo 8: ransferência de calor por condução Condução de calor em regime transiente Condução de calor em regime transiente Até o momento só foi analisada a transferência de calor por condução em regime
Capítulo 8: ransferência de calor por condução Condução de calor em regime transiente Condução de calor em regime transiente Até o momento só foi analisada a transferência de calor por condução em regime
UNIVRSIDADE EDUARDO MONDLANE Faculdade de Engenharia. 3º ano. Prof. Doutor Engº Jorge Nhambiu 1
 UNIVRSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 11 # 5. Métodos Numéricos em Transferência de Calor Formulação de Equações Diferenciais
UNIVRSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor 3º ano Prof. Doutor Engº Jorge Nhambiu 1 Aula 11 # 5. Métodos Numéricos em Transferência de Calor Formulação de Equações Diferenciais
PNV-2321 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR
 PNV-31 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR TRANSMISSÃO DE CALOR 1) INTRODUÇÃO Sempre que há um gradiente de temperatura no interior de um sistema ou quando há contato de dois sistemas com temperaturas
PNV-31 TERMODINÂMICA E TRANSFERÊNCIA DE CALOR TRANSMISSÃO DE CALOR 1) INTRODUÇÃO Sempre que há um gradiente de temperatura no interior de um sistema ou quando há contato de dois sistemas com temperaturas
Exame de Transmissão de Calor Mestrado Integrado em Engenharia Mecânica e Engenharia Aeroespacial 30 de Janeiro de º Semestre
 Eame de Transmissão de Calor Mestrado Integrado em Engenharia Mecânica e Engenharia Aeroespacial 30 de Janeiro de 2012 1º Semestre Observações: 1- Duração do eame: 3 h 2- Tempo aconselhado para a parte
Eame de Transmissão de Calor Mestrado Integrado em Engenharia Mecânica e Engenharia Aeroespacial 30 de Janeiro de 2012 1º Semestre Observações: 1- Duração do eame: 3 h 2- Tempo aconselhado para a parte
No escoamento sobre uma superfície, os perfis de velocidade e de temperatura têm as formas traduzidas pelas equações:
 Enunciados de problemas de condução do livro: Fundamentals of Heat and Mass Transfer, F.P. Incropera e D.P. DeWitt, Ed. Wiley (numeros de acordo com a 5ª Edição). Introdução à Convecção 6.10 - No escoamento
Enunciados de problemas de condução do livro: Fundamentals of Heat and Mass Transfer, F.P. Incropera e D.P. DeWitt, Ed. Wiley (numeros de acordo com a 5ª Edição). Introdução à Convecção 6.10 - No escoamento
FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO
 FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO PROF.: KAIO DUTRA Convecção Térmica O modo de transferência de calor por convecção é composto por dois mecanismos. Além da transferência
FENÔMENOS DE TRANSPORTES AULA 12 E 13 INTRODUÇÃO À CONVECÇÃO E CONDUÇÃO PROF.: KAIO DUTRA Convecção Térmica O modo de transferência de calor por convecção é composto por dois mecanismos. Além da transferência
Programa Analítico de Disciplina ENG278 Transferência de Calor e Massa
 0 Programa Analítico de Disciplina ENG78 Transferência de Calor e Massa Departamento de Engenharia Agrícola - Centro de Ciências Agrárias Número de créditos: Teóricas Práticas Total Duração em semanas:
0 Programa Analítico de Disciplina ENG78 Transferência de Calor e Massa Departamento de Engenharia Agrícola - Centro de Ciências Agrárias Número de créditos: Teóricas Práticas Total Duração em semanas:
Transferência de calor
 Transferência de calor 1.1 Calor: Forma de energia que se transmite espontaneamente de um corpo para o outro quando entre eles existir uma diferença de temperatura. O calor é uma energia em trânsito provocada
Transferência de calor 1.1 Calor: Forma de energia que se transmite espontaneamente de um corpo para o outro quando entre eles existir uma diferença de temperatura. O calor é uma energia em trânsito provocada
CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO
 CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO CONTEÚDO TRANSFERÊNCIA DE CALOR CONDUÇÃO LEI DE FOURIER CONDUTIVIDADE TÉRMICA DIFUSIVIDADE TÉRMICA CONDUÇÃO DE CALOR UNIDIMENSIONAL
CONDUÇÃO DE CALOR PÁTRICIA KUERTEN GUIZONI SUELI ALBERTON SALVALAGIO CONTEÚDO TRANSFERÊNCIA DE CALOR CONDUÇÃO LEI DE FOURIER CONDUTIVIDADE TÉRMICA DIFUSIVIDADE TÉRMICA CONDUÇÃO DE CALOR UNIDIMENSIONAL
Lista de exercícios Caps. 7 e 8 TMEC-030 Transferência de Calor e Massa Período especial 2017/2
 Lista de exercícios Caps. 7 e 8 TMEC-030 Transferência de Calor e Massa Período especial 2017/2 1. (Incropera et al., 6 ed., 7.2) Óleo de motor a 100ºC e a uma velocidade de 0,1 m/s escoa sobre as duas
Lista de exercícios Caps. 7 e 8 TMEC-030 Transferência de Calor e Massa Período especial 2017/2 1. (Incropera et al., 6 ed., 7.2) Óleo de motor a 100ºC e a uma velocidade de 0,1 m/s escoa sobre as duas
Condução de calor Transiente
 Fenômenos de Transporte Capitulo 8 cont. Condução de calor Transiente Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI Condução de calor transitória Se as condições de contorno térmica são dependentes
Fenômenos de Transporte Capitulo 8 cont. Condução de calor Transiente Prof. Dr. Christian J. Coronado Rodriguez IEM - UNIFEI Condução de calor transitória Se as condições de contorno térmica são dependentes
1ª Lista de Exercícios. Unidade Curricular: FNT22304 Fenômenos dos Transportes CONDUÇÃO
 1ª Lista de Exercícios Unidade Curricular: FNT22304 Fenômenos dos Transportes CONDUÇÃO 1.8 Um recipiente de baixo custo para comida e bebida é fabricado em poliestireno (isopor) de 25 mm de espessura (0,023
1ª Lista de Exercícios Unidade Curricular: FNT22304 Fenômenos dos Transportes CONDUÇÃO 1.8 Um recipiente de baixo custo para comida e bebida é fabricado em poliestireno (isopor) de 25 mm de espessura (0,023
Colégio Técnico de Lorena (COTEL)
 Colégio Técnico de Lorena (COTEL) Operações Unitárias Transferência de Calor Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas destinam-se exclusivamente a
Colégio Técnico de Lorena (COTEL) Operações Unitárias Transferência de Calor Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas destinam-se exclusivamente a
Profa.. Dra. Ana Maria Pereira Neto
 5/09/0 Universidade Federal do ABC BC309 Termodinâmica Aplicada Profa.. Dra. Ana Maria Pereira Neto [email protected] Bloco A, torre, sala 637 Calor, Trabalho e Primeira Lei da Termodinâmica 5/09/0
5/09/0 Universidade Federal do ABC BC309 Termodinâmica Aplicada Profa.. Dra. Ana Maria Pereira Neto [email protected] Bloco A, torre, sala 637 Calor, Trabalho e Primeira Lei da Termodinâmica 5/09/0
Transferência de Calor
 Transferência de Calor Escoamento Interno - Parte 1 Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Transferência de Calor Escoamento Interno - Parte 1 Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade Federal
Operações Unitárias II Lista de Exercícios 1 Profa. Dra. Milena Martelli Tosi
 1. Vapor d água condensado sobre a superfície externa de um tubo circular de parede fina, com diâmetro interno igual a 50 mm e comprimento igual a 6 m, mantém uma temperatura na superfície externa uniforme
1. Vapor d água condensado sobre a superfície externa de um tubo circular de parede fina, com diâmetro interno igual a 50 mm e comprimento igual a 6 m, mantém uma temperatura na superfície externa uniforme
Transferência de Calor
 Transferência de Calor Introdução à transferência de calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Introdução à transferência de calor Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Resolução comentada da P1 de 2017 de Transferência de Calor (PME3360)
 MECATRONE Vol. 2, n o 1 (2017) Texto Livre 2, pág. 1 Resolução comentada da P1 de 2017 de Transferência de Calor (PME3360) Éber Saj Porcacchia Resumo A disciplina de Transferência de Calor (PME3360) costuma
MECATRONE Vol. 2, n o 1 (2017) Texto Livre 2, pág. 1 Resolução comentada da P1 de 2017 de Transferência de Calor (PME3360) Éber Saj Porcacchia Resumo A disciplina de Transferência de Calor (PME3360) costuma
UNIVERSIDADE EDUARDO MONDLANE
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor Aula prática Nº 11 1 Aula Prática-11 Transferência de Massa Problema -8.1(I) Um recipiente contem um refrigerante gaseificado
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenharia Transmissão de calor Aula prática Nº 11 1 Aula Prática-11 Transferência de Massa Problema -8.1(I) Um recipiente contem um refrigerante gaseificado
ESZO Fenômenos de Transporte
 Universidade Federal do ABC ESZO 001-15 Fenômenos de Transporte Profa. Dra. Ana Maria Pereira Neto [email protected] Bloco A, torre 1, sala 637 Mecanismos de Transferência de Calor Calor Calor pode
Universidade Federal do ABC ESZO 001-15 Fenômenos de Transporte Profa. Dra. Ana Maria Pereira Neto [email protected] Bloco A, torre 1, sala 637 Mecanismos de Transferência de Calor Calor Calor pode
ESTE Aula 2- Introdução à convecção. As equações de camada limite
 Universidade Federal do ABC ESTE013-13 Aula - Introdução à convecção. As equações de camada limite EN 41: Aula As equações de camada limite Análise das equações que descrevem o escoamento em camada limite:
Universidade Federal do ABC ESTE013-13 Aula - Introdução à convecção. As equações de camada limite EN 41: Aula As equações de camada limite Análise das equações que descrevem o escoamento em camada limite:
EM34B Transferência de Calor 2
 EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha [email protected] Trocadores de Calor 2 Trocadores de Calor Introdução Os trocadores de calor são dispositivos que facilitam a transferência
EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha [email protected] Trocadores de Calor 2 Trocadores de Calor Introdução Os trocadores de calor são dispositivos que facilitam a transferência
Descrição Macroscópica de um Gás ideal
 Descrição Macroscópica de um Gás ideal O gás não tem volume fixo ou uma pressão fixa O volume do gás é o volume do recipiente A pressão do gás depende do tamanho do recipiente A equação de estado relaciona
Descrição Macroscópica de um Gás ideal O gás não tem volume fixo ou uma pressão fixa O volume do gás é o volume do recipiente A pressão do gás depende do tamanho do recipiente A equação de estado relaciona
TRANSP. BRAS. GAS. BOLÍVIA-BRASIL GERAL SIMULAÇÃO ÍNDICE DE REVISÕES DESCRIÇÃO E / OU FOLHAS ATINGIDAS
 GOPE CAT. : ÁREA DE ATIVIDADE: SERVIÇO: TÍTULO : TRANSP. BRAS. GAS. BOLÍVIA-BRASIL GERAL SIMULAÇÃO de 9 METODOLOGIA DE CÁLCULO DO COEFICIENTE GLOBAL DE TRANSFERÊNCIA DE CALOR REV. ÍNDICE DE REVISÕES DESCRIÇÃO
GOPE CAT. : ÁREA DE ATIVIDADE: SERVIÇO: TÍTULO : TRANSP. BRAS. GAS. BOLÍVIA-BRASIL GERAL SIMULAÇÃO de 9 METODOLOGIA DE CÁLCULO DO COEFICIENTE GLOBAL DE TRANSFERÊNCIA DE CALOR REV. ÍNDICE DE REVISÕES DESCRIÇÃO
Transferência de Calor
 Transferência de Calor Escoamento Sobre uma Placa Plana Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
Transferência de Calor Escoamento Sobre uma Placa Plana Filipe Fernandes de Paula [email protected] Departamento de Engenharia de Produção e Mecânica Faculdade de Engenharia Universidade
EP34D Fenômenos de Transporte
 EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha [email protected] Introdução à Transferência de Calor 2 Introdução à Transferência de Calor O que é Transferência de Calor? Transferência de
EP34D Fenômenos de Transporte Prof. Dr. André Damiani Rocha [email protected] Introdução à Transferência de Calor 2 Introdução à Transferência de Calor O que é Transferência de Calor? Transferência de
Lista de Exercícios para P1
 ENG 1012 Fenômenos de Transporte II - 2015.2 Lista de Exercícios para P1 Problema 1. Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e placa de gesso, como
ENG 1012 Fenômenos de Transporte II - 2015.2 Lista de Exercícios para P1 Problema 1. Uma casa possui uma parede composta com camadas de madeira, isolamento à base de fibra de vidro e placa de gesso, como
Universidade Federal de Sergipe, Departamento de Engenharia Química 2
 ELABORAÇÃO DE FERRAMENTA DE CÁLCULO PARA A DETERMINAÇÃO DO COEFICIENTE CONVECTIVO EM EXPERIMENTOS DE CONVECÇÃO FORÇADA AO REDOR DE UM CORPO SUBMERSO E ALETAS TORRES, F. C. O. 1, BARBOSA NETO, A. M. 2 1
ELABORAÇÃO DE FERRAMENTA DE CÁLCULO PARA A DETERMINAÇÃO DO COEFICIENTE CONVECTIVO EM EXPERIMENTOS DE CONVECÇÃO FORÇADA AO REDOR DE UM CORPO SUBMERSO E ALETAS TORRES, F. C. O. 1, BARBOSA NETO, A. M. 2 1
EM34B Transferência de Calor 2
 EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha [email protected] Convecção Forçada Escoamento Interno Parte I 2 Convecção Forçada: Escoamento Interno Definição Escoamento Interno: é um
EM34B Transferência de Calor 2 Prof. Dr. André Damiani Rocha [email protected] Convecção Forçada Escoamento Interno Parte I 2 Convecção Forçada: Escoamento Interno Definição Escoamento Interno: é um
Estudo do Comportamento e Desempenho de Aleta Tipo Pino
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA Estudo do Comportamento e Desempenho de Aleta Tipo Pino RELATÓRIO DE TRABALHO DE
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA Estudo do Comportamento e Desempenho de Aleta Tipo Pino RELATÓRIO DE TRABALHO DE
Lista de exercícios Caps. 4 e 5 TM-114 Transferência de Calor e Massa (Turma B) 2008/1
 Lista de exercícios Caps. 4 e 5 TM-114 Transferência de Calor e Massa (Turma B) 2008/1 1. (Incropera et al., 6 ed., 4.2) Uma placa retangular bidimensional está sujeita às condições de contorno especificadas.
Lista de exercícios Caps. 4 e 5 TM-114 Transferência de Calor e Massa (Turma B) 2008/1 1. (Incropera et al., 6 ed., 4.2) Uma placa retangular bidimensional está sujeita às condições de contorno especificadas.
Transferência de Calor Condução: paredes planas. Prof. Marco A. Simões
 Transferência de Calor Condução: paredes planas Prof. Marco A. Simões Objetivosda aula Entender o processo da condução térmica Aplicar a Lei de Fourier à condução térmica Entender o significado do coeficiente
Transferência de Calor Condução: paredes planas Prof. Marco A. Simões Objetivosda aula Entender o processo da condução térmica Aplicar a Lei de Fourier à condução térmica Entender o significado do coeficiente
LOQ Fenômenos de Transporte I
 LOQ 4083 - Fenômenos de Transporte I FT I 07 Equações básicas na forma integral para o volume de controle Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas
LOQ 4083 - Fenômenos de Transporte I FT I 07 Equações básicas na forma integral para o volume de controle Prof. Lucrécio Fábio dos Santos Departamento de Engenharia Química LOQ/EEL Atenção: Estas notas
Vicente Luiz Scalon. Disciplina: Transmissão de Calor
 Convecção Forçada Externa Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Método Empírico Camada Limite Teoria de Prandtl Solução de Blasius Convecção Laminar
Convecção Forçada Externa Vicente Luiz Scalon Faculdade de Engenharia/UNESP-Bauru Disciplina: Transmissão de Calor Sumário Método Empírico Camada Limite Teoria de Prandtl Solução de Blasius Convecção Laminar
Transferência de calor em superfícies aletadas
 Transferência de calor em superfícies aletadas Por ue usar aletas? Interior condução Na fronteira convecção = ha(ts - T) Para aumentar : - aumentar o h - diminuir T - aumentar a área de troca de calor
Transferência de calor em superfícies aletadas Por ue usar aletas? Interior condução Na fronteira convecção = ha(ts - T) Para aumentar : - aumentar o h - diminuir T - aumentar a área de troca de calor
