(2008/2009) Espaços vectoriais. Matemática 1º Ano - 1º Semestre 2008/2009. Mafalda Johannsen
|
|
|
- Otávio Lopes Sousa
- 6 Há anos
- Visualizações:
Transcrição
1 Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009
2 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores Independência Linear Transformações Lineares Base de um Espaço Vectorial Mudança de Base Determinar Coordenadas de um Vector em Diferentes Bases Valores e Vectores Próprios Diagonalização de uma Matriz Formas Quadráticas Estudo do Sinal das Formas Quadráticas
3 Características de um Espaço Vectorial Um espaço vectorial tem de respeitar todas estas propriedades: - Tem de ter origem, isto é, o nulo da dimensão onde está ( ); - Tem de ser fechado para a soma. Por outras palavras, o conjunto A diz-se fechado para a soma de elementos do conjunto se e só se: a,b A : a+b A; - Tem de ser fechado para a multiplicação por escalares, ou seja, se multiplicarmos um elemento do conjunto por outro elemento que pertença a IR, o resultado tem de fazer parte do conjunto do primeiro elemento : IR, b : A. Exemplo 1.1: IN é um espaço vectorial? Não, dado que não tem origem ou o nulo da dimensão (0 não pertence a IN). Exemplo 1.2: Q é um espaço vectorial? Tem origem (0 pertence a Q) e é fechado para a soma ( + =3, 3 ), no entanto não é fechado para a multiplicação escalar: x =, não pertence a Q. Dimensão do Espaço A dimensão de um espaço vectorial é sempre igual ao número de vectores da base: (x,y) dimensão 2 (x,y,z) dimensão 3 (x, z-x, z) dimensão 2
4 Subespaço Vectorial Um Subespaço Vectorial é um espaço mais pequeno, cujas propriedades de cima têm de ser respeitadas. Exemplo 1.3: é um subespaço de é subespaço de Exemplo 1.4: Diga se (x, y, 0) é subespaço de. É fechado para a adição vectorial: É fechado para a multiplicação escalar: (x1, y1, 0) + (x2, y2, 0) = (x1+x2, y1+y2, 0) Exemplo 1.5: Diga se (1, y, z) é subespaço de. Não é fechado para a adição vectorial, logo já não é subespaço: (1, y1, z1) + (1, y2, z2) = (2, y1+y2, z1+z2)
5 Combinação Linear de Vectores Uma combinação Linear de Vectores é algo do género: = são escalares e, e são vectores, sendo que é o resultado da combinação. Representação de Vectores = (a, b) (a, b) = a(1,0) + b(0,1) =
6 Independência Linear N vectores dizem-se linearmente independentes quando não for possível obter cada um deles à custa de combinações lineares feitas entre os restantes. Matematicamente, três vectores dizem-se linearmente independentes se e só se + + =, com = = = 0. Exemplo 2.1: (1,1) (1,0) (3,2) só serão linearmente independentes se λ1(1,1) + λ2(1,0) + λ3(3,2)=0 (, ) + (, 0) + (3, 2 ) = (0,0) (λ1+ λ2+3λ3, λ1+2λ3) = (0,0) Fixar uma constante: outro número qualquer) (a constante escolhida é aleatória, pode ser 2 como (-4, -2, 2) Agora substitui-se os pelos valores encontrados: -4(1,1) -2(1,0) +2(3,2) = (0,0) (-4,-4)+(-2,0)+(6,4) = (0,0) Pode-se concluir que não são linearmente independentes, pois para obter o vector nulo tivemos de utilizar ( = (-4, -2, 2) e, segundo a regra de independência linear, teríamos de ter usado (0, 0, 0).
7 Em, o máximo de vectores independentes entre si é n. Portanto, em há no máximo 30 vectores independentes e assim sucessivamente.
8 Porém, esta forma de avaliar a independência linear é bastante complexa. Podemos fazê-lo de uma forma muito mais simples: determinamos a dependência linear através da condensação de matrizes, com as operações anteriormente estudadas. Exemplo 2.2: Estude a independência linear do seguinte conjunto de vectores: -1; 2-2 ; 3x+1 (Caderno de Espaços Vectoriais) O vector -1 fica (1, 0, -1), dado que o coeficiente de é 1 e de x é 0. O vector 2-2 fica (-2, 0, 2) O vector 3x+1 fica (0, 3, 1) Portanto, em matriz fica: Depois de condensada, podemos concluir que não há independência linear: Exemplo 2.3: Verifique se os vectores (5, 0, 0), (3,2,0) e (4,3,1) são linearmente independentes. São linearmente independentes. Não é necessário operar a condensação, na medida em que já está feita.
9 Transformações Lineares As transformações lineares têm de possuir as seguintes propriedades: - Linear para a soma: Sendo os vectores (x, y) dois quaisquer vectores, teremos de verificar que T(x+y) = T(x) + T(y); -Linear para a multiplicação: T( x) = T(x). Uma transformação linear pode ser sempre representada pelo produto de uma matriz pelo vector que queremos transformar, isto é, T(x) = Ax, em que x é um vector. Exemplo 3.1: A transformação linear T de em definida por T(x, y, z) = (x, x+y+z) é linear. A transformação T de em definida por T(x, y, z) = (x, z+4) não é linear. Exemplo 3.2: Mostre que a transformação T de em definida por T(x, y, z) = (x, y, y+z) é linear. Neste exercício, temos de provar que a transformação é, de facto, linear. Como tal, é necessário montar e desmontar a transformação. Vejamos: A propriedade é T( + ) = ) + (isto é, provar que é linear para a soma e para a multiplicação) 1º Passo - Arranjar quaisquer x,y, z e colocar os fora das coordenadas, mas dentro da transformação: T( 1(x1, y1, z1) + 2(x2, y2, z2)) = 2º Passo Juntar os às coordenadas e somar os x s, os y s e os z s: = T( 1x1 + 2x2, 1y1 + 2y2, 1z1 + 2z2) =
10 3º Passo Substituir os x, y, z pelos do enunciado (isto é, x, y, y+z) e retirar o T: = ( 1x1 + 2x2, 1y1 + 2y2, 1(y1+z1) + 2(y2+z2) = 4º Passo Separam-se as coordenadas, ficando todas as que sejam 1 juntas e todas as que sejam 2 juntas também: = ( x1, 1y1, 1(y1+z1)) + ( 2x2, 2y2, 2(y2+z2)) = 5º Passo Pôr os em evidência: = 6º Passo Voltar à situação inicial, daí o T também aparecer novamente: = 1T(x1, y1, z1) + 2T(x2, y2, z2) Recapitulando: T( 1(x1, y1, z1) + 2(x2, y2, z2)) = = T( 1x1 + 2x2, 1y1 + 2y2, 1z1 + 2z2) = = ( 1x1 + 2x2, 1y1 + 2y2, 1(y1+z1) + 2(y2+z2) = = ( x1, 1y1, 1(y1+z1)) + ( 2x2, 2y2, 2(y2+z2)) = = = 1T(x1, y1, z1) + 2T(x2, y2, z2) Outros conceitos indissociáveis desta matéria são o núcleo da transformação e o contradomínio ou imagem da mesma. Considere-se a transformação Linear T de E em F. Chama-se núcleo de T ao conjunto de vectores de E que são transformados por T no vector nulo. A dimensão deste, também denominada nulidade, é a subtracção da dimensão do espaço de partida (neste caso, E) pela dimensão do contradomínio. A dimensão do contradomínio, por sua vez, é a característica (o r ) da matriz.
11 Por último, será relevante estudar a invertibilidade de uma transformação linear, isto é, analisar se esta é ou não invertível. Tal como acontece com qualquer função, a transformação linear é invertível apenas se for injectiva.
12 Base de um Espaço Vectorial Um conjunto de vectores ou elementos diz-se base de um espaço vectorial, se e só se for formado por vectores linearmente independentes e ainda gerar todo o espaço. Para gerar todo o espaço, a base tem de ter um número de vectores igual ao cardinal da dimensão do espaço, por exemplo: em (8, 4) e (1, 9) geram todo o espaço, visto que são dois vectores a gerar uma dimensão 2. Se, em vez de existirem os vectores (8, 4) e (1, 9), apenas houvesse o (8, 4), este já não geraria todo o espaço, na medida em que é um vector e a dimensão é 2. Portanto pode-se concluir que em há, no máximo, n vectores linearmente independentes que geram todo o espaço. Exemplo 4.1: Verifique se os seguintes vectores são linearmente independentes em : (1, 3); (2, 5); (0, 1). Num espaço vectorial de dimensão 2, 3 vectores são sempre linearmente dependentes. Exemplo 4.2: Diga se os vectores (1, 4, 5) e (0, 1, 2) podem constituir uma base do espaço respectivo. Neste caso, o espaço respectivo é, dado que cada vector é composto por três coordenadas, logo a dimensão do espaço é 3. Como tal, dois vectores nunca geram um espaço de dimensão 3, assim sendo, não formam uma base. Exemplo 4.3: Conclua se os vectores (3, 1); (3, 1) e (2, 1) podem constituir uma base em.
13 Num espaço vectorial de dimensão 2, três vectores são sempre linearmente dependentes, não podendo, deste modo, formar uma base. Atenção!: Quando nos é dado um vector e não se menciona a base em que ele vem expresso, é porque se está a considerar a base canónica. Base canónica de : (1,0); (0,1). Base Canónica de : (1,0,0); (0,1,0); (0,0,1). Resumindo: Dependência Base Espaço de Dimensão N Sistema de Geradores N-1 vectores Não Dependente/Independente Não N vectores Sim Dependente/Independente Não/Sim N+1 vectores Sim Dependente Não
14 Mudança de Base Existem três situações de mudança de base que podem ocorrer: 1º) Quando se deseja passar de uma base qualquer A para outra qualquer B; 2º) Quando se deseja passar da base canónica para uma base qualquer B; 3º) E quando se deseja passar de uma qualquer base B para a base canónica. 1º) Matriz que transforma coordenadas de uma base qualquer A para uma base qualquer B: A B 2º) Matriz que transforma coordenadas de uma base canónica para uma base qualquer B: 3º) Matriz que transforma coordenadas de uma base qualquer B para a base canónica: B
15 Exemplo 5.1: Considere a base V = de formada pelos vectores v1 = (2, -1, 3), v2 = (-1, 1, 1), v3 = (3, -1, 6). (Frequência de 29 de Janeiro de 2007) Este é o 2º caso de mudança de base, portanto opera-se a inversa da matriz Exemplo 5.2: Numa transformação T de tem na base a matriz A= Determine a matriz da transformação na base onde = + 2 = Este é, nitidamente, o 1º caso. Portanto, é necessário saber qual é a matriz A e qual a B. A matriz A corresponde à base velha, neste caso, é a matriz. A matriz B será então a base nova, ou seja, (são os coeficientes de e ). Logo fica:
16 Determinar Coordenadas de um Vector em Diferentes Bases 1º Caso: Sabem-se as coordenadas na base nova e querem-se na base velha Matriz mudança de base = Coordenadas da base velha Coordenadas da base nova 2º Caso: Sabem-se as coordenadas na base velha e querem-se na base nova Matriz mudança de base = Coordenadas na base nova Coordenadas na base velha
17 Exemplo 6.1: Dado o vector (1, 2, 1) na base canónica, escreva-o na base constituída pelos vectores (5, 0, 0); (3, 2, 0); (1, 2, 3). Este é o 2º Caso, dado que se sabem as coordenadas na base velha e pedem para as descobrirmos na base nova. A base velha é a canónica e a matriz é a matriz mudança de base. Logo, fica: = Exemplo 6.2: Sabe-se que a base A é constituída pelos vectores (1, 4, 5); (2, 3, 9); (2, 2, 7). Quais as coordenadas do vector (0, 0, 7) na base canónica? Este já é o 1º caso, portanto: =
18 Valores e Vectores Próprios Um vector diz-se próprio relativamente a uma transformação linear se e só se: T(x) = ax = x ( a é uma matriz) ax = x ax- x = 0 (a-λ)x = 0 (a-λi) = 0 Ao conjunto dos valores admissíveis para λ chamamos valores próprios associados aos vectores próprios da equação. Para tornar esta parte mais perceptível vejamos o seguinte exemplo: Exemplo 7.1: Seja a matriz A = (Caderno de Espaços Vectoriais) Determine os valores próprios de A e os correspondentes vectores próprios. Para começar, transforma-se a matriz num determinante, subtraem-se os λ aos valores da diagonal principal e iguala-se a zero: =0 Em seguida, utiliza-se a regra do determinante e descobrem-se os valores próprios:
19 (1-λ) (3-λ) (4x2) = 0 3 λ - 3λ = 0-4λ 5 = 0 λ = 1 λ = 5 1 e 5 são os valores próprios e com eles encontram-se os respectivos vectores próprios, substituindo os λ por 1 e 5, ampliando a matriz, condensando-a e fazendo um sistema: λ = 1: = = O vector próprio associado ao valor próprio 1, é: (0, 0) ou, escrito de outra forma: x (1, 0) λ = 5: = = O vector próprio associado ao valor próprio 5, é: x (1, 0)
20 Diagonalização de uma Matriz Em primeiro lugar, será necessário relembrar o conceito de matriz diagonal. Entende-se por matriz diagonal, a matriz que tiver todos os elementos iguais a zero, excepto os da diagonal principal (que podem ter qualquer valor, incluindo zero). Matriz diagonal 3x3: A = a, b, c IR Para se diagonalizar uma matriz tem que se seguir os seguintes passos: 1º Passo: Descobrir os valores próprios da matriz dada; 2º Passo: Descobrir os vectores próprios associados a cada valor próprio; 3º Passo: A matriz só será diagonizável se a multiplicidade algébrica for igual à multiplicidade geométrica; 4º Passo: A matriz que se obtém será, então, uma matriz diagonal, cuja diagonal principal contém os valores próprios da matriz inicial. Multiplicidade Algébrica: Número de vezes em que um valor próprio é solução do polinómio característico. Multiplicidade Geométrica: é o cardinal da base de vectores próprios associados a um valor próprio. Já se sabe de antemão que a matriz diagonal é formada pelos valores próprios, no entanto, ainda não foi explicado como é que se lá chega. Para se chegar à matriz
21 diagonal, aquilo que se faz à matriz inicial é: D = AP, onde D é a matriz diagonal, A a matriz inicial e P a matriz que tem como colunas os vectores próprios da matriz.
22 Exemplo 8.1: Seja P2 o espaço dos polinómios de grau 2 e considere-se a base. Seja T a transformação em P2 definida por T = p (x). A representação de T, na base fixada é feita pela matriz A = (Caderno de Espaços Vectoriais) Determine os valores próprios, os vectores próprios e diga se a transformação dada pode ser representada por uma matriz diagonal. Justifique. = 0 - = 0 λ = 0 λ = 0: O vector próprio associado ao valor próprio zero, será um vector do tipo (x, 0, 0) = x(1, 0, 0) A multiplicidade algébrica é 3, dado que o λ é 3 vezes solução, isto é, é 3 vezes um valor próprio. A multiplicidade geométrica é 1, dado que há um vector próprio, o (x, 0, 0). Portanto, a matriz não é diagonizável, visto que 1 3. Exemplo 8.2: Considere a transformação de em, representada em certa base pela matriz A = (Caderno de Espaços Vectoriais)
23 Determine os valores próprios e os vectores próprios associados. Determine a matriz diagonal que representa a transformação dada, embora numa outra base. Diga qual é essa base. = 0 λ = 1 λ = 1 λ = 3 λ = 1: (x, -2z, z) = x(1, 0, 0) + z(0, -2, 1) A multiplicidade geométrica de λ = 1 é 2, visto que tem dois vectores associados. A multiplicidade geométrica de λ = 1 é 2, dado que é duas vezes solução. Logo, a multiplicidade geométrica é igual à algébrica. No entanto, ainda não se pode afirmar que a matriz é diagonizável, na medida em que é necessário fazer os mesmos cálculos para λ = 3. Só se a multiplicidade algébrica e geométrica de λ = 3 forem iguais é que se pode diagonalizar. λ = 3: (z, 0, z) = z(1, 0, 1) A multiplicidade geométrica é 1 e a algébrica também, logo a matriz é diagonizável. Assim, a matriz diagonal será: D = P = (P tem como colunas os vectores próprios, logo esta é a base pedida no enunciado) Segundo a fórmula:
24 = Formas Quadráticas Uma forma quadrática é uma expressão que apenas apresenta termos de grau 2, por exemplo: + 2yx + 4. Uma forma quadrática pode ser sempre representada na seguinte forma: Pegando no exemplo + 2yx + 4, este pode ser representado assim: Os 1 s a negrito correspondem ao 2xy, ou seja, é obrigatório dividir por 2 sempre que o coeficiente corresponda a duas incógnitas. Exemplo 9.1: Seja a forma quadrática Q(xy) = 3 + 6xy +. Represente-a na forma matricial. Exemplo 9.2: Seja a forma quadrática Q(xy) = 2 + 5xy +. Represente-a na forma matricial.
25 Se a forma quadrática, em vez de ter duas variáveis (x, y), tiver três (x, y, z) fica: Exemplo 9.3: Seja a forma quadrática Q(xyz) = xy - 2yz + 4xz. Represente-a na forma matricial.
26 Estudo do Sinal da Forma Quadrática O sinal das formas quadráticas pode ser estudado através de dois métodos: - Pelos Valores Próprios; - Pelos Determinantes e Menores Principais. Pelos Valores Próprios Tal como diz o título, estudar o sinal através dos valores próprios é descobri-los e analisar-lhes os sinais. Se λ1 0 e λ2 0, então a forma quadrática é definida positiva. Se λ1 0 e λ2 0, a forma quadrática é definida negativa. Se λ1 0 e λ2 0 (ou vice-versa), a forma quadrática é semi-definida negativa. Se λ1 0 e λ2 0 (ou vice-versa), a forma quadrática é semi-definida positiva. Se λ1 0 e λ2 0 (ou vice-versa), a forma quadrática é indefinida. Exemplo 9.4: Estude o sinal da seguinte forma quadrática: Q(x, y) = xy. =0 ( ( ) 4 = λ + 3λ + + 6λ + 2 = 0 λ = -5,6 λ = -0, 355 A forma quadrática é definida negativa, dado que os dois valores próprios são negativos.
27 Pelos Determinantes e Menores Principais Seja uma forma quadrática na forma matricial Para descobrir se é definida positiva ou definida negativa, calcula-se o determinante da primeira linha e primeira coluna (D1 que neste caso é 2) e o da segunda linha e segunda coluna (D2): = -7 Se D1 > 0 D2 a forma quadrática é definida positiva Se D1 D2 0, a forma quadrática é definida negativa Neste exemplo, a forma quadrática é indefinida, mas vamos analisar como se ainda não soubéssemos, visto que ainda faltam as semi-definidas negativas e positivas: Para descobrir se é semi-definida positiva/negativa, calcula-se os menores principais de 1ª(Mp1 e Mp2) e 2ª(MP) ordem, exemplificando: Estes são os menores principais de 1ª ordem. Este é o menor principal de 2ª ordem, corta-se linhas e colunas imaginárias e calcula-se o determinante. Claro que se fosse uma matriz 3x3 só as linhas e colunas de 3ªordem é que seriam imaginárias e assim sucessivamente.
28 Se Mp1 0 Mp2 MP, a forma quadrática é semi-definida Positiva Se Mp1 0 Mp2 MP, a forma quadrática é semi-definida Negativa
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003. Funções reais de várias variáveis
 EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
ESPAÇOS LINEARES (ou vetoriais)
 Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
1. Considere a seguinte matriz dos vértices dum triângulo D = 0 2 3
 INSTITUTO SUPERIOR TÉCNICO - DEPARTAMENTO DE MATEMÁTICA 7 a LISTA DE PROBLEMAS E EXERCÍCIOS DE ÁLGEBRA LINEAR LEIC-Taguspark, LERCI, LEGI, LEE 1 o semestre 2006/07 - aulas práticas de 2006-12-04 e 2006-12-06
INSTITUTO SUPERIOR TÉCNICO - DEPARTAMENTO DE MATEMÁTICA 7 a LISTA DE PROBLEMAS E EXERCÍCIOS DE ÁLGEBRA LINEAR LEIC-Taguspark, LERCI, LEGI, LEE 1 o semestre 2006/07 - aulas práticas de 2006-12-04 e 2006-12-06
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Instituto Universitário de Lisboa
 Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
6. Verifique detalhadamente que os seguintes conjuntos são espaços vetoriais(com a soma e produto por escalar usuais):
 a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Expansão linear e geradores
 Espaços Vectoriais - ALGA - 004/05 Expansão linear e geradores Se u 1 ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u 1 ; u ;
Espaços Vectoriais - ALGA - 004/05 Expansão linear e geradores Se u 1 ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u 1 ; u ;
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
ESPAÇO VETORIAL REAL. b) Em relação à multiplicação: (ab) v = a(bv) (a + b) v = av + bv a (u + v ) = au + av 1u = u, para u, v V e a, b R
 ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
Lista 6: transformações lineares.
 Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
Diagonalização. Operador diagonalizável
 Operador linear Diagonalização Se T: V V for uma transformação linear definida no espaço vectorial V, então T designa-se por operador linear. A representação matricial de um operador linear depende da
Operador linear Diagonalização Se T: V V for uma transformação linear definida no espaço vectorial V, então T designa-se por operador linear. A representação matricial de um operador linear depende da
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
Ficha de Exercícios nº 1
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
5. Considere os seguintes subconjuntos do espaço vetorial F(R) das funções de R em R:
 MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
MAT3457 ÁLGEBRA LINEAR I 3 a Lista de Exercícios 1 o semestre de 2018 1. Verique se V = {(x, y) : x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação por escalar dadas por:
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0
![Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0 Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0](/thumbs/93/113642308.jpg) Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
ÁLGEBRA LINEAR I - MAT Em cada item diga se a afirmação é verdadeira ou falsa. Justifiquei sua resposta.
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 2 a Lista de
{ 1 2 3, 2 4 6, T
 Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
1 Autovetor e Autovalor 9. 2 Matrizes Ortogonais e Transformações Lineares Planas e Espaciais 55
 Capítulo LINE LINE Autovetor e Autovalor 9 Matrizes Ortogonais e Transformações Lineares Planas e Espaciais 55 Matrizes Simétricas, o Teorema Espectral e Operadores Auto-adjuntos 8 4 Formas Bilineares,
Capítulo LINE LINE Autovetor e Autovalor 9 Matrizes Ortogonais e Transformações Lineares Planas e Espaciais 55 Matrizes Simétricas, o Teorema Espectral e Operadores Auto-adjuntos 8 4 Formas Bilineares,
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Universidade Federal Fluminense - GAN
 Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
Conceitos Básicos INTRODUÇÃO 1 VETORES 1.1 REPRESENTAÇÃO DOS VETORES
 Conceitos Básicos INTRODUÇÃO Esse material foi criado por um motivo: o curso de álgebra linear II da UFRJ parte do princípio que o aluno de Engenharia da UFRJ que faz a disciplina já conhece alguns conceitos
Conceitos Básicos INTRODUÇÃO Esse material foi criado por um motivo: o curso de álgebra linear II da UFRJ parte do princípio que o aluno de Engenharia da UFRJ que faz a disciplina já conhece alguns conceitos
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 1 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
Álgebra Linear para LEIC - A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para LEIC - A Teste - 7 de Janeiro de 22 Versão A Duração: 9 minutos Resolução (com explicações detalhadas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para LEIC - A Teste - 7 de Janeiro de 22 Versão A Duração: 9 minutos Resolução (com explicações detalhadas
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Parte 2 - Espaços Vetoriais
 Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Parte 2 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
ÁLGEBRA LINEAR. Combinação Linear, Subespaços Gerados, Dependência e Independência Linear. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Combinação Linear, Subespaços Gerados, Dependência e Prof. Susie C. Keller Combinação Linear Sejam os vetores v 1, v 2,..., v n do espaço vetorial V e os escalares a 1, a 2,..., a n. Qualquer
ÁLGEBRA LINEAR Combinação Linear, Subespaços Gerados, Dependência e Prof. Susie C. Keller Combinação Linear Sejam os vetores v 1, v 2,..., v n do espaço vetorial V e os escalares a 1, a 2,..., a n. Qualquer
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Espaços Vectoriais. Espaços Vectoriais
 Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
AmigoPai. Matemática. Exercícios de Equação de 2 Grau
 AmigoPai Matemática Exercícios de Equação de Grau 1-Mai-017 1 Equações de Grau 1. (Resolvido) Identifique os coeficientes da seguinte equação do segundo grau: 3x (x ) + 17 = 0 O primeiro passo é transformar
AmigoPai Matemática Exercícios de Equação de Grau 1-Mai-017 1 Equações de Grau 1. (Resolvido) Identifique os coeficientes da seguinte equação do segundo grau: 3x (x ) + 17 = 0 O primeiro passo é transformar
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial
 TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
Parte 3 - Produto Interno e Diagonalização
 Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
3 a Avaliação Parcial - Álgebra Linear
 3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
MA71B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto. LISTA 5 - Espaços Vetoriais
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 5 - Espaços Vetoriais Desenvolvidas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 5 - Espaços Vetoriais Desenvolvidas
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
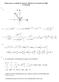 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
Capítulo 4 - Valores e Vectores Próprios
 Capítulo 4 - Valores e Vectores Próprios Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/ 17
Capítulo 4 - Valores e Vectores Próprios Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/ 17
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
Multiplicidade geométrica
 Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Valores e vectores próprios
 Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Questão 1: Seja V o conjunto de todos os pares ordenados de números reais. Denamos a adição e a multiplicação por escalar em V por
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 4 - Espaços Vetoriais Desenvolvidas
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Curitiba - DAMAT MA7B - Geometria Analítica e Álgebra Linear Profa. Dra. Diane Rizzotto Rossetto LISTA 4 - Espaços Vetoriais Desenvolvidas
1 a Lista de Exercícios MAT 3211 Álgebra Linear Prof. Vyacheslav Futorny
 1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
1 a Lista de Exercícios MAT 3211 Álgebra Linear - 213 - Prof. Vyacheslav Futorny 1 a parte: Resolução de sistemas de equações lineares, matrizes inversíveis 1. Para cada um dos seguintes sistemas de equações
7 temos que e u =
 Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Resolução do efólio B
 Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
2 Álgebra Linear (revisão)
 Teoria de Controle (sinopse) 2 Álgebra Linear (revisão) J. A. M. Felippe de Souza Neste capítulo vamos citar os principais tópicos de Álgebra Linear que são necessários serem revistos para o acompanhamento
Teoria de Controle (sinopse) 2 Álgebra Linear (revisão) J. A. M. Felippe de Souza Neste capítulo vamos citar os principais tópicos de Álgebra Linear que são necessários serem revistos para o acompanhamento
Resolução do 1 o Teste - A (6 de Novembro de 2004)
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
Transformações lineares
 Transformação linear (TL) Transformações lineares Sejam V e W espaços vectoriais. Uma função T : V W é chamada transformação linear de V em W se para todo o x, y Vec F se verifica: (a) (b) T(x + y) = T(x)
Transformação linear (TL) Transformações lineares Sejam V e W espaços vectoriais. Uma função T : V W é chamada transformação linear de V em W se para todo o x, y Vec F se verifica: (a) (b) T(x + y) = T(x)
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
PROBLEMAS DE ÁLGEBRA LINEAR
 PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
PROBLEMAS DE ÁLGEBRA LINEAR P. FREITAS Conteúdo. Números complexos. Sistemas de equações; método de eliminação de Gauss 3. Operações com matrizes 3 4. Inversão de matrizes 4 5. Característica e núcleo
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n
 Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n 1. Descrição do método e alguns exemplos Colocamos o seguinte problema: dado um conjunto finito: A = {a 1, a 2,...,
Método prático para extrair uma base de um conjunto de geradores de um subespaço de R n 1. Descrição do método e alguns exemplos Colocamos o seguinte problema: dado um conjunto finito: A = {a 1, a 2,...,
4. Tensores cartesianos em 3D simétricos
 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
Ficha de Trabalho 08 Transformações Lineares. (Aulas 19 a 22).
 F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
(x,y) x Exemplo: (x, y) ou f x. x = f x = 2xy. y = f y
 1 DEFINIÇÃO DE Chamamos de derivada parcial quando temos uma função que envolve mais de uma variável e queremos derivar em relação a uma delas. De forma geral, basta derivarmos em relação à variável de
1 DEFINIÇÃO DE Chamamos de derivada parcial quando temos uma função que envolve mais de uma variável e queremos derivar em relação a uma delas. De forma geral, basta derivarmos em relação à variável de
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química
 Código do Teste: 105 Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química 1. Para as matrizes A = ( 1 0 3 1 ) B = ( 5 4 1 0 2 1 3 1 ) C = 1 1 1 0 5 1
Código do Teste: 105 Álgebra Linear 1 ō Teste - 16/ 11/ 02 Cursos: Eng. Ambiente, Eng. Biológica, Eng. Química, Lic. Química 1. Para as matrizes A = ( 1 0 3 1 ) B = ( 5 4 1 0 2 1 3 1 ) C = 1 1 1 0 5 1
1 2 A, B 0 1. e C. 0 1
 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado respetivo. 1. No espaço vetorial R 4 considere
I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado respetivo. 1. No espaço vetorial R 4 considere
0 1. Assinale a alternativa verdadeira Q1. Seja A = (d) Os autovalores de A 101 são i e i. (c) Os autovalores de A 101 são 1 e 1.
 Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
w 1 = v 1 + v 2 + v 3 w 2 = 2v 2 + v 3 (1) w 3 = v 1 + 3v 2 + 3v 3 também são linearmente independentes. T =
 Independência e dependência linear ) a) Sejam v, v e v vectores linearmente independentes de um espaço linear S. Prove que os vectores também são linearmente independentes. Resolução Seja V a expansão
Independência e dependência linear ) a) Sejam v, v e v vectores linearmente independentes de um espaço linear S. Prove que os vectores também são linearmente independentes. Resolução Seja V a expansão
P2 de Álgebra Linear I Data: 10 de outubro de Gabarito
 P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
7 Formas Quadráticas
 Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Universidade Federal de Uberlândia Faculdade de Matemática
 Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
Álgebra Linear e Geometria Analítica. 7ª aula
 Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período
 www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 2013.2 OBS: Todas as alternativas corretas são as letras A. 1) Para encontrar o autovetor associado
www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 2013.2 OBS: Todas as alternativas corretas são as letras A. 1) Para encontrar o autovetor associado
MAT-27 Lista-09 Outubro/2011
 MAT-27 Lista-09 Outubro/2011 1. Determinar, se possível, uma matriz M M 2 (R) de maneira que M 1 AM seja diagonal nos seguintes casos: [ ] 2 4 (a) 3 13 [ ] 3 2 2 1 2. Achar uma matriz diagonal semelhante
MAT-27 Lista-09 Outubro/2011 1. Determinar, se possível, uma matriz M M 2 (R) de maneira que M 1 AM seja diagonal nos seguintes casos: [ ] 2 4 (a) 3 13 [ ] 3 2 2 1 2. Achar uma matriz diagonal semelhante
AUTOVALORES E AUTOVETORES
 AUTOVALORES E AUTOVETORES Prof a Simone Aparecida Miloca Definição 1 Uma tranformação linear T : V V é chamada de operador linear. Definição Seja T : V V um operador linear. existirem vetores não-nulos
AUTOVALORES E AUTOVETORES Prof a Simone Aparecida Miloca Definição 1 Uma tranformação linear T : V V é chamada de operador linear. Definição Seja T : V V um operador linear. existirem vetores não-nulos
Nota importante: U é a matriz condensada obtida no processo de condensação da matriz
 Decomposição P T LU A denominada decomposição P T L U é um processo que pode ser extremamente útil no cálculo computacional, na resolução de sistemas de equações lineares. Propriedade Seja A uma matriz
Decomposição P T LU A denominada decomposição P T L U é um processo que pode ser extremamente útil no cálculo computacional, na resolução de sistemas de equações lineares. Propriedade Seja A uma matriz
