Resolução do efólio B
|
|
|
- Giovanna Barreto Philippi
- 5 Há anos
- Visualizações:
Transcrição
1 Resolução do efólio B Álgebra Linear I Código: I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado respetivo. 1. Seja S ÔÔ1, 1, 4Õ, Ô0, 1, 3Õ, Ô1, 0, 1ÕÕ uma sequência de vetores de R 3. Então: a) S é um conjunto gerador, mas não é uma base de R 3. b) S é uma base de R 3, diferente da base canónica. c) S é a base canónica de R 3. d) dimüô1, 1, 4Õ, Ô0, 1, 3Õ, Ô1, 0, 1ÕÝ Seja A È M 6 6 ÔRÕ uma matriz com apenas três valores próprios, com multiplicidades algébricas iguais e tal que o produto dos valores próprios satisfaz λ 1 λ 2 λ 3 6. Então: a) O polinómio característico de A pode ser pôλõ Ôλ 1ÕÔλ 2ÕÔλ 3Õ. b) Uma matriz A nestas condições nunca é invertível. c) Os valores próprios de A podem ter multiplicidades geométricas diferentes. d) det A Para cada α È R, seja A α a matriz definida por A α α , e considere as 1 0 α seguintes afirmações: (i) A α é diagonal para todo o α; (ii) A α é diagonalizável para algum α; (iii) se o vetor  pertence ao núcleo de A α então α 1; (iv) o vetor  é um vetor próprio de A α para algum α. Então as afirmações verdadeiras são: a) (i) e (ii) c) (iii) e (iv) b) (ii) e (iii) d) (ii) e (iv) 4. Seja A È M 2 2 ÔRÕ uma matriz com polinómio característico pôλõ λ 2 1, e considere as seguintes afirmações: (i) A tem traço nulo; (ii) A é diagonalizável; (iii) det A 1; (iv) A tem um subespaço próprio com dimensão 2. e-fólio B 1
2 Então a lista completa das afirmações verdadeiras é: a) (i) e (iii) c) (i), (ii) e (iv) b) (ii) e (iii) d) (i), (ii) e (iii) II. Diga se é verdadeira ou falsa cada uma das afirmações nas alíneas a) e b) seguintes, justificando cuidadosamente a sua resposta através de uma demonstração ou de um contra-exemplo, consoante o que for apropriado. a) Se u é um vetor próprio de A então u é também um vetor próprio de A k para todo k 2. b) Se u é um vetor próprio de A k para algum k 2 então u é também um vetor próprio de A. III. Seja A Determine: (i) O polinómio característica de A. (ii) Uma base para cada um dos espaços próprios de A. (iii) A multiplicidade geométrica de cada valor próprio. (iv) Diga, justificadamente, se a matriz A é semelhante a uma matriz diagonal. IV. Seja T um endomorfismo de R 3, tal que onde Ôe 1, e 2, e 3 Õ b.c. R 3. T Ôe 1 Õ Ô1, 0, 1Õ, T Ôe 2 Õ Ô2, 1, 2Õ e T Ôe 3 Õ Ô1, 1, 1Õ, (i) Determine a matriz A MÔT, b.c. R 3, b.c. R 3Õ que representa a transformação T em relação à base canónica de R 3 no espaço de partida e no espaço de chegada. (ii) Determine uma base do núcleo de T. (iii) Determine a dimensão da imagem de T. (iv) Verifique que B ÔÔ 1, 0, 1Õ, Ô0, 1, 1Õ, Ô1, 1, 0ÕÕ é uma base de R 3 e determine a matriz C MÔT, B, b.c. R 3Õ que representa a transformação T em relação à base B no espaço de partida e à base canónica no espaço de chegada. V. Para cada n 2, seja J n È M n n ÔRÕ a matriz que tem todas as suas entradas iguais a Å 1, ou seja J n Determine os valores próprios e os espaços próprios de J n. (Sugestão: Comece por justificar que um dos valores próprios é λ 0 e determine a dimensão do espaço próprio associado E 0.) FIM 2 e-fólio B
3 Grupo I. 1. Uma vez que somando os 2 primeiros vetores de S se obtem o terceiro vetor, e portanto Ô1, 1, 4Õ Ô0, 1, 3Õ Ô1, 0, 1Õ 0, que é uma combinação linear nula, com coeficientes não todos nulos, a sequência de vetores é linearmente dependente. Assim, como estamos em R 3 que é um espaço de dimensão 3, concluimos que S não é uma base (nem um conjunto gerador), e portanto a dimensão do espaço gerado por S é certamente menor que a dimensão de R 3. Uma outra forma de concluir que os 3 vetores de S não são linearmente independentes é através do cálculo do determinante da matriz cujas linhas (ou colunas) são os vetores de S. Neste caso A alínea correta é d). 2. A matriz A é uma matriz de ordem 6, e portanto a soma das multiplicidades algébricas dos seus 3 valores próprios é igual a 6, e portanto a multiplicidade algébrica de cada valor próprio é igual a 2. Como A é uma matriz de ordem 6, o seu polinómio característico é de grau 6; como 0 não é valor próprio, a matriz A é uma matriz invertível; como λ 1 λ 2 λ 3 6 e cada valor próprio tem multiplicidade algébrica igual a 2, tem-se det A λ 2 1 λ2 2 λ2 3 Ôλ 1λ 2 λ 3 Õ Assim a alínea correta é c). 3. Como a matriz A α tem elementos não nulos fora da diagonal principal, é claro que não é diagonal para nenhum α. Para vermos se A α é diagonalizável vamos calcular os seus valores próprios: α λ λ 0 detôa α λi 3 Õ 0 1 λ 0 Ôα λõ 1 0 α λ 0 α λ λ 0 Ôα λõô1 λõôα λõ Ô1 λõ Ô1 λõöôα λõ 2 1 Ô1 λõôα λ 1ÕÔα λ 1Õ Ôλ 1ÕÔλ Ôα 1ÕÕÔλ Ôα 1ÕÕ, e portanto os valores próprios de A α são 1, α 1 e α 1. Escolhendo, por exemplo α 3, obtemos 3 valores próprios diferentes, 1, 4 e 2, e portanto A 3 é diagonalizável. O vetor Ô101Õ Â está no núcleo de A α A α Ô101Õ Â 0 α 1. Como A α Ô010Õ Â Ô010Õ Â, concluímos que Ô010Õ Â é um vetor de A α para todo o α com vetor próprio associado λ 1. A alínea correta é d). 4. Como pôλõ λ 2 1 Ôλ 1ÕÔλ 1Õ concluimos que os valores próprios de A são 1 e 1, e portanto Tr A e det A 1 Ô 1Õ 1. Além disso como A é de ordem 2 e tem 2 valores próprios distintos, é diagonalizável. Como A é de ordem 2 e tem 2 valores próprios distintos, cada um deles tem um espaço próprio de dimensão 1. A alínea correta é d). e-fólio B 3
4 Grupo II. a) Se u é um vetor próprio de A com valor próprio λ, então Au λu, e aplicando A aos dois lados desta igualdade tem-se AÔAuÕ AÔλuÕ ou seja A 2 u λôauõ λôλuõ λ 2 u, e podemos conjeturar que A k u λ k u para k 1. Usando o método de indução para mostrar a nossa conjetura, temos de provar o seguinte: Usando a hipótese de indução A n u λ n u A n 1 u λ n 1 u. A n 1 u AÔA n uõ AÔλ n uõ λ n ÔAuÕ λ n ÔλuÕ λ n 1 u, e portanto a afirmação é verdadeira. b) Para vermos porque é que esta afirmação é falsa podemos recordar que existem matrizes não identicamente nulas tais que A 2 0. Isso quer dizer que qualquer vetor não nulo é um vetor próprio de A 2 com valor próprio 0, e em geral esse vetor próprio de A 2 não é um vetor próprio de A. Um exemplo simples de uma matriz 2 2 nessa condições é Å 0 1 A. 0 0 Temos que A 2 Ô Õ, e portanto u Ô0 1ÕÂ é um vetor próprio de A 2 com valor próprio 0 pois A 2 u 0u 0, mas Au Ô1 0Õ Â λu, λ. Logo u não pode ser vetor próprio de A, e portanto a afirmação é falsa. Grupo III. (i) Por definição o polinómio característico de A é o determinante da matriz A λi 3. Como a matriz A λi 3 é uma matriz triangular, o seu determinante é igual ao produto dos elementos da diagonal principal. Também podiamos aplicar o Teorema de Laplace à 1 a coluna. Assim, p A ÔλÕ pôλõ Ô 1 λõô 1 λõô3 λõ Ô 1 λõ 2 Ô3 λõ Ôλ Ô 1ÕÕ 2 Ôλ 3Õ. (ii) Uma vez que os valores próprios são as raízes da equação característica pôλõ 0 concluímos imediatamente da alínea anterior que os valores próprios de A são λ 1 1 e λ 2 3, e que a multiplicidade algébrica (m.a) de 1 é igual a 2 e a de 3 é igual a 1. Por definição o espaço próprio associado a um valor próprio λ é igual ao espaço linear das soluções da equação ÔA λi 3 Õx 0. Para λ 1 1 tem-se A λ 1 I e portanto x y z 0 ² ± y 0 z 0 4z 0 y z 0 x y z x. Assim o espaço próprio associado a λ 1 1 é o espaço linear E λ1 E 1 gerado pelo vetor De modo inteiramente análogo para λ 2 3 tem-se A λ 2 I e portanto x ² 4x y 0 y 0 4y z 0 z 4y 16x x y x 1 4. ± z 0 0 z 16 4 e-fólio B 1 0 0
5 Assim o espaço próprio associado a λ 2 3 é o espaço linear E λ2 E 3 gerado pelo vetor (iii) Como a multiplicidade geométrica (m.g) de um valor próprio é a dimensão do seu espaço próprio, e cada um dos espaços próprios anteriores é gerado por um único vetor, temos que m.gô 1Õ 1 m.gô3õ. (iv) A é semelhante a uma matriz diagonal se e sómente se for diagonalizável, e podemos utilizar a Prop (3 a Ed.) ou a Prop (3 a Ed.), para mostrar que A não é diagonalizável. A Prop diz-nos que a matriz A de ordem n 3 é diagonalizável se e só se tiver 3 vetores próprios linearmente independentes, o que é impossível neste caso, pois A apenas tem 2 vetores próprios. A Prop diz-nos que a matriz A de ordem n 3 é diagonalizável se e só se a soma das multiplicidades geométricas dos seus valores próprios for igual a 3, mas neste caso tem-se Grupo IV. (i) A matriz A MÔT, b.c. R 3, b.c. R 3Õ que representa a transformação T em relação à base canónica der 3 no espaço de partida e no espaço de chegada é a matriz que tem por colunas as imagens por T dos vetores da base, ou seja é a matriz cujas colunas são T Ôe 1 Õ, T Ôe 2 Õe T Ôe 3 Õ, portanto A MÔT, b.c. R 3, b.c. R 3Õ (ii) O o núcleo de T é constituído pelas soluções do sistema Ax 0, ou seja x y 0 ² x 2y z 0 0 x 2y y 0 y z 0 x z y, ± z y z 0 x 2y z 0 e portanto o núcleo é um espaço linear gerado pelo vetor Ô1, 1, 1Õ der 3, logo dim Nuc T 1. (iii) O Teorema da Dimensão diz-nos que dimr 3 dim Nuc T dim ImT, neste caso 3 1 dim ImT e portanto dim ImT (iv) Para verificar que B ÔÔ 1, 0, 1Õ, Ô0, 1, 1Õ, Ô1, 1, 0ÕÕ é uma base de R 3 basta mostrar que os três vetores são linearmente independentes, pois num espaço de dimensão 3, quaisquer três vetores linearmente independentes são também geradores. Para vermos que os três vetores são linearmente independentes basta, por exemplo, mostrar que o determinante da matriz cujas colunas (ou linhas) são estes 3 vetores é não nulo. Tem-se Ô1 1Õ Para determinar a matriz C MÔT, B, b.c. R 3Õ que representa a transformação T em relação à base B no espaço de partida e à base canónica no espaço de chegada vamos utilizar dois métodos distintos. O primeiro consiste em escrever os vetores da base B à custa dos vetores da base canónica, ou seja como combinação linear dos três vetores Ôe 1, e 2, e 3 Õ e depois calcular a sua imagem e-fólio B 5
6 por T. Tem-se Ô 1, 0, 1Õ Ô1, 0, 0Õ Ô0, 0, 1Õ e 1 e 3, e portanto T ÔÔ 1, 0, 1ÕÕ T Ô e 1 e 3 Õ T Ôe 1 Õ T Ôe 3 Õ Ô1, 0, 1Õ Ô1, 1, 1Õ Ô0, 1, 0Õ. Para Ô0, 1, 1Õ tem-se Ô0, 1, 1Õ e 2 e 3 e portanto T ÔÔ0, 1, 1ÕÕ T Ôe 2 e 3 Õ T Ôe 2 Õ T Ôe 3 Õ Ô2, 1, 2Õ Ô1, 1, 1Õ Ô3, 2, 3Õ. Para Ô1, 1, 0Õ tem-se Ô1, 1, 0Õ e 1 e 2 e portanto T ÔÔ1, 1, 0ÕÕ T Ôe 1 e 2 Õ T Ôe 1 Õ T Ôe 2 Õ Ô1, 0, 1Õ Ô2, 1, 2Õ Ô 1, 1, 1Õ, e portanto C MÔT, B, b.c. R 3Õ O outro método consiste em usar matrizes de mudança de base, começando por determinar a matriz de mudança de base de B para b.c. R 3, ou seja MÔid R 3, B, b.c. R 3Õ, e depois usar a Prop. 5.42, neste caso simples, em que os espaços de partida e de chagada são R 3. Com a ajuda do seguinte diagrama B id R 3 MÔid R 3, B, b.c. R 3Õ b.c. R 3 T MÔT, b.c. R 3, b.c. R 3Õ b.c. R 3 T MÔT, B, b.c. R 3Õ tem-se MÔT, B, b.c. R 3Õ MÔT, b.c. R 3, b.c. R 3Õ MÔid R 3, B, b.c. R 3Õ. Designando os vetores da base B por Ôu, v, wõ, tem-se id R 3ÔuÕ Ô 1, 0, 1Õ Ô1, 0, 0Õ Ô0, 0, 1Õ Ô 1Õe 1 0e 2 1e 3 id R 3ÔvÕ Ô0, 1, 1Õ Ô0, 1, 0Õ Ô0, 0, 1Õ 0e 1 1e 2 1e 3 id R 3ÔwÕ Ô1, 1, 0Õ Ô0, 1, 0Õ Ô0, 0, 1Õ 1e 1 Ô 1Õe 2 0e 3, e portanto Finalmente MÔid R 3, B, b.c. R 3Õ MÔT, B, b.c. R 3Õ MÔT, b.c. R 3, b.c. R 3Õ MÔid R 3, B, b.c. R 3Õ e-fólio B
7 Grupo V. Uma vez que J n tem duas linhas iguais, a Prop garante que o seu determinante é nulo. Como pela Prop o determinante de J n é igual ao produto dos valores próprios, concluímos que 0 é valor próprio de J n. O espaço próprio associado ao valor próprio 0, E 0, corresponde ao núcleo de J n (pois J n 0I n J n ). Pela Prop ou 4.66, por exemplo, a matriz J n tem característica 1, e portanto, pela Prop. 4.69, o seu núcleo tem dimensão n rôj n Õ n 1. O valor próprio 0 tem multiplicidade algébrica no mínimo igual à multiplicidade geométrica, e portanto existe no máximo mais um valor próprio. Calculando detôj n λi n Õ já sabemos que vai ser um múltiplo de λ n 1. Para determinar o outro valor próprio vamos calcular o determinante de J n λi n, efetuando transformações nas linhas e nas colunas que não alteram o valor do determinante, 1 λ n λ n λ n λ n λ n λ λ λ λ λ λ λ onde a primeira transformação consiste em somar à primeira linha cada uma das outras linhas (l 1 l 2,..., l 1 l n ), e a segunda transformação consiste em somar a cada coluna, diferente da primeira, o simétrico da primeira coluna (c 2 c 1,..., c n c 1 ). esta última matriz é triangular e portanto o determinante é igual ao produto dos elementos da diagonal principal, n λ λ 0 0 Ôn λõô λõ n 1 Ô 1Õ n 1 ÔλÕ n 1 Ôn λõ λ Concluimos assim que o outro valor próprio é λ n, com multiplicidade algébrica (e geométrica) igual a 1. O espaço próprio associado a λ n é o núcleo da matriz 1 n n 1 1 J n ni n Æ, n ou de maneira mais sugestiva, consiste nas soluções de x x 1 x 2 Æ Æ. n x 2 Æ x n x n Como já sabemos que o valor próprio é λ n tem multiplicidade geométrica igual a 1, bastanos obter uma solução não nula, por exemplo o vetor definido por x 1 x 2 x n 1, e este vetor gera o espaço próprio do valor próprio n. FIM e-fólio B 7
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
MAT3458 ÁLGEBRA LINEAR II 2 a Lista de Exercícios 2 o semestre de 2018
 MAT3458 ÁLGEBRA LINEAR II 2 a Lista de Exercícios 2 o semestre de 2018 1. Verdadeiro ou falso? Justifique suas respostas. (i) Existe uma transformação linear T : P 3 (R) M 2 (R) cuja matriz em relação
MAT3458 ÁLGEBRA LINEAR II 2 a Lista de Exercícios 2 o semestre de 2018 1. Verdadeiro ou falso? Justifique suas respostas. (i) Existe uma transformação linear T : P 3 (R) M 2 (R) cuja matriz em relação
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
U.C Álgebra Linear I. 31 de janeiro de 2017
 Ministério da Ciência, Tecnologia e Ensino Superior p-fólio U.C. 21002 Álgebra Linear I 31 de janeiro de 2017 O p-fólio é composto por 4 grupos de questões e respetivas alíneas, contém 5 páginas e termina
Ministério da Ciência, Tecnologia e Ensino Superior p-fólio U.C. 21002 Álgebra Linear I 31 de janeiro de 2017 O p-fólio é composto por 4 grupos de questões e respetivas alíneas, contém 5 páginas e termina
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
0 1. Assinale a alternativa verdadeira Q1. Seja A = (d) Os autovalores de A 101 são i e i. (c) Os autovalores de A 101 são 1 e 1.
 Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0
![Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0 Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0](/thumbs/93/113642308.jpg) Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
 Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
 Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Resolução do efólio A Álgebra Linear I Código: 21002
 Resolução do efólio A Álgebra Linear I Código: I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio A Álgebra Linear I Código: I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
ESPAÇOS LINEARES (ou vetoriais)
 Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
1 2 A, B 0 1. e C. 0 1
 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado respetivo. 1. No espaço vetorial R 4 considere
I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado respetivo. 1. No espaço vetorial R 4 considere
Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período
 www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 4. OBS: Todas as alternativas corretas são as letras A. ) Devemos utilizar o teorema que diz: (Im(A
www.engenhariafacil.weebly.com Resolução das objetivas 3ª Prova de Álgebra Linear II da UFRJ, período 4. OBS: Todas as alternativas corretas são as letras A. ) Devemos utilizar o teorema que diz: (Im(A
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Álgebra Linear I - Lista 11. Autovalores e autovetores. Respostas. 1) Calcule os autovalores e autovetores das matrizes abaixo.
 Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Valores próprios (de uma matriz): tais que det(a I) = 0. Vectores próprios (de uma matriz) associados a um valor próprio : v 2 N (A I)n f0g
 Polinómio característico: det(a I) Valores próprios (de uma matriz): tais que det(a I) Vectores próprios (de uma matriz) associados a um valor próprio : v N (A I)n fg N (A I) é o subespaço próprio associado
Polinómio característico: det(a I) Valores próprios (de uma matriz): tais que det(a I) Vectores próprios (de uma matriz) associados a um valor próprio : v N (A I)n fg N (A I) é o subespaço próprio associado
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Verdadeiro ou falso?
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Segunda Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Verdadeiro ou falso?
Álgebra Linear I - Lista 12. Matrizes semelhantes. Diagonalização. Respostas
 Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Nota: Turma: MA 327 Álgebra Linear. Segunda Prova. Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 2006 Segunda Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Questão 1. A matriz de mudança da base ordenada
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 2006 Segunda Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Questão 1. A matriz de mudança da base ordenada
Álgebra Linear 1 o Teste
 Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 1 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
(a) (1,5) Obtenha os autovalores e autovetores de L. (b) (1,0) A matriz de L em relação à base canônica de M 2 2 é diagonalizável? Explique.
 Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Geometria anaĺıtica e álgebra linear
 Geometria anaĺıtica e álgebra linear Francisco Dutenhefner Departamento de Matematica ICEx UFMG 22/08/13 1 / 24 Determinante: teorema principal Teorema: Se A é uma matriz quadrada, então o sistema linear
Geometria anaĺıtica e álgebra linear Francisco Dutenhefner Departamento de Matematica ICEx UFMG 22/08/13 1 / 24 Determinante: teorema principal Teorema: Se A é uma matriz quadrada, então o sistema linear
A forma canônica de Jordan
 A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
Valores e vectores próprios
 Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
5. Seja A uma matriz qualquer. Assinale a afirmativa
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
AUTOVALORES E AUTOVETORES
 AUTOVALORES E AUTOVETORES Prof a Simone Aparecida Miloca Definição 1 Uma tranformação linear T : V V é chamada de operador linear. Definição Seja T : V V um operador linear. existirem vetores não-nulos
AUTOVALORES E AUTOVETORES Prof a Simone Aparecida Miloca Definição 1 Uma tranformação linear T : V V é chamada de operador linear. Definição Seja T : V V um operador linear. existirem vetores não-nulos
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
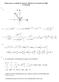 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
Resolução do efólio A
 Resolução do efólio A Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das armações a), b), c), d) é verdadeira. Indique-a marcando ˆ no quadrado
Resolução do efólio A Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das armações a), b), c), d) é verdadeira. Indique-a marcando ˆ no quadrado
3 a Avaliação Parcial - Álgebra Linear
 3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
Multiplicidade geométrica
 Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof. Juliana Coelho - 07h00-09h00
 Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof Juliana Coelho - 07h00-09h00 QUESTÃO 1 (2,0 pts - Considere os seguintes vetores de R3 : u = (3, 2, 2, v = (1, 3, 1 e w = ( 1, 4, 4 Responda as
Segunda prova de Álgebra Linear Aplicada - 20/02/2013 Prof Juliana Coelho - 07h00-09h00 QUESTÃO 1 (2,0 pts - Considere os seguintes vetores de R3 : u = (3, 2, 2, v = (1, 3, 1 e w = ( 1, 4, 4 Responda as
Álgebra Linear
 Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Perg 1 3 Val C Perg 2 2 Val B Perg 3 2 Val D Perg 4 3 Val A
 Instituto Superior Técnico Departamento de Matemática 1 o semestre 15/16 Nome: Número: Curso: Sala: 3 o TESTE DE ÁLGEBRA LINEAR LEE, LEGI, LEIC-T, LERC 19 de dezembro de 2015 (9:00) Teste 301 (soluções)
Instituto Superior Técnico Departamento de Matemática 1 o semestre 15/16 Nome: Número: Curso: Sala: 3 o TESTE DE ÁLGEBRA LINEAR LEE, LEGI, LEIC-T, LERC 19 de dezembro de 2015 (9:00) Teste 301 (soluções)
Álgebra linear A Primeira lista de exercícios
 Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Álgebra linear A Primeira lista de exercícios Prof. Edivaldo L. dos Santos (1) Verifique, em cada um dos itens abaixo, se o conjunto V com as operações indicadas é um espaço vetorial sobre R. {[ ] a b
Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan
 Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan Exercício 1. Seja A = (a i j ) uma matriz diagonal sobre
Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan Exercício 1. Seja A = (a i j ) uma matriz diagonal sobre
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
ÁLGEBRA LINEAR A FICHA 6. Por definição do determinante de uma matriz 3 3, tem-se det A = 7.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Aula 1 Autovetores e Autovalores de Matrizes Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17
 Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Parte 3 - Produto Interno e Diagonalização
 Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
GAAL - Primeira Prova - 06/abril/2013. Questão 1: Considere o seguinte sistema linear nas incógnitas x, y e z.
 GAAL - Primeira Prova - 06/abril/203 SOLUÇÕES Questão : Considere o seguinte sistema linear nas incógnitas x, y e z. x + ay z = x + y + 2z = 2 x y + az = a Determine todos os valores de a para os quais
GAAL - Primeira Prova - 06/abril/203 SOLUÇÕES Questão : Considere o seguinte sistema linear nas incógnitas x, y e z. x + ay z = x + y + 2z = 2 x y + az = a Determine todos os valores de a para os quais
Diagonalização de Operadores. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes.
 Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Segunda prova de Álgebra Linear - 01/07/2011 Prof. - Juliana Coelho
 Segunda prova de Álgebra Linear - 01/07/011 Prof - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1, pts
Segunda prova de Álgebra Linear - 01/07/011 Prof - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1, pts
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
GAAL Exercícios 6: Umas soluções
 GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
ÁLGEBRA LINEAR - MAT0024
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00
 Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00 [ ] 4 2 Questão 1. Seja T : R 2 R 2 o operador linear cuja matriz, com respeito à base canônica de R 2, é. 1 3 [ ] 2 0 Seja B uma base de R 2 tal que
Álgebra Linear II - Poli - Gabarito Prova SUB-tipo 00 [ ] 4 2 Questão 1. Seja T : R 2 R 2 o operador linear cuja matriz, com respeito à base canônica de R 2, é. 1 3 [ ] 2 0 Seja B uma base de R 2 tal que
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
Capítulo 5. Operadores Auto-adjuntos. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
U.C Álgebra Linear I Atividade Formativa 1
 Ministério da Educação e Ciência U.C. 2002 Álgebra Linear I Atividade Formativa I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira.
Ministério da Educação e Ciência U.C. 2002 Álgebra Linear I Atividade Formativa I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira.
Forma Canônica de Matrizes 2 2
 Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
ESPAÇO VETORIAL REAL. b) Em relação à multiplicação: (ab) v = a(bv) (a + b) v = av + bv a (u + v ) = au + av 1u = u, para u, v V e a, b R
 ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
ESPAÇO VETORIAL REAL Seja um conjunto V, não vazio, sobre o qual estão definidas as operações de adição e multiplicação por escalar, isto é: u, v V, u + v V a R, u V, au V O conjunto V com estas duas operações
Universidade Federal Fluminense - GAN
 Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
Solimá Gomes Pimentel Universidade Federal Fluminense IM - GAN Solimá Gomes Pimentel, ****- Matemática para Economia III/Solimá Gomes Pimentel 2pt, ; 31cm Inclui Bibliografia. 1. Matemática para Economia
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
Primeira prova de Álgebra Linear - 06/05/2011 Prof. - Juliana Coelho
 Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Álgebra Linear e Geometria Analítica D
 1 3 Departamento de Matemática Álgebra Linear e Geometria Analítica D Primeiro Teste 21 de Novembro de 2009 Nome: Número de caderno: PREENCHA DE FORMA BEM LEGÍVEL Grelha de Respostas A B C D 1 2 3 4 5
1 3 Departamento de Matemática Álgebra Linear e Geometria Analítica D Primeiro Teste 21 de Novembro de 2009 Nome: Número de caderno: PREENCHA DE FORMA BEM LEGÍVEL Grelha de Respostas A B C D 1 2 3 4 5
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
1 a Lista de Exercícios de MAT3458 Escola Politécnica 2 o semestre de 2016
 1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
Instituto Universitário de Lisboa
 Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
Instituto Universitário de Lisboa Departamento de Matemática Exercícios extra de Álgebra Linear Ano Lectivo 204/205 . Sejam A = 0 2 0 0 2 e B = 0 0 0 0. (a) Calcule, se possível, as matrizes AB, BA e B
3 o TESTE DE ÁLGEBRA LINEAR LCEIC-Taguspark, LCERC, LCEGI, LCEE (2 a Fase) 25 de Janeiro de 2008 (11:00) Teste 303
 Instituto Superior Técnico Departamento de Matemática 1 o semestre 07/08 Nome: Número: Curso: 3 o TESTE DE ÁLGEBRA LINEAR LCEIC-Taguspark, LCERC, LCEGI, LCEE (2 a Fase) 25 de Janeiro de 2008 (11:00) Teste
Instituto Superior Técnico Departamento de Matemática 1 o semestre 07/08 Nome: Número: Curso: 3 o TESTE DE ÁLGEBRA LINEAR LCEIC-Taguspark, LCERC, LCEGI, LCEE (2 a Fase) 25 de Janeiro de 2008 (11:00) Teste
