ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
|
|
|
- Ana Figueira Costa
- 8 Há anos
- Visualizações:
Transcrição
1 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: Semestre: Verão
2 Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA
3 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 3 PARTE 1 1 ç Considere o sistema de equações lineares nas incógnitas Bß Cß D, onde + e, são parâmetros reais: BC+D œ +B C +D œ " + BCD œ,$ a ç Discuta a natureza do sistema, em função dos parâmetros + e,. b ç Resolva-o, para +œ" e,œ", indicando ainda a solução geral do sistema homogéneo associado. c ç Faça +œ! e,œ$ e designe por Ea matriz simples do sistema: c1 ç Justifique que E é invertível e determine E ". c2 ç Resolva o sistema, recorrendo à matriz E " calculada na alínea anterior. Resposta 1a ç Levemos a matriz completa ÒE FÓdo sistema à forma escalonada, por condensação vertical: Para + œ", fica ainda: " " + " " + P+PÄP $ + " + "+! +" + +" +" " ",$ µ " $ PPÄP $ " $!! +," " " " " " " PÇP $ +œ"ê!!!! µ!! "," "!! ","!!!! Estamos, agora, em condições de fazer a discussão do sistema: Designando por < a característica da matriz E simples, por = a característica da matriz ÒE FÓ completa e por 8 œ $ o número de incógnitas, resumimos a discussão no quadro seguinte: Caso +, < = < œ = 8< " " Sim " Á" $ Não Natureza do sistema Possível simplesmente indeterminado Impossível $ " Sim " Possível simplesmente indeterminado % Á Á " $ $ Sim! Possível determinado 1b ç Para +œ "(caso $ ), o sistema é possivel e simplesmente indeterminado (independentemente do valor real de,). Para determinar a respectiva solução geral, basta agora fazer, œ " em " e levar a matriz completa à forma escalonada reduzida, por mais uma operação do tipo $ : " " " " "!! B œ C PPÄP " ",œ"ê!! " µ!! " Ê C œ C!!!!!!!! D œ Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
4 4 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) Deste modo, a solução geral do sistema é: BßCßD œcßcß œ!ß!ß C"ß"ß! à C O vector!ß!ß é uma solução particular de E\ œ F e C"ß "ß! é a solução geral do sistema homogéneo associado. 1c1 ç A discussão do sistema antes realizada mostra que, para +œ! e qualquer,, o sistema é determinado (caso %) e sê-lo-á, em particular, para,œ$: A matriz E terá característica <œ$, logo, Eé invertível e " "! T. Lap "! dete œ! "! œ œ " " " Então,! "! " " " " E œ E œ! œ!! dete adj!! " "! " T 1c2 ç Temos, sucessivamente, M " " " " E\ œ F Ê E E\ œ E F Ê E E \ œ E F $ "! " " ÊM\œ $ E FÊ\œE FÊ\œ!! " "! " ' Ê\œ " " œ " % 2015 Julho 15; 10:00 Ano Lectivo: Semestre: Verão
5 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 5 $! $ $ $ 2 ç Seja 0À Ä o endomorfismo de cuja matriz canónica é J œ " " ". "!! a ç Prove que ß "ß " é um vector próprio de 0. Qual o valor próprio associado? b ç Determine todos os valores próprios de 0, bem como as respectivas multiplicidades algébricas. c ç Sem efectuar quaisquer cálculos, mostre que o núcleo de 0 é!ß!ß! e conclua que 0 é um automorfismo de $. d ç Determine os subespaços próprios de 0 e indique uma base de $ em relação à qual a matriz de 0 seja "!! Hœ! "!!!. $ % e ç Considere a aplicação linear 1À Ä definida por 1Bß Cß D œ B Cß B Cß!ß D: e1 ç Justifique que 1 é injectiva e não sobrejectiva. e2 ç Determine a matriz de 1 0 em relação às bases canónicas dos espaços envolvidos e use-a para determinar 1 0BßCßD, para todo o BßCßD $. 2a ç As coordenadas na base canónica de Resposta $ da imagem do vector ß "ß " por 0 são $! % - " " " " œ œ " "!! " " Portanto, 0 ß"ß" œ ß"ß" o que mostra que ß"ß" é um vector próprio de 0 associado ao valor próprio - œ. 2b ç Aplicando o teorema de Laplace à coluna, o polinómio característico de 0 é dado por: $-! : 0 - œ detj -M$ œ " "- " "! - $- œ "- œ " $ " œ "-- -" œ -" - Conclui-se que o espectro de 0 é E0 œ "ß. A multiplicidade algébrica do valor próprio - œ " é e a multiplicidade algébrica do valor próprio - œ é "(consequentemente, também a geométrica). 2c ç Como! não é valor próprio de 0, segue-se que não existem vectores BßCßD não nulos tais que 0BßCßD œ! BßCßD œ!ß!ß!, ou seja, o único vector com imagem nula é o próprio vector nulo. Isto significa que o núcleo de 0 é!ß!ß!. Então, 0 é injectiva (um automorfismo de $ ). Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
6 6 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 2d ç Para determinar os subespaços próprios I-0, temos que calcular os vectores próprios de 0, resolvendo os sistemas homogéneos J-M \ œs, para cada - 0Þ ç Para - œ": $ - E!! "! "! "! "! B œ D " PÄP " " PPÄP " "! "! µ "! "! µ!!!! Ê C œ C PPÄP $ " $ "! "! "! "!!!!! D œ D A solução geral do sistema homogéneo duplamente indeterminado anterior é BßCßD œc!ß"ß! D "ß!ß" à CßD O subespaço próprio associado ao valor próprio - œ" é, pois: I"0 œc!ß"ß! D "ß!ß" ÀCßD œp!ß"ß! ß "ß!ß" Portanto, a multiplicidade geométrica o valor próprio " é 7 " œ dimi 0 œ 1 " ç Para - œ: "!! "!! B œ D PPÄP " " " "! µ! " "! Ê C œ D PPÄP $ " $ "!!!!!! D œ D A solução geral do sistema homogéneo simplesmente indeterminado anterior é D ß"ß" à D. O subespaço próprio associado ao valor próprio - œ é, pois: I0 œ D ß "ß " À D œ P ß "ß " Portanto, a multiplicidade geométrica o valor próprio é O quadro seguinte resume a situação de 0: 7 œ dimi 0 œ " 1 - I " P!ß "ß! ß "ß!ß " P ß "ß " " " 7 - œ $ - E0 Como a soma das multiplicidades geométricas dos valores próprios de 0 é igual a dim œ $, a função 0 é diagonalizável. A base /œ!ß"ß! ß "ß!ß" ß ß"ß" é formada exclusivamente por vectores próprios de 0 (associados respectivamente aos valores próprios "ß"ß ) pelo que, nessa base, a matriz de 0 é: "!! Hœdiag"ß "ß œ! "!!! 1 $ 2015 Julho 15; 10:00 Ano Lectivo: Semestre: Verão
7 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 7 Observe-se que a matriz diagonal H anterior é também a representação de 0 em relação, por exemplo, à base "ß!ß " ß!ß "ß! ß ß "ß " e ainda em relação às infinitas bases da forma + - +!ß"ß!, "ß!ß" ß-!ß"ß!. "ß!ß" ß> ß"ß" àcom Á! >Á! (porquê?),. 2e1 ç Como a dimensão do domínio é inferior à do codomínio, 1 não pode ser sobrejectiva. Por outro lado, a matriz canónica de 1 é É óbvio que a característica de " "! " "! Kœ!!!!! K (e de 1 ) é igual a $, o que mostra que 1 é injectiva. 2e2 ç A matriz canónica de 1 0 é " "! $! % " $ " "! " " KJ œ " " " œ!!!!!! "!!!!!! As coordenadas de 1 0BßCßD na base canónica de % são: % " $ %BC$D B " " BCD C œ!!!!!! D B Portanto, 1 0BßCßD œ %BC$DßBCDß!ßB Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
8 8 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 3 ç Em $, dotado do produto interno canónico, considere os vectores?t œ "ß!ß " œ!ß "ß " e At œ "ß "ß ". a ç Determine o ângulo entre?t e a projecção de At sobre?t. b ç Calcule a área do triângulo definido por?t c ç Usando determinantes, prove que a At é uma base de $. d ç Utilizando o processo de Gram-Schmidt, construa uma base ortogonal At. Resposta 3a ç O ângulo entre? t t é dado por:? ang? œ arccos? "ß!ß "!ß "ß " œ arccos "ß!ß "!ß "ß " " " 1 œ arccos œ arccos œ $ A projecção de At sobre?t é $, a partir da base At?t "ß"ß" "ß!ß"! proj?t At œ?t œ "ß!ß " œ "ß!ß " œ!ß!ß!? t?t "ß!ß" "ß!ß" 3b ç Sendo t-ß-ß- " t t$ a base canónica de $ (que é ortonormada para o produto interno usual), tem-se "! -t "! " "! " -t œ t- t- t- œ- t - t - t œ "ß"ß" " " " " "! " $ " $ " " -t $ A área do triângulo definido por?t será então: " " " œ "ß "ß " œ $ œ $ 2015 Julho 15; 10:00 Ano Lectivo: Semestre: Verão
9 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 9 3c ç Basta mostrar que At Á!: "! " At œ! " " œ"!!"!"œ$á! " " " 3d ç O método de ortogonalização de Gram-Schmidt permite obter uma sequência ortogonal /œ /tß/tß/t " $ a partir de uma sequência = At linearmente independente (esta condição é essencial e, como vimos na alínea anterior, ela verifica-se no presente problema). O referido método define a sequência ortogonal /t" ß/tß/t $ a partir da sequência linearmente independente =, por recorrência, de acordo com as expressões seguintes: /t " œ?t œ "ß!ß /t "!ß "ß " "ß!ß " /t œ@ t /t" œ!ß"ß" "ß!ß" /t" /t " "ß!ß " "ß!ß " œ!ß"ß" " " "ß!ß " œ "ß ß " At /t" At /t /t$ œ A t /t" /t /t" /t" /t /t " "ß "ß " "ß!ß " "ß "ß " "ß ß" " œ "ß "ß " "ß!ß " "ß!ß " "ß!ß " " " "ßß" "ßß" "ßß" œ "ß"ß"! "ß!ß"! "ßß" œ "ß"ß" Portanto, a sequência /t" ß/tß/t $ œ "ß!ß" ß"ßß" ß"ß"ß" é a base ortogonal pedida. Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
10 10 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) PARTE 2 1 ç Seja E uma matriz real quadrada de ordem 8 ". Atente nas seguintes proposições envolvendo E: T +ç a E é invertível Í dete E Á!. E 8ß8,ç a det - E œ - det E. 8ß8 - ßE -ç a EE œ E E 8ß8det det. " ".çdete œ Ê E œ adj E. A lista completa formada pelas proposições verdadeiras é: úç +ß -ß. úç,ß - ú ç +ß. úç +ß - Resposta Vejamos agora o valor de verdade das proposições: +ç Aproposição é verdadeira. Temos, sucessivamente, det T det T EE œ EdetE œdetedete œdete Á!ÍdetE Á!ÍEé invertível 8 8,çNeste caso, é det-e œ - dete. A igualdade -dete œ - detesó é verdadeira para E é singular - œ! - œ" - œ" 8ímpar A proposição dada é, pois, falsa. 8 -çneste caso, temos: detee œ dete œ dete. Por ser 8", a igualdade 8 dete œ detesó é verdadeira se Efor singular, isto é, se dete œ!. A proposição dada é, portanto, falsa..ç A proposição é verdadeira. A hipótese dete œ Á! mostra que E é invertível e então: " " " E œ adje œ adje œ adje dete "Î " Em face do exposto, a resposta correcta é a terceira, +ß Julho 15; 10:00 Ano Lectivo: Semestre: Verão
11 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 11 2 ç Seja I um espaço vectorial real e At vectores de I tais que?t Atœ?t$@t. Sendo J o subespaço de I gerado At, então: úç dimj œ! ú ç dimj œ " úç dimj œ úç dimj œ $ Resposta O enunciado permite-nos escrever At œ?t$@tœ?t$ %?t œ "!?t. Assim, At œ?t, %?t ß "!?t?tá9t Então, JœP?t, %?t ß"!?t œ P?t?tÁ9tÊdimJ œ" Concluímos que a opção correcta é a segunda. Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
12 12 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 3 ç Seja 0À $ Ä $ uma aplicação linear tal que 0 "ß!ß! œ "ß "ß! 0!ß "ß! œ!ß "ß " 0!ß!ß " œ "ß!ß ". Apenas uma das seguintes proposições é verdadeira. Assinale-a: ú 0 é sobrejectiva. ú A nulidade de 0 é igual a. ú 0 ß!ß" œ ß"ß". ú O núcleo de 0 é o subespaço gerado por "ß"ß". Resposta A matriz canónica J de 0 tem por colunas as coordenadas na base canónica de 0 "ß!ß!, 0!ß"ß! e 0!ß!ß", portanto: "! " Jœ " "!! " " A expressão geral de 0 é 0BßCßD œbdßbcßcd, como se mostra a seguir: "! " B BD " "! C œ BC! " " D CD A seguir, mostramos que a característica de 0 é igual a : "! " "! " "! " PPÄP " PPÄP $ $ " "! µ! " " µ! " "! " "! " "!!! ç A primeira proposição dada é falsa: Como a característica de 0 é $, 0 não é sobrejectiva. ç A segunda proposição dada é também falsa: A nulidade de 0 é igual a $ œ ". ç A terceira proposição é, igualmente, falsa: Temos, usando a expressão 0BßCßD œbdßbcßcd, com BßCßD œ ß!ß" : 0 ß!ß" œ "ß!ß!" œ $ßß" Á ß"ß" ç A última proposição dada é verdadeira: Por definição, tem-se Ker0 œbßcßdà0bßcßd œ!ß!ß! œbßcßdàbdßbcßcd œ!ß!ß! œbßcßdàbdœ! BCœ! CDœ! Trata-se, portanto, do espaço das soluções do sistema homogéneo anterior (espaço nulo de J ): "! "! "! "! "! "! B œ D PPÄP " PPÄP $ $ " "!! µ! " "! µ! " "! Ê C œ D! " "!! " "!!!!! D œ D 2015 Julho 15; 10:00 Ano Lectivo: Semestre: Verão
13 Álgebra Linear e Geometria Analítica - Resolução do Exame (Época de Recurso) 13 A solução geral é BßCßD œ DßDßD œ D "ß"ß " ; portanto, Ker0 œ D "ß "ß " À D œ > "ß "ß " À > œ P "ß "ß " A resposta correcta é, portanto, a última. Ano Lectivo: Semestre: Verão 2015 Julho 15; 10:00
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 20 de Fevereiro de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 20 de Fevereiro de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 1º Teste 29 de Abril de 2015; 18:30 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 1º Teste 29 de Abril de 2015; 18:30 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução da Repetição do 1º este 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução da Repetição do 1º este 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 1º Teste
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 07 de Maio de 2012 Ano Lectivo: 2011-2012 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução do
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do 1º este 07 de Maio de 2012 Ano Lectivo: 2011-2012 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução do
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 1º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste 01 de Fevereiro de 2013 Ano Lectivo: 2012-2013 Semestre: Inverno ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste 01 de Fevereiro de 2013 Ano Lectivo: 2012-2013 Semestre: Inverno ISEL è ADMat Secção de Álgebra ç ALGA Álgebra Linear e Geometria
EXAME DE ÁLGEBRA LINEAR (Semestre Alternativo, Alameda) GRUPO I
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise EXAME DE ÁLGEBRA LINEAR (Semestre Alternativo, Alameda) (24/JUNHO/2005) Duração: 3h Nome de Aluno: Número de Aluno: Curso:
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise EXAME DE ÁLGEBRA LINEAR (Semestre Alternativo, Alameda) (24/JUNHO/2005) Duração: 3h Nome de Aluno: Número de Aluno: Curso:
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Multiplicidade geométrica
 Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
ficha 2 determinantes
 Exercícios de Álgebra Linear ficha 2 determinantes Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 Determinantes 2 Sendo
Exercícios de Álgebra Linear ficha 2 determinantes Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 Determinantes 2 Sendo
Aulas práticas de Álgebra Linear
 Ficha 2 Determinantes Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores 1 o semestre 2016/17 Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto
Ficha 2 Determinantes Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores 1 o semestre 2016/17 Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto
Lista 6: transformações lineares.
 Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Álgebra Linear e Geometria Anaĺıtica
 Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
Álgebra Linear e Geometria Anaĺıtica 2016/17 MIEI+MIEB+MIEMN Slides da 4 a Semana de aulas Cláudio Fernandes (FCT/UNL) Departamento de Matemática 1 / 27 Programa 1 Matrizes 2 Sistemas de Equações Lineares
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Separe em grupos de folhas diferentes as resoluções dos grupos I e II das resoluções dos grupos III e IV GRUPO I (50 PONTOS)
 Faculdade de Ciências Económicas e Empresariais UCP MATEMÁTICA I FREQUÊNCIA 1 - versão A Duração: 15 minutos Durante a prova não serão prestados quaisquer tipo de esclarecimentos. Qualquer dúvida ou questão
Faculdade de Ciências Económicas e Empresariais UCP MATEMÁTICA I FREQUÊNCIA 1 - versão A Duração: 15 minutos Durante a prova não serão prestados quaisquer tipo de esclarecimentos. Qualquer dúvida ou questão
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
0 1. Assinale a alternativa verdadeira Q1. Seja A = (d) Os autovalores de A 101 são i e i. (c) Os autovalores de A 101 são 1 e 1.
 Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Álgebra Linear e Geometria Analítica D
 1 3 Departamento de Matemática Álgebra Linear e Geometria Analítica D Primeiro Teste 21 de Novembro de 2009 Nome: Número de caderno: PREENCHA DE FORMA BEM LEGÍVEL Grelha de Respostas A B C D 1 2 3 4 5
1 3 Departamento de Matemática Álgebra Linear e Geometria Analítica D Primeiro Teste 21 de Novembro de 2009 Nome: Número de caderno: PREENCHA DE FORMA BEM LEGÍVEL Grelha de Respostas A B C D 1 2 3 4 5
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral
 Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Departamento de Matemática
 Departamento de Matemática ALGA e Álgebra Linear Folhas Práticas - /6 EAmb/EC/EGI/EM Determinantes (*) Calcule o valor do determinante das seguintes matrizes A = + i, B = i, C = 6 i, D = 6 i i E = 6, F
Departamento de Matemática ALGA e Álgebra Linear Folhas Práticas - /6 EAmb/EC/EGI/EM Determinantes (*) Calcule o valor do determinante das seguintes matrizes A = + i, B = i, C = 6 i, D = 6 i i E = 6, F
Geometria anaĺıtica e álgebra linear
 Geometria anaĺıtica e álgebra linear Francisco Dutenhefner Departamento de Matematica ICEx UFMG 22/08/13 1 / 24 Determinante: teorema principal Teorema: Se A é uma matriz quadrada, então o sistema linear
Geometria anaĺıtica e álgebra linear Francisco Dutenhefner Departamento de Matematica ICEx UFMG 22/08/13 1 / 24 Determinante: teorema principal Teorema: Se A é uma matriz quadrada, então o sistema linear
Geometria Analítica e Álgebra Linear
 UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:
![1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com: 1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:](/thumbs/68/59802332.jpg) Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que:
 21002 - Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que: Verifique se o ficheiro que recebeu está correcto. O
21002 - Álgebra Linear I Ano lectivo 2015/16 Docente: António Araújo e-fólio A (20 a 30 de novembro) Para a resolução do e-fólio, aconselha-se que: Verifique se o ficheiro que recebeu está correcto. O
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA a LISTA DE EXERCÍCIOS DE MAT 7 II SEMESTRE DE 00 Professores: Flávia, Gustavo e Lana. Suponha que uma força
Produto interno no espaço vectorial R n
 ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
Álgebra Linear - 1 a lista de exercícios Prof. - Juliana Coelho
 Álgebra Linear - a lista de exercícios Prof. - Juliana Coelho - Considere as matrizes abaixo e faça o que se pede: M N O 7 P Q R 8 4 T S a b a Determine quais destas matrizes são simétricas. E antisimétricas?
Álgebra Linear - a lista de exercícios Prof. - Juliana Coelho - Considere as matrizes abaixo e faça o que se pede: M N O 7 P Q R 8 4 T S a b a Determine quais destas matrizes são simétricas. E antisimétricas?
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
Matemática- 2008/ Se possível, dê exemplos de: (no caso de não ser possível explique porquê)
 Matemática- 00/09. Se possível, dê exemplos de (no caso de não ser possível explique porquê) (a) Uma matriz do tipo ; cujos elementos principais sejam 0. (b) Uma matriz do tipo ; cujo elemento na posição
Matemática- 00/09. Se possível, dê exemplos de (no caso de não ser possível explique porquê) (a) Uma matriz do tipo ; cujos elementos principais sejam 0. (b) Uma matriz do tipo ; cujo elemento na posição
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
AULA Exercícios. DEMONSTRAR QUE UMA TRANSFORMAÇÃO É LINEAR Se A é uma matriz real m n e. u R, a aplicação T : R R tal que
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
EXERCÍCIOS DE ÁLGEBRA LINEAR. Prefácio 3. Parte 1. Sistemas de equações lineares 4. Parte 2. Matrizes 10. Parte 3.
 EXERCÍCIOS DE ÁLGEBRA LINEAR PEDRO MATIAS Conteúdo Prefácio 3 Parte 1. Sistemas de equações lineares 4 Parte 2. Matrizes 10 Parte 3. Determinantes 16 Parte 4. Geometria analítica 18 Parte 5. Espaços lineares
EXERCÍCIOS DE ÁLGEBRA LINEAR PEDRO MATIAS Conteúdo Prefácio 3 Parte 1. Sistemas de equações lineares 4 Parte 2. Matrizes 10 Parte 3. Determinantes 16 Parte 4. Geometria analítica 18 Parte 5. Espaços lineares
FACULDADE DE CIÊNCIAS ECONÓMICAS E EMPRESARIAIS. Matemática I 1 a Frequência: 27 de Outubro de 2009
 FACULDADE DE CIÊNCIAS ECONÓMICAS E EMPRESARIAIS Matemática I 1 a Frequência: 27 de Outubro de 2009 A frequência consiste em duas partes, tem uma duração de 2h30m e está cotado para 20 valores, é efectuado
FACULDADE DE CIÊNCIAS ECONÓMICAS E EMPRESARIAIS Matemática I 1 a Frequência: 27 de Outubro de 2009 A frequência consiste em duas partes, tem uma duração de 2h30m e está cotado para 20 valores, é efectuado
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Método de Gauss-Jordan e Sistemas Homogêneos
 Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Apontamentos das aulas teóricas de Álgebra Linear
 Apontamentos das aulas teóricas de Álgebra Linear Cursos: MEAmbi e MEBio 1 o Semestre 2015/2016 Prof Paulo Pinto http://wwwmathtecnicoulisboapt/ ppinto Conteúdo 1 Matrizes e sistemas lineares 1 11 Álgebra
Apontamentos das aulas teóricas de Álgebra Linear Cursos: MEAmbi e MEBio 1 o Semestre 2015/2016 Prof Paulo Pinto http://wwwmathtecnicoulisboapt/ ppinto Conteúdo 1 Matrizes e sistemas lineares 1 11 Álgebra
PROGRAMA ÁLGEBRA LINEAR, MEEC (AL-10) Aula teórica 32
 ÁLGEBRA LINEAR, MEEC (AL-10) Aula teórica 32 PROGRAMA 1. Sistemas de equações lineares e matrizes 1.1 Sistemas 1.2 Matrizes 1.3 Determinantes 2. Espaços vectoriais (ou espaços lineares) 2.1 Espaços e subespaços
ÁLGEBRA LINEAR, MEEC (AL-10) Aula teórica 32 PROGRAMA 1. Sistemas de equações lineares e matrizes 1.1 Sistemas 1.2 Matrizes 1.3 Determinantes 2. Espaços vectoriais (ou espaços lineares) 2.1 Espaços e subespaços
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
x 1 3x 2 2x 3 = 0 2 x 1 + x 2 x 3 6x 4 = 2 6 x x 2 3x 4 + x 5 = 1 ( f ) x 1 + 2x 2 3x 3 = 6 2x 1 x 2 + 4x 3 = 2 4x 1 + 3x 2 2x 3 = 4
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
Universidade Federal de Ouro Preto Departamento de Matemática MTM112 - Introdução à Álgebra Linear - Turmas 81, 82 e 84 Lista 1 - Tiago de Oliveira
 Universidade Federal de Ouro Preto Departamento de Matemática MTM2 - Introdução à Álgebra Linear - Turmas 8, 82 e 84 Lista - Tiago de Oliveira Reveja a teoria e os exercícios feitos em sala. 2 3 2 0. Sejam
Universidade Federal de Ouro Preto Departamento de Matemática MTM2 - Introdução à Álgebra Linear - Turmas 8, 82 e 84 Lista - Tiago de Oliveira Reveja a teoria e os exercícios feitos em sala. 2 3 2 0. Sejam
UFSC Matrizes. Prof. BAIANO
 UFSC Matrizes Prof. BAIANO Matrizes Classifique como Verdadeiro ou Falso ( F ) Uma matriz é dita retangular, quando o número de linhas é igual ao número de colunas. ( F ) A matriz identidade é aquela em
UFSC Matrizes Prof. BAIANO Matrizes Classifique como Verdadeiro ou Falso ( F ) Uma matriz é dita retangular, quando o número de linhas é igual ao número de colunas. ( F ) A matriz identidade é aquela em
Sebenta de exercícios de Álgebra Linear e Geometria Analítica. Curso: Eng. Topográ ca
 Sebenta de exercícios de Álgebra Linear e Geometria Analítica Curso: Eng. Topográ ca Ano Lectivo 009/010 4 de Setembro de 009 (Versão: 1.0) Índice Notações e terminologia ii 1 Revisão sobre noções elementares
Sebenta de exercícios de Álgebra Linear e Geometria Analítica Curso: Eng. Topográ ca Ano Lectivo 009/010 4 de Setembro de 009 (Versão: 1.0) Índice Notações e terminologia ii 1 Revisão sobre noções elementares
Introdução à Álgebra Linear - 1a lista de exercícios Prof. - Juliana Coelho
 Introdução à Álgebra Linear - a lista de exercícios Prof. - Juliana Coelho - Ache uma forma escalonada para cada matriz abaixo. (Lembre que a forma escalonada não é única, então você pode obter uma resposta
Introdução à Álgebra Linear - a lista de exercícios Prof. - Juliana Coelho - Ache uma forma escalonada para cada matriz abaixo. (Lembre que a forma escalonada não é única, então você pode obter uma resposta
PLANO DE ENSINO E APRENDIZAGEM
 SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR (A) DA DISCIPLINA:
SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR (A) DA DISCIPLINA:
Aula 5 - Produto Vetorial
 Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares
 FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
FATEC Notas de Aulas de Matrizes, Determinantes e Sistemas Lineares Prof Dr Ânderson Da Silva Vieira 2017 Sumário Introdução 2 1 Matrizes 3 11 Introdução 3 12 Tipos especiais de Matrizes 3 13 Operações
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Lista de Álgebra Linear Aplicada
 Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
0.1 Matrizes, determinantes e sistemas lineares
 SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ PARFOR MATEMÁTICA Lista de Exercícios para a Prova Substituta de Álgebra Linear 0.1 Matrizes, determinantes e sistemas lineares 1. Descreva explicitamente
SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ PARFOR MATEMÁTICA Lista de Exercícios para a Prova Substituta de Álgebra Linear 0.1 Matrizes, determinantes e sistemas lineares 1. Descreva explicitamente
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras EDIÇÃO, DISTRIBUIÇÃO E VENDAS SÍLABAS & DESAFIOS - UNIPESSOAL LDA. NIF:
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras EDIÇÃO, DISTRIBUIÇÃO E VENDAS SÍLABAS & DESAFIOS - UNIPESSOAL LDA. NIF:
Análise Dinâmica de Sistemas Mecânicos e Controle
 Análise Dinâmica de Sistemas Mecânicos e Controle Unidade 3 Espaço de Estados: álgebra e resolução das equações dinâmicas Prof. Thiago da Silva Castro [email protected] Para trabalhar no
Análise Dinâmica de Sistemas Mecânicos e Controle Unidade 3 Espaço de Estados: álgebra e resolução das equações dinâmicas Prof. Thiago da Silva Castro [email protected] Para trabalhar no
Sistemas lineares e matrizes, C = e C =
 1. Considere as matrizes ( 2 1 A 4 0 1 MATEMÁTICA I (M 195 (BIOLOGIA, BIOQUÍMICA E ARQUITETURA PAISAGISTA 2014/2015, B Sistemas lineares e matrizes ( 4 1 2 5 1 Verifique se está definida e, caso esteja,
1. Considere as matrizes ( 2 1 A 4 0 1 MATEMÁTICA I (M 195 (BIOLOGIA, BIOQUÍMICA E ARQUITETURA PAISAGISTA 2014/2015, B Sistemas lineares e matrizes ( 4 1 2 5 1 Verifique se está definida e, caso esteja,
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CURSO: CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROF.: MARCELO SILVA.
 UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CURSO: CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROF.: MARCELO SILVA Determinantes Introdução Como já vimos, matriz quadrada é a que tem o mesmo número
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CURSO: CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROF.: MARCELO SILVA Determinantes Introdução Como já vimos, matriz quadrada é a que tem o mesmo número
Sistemas de Equações Lineares e Matrizes
 Sistemas de Equações Lineares e Matrizes. Quais das seguintes equações são lineares em x, y, z: (a) 2x + 2y 5z = x + xy z = 2 (c) x + y 2 + z = 2 2. A parábola y = ax 2 + bx + c passa pelos pontos (x,
Sistemas de Equações Lineares e Matrizes. Quais das seguintes equações são lineares em x, y, z: (a) 2x + 2y 5z = x + xy z = 2 (c) x + y 2 + z = 2 2. A parábola y = ax 2 + bx + c passa pelos pontos (x,
A forma canônica de Jordan
 A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Produto Misto, Determinante e Volume
 15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
Instituto de Economia UFRJ Prof: Ary Álgebra Linear 2017/1 PROGRAMA
 Instituto de Economia UFRJ Prof: Ary Álgebra Linear 2017/1 PROGRAMA EMENTA: Vetores. Matrizes. Determinantes. Sistemas Lineares Transformações Lineares. Produto Vetorial. Produto Escalar. Espaços vetoriais.
Instituto de Economia UFRJ Prof: Ary Álgebra Linear 2017/1 PROGRAMA EMENTA: Vetores. Matrizes. Determinantes. Sistemas Lineares Transformações Lineares. Produto Vetorial. Produto Escalar. Espaços vetoriais.
2. (Ufrj 2003) Os números reais a, b, c e d formam, nesta ordem, uma progressão aritmética. Calcule o determinante da matriz
 1 Projeto Jovem Nota 10 1. (Uff 2000) Numa progressão aritmética, de termo geral aš e razão r, tem-se a=r=1/2. Calcule o determinante da matriz mostrada na figura adiante. 2. (Ufrj 2003) Os números reais
1 Projeto Jovem Nota 10 1. (Uff 2000) Numa progressão aritmética, de termo geral aš e razão r, tem-se a=r=1/2. Calcule o determinante da matriz mostrada na figura adiante. 2. (Ufrj 2003) Os números reais
Álgebra Linear I. Resumo e Exercícios P3
 Álgebra Linear I Resumo e Exercícios P3 Fórmulas e Resuminho Teórico Espaço Vetorial Qualquer conjunto V com 2 operações: Soma e Produto escalar, tal que 1. u + v + w = u + v + w u, v, w V 2. u + v = v
Álgebra Linear I Resumo e Exercícios P3 Fórmulas e Resuminho Teórico Espaço Vetorial Qualquer conjunto V com 2 operações: Soma e Produto escalar, tal que 1. u + v + w = u + v + w u, v, w V 2. u + v = v
Mensagem descodificada. Mensagem recebida. c + e
 Suponhamos que, num determinado sistema de comunicação, necessitamos de um código com, no máximo, q k palavras. Poderemos então usar todas as palavras a a 2 a k F k q de comprimento k. Este código será
Suponhamos que, num determinado sistema de comunicação, necessitamos de um código com, no máximo, q k palavras. Poderemos então usar todas as palavras a a 2 a k F k q de comprimento k. Este código será
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Aula 1 Autovetores e Autovalores de Matrizes Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17
 Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Os Quatro Subespaços Fundamentais
 Álgebra Linear e Geometria Analítica Texto de apoio Professor João Soares 7 páginas Universidade de Coimbra 26 de Novembro de 29 Os Quatro Subespaços Fundamentais Seja A uma matriz m n de elementos reais.
Álgebra Linear e Geometria Analítica Texto de apoio Professor João Soares 7 páginas Universidade de Coimbra 26 de Novembro de 29 Os Quatro Subespaços Fundamentais Seja A uma matriz m n de elementos reais.
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR
 UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROFESSOR: MARCELO SILVA 1. Introdução No ensino fundamental você estudou
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROFESSOR: MARCELO SILVA 1. Introdução No ensino fundamental você estudou
ÍNDICE MATRIZES SISTEMAS DE EQUAÇÕES LINEARES ESPAÇO VETORIAL REAL DE DIMENSÃO FINITA
 ÍNDICE MATRIZES Definição 1 Igualdade 2 Matrizes Especiais 2 Operações com Matrizes 3 Classificação de Matrizes Quadradas 9 Operações Elementares 11 Matriz Equivalente por Linha 11 Matriz na Forma Escalonada
ÍNDICE MATRIZES Definição 1 Igualdade 2 Matrizes Especiais 2 Operações com Matrizes 3 Classificação de Matrizes Quadradas 9 Operações Elementares 11 Matriz Equivalente por Linha 11 Matriz na Forma Escalonada
Diagonalização unitária e diagonalização ortogonal. (Positividade do produto interno) Raíz quadrada. Formas quadráticas.
 Aplicações: Diagonalização unitária e diagonalização ortogonal (Positividade do produto interno) Raíz quadrada Formas quadráticas Mínimos quadrados Produto externo e produto misto (Área do paralelogramo.
Aplicações: Diagonalização unitária e diagonalização ortogonal (Positividade do produto interno) Raíz quadrada Formas quadráticas Mínimos quadrados Produto externo e produto misto (Área do paralelogramo.
2. Calcule o determinante das seguintes matrizes usando o teorema de Laplace. ab (a) (b) (c) 2 5. (e) 0 a b a 0 c b c 0. (h)
 3.. determinante de uma riz página /5 departamento de emática universidade de aveiro. Determine o número de inversões e classifica qnto à paridade as seguintes permutações de {,, 3, 4, 5}: (3, 4,, 5, )
3.. determinante de uma riz página /5 departamento de emática universidade de aveiro. Determine o número de inversões e classifica qnto à paridade as seguintes permutações de {,, 3, 4, 5}: (3, 4,, 5, )
αx + 2y + (α + 1)z + 2αw = β 1. [40 pontos] Discuta o sistema em função dos parâmetros α, β e γ.
![αx + 2y + (α + 1)z + 2αw = β 1. [40 pontos] Discuta o sistema em função dos parâmetros α, β e γ. αx + 2y + (α + 1)z + 2αw = β 1. [40 pontos] Discuta o sistema em função dos parâmetros α, β e γ.](/thumbs/58/41749349.jpg) Católica Lisbon School of Business and Economics UCP MATEMÁTICA I MINI-TESTE 1 - versão A Duração: 90 minutos Durante a prova não serão prestados quaisquer tipo de esclarecimentos. Qualquer dúvida ou questão
Católica Lisbon School of Business and Economics UCP MATEMÁTICA I MINI-TESTE 1 - versão A Duração: 90 minutos Durante a prova não serão prestados quaisquer tipo de esclarecimentos. Qualquer dúvida ou questão
Álgebra Linear Teoria de Matrizes
 Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
(Todos os cursos da Alameda) Paulo Pinto
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Resumo das Aulas Teóricas de 2 o Semestre 2004/2005 (Todos os cursos da Alameda) Paulo Pinto Álgebra Linear Conteúdo Sistemas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Resumo das Aulas Teóricas de 2 o Semestre 2004/2005 (Todos os cursos da Alameda) Paulo Pinto Álgebra Linear Conteúdo Sistemas
Sistemas Lineares. Juliana Pimentel. juliana.pimentel. Sala Bloco A, Torre 2
 Sistemas Lineares Juliana Pimentel [email protected] http://hostel.ufabc.edu.br/ juliana.pimentel Sala 507-2 - Bloco A, Torre 2 O que é uma equação linear? O que é uma equação linear? Ex: 1)
Sistemas Lineares Juliana Pimentel [email protected] http://hostel.ufabc.edu.br/ juliana.pimentel Sala 507-2 - Bloco A, Torre 2 O que é uma equação linear? O que é uma equação linear? Ex: 1)
Capítulo 1. Matrizes e Sistema de Equações Lineares. 1.1 Corpos
 Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
Capítulo 1 Matrizes e Sistema de Equações Lineares Neste capítulo apresentaremos as principais de nições e resultados sobre matrizes e sistemas de equações lineares que serão necessárias para o desenvolvimento
Trabalhos e Exercícios 1 de Álgebra Linear
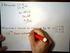 Trabalhos e Exercícios de Álgebra Linear Fabio Iareke 30 de março de 0 Trabalhos. Mostre que se A tem uma linha nula, então AB tem uma linha nula.. Provar as propriedades abaixo:
Trabalhos e Exercícios de Álgebra Linear Fabio Iareke 30 de março de 0 Trabalhos. Mostre que se A tem uma linha nula, então AB tem uma linha nula.. Provar as propriedades abaixo:
Universidade Federal de Uberlândia Faculdade de Matemática
 Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
Universidade Federal de Uberlândia Faculdade de Matemática Universidade Federal de Uberlândia Faculdade de Matemática Disciplina : Geometria Analítica e Álgebra Linear - GCI004 Assunto: Espaços vetoriais
ÁLGEBRA LINEAR SISTEMAS DE EQUAÇÕES LINEARES
 ÁLGEBRA LINEAR SISTEMAS DE EQUAÇÕES LINEARES Luís Felipe Kiesow de Macedo Universidade Federal de Pelotas - UFPel 1 / 14 Sistemas de Equações Lineares 1 Sistemas e Matrizes 2 Operações Elementares 3 Forma
ÁLGEBRA LINEAR SISTEMAS DE EQUAÇÕES LINEARES Luís Felipe Kiesow de Macedo Universidade Federal de Pelotas - UFPel 1 / 14 Sistemas de Equações Lineares 1 Sistemas e Matrizes 2 Operações Elementares 3 Forma
I Lista de Álgebra Linear /02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple
 1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
1 I Lista de Álgebra Linear - 2012/02 Matrizes-Determinantes e Sistemas Prof. Iva Zuchi Siple 1. Determine os valores de x e y que tornam verdadeira a igualdade ( x 2 + 5x x 2 ( 6 3 2x y 2 5y y 2 = 5 0
PROGRAMA DE DISCIPLINA
 PROGRAMA DE DISCIPLINA Disciplina: ÁLGEBRA LINEAR E CÁLCULO VETORIAL Código da Disciplina: NDC152 Curso: Engenharia Civil Semestre de oferta da disciplina: 2 Faculdade responsável: NÚCLEO DE DISCIPLINAS
PROGRAMA DE DISCIPLINA Disciplina: ÁLGEBRA LINEAR E CÁLCULO VETORIAL Código da Disciplina: NDC152 Curso: Engenharia Civil Semestre de oferta da disciplina: 2 Faculdade responsável: NÚCLEO DE DISCIPLINAS
. Repare que ao multiplicar os vetores (-1,1) e
 Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
