Lista 1 Matemática Pré-Vestibular Probabilidade
|
|
|
- Pedro Lucas Igor da Rocha de Sintra
- 8 Há anos
- Visualizações:
Transcrição
1 /0 Lista Matemática Pré-Vestibular Probabilidade PROF. WANZELLER. (ACAFE 0) Uma gaveta tem duas bolas azuis, três bolas brancas e cinco bolas vermelhas. Considere as afirmações a seguir, assinalando V para as verdadeiras e F para as falsas. ( ) Se retirarmos, consecutivamente e sem reposição, todas as bolas dessa gaveta e formarmos uma sequência com essas bolas, o número de sequências diferentes que podemos obter é. 0. ( ) Se retirarmos, sem reposição, três bolas dessa gaveta, uma a uma, a probabilidade de tirarmos, nessa ordem, bolas nas cores azul, branca e vermelha é. ( ) A probabilidade de se retirar, aleatoriamente, uma bola branca e, em seguida, sem reposição, retirar outra bola branca é inferior a 0%. ( ) O número de bolas amarelas que devem ser colocadas nessa gaveta, de modo que a probabilidade ao retirarmos, aleatoriamente, uma bola amarela seja igual a 8, é um número múltiplo de. A sequência correta, de cima para baixo, é: V F F V V V V F F F F V F V V F. (UNICAMP 0) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a: (FUVEST 0) Em um experimento probabilístico, Joana 8 0 retirará aleatoriamente bolas de uma caixa contendo bolas azuis e bolas vermelhas. Ao montar-se o experimento, colocamse bolas azuis na caixa: Quantas bolas vermelhas devem ser acrescentadas para que a probabilidade de Joana obter azuis seja?. (FGV 0) O torneio de futebol masculino nos Jogos Olímpicos de Verão 0 contará com times. Na Fase, serão formados quatro grupos com quatro times cada um. Cada time enfrentará, uma única vez, os demais times de seu próprio grupo. Suponha que os times sejam sorteados aleatoriamente entre os grupos (qualquer combinação de times por grupo pode ocorrer, com igual probabilidad. Suponha, também, que os times do Brasil e da Alemanha participem do torneio. Qual será o número total de jogos na Fase desse torneio? Nas condições estabelecidas no enunciado desta questão, qual é a probabilidade de que Brasil e Alemanha se enfrentem na Fase do torneio? João é fã de futebol e conseguiu ingressos para dois jogos da Fase do referido torneio. Considere que a chance de João obter ingresso para qualquer dos jogos da Fase seja a mesma. Nessas condições, qual é a probabilidade de que João assista a pelo menos um jogo da seleção do Brasil?. (ACAFE 0) O Exame de Papanicolau é um teste usado para o diagnóstico do câncer cervical (câncer de colo de útero), muitas vezes causado pela infecção do papiloma vírus humano, HPV. Para avaliar a qualidade de diagnóstico do Exame Papanicolau, 00 mulheres de uma determinada região foram submetidas ao teste, sendo que 00 estavam sadias (sem câncer) e 00 estavam doentes (com câncer). Após o teste, verificou-se que, dos resultados referentes às mulheres sadias, 0 eram negativo e, dos resultados referentes às mulheres doentes, 9 deram positivo. Analise as proposições abaixo e classifique-as em V - verdadeiras ou F - falsas. ( ) A probabilidade do teste Papanicolau ter resultado negativo, dentre as pacientes que não têm câncer, é de 8%. ( ) A probabilidade do teste Papanicolau ter resultado positivo, dentre as pacientes que realmente têm câncer, é 0, 9%. ( ) A probabilidade de uma paciente realmente ter câncer, dentre aquelas com resultado positivo no teste Papanicolau, é de 0, %. ( ) A probabilidade de uma paciente não ter câncer, dentre aquelas com resultado negativo no teste Papanicolau, é aproximadamente 98%. ( ) A probabilidade de uma paciente realmente ter câncer, dentre aquelas com resultado negativo no teste Papanicolau, é inferior a %. A sequência correta, de cima para baixo, é: V - V - F - F - V F - F - V - V - V V - F - V - F - F F - V - F - V V
2 /0. (UNESP 0) Um dado convencional e uma moeda, ambos não viciados, serão lançados simultaneamente. Uma das faces da moeda está marcada com o número e a outra com o número A probabilidade de que a média aritmética entre o número obtido da face do dado e o da face da moeda esteja entre e é igual a:. (INSPER 0) Em um curso de computação, uma das atividades consiste em criar um jogo da memória com as seis cartas mostradas a seguir. 8. (INSPER 0) A probabilidade de que o primeiro jogador forme um par em sua primeira tentativa é: (UERJ 0) Os consumidores de uma loja podem concorrer a brindes ao fazerem compras acima de R$ 00. Para isso, recebem um cartão de raspar no qual estão registradas letras do alfabeto em cinco linhas. Ao consumidor é informado que cada linha dispõe as seguintes letras, em qualquer ordem: linha {A, B, C, D, E}; linha {F, G, H, I, J}; linha {L, M, N, O, P}; linha {Q, R, S, T, U}; linha {V, X, Z}. Observe um exemplo desses cartões, com as letras ainda visíveis: Inicialmente, o programa embaralha as cartas e apresenta-as viradas para baixo. Em seguida, o primeiro jogador vira duas cartas e tenta formar um par. Suponha que o primeiro jogador tenha virado as duas cartas mostradas abaixo. Para que um consumidor ganhasse um secador, teria de raspar o cartão exatamente nas letras dessa palavra, como indicado abaixo: Como não foi feito par, o programa desvira as duas cartas e é a vez do segundo jogador, que utiliza a seguinte estratégia: ele vira uma das quatro cartas que não foi virada pelo primeiro jogador. Se a carta virada for um quadrado ou um triângulo, ele certamente forma um par, pois sabe onde está a carta correspondente. Caso contrário, ele vira uma das outras três cartas que ainda não foram viradas. A probabilidade de que o segundo jogador forme um par usando a estratégia descrita é: Considere um consumidor que receba um cartão para concorrer a um ventilador. Se ele raspar as letras corretas em cada linha para formar a palavra VENTILADOR, a probabilidade de que ele seja premiado corresponde a:
3 /0 0. (UEG 0) Pedro jogou dois dados comuns numerados de a. Sabendo-se que o produto dos números sorteados nos dois dados é múltiplo de, a probabilidade de terem sido sorteados os números e é uma em: (UERJ 0) Em uma urna, foram colocadas trinta bolas, numeradas de a 0. Uma dessas bolas foi sorteada aleatoriamente. Em relação a essa experiência, considerem-se os dois eventos abaixo:. (ESPM 0) Escolhendo-se ao acaso dois algarismos distintos do sistema decimal de numeração, a probabilidade de que a soma deles seja um número primo é: 0% 0% 0% % %. (PUC RJ 0) Eugênio tem três dados que são dodecaedros regulares, com os números inteiros de a escritos nas faces: Evento A: {a bola sorteada tem número menor ou igual a 0 }. Evento B: {a bola sorteada tem número maior do que k }. Sabendo que k 0, k e determine o valor de k. P( a b ),. (AFA 0) Em uma mesa há dois vasos com rosas. O vaso A contém 9 rosas das quais tem espinhos e o vaso B contém 8 rosas sendo que exatamente não tem espinhos. Retira-se, aleatoriamente, uma rosa do vaso A e coloca-se em B. Em seguida, retira-se uma rosa de B. A probabilidade de essa rosa retirada de B ter espinhos é: 8 8 ; 8 ; 8 8 ; 8 ;. (IFSP 0) O gráfico abaixo apresenta informações sobre os números de livros lidos no mês passado pelos alunos de uma determinada turma. Sabendo-se que a informação de todos os alunos consta nesse gráfico, e que não há aluno que leu mais de livros, utilize-o para responder à(s) questão(ões). Eugênio sorteia um número inteiro jogando os três dados simultaneamente e somando os três números obtidos (ou seja, ele soma os três números que aparecem na face de cima de cada um dos dados). Qual é a probabilidade de que o número sorteado seja igual a? Qual é a probabilidade de que o número sorteado seja igual a 0? Qual é a probabilidade de que o número sorteado seja maior ou igual a 0?. (Enem 0) Em uma central de atendimento, cem pessoas receberam senhas numeradas de até 00. Uma das senhas é sorteada ao acaso. Qual é a probabilidade de a senha sorteada ser um número de a 0? Escolhido aleatoriamente um aluno dessa turma, a probabilidade de o aluno escolhido não ter lido livro no mês passado é:,%, %,%, %,%
4 /0. (UERJ 0) Cada uma das 8 peças do jogo de dominó convencional, ilustradas abaixo, contêm dois números, de zero a seis, indicados por pequenos círculos ou, no caso do zero, por sua ausência.. (PUC PR 0) Em um grupo de 00 pessoas, 0 são homens e 80 são mulheres. Se a probabilidade de um homem estar com uma determinada doença é de 0, 0 e de uma mulher estar com a mesma doença é de 0,, qual é a probabilidade de uma pessoa deste grupo, escolhida ao acaso, estar com essa doença?. 9%. 9%., %. 0, %. 8, %. Admita um novo tipo de dominó, semelhante ao convencional, no qual os dois números de cada peça variem de zero a dez. Observe o desenho de uma dessas peças:. (Enem 0) No próximo final de semana, um grupo de alunos participará de uma aula de campo. Em dias chuvosos, aulas de campo não podem ser realizadas. A ideia é que essa aula seja no sábado, mas, se estiver chovendo no sábado, a aula será adiada para o domingo. Segundo a meteorologia, a probabilidade de chover no sábado é de 0% e a de chover no domingo é de %. A probabilidade de que a aula de campo ocorra no domingo é de: Considere que uma peça seja retirada ao acaso do novo dominó. Calcule a probabilidade de essa peça apresentar um número seis ou um número nove. 8. (PUC MG 0) Em uma população humana, a probabilidade 0 de um indivíduo ser mudo é estimada em 0000, a 8 probabilidade de ser cego é, e a probabilidade de ser 0000 mudo e cego é. Nesse caso, ser mudo não exclui a 0000 possibilidade de ser cego. Com base nessas informações, a probabilidade de um indivíduo, escolhido ao acaso, ser mudo ou cego é igual a: 0, 09 0, 0 0, 0 0, 0 9. (PUC RJ 0) Temos um baralho com 0 cartas, numeradas de a 0. Depois de embaralhar, viramos três cartas lado a lado sobre a mesa e somamos os três números que aparecem. Qual a probabilidade de a soma total ser? Qual a probabilidade de a soma total ser 9? 0. (UEG 0) A tabela a seguir apresenta a preferência de homens e mulheres em relação a um prato, que pode ser doce ou salgado, típico de certa região do Estado de Goiás. Sexo Preferências Doce Salgado Masculino 80 0 Feminino 0 0 0,%,%,% 0,% 0,% 0. (ITA 0) Três pessoas, aqui designadas por A, B e C, realizam o seguinte experimento: A recebe um cartão em branco e nele assinala o sinal ou o sinal, passando em seguida a B, que mantém ou troca o sinal marcado por A e repassa o cartão a C. Este, por sua vez, também opta por manter ou trocar o sinal do cartão. Sendo de a probabilidade de A escrever o sinal e de as respectivas probabilidades de B e C trocarem o sinal recebido, determine a probabilidade de A haver escrito o sinal sabendo-se ter sido este o sinal ao término do experimento.. (UEG 0) Evandro está pensando em convidar Ana Paula para ir ao cinema no próximo domingo, entretanto, ele sabe que se estiver chovendo nesse dia, a probabilidade de ela aceitar é de 0%; caso contrário, a probabilidade de ela aceitar é de 90%. Sabendo-se que a probabilidade de estar chovendo no domingo é de 0%, a probabilidade de Ana Paula aceitar o convite de Evandro é de: 0, 0 0, 0, 9 0, 0 Considerando-se os dados apresentados na tabela, a probabilidade de um desses indivíduos preferir o prato típico doce, sabendo-se que ele é do sexo feminino, é de: 0, 0, 0 0, 0 0, 0
5 /0. (FUVEST 0) De um baralho de 8 cartas, sete de cada naipe, Luís recebe cinco cartas: duas de ouros, uma de espadas, uma de copas e uma de paus. Ele mantém consigo as duas cartas de ouros e troca as demais por três cartas escolhidas ao acaso dentre as cartas que tinham ficado no baralho. A probabilidade de, ao final, Luís conseguir cinco cartas de ouros é: (UEPA 0) Leia o texto para responder à questão. Sabe-se que ler cria bons estudantes, melhora a capacidade de relacionamento e ativa os lugares certos do cérebro. Cultivar o hábito da leitura surte efeitos nítidos: desenvolve a imaginação, o vocabulário e o conhecimento. Não é acaso que jovens de grande promessa nos estudos e na carreira profissional sejam leitores vorazes. Pensando nisso, um jovem deseja presentear um amigo leitor com dois livros, entretanto fica na dúvida quanto ao estilo ficção ou não ficção. Decide sortear dois títulos distintos dentre 0 títulos de ficção e títulos de não ficção. (Fonte: Texto adaptado Revista Veja (edição ) Tomando por base as informações do texto, a probabilidade de esse jovem sortear, sucessivamente, um após o outro, dois títulos de ficção é: 8. (AFA 0) Um jogo é decidido com um único lançamento do dado cuja planificação está representada abaixo. 8. (EsPCEx 0) De uma caixa contendo 0 bolas numeradas de a 0 retiram-se duas bolas, sem reposição. A probabilidade do número da primeira bola ser divisível por e o número da segunda bola ser divisível por é: (UFSM 0) A tabela a seguir mostra o número de internações hospitalares da população idosa ( 0 ou mais anos de idad, numa determinada região, de acordo com as causas da internação. Causas N de internações Doenças cardíacas 80 Doenças cerebrovasculares 9 Doenças pulmonares Doenças renais Diabetes melito Fraturas de fêmur e ossos dos membros Hipertensão arterial Infecção de pele e tecido subcutâneo Pneumonia bacteriana Úlcera Considere que hipertensão arterial, doenças renais, doenças cardíacas e osteoporose estão associadas ao consumo excessivo de sódio e que as fraturas de fêmur e ossos dos membros são causadas pela osteoporose. Assim, a probabilidade de um idoso internado, escolhido ao acaso, ter como diagnóstico principal uma doença associada ao consumo excessivo de sódio, de acordo com a tabela, é igual a: 0, 0 0, 0 0, 0, 0, 0 0. (UNESP 0) Um dado viciado, que será lançado uma única vez, possui seis faces, numeradas de a. A tabela a seguir fornece a probabilidade de ocorrência de cada face. Participam desse jogo quatro pessoas: Carlos, que vencerá o jogo se ocorrer face preta ou menor que ; José vencerá se ocorrer face branca e número primo; Vicente vencerá caso ocorra face preta e número par; Antônio vencerá se ocorrer face branca ou número menor que. Nessas condições, é correto afirmar que: Vicente não tem chance de vencer. Carlos tem, sozinho, a maior probabilidade de vencer. a probabilidade de José vencer é o dobro da de Vicente. a probabilidade de Antônio vencer é maior do que a de Carlos. Número na face Probabilidade de ocorrência da face Sendo X o evento sair um número ímpar e Y um evento cuja probabilidade de ocorrência seja 90%, calcule a probabilidade de ocorrência de X e escreva uma possível descrição do evento Y.
6 /0. (Enem 0) Em uma escola, a probabilidade de um aluno compreender e falar inglês é de 0%. Três alunos dessa escola, que estão em fase final de seleção de intercâmbio, aguardam, em uma sala, serem chamados para uma entrevista. Mas, ao invés de chamá-los um a um, o entrevistador entra na sala e faz, oralmente, uma pergunta em inglês que pode ser respondida por qualquer um dos alunos. A probabilidade de o entrevistador ser entendido e ter sua pergunta oralmente respondida em inglês é:,% 0,% 0,%,% 90,% 0. (PUC PR 0) Um agricultor adquiriu 0 sementes de milho para fazer o plantio, com a garantia de que a probabilidade de germinação é de 0, 8 (independentes das outras). Ao utilizar a plantadeira manual, não percebeu que havia uma semente utilizada na safra anterior com probabilidade de germinação de 0, e esta se misturou às novas sementes. Assim, o agricultor plantou as sementes e destas, 0 germinaram. Dado que a probabilidade de uma semente germinar (velha ou nov é de 9, qual é a probabilidade de que a semente que não germinou tenha sido uma das sementes novas? 0. (UFU 0) Existe um grupo de n pessoas trabalhando em um escritório. Sabe-se que existem 80 maneiras de selecionar duas dessas pessoas para compor uma comissão representativa do grupo e a probabilidade de ser selecionado um homem desse grupo é 0, maior do que a probabilidade de escolha de uma mulher. Elabore e execute um plano de resolução de maneira a determinar: Qual é o valor de n. Quantos homens existem no grupo.. (PUC RJ 0) Em uma urna existem 0 bolinhas de cores diferentes, das quais sete têm massa de 00 gramas cada e as outras três têm massa de 00 gramas cada. Serão retiradas bolinhas, sem reposição. A probabilidade de que as bolinhas retiradas sejam as mais leves é de: (UPE 0) Dentre os esportes oferecidos aos estudantes de uma escola com. 000 alunos, temos o futebol como preferência, sendo praticado por 00 estudantes. 00 estudantes dessa mesma escola praticam natação, e 00 praticam ambos os esportes. Selecionando-se um estudante praticante de futebol para uma entrevista, qual a probabilidade de ele também praticar natação?. (Enem 0) Uma competição esportiva envolveu 0 equipes com 0 atletas cada. Uma denúncia à organização dizia que um dos atletas havia utilizado substância proibida. Os organizadores, então, decidiram fazer um exame antidoping. Foram propostos três modos diferentes para escolher os atletas que irão realizá-lo: Modo I: sortear três atletas dentre todos os participantes; Modo II: sortear primeiro uma das equipes e, desta, sortear três atletas; Modo III: sortear primeiro três equipes e, então, sortear um atleta de cada uma dessas três equipes. Considere que todos os atletas têm igual probabilidade de serem sorteados e que P(I), P(II) e P(III) sejam as probabilidades de o atleta que utilizou a substância proibida seja um dos escolhidos para o exame no caso do sorteio ser feito pelo modo I, II ou III. Comparando-se essas probabilidades, obtém-se: P( I ) P( III ) P( II ) P(I I ) P( I ) P(I II ) P( I ) P( II ) P(I II ) P( I ) P( II ) P(I II ) P( I ) P( II ) P(I II ). (UEL 0) Em uma cidade do Leste Europeu, cidadãos são indicados, anualmente, para concorrerem aos títulos de Cidadão Honorário e Cidadão Ilustre da Terra. Cada indicado pode receber apenas um dos títulos. Neste ano, a família Generoza conta com pessoas indicadas ao recebimento dos títulos. A partir dessas informações, determine a probabilidade de os cidadãos eleitos pertencerem à família Generoza. Justifique sua resposta apresentando os cálculos realizados 8. (PUC RJ 0) João joga dois dados comuns e soma os valores. Qual a probabilidade de a soma ser maior ou igual a 0?. 0
7 /0 9. (UFRGS 0) Um jogo consiste em responder corretamente as perguntas sorteadas, ao girar um ponteiro sobre uma roleta numerada de a 0, no sentido horário. O número no qual o ponteiro parar corresponde à pergunta a ser respondida. A cada número corresponde somente uma pergunta, e cada pergunta só pode ser sorteada uma vez. Caso o ponteiro pare sobre um número que já foi sorteado, o participante deve responder a próxima pergunta não sorteada, no sentido horário. Em um jogo, já foram sorteadas as perguntas,,,,, e 0. Assim, a probabilidade de que a pergunta seja a próxima a ser respondida é de: (PUC MG 0) Em certa pesquisa, um grupo de adultos e adolescentes foi solicitado a responder à seguinte pergunta: Você possui um telefone celular com linha ativa?. 8 8 Dos adolescentes entrevistados, seis responderam sim e treze, não. Já dentre os adultos consultados, dezessete responderam sim e os demais, não. Apurados os resultados, constatou-se que, escolhendo-se ao acaso uma das pessoas entrevistadas nessa pesquisa, a probabilidade de a mesma ser um adulto que não possui celular com linha ativa era de %. Com base nessas informações, é CORRETO afirmar que o total de pessoas entrevistadas nessa pesquisa é igual a:. (UNESP 0) Uma loja de departamentos fez uma pesquisa de opinião com. 000 consumidores, para monitorar a qualidade de atendimento de seus serviços. Um dos consumidores que opinaram foi sorteado para receber um prêmio pela participação na pesquisa. A tabela mostra os resultados percentuais registrados na pesquisa, de acordo com as diferentes categorias tabuladas. categorias percentuais ótimo regular péssimo não opinaram Se cada consumidor votou uma única vez, a probabilidade de o consumidor sorteado estar entre os que opinaram e ter votado na categoria péssimo é, aproximadamente: 0%. 0%. %. 9%. %.. (UDESC 0) Em uma associação serão eleitos um presidente, um tesoureiro e dois revisores. Cada membro vota em um candidato para presidente, um para tesoureiro e um para revisor. Supondo que haja candidatos para presidente, para tesoureiro e para revisor, então a probabilidade de todos os candidatos de um eleitor qualquer, que não anulou nem votou em branco, serem eleitos é de (Enem 0) Um protocolo tem como objetivo firmar acordos e discussões internacionais para conjuntamente estabelecer metas de redução de emissão de gases de efeito estufa na atmosfera. O quadro mostra alguns dos países que assinaram o protocolo, organizados de acordo com o continente ao qual pertencem. 9 0 Países da América do Norte Estados Unidos da América Canadá México Países da Ásia China Índia Japão Em um dos acordos firmados, ao final do ano, dois dos países relacionados serão escolhidos aleatoriamente, um após o outro, para verificar se as metas de redução do protocolo estão sendo praticadas. A probabilidade de o primeiro país escolhido pertencer à América do Norte e o segundo pertencer ao continente asiático é:. (FGV 0) Dois dados convencionais e honestos são lançados simultaneamente. A probabilidade de que a soma dos números das faces seja maior que, ou igual a, é: 8 8 9
8 /0. (UNESP 0) Renato e Alice fazem parte de um grupo de 8 pessoas que serão colocadas, ao acaso, em fila. Calcule a probabilidade de haver exatamente pessoas entre Renato e Alice na fila que será formada. Generalize uma fórmula para o cálculo da probabilidade do problema descrito acima com o mesmo grupo de " 8 pessoas, trocando " pessoas por "m pessoas, em que m. A probabilidade deverá ser dada em função de m.. (Mackenzie 0) Em uma das provas de uma gincana, cada um dos membros de cada equipe deve retirar, ao acaso, uma bola de uma urna contendo bolas numeradas de a 0, que deve ser reposta após cada retirada. A pontuação de uma equipe nessa prova é igual ao número de bolas com números pares sorteadas pelos seus membros. Assim, a probabilidade de uma equipe conseguir pelo menos um ponto é: (PUC RJ 0) Em uma urna existem 0 bolinhas de cores diferentes, das quais sete têm massa de 00 gramas cada e as outras três têm massa de 00 gramas cada. Serão retiradas bolinhas, sem reposição. A probabilidade de que a massa total das bolinhas retiradas seja de 900 gramas é de: (UFSM 0) A tabela mostra o resultado de uma pesquisa sobre tipos sanguíneos em que foram testadas 00 pessoas. Qual é a probabilidade de uma pessoa escolhida ao acaso ter sangue do tipo A ou A? Tipo de sangue O A B AB O A B AB Número de pessoas 8 0. (Unicamp 0) Uma loteria sorteia três números distintos entre doze números possíveis. Para uma aposta em três números, qual é a probabilidade de acerto? Se a aposta em três números custa R$,00, quanto deveria custar uma aposta em cinco números?. (UPF 0) Duas bolsas de estudo serão sorteadas entre 9 pessoas, sendo mulheres e homens. Considerando-se que uma pessoa desse grupo não pode ganhar as duas bolsas, qual a probabilidade de duas mulheres serem sorteadas? TOTAL (UEMG 0) Em uma empresa, foi feita uma pré-seleção para sorteio de uma viagem. Esta pré-seleção se iniciou com a distribuição, entre os funcionários, de fichas numeradas de a. Em seguida, foram selecionados os funcionários com as fichas numeradas, com as seguintes regras: ) Fichas com um algarismo: o algarismo tem que ser primo; ) Fichas com dois algarismos: a soma dos algarismos deverá ser um número primo. Após essa pré-seleção, Glorinha foi classificada para o sorteio. A probabilidade de Glorinha ganhar essa viagem no sorteio é de, aproximadamente: %. 8%. 9%. 0%. 9 8
9 /0. (UNESP 0) Em um condomínio residencial, há 0 casas e 0 terrenos sem edificações. Em um determinado mês, entre as casas, 0% dos proprietários associados a cada casa estão com as taxas de condomínio atrasadas, enquanto que, entre os proprietários associados a cada terreno, esse percentual é de 0%. De posse de todos os boletos individuais de cobrança das taxas em atraso do mês, o administrador do empreendimento escolhe um boleto ao acaso. A probabilidade de que o boleto escolhido seja de um proprietário de terreno sem edificação é de: (UPE 0) Em um certo país, as capitais Santo Antônio e São Bernardo são interligadas pelas rodovias AB, AB, AB e AB, e as capitais São Bernardo e São Carlos são interligadas pelas rodovias BC, BC 8, BC, BC e BC. Não existem rodovias interligando diretamente as capitais Santo Antônio e São Carlos. Se uma transportadora escolher aleatoriamente uma rota para o caminhoneiro Luís ir e voltar de Santo Antônio a São Carlos, qual a probabilidade de a rota sorteada conter, apenas, rodovias de numeração ímpar? % 9% 0% % 0%. (UEPA 0 Adaptado) Leia o trecho abaixo: Com as cidades imobilizadas por congestionamentos, os governos locais tomam medidas para evitar o colapso do sistema viário. Por exemplo, em Pequim, na China, serão sorteadas mensalmente 0 mil novas licenças de emplacamento para os 900 mil interessados. Para o sorteio, os 900 mil interessados foram divididos em 0 mil grupos com o mesmo número de integrantes. Texto adaptado da revista National Geographic Brasil, edição 9-A. Se num desses grupos estão presentes membros de uma mesma família, a probabilidade de essa família adquirir uma licença para emplacamento: é inferior a %. está compreendida entre % e %. está compreendida entre % e %. está compreendida entre % e %. é superior a %. Todo dia é ano novo no regato cristalino pequeno servo do mar nas ondas lavando as praias na clara luz do luar... Disponível em: < Acesso em:0 set. 0. Posteriormente, escreve no quadro um conjunto com cinco palavras A = {cervo, cativo, veado, prisioneiro, corço}. Por fim, solicita a um aluno que escolha aleatoriamente uma palavra do conjunto A que tenha o mesmo significado da palavra em negrito apresentada no poema. Diante do exposto, a probabilidade de que o aluno escolha uma palavra que não mude o significado da palavra servo é:. (PUC RS 0) Dois dados são jogados simultaneamente. A probabilidade de se obter soma igual a 0 nas faces de cima é: 8 0. (UFPR 0) Um programa de computador usa as vogais do alfabeto para gerar aleatoriamente senhas de letras. EEIOA e AEIOU, por exemplo, são duas senhas possíveis. Calcule a quantidade total de senhas que podem ser geradas pelo programa. Uma senha é dita insegura se possuir a mesma vogal em posições consecutivas. Por exemplo: AAEIO, EIIIO, UOUUO são senhas inseguras. Qual a probabilidade do programa gerar aleatoriamente uma senha insegura? 8. (UFRGS 0) Considere as retas r e s, paralelas entre si. Sobre a reta r, marcam-se pontos distintos: A, B e C; sobre a reta s, marcam-se dois pontos distintos: D e E. Escolhendo ao acaso um polígono cujos vértices coincidam com alguns desses pontos, a probabilidade de que o polígono escolhido seja um quadrilátero é de:. (UFG 0) Para discutir com seus alunos a ideia de sinônimo, um professor adota a seguinte estratégia de ensino: inicialmente, recita parte de um poema, transcrita a seguir: 9. (FGV 0) Dois eventos A e B de um espaço amostral são independentes. A probabilidade do evento A é P( A) 0, e a probabilidade da união de A com B é P AB 08,.. 9
10 /0 / / / / / Pode-se concluir que a probabilidade do evento B é: 0. (IFSP 0) O sangue humano é classificado em quatro tipos: A, B, AB e O. Além disso, também pode ser classificado pelo fator Rh em: Rh+ ou Rh. As pessoas do tipo O com Rh são consideradas doadoras universais e as do tipo AB com Rh+ são receptoras universais. Feita uma pesquisa sobre o tipo sanguíneo com 00 funcionários de uma clínica de estética, o resultado foi exposto na tabela a seguir. A B AB O Rh+ Rh 0 Um desses 00 funcionários será sorteado para um tratamento de pele gratuito. A probabilidade de que o sorteado seja doador universal é:,%. 0%. %.,%. 0%.. (ESPM 0) A distribuição dos alunos nas turmas de um curso é mostrada na tabela abaixo. A B C Homens Mulheres 8 Escolhendo-se uma aluna desse curso, a probabilidade de ela ser da turma A é: referentes à pesquisa, cujas respostas estão registradas no quadro abaixo, a universidade sorteou um tablet dentre os respondentes. Sabendo-se que o respondente sorteado consulta a internet para se manter informado diariamente, a probabilidade do sorteado ser um homem: é inferior a 0%. está compreendida entre 0% e 0%. está compreendida entre 0% e 0%. está compreendida entre 0% e 80%. é superior a 80%.. (Fuvest 0) O gamão é um jogo de tabuleiro muito antigo, para dois oponentes, que combina a sorte, em lances de dados, com estratégia, no movimento das peças. Pelas regras adotadas, atualmente, no Brasil, o número total de casas que as peças de um jogador podem avançar, numa dada jogada, é determinado pelo resultado do lançamento de dois dados. Esse número é igual à soma dos valores obtidos nos dois dados, se esses valores forem diferentes entre si; e é igual ao dobro da soma, se os valores obtidos nos dois dados forem iguais. Supondo que os dados não sejam viciados, a probabilidade de um jogador poder fazer suas peças andarem pelo menos oito casas em uma jogada é: 9 Mulheres Homens TOTAL DE JOVENS ENTREVISTADOS Ouvem apenas rádio. 0 Assistem televisão e consultam a internet. Assistem televisão e consultam internet. Utilizam apenas internet.. (UPE 0) Dois atiradores, André e Bruno, disparam simultaneamente sobre um alvo. - A probabilidade de André acertar no alvo é de 80%. - A probabilidade de Bruno acertar no alvo é de 0%. Se os eventos André acerta no alvo e Bruno acerta no alvo, são independentes, qual é a probabilidade de o alvo não ser atingido? % % 8% 0% 9%. (UEPA 0) Uma universidade realizou uma pesquisa online envolvendo jovens do ensino médio para saber quais meios de comunicação esses jovens utilizam para se informarem dos acontecimentos diários. Para incentivá-los a preencher os dados. (UEA 0) A tabela mostra o resultado de um levantamento feito para avaliar qualitativamente três empresas (X, Y e Z) que fazem a ligação fluvial entre duas localidades. Nesse 0
11 /0 levantamento, as pessoas entrevistadas deveriam relacionar as três empresas em ordem de preferência decrescente: Entrevistados Ordem de preferência relacionada,% X, Y, Z,0% X, Z, Y,% Y, X, Z,0% Y, Z, X,0% Z, X, Y,0% Z, Y, X denominado perfeito quando os halteres de mesma cor são colocados juntos. Nas figuras abaixo, podem-se observar dois exemplos de armazenamento perfeito: Escolhendo-se aleatoriamente uma das pessoas entrevistadas, a probabilidade de que ela prefira a empresa Y à empresa X é de:,%.,%. 0%. 8,%. %.. (UERJ 0) Um alvo de dardos é formado por três círculos concêntricos que definem as regiões I, II e III, conforme mostra a ilustração. Arrumando-se ao acaso os dez halteres, a probabilidade de que eles formem um armazenamento perfeito equivale a: (UNEB 0) Um atirador de dardos sempre acerta alguma região do alvo, sendo suas probabilidades de acertar as regiões I, II e III denominadas, respectivamente, PI, PII e PIII. Para esse atirador, valem as seguintes relações: - PII = PI - PIII = PII Calcule a probabilidade de que esse atirador acerte a região I exatamente duas vezes ao fazer dois lançamentos.. (UFG 0) Em um jogo de dados entre dois amigos, um deles lança um dado com seis faces, numeradas de a, e o outro lança um dado com doze faces, com formato de um dodecaedro regular, numeradas de a. Neste jogo, o número considerado no lançamento é aquele que estiver com a face voltada para cima. Em cada um dos dados, os números ocorrem com igual probabilidade. Para vencer o jogo, o jogador que lançar o dado com doze faces precisa obter no seu lançamento um número que seja múltiplo daquele que foi obtido no lançamento do dado com seis faces. Diante do exposto, determine a probabilidade do jogador que lançar o dado com doze faces vencer o jogo, cada vez que os dois jogadores lançarem os seus dados simultaneamente. 8. (UERJ 0) Em uma sala, encontram-se dez halteres, distribuídos em cinco pares de cores diferentes. Os halteres de mesma massa são da mesma cor. Seu armazenamento é De acordo com o texto, se Cebolinha lançar a sua moeda dez vezes, a probabilidade de a face voltada para cima sair cara, em pelo menos oito dos lançamentos, é igual a 8 8 RESOLUÇÃO
12 /0 azuis. Total de bolas: brancas vermelhas,, 0! 0 98! [V] P0 0!!!! [V] P( A,B,V ) [V] P( B,B ), % x x [F] P( Amarela ) x x0 x0 8!. Existem P modos de obter exatamente três caras! em lançamentos. Por outro lado, existem apenas duas maneiras de obter caras consecutivamente: ccck e kccc. Em consequência, a probabilidade pedida é, ou seja,.. Seja n o número de bolas vermelhas que deverão ser colocadas na caixa. Desse modo, como o número de casos favoráveis é n e o número de casos possíveis é, temos!!! n ( n )!! ( n )! n n 0 0 n.. O número de jogos será o produto do número de jogos em cada fase pelo total de chaves.! C,! ( ) O número de possibilidades de distribuir os times nas chaves será dado por: N( E ) C C C C,, 8,, O número de maneiras de Brasil e Alemanha se enfrentarem na primeira fase será dado por: N(A) = C, C, C8, C,. Portanto, a probabilidade de João assistir à pelo menos um dos jogos do Brasil será de: P 0 sadias( resultado negativo ) 00 sadias apos teste. 0 doentes( resultado positivo ) 00 mulheres 9 sadias( resultado negativo ) 00 doentes apos teste doentes( resultado positivo ) Portanto, [F] 0 0, 0 0% 00 [V] 9 0, 9 9% [F] 0, 098 0, 98% [V] 0, 98 98% 0 [V] 0, 0, % 0. Seja x a média aritmética entre o número obtido no dado e o da face da moeda. Lançando simultaneamente o dado e a moeda, é possível obter resultados distintos. Supondo x ], [, tem-se que os eventos favoráveis são (, ),(, ),(, ) e (, ). Em consequência, podemos afirmar que a probabilidade pedida é, ou seja,.. A probabilidade de que o segundo jogador ganhe na primeira tentativa, isto é, ao virar a primeira carta, é igual a. Assim, como a probabilidade dele ganhar ao virar a segunda carta é, tem-se que a probabilidade dele formar um par usando a estratégia descrita é igual a. 8. Virando a primeira carta, a probabilidade de que a próxima forme um par é igual a, pois apenas uma das cinco cartas restantes é igual à primeira. A multiplicação por garante que Brasil e Alemanha poderão pertencer a qualquer um dos quatro grupos: Portanto, a probabilidade pedida será dadas por:! C 8, C, C, C, P!! C, C!, C8, C,!! Vamos calcular a probabilidade de nenhum dos ingressos serem dos jogos do Brasil. Lembrando que o Brasil não participará apenas de jogos na primeira fase. 0 P 9. Calculando as probabilidades linha a linha:
13 /0 Linha letras { E, A, D } 0 0 Linha letra { I } Linha letras { N, L,O } 0 0 Linha letras {T, R } 0 0 Linha letra {V } Assim, a probabilidade de que o consumidor acerte todas as letras e seja premiado é de: Os possíveis números sorteados são (dados e ), (dados e ou e ), 9 (dados e ), (dados e ou e ), (dados e ), 8 (dados e ), (dados e ), (dados e ). Portanto a probabilidade de terem sido sorteados os números e é uma em 0.. O espaço amostral do experimento é {,,,, 0 }. Ademais, tem-se que A {,,,, 0 } e B { k, k,, 0}. Logo, vem #( A B ) 0 k e, assim, 0 k P( A B ) k. 0. Para saber a probabilidade total da rosa retirada do vaso B ter espinhos é preciso analisar os dois cenários da primeira rosa retirada do vaso A e colocada em B. Cenário : rosa retirada do vaso A e colocada em B tem espinhos. Probabilidade de retirar uma rosa com espinhos do vaso A: 9 ( rosas com espinhos do total 9) Probabilidade de, após a colocação de uma rosa com espinhos em B, retirar uma rosa com espinhos do vaso B: 9 com espinhos do novo total 8 9) que é a probabilidade do cenário acontecer ( rosas Cenário : rosa retirada do vaso A e colocada em B não tem espinhos. Probabilidade de retirar uma rosa sem espinhos do vaso A: 9 ( rosas sem espinhos do total 9) Probabilidade de, após a colocação de uma rosa com espinhos em B, retirar uma rosa com espinhos do vaso B: 9 com espinhos do novo total 8 9) 8 que é a probabilidade do cenário acontecer ( rosas A probabilidade total final de se retirar uma rosa com espinhos do vaso B será a soma das probabilidades destes dois cenários previstos: A turma possui 0 0 alunos. Logo, como alunos não leram nenhum livro no mês passado, segue que a probabilidade pedida é 00 %, %. 0. O número total de possibilidades de se escolher algarismos ao acaso entre os 0 algarismos disponíveis é de: 0! 0 98! 90 C0 C0 possibilidades!( 0 )! 8! O número total de possibilidades de escolha de dois algarismos cuja soma é um número primo é igual a: possibilidades Logo, a probabilidade de que, escolhendo-se ao acaso dois algarismos distintos, a soma deles seja um número primo é: 8 P 0, 0%. Total de resultados possíveis 8. A probabilidade P da soma ser acontece quando sair o em cada um dos dados, portanto, P 8. Para que a soma seja 0 o valor que pode acontecer nos dois primeiros dados é no mínimo 8, pois este valor será somado com no terceiro dado, daí temos os seguintes resultados possíveis para os dois primeiros dados: (,), (,), (,0), (,9), (,8), (,), (,) (,), (,), (,0), (,9), (,8), (, ) (0,), (0,), (0,0), (0,9), (0,8) (9,), (9,), (9,0), (9,9) (8,), (8,), (8,0) (,), (,) (,) É claro que para cada um destes 8 resultados temos um único resultado possível para o terceiro dado. 8 Portanto, a probabilidade pedida será P. 8 Novamente devemos observar a soma dos dois primeiros dados: pares de dados com soma 8: temos possibilidade para o terceiro dado pares de dados com soma 9: temos possibilidades para o terceiro dado pares de dados com soma 0: temos possibilidades para o terceiro dado pares de dados com soma : temos possibilidades para o terceiro dado pares de dados com soma : temos possibilidades para o terceiro dado pares de dados com soma : temos possibilidades para o terceiro dado par de dados com soma : temos possibilidades para o terceiro dado Total de resultados com soma maior ou igual a 0: 8
14 /0 Portanto, a probabilidade pedida será dada por: 8 P. 8. É imediato que a probabilidade pedida é igual a. Dominós que possuem o 0: dominós Dominós que possuem o 9: 0 dominós (pois o dominó (9, 0) já foi contado acim Dominós que possuem o 8: 9 dominós (pois os dominós (9, 8) e (9, 0) já foram contados acim e assim por diante... Portanto, o total de peças será ( ) Temos dominós que possuem o ou o 9: (dominó que possuem o e o 9) Portanto, a probabilidade pedida será dada por P 0, Existe apenas o subconjunto {,, } de três elementos de modo que a soma dos elementos seja. Portanto, a probabilidade pedida será dada por: P C 0! 0, 0!! Existem três subconjuntos do baralho de modo que a soma das cartas seja 9, são eles: {,, }, {,, } e {,, }. Portanto, a probabilidade pedida será dada por: P C 0! 0, 0 0!! 0 0. P 0, Homens doentes: 0, 0 0 8, Mulheres doentes: 0, 80 9, Portanto, a probabilidade pedida será 8, 9, 8 9 P 9% Para que a aula ocorra no domingo é necessário que chova no sábado e não chova no domingo. Assim, pode-se escrever: P( chover ) 0, 0 sáb P( chover ) 0, dom P( não chover ) P( chuva ) 0, 0, dom P( chover ) P( não chover ) 0, 0 0, 0,, % sáb dom. De acordo com o enunciado do problema podemos elaborar o segmente diagrama de árvore: dom Portanto, a probabilidade pedida será dada por: P. Se a probabilidade de estar chovendo no domingo é de 0%, entمo a probabilidade de nمo estar chovendo é de 00% 0% 0%. Desse modo, a probabilidade pedida é dada por 0, 0, 0, 0, 9 0, 9.. Luís pode receber cartas de ouros de! 0!!! maneiras e cartas quaisquer de modos.! 0! 0 Portanto, segue que a probabilidade pedida é igual a.. A probabilidade pedida é igual a Sejam A,C, J e V, respectivamente, os eventos que representam as vitórias de Antônio, Carlos, José e Vicente. Logo, segue que A {,,, }, C {,,, }, J {, } e V { }. Em consequência, como o espaço amostral possui eventos, podemos concluir que a probabilidade de vitória de cada um dos jogadores, na ordem estabelecida anteriormente, é,, e. Portanto, a probabilidade de José vencer é o dobro da de Vicente. 8. Divisíveis por : A {, 8,,, 0,, 8} e n( A) Divisíveis por : B {, 0,,, 0 } e n( B ) 0 Divisíveis por e : AB { 0, 0 } e n(ab ) Portanto, a probabilidade pedida será: P 0 9 0
15 / P 0, A probabilidade de sair um número ímpar será dada por: P( x ) % Poderemos admitir o evento Y como sendo Sair um número menor ou igual a quatro, pois neste caso, a probabilidade de ocorrência do evento Y seria dada por: P(y) = % A probabilidade de que um aluno não compreenda ou não fale inglês é 0, 0,. Logo, a probabilidade de que nenhum dos alunos compreenda ou fale inglês é 0, 0, 0, 0,. Portanto, a probabilidade de o entrevistador ser entendido e ter sua pergunta oralmente respondida em inglês é 0, 0,, %.. Das 0 sementes existe a possibilidade de não germinarem, pois 0% de 0 =. Temos então sementes que poderão não germinar num total de sementes. Aplicando agora a probabilidade condicional, temos: P 9.. Tem-se que n n! 80 80! ( n )! n ( n ) 0 9 n 0. Seja h o número de homens no grupo. Logo, vem h 0 h 0, h h.. Total de possibilidades para a escolha de três bolas: 0! C0, 0! ( 0 )! Portanto, a probabilidade será dada por p 0.. Sejam os eventos A: pratica futebol e B: pratica natação. Queremos calcular a probabilidade condicional P( B A). Logo, o resultado é n( A B ) 00 P( B A). n( A) 00. Além do atleta que utilizou a substância, deveremos escolher atletas dentre os 99 que não a utilizaram. Logo, temos 99 99!! 9! P( I ) ! 00! 9! No segundo modo, sorteada a equipe, deveremos escolher dois atletas dentre os 9 que não a utilizaram. Assim, vem 9 9!!! P( II ) ! 00!! Finalmente, no terceiro modo, deveremos escolher equipes em que não figura o jogador dopado e então sortear o jogador. Portanto, segue que 9 9!!! P( III ) ! 0 00!! As probabilidades são iguais.. Dois membros da família Generoza podem ser escolhidos de! modos.!!! Por outro lado, existem maneiras de! 9! escolher dois cidadãos quaisquer. Em consequência, a probabilidade pedida é dada por. 8. Número de elementos do Espaço amostral: n( E ). Evento A (A soma dos pontos ser maior ou igual a 0). A{(, ),(, ),(, ),(, ),(, ) e (, )} e n( A). Portanto, a probabilidade pedida será dada por: P 9. Números já sorteados que possibilitam as resposta da questão : {,,,,0}. Portanto, a probabilidade pedida será, P Adolescentes que responderam sim: Adolescente que responderam não: Adultos que responderam sim: Adultos que responderam não: x x 00x x 8x x 9. x 00 Portanto, o total de entrevistados é dado pela soma: 9.
16 /0. A probabilidade pedida é dada por 00% 0%. 8. Há modos de escolher um presidente, de escolher um! tesoureiro e maneiras de escolher dois!! revisores. Logo, pelo Princípio Multiplicativo, a eleição possui 80 resultados possíveis. Sejam P, P, P, P os candidatos a presidente, T,T,T os candidatos a tesoureiro e R, R,, R os candidatos a revisor. Suponhamos, sem perda de generalidade, que o voto de um determinado eleitor tenha sido ( P,T, R ). É fácil ver que o número de casos favoráveis para esse voto é igual a, pois existem revisores. Portanto, tem-se que a probabilidade pedida é igual a 80.. A probabilidade do primeiro país escolhido pertencer à América do Norte é de. A probabilidade do segundo pertencer ao continente asiático é de. A probabilidade de ambos os eventos ocorrerem será: O evento complementar do evento soma maior do que, ou igual a, é soma menor do que ou igual a, e diferente de, ou seja, {(, ),(, ),(, ),(, )}. Assim, como o espaço amostral possui elementos, segue que a resposta é Existem maneiras de posicionar Renato e Alice. Podemos dispor! m pessoas entre os dois de A,m maneiras. Além ( m )! disso, considerando agora as 8 ( m ) m pessoas restantes, temos P P ( m)! possibilidades. Por ( m ) m outro lado, podemos organizar o grupo em fila de P 8 8! modos, sem qualquer restrição. Desse modo, a probabilidade pedida é dada por! ( m )! ( m )! m. 8! 8 Em particular, se m, temos A probabilidade de um membro retirar uma bola ímpar é. Assim, a probabilidade de que a equipe não consiga nenhum ponto é.. Portanto, segue que a resposta é. Devemos considerar a retirada de bolinhas de 00 g para que a massa total seja 900g. Portanto, a probabilidade P pedida é: P Glorinha possui uma ficha cujo número pertence ao conjunto 9. {,,,,,,,, 0,, }. Por conseguinte, a probabilidade pedida é 00% 9%. - 8 P( A A ) P( A ) P( A ) Podemos sortear três números distintos entre doze possíveis de! 0 maneiras. Portanto, a probabilidade pedida! 9! é 0.! Uma aposta em cinco números corresponde a 0!! apostas de três números. Em consequência, uma aposta em cinco números deveria custar 0 R$ 0, Total de sorteios possíveis: C9, Total de sorteio onde os contemplados são mulheres: C, Portanto, a probabilidade pedida será dada por: P.. P: probabilidade pedida. 0% de 0 = % de 0 = Logo, P.. Pelo Princípio Fundamental da Contagem, o número total de rotas para ir e voltar de Santo Antônio a São Carlos é dado por 00. Por outro lado, o número de rotas com rodovias de numeração ímpar é igual a. Em consequência, o resultado pedido é 00 % 9 %. 00. Cada grupo possui integrantes. Logo, supondo 0000 que será sorteada uma licença para cada grupo, tem-se que a probabilidade pedida é 00 %, %.. A palavra servo no poema poderia ser substituída por cativo ou prisioneiro, portanto a probabilidade pedida será P.
17 /0. Número de elementos do Espaço Amostral: n( E ) Evento (a soma das faces ser 0): A, ;, ;, n(a). Portanto, a probabilidade pedida será: P e. Para cada posição temos escolhas. Logo, pelo Princípio Multiplicativo, podem ser geradas senhas. Temos escolhas para a primeira posição, escolhas apara a segunda posição, escolhas para a terceira posição, e assim por diante, até a quinta posição. Daí, pelo Princípio Multiplicativo, existem 80 senhas seguras. 8. Portanto, a probabilidade do programa gerar uma senha insegura é Sendo B o evento consulta a internet para se manter informado e A o evento homem, queremos calcular P( A B ). Logo, segue-se que o resultado é igual a P( A B ) , 9%.. Existem resultados possíveis, e os casos favoráveis são (, ),(, ),(, ),(, ),(, ),(, ),(, ),(, ),(, ),(, ), (, ),(, ),(, ),(, ),(, ),(, ) e (, ). Portanto, a probabilidade pedida é.. Como os eventos são independentes, a probabilidade pedida é dada por: ( 0, 8) ( 0, ) 0, 08 8%.. P =,% +,0% +,0% =,%.. PI + PII + PIII = PII = PI PIII = PI = PI Logo: PI + PI + PI = PI = /0 Portanto, a probabilidade pedida será P / 0 / 0 / 00 %. Número de triângulos com vértices nesses pontos: C, C, 0 9 Número de quadriláteros com vértices nesses pontos: C, C, Probabilidade de se escolher um quadrilátero: P Desde que A e B são independentes, tem-se P( A B ) P( A) P( B ). Portanto, do Teorema da Soma, vem P( A B ) P( A ) P( B ) P( A B ) 0, 8 0, P( B ) 0, P( B ) 0. 0 % , P( B ) 0, P( B ).. Queremos calcular a probabilidade condicional P( A aluna ). Sabemos que a turma A possui 8 alunas e que o total de alunas do curso é igual a 8 8. Portanto, a probabilidade pedida é Número de resultados possíveis:. Resultado da forma (a, em que b é múltiplo de a. (, ), (, ), (, )... (, ) e (, )... (, ), (, ), (, ), (, 8), (, 0), (, )... (, ), (, ), (, 9), (, )... (, ), (, 8), (, )... (, ), (, 0)... (, ), (, )... Total... 9 Portanto, a probabilidade era dada por, 9 P. 8. Um armazenamento perfeito pode ser feito de P! modos. Além disso, os halteres podem ser armazenados de (,,,, ) 0! P0!!!!! maneiras. Portanto, a probabilidade pedida é dada por!. 0! !!!!! 9. Espaço amostral dos 0 lançamentos: 0 = 0. Sair cara em pelo menos 8 moedas: C0, 8 C0, 9 C 00, 0. Logo, a probabilidade pedida será: P. 0 8
REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO ALUNO(A): Nº: MATEMÁTICA
 REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul MATEMÁTICA 0. (UFRGS - VESTIBULAR 205) Escolhe-se
REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul MATEMÁTICA 0. (UFRGS - VESTIBULAR 205) Escolhe-se
Resposta: Resposta: 4 ou seja, 1.
 1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
BANCO DE QUESTÕES TURMA PM-PE PROBABILIDADE
 01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
MATEMÁTICA MÓDULO 4 PROBABILIDADE
 PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
a) 6,0% b) 6,4% c) 7,2% d) 7,8% e) 8,0% a) 7. d) 14. total de lançamentos c) 15
 . (Ufsm 204) A tabela mostra o resultado de uma pesquisa sobre tipos sanguíneos em que foram testadas 600 pessoas. Qual é a probabilidade de uma pessoa escolhida ao acaso ter sangue do tipo A + ou A? 4.
. (Ufsm 204) A tabela mostra o resultado de uma pesquisa sobre tipos sanguíneos em que foram testadas 600 pessoas. Qual é a probabilidade de uma pessoa escolhida ao acaso ter sangue do tipo A + ou A? 4.
Chama-se evento todo subconjunto de um espaço amostral. PROBABILIDADE. Introdução
 Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Exercícios de Aprofundamento Mat. Combinação e Probabilidade
 1. (Unifesp 2015) Um tabuleiro de xadrez possui 64 casas quadradas. Duas dessas casas formam uma dupla de casas contíguas se estão lado a lado, compartilhando exatamente um de seus lados. Veja dois exemplos
1. (Unifesp 2015) Um tabuleiro de xadrez possui 64 casas quadradas. Duas dessas casas formam uma dupla de casas contíguas se estão lado a lado, compartilhando exatamente um de seus lados. Veja dois exemplos
INSTITUTO NOSSA SENHORA AUXILIADORA
 INSTITUTO NOSSA SENHORA AUXILIADORA ALUNO (A): Nº ANO: MATEMÁTICA DATA: / / Trim º Atividade LISTA DE REVISÃO PARA A ª AVALIAÇÃO Professora Rosa Godoy. (Fuvest 0) Francisco deve elaborar uma pesquisa sobre
INSTITUTO NOSSA SENHORA AUXILIADORA ALUNO (A): Nº ANO: MATEMÁTICA DATA: / / Trim º Atividade LISTA DE REVISÃO PARA A ª AVALIAÇÃO Professora Rosa Godoy. (Fuvest 0) Francisco deve elaborar uma pesquisa sobre
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
 COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
ANÁLISE COMBINATÓRIA II E PROBABILIDADE
 1. (Fac. Albert Einstein - Medicina 2016) Suponha que nos Jogos Olímpicos de 2016 apenas um representante do Brasil faça parte do grupo de atletas que disputarão a final da prova de natação dos 100 metros
1. (Fac. Albert Einstein - Medicina 2016) Suponha que nos Jogos Olímpicos de 2016 apenas um representante do Brasil faça parte do grupo de atletas que disputarão a final da prova de natação dos 100 metros
Exercícios. 1. (Uerj 2017) Considere o conjunto de números naturais abaixo e os procedimentos subsequentes:
 Probabilidade - Questões Extras Exercícios 1. (Uerj 01) Considere o conjunto de números naturais abaixo e os procedimentos subsequentes: A {0, 1,, 3, 4, 5, 6,, 8, 9} 1. Cada número primo de A foi multiplicado
Probabilidade - Questões Extras Exercícios 1. (Uerj 01) Considere o conjunto de números naturais abaixo e os procedimentos subsequentes: A {0, 1,, 3, 4, 5, 6,, 8, 9} 1. Cada número primo de A foi multiplicado
Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema.
 PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
Exercícios Obrigatórios
 Exercícios Obrigatórios ) (UFRGS/20) Observe a figura abaixo. Na figura, um triângulo equilátero está inscrito em um círculo, e um hexágono regular está circunscrito ao mesmo círculo. Quando se lança um
Exercícios Obrigatórios ) (UFRGS/20) Observe a figura abaixo. Na figura, um triângulo equilátero está inscrito em um círculo, e um hexágono regular está circunscrito ao mesmo círculo. Quando se lança um
Colégio Santa Dorotéia Área de Matemática Disciplina: Matemática Ano: 2º - Ensino Médio Professor: Elias
 Colégio Santa Dorotéia Área de Matemática Disciplina: Matemática Ano: 2º - Ensino Médio Professor: Elias Matemática Atividades para Estudos Autônomos Data: 5 / 6 / 2017 Aluno(a): N o : Turma: 1) (Ufes)
Colégio Santa Dorotéia Área de Matemática Disciplina: Matemática Ano: 2º - Ensino Médio Professor: Elias Matemática Atividades para Estudos Autônomos Data: 5 / 6 / 2017 Aluno(a): N o : Turma: 1) (Ufes)
PROBABILIDADE. c) 1/4 d) 1/12 e) nda MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS
 MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
Lista de exercícios de Matemática Eventos, espaço amostral e definição de probabilidade. Probabilidade condicional. Exercícios gerais.
 p: João Alvaro w: www.matemaniacos.com.br e: [email protected]. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
p: João Alvaro w: www.matemaniacos.com.br e: [email protected]. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
Matemática E Extensivo V. 5
 Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
01 - (UEM PR) um resultado "cara sobre casa preta" é (MACK SP)
 ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: [email protected] LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: [email protected] LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
LISTA 29 - PROBABILIDADE 1
 LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
Mat.Semana. PC Sampaio Alex Amaral Rafael Jesus Gabriel Ritter. (Fernanda Aranzate) Este conteúdo pertence ao Descomplica.
 17 PC Sampaio Alex Amaral Rafael Jesus Gabriel Ritter Semana (Fernanda Aranzate) Este conteúdo pertence ao Descomplica. Está vedada a cópia Probabilidade 08 jun Exercícios 01. Resumo 02. Exercícios de
17 PC Sampaio Alex Amaral Rafael Jesus Gabriel Ritter Semana (Fernanda Aranzate) Este conteúdo pertence ao Descomplica. Está vedada a cópia Probabilidade 08 jun Exercícios 01. Resumo 02. Exercícios de
PROBABILIDADE PROPRIEDADES E AXIOMAS
 PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
Questão 1. Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
 SE18 - Matemática LMAT 6A3 - Probabilidades condicionais Questão 1 (Enem 2017) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso
SE18 - Matemática LMAT 6A3 - Probabilidades condicionais Questão 1 (Enem 2017) Um morador de uma região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso
AULA 08 Probabilidade
 Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
b) 35 c) 14 d) 35 Gab: D
 0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
a) 3% b) 5% c) 7% d) 9% e) 12% 03. Uma população de pessoas acima de 60 anos de idade foi dividida nos seguintes dois grupos:
 REDE ISAA NEWTON ENSINO MÉDIO 2º ANO PROFESSOR: LUIANO VIEIRA DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul Matemática 01. Uma formiga, um rato e uma cobra atravessam um deserto.
REDE ISAA NEWTON ENSINO MÉDIO 2º ANO PROFESSOR: LUIANO VIEIRA DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul Matemática 01. Uma formiga, um rato e uma cobra atravessam um deserto.
Ciclo 3 Encontro 2 PROBABILIDADE. Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr.
 1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
Resoluções de Exercícios
 Resoluções de Exercícios MATEMÁTICA V Capítulo 05 Noções de Probabilidade Parte II 3 o ) P(I B) = Observação: Diagrama de Árvore Considere as probabilidades seguintes a) P(I) = = P(II) b) P(B I) = e P(V
Resoluções de Exercícios MATEMÁTICA V Capítulo 05 Noções de Probabilidade Parte II 3 o ) P(I B) = Observação: Diagrama de Árvore Considere as probabilidades seguintes a) P(I) = = P(II) b) P(B I) = e P(V
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
PROBABILIDADE. Numero de Resultados Desejado Numero de Resultados Possiveis EXERCÍCIOS DE AULA
 PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
Matemática E Extensivo V. 5
 Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
= 3 modos de escolher duas pessoas 2
 01. x/(x+0) /3 ó x 40 Resposta: E 0. [E] RESOLUÇÃO REVENEM 3 De acordo com o gráfico, temos que o número total de filhos é dado por 71 + 6 + 3. Portanto, como sete mães tiveram um único filho, segue que
01. x/(x+0) /3 ó x 40 Resposta: E 0. [E] RESOLUÇÃO REVENEM 3 De acordo com o gráfico, temos que o número total de filhos é dado por 71 + 6 + 3. Portanto, como sete mães tiveram um único filho, segue que
Q05. Ainda sobre os eventos A, B, C e D do exercício 03, quais são mutuamente exclusivos?
 LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
Probabilidade Condicional (grupo 2)
 page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
c) 17 b) 4 17 e) 17 21
 Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Lista Extra:Probabilidade +10-Mat1-2 anos
 Lista Extra:Probabilidade +10-Mat1-2 anos 1. (Upe 2014) Dois atiradores, André e Bruno, disparam simultaneamente sobre um alvo. - A probabilidade de André acertar no alvo é de 80%. - A probabilidade de
Lista Extra:Probabilidade +10-Mat1-2 anos 1. (Upe 2014) Dois atiradores, André e Bruno, disparam simultaneamente sobre um alvo. - A probabilidade de André acertar no alvo é de 80%. - A probabilidade de
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a
 Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Probabilidade Condicional
 18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
Estatística Aplicada. Prof. Carlos Alberto Stechhahn EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE. Administração. p(a) = n(a) / n(u)
 Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
EXERCÍCIOS REVISIONAIS SOBRE BINÔMIO DE NEWTON SISTEMAS LINEARES PROBABILIDADE 2 ANO
 QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
Aulas particulares. Conteúdo
 Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
avenida durante o período da pane, observando a cor da luz de cada um desses semáforos.
 1. (Enem) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante uma hora, e fixaram suas luzes unicamente em verde ou vermelho. Os semáforos funcionam
1. (Enem) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante uma hora, e fixaram suas luzes unicamente em verde ou vermelho. Os semáforos funcionam
MATEMÁTICA - 2 o ANO MÓDULO 43 PROBABILIDADE: CONDICIONAL E APLICAÇÕES GEOMÉTRICAS
 MATEMÁTICA - 2 o ANO MÓDULO 43 PROBABILIDADE: CONDICIONAL E APLICAÇÕES GEOMÉTRICAS Como pode cair no enem (ENEM) A vida na rua como ela é O Ministério do Desenvolvimento Social e Combate à Fome (MDS) realizou,
MATEMÁTICA - 2 o ANO MÓDULO 43 PROBABILIDADE: CONDICIONAL E APLICAÇÕES GEOMÉTRICAS Como pode cair no enem (ENEM) A vida na rua como ela é O Ministério do Desenvolvimento Social e Combate à Fome (MDS) realizou,
Lista de Análise Combinatória Pré-vestibular Noturno Professor: Leandro (Pinda)
 Lista de Análise Combinatória Pré-vestibular Noturno Professor: Leandro (Pinda) 1. (Famerp 2018) Lucas possui 6 livros diferentes e Milton possui 8 revistas diferentes. Os dois pretendem fazer uma troca
Lista de Análise Combinatória Pré-vestibular Noturno Professor: Leandro (Pinda) 1. (Famerp 2018) Lucas possui 6 livros diferentes e Milton possui 8 revistas diferentes. Os dois pretendem fazer uma troca
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA. ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_
 TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_ Análise Combinátoria, Probabilidade, Matrizes e Determinantes A resolução detalhada das questões
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_ Análise Combinátoria, Probabilidade, Matrizes e Determinantes A resolução detalhada das questões
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa.
 A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
De quantas formas distintas a estratégia desse cliente poderá ser posta em prática?
 1. (Enem 014) Um cliente de uma videolocadora tem o hábito de alugar dois filmes por vez. Quando os devolve, sempre pega outros dois filmes e assim sucessivamente. Ele soube que a videolocadora recebeu
1. (Enem 014) Um cliente de uma videolocadora tem o hábito de alugar dois filmes por vez. Quando os devolve, sempre pega outros dois filmes e assim sucessivamente. Ele soube que a videolocadora recebeu
ANÁLISE COMBINATÓRIA E PRINCÍPIO FUNDAMENTAL DA CONTAGEM
 1. (Fac. Albert Einstein - Medicin 2016) Suponha que nos Jogos Olímpicos de 2016 apenas um representante do Brasil faça parte do grupo de atletas que disputarão a final da prova de natação dos 100 metros
1. (Fac. Albert Einstein - Medicin 2016) Suponha que nos Jogos Olímpicos de 2016 apenas um representante do Brasil faça parte do grupo de atletas que disputarão a final da prova de natação dos 100 metros
Combinatória e Probabilidade
 Combinatória e Probabilidade 1. (Enem) Considere o seguinte jogo de apostas: Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados
Combinatória e Probabilidade 1. (Enem) Considere o seguinte jogo de apostas: Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
Lista de exercícios 02. Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática
 Lista de exercícios 02 Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática No Anhanguera você é + Enem Antes de iniciar a lista de exercícios leia atentamente as seguintes
Lista de exercícios 02 Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática No Anhanguera você é + Enem Antes de iniciar a lista de exercícios leia atentamente as seguintes
Análise Combinatória Intermediário
 Análise Combinatória Intermediário 1. (AFA) As senhas de acesso a um determinado arquivo de um microcomputador de uma empresa deverão ser formadas apenas por 6 dígitos pares, não nulos. Sr. José, um dos
Análise Combinatória Intermediário 1. (AFA) As senhas de acesso a um determinado arquivo de um microcomputador de uma empresa deverão ser formadas apenas por 6 dígitos pares, não nulos. Sr. José, um dos
Exercícios de Análise Combinatória 1) Quantos pares ordenados podemos formar com os elementos do conjunto A={0, 2, 3, 5, 6, 7, 8, 9}?
 Exercícios de Análise Combinatória 1) Quantos pares ordenados podemos formar com os elementos do conjunto A={0,, 3, 5,, 7, 8, 9}? ) Quantos pares ordenados com elementos distintos podemos formar com os
Exercícios de Análise Combinatória 1) Quantos pares ordenados podemos formar com os elementos do conjunto A={0,, 3, 5,, 7, 8, 9}? ) Quantos pares ordenados com elementos distintos podemos formar com os
Noções sobre Probabilidade
 Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
Exercícios de Probabilidade - Lista 1. Profa. Ana Maria Farias
 Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
( ) ( ) Questões tipo exame. O número pedido é: Questões tipo exame Pág Os algarismos 1 e 2 podem ocupar 5 A. posições diferentes.
 Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Módulo de Introdução à Probabilidade. Ferramentas Básicas. 2 a série E.M.
 Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística. Probabilidades
 Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
Questão 1. Qual a probabilidade de que esta pessoa tenha observado exatamente um sinal na cor verde? Questão 2
 SE18 - Matemática LMAT 6A2 - Introdução à teoria das probabilidades Questão 1 (Enem 2017) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante
SE18 - Matemática LMAT 6A2 - Introdução à teoria das probabilidades Questão 1 (Enem 2017) Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante
3º trimestre Sala de estudos Data: 29/09/17 Ensino Médio 2º ano classe: Prof. Maurício Nome: nº
 º trimestre Sala de estudos Data: 9/09/7 Ensino Médio º ano classe: Prof. Maurício Nome: nº. (Acafe 07) Uma prova consta de 7 questões de múltipla escolha, com 4 alternativas cada uma, e apenas uma correta.
º trimestre Sala de estudos Data: 9/09/7 Ensino Médio º ano classe: Prof. Maurício Nome: nº. (Acafe 07) Uma prova consta de 7 questões de múltipla escolha, com 4 alternativas cada uma, e apenas uma correta.
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
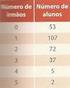 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
ESCOLA SECUNDÁRIA DE CASQUILHOS
 ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma B - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 04 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma B - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 04 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
TEMA 1 COMBINATÓRIA E PROBABILIDADES FICHAS DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 1 COMBINATÓRIA E PROBABILIDADES
 FICHAS DE TRABALHO.º ANO COMPILAÇÃO TEMA COMBINATÓRIA E PROBABILIDADES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA COMBINATÓRIA E PROBABILIDADES Matemática A.º Ano
FICHAS DE TRABALHO.º ANO COMPILAÇÃO TEMA COMBINATÓRIA E PROBABILIDADES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA COMBINATÓRIA E PROBABILIDADES Matemática A.º Ano
Aula 16 - Erivaldo. Probabilidade
 Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Prof.: Joni Fusinato
 Introdução a Teoria da Probabilidade Prof.: Joni Fusinato [email protected] [email protected] Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Introdução a Teoria da Probabilidade Prof.: Joni Fusinato [email protected] [email protected] Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Módulo de Introdução à Probabilidade. Ferramentas Básicas. 2 a série E.M.
 Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
UNIVERSIDADE FEDERAL DA PARAÍBA. Cálculo das Probabilidades e Estatística I. Segunda Lista de Exercícios
 UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
Questão 01 - (FGV /2015)
 SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR SARGENTO NADER ALVES DOS SANTOS SÉRIE/ANO: ª Série
SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR SARGENTO NADER ALVES DOS SANTOS SÉRIE/ANO: ª Série
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
Lista de exercícios Defina o espaço amostral para cada um dos seguintes experimentos aleatórios:
 UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
é um número natural 1. (Espcex (Aman) 2016) A solução da equação
 Lista de Exercícios: Substitutiva e A.P.E. 3º Trimestre 1. (Espcex (Aman) 2016) A solução da equação a) maior que nove. b) ímpar. c) cubo perfeito. d) divisível por cinco. e) múltiplo de três. 3!(x 1)!
Lista de Exercícios: Substitutiva e A.P.E. 3º Trimestre 1. (Espcex (Aman) 2016) A solução da equação a) maior que nove. b) ímpar. c) cubo perfeito. d) divisível por cinco. e) múltiplo de três. 3!(x 1)!
Matemática E Extensivo V. 5
 Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Probabilidade. C = {x 1 x < 30}, assinale o que for correto. 1. (Uepg 2014) Considerando o conjunto 2
 Probabilidade 1. (Uepg 014) Considerando o conjunto C = {x 1 x < 0}, assinale o que for correto. 01) O conjunto C tem subconjuntos. 0) Se A = {x 1< x 5}, então A C = {,, 4}. 04) Escolhendo-se, ao acaso,
Probabilidade 1. (Uepg 014) Considerando o conjunto C = {x 1 x < 0}, assinale o que for correto. 01) O conjunto C tem subconjuntos. 0) Se A = {x 1< x 5}, então A C = {,, 4}. 04) Escolhendo-se, ao acaso,
3. A probabilidade do evento de números pares. 4. O evento formado por número menor que três. 5. A probabilidade do evento número menor que três.
 1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
Probabilidade em espaços discretos. Prof.: Joni Fusinato
 Probabilidade em espaços discretos Prof.: Joni Fusinato [email protected] [email protected] Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
Probabilidade em espaços discretos Prof.: Joni Fusinato [email protected] [email protected] Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
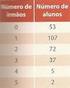 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
Matemática. Probabilidade Básica. Professor Dudan.
 Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
1 Definição Clássica de Probabilidade
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Módulo de Introdução à Probabilidade. O que é Probabilidade? 2 a série E.M.
 Módulo de Introdução à Probabilidade O que é Probabilidade? a série E.M. Probabilidade O que é Probabilidade? 1 Exercícios Introdutórios Exercício 1. Qual a probabilidade de, aleatoriamente, escolhermos
Módulo de Introdução à Probabilidade O que é Probabilidade? a série E.M. Probabilidade O que é Probabilidade? 1 Exercícios Introdutórios Exercício 1. Qual a probabilidade de, aleatoriamente, escolhermos
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan
 Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA. ( Segundo Acadêmico )
 TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundo Acadêmico ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti Análise Combinatória, Probabilidade, Logica, Matemática Financeira A resolução detalhada das
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundo Acadêmico ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti Análise Combinatória, Probabilidade, Logica, Matemática Financeira A resolução detalhada das
Exemplo 2: Considere um dado viciado em que as probabilidades P({1}) = P({3}) = P({5}) = k e P({2}) = P({4}) = P({6}) = 2k.
 Probabilidades Aulas 53 e 5 prof. Aguiar - 03 Aula 53 Probabilidades Exemplo : Considere um dado honesto: Os eventos elementares são {}, {}, {3}, {}, {5} e {6} A probabilidade de sair qualquer evento elementar
Probabilidades Aulas 53 e 5 prof. Aguiar - 03 Aula 53 Probabilidades Exemplo : Considere um dado honesto: Os eventos elementares são {}, {}, {3}, {}, {5} e {6} A probabilidade de sair qualquer evento elementar
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Propostas de resolução
 MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
Colégio Estadual Conselheiro Macedo Soares. Dependência de Matemática. 3º ano do Ensino Médio. Combinatória, Probabilidade Estatística.
 Colégio Estadual Conselheiro Macedo Soares Dependência de Matemática 3º ano do Ensino Médio Combinatória, Probabilidade Estatística Fábio Vinícius Professor de Matemática www.fabiovinicius.mat.br [email protected]
Colégio Estadual Conselheiro Macedo Soares Dependência de Matemática 3º ano do Ensino Médio Combinatória, Probabilidade Estatística Fábio Vinícius Professor de Matemática www.fabiovinicius.mat.br [email protected]
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
Portal da OBMEP. Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE. Fração como Probabilidade. Sexto Ano do Ensino Fundamental
 Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
ESPAÇO AMOSTRAL E EVENTO. 2) Jogando um dado ideal e anotando a face voltada para cima, teremos o espaço amostral E= {1,2,3,4,5,6}
 NOÇÕES DE PROBABILIDADE O estudo da probabilidade vem da necessidade de em certas situações, prevermos a possibilidade de ocorrência de determinados fatos. EXPERIMENTOS ALEATÓRIOS Experimentos aleatórios
NOÇÕES DE PROBABILIDADE O estudo da probabilidade vem da necessidade de em certas situações, prevermos a possibilidade de ocorrência de determinados fatos. EXPERIMENTOS ALEATÓRIOS Experimentos aleatórios
PROBABILIDADE - INTRODUÇÃO
 E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
TESTE GLOBAL PROBABILIDADES 12.º ANO
 TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
A B e A. Calcule as suas respectivas probabilidades.
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
PROBABILIDADE CONTEÚDOS
 PROBABILIDADE CONTEÚDOS Experimentos aleatórios Eventos Probabilidade Probabilidade de união de dois eventos Probabilidade de eventos independentes Probabilidade condicional AMPLIANDO SEUS CONHECIMENTOS
PROBABILIDADE CONTEÚDOS Experimentos aleatórios Eventos Probabilidade Probabilidade de união de dois eventos Probabilidade de eventos independentes Probabilidade condicional AMPLIANDO SEUS CONHECIMENTOS
12.º Ano de Escolaridade
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
