Estado triplo de tensão

Tamanho: px

Começar a partir da página:

Download "Estado triplo de tensão"

Laura Bugalho Cipriano
9 Há anos
Visualizações:

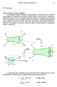
1 Estado triplo de tensão Tensões em um ponto Seja um ponto qualquer, pertencente a um corpo em equilíbrio, submetido às tensões representadas na figura. Com esta consideração, a força resultante no plano inclinado, epressa pelas suas componentes nas direções, e, pode ser determinada por: ( da) = da cos da cos da cos ( da) = da cos da cos da cos ( da) = da cos da cos da cos () Com isto, os três componentes ortogonais da tensão resultante são: = cos cos cos = cos cos cos () Figura Estado geral de tensões em um ponto. = cos cos cos Sabe-se que uma tensão é função de ponto e plano. Assim, para um plano inclinado, em relação aos apresentados na figura, irão atuar outras tensões, como mostra a figura. As três componentes da tensão, podem ser assim determinadas pelo produto de duas matries: = X = cos cos cos Observa-se, então, que qualquer seja o plano inclinado, a tensão nele resultante é igual ao produto entre a matri das tensões dos planos ortogonais e a matri dos co-senos dos ângulos do plano. Figura Tensão resultante em um plano qualquer de um estado geral de tensões. Os ângulos entre o plano considerado e os eios ; e, são, e, respectivamente. Os co-senos são chamados de co-senos diretores, e sua matri é chamada de matri dos co-senos diretores. A matri das tensões se dá o nome de Tensor (Τ). Ao tensor, não é possível se dar uma interpretação geométrica simples. Ele é encarado, apenas, Prof. José Carlos Morilla Estado triplo de tensão

2 como uma matri onde cada elemento representa uma das tensões encontradas na epressão. Desta maneira o tensor Τ, para um estado geral de tensões fica: mesma. Observa-se ainda que neste elemento inclinado ocorrem transformações nas tensões atuantes em cada plano já que ocorre mudança de plano. Τ = () Eios e Tensões Principais. A tensão que atua no plano inclinado pode ser representada por suas componentes: normal () e de cisalhamento (), como mostra a figura. Figura 4 inclinação do elemento em relação à posição inicial Figura tensão normal e de cisalhamento, componentes da tensão. A tensão normal resultante (), neste plano inclinado, é obtida por: = cos cos cos cos cos cos cos cos cos Note-se que, se o elemento inicial estiver inclinado em relação ao sistema apresentado, como se observa na figura 4, a tensão no plano inclinado deve permanecer a Assim, é possível eistir uma posição para o elemento, nestes planos tri-ortogonais, onde as tensões de cisalhamento sejam iguais a ero. A esta posição se dá o nome de posição principal, aos planos ortogonais se dá o nome de planos principais e às tensões normais que neles atuam se dá o nome de tensões principais. Estas tensões são indicadas por ; e, a partir da maior para a menor. Os planos respectivos onde atuam estas tensões, são indicados por ; e. Prof. José Carlos Morilla Estado triplo de tensão

3 = (8) figura 5 planos e tensões principais Chamando de ; e, os ângulos entre o plano inclinado e os planos principais ; e, respectivamente, é possível escrever: = X = (4) cos cos cos Assim, o tensor das tensões principais, é o tensor principal do estado de tensões. Τ = (5) Com isto, as componentes da tensão, ficam: = cos = = cos cos Lembrando que: (6) cos cos cos = (7) Das epressões 6 e 7, é possível escrever: Esta epressão mostra que os valores ; e, podem ser encarados como coordenadas da etremidade do vetor da tensão. O lugar geométrico das etremidades do vetor da tensão total forma um elipsóide, cujos semi-eios são as tensões principais ; e. O elipsóide chama-se elipsóide das tensões. Desta figura geométrica dedu-se que a maior das três tensões principais é o maior valor possível de tensão no conjunto de planos que passam pelo ponto. Dedu-se, ainda, que a menor das tensões principais é a menor das tensões normais. Determinação das tensões principais. Seja o estado de tensões da figura e um plano inclinado como o mostrado na figura. se este plano for um dos principais, a tensão resultante será uma tensão normal (). Assim, as componentes desta tensão normal podem ser escritas como: = ou seja: ( ) X cos ( ) = cos ( ) (9) cos Prof. José Carlos Morilla Estado triplo de tensão

4 cos cos cos () ( ) ( ) ( ) X = J J = () onde J = J Lembrando que: ( ) = cos ( ) = cos ( ) = cos é possível escrever: cos cos cos = J j = = (4) Círculo de Mohr para o Estado Triplo de Tensão. cos cos cos () = Lembrando que a matri dos co-senos diretores não pode ser nula (vide epressão 7), para que o produto mostrado na epressão seja nulo eiste a necessidade do determinante da matri das tensões ser igual a ero: Seja um ponto e suas tensões principais ; e. Seja, também um plano inclinado com um ângulo α, em relação aos planos e. = () figura 6 Planos principais; tensões principais e plano inclinado. Note-se aqui que, sendo uma tensão principal, seu valor independe do conhecimento prévio da posição do plano em que ela ocorre. Ele depende, apenas, do estado de tensões que atua no ponto. A solução do sistema apresentado na epressão é dada por: As tensões: normal e de cisalhamento, neste plano, podem ser determinadas por: = = senα Prof. José Carlos Morilla 4 Estado triplo de tensão cosα ()

5 Note-se que estas tensões podem, também, ser determinadas pelo Círculo de Mohr para o estado duplo de tensão. O mesmo tipo de estudo pode ser feito para um plano inclinado em relação aos planos e, como mostra a figura. Plano A (-)/ senα α ()/ (-)/ cosα figura 7 Círculo de Mohr para os planos ; e o inclinado Caso o plano esteja inclinado em relação aos planos e, como mostra a figura 8, tem-se o Círculo de Mohr apresentado na figura 9. figura Plano inclinado em relação aos planos e. O Círculo de Mohr para esta situação está mostrado na figura Plano C figura Círculo de Mohr para os planos ; e o inclinado figura 8 Plano inclinado em relação aos planos e. Note-se que é possível faer uma superposição dos Círculos de Mohr para os três casos. Isto pode ser observado na figura Plano B β figura 9 Círculo de Mohr para os planos ; e o inclinado figura Círculo de Mohr para os três estudos superpostos. Prof. José Carlos Morilla 5 Estado triplo de tensão

6 Um plano inclinado qualquer, em relação aos três planos, simultaneamente, como o mostrado na figura, tem seu ponto representativo na área limitada pelos três Círculos de Mohr (arbelos). Isto pode ser observado na figura 4.. Qualquer estado de tensão pode ser interpretado como um caso particular do estado triplo de tensão. As figuras 6 e 7, mostram, respectivamente, os estados de tração simples e cisalhamento puro. figura 6 Círculo de Mohr para a tração simples figura Plano inclinado qualquer e os planos principais Plano D figura 6 Círculo de Mohr para o cisalhamento puro figura 4 Círculo de Mohr para um plano qualquer.. Desde que seja conhecida uma das tensões principais, as demais podem ser determinadas por um estudo semelhante ao estado duplo de tensão. OBS:-. Usualmente a representação do Círculo de Mohr é feita, apenas, pelo semicírculo superior, como mostra a figura 5 figura 5 Representação usual do Círculo de Mohr. Prof. José Carlos Morilla 6 Estado triplo de tensão

Documentos relacionados

Estado duplo ou, Estado plano de tensões.

Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra