Probabilidade 2. Fascículo 11. Unidade 34
|
|
|
- Mauro Bayer Graça
- 7 Há anos
- Visualizações:
Transcrição
1 Probabilidade 2 Fascículo 11 Unidade 34
2
3 Probabilidade 2 Para início de conversa... Na unidade anterior observamos uma introdução ao estudo das probabilidades. Como exemplos, utilizamos o lançamento de moedas e de dados dentro de um espaço amostral, que é uma situação comum em nosso cotidiano. Uma atividade bastante também muito corriqueira em nosso dias é o jogo de cartas. Figura 1: Cartas de um baralho. Observe que nos exemplos e atividades resolvidos na unidade anterior não havia dependência entre as escolhas, isto é, foram feitas escolhas sobre a moeda lançada, sobre o dado lançado e assim por diante. São escolhas simples, onde uma decisão não depende da outra. Por exemplo, podemos verificar a probabilidade de escolher uma carta de naipe vermelho em um baralho. Matemática e suas Tecnologias Matemática 7
4 Figura 2: Naipes de um baralho. Como são 52 cartas e metade delas tem o naipe vermelho, teremos uma probabilidade de cinquenta por cento. Todavia, existem algumas situações onde os acontecimentos ficam dependentes uns dos outros. Nesta unidade iremos estudar estes casos, ou seja, quando existe mais de uma condição a ser avaliada ao determinarmos a probabilidade de um evento acontecer. Objetivos de aprendizagem Resolver problemas que envolvem probabilidade da união de eventos. Probabilidade de eventos complementares. Descrever o conceito de probabilidade Condicional. 8
5 Seção 1 Vamos lançar moedas e dados novamente e resolver alguns problemas diferentes? Vimos na aula passada como é interessante pensar sobre probabilidades utilizando moedas e dados, não é verdade? Então, vamos continuar utilizando estes objetos como referência para o nosso aprendizado, além de cartas e outros problemas que não envolvam jogos também. Probabilidade da união de dois eventos Vamos resolver um problema que consiste em descobrir a probabilidade de, no lançamento de dois dados, ocorrer a soma dos números obtidos nas faces superiores ser igual a 6 ou ocorrer um múltiplo de 3 em cada uma das faces superiores. Inicialmente poderíamos pensar que bastaria calcularmos a probabilidade de ocorrer a soma igual 6, que, como já vimos na aula anterior seria de superior, que seria de e somar com a probabilidade de ocorrer um múltiplo de 3 em cada face (visto que este evento: ocorrer um múltiplo de 3 em cada face superior têm 4 elementos: {(3,3), (3,6). (6,3). (6,6)} e o número de elementos do espaço amostral, como vimos na aula anterior é 36), encontrando = Matemática e suas Tecnologias Matemática 9
6 Mas, quando refletimos melhor sobre essa resposta, podemos observar que não é a solução correta, visto que utilizamos o elemento (3,3) em ambos os eventos, pois a soma dos números é igual a 6 e também cada um dos números é um múltiplo de 3. Portanto, a resposta correta seria Na seção 2, veremos de uma forma um pouco mais formal, o porquê desta retirada. CONHECENDO UM BARALHO Baralho francês de 52 cartas O principal baralho de 52 cartas em uso atualmente inclui 13 cartas de cada um dos quatro naipes franceses, paus ( ), ouros ( ), copas ( ) e espadas ( ), com cartas de figuras. Cada naipe inclui um ás, que descreve um único símbolo de seu naipe (muito grande, muitas vezes apenas o ás de espadas) um rei (representado pela letra K), uma rainha (representada pela letra Q), e um valete (representado pela letra J), cada um representado com um símbolo de seu naipe, com valores de dois a dez, com cada cartão mostrando o número de símbolos de seu naipe. Para além destas 52 cartas, baralhos comerciais geralmente incluem dois coringas. Em muitos jogos, os coringas não são usados. Os coringas são geralmente distinguidos pela cor. Baralho francês de 52 cartas Valete Dama Rei Paus Ouros Copas Espadas Este baralho é muito utilizado em problemas de probabilidades, assim como em diversos jogos, que podem utilizar probabilidade, como é o caso do poker. Fonte: (retirado do site: 10
7 Probabilidade e baralho. De um baralho de 52 cartas, uma é extraída ao acaso. Qual é a probabilidade de sair: a. Um valete de paus? b. Um quatro? c. Uma carta de copas? d. Um rei ou uma carta de espadas? Probabilidade de eventos complementares Já estudamos anteriormente que um evento é qualquer subconjunto de um espaço amostral W. Por exemplo, se em uma urna há 10 fichas numeradas de 1 a 10, o experimento retirar um número menor que 5 é dado por E = {1, 2, 3, 4}. Chamamos de evento complementar de E àquele que ocorrerá somente quando E não ocorrer, neste caso, o número retirado ser maior ou igual a 5. Representaremos por E c = {6, 7, 8, 9, 10}. Observemos ainda que E E c = W e que E E c = f Matemática e suas Tecnologias Matemática 11
8 Uma propriedade interessante de um espaço amostral finito e equiprovável Ω é que: Se E é um evento de Ω, e E c é o evento complementar de E, então P(E c ) = 1 P(E). Podemos verificar a veracidade desta afirmação de maneira simples! Como E E c = Ω e E E c = f, podemos escrever: n(e) + n(e c ) = n(ω) Dividindo os dois membros dessa igualdade por n(ω) 0, temos: c ne ( ) ne ( ) n( Ω) c + = PE ( ) + PE ( ) = 1. n( Ω) n( Ω) n( Ω) Daí, chegamos na afirmação desejada. Exemplo: De um baralho com 52 cartas, retiramos ao acaso, uma carta. Qual é a probabilidade de não sair um valete? Como há 4 valetes no baralho, sabemos que a probabilidade de retirarmos um valete, ao acaso, é de 4/52. Portanto, a probabilidade de não ocorrer um valete (evento complementar) é 1 4/52 = 48/52, simplificando temos 12/13. Retirando uma bola de uma urna Uma urna contém 100 bolas numeradas de 1 a 100. Uma bola é extraída ao acaso da urna. Qual a probabilidade de ser sorteada uma bola com número menor ou igual a 99? 12
9 Probabilidade condicional Condicional 1. Dependente de condição. 2. Que envolve condição, ou exprime circunstância de condição. 3. Gram Dizia-se do modo de verbo que enuncia o fato sob a dependência de uma condição; na N.G.B. desapareceu o modo condicional, que passou a denominar-se futuro do pretérito (simples e composto), enquadrado no modo indicativo. 4. Gram Qualificativo da conjunção subordinativa que liga exprimindo condição. sm 1 Condição. 2 Gram O modo condicional (V a acepção 3 do adj). sf Gram Conjunção subordinativa que introduz oração exprimindo uma hipótese ou condição necessária para que se realize ou não o que se expressa na principal: Se queres paz, defende-te. Eu não seria nada, caso você não existisse. Fonte: Do verbete acima, podemos concluir que a probabilidade condicional é aquela que envolve algum tipo de condição. Geralmente pretendemos encontrar a probabilidade de um evento ocorrer sabendo que ou dado que já ocorreu algo. Por exemplo: 1. Um dado é lançado e sabe-se que a face superior tem um número ímpar. Qual é a probabilidade de que o número obtido seja primo? Solução: Lembrando que um número é primo quando possui apenas dois divisores distintos, (1 e o próprio número) temos que, se chamarmos de G o evento: obter um nº primo, teremos que G = {3,5}, visto que o 1 não é primo por possuir um só divisor. Observe que, neste caso, o espaço amostral quer iremos utilizar não é Ω = {1,2,3,4,5,6}, pois já sabemos que na face superior tem um número ímpar, o que faz aumentar a nossa probabilidade, ou seja, utilizamos Ω ={1,3,5} como o novo espaço amostral e, com isso, temos como resultado: P(G) = ng ( ) 2 = n( Ω) Uma família planejou ter 3 crianças. Qual é a probabilidade de que a família tenha 3 meninas, já que a primeira criança que nasceu é menina? Considerando H como menino e M como menina, podemos considerar o espaço amostral relativo as possibilidades de nascimento como Ω = {HHH, HHM, HMH, HMM, MHH, MHM, MMH, MMM}. Mas como já sabemos que a primeira criança que nasceu é menina, o espaço amostral considerado deve ficar restrito às possibilidades onde o primeiro nascimento é menina, ou seja, Ω : {MHH, MHM, MMH, MMM}. Matemática e suas Tecnologias Matemática 13
10 Como queremos encontrar a probabilidade de que a família tenha 3 meninas, o evento K: nascer três meninas : {MMM}. Daí, P(K) = ¼. Novamente, ressalto aqui, que na próxima seção aprenderemos uma fórmula para calcular a probabilidade condicional, mas fique a vontade para utilizá-la quando desejar ou então resolva os problemas sem ela como fizemos nestes dois exemplos. Lançando dados, novamente! Jogam-se dois dados. Qual é a probabilidade de se obter 3 no primeiro dado, se a soma dos resultados é 6? Seção 2 Vamos rever alguns problemas de uma maneira diferente? Nesta seção veremos de uma forma um pouco diferente o que estudamos até agora nesta aula. Vamos lá! Sobre a probabilidade da união de dois eventos: Sejam A e B eventos de um mesmo espaço amostral Ω finito, não vazio e equiprovável (se esqueceu o que é, volta na aula anterior, encontre e releia! Isso é sempre uma boa atividade). Vamos encontrar uma expressão para a probabilidade de ocorrer o evento A ou o evento B, ou seja, a probabilidade de ocorrer o evento A B. (observem que o operador ou está relacionado a união, assim como o operador e está relacionado com a intersecção.) 14
11 Vimos na teoria dos conjuntos que n(a B) = n(a) + n(b) n(a B) Lembrando que como é um evento equiprovável, teremos n(ω) φ, assim podemos dividir toda a expressão acima por n(ω), o que nos permite achar a equação na ( B) na ( ) nb ( ) na ( B) = + n( Ω) n( Ω) n( Ω) n( Ω) Sabemos que a probabilidade de um evento é determinada pela razão entre o número de possibilidades do evento e o espaço amostral. Assim teremos: P(A B) = P(A) + P(B) P(A B) Caso esta interseção (A B) seja vazia, teremos: P(A B) = P(A) + P(B) Bem, definida esta equação, voltemos ao problema que já resolvemos na seção 1.1: descobrir a probabilidade de no lançamento de dois dados ocorrer a soma dos números obtidos nas faces superiores ser igual a 6 ou ocorrer um múltiplo de 3 em cada uma das faces superiores. Seja A o evento ocorrer a soma 6 e o evento B: ocorrer um múltiplo de 3 em cada uma das faces. Queremos descobrir P(A B). Temos que A:{(1,5), (2,4), (3,3), (4,2) e (5,1)} >>> n(a)=5 B:{(3,3), (3,6), (6,3),(6,6)} >>>>>>>>>>n(b)=4 A B: {(3,3)} >>>>>>>>>>>>>>>>>>>>n(a B)=1 Como estamos trabalhando com o lançamento de dois dados, sabemos que o total de possibilidades é n(ω)=36. Como, acabamos de ver que P(A B) = P(A) + P(B) P(A B), calculando as probabilidades temos que: P(A) = n(a)/ n(ω) = 5/36 P(B) = n(b)/ n(ω) = 4/36 P(A B)= n(a B)/ n(ω) = 1/36 Daí, P(A B) = 5/36 + 4/36 1/36 = 8/36, que é a resposta que encontramos anteriormente. Matemática e suas Tecnologias Matemática 15
12 Sobre a probabilidade condicional: Definição: Sejam A e B eventos de um espaço amostral Ω, finito e não vazio. A probabilidade condicional do evento A, sabendo que ocorreu o evento B, é indicada por P(A B) e é dada por: P(A B) = na ( B) nb ( ) Ou seja, a probabilidade condicional do evento A, sabendo que ocorreu o evento B é igual ao número de elementos da interseção de A com B dividido pelo número de elementos de B. Podemos chegar numa expressão equivalente a esta dividindo o numerador e o denominador do 2º membro por n(ω): P(A B) = na ( B) n( Ω) nb ( ) n( Ω) = P( A B) PB ( ) Voltemos ao problema 1) Um dado é lançado e sabe-se que a face superior tem um número ímpar. Qual é a probabilidade de que o número obtido seja primo? e resolvamos com a fórmula obtida. Chamando de evento A: o número obtido deve ser primo e o evento B: o número da face superior é impar. Queremos encontrar P(A B), visto que queremos encontrar a probabilidade do número ser primo sabendo que o nº da face superior é impar, correto? Sim! Então vamos continuar... Ω={1,2,3,4,5,6} >>>> n(ω)=6 A={2,3,5} B={1,3,5} >>>>>>>>>n(b)=3 A B={3,5}>>>>>>>>n(A B)=2 Daí, temos que: P(A B) = n(a B) / n(ω) = 2/6 P(B) = n(b) / n(ω) = 3/ Portanto, P(A B) = 6 =. = Que foi a mesma resposta que encontramos fazendo sem a fórmula. 16
13 Sobre o sexo dos filhos... Refaça a atividade: Uma família planejou ter 3 crianças. Qual é a probabilidade de que a família tenha 3 meninas, já que a primeira criança que nasceu é menina?, utilizando a fórmula. Conclusão Como observamos, algumas probabilidades são encontradas de forma simples, enquanto em outras há a presença da condicionalidade. Nestes casos é preciso verificar cada situação a parte. Podemos utilizar as fórmulas definidas nesta unidade, todavia a resolução pode ser feita de maneira analítica, sem a preocupação em decorar estas equações pré determinadas. Resumo A soma das probabilidades de um evento com seu complementar é igual a um. P(E) + P(E c ) = 1 Na probabilidade da união de dois eventos temos: P(A B) = P(A) + P(B) P(A B) Caso a interseção de A e B seja vazia, teremos P(A B) = P(A) + P(B). Na probabilidade condicional temos P(A B) = P(A B) / P(B). Matemática e suas Tecnologias Matemática 17
14 Veja ainda No site é possível acompanhar uma aula de probabilidade condicional com a resolução de exercícios. Referências Livros IEZZI, Gelso, et al. Matemática Ciência e Aplicações. 6ª edição, vol2. São Paulo, páginas. MORGADO, Augusto Cesar de Oliveira. Análise Combinatória e Probabilidade, 2ª edição, Rio de Janeiro, Imagens
15 Atividade 1 Observem que n(ω) = 52, visto que é o nº total de cartas de um baralho. Daí: a. Sendo A o evento: sair um valete de paus, teríamos n(a)=1, visto que só há um valete de paus e, portanto, P(A) = na ( ) 1 = 1, 9% n( Ω) 52 b. Sendo B o evento: sair um quatro, teríamos n(b)=4, visto que temos 4 naipes e um quatro de cada naipe. Portanto nb ( ) 4 = 7,6% n( Ω) 52. c. Sendo C o evento: sair uma carta de copas, teríamos n(c)=13, visto que temos 13 cartas de cada um dos 4 naipes e, portanto, nc ( ) 13 = = 25% n( Ω) 52. Sabemos que a probabilidade de sair um rei é a mesma de ocorrer um quatro, ou seja, 4/52, e a probabilidade de sair uma carta de espadas é a mesma de sair uma carta de copas, ou seja, é de, 13/52. Somando essas duas probabilidades temos, 17/52, mas temos que retirar a probabilidade de sair um rei de espadas, pois o contamos duas vezes, ou seja, temos que retirar 1/52, encontrando como resposta 16/52. Atividade 2 Se considerarmos o evento L: sortear uma bola com número menor ou igual a 99, vemos claramente que é mais simples encontrar o seu evento complementar L c : sortear uma bola com número maior que 99, visto que n(l c )=1, pois só temos o 100 maior que 99 na urna. Como n(ω)=100. Temos que P(L) = 1 P(L c ), ou seja P(L) = 1 1/100 = 99/100. Atividade 3 Jogam-se dois dados. Qual é a probabilidade de se obter 3 no primeiro dado, se a soma dos resultados é 6? Sabemos que a soma dos resultados é igual a 6. Portanto nosso Ω ={(1,5), (2,4), (3,3), (4,2), (5,1)}. Bem, nosso evento F: obter 3 no primeiro resultado : {(3,3)} e portanto a probabilidade procurada é P(F)= n(f)/n(ω) = 1/5. Matemática e suas Tecnologias Matemática 19
16 Atividade 4 Temos que W={HHH, HHM, HMH, HMM, MHH, MHM, MMH, MMM}, n(w) = 8 Chamando de A: família ter 3 meninas e B: a primeira criança que nasceu é menina, temos: A={MMM} B={MHH, MHM, MMH, MMM}>>>>>n(B)=4 A B={MMM}>>>>>>>>>>>>>>>>>n(A B)=1 Daí, temos que: P(A B) = n(a B) / n(w) = 1/8 P(B) = n(b) / n(w) = 4/ Portanto, P(A B) = 8 =. = = 25%
17 O que perguntam por aí? (ENEM -2012) José, Paulo e Antônio estão jogando dados não viciados, nos quais, em cada uma das seis faces, há um número de 1 a 6. Cada um deles jogará dois dados simultaneamente. José acredita que, após jogar seus dados, os números das faces voltadas para cima lhe darão uma soma igual a 7. Já Paulo acredita que sua soma será igual a 4 e Antônio acredita que sua soma será igual a 8. Com essa escolha, quem tem a maior probabilidade de acertar sua respectiva soma é a. Antônio, já que sua soma é a maior de todas as escolhidas. b. José e Antônio, já que há 6 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 4 possibilidades para a escolha de Paulo. c. José e Antônio, há que há 3 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 2 possibilidades para a escolha de Paulo. d. José, já que há 6 possibilidades para formar sua soma, 5 possibilidades para formar a soma de Antônio e apenas 3 possibilidades parar formar a soma de Paulo. e. Paulo, já que sua soma é a menor de todas. Resposta: Letra D. Comentário: Vimos na aula passada, o quadro do lançamento de dois dados: (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) 2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) Matemática e suas Tecnologias Matemática 21
18 4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6) Que fazendo a soma dos números que aparecem na face superior, gerou o quadro: Onde podemos observar, facilmente, que a soma 7 aparece 6 vezes, a soma 4 aparece apenas 3 vezes e a soma 8 aparece 5 vezes. Portanto quem tem a maior possibilidade de acertar é José, pois a soma 7 é a que aparece maior número de vezes no nosso quadro da soma. 22
19 Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente as 12 questões, acertar metade das respostas? (a) 1,55% (b) 1,35% (c) 1,25% (d) 1,05% Exercício 2 Lançando dois dados perfeitos, pergunta-se: Qual a probabilidade de que a soma dos resultados obtidos seja igual a 6? (a) 15,86% (b) 13,88% (c) 12,68% (d) 10,88% Exercício 3 Em uma urna existem bolas enumeradas de 1 a 15. Qualquer uma delas possui a mesma chance de ser retirada. Qual a probabilidade de se retirar uma bola com número par? (a) 40,3% (b) 38,4% (c) 43,6% (d) 46,6% Matemática e suas Tecnologias Matemática 23
20 Exercício 4 Em uma urna há 5 bolas verdes, numeradas de 1 a 5, e 6 bolas brancas, numeradas de 1 a 6. Dessa urna retiram- -se, sucessivamente e sem reposição, duas bolas. Quantas são as extrações nas quais a primeira bola sacada é verde e a segunda contém um número par? (a) 15 (b) 20 (c) 23 (d) 25 Exercício 5 Em uma mesa, estão espalhados 50 pares de cartas. As duas cartas de cada par são iguais e cartas de pares distintos são diferentes. Suponha que duas dessas cartas são retiradas da mesa ao acaso. Qual a probabilidade dessas duas cartas serem iguais? (a) 1/100 (b) 1/99 (c) 1/50 (d) 1/49 Exercício 6 Considere uma prova constituda de quatro questões cada uma com quatro alternativas, das quais apenas uma é correta. Um candidato decide fazer essa prova escolhendo, aleatoriamente, uma alternativa em cada questão. Qual a probabilidade desse candidato acertar exatamente uma questão? (a) 27/64 (b) 27/256 (c) 9/64 (d) 9/256 Exercício 7 Em um jogo de bingo são sorteadas, sem reposição, bolas numeradas de 1 a 75, e um participante concorre com a cartela reproduzida abaixo. Bingo
21 Qual é a probabilidade de que os três primeiros números sorteados estejam nessa cartela? (a) 1% (b) 2% (c) 3% (d) 4% Exercício 8 Em uma empresa, o risco de alguém se acidentar é dado pela razão 1 em 30. Qual a probabilidade de 3 funcionários se acidentarem? (a) 0,0037% (b) 0,0011% (c) 0,0017% (d) 0,0027% Exercício 9 Dois dados são lançados simultaneamente. Qual a probabilidade de que a soma seja 7? (a) 18,84% (b) 16,66% (c) 14,22% (d) 12,88% Exercício 10 Ao retirarmos uma bola de uma urna que contém 20 bolas numeradas de 1 a 20. Qual a probabilidade de a bola ser um número múltiplo de 3 ou ser primo? (a) 13/20 (b) 26/21 (c) 13/10 (d) 7/10 Exercício 11 Necessita-se organizar 3 livros de matemática, 2 de física e 4 de português em uma prateleira. De quantas maneiras podemos ordená-los de modo que os livros da mesma área de conhecimento fiquem sempre juntos? Matemática e suas Tecnologias Matemática 25
22 Exercício 12 Numa pesquisa sobre preferência entre dois refrigerantes, Coca-Cola e guaraná, obtivemos o seguinte resultado: 20 tomam guaraná, 15 tomam Coca- Cola, 08 tomam os dois e 03 não tomam nenhum dos dois. Qual a probabilidade de uma pessoa, que participou da pesquisa, tomar guaraná ou Coca-Cola? Exercício 13 Um aluno prestou vestibular em apenas duas universidades. Suponha que, em uma delas, a probabilidade de que ele seja aprovadoé de 30%, enquanto na outra, pelo fato de a prova ter sido mais fácil, a probabilidade de sua aprovação sobe para 40%. Qual a probabilidade desse aluno ser aprovado em pelo menos uma dessas universidades? Exercício 14 O quadro funcional de uma empresa é composto de 35 pessoas efetivas e 15 pessoas prestadoras de serviços. Do pessoal efetivo 20 são homens e do pessoal prestador de serviço e 5 são mulheres. Qual a probabilidade de uma pessoa ser homem ou prestar serviço? Exercício 15 Em uma população de aves, a probabilidade de um animal estar doente é 1/25. Quando uma ave está doente, a probabilidade de ser devorada por predadores é 1/4, e, quando não está doente, a probabilidade de ser devorada por predadores é 1/40. Escolhida uma ave aleatoriamente, qual a probabilidade de ela ser devorada por predadores? 26
23 Gabarito Exercício 1 A B C D Exercício 2 A B C D Exercício 3 A B C D Exercício 4 A B C D Exercício 5 A B C D Exercício 6 A B C D Matemática e suas Tecnologias Matemática 27
24 Exercício 7 A B C D Exercício 8 A B C D Exercício 9 A B C D Exercício 10 A B C D Exercício Exercício 12 5/6. Exercício 13 58%. 28
25 Exercício 14 7/10. Exercício 15 3/4%. Matemática e suas Tecnologias Matemática 29
26
Leon: Oi Lara, a primeira aula de probabilidade foi muito legal, né?
 Módulo 04 Aula 04 TÍTULO: Probabilidade Parte 2. Para início de conversa... Fazer quadrinhos do seguinte diálogo: Leon: Oi Lara, a primeira aula de probabilidade foi muito legal, né? Lara: É mesmo Leon,
Módulo 04 Aula 04 TÍTULO: Probabilidade Parte 2. Para início de conversa... Fazer quadrinhos do seguinte diálogo: Leon: Oi Lara, a primeira aula de probabilidade foi muito legal, né? Lara: É mesmo Leon,
Atividade extra. Exercício 1. Exercício 2. Exercício 3. Matemática e suas Tecnologias Matemática
 Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
Fascículo 11 Unidades 34, 35 e 36. Edição revisada 2016
 Edição revisada 2016 Fascículo 11 Unidades 34, 35 e 36 GOVERNO DO ESTADO DO RIO DE JANEIRO Governador Luiz Fernando de Souza Pezão Vice-Governador Francisco Oswaldo Neves Dornelles SECRETARIA DE ESTADO
Edição revisada 2016 Fascículo 11 Unidades 34, 35 e 36 GOVERNO DO ESTADO DO RIO DE JANEIRO Governador Luiz Fernando de Souza Pezão Vice-Governador Francisco Oswaldo Neves Dornelles SECRETARIA DE ESTADO
AULA 08 Probabilidade
 Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Matemática & Raciocínio Lógico
 Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
PROBABILIDADE - INTRODUÇÃO
 E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
Portal da OBMEP. Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE. Fração como Probabilidade. Sexto Ano do Ensino Fundamental
 Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
1 Definição Clássica de Probabilidade
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Estatística. Aula : Probabilidade. Prof. Ademar
 Estatística Aula : Probabilidade Prof. Ademar TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento. É um ramo da matemática que cria, elabora
Estatística Aula : Probabilidade Prof. Ademar TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento. É um ramo da matemática que cria, elabora
Lista de exercícios de Matemática Eventos, espaço amostral e definição de probabilidade. Probabilidade condicional. Exercícios gerais.
 p: João Alvaro w: www.matemaniacos.com.br e: [email protected]. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
p: João Alvaro w: www.matemaniacos.com.br e: [email protected]. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
Estatística Aplicada. Prof. Carlos Alberto Stechhahn EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE. Administração. p(a) = n(a) / n(u)
 Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
 COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
T o e r o ia a da P oba ba i b lida d de
 Teoria da Probabilidade Prof. Joni Fusinato Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso cotidiano. Usa o princípio básico do aprendizado humano que
Teoria da Probabilidade Prof. Joni Fusinato Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso cotidiano. Usa o princípio básico do aprendizado humano que
Prof.: Joni Fusinato
 Introdução a Teoria da Probabilidade Prof.: Joni Fusinato [email protected] [email protected] Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Introdução a Teoria da Probabilidade Prof.: Joni Fusinato [email protected] [email protected] Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Probabilidade Parte 1. Camyla Moreno
 Probabilidade Parte 1 Camyla Moreno Probabilidade A teoria das probabilidades é um ramo da Matemática que cria, elabora e pesquisa modelos para estudar experimentos ou fenômenos aleatórios. Principais
Probabilidade Parte 1 Camyla Moreno Probabilidade A teoria das probabilidades é um ramo da Matemática que cria, elabora e pesquisa modelos para estudar experimentos ou fenômenos aleatórios. Principais
Estatística. Disciplina de Estatística 2011/2 Curso de Administração em Gestão Pública Profª. Ms. Valéria Espíndola Lessa
 Estatística Disciplina de Estatística 20/2 Curso de Administração em Gestão Pública Profª. Ms. Valéria Espíndola Lessa Estatística Inferencial Estudos das Probabilidades (noção básica) Amostragens e Distribuição
Estatística Disciplina de Estatística 20/2 Curso de Administração em Gestão Pública Profª. Ms. Valéria Espíndola Lessa Estatística Inferencial Estudos das Probabilidades (noção básica) Amostragens e Distribuição
CAPÍTULO 3 PROBABILIDADE
 CAPÍTULO 3 PROBABILIDADE 1. Conceitos 1.1 Experimento determinístico Um experimento se diz determinístico quando repetido em mesmas condições conduz a resultados idênticos. Exemplo 1: De uma urna que contém
CAPÍTULO 3 PROBABILIDADE 1. Conceitos 1.1 Experimento determinístico Um experimento se diz determinístico quando repetido em mesmas condições conduz a resultados idênticos. Exemplo 1: De uma urna que contém
Estatística: Probabilidade e Distribuições
 Estatística: Probabilidade e Distribuições Disciplina de Estatística 2012/2 Curso: Tecnólogo em Gestão Ambiental Profª. Ms. Valéria Espíndola Lessa 1 Aula de Hoje 23/11/2012 Estudo da Probabilidade Distribuição
Estatística: Probabilidade e Distribuições Disciplina de Estatística 2012/2 Curso: Tecnólogo em Gestão Ambiental Profª. Ms. Valéria Espíndola Lessa 1 Aula de Hoje 23/11/2012 Estudo da Probabilidade Distribuição
Fascículo 11 Unidades 34, 35 e 36. 2ª Edição
 2ª Edição Fascículo 11 Unidades 34, 35 e 36 GOVERNO DO ESTADO DO RIO DE JANEIRO Governador Sergio Cabral Vice-Governador Luiz Fernando de Souza Pezão SECRETARIA DE ESTADO DE CIÊNCIA E TECNOLOGIA Secretário
2ª Edição Fascículo 11 Unidades 34, 35 e 36 GOVERNO DO ESTADO DO RIO DE JANEIRO Governador Sergio Cabral Vice-Governador Luiz Fernando de Souza Pezão SECRETARIA DE ESTADO DE CIÊNCIA E TECNOLOGIA Secretário
Estatística Aplicada. Prof. Carlos Alberto Stechhahn PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL.
 Estatística Aplicada Administração p(a) = n(a) / n(u) PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL Prof. Carlos Alberto Stechhahn 2014 1. Noções de Probabilidade Chama-se experimento
Estatística Aplicada Administração p(a) = n(a) / n(u) PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL Prof. Carlos Alberto Stechhahn 2014 1. Noções de Probabilidade Chama-se experimento
Adição de probabilidades. O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e):
 Adição de probabilidades O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e): Dois eventos A e B são ditos mutuamente exclusivos se, e somente se, A B
Adição de probabilidades O número de elementos da união dos conjuntos A e B n(aub) = n(a B) Dividindo os dois membros por n(e): Dois eventos A e B são ditos mutuamente exclusivos se, e somente se, A B
RESOLUÇÃO DAS ATIVIDADES E FORMALIZAÇÃO DOS CONCEITOS
 CENTRO UNIVERSITÁRIO FRANCISCANO Curso de Administração Disciplina: Estatística I Professora: Stefane L. Gaffuri RESOLUÇÃO DAS ATIVIDADES E FORMALIZAÇÃO DOS CONCEITOS Sessão 1 Experimentos Aleatórios e
CENTRO UNIVERSITÁRIO FRANCISCANO Curso de Administração Disciplina: Estatística I Professora: Stefane L. Gaffuri RESOLUÇÃO DAS ATIVIDADES E FORMALIZAÇÃO DOS CONCEITOS Sessão 1 Experimentos Aleatórios e
Aulas particulares. Conteúdo
 Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Ciclo 3 Encontro 2 PROBABILIDADE. Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr.
 1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
PROBABILIDADES PROBABILIDADE DE UM EVENTO EM UM ESPAÇO AMOSTRAL FINITO
 PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
Noções sobre Probabilidade
 Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
PROBABILIDADE PROPRIEDADES E AXIOMAS
 PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
Probabilidade em espaços discretos. Prof.: Joni Fusinato
 Probabilidade em espaços discretos Prof.: Joni Fusinato [email protected] [email protected] Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
Probabilidade em espaços discretos Prof.: Joni Fusinato [email protected] [email protected] Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES
 PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES 0 1 INTRODUÇÃO A teoria das probabilidades é utilizada para determinar as chances de um experimento aleatório acontecer. 1.1
PROBABILIDADE E ESTATÍSTICA UNIDADE V - INTRODUÇÃO À TEORIA DAS PROBABILIDADES 0 1 INTRODUÇÃO A teoria das probabilidades é utilizada para determinar as chances de um experimento aleatório acontecer. 1.1
MATEMÁTICA MÓDULO 4 PROBABILIDADE
 PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
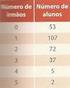 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Probabilidade. Professora Ana Hermínia Andrade. Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise
 Probabilidade Professora Ana Hermínia Andrade Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise Período 2016.2 Você reconhece algum desses experimentos? Alguns
Probabilidade Professora Ana Hermínia Andrade Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise Período 2016.2 Você reconhece algum desses experimentos? Alguns
Seja A um evento de um espaço amostral Ω finito, cujos elementos são igualmente prováveis. Define-se a probabilidade do evento A como
 Aula 7 Probabilidade Nesta aula você aprenderá a definição de probabilidade, estudará os axiomas e propriedades de uma lei de probabilidade e fará revisão dos seguintes conceitos de análise combinatória:
Aula 7 Probabilidade Nesta aula você aprenderá a definição de probabilidade, estudará os axiomas e propriedades de uma lei de probabilidade e fará revisão dos seguintes conceitos de análise combinatória:
3 NOÇÕES DE PROBABILIDADE
 3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
EXERCÍCIOS REVISIONAIS SOBRE BINÔMIO DE NEWTON SISTEMAS LINEARES PROBABILIDADE 2 ANO
 QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
Probabilidade Condicional (grupo 2)
 page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
INTRODUÇÃO ÀS PROBABILIDADES15
 INTRODUÇÃO ÀS PROBABILIDADES15 Vanderlei S. Bagnato 15.1 Introdução 15.2 Definição de Probabilidade 15.3 Adição de probabilidade 15.4 Multiplicação de probabilidades Referências Licenciatura em Ciências
INTRODUÇÃO ÀS PROBABILIDADES15 Vanderlei S. Bagnato 15.1 Introdução 15.2 Definição de Probabilidade 15.3 Adição de probabilidade 15.4 Multiplicação de probabilidades Referências Licenciatura em Ciências
PLANO DE TRABALHO 2 1º BIMESTRE 2014
 PLANO DE TRABALHO 2 1º BIMESTRE 2014 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: CIEP 343 PROFª EMÍLIA DINIZ LIGIÉRO PROFESSOR: ANA CRISTINA PEREIRA COSTA MATRÍCULA:
PLANO DE TRABALHO 2 1º BIMESTRE 2014 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: CIEP 343 PROFª EMÍLIA DINIZ LIGIÉRO PROFESSOR: ANA CRISTINA PEREIRA COSTA MATRÍCULA:
Q05. Ainda sobre os eventos A, B, C e D do exercício 03, quais são mutuamente exclusivos?
 LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
TEORIA DAS PROBABILIDADES
 TEORIA DAS PROBABILIDADES 1.1 Introdução Ao estudarmos um fenômeno coletivo, verificamos a necessidade de descrever o próprio fenômeno e o modelo matemático associado ao mesmo, que permita explicá-lo da
TEORIA DAS PROBABILIDADES 1.1 Introdução Ao estudarmos um fenômeno coletivo, verificamos a necessidade de descrever o próprio fenômeno e o modelo matemático associado ao mesmo, que permita explicá-lo da
PROBABILIDADE. É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral, é S.
 PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.
Chama-se evento todo subconjunto de um espaço amostral. PROBABILIDADE. Introdução
 Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Introdução à Estatística
 Introdução à Estatística Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB [email protected] Introdução a Probabilidade Existem dois tipos de experimentos:
Introdução à Estatística Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB [email protected] Introdução a Probabilidade Existem dois tipos de experimentos:
7- Probabilidade da união de dois eventos
 . 7- Probabilidade da união de dois eventos Sejam A e B eventos de um mesmo espaço amostral Ω. Vamos encontrar uma expressão para a probabilidade de ocorrer o evento A ou o evento B, isto é, a probabilidade
. 7- Probabilidade da união de dois eventos Sejam A e B eventos de um mesmo espaço amostral Ω. Vamos encontrar uma expressão para a probabilidade de ocorrer o evento A ou o evento B, isto é, a probabilidade
Princípios básicos de probabilidade e aplicação à genética
 Princípios básicos de probabilidade e aplicação à genética 1ª Parte: Princípios básicos de probabilidade Probabilidade é a chance que um evento tem de ocorrer, entre dois ou mais eventos possíveis. Por
Princípios básicos de probabilidade e aplicação à genética 1ª Parte: Princípios básicos de probabilidade Probabilidade é a chance que um evento tem de ocorrer, entre dois ou mais eventos possíveis. Por
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
Aula 16 - Erivaldo. Probabilidade
 Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Universidade Federal de Goiás Instituto de Matemática e Estatística
 Universidade Federal de Goiás Instituto de Matemática e Estatística Prova 1 de Probabilidade I Prof.: Fabiano F. T. dos Santos Goiânia, 15 de setembro de 2014 Aluno: Nota: Descreva seu raciocínio e desenvolva
Universidade Federal de Goiás Instituto de Matemática e Estatística Prova 1 de Probabilidade I Prof.: Fabiano F. T. dos Santos Goiânia, 15 de setembro de 2014 Aluno: Nota: Descreva seu raciocínio e desenvolva
Exercícios de Probabilidade - Lista 1. Profa. Ana Maria Farias
 Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Material Teórico - Módulo Probabilidade Condicional. Probabilidade Condicional - Parte 1. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Probabilidade Condicional Probabilidade Condicional - Parte 1 Segundo Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Probabilidade
Material Teórico - Módulo Probabilidade Condicional Probabilidade Condicional - Parte 1 Segundo Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Probabilidade
PROBABILIDADE CONTEÚDOS
 PROBABILIDADE CONTEÚDOS Experimentos aleatórios Eventos Probabilidade Probabilidade de união de dois eventos Probabilidade de eventos independentes Probabilidade condicional AMPLIANDO SEUS CONHECIMENTOS
PROBABILIDADE CONTEÚDOS Experimentos aleatórios Eventos Probabilidade Probabilidade de união de dois eventos Probabilidade de eventos independentes Probabilidade condicional AMPLIANDO SEUS CONHECIMENTOS
INTRODUÇÃO À PROBABILIDADE
 INTRODUÇÃO À PROBABILIDADE Foto extraída em http://www.alea.pt Profª Maria Eliane Universidade Estadual de Santa Cruz USO DE PROBABILIDADES EM SITUAÇÕES DO COTIDIANO Escolhas pessoais Previsão do tempo
INTRODUÇÃO À PROBABILIDADE Foto extraída em http://www.alea.pt Profª Maria Eliane Universidade Estadual de Santa Cruz USO DE PROBABILIDADES EM SITUAÇÕES DO COTIDIANO Escolhas pessoais Previsão do tempo
PROBABILIDADE E ESTATÍSTICA PROBABILIDADES
 PROBABILIDADE E ESTATÍSTICA PROBABILIDADES Bruno Baierle Maurício Furigo Prof.ª Sheila Regina Oro (orientadora) Edital 06/2013 - Produção de Recursos Educacionais Digitais Revisando - Análise combinatória
PROBABILIDADE E ESTATÍSTICA PROBABILIDADES Bruno Baierle Maurício Furigo Prof.ª Sheila Regina Oro (orientadora) Edital 06/2013 - Produção de Recursos Educacionais Digitais Revisando - Análise combinatória
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a
 Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Teoria das Probabilidades
 Capítulo 2 Teoria das Probabilidades 2.1 Introdução No capítulo anterior, foram mostrados alguns conceitos relacionados à estatística descritiva. Neste capítulo apresentamos a base teórica para o desenvolvimento
Capítulo 2 Teoria das Probabilidades 2.1 Introdução No capítulo anterior, foram mostrados alguns conceitos relacionados à estatística descritiva. Neste capítulo apresentamos a base teórica para o desenvolvimento
BANCO DE QUESTÕES TURMA PM-PE PROBABILIDADE
 01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
MATEMÁTICA A - 12o Ano Probabilidades - Distribuições de probabilidades
 MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
Resposta: Resposta: 4 ou seja, 1.
 1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
TÓPICO. Fundamentos da Matemática II INTRODUÇÃO ÀS PROBABILIDADES14. Licenciatura em Ciências USP/ Univesp. Vanderlei S. Bagnato
 INTRODUÇÃO ÀS PROBABILIDADES14 TÓPICO Vanderlei S. Bagnato Fundamentos da Matemática II 14.1 Introdução 14.2 Definição de Probabilidade 14.3 Adição de probabilidade 14.4 Multiplicação de Probabilidades
INTRODUÇÃO ÀS PROBABILIDADES14 TÓPICO Vanderlei S. Bagnato Fundamentos da Matemática II 14.1 Introdução 14.2 Definição de Probabilidade 14.3 Adição de probabilidade 14.4 Multiplicação de Probabilidades
Teoria das Probabilidades
 Teoria das Prof. Eduardo Bezerra (CEFET/RJ) 23 de fevereiro de 2018 Eduardo Bezerra (CEFET/RJ) Teoria das 2018.1 1 / 54 Roteiro Experimento aleatório, espaço amostral, evento 1 Experimento aleatório, espaço
Teoria das Prof. Eduardo Bezerra (CEFET/RJ) 23 de fevereiro de 2018 Eduardo Bezerra (CEFET/RJ) Teoria das 2018.1 1 / 54 Roteiro Experimento aleatório, espaço amostral, evento 1 Experimento aleatório, espaço
Probabilidades. Wagner H. Bonat Elias T. Krainski Fernando P. Mayer
 Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 2011/12 Distribuição de probabilidades 12.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
TEORIA DAS PROBABILIDADES
 TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento É um ramo da matemática que cria, elabora e pesquisa modelos para estudar experimentos
TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento É um ramo da matemática que cria, elabora e pesquisa modelos para estudar experimentos
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística. Probabilidades
 Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE. c) 1/4 d) 1/12 e) nda MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS
 MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
( ) ( ) Questões tipo exame. O número pedido é: Questões tipo exame Pág Os algarismos 1 e 2 podem ocupar 5 A. posições diferentes.
 Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
c) 17 b) 4 17 e) 17 21
 Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
3. Probabilidade P(A) =
 7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
Probabilidade e Estatística
 Aula 3 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Aula 3 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Conteúdo: Aula 2. Probabilidade e Estatística. Professora: Rosa M. M. Leão
 Aula 2 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
Aula 2 Professora: Rosa M. M. Leão Probabilidade e Estatística Conteúdo: 1.1 Por que estudar? 1.2 O que é? 1.3 População e Amostra 1.4 Um exemplo 1.5 Teoria da Probabilidade 1.6 Análise Combinatória 3
ESTATÍSTICA I LISTA DE EXERCÍCIOS 2 GABARITO
 ESTATÍSTICA I LISTA DE EXERCÍCIOS 2 GABARITO 1. (Magalhães e Lima, pg 40) Para cada um dos casos abaixo, escreva o espaço amostral correspondente e conte seus elementos: (a) Uma moeda é lançada duas vezes
ESTATÍSTICA I LISTA DE EXERCÍCIOS 2 GABARITO 1. (Magalhães e Lima, pg 40) Para cada um dos casos abaixo, escreva o espaço amostral correspondente e conte seus elementos: (a) Uma moeda é lançada duas vezes
REGRAS PARA CÁLCULO DE PROBABILIDADES
 REGRAS PARA CÁLCULO DE PROBABILIDADES Prof. Dr. Lucas Santana da Cunha http://www.uel.br/pessoal/lscunha/ 15 de abril de 2019 Londrina 1 / 17 As probabilidades sempre se referem a ocorrência de eventos
REGRAS PARA CÁLCULO DE PROBABILIDADES Prof. Dr. Lucas Santana da Cunha http://www.uel.br/pessoal/lscunha/ 15 de abril de 2019 Londrina 1 / 17 As probabilidades sempre se referem a ocorrência de eventos
Teoria das probabilidades
 Teoria das probabilidades Prof. Dr. Lucas Santana da Cunha email: [email protected] http://www.uel.br/pessoal/lscunha/ 25 de abril de 2018 Londrina 1 / 22 Conceitos probabiĺısticos são necessários para se
Teoria das probabilidades Prof. Dr. Lucas Santana da Cunha email: [email protected] http://www.uel.br/pessoal/lscunha/ 25 de abril de 2018 Londrina 1 / 22 Conceitos probabiĺısticos são necessários para se
Fração como Probabilidade - União e Interseção de Eventos. Sexto Ano do Ensino Fundamental
 Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade - União e Interseção de Eventos Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio
Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade - União e Interseção de Eventos Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio
O conceito de probabilidade
 A UA UL LA O conceito de probabilidade Introdução Nesta aula daremos início ao estudo da probabilidades. Quando usamos probabilidades? Ouvimos falar desse assunto em situações como: a probabilidade de
A UA UL LA O conceito de probabilidade Introdução Nesta aula daremos início ao estudo da probabilidades. Quando usamos probabilidades? Ouvimos falar desse assunto em situações como: a probabilidade de
Teoria das Probabilidades
 08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
NOÇÕES DE PROBABILIDADE
 NOÇÕES DE PROBABILIDADE ? CARA? OU? COROA? 2 ? Qual será o rendimento da Caderneta de Poupança até o final deste ano??? E qual será a taxa de inflação acumulada em 2011???? Quem será o próximo prefeito
NOÇÕES DE PROBABILIDADE ? CARA? OU? COROA? 2 ? Qual será o rendimento da Caderneta de Poupança até o final deste ano??? E qual será a taxa de inflação acumulada em 2011???? Quem será o próximo prefeito
3. A probabilidade do evento de números pares. 4. O evento formado por número menor que três. 5. A probabilidade do evento número menor que três.
 1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
Teoria das Probabilidades
 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Matemática. Probabilidade Básica. Professor Dudan.
 Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
ELEMENTOS DE PROBABILIDADE. Prof. Paulo Rafael Bösing 25/11/2015
 ELEMENTOS DE PROBABILIDADE Prof. Paulo Rafael Bösing 25/11/2015 ELEMENTOS DE PROBABILIDADE Def.: Um experimento é dito aleatório quando o seu resultado não for previsível antes de sua realização, ou seja,
ELEMENTOS DE PROBABILIDADE Prof. Paulo Rafael Bösing 25/11/2015 ELEMENTOS DE PROBABILIDADE Def.: Um experimento é dito aleatório quando o seu resultado não for previsível antes de sua realização, ou seja,
TESTE GLOBAL PROBABILIDADES 12.º ANO
 TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
PROBABILIDADE. Numero de Resultados Desejado Numero de Resultados Possiveis EXERCÍCIOS DE AULA
 PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
NOÇÕES DE PROBABILIDADE
 NOÇÕES DE PROBABILIDADE Experimento Aleatório Experimento Aleatório: procedimento que, ao ser repetido sob as mesmas condições, pode fornecer resultados diferentes Exemplos:. Resultado no lançamento de
NOÇÕES DE PROBABILIDADE Experimento Aleatório Experimento Aleatório: procedimento que, ao ser repetido sob as mesmas condições, pode fornecer resultados diferentes Exemplos:. Resultado no lançamento de
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan
 Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
PROBABILIDADE. Aula 2 Probabilidade Básica. Fernando Arbache
 PROBABILIDADE Aula 2 Probabilidade Básica Fernando Arbache Probabilidade Medida da incerteza associada aos resultados do experimento aleatório Deve fornecer a informação de quão verossímil é a ocorrência
PROBABILIDADE Aula 2 Probabilidade Básica Fernando Arbache Probabilidade Medida da incerteza associada aos resultados do experimento aleatório Deve fornecer a informação de quão verossímil é a ocorrência
CADERNO DE EXERCÍCIOS 3B
 CADERNO DE EXERCÍCIOS B Ensino Médio Matemática Conteúdo Habilidade da Questão Matriz da EJA/FB Equação Exponencial H7 Probabilidade. H7 . Em qual das equações exponenciais temos o valor de x maior ou
CADERNO DE EXERCÍCIOS B Ensino Médio Matemática Conteúdo Habilidade da Questão Matriz da EJA/FB Equação Exponencial H7 Probabilidade. H7 . Em qual das equações exponenciais temos o valor de x maior ou
Matemática E Extensivo V. 5
 Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Aula 10 - Erivaldo. Probabilidade
 Aula 10 - Erivaldo Probabilidade Experimento determinístico Dizemos que um experimento é determinístico quando repetido em condições semelhantes conduz a resultados idênticos. Experimento aleatório Dizemos
Aula 10 - Erivaldo Probabilidade Experimento determinístico Dizemos que um experimento é determinístico quando repetido em condições semelhantes conduz a resultados idênticos. Experimento aleatório Dizemos
Probabilidade. Ricardo Ehlers Departamento de Matemática Aplicada e Estatística Universidade de São Paulo
 Probabilidade Ricardo Ehlers [email protected] Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Experimento aleatório Definição. Qualquer experimento cujo resultado não pode
Probabilidade Ricardo Ehlers [email protected] Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Experimento aleatório Definição. Qualquer experimento cujo resultado não pode
SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE
 SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE Trabalho apresentado ao curso de Formação Continuada da Fundação CECIERJ - Consórcio CEDERJ. Orientadora: Danubia de Araujo Machado (Tutora) Grupo 2 Série:
SULIMAR GOMES SILVA INTRODUÇÃO À PROBABILIDADE Trabalho apresentado ao curso de Formação Continuada da Fundação CECIERJ - Consórcio CEDERJ. Orientadora: Danubia de Araujo Machado (Tutora) Grupo 2 Série:
