Álgebra A - Aula 11 RSA
|
|
|
- Juan Aragão Escobar
- 8 Há anos
- Visualizações:
Transcrição
1 Álgebra A - Aula 11 RSA Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre
2 Criptografia RSA- pré-codificação Converter a mensagem em uma seqüência de números pré-codificação. Letras A a Z (maiúsculas) + espaços em branco entre palavras (99). A = 10, B = 11, etc, Z = 35. Números com exatamente dois algarismos.
3 Pré-codificação Chave pública: n = p.q, p e q primos. Devemos quebrar a mensagem em blocos: números menores que n. Orientações: Não começar com o número 0 (problemas na decodificação). Os blocos não devem corresponder a nenhuma unidade linguística (palavra, letra, etc): decodificação por contagem de freqüência fica impossível.
4 Codificando Para codificar: n = p.q e inteiro positivo e que seja inversível módulo φ(n). Em outras palavras, mdc(e, φ(n)) = mdc(e, (p 1).(q 1)) = 1 Chamaremos o par (n, e) a chave de codificação RSA. Codificando cada bloco b: do sistema C(b) b e (mod n) Onde 0 C(b) < n. Importante: Não reunir os blocos após a codificação.
5 Exemplo Paraty é linda: Tome n = = 143. Quebrando a mensagem em blocos: Como φ(143) = = 120, tomamos e = 7. Logo, C(25) (mod 143) (mod 143) (mod 143) (mod 143) (mod 143) 64 (mod 143) Obtemos assim a seguinte mensagem cifrada:
6 Decodificando (n, d) = chave de decodificação onde d é o inverso de e módulo φ(n). D(c) é dado por: D(c) c d (mod n) onde 0 D(c) < n. Observe que é muito fácil calcular d, desde que φ(n) e e sejam conhecidos: basta aplicar o algoritmo euclideano estendido. Entretanto, se não conhecemos p e q é praticamente impossível calcular d.
7 Exemplo Voltando ao nosso exemplo, temos que n = 143 e e = 7. Para calcular d, usamos o algoritmo euclideano estendido: 120 = = 1 = ( 17).7 Logo o inverso de 7 módulo 120 é 17. Como d deve ser usado como um expoente, precisamos que d seja positivo. Logo tomamos d = = 103.
8 Funciona? Pergunta óbvia que surge: D(C(b)) = b? Ou seja, decodificando um bloco de mensagem codificada, encontramos um bloco da mensagem original? Consideremos então n = p.q. Vamos provar que DC(b) b (mod n) E por que não a igualdade? Observe que DC(b) e b são menores que n 1. Por isso escolhemos b menor que n e mantivemos os blocos separados depois da codificação!
9 Funciona! Por definição: DC(b) (b e ) d b e.d (mod n) Mas d é o inverso de e módulo φ(n). Logo existe inteiro k tal que ed = 1 + kφ(n). Logo, b ed b 1+kφ(n) (b φ(n) ) k.b (mod n) Se mdc(b, n) = 1, então podemos usar o teorema de Euler: b ed (b φ(n) ) k.b b (mod n)
10 Funciona! Se b e n não são primos entre si, observe que n = p.q, p e q primos distintos. Logo, b ed b 1+kφ(n) (b (p 1) ) k.(q 1).b (mod p) Se mdc(b, p) = 1, então podemos usar o teorema de Fermat (b p 1 1 (mod p)). Se não, temos que p b e portanto b ed b 0 (mod p)
11 Funciona! Logo, b ed b (mod p) qualquer que seja b. Fazemos o mesmo para o primo q, obtendo: b ed b (mod q) Portanto, como queríamos. b ed b (mod p.q)
12 Porque o RSA é seguro O RSA só é seguro se for difícil calcular d quando apenas o par (n, e) é conhecido. Mas d somente se φ(n): fatoração de n. Por que não outro processo para calcular d e φ(n)? Resposta: φ(n) = (p 1).(q 1) = pq (p + q) + 1 = n (p + q) + 1 Logo, (p + q) = n φ(n) + 1 e (p + q) 2 4n = (p 2 + q 2 + 2pq) 4pq = (p q) 2 Logo, p q = (p + q) 2 4n
13 Porque o RSA é seguro Outro jeito de quebrar o RSA seria achar um algoritmo que calcule d diretamente a partir de n e e. Como ed 1 (mod φ(n)), isto implica que conhecemos um múltiplo de φ(n). Isso também é suficiente para fatorar n (prova complicada). A última alternativa seria achar b a partir da forma reduzida de b e módulo n sem achar d. Bom, ninguém conseguiu fazer isso até agora... Acredita-se que quebrar o RSA e fatorar n sejam problemas equivalentes, apesar disso não ter sido demonstrado.
14 Escolhendo primos RSA de chave pública (n, e), n com aproximadamente r algarismos. Escolha um primo p entre 4r 10 e 45r 10r 100 algarismos e q próximo de p. Tamanho da chave recomendado atualmente: 768 bits. n terá 231 algarismos. p e q: 104 e 127 algarismos respectivamente. Importante: p 1, q 1, p + 1, p 1 não tenham fatores primos pequenos, pois senão seria fácil fatorar n.
15 Escolhendo primos Para encontrar p e q, seguiremos a seguinte estratégia: 1. Tome um número s ímpar. 2. Verifique se s é divisível por um primo menor que Aplique o teste de Miller a s usando como base os 10 primeiros primos. Se x é um número da ordem de , no intervalo entre x e x existem aproximadamente 34 primos dentre 560 números que passam a etapa (1) da estratégia acima...
16 Assinaturas Apenas codificar mensagens não basta: sistema é de chave pública. Um hacker poderia facilmente mandar instruções ao banco para que o seu saldo bancário fosse transferido para uma outra conta. Por isso, o banco precisa de uma garantia de que a mensagem teve origem em um usuário autorizado. Ou seja, a mensagem tem que ser assinada.
17 Assinaturas C m e D m : codificação e decodificação do Mário e de C a e D a as funções do Allan.b: de Mário para Allan. Mensagem assinada: C a (D m (b)) Para ler a mensagem: Allan aplica D a e depois C m. Observe que C m é público. Se a mensagem fizer sentido, é certo que a origem foi mesmo o Mário! Mas cuidado! Esse sistema pode ser usado para quebrar o RSA, como em 1995 por um consultor em assuntos de segurança de computadores...
18 Exercícios propostos - Capítulo 11 1,2,3,4,6
¹CPTL/UFMS, Três Lagoas, MS,Brasil, oliveiralimarafael@hotmail.com. ²CPTL/UFMS, Três Lagoas, MS, Brasil.
 Encontro de Ensino, Pesquisa e Extensão, Presidente Prudente, 22 a 25 de outubro, 2012 36 INTRODUÇÃO A CRIPTOGRAFIA RSA Rafael Lima Oliveira¹, Prof. Dr. Fernando Pereira de Souza². ¹CPTL/UFMS, Três Lagoas,
Encontro de Ensino, Pesquisa e Extensão, Presidente Prudente, 22 a 25 de outubro, 2012 36 INTRODUÇÃO A CRIPTOGRAFIA RSA Rafael Lima Oliveira¹, Prof. Dr. Fernando Pereira de Souza². ¹CPTL/UFMS, Três Lagoas,
CONCEITOS MATEMÁTICOS ENVOLVIDOS NO FUNCIONAMENTO DA CRIPTOGRAFIA RSA
 CONCEITOS MATEMÁTICOS ENVOLVIDOS NO FUNCIONAMENTO DA CRIPTOGRAFIA RSA Cristiane Moro 1 Raquel Cerbaro 2 Andréia Beatriz Schmid 3 Resumo: A criptografia visa garantir que somente pessoas autorizadas tenham
CONCEITOS MATEMÁTICOS ENVOLVIDOS NO FUNCIONAMENTO DA CRIPTOGRAFIA RSA Cristiane Moro 1 Raquel Cerbaro 2 Andréia Beatriz Schmid 3 Resumo: A criptografia visa garantir que somente pessoas autorizadas tenham
Nome: Paulo Eduardo Rodrigues de Oliveira Nome: Pedro Thiago Ezequiel de Andrade Nome: Rafael Lucas Gregório D'Oliveira. Rsa
 Nome: Paulo Eduardo Rodrigues de Oliveira Nome: Pedro Thiago Ezequiel de Andrade Nome: Rafael Lucas Gregório D'Oliveira RA:063570 RA:063696 RA:063824 Rsa Introdução: Criptografia (Do Grego kryptós, "escondido",
Nome: Paulo Eduardo Rodrigues de Oliveira Nome: Pedro Thiago Ezequiel de Andrade Nome: Rafael Lucas Gregório D'Oliveira RA:063570 RA:063696 RA:063824 Rsa Introdução: Criptografia (Do Grego kryptós, "escondido",
Criptografia fragilidades? GRIS-2011-A-003
 Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Ciência da Computação Grupo de Resposta a Incidentes de Segurança Rio de Janeiro, RJ - Brasil Criptografia O que é, porque
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Ciência da Computação Grupo de Resposta a Incidentes de Segurança Rio de Janeiro, RJ - Brasil Criptografia O que é, porque
Resíduos Quadráticos e Fatoração: uma aplicação à criptoanálise do RSA
 Resíduos Quadráticos e Fatoração: uma aplicação à criptoanálise do RSA Charles F. de Barros 20 de novembro de 2008 Resumo Faremos uma breve introdução ao conceito de resíduos quadráticos, descrevendo em
Resíduos Quadráticos e Fatoração: uma aplicação à criptoanálise do RSA Charles F. de Barros 20 de novembro de 2008 Resumo Faremos uma breve introdução ao conceito de resíduos quadráticos, descrevendo em
Criptografia e Segurança em Redes Capítulo 9. Quarta Edição William Stallings
 Criptografia e Segurança em Redes Capítulo 9 Quarta Edição William Stallings Capítulo 9 - Public Key Cryptography e RSA Cada egípicio recebia dois nomes que eram conhecidos respectivamente como o nome
Criptografia e Segurança em Redes Capítulo 9 Quarta Edição William Stallings Capítulo 9 - Public Key Cryptography e RSA Cada egípicio recebia dois nomes que eram conhecidos respectivamente como o nome
Aulas de PHP Criptografia com Cifra de César. Paulo Marcos Trentin paulo@paulotrentin.com.br http://www.paulotrentin.com.br
 Aulas de PHP Criptografia com Cifra de César Paulo Marcos Trentin paulo@paulotrentin.com.br http://www.paulotrentin.com.br Cifra de César com ISO-8859-1 A cifra de Cesar existe há mais de 2000 anos. É
Aulas de PHP Criptografia com Cifra de César Paulo Marcos Trentin paulo@paulotrentin.com.br http://www.paulotrentin.com.br Cifra de César com ISO-8859-1 A cifra de Cesar existe há mais de 2000 anos. É
Números Primos e Criptografia RSA
 Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
Números Primos e Criptografia RSA Jean Carlo Baena Vicente Matemática - UFPR Orientador: Carlos Henrique dos Santos 6 de outubro de 2013 Sumário Criptografia RSA Por que o RSA funciona? Fatoração Primalidade
Assinatura Digital: problema
 Assinatura Digital Assinatura Digital Assinatura Digital: problema A autenticidade de muitos documentos, é determinada pela presença de uma assinatura autorizada. Para que os sistemas de mensagens computacionais
Assinatura Digital Assinatura Digital Assinatura Digital: problema A autenticidade de muitos documentos, é determinada pela presença de uma assinatura autorizada. Para que os sistemas de mensagens computacionais
MA14 - Aritmética Unidade 24 Resumo
 MA14 - Aritmética Unidade 24 Resumo Introdução à Criptografia Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
MA14 - Aritmética Unidade 24 Resumo Introdução à Criptografia Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
Aritmética Binária e. Bernardo Nunes Gonçalves
 Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
INE5403 - Fundamentos de Matemática Discreta para a Computação
 INE5403 - Fundamentos de Matemática Discreta para a Computação 2) Fundamentos 2.1) Conjuntos e Sub-conjuntos 2.2) Números Inteiros 2.3) Funções 2.4) Seqüências e Somas 2.5) Crescimento de Funções Divisão
INE5403 - Fundamentos de Matemática Discreta para a Computação 2) Fundamentos 2.1) Conjuntos e Sub-conjuntos 2.2) Números Inteiros 2.3) Funções 2.4) Seqüências e Somas 2.5) Crescimento de Funções Divisão
Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano. Prof. Angelo Papa Neto
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
Universidade Federal de São Carlos Departamento de Matemática 083020 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/04/2008
 Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
Universidade Federal de São Carlos Departamento de Matemática 08300 - Curso de Cálculo Numérico - Turma E Resolução da Primeira Prova - 16/0/008 1. (0 pts.) Considere o sistema de ponto flutuante normalizado
Bases Matemáticas. Aula 2 Métodos de Demonstração. Rodrigo Hausen. v. 2013-7-31 1/15
 Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
Bases Matemáticas Aula 2 Métodos de Demonstração Rodrigo Hausen v. 2013-7-31 1/15 Como o Conhecimento Matemático é Organizado Definições Definição: um enunciado que descreve o significado de um termo.
Arquitetura de Rede de Computadores
 TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
Soluções de Questões de Matemática do Centro Federal de Educação Tecnológica Celso Suckow da Fonseca CEFET/RJ
 Soluções de Questões de Matemática do Centro Federal de Educação Tecnológica Celso Suckow da Fonseca CEFET/RJ. Questão Sistemas de Numeração No sistema de numeração de base 2, o numeral mais simples de
Soluções de Questões de Matemática do Centro Federal de Educação Tecnológica Celso Suckow da Fonseca CEFET/RJ. Questão Sistemas de Numeração No sistema de numeração de base 2, o numeral mais simples de
Definição. A expressão M(x,y) dx + N(x,y)dy é chamada de diferencial exata se existe uma função f(x,y) tal que f x (x,y)=m(x,y) e f y (x,y)=n(x,y).
 PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Somatórias e produtórias
 Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Tópico 3. Limites e continuidade de uma função (Parte 2)
 Tópico 3. Limites e continuidade de uma função (Parte 2) Nessa aula continuaremos nosso estudo sobre limites de funções. Analisaremos o limite de funções quando o x ± (infinito). Utilizaremos o conceito
Tópico 3. Limites e continuidade de uma função (Parte 2) Nessa aula continuaremos nosso estudo sobre limites de funções. Analisaremos o limite de funções quando o x ± (infinito). Utilizaremos o conceito
SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2
 SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2 1.1 Introdução... 2 1.2 Estrutura do IP... 3 1.3 Tipos de IP... 3 1.4 Classes de IP... 4 1.5 Máscara de Sub-Rede... 6 1.6 Atribuindo um IP ao computador... 7 2
SUMÁRIO 1. AULA 6 ENDEREÇAMENTO IP:... 2 1.1 Introdução... 2 1.2 Estrutura do IP... 3 1.3 Tipos de IP... 3 1.4 Classes de IP... 4 1.5 Máscara de Sub-Rede... 6 1.6 Atribuindo um IP ao computador... 7 2
Título. Breve descrição da aula. Competência(s) desenvolvida(s) Conteúdo(s) desenvolvido(s).
 Universidade Federal de Goiás Campus Catalão Alunos: Bruno Castilho Rosa Laura Thaís Lourenço Géssica Cristina dos Reis Lucas Borges de Faria Orientador: Igor Lima Seminário Semanal de Álgebra Notas de
Universidade Federal de Goiás Campus Catalão Alunos: Bruno Castilho Rosa Laura Thaís Lourenço Géssica Cristina dos Reis Lucas Borges de Faria Orientador: Igor Lima Seminário Semanal de Álgebra Notas de
8 8 (mod 17) e 3 34 = (3 17 ) 2 9 (mod 17). Daí que 2 67 + 3 34 8 + 9 0 (mod 17), o que significa que 2 67 + 3 34 é múltiplo de 17.
 Prova Teoria de Números 23/04/203 Nome: RA: Escolha 5 questões.. Mostre que 2 67 + 3 34 é múltiplo de 7. Solução: Pelo teorema de Fermat 2 6 (mod 7 e 3 7 3 (mod 7. Portanto, 2 67 = 2 64+3 = ( 2 6 4 8 8
Prova Teoria de Números 23/04/203 Nome: RA: Escolha 5 questões.. Mostre que 2 67 + 3 34 é múltiplo de 7. Solução: Pelo teorema de Fermat 2 6 (mod 7 e 3 7 3 (mod 7. Portanto, 2 67 = 2 64+3 = ( 2 6 4 8 8
Escola Secundária c/3º CEB José Macedo Fragateiro. Curso Profissional de Nível Secundário. Componente Técnica. Disciplina de
 Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
Escola Secundária c/3º CEB José Macedo Fragateiro Curso Profissional de Nível Secundário Componente Técnica Disciplina de Sistemas Digitais e Arquitectura de Computadores 29/21 Módulo 1: Sistemas de Numeração
Algoritmos criptográficos de chave pública
 Algoritmos criptográficos de chave pública Histórico - A descoberta em 1976 por Diffie, Hellman e Merkle de algoritmos criptográficos assimétricos, onde a segurança se baseia nas dificuldades de 1. Deduzir
Algoritmos criptográficos de chave pública Histórico - A descoberta em 1976 por Diffie, Hellman e Merkle de algoritmos criptográficos assimétricos, onde a segurança se baseia nas dificuldades de 1. Deduzir
Seqüências, Limite e Continuidade
 Módulo Seqüências, Limite e Continuidade A partir deste momento, passaremos a estudar seqüência, ites e continuidade de uma função real. Leia com atenção, caso tenha dúvidas busque indicadas e também junto
Módulo Seqüências, Limite e Continuidade A partir deste momento, passaremos a estudar seqüência, ites e continuidade de uma função real. Leia com atenção, caso tenha dúvidas busque indicadas e também junto
Aplicações de Combinatória e Geometria na Teoria dos Números
 Aplicações de Combinatória e Geometria na Teoria dos Números Nesse artigo vamos discutir algumas abordagens diferentes na Teoria dos Números, no sentido de envolverem também outras grandes áreas, como
Aplicações de Combinatória e Geometria na Teoria dos Números Nesse artigo vamos discutir algumas abordagens diferentes na Teoria dos Números, no sentido de envolverem também outras grandes áreas, como
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade
 REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
Prof. Flávio Henrique de Lima Araújo 19
 Um pouco mais sobre as funções matemáticas Em primeiro lugar precisamos ter em mente que o EXCEL é uma ferramenta poderosa que nos dá condição de trabalhar com planilhas eletrônicas, ou seja, com funções,
Um pouco mais sobre as funções matemáticas Em primeiro lugar precisamos ter em mente que o EXCEL é uma ferramenta poderosa que nos dá condição de trabalhar com planilhas eletrônicas, ou seja, com funções,
Venda segura. Série Matemática na Escola
 Venda segura Série Objetivos 1. Apresentar alguns conceitos de criptografia de chave pública; 2. Contextualizar o assunto através de exemplos práticos. 3. Motivar o estudo de operações matemáticas envolvendo
Venda segura Série Objetivos 1. Apresentar alguns conceitos de criptografia de chave pública; 2. Contextualizar o assunto através de exemplos práticos. 3. Motivar o estudo de operações matemáticas envolvendo
MA14 - Aritmética Unidade 4. Representação dos Números Inteiros (Sistemas de Numeração)
 MA14 - Aritmética Unidade 4 Representação dos Números Inteiros (Sistemas de Numeração) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo
MA14 - Aritmética Unidade 4 Representação dos Números Inteiros (Sistemas de Numeração) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo
1. NÍVEL CONVENCIONAL DE MÁQUINA
 1. NÍVEL CONVENCIONAL DE MÁQUINA Relembrando a nossa matéria de Arquitetura de Computadores, a arquitetura de Computadores se divide em vários níveis como já estudamos anteriormente. Ou seja: o Nível 0
1. NÍVEL CONVENCIONAL DE MÁQUINA Relembrando a nossa matéria de Arquitetura de Computadores, a arquitetura de Computadores se divide em vários níveis como já estudamos anteriormente. Ou seja: o Nível 0
Sistemas de Numerações.
 Matemática Profº: Carlos Roberto da Silva; Lourival Pereira Martins. Sistema de numeração: Binário, Octal, Decimal, Hexadecimal; Sistema de numeração: Conversões; Sistemas de Numerações. Nosso sistema
Matemática Profº: Carlos Roberto da Silva; Lourival Pereira Martins. Sistema de numeração: Binário, Octal, Decimal, Hexadecimal; Sistema de numeração: Conversões; Sistemas de Numerações. Nosso sistema
Prof. Roberto Franciscatto 4º Semestre - TSI - CAFW. Free Powerpoint Templates Page 1
 Segurança na Web Cap. 4: Protocolos de Segurança Prof. Roberto Franciscatto 4º Semestre - TSI - CAFW Page 1 é definido como um procedimento seguro para se regular a transmissão de dados entre computadores
Segurança na Web Cap. 4: Protocolos de Segurança Prof. Roberto Franciscatto 4º Semestre - TSI - CAFW Page 1 é definido como um procedimento seguro para se regular a transmissão de dados entre computadores
VALE PARA 1, PARA 2, PARA 3,... VALE SEMPRE?
 VALE PARA 1, PARA 2, PARA 3,.... VALE SEMPRE? Renate Watanabe As afirmações abaio, sobre números naturais, são verdadeiras para os números 1, 2, 3 e muitos outros. Perguntamos: elas são verdadeiras sempre?
VALE PARA 1, PARA 2, PARA 3,.... VALE SEMPRE? Renate Watanabe As afirmações abaio, sobre números naturais, são verdadeiras para os números 1, 2, 3 e muitos outros. Perguntamos: elas são verdadeiras sempre?
PROJETO DE REDES www.projetoderedes.com.br
 PROJETO DE REDES www.projetoderedes.com.br Curso de Tecnologia em Redes de Computadores Disciplina: Redes I Fundamentos - 1º Período Professor: José Maurício S. Pinheiro AULA 2: Transmissão de Dados 1.
PROJETO DE REDES www.projetoderedes.com.br Curso de Tecnologia em Redes de Computadores Disciplina: Redes I Fundamentos - 1º Período Professor: José Maurício S. Pinheiro AULA 2: Transmissão de Dados 1.
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
Microsoft Excel 2007
 Microsoft Excel 2007 O Microsoft Excel é um aplicativo para a construção e edição de planilhas eletrônicas, que permite o trabalho com: formulários, tabelas, gráficos e outros. 2.1 CONCEITOS INICIAIS:
Microsoft Excel 2007 O Microsoft Excel é um aplicativo para a construção e edição de planilhas eletrônicas, que permite o trabalho com: formulários, tabelas, gráficos e outros. 2.1 CONCEITOS INICIAIS:
Auditoria e Segurança da Informação GSI536. Prof. Rodrigo Sanches Miani FACOM/UFU
 Auditoria e Segurança da Informação GSI536 Prof. Rodrigo Sanches Miani FACOM/UFU Revisão Criptografia de chave simétrica; Criptografia de chave pública; Modelo híbrido de criptografia. Criptografia Definições
Auditoria e Segurança da Informação GSI536 Prof. Rodrigo Sanches Miani FACOM/UFU Revisão Criptografia de chave simétrica; Criptografia de chave pública; Modelo híbrido de criptografia. Criptografia Definições
2. Representação Numérica
 2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
37ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 1 (6º e 7º anos do Ensino Fundamental) GABARITO
 GABARITO NÍVEL 1 37ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 1 (6º e 7º anos do Ensino Fundamental) GABARITO 1) C 6) A 11) D 16) C 2) D 7) C 12) C 17) D 3) E 8) B 13) E 18) A 4) E 9) B 14)
GABARITO NÍVEL 1 37ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 1 (6º e 7º anos do Ensino Fundamental) GABARITO 1) C 6) A 11) D 16) C 2) D 7) C 12) C 17) D 3) E 8) B 13) E 18) A 4) E 9) B 14)
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE ESCOLA AGRÍCOLA DE JUNDIAÍ EAJ - PRONATEC / REDE etec MÓDULO III DESENVOLVIMENTO PROFESSOR ADDSON COSTA
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE ESCOLA AGRÍCOLA DE JUNDIAÍ EAJ - PRONATEC / REDE etec MÓDULO III DESENVOLVIMENTO PROFESSOR ADDSON COSTA RESUMO DE AULA CRIAÇÃO E MANIPULAÇÃO DO BANCO DE DADOS
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE ESCOLA AGRÍCOLA DE JUNDIAÍ EAJ - PRONATEC / REDE etec MÓDULO III DESENVOLVIMENTO PROFESSOR ADDSON COSTA RESUMO DE AULA CRIAÇÃO E MANIPULAÇÃO DO BANCO DE DADOS
Respostas de MAIO. A sequência é formada elevando-se ao quadrado os números 2,3,4... e somandolhes 2 em cada caso.
 Respostas de MAIO Dia 1: O menor número de ovos é 91. Dia 2: O nível da água baixa. No barquinho, a moeda desloca a mesma massa de água que a do barquinho, portanto, um volume maior que o da moeda. Na
Respostas de MAIO Dia 1: O menor número de ovos é 91. Dia 2: O nível da água baixa. No barquinho, a moeda desloca a mesma massa de água que a do barquinho, portanto, um volume maior que o da moeda. Na
EA773 - Experimento 5
 EA773 - Experimento 5 Wu Shin - Ting DCA - FEEC - Unicamp 19 de Novembro de 2009 O projeto consiste em implementar uma calculadora com memória com uso de barramento de 8 bits. Neste documento são discutidos
EA773 - Experimento 5 Wu Shin - Ting DCA - FEEC - Unicamp 19 de Novembro de 2009 O projeto consiste em implementar uma calculadora com memória com uso de barramento de 8 bits. Neste documento são discutidos
Contagem II. Neste material vamos aprender novas técnicas relacionadas a problemas de contagem. 1. Separando em casos
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 5 Contagem II Neste material vamos aprender novas técnicas relacionadas a problemas de contagem. 1. Separando em
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 5 Contagem II Neste material vamos aprender novas técnicas relacionadas a problemas de contagem. 1. Separando em
FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/2008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO
 1 FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO Nílson José Machado njmachad@usp.br Sempre que pensamos em grandezas que
1 FEUSP- SEMINÁRIOS DE ENSINO DE MATEMÁTICA-1º semestre/008 CÁLCULO DIFERENCIAL E INTEGRAL NA ESCOLA BÁSICA: POSSÍVEL E NECESSÁRIO Nílson José Machado njmachad@usp.br Sempre que pensamos em grandezas que
Manual de operação. BS Ponto Versão 5.1
 Manual de operação BS Ponto Versão 5.1 conteúdo 1. Instalação do sistema Instalando o BS Ponto Configurando o BS Ponto 2. Cadastrando usuários Cadastro do usuário Master Alterando a senha Master Cadastro
Manual de operação BS Ponto Versão 5.1 conteúdo 1. Instalação do sistema Instalando o BS Ponto Configurando o BS Ponto 2. Cadastrando usuários Cadastro do usuário Master Alterando a senha Master Cadastro
Sistemas de Numeração. 1 Introdução aos sistemas numeração
 Sistemas de Numeração 1 Introdução aos sistemas numeração Sistemas de Numeração Base Decimal Base Binária Base Octal Base Hexadecimal Sistemas de numeração ria\base Oct tal\ Base He exadecimal l\base Biná
Sistemas de Numeração 1 Introdução aos sistemas numeração Sistemas de Numeração Base Decimal Base Binária Base Octal Base Hexadecimal Sistemas de numeração ria\base Oct tal\ Base He exadecimal l\base Biná
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB
 NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
2 A Derivada. 2.1 Velocidade Média e Velocidade Instantânea
 2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
(a 1 + a 100 ) + (a 2 + a 99 ) + (a 3 + a 98 ) +... + (a 50 + a 51 ).
 Questão 1. A sequência 0, 3, 7, 10, 14, 17, 21,... é formada a partir do número 0 somando-se alternadamente 3 ou 4 ao termo anterior, isto é: o primeiro termo é 0, o segundo é 3 a mais que o primeiro,
Questão 1. A sequência 0, 3, 7, 10, 14, 17, 21,... é formada a partir do número 0 somando-se alternadamente 3 ou 4 ao termo anterior, isto é: o primeiro termo é 0, o segundo é 3 a mais que o primeiro,
Manual de Instalação e Configuração do Primeiro Backup Versão PRO
 Manual de Instalação e Configuração do Primeiro Backup Versão PRO Instalação do gbackup Pro Para instalar o gbackup Pro em seu computador ou servidor, basta seguir as seguintes etapas: Após baixar a instalação
Manual de Instalação e Configuração do Primeiro Backup Versão PRO Instalação do gbackup Pro Para instalar o gbackup Pro em seu computador ou servidor, basta seguir as seguintes etapas: Após baixar a instalação
Teoria dos Números. A Teoria dos Números é a área da matemática que lida com os números inteiros, isto é, com o conjunto
 Teoria dos Números 1 Noções Básicas A Teoria dos Números é a área da matemática que lida com os números inteiros, isto é, com o conjunto Z = {..., 4, 3, 2, 1, 0, 1, 2, 3, 4...}. Ela permite resolver de
Teoria dos Números 1 Noções Básicas A Teoria dos Números é a área da matemática que lida com os números inteiros, isto é, com o conjunto Z = {..., 4, 3, 2, 1, 0, 1, 2, 3, 4...}. Ela permite resolver de
1. Sistemas de numeração
 1. Sistemas de numeração Quando mencionamos sistemas de numeração estamos nos referindo à utilização de um sistema para representar uma numeração, ou seja, uma quantidade. Sistematizar algo seria organizar,
1. Sistemas de numeração Quando mencionamos sistemas de numeração estamos nos referindo à utilização de um sistema para representar uma numeração, ou seja, uma quantidade. Sistematizar algo seria organizar,
UNIVERSIDADE ESTADUAL DE GOIÁS UNIDADE UNIVERSITÁRIA DE JUSSARA LICENCIATURA EM MATEMÁTICA ANA PAULA ALVES MACHADO DE LIMA
 UNIVERSIDADE ESTADUAL DE GOIÁS UNIDADE UNIVERSITÁRIA DE JUSSARA LICENCIATURA EM MATEMÁTICA ANA PAULA ALVES MACHADO DE LIMA A HISTÓRIA DA CRIPTOGRAFIA E A APLICAÇÃO DE TEORIA DOS NÚMEROS EM CRIPTOGRAFIA
UNIVERSIDADE ESTADUAL DE GOIÁS UNIDADE UNIVERSITÁRIA DE JUSSARA LICENCIATURA EM MATEMÁTICA ANA PAULA ALVES MACHADO DE LIMA A HISTÓRIA DA CRIPTOGRAFIA E A APLICAÇÃO DE TEORIA DOS NÚMEROS EM CRIPTOGRAFIA
Configuração do cliente de e-mail Thunderbird para usuários DAC
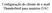 Configuração do cliente de e-mail Thunderbird para usuários DAC A. Configurando a autoridade certificadora ICPEdu no Thunderbird Os certificados utilizados nos serviços de e-mail pop, imap e smtp da DAC
Configuração do cliente de e-mail Thunderbird para usuários DAC A. Configurando a autoridade certificadora ICPEdu no Thunderbird Os certificados utilizados nos serviços de e-mail pop, imap e smtp da DAC
GERAÇÃO DE NOTA FISCAL PAULISTA BEMATECH RESTEQ RESOLVE TECNOLOGIA BEMATECH 1
 BEMATECH 1 Procedimento passo a passo para gerar o arquivo da Nota Fiscal Paulista utilizando o aplicativo da Bematech WINMFD2 Neste aplicativo, existem dois modos para gerar o arquivo corretamente. 1º
BEMATECH 1 Procedimento passo a passo para gerar o arquivo da Nota Fiscal Paulista utilizando o aplicativo da Bematech WINMFD2 Neste aplicativo, existem dois modos para gerar o arquivo corretamente. 1º
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Teoremas de Fermat, Wilson, Wolstenholme e Euler. 1 Os teoremas de Wilson e Wolstenholme
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 6 Teoremas de Fermat, Wilson, Wolstenholme e Euler 1 Os teoremas de Wilson e Wolstenholme Uma aplicação
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 6 Teoremas de Fermat, Wilson, Wolstenholme e Euler 1 Os teoremas de Wilson e Wolstenholme Uma aplicação
Exercícios de Fixação Pseudocódigo e Estruturas Básicas de Controle
 Disciplina: TCC-00.7 Prog. de Computadores III Professor: Leandro Augusto Frata Fernandes Turma: A- Data: / / Exercícios de Fixação Pseudocódigo e Estruturas Básicas de Controle. Construa um algoritmo
Disciplina: TCC-00.7 Prog. de Computadores III Professor: Leandro Augusto Frata Fernandes Turma: A- Data: / / Exercícios de Fixação Pseudocódigo e Estruturas Básicas de Controle. Construa um algoritmo
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas CMP1132 Processo e qualidade de software II Prof. Me. Elias Ferreira Sala: 402 E Quarta-Feira:
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas CMP1132 Processo e qualidade de software II Prof. Me. Elias Ferreira Sala: 402 E Quarta-Feira:
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
CAPÍTULO 6 - ESTRUTURA DE SELEÇÃO
 6.1 - INTRODUÇÃO CAPÍTULO 6 - ESTRUTURA DE SELEÇÃO Existem problemas que podem ter mais de um caminho a ser seguido para seleção correta, ou existem restrições em suas soluções. O sujeito que irá executar
6.1 - INTRODUÇÃO CAPÍTULO 6 - ESTRUTURA DE SELEÇÃO Existem problemas que podem ter mais de um caminho a ser seguido para seleção correta, ou existem restrições em suas soluções. O sujeito que irá executar
Manual RbCripto. Sobre o RbCripto. Requisitos. Estatísticas de exemplo. Criptografia assimétrica versus criptografia simétrica. Como usar o programa
 Manual RbCripto Sobre o RbCripto O RbCripto é um programa simples que foi concebido com fins acadêmicos. É capaz de realizar a encriptação e decriptação de arquivos usando o moderno conceito de curvas
Manual RbCripto Sobre o RbCripto O RbCripto é um programa simples que foi concebido com fins acadêmicos. É capaz de realizar a encriptação e decriptação de arquivos usando o moderno conceito de curvas
No cálculo de porcentagem com operações financeiras devemos tomar muito cuidado para verificar sobre quem foi calculada essa porcentagem.
 1º BLOCO... 2 I. Porcentagem... 2 Relacionando Custo, Venda, Lucro e Prejuízo... 2 Aumentos Sucessivos e Descontos Sucessivos... 3 II. Juros Simples... 3 III. Juros Compostos... 4 2º BLOCO... 6 I. Operadores...
1º BLOCO... 2 I. Porcentagem... 2 Relacionando Custo, Venda, Lucro e Prejuízo... 2 Aumentos Sucessivos e Descontos Sucessivos... 3 II. Juros Simples... 3 III. Juros Compostos... 4 2º BLOCO... 6 I. Operadores...
Capítulo 7 Medidas de dispersão
 Capítulo 7 Medidas de dispersão Introdução Para a compreensão deste capítulo, é necessário que você tenha entendido os conceitos apresentados nos capítulos 4 (ponto médio, classes e frequência) e 6 (média).
Capítulo 7 Medidas de dispersão Introdução Para a compreensão deste capítulo, é necessário que você tenha entendido os conceitos apresentados nos capítulos 4 (ponto médio, classes e frequência) e 6 (média).
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE. Prof. Dr. Daniel Caetano 2012-1
 ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
Contagem I. Figura 1: Abrindo uma Porta.
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 4 Contagem I De quantos modos podemos nos vestir? Quantos números menores que 1000 possuem todos os algarismos pares?
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 4 Contagem I De quantos modos podemos nos vestir? Quantos números menores que 1000 possuem todos os algarismos pares?
Polos Olímpicos de Treinamento. Aula 2. Curso de Teoria dos Números - Nível 2. Divisibilidade II. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula Divisibilidade II Definição 1. Dados dois inteiros a e b, com a 0, dizemos que a divide b ou que a é um divisor
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula Divisibilidade II Definição 1. Dados dois inteiros a e b, com a 0, dizemos que a divide b ou que a é um divisor
ALGORITMOS PARTE 01. Fabricio de Sousa Pinto
 ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
ALGORITMOS PARTE 01 Fabricio de Sousa Pinto Algoritmos: Definição 2 É uma sequência de instruções finita e ordenada de forma lógica para a resolução de uma determinada tarefa ou problema. Algoritmos 3
INTRODUÇÃO À MATEMÁTICA FINANCEIRA
 INTRODUÇÃO À MATEMÁTICA FINANCEIRA SISTEMA MONETÁRIO É o conjunto de moedas que circulam num país e cuja aceitação no pagamento de mercadorias, débitos ou serviços é obrigatória por lei. Ele é constituído
INTRODUÇÃO À MATEMÁTICA FINANCEIRA SISTEMA MONETÁRIO É o conjunto de moedas que circulam num país e cuja aceitação no pagamento de mercadorias, débitos ou serviços é obrigatória por lei. Ele é constituído
Sistemas de Numeração. Introdução ao Computador 2010/1 Renan Manola
 Sistemas de Numeração Introdução ao Computador 2010/1 Renan Manola Introdução Em sistemas digitais o sistema de numeração binário é o mais importante, já fora do mundo digital o sistema decimal é o mais
Sistemas de Numeração Introdução ao Computador 2010/1 Renan Manola Introdução Em sistemas digitais o sistema de numeração binário é o mais importante, já fora do mundo digital o sistema decimal é o mais
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
Questionário de Estudo - P1 Criptografia
 Questionário de Estudo - P1 Criptografia 1) A criptografia e a criptoanálise são dois ramos da criptologia. Qual a diferença entre essas duas artes? Enquanto a Criptografia é a arte de esconder dados e
Questionário de Estudo - P1 Criptografia 1) A criptografia e a criptoanálise são dois ramos da criptologia. Qual a diferença entre essas duas artes? Enquanto a Criptografia é a arte de esconder dados e
Este material traz a teoria necessária à resolução das questões propostas.
 Inclui Teoria e Questões Inteiramente Resolvidas dos assuntos: Contagem: princípio aditivo e multiplicativo. Arranjo. Permutação. Combinação simples e com repetição. Lógica sentencial, de primeira ordem
Inclui Teoria e Questões Inteiramente Resolvidas dos assuntos: Contagem: princípio aditivo e multiplicativo. Arranjo. Permutação. Combinação simples e com repetição. Lógica sentencial, de primeira ordem
Organização e Arquitetura de Computadores I
 Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Organização e Arquitetura de Computadores I Aritmética Computacional Slide 1 Sumário Unidade Lógica e Aritmética Representação de Números Inteiros Aritmética de Números Inteiros Representação de Números
Linguagem algorítmica: Portugol
 Programação de Computadores I Aula 03 Linguagem algorítmica: Portugol José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/34 Introdução I Lógica A lógica é usada
Programação de Computadores I Aula 03 Linguagem algorítmica: Portugol José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/34 Introdução I Lógica A lógica é usada
Princípio da Indução Matemática: P(1) verdadeira ( k)[p(k) verdadeira P(k+1) verdadeira] ENTÃO P(n) verdadeira para todos os n inteiros positivos
![Princípio da Indução Matemática: P(1) verdadeira ( k)[p(k) verdadeira P(k+1) verdadeira] ENTÃO P(n) verdadeira para todos os n inteiros positivos Princípio da Indução Matemática: P(1) verdadeira ( k)[p(k) verdadeira P(k+1) verdadeira] ENTÃO P(n) verdadeira para todos os n inteiros positivos](/thumbs/26/7178858.jpg) Indução Matemática Princípio da Indução Matemática: P(1) verdadeira ( k)[p(k) verdadeira P(k+1) verdadeira] ENTÃO P(n) verdadeira para todos os n inteiros positivos O Princípio da Indução Matemática é
Indução Matemática Princípio da Indução Matemática: P(1) verdadeira ( k)[p(k) verdadeira P(k+1) verdadeira] ENTÃO P(n) verdadeira para todos os n inteiros positivos O Princípio da Indução Matemática é
ARQUITETURA DE COMPUTADORES. Sistemas de Numeração. 1 Arquitetura de Computadores
 ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
ARQUITETURA DE COMPUTADORES Sistemas de Numeração 1 Sistemas de Numeração e Conversão de Base Sistema Decimal É o nosso sistema natural. Dígitos 0,1,2,3,4,5,6,7,8 e 9. Números superiores a 9; convencionamos
Sistemas de Numeração
 Sistemas de Numeração Representação da Informação para seres humanos Números (1,2,3,4...) Letras (a,a,b,b,c,c...) Sinais de pontuação (:,;...) Operadores aritméticos (+,-,x,/) Representação da Informação
Sistemas de Numeração Representação da Informação para seres humanos Números (1,2,3,4...) Letras (a,a,b,b,c,c...) Sinais de pontuação (:,;...) Operadores aritméticos (+,-,x,/) Representação da Informação
X.0 Sucessões de números reais 1
 «Tal como a tecnologia requer as tøcnicas da matemætica aplicada, tambøm a matemætica aplicada requer as teorias do nœcleo central da matemætica pura. Da l gica matemætica topologia algøbrica, da teoria
«Tal como a tecnologia requer as tøcnicas da matemætica aplicada, tambøm a matemætica aplicada requer as teorias do nœcleo central da matemætica pura. Da l gica matemætica topologia algøbrica, da teoria
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Dicas para a 6 a Lista de Álgebra 1 (Conteúdo: Homomorfismos de Grupos e Teorema do Isomorfismo para grupos) Professor: Igor Lima.
 Dicas para a 6 a Lista de Álgebra 1 (Conteúdo: Homomorfismos de Grupos e Teorema do Isomorfismo para grupos) Professor: Igor Lima. 1 /2013 Para calcular Hom(G 1,G 2 ) ou Aut(G) vocês vão precisar ter em
Dicas para a 6 a Lista de Álgebra 1 (Conteúdo: Homomorfismos de Grupos e Teorema do Isomorfismo para grupos) Professor: Igor Lima. 1 /2013 Para calcular Hom(G 1,G 2 ) ou Aut(G) vocês vão precisar ter em
1. Explicando Roteamento um exemplo prático. Através da análise de uns exemplos simples será possível compreender como o roteamento funciona.
 Aula 14 Redes de Computadores 24/10/07 Universidade do Contestado UnC/Mafra Sistemas de Informação Prof. Carlos Guerber ROTEAMENTO EM UMA REDE DE COMPUTADORES A máscara de sub-rede é utilizada para determinar
Aula 14 Redes de Computadores 24/10/07 Universidade do Contestado UnC/Mafra Sistemas de Informação Prof. Carlos Guerber ROTEAMENTO EM UMA REDE DE COMPUTADORES A máscara de sub-rede é utilizada para determinar
Trabalho 2 Fundamentos de computação Gráfica
 Trabalho 2 Fundamentos de computação Gráfica Processamento de Imagens Aluno: Renato Deris Prado Tópicos: 1- Programa em QT e C++ 2- Efeitos de processamento de imagens 1- Programa em QT e C++ Para o trabalho
Trabalho 2 Fundamentos de computação Gráfica Processamento de Imagens Aluno: Renato Deris Prado Tópicos: 1- Programa em QT e C++ 2- Efeitos de processamento de imagens 1- Programa em QT e C++ Para o trabalho
ESTRUTURAS DE DADOS II
 ESTRUTURAS DE DADOS II Msc. Daniele Carvalho Oliveira Doutoranda em Ciência da Computação - UFU Mestre em Ciência da Computação UFU Bacharel em Ciência da Computação - UFJF Conteúdo Programático 1. Introdução
ESTRUTURAS DE DADOS II Msc. Daniele Carvalho Oliveira Doutoranda em Ciência da Computação - UFU Mestre em Ciência da Computação UFU Bacharel em Ciência da Computação - UFJF Conteúdo Programático 1. Introdução
PARANÁ GOVERNO DO ESTADO
 A COMUNICAÇÃO NA INTERNET PROTOCOLO TCP/IP Para tentar facilitar o entendimento de como se dá a comunicação na Internet, vamos começar contando uma história para fazer uma analogia. Era uma vez, um estrangeiro
A COMUNICAÇÃO NA INTERNET PROTOCOLO TCP/IP Para tentar facilitar o entendimento de como se dá a comunicação na Internet, vamos começar contando uma história para fazer uma analogia. Era uma vez, um estrangeiro
