Folheações de grau um no plano projetivo e matrizes de traço nulo
|
|
|
- Larissa Molinari Anjos
- 5 Há anos
- Visualizações:
Transcrição
1 V Bienal da SBM Sociedade Brasileira de Matemática UFPB - Universidade Federal da Paraíba 18 a de outubro de 010 Folheações de grau um no plano projetivo e matrizes de traço nulo Flaviano Bahia & Vivana Ferrer Sumário 1 Introdução 1 Preliminares 3.1 O plano projetivo Folheações em P Campos vetoriais em P O espaço de campos vetoriais de grau d em P formas em P O espaço de 1-formas de grau d em P Campos vs 1-formas Singularidades Singularidades de campos de vetores e de 1-formas Tipos de Singularidades Folheações de grau 1 em P vs Matrizes 3 3 de traço nulo 15 6 Espaço de parâmetros para folheações com cada tipo de singularidade 18 1 Introdução O estudo de folheações holomorfas tem tido um enorme avanço nos últimos tempos. Trabalhos de J.P. Jouanolou, D. Cerveau, A. Lins-Neto, J.V. Pereira, F. Cukierman, O. Calvo-Andrade, X. Gómez-Mont e outros focam o interesse em aspectos globais, estudando questões como a não-)existência de soluções algébricas, descrição das componentes dos espaços de folheações de codimensão 1, etc. Nosso ponto de vista segue o da geometria enumerativa clássica, onde são consideradas perguntas tais como: Quantas curvas passam por uma quantidade apropriada de pontos em posição geral? Achar o grau do espaço de curvas planas tendo uma singularidade de odem dado, etc. Em este trabalho consideramos perguntas similares para espaços de folheações. Vamos nos centrar no caso de folheações =campos vetoriais) de grau um no plano projetivo complexo. O espaço de campos vetoriais de grau um no plano projetivo forma um espaço projetivo de dimensão 7, P 7. As singularidades de um campo vetorial são os pontos onde o campo se anula, i.e., nas singularidades não temos uma direção determinada. Existem vários tipos de singularidades, que definiremos no trabalho. UFSJ, MG, Brasil, bahia flaviano@yahoo.com.br IMPA, RJ, Brasil, vivisferrer@gmail.com
2 Queremos estudar que tipos de singularidades pode ter uma folheação de grau um campo vetorial de grau um), e os subespaços de P 7 de folheações que apresentam alguma singularidade de cada um desses tipos. Fixado um tipo de singularidade, vamos descrever as folheações que apresentam esse tipo de singularidade e um espaço de parâmetros para estas folheções. Com esta descrição vamos calcular codimensão e grau destes espaços de parâmetros em P 7. O grau do espaço M P 7 de campos vetoriais com singularidade de tipo dado tem a seguinte interpretação geométrica: é o número de campos vetoriais X apresentando uma singularidade do tipo prefixado e que são tangentes a um número adequado = codm) de retas com um ponto marcado, i.e., o campo X p) é paralelo a l, para um número adequado de pares ponto, reta) no conjunto {p, l) p l}. O caso de campos vetoriais de grau um, se simplifica usando a correspondência existente provada por Jouanoulou [5]) entre campos de grau um e matrizes 3 3 de trazo nulo. Mostraremos como é obtida esta correspondência e faremos um dicionário entre folheações de grau um e matrizes. Esta correspondencia identifica órbitas da ação de GL 3 C) por mudança coordenadas nos campos, com órbitas pela a açao de GL 3 C) por conjugação nas matrizes. Em particular, identificaremos os tipos de singularidades que correspondem com as possíveis formas de Jordan para matrizes. Explorando a correspondência acima, obteremos o grau dos espaços de campos vetoriais com singularidade de tipo prefixado, olhando para eles como espaços de matrizes com determinada forma de Jordan. O grau dos estratos determinados por forma de Jordan são conhecidos, mas nos casos mais simples mostraremos com é obtido esse grau. Esperamos que este trabalho seja uma útil e pela vez compreensível) introdução a problemas enumerativos, assim como ao estudo da geometria dos espaços de folheações. No trabalho daremos todas as definições necessárias, num nível adequado para um aluno de final de graduação. Serão necessarios conhecimentos básicos de álgebra linear, polinômios em várias variáveis, campos de vetores e 1-formas diferenciais. Referências para o estudo de folheações são as notas de Gómez-Mont e Ortíz Bobadilla [4] ou o livro de Lins-Neto e Scardua [6]. Para o estudo de folheações de grau quaisquer) desde o ponto de vista enumerativo, ver a tese []. A seguir detalhamos o conteúdo de cada seção. A Seção contém uma breve discusão sobre o plano projetivo P, o qual será o ambiente onde trabalharemos. Na Seção 3 definiremos campo de vetores em P, discutiremos suas expressões globais e locais e como obter uma expressão a partir da outra. Isto motivará a definição de folheação holomorfa de dimensão um. Calcularemos a dimensão do espaço de campos de vetores de grau d em P. Ainda no capítulo serão estudados 1-formas diferenciáveis e como uma 1-forma pode estar relacionada com um campo de vetores. Assim definiremos também uma folheação holomorfa de dimensão um em P através de uma 1-forma. Dada uma folheação definida por um campo de vetores, mostraremos como encontrar a expressão de uma 1-forma que define a mesma folheação e também mostraremos o caminho inverso. Na Seção 4 definiremos singularidade de um campo de vetores e de uma 1-forma, e mostraremos que um campo de vetores de grau 1 em P genérico tem 3 singularidades. A partir daí classificaremos estas singularidades e apresentaremos exemplos de campos de vetores que apresentam cada um dos tipos de singularidades. Na Seção 5 mostraremos o isomorfismo existente entre campos de vetores de grau 1 em P e matrizes 3 3 de traço nulo. Exploraremos este isomorfismo para dar uma relação entre os tipos de singularidades introduzidas no capítulo 3 com as possíveis formas de Jordan de uma matriz 3 3 de traço nulo. Por fim, na Seção 6 calcularemos a dimensão e o grau da subvariedade do espaço das folheações que apresenta cada um dos tipos de singularidades.
3 Preliminares.1 O plano projetivo. Nesta seção vamos definir e estudar o plano projetivo complexo P = CP. Uma excelente referência para estudar o plano projetivo e curvas planas é o livro de Fulton [3]. Como motivação para definir o plano projetivo P, vamos começar trabalhando no plano afim A := C e conhecendo um pouco de curvas algébricas nele. Uma curva algébrica de grau k no plano afim é o conjunto de zeros de um polinômio fx, y) C[x, y] de grau k. A motivação para se definir o plano projetivo é que queremos que dadas duas curvas em P de grau k 1 e k respectivamente, elas tenham k 1 k pontos de interseção. Observe no plano afim o seguinte exemplo: Exemplo.1. Sejam as curvas x + y + 1 = 0 e x + y 1 = 0. Temos que em A sua interseção é vazia, mas por outro lado ambas curvas são de grau 1, logo queremos que a interseção delas seja 1 ponto. Observando geometricamente, temos que as duas curvas citadas acima são duas retas paralelas. Então a ideia de definir o plano projetivo P será a de compactificar o plano afim A, adicionando um ponto para cada direção no plano afim este ponto será a interseção das retas, o que elas tem em comum). Definição de plano projetivo. Uma maneira de obter a compactificação de A como acima é definir P como sendo o conjunto de todas as retas passando pela origem em C 3. Representaremos este conjunto como o quociente de C 3 \{0} por uma relação de equivalência que identifica z :=, z 1, z ) com w := w 0, w 1, w ) se e só se existe λ 0 tal que, z 1, z ) = λw 0, w 1, w ) i.e. se z e w definem a mesma direção em C 3 ). Vamos representar a classe de equivalência que contém, z 1, z ) por : z 1 : z ). Daí temos Veremos A P da seguinte maneira: P = { : z 1 : z );, z 1, z ) 0, 0, 0)} A P x, y) 1 : x : y) Isto nos leva a perceber que P pode descrito como a união de 3 conjuntos que são isomorfos a A, a saber: U i := { : z 1 : z ) P ; z i 0} Temos P = U 0 U 1 U e os conjuntos U i são chamados de abertos coordenados ou cartas afins). Os isomorfismos entre U i e A são dados da seguinte maneira: Para i = 0 ϕ 0 : U 0 A : z 1 : z ) z1, z ) Para i = 1 ϕ 1 : U 1 A : z 1 : z ) z0 z 1, z z 1 ) Para i = ϕ 0 : U A : z 1 : z ) z0 z, z1 z ) Quando denotamos um ponto p U i pelas coordenadas dadas por ϕ i p) dizemos que p está escrito em coordenadas locais. No caso especial em que i = 0 escreveremos p = x, y). Associada a cada aberto U i, em P temos sua correspodente reta no infinito l i definida pela equação z i = 0. Assim P pode também ser pensado como a completação de U i com a reta no infinito l i. Por exemplo completando o aberto U 0 obtemos P = { : z 1 : z ) 0} {0 : z 1 : z )} = U 0 l 0.
4 Curvas algébricas em P. Façamos a seguinte pergunta agora: como são as curvas algébricas em P? Baseados na ideia de curvas algébricas em A parece natural definir uma curva algébrica em P como sendo o conjunto dos zeros de um polinômio em C[, z 1, z ], mas observe que isto pode gerar algum problema, pois temos diferentes maneiras de representar um mesmo ponto. Por exemplo, seja F, z 1, z ) = z 1 + z + 1 e o ponto p := 1 : 0 : 1) = : 0 : ), então temos 0 = F 1, 0, 1) F, 0, ) = 1. O ponto p está o não na curva F = 0? Isto mostra que os zeros de este polinômio não definem um subconjunto em P. A condição para que os zeros de um polinômio F C[, z 1, z ] defina um subconjunto de P = C3 \{0} é que se um ponto anula F, todos os pontos equivalentes pela relação também anulem F i.e., F, z 1, z ) = 0 implica F λ, λz 1, λz ) = 0 para todo λ C. Os polinômios que satisfazem a condição acima chamam-se polinômios homogêneos. Definição.1. Dizemos que um polinômio F, z 1, z ) é homogêneo de grau d se F, z 1, z ) = a ijl z0z i j 1 zl, com a ijl C. i+j+l=d Isto é equivalente à condição F λ, λz 1, λz ) = λ d F, z 1, z ) para todo λ C. Assim se F é um polinômio homogêneo e F se anula em, z 1, z ), então F se anula em qualquer representante do ponto : z 1 : z ). Com isto podemos definir uma curva algébrica em P de grau k como sendo os zeros de um polinômio homogêneo de grau k em C[, z 1, z ]. Notaremos ZF ) = { : z 1 : z ) F : z 1 : z ) = 0} à curva definida por F. Exercício.1. Relação de Euler: a igualdade: Dica: Mostre primeiro para o monômio a ijl z i 0z j 1 zl. Mostre que se F, z 1, z ) é um polinômio homogêneo de grau d então vale F + z 1 F + z F z = df Notação. Em todo o trabalho, S d denotará o conjunto de polinômios homogêneos de grau d em três variáveis. Homogeneização. Dado um polinômio f C[x, y] de grau d, vamos dizer que F C[, z 1, z ] é a homogeneização de f em quando F = z0f d z 1, z ). Leitor, mostre que F é homogêneo. Com este processo de homogeneização, estamos adicionando um ponto completando) as curvas definidas em U 0. Por exemplo, voltando ao exemplo.1, consideremos as retas l 1 = Zx+y +1) e l = Zx+y 1), homogeneizando obtemos curvas definidas pelos polinômios F 1 := z 1 + z + e F := z 1 + z Observe que agora estas curvas se intersectam no ponto 0 : 1 : 1), que representa a direção comum de l 1 e l. O ponto 0 : 1 : 1) não está na carta U 0, ele está de fato na reta no infinito correspondente a U 0 i.e. Z )). Exemplo.. Mais um exemplo, considere as curvas de grau dois definidas em U 0, por e f 1 := x y x f := x y, queremos ter dois = grauf 1 )grauf )) pontos na interseção. Em principio só temos o ponto 0, 0) na interseção, leitor: verifique. Homogeneizando obtemos F 1 := z 1 z z 1 e F := z 1 z, estas duas curvas se intersetam nos pontos 1 : 0 : 0) U 0 que já tinhamos) e 0 : 1 : 1), que está na reta no infinito da carta U 0. Dado um polinômio F, z 1, z ) homogêneo, dizemos que fx, y) := F 1, x, y) é a desomogeneização de F na variável. Este é o processo inverso da homogeneização, e permite ver localmente as curvas definidas em P.
5 Espaço tangente a P. Definimos o espaço tangente a P num ponto p U i como sendo T p P := T ϕip)c. { } Quando p U 0, denotaremos x p), y p) uma base de T p P. O espaço projetivo de dimensão n. Generalizando a definição de P, definimos P n como sendo o conjunto das retas que passam pela origem em C n+1. Análogo a P, escreveremos P n = { : z 1 : : z n ), z 1,, z n ) 0}. Pode se encontrar uma cobertura de P n por abertos coordenados, analogo ao feito para P. Ver Fulton [3]. O espaço projetivo associado a um espaço vetorial V. Generalizando um pouco mais, definimos o espaço projetivo associado a um espaço vetorial V, de dimensão n + 1, como sendo PV ) := V \ {0} onde v w se e somente se existe λ C tal que w = λv. Obviamente, PV ) P n, mas as vezes é necesario poner em evidencia qual é o espaço vetorial que estamos projetivizando. 3 Folheações em P. 3.1 Campos vetoriais em P. Um campo de vetores é uma correspondência X que associa a cada ponto p P, uma direção tangente X p) T p P. Permitiremos que esta correspondência se anule em alguns pontos em um conjunto finito de pontos). Dependendo da regularidade continua, diferenciável, holomorfa, polinomial, etc) desta correspondência o campo chama-se continuo, diferenciável, holomorfo, polinomial, etc. Trabalharemos com campos que são polinomiais, e não escreveremos mais a palavra polinomial. Em cada aberto coordenado, um campo é dado por dois polinômios b 1, b nas coordenadas locais. Se x, y) são coordenadas locais de U 0 e notamos { x p), y p)} uma base de T pp temos X p) = b 1 p) x p) + b p) y p). Aceitaremos o fato de que esta base { x p), y p)} varia regularmente com o ponto p, e escrevemos { x, y } desconsiderando o ponto p. Se a reta no infinito da carta U 0 i.e. l 0 := Z )) não é solucão de X, então dizemos que o campo acima tem grau d, onde d = max i=1, {graub i )} 1, este é o caso geral. Se a reta no infinito é solução, então o grau é d = max i=1, {graub i )}. Para um significado geometrico do grau de um campo ver []. Descrição global de um campo. Note que a definição de campo de vetores acima é dada apenas em um aberto coordenado, isto nos motiva a perguntar se é possível dar uma descrição global de um campo de vetores em P. Veremos agora que isto{ é possível. } Para isto definimos,, z a base canônica de T 0 C 3, onde 0 = 0, 0, 0). Um campo de vetores em P é dado por três polinômios homogêneos de igual grau que denotaremos d) F 0, F 1, F, nas variáveis {, z 1, z }: X = F 0 + F 1 + F 3.1) z
6 Em princípio X define um campo em C 3. Para obter um campo em P é relevante observar que na construção de P identificamos vetores de C 3 \ {0} que se encontram na mesma reta pelo origem. Isto implica que o campo radial R := + z 1 + z z é o campo nulo em P. Logo a representação de um campo de vetores em P não é única, pois o campo 3.1) pode ser representado por X + GR, onde G é quaisquer polinômio homogêneo de grau d 1. Uma forma de evitar esta falta de unicidade, é trabalhar com campos que tenham divergência zero, isto é, se escolhemos X como em 3.1) e com divergência zero este é único no conjunto de representantes {X +GR G S d 1 }. Lembramos aqui que a divergência de um campo como em 3.1) é por definição DivX ) := F 0 + F 1 + F z. Lema 3.1. Se X tem divergência nula, e X é outro representante do mesmo campo em P com divergência nula, então X = X Prova: Suponha que X tem divergência nula, e X + GR é outro representante do mesmo campo em P. Temos DivX + GR) = DivX ) + DivGR) = 0 + G + Gz 1 + Gz z = G + z 1 G + z G z + 3G = d + )G. A última igualdade foi obtida da relação de Euler ver exercício.1): Se G é um polinômio homogêneo de grau n, então vale G G G + z 1 + z = ng. z Concluímos então que DivX + GR) = 0 se e somente se G = 0, i.e., o único representante do campo em P com divergência zero é X. Expressão local de um campo. Dado um campo em sua expressão global, como encontrar sua expressão local em um aberto coordenado? Discutiremos agora este processo. Também veremos o processo inverso i.e., dado um campo em sua forma local, como obter sua forma global) na Seção 3.5. Se X é como em 3.1), podemos deduzir a forma local do campo em U 0 como segue. Sejam x, y) as coordenadas locais de U 0, i.e., x = z1 e y = z e : z 1 : z ) = 1 : x : y). Lema 3.. A forma local do campo X em 3.1), é dada, nas coordenadas locais x, y) por Onde f i x, y) := F i 1, x, y). X U0 = f 1 xf 0 ) x + f yf 0 ) y. Prova: Começamos por observar que esta forma local não depende do representante. De fato, se X + GR é outro representante, então a forma local seria [f 1 + xg) xf 0 + g)] x + [f + yg) yf 0 + g)] y = f 1 xf 0 ) x + f yf 0 ) y, onde gx, y) := G1, x, y). Seja então X = F 0 + F 1 x + F z.
7 A expressão de X em U 0 é a mesma que a de X, e a mesma que a de X F 0 R = F 1 z 1 F 0 ) + F z F 0 ) z que é f 1 xf 0 ) x + f yf 0 ) y simplesmente trocando : z 1 : z ) por 1, x, y). Ver [6] para a relação entre a forma local em uma carta e em outra, i.e. se p U i U j, então existe a seguinte relação entre as formas locais X i = u ij X j, onde u ij não se anula em U i U j. Quando trabalhamos com campos de vetores, estamos interessados nas direções tangentes determinadas pelo campo, e não no comprimento dos vetores X p). Logo vamos a considerar dois campos que diferem em um múltiplo escalar como iguais: X λx para todo λ C \ {0}. Com todas as considerações anteriores podemos dar a definição de campo de vetores em P com a que trabalharemos em estas notas. Definição 3.1. Um campo de vetores folheação) em P é dado a menos de multiplos não nulos) por um trio de polinômios homogêneos do mesmo grau F 0, F 1, F ) satisfazendo a seguinte relação F 0 + F 1 + F z = O espaço de campos vetoriais de grau d em P. Se consideramos a definição 3.1 acima, e consideramos bases para os espaços de polinômios homogêneos de grau d podemos contar o número de parâmetros necessários para obter um campo de vetores. Logo teremos um espaço vetorial onde moram os campos sem desconsiderar ainda os múltiplos complexos). Começamos calculando a dimensão de S d. Lema 3.3. A dimensão do espaço vetorial formado pelos polinômios homogêneos de grau d em três variáveis é igual a ) d+ = d+)d+1). Prova: A afirmação é clara para d = 1. Procedemos por indução em d, se H é um polinômio homogêneo de grau d nas variáveis, z 1, z, então podemos escrever de forma única H = H 0 + z 1 H 1 + λz d, onde H 0 é um polinômio de grau d 1 nas variáveis, z 1, z e H 1 é um polinômio de grau d 1 nas variáveis z 1, z. Por indução o número de coeficientes de H 0 é ) d+1. Por outro lado é fácil mostrar que o número de coeficientes de H é d. Logo o número de coeficientes de H é ) d+1 + d + 1 = d+ ). Temos então que o número de parâmetros necessários para definir o trio de polinômios homogêneos de grau d, F 0, F 1, F ) = à dimensão do espaço vetorial onde mora o trio) é 3 ) d+. Consideramos agora a condição da anulação da divergência no trio F 0, F 1, F ), i.e., F 0 + F 1 + F z = 0. 3.) O número de equações que tem que satisfazer os coeficientes do trio e igual a dimensão do espaço de polinômios homogêneos de grau d 1. Pois satisfazer 3.) equivale a zerar cada um dos coeficientes do polinômio homogêneo F de grau d 1: 0 + F1 + F z de onde obtemos ) d+1 equações independentes. Com estas considerações temos provado a seguinte proposição. Proposição 3.1. A dimensão do espaço vetorial V dos campos de grau d em P é ) ) d + d = d + 1)d + 3).
8 Espaço de parâmetros para folheações de grau d. Como estamos interessados só na direção dos vetores definidos por um campo, desconsideramos múltiplos escalares. Esto é, consideramos agora a identificação de campos que diferem em um multiplo complexo não nulo e obtemos que o espaço de folheações de grau d se identifica ao espaço projetivo das retas que passam pela origem de V, i.e., P N = PV ), onde N = d + 1)d + 3) 1. d = 1. No caso em que estamos interessados em este trabalho d = 1, obtemos que o espaço de folheações de grau um em P é um espaço projetivo de dimensão 7, P formas em P Até agora definimos folheações através de campos de vetores. Nosso objetivo agora é definir folheações holomorfas através de 1-formas diferenciáveis. Para isso vamos relembrar alguns conceitos de álgebra linear. Espaço Dual de um espaço vetorial. Dado um espaço vetorial U sobre C, o espaço vetorial dual de U, que denotaremos U, é o conjunto de todos os funcionais lineares de U. U = {ω : U C; w é linear}. Leitor, verifique que U é um espaço vetorial. Se B = {v 1,..., v n } é uma base de U, chama-se base dual de B à base do espaço vetorial U formada pelos funcionales lineares ω i : U C tais que ω i v j ) = δ i,j. Isto é ω i v j ) = Assim, se um vetor v U se expressa na base B como { 1 se i = j 0 se i j v = i a i v i, onde a i C temos que a j = ω j v). Leitor: verifique este fato! Observe que se para cada elemento ω U, consideramos ker ω U, obtemos que cada elemento ω U define um subespaço linear de U de codimensão um i.e. um hiperplano de U). Espaço Cotangente. Definimos o espaço cotangente a P em um ponto p P, como o espaço vetorial dual do espaço tangente. Denotamos Ω p := T p P ) No aberto coordenado U 0 com coordenadas locais x, y), e denotando como antes { x p), } y p) a base de T p P, denotaremos {d p x, d p y} a correspondente base dual, i.e., os funcionais lineares definidos por d p x x p)) = 1, d p x y p)) = 0, d p y y d p y x p)) = 1, p)) = 0, Também esta base varia regularmente com p P, e notaremos {dx, dy} a base que em cada ponto p é {d p x, d p y}.
9 1-formas. Análogo à definição de campo de vetores, definimos uma 1-forma em P como uma correspondência ω que associa a cada ponto p P, um funcional ωp) Ω p. Trabalharemos com 1-formas polinomiais, i.e., a correspondência acima depende polinomialmente de p. Como no caso de campos de vetores vemos como representar uma 1-forma no aberto U 0 utilizando as coordenadas locais x, y). Neste aberto uma 1-forma é dada por dois polinômios a 1 x, y), a x, y): ω = a 1 dx + a dy Descrição global de uma 1-forma. Vamos agora estender uma 1-forma dada em sua expressão local, a uma forma global em P. Começaremos definindo Ω 0 C 3 := T 0 C 3 ) e denotemos {d, dz 1, dz } a base de Ω 0 C 3 dual da base {,, z } de T 0 C 3. Observe que x = z1 Mudando de variáveis temos a igualdade ω = a 1 dx + a dy = 1 [ z 1 a 1 e y = z, e usando as regras de derivação obtemos dx = z0dz1 z1dz0 z 0 z1, z e dy = z0dz zdz0. z0 ) z z1 a, z )) z1 d + a 1, z ) z1 dz 1 + a, z ) ] dz desconsiderando o múltiplo 1 temos a 1-forma z 1 z1 a 1, z ) z z1 a, z )) z1 d + a 1, z ) z1 dz 1 + a, z ) dz Seja d = max i=1, {graua i )}. Definimos A 0 := z0 d+1 z 1 z1 a 1, z ) z z1 a, z )) A 1 := z d+1 0 a 1 z1, z A := z d+1 0 a z1, z Observe que A 0, A 1 e A são polinômios homogêneos nas variáveis {, z 1, z } e de mesmo grau d + 1. Ainda temos que A 0, A 1 e A satisfazem a relação A 0 + z 1 A 1 + z A = 0. Assim uma 1-forma polinomial de grau d) em P é dada por três polinômios homogêneos de grau d + 1 nas variáveis {, z 1, z }, que denotaremos A 0, A 1, A : ) ) que satisfazem a seguinte relação Veremos o exemplo a seguir: ω := A 0 d + A 1 dz 1 + A dz 3.3) A 0 + z 1 A 1 + z A = ) Exemplo 3.1. Dada a 1-forma ω = xdx + ydy definida em U 0, queremos encontrar uma expressão global para esta forma em P. Temos que a 1 x, y) = x e a x, y) = y, daí temos A 0 = z0 z 1 z1 a 1, z ) z z1 a, z )) = z0 z 1 z 1 z ) z = z1 z A 1 = z0a z1 1, z ) = z 1 A = z0a z1, z ) = z Daí uma expressão global para ω é ω = z 1 z )d + z 1 dz 1 + z dz
10 Expressão local de uma 1-forma. Vamos fazer agora o processo inverso, isto é, dado uma 1-forma na sua expressão global em P, queremos encontrar sua expressão local em U 0. Se ω é como em 3.3), fazendo a mudança de variáveis : z 1 : z ) = 1 : x : y) no aberto coordenado U 0, obtemos a forma local da 1-forma em U 0. Lema 3.4. A forma local do campo ω em 3.3), é dada, nas coordenadas locais x, y) de U 0, por ω U0 = a 1 dx + a dy. Onde a i x, y) := A i 1, x, y). Prova: Fazemos a mudança de variáveis x = z1 { e y = z. Usando as regras de derivação obtemos dz 1 = dx + xd, Substituindo estas identidades em 3.3) obtemos: dz = dy + yd ω U0 = A 1 dx + A dy + A 0 + xa 1 + ya )d. Agora, pela condição 3.4), os polinômios A 0, A 1, A satisfazem A 0 + xa 1 + ya = 0 o que prova a afirmação. 1-formas como distribução de direções. funcional linear em T p P : Lembrando que se ω é uma 1-forma e p P, então ωp) é um ωp) : T p P C, temos que o núcleo deste funcional linear Kerωp)), será uma reta de T p P passando pela origem. Deste modo obtemos uma correspondência p Kerωp)), que associa a cada ponto p P uma reta em T p P. Uma correspondência deste tipo chama-se distribuição de subespaços tangentes, em este caso trata-se de uma distribuição de retas tangentes. Logo uma distribução polinomial de vetores tangentes a P pode ser dada tanto por um campo, como na seção anterior, como por uma 1-forma. Explicitamente, para cada p P, podemos definir um vetor de T p P como a direção X p) ou como um vetor em Kerωp)). Assim se um campo de vetores e uma 1-forma definem a mesma distribução de vetores devemos ter que para cada p P então X p) Kerωp)), isto é: ωp)x p)) = 0 p U 0. Se escrevemos em coordenadas locais X = b 1 x + b y e ω = a 1dx + a dy. Da definição de bases duais obtemos a relação Leitor: Verifique! a 1 b 1 + a b = ) Análogo ao caso de campos, quando trabalhamos com 1-formas, estamos interessados em Kerω) = Kerλω) para todo λ C \ {0}. Assim obtemos a definição correta de folheação definida por uma 1-forma. Definição 3.. Uma folheação de grau d, definida por uma 1-forma em P é dada a menos de múltiplos não nulos) por um trio de polinômios homogêneos de grau d + 1, A 0, A 1, A satisfazendo a relação 3.4) A 0 + z 1 A 1 + z A = 0.
11 3.4 O espaço de 1-formas de grau d em P. Usando a definição anterior, voltamos a calcular a dimensão do espaço vetorial de folheações de grau d em P. Lembrando que a dimensão do espaço dos polinômios homogêneos de grau d em 3 variáveis é ) d+. Logo o número de parâmetros necessários para se definir um trio de polinômios homogêneos de grau d + 1 em 3 variáveis é 3 ) d+3. Pedir a condição de que z0 A 0 + z 1 A 1 + z A = 0 é pedir que um polinômio de grau d + se anule, ou seja, é pedir ) d+4 condições lineares. Concluímos então que a dimensão do espaço das 1-formas de grau d satisfazendo a condição A 0 + z 1 A 1 + z A = 0 é ) ) d + 3 d = d + 3)d + 1). 3.5 Campos vs 1-formas. Já vimos a relação existente entre as formas locais de um campo e de uma 1-forma definindo a mesma folheação em P ver equação 3.5)). Estudamos agora a relação entre as expressões globais de um campo e uma 1-forma definindo a mesma folheação em P. Ou seja, dado um campo em sua expressão global X = F 0 + F 1 + F z tal que DivX ) = 0, como encontrar uma 1-forma ω = A 0 d + A 1 dz 1 + A dz que define a mesma folheação que X, e vice-versa. Campo 1-forma. Dada a expressão local para o campo X em U 0 temos que X ωp)) = 0, p U 0, nosso objetivo será encontrar uma expressão local para uma tal ω, e finalmente encontrar uma expressão global para ω. Seja X = F 0 + F 1 + F z um campo de vetores de grau d tal que DivX ) = 0, uma expressão para X no aberto coordenada U 0 é f 1 xf 0 ) x + f yf 0 ) y, onde f 0, f 1 e f são as desomogeneizações de F 0, F 1 e F. Agora utilizando X ω) 0 em U 0, temos que uma expressão local para a 1-forma ω que define a mesma folheção que X será ω = f yf 0 )dx f 1 xf 0 )dy. Queremos agora uma expressão global para ω. Esta expressão será ω = A 0 d + A 1 dz 1 + A dz, onde A 0 = z0 d+1 z1 f z f 0 ) = z 1 F + z 1 z F 0 + z F 1 z z 1 F 0 = z F 1 z 1 F A 1 = z d+1 0 f z = F z F 0 f 0 ) A = z d+1 0 f 1 z1 = z 1 F 0 F 1 f 0 ) ) z 1, z ) z 1, z + z f 1 z1 f 0 ) ) z 1, z z 1, z )) Concluímos então que a expressão global da forma que define a mesma folheação de X é ω = z F 1 z 1 F )d + F z F 0 )dz 1 + z 1 F 0 F 1 )dz. 1-forma Campo. Reciprocamente, podemos obter os coeficientes da expressão global do campo, a partir dos coeficientes da expressão global da forma. Lema 3.5. Se A 0, A 1, A são polinômios homogêneos de grau d + 1 satisfazendo a relação A 0 + z 1 A 1 + z A = 0, então existem polinômios homogêneos F 0, F 1, F de grau d tais que A 0 = z F 1 z 1 F A 1 = F z F 0 3.6) A = z 1 F 0 F 1
12 Prova: Da relação A 0 + z 1 A 1 + z A = 0 podemos escrever A 0 = z 1 A 1 z A 3.7) escrevendo A 0 = z 1 G + z G 1 + λz d+1 0 e substituindo em 3.7) obtemos λ = 0. Logo A 0 = z 1 G + z G 1. Substituindo em 3.7) esta igualdade e reagrupando obtemos de onde deduzimos que z 1 divide a G 1 + A e z divide G + A 1. { G 1 + A = z 1 G 0 G + A 1 = z G 3 z 1 G + A 1 ) = z G 1 + A ) 3.8) Sustituindo estas relações em 3.8), deducimos que G 3 = G 0. Então A = z 1 G 0 G 1 e A 1 = z G 0 G. Definindo F 0 := G 0, F 1 := G 1 e F := G, obtemos as relações procuradas. Veremos um exemplo a seguir: Exemplo 3.. Seja o campo de vetores dado por: X = z z 1, z então a 1-forma ω que define a mesma folheação que X é dada por ω = z 1 + z )d z 1 dz 1 z dz As relações entre o campo e a forma que definem a mesma folheação encontradas acima podem ser usadas para calcular a expressão global de um campo dado em sua forma local, i.e., dado um campo em sua forma local X = b 1 x + b y onde b 1, b são polinômios com d + 1 = max i=1, {graub i )} A forma local da 1-forma associada é b dx b 1 dy. Pelo visto anteriormente a expressão global de esta forma é: ω = A 0 d + A 1 dz 1 + A dz onde A 0 = z0 d+1 z 1 z1 b, z ) + z z1 b 1, z )) A 1 = z0 d+1 z1 b, z ) A = z d+1 0 b 1 z1, z E daqui podemos obter F 0, F 1, F como no Lema 3.5. Veamos um exemplo: Exemplo 3.3. Seja o campo de vetores em U 0 dado por X x, y) = y x x y. Queremos encontrar uma expressão global para este campo em P tal que o divergente seja nulo. Neste caso b 1 x, y) = y e b x, y) = x. Logo z1 ) + z ) 3 ) ) A 0 = z 3 0 = z 1 + z 3 A 1 = z0 3 z 1 = z z 0z 1 0 ) A = z0 3 z = zz 0
13 Logo as coordendas do campo são F 0 = 0, F 1 = z e F = z 1. Observe que DivX ) = 0. Com isto concluímos que uma expressão global para o campo é X = z z 1 z Exercício 3.1. Seja o campo de vetores em U 0 dado por X x, y) = x x + y y. Encontre uma expressão global para este campo em P tal que o divergente seja nulo. 4 Singularidades Um dos focos no estudo de folheações holomorfas é o estudo de singularidades das folheações. Há uma tentativa de classificar o tipo de singularidades que pode presentar uma folheação e também de calcular o grau do subconjunto de folheações que apresentam um certo tipo de singularidades. Para folheções de grau d > 1, resultados de Campillo e Olivares [1] mostram que uma folheação fica determinada pelas suas singularidades considerando multiplicidades). Neste sentido este trabalho é o complementar de este resultado, veremos que uma folheação de grau um não é determinada pelas suas singularidades e estudaremos o espaço das folheações que apresentam cada tipo de singularidade. Nesta seção vamos definir singularidade de um campo de vetores e singularidade de uma 1-forma, e depois definiremos os tipos de singularidades que nos interessam e que, como veremos logo, são as únicas possíveis). 4.1 Singularidades de campos de vetores e de 1-formas Começaremos definindo singularidade de um campo de vetores. Definição 4.1. Dado um campo de vetores X, dizemos que um ponto p é singularidade de X se o vetor X p) T p P for nulo. Se p U i, então p é uma singularidade de X se anula a expressão local de X no aberto U i. Analogamente definimos singularidades em 1-formas. Definição 4.. Dado uma 1-forma ω, um ponto p U i, é uma singularidade de ω se p anula a expressão local de ω em U i. As definições anteriores não dependem do aberto coordenado U i tal que p U i. Exercício 4.1. Se ω = A 0 d + A 1 dz 1 + A dz é a expressão global de ω, então, as singularidades de ω são exatamente os zeros comuns de A 0, A 1, A. Exercício 4.. Usando o exercício anterior prove que o conjunto de singularidades de um campo X = F 0 + F 1 + F z [ ] F 0 F 1 F é o conjunto de zeros dos menores dois por dois da matriz. z 1 z Dica: use a relação entre as expressões globais do campo e da forma. Deduza que p P é uma singularidade de X se e só se X p) = λrp) para algúm λ C. Podemos nos perguntar se é possível contar as singularidades de um campo de vetores de grau d em P. E a resposta é que um campo de vetores de grau d onde o conjunto de singularidades for um conjunto discreto tem d + d + 1 singularidades contando com multiplicidades. Para se mostrar isto é necessário utilizar técnicas de teoria de interseção, que não é o foco deste curso. Mas daremos uma demonstração para o caso onde d = 1. Teorema 4.1. Um campo de vetores genérico em P de grau 1, tem 3 singularidades. Genérico aqui quer dizer que existe um aberto do espaço P 7 de folheações ao qual o campo pertece.
14 Prova: A expressão global para um campo de vetores de grau 1 em P é dada por X = a 11 + a 1 z 1 + a 13 z ) + a 1 + a z 1 + a 3 z ) + a 31 + a 3 z 1 + a 33 z ) z Um ponto p = : z 1 : z ) é singularidade de X se X p) = λrp), para algum λ C e R é o campo radial. Daí teremos a 11 + a 1 z 1 + a 13 z = λ a 1 + a z 1 + a 3 z = λz 1 a 31 + a 3 z 1 + a 33 z = λz Tomando a matriz de coeficiente desde sistema B = [a ij ], das igualdades acima vemos que p = : z 1 : z ) é uma singularidade de X se e somente se v =, z 1, z ) é um autovetor de B. A hipóteses de o campo ser genérico implica que a matriz de coeficientes B é genérica, logo tem 3 autovalores distintos o polinômio característico não tem raízes repetidas), de onde obtemos 3 autovetores independentes. 4. Tipos de Singularidades Nosso objetivo agora é distinguir diferentes tipos de singularidades que se apresentam em um campo de vetores de grau 1 em P. Degenerações. Estudaremos os seguintes tipos de degenerações nas singularidades. Veremos na seguinte seção que de fato estas degenerações são as únicas possíveis. Definição 4.3. Se p U 0 é uma singularidade de um campo X, e b 1 x + b [ b1 x o jacobiano de X como a matriz J p X := p) b 1 y p) ] b x p) b y p). Consideraremos os seguintes tipos de degenerações nas singularidades: y é a expressão local de X, definimos 1. Tipo 1. det J p X = 0.. Tipo. det J p X = trj p X ) = 0 i.e. a matriz J p X é nilpotente. 3. Tipo 3. J p X CId; neste caso se diz que p é uma singularidade radial. 4. Tipo 4. J p X = 0. Singularidade de ordem maior que um. Exemplo 4.1. Observe os diferentes exemplos de campos de vetores a seguir: X 1 = 3 + z 1 + z z. X 1 é um campo onde os pontos 1 : 0 : 0), 0 : 1 : 0) e 0 : 0 : 1) são singularidades. Exercício 4.3. Observe que os autovalores 3,, 1 com autovetores 1, 0, 0), 0, 1, 0) e 0, 0, 1)) da matriz B 1 da prova do teorema 4.1, tem multiplicidade algébrica e geométrica igual a 1. X = z 1 + ) + z 1 z z. X é um campo com singularidades nos pontos 1 : 0 : 0) e 0 : 0 : 1). Exercício 4.4. Prove que como autovalor da matriz B da prova do teorema 4.1, 1 tem multiplicidade algébrica igual a, e geométrica igual a 1, e tem multiplicidade algébrica=multiplicidade geométrica) igual a 1. Identifique este tipo de campo com alguma das degenerações da definição acima.
15 X 3 = z 1 + z. X 3 é um campo onde 1 : 0 : 0) é a única singularidade. Exercício 4.5. Prove que como autovalor de B 3 da prova do teorema 4.1, 0 tem multiplicidade algébrica igual a 3 e geométrica igual a 1. Identifique este tipo de campo com alguma das degenerações da definição acima. X 4 = + z 1 + z z. X 4 é um campo onde o ponto 1 : 0 : 0) é singular e todos os pontos da forma 0 : a : b), com a, b C também são singulares. Este é um campo que tem infinitas singularidades pois tem a reta = 0 no conjunto singular. Exercício 4.6. Prove que como autovalor da matriz B 4 da prova do teorema 4.1, tem multiplicidade algébrica e geométrica) igual a 1, e 1 tem multiplicidade algébrica igual a 1 e geométrica igual a. O que podemos dizer da matriz B 4? Identifique este tipo de campo com alguma das degenerações da definição acima. X 5 = z. X 5 é um campo onde os pontos da forma a : b : 0) onde a, b C são singulares. Exercício 4.7. O que podemos dizer da matriz B 5? Identifique este tipo de campo com alguma das degenerações da definição acima. 5 Folheações de grau 1 em P vs Matrizes 3 3 de traço nulo Na seção anterior apresentamos 5 tipos de singularidades de campos de vetores de grau 1 em P. Nosso objetivo agora é descrever o espaço das folheações que apresentam cada um dos tipos de singularidades, através de matrizes de traço nulo. Associaremos a cada tipo de singularidade, um tipo de forma canônica Jordan nas matrizes. Em particular obteremos que os quatro tipos de degenerações nas singularidades apresentados anteriormente são todos os possíveis. Primeiramente, motivados pela prova do teorema 4.1, vamos exibir uma bijeção entre campos de vetores de grau 1 em P e matrizes 3 3 de traço nulo. A expressão global de um campo de vetores de grau 1 em P é onde a ij C. X = a 11 + a 1 z 1 + a 13 z ) + a 1 + a z 1 + a 3 z ) + a 31 + a 3 z 1 + a 33 z ) z Exercício 5.1. Prove que DivX = trb) = a 11 + a + a 33 ; onde B é matriz correspondente a X como na prova do Teorema 4.1. Assim obtemos uma bijeção do espaço dos campos de vetores de grau 1 em P no espaço das matrizes 3 3 de traço nulo definida por X B = [a ij ]. Dizemos que a matriz B é a matriz associada ao campo X. Notação. sl 3 C) denota o espaço vetorial de matrizes 3 3 de trazo nulo. Gl 3 C) denota o grupo de matrizes 3 3 inversíveis. Teorema 5.1. Existe uma bijeção θ : V sl 3 C) que faz corresponder a cada campo sua matriz associada.
16 Além disso, se considerarmos a ação de Gl 3 C) por mudança de coordenadas lineares em V, então o mapa θ é Gl 3 C) equivariante, para a seguinte ação em de Gl 3 C) em sl 3 : g, B) detg)g 1 Bg. Isto significa que se g GL 3 C) e X é o campo X onde fizemos a mudanca de variáveis definida por g, então θx ) = detg)g 1 θx )g. Prova: O único que falta provar é a afirmação da equivariância, esta prova não é difícil se reduz a uma mudança de variáveis e muitas contas) e se encontra em Jouanolou [5]. Como importante consequência deste Teorema obtemos que a clasificação de campos a menos de mudança de coordenadas lineares é equivalente à clasificação de matrizes de trazo nulo pela sua forma de Jordan, i.e. pelos tipos de órbitas classes de equivalência) que aparecem quando consideremos a ação de Gl 3 C) em sl 3 C) como no Teorema acima. Logo, se conhecemos todos os tipos de formas de Jordan, e fazemos corresponder a cada um destos tipos, campos com um tipo de singularidade, os tipos de singularidades que obtemos por este processo serão as únicos possíveis. Mãos à obra: Começamos relembrando algun fatos sobre formas de Jordan. Reelembrando um pouco sobre formas canônicas de Jordan. A forma canônica de Jordan é uma forma de representar uma matriz através de uma outra matriz semelhante à original que é uma matriz diagonal somada a uma matriz nilpotente possivelmente nula). Dizemos que uma matriz A é semelhante a uma matriz B se existe uma matriz invertível g GL 3 C) tal que B = gag 1. Se A é uma matriz, na sua forma canônica de Jordan a diagonal é preenchida pelos autovalores da matriz. Escrevemos A = D +N, onde D é uma matriz diagonal com os autovetores da matriz, e N é uma matriz nilpotente. No caso quenos ocupa, i.e., de matrizes 3 3 as possíveis matrizes nilpotentes são : , 0 0 0, 0 0 0, onde as duas últimas são equivalentes tem igual forma de Jordan) Lembramos que o traço de uma matriz é igual a soma de seus autovalores. Não é difícil provar que as possíveis formas canônicas de Jordan de uma matriz 3 3 de traço nulo são: A 1 = α β α β A 4 =, A = α α α α α α e A 5 =, A 3 = onde α 0. Para maior conhecimento sobre o assunto consulte o livro Linear Algebra de Hoffman e Kunze [7] ou seu livro de Algebra Linear favorito., Correspondência entre formas de Jordan e degenerações. um tipo de forma de Jordan. A seguir associamos a cada tipo de degeneração Proposição 5.1. A correspondência entre degenerações e formas de Jordan é como segue: α Degeneração de tipo 1. forma de Jordan = 0 α 0, com α α
17 . Degeneração de tipo. forma de Jordan = 3. Degeneração de tipo 3. forma de Jordan = 4. Degeneração de tipo 4. forma de Jordan = Prova: α α α , com α 0. Suponhamos que a singularidade é p = 1 : 0 : 0). Começamos observando que se X = a 11 + a 1 z 1 + a 13 z ) + a 1 + a z 1 + a 3 z ) + a 31 + a 3 z 1 + a 33 z ) z a forma local de X em U 0 tem coordenadas e b 1 = a 1 + a x + a 3 y) xa 11 + a 1 x + a 13 y) b = a 31 + a 3 x + a 33 y) ya 11 + a 1 x + a 13 y). O fato de que p = 1 : 0 : 0) é um autovetor da matriz B associada ao campo implica que a 11 é um autovalor a 11 a 1 a 13 de B é que a 1 = a 31 = 0. Leitor: verifique! Logo B = 0 a a 3. 0 a 3 a [ 33 ] a a 3 Observe agora que, pela definição de jacobiano, temos J p X = a 11 Id. a 3 a 33 [ ] a a 3 1. Pelo provado acima a condição detj p X ) = 0 impõe que a 11 seja um autovalor de. a 3 a 33 Ou seja, a matriz B tem um autovalor repetido, a forma de Jordan mais geral de este tipo de matrizes é α α α. Em este caso a condição impõe, além do anterior, a a 11 + a 33 a 11 = 0, e como trb = 0, temos a 11 = Verifique!). A forma de Jordan mais geral para matrizes com único autovalor zero é Neste caso a condição impõe: [ a a 11 a 3 a 3 a 33 a 11 é diagonalizável, com um autovalor repetido. A forma de Jordan para esta matriz é ] = λid, logo a = a 33, a 3 = a 3 = 0 i.e. a matriz B α α α 4. Neste caso condição impõe: a 11 = a = a 33 que como o traço de B é zero, implica a 11 = a = a 33 = 0), e a 3 = a 3 = 0. Logo B tem um único autovalor que é 0 com multiplicidade geométrica i.e. o autoespaço associado tem dimensão ). A forma de Jordan mais geral para matrizes desta maneira é
18 Exercício 5.. Verifique os detalhes da demostração anterior. 6 Espaço de parâmetros para folheações com cada tipo de singularidade Nesta seção temos dois objetivos, primeiramente daremos a forma explícita de um campo presentando cada um dos tipos de singularidades, e sem segundo lugar vamos calcular a dimensão e o grau das subvariedades M i de P 7 formadas por campos com singularidade de tipo i. Para estes cálculos usamos a correspondência com os tipos de forma de Jordan nas matrizes. Alguns graus são fáceis de calcular, para os restantes damos referências para os resultados usados para calcularlos. Observe que a forma canônica de Jordan genérica é três singularidades distintas e estes campos são da forma α β α β α β) + αz 1 + βz. z. Logo o campo genérico em P 7 tem Teorema 6.1. Seja M i P 7 a subvariedade dos campos que tem singularidade do tipo i. dimensão e o grau de M i respectivamente. Então vale: Notemos d i e g i a 1. d 1 = 6 e g 1 = 6. Um elemento típico de M 1 é da forma X = α + z 1 ) + αz 1 αz. z. d = 5 e g = 6. Um elemento típico de M é da forma X = z 1 + z. 3. d 3 = 4 e g 3 = 6. Um elemento típico de M 3 é da forma X = α + αz 1 + αz. z 4. d 4 = 3 e g 4 = 6. Um elemento típico de M 4 é da forma X = z. Prova: O polinômio característico de uma matriz B, 3 3 é da forma X B t) = t 3 + a 1 t + a t + a 3 onde a 1 = trb), a = tr B) e a 3 = detb). Onde B é a matriz formada pelos menores de B. Logo a i é um polinômio de grau i nos coeficiente da matriz B. Em nosso caso, como trb) = 0 temos a 1 = Pela Proposição 5.1, as matrizes correspondentes a degenerações de tipo 1 se caracterizam por ter um autovalor repetido, logo esta subvariedade é definida simplesmente pelo discriminante do polinômio característico. Este discriminante é = 7a 3 + 4a 3 a a 3 a 1a 18a 1 a a
19 em nosso caso a 1 = 0) temos = 7a 3 + 4a 3 que é um polinômio de grau 6 nos coeficientes da matriz B. Deduzimos então que M 1 é uma hipersuperfície de grau 6 em P 7.. Pela Proposição 5.1, as matrizes correspondentes a degenerações de tipo se caracterizam por ser ter todos os autovalores nulos, daí seu polinômio característico é t 3, logo esta subvariedade é definida pela interseção de duas hipersuperfícies em P 7, a saber a = a 3 = 0, onde a é um polinomio de grau nos coeficientes da matriz B e a 3 é um polinomio de grau 3 nos coeficientes da matriz B. Logo dim M = 7 = 5 e o grau de M é 3 = Os casos 3 e 4 serão tratados juntos. As matrizes correspondentes a degenerações de tipo 4 se caracterizam por ser de posto 1. É claro que a dimensão de M 4 é 3, se consideramos a condição de traço nulo. Uma forma clássica de descrever este tipo de matrizes é como sendo a imagem do morfismo de Segre dado por Leitor, mostre que este mapa é injetivo). σ : P P P 8 y 0 x 0 y 0 x 1 y 0 x σx 0 : x 1 : x ), y 0 : y 1 : y )) = y 1 x 0 y 1 x 1 y 1 x y x 0 y x 1 y x É conhecido o fato de que este morfismo é uma isomorfismo sobre sua imagem, que são justamente as matrizes de posto 1. O grau desta variedade dentro de P 8 é 6. Se impormos a condição de traço nulo nada muda, pois estamos intersetando com um hiperplano de P 8 uma equação linear nos coeficientes de matriz). Daí temos que o grau de M 4 é 6. Estas mesmas ideias podem ser usadas para calcular dimensão e grau de M 3. É fácil ver que os campos que tem o tipo de singularidade 3, são da forma X = α + αz 1 + αz. z Estes campos são caracterizados por ter a matriz associada um autoespaço de dimensão dois e um de dimensão um. Podemos então parametrizar M 3 com a reta correspondente ao autoespaço de dimensão dois) e o ponto correspondente ao autoespaço de dimensão um). Notamos ˇP := PČ3 ) o espaço projetivo que parametriza retas de P. Assim, um ponto [a 0 : a 1 : a ] ˇP representa à reta de P dada pela equação a 0 + a 1 z 1 + a z = 0. Podemos então definir um mapa ρ : P ˇP P 7 tal que a imagem ρp, l) é uma matriz de trazo nulo, com p como autovetor e a reta l como autoespaço. É fácil achar a expressão de este mapa ver exercício 6.1): [p 0 : p 1 : p ], [a 0 : a 1 : a ]) a 1 p 1 a 0 p 0 a p 3a 1 p 0 3p 0 a 3a 0 p 1 a 0 p 0 a 1 p 1 p a 3p 1 a 3a 0 p 3a 1 p a 1 p 1 + a 0 p 0 + a p
20 É possível provar que este morfismo é uma isomorfismo sobre sua imagem. O grau da sua imagem que é M 3 ) dentro de P 7 é 6, esto pode ser provado de forma análoga ao cálculo do grau da imagem de σ Segre). Logo a dimensão de M 3 é 4 e o grau é 6. Deixamos ao leitor a tarefa de achar a cara dos campos com cada tipo de singularidade. Exercício Dados um ponto p = [p 0 : p 1 : p ] e uma reta de equação a 0 + a 1 z 1 + a z = 0, ache uma matriz de trazo nulo, que tenha p 0, p 1, p ) como autovetor e tal que restrita ao subespaço de dimensão dois dado pela equação a 0 + a 1 z 1 + a z = 0 seja um múltiplo da identidade.. Encontre uma expressão explícita para o mapa ρ. 3. Observe que em principio ρ está definido para p l, mas a incidencia p l é dada por uma equação, então fatorando esta equação) o mapa extende-se a todos os pares p, l) P ˇP. 4. Alternativamente, a forma explícita do mapa ρ pode ser achada da seguinte forma: a) As 1-formas que tem singularidades do tipo 3 são da forma: ω = LF dg GdF ) onde L, F, G são polinômios de grau um, i.e. ω tem uma reta l := ZL) no lugar singular, e tem uma singularidade radial no ponto p = ZF, G). b) Usando a parte anterior podemos parametrizar 1-formas com singularidade do tipo 3, por a reta l ˇP e o ponto p = ZF, G) P esta é a informação que contém o mapa ρ). c) Dado um par p, l) P ˇP, encontre as equações que definem o ponto, i.e. os polinômios lineares F, G tais que {p} = ZF, G). Ache o campo correspondente à 1-forma ω = LF dg Gdf), onde L é a equação da reta l. d) Ache a matriz associada ao campo do item anterior, esta é ρp, l). Exercício 6.. Para cada tipo de singularidade encontre a 1-forma típica que presenta esse tipo de singularidade. Referências [1]campillo, a. and olivares, j. A plane foliation of degree different from 1 is determined by its singular scheme. Comptes Rendus de l Académie des Sciences - Series I - Mathematics Volume 38, Issue 10, 15 May 1999, Pages [] ferrer, v. - Aspectos enumerativos de Folheações Holomorfas. pgmat/teses/tese04.pdf. Doctoral Thesis, UFMG [3] fulton, w. - Algebraic Curves. W. A. Benjamin, new York, [4] gómez mont, x. e ortíz bobadilla, l. - Sistemas dinámicos holomorfos en superficies. Sociedad Matemática Mexicana, México City, [5] jouanolou, j. p. - Equations de Pfaff algébriques. Lectures Notes in Mathematics, 708. Springer-Verlag, [6] lins neto, a. e scardua, b. - Folheações Algébricas Complexas. 1 Colóquio Brasileiro de Matemática, IMPA, [7] hoffman, k. m. e kunze, r. - Linear Algebra. Editora Prentice Hall, 1971.
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Capítulo 5. Operadores Auto-adjuntos. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Polinômio Mínimo e Operadores Nilpotentes
 Capítulo 9 Polinômio Mínimo e Operadores Nilpotentes Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 9 Polinômio Mínimo e Operadores Nilpotentes Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Apostila Minicurso SEMAT XXVII
 Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
Um Estudo Sobre Espaços Vetoriais Simpléticos
 Um Estudo Sobre Espaços Vetoriais Simpléticos Fabiano Borges da Silva Lívia T. Minami Borges 28 de novembro de 2015 Resumo O presente artigo estuda de maneira detalhada espaços vetoriais que possuem uma
Um Estudo Sobre Espaços Vetoriais Simpléticos Fabiano Borges da Silva Lívia T. Minami Borges 28 de novembro de 2015 Resumo O presente artigo estuda de maneira detalhada espaços vetoriais que possuem uma
Conceitos Básicos sobre Representações e Caracteres de Grupos Finitos. Ana Cristina Vieira. Departamento de Matemática - ICEx - UFMG
 1 Conceitos Básicos sobre Representações e Caracteres de Grupos Finitos Ana Cristina Vieira Departamento de Matemática - ICEx - UFMG - 2011 1. Representações de Grupos Finitos 1.1. Fatos iniciais Consideremos
1 Conceitos Básicos sobre Representações e Caracteres de Grupos Finitos Ana Cristina Vieira Departamento de Matemática - ICEx - UFMG - 2011 1. Representações de Grupos Finitos 1.1. Fatos iniciais Consideremos
Capítulo 6. Operadores Ortogonais. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT0032 11 a Lista de
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
Capítulo 2. Ortogonalidade e Processo de Gram-Schmidt. Curso: Licenciatura em Matemática
 Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Introduzir os conceitos de base e dimensão de um espaço vetorial. distinguir entre espaços vetoriais de dimensão fnita e infinita;
 META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
META Introduzir os conceitos de base e dimensão de um espaço vetorial. OBJETIVOS Ao fim da aula os alunos deverão ser capazes de: distinguir entre espaços vetoriais de dimensão fnita e infinita; determinar
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
 Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
 1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 1 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
UFPB - CCEN - DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA a LISTA DE EXERCÍCIOS PERÍODO 0 Os exercícios 0 8 trazem um espaço vetorial V e um seu subconjunto W Sempre que W for um subespaço
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham.
 Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Capítulo 7. Operadores Normais. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 7 Operadores Normais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 7: Operadores Normais Meta
Capítulo 7 Operadores Normais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 7: Operadores Normais Meta
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan
 Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan Exercício 1. Seja A = (a i j ) uma matriz diagonal sobre
Universidade Federal do Paraná Centro Politécnico ET-DMAT Prof. Maria Eugênia Martin Tópicos de Álgebra Linear Verão 2019 Lista 4: Formas de Jordan Exercício 1. Seja A = (a i j ) uma matriz diagonal sobre
Aula 19 Operadores ortogonais
 Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
ÁLGEBRA LINEAR - MAT0024
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR - MAT0024 11 a Lista de exercícios
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
 Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Aula 1 Autovetores e Autovalores de Matrizes Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17
 Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
CÔNICAS PROJETIVAS SEMANA OLÍMPICA 2015 NÍVEL UNIVERSITÁRIO
 CÔNICAS PROJETIVAS SEMANA OLÍMPICA 2015 NÍVEL UNIVERSITÁRIO PROF. LUCIANO MONTEIRO DE CASTRO Conteúdo Introdução 1 Espaços Projetivos 2 1. A Reta Projetiva Real: P 1 (R) 2 1.1. Coordenadas Projetivas ou
CÔNICAS PROJETIVAS SEMANA OLÍMPICA 2015 NÍVEL UNIVERSITÁRIO PROF. LUCIANO MONTEIRO DE CASTRO Conteúdo Introdução 1 Espaços Projetivos 2 1. A Reta Projetiva Real: P 1 (R) 2 1.1. Coordenadas Projetivas ou
FUNCIONAIS LINEARES: ESPAÇO DUAL E ANULADORES
 FUNCIONAIS LINEARES: ESPAÇO DUAL E ANULADORES Eduardo de Souza Böer - eduardoboer04@gmail.com Universidade Federal de Santa Maria, Campus Camobi, 97105-900-Santa Maria, RS, Brasil Saradia Sturza Della
FUNCIONAIS LINEARES: ESPAÇO DUAL E ANULADORES Eduardo de Souza Böer - eduardoboer04@gmail.com Universidade Federal de Santa Maria, Campus Camobi, 97105-900-Santa Maria, RS, Brasil Saradia Sturza Della
A forma canônica de Jordan
 A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
A forma canônica de Jordan 1 Matrizes e espaços vetoriais Definição: Sejam A e B matrizes quadradas de orden n sobre um corpo arbitrário X. Dizemos que A é semelhante a B em X (A B) se existe uma matriz
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero.
 Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
Campos de Vetores sem Curvas Algébricas Tangentes
 Campos de Vetores sem Curvas Algébricas Tangentes Um Enfoque Computacional S. C. Coutinho UFRJ Colóquio 2005 p. 1/44 Campos de vetores Um campo de vetores polinomial no plano C 2 é uma aplicação Φ : C
Campos de Vetores sem Curvas Algébricas Tangentes Um Enfoque Computacional S. C. Coutinho UFRJ Colóquio 2005 p. 1/44 Campos de vetores Um campo de vetores polinomial no plano C 2 é uma aplicação Φ : C
Álgebra Linear Diagonalização de Operadores
 Introdução e Motivação Preliminares Diagonalização de Operadores Aplicações Referências Álgebra Linear Diagonalização de Operadores Universidade Estadual Vale do Acaraci - Sobral - CE Semana da Matemática
Introdução e Motivação Preliminares Diagonalização de Operadores Aplicações Referências Álgebra Linear Diagonalização de Operadores Universidade Estadual Vale do Acaraci - Sobral - CE Semana da Matemática
Forma Canônica de Matrizes 2 2
 Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
5 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2009
 5 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 29 Soluções dos exercícios Devido ao fato de A ser simétrica, existe uma base ortonormal {u,, u n } formada por autovetores de A, então
5 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 29 Soluções dos exercícios Devido ao fato de A ser simétrica, existe uma base ortonormal {u,, u n } formada por autovetores de A, então
MAE125 Álgebra Linear /1 Turmas EQN/QIN
 MAE25 Álgebra Linear 2 205/ Turmas EQN/QIN Planejamento (última revisão: 0 de junho de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na semana seguinte à aula e valem nota Todas
MAE25 Álgebra Linear 2 205/ Turmas EQN/QIN Planejamento (última revisão: 0 de junho de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na semana seguinte à aula e valem nota Todas
1 a Lista de Exercícios de MAT3458 Escola Politécnica 2 o semestre de 2016
 1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
1 a Lista de Exercícios de MAT3458 Escola Politécnica o semestre de 16 1 Para que valores de t R a função definida por (x 1, x ), (y 1, y ) = x 1 y 1 + tx y é um produto interno em R? Para cada par de
Cúbicas Reversas e Redes de Quádricas
 Cúbicas Reversas e Redes de Quádricas I. Vainsencher M.A.G. Zarzar 1999 Uma cúbica reversa é a imagem da aplicação P 1 [t, u] [t 3, t 2 u, tu 2, u 3 ] P 3, para uma escolha adequada de coordenadas homogêneas
Cúbicas Reversas e Redes de Quádricas I. Vainsencher M.A.G. Zarzar 1999 Uma cúbica reversa é a imagem da aplicação P 1 [t, u] [t 3, t 2 u, tu 2, u 3 ] P 3, para uma escolha adequada de coordenadas homogêneas
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
MAT 1202 ÁLGEBRA LINEAR II SUBESPACCOS FUNDAMENTAIS E TRANSF. LINEARES 23/08/12 Profs. Christine e Pedro
 MAT 1202 ÁLGEBRA LINEAR II 2012.2 SUBESPACCOS FUNDAMENTAIS E TRANSF. LINEARES 23/08/12 Profs. Christine e Pedro 1. Subespaços Fundamentais de uma Matriz (1.1) Definição. Seja A uma matriz retangular m
MAT 1202 ÁLGEBRA LINEAR II 2012.2 SUBESPACCOS FUNDAMENTAIS E TRANSF. LINEARES 23/08/12 Profs. Christine e Pedro 1. Subespaços Fundamentais de uma Matriz (1.1) Definição. Seja A uma matriz retangular m
Álgebra Linear /2 Turma EM1 (unificada)
 Álgebra Linear 2 2013/2 Turma EM1 (unificada) Planejamento preliminar (última revisão: 3/4/2013) Os exercícios correspondentes a cada aula serão discutidos na aula seguinte e não valem nota Este planejamento
Álgebra Linear 2 2013/2 Turma EM1 (unificada) Planejamento preliminar (última revisão: 3/4/2013) Os exercícios correspondentes a cada aula serão discutidos na aula seguinte e não valem nota Este planejamento
Prova de seleção ao Mestrado e/ou Programa de Verão. Programas: ICMC-USP, UFAL, UFRJ
 Prova de seleção ao Mestrado e/ou Programa de Verão Programas: ICMC-USP, UFAL, UFRJ Nome: Identidade (Passaporte): Assinatura: Instruções (i) O tempo destinado a esta prova é de 5 horas. (ii) 25 porcento
Prova de seleção ao Mestrado e/ou Programa de Verão Programas: ICMC-USP, UFAL, UFRJ Nome: Identidade (Passaporte): Assinatura: Instruções (i) O tempo destinado a esta prova é de 5 horas. (ii) 25 porcento
Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α).
![Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α). Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α).](/thumbs/77/75469525.jpg) Teoria de Galois Vamos nos restringir a car. zero. Seja K/F uma extensão finita de corpos. O grupo de Galois G(K/F ) é formado pelos isomorfismos ϕ : K K tais que x F, ϕ(x) = x. Lema. G(K/F ) [K : F ].
Teoria de Galois Vamos nos restringir a car. zero. Seja K/F uma extensão finita de corpos. O grupo de Galois G(K/F ) é formado pelos isomorfismos ϕ : K K tais que x F, ϕ(x) = x. Lema. G(K/F ) [K : F ].
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-458 Álgebra Linear para Engenharia II Terceira Lista de Eercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Seja V um espaço vetorial
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-458 Álgebra Linear para Engenharia II Terceira Lista de Eercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Seja V um espaço vetorial
Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa
 MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
Álgebra Linear I - Aula 10. Roteiro
 Álgebra Linear I - Aula 10 1. Combinação linear de vetores. 2. Subespaços e geradores. Roteiro 1 Combinação linear de vetores Definição 1 (Combinação linear de vetores). Dada um conjunto de vetores U =
Álgebra Linear I - Aula 10 1. Combinação linear de vetores. 2. Subespaços e geradores. Roteiro 1 Combinação linear de vetores Definição 1 (Combinação linear de vetores). Dada um conjunto de vetores U =
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica. Sistemas com três variáveis - Parte 1. Terceiro Ano do Ensino Médio
 Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Álgebra Linear I - Aula 18
 Álgebra Linear I - Aula 18 1. Matrizes semelhantes. 2. Matriz de uma transformação linear em uma base. Roteiro 1 Matrizes semelhantes Definição 1 (Matrizes semelhantes). Considere duas matrizes quadradas
Álgebra Linear I - Aula 18 1. Matrizes semelhantes. 2. Matriz de uma transformação linear em uma base. Roteiro 1 Matrizes semelhantes Definição 1 (Matrizes semelhantes). Considere duas matrizes quadradas
Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α).
![Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α). Lema. G(K/F ) [K : F ]. Vamos demonstrar usando o Teorema do Elemento Primitivo, a ser provado mais adiante. Assim, K = F (α).](/thumbs/83/88296130.jpg) Teoria de Galois Vamos nos restringir a car. zero. Seja K/F uma extensão finita de corpos. O grupo de Galois G(K/F ) é formado pelos isomorfismos ϕ : K K tais que x F, ϕ(x) = x. Lema. G(K/F ) [K : F ].
Teoria de Galois Vamos nos restringir a car. zero. Seja K/F uma extensão finita de corpos. O grupo de Galois G(K/F ) é formado pelos isomorfismos ϕ : K K tais que x F, ϕ(x) = x. Lema. G(K/F ) [K : F ].
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais
 Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
Unidade 5 - Subespaços vetoriais. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa. 10 de agosto de 2013
 MA33 - Introdução à Álgebra Linear Unidade 5 - Subespaços vetoriais A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Às vezes, é necessário detectar, dentro
MA33 - Introdução à Álgebra Linear Unidade 5 - Subespaços vetoriais A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Às vezes, é necessário detectar, dentro
GEOMETRIA E ÁLGEBRA DOS NÚMEROS COMPLEXOS
 GEOMETRIA E ÁLGEBRA DOS NÚMEROS COMPLEXOS Aluno: Adailton José do Nascimento Sousa Orientador: David Francisco Martinez Torres e Ricardo Alonso Introdução Os números complexos são muitas vezes interpretados
GEOMETRIA E ÁLGEBRA DOS NÚMEROS COMPLEXOS Aluno: Adailton José do Nascimento Sousa Orientador: David Francisco Martinez Torres e Ricardo Alonso Introdução Os números complexos são muitas vezes interpretados
Capítulo 2. f : A B. elementos A com elementos de B ilustradas nos seguintes diagramas.
 Capítulo 2 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Capítulo 2 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Material Teórico - Módulo: Vetores em R 2 e R 3. Operações Envolvendo Vetores. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Capítulo 2. f : A B. 3. A regra em (3) não define uma função de A em B porque 4 A está associado a mais de um. elemento de B.
 Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
3 a Avaliação Parcial - Álgebra Linear
 3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
7. Sejam U, W subespaços vetoriais de um espaço vetorial V sobre um corpo K. Prove que U W é um subespaço vetorial de V se e somente se U W ou W U.
 Lista de Álgebra Linear - Prof. Edson Iwaki 1. Quais dos subconjuntos são R subespaços vetoriais? Ache uma base para os que forem. (a) S = {(x, y, z) R 3 x 0} R 3 (b) S = {(x, y, z) R 3 x = 0} R 3 (c)
Lista de Álgebra Linear - Prof. Edson Iwaki 1. Quais dos subconjuntos são R subespaços vetoriais? Ache uma base para os que forem. (a) S = {(x, y, z) R 3 x 0} R 3 (b) S = {(x, y, z) R 3 x = 0} R 3 (c)
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
EXERCÍCIOS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2458 Álgebra Linear para Engenharia II Primeira Lista de Exercícios - Professor: Equipe da Disciplina 1. Em R 3, sejam S 1
Autovalores e Autovetores Determinante de. Motivando com Geometria Definição Calculando Diagonalização Teorema Espectral:
 Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
GABRIEL BUJOKAS
 APLICAÇÕES DE ÁLGEBRA LINEAR À COMBINATÓRIA GABRIEL BUJOKAS (GBUJOKAS@MIT.EDU) A gente vai discutir algumas das aplicações clássicas de álgebra linear à combinatória. Vamos começar relembrando alguns conceitos
APLICAÇÕES DE ÁLGEBRA LINEAR À COMBINATÓRIA GABRIEL BUJOKAS (GBUJOKAS@MIT.EDU) A gente vai discutir algumas das aplicações clássicas de álgebra linear à combinatória. Vamos começar relembrando alguns conceitos
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
MAE125 Álgebra Linear /2 Turmas EQN/QIN
 MAE25 Álgebra Linear 2 205/2 Turmas EQN/QIN Planejamento (última revisão: 26 de outubro de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na aula seguinte e valem nota Todas as
MAE25 Álgebra Linear 2 205/2 Turmas EQN/QIN Planejamento (última revisão: 26 de outubro de 205) Os exercícios correspondentes a cada aula serão cobrados oralmente na aula seguinte e valem nota Todas as
Fabio Augusto Camargo
 Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
GAAL Exercícios 6: Umas soluções
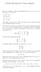 GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
O TEOREMA ESPECTRAL PARA OPERADORES SIMÉTRICOS. Marco Antonio Travassos 1, Fernando Pereira Sousa 2
 31 O TEOREMA ESPECTRAL PARA OPERADORES SIMÉTRICOS Marco Antonio Travassos 1, Fernando Pereira Sousa 2 1 Aluno do Curso de Matemática CPTL/UFMS, bolsista do Grupo PET Matemática/CPTL/UFMS; 2 Professor do
31 O TEOREMA ESPECTRAL PARA OPERADORES SIMÉTRICOS Marco Antonio Travassos 1, Fernando Pereira Sousa 2 1 Aluno do Curso de Matemática CPTL/UFMS, bolsista do Grupo PET Matemática/CPTL/UFMS; 2 Professor do
3 Sistema de Steiner e Código de Golay
 3 Sistema de Steiner e Código de Golay Considere o sistema de Steiner S(5, 8, 24, chamaremos os seus blocos de octads. Assim, as octads são subconjuntos de 8 elementos de um conjunto Ω com 24 elementos
3 Sistema de Steiner e Código de Golay Considere o sistema de Steiner S(5, 8, 24, chamaremos os seus blocos de octads. Assim, as octads são subconjuntos de 8 elementos de um conjunto Ω com 24 elementos
= 2 sen(x) (cos(x) (b) (7 pontos) Pelo item anterior, temos as k desigualdades. sen 2 (2x) sen(4x) ( 3/2) 3
 Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Álgebra Linear /2 Turma 11852
 Álgebra Linear 2 202/2 Turma 852 Planejamento (última revisão: 26/0/202) Os exercícios correspondentes a cada aula serão cobrados oralmente na aula seguinte e valem nota Todas as referências e exercícios
Álgebra Linear 2 202/2 Turma 852 Planejamento (última revisão: 26/0/202) Os exercícios correspondentes a cada aula serão cobrados oralmente na aula seguinte e valem nota Todas as referências e exercícios
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
23 e 24. Forma Quadrática e Equação do Segundo Grau em R 3. Sumário
 23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
Álgebra Linear Teoria de Matrizes
 Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
Álgebra Linear Teoria de Matrizes 1. Sistemas Lineares 1.1. Coordenadas em espaços lineares: independência linear, base, dimensão, singularidade, combinação linear 1.2. Espaço imagem (colunas) - Espaço
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista de exercícios 6 Espaços Vetoriais
 Universidade Federal do Paraná semestre 016. Algebra Linear, Olivier Brahic Lista de exercícios 6 Espaços Vetoriais Exercícios da Seção 3. Exercício 1: Determine se os seguintes conjuntos formam subespaços
Universidade Federal do Paraná semestre 016. Algebra Linear, Olivier Brahic Lista de exercícios 6 Espaços Vetoriais Exercícios da Seção 3. Exercício 1: Determine se os seguintes conjuntos formam subespaços
1 Matrizes Ortogonais
 Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
A forma canônica de Jordan e aplicações. 2 Resultados. 2.1 Triangularização. Marcos Alves dos Santos e José Carlos Corrêa Eidam(Orientador)
 A forma canônica de Jordan e aplicações Marcos Alves dos Santos e José Carlos Corrêa Eidam(Orientador) Universidade de São Paulo (USP), Brasil marcos.santos@usp.br Universidade de São Paulo (USP), Brasil
A forma canônica de Jordan e aplicações Marcos Alves dos Santos e José Carlos Corrêa Eidam(Orientador) Universidade de São Paulo (USP), Brasil marcos.santos@usp.br Universidade de São Paulo (USP), Brasil
1 Grupos (23/04) Sim(R 2 ) T T
 1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
1 Álgebra linear matricial
 MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
MTM510019 Métodos Computacionais de Otimização 2018.2 1 Álgebra linear matricial Revisão Um vetor x R n será representado por um vetor coluna x 1 x 2 x =., x n enquanto o transposto de x corresponde a
Aula 22 Derivadas Parciais - Diferencial - Matriz Jacobiana
 Derivadas Parciais - Diferencial - Matriz Jacobiana MÓDULO 3 - AULA 22 Aula 22 Derivadas Parciais - Diferencial - Matriz Jacobiana Introdução Uma das técnicas do cálculo tem como base a idéia de aproximação
Derivadas Parciais - Diferencial - Matriz Jacobiana MÓDULO 3 - AULA 22 Aula 22 Derivadas Parciais - Diferencial - Matriz Jacobiana Introdução Uma das técnicas do cálculo tem como base a idéia de aproximação
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Convergência em espaços normados
 Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Álgebra Linear I - Aula 19
 Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Agradecimentos. Aos colegas da pós-graduação que me fizeram sentir em casa, mesmo eu sendo o único da turma que não era de Belo Horizonte. Valeu!
 Agradecimentos Antes de tudo, quero agradecer a Deus. Ele tem me abençoado todos os dias da minha vida. Pois dele, por Ele e para Ele são todas as coisas. A Ele seja a glória para sempre! Amém. Quero agradecer
Agradecimentos Antes de tudo, quero agradecer a Deus. Ele tem me abençoado todos os dias da minha vida. Pois dele, por Ele e para Ele são todas as coisas. A Ele seja a glória para sempre! Amém. Quero agradecer
EDOs lineares de coeficientes constantes via Álgebra Linear
 EDOs lineares de coeficientes constantes via Álgebra Linear Lucas Seco 26 de Dezembro de 2012 Sempre ouvi falar que a solução de EDOs lineares homogêneas de coeficientes constantes bem como o Método dos
EDOs lineares de coeficientes constantes via Álgebra Linear Lucas Seco 26 de Dezembro de 2012 Sempre ouvi falar que a solução de EDOs lineares homogêneas de coeficientes constantes bem como o Método dos
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
