ÁLGEBRA 1. Departamento de Matemática UDESC - Joinville

Transcrição

1 ÁLGEBRA 1 Departamento de Matemática UDESC - Joinville

2 Conteúdo 1 CURVAS Cilindros projetantes de uma curva Exemplo Construção geométrica da curva formada pela interseção de seus cilindros projetantes Exemplos Exercícios Equações Paramétricas Exemplo Equações paramétricas de algumas curvas Exemplos Equação vetorial das curvas Exemplos Exercícios SISTEMAS DE COORDENADAS.1 Coordenadas polares no R Exemplo Relação entre o Sistema de Coordenadas Cartesianas Retangulares e o Sistema de Coordenadas Polares Exemplos Gráficos de Equações em Coordenadas Polares Exemplos Algumas Equações em Coordenadas Polares e seus respectivos Gráficos Exercícios Respostas Coordenadas polares no R Coordenadas cilíndricas Coordenadas esféricas Exemplos Exercícios Respostas TRANSFORMAÇÃO DE COORDENADAS Translação de eixos coordenados Exemplos Exercícios Respostas Rotação dos eixos coordenados Exemplos Exercícios Respostas

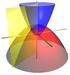
3 3 1 CURVAS 1.1 Cilindros projetantes de uma curva Dada uma curva C no espaço é possível obter três cilindros retos cujas interseções fornecem a curva C. Estes cilindros são obtidos projetando-se a curva em cada um dos planos coordenados. Portanto, projetando a curva no plano xy teremos um cilindro cuja diretriz é a curva C e a geratriz é o eixo z, projetando a curva no plano xz teremos um cilindro cuja diretriz é a curva C e a geratriz é o eixo y e projetando a curva no plano yz teremos um cilindro cuja diretriz é a curva C e a geratriz é o eixo x. Figura 1: Dada uma curva no espaço representada pela interseção das superfícies g(x, y, z) = 0, (1) f(x, y, z) = 0, podemos representá-la analiticamente por qualquer das equações de duas superfícies que se interceptam segundo a mesma curva. As superfícies mais amenas para se trabalhar são os cilindros e dada uma curva no espaço podemos sempre obter esta mesma curva através da interseção de dois cilindros.

4 4 Com efeito, consideramos os sistemas equivalentes ao sistema (1) formado por um par qualquer das equações F (x, y) = 0, G(y, z) = 0, H(x, z) = 0, resultante da eliminação respectiva das variáveis z, x, y. Cada um desses sistemas representa a mesma curva C. Geometricamente, estes cilindros são obtidos projetando-se a curva nos três planos coordenados e, por isso, são chamados cilindros projetantes da curva Exemplo 1. Determinar os cilindros projetantes da curva dada pela interseção das superfícies 4x + y + z 7 = 0, () x + y z + 1 = 0. Para eliminar a variável x, multiplicamos a segunda equação por e a primeira por 1 e em seguida somamos as duas equações Obtemos o cilindro hiperbólico 4x y z + 7 = 0, 4x + y z + = 0. 3z y = 9. (3) Para eliminar a variável y, devemos retornar ao sistema () e multiplicar a segunda equação por 1 e somar com a primeira equação Obtemos o cilindro circular 4x + y + z 7 = 0, x y + z 1 = 0. x + z = 4. (4) Para eliminar a variável z, voltamos ao sistema () e adicionamos as duas equações 4x + y + z 7 = 0, x + y z + 1 = 0.

5 5 Encontramos como resultado o cilindro circular 3x + y = 3. (5) A mesma curva representada pelo sistema () pode ser ser substituído por qualquer um dos sistemas seguintes formados pelos cilindros projetantes da curva: { 3x + y = 3 x + z = 4, (6) { 3x + y = 3 3z y = 9, (7) { x + z = 4 3z y = 9. (8) 1. Construção geométrica da curva formada pela interseção de seus cilindros projetantes Para traçar a curva de interseção de dois cilindros projetantes não é necessário desenhar os cilindros completos, basta apenas desenhar as curvas diretrizes de cada cilindro nos planos coordenados correspondentes e através de segmentos paralelos aos eixos coordenados obter cada ponto da curva de interseção. Para exemplificar, considere os dois cilindros projetantes { y = x y + z = 4. (9) Inicialmente, desenhamos cada cilindro separadamente e em seguida construímos a curva de interseção dos dois cilindros: (a) Cilindro parabólico y = x (Figura ). Note que no plano xy temos a parábola y = x. (b) Cilindro circular y + z = 4 (Figura 3). Note que no plano yz temos a circunferência y + z = 4. (c) Vamos agora desenhar os dois cilindros conjuntamente no mesmo sistema de coordenadas (Figuras 4 e 5). (d) Vamos agora traçar a curva de interseção dos dois cilindros e para isso necessitamos apenas das curvas diretrizes nos respectivos planos coordenados (Figura 6). Depois de obter a curva de interseção podemos então desenhar os cilindros para termos uma visualização completa dos destes e da curva de interseção. Para simplificar a obtenção da curva de interseção adotaremos sempre o primeiro octante para efetuarmos o traçado. Para os outros octantes o procedimento é o mesmo. Além disso, por simetria, podemos sempre inferir qual será a curva completa.

6 6 Figura : Figura 3:

7 7 Figura 4: Figura 5:

8 8 Figura 6: Claramente os pontos A e B pertencem a curva de interseção mas também podem ser obtidos usando-se a técnica geral de construção da curva de interseção que vamos agora descrever. Vamos tomar um ponto P qualquer de uma das curvas e através de segmentos paralelos aos eixos coordenados ir de encontro a um ponto da outra curva. Na Figura 7 partimos do ponto P da curva z + y = 4 e vamos de encontro ao ponto Q da curva y = x. Para isso, traçamos inicialmente o segmento P M paralelo ao eixo z e em seguida o segmento MQ paralelo ao eixo x. O ponto C (Figura 8) da curva de interseção dos dois cilindros é agora obtido através da interseção da reta r que passa pelo ponto Q e é paralela ao segmento P M com a reta s que passa pelo ponto P e é paralela ao segmento QM. Utilizando este mesmo procedimento com vários pontos obtemos a curva de interseção (Figura 9) Exemplos 1. Obter a curva de interseção dos cilindros x + y = 1 e x + z = 1. Vamos apenas desenhar as curvas diretrizes nos planos coordenados somente no primeiro octante e, através do processo descrito acima, encontrar a curva de interseção dos cilindros (Figura 10). A seguir, representamos no primeiro octante o desenho completo da interseção dos dois cilindros (Figura 11).. Determinar dois cilindros projetantes da curva gerada pela interseção das superfícies dadas abaixo e obter um desenho da curva de interseção das superfícies, no primeiro octante, do sistema 0x, 0y e 0z. { 7x + 14y + 63z 8y = 63 6x + 3y 7z 4y + 7 = 0. (10) Para obter os cilindros projetantes devemos trabalhar com as equações de modo a eliminar sucessivamente as variávieis x, y e z. Para melhor trabalhar com as equações, observe que

9 9 Figura 7: podemos simplificá-las um pouco, dividindo a primeira equação por 7 e a segunda por 3. Fazendo isso temos: { x + y + 9z 4y = 9 6x + y 9z 8y = 9. (11) Observe que facilmente podemos eliminar a variável z somando as duas equações acima 3x + 3y 1y = 0. (1) Para eliminar a variável x, multiplicamos a primeira equação por e subtraímos a segunda equação da primeira, { x + 4y + 18z 8y = 18 x + y 9z 8y = 9. Obtemos, 3y + 7z = 7. (13) Observe que neste caso não vamos conseguir eliminar facilmente a variável y, mas como já temos as equações (1) e (13) de dois cilindros projetantes, vamos usá-las para obter a curva de interseção.

10 10 Figura 8: Note que na equação 3x + 3y 1y = 0 temos y e y. Logo, devemos completar os quadrados de modo a obter uma equação mais simples para podermos identificar a curva e fazer seu desenho. Ou seja, 3x + 3y 1y = 0 x + y 4y = 0 x + y 4y = 0 x + ( y 4y + 4 ) 4 = 0 x + ( y 4y + 4 ) = 4 x + (y ) = 4 Portanto, obtemos os cilindros projetantes, x + (y ) = 4, que é um cilindro circular e (14) y 9 + z = 1, que é um cilindro elíptico. (15)

11 11 Figura 9: Figura 10:

12 1 Figura 11: Observe que o primeiro cilindro é gerado por uma circunferência de raio, no plano xy, com centro no ponto C(0, ) e o segundo cilindro é gerado por uma elipse, no plano yz, com semi-eixo maior 3 no eixo y e semi-eixo menor 1 no eixo z (Figura 1). 3. Aplicando o mesmo procedimento descrito acima, obter a curva de interseção dos cilindros, no primeiro octante, dados por: z = 1 y x + (y ) = 1 Note que neste caso devemos ter y > 0. As curvas estão representadas na Figura 13.

13 13 Figura 1: 1.. Exercícios 1. Determinar os cilindros projetantes e construir a curva dada pela interseção das superfícies no primeiro octante, quando for possível. Caso não seja possível no primeiro, escolha outro octante. (a) x + y + z = e x y z + 1 = 0 (b) x + y + z + z = 14 e x y z + 3z = 0 (c) 4x + y + z = 7 e x + y z + 1 = 0 (d) x 3y 3x + z = 0 e x + y + x + z = 0 (e) x + 3y + z = 1 e x y 3z + 4 = 0 (f) 3y + x + z = 1 e y x + z = 4 (g) y + 4z 3x = 4 e y z + x = 0 (h) y + 4z 3x = 4 e y z + x = 4 (i) x + y + 9z 4y = 9 e x + y 9z 8y + 9 = 0 (j) 180y + 9x + 4z = 180 sen x + 36 e 36y + 9x + 4z = 36 sen x + 36 (k) x y + 8z + 4y = 0 e x + y + 4z 4y = 0

14 14 Figura 13: 1.3 Equações Paramétricas Uma curva no espaço pode ser representada por três equações da forma x = f(t) y = g(t) z = h(t) (16) onde cada coordenada do ponto da curva depende de um parâmetro t. Convenciona-se usar a notação t para o parâmetro em virtude das equações paramétricas serem usadas na Física para representar o movimento de uma partícula em função do tempo. Mas, podemos usar outras notações para o parâmetro, como por exemplo θ e s, quando for conveniente. Se na primeira equação isolarmos o valor de t e substituimos este valor nas outras duas equações teremos as equações da curva na forma cartesiana, F (x, y) = 0 G(x, z) = 0. (17) Estas são as equações cartesianas dos cilindros projetante da curva (16) Exemplo Fazer um desenho da curva x = 1 y = t. (18) z = t

15 15 Para fazer o esboço da curva podemos proceder de dois modos: 1. Determinamos cada ponto da curva atribuindo valores ao parâmetro t, como na tabela abaixo. t x y z Marcamos cada um dos pontos no sistema tridimensional P 1 (1, 4, 16), P (1, 3, 9), P 3 (1,, 4), P 4 (1, 1, 1), P 5 (1, 0, 0), P 6 (1, 1, 1), P 7 (1,, 4), P 8 (1, 3, 9), P 9 (1, 4, 16), como na Figura 14. Figura 14: Em seguida unimos os pontos para visualizarmos a curva (Figura 15). É claro que quanto mais pontos tivermos mais preciso será o traçado da curva. As equações paramétricas são ideais para fazermos traçados de curvas no computador pois o computador pode calcular em pouquíssimo tempo uma grande quantidade de parâmetros e pontos da curva.. Outra maneira é passar as equações paramétricas para a forma de equações cartesianas, respectivamente, como dadas abaixo,

16 16 Figura 15: x = 1 y = t, (19) z = t { x = 1 z = y. (0) Logo, temos uma parábola em cima do plano x = 1. Ou seja, é a projeção da parábola de equação z = y do plano yz sobre o plano x = 1 (Figura 15) Equações paramétricas de algumas curvas 1. Circunferência com Centro C(x 0, y 0 ) e raio r no plano:. Elipse com centro C(x 0, y 0 ) e semi-eixos a e b no plano: { x(θ) = x0 + r cos θ y(θ) = y 0 + r sen θ. (1) { x(θ) = x0 + a cos θ y(θ) = y 0 + b sen θ. ()

17 17 3. Reta com vetor diretor v = (a, b, c) passando pelo ponto P (x 0, y 0, z 0 ) no espaço: x(t) = x 0 + at y(t) = y 0 + bt z(t) = z 0 + c(t). (3) Exemplos 1. Desenhe a curva x = cos θ y = sen θ z = 3. (4) Passando para coordenadas cartesianas temos { x + y = 4 z = 3. (5) Portanto, a curva é uma circuferência em cima do plano z = 3 e a projeção dessa curva no plano xy é a circunferência x + y = 4 (Figura 16). Figura 16:

18 18. Desenhe a curva x = y = cos θ z = sen θ. (6) Portanto, temos uma cir- Observe que a curva no plano yz é uma circuferência de raio. cuferência de raio em cima do plano x = (Figura 17). Figura 17: 3. Desenhe a curva x = y = cos θ z = 3 sen θ. (7) 1.4 Equação vetorial das curvas Uma curva pode ser determinada pelo vetor posição de cada ponto da curva. Neste caso, cada ponto da curva será dado por um vetor cuja extremidade se encontra nesse ponto. Uma equação vetorial é da forma, r(t) = x(t) i + y(t) j + z(t) k. (8)

19 Exemplos 1. Desenhar a curva r(t) = (t + ) i + (t 4) j + (1 t) k. Para cada valor de t teremos um vetor que indicará um ponto da curva, como na tabela abaixo. t r(t) 0 i 4 j + k 1 i 6 j + k 1 3 i j 8 j + 3 k 4 i 1 k (9) Para obter a curva, representamos os vetores no espaço, localizamos a extremidade de cada vetor e unimos os pontos das extremidades (Figura 18). Figura 18: Assim como no caso da equações paramétricas, necessitamos um grande número de vetores

20 0 para traçarrmos a curva. Podemos ter uma idéia da curva passando a equação vetorial para equações paramétricas e daí para equações cartesianas. Deste modo podemos usar todo o nosso conhecimento anterior. Com a equação vetorial r(t) = (t + ) i + (t 4) j + (1 t) k, obtemos as equações paramétricas x(t) = + t y(t) = 4 + t z(t) = 1 t que possuem vetor diretor v = (1, 1) e ponto P (, 4, 1) (Figura 19).. (30) Figura 19:. Seguindo o mesmo procedimento do exemplo anterior, desenhe a curva r(t) = cos(t) i + sen (t) j + 4 k Exercícios 1. Escrever as equações paramétricas das seguintes curvas: (a) x + y + z = 16 e z =,

21 1 (b) x + y + z = 9 e y = x, (c) x + y = 1 e y = z, (d) x + y + z = e x y z + 1 = 0, (e) x + y = 4 e x + y z = 0.. Desenhar a curva x = 4 cos t, y = 9 sen t, z = Desenhar a curva x = t, y = 0, z = e t. 4. Escrever a equação cartesiana da curva x = cos t, y = sen t, z = cos t + sen t. 5. Construir a curva cujas equações vetoriais são dadas abaixo: (a) r(t) = ( t 3) i + (t 4) j + (4t 7) k, (b) r(t) = t i + 4t j + t k, (c) r(t) = cos θ i + cos θ j + sen θ k, (d) r(t) = 4 sen θ i + cos θ j + sen θ k. 6. Fazer o desenho, no primeiro octante, da curva cujas equações paramétrica são dadas por x = 4 sen t + 6 y = 6 cos t. z = 4 sen t 7. Determine a equação vetorial que representa a curva de intersecção das superfícies x + y = 1 e y + z =. Faça um esboço da curva. 8. Parametrize a curva de intersecção das superfícies dadas an seguir: (a) (b) { x = y + z x + y + z =, { x + z = 4 y = 9 x 4z. 9. Represente no primeiro octante a curva cuja equação vetorial é dada abaixo: (a) r(t) = (t, t, cos t), (b) r(t) = (3 1 cos t, 3 sen t, cos t).

22 SISTEMAS DE COORDENADAS.1 Coordenadas polares no R Fonte: Cálculo A. Funções. Limite. Derivação. Integração. Diva Marília Flemming. Mírian Buss Gonçalves. Até o presente momento, localizamos um ponto no plano por meio de suas coordenadas cartesianas retangulares. Existem outros sistemas de coordenadas. Um sistema bastante utilizado é o sistema de coordenadas polares. No sistema de coordenadas polares, as coordenadas consistem de uma distância e da medida de um ângulo em relação a um ponto fixo e a uma semireta fixa. A Figura 1 ilustra um ponto P num sistema de coordenadas polares. O ponto fixo, denotado por O, é chamado pólo ou origem. A semireta fixa OA é chamada. O ponto P fica bem determinado através do par ordenado (r, θ), onde r representa a distância entre a origem e o ponto P, e θ representa a medida, em radianos, do ângulo orientado AOP. O segmento OP, muitas vezes, é chamado raio. P Pólo r ou origem θ O A Figura 1 Usaremos as seguintes convenções: (i) Se o ângulo AOP for descrito no sentido anti-horário, então θ > 0. Caso contrário, teremos θ < 0. (ii) Se r < 0, o ponto P estará localizado na extensão do lado terminal do ângulo (iii) O par ordenado (0, θ), θ qualquer, representará o pólo. AOP..1.1 Exemplo 1. Representar num sistema de coordenadas polares os seguintes pontos: (a) P 1 (, /4) (b) P (, /4) (c) P 3 (, /4) (d) P 4 (, /4) As Figuras (a) e (b), representam os pontos P 1 e P, respectivamente. P 1 r = θ = 4 O (a) r = P Figura θ = 4 O (b)

23 3 As Figuras 3 (a) e 3 (b), mostram os pontos P 3 e P 4, respectivamente. P 3 r = O θ = 4 O θ = 4 r = (a) (b) P 4 Figura 3.1. Relação entre o Sistema de Coordenadas Cartesianas Retangulares e o Sistema de Coordenadas Polares. Em várias situações, surge a necessidade de nos referirmos a ambas, coordenadas cartesianas e coordenadas polares de um ponto P. Para visualizar isto, fazemos a origem do primeiro sistema coincidir com o pólo do segundo sistema, o com o eixo positivo dos x e o raio para o qual θ = / com o eixo positivo dos y (ver Figura 4). Y O θ = A X Figura 4 Supondo que P seja um ponto com coordenadas cartesianas (x, y) e coordenadas polares (r, θ), vamos analisar o caso em que o ponto P está no primeiro quadrante. A Figura 5 (a) e (b) ilustra o caso para r > 0 e r < 0, respectivamente.

24 4 Y Y y P r θ x (a) X -x y θ -y P (b) x X Figura 5 Podemos observar que: (i) Para r > 0, temos cos θ = x r e sen θ = y r. (ii) Para r < 0, temos cos θ = x y e sen θ =. r r Portanto, { x = r cos θ y = r sen θ. (31) Pode-se verificar a validade das relações encontradas, no caso em que o ponto P se encontra sobre um dos eixos ou num outro quadrante. Usando (31), podemos deduzir outra relação muito usada. Elevando ambos os membros das equações em (31) ao quadrado, podemos escrever { x = r cos θ y = r sen θ. Adicionando membro a membro, obtemos: x + y = r cos θ + r sen θ ou x + y = r. Portanto, r = ± x + y. (3)

25 5.1.3 Exemplos 1. Encontrar as coordenadas cartesianas do ponto cujas coordenadas polares são ( 4, 7/6). Y Solução. A Figura 6 ilustra este ponto. Temos, x = r cos θ e y = r sen θ = 4 cos ( 7 6 ) = 4 sen 7 ) 6 = 4 3 = 4 ( 1 = 3 =. Portanto, ( 3, ) são as coordenadas cartesianas do ponto dado. y 7 6 P x X Figura 6. Encontrar (r, θ), supondo r < 0 e 0 θ < para o ponto P, cujas coordenadas cartesianas são ( 3, 1). Y Solução. A Figura 7 ilustra o ponto P. r = x + y = = ; cos θ = x r = 3 = 3 sen θ = y r = 1 = 1. Portanto, θ = 5 6. e P X Figura Gráficos de Equações em Coordenadas Polares. O gráfico de F (r, θ) = 0 é formado por todos os pontos cujas coordenadas polares satisfazem a equação. É comum apresentarmos a equação numa forma explícita, isto é, r = f(θ). Na prática, os seguintes procedimentos poderão nos auxiliar no esboço do gráfico: (i) calcular os pontos de máximo e/ou mínimos; (ii) encontrar os valores de θ para os quais a curva passa pelo pólo; (iii) verificar simetrias. Se, a equação não se altera quando substituirmos r por r, existe simetria em relação à origem; a equação não se altera quando substituirmos θ por θ, existe simetria em relação ao eixo polar;

26 6 a equação não se altera quando substituirmos θ por θ, existe simetria em relação ao eixo θ =..1.5 Exemplos 1. Esboçar a curva r = (1 cos θ). Como a equação não se altera ao substituirmos θ por θ, isto é r = (1 cos θ) = (1 cos( θ)), concluímos que existe simetria em relação ao. Logo, basta analisar valores de θ tais que 0 θ. Para 0 θ, encontramos um ponto de máximo (4, ) e um ponto de mínimo (0, 0). Observamos que, considerando r = f(θ), os pontos de máximos e mínimos podem ser encontrados de maneira análoga aos da Seção 5.7 (Cálculo A). A Tabela 1 mostra alguns pontos da curva, cujo esboço é mostrado na Figura 8. Tabela 1 θ r Figura 8. Esboçar a curva r = cos θ. Analisando as simetrias, temos que (a) A curva é simétrica em relação ao eixo dos x, pois r = cos( θ) = cos θ. (b) A curva é simétrica em relação ao eixo dos y, pois r = cos[( θ)] = cos( θ) = cos θ. Logo, basta fazer uma tabela para 0 θ. Em 0 θ, a curva passa pelo pólo quando θ = 4, pois r = f ( ) 4 = cos 4 = cos = 0. Podemos ainda verificar que, para 0 θ, temos um ponto de máximo (, 0) e um ponto de mínimo (, /). Usando a Tabela e os resultados anteriores, esboçamos a curva vista na Figura 9. Tabela θ r θ = θ = 3 θ = 4 θ = 6 θ = 0 Figura 9

27 7.1.6 Algumas Equações em Coordenadas Polares e seus respectivos Gráficos. (I) Equações de retas. (a) θ = θ 0 ou θ = θ 0 ± n, n Z é uma reta que passa pelo pólo e faz um ângulo de θ 0 ou θ 0 ± n radianos com o (ver Figura 10). θ 0 O A Figura 10 (b) r sen θ = a e r cos θ = b, a, b R, são retas paralelas aos eixos polar e /, respectivamente (ver Figuras 11 e 1). a A A [r sen θ = a, a > 0] Figura 11 a [r sen θ = a, a < 0] b A b A [r cos θ = b, b > 0] (II) Circunferências. Figura 1 [r cos θ = b, b < 0] (a) r = c, c R é uma circunferência centrada no pólo e raio c (ver Figura 13). o A Figura 13

28 8 (b) r = a cos θ é uma circunferência de centro no, tangente ao eixo θ = /: se a > 0, o gráfico está à direita do pólo; se a < 0, o gráfico está à esquerda do pólo (ver Figura 14). P (r, θ) θ 0 (a, 0) A [r = a cos θ, a > 0] a A [r = a cos θ, a < 0] Figura 14 (c) r = b sen θ é uma circunferência de centro no eixo / e que tangencia o : se b > 0, o gráfico está acima do pólo; se b < 0, o gráfico está abaixo do pólo (ver Figura 15). b 0 A A [r = b sen θ, b > 0] b [r = b sen θ, b < 0] Figura 15 (III) Limaçons. r = a ± b cos θ ou r = a ± b sen θ, onde a, b R são limaçons. Temos, se b > a, então o gráfico tem um laço (ver Figura 16);

29 9 r = a + b cos θ r = a b cos θ r = a + b sen θ r = a b sen θ Figura 16 se b = a, então o gráfico tem o formato de um coração, por isso é conhecido como Cardióide (ver Figura 17); r = a(1 + cos θ) r = a(1 cos θ) r = a(1 + sen θ) Figura 17 r = a(1 sen θ)

30 30 se b < a, então o gráfico não tem laço (ver Figura 18). r = a + b cos θ r = a b cos θ r = a + b sen θ r = a b sen θ (IV) Rosáceas. Figura 18 Observamos que na Figura 16 usamos a = 1 e b =, na Figura 17 usamos a = b = 1 e na Figura 18 usamos a = 3 e b =. r = a cos nθ ou r = a sen nθ, onde a R e n ℵ são rosáceas: se n é par temos uma rosácea de n pétalas (ver Figura 19); r = a cos nθ Figura 19 r = a sen nθ se n é ímpar temos uma rosácea de n pétalas (ver Figura 0).

31 31 r = a sen nθ Figura 0 r = a cos nθ Observamos que na Figura 19 usamos a = 1 e n = 4, na Figura 0 usamos a = 1 e n = 5. (V) Lemniscatas. r = ±a cos θ ou r = ±a sen θ, onde a R são lemniscatas (ver Figura 1). θ = 3 4 θ = 4 θ = 3 4 θ = 4 r = a cos θ r = a cos θ r = a sen θ Figura 1 r = a sen θ Observamos que na Figura 1 usamos a = 1.

32 3 (IV) Espirais. As equações seguintes representam algumas espirais: (a) rθ = a, a > 0 espiral hiperbólica; (b) r = aθ, a > 0 espiral de Arquimedes; (c) r = e aθ espiral logarítmica; (d) r = θ espiral parabólica. As Figuras a 5 ilustram estas espirais. (a, ) (a, ) rθ = a (θ > 0) Figura rθ = a (θ < 0) Figura 3 r = aθ (θ 0) r = e aθ Figura 4 r = θ Figura 5 r = θ

33 Exercícios 1. Demarcar os seguintes pontos no sistema de coordenadas polares. (a) P 1 (4, /4) (b) P (4, /4) (c) P 3 ( 4, /4) (d) P 4 ( 4, /4). Demarcar os seguintes pontos no sistema de coordenadas polares e encontrar suas coordenadas cartesianas. (a) P 1 (3, /3) (b) P ( 3, /3) (c) P 3 (3, /3) (d) P 4 ( 3, /3) 3. Encontrar as coordenadas cartesianas dos seguintes pontos dados em coordenadas polares. (a) (, /3) (b) (4, 5/8) (c) (3, 13/4) (d) ( 10, /) (e) ( 10, 3/) (f) (1, 0) 4. Encontrar um par de coordenadas polares dos seguintes pontos: (a) (1, 1) (b) ( 1, 1) 5. Usar (a) r > 0 e 0 θ < ; (b) r < 0 e 0 θ < ; (c) ( 1, 1) (d) (1, 1) (c) r > 0 e < θ 0; (d) r < 0 e < θ 0; para descrever os pontos P 1 ( 3, 1) e P (, ), em coordenadas polares. 6. Identificar e transformar as seguintes equações para coordenadas polares. (a) x + y = 4 (b) x = 4 (c) y = (d) y + x = 0 (e) x + y x = 0 (f) x + y 6y = 0 7. Transformar as seguintes equações para coordenadas cartesianas e identificá-las. (a) r = cos θ (b) r = sen θ (c) r = 1 cos θ+ sen θ (d) r = a, a > Nos exercícios a seguir esboçar o gráfico das curvas em coordenadas polares. (a) r = 1 + cos θ (b) r = 1 sen θ (c) r = a ± b cos θ, a = e b = 3; a = 3 e b = ; a = b = 3 (d) r = cos 3θ (e) r = cos 3θ (f) r = sen θ (g) r = cos θ (h) r = sen θ (i) r = a ± b sen θ, a = e b = 3; a = 3 e b = ; a = b = (j) r = sen 3θ

34 34 (k) θ = /4 (l) θ = /9 (m) r = 4 cos θ (n) r = 3θ, θ 0 (o) r = 4 sen θ (p) r = e θ, θ 0 (q) r = (r) r = 10 cos θ (s) r = cos θ (t) r = 1 sen θ (u) r = e θ/3 (v) r = θ (w) r cos θ = 5 (x) 5r cos θ = Respostas (a) (3/, 3 3/) (b) ( 3/, 3 3/) (c) (3/, 3 3/) (d) ( 3/, 3 3/) (3a) (1, 3) (3b) ( , ) (3c) ( 3 /, 3 /) (3d) (0, 10) (3e) (0, 10) (3f) (1, 0) (4a) (, /4) (4b) (, 3/4) (4c) (, 5/4) (4d) (, 7/4) (5a) P 1 (, 11/6); P (, 5/4) (5b) P 1 (, 5/6); P (, /4) (5c) P 1 (, /6); P (, 3/4) (5d) P 1 (, 7/6); P (, 7/4) (6a) r = ± (6b) r cos θ = 4 (6c) r sen θ = (6d) θ = 3 + k, k Z 4 (6e) r = cos θ (6f) r = 6 sen θ (7a) x + y x = 0 (7b) x + y y = 0 (7c) x + y = 1 (7d) x + y = a. Coordenadas polares no R 3 Fonte:Geometria Analítica. Coleção Schaum. Joseph H. Kindle. Z No espaço, além das coordenadas cartesianas retangulares, três outros sistemas são freqüentemente empregados: os de coordenadas polares, cilíndricas e esféricas. As coordenadas polares do ponto P no espaço, Fig. 1, são (r, α, β, γ), onde r, raio vetor, designa a distância OP e α, β e γ são ângulos diretores de OP. As relações entre coordenadas polares e retangulares do ponto P são γ r β O α X Figura 1 P (x, y, z) (r, α, β, γ) Y

35 35 x = r cos α y = r cos β z = r cos γ. (33) r = ± x + y + z, cos α = x r, cos β = y r, cos γ = z r, r 0. (34) Uma vez que cos α + cos β + cos γ = 1, as quatro coordenadas não são independentes. Por exemplo, para α = 60 e β = 45, temos cos γ = 1 cos α cos β = = 1. Da condição 4 4 γ 180 deduz-se: γ = 60 ou Coordenadas cilíndricas No sistema de coordenadas cilíndricas, um ponto P (x, y, z), Fig., é localizado pelas coordenadas r, θ, z, devendo-se notar que r e θ são as coordenadas polares da projeção Q do ponto P no plano xy. Para designar essas coordenadas, escrevemos: (r, θ, z). As relações entre coordenadas cilíndricas e retangulares são Z P (x, y, z) P (r, θ, z) z O θ r X Figura Y x = r cos θ y = r sen θ z = z. (35) r = ± x + y, θ = arctan y x. (36) O ângulo θ não sofre restrição de valor, podendo r receber valores negativos, como em coordenadas polares..4 Coordenadas esféricas Seja P (x, y, z) um ponto qualquer do espaço e Q, sua projeção no plano xy. Chamemos de r a distância OP, como em coordenadas polares. Designemos o ângulo ZOP por φ. Consideremos o ângulo φ como positivo e capaz de variar no 0 φ 180. Designemos o ângulo XOQ por θ. Os símbolos r, θ e φ tomam o nome de coordenadas esféricas do ponto P e representam-se por P (r, θ, φ); r é o raio vetor, θ é a longitude e φ é a co-latitude de P. O ângulo θ pode receber qualquer valor. Do triângulo retângulo OP Q, deduzimos OQ = r sen φ, QP = r cos φ. (37)

36 36 Z r P (x, y, z) P (r, θ, φ) φ O θ M Q X Figura 3 Y Do triângulo retângulo OM Q tiramos OM = OQ cos θ, MQ = OQ sen θ. Portanto, x = OM = r sen φ cos θ y = MQ = r sen φ sen θ z = QP = r cos φ. (38) r = ± x + y + z, θ = arctan y x, φ = arccos z r. (39) Nos problemas que envolvem a determinação de áreas e volumes pelo cálculo, o trabalho muito se simplifica com o emprego de coordenadas cilíndricas ou esféricas. As coordenadas cilíndricas mostram-se particularmente úteis quando a superfície limite é de revolução..5 Exemplos 1. Determinar as coordenadas polares, cilíndricas e esféricas do ponto de coordenadas retangulares (1,, ). Solução Coordenadas polares. r = x + y + z = 1 + ( ) + = 9 = 3. α = arccos x r = arccos 1 3 = 70 3, ) β = arccos y r ( = arccos 3 = , γ = arccos z r = arccos 3 = Resposta: (3, 70 3, , ). Coordenadas cilíndricas. r = x + y = 1 + ( ) = 5. θ = arctan y x = arctan = 96 34, z =. Resposta: ( 5, 96 34, ). Coordenadas esféricas. r = x + y + z = 1 + ( ) + = 9 = 3. θ = arctan y x = arctan = 96 34, φ = arccos z r = arccos 3 = 48 11, Resposta: (3, 96 34, ).. Determinar as coordenadas cartesianas ortogonais do ponto, cujas coordenadas cilíndricas são (6, 10, ).

37 37 Solução. x = r cos θ = 6 cos 10 = 3, y = r sen θ = 6 sen 10 = 3 3, z =. Resposta: ( 3, 3 3, ). 3. Determinar as coordenadas retangulares do ponto de coordenadas esféricas (4, 45, 30 ). Solução. x = r sen φ cos θ = 4 sen 30 cos( 45 ) =, y = r sen φ sen θ = 4 sen 30 sen ( 45 ) =, z = r cos φ = 4 cos 30 = 3. Resposta: (,, 3). 4. Determinar as coordenadas cartesianas do ponto, cujas coordenadas polares são (3, 10, 10, 135 ). Solução. x = r cos α = 3 cos 10 = 3, y = r cos β = 3 cos 10 = 3, z = r cos γ = 3 cos 135 = 3 ( ) Resposta: 3, 3, Determinar as coordenadas cartesianas, polares e esféricas de um ponto, cujas coordenadas cilíndricas são (6, 10, 4). Solução Retangulares. x = r cos θ = 6 cos 10 = 3, y = r sen θ = 6 sen 10 = 3, z = 4. Resposta: ( 3, 3 3, 4). Polares. r = x + y + z = ( 3) + (3 3) + 4 = 13. α = arccos x r = arccos 3 13 = , β = arccos y r = arccos = 46 7, γ = arccos z r = arccos 4 13 = Resposta: ( 13, , 46 7, ). Esféricas. r = x + y + z = θ = arctan y x = arctan = 10, φ = arccos z r = arccos 4 13 = 56 19, Resposta: ( 13, 10, ). ( 3) + (3 3) + 4 = 13

38 38 6. Passar a equação x + y + z x 3y z + = 0 para coordenadas cilíndricas. Solução. Empreguemos as fórmulas x = r cos θ, y = r sen θ e z = z. Substituindo, na equação dada, x, y e z pelos valores acima, vem r cos θ + r sen θ + z r cos θ 3r sen θ z + = 0. Simplificando, resulta r r( cos θ + 3 sen θ) + z z + = Passar a equação x + 3y 6z = 0 para coordenadas esféricas. Solução. Empreguemos as fórmulas x = r sen φ cos θ, y = r sen φ sen θ e z = r cos φ. Substituindo, temos r sen φ cos θ + 3r sen φ sen θ 6r cos φ = 0 ou r sen φ cos θ + 3r sen φ sen θ 6 cos φ = Exprimir a equação r + 6 sen φ cos θ + 4 sen φ sen θ 8 cos φ = 0, em coordenadas retangulares. Solução. A equação dada está expressa em coordenadas esféricas. Podemos Multiplicá-la por r. Empregando os valores de x, y, z, dados no problema 7, obtemos r + 6r sen φ cos θ + 4r sen φ sen θ 8r cos φ = 0, ou x + y + z + 6x + 4y 8z = 0. Esta é a equação de uma esfera com centro em ( 3,, 4) e raio r = Reduzir a equação z = r cos θ, expressa em coordenadas cilíndricas, a coordenadas cartesianas ortogonais. Solução. Façamos cos θ = cos θ sen θ. Teremos então z = r (cos θ sen θ) = r cos θ r sen θ. Como r cos θ = x e r sen θ = y, a equação pedida é z = x y. 10. Transformar x + y z = 5 em uma equação do sistema polar. Solução. Em coordenadas polares, temos x = r cos α, y = r cos β, z = r cos γ. Portanto, a equação se transforma em r cos α + r cos β r cos γ = 5 ou r (cos α + cos β cos γ) = 5. Como cos α + cos β + cos γ = 1, a equação pedida é r (1 cos γ) = Passar a equação cos γ = r cos α cos β, expressa em coordenadas polares, para o sistema cartesiano ortogonal. Solução. Multipliquemos ambos os membros da equação dada por r. Teremos r cos γ = r cos α cos β. Como r cos γ = z, r cos α = x e r cos β = y, a equação pedida é z = xy..6 Exercícios 1. Determinar as coordenadas polares dos seguintes pontos: (a) (0, 1, 1) (b) (0,, ) (c) (1,, ) (d) (6, 3, ) (e) (8, 4, 1). Determinar as coordenadas cilíndricas dos pontos do problema 1.

39 39 3. Determinar as coordenadas esféricas do problema1. 4. Determinar as coordenadas retangulares dos pontos, cujas coordenadas polares são: (a) (, 90, 30, 60 ) (b) (3, 60, 45, 10 ) (c) (4, 10, 10, 135 ) (d) (3, 150, 60, 90 ) (e) (, 45, 10, 60 ) 5. Determinar as coordenadas ortogonais dos pontos, cujas coordenadas cilíndricas são: (a) (6, 10, ) (b) (1, 330, ) (c) (4, 45, ) (d) (8, 10, 3) (e) (6, 30, 3) 6. Determinar as coordenadas retangulares dos pontos, cujas coordenadas esféricas são: (a) (4, 10, 30 ) (b) (3, 10, 40 ) (c) (6, 330, 60 ) (d) (5, 150, 10 ) (e) (, 180, 70 ) 7. Determinar as coordenadas esféricas dos pontos, cujas coordenadas cilíndricas são: (a) (8, 10, 6) (b) (4, 30, 3) (c) (6, 135, ) (d) (3, 150, 4) (e) (1, 90, 5) 8. Transformar as seguintes equações nas correspondentes do sistema esférico. (a) 3x 3y = 8z (b) x y z = a (c) 3x + 5y z = 6 9. Transformar as coordenadas retangulares das equações dadas em coordenadas cilíndricas: (a) 5x + 4y = 0 (b) 5x 4y + x + 3y = 0 (c) x + y 8x = 0 (d) x y + y 6 = 0 (e) x + y z = a 10. As superfícies dadas por suas equações estão expressas em coordenadas cilíndricas. Referí-las ao sistema cartesiano ortogonal e identificá-las. (a) r + 3z = 36 (b) r = a sen θ (c) r + z = 16 (d) θ = 45 (e) r z = Referir ao sistema polar os lugares das seguintes equações cartesianas. (a) x + y + 4z = 0 (c) x +3y +z 6x +y = 0 (b) x + y z = a (d) z = xy 1. Transformar as seguintes equações, dadas em coordenadas esféricas, em equações de coordenadas retangulares e identificá-las. (a) r = 5a cos φ (c) r sen φ = a (b) θ = 60 (d) r = Transformar as seguintes equações polares em equações cartesianas retangulares: (a) r(cos α + cos β + cos γ) = 5 (b) r ( cos α 1) = 5 (c) cos γ = r(cos α cos β) (d) r r cos γ 4r cos γ = 0

40 40.7 Respostas (8a) 3r sen φ cos θ = 8 cos θ (8b) r ( sen φ cos θ cos φ) = a (8c) r(3 sen φ cos θ + 5 sen φ sen θ cos φ) = 6 (9a) θ = arctan( 5/4) (9b) 5r cos θ 4r sen θ + cos θ + 3 sen θ = 0 (9c) r 8 cos θ = 0 (9d) r cos θ + r sen θ 6 = 0 (9e) r z = a (10a) x + y + 3z = 36. Elipsóide de revolução. (10b) x + y = ay. Cilindro circular reto. (10c) x + y + z = 16. Esfera. (10d) y = x. Plano. (10e) x + y z = 1. Hiperbolóide de uma folha. (11a) r(cos α + cos β) + 4 cos γ = 0 ou r(1 cos γ) + 4 cos γ = 0 (11b) r (1 cos γ) = a (11c) r( + cos β) 6 cos α + cos β = 0 (11d) cos γ = r cos α cos β (1a) x + y + z = 5az (1b) y = 3x (1c) x + y = a (1d) x + y + z = 16 (13a) x + y + z = 5 (13b) x y z = 5 (13c) z = x y (13d) x + y 4z = 0

41 41 3 TRANSFORMAÇÃO DE COORDENADAS Fonte:Geometria Analítica. Charles H. Lehmann. Um dos principais objetivos da Geometria Analítiva é a determinação das propriedades de várias curvas e configurações geométricas. Sobre a base de alguns conceitos fundamentais já fizemos um estudo da linha reta e da circunferência. Naturalmente esperamos continuar esta investigação relativamente a outras curvas. Entretanto, a medida que progredirmos em nosso trabalho, verificaremos que as curvas e suas equações se tornam mais complicadas e mais difíceis de serem analisadas. Em consequência torna-se expediente, em várias ocasiões, introduzir novos recursos a fim de facilitar o estudo destas curvas. Assim, nesta altura, é conveniente introduzir a noção de transformação de coordenadas, um recurso que nos possibilita simplificar as equações de muitas curvas. Uma transformação é o processo de mudar uma relação, expressão ou figura em outra. Uma tranformação é uma operação por meio da qual uma relação, expressão ou figura é mudada em outra de acordo com uma dada lei. Analiticamente a lei dada é expressa por uma ou mais equações denominadas equações de transformação. Transformação de coordenadas. Consideremos uma circunferência de raio r cuja equação é dada na forma padrão Y O Y P O (h,k) X X (x h) + (y k) = r (40) onde as coordenadas (h, k) do centro O são ambas diferentes de zero (Fig. 1). Se esta circunferência é mudada, a qualquer respeito, sendo colocada com seu centro na origem O, sua equação assume a forma canônica mais simples x + y = r. (41) Figura 1 Mas o mesmo efeito pode ser produzido sem mover a figura. Em vez disso, podemos mover os eixos coordenados paralelamente a si mesmos, respectivamente, no plano coordenado de maneira que a origem O coincida com o centro O (h, k) da circunferência e os eixos coordenados tomam as posições paralelas designadas pelos novos eixos X e Y na Fig. 1. Seja P qualquer ponto sobre a circunferência. As coordenadas de P são (x, y) quando referidas aos eixos originais X e Y, mas evidentemente, são diferentes quando referidas aos novos eixos X e Y. Sejam designadas por (x, y ) as novas coordenadas de P. Então a equação da circunferência referida aos novos eixos X e Y é dada pela forma canônica simples x + y = r. (4) Vemos, então, que movendo os eixos coordenados paralelamente a si mesmos, respectivamente, transformamos as coordenadas (x, y) de um ponto qualquer sobre a circunferência nas coordenadas (x, y ) e, como consequência, transformamos a equação (40) na forma (4) mais simples. A operação de mover os eixos coordenados no plano coordenado para uma posição diferente de maneira que os

42 4 novos eixos sejam paralelos aos antigos eixos, semelhante e respectivamente orientados, é denominada translação dos eixos coordenados. Veremos mais adiante que algumas equações podem ser transformadas para formas mais simples por uma rotação dos eixos coordenados em torno de sua origem como ponto fixo. 3.1 Translação de eixos coordenados. A fim de simplificar equações por translação dos eixos coordenados necessitaremos do seguinte teorema. Teorema 1. Se os eixos coordenados são transladados para uma nova origem O (h, k) e se as coordenadas de qualquer ponto P antes e depois da translação são (x, y) e (x, y ), respectivamente, então as equações de transformação das antigas para as novas coordenadas são dadas por { x = x + h y = y + k Demonstração. Os antigos eixos X e Y e os novos eixos transladados X e Y estão representados na Fig. onde as coordenadas da nova origem O são (h, k) em relação aos antigos eixos. Desde o ponto P são traçadas perpendiculares a ambos os conjuntos de eixos e os novos eixos estão prolongados até interceptarem os antigos eixos, dando-nos assim todos os pontos apresentados na figura. Y F B Y E O (h,k) P C X (43) Usando a relação fundamental para segmentos retilíneos orientados, temos de imediato, por meio da figura x = OD = OA + AD = OA + O C = h + x. (44) Semelhantemente O A D X y = OF = OB + BF = OB + O E = k + y. (45) Figura Exemplos 1. Transformar a equação x 3 3x y + 3x + 4y 5 = 0 (46) por translação dos eixos coordenados à nova origem (1, ). Desenhar o lugar geométrico e mostrar ambos os conjuntos de eixos. Solução. Pelo Teorema 1 as equações de transformação são x = x + 1 e y = y + Se substituirmos estes valores de x e y na equação (46) obteremos

43 43 Y Y (x + 1) 3 3(x + 1) (y + ) + 3(x + 1) + 4(y + ) 5 = 0. O X Desenvolvendo e simplificando esta última equação obtemos a equação transformada procurada O 1 X x 3 y = 0. (47) O lugar geométrico, uma parábola semi-cúbica, está representado na Fig. 3. Figura 3 No exemplo 1 a nova origem foi especificada. Usualmente, entretanto, as coordenadas da nova origem não são dadas, mas devem ser determinadas. O processo em tal caso é ilustrado no exemplo seguinte.. Por uma translação dos eixos coordenados transformar a equação x 4y + 6x + 8y + 1 = 0 em outra equação desprovida de termos do primeiro grau. Desenhar o lugar geométrico e mostrar ambos os conjuntos de eixos. Solução. Neste caso particular podemos usar dois métodos diferentes, o primeiro sendo o mais geral. Primeiro método. Se substituirmos na equação acima os valores de x e y dados pelas equações de transformação no Teorema 1, obtemos a equação transformada (x + h) 4(y + k) + 6(x + h) + 8(y + k) + 1 = 0 que, após desenvolvimentos e redução de termos semelhantes assume a forma x 4y + (h + 6)x (8k 8)y + h 4k + 6h + 8k + 1 = 0. (48) Uma vez que a equação transformada deve ser desprovida de termos do primeiro grau, fazemos iguais a zero os coeficientes de x e y na equação (48). Assim temos: Y Y h + 6 = 0 e 8k 8 = 0 donde h = 3 e k = 1. O 3 1 O X X Logo, a nova origem é o ponto ( 3, 1). Se substituirmos estes valores de h e k em (48) obtemos a equação procurada x 4y 4 = 0. (49) Figura 4 O lugar geométrico, uma hipérbole, está representado na Fig. 4.

44 44 Segundo método. No caso de equações do segundo grau desprovidas do termo em xy é possível efetuar a transformação pelo método de completar os quadrados. Assim, os termos da equação x 4y + 6x + 8y + 1 = 0 podem ser reagrupados na forma Então completando os quadrados, obtemos (x + 6x) 4(y y) = 1. donde (x + 6x + 9) 4(y y + 1) = (x + 3) 4(y 1) = 4. (50) Se na equação (50) fazemos as substituições x + 3 = x e y 1 = y (51) obtemos de imediato a equação procurada (49). Obviamente, de (51) temos as equações de transformação x = x 3 e y = y + 1. No exemplo o tipo de simplificação desejada é especificado; em caso contrário, procuramos efetuar o maior número de simplificações possíveis, como ilustrado no exemplo seguinte. 3. Por uma translação dos eixos coordenados, simplificar a equação y 4x 6y + 17 = 0. (5) Solução. Como no primeiro método do exemplo substituímos na equação (5) os valores de x e y dados pelas equaçòes de transformação no Teorema 1. Temos então que pode ser escrita na forma (y + k) 4(x + h) 6(y + k) + 17 = 0 y 4x + (k 6)y + k 4h 6k + 17 = 0. (53) Nossa próxima etapa é determinar os valores de h e k que simplificarão a equação (53). Podemos eliminar o termo em y, mas não podemos eliminar o termo em x uma vez que seu coeficiente é 4. Neste caso, porém, podemos eliminar o termo constante. Em conseqüência escrevemos donde k 6 = 0 e k 4h 6k + 17 = 0 k = 3 e h =. Para estes valores de h e k a equação (53) se reduz à forma procurada y 4x = 0.

45 Exercícios 1. Em cada um dos exercícios, transformar a equação dada por translação dos eixos coordenados para a nova origem indicada. (a) x + y + x 6y + 6 = 0; ( 1, 3). (b) 3x + y + 1x 4y + 8 = 0; (, 1). (c) 4x y 8x 10y 5 = 0; (1, 5). (d) y 3 x + 3y 4x + 3y 3 = 0; (, 1). (e) xy 3x + 4y 13 = 0; ( 4, 3).. Em cada um dos exercícios, por uma translação dos eixos coordenados, transformar a equação dada em outra desprovida de termos do primeiro grau. Usar o primeiro método de exemplo ilustrativo. (a) x + y + 16x 4y + 3 = 0. (b) 3x + y + 18x 8y + 9 = 0. (c) 3x y 4x 4y = 0. (d) xy x + y 10 = 0. (e) 8x 3 + 4x 4y + 4x 1y 1 = Em cada um dos exercícios, por uma translaçào dos eixos coordenados, transformar a equação dada em outra desprovida de termos do primeiro grau. Usar o segundo método do exemplo ilustrativo. (a) 4x + 4y + 3x 4y + 45 = 0. (b) x + 5y 8x + 0y = 0. (c) x 3y + 6x + 6y + 3 = 0. (d) 1x + 18y 1x + 1y 1 = 0. (e) 1x 18y 1x 1y 5 = Em cada um dos exercícios, simplificar a equação dada por uma translação dos eixos coordenados. (a) x + 8x 3y + 10 = 0. (b) 16x + 16y + 8x 48y + 5 = 0. (c) 7x + 36y 48x + 36y 55 = 0. (d) y 6x 4x y 3 = 0. (e) 30xy + 4x 5y Respostas (1a) x + y = 4. (1b) 3x + y = 6. (1c) 4x y = 4. (1d) y 3 x = 0. (1e) x y = 1. (a) x + y = 4. (b) 3x + y = 6. (c) 3x y = 1. (d) x y = 8. (e) x 3 y = 0. (3a) x + y = 5. (3b) x + 5y = 10. (3c) x 3y = 3. (3d) x + 3y = 1. (3e) x 3y = 1 (4a) x 3y = 0. (4b) x + y =. (4c) x + y =. (4d) y 6x = 9. (4e) x y =.

46 46 3. Rotação dos eixos coordenados. A fim de simplificar equações por rotação dos eixos coordenados necessitaremos do seguinte teorema. Teorema. Se os eixos coordenados são girados de um ângulo θ em torno de sua origem O como ponto fixo e se as coordenadas de qualquer ponto P são (x, y) e (x, y ) antes e depois da rotação, respectivamente, então as equações de transformação das antigas para as novas coordenadas são dadas por { x = x cos θ y sen θ y = x sen θ + y cos θ. Demonstração. Na Fig. 5 estão representados os antigos eixos X e Y e os novos eixos X e Y oriundos da rotação. Desde o ponto P tracemos a ordenada AP sobre o eixo X, a ordenada A P sobre o eixo X e o segmento retilíneo OP. Seja ângulo P OA = φ e OP = r. Então, das definições das funções trigonométricas, temos: Y Y P r X A φ θ O A X De (54), temos: x = OA = r cos(θ + φ) (54) y = AP = r sen (θ + φ) (55) x = OA = r cos φ y = A P = r sen φ. x = r cos(θ + φ) = r cos θ cos φ r sen θ sen φ. (56) Figura 5 Se nesta última equação substituirmos os valores dados por (56) obtemos a primeira equação de transformação Semelhantemente de (55) x = x cos θ y sen θ. y = r sen (θ + φ) = r sen θ cos φ + r cos θ sen φ donde, de (56), temos a segunda equação de transformação y = x sen θ + y cos θ. Nota. Para nossas finalidades será necessário girar os eixos coordenados apenas de um ângulo com valor suficiente para colocar um ou outro dos eixos coincidente com, ou paralelo a, qualquer reta fixa dada no plano coordenado. Em conseqüência restringiremos, geralmente, os valores de ângulo de rotação θ ao intervalo dado por 0 θ < 90.

47 Exemplos 1. Transformar a equação x + 3xy + y = 4 (57) por rotação dos eixos coordenados de um ângulo de 30. Desenhar o lugar geométrico e mostrar ambos os conjuntos de eixos. Solução. Pelo teorema as equações de transformação são Y Y X 30 O X 3 x 1 y 3 y. x = x cos 30 y sen 30 = y = x sen 30 + y cos 30 = 1 x + Se estes valores de x e y são substituídos na equação (57) obtemos ( 3 x 1 y ) ( ( x 1 y ) 1 ( + 1 x + 3 y ) = 4. x + 3 y ) Desenvolvendo e simplificando esta última equação obtemos a equação transformada pedida 5x + y = 8. (58) Figura 6 O lugar geométrico, uma elipse, está representado na Fig. 6. No exemplo 1 o ângulo de rotação θ é dado. Geralmente, entretanto, o ângulo de rotação deve ser determinado a fim de alcançar alguma condição estabelecida. O principal emprego para a rotação de eixos é a remoção do termo em xy das equações de segundo grau.. Por uma rotação dos eixos coordenados transformar a equação 9x 4xy + 16y 40x 30y = 0 (59) em outra equação desprovida do termo x y. Desenhar o lugar geométrico e mostrar ambos os conjuntos de eixos. Solução. Se substituirmos na equação (59) os valores de x e y dados pelas equações de transformação no teorema, obtemos 9(x cos θ y sen θ) 4(x cos θ y sen θ)(x sen θ + y cos θ) + 16(x sen θ + y cos θ) 40(x cos θ y sen θ) 30(x sen θ + y cos θ) = 0 que, após desenvolvimento e redução de termos semelhantes, assume a forma (9 cos θ 4 cos θ sen θ + 16 sen θ)x + (14 sen θ cos θ + 4 sen θ 4 cos θ)x y +(9 sen θ + 4 sen θ cos θ + 16 cos θ)y (40 cos θ + 30 sen θ)x + (40 sen θ 30 cos θ)y = 0. (60)

48 48 Visto que a equação transformada deve ser desprovida de termos em x y, igualamos a zero o coeficiente de x y em (60) e obtemos 14 sen θ cos θ + 4 sen θ 4 cos θ = 0. Ora, sen θ = sen θ cos θ e cos θ = cos θ sen θ. Logo a última relação pode ser escrita donde 7 sen θ 4 cos θ = 0 tan θ = 4 7. De acordo com a nota ao teorema, o ângulo θ estará restrito ao primeiro quadrante, de maneira que θ se situará no primeiro ou no segundo quadrantes onde o cosseno e a tangente de um ângulo concordam em sinal. Da mesma forma, sen θ e cos θ serão negativos. Logo, a partir do valor de tan θ dado acima, temos: cos θ = 7 5. A fim de efetuar a simplificação da equação (60) necessitamos os valores de sen θ e cos θ, que podem ser obtidos pelas fórmulas do ângulo metade da Trigonometria. Assim, e Y Y O X θ X sen θ = 1 cos θ = cos θ = 1+cos θ = = = 4 5. Se estes valores de sen θ e cos θ são substituídos na equação (60), temos: ( ) ( ) x x y ( ) y (3 + 18)x + (4 4)y = 0 que se reduz à equação transformada procurada y x = 0. (61) O lugar geométrico, uma parábola, está mostrado na Figura 7 Fig. 7. Nota. Evidentemente é muito mais fácil desenhar o lugar geométrico da equação (61) relativa aos eixos X e Y do que desenhar o lugar geométrico da equação (59) relativa aos eixos X e Y. Mais ainda, as propriedades da parábola podem ser obtidas muito mais facilmente da equação (61) mais simples. 3. Por transformação de coordenadas simplificar a equação 3x xy + 3y x 10y + 9 = 0. (6) Desenhar o lugar geométrico e todos os conjuntos de eixos coordenados. Solução. Uma vez que em (6) os termos de segundo grau não formam um quadrado perfeito, podemos primeiramente transladar os eixos para uma nova origem (h, k). Logo, usando as equações de transformação do Teorema 1, obtemos da equação (6)

49 49 3(x + h) (x + h)(y + k) + 3(y + k) (x + h) 10(y + k) + 9 = 0 que, depois de desenvolvimento, simplificação e redução de termos semelhantes, assume a forma 3x xy + 3y + (6h k )x + ( h + 6k 10)y + (3h hk + 3k h 10k + 9) = 0. (63) A fim de eliminar os termos de primeiro grau em (63) fazemos seus coeficientes iguais a zero. Isto nos dá o sistema 6h k = 0 h + 6k 10 = 0 cuja solução é h = 1 e k =. Substituindo estes valores de h e k em (63) obtemos 3x x y + 3y = 0. (64) A seguir, por rotação de eixos, usando as equações do Teorema, obtemos da equação (64) 3(x cos θ y sen θ) (x cos θ y sen θ)(x sen θ + y cos θ) + 3(x sen θ + y cos θ) = 0 que se reduz a Y (3 cos θ sen θ cos θ + 3 sen θ)x + ( sen θ cos θ)x y +(3 sen θ + sen θ cos θ + 3 cos θ)y = 0. Y X Y 45 O X (65) A fim de eliminar o termo x y de (65) fazemos seu coeficiente igual a zero, obtendo assim sen θ cos θ = 0 donde θ = 45 de acordo com a nota do Teorema. Substituindo este valor de θ em (65) e simplificando, obtemos a equação procurada x + y 1 = 0. (66) O 1 Figura 9 X O lugar geométrico da equação (66), uma elipse, e todos os conjuntos de eixos coordenados estão representados na Fig Exercícios 1. Determinar as novas coordenadas do ponto (3, 4) quando os eixos coordenados são girados de um ângulo de 30.. Determinar as novas coordenadas dos pontos (1, 0) e (0, 1) quando os eixos coordenados são girados de um ângulo de 90.

50 50 3. Em cada um dos exercícios seguintes transformar a equação dada por rotação dos eixos coordenados do ângulo indicado. (a) x+5y 3 = 0; arctan.5. (b) x xy + y x = 0; 45. (c) 3y + 3xy 1 = 0; 60. (d) 5x + 3xy + y 4 = 0; arcsen (e) 11x + 4xy + 4y 0 = 0; arctan (f) x 4 + y 4 + 6x y 3 = 0; Por rotação dos eixos coordenados transformar a equação x y = 0 em outra equação desprovida do termo em x. 5. Por rotação dos eixos coordenados transformar a equação x + y = 0 em outra equação desprovida do termo y. 6. Em cada um dos exercícios seguintes, por uma rotação dos eixos coordenados, transformar a equação dada em outra equação desprovida do termo em x y. (a) 4x + 4xy + y + 5x = 1. (b) 9x + 3xy + 9y = 5. (c) 5x + 4xy + y =. (d) x 5xy + y = 0. (e) x xy + y 4 = 0. (f) 16x + 4xy + 9y + 5x = A equação de uma circunferência é x +y = r. Mostrar que a forma desta equação permanece sem modificação quando referida aos eixos coordenados que foram girados de qualquer ângulo θ. Diz-se então que esta equação é invariante quanto à rotação. 8. Em cada um dos exercícios abaixo, simplificar a equação dada por transformação de coordenadas. (a) x 10xy + y 10x + y + 13 = 0. (b) 5x 7xy + 73y 104x + 7y 48. (c) 16x + 4xy + 9y + 60x 80y = 0. (d) 3x + y 5 = 0. (e) x + xy + y x 10y + 11 = Determinar as novas coordenadas do ponto ( 1, 3) quando os eixos coordenados são, primeiramente, transladados à nova origem (4, 5) e, então, girados de um ângulo de Determinar as novas coordenadas do ponto (, ) quando os eixos coordenados são, primeiramente, girados de um ângulo de 45 e, então, transladados à nova origem ( 1, 1). 11. Por translação dos eixos coordenados à nova origem (3, 3), seguida pela rotação dos eixos de um ângulo de 30, as coordenadas de um certo ponto P são transformadas em (7, 6). Determinar as coordenadas de P em relação aos eixos originais. 1. Por translação dos eixos coordenados à nova origem (1, 1), seguida pela rotação dos eixos de um ângulo de 45, a equação de um certo lugar geométrico é transformada em x y =. Determinar a equação do lugar geométrico em relação aos eixos originais.