Agente Penitenciário
|
|
|
- Mafalda da Rocha Malheiro
- 7 Há anos
- Visualizações:
Transcrição
1 Agente Penitenciário Questões La Salle Raciocínio Lógico Prof. Edgar Abreu
2
3 Raciocínio Lógico QUESTÕES LA SALLE MUNICÍPIO DE CANOAS 2015 TÉCNICO EM TRÂNSITO E TRANSPORTES 1. A negação da proposição "Arthur comprou um carro, mas João não anda de bicicleta" é: a) Arthur não comprou um carro ou João anda de bicicleta. b) Se Arthur não comprou um carro, então João anda de bicicleta. c) Arthur comprou um carro ou João não anda de bicicleta. d) Arthur não comprou um carro e João anda de bicicleta. e) Arthur comprou um carro e João anda de bicicleta. 2. Sabendo que "todo o problema complexo é um problema interessante" e "alguns problemas interessantes são fáceis de resolver", então se pode afirmar logicamente que: a) Todo problema fácil de resolver é um problema complexo. b) Todo problema complexo é fácil de resolver. c) Existem problemas que são fáceis de resolver, mas não são complexos. d) Alguns problemas fáceis de resolver são interessantes. e) Alguns problemas complexos são fáceis de resolver. 3. Três amigos, João, Paula e Carlos, decidem medir e comparar as suas alturas. Após realizarem as medições, cada um dos três amigos faz uma afirmação, conforme abaixo: João: "- A minha altura é igual a 1,70m e sou o mais baixo entre nós três". Paula: "- A minha altura é igual a 1,75m e não sou a mais alta entre nós três". Carlos: "- A minha altura é igual a 1,60m e não sou o mais baixo entre nós três". Sabe-se que apenas um dos três amigos mentiu. Logo é possível afirmar sobre a altura e afirmações de João, Paula e Carlos que: a) João mentiu e Paula é a mais alta. b) Paula mentiu e Paula é a mais alta. c) Paula mentiu e João é o mais alto. d) Carlos mentiu e João é o mais alto. e) Carlos mentiu e Carlos é o mais alto. 3
4 CANOASTEC 2015 TÉCNICO ADMINISTRATIVO 4. A negação da proposição composta "Pedro mora em Canoas, mas Maria mora em Porto Alegre" é: a) Pedro não mora em Canoas, mas Maria mora em Porto Alegre. b) Pedro e Maria não moram em Canoas. c) Se Pedro mora em Canoas, então Maria não mora em Porto Alegre. d) Se Maria mora em Porto Alegre, então Pedro mora em Canoas. e) Pedro não mora em Canoas ou Maria mora em Porto Alegre. 5. Sabe-se que é verdade que todos os Alfas são Betas e alguns Betas são Sigmas. Então, é correto e lógico afirmar que: a) Alguns Alfas são Sigmas. b) Alguns Sigmas são Alfas. c) Alguns Betas são Altas. d) Todos os Sigmas são Setas. e) Todos os Setas são Alfas. 6. No esquema abaixo está representada uma rede de movimentos entre círculos numerados, onde só é possível o deslocamento de um círculo para o outro seguindo o sentido das flechas. Por exemplo, é possível sair do círculo 3 e ir até o círculo 7 em três movimentos: Note que cada movimento representa uma passagem de um círculo para outro círculo distinto. Neste contexto apresentado, é correto afirmar que o número mínimo de movimentos tal que é possível sair do círculo 1 e retornar para este mesmo círculo, passando pelo círculo 9, é igual a: a) 4. b) 6. c) 8. d) 10. e) Em uma pesquisa foram entrevistadas 200 pessoas para averiguar a aprovação ou reprovação dos Jornais A, B e C no mercado. Entre os entrevistados, 15 pessoas não aprovaram nenhum dos jornais e 35 aprovaram apenas o Jornal B. Sabe-se que o número de entrevistados que aprovaram o Jornal A é igual a 115 e o número de entrevistados que aprovaram o Jornal C é igual a
5 SUSEPE (Agente Administrativo) Raciocínio Lógico Prof. Edgar Abreu É correto afirmar que o número de pessoas entrevistada que aprovaram os Jornais A e C é igual a: a) 30 b) 35 c) 45 d) 65 e) Artur, Beto e Cassiano foram a uma pastelaria de Canoas e solicitaram para comer um pastel de carne, um pastel de frango e um pastel de queijo. Para beber, os três amigos pediram um suco de uva, um refrigerante e uma água. Sabendo que cada um dos três citados solicitou apenas um pastel e uma bebida, analise as seguintes afirmações verdadeiras: I Quem solicitou o pastel de frango não pediu suco de uva. II Quem pediu refrigerante comeu um pastel de carne. III Beto não pediu pastel de carne. É correto afirmar que, se Artur pediu o suco de uva, então: a) Beto pediu um refrigerante. b) Cassiano pediu o pastel de carne. c) Artur pediu o pastel de frango. d) Beto pediu o pastel de carne. e) Cassiano pediu uma água. CRO-RS 2014 FISCAL 9. A negação da frase "Nem todos brasileiros gostam de carnaval" é: a) Não existe brasileiro que não gosta de carnaval. b) Não existe brasileiro que gosta de carnaval. c) Todo brasileiro não gosta de carnaval. d) Existem brasileiros que não gostam de carnaval. e) Existem brasileiros que gostam de carnaval, mas também existem brasileiros que não gostam de carnaval. 10. Sabendo que "João mora em Porto Alegre ou Maria mora em Tramandaí" é uma proposição verdadeira, assinale a alternativa que apresenta uma proposição composta logicamente FALSA: a) João não mora em Porto Alegre e Maria mora em Tramandaí. b) João não mora em Porto Alegre e Maria não mora em Tramandaí. c) João mora em Porto Alegre e Maria não mora em Tramandaí. d) João mora em Porto Alegre e Maria mora em Tramandaí. e) João e Maria não moram em Porto Alegre. 5
6 CRO-RS 2015 AGENTE ADMINISTRATIVO 11. A proposição "se André foi à festa, então Bruna foi ao show" é logicamente equivalente a: a) André foi à festa e Bruna foi ao show. b) André não foi à festa ou Bruna foi ao show. c) André foi à festa ou Bruna não foi ao show. d) Se Bruna foi ao show, então André foi à festa. e) Se André não foi à festa, então Bruna não foi ao show. 12. A negação lógica da proposição "todas as pessoas gostam de ir ao cinema ou ir ao teatro" é: a) nenhuma pessoa gosta de ir ao cinema ou ir ao teatro. b) nenhuma pessoa gosta de ir ao cinema e ir ao teatro. c) existe pelo menos uma pessoa que não gosta de ir ao cinema nem gosta de ir ao teatro. d) existe pelo menos uma pessoa que não gosta de ir ao cinema ou não gosta de ir ao teatro. e) algumas pessoas gostam de ir ao cinema e ir ao teatro. 13. Durante uma entrevista com 200 crianças, verificou-se a utilização da maçã ou da banana na alimentação semanal dos entrevistados. Entre os entrevistados, 40 crianças confirmaram não utilizar nenhuma das duas frutas, 120 utilizam maçã e 140 utilizam banana na sua alimentação semanal. É correto afirmar que o número de crianças desta entrevista que utilizam ambas as frutas na alimentação semanal é igual a: a) 40. b) 60. c) 80. d) 100. e) 120. MUNICÍPIO DE CANOAS 2015 PROFISSIONAL DE EDUCAÇÃO FÍSICA 14. Sabendo que "todo gaúcho gosta de churrasco" e "algumas pessoas que gostam de churrasco também gostam de lasanha", decorre logicamente destas proposições que: a) todo gaúcho gosta de lasanha. b) todos que gostam de churrasco são gaúchos. c) existe quem goste de lasanha e não é gaúcho. d) existe quem goste de lasanha e de churrasco. e) não existe gaúcho que goste de lasanha. 15. Sobre a negação de proposições lógicas, analise as afirmações abaixo. I A negação da proposição simples "x é um número maior que 5" é "x é um número menor que 5". II A negação da proposição composta "Carlos sabe nadar e Maria sabe andar de bicicleta" é "Carlos não sabe nadar e Maria não sabe andar de bicicleta". 6
7 SUSEPE (Agente Administrativo) Raciocínio Lógico Prof. Edgar Abreu III A negação da proposição composta "todos os alunos falam inglês ou espanhol, mas não sabem matemática" é "existe pelo menos um aluno que não fala inglês nem espanhol ou sabe matemática". Das afirmações acima, qual(is) está(ão) correta(s)? a) Apenas a I. b) Apenas a II. c) Apenas a III. d) Apenas I e III. e) Apenas II e III. 16. Em uma urna estão 20 bolas de cores únicas: 3 verdes, 4 azuis, 5 vermelhas e 8 pretas. Um jogo consiste em sortear ao acaso 10 bolas, sem reposição, desta urna e somar os pontos obtidos, de acordo a cor de cada bola segundo o quadro de pontuações abaixo: Cor da bola Pontuação (pontos) Verde 20 Azul 15 Vermelha 10 Preta 5 Se uma pessoa alcança a pontuação de 145 pontos neste jogo, então é possível afirmar que o número máximo de bolas pretas que podem ter sido sorteadas é igual a: a) 1 b) 2 c) 3 d) 5 e) 8 MUNICÍPIO DE CANOAS 2015 GUARDA MUNICIPAL 17. A proposição lógica "todos Blanchet são Dark" é equivalente à proposição expressa na alternativa: a) Nenhum Blanchet é Dark. b) Todos Dark são Blanchet. c) Existe Blanchet que seja Dark. d) Existe pelo menos um Blanchet que não é Dark. e) Não existe Blanchet que não seja Dark. 18. Admita que a proposição "Carolina é guarda municipal" é verdadeira e a proposição "Pedro mora em Canoas" é falsa. Analise as proposições compostas abaixo. I Se Pedro mora em Canoas, então Carolina é guarda municipal. II Carolina é guarda municipal e Pedro mora em Canoas. 7
8 III Carolina não é guarda municipal ou Pedro não mora em Canoas. Das proposições compostas acima, qual(is) possui(em) valor lógico verdadeiro? a) Apenas a I. b) Apenas a II. c) Apenas a III d) Apenas I e III. e) Apenas II e III. 19. André, Bianca, Camila e Diogo trabalham em um prédio de 5 andares. Neste prédio os andares são nomeados como sendo 1º, 2º, 3º, 4º e 5º andar, do mais baixo para o mais alto respectivamente. Sobre os andares em que André, Bianca, Camila e Diogo trabalham, pode-se afirmar as seguintes proposições: I Todos trabalham em andares diferentes. II Entre os andares onde trabalham Diogo e Bianca existe apenas um andar, onde nenhum destes quatro trabalha. III Camila trabalha no andar imediatamente abaixo do andar em que trabalha Bianca. IV Diogo trabalha em um andar que fica mais alto do que o andar em que André trabalha. Sabendo que as informações apresentadas são verdadeiras, sobre os andares neste prédio onde André, Bianca, Camila e Diogo trabalham, é correto afirmar que a) André trabalha no 1º andar. b) Bianca trabalha no 2º andar. c) Camila trabalha no 3º andar. d) Bianca trabalha no 4º andar. e) Diogo trabalha no 4º andar. MUNICÍPIO DE NOVO HAMBURGO 2014 ASSISTENTE ADMINISTRATIVO 20. A negação da frase:"em Novo Hamburgo, todos os pares de sapatos estão em liquidação de inverno" é: a) Em Novo Hamburgo, todos os sapatos não estão em liquidação de inverno. b) Nenhum sapato está em liquidação de inverno em Novo Hamburgo. c) Existem alguns pares de sapatos, em Novo Hamburgo, que estão em liquidação de inverno. d) Pelo menos um par de sapatos não está em liquidação de inverno em Novo Hamburgo. e) Nenhum par de sapatos, em Novo Hamburgo, não está em liquidação de inverno. 21. Um grupo empresarial, afim de investir em cultura na sua empresa, entrevistou 150 funcionários para verificar a preferência entre cinema e teatro. Entre os entrevistados, 30 afirmaram não gostar de nenhuma das duas opções. Além disso, o número de entrevistados que afirmou gostar de teatro é a metade do número de entrevistados que afirmou gostar apenas de cinema. Pode-se então concluir que o número de pessoas que afirmou gostar de teatro é: a) 30 b)
9 SUSEPE (Agente Administrativo) Raciocínio Lógico Prof. Edgar Abreu c) 50 d) 60 e) Sejam as proposições: A: "p q" e B: " p q ", considere as afirmações abaixo: I A proposição B A é uma tautologia. II A proposição B A é uma contradição. III A proposição B não é ação da proposição A. Das afirmações acima, qual(is) está(ão) correta(s)? a) Apenas a I. b) Apenas a II. c) Apenas a III. d) Apenas li e III. e) Apenas I e II. Gabarito: 1. A 2. D 3. E 4. C 5. C 6. D 7. E 8. B 9. A 10. B 11. B 12. C 13. D 14. D 15. C 16. A 17. E 18. D 19. A 20. D 21. B 22. C 9
Questões Raciocínio Lógico e Matemática Financeira Prof. Edgar Abreu
 Questões Raciocínio Lógico e Matemática Financeira Prof. Edgar Abreu Raciocínio Lógico e Matemática Financeira IRGA 2016 TÉCNICO ORIZICOLA 21. Considere que a proposição composta "se Carlos é gaúcho e
Questões Raciocínio Lógico e Matemática Financeira Prof. Edgar Abreu Raciocínio Lógico e Matemática Financeira IRGA 2016 TÉCNICO ORIZICOLA 21. Considere que a proposição composta "se Carlos é gaúcho e
...
 1. (FHGV 2015) Segundo a teoria da lógica, a negação da proposição alguns motoristas não respeitam as leis de trânsito é: (A) Existem motoristas que não respeitam as leis de trânsito. (B) Todos os motoristas
1. (FHGV 2015) Segundo a teoria da lógica, a negação da proposição alguns motoristas não respeitam as leis de trânsito é: (A) Existem motoristas que não respeitam as leis de trânsito. (B) Todos os motoristas
A CASA DO SIMULADO DESAFIO QUESTÕES MINISSIMULADO 17/360
 1 DEMAIS SIMULADOS NO LINK ABAIXO CLIQUE AQUI REDE SOCIAL SIMULADO 17/360 RLM INSTRUÇÕES TEMPO: 30 MINUTOS MODALIDADE: CERTO OU ERRADO 30 QUESTÕES CURTA NOSSA PÁGINA MATERIAL LIVRE Este material é GRATUITO
1 DEMAIS SIMULADOS NO LINK ABAIXO CLIQUE AQUI REDE SOCIAL SIMULADO 17/360 RLM INSTRUÇÕES TEMPO: 30 MINUTOS MODALIDADE: CERTO OU ERRADO 30 QUESTÕES CURTA NOSSA PÁGINA MATERIAL LIVRE Este material é GRATUITO
PROVA TESTE ANPAD - RL EDIÇÃO FEVEREIRO O próximo número da seqüência 11, 33, 97, 2715 é A) B) C) D) E) 9230.
 PROVA TESTE ANPAD - RL EDIÇÃO FEVEREIRO 2008 1. O próximo número da seqüência 11, 33, 97, 2715 é A) 5430. B) 7116. C) 7251. D) 8131. E) 9230. 2. Em uma festa estão expostas 4 jarras com cores distintas
PROVA TESTE ANPAD - RL EDIÇÃO FEVEREIRO 2008 1. O próximo número da seqüência 11, 33, 97, 2715 é A) 5430. B) 7116. C) 7251. D) 8131. E) 9230. 2. Em uma festa estão expostas 4 jarras com cores distintas
Raciocínio Lógico Matemático
 Raciocínio Lógico Matemático Diagramas lógicos Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou existem B que são A. Negação: Trocar TODO
Raciocínio Lógico Matemático Diagramas lógicos Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou existem B que são A. Negação: Trocar TODO
Analista Área Administração
 Analista Área Administração Questões - Aula 6 Raciocínio Lógico-Matemático Prof. Edgar Abreu Raciocínio Lógico 1. (FCC 2016 METRO Superior Engenheiro) Considere as afirmações verdadeiras: I Se chove,
Analista Área Administração Questões - Aula 6 Raciocínio Lógico-Matemático Prof. Edgar Abreu Raciocínio Lógico 1. (FCC 2016 METRO Superior Engenheiro) Considere as afirmações verdadeiras: I Se chove,
Questões de Concursos Aula 04 CEF RACIOCÍNIO LÓGICO. Prof. Fabrício Biazotto
 Questões de Concursos Aula 04 CEF RACIOCÍNIO LÓGICO Prof. Fabrício Biazotto Raciocínio Lógico 1. Julgue os itens a seguir: A seguinte argumentação é inválida. Premissa 1: Todo funcionário que sabe lidar
Questões de Concursos Aula 04 CEF RACIOCÍNIO LÓGICO Prof. Fabrício Biazotto Raciocínio Lógico 1. Julgue os itens a seguir: A seguinte argumentação é inválida. Premissa 1: Todo funcionário que sabe lidar
IBGE- RACIOCÍNIO LÓGICO & MATEMÁTICA. Josimar Padilha
 IBGE- RACIOCÍNIO LÓGICO & MATEMÁTICA Josimar Padilha 01- Ano: 2016 Banca: FGV João olhou as dez bolas que havia em um saco e afirmou: Todas as bolas desse saco são pretas". Sabe-se que a afirmativa de
IBGE- RACIOCÍNIO LÓGICO & MATEMÁTICA Josimar Padilha 01- Ano: 2016 Banca: FGV João olhou as dez bolas que havia em um saco e afirmou: Todas as bolas desse saco são pretas". Sabe-se que a afirmativa de
Exame Analítico Questão 1: Se não fumo, bebo. Se estou cansado, fumo. Se fumo, não estou cansado. Se não estou cansado, não bebo.
 Exame Analítico 2009 Questão 1: Se não fumo, bebo. Se estou cansado, fumo. Se fumo, não estou cansado. Se não estou cansado, não bebo. Logo, a) Não fumo, estou cansado e não bebo. b) Fumo, estou cansado
Exame Analítico 2009 Questão 1: Se não fumo, bebo. Se estou cansado, fumo. Se fumo, não estou cansado. Se não estou cansado, não bebo. Logo, a) Não fumo, estou cansado e não bebo. b) Fumo, estou cansado
CANOAS ASSISTENTE LEGISLATIVO
 REVISÃO CANOAS - 2014 - ASSISTENTE LEGISLATIVO Sobre os números reais é correto afirmar que: a)o número 35 é primo. b)o número 91 é um quadrado perfeito. c)o número fracionário 29/4 é maior que 6 e menor
REVISÃO CANOAS - 2014 - ASSISTENTE LEGISLATIVO Sobre os números reais é correto afirmar que: a)o número 35 é primo. b)o número 91 é um quadrado perfeito. c)o número fracionário 29/4 é maior que 6 e menor
Aula 1 Teoria com resolução de questões FGV
 Aula 1 Teoria com resolução de questões FGV AULA 01 Olá futuro servidor do TRT 12, Meu nome é Fabio Paredes, sou professor de Raciocínio Lógico Matemático e terei o prazer de ajudá-los nesta árdua missão
Aula 1 Teoria com resolução de questões FGV AULA 01 Olá futuro servidor do TRT 12, Meu nome é Fabio Paredes, sou professor de Raciocínio Lógico Matemático e terei o prazer de ajudá-los nesta árdua missão
Noções de Lógica. Proposições Frases para as quais se pode atribuir o valor verdadeiro ou falso. Exs: 1) Quatro vezes três é igual a 12.
 Noções de Lógica Proposições Frases para as quais se pode atribuir o valor verdadeiro ou falso. Exs: 1) Quatro vezes três é igual a 12. 2) Florianópolis é capital de SC. 3) O Brasil faz fronteira com a
Noções de Lógica Proposições Frases para as quais se pode atribuir o valor verdadeiro ou falso. Exs: 1) Quatro vezes três é igual a 12. 2) Florianópolis é capital de SC. 3) O Brasil faz fronteira com a
TESTES LÓGICOS FECHADOS
 TESTES LÓGICOS FECHADOS 1) (UFPE) Considerando que em uma festa existem 15 pessoas, não podemos afirmar que a) pelo menos duas nasceram no mesmo mês do ano. b) pelo menos três nasceram no mesmo dia da
TESTES LÓGICOS FECHADOS 1) (UFPE) Considerando que em uma festa existem 15 pessoas, não podemos afirmar que a) pelo menos duas nasceram no mesmo mês do ano. b) pelo menos três nasceram no mesmo dia da
Matemática. Lógica Proposicional. Professor Dudan
 Matemática Lógica Proposicional Professor Dudan DIAGRAMAS LÓGICOS Diagramas lógicos ü Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou
Matemática Lógica Proposicional Professor Dudan DIAGRAMAS LÓGICOS Diagramas lógicos ü Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou
Questões de Concursos Aula 02 CEF RACIOCÍNIO LÓGICO. Prof. Fabrício Biazotto
 Questões de Concursos Aula 02 CEF RACIOCÍNIO LÓGICO Prof. Fabrício Biazotto Raciocínio Lógico 1. Considere as afirmações: I. A camisa é azul ou a gravata é branca. II. Ou o sapato é marrom ou a camisa
Questões de Concursos Aula 02 CEF RACIOCÍNIO LÓGICO Prof. Fabrício Biazotto Raciocínio Lógico 1. Considere as afirmações: I. A camisa é azul ou a gravata é branca. II. Ou o sapato é marrom ou a camisa
RLM A MELHOR DISCIPLINA DOS CONCURSOS. d) 16.
 Proposição d) 16. Órgão: PM-AL Prova: Bombeiro A respeito de proposições lógicas, julgue os itens a seguir. Considere que P e Q sejam as seguintes proposições: P: Se a humanidade não diminuir a produção
Proposição d) 16. Órgão: PM-AL Prova: Bombeiro A respeito de proposições lógicas, julgue os itens a seguir. Considere que P e Q sejam as seguintes proposições: P: Se a humanidade não diminuir a produção
MATEMÁTICA Questões comentadas Daniela Arboite
 MATEMÁTICA Questões comentadas Daniela Arboite TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por qualquer meio ou processo. A violação de direitos autorais é punível
MATEMÁTICA Questões comentadas Daniela Arboite TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por qualquer meio ou processo. A violação de direitos autorais é punível
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
RACIOCÍNIO LÓGICO
 RACIOCÍNIO LÓGICO 01- Analise as premissas e a conclusão do argumento a seguir e responda se é VÁLIDO ou NÃO. "Basta ser estudioso para vencer no concurso; ora, todos os alunos do curso Degrau Cultural
RACIOCÍNIO LÓGICO 01- Analise as premissas e a conclusão do argumento a seguir e responda se é VÁLIDO ou NÃO. "Basta ser estudioso para vencer no concurso; ora, todos os alunos do curso Degrau Cultural
MATEMÁTICA E RACIOCÍNIO LÓGICO
 MATEMÁTICA E RACIOCÍNIO LÓGICO Raciocínio lógico: resolução de problemas envolvendo frações, conjuntos, porcentagens, sequencias (com números, com figuras, de palavras). Raciocínio lógico-matemático: proposições,
MATEMÁTICA E RACIOCÍNIO LÓGICO Raciocínio lógico: resolução de problemas envolvendo frações, conjuntos, porcentagens, sequencias (com números, com figuras, de palavras). Raciocínio lógico-matemático: proposições,
Descrevendo um conjunto
 Conjuntos Veja os seguintes exemplos: Jogadores de um time Lista de compras Números Inteiros Alfabeto Se você está familiarizado com estes exemplos, é claro que você tem a ideia do que é um conjunto, podemos
Conjuntos Veja os seguintes exemplos: Jogadores de um time Lista de compras Números Inteiros Alfabeto Se você está familiarizado com estes exemplos, é claro que você tem a ideia do que é um conjunto, podemos
ESTRUTURAS LÓGICAS/LÓGICA DE ARGUMENTAÇÃO/TAUTOLOGIA/TABELA VERDADE
 ESTRUTURAS LÓGICAS/LÓGICA DE ARGUMENTAÇÃO/TAUTOLOGIA/TABELA VERDADE Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito,
ESTRUTURAS LÓGICAS/LÓGICA DE ARGUMENTAÇÃO/TAUTOLOGIA/TABELA VERDADE Ser síndico não é fácil. Além das cobranças de uns e da inadimplência de outros, ele está sujeito a passar por desonesto. A esse respeito,
Tema I Introdução à lógica bivalente e à teoria de conjuntos
 Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade 1 Proposições Páginas 13 a 9 1. a) 3 é uma designação. b) 3 = 6 é uma proposição. c) é o único número primo par é uma proposição. d)
Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade 1 Proposições Páginas 13 a 9 1. a) 3 é uma designação. b) 3 = 6 é uma proposição. c) é o único número primo par é uma proposição. d)
Prova TCE/SP Resolvida Raciocínio Lógico e Matemático Agente da Fiscalização. Prof. Thiago Cardoso. Olá, Alunos, tudo bem?
 Olá, Alunos, tudo bem? A prova do TCE/SP 2017 foi dentro do esperado, um pouco acima do nível de dificuldade padrão da Vunesp, porém, nada do outro mundo. Nesse arquivo, estamos corrigindo a prova de.
Olá, Alunos, tudo bem? A prova do TCE/SP 2017 foi dentro do esperado, um pouco acima do nível de dificuldade padrão da Vunesp, porém, nada do outro mundo. Nesse arquivo, estamos corrigindo a prova de.
matematicautodidata.com
 Exercite! Data: Nota: Nome: Tópico: Médio 01 - Conjuntos 1. Dê os elementos dos seguintes conjuntos: (a) A = {x x é a letra da palavra autodidata } (b) B = {x x é o estado do sudeste do Brasil } (c) C
Exercite! Data: Nota: Nome: Tópico: Médio 01 - Conjuntos 1. Dê os elementos dos seguintes conjuntos: (a) A = {x x é a letra da palavra autodidata } (b) B = {x x é o estado do sudeste do Brasil } (c) C
Simulado 01 de Lógica ANPAD para junho de 2017
 1 Simulado 01 de Lógica ANPAD para junho de 2017 Nome : Instruções 1- Esta prova contém 17 questões de lógica sentencial 2- Esta prova deverá ser feita em um tempo máximo de 43 minutos sob pena de perder
1 Simulado 01 de Lógica ANPAD para junho de 2017 Nome : Instruções 1- Esta prova contém 17 questões de lógica sentencial 2- Esta prova deverá ser feita em um tempo máximo de 43 minutos sob pena de perder
Matemática e Raciocínio Lógico Homeopatia 3 Prof. Dudan
 Matemática e Raciocínio Lógico Homeopatia 3 Prof. Dudan Matemática e Raciocínio Aula Lógico XX Tautologia e Contradição 1. (2012 FUNDATEC PROCERGS Técnico de Nível Médio Técnico em Segurança do Trabalho)
Matemática e Raciocínio Lógico Homeopatia 3 Prof. Dudan Matemática e Raciocínio Aula Lógico XX Tautologia e Contradição 1. (2012 FUNDATEC PROCERGS Técnico de Nível Médio Técnico em Segurança do Trabalho)
OS 70 TONS DE RACIOCÍNIO LÓGICO
 OS 70 TONS DE RACIOCÍNIO LÓGICO DIAGRAMAS LÓGICOS Diagramas lógicos Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou existem B que são
OS 70 TONS DE RACIOCÍNIO LÓGICO DIAGRAMAS LÓGICOS Diagramas lógicos Todo Sinônimos: qualquer um ou outra similar. Representação: Conclusão: Todo A é B. Alguns elementos de B são A ou existem B que são
Raciocínio Lógico. Argumento com Quantificadores Válidos (Silogismo) Professor Edgar Abreu.
 Raciocínio Lógico Argumento com Quantificadores Válidos (Silogismo) Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico ARGUMENTO COM QUANTIFICADORES VÁLIDO SILOGISMO QUESTÃO COMENTADA
Raciocínio Lógico Argumento com Quantificadores Válidos (Silogismo) Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico ARGUMENTO COM QUANTIFICADORES VÁLIDO SILOGISMO QUESTÃO COMENTADA
Combinatória e Probabilidade
 Combinatória e Probabilidade 1. (Enem) Considere o seguinte jogo de apostas: Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados
Combinatória e Probabilidade 1. (Enem) Considere o seguinte jogo de apostas: Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados
CEM. RLM Equivalência Lógica
 CEM CADERNO DE EXERCÍCIOS MASTER Período 2006 2016 1) IBFC - Agente Penitenciário (SEDS MG)-2014 De acordo com raciocínio lógico matemático a frase O Brasil não foi campeão ou o presidente foi ao comício
CEM CADERNO DE EXERCÍCIOS MASTER Período 2006 2016 1) IBFC - Agente Penitenciário (SEDS MG)-2014 De acordo com raciocínio lógico matemático a frase O Brasil não foi campeão ou o presidente foi ao comício
APRENDENDO RACIOCÍNIO LÓGICO
 APRENDENDO RACIOCÍNIO LÓGICO QUESTÕES DE HIPÓTESES, VERDADE e MENTIRAS PREFEITURA DE PORTO ALEGRE 2016 A palavra que completa o grupo formado por maçã, mamão, manga, maracujá, melancia é: a) Jabuticaba.
APRENDENDO RACIOCÍNIO LÓGICO QUESTÕES DE HIPÓTESES, VERDADE e MENTIRAS PREFEITURA DE PORTO ALEGRE 2016 A palavra que completa o grupo formado por maçã, mamão, manga, maracujá, melancia é: a) Jabuticaba.
DOUGLAS LÉO RACIOCÍNIO LÓGICO MATEMÁTICO
 DOUGLAS LÉO RACIOCÍNIO LÓGICO MATEMÁTICO 1 - (FEPESE - CAU-SC ASSISTENTE ADMINISTRATIVO -2013 ) Um pintor dispõe de tinta em 7 cores diferentes para pintar 3 paredes. Sabendo-se que cada parede deve ser
DOUGLAS LÉO RACIOCÍNIO LÓGICO MATEMÁTICO 1 - (FEPESE - CAU-SC ASSISTENTE ADMINISTRATIVO -2013 ) Um pintor dispõe de tinta em 7 cores diferentes para pintar 3 paredes. Sabendo-se que cada parede deve ser
ACLÉSIO MOREIRA RACIOCÍNIO LÓGICO
 ACLÉSIO MOREIRA RACIOCÍNIO LÓGICO LÓGICA PROPOSICIONAL 01. (IBFC 2016) A conjunção entre duas proposições compostas é verdadeira se: a) os valores lógicos de ambas as proposições forem falsos b) se o valor
ACLÉSIO MOREIRA RACIOCÍNIO LÓGICO LÓGICA PROPOSICIONAL 01. (IBFC 2016) A conjunção entre duas proposições compostas é verdadeira se: a) os valores lógicos de ambas as proposições forem falsos b) se o valor
Expoente 10 Dossiê do Professor 2
 Expoente 0 Dossiê do Professor Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade Proposições Páginas a 9. a) é uma designação. b) = 6 é uma proposição. c) é o único número primo par
Expoente 0 Dossiê do Professor Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade Proposições Páginas a 9. a) é uma designação. b) = 6 é uma proposição. c) é o único número primo par
Raciocínio Lógico. 06- A quantidade de anagramas que podem ser formados com as letras da palavra MINISTÉRIO é inferior a
 Raciocínio Lógico 01- Se Carlos é surfista, então Julia não é tenista. Se Julia não é tenista, então Michelle anda de skate. Se Michelle anda de skate, então Lucas não é patinador. Ora, Lucas é patinador.
Raciocínio Lógico 01- Se Carlos é surfista, então Julia não é tenista. Se Julia não é tenista, então Michelle anda de skate. Se Michelle anda de skate, então Lucas não é patinador. Ora, Lucas é patinador.
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
ANÁLISE COMBINATÓRIA
 ANÁLISE COMBINATÓRIA DEFINIÇÃO Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e representamos por n!. Exemplo: 7! = 7.6.5.4.3.2.1 12! = 12.11.10.9.8.7.6.5.4.3.2.1
ANÁLISE COMBINATÓRIA DEFINIÇÃO Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e representamos por n!. Exemplo: 7! = 7.6.5.4.3.2.1 12! = 12.11.10.9.8.7.6.5.4.3.2.1
A CASA DO SIMULADO DESAFIO QUESTÕES MINISSIMULADO 69/360
 1 DEMAIS SIMULADOS NO LINK ABAIXO CLIQUE AQUI REDE SOCIAL SIMULADO 69/360 RLM INSTRUÇÕES TEMPO: 30 MINUTOS MODALIDADE: CERTO OU ERRADO 30 QUESTÕES CURTA NOSSA PÁGINA MATERIAL LIVRE Este material é GRATUITO
1 DEMAIS SIMULADOS NO LINK ABAIXO CLIQUE AQUI REDE SOCIAL SIMULADO 69/360 RLM INSTRUÇÕES TEMPO: 30 MINUTOS MODALIDADE: CERTO OU ERRADO 30 QUESTÕES CURTA NOSSA PÁGINA MATERIAL LIVRE Este material é GRATUITO
c) 35. d) 37. e) 45.
 LISTA DE EXERCÍCIOS CONJUNTOS PROF: Paulo Vinícius Questão 1) Em uma determinada turma, há alunos que praticam futebol (conjunto A), que praticam basquetebol (conjunto B) e que praticam futebol e basquetebol
LISTA DE EXERCÍCIOS CONJUNTOS PROF: Paulo Vinícius Questão 1) Em uma determinada turma, há alunos que praticam futebol (conjunto A), que praticam basquetebol (conjunto B) e que praticam futebol e basquetebol
CPV O Cursinho que Mais Aprova na GV
 CPV O Cursinho que Mais Aprova na GV FGV ADM 05/junho/06 MATEMÁTICA APLICADA 0. Para a construção de uma janela na sala de um teatro, existe a dúvida se ela deve ter a forma de um retângulo, de um círculo
CPV O Cursinho que Mais Aprova na GV FGV ADM 05/junho/06 MATEMÁTICA APLICADA 0. Para a construção de uma janela na sala de um teatro, existe a dúvida se ela deve ter a forma de um retângulo, de um círculo
Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu
 Auditor Fiscal Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu Raciocínio Lógico SILOGISMO Silogismo Categórico é uma forma de raciocínio lógico na qual há duas premissas e uma conclusão distinta
Auditor Fiscal Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu Raciocínio Lógico SILOGISMO Silogismo Categórico é uma forma de raciocínio lógico na qual há duas premissas e uma conclusão distinta
Observando o primeiro dado, podemos concluir que abaixo da letra F está a letra B. Dessa forma a letra que está faltando no último dado é a letra B.
 1 Neste capítulo o objetivo é estabelecer relações entre as proposições dos argumentos para chegarmos nas conclusões corretas. Para isso, reescrevemos os argumentos usando tabelas que sintetizem suas informações.
1 Neste capítulo o objetivo é estabelecer relações entre as proposições dos argumentos para chegarmos nas conclusões corretas. Para isso, reescrevemos os argumentos usando tabelas que sintetizem suas informações.
Matemática Discreta e Raciocínio Lógico
 Matemática Discreta e Raciocínio Lógico 51. (ABC) A negação de o gato mia e o rato chia é: (A) o gato não mia e o rato não chia; (B) o gato mia ou o rato chia; (C) o gato não mia ou o rato não chia; (D)
Matemática Discreta e Raciocínio Lógico 51. (ABC) A negação de o gato mia e o rato chia é: (A) o gato não mia e o rato não chia; (B) o gato mia ou o rato chia; (C) o gato não mia ou o rato não chia; (D)
Matemática Computacional
 Matemática Computacional SLIDE 1I Professor Júlio Cesar da Silva [email protected] site: http://eloquium.com.br/ twitter: @profjuliocsilva facebook: https://www.facebook.com/paginaeloquium Google+:
Matemática Computacional SLIDE 1I Professor Júlio Cesar da Silva [email protected] site: http://eloquium.com.br/ twitter: @profjuliocsilva facebook: https://www.facebook.com/paginaeloquium Google+:
OPERAÇÕES COM CONJUNTOS
 OPERAÇÕES COM CONJUNTOS Vamos estudar agora problemas envolvendo as operações entre conjuntos que serão solucionados utilizando-se os diagramas de Venn. 01. Uma escola oferece reforço escolar em todas
OPERAÇÕES COM CONJUNTOS Vamos estudar agora problemas envolvendo as operações entre conjuntos que serão solucionados utilizando-se os diagramas de Venn. 01. Uma escola oferece reforço escolar em todas
OBS.1: As palavras Se e então podem estar ocultas na. Proposição
 RACIOCÍNIO LÓGICO PRO. IGOR BRASIL 1) Proposição: Observação!!! Não são proposições 1. 2. 3. 4. 5. 6. 7. 2) Conectivos São utilizados em proposições.» O conectivo e é conhecido por, representado pelo símbolo
RACIOCÍNIO LÓGICO PRO. IGOR BRASIL 1) Proposição: Observação!!! Não são proposições 1. 2. 3. 4. 5. 6. 7. 2) Conectivos São utilizados em proposições.» O conectivo e é conhecido por, representado pelo símbolo
Não sou o melhor, sei disso, mas faço o melhor que posso!! RANILDO LOPES
 Lógica Matemática e Computacional Não sou o melhor, sei disso, mas faço o melhor que posso!! RANILDO LOPES 2. Conceitos Preliminares 2.1. Sentença, Verdade e Proposição Cálculo Proposicional Como primeira
Lógica Matemática e Computacional Não sou o melhor, sei disso, mas faço o melhor que posso!! RANILDO LOPES 2. Conceitos Preliminares 2.1. Sentença, Verdade e Proposição Cálculo Proposicional Como primeira
AULA 08 Probabilidade
 Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória. 1º Teste de avaliação.
 Escola Secundária com º ciclo D. Dinis 1º Ano de Matemática A Tema I Probabilidades e Combinatória 1º Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas
Escola Secundária com º ciclo D. Dinis 1º Ano de Matemática A Tema I Probabilidades e Combinatória 1º Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
Matemática Questões - Revisão Prof. Dudan
 Soldado Matemática Questões - Revisão Prof. Dudan Matemática 1. Uma empresa com 200 funcionários oferece cursos de capacitação em inglês e em informática a seus funcionários. Sabe-se que 50 funcionários
Soldado Matemática Questões - Revisão Prof. Dudan Matemática 1. Uma empresa com 200 funcionários oferece cursos de capacitação em inglês e em informática a seus funcionários. Sabe-se que 50 funcionários
a) 5 cadernos - b) 2 cadernos e 3 hidrocores - c) 1 mochila, 1 lancheira e 1 cantil - d) 2 caderno e 2 lápis de cor -
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 2º ANO - ENSINO FUNDAMENTAL ========================================================================== 01- Observe os produtos e seus preços.
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - MATEMÁTICA - 2º ANO - ENSINO FUNDAMENTAL ========================================================================== 01- Observe os produtos e seus preços.
Raciocínio. Lógico. Matemático
 Raciocínio Lógico Matemático # DICA 1 # LEMBRAR-SE DOS CONJUNTOS NUMÉRICOS ELEMENTARES Números Naturais N = {0, 1, 2, 3, 4,... } Números Inteiros Z = {..., -4, -3, -2, -1, 0, 1, 2, 3,... } Números Racionais
Raciocínio Lógico Matemático # DICA 1 # LEMBRAR-SE DOS CONJUNTOS NUMÉRICOS ELEMENTARES Números Naturais N = {0, 1, 2, 3, 4,... } Números Inteiros Z = {..., -4, -3, -2, -1, 0, 1, 2, 3,... } Números Racionais
Dante Então, nas férias,
 1. Nas férias, Carmem não foi ao cinema. Sabe-se que sempre que q Denis viaja, Denis fica feliz. Sabe-se, também, que nas férias, ou Dante vai à praia ou vai à piscina. Sempre que Dante vai à piscina,
1. Nas férias, Carmem não foi ao cinema. Sabe-se que sempre que q Denis viaja, Denis fica feliz. Sabe-se, também, que nas férias, ou Dante vai à praia ou vai à piscina. Sempre que Dante vai à piscina,
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a
 Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Aprendendo. Raciocínio. Lógico
 Aprendendo Raciocínio Lógico Raciocínio Lógico Equivalência de Proposições Compostas Duas proposições são consideradas EQUIVALENTES entre si, quando elas transmitem a mesma ideia. De forma prática, dizemos
Aprendendo Raciocínio Lógico Raciocínio Lógico Equivalência de Proposições Compostas Duas proposições são consideradas EQUIVALENTES entre si, quando elas transmitem a mesma ideia. De forma prática, dizemos
AULA 00. Raciocínio Lógico. Aula Demonstrativa Professor Henrique Tiezzi.
 AULA 00 Raciocínio Lógico Aula Demonstrativa Professor Henrique Tiezzi www.pontodosconcursos.com.br www.pontodosconcursos.com.br Professor Henrique Tiezzi 1 Aula 00 Aula Demonstrativa Aula Conteúdo Programático
AULA 00 Raciocínio Lógico Aula Demonstrativa Professor Henrique Tiezzi www.pontodosconcursos.com.br www.pontodosconcursos.com.br Professor Henrique Tiezzi 1 Aula 00 Aula Demonstrativa Aula Conteúdo Programático
24/09/2017 LÓGICA MATEMÁTICA
 LÓGICA MATEMÁTICA Um aprendizado Definitivo! 0. Considere todas as placas de veículos desde NCD-4000 até NCD-9999. O número de placas que possuem os dígitos todos diferentes é: a) 2.520; b) 3.024; c) 3.528;
LÓGICA MATEMÁTICA Um aprendizado Definitivo! 0. Considere todas as placas de veículos desde NCD-4000 até NCD-9999. O número de placas que possuem os dígitos todos diferentes é: a) 2.520; b) 3.024; c) 3.528;
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa.
 A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
Atividade extra. Exercício 1. Exercício 2. Exercício 3. Matemática e suas Tecnologias Matemática
 Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
2) Transforme as potenciações em multiplicações e as resolva.
 TRABALHO DE RECUPERAÇÃO EM MATEMÁTICA º TRIMESTRE Nome: nº: Ano: 7º E.F.II Data: / / 016 Professor: Carlos 1) Que barra representa: a) Metade da metade da barra marrom. b) Metade de um quarto da barra
TRABALHO DE RECUPERAÇÃO EM MATEMÁTICA º TRIMESTRE Nome: nº: Ano: 7º E.F.II Data: / / 016 Professor: Carlos 1) Que barra representa: a) Metade da metade da barra marrom. b) Metade de um quarto da barra
Ano lectivo Ficha de trabalho nº 3
 Disciplina Ano M.A.C.S. 11º Ano lectivo Ficha de trabalho nº 3 2014/2015 Probabilidades 1. Um estojo tem 5 marcadores, 5 canetas e 3 lapiseiras. Retiram-se dois objectos do estojo, ao acaso, sucessivamente
Disciplina Ano M.A.C.S. 11º Ano lectivo Ficha de trabalho nº 3 2014/2015 Probabilidades 1. Um estojo tem 5 marcadores, 5 canetas e 3 lapiseiras. Retiram-se dois objectos do estojo, ao acaso, sucessivamente
FCC TRF/3ª 2016) RESOLUÇÃO:
 Para ajudar aos candidatos a estudar para o primeiro concurso da Artesp, FOLHA DIRIGIDA oferece mais um teste de matemática. As questões foram elaboradas pelo professor de Matemática e Raciocínio Lógico,
Para ajudar aos candidatos a estudar para o primeiro concurso da Artesp, FOLHA DIRIGIDA oferece mais um teste de matemática. As questões foram elaboradas pelo professor de Matemática e Raciocínio Lógico,
Estatística Aplicada. Prof. Carlos Alberto Stechhahn EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE. Administração. p(a) = n(a) / n(u)
 Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
30 s. Matemática Volume Questão O valor de 2, é: a) 1,2 b) 1, c) 1,5 d) Um número entre 0,5 e 1
 30 s Matemática Volume 5 1. Questão Determine a soma e o produto das raízes 7x + x + 5 = 0.. Questão O valor de,777... é: a) 1, b) 1,666... c) 1,5 d) Um número entre 0,5 e 1 3. Questão Para que a média
30 s Matemática Volume 5 1. Questão Determine a soma e o produto das raízes 7x + x + 5 = 0.. Questão O valor de,777... é: a) 1, b) 1,666... c) 1,5 d) Um número entre 0,5 e 1 3. Questão Para que a média
RLM Material de Apoio Professor Jhoni Zini
 1 - José, Luís e Mário são funcionários públicos nas funções de auditor, analista e técnico, não necessariamente nessa ordem. Sabe-se que José não é analista, que o técnico será o primeiro dos três a se
1 - José, Luís e Mário são funcionários públicos nas funções de auditor, analista e técnico, não necessariamente nessa ordem. Sabe-se que José não é analista, que o técnico será o primeiro dos três a se
Matemática 5 o ano Unidade 8
 Matemática 5 o ano Unidade 8 Nome: Unidade 8 Data: 1. Observe a imagem a seguir. Rua Paz Rua Sabedoria Rua Amizade Rua Paciência Seamartini/Shutter Identifique quais ruas são: a) paralelas. b) concorrentes.
Matemática 5 o ano Unidade 8 Nome: Unidade 8 Data: 1. Observe a imagem a seguir. Rua Paz Rua Sabedoria Rua Amizade Rua Paciência Seamartini/Shutter Identifique quais ruas são: a) paralelas. b) concorrentes.
MATEMÁTICA. Alfa. Durão
 MATEMÁTICA SSA 2ª Fase 13. O Banco Dinheiro Fácil movimentou a quantia de 240 bilhões de reais no ano de 2013. Suponhamos que um conjunto de dez cédulas de R$ 50,00 tem massa equivalente a um grama. Qual
MATEMÁTICA SSA 2ª Fase 13. O Banco Dinheiro Fácil movimentou a quantia de 240 bilhões de reais no ano de 2013. Suponhamos que um conjunto de dez cédulas de R$ 50,00 tem massa equivalente a um grama. Qual
Matemática & Raciocínio Lógico
 Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur QUESTÕES DE RACIOCÍNIO LÓGICO PARTE I 1. A negação da afirmação: Vai fazer frio
Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur QUESTÕES DE RACIOCÍNIO LÓGICO PARTE I 1. A negação da afirmação: Vai fazer frio
CASA TRIBUNAIS RACIOCÍNIO LÓGICO
 CASA TRIBUNAIS RACIOCÍNIO LÓGICO Quantificadores Prof. Bruno Villar www.acasadoconcurseiro.com.br Raciocínio Lógico QUANTIFICADORES Definição: É um termo utilizado para quantificar uma expressão. Os quantificadores
CASA TRIBUNAIS RACIOCÍNIO LÓGICO Quantificadores Prof. Bruno Villar www.acasadoconcurseiro.com.br Raciocínio Lógico QUANTIFICADORES Definição: É um termo utilizado para quantificar uma expressão. Os quantificadores
Resolução da Prova de Raciocínio Lógico da Agente Penitenciário/MA, aplicada em 24/04/2016.
 de Raciocínio Lógico da gente Penitenciário/M, aplicada em 24/04/206. - sentença Se Maria é médica, então Silvio é engenheiro. é logicamente equivalente a () se Maria é médica, então Silvio é engenheiro.
de Raciocínio Lógico da gente Penitenciário/M, aplicada em 24/04/206. - sentença Se Maria é médica, então Silvio é engenheiro. é logicamente equivalente a () se Maria é médica, então Silvio é engenheiro.
XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução da prova 1 a fase Nível de agosto de 2017
 UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução da prova 1 a fase
UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução da prova 1 a fase
4 3 10! Resposta pedida: 3! x 4! = 144 Resposta: C
 ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
24 de outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
3. A probabilidade do evento de números pares. 4. O evento formado por número menor que três. 5. A probabilidade do evento número menor que três.
 1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
RACIOCÍNIO LÓGICO. rascunho. NÍVEL: Médio DATA: 08/05/2016 QUESTÕES: 07
 Considere a seguinte informação para responder às quatro próximas questões: a Prefeitura do Município de São Paulo (PMSP) é subdividida em 32 subprefeituras e cada uma dessas subprefeituras administra
Considere a seguinte informação para responder às quatro próximas questões: a Prefeitura do Município de São Paulo (PMSP) é subdividida em 32 subprefeituras e cada uma dessas subprefeituras administra
Conteúdos: Análise Combinatória, Conjuntos, Fatorial e Binomial.
 Lista de exercícios Prof: Maurício Baffi 06/2017 Ensino Médio - 3º ano Conteúdos: Análise Combinatória, Conjuntos, Fatorial e Binomial. 1. (G1 - ifsul 2017) Em uma consulta à comunidade acadêmica sobre
Lista de exercícios Prof: Maurício Baffi 06/2017 Ensino Médio - 3º ano Conteúdos: Análise Combinatória, Conjuntos, Fatorial e Binomial. 1. (G1 - ifsul 2017) Em uma consulta à comunidade acadêmica sobre
2. Construa as tabelas verdade das seguintes proposições, indicando quaisquer tautologias ou contradições:
 FACULDADE DE TECNOLOGIA SENAC PELOTAS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas Matemática Aplicada Edécio Fernando Iepsen 1. Traduza para a linguagem natural as fórmulas abaixo,
FACULDADE DE TECNOLOGIA SENAC PELOTAS Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas Matemática Aplicada Edécio Fernando Iepsen 1. Traduza para a linguagem natural as fórmulas abaixo,
RACIOCÍNIO LÓGICO. Parte 3. Diagramas de Venn(Conjuntos). Prof. Renato Oliveira
 RACIOCÍNIO LÓGICO. Parte 3. Prof. Renato Oliveira 1) Em uma pesquisa realizada sobre a preferência de cores de automóveis, os entrevistados afirmaram que: I- 90 entrevistados preferem a cor vermelha; II-
RACIOCÍNIO LÓGICO. Parte 3. Prof. Renato Oliveira 1) Em uma pesquisa realizada sobre a preferência de cores de automóveis, os entrevistados afirmaram que: I- 90 entrevistados preferem a cor vermelha; II-
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
EXERCÍCIOS REVISIONAIS SOBRE BINÔMIO DE NEWTON SISTEMAS LINEARES PROBABILIDADE 2 ANO
 QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA. ( Segundo Acadêmico )
 TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundo Acadêmico ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti Análise Combinatória, Probabilidade, Logica, Matemática Financeira A resolução detalhada das
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundo Acadêmico ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti Análise Combinatória, Probabilidade, Logica, Matemática Financeira A resolução detalhada das
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
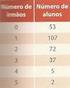 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Lógica/oitavos anos do E. Fundamental II/ Listagem de estudos referência para prova- PUPO
 Lógica/oitavos anos do E. Fundamental II/ Listagem de estudos referência para prova- PUPO 1- Analise as proposições abaixo e a seguir atribua a cada uma delas valor lógico: a) Se A é um conjunto de 3 elementos
Lógica/oitavos anos do E. Fundamental II/ Listagem de estudos referência para prova- PUPO 1- Analise as proposições abaixo e a seguir atribua a cada uma delas valor lógico: a) Se A é um conjunto de 3 elementos
RACIOCÍNIO LÓGICO TEORIA 86 EXERCÍCIOS POR ASSUNTOS RESOLVIDOS E QUESTÕES DE PROVAS DE CONCURSOS. Edição junho 2017
 RACIOCÍNIO LÓGICO TEORIA 86 EXERCÍCIOS POR ASSUNTOS RESOLVIDOS E QUESTÕES DE PROVAS DE CONCURSOS Edição junho 2017 TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por
RACIOCÍNIO LÓGICO TEORIA 86 EXERCÍCIOS POR ASSUNTOS RESOLVIDOS E QUESTÕES DE PROVAS DE CONCURSOS Edição junho 2017 TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por
n > n > n > 4 LETRA E
 01) Antônio foi ao banco conversar com seu gerente sobre investimentos. Ele tem um capital inicial de R$ 2.500,00 e deseja saber depois de quanto tempo de investimento esse capital, aplicado a juros compostos,
01) Antônio foi ao banco conversar com seu gerente sobre investimentos. Ele tem um capital inicial de R$ 2.500,00 e deseja saber depois de quanto tempo de investimento esse capital, aplicado a juros compostos,
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA. ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_
 TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_ Análise Combinátoria, Probabilidade, Matrizes e Determinantes A resolução detalhada das questões
TRABALHO DE RECUPERAÇÃO FINAL DE MATEMÁTICA ( Segundos Técnicos ) NOME: TURMA: Nº PROFESSOR: Daniel Verotti_ Análise Combinátoria, Probabilidade, Matrizes e Determinantes A resolução detalhada das questões
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO ESCOLA DE SARGENTOS DAS ARMAS (ESCOLA SARGENTO MAX WOLF FILHO)
 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO ESCOLA DE SARGENTOS DAS ARMAS (ESCOLA SARGENTO MAX WOLF FILHO) EXAME INTELECTUAL AOS CURSOS DE FORMAÇÃO E GRADUAÇÃO DE SARGENTOS 2020-21 SOLUÇÃO DAS QUESTÕES DE
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO ESCOLA DE SARGENTOS DAS ARMAS (ESCOLA SARGENTO MAX WOLF FILHO) EXAME INTELECTUAL AOS CURSOS DE FORMAÇÃO E GRADUAÇÃO DE SARGENTOS 2020-21 SOLUÇÃO DAS QUESTÕES DE
Matemática CONJUNTOS NUMÉRICOS. Professor Dudan
 Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Matemática CONJUNTOS NUMÉRICOS Professor Dudan Números Naturais (IN) Definição: N = {0, 1, 2, 3, 4,... } Subconjuntos N * = { 1, 2, 3, 4,... } naturais não nulos. Números Inteiros (Z) Definição Z = {...,
Lógica Matemática. Luan Arjuna
 Lógica Matemática Luan Arjuna 1 Introdução Neste material estudaremos lógica matemática, um assunto de extrema importância para quem deseja estudar matemática olímpica. Para esse estudo, não serão necessários
Lógica Matemática Luan Arjuna 1 Introdução Neste material estudaremos lógica matemática, um assunto de extrema importância para quem deseja estudar matemática olímpica. Para esse estudo, não serão necessários
