A atmosfera e a radiação solar
|
|
|
- Helena Batista Cordeiro
- 7 Há anos
- Visualizações:
Transcrição
1 @cláudi lobto Simone oliveir A tmosfer e rdição solr A tmosfer tem: > um limite inferior que mrc o seu início e que corresponde o nível médio ds águs do mr (0 metros) superfície d Terr; > um limite superior, que, o contrário do inferior, é difícil de determinr, ms que segundo os cientists oscil entre os 800 e os 1000 quilómetros de ltitude. A tmosfer e su composição químic A tmosfer é constituíd por r tmosférico. Este é essencilmente constituído por um mistur de gses, que contêm em suspensão minúsculs prtículs sólids de poeir, de fumo e de prtículs líquids ( águ encontr-se n tmosfer nos três estdos: gsoso, líquido e sólido). Em relção o volume de r, os constituintes d tmosfer mis importntes são os que, no seu conjunto, representm cerc de 99,96% do volume d homosfer: > o zoto (78,08%), > o oxigénio (20,95%), > o árgon (0,93%). Oxigénio 21% Azoto 78% Árgon (0,93%) Dióxido de crbono (0,033%) Hélio (0,00052%) Outros gses 1% Metno cripton, (0,00066%) xénon, hidrogénio, ozono, etc. 1
2 @cláudi lobto Simone oliveir Nest encontrm-se ind os gses rros (néon, hélio, crípton, hidrogénio, xénon, rdão, metno e óxido de nitroso), que, no totl, ocupm menos de 0,01% do volume d homosfer. Estes constituintes designm-se por gses de concentrção permnente, por se encontrrem em proporções que se mntêm reltivmente constntes. No entnto, n tmosfer encontrm-se gses cujs proporções vrim, mis ou menos centudmente, no tempo e no espço gses de concentrção vriável. Os mis importntes, um vez que têm um ppel relevnte, do ponto de vist meteorológico, são: > o vpor de águ, que diminui em ltitude (cerc de 75% cumul-se nos primeiros 4 km de ltitude); > o dióxido de crbono, que diminui em ltitude (cerc de 75% concentrm-se nos 10 km de ltitude); > o ozono, que ument em ltitude ( su mior concentrção ocorre sensivelmente entre os 20 e os 50 km de ltitude). Além destes gses existem n tmosfer prtículs sólids. As poeirs, fumos, sis mineris e microrgnismos presentes n tmosfer são muito importntes do ponto de vist meteorológico, pois é em torno dels que se dá condensção do vpor de águ (núcleos de condensção). Os fumos e s poeirs existentes n tmosfer ds ciddes são responsáveis pel formção de nebulosidde. A tmosfer e su estrutur verticl Os meteorologists, pr preverem evolução d tmosfer, devem considerá-l como um todo. Ms tmosfer present um estrutur físic complex, o que levou que os meteorologists, tenhm procedido um divisão teóric, com bse n vrição d tempertur em ltitude, isto é, d su estrutur térmic verticl grdiente térmico verticl, pr que determinds regiões possm ser estudds seprdmente. Assim, tmosfer é formd por um série de cmds ou zons esférics, com crcterístics própris. Ests cmds designm-se por: > Troposfer, desde superfície terrestre té sensivelmente os km de ltitude; o seu limite superior é Tropopus. > Estrtosfer, desde os km de ltitude té os km de ltitude; o seu limite superior é Estrtopus. > Mesosfer, desde os km de ltitude té os 80 km de ltitude; o limite superior é Mesopus. > Termosfer, desde mesopus té proximdmente os km de ltitude; o seu limite superior é Termopus. 2
3 10 cláudi lobto Simone oliveir 500 km Termosfer Limites: entre os 80 km e os km de ltitude. Limite superior: termopus Tempertur: mntém-se reltivmente constnte té os 90 km de ltitude (cmd isotérmic); ument prtir dos cerc de 90 km de ltitude. Termosfer 110 Mesosfer Limites: entre os km e os 80 km de ltitude. Limite superior: mesopus. Tempertur: diminui em ltitude km Altitude cim d superfície terrestre (km) Estrtosfer Limites: entre os km e os km de ltitude. Limite superior: estrtopus. Tempertur: mntém-se reltivmente constnte té os km de ltitude (cmd isotérmic); ument grdulmente té os cerc de 32 km de ltitude; ument rpidmente prtir dos cerc de 32 km de ltitude. Mesosfer km fer Estrtos Troposfer Limites: entre superfície terrestre e os km de ltitude. Limite superior: tropopus. Tempertur: diminui em ltitude km r osfe Trop r Nível do m Tempertur (ºC) Troposfer A Troposfer é um cmd chtd nos polos, o que se deve: > à contrção do r provocd pels bixs temperturs; > o efeito d forç centrífug resultnte do movimento de rotção do nosso plnet. 3
4 @cláudi lobto Simone oliveir Troposfer 6 8 km Polo Norte km Equdor km Polo Sul 6 8 km Tropopus A espessur médi d Troposfer é de cerc de 11 km 12 km, diminuindo em ltitude, isto é, do equdor (16 km 18 km) pr os polos (6 km 8 km). A Troposfer é quecid pel bse, ou sej, tempertur n Troposfer sofre um decréscimo em ltitude, um vez que: > rdição terrestre é principl fonte clorífic d Troposfer; logo, à medid que ument distânci à fonte de clor tempertur diminui; > à medid que ument ltitude, diminuem os gses seletivos, ou sej, s quntiddes de dióxido de crbono, de vpor de águ e de prtículs sólids, que são os principis retentores d rdição solr e, sobretudo, d rdição terrestre (energi clorífic libertd pel Terr). Diminuindo estes componentes em ltitude, bsorção de energi vi tmbém diminuindo, o que conduz o decréscimo d tempertur. Estrtosfer A Estrtosfer é cmd que se locliz entre Troposfer e Mesosfer. N bix Estrtosfer existem dus fixs de ventos (um no hemisfério norte e outr no hemisfério sul) horizontis, muito fortes, com um velocidde que vri entre os 100 km/h e os 250 km/h. Designm-se de jet-strems ou correntes de jto e deslocm-se no sentido do movimento de rotção d Terr de oeste pr este. A Estrtosfer é quecid pelo topo. Deste modo, Estrtosfer tem um grdiente térmico verticl negtivo, isto é, tempertur ument em ltitude. Apresent um tempertur reltivmente constnte té sensivelmente os km de ltitude cmd isotérmic. A prtir dest ltitude, tempertur ument, primeiro e té sensivelmente os 32 km de ltitude de um form ligeir e, depois, té à Estrtopus, de form muito rápid cmd quente (ou de ozono). Assim, bsorção d rdição ultrviolet pelo ozono, que se concentr nest cmd, sobretudo entre os 20 km e os 50 km cmd de ozono provoc um umento d tempertur, que tinge vlores quse tão elevdos como os sentidos à superfície d Terr. Polo Norte Polo Sul 60º 4
5 @cláudi lobto Simone oliveir Mesosfer É cmd que se locliz entre Estrtosfer e Termosfer. O comportmento térmico dest cmd é semelhnte o que se encontr n Troposfer. Deste modo, tempertur decresce em ltitude, tingindo os 90 ºC n Mesopus. Este fenómeno é explicdo por est cmd tmosféric ser quecid pel bse, sendo, então, lt Estrtosfer su fonte clorífic. Termosfer Após Mesosfer, e té sensivelmente os 500 km 600 km, surge Termosfer. A Termosfer é um cmd que regist, té sensivelmente os 90 km de ltitude, um tempertur reltivmente constnte (cmd isotérmic). A prtir dí tempertur ument rpidmente, chegndo mesmo tingir os 2000 ºC n Termopus (grdiente térmico verticl negtivo). O umento d tempertur em ltitude deve-se à bsorção ds rdições ultrviolets pelo oxigénio tómico e pel intensificção dos rios solres e outrs estrels sobre s prtículs gsoss ionizds. Como estes processos umentm em ltitude, tempertur ument no mesmo sentido. 5
Lista de Exercícios de Física II - Gabarito,
 List de Exercícios de Físic II - Gbrito, 2015-1 Murício Hippert 18 de bril de 2015 1 Questões pr P1 Questão 1. Se o bloco sequer encost no líquido, leitur n blnç corresponde o peso do líquido e cord sustent
List de Exercícios de Físic II - Gbrito, 2015-1 Murício Hippert 18 de bril de 2015 1 Questões pr P1 Questão 1. Se o bloco sequer encost no líquido, leitur n blnç corresponde o peso do líquido e cord sustent
Psicrometria e balanços entálpicos
 álculo d entlpi Psicrometri e blnços entálpicos m Psicrometri pr o cálculo d entlpi dum corrente de r recorre-se à entlpi específic. egundo crt que usmos em PQ entlpi específic vem express em J/g de r
álculo d entlpi Psicrometri e blnços entálpicos m Psicrometri pr o cálculo d entlpi dum corrente de r recorre-se à entlpi específic. egundo crt que usmos em PQ entlpi específic vem express em J/g de r
No início. Desgaseificação do seu interior de gases voláteis. Os gases libertados constituíram a atmosfera primitiva da Terra.
 A Atmosfera A Terra tem aproximadamente 4,5 biliões de anos e quando se formou era bastante diferente da Terra que conhecemos hoje. Assim também aconteceu com a atmosfera terrestre que nem sempre apresentou
A Atmosfera A Terra tem aproximadamente 4,5 biliões de anos e quando se formou era bastante diferente da Terra que conhecemos hoje. Assim também aconteceu com a atmosfera terrestre que nem sempre apresentou
1. A tabela mostra a classificação das ondas eletromagnéticas em função das suas frequências.
 1. A tbel mostr clssificção ds onds eletromgnétics em função ds sus frequêncis. Região do espectro eletromgnético Onds de rádio Fix de frequênci (Hz) Micro-onds 9,0 10 Infrvermelho Visível Ultrviolet Rios
1. A tbel mostr clssificção ds onds eletromgnétics em função ds sus frequêncis. Região do espectro eletromgnético Onds de rádio Fix de frequênci (Hz) Micro-onds 9,0 10 Infrvermelho Visível Ultrviolet Rios
UNIDADE II 1. INTRODUÇÃO
 Instlções Elétrics Interns UNIDADE II RESISTÊNCIA E RESISTIVIDADE DO TERRENO 1. INTRODUÇÃO Pr grntir o bom funcionmento do terrmento é necessário ssegurr um corret união ds prtes metálics d instlção, um
Instlções Elétrics Interns UNIDADE II RESISTÊNCIA E RESISTIVIDADE DO TERRENO 1. INTRODUÇÃO Pr grntir o bom funcionmento do terrmento é necessário ssegurr um corret união ds prtes metálics d instlção, um
Quantidade de oxigênio no sistema
 EEIMVR-UFF Refino dos Aços I 1ª Verificção Junho 29 1. 1 kg de ferro puro são colocdos em um forno, mntido 16 o C. A entrd de oxigênio no sistem é controld e relizd lentmente, de modo ir umentndo pressão
EEIMVR-UFF Refino dos Aços I 1ª Verificção Junho 29 1. 1 kg de ferro puro são colocdos em um forno, mntido 16 o C. A entrd de oxigênio no sistem é controld e relizd lentmente, de modo ir umentndo pressão
BIOLOGIA E GEOLOGIA 10 Guerner Dias Paula Guimarães Paulo Rocha
 Guerner Dis Pul Guimrães Pulo Roch EXERCÍCIO TIPO EXAME 10.º ANO Nome Turm N.º Dt Robot Curiosity encontr pists de mudnçs n tmosfer de Mrte O robot d NASA com o tmnho de um crro, Curiosity (figur 1), está
Guerner Dis Pul Guimrães Pulo Roch EXERCÍCIO TIPO EXAME 10.º ANO Nome Turm N.º Dt Robot Curiosity encontr pists de mudnçs n tmosfer de Mrte O robot d NASA com o tmnho de um crro, Curiosity (figur 1), está
6-1 Determine a primitiva F da função f que satisfaz a condição indicada, em cada um dos casos seguintes: a) f(x) = sin 2x, F (π) = 3.
 6 Fich de eercícios de Cálculo pr Informátic CÁLCULO INTEGRAL 6- Determine primitiv F d função f que stisfz condição indicd, em cd um dos csos seguintes: ) f() = sin, F (π) = 3. b) f() = 3 + +, F (0) =
6 Fich de eercícios de Cálculo pr Informátic CÁLCULO INTEGRAL 6- Determine primitiv F d função f que stisfz condição indicd, em cd um dos csos seguintes: ) f() = sin, F (π) = 3. b) f() = 3 + +, F (0) =
ESTRUTURAS DE BETÃO ARMADO I 11 ESTADO LIMITE DE RESISTÊNCIA À FLEXÃO COMPOSTA E DESVIADA
 11 ESTADO LIMITE DE RESISTÊNCIA À FLEXÃO COMPOSTA E DESVIADA PROGRAMA 1.Introdução o etão rmdo 2.Bses de Projecto e Acções 3.Proprieddes dos mteriis: etão e ço 4.Durilidde 5.Estdos limite últimos de resistênci
11 ESTADO LIMITE DE RESISTÊNCIA À FLEXÃO COMPOSTA E DESVIADA PROGRAMA 1.Introdução o etão rmdo 2.Bses de Projecto e Acções 3.Proprieddes dos mteriis: etão e ço 4.Durilidde 5.Estdos limite últimos de resistênci
Curso Básico de Fotogrametria Digital e Sistema LIDAR. Irineu da Silva EESC - USP
 Curso Básico de Fotogrmetri Digitl e Sistem LIDAR Irineu d Silv EESC - USP Bses Fundmentis d Fotogrmetri Divisão d fotogrmetri: A fotogrmetri pode ser dividid em 4 áres: Fotogrmetri Geométric; Fotogrmetri
Curso Básico de Fotogrmetri Digitl e Sistem LIDAR Irineu d Silv EESC - USP Bses Fundmentis d Fotogrmetri Divisão d fotogrmetri: A fotogrmetri pode ser dividid em 4 áres: Fotogrmetri Geométric; Fotogrmetri
Aula de solução de problemas: cinemática em 1 e 2 dimensões
 Aul de solução de problems: cinemátic em 1 e dimensões Crlos Mciel O. Bstos, Edurdo R. Azevedo FCM 01 - Físic Gerl pr Químicos 1. Velocidde instntâne 1 A posição de um corpo oscil pendurdo por um mol é
Aul de solução de problems: cinemátic em 1 e dimensões Crlos Mciel O. Bstos, Edurdo R. Azevedo FCM 01 - Físic Gerl pr Químicos 1. Velocidde instntâne 1 A posição de um corpo oscil pendurdo por um mol é
Física. , penetra numa lâmina de vidro. e sua velocidade é reduzida para v vidro = 3
 Questão 6 Um torre de ço, usd pr trnsmissão de televisão, tem ltur de 50 m qundo tempertur mbiente é de 40 0 C. Considere que o ço dilt-se, linermente, em médi, n proporção de /00.000, pr cd vrição de
Questão 6 Um torre de ço, usd pr trnsmissão de televisão, tem ltur de 50 m qundo tempertur mbiente é de 40 0 C. Considere que o ço dilt-se, linermente, em médi, n proporção de /00.000, pr cd vrição de
Desvio do comportamento ideal com aumento da concentração de soluto
 Soluções reis: tividdes Nenhum solução rel é idel Desvio do comportmento idel com umento d concentrção de soluto O termo tividde ( J ) descreve o comportmento de um solução fstd d condição idel. Descreve
Soluções reis: tividdes Nenhum solução rel é idel Desvio do comportmento idel com umento d concentrção de soluto O termo tividde ( J ) descreve o comportmento de um solução fstd d condição idel. Descreve
Trigonometria FÓRMULAS PARA AJUDÁ-LO EM TRIGONOMETRIA
 Trigonometri é o estudo dos triângulos, que contêm ângulos, clro. Conheç lgums regrs especiis pr ângulos e váris outrs funções, definições e trnslções importntes. Senos e cossenos são dus funções trigonométrics
Trigonometri é o estudo dos triângulos, que contêm ângulos, clro. Conheç lgums regrs especiis pr ângulos e váris outrs funções, definições e trnslções importntes. Senos e cossenos são dus funções trigonométrics
Matemática. Atividades. complementares. 9-º ano. Este material é um complemento da obra Matemática 9. uso escolar. Venda proibida.
 9 ENSINO 9-º no Mtemátic FUNDMENTL tividdes complementres Este mteril é um complemento d obr Mtemátic 9 Pr Viver Juntos. Reprodução permitid somente pr uso escolr. Vend proibid. Smuel Csl Cpítulo 6 Rzões
9 ENSINO 9-º no Mtemátic FUNDMENTL tividdes complementres Este mteril é um complemento d obr Mtemátic 9 Pr Viver Juntos. Reprodução permitid somente pr uso escolr. Vend proibid. Smuel Csl Cpítulo 6 Rzões
4 SISTEMAS DE ATERRAMENTO
 4 SISTEMAS DE ATEAMENTO 4. esistênci de terr Bix frequênci considerr o solo resistivo CONEXÃO À TEA Alt frequênci considerr cpcitânci indutânci e resistênci Em lt frequênci inclui-se s áres de telecomunicções
4 SISTEMAS DE ATEAMENTO 4. esistênci de terr Bix frequênci considerr o solo resistivo CONEXÃO À TEA Alt frequênci considerr cpcitânci indutânci e resistênci Em lt frequênci inclui-se s áres de telecomunicções
LISTA DE EXERCÍCIOS #6 - ELETROMAGNETISMO I
 LIST DE EXERCÍCIOS #6 - ELETROMGNETISMO I 1. N figur temos um fio longo e retilíneo percorrido por um corrente i fio no sentido indicdo. Ess corrente é escrit pel epressão (SI) i fio = 2t 2 i fio Pr o
LIST DE EXERCÍCIOS #6 - ELETROMGNETISMO I 1. N figur temos um fio longo e retilíneo percorrido por um corrente i fio no sentido indicdo. Ess corrente é escrit pel epressão (SI) i fio = 2t 2 i fio Pr o
Processo TIG. Eletrodo (negativo) Argônio. Arco elétrico Ar Ar + + e - Terra (positivo)
 Processo TIG No processo de soldgem rco sob proteção gsos, região se unir é quecid té que se tinj o ponto de fusão, pr que isto ocorr, é fornecid um energi trvés do rco elétrico, que irá fundir tnto o
Processo TIG No processo de soldgem rco sob proteção gsos, região se unir é quecid té que se tinj o ponto de fusão, pr que isto ocorr, é fornecid um energi trvés do rco elétrico, que irá fundir tnto o
PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 2012 1 a Fase RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 01 1 Fse Prof. Mri Antôni Gouvei. QUESTÃO 83. Em 010, o Instituto Brsileiro de Geogrfi e Esttístic (IBGE) relizou o último censo populcionl brsileiro, que mostrou
PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 01 1 Fse Prof. Mri Antôni Gouvei. QUESTÃO 83. Em 010, o Instituto Brsileiro de Geogrfi e Esttístic (IBGE) relizou o último censo populcionl brsileiro, que mostrou
{ 2 3k > 0. Num triângulo, a medida de um lado é diminuída de 15% e a medida da altura relativa a esse lado é aumentada
 MATEMÁTICA b Sbe-se que o qudrdo de um número nturl k é mior do que o seu triplo e que o quíntuplo desse número k é mior do que o seu qudrdo. Dess form, k k vle: ) 0 b) c) 6 d) 0 e) 8 k k k < 0 ou k >
MATEMÁTICA b Sbe-se que o qudrdo de um número nturl k é mior do que o seu triplo e que o quíntuplo desse número k é mior do que o seu qudrdo. Dess form, k k vle: ) 0 b) c) 6 d) 0 e) 8 k k k < 0 ou k >
No início. Desgaseificação do seu interior de gases voláteis. Os gases libertados constituíram a atmosfera primitiva da Terra.
 A Atmosfera A Terra tem aproximadamente 4,5 biliões de anos e quando se formou era bastante diferente da Terra que conhecemos hoje. Assim também aconteceu com a atmosfera terrestre que nem sempre apresentou
A Atmosfera A Terra tem aproximadamente 4,5 biliões de anos e quando se formou era bastante diferente da Terra que conhecemos hoje. Assim também aconteceu com a atmosfera terrestre que nem sempre apresentou
Potencial Elétrico. Evandro Bastos dos Santos. 14 de Março de 2017
 Potencil Elétrico Evndro Bstos dos Sntos 14 de Mrço de 2017 1 Energi Potencil Elétric Vmos começr fzendo um nlogi mecânic. Pr um corpo cindo em um cmpo grvitcionl g, prtir de um ltur h i té um ltur h f,
Potencil Elétrico Evndro Bstos dos Sntos 14 de Mrço de 2017 1 Energi Potencil Elétric Vmos começr fzendo um nlogi mecânic. Pr um corpo cindo em um cmpo grvitcionl g, prtir de um ltur h i té um ltur h f,
1 heae. 1 hiai 1 UA. Transferência de calor em superfícies aletadas. Tot. Por que usar aletas? Interior condução Na fronteira convecção
 Trnsferênci de clor em superfícies letds Por ue usr lets? Interior condução N fronteir convecção = ha(ts - T Pr umentr : - umentr o h - diminuir T - umentr áre A Intensificção d trnsferênci de clor Exemplo:
Trnsferênci de clor em superfícies letds Por ue usr lets? Interior condução N fronteir convecção = ha(ts - T Pr umentr : - umentr o h - diminuir T - umentr áre A Intensificção d trnsferênci de clor Exemplo:
P1 de CTM OBS: Esta prova contém 7 páginas e 6 questões. Verifique antes de começar.
 P de CTM 0. Nome: Assintur: Mtrícul: Turm: OBS: Est prov contém 7 págins e 6 questões. Verifique ntes de começr. Tods s resposts devem ser justificds. Não é permitido usr clculdor. As questões podem ser
P de CTM 0. Nome: Assintur: Mtrícul: Turm: OBS: Est prov contém 7 págins e 6 questões. Verifique ntes de começr. Tods s resposts devem ser justificds. Não é permitido usr clculdor. As questões podem ser
MINISTÉRIO DA AGRICULTURA, PECUÁRIA E ABASTECIMENTO
 MINISTÉRIO DA AGRICULTURA, PECUÁRIA E ABASTECIMENTO SECRETARIA DE POLÍTICA AGRÍCOLA DEPARTAMENTO DE GESTÃO DE RISCO RURAL PORTARIA Nº 193, DE 8 DE JUNHO DE 2011 O DIRETOR DO DEPARTAMENTO DE GESTÃO DE RISCO
MINISTÉRIO DA AGRICULTURA, PECUÁRIA E ABASTECIMENTO SECRETARIA DE POLÍTICA AGRÍCOLA DEPARTAMENTO DE GESTÃO DE RISCO RURAL PORTARIA Nº 193, DE 8 DE JUNHO DE 2011 O DIRETOR DO DEPARTAMENTO DE GESTÃO DE RISCO
No mecanismo de Lindemann-Hinshelwood admite-se que a molécula do reagente A torna-se excitada em colisão com outra molécula de A.
 Aul: 30 Temátic: Reções Unimoleculres e Ctlisores Vmos continur noss nálise cinétic em função e um mecnismo e reção. Depois fremos um introução um novo tópico isciplin, os ctlisores. 1. Reções unimoleculres
Aul: 30 Temátic: Reções Unimoleculres e Ctlisores Vmos continur noss nálise cinétic em função e um mecnismo e reção. Depois fremos um introução um novo tópico isciplin, os ctlisores. 1. Reções unimoleculres
EXPRESSÕES DE CÁLCULO DO ÍNDICE IREQ
 EXPRESSÕES DE CÁLCULO DO ÍNDICE IREQ EXPRESSÕES DE CÁLCULO DO ÍNDICE IREQ No presente nexo presentm-se s expressões de cálculo utilizds pr determinção do índice do Isolmento Térmico do Vestuário Requerido,
EXPRESSÕES DE CÁLCULO DO ÍNDICE IREQ EXPRESSÕES DE CÁLCULO DO ÍNDICE IREQ No presente nexo presentm-se s expressões de cálculo utilizds pr determinção do índice do Isolmento Térmico do Vestuário Requerido,
MATEMÁTICA 1ª QUESTÃO. x é. O valor do limite. lim x B) 1 E) 1 2ª QUESTÃO. O valor do limite. lim A) 0 B) 1 C) 2 D) 3 E) 4
 MATEMÁTICA ª QUESTÃO O vlor do limite lim x 0 x x é A) B) C) D) 0 E) ª QUESTÃO O vlor do limite x 4 lim x x x é A) 0 B) C) D) E) 4 ª QUESTÃO Um equção d ret tngente o gráfico d função f ( x) x x no ponto
MATEMÁTICA ª QUESTÃO O vlor do limite lim x 0 x x é A) B) C) D) 0 E) ª QUESTÃO O vlor do limite x 4 lim x x x é A) 0 B) C) D) E) 4 ª QUESTÃO Um equção d ret tngente o gráfico d função f ( x) x x no ponto
Conceitos de Cavitação. Capítulo 8: Conceitos de Cavitação
 Conceitos de Cvitção Cpítulo 8: Conceitos de Cvitção Cpítulo 8: Conceitos de Cvitção Introdução Os fluidos podem pssr do estdo líquido pr o gsoso dependendo ds condições de pressão e tempertur que estão
Conceitos de Cvitção Cpítulo 8: Conceitos de Cvitção Cpítulo 8: Conceitos de Cvitção Introdução Os fluidos podem pssr do estdo líquido pr o gsoso dependendo ds condições de pressão e tempertur que estão
Isso ocorre quando dois átomos de carbono fazem apenas ligações sigma. Observe a figura abaixo:
 1. Isomeri Espcil ou Geométric Qundo ligção entre dois átomos de crono permite que hj rotção entre eles, posição que os ligntes de um átomo de crono ssumem em relção os ligntes do outro átomo de crono
1. Isomeri Espcil ou Geométric Qundo ligção entre dois átomos de crono permite que hj rotção entre eles, posição que os ligntes de um átomo de crono ssumem em relção os ligntes do outro átomo de crono
SUPORTE METEOROLÓGICO DE SUPERFÍCIE PARA O MONITORAMENTO DE PRECIPITAÇÃO NA AMAZÔNIA. David Mendes. UFPA,
 SUPORTE METEOROLÓGICO DE SUPERFÍCIE PARA O MONITORAMENTO DE PRECIPITAÇÃO NA AMAZÔNIA. Dvid Mendes UFPA, emil: [email protected] ABSTRACT. This pper presents n nlyses of the Rhythm nd the vribility of the Amzonin
SUPORTE METEOROLÓGICO DE SUPERFÍCIE PARA O MONITORAMENTO DE PRECIPITAÇÃO NA AMAZÔNIA. Dvid Mendes UFPA, emil: [email protected] ABSTRACT. This pper presents n nlyses of the Rhythm nd the vribility of the Amzonin
ASTRONOMIA DO SISTEMA SOLAR CONCEITOS INICIAIS
 ASTRONOMIA DO SISTEMA SOLAR CONCEITOS INICIAIS 1 ASTRONOMIA DO SISTEMA SOLAR CONCEITOS INICIAIS 1 O TAMANHO DOS ASTROS 2 O TAMANHO DOS ASTROS Grnde prte dos stros possui form esféric. Pr eles, o seu tmnho
ASTRONOMIA DO SISTEMA SOLAR CONCEITOS INICIAIS 1 ASTRONOMIA DO SISTEMA SOLAR CONCEITOS INICIAIS 1 O TAMANHO DOS ASTROS 2 O TAMANHO DOS ASTROS Grnde prte dos stros possui form esféric. Pr eles, o seu tmnho
ROTAÇÃO DE CORPOS SOBRE UM PLANO INCLINADO
 Físic Gerl I EF, ESI, MAT, FQ, Q, BQ, OCE, EAm Protocolos ds Auls Prátics 003 / 004 ROTAÇÃO DE CORPOS SOBRE UM PLANO INCLINADO. Resumo Corpos de diferentes forms deslocm-se, sem deslizr, o longo de um
Físic Gerl I EF, ESI, MAT, FQ, Q, BQ, OCE, EAm Protocolos ds Auls Prátics 003 / 004 ROTAÇÃO DE CORPOS SOBRE UM PLANO INCLINADO. Resumo Corpos de diferentes forms deslocm-se, sem deslizr, o longo de um
UNESP - FEIS - DEFERS
 UNESP - FEIS - DEFERS DISCIPLINA: ARMAZENAMENTO E BENEFICIAMENTO DE GRÃOS Exercício Modelo sobre Secgem de Grãos Como técnico contrtdo pr ssessorr u propriedde produtor de milho pr grãos, efetur u nálise
UNESP - FEIS - DEFERS DISCIPLINA: ARMAZENAMENTO E BENEFICIAMENTO DE GRÃOS Exercício Modelo sobre Secgem de Grãos Como técnico contrtdo pr ssessorr u propriedde produtor de milho pr grãos, efetur u nálise
1º Teste (Repescagem) de Mecânica Aplicada II
 MEAer / MEMEc / LEAN Ano Lectivo de 01/013 Instituto Superior Técnico 1 de Junho de 013 1º Teste (Repescgem) de Mecânic Aplicd II Este teste é constituído por 3 problems e tem durção de um hor e mei. Justifique
MEAer / MEMEc / LEAN Ano Lectivo de 01/013 Instituto Superior Técnico 1 de Junho de 013 1º Teste (Repescgem) de Mecânic Aplicd II Este teste é constituído por 3 problems e tem durção de um hor e mei. Justifique
Introdução ao estudo de equações diferenciais
 MTDI I - 2007/08 - Introdução o estudo de equções diferenciis 63 Introdução o estudo de equções diferenciis Existe um grnde vriedde de situções ns quis se desej determinr um quntidde vriável prtir de um
MTDI I - 2007/08 - Introdução o estudo de equções diferenciis 63 Introdução o estudo de equções diferenciis Existe um grnde vriedde de situções ns quis se desej determinr um quntidde vriável prtir de um
SEL 329 CONVERSÃO ELETROMECÂNICA DE ENERGIA. Aula 14
 SEL 329 CONVERSÃO ELETROMECÂNCA DE ENERGA Aul 14 Aul de Hoje Gerdor CC Composto Gerdor Série nterpolos Gerdor CC com Excitção Compost Estrutur Básic Utiliz combinções de enrolmentos de cmpo em série e
SEL 329 CONVERSÃO ELETROMECÂNCA DE ENERGA Aul 14 Aul de Hoje Gerdor CC Composto Gerdor Série nterpolos Gerdor CC com Excitção Compost Estrutur Básic Utiliz combinções de enrolmentos de cmpo em série e
Phoenix do Brasil Ltda.
 RESISTOR DE FIO AXIAL - AC CARACTERÍSTICAS Resistores de uso gerl Alt potênci em tmnho compcto Alto desempenho em plicções de pulso Váris opções de pré-form dos terminis Revestimento pr lt tempertur TECNOLOGIA
RESISTOR DE FIO AXIAL - AC CARACTERÍSTICAS Resistores de uso gerl Alt potênci em tmnho compcto Alto desempenho em plicções de pulso Váris opções de pré-form dos terminis Revestimento pr lt tempertur TECNOLOGIA
E m Física chamam-se grandezas àquelas propriedades de um sistema físico
 Bertolo Apêndice A 1 Vetores E m Físic chmm-se grndezs àquels proprieddes de um sistem físico que podem ser medids. Els vrim durnte um fenômeno que ocorre com o sistem, e se relcionm formndo s leis físics.
Bertolo Apêndice A 1 Vetores E m Físic chmm-se grndezs àquels proprieddes de um sistem físico que podem ser medids. Els vrim durnte um fenômeno que ocorre com o sistem, e se relcionm formndo s leis físics.
FUNÇÕES. Mottola. 1) Se f(x) = 6 2x. é igual a (a) 1 (b) 2 (c) 3 (d) 4 (e) 5. 2) (UNIFOR) O gráfico abaixo. 0 x
 FUNÇÕES ) Se f() = 6, então f ( 5) f ( 5) é igul () (b) (c) 3 (d) 4 (e) 5 ) (UNIFOR) O gráfico bio 0 () não represent um função. (b) represent um função bijetor. (c) represent um função não injetor. (d)
FUNÇÕES ) Se f() = 6, então f ( 5) f ( 5) é igul () (b) (c) 3 (d) 4 (e) 5 ) (UNIFOR) O gráfico bio 0 () não represent um função. (b) represent um função bijetor. (c) represent um função não injetor. (d)
Resoluções dos exercícios propostos
 os fundmentos d físic 1 Unidde D Cpítulo 11 Os princípios d Dinâmic 1 P.230 prtícul está em MRU, pois resultnte ds forçs que gem nel é nul. P.231 O objeto, livre d ção de forç, prossegue por inérci em
os fundmentos d físic 1 Unidde D Cpítulo 11 Os princípios d Dinâmic 1 P.230 prtícul está em MRU, pois resultnte ds forçs que gem nel é nul. P.231 O objeto, livre d ção de forç, prossegue por inérci em
Projecções Cotadas. Luís Miguel Cotrim Mateus, Assistente (2006)
 1 Projecções Cotds Luís Miguel Cotrim Mteus, Assistente (2006) 2 Nestes pontmentos não se fz o desenvolvimento exustivo de tods s mtéris, focndo-se pens lguns items. Pelo indicdo, estes pontmentos não
1 Projecções Cotds Luís Miguel Cotrim Mteus, Assistente (2006) 2 Nestes pontmentos não se fz o desenvolvimento exustivo de tods s mtéris, focndo-se pens lguns items. Pelo indicdo, estes pontmentos não
fundamental do cálculo. Entretanto, determinadas aplicações do Cálculo nos levam a formulações de integrais em que:
 Cpítulo 8 Integris Imprópris 8. Introdução A eistênci d integrl definid f() d, onde f é contínu no intervlo fechdo [, b], é grntid pelo teorem fundmentl do cálculo. Entretnto, determinds plicções do Cálculo
Cpítulo 8 Integris Imprópris 8. Introdução A eistênci d integrl definid f() d, onde f é contínu no intervlo fechdo [, b], é grntid pelo teorem fundmentl do cálculo. Entretnto, determinds plicções do Cálculo
Física D Extensivo V. 2
 Físic D Extensivo V. Exercícios 01) ) 10 dm =,1. 10 5 cm b) 3,6 m = 3,6. 10 3 km c) 14,14 cm = 14,14. 10 dm d) 8,08 dm = 8,08. 10 3 cm e) 770 dm = 7,7. 10 1 m 0) ) 5,07 m = 5,07. 10 dm b) 14 dm = 1,4.
Físic D Extensivo V. Exercícios 01) ) 10 dm =,1. 10 5 cm b) 3,6 m = 3,6. 10 3 km c) 14,14 cm = 14,14. 10 dm d) 8,08 dm = 8,08. 10 3 cm e) 770 dm = 7,7. 10 1 m 0) ) 5,07 m = 5,07. 10 dm b) 14 dm = 1,4.
ATMOSFERA Temperatura, pressão, densidade e grandezas associadas.
 ATMOSFERA Temperatura, pressão, densidade e grandezas associadas. As camadas na atmosfera são: Troposfera. Estratosfera. Mesosfera Termosfera Exosfera As camadas na atmosfera são definidas a partir de
ATMOSFERA Temperatura, pressão, densidade e grandezas associadas. As camadas na atmosfera são: Troposfera. Estratosfera. Mesosfera Termosfera Exosfera As camadas na atmosfera são definidas a partir de
3. Cálculo integral em IR 3.1. Integral Indefinido 3.1.1. Definição, Propriedades e Exemplos
 3. Cálculo integrl em IR 3.. Integrl Indefinido 3... Definição, Proprieddes e Exemplos A noção de integrl indefinido prece ssocid à de derivd de um função como se pode verificr prtir d su definição: Definição
3. Cálculo integrl em IR 3.. Integrl Indefinido 3... Definição, Proprieddes e Exemplos A noção de integrl indefinido prece ssocid à de derivd de um função como se pode verificr prtir d su definição: Definição
Lista 7.1 Formas Quadráticas; Conjunto Convexo; Função Convexa
 Fculdde de Economi d Universidde Nov de isbo pontmentos Cálculo II ist 7.1 Forms Qudrátics; Conjunto Convexo; Função Convex 1. Form qudrátic de n vriáveis reis (Q): Polinómio de º gru de n vriáveis reis
Fculdde de Economi d Universidde Nov de isbo pontmentos Cálculo II ist 7.1 Forms Qudrátics; Conjunto Convexo; Função Convex 1. Form qudrátic de n vriáveis reis (Q): Polinómio de º gru de n vriáveis reis
UNITAU APOSTILA. SUCESSÃO, PA e PG PROF. CARLINHOS
 ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA SUCESSÃO, PA e PG PROF. CARLINHOS NOME DO ALUNO: Nº TURMA: blog.portlpositivo.com.br/cpitcr 1 SUCESSÃO OU SEQUENCIA NUMÉRICA Sucessão ou seqüênci
ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA SUCESSÃO, PA e PG PROF. CARLINHOS NOME DO ALUNO: Nº TURMA: blog.portlpositivo.com.br/cpitcr 1 SUCESSÃO OU SEQUENCIA NUMÉRICA Sucessão ou seqüênci
INTEGRAIS DEFINIDAS. Como determinar a área da região S que está sob a curva y = f(x) e limitada pelas retas verticais x = a, x = b e pelo eixo x?
 INTEGRAIS DEFINIDAS O Prolem d Áre Como determinr áre d região S que está so curv y = f(x) e limitd pels rets verticis x =, x = e pelo eixo x? Um idei é proximrmos região S utilizndo retângulos e depois
INTEGRAIS DEFINIDAS O Prolem d Áre Como determinr áre d região S que está so curv y = f(x) e limitd pels rets verticis x =, x = e pelo eixo x? Um idei é proximrmos região S utilizndo retângulos e depois
INTEGRAIS DEFINIDAS. Como determinar a área da região S que está sob a curva y = f(x) e limitada pelas retas verticais x = a, x = b e pelo eixo x?
 INTEGRAIS DEFINIDAS O Prolem d Áre Como determinr áre d região S que está so curv y = f(x) e limitd pels rets verticis x =, x = e pelo eixo x? Um idei é proximrmos região S utilizndo retângulos e depois
INTEGRAIS DEFINIDAS O Prolem d Áre Como determinr áre d região S que está so curv y = f(x) e limitd pels rets verticis x =, x = e pelo eixo x? Um idei é proximrmos região S utilizndo retângulos e depois
8.1 Áreas Planas. 8.2 Comprimento de Curvas
 8.1 Áres Plns Suponh que um cert região D do plno xy sej delimitd pelo eixo x, pels rets x = e x = b e pelo grá co de um função contínu e não negtiv y = f (x) ; x b, como mostr gur 8.1. A áre d região
8.1 Áres Plns Suponh que um cert região D do plno xy sej delimitd pelo eixo x, pels rets x = e x = b e pelo grá co de um função contínu e não negtiv y = f (x) ; x b, como mostr gur 8.1. A áre d região
ATIVIDADE AVALIATIVA
 Climatologia 2. Atmosfera Terrestre ATIVIDADE AVALIATIVA Valor: 1,0 Tempo para responder: 15min 1) Qual a importância da concentração dos gases que compõe a atmosfera terrestre, em termos físicos e biológicos?
Climatologia 2. Atmosfera Terrestre ATIVIDADE AVALIATIVA Valor: 1,0 Tempo para responder: 15min 1) Qual a importância da concentração dos gases que compõe a atmosfera terrestre, em termos físicos e biológicos?
Professora: Profª Roberta Nara Sodré de Souza
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICAS INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA-CAMPUS ITAJAÍ Professor: Profª Robert Nr Sodré de Souz Função
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICAS INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA-CAMPUS ITAJAÍ Professor: Profª Robert Nr Sodré de Souz Função
Escola: Nome: Turma: N.º: Data: / / FICHA DE TRABALHO 1. troposfera a radiação termosfera. gasosa estratosfera os fenómenos. mesosfera o ar O ozono
 Conteúdo: Camadas da Atmosfera FICHA DE TRABALHO 1 troposfera a radiação termosfera gasosa estratosfera os fenómenos mesosfera o ar O ozono A atmosfera terrestre, camada que envolve a Terra, com cerca
Conteúdo: Camadas da Atmosfera FICHA DE TRABALHO 1 troposfera a radiação termosfera gasosa estratosfera os fenómenos mesosfera o ar O ozono A atmosfera terrestre, camada que envolve a Terra, com cerca
Física D Extensivo V. 2
 GITO Físic D Extensivo V. Exercícios 01) ) 10 dm =,1. 10 5 cm b) 3,6 m = 3,6. 10 3 km c) 14,14 cm = 14,14. 10 dm d) 8,08 dm = 8,08. 10 3 cm e) 770 dm = 7,7. 10 1 m 0) ) 5,07 m = 5,07. 10 dm b) 14 dm =
GITO Físic D Extensivo V. Exercícios 01) ) 10 dm =,1. 10 5 cm b) 3,6 m = 3,6. 10 3 km c) 14,14 cm = 14,14. 10 dm d) 8,08 dm = 8,08. 10 3 cm e) 770 dm = 7,7. 10 1 m 0) ) 5,07 m = 5,07. 10 dm b) 14 dm =
Atmosfera terrestre. Camada fina, gasosa, sem cheiro, sem cor e sem gosto, presa à Terra pela força da gravidade.
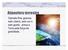 Atmosfera terrestre Camada fina, gasosa, sem cheiro, sem cor e sem gosto, presa à Terra pela força da gravidade. Atmosfera terrestre - Composição 99,9% da atmosfera é constituída por apenas quatro gases:
Atmosfera terrestre Camada fina, gasosa, sem cheiro, sem cor e sem gosto, presa à Terra pela força da gravidade. Atmosfera terrestre - Composição 99,9% da atmosfera é constituída por apenas quatro gases:
15 aulas. Qual o número m ximo de faltas que ele ainda pode ter? (A) 9 (B) 10 (C) 12 (D) 16 (E) 24
 Pré-AFA 2017 Simuldo A 28 de junho de 2017 Questão 1 (CFN) Qul é o número nturl que elevdo o qudrdo é igul o seu triplo somdo com 0? (A) 5 (B) 6 (C) 8 (D) 9 Questão 2 (CFN) Sbendo-se que tn(0 ) =, o vlor
Pré-AFA 2017 Simuldo A 28 de junho de 2017 Questão 1 (CFN) Qul é o número nturl que elevdo o qudrdo é igul o seu triplo somdo com 0? (A) 5 (B) 6 (C) 8 (D) 9 Questão 2 (CFN) Sbendo-se que tn(0 ) =, o vlor
Resolução A primeira frase pode ser equacionada como: QUESTÃO 3. Resolução QUESTÃO 2 QUESTÃO 4. Resolução
 (9) - www.elitecmpins.com.br O ELITE RESOLVE MATEMÁTICA QUESTÃO Se Améli der R$, Lúci, então mbs ficrão com mesm qunti. Se Mri der um terço do que tem Lúci, então est ficrá com R$, mis do que Améli. Se
(9) - www.elitecmpins.com.br O ELITE RESOLVE MATEMÁTICA QUESTÃO Se Améli der R$, Lúci, então mbs ficrão com mesm qunti. Se Mri der um terço do que tem Lúci, então est ficrá com R$, mis do que Améli. Se
Física 1 Capítulo 3 2. Acelerado v aumenta com o tempo. Se progressivo ( v positivo ) a m positiva Se retrógrado ( v negativo ) a m negativa
 Físic 1 - Cpítulo 3 Movimento Uniformemente Vrido (m.u.v.) Acelerção Esclr Médi v 1 v 2 Movimento Vrido: é o que tem vrições no vlor d velocidde. Uniddes de celerção: m/s 2 ; cm/s 2 ; km/h 2 1 2 Acelerção
Físic 1 - Cpítulo 3 Movimento Uniformemente Vrido (m.u.v.) Acelerção Esclr Médi v 1 v 2 Movimento Vrido: é o que tem vrições no vlor d velocidde. Uniddes de celerção: m/s 2 ; cm/s 2 ; km/h 2 1 2 Acelerção
FÍSICA. 16) Uma pedra é solta de um penhasco e leva t 1 segundos para chegar no solo. Se t 2 é o
 FÍSICA 16) Um pedr é solt de um penhsco e lev t 1 segundos pr chegr no solo. Se t 2 é o tempo necessário pr pedr percorrer primeir metde do percurso, então podemos firmr que rzão entre t 1 e t 2 vle: A)
FÍSICA 16) Um pedr é solt de um penhsco e lev t 1 segundos pr chegr no solo. Se t 2 é o tempo necessário pr pedr percorrer primeir metde do percurso, então podemos firmr que rzão entre t 1 e t 2 vle: A)
CÁLCULO I. 1 Funções denidas por uma integral
 CÁLCULO I Prof. Mrcos Diniz Prof. André Almeid Prof. Edilson Neri Júnior Prof. Emerson Veig Prof. Tigo Coelho Aul n o 26: Teorem do Vlor Médio pr Integris. Teorem Fundmentl do Cálculo II. Funções dds por
CÁLCULO I Prof. Mrcos Diniz Prof. André Almeid Prof. Edilson Neri Júnior Prof. Emerson Veig Prof. Tigo Coelho Aul n o 26: Teorem do Vlor Médio pr Integris. Teorem Fundmentl do Cálculo II. Funções dds por
