Fotónica. Nesta primeira parte do trabalho pretende-se obter uma representação gráfica da curva lemniscata de Bernoulli.

Transcrição

1 Fotónica Ano Lectivo: 4/5 Trabalho T Pretende-se neste trabalho utilizar os conhecimentos adquiridos em álgebras (geométricas) de Clifford para algumas aplicações nomeadamente na representação gráfica em MATLAB Estuda-se também o movimento hiperbólico uma aplicação específica da álgebra do espaçotempo de Minkowski (plano hiperbólico) PARTE A Nesta primeira parte do trabalho pretende-se obter uma representação gráfica da curva lemniscata de Bernoulli Seja z x ye um spinor de ie z x y x i y e tal que com p z p e Comece por provar que e e z p z p z p p Portanto (explique porquê) z p p Faça agora Página Fotónica Trabalho T

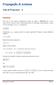
2 p z exp e cos e sin z x y 4 Nestas condições mostre que z p cos Mostre ainda que x y y x tan cos x y y x tan Podemos então concluir o seguinte: a lemniscata tem a equação cartesiana que se indica a seguir x y p x y Assim a lemniscata obedece às equações paramétricas pcos cos x cos x x y p cos y sin y psin cos Note que o ramo direito se obtém fazendo 4 4 O ramo esquerdo por sua vez obtém-se fazendo A figura a obter encontra-se representada a seguir Página Fotónica Trabalho T

3 PARTE B Nesta segunda parte do trabalho pretende-se obter uma representação gráfica de várias cónicas com o mesmo pericentro (antónimo de apocentro) No caso de uma órbita em torno da Terra o pericentro designa-se por perigeu e o apocentro por apogeu No caso de uma órbita em torno do Sol o pericentro designa-se por periélio e o apocentro por afélio Uma cónica é representada genericamente pela seguinte equação em coordenadas polares: r cos Designa-se por o semi-latus rectum e por a excentricidade Note-se que d sendo d a distância da directriz da cónica ao foco considerado como pericentro (correspondente ao ponto para o qual a distância r assume o valor mínimo) Quando a cónica degenera numa circunferência Para a cónica é uma elipse Para a cónica representa uma parábola E finalmente quando a cónica é uma hipérbole Suponhamos que em coordenadas cartesianas o foco corresponde ao centro O x y e o pericentro ao ponto P x p y Nestas condições a equação das cónicas com os mesmos foco e pericentro é dada com p por p r cos Note-se que o pericentro ocorre para a que corresponde portanto r p Em coordenadas cartesianas vem então: xr y r cos sin p p cos cos sin cos Note-se que deste modo a equação genérica de uma cónica corresponde ao spinor z x y e r exp e r r cos Pretende-se que represente numa única figura as cónicas correspondentes a: (i) (circunferência); (ii) 8 (elipse); (iii) (parábola); (iv) 5 (hipérbole) Considere em todos os casos p A figura a obter é a representada na página seguinte Note que para efeitos de representação gráfica o valor máximo x max de todas as curvas (à excepção da circunferência) deve coincidir com o valor da elipse ie sendo a excentricidade da elipse (o valor numérico aqui adoptado é 8 ) tem-se Página 3 Fotónica Trabalho T

4 x max p PARTE C Nesta terceira parte do trabalho pretende-se obter uma representação gráfica de uma elipse e de uma hipérbole Em ambos os casos a equação é agora caracterizada por um vector r xe ye C B é a base ortonormada da parte ímpar da álgebra (geométrica) do plano em que e e euclidiano Para ambas as cónicas considere sin cos a a cos e e b b sin e e com 3 a b a b No caso da elipse a equação é dada por r a cos b sin a b Para a elipse faça Página 4 Fotónica Trabalho T

5 a elipse b A correspondente figura encontra-se a seguir No caso da hipérbole a equação é dada por r a cosh b sinh a b Para a hipérbole faça a 5 hipérbole b Deve no caso da hipérbole representar as duas assímptotas A correspondente figura encontra-se a seguir (na página seguinte) Página 5 Fotónica Trabalho T

6 De acordo com a mecânica clássica newtoniana as órbitas planetárias (dos planetas do sistema solar em torno do Sol) obedecem às leis de Kepler: são as trajectórias de uma massa (pontual) sob a acção de uma força gravitacional central (no foco) inversamente proporcional ao quadrado da distância (do planeta ao foco ocupado pelo Sol) Seja M a massa do Sol (no foco) e m a massa do planeta (que orbita em torno do Sol) A energia total do movimento (ie a soma da energia cinética com a energia potencial) é uma constante E dada por (em que v é a velocidade do planeta e r a sua distância ao Sol) k mk E m v constante k G M m r 3 sendo G a constante de gravitação universal: G m kg s Uma trajectória elíptica corresponde a ter-se corresponde E Uma trajectórica parabólica E Uma trajectória hiperbólica corresponde a E a trejectória circular corresponde a mk E O caso particular de uma No caso relativista a órbita elíptica correspondente a E dá lugar a uma precessão da elipse Esta precessão claramente observável no caso da órbita de Mercúrio corresponde (no caso geral) a uma equação da forma r cos Página 6 Fotónica Trabalho T

7 Quando a órbita é exactamente elíptica A precessão da órbita observa-se para As correspondentes equações paramétricas correspondem a xr y r cos cos cos sin sin cos As três figuras seguintes representam sempre a situação em que e 8 Porém no primeiro caso tem-se (órbita elítica) e fez-se ; no segundo caso tem-se 95 e fez-se ; no terceiro caso tem-se (tal como no caso anterior) 95 mas agora fez-se 4 Página 7 Fotónica Trabalho T

8 PARTE D Nesta quarta parte do trabalho pretende-se obter uma representação gráfica do sistema de coordenadas bipolares Começa-se por considerar dois vectores constantes ab tais que ade b d e e ainda o vector variável r xe ye Como anteriormente e e do plano euclidiano B é a base ortonormada da parte ímpar da álgebra (geométrica) A primeira tarefa desta parte do trabalho consiste em analisar a representação gráfica da equação (escrita em ) exp a r b r e Mostre primeiro que x y d y d e a r b r x d y Logo atendendo a que exp e cos e sin Página 8 Fotónica Trabalho T

9 obtêm-se as seguintes equações paramétricas x y d x d y yd x d y cos sin das quais se tira por divisão ordenada cot x y d yd Atendendo à identidade csc tan infere-se então a equação paramétrica da primeira família de circunferências: primeira família de circunferências x y d cot d csc Por outro lado atendendo a que a r b r expe b r a r expe a r b r b r a r b r a r r b r a e ainda a que r a r b x d y x d y infere-se portanto que x y d x d xd x d y x y d x d y x y d x d xd x y d Introduzamos agora o novo parâmetro tal que e ln Nestas condições obtém-se sucessivamente Página 9 Fotónica Trabalho T

10 exp cosh sinh tanh exp exp cosh sinh tanh Logo das duas expressões alternativas para coth x y d xd Assim atendendo à identidade coth csch resulta obtém-se a equação paramétrica da segunda família de circunferências: segunda família de circunferências x d coth y d csch Estas duas famílias de circunferências revelam duas formas alternativas de descrever o plano A saber: ) Coordenadas cartesianas: x y x & y ; ) Coordenadas bipolares: & Nas coordenadas bipolares existem dois pontos especiais P d a de P d b de que correspondem respectivamente a e a Quando se faz obtém-se o segmento de recta que une estes dois pontos: PP Questão: O que se obtém para e quando se faz? Note-se que as equações paramétricas das duas famílias de circunferências são dadas pelas equações seguintes (verificar!): equações paramétricas x y cosh cosh sinh cos d sin cos d Representar as duas famílias de circunferências para: Página Fotónica Trabalho T

11 ; Nota importante: Só deve incluir na representação gráfica a parte de cada curva que se encontra no interior da região delimitada pela circunferência x y R com R d sin 5 cos 5 tal como se ilustra na figura seguinte PARTE E Nesta quinta parte do trabalho analisa-se em termos da álgebra o movimento hiperbólico Este tipo de movimento em teoria da relatividade restrita é o análogo do movimento uniformemente acelerado da mecânica newtoniana Tem-se (álgebra geométrica do plano hiperbólico) Página Fotónica Trabalho T

12 em que r t e xe t x & e e & e e O espaço quadrático tem portanto a métrica e e e e e e e e G Um multivector genérico u tem a forma u a e a e e e e e onde u a u e u e e e e e e e e e e e e e e e e e e e e e A tabuada de apresenta-se a seguir e e e e e e e e e e e e Dados dois vectores interno como segue: ab tais que a a e a e e b b e b e define-se o produto ab a b a b Assim na sub-álgebra par tem-se u e u e e e Além disso porque Cen e e vem u exp exp e exp exp e exp cosh e sinh No entanto o reverso de u a e é o multivector u a e Mas então a e a e a e a a ae e e a uu a a ae uu dado que Página Fotónica Trabalho T

13 ae a e a e e a e a e e a e a e a e a e a e ae e a ie o bivector unitário da álgebra anticomuta com todos os vectores Define-se o conjugado de Clifford do multivector u a e como sendo u a e de forma que u u a e uu a Podemos estabelecer a norma (que neste caso pode ser positiva negativa ou nula) u uu a Em particular tem-se a a a a a a a a a e e e e e e Este vector a diz-se: (i) do tipo tempo se a a a a a a ; (iii) do tipo espaço se a a a escrever ; (ii) do tipo luz se No caso (i) podemos a a e a e f \ f a exp f cosh f sinh ; no caso (ii) é exp a e e a e e e e ; no caso (iii) é a a e a e f \ f a exp f cos f sin Represente o plano de Minkowski (ou plano hiperbólico) tal como se indica na primeira figura contida na página seguinte Devido ao facto da métrica não ser euclidiana ie ter-se G I os vectores f e f são unitários tal como e e e (tal como provam as hipérboles de calibração t x e x t ): e e f f Usam-se unidades geométricas em que se considera c Assim as duas assímptotas correspondem a t x e t x Página 3 Fotónica Trabalho T

14 Consideremos agora a linha de universo de uma partícula material descrita pela sequência contínua de acontecimentos (em que é o tempo próprio medido por um relógio ideal movendose em conjunto com a partícula) t x r e e f Portanto vem re t xe t x e r e x r re e r t x t x t x t x t Página 4 Fotónica Trabalho T

15 Assim o teorema de Minkowski estabelece que o tempo próprio é t t t x t x Apresente uma ilustração gráfica deste teorema: num diagrama de Minkowski considere um acontecimento x t A do tipo tempo e marque nesse diagrama as coordenadas t t e ; dê uma interpretação física A A A velocidade absoluta desta partícula é dada por dr d t d x d t u e e f d d d t d u d t d x t t d e e d t u f Seja então o bivector da velocidade (normalizada) relativa t t β e β Seja ainda v e a velocidade absoluta do laboratório (referencial inercial) onde se observa o movimento da partícula Então como v dt t dt u v u v u v d β u t d β v dt vu u v u v t d β dt u v u v β d u v Como dt u u v vu β d define-se o coeficiente de Lorentz dt d u v uv β u e e f Note-se que Página 5 Fotónica Trabalho T

16 u v β u v u v u v vu u v u v vu u v u v u v u v pelo que atendendo a que se tem u v vu u v infere-se u v u v β β u v u v u v A aceleração própria da partícula define-se como d u u d Deste modo vem (em que o ponto por cima designa derivação em relação ao tempo próprio) d d d uv β β β a u v β a d t d t d t uma vez que d t d β a ae d d t onde a é a aceleração relativa Tratando-se de movimento unidimensional vem ainda (com a a ) d d d a a d u e e a d t d t d t e e e f e d t pois f e e e f f f e e e f f De resulta também e f d d d d d a d t d t d t d t d t 3 3 Assim infere-se que u f u u f 3 a 3 a f u Designa-se deste modo por o valor da aceleração própria (ou absoluta) da partícula Notese que é sempre Página 6 Fotónica Trabalho T

17 u u u u u No chamado movimento hiperbólico a partícula material descreve uma linha de universo tal que movimento hiperbólico x t X em que X x é uma constante Daqui resulta imediatamente que d x t t x x d x t dt t X dt x X X t X Logo como d X t X sinh t X sinh d t t X X X infere-se com base na equação da linha de universo que x X cosh X Portanto obtém-se t t tanh x t X X x t cosh X X X Note-se que t t t X X X X X sinh ln A aceleração relativa tem o valor d X a dt t X 3 Consequentemente a aceleração absoluta é dada por a X 3 Página 7 Fotónica Trabalho T

18 Prova-se assim que o movimento hiperbólico tem aceleração própria constante ie é o equivalente ao movimento uniformemente acelerado da mecânica newtoniana Com efeito consideremos a nova trajectória x X t X x X t X Restauremos de momento as unidades SI: c c 4 c c t c c x c t t c c onde a aproximação é válida para c t Obtém-se assim x t como é bem conhecido no caso do movimento com aceleração constante em mecânica newtoniana Para terminar esta parte vai-se introduzir o parâmetro da rapidez tal que tanh X As equações paramétricas do movimento hiperbólico escrevem-se então na forma x X cosh t X sinh Represente graficamente a linha de universo para X 3 5 Note que um fotão emitido em x no instante t nunca será capaz de alcançar a partícula apesar da velocidade desta ser sempre inferior à do fotão Página 8 Fotónica Trabalho T

19 PARTE F Nesta sexta e última parte do trabalho recupera-se o paradoxo dos gémeos já analisado no primeiro trabalho Porém aqui o gémeo astronauta (ALICE) tem uma linha de universo curva correspondente a movimento hiperbólico (estudado na parte anterior) A linha de universo de BOB é a mesma do trabalho T A linha de universo de ALICE corresponde a três troços Sejam T o tempo total decorrido de acordo com BOB e T o tempo total decorrido de acordo com ALICE A aceleração própria de ALICE tem como módulo o valor T em unidades geométricas (em que c ) como as que aqui se adoptam Em unidades SI é c T Introduziu-se aqui o parâmetro adimensional que caracteriza uma dada linha de universo de ALICE A primeira parte da linha de universo de ALICE é: T T t x t t 4 T A segunda parte é: Página 9 Fotónica Trabalho T

20 T 3 T T t t x t 4 4 T 6 Finalmente a terceira parte é: 3 T T t t T xt 4 T A primeira hipérbole (ie a que corresponde à primeira parte da linha de universo) é: t x T T A segunda hipérbole é: x t T 6 T A terceira hipérbole é: t x T T A máxima distância entre ALICE e BOB corresponde a T T t L 6 O tempo próprio da ALICE é dado por T t 4 T t T 3T sinh T t T 4 4 3T t T 4 e a relação entre os tempos totais de cada um dos gémeos é T 4 sinh T 4 Represente graficamente as linhas de universo de ALICE para T e 8 4 Página Fotónica Trabalho T

21 Na figura seguinte represente T em função de t T também para 8 4 Na figura anexa da página seguinte pretende-se ilustrar a relação dos dois tempos totais T T em função do parâmetro (para ) Página Fotónica Trabalho T

22 Tem-se T lim T Explique porquê O trabalho deve incluir uma secção intitulada Introdução bem como uma secção intitulada Conclusões Todos os programas MATLAB desenvolvidos devem aparecer em ANEXO ao trabalho Nota Final Este trabalho deve ser apresentado para avaliação de duas formas distintas: numa versão PDF (a enviar para o professor responsável: carlospaiva@lxitpt) e numa versão física ie em papel (a entregar na Área Científica de Telecomunicações) Pode e deve ser utilizada a cor nas figuras mesmo se a versão em papel for a preto e branco Sugere-se que as figuras criadas em MATLAB sejam comentadas (com expressões matemáticas) em PowerPoint Assim as figuras criadas em MATLAB serão exportadas para o PowerPoint no formato TIFF Da mesma forma ao integrar as figuras do PowerPoint num documento WORD deve-se utilizar o formato TIFF O WORD e o PowerPoint têm a possibilidade de integrar o programa MathType que melhora consideravelmente a escrita de fórmulas matemáticas Página Fotónica Trabalho T