CÁLCULO III - MAT 216- IFUSP- Semestre 1 de 2014 Professor Oswaldo Rio Branco de Oliveira
|
|
|
- Andreia do Amaral Carneiro
- 6 Há anos
- Visualizações:
Transcrição
1 CÁLCULO III - MAT 16- IFUSP- Semestre 1 de 014 Professor Oswaldo Rio Branco de Oliveira MULTIPLICADORES DE LAGRANGE: INTERPRETAÇÕES E EXEMPLOS Definições: Seja f Ω R, com Ω aberto em R n. Um ponto p em Ω é: Crítico, ou estacionário, da função f, se f(p)=0. Um máximo [mínimo] local da função f se existe um raio r> 0 tal que f(p) f(x) [f(p) f(x)], para todo x na intersecção B(p;r) Ω. Extremante local de f se p é ponto de máximo [mínimo] local de f. Extremante local de f em um subconjunto A de Ω, se p está em A e p é ponto de máximo [mínimo] local da função f restrita a A. Teorema 1. Sejam f e g funções em C 1 (Ω;R), com Ω aberto em R, e L a curva de nível 0 de g, com g 0 nos pontos de L. Seja p um extremante local de f em L. Temos (1.1) f(p)=λ g(p), para algum λ em R. f γ (t 0 ) g p B L=g 1 (0) f c=f(p) R Figura 1: Teorema de Lagrange no Plano
2 Prova. (Vide Figura 1.) Localmente, em p, pelo Teorema da Função Implícita L é uma curva γ(t) com γ(0)=p e γ (0) 0. Assim,(f γ)(t) têm extremante em t=0. Portanto(f γ) (0)=0 e, pela regra da cadeia, f(p) γ (0). Também temos g γ 0, g(p) γ (0), γ (0) 0 e g(p) 0. Logo, f(p) é paralelo a g(p) 0. Donde, a tese Interpretações Geométricas para o Teorema 1 (Lagrange). y y f(p)=λ g(p) f(p) c 4 =f(p) p A B C curvas de nível a, b e c de f a<b=f(p)<c x L g(x,y)=0 L g(x,y)=0 c c c 1 x Figura : Ilustrações A e B (complementares) para o Teorema de Lagrange Interpretação para Figura -A (à esquerda). Suponha f(p) 0 oblíquo a L em p. Então, a curva C de nível f(p), de f, cruza a curva L e as curvas de nível c, de f, para c f(p), com gráficos próximos a C, também cruzam L e, orientando-as na direção de crescimento de c (a direção do gradiente) vemos que p não é ponto de máximo, nem de mínimo, local de f em L, contra a hipótese. Donde f(p) é ortogonal a L, assim como g(p). Logo, o vetor f(p) é paralelo a g(p). Interpretação para Figura -B (à direita): Representemos as curvas de nível c 1 < c < c < c 4 = f(x 0,y 0 )=f(p) no sentido de crescimento de f [i.e., no sentido de f(p)]. Claramente o valor máximo de f sobre a curva L={(x,y) g(x,y)=0}, corresponde ao maior valor c tal que a curva de nível f(x,y)=c intercepta a curva L. Em tal ponto p de intersecção tais curvas tem mesma reta tangente e mesma reta normal, as quais a priori tem direção f(p) e g(p) (Figura -B), respectivamente. Logo, tais vetores são paralelos e f(p) é um múltiplo de g(p) já que este é não nulo.
3 Observações. Mantenhamos a notação do Teorema 1 e de sua prova. (1) Suponhamos que p é ponto crítico de f. Então, pondo λ=0 temos f(p)= 0 = λ g(p). Porém, não existe λ tal que 0 g(p)= λ f(p). Neste sentido, a equação (1.1) é a melhor possível. () Pontos críticos de f pertencentes a L, são candidatos a extremantes locais de f restrita a L. () Se f 0 em todo ponto, localmente parametrizamos a curva de nível c=f(p), de f, por uma curva δ, com δ 0. Esta curva tem vetor tangente ortogonal a f(p). Logo, δ (p) g(p). No ponto p, visto que os vetores tangentes δ e γ são não nulos e ortogonais a g(p), vemos que δ e γ são múltiplos um do outro. Donde as curvas L=g 1 (0) e a de nível c=f(p) da função f, tangenciam-se em p. (4) Os extremantes saem do sistema f(x,y)=λ g(x,y) g(x,y)=0, que é equivalente ao sistema f =λ g f y =λ g y g(x,y)=0. (5) Na equação(1.1)[i.e., f(p) = λ g(p)], é possível eliminar o parâmetro λ (a conveniência depende do problema). Basta resolvermos f g f y g y (p) = 0. A questão da determinação dos extremantes locais de f sobre a curva {(x,y) g(x,y)=0} é usualmente referida como o problema da determinação dos máximos e mínimos de f sujeita à restrição g(x,y)=0 ou, dos máximos e mínimos condicionados de f sujeita à condição g(x,y)=0. Vejamos alguns conceitos úteis ao Método dos Multiplicadores de Lagrange.
4 Definições Topológicas. Sejam A e K dois subconjuntos de R n. A é fechado se seu complementar R n {A}=A c é aberto. K é compacto se é fechado e limitado. Teorema (Weierstrass). Seja f K R uma função contínua em um compacto K de R n. Então, f assume valor máximo e valor mínimo em K. Prova. Vide página destinada ao curso. Exemplo 1. Determineacurvadeníveldef(x,y)=x +16y quetangencia a curva (ramo de hipérbole) xy=1, x>0 e y>0. Dê o ponto de tangência. Solução. y xy= f(, 1 ) x x +16y =8,x 0 Figura : Ilustração ao Exemplo 1 No ponto(x 0,y 0 ) em que as curvas se tangenciam seus vetores tangentes são paralelos e seus vetores normais também. O normal à curva de nível é f e o normal à hipérbole xy= 1 é g(x 0,y 0 )=(y 0,x 0 ) (não nulo pois x 0 y 0 =1). Obtemos f(x 0,y 0 )=λ g(x 0,y 0 ) para algum λ R e, x 0,y 0 =λ y 0,x 0. Logo, x 0.y 0 = λy 0.λx 0 e, como x 0 y 0 = 1, obtemos 64=λ e λ=±8. Como x 0 > 0 e y 0 > 0, não temos λ= 8. Donde segue x 0 = 4y 0 e portanto, 1=x 0 y 0 =4y0 e assim encontramos y 0= 1 e x 0= e o ponto de tangência (x 0,y 0 )=(, 1 ). A curva de nível é a elipse dada por x +16y =f(, 1 )=4+4=8 4
5 Exemplo. Analise os máximos e mínimos de f(x,y)=x xy+y, com a restrição x +y =1. Solução. Sejam a elipse E={(x,y) x +y = 1} e a função g(x,y)=x +y 1. Então, E= g 1 (0) e g=(x,4y) 0 sobre E. Como f é contínua e E é compacto, por Weierstrass, f assume máximo e mínimo em E. Por multiplicadores de Lagrange, para tais extremantes existe λ em R tal que f(x,y)=λ g(x,y) x +y =1 ou, (x y, x+6y)=λ(x,4y) x +y =1. Eliminando o parâmetro λ na primeira equação do sistema à direita temos, x y 6y x =0 y(x y) x(y x)=0. x 4y Porém, temos 0=(xy y ) (xy x )=(x y)(x+y). Assim, obtemos as soluções P =(y,y) ou Q=( y,y). Como P e Q pertencem à elipse concluímos que (y) +y =1 ou y=± 1 6 ou P=±( 6, 1 6 ) ou y +y =1 y=± 1. Q=±( 1, 1 ). Computemos f em P e em Q. Como f( x, y)=f(x,y) temos, f( 6, 1 6 ) =f( 6, 1 6 ) = 1 f( 1, 1 ) =f( 1, 1 ) =. Ospontos±( 1, 1 )sãodemáximoeospontos±( 6, 1 6 )sãodemínimo 5
6 Teorema. Sejam f e g em C 1 (Ω;R), com Ω um aberto em R. Consideremos a superfície de nível S= g 1 (0), com g 0 em todo ponto de S. Seja p, em S, um extremante local de f restrita a S. Então temos f(p)=λ g(p), para algum λ R. Interpretação. (Análoga ao caso planar.) Se f(p) 0 é oblíquo a S em p (i.e., aoplanoπ tangenteas emp), entãoasuperfícies denívelf(p), def, cruza S em p e as superfícies de nível c, de f, para valores de c próximos de f(p), também cruzam S e orientando-as na direção f(p), de crescimento de c, vemos que p não é extremante de f, contra a hipótese. Logo, f(p) é ortogonal a S, assim como g(p) 0. Donde f(p) e g(p) são paralelos. Prova. PeloTeoremadasFunçõesImplícitas, S élocalmenteemp=(x 0,y 0,z 0 )(i.e., em uma bola aberta contendo p), o gráfico de uma função z=ϕ(x,y), com o par(x,y) numa vizinhança de(x 0,y 0 ) e ϕ(x 0,y 0 )=z 0. Pelas hipóteses, dada uma curva arbitrária γ no gráfico de ϕ, satisfazendo γ(0)=p, a função (f γ)temmáximooumínimoemt=0. Logo, f(p) γ (0). Assim, f(p) é ortogonal ao plano π, tangente ao gráfico de ϕ em p. Claramente g(p) é ortogonal ao gráfico de ϕ e, portanto, ao plano π). z g(p) f(p) z 0 S p γ π y 0 y x 0 x Figura 4: Ilustração ao Teorema. Logo, f(p) e g(p) 0 são paralelos. Donde concluímos a tese 6
7 Observação 6. No Teorema também é simples eliminar o parâmetro λ. A resolubilidade da equação f(p)=λ g(p) equivale à de i j k f f f (p) = 0. g y g z g z Exemplo. Encontre o único ponto P no plano x+y+z=1 cuja soma dos quadrados das distâncias de P a(0,0,0) e a(1,1,1) é mínima. Solução. Geometricamente, se K é um disco fechado e limitado que contém os pontos dados e intersecta o plano π dado, o ponto procurado pertence a K π e é então o mínimo absoluto da função (quadrado da distância) D(x,y,z)=(x 0) +(y 0) +(z 0) +(x 1) +(y 1) +(z 1) restrita ao compacto K π. O Teorema de Weierstrass assegura a existência de tal mínimo. Pelo Teorema os extremantes de D(x,y,z) com a restrição x+y+z=1 satisfazem: D(x,y,z)=λ,,1, λ em R, ou, eliminando o parâmetro λ, i j k i j k x+(x 1) y+(y 1) z+(z 1) = x 1 y 1 z 1 0= 1 1 Desta forma é claro que desenvolvendo o segundo determinante pela primeiralinhatemos,(y 1 4z+) i (x 1 6z+) j+(4x 6y+) k= 0 e portanto, y=4z 1 e x=z 1. Donde, substituindo na equação do plano, obtemos (z 1)+(4z 1)+z=1. Finalmente, z= , y=, x= e P 0=( 4 14,5 14,16 14 ).. Atenção. Neste caso podemos eliminar λ mais simplesmente com as equações x+(x 1) = y+(y 1) = z+(z 1) 1 (=λ) 7
8 Exemplo 4. Consideremos o plano π ax+by+cz+d=0, a +b +c 0. (a) Determine o ponto P 1 =(x 1,y 1,z 1 ) no plano π mais próximo à origem. (b) Com o método utilizado em (a) mostre que a distância de todo ponto P 0 =(x 0,y 0,z 0 ) ao plano é dada pela fórmula: 1 Solução. ax 0 +by 0 +cz 0 +d a +b +c. (a) Geometricamente sabemos que existe tal ponto P 1 =(x 1,y 1,z 1 ) e que P 1 =(0,0,0) se d=0. Passemos à determinação do mínimo da função Φ(x,y,z)=x +y +z, o quadrado da distância, sujeita à restrição ax+by+cz+d=0. Utilizando multiplicadores de Lagrange temos, Φ(P 1 )=(x 1,y 1,z 1 )=λ(a,b,c). Logo, P 1 =(x 1,y 1,z 1 )= λ (a,b,c) e, substituindo tais coordenadas para P 0 na equação para π temos 0=ax 1 +by 1 +cz 1 +d= λ (a +b +c )+d. Donde, λ = d a +b +c. Assim, o ponto de π mais próximo à origem é d P 1 = a +b +c (a,b,c). (b) Geometricamente é claro que existe em π o ponto P =(x,y,z ) mais próximo de P 0 =(x 0,y 0,z 0 ). Claramente, P é ponto de mínimo absoluto da função Ψ(x,y,z)=(x x 0 ) +(y y 0 ) +(z z 0 ) restrita ao plano ax+by+cz+d=0, que avalia o quadrado da distância dos pontos doplanoπ aopontop 0. AplicandomultiplicadoresdeLagrangetemos, Ψ(P )=((x x 0 ),(y y 0 ),(z z 0 ))=µ(a,b,c). Portanto, P 0 P = µ (a,b,c) e a distância de P ao plano π, dada pelo módulo do vetor P 0 P, é então µ (a,b,c). Visto que P =P 0 + µ (a,b,c) pertence a π temos a(x 0 + µ a)+b(y 0+ µ b)+c(z 0+ µ c)+d=0. Donde, µ (a +b +c )= (ax 0 +by 0 +cz 0 +d). Finalmente, a distância procurada é µ µ a,b,c = (a + b + c ) a + b + c 8 = ax 0+ by 0 + cz 0 + d a +b +c.
9 P 0 =(x 0,y 0,z 0 ) n π P =(x,y,z ) Figura 5: A distância de um ponto a um plano. Solução (Geométrica, simples e sem multiplicadores de Lagrange): Se P, pertencente a π, é o pé da perpendicular por P 0 ao plano π temos que P 0 P é paralelo ao vetor normal a π, n π = a,b,c 0. Logo, existe λ em R tal que P 0 P = λ a,b,c e portanto a distância de P 0 a π é P 0 P. Porém, da identidade P =P 0 + P 0 P =P 0 +λ a,b,c, segue que 0=a(x 0 +λa)+b(y 0 +λb)+c(z 0 +λc)+d=0, e assim, λ(a +b +c )= (ax 0 +by 0 +cz 0 +d) e λ= ax 0+by 0 +cz 0 +d a +b +c. Donde, P 0 P = λ a,b,c = ax 0+ by 0 + cz 0 + d a +b +c Recordemos que: se u, v e w são vetores em R tais que u v 0 e w é ortogonal a u v então w é combinação linear de u e v. Teorema. Consideremos três funções f, g e h em C 1 (Ω;R), com Ω um aberto em R, e a intersecção de duas superfícies de nível zero L={P=(x,y,z) em Ω g(p)=0 e h(p)=0}. Suponhamos que g(x,y,z) h(x,y,z) 0, para todo(x,y,z) em L. Suponhamos que P 0 =(x 0,y 0,z 0 ) é um extremante local de f sobre L. Então, existem λ 1 em R e λ em R tais que f(p 0 )=λ 1 g(p 0 )+λ h(p 0 ). 9
10 h(x,y,z)=0 g f γ h g(x,y,z)=0 Figura 6: Ilustração ao Teorema. Prova. Pelas hipóteses (vide o Teorema das Funções Implícitas) temos que localmente, em P 0, L é uma curva γ= γ(t), com γ(0)=p 0 e γ (0) 0. Como Im(γ) está contida na superfície de nível zero de g, segue que o vetor g(p 0 ) é ortogonal a γ (0) e, analogamente, o vetor h(p 0 ) é ortogonal a γ (0) (vide Figura 5). Portanto, γ (0) é paralelo a g(p 0 ) h(p 0 ). Ainda, a função(f γ)(t) tem máximo, ou mínimo, local em t=0e f(p 0 ) γ (0) 0. Assim, temos f(p 0 ) g(p 0 ) h(p 0 ). Donde segue que o vetor f(p 0 ) é combinação linear de g(p 0 ) e h(p 0 ) Observação 7. É possível eliminar os parâmetros λ 1 e λ. No Teorema temos a identidade f(p 0 )=λ 1 g(p 0 )+λ h(p 0 ) se, e somente se, f g h f y g y h f z g z h z (P 0 ) = 0. Observação 8. Os sistemas encontrados nos teoremas acima são redutíveis a uma única equação vetorial, eliminando equações de restrição e acrescentando variáveis. Para o Teorema, e analogamente para os demais, definimos a funçãolem cinco variáveis livres (vide Exemplo 6, a seguir), ou não condicionadas, L(x,y,z,λ,µ)=f(x,y,z) λg(x,y,z) µh(x,y,z). 10
11 As soluções do sistema mencionado são os pontos de máximo ou mínimo não-condicionados de L, os quais se encontram entre seus (de L) pontos críticos e satisfazem, L(x,y,z,λ,µ)= fx λg x µh x,f y λg y µh y,f z λg z µh z, g, h = 0, que é um problema sem condições de restrição e simétrico no sentido que as variáveis tem igual importância. Esta formatação do problema é elegante e trivialmente generalizável para uma função f com qualquer número de variáveis e com qualquer número de restrições. Definição. A variável λ (ou µ) é um multiplicador de Lagrange. Em Economia, Geometria Diferencial, Cálculo das Variações, etc. o multiplicador λ é convenientemente interpretado e tem importância por si só. Exemplo 5. Determine os pontos mais afastados da origem e com coordenadas sujeitas às restrições x +4y +z =4 e x+y+z=1. Solução. Determinemos os pontos que maximizam a função D(x,y,z)=x +y +z, o quadrado da distância de(x,y,z) a(0,0,0) com as restrições g(x,y,z)=0 e h(x,y,z)=0, com g(x,y,z)=x+y+z 1 e h(x,y,z)=x +4y +z 4. Tais pontos pertencem à intersecção do elipsóide g= 0 com o plano h=0, a qual é um compacto K de R. Como D é contínua, D assume máximo e mínimo em K. Pela Observação 7 ao Teorema, se P 0 =(x 0,y 0,z 0 ) é extremante local de D sobre K={(x,y,z) g=0 e h=0} temos x 0 y 0 z =4 x 0 y 0 z = 0. x 0 8y 0 z 0 x 0 4y 0 z 0 Logo, 0=x 0 (z 0 4y 0 ) y 0 (z 0 x 0 )+z 0 (4y 0 x 0 )=y 0 (z 0 x 0 ) e temos y 0 =0 ou z 0 =x 0. Se y 0 =0 obtemos x+z=1 x +z =4, x +(1 x) =4 x x =0 x= 1± 7. 11
12 Assim, P 1 =( 1+ 7,0, 1 7 ) e P =( 1 7,0, 1+ 7 ) são candidatos a extremantes. Se z 0 =x 0 temos, x+y=1 x +4y =4 y=1 x x +y = x +(1 x) = 9x 8x=0 x=0 ou x= 8 9. Neste caso os candidatos são P =(0,1,0) e P 4 =( 8 9, 7 9, 8 9 ). Comparando os valores D(P 1 )=D(P )=4, D(P )=1eD(P 4 )= constatamos que P 1 e P são os pontos desejados Exemplo 6. Determine o ponto sobre a reta de intersecção dos planos x+y+z=1 e x y+z=4 que está mais próximo à origem. Solução. Minimizemosx +y +z comasrestriçõesx+y+z 1=0e x y+z 4=0. Definindo L(x,y,z,λ,µ)=x +y +z λ(x+y+z 1) µ( x y+z 4), resolvamos o sistema L =x λ+µ=0, L =y λ+µ=0, y L z Das três primeiras equações temos, x= λ µ =z λ µ=0, L λ = (x+y+z 1)=0, L µ =(x+y z+4)=0., y= λ µ, z= λ+µ que substituídas na quarta e na quinta equações e então simplificando fornecem e λ= λ µ = λ 14µ = 8, 54 e µ= 75. Donde concluímos, x= 11 15, y= , e z= 16 15
13 No espaço R n, chamamos um subespaço vetorial de dimensão n 1 de hiperplano (se n=, um hiperplano é um plano passando pela origem). Exemplo 7. Seja f R n R diferenciável e tal que a restrição de f a um hiperplano π tem um máximo em um ponto P no hiperplano. Verifique que dado um vetor arbitrário v unitário e paralelo a π então temos f v (P)= f(p) v =0. Isto é, f(p) é ortogonal a π. Supondo n o vetor normal ao hiperplano π conclua que existe λ em R tal que f(p)=λ n. Seja Ω um aberto em R n, n fixo em N. Como consequência do Teorema da Função Implícita para uma função g em C 1 (Ω;R), mostremos que vale um resultado análogo aos teoremas 1 e, no espaço n-dimensional. Teorema 4. Sejam f e g, ambas em C 1 (Ω;R), e S={x Ω g(x)=0}, a superfície de nível zero de g, com g(x) 0 para todo x em S. Seja P, em S, um extremante local de f restrita a S. Então, existe λ em R tal que f(p)=λ g(p). Interpretação. A superfície solução S da equação g(x) = 0 possui hiperplano tangente π e para toda curva γ em S, γ(0)=p, a composta f γ tem um extremante em P. Donde, f(p) é ortogonal ao vetor tangente γ (0) em π. Assim, f(p) e g(p) são ortogonais a π. A conclusão é então trivial. Prova. Vide a prova para Multiplicadores de Lagrange em várias variáveis. 1
14 Teorema 5. Sejam f em C 1 (R n ;R) e g=(g 1,...,g m ) em C 1 (R n ;R m ), com m<n. Suponhamos que f tem um extremante local no ponto P em S= g 1 (0,...,0). Suponhamos também que o conjunto{ g 1,..., g m } é linearmenteindependenteemr n emtodoponto. Então,existemmnúmeros reais λ 1,...,λ m tais que f(p)=λ 1 g 1 (P)+ +λ m g m (P). Interpretação. Consideremos, para cada j= 1,...,m, o hiperplano em R n tangente à superfície gj 1 (0) no ponto P. A intersecção destes hiperplanos é o espaço vetorial V tangente a S e de dimensão n m. O espaço vetorial V ortogonal a V, tem dimensão m. O conjunto{ g 1 (P),..., g m (P)} é ortogonalav eportantoumabasedev. Ainda,dadaumacurvaarbitrária γ em S, com γ(0)=p, temos que a função f γ tem um extremante em t=0 e assim, f(p) é ortogonal a γ (0). Logo, o vetor f(p) é ortogonal a V e uma combinação linear de g 1 (P),..., g m (P). Máximos e mínimos, locais e absolutos, de uma função f em C 1 (K;R), K um compacto. Definições topológicas. Seja A um subconjunto de R n. O ponto P de A, é um ponto interior de A se existe uma bola aberta, não vazia, centrada em P e contida em A. Isto é, se existe r>0 tal que B(P;r) está contida em A. O ponto P de R n é um ponto de fronteira de A se toda bola aberta, não vazia, centrada em P intersecta A e também R n A=A C, o complementar de A. Isto é, se para todo r>0, temos B(P;r) A e também B(P;r) A C. O interior de A, int(a), é o conjunto dos pontos interiores de A. A fronteira de A, A, é o conjunto dos pontos de fronteira de A. 14
15 Dado P em A, temos uma só das possibilidades: ou P int(a), ou P A. Notemos que: (A) Pelo Teorema de Weierstrass f assume máximo e mínimo, absolutos. (B) Os pontos de máximo e mínimo locais e interiores a K são pontos críticos de f. Isto é, em tais pontos o gradiente se anula. Assim, adotamos o procedimento abaixo. (1) Restringindo f a int(k) determinamos os pontos críticos, candidatos a extremantes. () Encontramos os possíveis pontos de máximo e mínimo de f sobre a fronteira, K, ou elementarmente ou por multiplicadores de Lagrange. () Os extremantes absolutos estão entre os valores de f nos pontos acima obtidos. Exemplo 8. Dada f(x,y)=6x +18xy+4y 6x 10y+5, determine os extremantes e os máximos e mínimos locais e absolutos de f no quadrado K={(x,y) x 1 e y 1}. Solução. Os pontos críticos de f são dados pela equação f = 1x+18y 6,18x+8y 10 = 0,0 x+y 1=0 e 9x+4y 5=0 Logo, o único ponto crítico no interior de K é P 0 =( 11 19, 1 19 ). A matriz hessiana de f é, H f = e então, f xx (P 0 )=1>0eodeterminante hessiano H f (P 0 ) é negativo. Logo, P 0 é ponto de sela e f não tem máximo ou mínimo local em int(d). Assim, o máximo e o mínimo absolutos pertencem à fronteira de K, K={ 1} [ 1,1] {1} [ 1,1] [ 1,1] { 1} [ 1,1] {1}. 15
16 y f=λ j 1 f f=λ i 1 1 x 1 f Figura 7: Ilustração ao Exemplo 7 Na figura abaixo as setas indicam a direção do vetor ortogonal a K. Os extremantes locais na fronteira de K, mas não um vértice, satisfazem (v. Teorema ): Em{ 1} ] 1,1[ temos x= 1 e 0=f y = 18+8y 10; logo, y=7/, possibilidade que descartamos. Em{1} ] 1,1[ temos x=1e0=f y =18+8y 10; logo, y= 1 e P 1 =(1, 1) que não pertence ao segmento considerado, é um vértice e será analizado à parte. Em] 1,1[ { 1} temos y= 1 e 0=f x = 1x 18 6; logo, x=, que também descartamos. Em] 1,1[ {1} temos y=1e0=f x =1x+18 6; logo, x= 1 e P =( 1,1) que não pertence ao segmento considerado, é um vértice e será analizado à parte. Finalmente, os pontos de máximo e o mínimo se encontram entre o vértices. Temos, f(1,1)=17, f( 1, 1)=49, f(1, 1)=+1, e f( 1,+1)= 7. Resposta: Não existem máximo ou mínimo locais e interiores. Ainda, f( 1,+1)= 7 é o mínimo absoluto e f( 1, 1)=49 é o máximo absoluto 16
17 Exemplo 9. Determine os pontos de máximo e mínimo absoluto da função f(x,y,z)=x +y +z +x+y sobre o compacto M={(x,y,z) R x +y +z 4 e z 1}. Solução. Pelo Teorema de Weierstrass a função f admite pontos de máximo e mínimo absolutos em M. Se tais pontos estiverem no interior de M então eles são pontos críticos. Os pontos críticos de f satisfazem f= x+1,y+1,z = 0,0,0 e portanto o único ponto crítico( 1/, 1/,0) não pertence ao interior de M e assim os extremantes de f pertencem à fronteira de M, M. Então, um extremante P 0 arbitrário pertence a M 1 ={(x,y,z) x +y +z =4ez>1} ou M ={(x,y,1) x +y <} ou M ={(x,y,z) x +y +z =4 e z=1}. Se P 0 =(x 0,y 0,z 0 ) estiver em M 1, por Multiplicadores de Lagrange temos, f= x0 +1,y 0 +1,z 0 =λ x 0,y 0,z 0 e portanto z 0 = λz 0 e então : ou temos λ=1 ou temos z 0 = 0. Se z 0 = 0, então P 0 não pertence a M 1 e descartamos tal possibilidade. Se λ=1 então temos x 0 +1=x 0, uma contradição! Se P 0 pertence a M (onde temos z 0 =1) então segue x 0 +1,y 0 +1,z 0 =λ 0,0,1. Logo, encontramos o candidato P 1 =( 1/, 1/,1). Se P 0 pertence a M então P 0 é extremante condicionado de f(x,y,z)=x +y +x+y+z, x +y +z =4 z=1. Pelo Método dos Multiplicadores de Lagrange obtemos f(p 0 )=λ 1 x 0 +1,y 0 +1,z 0 +λ 0,0,1. 17
18 Logo, x 0 +1 y 0 +1 x 0 y 0 = Donde segue y 0 (x 0 + 1) x 0 (y 0 + 1)=0ey 0 = x 0. Substituindo na equação da esfera segue x 0 = e x 0=± 6/. Desta forma, encontramos os candidatos P =( 6, 6,1) e P =( 6, 6,1). Como f(p 1 )= 1, f(p )=4+ 6 e f(p )=4 6, concluímos que P 1 é ponto de mínimo absoluto e P é ponto de máximo absoluto Exemplo 10 (Um Argumento Importante). Argumento: Seja S={(x,y,z) f(x,y,z)=0} a superfície de nível 0 de uma função f Ω R, Ω um aberto de R, com f de classe C 1 e f(x,y,z) 0, para todo(x,y,z) em S. Seja P 1 =(x 1,y 1,z 1 ) em R tal que P 1 não pertence a S. Suponhamos que P 0 é o ponto em S que realiza a distância do ponto P 1 à superfície S [isto é, vale a desigualdade P 1 P 0 P 1 P, para todo P em S]. Então temos, P 0 P 1 =λ f(p 0 ) para algum λ R. Donde segue, P 0 P 1 S. Consequentemente obtemos: P 0 P 1 γ (t 0 ), se γ é uma curva arbitrária de classe C 1, em S, tal que γ(t 0 )=P 0. Prova. Seja D(x,y,z)=(x x 1 ) +(y y 1 ) +(z z 1 ) definida em R. Considerando um disco fechado D(P 1 ;R) centrado em P 1 e com raio R>0 suficientemente grande tal que K = D(P 1 ;R) S, temos que K é compacto (pois fechado e limitado). Pelo Teorema de Weierstrass a função D restrita a K assume um valor mínimo em algum ponto P S. É claro que P é o ponto P 0 procurado, que realiza a distância de P 1 à superfície S. Então, como D restrita a S assume valor mínimo em P 0 S, pelo Método dos Multiplicadores de Lagrange é válida a equação: (D)(P0 )=λ f(p 0 ), para algum λ R. 18
19 Computemos o gradiente de D(x,y,z). É fácil ver que (D)= (x x1 ),(y y 1 ),(z z 1 ), e portanto, (D)(P0 )= x 0 x 1,y 0 y 1,z 0 z 1 = P 0 P 1, e assim temos (notemos, abaixo, que a constante é absorvível por λ) P 0 P 1 =λ f(p 0 ) REFERÊNCIAS 1. Apostol, T. M., Análisis Matemático, Editorial Reverté, Guidorizzi, H. L., Um Curso de Cálculo, Vol 1 e, 5 ed., Ed. LTC, 00.. Lima, E., Curso de Análise, Vol., IMPA, Simmons, G. F., Cálculo com Geometria Analítica, Vol, McGraw- Hill, Departamento de Matemática, Universidade de São Paulo São Paulo, SP - Brasil oliveira@ime.usp.br 19
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 se define da seguinte maneira:
 Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Aula 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r se define da seguinte maneira: (r1, r ) 0o se r1 e r são coincidentes, Se as retas são concorrentes, isto
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
Distância entre duas retas. Regiões no plano
 Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
Capítulo 4 Distância entre duas retas. Regiões no plano Nesta aula, veremos primeiro como podemos determinar a distância entre duas retas paralelas no plano. Para isso, lembramos que, na aula anterior,
MAT Lista de exercícios
 1 Curvas no R n 1. Esboce a imagem das seguintes curvas para t R a) γ(t) = (1, t) b) γ(t) = (t, cos(t)) c) γ(t) = (t, t ) d) γ(t) = (cos(t), sen(t), 2t) e) γ(t) = (t, 2t, 3t) f) γ(t) = ( 2 cos(t), 2sen(t))
1 Curvas no R n 1. Esboce a imagem das seguintes curvas para t R a) γ(t) = (1, t) b) γ(t) = (t, cos(t)) c) γ(t) = (t, t ) d) γ(t) = (cos(t), sen(t), 2t) e) γ(t) = (t, 2t, 3t) f) γ(t) = ( 2 cos(t), 2sen(t))
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
APLICAÇÕES NA GEOMETRIA ANALÍTICA
 4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
4 APLICAÇÕES NA GEOMETRIA ANALÍTICA Gil da Costa Marques 4.1 Geometria Analítica e as Coordenadas Cartesianas 4. Superfícies 4..1 Superfícies planas 4.. Superfícies limitadas e não limitadas 4.3 Curvas
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
14 AULA. Vetor Gradiente e as Derivadas Direcionais LIVRO
 1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
1 LIVRO Vetor Gradiente e as Derivadas Direcionais 14 AULA META Definir o vetor gradiente de uma função de duas variáveis reais e interpretá-lo geometricamente. Além disso, estudaremos a derivada direcional
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
1. Extremos de uma função
 Máximo e Mínimo de Funções de Várias Variáveis 1. Extremos de uma função Def: Máximo Absoluto, mínimo absoluto Seja f : D R R função (i) Dizemos que f assume um máximo absoluto (ou simplesmente um máximo)
Máximo e Mínimo de Funções de Várias Variáveis 1. Extremos de uma função Def: Máximo Absoluto, mínimo absoluto Seja f : D R R função (i) Dizemos que f assume um máximo absoluto (ou simplesmente um máximo)
Exercício 1: Encontre o ângulo emtre os vetores v e w em cada um dos seguintes:
 Universidade Federal do Paraná 2 semestre 2016. Algebra Linear Olivier Brahic Lista de exercícios 1 Ortogonalidade Exercícios da Seção 5.1 Exercício 1: Encontre o ângulo emtre os vetores v e w em cada
Universidade Federal do Paraná 2 semestre 2016. Algebra Linear Olivier Brahic Lista de exercícios 1 Ortogonalidade Exercícios da Seção 5.1 Exercício 1: Encontre o ângulo emtre os vetores v e w em cada
Sistemas de equações lineares com três variáveis
 18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
18 Sistemas de equações lineares com três variáveis Sumário 18.1 Introdução....................... 18. Sistemas de duas equações lineares........... 18. Sistemas de três equações lineares........... 8
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Aula 4 Colinearidade, coplanaridade e dependência linear
 Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Aula 4 Colinearidade, coplanaridade e dependência linear MÓDULO 1 - AULA 4 Objetivos Compreender os conceitos de independência e dependência linear. Estabelecer condições para determinar quando uma coleção
Álgebra Linear e Geometria Anaĺıtica. Vetores, Retas e Planos
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 3 Vetores, Retas e lanos roduto interno em R n [3 01] Dados os vetores X =
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 3 Vetores, Retas e lanos roduto interno em R n [3 01] Dados os vetores X =
Aula 10 Produto interno, vetorial e misto -
 MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Aula 15 Superfícies quádricas - cones quádricos
 Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Aula 15 Superfícies quádricas - cones quádricos MÓDULO - AULA 15 Objetivos Definir e estudar os cones quádricos identificando suas seções planas. Analisar os cones quádricos regrados e de revolução. Cones
Geometria Analítica. Superfícies. Prof Marcelo Maraschin de Souza
 Geometria Analítica Superfícies Prof Marcelo Maraschin de Souza Superfícies Quadráticas A equação geral do 2º grau nas três variáveis x,y e z ax 2 + by 2 + cz 2 + 2dxy + 2exz + 2fyz + mx + ny + pz + q
Geometria Analítica Superfícies Prof Marcelo Maraschin de Souza Superfícies Quadráticas A equação geral do 2º grau nas três variáveis x,y e z ax 2 + by 2 + cz 2 + 2dxy + 2exz + 2fyz + mx + ny + pz + q
Ricardo Bianconi. Fevereiro de 2015
 Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
Seções Cônicas Ricardo Bianconi Fevereiro de 2015 Uma parte importante da Geometria Analítica é o estudo das curvas planas e, em particular, das cônicas. Neste texto estudamos algumas propriedades das
4.1 posição relativas entre retas
 4 P O S I Ç Õ E S R E L AT I VA S Nosso objetivo nesta seção é entender a posição relativa entre duas retas, dois planos e ou uma reta e um plano, isto é, se estes se interseccionam, se são paralelos,
4 P O S I Ç Õ E S R E L AT I VA S Nosso objetivo nesta seção é entender a posição relativa entre duas retas, dois planos e ou uma reta e um plano, isto é, se estes se interseccionam, se são paralelos,
Aula 18 Cilindros quádricos e identificação de quádricas
 MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
MÓDULO 2 - AULA 18 Aula 18 Cilindros quádricos e identificação de quádricas Objetivos Estudar os cilindros quádricos, analisando suas seções planas paralelas aos planos coordenados e estabelecendo suas
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
1. Qual éolugar geométrico dos pontosequidistantes de A = (1,0,0),B = ( 1,1,0),C = (0,2,0) e D = (0,0,0).
 Universidade Federal Fluminense PURO Instituto de Ciência e Tecnologia Departamento de Física e Matemática Geometria Analítica e Cálculo Vetorial 7 a Lista de Exercícios 1/2011 Distâncias Observação: Todos
Universidade Federal Fluminense PURO Instituto de Ciência e Tecnologia Departamento de Física e Matemática Geometria Analítica e Cálculo Vetorial 7 a Lista de Exercícios 1/2011 Distâncias Observação: Todos
MAT Poli Roteiro de Estudos sobre as Cônicas
 MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
Cálculo a Várias Variáveis I - MAT Cronograma para P2: aulas teóricas (segundas e quartas)
 Cálculo a Várias Variáveis I - MAT 116 0141 Cronograma para P: aulas teóricas (segundas e quartas) Aula 10 4 de março (segunda) Aula 11 6 de março (quarta) Referências: Cálculo Vol James Stewart Seções
Cálculo a Várias Variáveis I - MAT 116 0141 Cronograma para P: aulas teóricas (segundas e quartas) Aula 10 4 de março (segunda) Aula 11 6 de março (quarta) Referências: Cálculo Vol James Stewart Seções
GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA. 03/01/ GGM - UFF Dirce Uesu Pesco
 GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA 03/01/2013 - GGM - UFF Dirce Uesu Pesco CÔNICAS Equação geral do segundo grau a duas variáveis x e y onde A, B e C não são simultaneamente
GEOMETRIA ANALÍTICA E CÁLCULO VETORIAL GEOMETRIA ANALÍTICA BÁSICA 03/01/2013 - GGM - UFF Dirce Uesu Pesco CÔNICAS Equação geral do segundo grau a duas variáveis x e y onde A, B e C não são simultaneamente
Álgebra Linear e Geometria Anaĺıtica. Cónicas e Quádricas
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
Produto Interno - Mauri C. Nascimento - Depto. de Matemática - FC UNESP Bauru
 1 Produto Interno - Mauri C. Nascimento - Depto. de Matemática - FC UNESP Bauru Neste capítulo vamos considerar espaços vetoriais sobre K, onde K = R ou K = C, ou seja, os espaços vetoriais podem ser reais
1 Produto Interno - Mauri C. Nascimento - Depto. de Matemática - FC UNESP Bauru Neste capítulo vamos considerar espaços vetoriais sobre K, onde K = R ou K = C, ou seja, os espaços vetoriais podem ser reais
Superfícies e Curvas no Espaço
 Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Notas de Aula - Espaços Vetoriais I
 Notas de Aula - Espaços Vetoriais I 1 O espaço vetorial R 2 A definição de espaço vetorial que veremos adiante faz uso da ideia de operações definidas sobre um conjunto. Iniciaremos nosso estudo explorando
Notas de Aula - Espaços Vetoriais I 1 O espaço vetorial R 2 A definição de espaço vetorial que veremos adiante faz uso da ideia de operações definidas sobre um conjunto. Iniciaremos nosso estudo explorando
Cálculo III. Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani
 Cálculo III Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani Primeiro Semestre de 21 2 Sumário 1 A Fórmula de Taylor 5 2 Máximos e mínimos 13 3 O problema de um vínculo 29 4 O problema de dois
Cálculo III Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani Primeiro Semestre de 21 2 Sumário 1 A Fórmula de Taylor 5 2 Máximos e mínimos 13 3 O problema de um vínculo 29 4 O problema de dois
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
1 Diferenciabilidade e derivadas direcionais
 UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani
 Cálculo III Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani Sumário 1 A Fórmula de Taylor 5 1.1 Fórmula e polinômio de Taylor para funções de uma variável.................. 5 1. Fórmula e polinômio
Cálculo III Alexandre N. Carvalho, Wagner V. L. Nunes e Sérgio L. Zani Sumário 1 A Fórmula de Taylor 5 1.1 Fórmula e polinômio de Taylor para funções de uma variável.................. 5 1. Fórmula e polinômio
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - ula 2 1. Vetores. 2. Distâncias. 3. Módulo de um vetor. Roteiro 1 Vetores Nesta seção lembraremos brevemente os vetores e suas operações básicas. Definição de vetor. Vetor determinado
Álgebra Linear I - ula 2 1. Vetores. 2. Distâncias. 3. Módulo de um vetor. Roteiro 1 Vetores Nesta seção lembraremos brevemente os vetores e suas operações básicas. Definição de vetor. Vetor determinado
Álgebra Linear I - Aula 9. Roteiro
 Álgebra Linear I - Aula 9 1. Distância entre duas retas. 2. A perpendicular comum a duas retas. 3. Posições relativas. Roteiro 1 Distância entre duas retas r e s Calcularemos a distância entre duas retas
Álgebra Linear I - Aula 9 1. Distância entre duas retas. 2. A perpendicular comum a duas retas. 3. Posições relativas. Roteiro 1 Distância entre duas retas r e s Calcularemos a distância entre duas retas
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Curso de Geometria Analítica
 Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 10 - Posições relativas entre Pontos Retas e Planos. I.
Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática - Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 10 - Posições relativas entre Pontos Retas e Planos. I.
Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105
 Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105 2 de fevereiro de 2017 Esta lista contém exercícios de [1], [2] e [3]. Os exercícios estão separados por aulas em ordem decrescente de aula.
Lista de Exercícios Geometria Analítica e Álgebra Linear MAT 105 2 de fevereiro de 2017 Esta lista contém exercícios de [1], [2] e [3]. Os exercícios estão separados por aulas em ordem decrescente de aula.
Análise Convexa. 1. Conjuntos convexos 1.1. Casca convexa, ponto extremo, cone. 2. Hiperplanos: suporte, separador, teorema da separação
 Análise Convexa 1. Conjuntos convexos 1.1. Casca convexa, ponto extremo, cone 2. Hiperplanos: suporte, separador, teorema da separação 3. Funções convexas 4. Teoremas de funções convexas 5. Conjunto poliedral
Análise Convexa 1. Conjuntos convexos 1.1. Casca convexa, ponto extremo, cone 2. Hiperplanos: suporte, separador, teorema da separação 3. Funções convexas 4. Teoremas de funções convexas 5. Conjunto poliedral
Universidade dos Açores Departamento de Matemática Curso de Informática Redes e Multimédia Cálculo II
 Universidade dos Açores Departamento de Matemática Curso de Informática Redes e Multimédia Cálculo II Tema : Cálculo diferencial de funções de duas variáveis Este teto foi retirado do manual de apoio à
Universidade dos Açores Departamento de Matemática Curso de Informática Redes e Multimédia Cálculo II Tema : Cálculo diferencial de funções de duas variáveis Este teto foi retirado do manual de apoio à
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Equações não lineares
 DMPA IME UFRGS Cálculo Numérico Índice Raizes de polinômios 1 Raizes de polinômios 2 raizes de polinômios As equações não lineares constituídas por polinômios de grau n N com coeficientes complexos a n,a
DMPA IME UFRGS Cálculo Numérico Índice Raizes de polinômios 1 Raizes de polinômios 2 raizes de polinômios As equações não lineares constituídas por polinômios de grau n N com coeficientes complexos a n,a
REVISÃO - DESIGUALDADE, MÓDULO E FUNÇÕES
 REVISÃO - DESIGUALDADE, MÓDULO E FUNÇÕES Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br 1 REVISÃO
REVISÃO - DESIGUALDADE, MÓDULO E FUNÇÕES Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br 1 REVISÃO
Simulado 1 Matemática IME Soluções Propostas
 Simulado 1 Matemática IME 2012 Soluções Propostas 1 Para 0, temos: para cada um dos elementos de, valores possíveis em (não precisam ser distintos entre si, apenas precisam ser pertencentes a, pois não
Simulado 1 Matemática IME 2012 Soluções Propostas 1 Para 0, temos: para cada um dos elementos de, valores possíveis em (não precisam ser distintos entre si, apenas precisam ser pertencentes a, pois não
MAP2110 Matemática e Modelagem
 1 Reta e Plano MAP2110 Matemática e Modelagem Folha de Estudos 4 1 o semestre de 2010 Prof. Claudio H. Asano 1.1 Encontre as equações paramétricas e simétricas da reta que passa pelos pontos A e B. Em
1 Reta e Plano MAP2110 Matemática e Modelagem Folha de Estudos 4 1 o semestre de 2010 Prof. Claudio H. Asano 1.1 Encontre as equações paramétricas e simétricas da reta que passa pelos pontos A e B. Em
Geometria Analítica II - Aula
 Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Geometria Analítica II - Aula 0 94 Aula Coordenadas Cilíndricas e Esféricas Para descrever de modo mais simples algumas curvas e regiões no plano introduzimos anteriormente as coordenadas polares. No espaço
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
MAT Cálculo a Várias Variáveis I. Período
 MAT116 - Cálculo a Várias Variáveis I Integração Tripla Período 01.1 1 Exercícios Exercício 1 Considere a região = {(x, y, z) R 3 x + y z 1}. 9 1. Calcule o volume de.. Determine o valor de b de forma
MAT116 - Cálculo a Várias Variáveis I Integração Tripla Período 01.1 1 Exercícios Exercício 1 Considere a região = {(x, y, z) R 3 x + y z 1}. 9 1. Calcule o volume de.. Determine o valor de b de forma
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
3. Obter a equação do plano que contém os pontos A = (3, 0, 1), B = (2, 1, 1) e C = (3, 2, 2).
 Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
10 AULA. Funções de Varias Variáveis Reais a Valores LIVRO
 1 LIVRO Funções de Varias Variáveis Reais a Valores Reais META Estudar o domínio, o gráfico e as curvas de níveis de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de domínio
1 LIVRO Funções de Varias Variáveis Reais a Valores Reais META Estudar o domínio, o gráfico e as curvas de níveis de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de domínio
Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016
 Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016 Parte A 1. Identifique e esboce as superfícies quádricas x 2 + 4y 2 + 9z 2 = 1 x 2 y 2 + z 2 = 1 (c) y = 2x 2 + z 2 (d) x = y 2 z 2
Lista de Exercícios de Cálculo 3 Módulo 1 - Terceira Lista - 02/2016 Parte A 1. Identifique e esboce as superfícies quádricas x 2 + 4y 2 + 9z 2 = 1 x 2 y 2 + z 2 = 1 (c) y = 2x 2 + z 2 (d) x = y 2 z 2
Lista Determine o volume do sólido contido no primeiro octante limitado pelo cilindro z = 9 y 2 e pelo plano x = 2.
 UFPR - Universidade Federal do Paraná Departamento de Matemática CM042 - Cálculo II (Turma B) Prof. José Carlos Eidam Lista 3 Integrais múltiplas. Calcule as seguintes integrais duplas: (a) R (2y 2 3x
UFPR - Universidade Federal do Paraná Departamento de Matemática CM042 - Cálculo II (Turma B) Prof. José Carlos Eidam Lista 3 Integrais múltiplas. Calcule as seguintes integrais duplas: (a) R (2y 2 3x
Ponto 1) Representação do Ponto
 Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
Ponto 1) Representação do Ponto Universidade Federal de Pelotas Cálculo com Geometria Analítica I Prof a : Msc. Merhy Heli Rodrigues Plano Cartesiano, sistemas de coordenadas: pontos e retas Na geometria
SEMINÁRIOS DE ENSINO DE MATEMÁTICA (SEMA FEUSP) SERÁ O INFINITO UM PONTO?
 SMINÁRIS D NSIN D MATMÁTICA (SMA FUSP) SRÁ INFINIT UM PNT? Sergio Alves IM USP salves@ime.usp.br Inspirado no artigo de mesmo título publicado na Revista ducação e Matemática, Nº 95, Portugal (2007) :
SMINÁRIS D NSIN D MATMÁTICA (SMA FUSP) SRÁ INFINIT UM PNT? Sergio Alves IM USP salves@ime.usp.br Inspirado no artigo de mesmo título publicado na Revista ducação e Matemática, Nº 95, Portugal (2007) :
Lista 3: Geometria Analítica
 Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA 1 a LISTA DE EXERCÍCIOS DE MAT 17 1. Suponha que uma força de 1 newtons é aplicada em um objeto ao longo do
Álgebra Linear. Sérgio L. Zani
 Álgebra Linear Sérgio L Zani Segundo Semestre de 2001 2 Sumário 1 Espaços Vetoriais 5 11 Introdução e Exemplos 5 12 Propriedades 8 2 Subespaços Vetoriais 9 21 Introdução e Exemplos 9 22 Propriedades 10
Álgebra Linear Sérgio L Zani Segundo Semestre de 2001 2 Sumário 1 Espaços Vetoriais 5 11 Introdução e Exemplos 5 12 Propriedades 8 2 Subespaços Vetoriais 9 21 Introdução e Exemplos 9 22 Propriedades 10
GGM Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 20/12/2012- GGM - UFF Dirce Uesu
 GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
GGM0016 Geometria Analítica e Cálculo Vetorial Geometria Analítica Básica 0/1/01- GGM - UFF Dirce Uesu CÔNICAS DEFINIÇÃO GEOMÉTRICA Exercício: Acesse o sitio abaixo e use o programa: http://www.professores.uff.br/hjbortol/disciplinas/005.1/gma04096/applets/conic/co
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho
 Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
Álgebra Linear - 2 a lista de exercícios Prof. - Juliana Coelho 1 - Verifique que os conjuntos V abaixo com as operações dadas não são espaços vetoriais explicitando a falha em alguma das propriedades.
n. 18 Estudo da reta: ângulo, paralelismo, ortogonalidade, coplanaridade e interseção entre retas Ângulo entre duas retas
 n. 18 Estudo da reta: ângulo, paralelismo, ortogonalidade, coplanaridade e interseção entre retas Ângulo entre duas retas Sejam as retas r1, que passa pelo ponto A (x1, y1, z1) e tem a direção de um vetor
n. 18 Estudo da reta: ângulo, paralelismo, ortogonalidade, coplanaridade e interseção entre retas Ângulo entre duas retas Sejam as retas r1, que passa pelo ponto A (x1, y1, z1) e tem a direção de um vetor
Números Reais. Víctor Arturo Martínez León b + c ad + bc. b c
 Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Instituto de Fıśica UFRJ Mestrado em Ensino profissional
 Instituto de Fıśica UFRJ Mestrado em Ensino profissional Tópicos de Fıśica Clássica II 1 a Lista de Exercıćios egundo emestre de 2008 Prof. A C Tort Exercıćio 1 O operador nabla Começamos definindo o operador
Instituto de Fıśica UFRJ Mestrado em Ensino profissional Tópicos de Fıśica Clássica II 1 a Lista de Exercıćios egundo emestre de 2008 Prof. A C Tort Exercıćio 1 O operador nabla Começamos definindo o operador
n. 17 ESTUDO DA RETA: equações Uma direção e um ponto determinam uma reta Dois pontos determinam uma reta
 n. 17 ESTUDO DA RETA: equações Uma direção e um ponto determinam uma reta Dois pontos determinam uma reta Equação geral de uma reta Para determinar a equação geral de uma reta utilizamos os conceitos relacionados
n. 17 ESTUDO DA RETA: equações Uma direção e um ponto determinam uma reta Dois pontos determinam uma reta Equação geral de uma reta Para determinar a equação geral de uma reta utilizamos os conceitos relacionados
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.6 Derivadas Direcionais e o Vetor Gradiente Nesta seção, vamos aprender como encontrar: As taxas de variação de uma função de duas ou mais variáveis
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.6 Derivadas Direcionais e o Vetor Gradiente Nesta seção, vamos aprender como encontrar: As taxas de variação de uma função de duas ou mais variáveis
Figura disponível em: <http://soumaisenem.com.br/fisica/conhecimentos-basicos-e-fundamentais/grandezas-escalares-egrandezas-vetoriais>.
 n. 7 VETORES vetor é um segmento orientado; são representações de forças, as quais incluem direção, sentido, intensidade e ponto de aplicação; o módulo, a direção e o sentido caracterizam um vetor: módulo
n. 7 VETORES vetor é um segmento orientado; são representações de forças, as quais incluem direção, sentido, intensidade e ponto de aplicação; o módulo, a direção e o sentido caracterizam um vetor: módulo
Bacharelado em Ciência e Tecnologia 2ª Lista de Exercícios - Geometria Analítica
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO DEPARTAMENTO DE CIÊNCIAS AMBIENTAIS Bacharelado em Ciência e Tecnologia ª Lista de Exercícios - Geometria Analítica 008. ) São dados os pontos
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO DEPARTAMENTO DE CIÊNCIAS AMBIENTAIS Bacharelado em Ciência e Tecnologia ª Lista de Exercícios - Geometria Analítica 008. ) São dados os pontos
O PLANO...> Equação do Plano
 Equação do Plano O PLANO...> Equação vetorial de um Plano Equações Paramétricas do Plano Equações Geral de um Plano Casos Particulares da Equações Geral de um Plano Vetor normal a um plano Feixe de Planos
Equação do Plano O PLANO...> Equação vetorial de um Plano Equações Paramétricas do Plano Equações Geral de um Plano Casos Particulares da Equações Geral de um Plano Vetor normal a um plano Feixe de Planos
Resumo com exercícios resolvidos dos assuntos:
 www.engenhariafacil.weebly.com (0)- Considerações iniciais: Resumo com exercícios resolvidos dos assuntos: Máximos e mínimos absolutos e Multiplicador de Lagrange -Grande parte das funções não possui máximos
www.engenhariafacil.weebly.com (0)- Considerações iniciais: Resumo com exercícios resolvidos dos assuntos: Máximos e mínimos absolutos e Multiplicador de Lagrange -Grande parte das funções não possui máximos
Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b. a) a = 3, b, b R. b) a = 3 e b = 1. c) a = 3 e b 1. d) a 3
 01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
01 Na forma reduzida, temos: (r) y = 3x + 1 (s) y = ax + b a) a = 3, b, b R b) a = 3 e b = 1 c) a = 3 e b 1 d) a 3 1 0 y = 3x + 1 m = 3 A equação que apresenta uma reta com o mesmo coeficiente angular
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.2 Limites e Continuidade Nesta seção, aprenderemos sobre: Limites e continuidade de vários tipos de funções. LIMITES E CONTINUIDADE Vamos comparar o
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.2 Limites e Continuidade Nesta seção, aprenderemos sobre: Limites e continuidade de vários tipos de funções. LIMITES E CONTINUIDADE Vamos comparar o
NOTAÇÕES. R : conjunto dos números reais C : conjunto dos números complexos
 NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
Geometria Analítica. Cônicas. Prof. Vilma Karsburg
 Geometria Analítica Cônicas Prof. Vilma Karsburg Cônicas Sejam duas retas e e g concorrentes em O e não perpendiculares. Considere e fixa e g girar 360 em torno de e, mantendo constante o ângulo entre
Geometria Analítica Cônicas Prof. Vilma Karsburg Cônicas Sejam duas retas e e g concorrentes em O e não perpendiculares. Considere e fixa e g girar 360 em torno de e, mantendo constante o ângulo entre
Matriz Hessiana e Aplicações
 Matriz Hessiana e Aplicações Sadao Massago Dezembro de 200 Sumário Introdução 2 Matriz Jacobiana 3 Matriz hessiana 2 4 Talor de primeira e segunda ordem 2 5 Classicação dos pontos críticos 3 A Procedimeno
Matriz Hessiana e Aplicações Sadao Massago Dezembro de 200 Sumário Introdução 2 Matriz Jacobiana 3 Matriz hessiana 2 4 Talor de primeira e segunda ordem 2 5 Classicação dos pontos críticos 3 A Procedimeno
6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES
 47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA
 EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
EXERCICIOS DE APROFUNDAMENTO - MATEMÁTICA - RETA - 015 1. (Unicamp 015) Seja r a reta de equação cartesiana x y 4. Para cada número real t tal que 0 t 4, considere o triângulo T de vértices em (0, 0),
O problema proposto possui alguma solução? Se sim, quantas e quais são elas?
 PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
PROVA PARA OS ALUNOS DE 3º ANO DO ENSINO MÉDIO 1) Considere o seguinte problema: Vitor ganhou R$ 3,20 de seu pai em moedas de 5 centavos, 10 centavos e 25 centavos. Se recebeu um total de 50 moedas, quantas
MAT 105- Lista de Exercícios
 1 MAT 105- Lista de Exercícios 1. Determine as áreas dos seguintes polígonos: a) triângulo de vértices (2,3), (5,7), (-3,4). Resp. 11,5 b) triângulo de vértices (0,4), (-8,0), (-1,-4). Resp. 30 c) quadrilátero
1 MAT 105- Lista de Exercícios 1. Determine as áreas dos seguintes polígonos: a) triângulo de vértices (2,3), (5,7), (-3,4). Resp. 11,5 b) triângulo de vértices (0,4), (-8,0), (-1,-4). Resp. 30 c) quadrilátero
Então (τ x, ) é um conjunto dirigido e se tomarmos x U U, para cada U vizinhança de x, então (x U ) U I é uma rede em X.
 1. Redes Quando trabalhamos no R n, podemos testar várias propriedades de um conjunto A usando seqüências. Por exemplo: se A = A, se A é compacto, ou se a função f : R n R m é contínua. Mas, em espaços
1. Redes Quando trabalhamos no R n, podemos testar várias propriedades de um conjunto A usando seqüências. Por exemplo: se A = A, se A é compacto, ou se a função f : R n R m é contínua. Mas, em espaços
Algebra Linear S ergio Lu ıs Zani
 Álgebra Linear Sérgio Luís Zani 2 Sumário 1 Espaços Vetoriais 7 1.1 Introdução e Exemplos.......................... 7 1.2 Propriedades............................... 12 1.3 Exercícios.................................
Álgebra Linear Sérgio Luís Zani 2 Sumário 1 Espaços Vetoriais 7 1.1 Introdução e Exemplos.......................... 7 1.2 Propriedades............................... 12 1.3 Exercícios.................................
x 1 3x 2 2x 3 = 0 2 x 1 + x 2 x 3 6x 4 = 2 6 x x 2 3x 4 + x 5 = 1 ( f ) x 1 + 2x 2 3x 3 = 6 2x 1 x 2 + 4x 3 = 2 4x 1 + 3x 2 2x 3 = 4
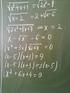 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-47 Álgebra Linear para Engenharia I Primeira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS. Resolva os seguintes sistemas:
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
Lista de exercícios 7 Independência Linear.
 Universidade Federal do Paraná semestre 6. Algebra Linear Olivier Brahic Lista de exercícios 7 Independência Linear. Exercício : Determine se os seguintes vetores são linearmente independentes em R : (
Universidade Federal do Paraná semestre 6. Algebra Linear Olivier Brahic Lista de exercícios 7 Independência Linear. Exercício : Determine se os seguintes vetores são linearmente independentes em R : (
Uma breve história da Geometria Diferencial (até meados do s
 Uma breve história da Geometria Diferencial (até meados do século XIX) 29 de novembro de 2006 Os postulados de Euclides ( 300 a.c.) Os postulados de Euclides ( 300 a.c.) 1- Dois pontos distintos determinam
Uma breve história da Geometria Diferencial (até meados do século XIX) 29 de novembro de 2006 Os postulados de Euclides ( 300 a.c.) Os postulados de Euclides ( 300 a.c.) 1- Dois pontos distintos determinam
Geometria Analítica. Números Reais. Faremos, neste capítulo, uma rápida apresentação dos números reais e suas propriedades, mas no sentido
 Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações.
 Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações. 11º Ano Paralelismo e perpendicularidade de retas No espaço, duas
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria IV Paralelismo e perpendicularidade. Sistemas de equações. 11º Ano Paralelismo e perpendicularidade de retas No espaço, duas
Todos os exercícios sugeridos nesta apostila se referem ao volume 3. MATEMÁTICA III 1 ESTUDO DA CIRCUNFERÊNCIA
 DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
DEFINIÇÃO... EQUAÇÃO REDUZIDA... EQUAÇÃO GERAL DA CIRCUNFERÊNCIA... 3 RECONHECIMENTO... 3 POSIÇÃO RELATIVA ENTRE PONTO E CIRCUNFERÊNCIA... 1 POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA... 17 PROBLEMAS
Funções de duas (ou mais)
 Lista 5 - CDI II Funções de duas (ou mais) variáveis. Seja f(x, y) = x+y x y, calcular: f( 3, 4) f( 2, 3 ) f(x +, y ) f( x, y) f(x, y) 2. Seja g(x, y) = x 2 y, obter: g(3, 5) g( 4, 9) g(x + 2, 4x + 4)
Lista 5 - CDI II Funções de duas (ou mais) variáveis. Seja f(x, y) = x+y x y, calcular: f( 3, 4) f( 2, 3 ) f(x +, y ) f( x, y) f(x, y) 2. Seja g(x, y) = x 2 y, obter: g(3, 5) g( 4, 9) g(x + 2, 4x + 4)
Cálculo Diferencial e Integral Química Notas de Aula
 Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Matemática. Resolução das atividades complementares. M21 Geometria Analítica: Cônicas
 Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
Resolução das atividades complementares Matemática M Geometria Analítica: Cônicas p. FGV-SP) Determine a equação da elipse de centro na origem que passa pelos pontos A, 0), B, 0) e C0, ). O centro da elipse
Matemática I Cálculo I Unidade B - Cônicas. Profª Msc. Débora Bastos. IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE
 Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
Unidade B - Cônicas Profª Msc. Débora Bastos IFRS Campus Rio Grande FURG UNIVERSIDADE FEDERAL DO RIO GRANDE 22 12. Cônicas São chamadas cônicas as curvas resultantes do corte de um cone duplo com um plano.
