X - D U A L I D A D E
|
|
|
- Cíntia Olivares Bayer
- 9 Há anos
- Visualizações:
Transcrição
1 X - D U A L I D A D E 1 - Introdução. Regras de transformação "Primal - Dual" Consideremos os dois problemas P1 e P2 de Programação Linear seguintes: P1 : n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk bi k = 1 Xk 0 i = 1, 2,..., m k = 1, 2,..., n P2 : m Minimizar G = Σ bi. Ui i = 1 m Σ aik. Ui ck i = 1 Ui 0 k = 1, 2,..., n i = 1, 2,..., m ou, utilizando a notação matricial: P1 : Maximizar F = C. X A. X b X 0 n P2 : Minimizar G = bt. U AT. U CT U 0 m 100
2 Na representação anterior, o vector das incógnitas de P1, X, é um vector coluna ( n x 1 ), o vector das incógnitas de P2, U, é um vector coluna ( m x 1 ), C é um vector linha ( 1 x n ), A é uma matriz ( m x n ) e b é um vector coluna ( m x 1 ). De notar que 0 n é o vector nulo do tipo ( n x 1 ) e que 0 m é o vector nulo do tipo ( m x 1 ). P1 e P2 formam um par de problemas duais, isto é, P1 é o problema dual de P2 e vice-versa. Algumas Regras de Transformação "Primal-Dual" podem ser enunciadas: R1 : A cada restrição do problema primal corresponde uma variável do problema dual. A cada variável do problema primal corresponde uma restrição do problema dual. R1 : restrição P variável D ; variável P restrição D R2 : A matriz dos coeficientes das restrições do problema dual é a transposta da matriz dos coeficientes das restrições do correspondente problema primal. R2 : A P = AT D ; A D = AT P R3 : Os termos independentes das restrições de um dos problemas (primal/dual) são os coeficientes da função objectivo no outro problema (dual/primal). R3 : Termos independentes P Coeficientes da f.o. D Termos independentes D Coeficientes da f.o. P R4 : A um problema primal de maximização com restrições do tipo e variáveis não negativas, corresponde um problema dual de minimização com restrições do tipo e variáveis não negativas. R4 : Problema Primal Max restrições ' ' variáveis ' 0 ' Problema Dual Min restrições ' ' variáveis ' 0 ' Para podermos aplicar as 'Regras de Transformação' apresentadas, resolvamos os seguintes exercícios: 101
3 Ex.1 : Escreva o dual do problema de Programação Linear seguinte: MAX F = 2. X X2 2. X1-3. X X X X X X1-2. X2 7 X1, X2 0. Resolução : MIN G = 4. U U U U4 2. U1-1. U U U U U U3-2. U4 3 U1, U2, U3, U4 0. Note-se que o problema primal apresentado tem m = 4 (número de equações) e n = (número de incógnitas), pelo que a sua resolução pelo Algoritmo Simplex Revisto implicaria a manipulação (incluindo inversão) de matrizes B ( 4 x 4 ). O problema dual correspondente tem m = 2 (número de equações) e n = (número de incógnitas), pelo que a sua resolução pelo Algoritmo Simplex Revisto implicaria a manipulação de matrizes B ( 2 x 2 )! Assim, a priori, é mais fácil resolver o problema dual, já que este corresponderá a um menor esforço de cálculo... Posteriormente retomaremos esta questão. Ao observarmos as 'Regras de Transformação' apresentadas, em particular a regra R4 : Problema Primal Max restrições ' ' variáveis ' 0 ' Problema Dual Min restrições ' ' variáveis ' 0 ' pode surgir-nos uma interrogação: O que acontece se uma das restrições for uma desigualdade de 'sentido oposto' à regra " Max ; restrição / Min ; restrição "? Para tentarmos responder a esta questão, poderemos considerar o seguinte exercício:, 102
4 Ex.2 : Escreva o dual do problema de Programação Linear seguinte: MIN F = 4. X X X3 2. X X X X1-1. X X X X3 5 X1, X2, X3, X X2-3. X3 4 Resolução : A terceira restrição pode ser re-escrita de modo a respeitar a regra " Min ; restrição " : 1. X1-3. X2-4. X3-5. Ter-se-ia, então, o seguinte problema dual: MAX G = 5. U U2-5. U U4 2. U U U U1-1. U2-3. U U U1-4. U3-3. U4 1 U1, U2, U3, U4 0. Para mantermos as regras anteriormente enunciadas, muito especialmente, R2 e R3 deveríamos ter os simétricos dos coeficientes de U3 (relativamente ao problema dual apresentado), o que se consegue facilmente considerando U3 0, ou seja, MAX G = 5. U U U U4 2. U U2-1. U U1-1. U U U U U3-3. U4 1 U1, U2, U4 0 ; U3 0. Poderemos, assim, enunciar uma nova Regra de Transformação "Primal-Dual" : R5 : A uma restrição do problema primal de tipo 'oposto' à regra " Max / restrições ; Min / restrições " corresponderá no problema dual, uma variável não positiva, e vice-versa. 103
5 R5 : Problema Primal Max restrição ' ' Problema Dual Min variável ' 0 ' Problema Primal Max variável ' 0 ' Problema Dual Min restrição ' ' Aproveitemos o problema dual do exercício nº 2 anterior e determinemos o correspondente problema dual: MAX G = 5. U U U U4 2. U U2-1. U U1-1. U U U U U3-3. U4 1 U1, U2, U4 0 ; U3 0. Resolução : MIN F = 4. X X X3 2. X X X X1-1. X X X X3 5 X1, X2, X3, X X2-3. X3 4 F Não sei se notaram, mas o dual do 'problema dual' é igual ao 'problema primal'! Para aplicarmos as 'regras de transformação' apresentadas, resolvamos agora o exercício seguinte: I 104
6 Ex.3 Escreva o dual do problema de Programação Linear seguinte: MAX G = 2. X X X3 3. X1-2. X X1-1. X X X X2-1. X3 4 X1, X2 0 ; X3 0. Resolução : MIN F = 5. U U U3 3. U U U U1-1. U U U2-1. U3 4 U1, U3 0 ; U2 0. Já sabemos o que fazer se uma das restrições for uma desigualdade de 'sentido oposto' à regra " Max ; restrição / Min ; restrição ". Mas, o que fazer se se tiver uma restrição do tipo ' = '? Para tentarmos responder a esta questão, poderemos considerar o seguinte exercício: Ex.4 : Escreva o dual do problema de Programação Linear seguinte: MAX F = 2. X X2-1. X X X1-1. X X1-2. X2 = 3 3. X X2 7 X1, X2, X3, X
7 Resolução : A terceira restrição pode ser re-escrita do modo seguinte: 2. X1-2. X X1-2. X2 3, ou, equivalentemente: 2. X1-2. X X X2-3. Ter-se-ia, então, o seguinte problema: MAX F = 2. X X2-1. X X X1-1. X X1-2. X X X X X2 7 X1, X2 0. A este problema corresponde o seguinte dual: MIN G = 5. U U U3-3. U U5-1. U U U3-2. U U U1-1. U2-2. U U U5 3 U1, U2, U3, U4, U5 0. Os coeficientes das variáveis não negativas U3 e U4 são simétricos, pelo que poderemos fazer a substituição V = U3 - U4, com V R: MIN G = 5. U U V + 7. U5-1. U U V + 3. U U1-1. U2-2. V + 5. U5 3 U1, U2, U5 0 ; V R. Se designarmos V por U3 e U5 por U4, poderemos escrever o problema dual do problema dado na forma seguinte: 106
8 MIN G = 5. U U U U4-1. U U U U U1-1. U2-2. U U4 3 U1, U2, U4 0 ; U3 R. Poderemos, assim, enunciar uma nova Regra de Transformação "Primal-Dual" : R6 : A uma restrição do problema primal de tipo 'igualdade' corresponderá no problema dual, uma variável livre, e vice-versa. R6 : Problema Primal restrição ' = ' Problema Dual variável ' R ' Exercitemos a utilização das 'regras de transformação' apresentadas, com o exercício seguinte: Ex.5 Escreva o dual do problema de Programação Linear seguinte: MIN F = 2. X X X X4 2. X1-3. X2-5. X X1-2. X X X X3-1. X4 = 7 X1, X4 0 ; X2 0; X3 R. Resolução : MAX G = 20. U U U3 2. U U U U U1-2. U U3 = 4 1. U2-1. U3 2 U1 0, U2 0 ; U3 R. Sintetizemos, agora as Relações "Primal - Dual" no quadro seguinte: 107
9 Relações ' Primal Dual ' Problema de Maximização Problema de Minimização i-ésima restrição i = 1, 2,..., m. k-ésima variável k = 1, 2,..., m. matriz dos coeficientes das restrições A ( m x n ) coeficientes da função objectivo c k, C ( 1 x n ) k = 1, 2,..., n. termos independentes das restrições b i, b ( m x 1 ) i = 1, 2,..., m. = 0 R 0 0 R 0 = i-ésima variável i = 1, 2,..., m. k-ésima restrição k = 1, 2,..., m. matriz dos coeficientes das restrições AT ( n x m ) termos independentes das restrições c k, CT ( 1 x n ) k = 1, 2,..., n. coeficientes da função objectivo b i, bt ( 1 x m ) i = 1, 2,..., n. Nota: Quadro adaptado de 'Programação Linear' ( vol. II ), Guerreiro et al, Mc Graw Hill E aproveitemos as 'regras de transformação' apresentadas, para resolver o exercício seguinte: Ex.6 Escreva o dual do problema tipo de Programação Linear apresentado na sua 'forma standard': n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk = bi k = 1 Xk 0 i = 1, 2,..., m k = 1, 2,..., n Resolução : m Minimizar G = Σ bi. Ui i = 1 m Σ aik. Ui ck i = 1 Ui R k = 1, 2,..., n i = 1, 2,..., m 108
10 2 - Propriedades Fundamentais da Dualidade P1 : O dual do problema dual de um dado problema de Programação Linear é o próprio problema de Programação Linear. P2: Considerando o problema primal, um problema de Programação Linear cujo objectivo é maximizar a função objectivo F, pode garantir-se que o o valor da função objectivo F ( F = C.X ) não excede o valor da função objectivo G ( g = bt. U ) qualquer solução admissível do problema dual, ou seja, n m F = Σ ck. Xk G = Σ bi. Ui, para ( Xk ), ( Ui ) soluções k = 1 i = 1 admissíveis do problema primal e dual, respectivamente. P3 : P4 : Se X* = [ X1*, X2*,..., Xn* ]T e U* = [ U1*, U2*,..., UM* ]T são soluções admissíveis para os problemas primal e dual, respectivamente, tais que. n m F* = Σ ck. Xk* = G* = Σ bi. Ui*, k = 1 i = 1 então X* e U* são as soluções óptimas do problema primal e do problema dual, respectivamente. Para qualquer par de problemas primal-dual, a existncia de solução óptima finita para um deles garante a existncia de solução óptima finita para o outro, verificando-se F* = G*. Esquematicamente, pode indicar-se: Min G F* = G* [em geral, F G ( ver P2 ), mas, Max F no "óptimo finito", F* = G* ( P4 ).] Recordemo-nos que F* = C. X* = C B. X B * = C B. B-1. b e que G* = bt. U* = U*T. b. ( relativamente à base óptima do problema primal ) Assim, se F* = G * ( P4 ), U*T. b = C B. B-1. b, ou seja, U*T = C B. B-1 ( relativamente à base óptima do problema primal ). Assim, se um problema de Programação Linear admitir solução óptima finita, a partir da sua base óptima será possível determinar a solução óptima do correspondente problema dual. De notar que o valor óptimo das variáveis duais intervém no cálculo dos coeficientes r (a partir dos quais se verifica a optimalidade das soluções de um problema de Programação 109
11 Linear). Com efeito, relativamente à solução óptima de um problema de Programação Linear pode escrever-se r* = - C D + ( C B. B-1 ). D 0, o que é equivalente a r* = - C D + ( U*T ). D 0. Particularmente interessante se torna a determinação da solução óptima do problema dual quando é possível escrever-se o problema primal na forma: B D 1 I b è I B-1. D 1 B-1 B-1. b - C B - C D C D1 + C B. B-1. D 1 C B. B-1 C B. B-1. b Estando agora clara a relação entre o par de problemas primal-dual, poderemos retomar as considerações feitas no final da resolução do exercício nº1. Então, referimos que o problema primal apresentado tinha m = 4 (número de equações) e n = (número de incógnitas), pelo que a sua resolução pelo Algoritmo Simplex Revisto implicaria a manipulação (incluindo inversão) de matrizes B ( 4 x 4 ), enquanto que o problema dual correspondente tinha m = 2 (número de equações) e n = (número de incógnitas), pelo que a sua resolução pelo Algoritmo Simplex Revisto implicaria a manipulação de matrizes B ( 2 x 2 )! Concluímos, então, que, a priori, seria mais fácil resolver o problema dual, já que este corresponderia a um menor esforço de cálculo... Poderemos generalizar o raciocínio apresentado e referir que, dado um problema de Programação Linear que se pretende resolver, deve verificar-se se a resolução do correspondente problema dual não será mais fácil. Em caso afirmativo, deverá determinar-se a solução óptima do problema dual e, a partir da correspondente base óptima, determinar a solução óptima do problema (primal) dado. De recordar que quanto maior for o número de restrições de um problema de Programação Linear, maior será a ordem das correspondentes matrizes B e, consequentemente, maior será o volume de cálculo envolvido. Assim, dado um problema de Programação Linear, se o número de restrições for muito superior ao número de incógnitas (não incluindo as variáveis de folga) deve resolver- -se o correspondente problema dual, já que as matrizes B Primal ( m x m ) são de ordem muito superior que as matrizes B Dual. Para terminarmos a indicação das propriedades fundamentais da Dualidade, refiramos ainda mais duas propriedades: U*T P5: Um problema de Programação Linear admite solução óptima finita se e só se existirem soluções admissíveis para esse problema e para o seu dual. P6: Se um problema de Programação Linear não admitir solução óptima finita, então o correspondente dual não tem soluções admissíveis. Primal (Max F) Dual (Min G) Explo. Problema Possível S Explo. Problema Impossível S = Problema Possível 1 F* = G* ambos problemas 3 G* - o problema dual S tm solução óptima finita não tem solução óptima finita Problema Impossível 2 F* + o problema primal Nenhum dos problemas tem 4 S = não tem solução óptima finita soluções admissíveis Exemplos das situações referidas no Quadro anterior (resolva os problemas graficamente): 110
12 Explo. Problema Primal Problema Dual 1 Max F = 5. X sujeito a X + Y = 1 X, Y 0 X* = 1, Y * = 0 ; F* = 5 Min G = U sujeito a U 5 U 0 U R X* = 1, Y * = 0 ; F* = 5 2 Max F = X + Y sujeito a X - Y = 2 X, Y 0 F* + Min G = 2. U sujeito a U 1 - U 1 Problema impossível ( S = ) 3 Max F = - X sujeito a - X = 4 X 0 Problema impossível ( S = ) Min G = 4. U sujeito a - U - 1 U R G* - 4 Max F = X + Y sujeito a -X +Y = 4 X -Y = 4 X, Y 0 Problema impossível ( S = ) Min G = 4. U + 4. V sujeito a - U + V 1 U - V 1 Problema impossível ( S = ) Nota: Exemplos retirados de 'Programação Linear' ( vol. II ), Guerreiro et al, Mc Graw Hill 3 - Teorema da Complementaridade Considerando o par de problemas 'primal-dual' Problema 'primal': Max F = C. X sujeito a A. X b X 0 Problema 'dual': Min G = bt. U poderemos enunciar o Terorema da Complementaridade: sujeito a AT. U CT U 0, 111
13 É condição necessária e suficiente para que X e U, soluções admissíveis dos problemas primal e dual, respectivamente, sejam soluções óptimas, que verifiquem as seguintes condições: X k * > 0 U*T. a k = c k [ 1 ] U*T. a k > c k X k * = 0 [ 2 ] U i * > 0 ai. X* = b i [ 3 ] ai. X* < b i U i * = 0 [ 4 ] para i = 1, 2,..., m e k = 1, 2,..., n e representando a k e ai, respectivamente, a k-ésima coluna e a i-ésima linha de A. De acordo com o Teorema da Complementaridade, podemos concluir que, relativamente à solução óptima: se uma 'variável primal' é positiva, então a correspondente 'restrição dual' é activa [ 1 ] e que se uma 'restrição dual' é não activa, então a correspondente 'variável primal' é nula [ 2 ]. se uma 'variável dual' é positiva, então a correspondente 'restrição primal' é activa [ 3 ] e que se uma 'restrição primal' é não activa, então a correspondente 'variável dual' é nula [ 4 ]. Poderemos sintetizar o Teorema da Complementaridade, nas afirmações seguintes: Relativamente às soluções óptimas do par de problemas 'primal-dual' de Programação Linear, é nulo o produto da k-ésima 'variável primal' pela variável de folga correspondente à k- ésima 'restrição dual': m x k *. [ ( Σ aik. ui* ) - ck ] = 0 x k *. um+k* = 0 i = 1 k = 1, 2,..., n é nulo o produto da i-ésima 'variável dual' pela variável de folga correspondente à i-ésima 'restrição primal': n u i *. [ ( Σ aik. xk* ) - bi ] = 0 u i *. xn+i* = 0 k = 1 i = 1, 2,..., m Consideremos o seguinte par de problemas 'primal-dual' de Programação Linear: 112
14 sujeito a Max F = 2 X X 2 Min G = 5 U U U 3 sujeito a 3 X X U U U X 1-1 X U 1-1 U U X X 2 4 U 1, U 2, U 3 0 X 1, X 2 0 O Teorema da Complementaridade permite afirmar que, relativamente ao óptimo: X 1 * > 0 3 U 1 * + 6 U 2 * + 2 U 3 * = 2 X 2 * > 0 4 U 1 * - 1 U 2 * + 4 U 3 * = 3 3 U 1 * + 6 U 2 * + 2 U 3 * > 2 X 1 * = 0 4 U 1 * - 1 U 2 * + 4 U 3 * > 3 X 2 * = 0 U 1 * > 0 3 X 1 * + 4 X 2 * = 5 U 2 * > 0 6 X 1 * - 1 X 2 * = 3 U 3 * > 0 2 X 1 * + 4 X 2 * = 4 3 X 1 * + 4 X 2 * < 5 U 1 * = 0 6 X 1 * - 1 X 2 * < 3 U 2 * = 0 2 X 1 * + 4 X 2 * < 4 U 3 * = 0 Resolva, recorrendo ao Método gráfico o problema 'primal' dado. [ Nós aguardamos, pacatamente, que resolva mesmo o problema! ] Como pode observar, a 1ª restrição é dominada pelas duas outras. A solução óptima do problema ( X 1 * = 8/13 ; X 2 * = 9/13, com F* = 43/13 ) corresponde à intersecção das rectas respeitantes à 2ª e 3ª restrições. Assim, relativamente ao óptimo, podemos concluir que a 2ª e a 3ª restrições são activas (isto é, tm folga nulas). Pelo Teorema da Complementaridade, podemos, imediatamente, concluir que se a 1ª restrição é a única restrição não activa, então a correspondente variável dual, U 1 * é a única variável dual 'original' nula. Mas, se o problema dual tem duas restrições (e trs variáveis 'originais'), então as correspondentes matrizes B são do tipo ( 2 x 2 ). Ora se U 1 * é nula, então U 2 * e U 3 * serão obrigatoriamente não nulas, isto é pertencerão à base óptima do problema dual. Como, neste caso, é mais fácil resolver analiticamente o problema dual do que o problema primal e já sabemos quais as variáveis que integram a respectiva base óptima
15 F... resolva o problema 'dual' utilizando a formulação matricial do Simplex. [ Nós aguardamos, pacatamente, que resolva mesmo o problema! ] Deve ter obtido U 2 * = 1/13 ; U 3 * = 10/13, com G* = 43/13 [ Claro que se tinha que obter F* = G *! ]. A partir do problema 'dual' pode obter a solução óptima do problema 'primal' (calculando C B. B-1 relativamente à base óptima do problema 'dual') - deve obter X 1 * = 8/13 ; X 2 * = 9/13, verificando os resultados obtidos anteriormente. Relativamente à solução óptima, os valores assumidos pelas variáveis duais costumam ser designados por preços-sombra associados às restrições do problema primal. A uma 'restrição primal' não activa corresponde um preço-sombra nulo. Um preço-sombra não nulo corresponde a uma restrição activa. A designação de preço-sombra, prende-se com o facto de, em aplicações de carácter económico, o preço-sombra correspondente a uma dada 'restrição primal' representar a quantia máxima que estaríamos dispostos a pagar para incrementar em uma unidade a disponibilidade do correspondente recurso (isto é, aumentar em uma unidade o termo independente da restrição). Se se alterar os termos independentes do problema primal (que, em geral, exprimem disponibilidades de recursos) - e se se mantiver a mesma base - é possível calcular facilmente a variação produzida na função objectivo: Com efeito, sabemos que F = C B. B-1. b = UT. b, pelo que se se alterar b para b' = b + b, ter-se-á: F' = UT. b' = UT. ( b + b ) = UT. b + UT. b = F + UT. b, ou seja, F = F' - F = UT. b, isto é, F = UT. b, ou seja os valores óptimos das variáveis duais constituem coeficientes de sensibilidade da função objectivo, em relação aos termos independentes das restrições. Apliquemos algumas das noções apresentadas, a partir da análise do seguinte par de problemas 'primal-dual' de Programação Linear: sujeito a Min F = - X X 2 Max G = 5 U U U 3 Max P = 1 X 1-2 X 2 sujeito a 1 X X X 3 = 10 1 X X 2-1 X 4 = 5 1 X 1-1 X X 5 = 0 X 1, X 2, X 3, X 4, X 5 0 sujeito a 1 X X U U U X X U U 2-1 U X 1-1 X 2 0 U 1 0 ; U 2 0 ; U 3 0 X 1, X 2 0 X /2 F 5/ X1
16 Como se pode observar, pela resolução gráfica, a solução óptima do problema 'primal' é ( X 1 * = 5/2 ; X 2 * = 5/2 ), a que corresponde F* = 5/2. De notar que o vértice do espaço de soluções admissíveis correspondente à solução óptima é definido pela intersecção da 2ª e 3ª restrições, ou seja, a base óptima é ( X 1 ; X 2 ; X 3 ), já que X 3 *é a variável de folga correspondente à primeira restrição. Por outro lado, se a 2ª e 3ª 'restrições primais' são activas, então, as correspondentes variáveis duais estarão na base correspondente à solução óptima do problema dual, isto é, essa base é ( U 2 ; U 3 ). F Utilizando a formulação matricial do Simplex, verifique que ( X 1 ; X 2 ; X 3 ) é a base óptima do problema primal.... Deve ter obtido r = [ + 1/2 ; + 3/2 ], ( X1* = 5/2 ; X2* = 5/2 ) e P*= - 5/2 F * = 5/2 F A partir da base óptima do problema primal, determine a solução óptima do problema dual.... Deve ter obtido UT* = [ 0 ; + 1/2 ; - 3/2 ], isto é, U1* = 0 ; U2* = + 1/2 ; U3* = - 3/2.... De notar que G* = 5/2 = F* ü F Utilizando a formulação matricial do Simplex, aplicada ao problema dual (na forma standard), verifique que ( U 2 ; U' 3 ) é a base óptima desse problema.... Não se esqueça de fazer U 3 = - U' 3. Deverá obter U2* = + 1/2 ; U'3* = + 3/2. F Utilizando a formulação matricial do Simplex, aplicada à base óptima do problema dual, verifique a solução óptima do problema primal.... Deverá obter ( X1* = 5/2 ; X2* = 5/2 ). Recordemo-nos que X 1 * = 5/2 ; X 2 * = 5/2, pelo que facilmente determinamos os valores correspondentes das variáveis de folga X 3 *, X 4 * e X 5 * : X 3 * = 10 - ( X 1 * + X 2 * ) = 5 e X 4 * = X 5 * = = 0 (de recordar que a 2ª e 3ª 'restrições primais' são activas, pelo que as correspondentes variáveis de folga são nulas). Por outro lado, U1* = 0 ; U2* = + 1/2 ; U3* = - 3/2, pelo que os valores das correspondentes variáveis de folga do problema dual serão U4* = ( U 1 *+ U 2 * + U 3 * ) = 0 e U5* = 2 - ( 1 U 1 * + 1 U 2 * - 1 U 3 ) = 0 (ou seja as duas 'restrições duais' são activas). Verifiquemos o cumprimento das condições estabelecidas pelo Teorema da Complementaridade: X 3 *. U 1 * = = 0 ü X 4 *. U 2 * = /2 = 0 ü X 5 *. U 3 * = 0 0. (-3/2) = 0 ü X 1 *. U 4 * = 0 5/2. 0 = 0 ü X 2 *. U 5 * = 0 5/2. 0 = 0 ü Aproveitemos para retomar a noção de preço-sombra. Comecemos com U2* = + 1/2. Tal indica-nos que, se se incrementar uma unidade ao termo independente da segunda 'restrição primal', a função objectivo F sofrerá um incremento de + 1/2 ( o que, por acaso, não nos interessaria muito, já que o objectivo do problema primal é Minimizar F! ). De notar que o que se referiu só é válido na hipótese de se manter óptima a mesma base! 115
17 F Considere o problema primal 'alterado' (na forma standard): Max P = 1 X 1-2 X 2 sujeito a 1 X X X 3 = 10 1 X X 2-1 X 4 = X 1-1 X X 5 = 0 X 1, X 2, X 3, X 4, X 5 0 Utilizando a formulação matricial do Simplex, verifique que ( X 1 ; X 2 ; X 3 ) se mantém a base óptima do problema primal.... Deve ter obtido r = [ + 1/2 ; + 3/2 ], ( X1* = 3 ; X2* = 3 ) e P*= - 3 F * = 3 = 5/2 + 1/2 F*orig. U2* Se considerermos, agora, U3* = - 3/2, tal indicar-nos-á que, a um incremento de uma unidade no termo independente da terceira 'restrição primal', a função objectivo F sofrerá um 'incremento' de - 3/2 ( o que, por acaso, nos interessaria, já que o objectivo do problema primal é Minimizar F! ). ( Continuamos a assumir que se mantem óptima a mesma base! ) F Considere o problema primal 'alterado' (na forma standard): Max P = 1 X 1-2 X 2 sujeito a 1 X X X 3 = 10 1 X X 2-1 X 4 = 5 1 X 1-1 X X 5 = X 1, X 2, X 3, X 4, X 5 0 Utilizando a formulação matricial do Simplex, verifique que ( X 1 ; X 2 ; X 3 ) se mantém a base óptima do problema primal.... Deve ter obtido r = [ + 1/2 ; + 3/2 ], ( X1* = 3 ; X2* = 2 ) e P*= - 1 F * = 1 = 5/2 + (- 3/2) F*orig. U3* Assim, a Dualidade tem, pelo menos, duas importantes aplicações: por um lado, relativamente a um per de problemas 'primal-dual' de Programação Linear, permite-nos resolver o problema 'mais simples' e obter a solução de ambos; por outro lado, os valores óptimos das variáveis duais de um problema de Programação Linear podem ser encarados como coeficientes de sensibilidade da função objectivo, face a eventuais variações dos termos independentes ('disponibilidades de recursos'), o que é muito importante, numa interpretação de 'caractér económico'. 116
IV - P R O G R A M A Ç Ã O L I N E A R :
 IV - P R O G R A M A Ç Ã O L I N E A R : C O N C E I T O S F U N D A M E N T A I S Consideremos um problema de Programação Linear apresentado na sua forma standard: Maximizar F = c1. X1 + c2. X2 + c3.
IV - P R O G R A M A Ç Ã O L I N E A R : C O N C E I T O S F U N D A M E N T A I S Consideremos um problema de Programação Linear apresentado na sua forma standard: Maximizar F = c1. X1 + c2. X2 + c3.
IX - A N Á L I S E D E S E N S I B I L I D A D E
 IX - A N Á L I S E D E S E N S I B I L I D A D E A N Á L I S E P Ó S - O P T I M A L I D A D E Recordemos o exercício apresentado para ilustrar a aplicação do Algoritmo Simplex Revisto: Consideremos o
IX - A N Á L I S E D E S E N S I B I L I D A D E A N Á L I S E P Ó S - O P T I M A L I D A D E Recordemos o exercício apresentado para ilustrar a aplicação do Algoritmo Simplex Revisto: Consideremos o
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. IV Modelo Dual
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
CAPÍTULO 4. Teoria da Dualidade
 CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
Investigação Operacional
 Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
2º Semestre 2002/2003 Problemas Resolvidos
 RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº3: Dualidade. Interpretação Económica.
 Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
Índice. Prefácio Os modelos de programação linear e a investigação operacional 17
 Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Pesquisa Operacional
 Pesquisa Operacional Teoria da Dualidade Profa. Sheila Morais de Almeida DAINF-UTFPR-PG outubro - 2015 Problema Dual Cada problema de Programa de Programação Linear está associado a um outro problema de
Pesquisa Operacional Teoria da Dualidade Profa. Sheila Morais de Almeida DAINF-UTFPR-PG outubro - 2015 Problema Dual Cada problema de Programa de Programação Linear está associado a um outro problema de
Simplex. Investigação Operacional José António Oliveira Simplex
 18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
Combinando inequações lineares
 Combinando inequações lineares A multiplicação por um número > 0 não altera uma inequação 2x x 5 4x 2x 10 1 2 1 2 A soma de duas inequações (com o mesmo sentido) produz uma inequação válida x 3x x 3 1
Combinando inequações lineares A multiplicação por um número > 0 não altera uma inequação 2x x 5 4x 2x 10 1 2 1 2 A soma de duas inequações (com o mesmo sentido) produz uma inequação válida x 3x x 3 1
A Dualidade em Programação Linear
 Investigação Operacional- 2009/10 - Programas Lineares 14 A Dualidade em Programação Linear Para melhor ilustrar este conceito vamos estudar dois problemas intimamente relacionadas: o problema da dona
Investigação Operacional- 2009/10 - Programas Lineares 14 A Dualidade em Programação Linear Para melhor ilustrar este conceito vamos estudar dois problemas intimamente relacionadas: o problema da dona
O Problema de Transportes
 Investigação Operacional- 00/0 - Problemas de Transportes 8 O Problema de Transportes O problema geral de transportes consiste em determinar a forma mais económica de enviar um bem que está disponível
Investigação Operacional- 00/0 - Problemas de Transportes 8 O Problema de Transportes O problema geral de transportes consiste em determinar a forma mais económica de enviar um bem que está disponível
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
Programação Linear - Parte 5
 Matemática Industrial - RC/UFG Programação Linear - Parte 5 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 5 1/2016 1 / 29 Dualidade Os parâmetros de entrada são dados de acordo com
Matemática Industrial - RC/UFG Programação Linear - Parte 5 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 5 1/2016 1 / 29 Dualidade Os parâmetros de entrada são dados de acordo com
Investigação Operacional
 Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Investigação Operacional
 Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
Combinando inequações lineares
 Combinando inequações lineares A multiplicação por um número > 0 não altera uma inequação 2x x 5 4x 2x 0 2 2 A soma de duas inequações (com o mesmo sentido) produz uma inequação válida x 3x + x 3 2 + 5x
Combinando inequações lineares A multiplicação por um número > 0 não altera uma inequação 2x x 5 4x 2x 0 2 2 A soma de duas inequações (com o mesmo sentido) produz uma inequação válida x 3x + x 3 2 + 5x
Programação Linear. Dualidade
 Programação Linear Dualidade Dualidade Já vimos em sala que para cada PPL existe um outro PL chamado dual, que consiste em modelar um problema que utiliza os mesmos dados que o original, mas alterando
Programação Linear Dualidade Dualidade Já vimos em sala que para cada PPL existe um outro PL chamado dual, que consiste em modelar um problema que utiliza os mesmos dados que o original, mas alterando
Método do Big M. Análise de Sensibilidade
 A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
Professor João Soares 20 de Setembro de 2004
 Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
PESQUISA OPERACIONAL I
 PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza [email protected] www.engenharia-puro.com.br/edwin/po-i.html Dualidade Introdução Uma das mais importantes descobertas no início do
PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza [email protected] www.engenharia-puro.com.br/edwin/po-i.html Dualidade Introdução Uma das mais importantes descobertas no início do
sujeito a: 30x x (madeira) 5x x (horas de trabalho) x 1, x 2 0
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
Teoremas de dualidade
 Teoremas de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Teoremas de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Simplex. Transparências de apoio à leccionação de aulas teóricas. c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Simplex Transparências de apoio à leccionação de aulas teóricas Versão 3 c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear abordagem algébrica max sujeito a: n
Simplex Transparências de apoio à leccionação de aulas teóricas Versão 3 c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear abordagem algébrica max sujeito a: n
Investigação Operacional
 Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
CAPÍTULO 3. Método Simplex
 CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
Investigação Operacional
 Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081. PROF. IVO CHAVES DA SILVA JUNIOR
 UNIVERSIDADE FEDERAL DE JUIZ DE FORA Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081 PROF. IVO CHAVES DA SILVA JUNIOR E-mail: [email protected] Aula Número: 07 Programação Linear Últimas
UNIVERSIDADE FEDERAL DE JUIZ DE FORA Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081 PROF. IVO CHAVES DA SILVA JUNIOR E-mail: [email protected] Aula Número: 07 Programação Linear Últimas
Investigação Operacional
 Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Teoria de dualidade. Marina Andretta ICMC-USP. 19 de outubro de 2016
 Teoria de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Teoria de dualidade Marina Andretta ICMC-USP 19 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Programação Linear M É T O D O S : E S T A T Í S T I C A E M A T E M Á T I C A A P L I C A D A S D e 1 1 d e m a r ç o a 2 9 d e a b r i l d e
 Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo
 Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br 2018/2 - PCC174/BCC464 Aula Prática - Laboratório COM30!1 Breve Revisão Modelagem Método gráfico O Algoritmo Simplex
Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br 2018/2 - PCC174/BCC464 Aula Prática - Laboratório COM30!1 Breve Revisão Modelagem Método gráfico O Algoritmo Simplex
Programação Linear. Rosa Canelas 2010
 Programação Linear Rosa Canelas 2010 Problemas de Optimização São problemas em que se procura a melhor solução (a que dá menor prejuízo, maior lucro, a que é mais eficiente, etc.) Alguns destes problemas
Programação Linear Rosa Canelas 2010 Problemas de Optimização São problemas em que se procura a melhor solução (a que dá menor prejuízo, maior lucro, a que é mais eficiente, etc.) Alguns destes problemas
Optimização/Matemática II (Eco)
 Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Método Simplex dual. Marina Andretta ICMC-USP. 24 de outubro de 2016
 Método Simplex dual Marina Andretta ICMC-USP 24 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Método Simplex dual Marina Andretta ICMC-USP 24 de outubro de 2016 Baseado no livro Introduction to Linear Optimization, de D. Bertsimas e J. N. Tsitsiklis. Marina Andretta (ICMC-USP) sme0211 - Otimização
Vânio Correia Domingos Massala
 Optimização e Decisão 06/0/008 Método do Simplex Vânio Correia - 5567 Domingos Massala - 58849 INSTITUTO SUPERIOR TÉCNICO Generalidades do Método do Simplex Procedimento algébrico iterativo para resolver
Optimização e Decisão 06/0/008 Método do Simplex Vânio Correia - 5567 Domingos Massala - 58849 INSTITUTO SUPERIOR TÉCNICO Generalidades do Método do Simplex Procedimento algébrico iterativo para resolver
Programação Linear Inteira. C. Requejo (UA) Métodos de Investigação Operacional MIO / 30
 Programação Linear Inteira Programação Linear Inteira C. Requejo (UA) Métodos de Investigação Operacional MIO 2016 1 / 30 Programação Linear Inteira Programação Linear Inteira Resolução de problemas de
Programação Linear Inteira Programação Linear Inteira C. Requejo (UA) Métodos de Investigação Operacional MIO 2016 1 / 30 Programação Linear Inteira Programação Linear Inteira Resolução de problemas de
PROGRAMAÇÃO LINEAR. Tipo de problemas: cálculo do plano óptimo de distribuição de mercadorias; minimiação de desperdícios no corte de materiais;
 PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Revisão Método Simplex Solução básica factível: xˆ xˆ, xˆ N em que xˆ N 0 1 xˆ b 0 Solução geral
Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Revisão Método Simplex Solução básica factível: xˆ xˆ, xˆ N em que xˆ N 0 1 xˆ b 0 Solução geral
Slide 1. c 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Programação Linear e Método Simplex Slide 1 Transparências de apoio à leccionação de aulas teóricas Versão 1 c 1998 Programação Linear e Método Simplex 1 Slide 2 Toda a teoria deve ser feita para poder
Programação Linear e Método Simplex Slide 1 Transparências de apoio à leccionação de aulas teóricas Versão 1 c 1998 Programação Linear e Método Simplex 1 Slide 2 Toda a teoria deve ser feita para poder
TP052-PESQUISA OPERACIONAL I Algoritmo Dual Simplex. Prof. Volmir Wilhelm Curitiba, Paraná, Brasil
 TP052-PESQUISA OPERACIONAL I Algoritmo Dual Simplex Prof. Volmir Wilhelm Curitiba, Paraná, Brasil Algoritmo Dual Simplex Motivação max sa Z = cx Ax = b x 0 escolhida uma base viável max sa Z = c B x B
TP052-PESQUISA OPERACIONAL I Algoritmo Dual Simplex Prof. Volmir Wilhelm Curitiba, Paraná, Brasil Algoritmo Dual Simplex Motivação max sa Z = cx Ax = b x 0 escolhida uma base viável max sa Z = c B x B
No eixo das ordenadas o ponto B tem abcissa nula (x 1 = 0) pelo que a equação se reduz a 20x 2 = 300. Madeira. C(10,10) não é admissível.
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 Programação Não Linear Aula 7: Programação Não-Linear - Funções de Várias variáveis Vector Gradiente; Matriz Hessiana; Conveidade de Funções e de Conjuntos; Condições óptimas de funções irrestritas; Método
Programação Não Linear Aula 7: Programação Não-Linear - Funções de Várias variáveis Vector Gradiente; Matriz Hessiana; Conveidade de Funções e de Conjuntos; Condições óptimas de funções irrestritas; Método
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i Cap. VII - Interpretação económica do modelo de
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i Cap. VII - Interpretação económica do modelo de
Investigação Operacional 1. Transparências de apoio à leccionação de aulas teóricas. x j - valor da variável de decisão j;
 Investigação Operacional 1 Programação Linear Slide 1 Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Programação Linear Modelos Slide 2 Forma geral
Investigação Operacional 1 Programação Linear Slide 1 Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Programação Linear Modelos Slide 2 Forma geral
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010
 DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
Ficha de trabalho Decomposição e resolução de equações e inequações polinomiais
 Ficha de trabalho Decomposição e resolução de equações e inequações polinomiais 1. Verifique, recorrendo ao algoritmo da divisão, que: 6 4 0x 54x + 3x + é divisível por x 1.. De um modo geral, que relação
Ficha de trabalho Decomposição e resolução de equações e inequações polinomiais 1. Verifique, recorrendo ao algoritmo da divisão, que: 6 4 0x 54x + 3x + é divisível por x 1.. De um modo geral, que relação
Frequência / Exame de 1. a Época
 ISCTE - Instituto Universitário de Lisboa Licenciaturas: Gestão, Finanças e Contabilidade, Gestão e Engenharia Industrial, Marketing e Economia Frequência / Exame de 1. a Época OPTIMIZAÇÃO / MATEMÁTICA
ISCTE - Instituto Universitário de Lisboa Licenciaturas: Gestão, Finanças e Contabilidade, Gestão e Engenharia Industrial, Marketing e Economia Frequência / Exame de 1. a Época OPTIMIZAÇÃO / MATEMÁTICA
Pesquisa Operacional
 Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Programação Linear. MÉTODOS QUANTITATIVOS: ESTATÍSTICA E MATEMÁTICA APLICADAS De 30 de setembro a 13 de novembro de 2011 prof. Lori Viali, Dr.
 Programação Linear São problemas complexos, muitas vezes de difícil solução e que envolvem significativas reduções de custos, melhorias de tempos de processos, ou uma melhor alocação de recursos em atividades.
Programação Linear São problemas complexos, muitas vezes de difícil solução e que envolvem significativas reduções de custos, melhorias de tempos de processos, ou uma melhor alocação de recursos em atividades.
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Dualidade A eoria da Dualidade é um dos mais importantes tópicos da Programação Linear (PL). Estudos
Otimização Linear Profª : Adriana Departamento de Matemática [email protected] wwwp.fc.unesp.br/~adriana Dualidade A eoria da Dualidade é um dos mais importantes tópicos da Programação Linear (PL). Estudos
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
Problemas de Transportes e de Afectação
 CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A
 PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A Prof.ª: Maria João Mendes Vieira ESC 11MatA 2012/2013 PROGRAMAÇÃO LINEAR A programação linear é uma "ferramenta" matemática que permite encontrar a solução ótima
PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A Prof.ª: Maria João Mendes Vieira ESC 11MatA 2012/2013 PROGRAMAÇÃO LINEAR A programação linear é uma "ferramenta" matemática que permite encontrar a solução ótima
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Análise e Síntese de Algoritmos. Programação Linear CLRS, Cap. 29
 Análise e Síntese de Algoritmos Programação Linear CLRS, Cap. 29 Conteto Algoritmos em Grafos (CLRS, Cap. 22-26)... Fluos máimos em grafos (CLRS, Cap. 26) Programação Linear (CLRS, Cap. 29) Programação
Análise e Síntese de Algoritmos Programação Linear CLRS, Cap. 29 Conteto Algoritmos em Grafos (CLRS, Cap. 22-26)... Fluos máimos em grafos (CLRS, Cap. 26) Programação Linear (CLRS, Cap. 29) Programação
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 8 : O método Simplex. Casos particulares. Empate no critério de entrada. Óptimo não finito. Soluções óptimas alternativas. Degenerescência. INÍCIO Forma Padrão Faculdade
1 Programação Linear (PL) Aula 8 : O método Simplex. Casos particulares. Empate no critério de entrada. Óptimo não finito. Soluções óptimas alternativas. Degenerescência. INÍCIO Forma Padrão Faculdade
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL
 INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
1 Despacho económico
 Trânsito de potência difuso DC com despacho incorporado Documento complementar à dissertação José Iria [email protected] - 10-03-2011 1 Despacho económico 1.1 Considerações Gerais O problema de decisão
Trânsito de potência difuso DC com despacho incorporado Documento complementar à dissertação José Iria [email protected] - 10-03-2011 1 Despacho económico 1.1 Considerações Gerais O problema de decisão
Resolvendo algebricamente um PPL
 Capítulo 6 Resolvendo algebricamente um PPL 6.1 O método algébrico para solução de um modelo linear A solução de problemas de programação linear com mais de duas variáveis, não pode ser obtida utilizando-se
Capítulo 6 Resolvendo algebricamente um PPL 6.1 O método algébrico para solução de um modelo linear A solução de problemas de programação linear com mais de duas variáveis, não pode ser obtida utilizando-se
Aula 07: Análise de sensibilidade (2)
 Aula 07: Análise de sensibilidade (2) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously Aulas anteriores: Dualidade
Aula 07: Análise de sensibilidade (2) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously Aulas anteriores: Dualidade
Prof.: Eduardo Uchoa.
 Análise de sensibilidade Prof.: Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi 1 Análise de Sensibilidade Uma vez que já se tenha resolvido um PL, existem técnicas para avaliar como pequenas alterações
Análise de sensibilidade Prof.: Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi 1 Análise de Sensibilidade Uma vez que já se tenha resolvido um PL, existem técnicas para avaliar como pequenas alterações
Problemas em Programação Linear Resolução e Análise de Sensibilidade
 Problemas em Programação Linear Resolução e Análise de Sensibilidade 24-25 Junho 2014 Metodologias de apoio à decisão nas Ciências Agrárias Eemplo: Formulação Um agricultor pretende cultivar 80 ha de terra
Problemas em Programação Linear Resolução e Análise de Sensibilidade 24-25 Junho 2014 Metodologias de apoio à decisão nas Ciências Agrárias Eemplo: Formulação Um agricultor pretende cultivar 80 ha de terra
Matemática I. Capítulo 3 Matrizes e sistemas de equações lineares
 Matemática I Capítulo 3 Matrizes e sistemas de equações lineares Objectivos Matrizes especiais e propriedades do produto de matrizes Matriz em escada de linhas Resolução de sistemas de equações lineares
Matemática I Capítulo 3 Matrizes e sistemas de equações lineares Objectivos Matrizes especiais e propriedades do produto de matrizes Matriz em escada de linhas Resolução de sistemas de equações lineares
Indicação de uma possível resolução do exame
 Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Recursos críticos disponíveis: Madeira 300 metros Horas de trabalho 110 horas
 I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
II. Programação Linear (PL)
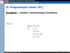 II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
1 NOTAS DE AULA FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA. Professor Doutor: Jair Silvério dos Santos
 FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA 1 NOTAS DE AULA Professor Doutor: Jair Silvério dos Santos (i) Matrizes Reais Uma matriz real é o seguinte arranjo de números reais : a 11 a 12 a 13 a 1m a 21
FFCLRP-USP - VETORES E GEOMETRIA ANALÍTICA 1 NOTAS DE AULA Professor Doutor: Jair Silvério dos Santos (i) Matrizes Reais Uma matriz real é o seguinte arranjo de números reais : a 11 a 12 a 13 a 1m a 21
Capítulo 3. O Método Primal Simplex
 Capítulo 3 O Método Primal Simplex 3.. Introdução Neste Capítulo, apresenta-se o método de resolução de problemas de programação linear mais utilizado, isto é, o método primal simplex. Assim, apresenta-se
Capítulo 3 O Método Primal Simplex 3.. Introdução Neste Capítulo, apresenta-se o método de resolução de problemas de programação linear mais utilizado, isto é, o método primal simplex. Assim, apresenta-se
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL
 INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL Teste A CURSOS: EMP e EEM 00/00 Data: 1 de Novembro de 00 Duração: 19:0 às 1:0 Instruções:
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL Teste A CURSOS: EMP e EEM 00/00 Data: 1 de Novembro de 00 Duração: 19:0 às 1:0 Instruções:
Unidade 4 - Matrizes elementares, resolução de sistemas. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa. 10 de agosto de 2013
 MA33 - Introdução à Álgebra Linear Unidade 4 - Matrizes elementares, resolução de sistemas A Hefez e C S Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Nesta unidade, veremos
MA33 - Introdução à Álgebra Linear Unidade 4 - Matrizes elementares, resolução de sistemas A Hefez e C S Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto de 2013 Nesta unidade, veremos
Programação Linear/Inteira - Aula 5
 Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
4- Dualidade em Programação Linear
 4- Dualidade em Programação Linear 4.1- Introdução Considere o problema clássico da dieta: (problema primal): Quer-se consumir quantidades de determinados alimentos de tal forma a satisfazer as necessidades
4- Dualidade em Programação Linear 4.1- Introdução Considere o problema clássico da dieta: (problema primal): Quer-se consumir quantidades de determinados alimentos de tal forma a satisfazer as necessidades
Programação Linear. (4ª parte) Informática de Gestão Maria do Rosário Matos Bernardo 2016
 Programação Linear (4ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Análise de sensibilidade Relatório de reposta Relatório de sensibilidade Relatório de limites Desafio:
Programação Linear (4ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Análise de sensibilidade Relatório de reposta Relatório de sensibilidade Relatório de limites Desafio:
Programação Linear (PL) Solução algébrica - método simplex
 Universidade Federal de Itajubá Instituto de Engenharia de Produção e Gestão Pesquisa Operacional Simplex Prof. Dr. José Arnaldo Barra Montevechi Programação Linear (PL) Solução algébrica - método simplex
Universidade Federal de Itajubá Instituto de Engenharia de Produção e Gestão Pesquisa Operacional Simplex Prof. Dr. José Arnaldo Barra Montevechi Programação Linear (PL) Solução algébrica - método simplex
Modelos de Apoio à Decisão. Programação Linear. Rui Cunha Marques
 Modelos de Apoio à Decisão Programação Linear Rui Cunha Marques / Metodologia: Análise Sistémica Modelo: representação adequada (face aos objectivos do estudo) do sistema em análise que sendo passível
Modelos de Apoio à Decisão Programação Linear Rui Cunha Marques / Metodologia: Análise Sistémica Modelo: representação adequada (face aos objectivos do estudo) do sistema em análise que sendo passível
Programação Linear - Parte 3
 Matemática Industrial - RC/UFG Programação Linear - Parte 3 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 3 1/2016 1 / 26 O Método Simplex Encontre o vértice ótimo pesquisando um subconjunto
Matemática Industrial - RC/UFG Programação Linear - Parte 3 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 3 1/2016 1 / 26 O Método Simplex Encontre o vértice ótimo pesquisando um subconjunto
Métodos Numéricos - Notas de Aula
 Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Otimização Aplicada à Engenharia de Processos
 Otimização Aplicada à Engenharia de Processos Aula 4: Programação Linear Felipe Campelo http://www.cpdee.ufmg.br/~fcampelo Programa de Pós-Graduação em Engenharia Elétrica Belo Horizonte Março de 2013
Otimização Aplicada à Engenharia de Processos Aula 4: Programação Linear Felipe Campelo http://www.cpdee.ufmg.br/~fcampelo Programa de Pós-Graduação em Engenharia Elétrica Belo Horizonte Março de 2013
3- O MÉTODO SIMPLEX Introdução e fundamentos teóricos para o Método Simplex
 3- O MÉTODO SIMPLEX 3.1- Introdução O Método Simplex é uma técnica utilizada para se determinar, numericamente, a solução ótima de um modelo de Programação Linear. Será desenvolvido inicialmente para Problemas
3- O MÉTODO SIMPLEX 3.1- Introdução O Método Simplex é uma técnica utilizada para se determinar, numericamente, a solução ótima de um modelo de Programação Linear. Será desenvolvido inicialmente para Problemas
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Exemplo: Maximização de lucros em uma chocolateria que produz os seguintes produtos: (1) Chocolate Pyramide (2) Chocolate Pyramide Nuit
 Universidade Tecnológica Federal do Paraná Professor Murilo V. G. da Silva Notas de aula Estrutura de Dados 2 (Aula 09) Conteúdos da Aula: [DPV06 7.1, 7.2, 7.3] [Observação: Estas notas de aula são apenas
Universidade Tecnológica Federal do Paraná Professor Murilo V. G. da Silva Notas de aula Estrutura de Dados 2 (Aula 09) Conteúdos da Aula: [DPV06 7.1, 7.2, 7.3] [Observação: Estas notas de aula são apenas
Métodos de Pesquisa Operacional
 Métodos de Pesquisa Operacional Programação Linear é a parte da Pesquisa Operacional que trata da modelagem e resolução de problemas formulados com funções lineares. Programação Linear } Métodos de Resolução
Métodos de Pesquisa Operacional Programação Linear é a parte da Pesquisa Operacional que trata da modelagem e resolução de problemas formulados com funções lineares. Programação Linear } Métodos de Resolução
Análise de Sensibilidade. Investigação Operacional. Análise de Sensibilidade aos coeficientes da FO. Análise de Sensibilidade
 nálise de Sensibilidade Investigação Operacional rogramação Linear (arte II) 2/2 Nuno Moreira/milcar rantes/ui Marques/Marta Gomes Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território
nálise de Sensibilidade Investigação Operacional rogramação Linear (arte II) 2/2 Nuno Moreira/milcar rantes/ui Marques/Marta Gomes Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território
O método Simplex Aplicado ao Problema de Transporte (PT).
 Prof. Geraldo Nunes Silva (Revisado por Socorro Rangel) Estas notas de aula são Baseadas no livro: Hillier, F. S. e G. J. Lieberman. Introdução à Pesquisa Operacional, Campus, a ed., 9 Agradeço a Professora
Prof. Geraldo Nunes Silva (Revisado por Socorro Rangel) Estas notas de aula são Baseadas no livro: Hillier, F. S. e G. J. Lieberman. Introdução à Pesquisa Operacional, Campus, a ed., 9 Agradeço a Professora
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
O Método Simplex. Prof. Gustavo Peixoto Silva Departamento de Computação Univ. Federal de Ouro Preto
 O Método Simplex Prof. Gustavo Peixoto Silva Departamento de Computação Univ. Federal de Ouro Preto O Método Simplex para Problemas de Maximização Max Z(X) = 5X 1 + 2X 2 sujeito a X 1 = 0 X 2
O Método Simplex Prof. Gustavo Peixoto Silva Departamento de Computação Univ. Federal de Ouro Preto O Método Simplex para Problemas de Maximização Max Z(X) = 5X 1 + 2X 2 sujeito a X 1 = 0 X 2
Unidade: Modelo Simplex e Modelo Dual. Unidade I:
 Unidade: Modelo Simplex e Modelo Dual Unidade I: 0 Unidade: Modelo Simplex e Modelo Dual Segundo Wikipédia (2008), em teoria da otimização matemática, o algoritmo simplex de George Dantiz é uma técnica
Unidade: Modelo Simplex e Modelo Dual Unidade I: 0 Unidade: Modelo Simplex e Modelo Dual Segundo Wikipédia (2008), em teoria da otimização matemática, o algoritmo simplex de George Dantiz é uma técnica
Investigação Operacional
 Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 2004.02.09 Duração: 2 horas Nome: Teórica Responda a cada afirmação com (V) Verdadeira ou (F) Falsa. Por cada
Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 2004.02.09 Duração: 2 horas Nome: Teórica Responda a cada afirmação com (V) Verdadeira ou (F) Falsa. Por cada
Programa de Unidade Curricular
 Programa de Unidade Curricular Faculdade Ciências Empresariais Licenciatura Ciências Económicas e Empresariais Unidade Curricular Investigação Operacional Semestre: 5 Nº ECTS: 6,0 Regente José Manuel Brito
Programa de Unidade Curricular Faculdade Ciências Empresariais Licenciatura Ciências Económicas e Empresariais Unidade Curricular Investigação Operacional Semestre: 5 Nº ECTS: 6,0 Regente José Manuel Brito
Programação Linear. Dual Simplex: Viabilidade Dual Método Dual Simplex
 Programação Linear Dual Simplex: Viabilidade Dual Viabilidade Dual Considere o par de problemas primal (P) dual (D). Agora já sabemos como encontrar a solução de um desses PPL a partir da solução do outro.
Programação Linear Dual Simplex: Viabilidade Dual Viabilidade Dual Considere o par de problemas primal (P) dual (D). Agora já sabemos como encontrar a solução de um desses PPL a partir da solução do outro.
