Tarefa nº 9. (Plano de trabalho nº 4)

Tamanho: px

Começar a partir da página:

Download "Tarefa nº 9. (Plano de trabalho nº 4)"

Nathalia Bentes Meneses
9 Há anos
Visualizações:

1 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Tarefa nº 9 VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO CUBO Pretende-se, com esta actividade, e utilizando o que estudou e trabalhou até aqui (secções no cubo) que parta para a descoberta de novos poliedros. 1. Com o cubo e com o material de que dispõe na sua mesa, substitua cada aresta por um vértice situado no seu ponto médio. Caracterize o novo sólido que obteve. Nota: Se não conseguir descobrir o seu nome utilize o programa Poly no computador. 2. Relacione os volumes do cubo e do sólido obtido. 3. Faça um pequeno relatório da actividade realizada. Na elaboração do seu relatório não deve esquecer, entre outros, os aspectos seguintes: Título Objectivo do trabalho. Material utilizado. Descrição do processo utilizado para a descoberta, das tentativas realizadas e das dificuldades encontradas. Conclusões. Comentários acerca do interesse e gozo suscitados por esta actividade. Clareza e correcção da linguagem utilizada. Identificação do autor do trabalho, da escola, da data, do ano e da turma. PROFESSORA: Rosa Canelas 1

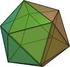
2 Tarefa nº 9 proposta de resolução VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO CUBO Objectivo da tarefa: Utilizando a matéria já estudada até aqui (secções no cubo) descobrir novos poliedros. A tarefa divide-se em duas etapas: o Descobrir o poliedro e caracterizá-lo. o Comparar o volume do poliedro obtido com o do cubo. D 1ª etapa: Com o cubo em acetato e uma caneta apropriada que C tínhamos em cima da mesa, substituímos cada aresta por um vértice situado no seu ponto médio e obtivemos o poliedro da figura, que tem 6 faces quadradas (uma por cada face do cubo) e 8 triangulares (uma por cada vértice do cubo), 12 vértices (um por cada A B aresta do cubo) e 24 arestas todas iguais a a 2, sendo a a aresta 2 do cubo. Este novo poliedro, irregular, chama-se cuboctaedro como verificámos ao consultar os sólidos arquimedeanos, em planificação e montados, do Poly. 2ª etapa: Para relacionar os volumes do cubo e do cuboctaedro tivemos que pensar na pirâmide [ABCD], cuja base é um triângulo rectângulo com os dois catetos iguais a a 2 e com altura igual à a a a medida dos catetos. A área da base é a a a = e o volume é =. O volume do cuboctaedro vai ser igual à diferença entre o volume do cubo (a 3 ) e o volume das 8 pirâmides 3 3 a a 8 =. Então o volume do octaedro é dado por a 5a a =. 6 6 Podemos finalmente concluir que o volume do cuboctaedro é 5 6 do volume do cubo. PROFESSORA: Rosa Canelas 2

3 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Tarefa nº 9 VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO OCTAEDRO Pretende-se, com esta actividade, e utilizando o que estudou e trabalhou até aqui (secções no cubo) que parta para a descoberta de novos poliedros. 1. Com o octaedro e com o material de que dispõe na sua mesa, substitua cada aresta por um vértice situado no seu ponto médio. Caracterize o novo sólido que obteve. Nota: Se não conseguir descobrir o seu nome utilize o programa Poly no computador. 2. Relacione os volumes do octaedro e do sólido obtido. 3. Faça um pequeno relatório da actividade realizada. Na elaboração do seu relatório não deve esquecer, entre outros, os aspectos seguintes: Título Objectivo do trabalho. Material utilizado. Descrição do processo utilizado para a descoberta, das tentativas realizadas e das dificuldades encontradas. Conclusões. Comentários acerca do interesse e gozo suscitados por esta actividade. Clareza e correcção da linguagem utilizada. Identificação do autor do trabalho, da escola, da data, do ano e da turma. PROFESSORA: Rosa Canelas 3

4 Tarefa nº 9 proposta de resolução VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO OCTAEDRO Objectivo da tarefa: Utilizando a matéria já estudada até aqui (secções no cubo) descobrir novos poliedros. V A tarefa divide-se em duas etapas: R S o Descobrir o poliedro e caracterizá-lo. Q o Comparar o volume do poliedro obtido com o do octaedro. O T 1ª etapa: Com o octaedro em acetato e uma caneta de acetato que tínhamos em cima da mesa, substituímos cada aresta por um vértice situado no seu ponto médio e obtivemos o poliedro da figura, que tem 6 faces quadradas (uma por cada vértice do octaedro) e 8 triangulares (uma por cada face do octaedro), 12 vértices (um por cada L M N aresta do octaedro) e 24 arestas todas iguais a a, sendo a a aresta 2 do octaedro. Este novo poliedro, irregular, chama-se cuboctaedro como verificámos ao consultar os sólidos arquimedeanos, em planificação e montados, do Poly. 2ª etapa: Para relacionar os volumes do octaedro e do cuboctaedro tivemos que pensar: o que o octaedro é resultado de duas pirâmides quadrangulares regulares iguais, coladas pela base. o que o cuboctaedro se obtém do octaedro quando tiramos 6 pirâmides quadrangulares regulares iguais à pirâmide [VQRST]. o As duas pirâmides são semelhantes e a razão de semelhança entre a menor e a maior é 1 2. o O volume da pirâmide menor vai ser 1 8 do volume da maior porque a razão dos volumes de duas figuras semelhantes é o cubo da razão de semelhança. o Porque o octaedro é formado por duas pirâmides das grandes o volume da pirâmide [VQRST] é 1 do volume do octaedro. 16 o O volume das seis pirâmides vai ser 6 16 o O volume do cuboctaedro é então do volume do octaedro. do volume do octaedro. Podemos finalmente concluir que o volume do cuboctaedro é 5 8 do volume do octaedro. PROFESSORA: Rosa Canelas 4

5 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Tarefa nº 9 VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO TETRAEDRO Pretende-se, com esta actividade, e utilizando o que estudou e trabalhou até aqui (secções no cubo) que parta para a descoberta de novos poliedros. 1. Com o tetraedro e com o material de que dispõe na sua mesa, substitua cada aresta por um vértice situado no seu ponto médio. Caracterize o novo sólido que obteve. Nota: Se não conseguir descobrir o seu nome utilize o programa Poly no computador. 2. Relacione os volumes do tetraedro e do sólido obtido. 3. Faça um pequeno relatório da actividade realizada. Na elaboração do seu relatório não deve esquecer, entre outros, os aspectos seguintes: Título Objectivo do trabalho. Material utilizado. Descrição do processo utilizado para a descoberta, das tentativas realizadas e das dificuldades encontradas. Conclusões. Comentários acerca do interesse e gozo suscitados por esta actividade. Clareza e correcção da linguagem utilizada. Identificação do autor do trabalho, da escola, da data, do ano e da turma. PROFESSORA: Rosa Canelas 5

6 Tarefa nº 9 proposta de resolução VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO TETRAEDRO Objectivo da tarefa: Utilizando a matéria já estudada até aqui (secções no cubo) descobrir novos poliedros. A tarefa divide-se em duas etapas: o Descobrir o poliedro e caracterizá-lo. o Comparar o volume do poliedro obtido com o do tetraedro. 1ª etapa: Com o tetraedro em acetato e uma caneta de acetato que tínhamos em cima da mesa, substituímos cada aresta por um vértice situado no seu ponto médio e obtivemos o poliedro da figura, que tem 8 faces triangulares. a 2 é a medida de cada aresta do poliedro, sendo a a aresta do octaedro. Este novo poliedro, regular, chama-se octaedro como já sabíamos. 2ª etapa: Para relacionar os volumes do tetraedro e do octaedro tivemos que pensar: o Que o octaedro se obtém do tetraedro quando tiramos 4 tetraedros com aresta igual a metade da aresta do tetraedro. o Os dois tetraedros são semelhantes e a razão de semelhança entre o menor e o maior é 1 2. o O volume do tetraedro menor vai ser 1 8 do volume do maior, porque a razão dos volumes de duas figuras semelhantes é o cubo da razão de semelhança. o O volume das 4 pirâmides vai, portanto, ser 4 8 do volume do tetraedro. o O volume do octaedro é então 4 8 do volume do tetraedro. Podemos finalmente concluir que o volume do octaedro é 1 do volume do tetraedro. 2 PROFESSORA: Rosa Canelas 6

Documentos relacionados

Escola Secundária com 3º ciclo D. Dinis. 10º Ano de Matemática A. Geometria no Plano e no Espaço I

Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Geometria no Plano e no Espaço I Trabalho de casa nº 7 GRUPO I 1. Num certo prisma, cada uma das bases tem n vértices. Quantas faces e quantas