Geometria Euclidiana II
|
|
|
- Manuel Barateiro Quintão
- 8 Há anos
- Visualizações:
Transcrição
1 Geometria Euclidiana II Professor Fabrício Oliveira Universidade Federal Rural do Semiárido 17 de outubro de 2010
2 O nosso curso Tópicos abordados Poliedros Convexos
3 O nosso curso Tópicos abordados Poliedros Convexos Prisma
4 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide
5 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide Cilindro
6 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide Cilindro Cone
7 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide Cilindro Cone Esfera
8 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide Cilindro Cone Esfera Inscrição e circunscrição de sólidos
9 O nosso curso Tópicos abordados Poliedros Convexos Prisma Pirâmide Cilindro Cone Esfera Inscrição e circunscrição de sólidos Superfícies e sólidos de revolução.
10 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que:
11 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que: Dois poĺıgonos não estão no mesmo plano
12 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que: Dois poĺıgonos não estão no mesmo plano Cada lado de um poĺıgono é comum a dois e somente dois poĺıgonos
13 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que: Dois poĺıgonos não estão no mesmo plano Cada lado de um poĺıgono é comum a dois e somente dois poĺıgonos O plano de cada poĺıgono deixa os demais poĺıgonos num mesmo semiespaço.
14 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que: Dois poĺıgonos não estão no mesmo plano Cada lado de um poĺıgono é comum a dois e somente dois poĺıgonos O plano de cada poĺıgono deixa os demais poĺıgonos num mesmo semiespaço.
15 Poliedros Convexos Seja n 4 um número finito de poĺıgonos convexos, tais que: Dois poĺıgonos não estão no mesmo plano Cada lado de um poĺıgono é comum a dois e somente dois poĺıgonos O plano de cada poĺıgono deixa os demais poĺıgonos num mesmo semiespaço. Definição de poliedro convexo Um poliedro convexo é a interseção dos semiespaços que contém os poĺıgonos acima.
16 Um pouco de história A vida de Euler Leonard Euler era Suiço e nasceu na cidade de Basiléia em 1707, viveu até 1783.
17 Um pouco de história A vida de Euler Leonard Euler era Suiço e nasceu na cidade de Basiléia em 1707, viveu até Ele desenvolveu tanta matemática que sua obra abrange mais de 75 volmes.
18 Um pouco de história A vida de Euler Leonard Euler era Suiço e nasceu na cidade de Basiléia em 1707, viveu até Ele desenvolveu tanta matemática que sua obra abrange mais de 75 volmes. Ele desenvolveu várias áreas da matemática como a Teoria dos Números, a Probabilidade, Equações Diferenciais e a Geometria.
19 Um pouco de história A vida de Euler Leonard Euler era Suiço e nasceu na cidade de Basiléia em 1707, viveu até Ele desenvolveu tanta matemática que sua obra abrange mais de 75 volmes. Ele desenvolveu várias áreas da matemática como a Teoria dos Números, a Probabilidade, Equações Diferenciais e a Geometria. Ficou cego em 1766 e nos últimos 17 anos de sua vida, mesmo cego, não diminuiu seu ritmo de publicações, alguns dizem que até aumentou a quantidade de artigos publicados.
20 Software Poly Veja alguns exemplos de poliedros convexos
21 Poliedros Convexos Conceitos Um poliedro convexo é composto dos seguintes elementos:
22 Poliedros Convexos Conceitos Um poliedro convexo é composto dos seguintes elementos: Faces(F ) que são os poĺıgonos do poliedro
23 Poliedros Convexos Conceitos Um poliedro convexo é composto dos seguintes elementos: Faces(F ) que são os poĺıgonos do poliedro Arestas(A) que são os lados dos poĺıgonos
24 Poliedros Convexos Conceitos Um poliedro convexo é composto dos seguintes elementos: Faces(F ) que são os poĺıgonos do poliedro Arestas(A) que são os lados dos poĺıgonos Vértices(V ) que são vértices das faces
25 Poliedros Convexos Conceitos Um poliedro convexo é composto dos seguintes elementos: Faces(F ) que são os poĺıgonos do poliedro Arestas(A) que são os lados dos poĺıgonos Vértices(V ) que são vértices das faces Ângulos que são os ângulos dos poĺıgonos das faces
26 Poliedros Convexos Relação de Euler Os elementos de um poliedro convexo se relacionam segundo uma famosa relação matemática. Esta relação foi encontrada por Euler em 1758, então com 51 anos.
27 Poliedros Convexos Relação de Euler Os elementos de um poliedro convexo se relacionam segundo uma famosa relação matemática. Esta relação foi encontrada por Euler em 1758, então com 51 anos. A relação diz o seguinte:
28 Poliedros Convexos Relação de Euler Os elementos de um poliedro convexo se relacionam segundo uma famosa relação matemática. Esta relação foi encontrada por Euler em 1758, então com 51 anos. A relação diz o seguinte:
29 Poliedros Convexos Relação de Euler Os elementos de um poliedro convexo se relacionam segundo uma famosa relação matemática. Esta relação foi encontrada por Euler em 1758, então com 51 anos. A relação diz o seguinte: Relação de Euler Em um poliedro convexo com V vértices, A arestas e F faces, temos a relação V A + F = 2
30 Poliedros Convexos Exemplificando relação Euler Vamos verificar a relação de Euler nos sólidos seguintes.
31 Poliedros Convexos Exemplo e exercício Exemplo Um poliedro convexo de onze faces tem seis faces triangulares e cinco faces quadrangulares. Calcule o número de arestas e de vértices do poliedro.
32 Poliedros Convexos Exemplo e exercício Exemplo Um poliedro convexo de onze faces tem seis faces triangulares e cinco faces quadrangulares. Calcule o número de arestas e de vértices do poliedro. Exercício Num poliedro convexo de 10 arestas, o número de faces é igual ao número de vértices. Quantas faces tem esse poliedro?
33 Poliedros Convexos Exemplo e exercício Exemplo Um poliedro convexo de onze faces tem seis faces triangulares e cinco faces quadrangulares. Calcule o número de arestas e de vértices do poliedro. Exercício Num poliedro convexo de 10 arestas, o número de faces é igual ao número de vértices. Quantas faces tem esse poliedro? Exercício Um poliedro convexo apresenta faces quadrangulares e triangulares. Calcule o número de faces, vértices e arestas desse poliedro, sabendo que o número de arestas é o quadrúplo do número de faces triangulares e o número de faces quadrangulares é igual a 5.
34 Poliedros Convexos Soma ângulos internos das faces Em um poliedro convexo temos a seguinte propriedade
35 Poliedros Convexos Soma ângulos internos das faces Em um poliedro convexo temos a seguinte propriedade
36 Poliedros Convexos Soma ângulos internos das faces Em um poliedro convexo temos a seguinte propriedade Propriedade A soma(em graus) dos ângulos internos de todas as faces de um poliedro convexo é S = (V 2)360 o em que V é o número de vértices do poliedro.
37 Poliedros de Platão Conceito Definindo poliedro de platão Um poliedro é chamado poliedro de platão se
38 Poliedros de Platão Conceito Definindo poliedro de platão Um poliedro é chamado poliedro de platão se Todas as faces tem o mesmo número (n) de arestas
39 Poliedros de Platão Conceito Definindo poliedro de platão Um poliedro é chamado poliedro de platão se Todas as faces tem o mesmo número (n) de arestas Todas os ângulos poliedricos têm o mesmo número (m) de arestas
40 Poliedros de Platão Conceito Definindo poliedro de platão Um poliedro é chamado poliedro de platão se Todas as faces tem o mesmo número (n) de arestas Todas os ângulos poliedricos têm o mesmo número (m) de arestas Vale a relação de Euler V A + F = 2
41 Poliedros de Platão Tabela Podemos, então construir a tabela seguinte com os Poliedros de Platão existentes.
42 Poliedros de Platão Tabela m n A V F Nome Tetraedro Hexaedro Octaedro Dodecaedro Icosaedro
43 Poliedros Regulares Conceito Um poliedro é regular quando
44 Poliedros Regulares Conceito Um poliedro é regular quando Suas faces são poĺıgonos regulares
45 Poliedros Regulares Conceito Um poliedro é regular quando Suas faces são poĺıgonos regulares Seus ângulos poliédricos são congruentes
46 Poliedros Regulres Tipos São cinco os poliedros regulares
47 Poliedros Regulres Tipos São cinco os poliedros regulares Tetraedro Regular
48 Poliedros Regulres Tipos São cinco os poliedros regulares Tetraedro Regular Hexaedro Regular
49 Poliedros Regulres Tipos São cinco os poliedros regulares Tetraedro Regular Hexaedro Regular Octaedro Regular
50 Poliedros Regulres Tipos São cinco os poliedros regulares Tetraedro Regular Hexaedro Regular Octaedro Regular Dodecaedro Regular
51 Poliedros Regulres Tipos São cinco os poliedros regulares Tetraedro Regular Hexaedro Regular Octaedro Regular Dodecaedro Regular Icosaedro Regular.
52 Poliedros Exemplo e exercício Exemplo Um poliedro convexo de 15 arestas tem somente faces quadrangulares e pentagonais. Quantas faces tem de cada tipo se a soma dos ângulos das faces é 32 ângulos retos.
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados.
 POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
POLIEDROS AULA I. Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 POLIEDROS AULA I Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos POLIEDROS Vértice Face Aresta 1) Definição de POLIEDRO: É uma região do espaço delimitada por um conjunto finito de polígonos,
POLIEDROS AULA I Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos POLIEDROS Vértice Face Aresta 1) Definição de POLIEDRO: É uma região do espaço delimitada por um conjunto finito de polígonos,
GEOMETRIA MÉTRICA. As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases.
 GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
Poliedros Teoria. Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades:
 Poliedros Teoria Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades: P1. Todo polígono da Superfície Poliédrica possui algum lado
Poliedros Teoria Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades: P1. Todo polígono da Superfície Poliédrica possui algum lado
Lista de exercícios 04 Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática
 Lista de exercícios 04 Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática Antes de iniciar a lista de exercícios leia atentamente as seguintes orientações: É fundamental
Lista de exercícios 04 Aluno (a): Turma: 2ª série: (Ensino médio) Professor: Flávio Disciplina: Matemática Antes de iniciar a lista de exercícios leia atentamente as seguintes orientações: É fundamental
Mat. Monitor: Roberta Teixeira
 1 Mat. Professore: Alex Amaral Monitor: Roberta Teixeira 2 Poliedros 19 set RESUMO Poliedros São sólidos geométricos formados por vértices, arestas e faces, cujas superfícies são polígonos planos (triângulos,
1 Mat. Professore: Alex Amaral Monitor: Roberta Teixeira 2 Poliedros 19 set RESUMO Poliedros São sólidos geométricos formados por vértices, arestas e faces, cujas superfícies são polígonos planos (triângulos,
Prof. Márcio Nascimento. 1 de abril de 2015
 Geometria dos Sólidos Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Geometria
Geometria dos Sólidos Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Geometria
GEOMETRIA MÉTRICA ESPACIAL
 GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
RELATÓRIO Data: , e
 RELATÓRIO Data:25.06.2015, 26.06.2015 e 29.06.2015 Objetivo(s) Objetivo Geral: - Abordar conceitos de geometria espacial e plana por meio da construção, manipulação e planificação dos poliedros de Platão.
RELATÓRIO Data:25.06.2015, 26.06.2015 e 29.06.2015 Objetivo(s) Objetivo Geral: - Abordar conceitos de geometria espacial e plana por meio da construção, manipulação e planificação dos poliedros de Platão.
ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA POLIEDROS PROF. CARLINHOS
 ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA POLIEDROS PROF. CARLINHOS 1 Sólidos Geométricos Introdução Grande parte dos objetos que nos são familiares tem formas geométricas definidas; são
ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA POLIEDROS PROF. CARLINHOS 1 Sólidos Geométricos Introdução Grande parte dos objetos que nos são familiares tem formas geométricas definidas; são
GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR
 GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR Sólidos geométricos PARA COMEÇAR... No mundo de hoje, as inúmeras obras de engenharia, arquitetura, artes plásticas etc. mostram a imensa quantidade de formas que
GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR Sólidos geométricos PARA COMEÇAR... No mundo de hoje, as inúmeras obras de engenharia, arquitetura, artes plásticas etc. mostram a imensa quantidade de formas que
GEOMETRIA ESPACIAL TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO REGULARES RETO POLIEDROS OBLÍQUO PRISMA REGULAR IRREGULARES RETA OBLÍQUA PIRÂMIDE
 GEOMETRIA ESPACIAL SÓLIDOS GEOMÉTRICOS POLIEDROS REGULARES SÓLIDOS DE REVOLUÇÃO IRREGULARES CONE TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO ESFERA CILINDRO PRISMA PIRÂMIDE RETO OBLÍQUO RETO RETO
GEOMETRIA ESPACIAL SÓLIDOS GEOMÉTRICOS POLIEDROS REGULARES SÓLIDOS DE REVOLUÇÃO IRREGULARES CONE TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO ESFERA CILINDRO PRISMA PIRÂMIDE RETO OBLÍQUO RETO RETO
PROPOSTA DIDÁTICA. 3. Desenvolvimento da proposta didática (10 min) - Acomodação dos alunos, apresentação dos bolsistas e realização da chamada.
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
1 POLIEDROS 2 ELEMENTOS 4 POLIEDROS REGULARES 3 CLASSIFICAÇÃO. 3.2 Quanto ao número de faces. 4.1 Tetraedro regular. 3.
 Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones)
 Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
NDMAT Núcleo de Desenvolvimentos Matemáticos
 01) Determine o número de vértices de um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 pentagonal e 2 hexagonais. 07) Um poliedro de sete vértices tem cinco ângulos tetraédricos
01) Determine o número de vértices de um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 pentagonal e 2 hexagonais. 07) Um poliedro de sete vértices tem cinco ângulos tetraédricos
Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO
 Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre/2013 Aluno(a): Número: Turma: 1) Coloque V ou F, conforme
Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre/2013 Aluno(a): Número: Turma: 1) Coloque V ou F, conforme
Geometria Espacial: Sólidos Geométricos
 Aluno(a): POLIEDROS E PRISMA (1º BIM) Noções Sobre Poliedros Denominam-se sólidos geométricos as figuras geométricas do espaço. Entre os sólidos geométricos, destacamos os poliedros e os corpos redondos.
Aluno(a): POLIEDROS E PRISMA (1º BIM) Noções Sobre Poliedros Denominam-se sólidos geométricos as figuras geométricas do espaço. Entre os sólidos geométricos, destacamos os poliedros e os corpos redondos.
Poliedros AULA Introdução Denições
 AULA 13 13.1 Introdução Nesta aula estudaremos os sólidos formados por regiões do espaço (faces), chamados poliedros. O conceito de poliedro está para o espaço assim como o conceito de polígono está para
AULA 13 13.1 Introdução Nesta aula estudaremos os sólidos formados por regiões do espaço (faces), chamados poliedros. O conceito de poliedro está para o espaço assim como o conceito de polígono está para
Aula 26 Poliedros. Objetivos. Identificar poliedros. Aplicar o Teorema de Euler
 MÓDULO 2 - AULA 26 Aula 26 Poliedros Objetivos Identificar poliedros Aplicar o Teorema de Euler Introdução Nesta aula estudaremos outros exemplos de figuras no espaço: os poliedros Começaremos com a definição
MÓDULO 2 - AULA 26 Aula 26 Poliedros Objetivos Identificar poliedros Aplicar o Teorema de Euler Introdução Nesta aula estudaremos outros exemplos de figuras no espaço: os poliedros Começaremos com a definição
MATEMÁTICA - 3 o ANO MÓDULO 50 POLIEDROS
 MATEMÁTICA - 3 o ANO MÓDULO 50 POLIEDROS Tetraedro regular Hexaedro regular Octaedro regular Dodecaedro regular Icosaedro regular B C A F D G E H Como pode cair no enem O poliedro da figura (uma invenção
MATEMÁTICA - 3 o ANO MÓDULO 50 POLIEDROS Tetraedro regular Hexaedro regular Octaedro regular Dodecaedro regular Icosaedro regular B C A F D G E H Como pode cair no enem O poliedro da figura (uma invenção
FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL
 FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL Tarefa 1 Aluno: Thiago Milani Cabral Grupo 2 Tutora: Susi Cristine
FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL Tarefa 1 Aluno: Thiago Milani Cabral Grupo 2 Tutora: Susi Cristine
Poliedross. ANOTAÇÕES EM AULA Capítulo 23 Poliedros 1.5 CONEXÕES COM A MATEMÁTICA
 Poliedross 1.5 Superfície poliédrica fechada Uma superfície poliédrica fechada é composta de um número finito (quatro ou mais) de superfícies poligonais planas, de modo que cada lado de uma dessas superfícies
Poliedross 1.5 Superfície poliédrica fechada Uma superfície poliédrica fechada é composta de um número finito (quatro ou mais) de superfícies poligonais planas, de modo que cada lado de uma dessas superfícies
Plano de Trabalho 2. Introdução à Geometria Espacial
 FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 1º Bimestre/2013 Plano de Trabalho 2 Introdução à Geometria Espacial Cursista: Izabel Leal Vieira Tutor: Cláudio Rocha de Jesus 1 SUMÁRIO INTRODUÇÃO........................................
FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 1º Bimestre/2013 Plano de Trabalho 2 Introdução à Geometria Espacial Cursista: Izabel Leal Vieira Tutor: Cláudio Rocha de Jesus 1 SUMÁRIO INTRODUÇÃO........................................
Lista de exercícios 05. Aluno (a) : Série: 2º ano (Ensino médio) Professor: Flávio Disciplina: Matemática
 Lista de exercícios 05 Aluno (a) : Série: 2º ano (Ensino médio) Professor: Flávio Disciplina: Matemática No Anhanguera você é + Enem Observações: Data da entrega: 29/08/2015. A lista deverá apresentar
Lista de exercícios 05 Aluno (a) : Série: 2º ano (Ensino médio) Professor: Flávio Disciplina: Matemática No Anhanguera você é + Enem Observações: Data da entrega: 29/08/2015. A lista deverá apresentar
ESI COLÉGIO NOSSA SENHORA AUXILIADORA Cascavel
 ESI COLÉGIO NOSSA SENHORA AUXILIADORA Cascavel VA RECUPERAÇÃO Matemática UNIDADE LETIVA 2º Bimestre DATA / /2018 NOME Nº SÉRIE 2ª. PROFESSOR Antonio VALOR 2,0 NOTA 2 Dadas as matrizes de ordem 3. Sendo
ESI COLÉGIO NOSSA SENHORA AUXILIADORA Cascavel VA RECUPERAÇÃO Matemática UNIDADE LETIVA 2º Bimestre DATA / /2018 NOME Nº SÉRIE 2ª. PROFESSOR Antonio VALOR 2,0 NOTA 2 Dadas as matrizes de ordem 3. Sendo
Os Poliedros Platônicos. Por que existem só 5 sólidos platônicos?
 Os Poliedros Platônicos Por que existem só 5 sólidos platônicos? Introdução O sufixo edro vem da palavra grega hédra que significa face. Os prefixos, também oriundos do grego, indicam a quantidade de faces
Os Poliedros Platônicos Por que existem só 5 sólidos platônicos? Introdução O sufixo edro vem da palavra grega hédra que significa face. Os prefixos, também oriundos do grego, indicam a quantidade de faces
1ª Parte SÓLIDOS GEOMÉTRICOS. Prof. Danillo Alves 6º ano Matutino
 1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
III REPRESENTAÇÃO DO PLANO. 1. Representação do plano Um plano pode ser determinado por: a) três pontos não colineares
 59 MINISTÉRIO DA EDUCAÇÃO - UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS - DEPARTAMENTO DE EXPRESSÃO GRÁFICA Professora Deise Maria Bertholdi Costa Disciplina CD020 Geometria Descritiva Curso
59 MINISTÉRIO DA EDUCAÇÃO - UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS - DEPARTAMENTO DE EXPRESSÃO GRÁFICA Professora Deise Maria Bertholdi Costa Disciplina CD020 Geometria Descritiva Curso
MATEMÁTICA. Geometria Espacial
 MATEMÁTICA Geometria Espacial Professor : Dêner Rocha Monster Concursos 1 Geometria Espacial Conceitos primitivos São conceitos primitivos (e, portanto, aceitos sem definição) na Geometria espacial os
MATEMÁTICA Geometria Espacial Professor : Dêner Rocha Monster Concursos 1 Geometria Espacial Conceitos primitivos São conceitos primitivos (e, portanto, aceitos sem definição) na Geometria espacial os
Exercícios de Matemática Poliedros
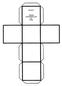
 Exercícios de Matemática Poliedros 3. (Unitau) Se dobrarmos convenientemente as linhas tracejadas das figuras a seguir, obteremos três modelos de figuras espaciais cujos nomes são: 1. (Uerj) O poliedro
Exercícios de Matemática Poliedros 3. (Unitau) Se dobrarmos convenientemente as linhas tracejadas das figuras a seguir, obteremos três modelos de figuras espaciais cujos nomes são: 1. (Uerj) O poliedro
Geometria Descritiva. Revisão: Polígonos regulares/irregulares. Linhas e Pontos pertencentes a Faces/Arestas de Poliedros
 Geometria Descritiva Revisão: Polígonos regulares/irregulares Linhas e Pontos pertencentes a Faces/Arestas de Poliedros - Os Poliedros em estudo em GD podem ser: regulares (cujas fases são polígonos regulares,
Geometria Descritiva Revisão: Polígonos regulares/irregulares Linhas e Pontos pertencentes a Faces/Arestas de Poliedros - Os Poliedros em estudo em GD podem ser: regulares (cujas fases são polígonos regulares,
U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA!
 1 U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA! http://ueedgartito.wordpress.com RESUMO DE GEOMETRIA ESPACIAL São conceitos primitivos ( e, portanto,
1 U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA! http://ueedgartito.wordpress.com RESUMO DE GEOMETRIA ESPACIAL São conceitos primitivos ( e, portanto,
Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF
 Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF 01) Observando a figuras e simplesmente contando, determine o número de faces, arestas e o vértices
Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF 01) Observando a figuras e simplesmente contando, determine o número de faces, arestas e o vértices
Plano de Trabalho sobre Introdução à Geometria Espacial
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: C. E. Madre Teresa de Calcutá. PROFESSORA: Angela Saida Alvarez Jacob. GRUPO 6 MATRÍCULA: 0913098-0 TURMA: 2 ano.
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: C. E. Madre Teresa de Calcutá. PROFESSORA: Angela Saida Alvarez Jacob. GRUPO 6 MATRÍCULA: 0913098-0 TURMA: 2 ano.
Dupla Projeção Ortogonal. PARTE III REPRESENTAÇÃO DO PLANO 1. Representação do plano Um plano pode ser determinado por: a) três pontos não colineares
 31 PARTE III REPRESENTAÇÃ D PLAN 1. Representação do plano Um plano pode ser determinado por: a) três pontos não colineares b) um ponto e uma reta que não se pertencem 32 c) duas retas concorrentes d)
31 PARTE III REPRESENTAÇÃ D PLAN 1. Representação do plano Um plano pode ser determinado por: a) três pontos não colineares b) um ponto e uma reta que não se pertencem 32 c) duas retas concorrentes d)
Poliedros 1 ARESTAS FACES VERTICES. Figura 1.1: Elementos de um poliedro
 Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
PLANO DE TRABALHO SOBRE GEOMETRIA ESPACIAL. H07 Relacionar diferentes poliedros ou corpos redondos com suas planificações.
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: COLÉGIO ESTADUAL PAULINO PINHEIRO BAPTISTA PROFESSORA: PATRÍCIA DOMINGUES DE SOUZA MATRÍCULA: 0912303-5 TUTOR: SUSI
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: COLÉGIO ESTADUAL PAULINO PINHEIRO BAPTISTA PROFESSORA: PATRÍCIA DOMINGUES DE SOUZA MATRÍCULA: 0912303-5 TUTOR: SUSI
Questão 1. Com base nas informações, qual é a quantidade de cores que serão utilizadas na pintura das faces do troféu?
 SE18 - Matemática LMAT 6C4 - Poliedros convexos Questão 1 (Enem 2015) Para o modelo de um troféu foi escolhido um poliedro P, obtido a partir de cortes nos vértices de um cubo. Com um corte plano em cada
SE18 - Matemática LMAT 6C4 - Poliedros convexos Questão 1 (Enem 2015) Para o modelo de um troféu foi escolhido um poliedro P, obtido a partir de cortes nos vértices de um cubo. Com um corte plano em cada
3º trimestre SALA DE ESTUDOS Data: 25/09/18 Ensino Médio 2º ano classe: Prof. Maurício Nome: nº
 3º trimestre SALA DE ESTUDOS Data: 5/09/18 Ensino Médio º ano classe: Prof. Maurício Nome: nº.. 1. (Uem 018) Sobre geometria espacial, assinale o que for correto. 01) Dois planos sempre se interceptam.
3º trimestre SALA DE ESTUDOS Data: 5/09/18 Ensino Médio º ano classe: Prof. Maurício Nome: nº.. 1. (Uem 018) Sobre geometria espacial, assinale o que for correto. 01) Dois planos sempre se interceptam.
Os Poliedros de Platão
 Os Poliedros de Platão Poliedro é um sólido geométrico cuja superfície é composta por um número finito de faces, cujos vértices são formados por três ou mais arestas em três dimensões (eixo dos "X", "Y",
Os Poliedros de Platão Poliedro é um sólido geométrico cuja superfície é composta por um número finito de faces, cujos vértices são formados por três ou mais arestas em três dimensões (eixo dos "X", "Y",
Figuras Geométricas planas e espaciais. Rafael Carvalho
 Figuras Geométricas planas e espaciais Rafael Carvalho Figuras geométricas planas Na geometria plana vamos então nos atentar ao método de cálculo da área das figuras geométricas planas. Sendo elas os polígonos,
Figuras Geométricas planas e espaciais Rafael Carvalho Figuras geométricas planas Na geometria plana vamos então nos atentar ao método de cálculo da área das figuras geométricas planas. Sendo elas os polígonos,
PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas
 PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas 1 Escalas escala medida _ no _ desenho medida _ real _ ou _ verdadeira _ grandeza D VG Escala de ampliação Objeto real
PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas 1 Escalas escala medida _ no _ desenho medida _ real _ ou _ verdadeira _ grandeza D VG Escala de ampliação Objeto real
ATIVIDADE DE RECUPERAÇÃO PARALELA 2º Trimestre 3º EM DISCIPLINA: Álgebra
 ATIVIDADE DE RECUPERAÇÃO PARALELA 2º Trimestre º EM DISCIPLINA: Álgebra Observação: Antes de responder às atividades, releia o material de orientação de estudos Números Complexos 1) Na figura a seguir,
ATIVIDADE DE RECUPERAÇÃO PARALELA 2º Trimestre º EM DISCIPLINA: Álgebra Observação: Antes de responder às atividades, releia o material de orientação de estudos Números Complexos 1) Na figura a seguir,
V = 12 A = 18 F = = 2 V=8 A=12 F= = 2
 Por: Belchior, Ismaigna e Jannine Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V - A + F = 2 em que V é o número de vértices, A é o número de arestas e F, o número de faces. Observe
Por: Belchior, Ismaigna e Jannine Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V - A + F = 2 em que V é o número de vértices, A é o número de arestas e F, o número de faces. Observe
singular Lista 1 de exercícios - Áreas das principais figuras planas e poliedros 3C17/27 - Prof.Liana (11/03/2016)
 singular Lista 1 de exercícios - Áreas das principais figuras planas e poliedros 3C17/7 - Prof.Liana (11/03/016) 1. (FGV ) Em um mesmo plano estão contidos um quadrado de 9 cm de lado e um círculo de 6
singular Lista 1 de exercícios - Áreas das principais figuras planas e poliedros 3C17/7 - Prof.Liana (11/03/016) 1. (FGV ) Em um mesmo plano estão contidos um quadrado de 9 cm de lado e um círculo de 6
Sólidos Geométricos, Poliedros e Volume Prof. Lhaylla Crissaff
 Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
Posições relativas entre elementos geométricos no espaço
 Geometria no espaço Posições relativas entre elementos geométricos no espaço Plano: constituído por três pontos distintos e não colineares; o plano é bidimensional (tem duas dimensões: altura e largura);
Geometria no espaço Posições relativas entre elementos geométricos no espaço Plano: constituído por três pontos distintos e não colineares; o plano é bidimensional (tem duas dimensões: altura e largura);
FORMAÇÃO CONTINUADA EM MATEMÁTICA TAREFA 4 MARCIA LEPSCH FERREIRA BARCELLOS. Matemática 2º ano - 1º Bimestre. Grupo: 4
 FORMAÇÃO CONTINUADA EM MATEMÁTICA TAREFA 4 MARCIA LEPSCH FERREIRA BARCELLOS Matemática 2º ano - 1º Bimestre Grupo: 4 Tutor: Maria Cláudia Padilha Tostes Plano de trabalho: Geometria Espacial Introdução:
FORMAÇÃO CONTINUADA EM MATEMÁTICA TAREFA 4 MARCIA LEPSCH FERREIRA BARCELLOS Matemática 2º ano - 1º Bimestre Grupo: 4 Tutor: Maria Cláudia Padilha Tostes Plano de trabalho: Geometria Espacial Introdução:
ESTADO DE ALAGOAS UNIVERSIDADE ESTADUAL DE ALAGOAS - UNEAL PRÓ-REITORIA DE GRADUAÇÃO - PROGRAD Reitoria Arapiraca PLANO DE MONITORIA
 PLANO DE MONITORIA CAMPUS: Campus III - Palmeira dos Índios CURSO: Matemática ANO LETIVO: 2017 PROFESSOR ORIENTADOR: ELIELSON MAGALHÃES LIMA DISCIPLINA: Geometria Euclidiana Espacial EXISTE DISCIPLINA
PLANO DE MONITORIA CAMPUS: Campus III - Palmeira dos Índios CURSO: Matemática ANO LETIVO: 2017 PROFESSOR ORIENTADOR: ELIELSON MAGALHÃES LIMA DISCIPLINA: Geometria Euclidiana Espacial EXISTE DISCIPLINA
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
POLIEDROS REGULARES. São os poliedros cujas faces são polígonos regulares iguais entre si, e cujos ângulos poliédricos são todos iguais.
 1 POLIEDROS REGULARES DEFINIÇÃO E CLASSIFICAÇÃO DE POLIEDROS Do grego - poly (muitas) + edro (face). Os poliedros fazem parte do pensamento grego, foram estudados pelos grandes filósofos da antiguidade
1 POLIEDROS REGULARES DEFINIÇÃO E CLASSIFICAÇÃO DE POLIEDROS Do grego - poly (muitas) + edro (face). Os poliedros fazem parte do pensamento grego, foram estudados pelos grandes filósofos da antiguidade
EXERCÍCOS DE REVISÃO - 1º ANO ENSINO MÉDIO
 EXERÍOS DE REVISÃO - 1º NO ENSINO MÉDIO 1.- Para a função definida por f(x) = - 2x 2 + x + 1, determine as coordenadas do vértice e decida se ele representa um ponto de máximo ou de mínimo, explicando
EXERÍOS DE REVISÃO - 1º NO ENSINO MÉDIO 1.- Para a função definida por f(x) = - 2x 2 + x + 1, determine as coordenadas do vértice e decida se ele representa um ponto de máximo ou de mínimo, explicando
REGULARES POLIEDROS IRREGULARES
 GEOMETRIA ESPACIAL ESFERA OBLÍQUO RETO CILINDRO OBLÍQUO RETO CONE SÓLIDOS DE REVOLUÇÃO REGULAR OBLÍQUA RETA PIRÂMIDE REGULAR OBLÍQUO RETO PRISMA IRREGULARES ICOSAEDRO DODECAEDRO OCTAEDRO HEXAEDRO TETRAEDRO
GEOMETRIA ESPACIAL ESFERA OBLÍQUO RETO CILINDRO OBLÍQUO RETO CONE SÓLIDOS DE REVOLUÇÃO REGULAR OBLÍQUA RETA PIRÂMIDE REGULAR OBLÍQUO RETO PRISMA IRREGULARES ICOSAEDRO DODECAEDRO OCTAEDRO HEXAEDRO TETRAEDRO
Poliedro de Escher (dodecaedro rômbico estrelado) (Jogos de Engenho S1 Laboratório de Educação Matemática) Parte 1:
 Poliedro de Escher (dodecaedro rômbico estrelado) (Jogos de Engenho S1 Laboratório de Educação Matemática) Parte 1: Observando a natureza A primeira descrição formal do dodecaedro rômbico deve-se a Kepler,
Poliedro de Escher (dodecaedro rômbico estrelado) (Jogos de Engenho S1 Laboratório de Educação Matemática) Parte 1: Observando a natureza A primeira descrição formal do dodecaedro rômbico deve-se a Kepler,
Recursos para Estudo / Atividades
 COLÉGIO NOSSA SENHORA DA PIEDADE Programa de Recuperação Final 3ª Etapa 2014 Disciplina: Matemática Série: 2ª Professor (a): Ana Cristina Turma: FG Caro aluno, você está recebendo o conteúdo de recuperação.
COLÉGIO NOSSA SENHORA DA PIEDADE Programa de Recuperação Final 3ª Etapa 2014 Disciplina: Matemática Série: 2ª Professor (a): Ana Cristina Turma: FG Caro aluno, você está recebendo o conteúdo de recuperação.
Construção dos Poliedros: Cubo e Tetraedro e suas Aplicações
 Construção dos Poliedros: Cubo e Tetraedro e suas Aplicações Rita de Cássia Pavani Lamas, Departamento de Matemática, IBILCE-UNESP [email protected] Uma aplicação da congruência de triângulos e polígonos
Construção dos Poliedros: Cubo e Tetraedro e suas Aplicações Rita de Cássia Pavani Lamas, Departamento de Matemática, IBILCE-UNESP [email protected] Uma aplicação da congruência de triângulos e polígonos
Poliedros. MA13 - Unidade 22. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT
 Poliedros MA13 - Unidade 22 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Poliedros Poliedro é um objeto da Matemática que pode ser definido com diversos
Poliedros MA13 - Unidade 22 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Poliedros Poliedro é um objeto da Matemática que pode ser definido com diversos
Unidade 9 Geometria Espacial. Poliedros Volume de sólidos geométricos Princípio de Cavalieri
 Unidade 9 Geometria Espacial Poliedros Volume de sólidos geométricos Princípio de Cavalieri Poliedros palavra poliedro tem sua origem no idioma grego (poly significa, muitos, e hedra, faces). Poliedro
Unidade 9 Geometria Espacial Poliedros Volume de sólidos geométricos Princípio de Cavalieri Poliedros palavra poliedro tem sua origem no idioma grego (poly significa, muitos, e hedra, faces). Poliedro
Professor Diego - Tarefa (UFJF MG) Observe, abaixo, uma imagem desse vírus que tem a forma de um sólido geométrico.
 Professor Diego - Tarefa 10 01. (UFJF MG) Observe, abaixo, uma imagem desse vírus que tem a forma de um sólido geométrico. Qual é a planificação do sólido representado por esse vírus? Disponível em:
Professor Diego - Tarefa 10 01. (UFJF MG) Observe, abaixo, uma imagem desse vírus que tem a forma de um sólido geométrico. Qual é a planificação do sólido representado por esse vírus? Disponível em:
Apostila de Matemática II 3º bimestre/2016. Professora : Cristiane Fernandes
 Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2. Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 -
 Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2 Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 - Formação Continuada em Matemática Fundação CECIERJ / Consórcio CEDERJ MATEMÁTICA 2º ANO/ENS.
Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2 Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 - Formação Continuada em Matemática Fundação CECIERJ / Consórcio CEDERJ MATEMÁTICA 2º ANO/ENS.
INTRODUÇÃO À GEOMETRIA ESPACIAL
 Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 1º Bimestre/2014 Plano de Trabalho INTRODUÇÃO À GEOMETRIA ESPACIAL Tarefa 1 Cursista: Wendel do Nascimento Pinheiro
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 1º Bimestre/2014 Plano de Trabalho INTRODUÇÃO À GEOMETRIA ESPACIAL Tarefa 1 Cursista: Wendel do Nascimento Pinheiro
1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente:
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 2014 1ª. SÉRIE 1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente: 2.-Ao fazer uma
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 2014 1ª. SÉRIE 1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente: 2.-Ao fazer uma
Poliedros / Prismas-2 s-2018-mat2
 Poliedros / Prismas- s-08-mat. (Uece ) Um poliedro convexo tem faces, sendo 0 hexágonos e pentágonos. O número de vértices deste polígono: a) 90. b) 7. c) 60. d) 56.. (Ifsp ) A figura mostra uma peça feita
Poliedros / Prismas- s-08-mat. (Uece ) Um poliedro convexo tem faces, sendo 0 hexágonos e pentágonos. O número de vértices deste polígono: a) 90. b) 7. c) 60. d) 56.. (Ifsp ) A figura mostra uma peça feita
UNIVERSIDADE FEDERAL DE ALAGOAS CENTRO DE EDUCAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE CIÊNCIAS E MATEMÁTICA JOSÉ WELLINGTON SANTOS SILVA
 UNIVERSIDADE FEDERAL DE ALAGOAS CENTRO DE EDUCAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE CIÊNCIAS E MATEMÁTICA JOSÉ WELLINGTON SANTOS SILVA SEQUÊNCIA DIDÁTICA PARA O ESTUDO DE SÓLIDOS GEOMÉTRICOS COM
UNIVERSIDADE FEDERAL DE ALAGOAS CENTRO DE EDUCAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE CIÊNCIAS E MATEMÁTICA JOSÉ WELLINGTON SANTOS SILVA SEQUÊNCIA DIDÁTICA PARA O ESTUDO DE SÓLIDOS GEOMÉTRICOS COM
Geometria Espacial. Projetos SEEDUC Formação Continuada. Matemática 2ª Série do ensino médio 1º Bimestre
 Projetos SEEDUC Formação Continuada Geometria Espacial Matemática 2ª Série do ensino médio 1º Bimestre Plano de Trabalho 2 Professora: Viviane de Almeida Ramos Tutor: Claudio Rocha de Jesus Grupo: 6 Introdução
Projetos SEEDUC Formação Continuada Geometria Espacial Matemática 2ª Série do ensino médio 1º Bimestre Plano de Trabalho 2 Professora: Viviane de Almeida Ramos Tutor: Claudio Rocha de Jesus Grupo: 6 Introdução
AULA 02 AULA 01 (D) 9. ITEM 01 No lançamento de um dado e uma moeda, qual é a probabilidade de se obter cara na moeda e face 5 no dado?
 AULA 01 No lançamento de um dado e uma moeda, qual é a probabilidade de se obter cara na moeda e face 5 no dado? Em um conjunto de 50 cartões numerados de 1 a 50, retirando ao acaso um desses cartões,
AULA 01 No lançamento de um dado e uma moeda, qual é a probabilidade de se obter cara na moeda e face 5 no dado? Em um conjunto de 50 cartões numerados de 1 a 50, retirando ao acaso um desses cartões,
 10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
Módulo de Geometria Espacial I - Fundamentos. Poliedros. 3 ano/e.m.
 Módulo de Geometria Espacial I - Fundamentos Poliedros. ano/e.m. Geometria Espacial I - Fundamentos Poliedros. 1 Exercícios Introdutórios Exercício 1. Um poliedro convexo tem 6 faces e 1 arestas. Determine
Módulo de Geometria Espacial I - Fundamentos Poliedros. ano/e.m. Geometria Espacial I - Fundamentos Poliedros. 1 Exercícios Introdutórios Exercício 1. Um poliedro convexo tem 6 faces e 1 arestas. Determine
Noções de Geometria. Professora: Gianni Leal 6º B.
 Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
GEOMETRIA ESPACIAL CONTEÚDOS. Capacidade e volume Poliedros Pirâmides Cilindros Cone Esfera AMPLIANDO SEUS CONHECIMENTOS
 GEOMETRIA ESPACIAL CONTEÚDOS Capacidade e volume Poliedros Pirâmides Cilindros Cone Esfera AMPLIANDO SEUS CONHECIMENTOS Capacidade e volume Na receita de bolo estava indicado 500 ml de leite ou 500 cm³?
GEOMETRIA ESPACIAL CONTEÚDOS Capacidade e volume Poliedros Pirâmides Cilindros Cone Esfera AMPLIANDO SEUS CONHECIMENTOS Capacidade e volume Na receita de bolo estava indicado 500 ml de leite ou 500 cm³?
6º - Duas retas são concorrentes se tiverem apenas um ponto em comum.
 3º - Pontos colineares pertencem à mesma reta. 4º- Três pontos determinam um único plano. 5º - Se uma reta contém dois pontos de um plano, esta reta está contida neste plano. 6º - Duas retas são concorrentes
3º - Pontos colineares pertencem à mesma reta. 4º- Três pontos determinam um único plano. 5º - Se uma reta contém dois pontos de um plano, esta reta está contida neste plano. 6º - Duas retas são concorrentes
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL
 ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL Gilmara Teixeira Barcelos - Centro Federal de Educação Tecnológica de Campos (CEFET- Campos) - [email protected] Silvia Cristina Freitas Batista
ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL Gilmara Teixeira Barcelos - Centro Federal de Educação Tecnológica de Campos (CEFET- Campos) - [email protected] Silvia Cristina Freitas Batista
Geometria Espacial Profº Driko
 Geometria Espacial Profº Driko PRISMAS Sejam α e β dois planos paralelos distintos, uma reta r secante a esses planos e uma região poligonal convexa A1A2A3...An contida em α. Consideremos todos os segmentos
Geometria Espacial Profº Driko PRISMAS Sejam α e β dois planos paralelos distintos, uma reta r secante a esses planos e uma região poligonal convexa A1A2A3...An contida em α. Consideremos todos os segmentos
O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem.
 TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
REGULARES POLIEDROS IRREGULARES
 GEOMETRIA ESPACIAL ESFERA OBLÍQUO RETO CILINDRO OBLÍQUO RETO CONE SÓLIDOS DE REVOLUÇÃO REGULAR OBLÍQUA RETA PIRÂMIDE REGULAR OBLÍQUO RETO PRISMA IRREGULARES ICOSAEDRO DODECAEDRO OCTAEDRO HEXAEDRO TETRAEDRO
GEOMETRIA ESPACIAL ESFERA OBLÍQUO RETO CILINDRO OBLÍQUO RETO CONE SÓLIDOS DE REVOLUÇÃO REGULAR OBLÍQUA RETA PIRÂMIDE REGULAR OBLÍQUO RETO PRISMA IRREGULARES ICOSAEDRO DODECAEDRO OCTAEDRO HEXAEDRO TETRAEDRO
Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides
 Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides Cursista: Marta Vieira de Andrade. 1 Série: 2ª. Tutor: Andréa Silva
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides Cursista: Marta Vieira de Andrade. 1 Série: 2ª. Tutor: Andréa Silva
3ª Ficha de Trabalho
 SOL SUNÁRI LRTO SMPIO 3ª icha de Trabalho MTMÁTI - 10º no 01/013 1ª. Parte : ( Questões Múltiplas ) 1. O perímetro do retângulo é igual a: ( ) 0 8 ( ) 10 8 ( ) 5 3 10 ( ) 100 15 15 75. diagonal de um quadrado
SOL SUNÁRI LRTO SMPIO 3ª icha de Trabalho MTMÁTI - 10º no 01/013 1ª. Parte : ( Questões Múltiplas ) 1. O perímetro do retângulo é igual a: ( ) 0 8 ( ) 10 8 ( ) 5 3 10 ( ) 100 15 15 75. diagonal de um quadrado
4. Superfícies e sólidos geométricos
 4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
CURSO: Licenciatura em Matemática TURMA: LM 2011/01_1ºSEM PROFESSOR: NÍCOLAS MORO MÜLLER PLANO DE ENSINO
 CURSO: Licenciatura em Matemática TURMA: LM 2011/01_1ºSEM PROFESSOR: NÍCOLAS MORO MÜLLER PLANO DE ENSINO DISCIPLINA: 030362 Geometria Espacial DURAÇÃO: Semestral CARGA HORÁRIA TOTAL: 45 horas CARGA HORÁRIA
CURSO: Licenciatura em Matemática TURMA: LM 2011/01_1ºSEM PROFESSOR: NÍCOLAS MORO MÜLLER PLANO DE ENSINO DISCIPLINA: 030362 Geometria Espacial DURAÇÃO: Semestral CARGA HORÁRIA TOTAL: 45 horas CARGA HORÁRIA
Matemática - 3C12/14/15/16/26 Lista 2
 Matemática - 3C12/14/15/16/26 Lista 2 Poliedros Convexos 1) Determine qual é o poliedro convexo e fechado que tem 6 vértices e 12 arestas. 2) Determine o nº de vértices de dodecaedro convexo que tem 20
Matemática - 3C12/14/15/16/26 Lista 2 Poliedros Convexos 1) Determine qual é o poliedro convexo e fechado que tem 6 vértices e 12 arestas. 2) Determine o nº de vértices de dodecaedro convexo que tem 20
PRISMAS E PIRÂMIDES 1. DEFINIÇÕES (PRISMAS) MATEMÁTICA. Prisma oblíquo: as arestas laterais são oblíquas aos planos das bases.
 PRISMAS E PIRÂMIDES. DEFINIÇÕES (PRISMAS) Chama-se prisma todo poliedro convexo composto por duas faces (bases) que são polígonos congruentes contidos em planos paralelos e as demais faces (faces laterais)
PRISMAS E PIRÂMIDES. DEFINIÇÕES (PRISMAS) Chama-se prisma todo poliedro convexo composto por duas faces (bases) que são polígonos congruentes contidos em planos paralelos e as demais faces (faces laterais)
Elementos de um poliedro
 RELAÇÃO DE EULER 1 Elementos de um poliedro A Face Vértice B Aresta C D Imagem: Pablo rigel / public domain O ponto A é um dos vértices desse poliedro. O segmento de reta AB é uma das arestas. A região
RELAÇÃO DE EULER 1 Elementos de um poliedro A Face Vértice B Aresta C D Imagem: Pablo rigel / public domain O ponto A é um dos vértices desse poliedro. O segmento de reta AB é uma das arestas. A região
Lista de exercícios de Geometria Espacial 2017 Prof. Diego. Assunto 1 Geometria Espacial de Posição
 Assunto 1 Geometria Espacial de Posição (01). Considere um plano a e um ponto P qualquer no espaço. Se por P traçarmos a reta perpendicular a a, a intersecção dessa reta com a é um ponto chamado projeção
Assunto 1 Geometria Espacial de Posição (01). Considere um plano a e um ponto P qualquer no espaço. Se por P traçarmos a reta perpendicular a a, a intersecção dessa reta com a é um ponto chamado projeção
Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Espacial 2º Ano APROFUNDAMENTO/REFORÇO
 Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Espacial 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre 2012 Aluno(a): Número: Turma: 1) Resolva
Colégio Adventista Portão EIEFM MATEMÁTICA Geometria Espacial 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre 2012 Aluno(a): Número: Turma: 1) Resolva
Volume do dodecaedro e do icosaedro
 Capítulo Volume do dodecaedro e do icosaedro.1 Introdução. Os cálculos do volume dos sólidos platônicos que geralmente são abordados pelos livros didáticos de Matemática do ensino médio, resumem-se ao
Capítulo Volume do dodecaedro e do icosaedro.1 Introdução. Os cálculos do volume dos sólidos platônicos que geralmente são abordados pelos livros didáticos de Matemática do ensino médio, resumem-se ao
PROPOSTA DIDÁTICA. 2. Objetivo(s) da proposta didática - Reconhecer o que é um sólido geométrico e suas características.
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Jéssica Marilda Gomes Mendes 1.2 Público alvo: Alunos de 6º a 9º ano e Magistério 1.3 Duração: 2 aulas de 2 h e 30 min cada 1.4 Conteúdo
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Jéssica Marilda Gomes Mendes 1.2 Público alvo: Alunos de 6º a 9º ano e Magistério 1.3 Duração: 2 aulas de 2 h e 30 min cada 1.4 Conteúdo
EXPLORANDO O SOFTWARE POLY- PRO Natália Lummertz 1 Sabrini Micheli da Silva dos Anjos 2 RESUMO
 EXPLORANDO O SOFTWARE POLY- PRO Natália Lummertz 1 Sabrini Micheli da Silva dos Anjos 2 RESUMO O Poly-pro é um software matemático que pode ser utilizado no conteúdo de Geometria Espacial. Com o poly pode-se
EXPLORANDO O SOFTWARE POLY- PRO Natália Lummertz 1 Sabrini Micheli da Silva dos Anjos 2 RESUMO O Poly-pro é um software matemático que pode ser utilizado no conteúdo de Geometria Espacial. Com o poly pode-se
Chama-se poliedro a uma figura geométrica, a três dimensões, cujas faces são polígonos. Um poliedro regular é aquele em que as faces são polígonos
 Ana Salgado INTRODUÇÃO Acedendo ao site The Geometry Junkyard, encontrei o link All the junk in one big pile onde escolhi o tema Poly. Poly, é um programa para explorar várias classes de poliedros, incluindo
Ana Salgado INTRODUÇÃO Acedendo ao site The Geometry Junkyard, encontrei o link All the junk in one big pile onde escolhi o tema Poly. Poly, é um programa para explorar várias classes de poliedros, incluindo
Formação Continuada em Matemática Fundação Cecierj/consórcio CEDERJ
 Formação Continuada em Matemática Fundação Cecierj/consórcio CEDERJ Matemática 2ºAno-1º Bimestre/2013 PLANO DE TRABALHO 2 Cursista: Werbert Augusto Coutinho Tutor(a): Daiana da Silva Leite Grupo: 2 INTRODUÇÃO
Formação Continuada em Matemática Fundação Cecierj/consórcio CEDERJ Matemática 2ºAno-1º Bimestre/2013 PLANO DE TRABALHO 2 Cursista: Werbert Augusto Coutinho Tutor(a): Daiana da Silva Leite Grupo: 2 INTRODUÇÃO
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria. Aluno(a):. Nº.
 COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
Poliedros. INF2604 Geometria Computacional. Waldemar Celes. Departamento de Informática, PUC-Rio. W.
 Poliedros INF2604 Geometria Computacional Waldemar Celes [email protected] Departamento de Informática, PUC-Rio W. Celes Poliedros 1 Poliedros Poliedros Região 3D delimitada por uma fronteira composta
Poliedros INF2604 Geometria Computacional Waldemar Celes [email protected] Departamento de Informática, PUC-Rio W. Celes Poliedros 1 Poliedros Poliedros Região 3D delimitada por uma fronteira composta
CLASSIFICAÇÃO DOS POLIEDROS
 COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
PROPOSTA DIDÁTICA. Desenvolvimento da proposta didática (10 min) Acomodação dos alunos em semicírculo e realização da chamada.
 PROPOSTA DIDÁTICA Dados de Identificação 1.1 Nome do bolsista: Mariely Rodrigues Anger. 1.2 Público alvo: 6º e 7º ano 1.3 Duração: 2 horas 1.4 Conteúdos desenvolvidos: Noções primitivas de Geometria; Identificação
PROPOSTA DIDÁTICA Dados de Identificação 1.1 Nome do bolsista: Mariely Rodrigues Anger. 1.2 Público alvo: 6º e 7º ano 1.3 Duração: 2 horas 1.4 Conteúdos desenvolvidos: Noções primitivas de Geometria; Identificação
