Mistério geométrico e planificação
|
|
|
- Victor Natan Figueira Rios
- 9 Há anos
- Visualizações:
Transcrição
1 X 2 = Mistério geométrico e planificação nós na sala de aula - módulo: matemática 4º e 5º anos - unidade 9 Esta atividade tem como objetivo desafiar os seus alunos a reconhecer as figuras geométricas planas e os sólidos geométricos. Público-alvo: 4º e 5º anos Duração: 5 aulas Expectativas de aprendizagem Identificar figuras geométricas. Identificar sólidos geométricos. Recursos e materiais necessários Laboratório de informática com acesso à Internet Jogo digital: Uma cidade interativa - Mistério geométrico Figuras planificadas (fornecidas) Aplicação Preparação Imprima cópias da figuras planificadas disponíveis ao final da proposta pedagógica. Vide anexo. Verifique o número de cópias necessárias, de acordo com a quantidade de alunos da classe. Aulas 1 e 2 Conduza os alunos ao laboratório de informática e peça para que acessem o jogo: Copyright 2013 Abril Educação - Todos os direitos reservados 1
2 X 2 = Mistério geométrico e planificação nós na sala de aula - módulo: matemática 4º e 5º anos - unidade 9 Uma cidade interativa - Mistério geométrico Esta atividade poderá ser feita em dupla ou individualmente, dependendo do número de computadores. O jogo é composto por três níveis. Inicie com o nível 01 que trata das figuras planas. O reconhecimento dessas figuras por parte dos alunos é importante, pois são figuras que eles já têm contato no dia a dia. Caso tenham alguma dificuldade em reconhecê-las, tente dar dicas de onde elas podem ser encontradas. Se possível, utilize materiais que estão no laboratório. O mesmo deve ser feito com os níveis dois e três, só que agora com figuras tridimensionais. Talvez os materiais do laboratório não sejam os ideais para utilizar como exemplo, então utilize as embalagens dos alimentos. Nos dois últimos níveis se quiser ir mais além, pergunte números de arestas, faces e vértices. Aulas 3 e 5 Nas aulas anteriores, os alunos já visualizaram os sólidos geométricos. Agora é a hora de trabalhar a planificação de alguns deles. Distribua a ficha de atividades para seus alunos e solicite que eles anotem quais são os sólidos que foram planificados e o nome das suas faces, números de arestas, faces e vértices, quando possível. Copyright 2013 Abril Educação - Todos os direitos reservados 2
3 X 2 = Mistério geométrico e planificação nós na sala de aula - módulo: matemática 4º e 5º anos - unidade 9 Confira o gabarito dessa atividade no final desta proposta pedagógica. Vide Anexo. Neste tipo de atividade os alunos demonstram dificuldades, pois muitos ainda não têm a percepção que formas podem se transformar em sólidos. Durante esta atividade, tire as dúvidas que forem surgindo em relação aos nomes dos sólidos geométricos e das figuras, dê exemplos de situações do dia a dia em que elas aparecem. Depois, peça para que os alunos recortem e montem as figuras. Copyright 2013 Abril Educação - Todos os direitos reservados 3
4
5
6
7 As faces são quadrados Cubo Prisma triangular As faces são 02 triângulos e 03 retângulos As faces são triangulos Tetraedro Base em formato circular Cone Suas bases são círculos Cilindro Suas faces são 2 quadrados e 4 retângulos Prisma quadrangular
Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2. Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 -
 Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2 Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 - Formação Continuada em Matemática Fundação CECIERJ / Consórcio CEDERJ MATEMÁTICA 2º ANO/ENS.
Março/2013 CECIERJ CEDERJ PLANO DE TRABALHO 2 Introdução à Geometria Espacial Danielle Gomes Gioseffi - 0 - Formação Continuada em Matemática Fundação CECIERJ / Consórcio CEDERJ MATEMÁTICA 2º ANO/ENS.
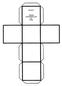 10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
Matemática 6.º ano. 1. Determine o valor das seguintes expressões e apresente o resultado como uma potência. Mostre como chegou ao resultado.
 1. Determine o valor das seguintes expressões e apresente o resultado como uma potência. Mostre como chegou ao resultado. a) ( 3 4 )25 : ( 3 4 )15 5 10 b) 15 35 : 5 35 3 45 2. Calcule o valor das seguintes
1. Determine o valor das seguintes expressões e apresente o resultado como uma potência. Mostre como chegou ao resultado. a) ( 3 4 )25 : ( 3 4 )15 5 10 b) 15 35 : 5 35 3 45 2. Calcule o valor das seguintes
PROPOSTA DIDÁTICA. Desenvolvimento da proposta didática (10 min) Acomodação dos alunos em semicírculo e realização da chamada.
 PROPOSTA DIDÁTICA Dados de Identificação 1.1 Nome do bolsista: Mariely Rodrigues Anger. 1.2 Público alvo: 6º e 7º ano 1.3 Duração: 2 horas 1.4 Conteúdos desenvolvidos: Noções primitivas de Geometria; Identificação
PROPOSTA DIDÁTICA Dados de Identificação 1.1 Nome do bolsista: Mariely Rodrigues Anger. 1.2 Público alvo: 6º e 7º ano 1.3 Duração: 2 horas 1.4 Conteúdos desenvolvidos: Noções primitivas de Geometria; Identificação
D3 Relacionar diferentes poliedros ou corpos redondos com suas planificações ou vistas. ***********************************
 Observe o prisma hexagonal regular ilustrado a seguir: Dentre as alternativas a seguir, a que representa uma planificação para esse sólido é *********************************** Ao fazer um molde de um
Observe o prisma hexagonal regular ilustrado a seguir: Dentre as alternativas a seguir, a que representa uma planificação para esse sólido é *********************************** Ao fazer um molde de um
Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF
 Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF 01) Observando a figuras e simplesmente contando, determine o número de faces, arestas e o vértices
Nome: Nº Ano: Turma: Disciplina: Professor: Data: / / GABARITO - LISTA DE REFORÇO MATEMÁTICA 2 0 ANO EF 01) Observando a figuras e simplesmente contando, determine o número de faces, arestas e o vértices
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de Matemática de 4ª Série Fundamental
 Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de de 4ª Série Fundamental TEMA I ESPAÇO E FORMA A compreensão do espaço com suas dimensões e formas de constituição são elementos necessários
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de de 4ª Série Fundamental TEMA I ESPAÇO E FORMA A compreensão do espaço com suas dimensões e formas de constituição são elementos necessários
PROPOSTA DIDÁTICA. 3. Desenvolvimento da proposta didática (10 min) - Acomodação dos alunos, apresentação dos bolsistas e realização da chamada.
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ. Matemática 2º Ano 3º Bimestre/2012
 Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 Pirâmides e Cones Cursista: Ângela Pereira Cerqueira Halfeld Tutora: Ana Paula
Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 Pirâmides e Cones Cursista: Ângela Pereira Cerqueira Halfeld Tutora: Ana Paula
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados.
 POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria. Aluno(a):. Nº.
 COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
Capitulo 4 Figuras Geométricas Planas
 Página16 Capitulo 4 Figuras Geométricas Planas Ponto O ponto é a figura geométrica mais simples, não tem dimensão (comprimento, largura e altura) e é determinado pelo cruzamento de duas linhas. Identificação
Página16 Capitulo 4 Figuras Geométricas Planas Ponto O ponto é a figura geométrica mais simples, não tem dimensão (comprimento, largura e altura) e é determinado pelo cruzamento de duas linhas. Identificação
Exercícios complementares
 Exercícios complementares Conteúdo(s) abordado(s): o olume de figuras geométricas especiais ( cilindro, cubo, pirâmide, prisma e cones) Os conteúdos abordados neste material fazem parte dos blocos de conteúdos
Exercícios complementares Conteúdo(s) abordado(s): o olume de figuras geométricas especiais ( cilindro, cubo, pirâmide, prisma e cones) Os conteúdos abordados neste material fazem parte dos blocos de conteúdos
Apostila de Matemática II 3º bimestre/2016. Professora : Cristiane Fernandes
 Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
1ª Parte SÓLIDOS GEOMÉTRICOS. Prof. Danillo Alves 6º ano Matutino
 1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
1 POLIEDROS 2 ELEMENTOS 4 POLIEDROS REGULARES 3 CLASSIFICAÇÃO. 3.2 Quanto ao número de faces. 4.1 Tetraedro regular. 3.
 Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Prismas e. cilindros
 FORMAÇÃO CONTINUADA MATEMÁTICA PLANO DE TRABALHO 2 2º BIMESTRE Prismas e cilindros NOME: JOSIANE ALVES DA SILVA 2ª SÉRIE DO ENSINO MÉDIO TUTURA: SUSI CRISTINA GRUPO: 03 2014 SUMÁRIO 1 Introdução... 03
FORMAÇÃO CONTINUADA MATEMÁTICA PLANO DE TRABALHO 2 2º BIMESTRE Prismas e cilindros NOME: JOSIANE ALVES DA SILVA 2ª SÉRIE DO ENSINO MÉDIO TUTURA: SUSI CRISTINA GRUPO: 03 2014 SUMÁRIO 1 Introdução... 03
C O L É G I O F R A N C O - B R A S I L E I R O
 C O L É G I O F R A N C O - B R A S I L E I R O Nome: N.º: Turma: Professor: IRAN MARCELINO Ano: ª Data: / / 014 CONTEÚDO: LISTA DE RECUPERAÇÃO (MATEMÁTICA ) Equação modular Inequação modular Áreas de
C O L É G I O F R A N C O - B R A S I L E I R O Nome: N.º: Turma: Professor: IRAN MARCELINO Ano: ª Data: / / 014 CONTEÚDO: LISTA DE RECUPERAÇÃO (MATEMÁTICA ) Equação modular Inequação modular Áreas de
Matemática GEOMETRIA ESPACIAL. Professor Dudan
 Matemática GEOMETRIA ESPACIAL Professor Dudan CUBO Um hexaedro é um poliedro com 6 faces, um paralelepípedo retângulo com todas as arestas congruentes ( a= b = c). Exemplo O volume de uma caixa cúbica
Matemática GEOMETRIA ESPACIAL Professor Dudan CUBO Um hexaedro é um poliedro com 6 faces, um paralelepípedo retângulo com todas as arestas congruentes ( a= b = c). Exemplo O volume de uma caixa cúbica
FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL
 FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL Tarefa 1 Aluno: Thiago Milani Cabral Grupo 2 Tutora: Susi Cristine
FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ/ CONSÓRCIO CEDERJ PLANO DE TRABALHO MATEMÁTICA 2º ANO 1º BIMESTRE/2014 GEOMETRIA ESPACIAL Tarefa 1 Aluno: Thiago Milani Cabral Grupo 2 Tutora: Susi Cristine
Noções de Geometria. Professora: Gianni Leal 6º B.
 Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ COLÉGIO ESTADUAL DOM JOÃO VI
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ COLÉGIO ESTADUAL DOM JOÃO VI Professora: ANA PAULA LIMA Matrículas: 09463027/09720475 Série: 2º ANO ENSINO MÉDIO Tutora: KARINA
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ COLÉGIO ESTADUAL DOM JOÃO VI Professora: ANA PAULA LIMA Matrículas: 09463027/09720475 Série: 2º ANO ENSINO MÉDIO Tutora: KARINA
Matéria: Matemática Assunto: Volume Prof. Dudan
 Matéria: Matemática Assunto: Volume Prof. Dudan Matemática VOLUME DEFINIÇÃO As medidas de volume possuem grande importância nas situações envolvendo capacidades de sólidos. Podemos definir volume como
Matéria: Matemática Assunto: Volume Prof. Dudan Matemática VOLUME DEFINIÇÃO As medidas de volume possuem grande importância nas situações envolvendo capacidades de sólidos. Podemos definir volume como
VOLUME DE PIRÂMIDES E CONES
 VOLUME DE PIRÂMIDES E CONES PLANO DE TRABALHO 2 CURSO DE FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ / CONSÓRCIO CEDERJ PROJETO SEEDUC MATEMÁTICA 2º ANO 3º BIMESTRE / 2012 PLANO DE TRABALHO TAREFA
VOLUME DE PIRÂMIDES E CONES PLANO DE TRABALHO 2 CURSO DE FORMAÇÃO CONTINUADA EM MATEMÁTICA FUNDAÇÃO CECIERJ / CONSÓRCIO CEDERJ PROJETO SEEDUC MATEMÁTICA 2º ANO 3º BIMESTRE / 2012 PLANO DE TRABALHO TAREFA
Cones, cilindros, esferas e festividades, qual a ligação?
 Cones, cilindros, esferas e festividades, qual a ligação? Helena Sousa Melo [email protected] Professora do Departamento de Matemática da Universidade dos Açores Publicado no jornal Correio dos Açores em 5
Cones, cilindros, esferas e festividades, qual a ligação? Helena Sousa Melo [email protected] Professora do Departamento de Matemática da Universidade dos Açores Publicado no jornal Correio dos Açores em 5
Durante a atividade Divida os alunos em duplas; 1 - Peça para que cada dupla inicie a atividade; 2 - Depois de reconhecer e classificar os tipos de fi
 Geometria 3ª atividade Relacionando formas Introdução Após várias atividades que possibilitaram a classificação das formas tridimensionais desejamos que os alunos continuem a percebê-las e que possam ser
Geometria 3ª atividade Relacionando formas Introdução Após várias atividades que possibilitaram a classificação das formas tridimensionais desejamos que os alunos continuem a percebê-las e que possam ser
PLANO DE TRABALHO SOBRE GEOMETRIA ESPACIAL. H07 Relacionar diferentes poliedros ou corpos redondos com suas planificações.
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: COLÉGIO ESTADUAL PAULINO PINHEIRO BAPTISTA PROFESSORA: PATRÍCIA DOMINGUES DE SOUZA MATRÍCULA: 0912303-5 TUTOR: SUSI
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: COLÉGIO ESTADUAL PAULINO PINHEIRO BAPTISTA PROFESSORA: PATRÍCIA DOMINGUES DE SOUZA MATRÍCULA: 0912303-5 TUTOR: SUSI
Exercícios Obrigatórios
 Exercícios Obrigatórios 1) (UFRGS) A figura abaixo, formada por trapézios congruentes e triângulos equiláteros, representa a planificação de um sólido. Esse sólido é um (a) tronco de pirâmide. (b) tronco
Exercícios Obrigatórios 1) (UFRGS) A figura abaixo, formada por trapézios congruentes e triângulos equiláteros, representa a planificação de um sólido. Esse sólido é um (a) tronco de pirâmide. (b) tronco
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones)
 Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
DEPENDÊNCIA 2º ANO MATEMÁTICA
 DEPENDÊNCIA 2º ANO MATEMÁTICA ----------------- QUESTÃO 1 ------------------- são problemas de contagem que envolvem situações nas quais a ordem não é importante. a) Permutações b) Permutações com repetição
DEPENDÊNCIA 2º ANO MATEMÁTICA ----------------- QUESTÃO 1 ------------------- são problemas de contagem que envolvem situações nas quais a ordem não é importante. a) Permutações b) Permutações com repetição
CAMINHOS DA GEOMETRIA NA ERA DIGITAL
 CAMINHOS DA GEOMETRIA NA ERA DIGITAL GT 05 Educação Matemática: tecnologias informáticas e educação à distância Tatiana Schmitz UNISINOS [email protected] Ana Paula de Quadros UNISINOS [email protected]
CAMINHOS DA GEOMETRIA NA ERA DIGITAL GT 05 Educação Matemática: tecnologias informáticas e educação à distância Tatiana Schmitz UNISINOS [email protected] Ana Paula de Quadros UNISINOS [email protected]
PROPOSTA DIDÁTICA. 2. Objetivo(s) da proposta didática - Reconhecer o que é um sólido geométrico e suas características.
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Jéssica Marilda Gomes Mendes 1.2 Público alvo: Alunos de 6º a 9º ano e Magistério 1.3 Duração: 2 aulas de 2 h e 30 min cada 1.4 Conteúdo
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Jéssica Marilda Gomes Mendes 1.2 Público alvo: Alunos de 6º a 9º ano e Magistério 1.3 Duração: 2 aulas de 2 h e 30 min cada 1.4 Conteúdo
CLASSIFICAÇÃO DOS POLIEDROS
 COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR
 GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR Sólidos geométricos PARA COMEÇAR... No mundo de hoje, as inúmeras obras de engenharia, arquitetura, artes plásticas etc. mostram a imensa quantidade de formas que
GEOMETRIA ESPACIAL PROF. VALDIR AGUIAR Sólidos geométricos PARA COMEÇAR... No mundo de hoje, as inúmeras obras de engenharia, arquitetura, artes plásticas etc. mostram a imensa quantidade de formas que
Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides
 Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides Cursista: Marta Vieira de Andrade. 1 Série: 2ª. Tutor: Andréa Silva
Formação Continuada em MATEMÁTICA Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2013 Plano de Trabalho 2 Pirâmides Cursista: Marta Vieira de Andrade. 1 Série: 2ª. Tutor: Andréa Silva
ESPAÇO E FORMA. CURSO: Pró-Letramento. TURMA: Revezamento. ÁREA: Matemática. CONTEÚDO: Espaço e Forma. TEMA: Dobradura, Tangram e Mosaicos
 ESPAÇO E FORMA CURSO: Pró-Letramento TURMA: Revezamento ÁREA: Matemática CONTEÚDO: Espaço e Forma TEMA: Dobradura, Tangram e Mosaicos DATA DO ENCONTRO: 22/08/2012 a 24/08/2012 PROFESSOR RESPONSÁVEL: Profª
ESPAÇO E FORMA CURSO: Pró-Letramento TURMA: Revezamento ÁREA: Matemática CONTEÚDO: Espaço e Forma TEMA: Dobradura, Tangram e Mosaicos DATA DO ENCONTRO: 22/08/2012 a 24/08/2012 PROFESSOR RESPONSÁVEL: Profª
Escola Secundária com 3º Ciclo D. Dinis Curso Profissional de Técnico de Informática de Gestão Teste Diagnóstico do módulo A1
 Nome: Nº 10º IG 1ª Parte 1. Qual é o perímetro da estrela representada na figura ao lado, sabendo que é formada por quatro circunferências, cada uma com 5 cm de raio, um quadrado e quatro triângulos equiláteros?
Nome: Nº 10º IG 1ª Parte 1. Qual é o perímetro da estrela representada na figura ao lado, sabendo que é formada por quatro circunferências, cada uma com 5 cm de raio, um quadrado e quatro triângulos equiláteros?
Resumo de Geometria Espacial Métrica
 1) s. esumo de Geometria Espacial Métrica Extensivo - São João da Boa Vista Matemática - Base Base Base Base Base oblíquo reto quadrangular regular exagonal regular triangular regular Base Fórmulas dos
1) s. esumo de Geometria Espacial Métrica Extensivo - São João da Boa Vista Matemática - Base Base Base Base Base oblíquo reto quadrangular regular exagonal regular triangular regular Base Fórmulas dos
PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas
 PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas 1 Escalas escala medida _ no _ desenho medida _ real _ ou _ verdadeira _ grandeza D VG Escala de ampliação Objeto real
PLANTA BAIXA AULA 02 (parte I) Introdução ao Desenho Técnico (continuação) Escalas 1 Escalas escala medida _ no _ desenho medida _ real _ ou _ verdadeira _ grandeza D VG Escala de ampliação Objeto real
Geometria Espacial Pirâmides
 Formação Continuada em MATEMÁTICA Matemática 2 Ano 3º Bimestre/2012 Plano de Trabalho Geometria Espacial Pirâmides Tarefa 2 Cursista: Maria do Carmo de Souza Ribeiro Tutor: Hannibal Escobar R. H. de Carvalho
Formação Continuada em MATEMÁTICA Matemática 2 Ano 3º Bimestre/2012 Plano de Trabalho Geometria Espacial Pirâmides Tarefa 2 Cursista: Maria do Carmo de Souza Ribeiro Tutor: Hannibal Escobar R. H. de Carvalho
Metas/Objetivos/Domínios Conteúdos/Competências/Conceitos Número de Aulas
 COLÉGIO DE SANTA DOROTEIA LISBOA ANO LETIVO 2018/2019 Planificação (Conteúdos)... Período Letivo: 1.º DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: MATEMÁTICA ANO: 6.º Metas/Objetivos/Domínios Conteúdos/Competências/Conceitos
COLÉGIO DE SANTA DOROTEIA LISBOA ANO LETIVO 2018/2019 Planificação (Conteúdos)... Período Letivo: 1.º DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: MATEMÁTICA ANO: 6.º Metas/Objetivos/Domínios Conteúdos/Competências/Conceitos
Adriana da Silva Santi Coord. Pedagógica de Matemática SMED - Abril/2015
 GEOMETRIA Adriana da Silva Santi Coord. Pedagógica de Matemática SMED - Abril/2015 O MATERIAL COMO SUPORTE DO PENSAMENTO Muita gente usa o material na sala de aula como se a Geometria estivesse no material.
GEOMETRIA Adriana da Silva Santi Coord. Pedagógica de Matemática SMED - Abril/2015 O MATERIAL COMO SUPORTE DO PENSAMENTO Muita gente usa o material na sala de aula como se a Geometria estivesse no material.
cubo a partir de sua planificação e nele nomear vértices, arestas e faces, além de verificar as posições das diagonais das faces e da diagonal do cubo
 Guia do Professor CAMINHANDO PELAS FACES DE UM CUBO Introdução O estudo das formas geométricas não planas acompanha os alunos desde as séries iniciais do Ensino Fundamental. Todavia, quando no Ensino Médio
Guia do Professor CAMINHANDO PELAS FACES DE UM CUBO Introdução O estudo das formas geométricas não planas acompanha os alunos desde as séries iniciais do Ensino Fundamental. Todavia, quando no Ensino Médio
Metas Curriculares Conteúdos Aulas Previstas. - Números primos; - Crivo de Eratóstenes;
 ANO LETIVO 2017/2018... 1º PERÍODO - (13 de setembro a 15 de dezembro) DEPARTAMENTO DE MATEMÁTICA /INFORMÁTICA DISCIPLINA: Matemática (6º Ano) METAS CURRICULARES/CONTEÚDOS Metas Curriculares Conteúdos
ANO LETIVO 2017/2018... 1º PERÍODO - (13 de setembro a 15 de dezembro) DEPARTAMENTO DE MATEMÁTICA /INFORMÁTICA DISCIPLINA: Matemática (6º Ano) METAS CURRICULARES/CONTEÚDOS Metas Curriculares Conteúdos
EXERCÍCIOS DE AULA - 01
 EXERCÍCIOS DE AULA - 01 Representação de objectos em axonometria normalizada FA.ULisboa Ano lectivo 2017/2018 1º semestre Professor Luís Mateus ([email protected]) Notas: 1) Resolva os exercícios
EXERCÍCIOS DE AULA - 01 Representação de objectos em axonometria normalizada FA.ULisboa Ano lectivo 2017/2018 1º semestre Professor Luís Mateus ([email protected]) Notas: 1) Resolva os exercícios
ÁREA. Unidades de medida de área. Prof. Patricia Caldana
 ÁREA Prof. Patricia Caldana Área ou superfície de uma figura plana tem a ver com o conceito (primitivo) de sua extensão (bidimensional). Usamos a área do quadrado de lado unitário como referência de unidade
ÁREA Prof. Patricia Caldana Área ou superfície de uma figura plana tem a ver com o conceito (primitivo) de sua extensão (bidimensional). Usamos a área do quadrado de lado unitário como referência de unidade
FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS
 FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS Professora: Vanessa Bayerl Cesana PLANA Figuras poligonais e não poligonais. Forma, número de lados,
FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS Professora: Vanessa Bayerl Cesana PLANA Figuras poligonais e não poligonais. Forma, número de lados,
ESCOLA E.B. 2,3/S CUNHA RIVARA ARRAIOLOS Ano Letivo 2017/2018
 ESCOLA E.B. 2,3/S CUNHA RIVARA ARRAIOLOS Ano Letivo 17/18 PLANIFICAÇÃO DA DISCIPLINA DE MATEMÁTICA 6º ANO DE ESCOLARIDADE PERÍODO UNIDADES DIDÁTICAS Aulas 1.º Período 78 Aulas 1. Números naturais 25 (Articula
ESCOLA E.B. 2,3/S CUNHA RIVARA ARRAIOLOS Ano Letivo 17/18 PLANIFICAÇÃO DA DISCIPLINA DE MATEMÁTICA 6º ANO DE ESCOLARIDADE PERÍODO UNIDADES DIDÁTICAS Aulas 1.º Período 78 Aulas 1. Números naturais 25 (Articula
Roteiro de Estudos do 2º Trimestre 2ª Série Disciplina: Geometria Professor: Hugo P.
 Roteiro de Estudos do º Trimestre ª Série Disciplina: Geometria Professor: Hugo P Conteúdos para Avaliação Trimestral: Pirâmides; Cones; Cilindros; Cálculos de área lateral; área total; volume Problemas
Roteiro de Estudos do º Trimestre ª Série Disciplina: Geometria Professor: Hugo P Conteúdos para Avaliação Trimestral: Pirâmides; Cones; Cilindros; Cálculos de área lateral; área total; volume Problemas
APRENDENDO PROBABILIDADE E GEOMETRIA POR MEIO DO JOGO AS ROLETAS E OS SÓLIDOS
 1 APRENDENDO PROBABILIDADE E GEOMETRIA POR MEIO DO JOGO AS ROLETAS E OS SÓLIDOS Daniela Souza Lima SEEDF e FAJESU [email protected] Raquel Souza Lima de Moura SEEDF [email protected] Resumo
1 APRENDENDO PROBABILIDADE E GEOMETRIA POR MEIO DO JOGO AS ROLETAS E OS SÓLIDOS Daniela Souza Lima SEEDF e FAJESU [email protected] Raquel Souza Lima de Moura SEEDF [email protected] Resumo
Hewlett-Packard PIRÂMIDES. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hewlett-Packard PIRÂMIDES Aulas 01 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário PIRÂMIDES... 1 CLASSIFICAÇÃO DE UMA PIRÂMIDE... 1 EXERCÍCIOS FUNDAMENTAIS... 2 ÁREAS EM UMA PIRÂMIDE...
Hewlett-Packard PIRÂMIDES Aulas 01 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário PIRÂMIDES... 1 CLASSIFICAÇÃO DE UMA PIRÂMIDE... 1 EXERCÍCIOS FUNDAMENTAIS... 2 ÁREAS EM UMA PIRÂMIDE...
Geometria Espacial - AFA
 Geometria Espacial - AFA 1. (AFA) O produto da maior diagonal pela menor diagonal de um prisma hexagonal regular de área lateral igual a 1 cm e volume igual a 1 cm é: 10 7. 0 7. 10 1. (D) 0 1.. (AFA) Qual
Geometria Espacial - AFA 1. (AFA) O produto da maior diagonal pela menor diagonal de um prisma hexagonal regular de área lateral igual a 1 cm e volume igual a 1 cm é: 10 7. 0 7. 10 1. (D) 0 1.. (AFA) Qual
2 CILINDRO E ESFERA 1 CUBO E ESFERA. 2.1 Cilindro inscrito. 1.1 Cubo inscrito. 2.2 Cilindro circunscrito. 1.2 Cubo circunscrito
 Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
Cursista: Jacqueline Garcia Pereira. 2º ano do Ensino Médio. Grupo 4. Tutor: Deivis de Oliveira Alves. Número de matrícula:
 Formação continuada Projeto SEEDUC Cursista: Jacqueline Garcia Pereira 2º ano do Ensino Médio Grupo 4 Tutor: Deivis de Oliveira Alves Número de matrícula: 2422699 SUMÁRIO INTRODUÇÃO...3 DESENVOLVIMENTO...4
Formação continuada Projeto SEEDUC Cursista: Jacqueline Garcia Pereira 2º ano do Ensino Médio Grupo 4 Tutor: Deivis de Oliveira Alves Número de matrícula: 2422699 SUMÁRIO INTRODUÇÃO...3 DESENVOLVIMENTO...4
3 O ANO EM. Lista de Recuperação tri2. Matemática II RAPHAEL LIMA
 3 O ANO EM Matemática II RAPHAEL LIMA Lista de Recuperação tri2 1. Uma indústria de cerâmica localizada no município de São Miguel do Guamá no estado do Pará fabrica tijolos de argila (barro) destinados
3 O ANO EM Matemática II RAPHAEL LIMA Lista de Recuperação tri2 1. Uma indústria de cerâmica localizada no município de São Miguel do Guamá no estado do Pará fabrica tijolos de argila (barro) destinados
Plano de Trabalho sobre Introdução à Geometria Espacial
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: C. E. Madre Teresa de Calcutá. PROFESSORA: Angela Saida Alvarez Jacob. GRUPO 6 MATRÍCULA: 0913098-0 TURMA: 2 ano.
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ / SEEDUC-RJ COLÉGIO: C. E. Madre Teresa de Calcutá. PROFESSORA: Angela Saida Alvarez Jacob. GRUPO 6 MATRÍCULA: 0913098-0 TURMA: 2 ano.
ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO
 ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO 2011-2012 Sólidos Geométricos NOME: Nº TURMA: Polígonos Um polígono é uma figura geométrica plana limitada por uma linha fechada.
ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO 2011-2012 Sólidos Geométricos NOME: Nº TURMA: Polígonos Um polígono é uma figura geométrica plana limitada por uma linha fechada.
KITS DIDÁTICOS ÁREA: QUÍMICA
 KITS DIDÁTICOS Os KITS DIDÁTICOS apresentados a seguir foram obtidos a partir de recursos oriundos de parceria firmada em UFPR - Campus Jandaia do Sul e o Rotary Clube local. Os materiais doados possibilitam
KITS DIDÁTICOS Os KITS DIDÁTICOS apresentados a seguir foram obtidos a partir de recursos oriundos de parceria firmada em UFPR - Campus Jandaia do Sul e o Rotary Clube local. Os materiais doados possibilitam
Exercícios de Revisão
 Professor: Cassio Kiechaloski Mello Disciplina: Matemática Exercícios de Revisão Geometria Analítica Geometria Plana Geometria Espacial Números Complexos Polinômios Na prova de recuperação final, não será
Professor: Cassio Kiechaloski Mello Disciplina: Matemática Exercícios de Revisão Geometria Analítica Geometria Plana Geometria Espacial Números Complexos Polinômios Na prova de recuperação final, não será
FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 2º Bimestre/2014. Plano de Trabalho 2 : Geometria Espacial - Prismas e Cilindros
 FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 2º Bimestre/2014 Plano de Trabalho 2 : Geometria Espacial - Prismas e Cilindros Tarefa 2 Cursista:Thereza Christina da Silva Cabral Tutora: Susi Cristine
FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 2º Bimestre/2014 Plano de Trabalho 2 : Geometria Espacial - Prismas e Cilindros Tarefa 2 Cursista:Thereza Christina da Silva Cabral Tutora: Susi Cristine
Trabalhando com o material dourado ou similares
 Essa atividade com o material dourado tem por objetivo facilitar a compreensão do aluno de forma concreta em relação ao sistema de numeração decimal. Composto por cubinhos, barrinhas e placas, esse material
Essa atividade com o material dourado tem por objetivo facilitar a compreensão do aluno de forma concreta em relação ao sistema de numeração decimal. Composto por cubinhos, barrinhas e placas, esse material
Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides. 3 ano/e.m.
 Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides Pirâmide ano/em Pirâmide Geometria Espacial II - volumes e áreas de prismas e pirâmides 1 Exercícios Introdutórios Exercício 1 Determine
Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides Pirâmide ano/em Pirâmide Geometria Espacial II - volumes e áreas de prismas e pirâmides 1 Exercícios Introdutórios Exercício 1 Determine
Matemática - 3C12/14/15/16/26 Lista 2
 Matemática - 3C12/14/15/16/26 Lista 2 Poliedros Convexos 1) Determine qual é o poliedro convexo e fechado que tem 6 vértices e 12 arestas. 2) Determine o nº de vértices de dodecaedro convexo que tem 20
Matemática - 3C12/14/15/16/26 Lista 2 Poliedros Convexos 1) Determine qual é o poliedro convexo e fechado que tem 6 vértices e 12 arestas. 2) Determine o nº de vértices de dodecaedro convexo que tem 20
Avaliação 2 - MA Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL Avaliação - MA1-015 - Gabarito Questão 01 [,00 ] Considere um cilindro sólido de altura R, cujas bases são dois círculos de raio R, do qual são retirados
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL Avaliação - MA1-015 - Gabarito Questão 01 [,00 ] Considere um cilindro sólido de altura R, cujas bases são dois círculos de raio R, do qual são retirados
Recursos para Estudo / Atividades
 COLÉGIO NOSSA SENHORA DA PIEDADE Programa de Recuperação Final 3ª Etapa 2014 Disciplina: Matemática Série: 2ª Professor (a): Ana Cristina Turma: FG Caro aluno, você está recebendo o conteúdo de recuperação.
COLÉGIO NOSSA SENHORA DA PIEDADE Programa de Recuperação Final 3ª Etapa 2014 Disciplina: Matemática Série: 2ª Professor (a): Ana Cristina Turma: FG Caro aluno, você está recebendo o conteúdo de recuperação.
MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina Instituto de Matemática da UFRGS
 MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina [email protected] Instituto de Matemática da UFRGS Neste minicurso vamos trabalhar com os recursos do GeoGebra 3D e discutir possibilidades
MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina [email protected] Instituto de Matemática da UFRGS Neste minicurso vamos trabalhar com os recursos do GeoGebra 3D e discutir possibilidades
GEOMETRIA MÉTRICA. As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases.
 GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
PROGRAMAÇÃO DA 2ª ETAPA 2º ANO Helaine e Thaciana
 PROGRAMAÇÃO DA 2ª ETAPA 2º ANO Helaine e Thaciana MATEMÁTICA Qual é o nosso afã de cada dia? É tentar sempre o melhor, mas não se cansar de tentar. Santo Agostinho CONTEÚDOS: Livro: Projeto Ápis Matemática
PROGRAMAÇÃO DA 2ª ETAPA 2º ANO Helaine e Thaciana MATEMÁTICA Qual é o nosso afã de cada dia? É tentar sempre o melhor, mas não se cansar de tentar. Santo Agostinho CONTEÚDOS: Livro: Projeto Ápis Matemática
OS PRISMAS. 1) Definição e Elementos :
 1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
JOGOS COMO FERRAMENTAS NO ENSINO DA GEOMETRIA ESPACIAL
 JOGOS COMO FERRAMENTAS NO ENSINO DA GEOMETRIA ESPACIAL Evanildo Franco de Jesus [email protected] Daniela Lannes da Silva [email protected] Noé Franco de Jesus [email protected] Ranaí Gonçalves
JOGOS COMO FERRAMENTAS NO ENSINO DA GEOMETRIA ESPACIAL Evanildo Franco de Jesus [email protected] Daniela Lannes da Silva [email protected] Noé Franco de Jesus [email protected] Ranaí Gonçalves
FORMAÇÃO CONTINUADA EM MATEMÁTICA. Matemática 2º Ano 3º Bimestre/2012. Plano de Trabalho 2 PIRÂMIDES E CONES
 FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 PIRÂMIDES E CONES Cursista: Izabel Leal Vieira Tutor: Paulo Alexandre Alves de Carvalho 1 SUMÁRIO INTRODUÇÃO.......................................
FORMAÇÃO CONTINUADA EM MATEMÁTICA Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 PIRÂMIDES E CONES Cursista: Izabel Leal Vieira Tutor: Paulo Alexandre Alves de Carvalho 1 SUMÁRIO INTRODUÇÃO.......................................
Lista de exercícios - 2os anos - matemática 2 - prova Para se fabricar uma caixa de sabão em pó com 25 cm de altura, 16 cm de largura e
 Lista de exercícios - 2os anos - matemática 2 - prova 7-2013 Professores: Cebola, Figo, Guilherme, Rod e Sandra 1 - Para se fabricar uma caixa de sabão em pó com 25 cm de altura, 16 cm de largura e 5 cm
Lista de exercícios - 2os anos - matemática 2 - prova 7-2013 Professores: Cebola, Figo, Guilherme, Rod e Sandra 1 - Para se fabricar uma caixa de sabão em pó com 25 cm de altura, 16 cm de largura e 5 cm
Plano de Trabalho. Introdução à Geometria Espacial. Fundação CECIERJ/ Consórcio CEDERJ. Tarefa 2. Matemática 2 ano 1 bimestre/2013
 Fundação CECIERJ/ Consórcio CEDERJ Plano de Trabalho Introdução à Geometria Espacial Disponível em universododownloadgratis.blogspot.com Matemática 2 ano 1 bimestre/2013 Tarefa 2 Cursista: Barbara B. dos
Fundação CECIERJ/ Consórcio CEDERJ Plano de Trabalho Introdução à Geometria Espacial Disponível em universododownloadgratis.blogspot.com Matemática 2 ano 1 bimestre/2013 Tarefa 2 Cursista: Barbara B. dos
Guia do professor - Fábrica de Cubos e Mosaicos
 Guia do professor - Fábrica de Cubos e Mosaicos Introdução Os mosaicos são uma das mais bonitas criações, estando presente em tapeçarias, decoração de interiores, vitrais, cobertura de piso, em obras de
Guia do professor - Fábrica de Cubos e Mosaicos Introdução Os mosaicos são uma das mais bonitas criações, estando presente em tapeçarias, decoração de interiores, vitrais, cobertura de piso, em obras de
INSTITUTO GEREMÁRIO DANTAS COMPONENTE CURRICULAR: MATEMÁTICA II EXERCÍCIOS DE RECUPERAÇÃO FINAL 2016
 INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (1) 1087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): º Ano:C1 Nº Professora: Marcilene Siqueira Gama COMPONENTE CURRICULAR:
INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (1) 1087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): º Ano:C1 Nº Professora: Marcilene Siqueira Gama COMPONENTE CURRICULAR:
Tarefa nº 9. (Plano de trabalho nº 4)
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Tarefa nº 9 VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO CUBO Pretende-se, com esta actividade, e utilizando o que estudou e trabalhou até
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Tarefa nº 9 VAMOS DESCOBRIR NOVOS POLIEDROS A PARTIR DO CUBO Pretende-se, com esta actividade, e utilizando o que estudou e trabalhou até
AXIOMAS DA GEOMETRIA EUCLIDIANA EM ATIVIDADES EXPERIMENTAIS
 AXIOMAS DA GEOMETRIA EUCLIDIANA EM ATIVIDADES EXPERIMENTAIS Rita de Cássia Pavani LAMAS 1 Resumo: Este trabalho utiliza os axiomas da geometria euclidiana espacial na construção e definição de figuras
AXIOMAS DA GEOMETRIA EUCLIDIANA EM ATIVIDADES EXPERIMENTAIS Rita de Cássia Pavani LAMAS 1 Resumo: Este trabalho utiliza os axiomas da geometria euclidiana espacial na construção e definição de figuras
Figuras tri, tchê! Dinâmica 6. Professor. 2ª Série 2º Bimestre. Professor, nesta dinâmica, você irá desenvolver as seguintes etapas com seus alunos.
 Reforço escolar M ate mática Figuras tri, tchê! Dinâmica 6 2ª Série 2º Bimestre DISCIPLINA Série CAMPO CONCEITO Professor Matemática Ensino Médio 2ª Geométrico DINÂMICA Figuras tri, tchê! Geometria espacial:
Reforço escolar M ate mática Figuras tri, tchê! Dinâmica 6 2ª Série 2º Bimestre DISCIPLINA Série CAMPO CONCEITO Professor Matemática Ensino Médio 2ª Geométrico DINÂMICA Figuras tri, tchê! Geometria espacial:
PRISMAS E CILINDROS. Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ. Matemática 2º ano / 2º Bimestre/ 2013 PLANO DE TRABALHO
 Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º ano / 2º Bimestre/ 2013 PLANO DE TRABALHO PRISMAS E CILINDROS TAREFA 2: Cursista: Vanessa de Souza Machado Matrícula: 00/0974440-0
Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º ano / 2º Bimestre/ 2013 PLANO DE TRABALHO PRISMAS E CILINDROS TAREFA 2: Cursista: Vanessa de Souza Machado Matrícula: 00/0974440-0
LEIA ATENTAMENTE AS INSTRUÇÕES
 Matemática e suas Tecnologias CÓDIGO DA PROVA / SIMULADO Aluno(a): POMA - 3 Matemática Questões Professores: Guilherme Neydiwan 01-5 6-45 ª Série 3º Bimestre - N 30 / 09 / 016 LEIA ATENTAMENTE AS INSTRUÇÕES
Matemática e suas Tecnologias CÓDIGO DA PROVA / SIMULADO Aluno(a): POMA - 3 Matemática Questões Professores: Guilherme Neydiwan 01-5 6-45 ª Série 3º Bimestre - N 30 / 09 / 016 LEIA ATENTAMENTE AS INSTRUÇÕES
Roteiro de estudos para recuperação final
 Roteiro de estudos para recuperação final Disciplina: Matemática 1 Professor (a): Pedro Costa Júnior Semelhança de triângulos. Apostila 2 - Bernoulli: 6V Módulo: 5 Frente B Páginas: 37 a 44. Fixação (3
Roteiro de estudos para recuperação final Disciplina: Matemática 1 Professor (a): Pedro Costa Júnior Semelhança de triângulos. Apostila 2 - Bernoulli: 6V Módulo: 5 Frente B Páginas: 37 a 44. Fixação (3
2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 1 TETRAEDRO REGULAR. 2.1 Área lateral. 2.2 Área da base. 2.3 Área total. 2.4 Volume
 Matemática Pedro Paulo GEOMETRIA ESPACIAL VI são 1 TETRAEDRO REGULAR É uma piramide regular triangular, cujas faces triângulos equiláteros de lado 2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 2.1 Área lateral
Matemática Pedro Paulo GEOMETRIA ESPACIAL VI são 1 TETRAEDRO REGULAR É uma piramide regular triangular, cujas faces triângulos equiláteros de lado 2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 2.1 Área lateral
EXERCICIOS - ÁREAS E ÂNGULOS:
 EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
VOLUMES DE SÓLIDOS GEOMÉTRICOS. l = Aresta ou lado da base
 1 VOLUMES DE SÓLIDOS GEOMÉTRICOS Nomenclatura: P = Perímetro da ase a = Apótema da ase A FL = Área de uma face lateral At = Área total l = Aresta ou lado da ase A = Área da ase d = Diagonal da ase Al =
1 VOLUMES DE SÓLIDOS GEOMÉTRICOS Nomenclatura: P = Perímetro da ase a = Apótema da ase A FL = Área de uma face lateral At = Área total l = Aresta ou lado da ase A = Área da ase d = Diagonal da ase Al =
PLANO DE ESTUDOS DE MATEMÁTICA - 6.º ANO PERFIL DO ALUNO 1.º PERÍODO. DOMÍNIOS SUBDOMÍNIOS/CONTEÚDOS OBJETIVOS n.º de aulas
 DE MATEMÁTICA - 6.º ANO Ano Letivo 2014 2015 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de conhecer e aplicar propriedades dos números primos; representar e comparar números
DE MATEMÁTICA - 6.º ANO Ano Letivo 2014 2015 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de conhecer e aplicar propriedades dos números primos; representar e comparar números
PLANO DE ESTUDOS DE MATEMÁTICA 6.º ANO
 DE MATEMÁTICA 6.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de conhecer e aplicar propriedades dos números primos; representar e comparar números
DE MATEMÁTICA 6.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de conhecer e aplicar propriedades dos números primos; representar e comparar números
Pirâmide, cone e esfera
 A UA UL LA Pirâmide, cone e esfera Introdução Dando continuidade à unidade de Geometria Espacial, nesta aula vamos estudar mais três dos sólidos geométricos: a pirâmide, o cone e a esfera. Nossa aula A
A UA UL LA Pirâmide, cone e esfera Introdução Dando continuidade à unidade de Geometria Espacial, nesta aula vamos estudar mais três dos sólidos geométricos: a pirâmide, o cone e a esfera. Nossa aula A
Sólidos Inscritos e Circunscritos 3.º Ano
 Sólidos Inscritos e Circunscritos 3.º Ano 1. (Fuvest 2013) Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é a) 2 3 b) 4 c) 3 2 d)3 3
Sólidos Inscritos e Circunscritos 3.º Ano 1. (Fuvest 2013) Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é a) 2 3 b) 4 c) 3 2 d)3 3
(Matemática e Ciências Naturais) Grupo 230) Ano Letivo 2017 /2018
 1 - PLANIFICAÇÃO ANUAL DE MATEMÁTICA 1.1-5º ANO Números Naturais CONTEÚDOS PERÍODO As operações: Adição, subtração, e multiplicação e divisão Expressões numéricas números pelo respetivo máximo divisor
1 - PLANIFICAÇÃO ANUAL DE MATEMÁTICA 1.1-5º ANO Números Naturais CONTEÚDOS PERÍODO As operações: Adição, subtração, e multiplicação e divisão Expressões numéricas números pelo respetivo máximo divisor
1. Encontre a equação das circunferências abaixo:
 Nome: nº Professor(a): Série: 2ª EM. Turma: Data: / /2013 Nota: Sem limite para crescer Exercícios de Matemática II 2º Ano 2º Trimestre 1. Encontre a equação das circunferências abaixo: 2. Determine o
Nome: nº Professor(a): Série: 2ª EM. Turma: Data: / /2013 Nota: Sem limite para crescer Exercícios de Matemática II 2º Ano 2º Trimestre 1. Encontre a equação das circunferências abaixo: 2. Determine o
