Modulação em Largura de Pulso - PWM
|
|
|
- Maria Fernanda Antas Carreira
- 9 Há anos
- Visualizações:
Transcrição
1 Mdulaçã e Largura de Puls - PWM O sisea PWM cnsise e variar a largura d puls da pradra, prprcinalene a sinal dulane, anend cnsanes a apliude e inerval de ep a que s pulss se repee. Pdes classifica PWM c: - PWM siéric, quand es variações e abs s brds d puls. - PWM assiéric, quand es variações e apenas u brd de cada vez. A figura abaix sra as fras de nda d PWM. A largura insanânea d puls é ua funçã d sinal dulane dada pr: ( ) = K e ( ) nde () é a largura insanânea d puls; K é a cnsane d circui duladr, capaz de cnverer as variações de ensã de e() e variações da largura de (). K= s/v (segunds pr Vl) Se uilizars u sinal dulane cssenidal, c ua expressã d ip: e ( ) = E csω Prf.ª Irene
2 Enã eres seguine desenvlvien: ( ) = K E csω PRINCÍPIOS DE COMUNICAÇÃO II K E ( ) = csω Definis índice de dulaçã PWM: K E = nde 0 O fra ideal para a pradra re-de-pulss que vai ser dulada e PWM é c cicl de rabalh de 50%, u seja, u re-de-pulss siéric. Cnfre desrad pela equações abaix: ( ) = K E csω Quand csω = áx = K. E () = áx Quand csω = - ín = K. E () = ín Se cnsiderars a áxia largura d puls dulad cincidene c períd e a ínia largura send nula, eres: = K. E Reslvend as duas equações, es áx ín = K. E = 2 U re-de-pulss desenvlvida e Série de Furier, send descri c: E. e ( ) = 2E π n=.sen n nπ.cs nω N cas d sinal dulad PWM, a invés de, es () na expressã final. Enã: E.( ) 2E e( ) = π E. 2E e( ) =.( csω) π E. e( ) =. E. n= nπ ( ).sen.csnω n n= 2E csω π nπ.sen n n= nπ.sen n.( csω ).csnω. nπ csω.csnω Prf.ª Irene 2
3 Send que pdes definir s seguines ers:. E. valr cnsane, independene d ep, é valr édi d sinal dulad e().. E. 2. csω raia crrespndene a sinal dulane, pis esá siuada na velcidade w E π n. π. n.. π...sen n=.cs ω.csnω que é a funçã de Bessel, e que desenvlve nua sária de cssenóides de velcidades angulares úliplas de w. C essa parcela esá uliplicada pr csnω e FM, cenrad e u harônic da pradra., eres para cada valr n, u especr selhane a d sinal dulad Na figura abaix sras especr de apliudes d sinal dulad PWM Largura de Faixa Ocupada pel Sinal Mdulad A largura de faixa de u re-de- pulss é dada pr: B = N cas de u sinal PWM, es = ( ) e, para deerinars a air largura de faixa cupada pel sinal dulad PWM, cnsideres ( ) =. Assi: in = ( ) e B = ( = ) in c < Prf.ª Irene 3
4 Cicuis Mduladres PWM PRINCÍPIOS DE COMUNICAÇÃO II O principi básic para u duladr PWM é fazer c que ua variaçã de apliude se cnvera, de fra linear, e variaçã d espaç de ep ranscrrids enre dis evens. Uilizand a sa d sinal dulane c ua rapa, siérica u assiérica, bida a parir da pradra é pssível fazer essa dulaçã. Ver figura: O circui R2, C2 é u inegradr que ransfra a pradra e ua nda riangular que acplada pr C3 e R3, sa-se a sinal dulane (R, C) aravés d peracinal A. O divisr resisiv frad pr R6, R7 e P ajusa nível DC da ensã de saída d sadr, para rná-la cpaível c a ensã de dispar d Schi-rigger. O nível de dispar d Schi- rigger é cnsane e dad pels própris cpnenes d circui e a variars a psiçã d cursr P aleras a prfundidade de dulaçã dada a pradra. Pdes deduzir que se fixads e E M, penciôer P alera índice de dulaçã, send respnsável pel K d circui. Na figura sras a analise d sinal e cada pn d circui. Prf.ª Irene 4
5 Na figura abaix sras ua alernaiva de duladr PWM assiéric de brd esquerd e u inegradr para gerar PWM de brd direi c seus respecivs sinais. E abs s inegradres, resisr R3 é ui enr que R2, de aneira que a carga d capacir seja lena, feia sene pr r2, e a descarga é rápida, feia pr R3 e paralel c R2. O cpraen d segund circui é invers d prieir. Prf.ª Irene 5
6 Our d de geraçã d sinal PWM é aravés d CI 555 u 556, cnfre figura abaix. A pradra gerada inernaene pr esse duladr é u re-de-pulss c freqüência dada pr:,44 f = ( R 2. R2). C e cicl de rabalh R2 c = R 2. R2 Dedulaçã d Sinal PWM A dedulaçã d sinal PWM pde ser feia pr dis prcesss:.uilizand u circui deer de envlória c u filr passa-baixas. O incnveniene dese prcess é que há ua ineviável inerferência das bandas laerais relaivas a f, causand ua disrçã que só pderia ser eliinada se auenásses ui f. Ocrre que esse auen exigiria ua largura de faixa ui air que aquela calculada, rnand sisea inviável e funçã da largura de faixa cupada. Prf.ª Irene 6
7 Enã, a ser auen de f aé pn e que iss prvque ua disrçã lerável n sinal recuperad, anend a largura da faixa riginalene deerinada. and pr base s valres de Bessel, pdes chegar a u cnjun de equações que define a freqüência ínia de pradra, e funçã d índice de dulaçã e da freqüência d sinal dulane, end c parâer a disrçã. Essas expressões, girara e rn d inerval 0 < <. Disrçã de %: f f. (3,5 2,5. ) Disrçã de 2%: f f. (2,9 2,2. ) Disrçã de 5%: f f. (2,2 2. ) Disrçã de 0%: f f. (2 ) Essas expressões leva e cna que cicl de rabalh da pradra é de 50%. Ours valres d cicl de rabalh prvca variações n er que esá uliplicand índice de dulaçã. Na dulaçã PWM, a bservância resria d erea da Asrage (u seja: f = 2. f) prvcará ua disrçã n sinal recuperad seguraene air que 0%. Prf.ª Irene 7
8 2.O ur prcess é chaad de Dedulaçã Indirea e cnsise e cnverer sinal PWM e PAM, fazend pserirene ua asrage c reençã e ua filrage passa-baixas, para recuperar a infraçã. A figura abaix sra u diagraa de blcs básics para ese deduladr. A figura abaix sra as fras de nda relacinadas as pns nuerads n diagraa de Prf.ª Irene 8
9 blcs d deduladr. Cnvé bservar que a elhr pçã d ip de PWM a usar para esa dedulaçã é assiéric de brd direi, pis ds s insanes de sincrnis sã bids e relaçã a brd de subida d puls dulad PWM. Our dealhe é relaiv às fras de nda ns pns 6 e 7, que supõe circui já e funcinaen, pis se ese ivesse sid ligad e cndições iniciais nulas, n insane d iníci d gráfic, a fra de nda deveria iniciar e zer. Prf.ª Irene 9
Modulação em Amplitude de Pulso PAM
 Mdulaçã em Amplitude de Puls PAM PRINCÍPIOS DE COMUNICAÇÃO II O sistema PAM é aquele nde se aplica diretamente cnceit de um sinal amstrad, pis sinal mdulad pde ser cmpreendid cm prdut d sinal mdulante
Mdulaçã em Amplitude de Puls PAM PRINCÍPIOS DE COMUNICAÇÃO II O sistema PAM é aquele nde se aplica diretamente cnceit de um sinal amstrad, pis sinal mdulad pde ser cmpreendid cm prdut d sinal mdulante
Modulação em Amplitude com Faixa Lateral Simples (AM-SSB)
 Modulação e Apliude co Faixa Laeral iples (AM-B) O faor que levou a se desenvolver o AM - B foi a necessidade de se oer u sisea que ocupasse a enor faixa possível no especro e ivesse o áxio aproveiaeno
Modulação e Apliude co Faixa Laeral iples (AM-B) O faor que levou a se desenvolver o AM - B foi a necessidade de se oer u sisea que ocupasse a enor faixa possível no especro e ivesse o áxio aproveiaeno
Teoria para Laboratório 2º Bimestre
 Teoria para Laboratório 2º Biestre Prof.ª Irene 1 MODULAÇÃO EM LARGURA DE PULSO - PWM SISTEMAS DE COMUNICAÇÃO I - LABORATÓRIO O sistea PWM consiste e variar a largura do pulso da portadora, proporcionalente
Teoria para Laboratório 2º Biestre Prof.ª Irene 1 MODULAÇÃO EM LARGURA DE PULSO - PWM SISTEMAS DE COMUNICAÇÃO I - LABORATÓRIO O sistea PWM consiste e variar a largura do pulso da portadora, proporcionalente
Para uma linha de transmissão, o fluxo de potência ativa entre duas barras é dado por:
 Análise de Sisteas de tência (AS Flu de carga linearizad E funçã da grande siplificaçã prprcinada nas equações d flu de carga, s dels linearizads apresenta grande utilidade n planejaent da peraçã e da
Análise de Sisteas de tência (AS Flu de carga linearizad E funçã da grande siplificaçã prprcinada nas equações d flu de carga, s dels linearizads apresenta grande utilidade n planejaent da peraçã e da
UMC/ACET/ Wilson Yamaguti/Edson Gusella Jr. 6.1 Lab. Telecomunicações 2010. EXPERIÊNCIA 6 MODULAÇÃO PWM e PCM
 UMC/ACET/ Wilson Yaaguti/Edson Gusella Jr. 6.1 Lab. Telecounicações 21 1. Introdução EXPERIÊNCIA 6 MODULAÇÃO PWM e PCM Nesta experiência pretende-se conhecer a odulação PWM ou PDM couente usados no controle
UMC/ACET/ Wilson Yaaguti/Edson Gusella Jr. 6.1 Lab. Telecounicações 21 1. Introdução EXPERIÊNCIA 6 MODULAÇÃO PWM e PCM Nesta experiência pretende-se conhecer a odulação PWM ou PDM couente usados no controle
Capítulo. Meta deste capítulo Entender o princípio de funcionamento de osciladores controlados por tensão.
 1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
Helio Marcos Fernandes Viana
 1 UNtas de aulas de Estradas (parte 6) Heli Marcs Fernandes Viana UCnteúd da parte 6 Exercícis 1. ) Pede-se deterinar s eleents da curva circular hrizntal: T, D, E, 0, d, d, E(PC) e E(PT). Ainda, pede-se
1 UNtas de aulas de Estradas (parte 6) Heli Marcs Fernandes Viana UCnteúd da parte 6 Exercícis 1. ) Pede-se deterinar s eleents da curva circular hrizntal: T, D, E, 0, d, d, E(PC) e E(PT). Ainda, pede-se
Capítulo VII. Elementos Armazenadores de Energia
 Capíul VII Elemens Armazenadres de Energia 7. Inrduçã Nese capíul serã esudads dis elemens armazenadres de energia cnhecids cm indur e capacir. O primeir cnsise em um elemen que armazena energia em camp
Capíul VII Elemens Armazenadres de Energia 7. Inrduçã Nese capíul serã esudads dis elemens armazenadres de energia cnhecids cm indur e capacir. O primeir cnsise em um elemen que armazena energia em camp
EEL-001 CIRCUITOS ELÉTRICOS ENGENHARIA DA COMPUTAÇÃO
 EE- CRCUOS EÉRCOS 8 UNFE,FS, Rev BDB EE- CRCUOS EÉRCOS ENGENHARA DA COMPUAÇÃO CAPÍUO 4 4 AOR MÉDO E AOR EFCAZ (RMS) DE UM SNA 4 PROPREDADES DAS FORMAS DE ONDA PERÓDCAS 4 Definições v() senϖ v() v( +) valr
EE- CRCUOS EÉRCOS 8 UNFE,FS, Rev BDB EE- CRCUOS EÉRCOS ENGENHARA DA COMPUAÇÃO CAPÍUO 4 4 AOR MÉDO E AOR EFCAZ (RMS) DE UM SNA 4 PROPREDADES DAS FORMAS DE ONDA PERÓDCAS 4 Definições v() senϖ v() v( +) valr
MECÂNICA DE PRECISÃO - ELETRÔNICA I - Prof. NELSON M. KANASHIRO FILTRO CAPACITIVO
 . INTRODUÇÃO Na saída dos circuios reificadores, viso na aula anerior, emos ensão pulsane que não adequada para o funcionameno da maioria dos aparelhos elerônicos. Esa ensão deve ser conínua, semelhane
. INTRODUÇÃO Na saída dos circuios reificadores, viso na aula anerior, emos ensão pulsane que não adequada para o funcionameno da maioria dos aparelhos elerônicos. Esa ensão deve ser conínua, semelhane
Modulação Angular. Telecomunicações. Modulação em Frequência (FM) - 1
 Teleouniações Modulação e Frequênia (FM) - 1 Modulação Angular o Nos siseas de odulação e apliude a saída do odulador onsise nua poradora o ariações de apliude. o Na odulação e frequênia o sinal à saída
Teleouniações Modulação e Frequênia (FM) - 1 Modulação Angular o Nos siseas de odulação e apliude a saída do odulador onsise nua poradora o ariações de apliude. o Na odulação e frequênia o sinal à saída
3. Apreçamento CDS. 3.1 Risco-Neutro
 9 3. Apreçamen CDS O cálcul d spread de um CDS pde ser fei igualand-se s fluxs de caixa em ambas as siuações d CDS, cm s pagamens ds prêmis aé even de inadimplência e após even cm a liquidaçã d cnra. A
9 3. Apreçamen CDS O cálcul d spread de um CDS pde ser fei igualand-se s fluxs de caixa em ambas as siuações d CDS, cm s pagamens ds prêmis aé even de inadimplência e após even cm a liquidaçã d cnra. A
EXERCÍCIOS. 1. Comentar a ordem e molecularidade das seguintes reações, bem como a possibilidade da reação ser elementar. + 3H 2
 EXERCÍCIOS. Cmenar a rdem e mleularidade das seguines reações, bem m a pssibilidade da reaçã ser elemenar. (a) N 2 + 3H 2 2NH 3 (b) 2NH 3 N 2 + 3H 2 (inversa da anerir) () H 2 H + H MT 236 - Físi-Químia
EXERCÍCIOS. Cmenar a rdem e mleularidade das seguines reações, bem m a pssibilidade da reaçã ser elemenar. (a) N 2 + 3H 2 2NH 3 (b) 2NH 3 N 2 + 3H 2 (inversa da anerir) () H 2 H + H MT 236 - Físi-Químia
Roteiro de Integração Numérica (Método de Euler) Análise de Experimentos Virtuais
 Experients Virtuais (WEB) Rteir de Integraçã Nuérica (Métd de Euler) Análise de Experients Virtuais Quand ua partícula se ve sb influência de frças c resultante cnstante, sua aceleraçã tabé é cnstante,
Experients Virtuais (WEB) Rteir de Integraçã Nuérica (Métd de Euler) Análise de Experients Virtuais Quand ua partícula se ve sb influência de frças c resultante cnstante, sua aceleraçã tabé é cnstante,
TOE-50: Correção do fator de potência para cargas não lineares. Prof. Cassiano Rech
 TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech [email protected] 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech [email protected] 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
4. SINAL E CONDICIONAMENTO DE SINAL
 4. SINAL E CONDICIONAMENO DE SINAL Sumário 4. SINAL E CONDICIONAMENO DE SINAL 4. CARACERÍSICAS DOS SINAIS 4.. Período e frequência 4..2 alor médio, valor eficaz e valor máximo 4.2 FILRAGEM 4.2. Circuio
4. SINAL E CONDICIONAMENO DE SINAL Sumário 4. SINAL E CONDICIONAMENO DE SINAL 4. CARACERÍSICAS DOS SINAIS 4.. Período e frequência 4..2 alor médio, valor eficaz e valor máximo 4.2 FILRAGEM 4.2. Circuio
Lista de Exercícios Funções
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL Faculdade de Matemática Departament de Matemática Cálcul Dierencial e Integral I Lista de Eercícis Funções ) O gráic abai epressa a temperatura em
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL Faculdade de Matemática Departament de Matemática Cálcul Dierencial e Integral I Lista de Eercícis Funções ) O gráic abai epressa a temperatura em
CAPÍTULO 9. y(t). y Medidor. Figura 9.1: Controlador Analógico
 146 CAPÍULO 9 Inrodução ao Conrole Discreo 9.1 Inrodução Os sisemas de conrole esudados aé ese pono envolvem conroladores analógicos, que produzem sinais de conrole conínuos no empo a parir de sinais da
146 CAPÍULO 9 Inrodução ao Conrole Discreo 9.1 Inrodução Os sisemas de conrole esudados aé ese pono envolvem conroladores analógicos, que produzem sinais de conrole conínuos no empo a parir de sinais da
QUARTA EXPERIÊNCIA DO LABORATÓRIO DE ONDAS TRANSFORMADORES DE QUARTO DE ONDA EWALDO ÉDER CARVALHO SANTANA JÚNIOR EE06115-67 TURMA2
 UNIVERSIDADE FEDERA DO MARANHÃO CENTRO DE CIÊNCIAS EXATAS E TECNOOGIA DEPARTAMENTE DE ENGENHARIA DA EETRICIDADE ABORATÓRIO DE ONDAS EETROMAGNÉTICAS QUARTA EXPERIÊNCIA DO ABORATÓRIO DE ONDAS TRANSFORMADORES
UNIVERSIDADE FEDERA DO MARANHÃO CENTRO DE CIÊNCIAS EXATAS E TECNOOGIA DEPARTAMENTE DE ENGENHARIA DA EETRICIDADE ABORATÓRIO DE ONDAS EETROMAGNÉTICAS QUARTA EXPERIÊNCIA DO ABORATÓRIO DE ONDAS TRANSFORMADORES
Entre multiplicar por 1 e somar 1, o maior resultado é obtido no segundo caso, logo devemos também colocar um sinal de adição antes do 1:
 QUESTÃO C a ultiplicar qualquer núer pr 0 resultad é 0, nã cntribuind assi para axiizar resultad da expressã, deves clcar sinais de adiçã ds dis lads d 0: 2 + 0 + 9 Entre ultiplicar pr e sar, air resultad
QUESTÃO C a ultiplicar qualquer núer pr 0 resultad é 0, nã cntribuind assi para axiizar resultad da expressã, deves clcar sinais de adiçã ds dis lads d 0: 2 + 0 + 9 Entre ultiplicar pr e sar, air resultad
Teoria das Comunicações Prof. André Noll Barreto Prova 2
 Prova Aluno: Marícula: Quesão 1 ( ponos) Dado um sinal m = 1 deermine as expressões dos sinais modulados para as seguines modulações (0,5 ponos cada): a)am, com índice de modulação = m p A = 1 b)dsb-sc
Prova Aluno: Marícula: Quesão 1 ( ponos) Dado um sinal m = 1 deermine as expressões dos sinais modulados para as seguines modulações (0,5 ponos cada): a)am, com índice de modulação = m p A = 1 b)dsb-sc
MODULAÇÃO. Modulação. AM Amplitude Modulation Modulação por amplitude 24/02/2015
 ODUAÇÃO... PW DIGITA odulação odulação éamodificaçãoinencional e conrolada de um sinal original oalmene conhecido por meio de um ouro sinal, que se deseja ransporar. Esa modificação permie o ranspore do
ODUAÇÃO... PW DIGITA odulação odulação éamodificaçãoinencional e conrolada de um sinal original oalmene conhecido por meio de um ouro sinal, que se deseja ransporar. Esa modificação permie o ranspore do
CAPÍTULO 5 Problemas resolvidos. a c
 CAPÍTUO 5 Prbleas reslids a c Prblea A aceleraçã laeral áia que u carr pde er se derrapar, rafegand e pisa hriznal, é deninada aderência laeral, e usualene é epressa e ers da aceleraçã da graidade Assi,
CAPÍTUO 5 Prbleas reslids a c Prblea A aceleraçã laeral áia que u carr pde er se derrapar, rafegand e pisa hriznal, é deninada aderência laeral, e usualene é epressa e ers da aceleraçã da graidade Assi,
Exercícios complementares às notas de aulas de Estradas (parte 7) Curvas horizontais de transição
 1 Exercícis cpleentares às ntas de aulas de Estradas (parte 7) Heli Marcs Fernandes Viana Tea: urvas hrizntais de transiçã Heli Marcs Fernandes Viana 2 Exercíci 1 Para realizaçã d prjet de ua curva hrizntal
1 Exercícis cpleentares às ntas de aulas de Estradas (parte 7) Heli Marcs Fernandes Viana Tea: urvas hrizntais de transiçã Heli Marcs Fernandes Viana 2 Exercíci 1 Para realizaçã d prjet de ua curva hrizntal
Universidade Federal do Rio de Janeiro
 Universidade Federal do Rio de Janeiro Circuios Eléricos I EEL42 Coneúdo 8 - Inrodução aos Circuios Lineares e Invarianes...1 8.1 - Algumas definições e propriedades gerais...1 8.2 - Relação enre exciação
Universidade Federal do Rio de Janeiro Circuios Eléricos I EEL42 Coneúdo 8 - Inrodução aos Circuios Lineares e Invarianes...1 8.1 - Algumas definições e propriedades gerais...1 8.2 - Relação enre exciação
Espaço SENAI. Missão do Sistema SENAI
 Sumário Inrodução 5 Gerador de funções 6 Caracerísicas de geradores de funções 6 Tipos de sinal fornecidos 6 Faixa de freqüência 7 Tensão máxima de pico a pico na saída 7 Impedância de saída 7 Disposiivos
Sumário Inrodução 5 Gerador de funções 6 Caracerísicas de geradores de funções 6 Tipos de sinal fornecidos 6 Faixa de freqüência 7 Tensão máxima de pico a pico na saída 7 Impedância de saída 7 Disposiivos
Física A Extensivo V. 2
 Eensi V. Eercícis 1) 8 m. Num cer insane: 4 m/s 1 m/s 6 m/s C 6 18 Equações hrárias: : + 4 : X 6 + C: X C 18 + 6 siçã desejada: X (m) 8. Verdadeira. + a. + 5 + 5. 1 m/s 16. Verdadeira. + a. + 5. (8) m/s
Eensi V. Eercícis 1) 8 m. Num cer insane: 4 m/s 1 m/s 6 m/s C 6 18 Equações hrárias: : + 4 : X 6 + C: X C 18 + 6 siçã desejada: X (m) 8. Verdadeira. + a. + 5 + 5. 1 m/s 16. Verdadeira. + a. + 5. (8) m/s
Modulação por Pulsos
 Modulação por Pulsos Propriedades Amostragem de sinais Modulação por amplitude de pulso (PAM) Modulação por pulso codificado (PCM) Modulação por largura de pulso (PWM) Modulação por posição de pulso (PPM)
Modulação por Pulsos Propriedades Amostragem de sinais Modulação por amplitude de pulso (PAM) Modulação por pulso codificado (PCM) Modulação por largura de pulso (PWM) Modulação por posição de pulso (PPM)
Reatores Enzimáticos. EQB4383 Enzimologia Industrial. M.A.Z. Coelho
 Reatres Enziátics TIPOS DE REATORES USADOS COM ENZIMAS Os prcesss que utiliza enzias ibilizadas pde ser cnduzids de fra cntínua u e batelada. O sistea ais cu é de tanque agitad e batelada (STR). E alguns
Reatres Enziátics TIPOS DE REATORES USADOS COM ENZIMAS Os prcesss que utiliza enzias ibilizadas pde ser cnduzids de fra cntínua u e batelada. O sistea ais cu é de tanque agitad e batelada (STR). E alguns
Capítulo 2: Proposta de um Novo Retificador Trifásico
 30 Capíulo 2: Proposa de um Novo Reificador Trifásico O mecanismo do descobrimeno não é lógico e inelecual. É uma iluminação suberrânea, quase um êxase. Em seguida, é cero, a ineligência analisa e a experiência
30 Capíulo 2: Proposa de um Novo Reificador Trifásico O mecanismo do descobrimeno não é lógico e inelecual. É uma iluminação suberrânea, quase um êxase. Em seguida, é cero, a ineligência analisa e a experiência
Modulação AM - DSB. Sinal Modulante + = () ( ) ( ) k = Eficiência do modulador. Sinal Portador AM - DSB
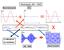 Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
CIRCUITO SÉRIE/PARALELO Prof. Antonio Sergio-D.E.E-CEAR-UFPB.
 CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
Questão 11. Questão 12. Resposta. Resposta S 600. Um veículo se desloca em trajetória retilínea e sua velocidade em função do tempo é apresentada
 Questã Um veícul se deslca em trajetória retilínea e sua velcidade em funçã d temp é apresentada na fiura. a) Identifique tip de mviment d veícul ns intervals de temp de 0 a 0 s,de 0 a 30 s e de 30 a 0
Questã Um veícul se deslca em trajetória retilínea e sua velcidade em funçã d temp é apresentada na fiura. a) Identifique tip de mviment d veícul ns intervals de temp de 0 a 0 s,de 0 a 30 s e de 30 a 0
INTRODUÇÃO. 1. MODULAÇÃO POR CÓDIGO DE PULSO - PCM 1.1
 ETFSC UNED/SJ CURSO DE TELEFONIA DIGITAL CAPÍTULO. MODULAÇÃO POR CÓDIGO DE PULSO - PCM. INTRODUÇÃO. Uma grande pare dos sinais de inormações que são processados em uma rede de elecomunicações são sinais
ETFSC UNED/SJ CURSO DE TELEFONIA DIGITAL CAPÍTULO. MODULAÇÃO POR CÓDIGO DE PULSO - PCM. INTRODUÇÃO. Uma grande pare dos sinais de inormações que são processados em uma rede de elecomunicações são sinais
Questão 1. Questão 3. Questão 2. alternativa B. alternativa E. alternativa B
 Questã 1 Uma pesquisa de mercad sbre determinad eletrdméstic mstru que 7% ds entrevistads preferem a marca X, 40% preferem a marca Y, 0% preferem a marca Z, 5% preferem X e Y, 8% preferem Y e Z, % preferem
Questã 1 Uma pesquisa de mercad sbre determinad eletrdméstic mstru que 7% ds entrevistads preferem a marca X, 40% preferem a marca Y, 0% preferem a marca Z, 5% preferem X e Y, 8% preferem Y e Z, % preferem
I, determine a matriz inversa de A. Como A 3 3 A = 2 I; fatorando o membro esquerdo dessa igualdade por A, temos a expressão
 VTB 008 ª ETAPA Sluçã Cmentada da Prva de Matemática 0 Em uma turma de aluns que estudam Gemetria, há 00 aluns Dentre estes, 0% fram aprvads pr média e s demais ficaram em recuperaçã Dentre s que ficaram
VTB 008 ª ETAPA Sluçã Cmentada da Prva de Matemática 0 Em uma turma de aluns que estudam Gemetria, há 00 aluns Dentre estes, 0% fram aprvads pr média e s demais ficaram em recuperaçã Dentre s que ficaram
Universidade Federal do Rio Grande do Sul Escola de Engenharia de Porto Alegre Departamento de Engenharia Elétrica ANÁLISE DE CIRCUITOS II - ENG04031
 Universidade Federal do io Grande do Sul Escola de Engenharia de Poro Alegre Deparameno de Engenharia Elérica ANÁLISE DE CICUITOS II - ENG43 Aula 5 - Condições Iniciais e Finais de Carga e Descarga em
Universidade Federal do io Grande do Sul Escola de Engenharia de Poro Alegre Deparameno de Engenharia Elérica ANÁLISE DE CICUITOS II - ENG43 Aula 5 - Condições Iniciais e Finais de Carga e Descarga em
Gabarito Prova de 1º e 2º anos
 Gabari Pra de º e º ans. Cada arca após ua la cplea percrre ua disância d i= π i + L, u seja: d = π + 6π 8π d = π e d3 = π = Se i é a elcidade de cada arca, ua la cplea é efeuada n ep As arcas irã cincidir
Gabari Pra de º e º ans. Cada arca após ua la cplea percrre ua disância d i= π i + L, u seja: d = π + 6π 8π d = π e d3 = π = Se i é a elcidade de cada arca, ua la cplea é efeuada n ep As arcas irã cincidir
Primeira Lista de Exercícios
 TP30 Modulação Digial Prof.: MSc. Marcelo Carneiro de Paiva Primeira Lisa de Exercícios Caracerize: - Transmissão em Banda-Base (apresene um exemplo de especro de ransmissão). - Transmissão em Banda Passane
TP30 Modulação Digial Prof.: MSc. Marcelo Carneiro de Paiva Primeira Lisa de Exercícios Caracerize: - Transmissão em Banda-Base (apresene um exemplo de especro de ransmissão). - Transmissão em Banda Passane
SANTA CASA 2018 MEDICINA DISCURSIVAS FACULDADE DE CIÊNCIAS MÉDICAS DA SANTA CASA DE SÃO PAULO
 Prfessra Snia SANTA ASA 018 MEDIINA DISURSIVAS FAULDADE DE IÊNIAS MÉDIAS DA SANTA ASA DE SÃ PAUL 09. Até ent, nã existe cura para a dença de Alzheier. Acredita-se que parte ds sintas da dença decrra de
Prfessra Snia SANTA ASA 018 MEDIINA DISURSIVAS FAULDADE DE IÊNIAS MÉDIAS DA SANTA ASA DE SÃ PAUL 09. Até ent, nã existe cura para a dença de Alzheier. Acredita-se que parte ds sintas da dença decrra de
S3 - Explicação sobre endereço e/ou número de telefone dos EUA
 S3 - Explicaçã sbre endereç e/u númer de telefne ds EUA Nme Númer da Cnta (se huver) A preencher seu Frmulári W-8 d IRS, vcê afirma nã ser cidadã u residente ds EUA u utra cntraparte ds EUA para efeit
S3 - Explicaçã sbre endereç e/u númer de telefne ds EUA Nme Númer da Cnta (se huver) A preencher seu Frmulári W-8 d IRS, vcê afirma nã ser cidadã u residente ds EUA u utra cntraparte ds EUA para efeit
INF Técnicas Digitais para Computação. Conceitos Básicos de Circuitos Elétricos. Aula 3
 INF01 118 Técnicas Digiais para Compuação Conceios Básicos de Circuios Eléricos Aula 3 1. Fones de Tensão e Correne Fones são elemenos aivos, capazes de fornecer energia ao circuio, na forma de ensão e
INF01 118 Técnicas Digiais para Compuação Conceios Básicos de Circuios Eléricos Aula 3 1. Fones de Tensão e Correne Fones são elemenos aivos, capazes de fornecer energia ao circuio, na forma de ensão e
Sinais e Sistemas. Caderno de Exercícios de Casa (Horas não presenciais) (Compilação de exercícios de exames)
 Sinais e Sisemas Caderno de Exercícios de Casa (Horas não presenciais) (Compilação de exercícios de exames) Capíulo - Sinais. Escreva as linhas de código em Malab para criar e represenar os seguines sinais:
Sinais e Sisemas Caderno de Exercícios de Casa (Horas não presenciais) (Compilação de exercícios de exames) Capíulo - Sinais. Escreva as linhas de código em Malab para criar e represenar os seguines sinais:
INTRODUÇÃO TEÓRICA - EXPERIÊNCIA 3. Comportamento de Componentes Passivos
 UNIVERSIDADE DE SÃO PAULO ESCOLA POLIÉCNICA Deparameno de Engenharia de Sisemas Elerônicos PSI - EPUSP PSI 3031/3212 - LABORAÓRIO DE CIRCUIOS ELÉRICOS INRODUÇÃO EÓRICA - EXPERIÊNCIA 3 Comporameno de Componenes
UNIVERSIDADE DE SÃO PAULO ESCOLA POLIÉCNICA Deparameno de Engenharia de Sisemas Elerônicos PSI - EPUSP PSI 3031/3212 - LABORAÓRIO DE CIRCUIOS ELÉRICOS INRODUÇÃO EÓRICA - EXPERIÊNCIA 3 Comporameno de Componenes
Seção 5: Equações Lineares de 1 a Ordem
 Seção 5: Equações Lineares de 1 a Ordem Definição. Uma EDO de 1 a ordem é dia linear se for da forma y + fx y = gx. 1 A EDO linear de 1 a ordem é uma equação do 1 o grau em y e em y. Qualquer dependência
Seção 5: Equações Lineares de 1 a Ordem Definição. Uma EDO de 1 a ordem é dia linear se for da forma y + fx y = gx. 1 A EDO linear de 1 a ordem é uma equação do 1 o grau em y e em y. Qualquer dependência
2 Conceitos de transmissão de dados
 2 Conceios de ransmissão de dados 2 Conceios de ransmissão de dados 1/23 2.2.1 Fones de aenuação e disorção de sinal 2.2.1 Fones de aenuação e disorção do sinal (coninuação) 2/23 Imperfeições do canal
2 Conceios de ransmissão de dados 2 Conceios de ransmissão de dados 1/23 2.2.1 Fones de aenuação e disorção de sinal 2.2.1 Fones de aenuação e disorção do sinal (coninuação) 2/23 Imperfeições do canal
Análise do FET para pequenos sinais
 EN2719 ispsitivs Eletrônics AULA 19 Análise d FET para pequens sinais Prf. dri eina Muñz [email protected] T1 2018 EN 2719 ispsitivs Eletrônics Cnteúd Análise d JFET, MOFET depleçã e MOFET intensificaçã
EN2719 ispsitivs Eletrônics AULA 19 Análise d FET para pequens sinais Prf. dri eina Muñz [email protected] T1 2018 EN 2719 ispsitivs Eletrônics Cnteúd Análise d JFET, MOFET depleçã e MOFET intensificaçã
AULA PRÉ-TEÓRICA 03 CONVERSORES CC-CC 2 GERAÇÃO DOS SINAIS DE COMANDO (PWM) NO ARDUINO
 Pré-Teórica 3 Cnverre cc-cc Buck e B cm filr INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA DEPARTAMENTO ACADÊMICO DE ELETRÔNICA CURSO TÉCNICO DE ELETRÔNICA Elerônica de Pência AULA
Pré-Teórica 3 Cnverre cc-cc Buck e B cm filr INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA DEPARTAMENTO ACADÊMICO DE ELETRÔNICA CURSO TÉCNICO DE ELETRÔNICA Elerônica de Pência AULA
MOVIMENTO RELATIVO. Não existe um referencial absoluto. Velocidade Relativa. v B. v A. Velocidades de A e B medidas pelo observador O B = A = dr
 1 MOVIMEO ELIVO O mimen é um cncei reli cu descriçã depende de um referencil específic esclhid pel bserdr. Diferenes bserdres usnd sisems referenciis diferenes bém diferenes descrições de um mesm mimen.
1 MOVIMEO ELIVO O mimen é um cncei reli cu descriçã depende de um referencil específic esclhid pel bserdr. Diferenes bserdres usnd sisems referenciis diferenes bém diferenes descrições de um mesm mimen.
Radar CW. Aplicações:
 Radar CW Aplicações: Deerinação de velocidade de veículos Deerinação de velocidade de projéceis, ísseis, ec, e aplicações desporivas Taxa de subida e ake-o verical Alíero Operações de docage no espaço
Radar CW Aplicações: Deerinação de velocidade de veículos Deerinação de velocidade de projéceis, ísseis, ec, e aplicações desporivas Taxa de subida e ake-o verical Alíero Operações de docage no espaço
EN2607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 1 2 quadrimestre 2011
 EN67 Transformadas em Sinais e Sisemas Lineares Lisa de Exercícios Suplemenares quadrimesre Figura Convolução (LATHI, 998) (N) (HAYKIN; VEEN,, p 79) O pulso rapezoidal x( ) da figura a seguir é aplicado
EN67 Transformadas em Sinais e Sisemas Lineares Lisa de Exercícios Suplemenares quadrimesre Figura Convolução (LATHI, 998) (N) (HAYKIN; VEEN,, p 79) O pulso rapezoidal x( ) da figura a seguir é aplicado
Física. Física Módulo 1
 Física Módulo 1 Nesa aula... Movimeno em uma dimensão Aceleração e ouras coisinhas O cálculo de x() a parir de v() v( ) = dx( ) d e x( ) x v( ) d = A velocidade é obida derivando-se a posição em relação
Física Módulo 1 Nesa aula... Movimeno em uma dimensão Aceleração e ouras coisinhas O cálculo de x() a parir de v() v( ) = dx( ) d e x( ) x v( ) d = A velocidade é obida derivando-se a posição em relação
COMPARAÇÃO DE CURVAS DE SOBREVIVÊNCIA
 COMPARAÇÃO DE CURVAS DE SOBREVIVÊNCIA O prblema de cmparaçã de distribuições de sbrevivências surge cm freqüência em estuds de sbrevivência. Pr exempl, pde ser de interesse cmparar dis trataments para
COMPARAÇÃO DE CURVAS DE SOBREVIVÊNCIA O prblema de cmparaçã de distribuições de sbrevivências surge cm freqüência em estuds de sbrevivência. Pr exempl, pde ser de interesse cmparar dis trataments para
Teoria da Comunicação. Prof. Andrei Piccinini Legg Aula 09
 Teoria da Comuniação Pro. Andrei Piinini Legg Aula 09 Inrodução Sabemos que a inormação pode ser ransmiida aravés da modiiação das araerísias de uma sinusóide, hamada poradora do sinal de inormação. Se
Teoria da Comuniação Pro. Andrei Piinini Legg Aula 09 Inrodução Sabemos que a inormação pode ser ransmiida aravés da modiiação das araerísias de uma sinusóide, hamada poradora do sinal de inormação. Se
Figura 1 Carga de um circuito RC série
 ASSOIAÇÃO EDUAIONAL DOM BOSO FAULDADE DE ENGENHAIA DE ESENDE ENGENHAIA ELÉTIA ELETÔNIA Disciplina: Laboraório de ircuios Eléricos orrene onínua 1. Objeivo Sempre que um capacior é carregado ou descarregado
ASSOIAÇÃO EDUAIONAL DOM BOSO FAULDADE DE ENGENHAIA DE ESENDE ENGENHAIA ELÉTIA ELETÔNIA Disciplina: Laboraório de ircuios Eléricos orrene onínua 1. Objeivo Sempre que um capacior é carregado ou descarregado
UTFPR CURSO DE ENGENHARIA ELETRÔNICA FUNDAMENTOS DE COMUNICAÇÕES - PROF. EMILIO WILLE EXERCÍCIOS PROPOSTOS
 UTFPR CURSO DE ENGENHRI EETRÔNIC FUNDMENTOS DE COMUNICÇÕES - PROF. EMIIO WIE EXERCÍCIOS PROPOSTOS ) Prove que a Série Trigonomérica de Fourier para o sinal periódico abaixo ( = e = T o /) é dada por: gp()
UTFPR CURSO DE ENGENHRI EETRÔNIC FUNDMENTOS DE COMUNICÇÕES - PROF. EMIIO WIE EXERCÍCIOS PROPOSTOS ) Prove que a Série Trigonomérica de Fourier para o sinal periódico abaixo ( = e = T o /) é dada por: gp()
matemática 2 Questão 7
 Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
Correntes alternadas. circuito com corrente estacionária fi V = RI; P = RI 2 circuito puramente resistivo (resistores R) V L.
 Eleents lineares Fi vist: rrentes alternadas circuit c crrente estacinária fi V RI; P RI circuit puraente resistiv (resistres R) quand a crrente nã é estacinária fi aparece fe induzida V L ε ind L di dt
Eleents lineares Fi vist: rrentes alternadas circuit c crrente estacinária fi V RI; P RI circuit puraente resistiv (resistres R) quand a crrente nã é estacinária fi aparece fe induzida V L ε ind L di dt
Circuitos de Corrente Alternada I
 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Resposta de R, L e C em CA e Potência Média
 Institut Federal de Educaçã, Ciência e Tecnlgia de Santa Catarina Departaent Acadêic de Eletrônica Retificadres Respsta de R, e C e CA e Ptência Média Prf. Clóvis Antôni Petry. Flrianóplis, fevereir de
Institut Federal de Educaçã, Ciência e Tecnlgia de Santa Catarina Departaent Acadêic de Eletrônica Retificadres Respsta de R, e C e CA e Ptência Média Prf. Clóvis Antôni Petry. Flrianóplis, fevereir de
Introdução aos multivibradores e circuito integrado 555
 2 Capíulo Inrodução aos mulivibradores e circuio inegrado 555 Mea dese capíulo Enender o princípio de funcionameno dos diversos ipos de mulivibradores e esudo do circuio inegrado 555. objeivos Enender
2 Capíulo Inrodução aos mulivibradores e circuio inegrado 555 Mea dese capíulo Enender o princípio de funcionameno dos diversos ipos de mulivibradores e esudo do circuio inegrado 555. objeivos Enender
67.301/1. RLP 10 & 20: Controlador pneumático de volume-caudal. Sauter Components
 7./ RL & : Conrolador pneumáico de volume-caudal Usado em conjuno com um prao orifício ou com um sensor de pressão dinâmica e um acuador pneumáico de regiso para conrolo do volume de ar em sisemas de ar
7./ RL & : Conrolador pneumáico de volume-caudal Usado em conjuno com um prao orifício ou com um sensor de pressão dinâmica e um acuador pneumáico de regiso para conrolo do volume de ar em sisemas de ar
Lista de Exercícios n o.1. 1) O diodo do circuito da Fig. 1(a) se comporta segundo a característica linearizada por partes da Fig 1(b). I D (ma) Fig.
 Universidade Federal da Bahia EE isposiivos Semiconduores ENG C41 Lisa de Exercícios n o.1 1) O diodo do circuio da Fig. 1 se compora segundo a caracerísica linearizada por pares da Fig 1. R R (ma) 2R
Universidade Federal da Bahia EE isposiivos Semiconduores ENG C41 Lisa de Exercícios n o.1 1) O diodo do circuio da Fig. 1 se compora segundo a caracerísica linearizada por pares da Fig 1. R R (ma) 2R
Capacitores e Indutores
 Capaciores e Induores Um capacior é um disposiivo que é capaz de armazenar e disribuir carga elérica em um circuio. A capaciância (C) é a grandeza física associada a esa capacidade de armazenameno da carga
Capaciores e Induores Um capacior é um disposiivo que é capaz de armazenar e disribuir carga elérica em um circuio. A capaciância (C) é a grandeza física associada a esa capacidade de armazenameno da carga
Circuitos Elétricos I EEL420
 Universidade Federal do Rio de Janeiro Circuios Eléricos I EEL420 Coneúdo 1 - Circuios de primeira ordem...1 1.1 - Equação diferencial ordinária de primeira ordem...1 1.1.1 - Caso linear, homogênea, com
Universidade Federal do Rio de Janeiro Circuios Eléricos I EEL420 Coneúdo 1 - Circuios de primeira ordem...1 1.1 - Equação diferencial ordinária de primeira ordem...1 1.1.1 - Caso linear, homogênea, com
GERAÇÃO DE PREÇOS DE ATIVOS FINANCEIROS E SUA UTILIZAÇÃO PELO MODELO DE BLACK AND SCHOLES
 XXX ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO Mauridade e desafios da Engenharia de Produção: compeiividade das empresas, condições de rabalho, meio ambiene. São Carlos, SP, Brasil, 1 a15 de ouubro de
XXX ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO Mauridade e desafios da Engenharia de Produção: compeiividade das empresas, condições de rabalho, meio ambiene. São Carlos, SP, Brasil, 1 a15 de ouubro de
Questão 1. Questão 3. Questão 2. Questão 4. Resposta. Resposta. Resposta. ATENÇÃO: Escreva a resolução COM- PLETA de cada questão no espaço reservado
 ATENÇÃO: Escreva a resluçã COM- PLETA de cada questã n espaç reservad para a mesma. Nã basta escrever apenas resultad final: é necessári mstrar s cálculs racicíni utilizad. Questã Caminhand sempre cm a
ATENÇÃO: Escreva a resluçã COM- PLETA de cada questã n espaç reservad para a mesma. Nã basta escrever apenas resultad final: é necessári mstrar s cálculs racicíni utilizad. Questã Caminhand sempre cm a
Construindo Tecnologia
 Cmand Bimanual Cnstruind Tecnlgia Quem sms Safety Divisin Desde 1967 a ACE SCHMERSAL prduz equipaments para Autmaçã e Sistemas de Segurança, cntand cm mais de 300 clabradres em sua fábrica n Brasil, instalada
Cmand Bimanual Cnstruind Tecnlgia Quem sms Safety Divisin Desde 1967 a ACE SCHMERSAL prduz equipaments para Autmaçã e Sistemas de Segurança, cntand cm mais de 300 clabradres em sua fábrica n Brasil, instalada
