ponto P terá as projecções P 1 e P 2. E o eixo X passa para X. Vamos ver o que acontece no plano do
|
|
|
- Heloísa Carlos Oliveira
- 8 Há anos
- Visualizações:
Transcrição
1 Mudança de planos 1- Introdução As projecções de uma figura só representam as suas verdadeiras grandezas se essa figura está contida num plano paralelo aos planos de projecção. Caso contrário as projecções e a verdadeira grandeza têm valores diferentes. Mantendo fixa a figura a projectar, podemos contudo mudar os planos de projecção, mantendo-os de qualquer das formas perpendiculares um ao outro, ou seja, mantendo um sistema de projecções ortogonais, e tornar assim um dos planos paralelo ao plano da figura. Temos assim uma das projecções igual à verdadeira grandeza. A este processo chamamos mudança de planos. Para executarmos este processo só podemos mudar um plano de cada vez, e com a condição de os dois planos de projecção se manterem sempre perpendiculares. 2- Transformação das projecções de um ponto 2.1- Mudança do plano frontal Consideremos um ponto P e as sua projecções P 1 e P 2 em ϕ o e ν o. Imaginemos que o plano frontal (ϕ o ) roda para uma nova posição (ϕ o ), mantendo-se perpendicular a ν o. Neste novo sistema de projecções o ponto P terá as projecções P 1 e P 2. E o eixo X passa para X. Vamos ver o que acontece no plano do Se mesma no novo sistema, ou seja, P 1 coincide com P 1. Por outro lado a cota de P no novo sistema de projecções também é a mesma, logo, como P 2 tem de estar na perpendicular a X que passa em P 1, facilmente o encontramos, basta a partir de X marcar a cota. papel. o plano horizontal se mantém, a projecção horizontal do ponto também vai ser a 1
2 2.2- Mudança do plano horizontal Neste caso é a projecção frontal que se mantém e o afastamento é o mesmo. 3- Transformação das projecções de uma recta 3.1- Transformar uma recta de nível numa recta de topo Como uma recta de nível é paralela ao plano horizontal, e uma recta de topo é perpendicular ao plano frontal, se tivermos uma recta de nível, podemos rodar o plano frontal, mantendo-o sempre perpendicular ao plano horizontal, até este ficar perpendicular recta. Ficamos assim com um sistema de projecções onde a recta passa a ser de topo. O novo eixo (X ) é agora perpendicular a n 1. à 3.2- Transformar uma recta de frente em recta vertical Mudamos o plano horizontal até ficar perpendicular à recta X vai ficar perpendicular a f Transformar uma recta oblíqua em recta de nível. Mudamos o plano horizontal até ficar paralelo à recta. X vai ficar paralelo a r 2. 2
3 3.4- Transformar uma recta oblíqua em recta de frente Mudamos o plano frontal até ficar paralelo à recta X vai ficar paralelo a r 1. Nota: O facto de considerarmos as novas projecções para um ou para o outro lado do novo eixo, não acarreta nenhum problema. Apenas devemos ter em atenção o seguinte. Marcando coordenadas com determinado sinal para um lado do eixo, todas as do mesmo sinal devem ser marcadas para esse lado, e para o outro lado as de sinal contrário. 4- Transformação dos elementos de um plano 4.1- Transformar um plano de topo num de nível Neste caso o novo eixo X vai ficar paralelo ao traço frontal do plano. O novo traço frontal vai ficar coincidente com o antigo, quer isto dizer que houve uma mudança do plano horizontal de projecção. Se o plano de topo for definido por duas rectas concorrentes, como é de topo, as projecções frontais das duas rectas são coincidentes, para o transformar num plano de nível fazemos uma mudança do plano horizontal de projecção, ficando o novo eixo X, paralelo às projecções frontais das rectas. 3
4 4.2- Transformação dos traços de um plano Mudança do plano frontal de projecção Neste caso o traço horizontal mantém-se. Os traços que no sistema inicial se cruzavam no ponto O de X, vão passar a ter o seu ponto de cruzamento em O de X. Se considerarmos o ponto P de α, que tem P 1 no cruzamento dos dois eixos X e X, P é do traço frontal inicial e vai ser do traço frontal do novo sistema, logo achando P 2 e unindo-o a O temos o novo traço frontal Mudança do plano horizontal de projecções 5- Estudo da recta de perfil Se fizermos uma mudança de plano horizontal, fazendo as mudanças de A e B, obtemos a recta no novo sistema. O ponto onde a nova projecção encontra X, dá-nos a nova projecção horizontal do traço frontal, o ponto onde a nova projecção encontra X, dá-nos a nova projecção do traço horizontal. A partir destes pontos podemos obter as projecções no sistema inicial. Nota: Podíamos ter optado por uma mudança do plano frontal. 4
5 6- Determinar a verdadeira grandeza de um segmento oblíquo AB Dadas as projecções de AB, se considerarmos uma mudança do plano horizontal, tal que o novo eixo X fique paralelo à projecção frontal de AB, este fica de nível, logo A 1 ívelb 1 dá-nos a verdadeira grandeza de AB. Notar que A 1 foi marcado para um lado de X e B 1 para outro lado, uma vez que o afastamento de A é positivo e o de B negativo. 7- Caso em que é necessário fazer mais do que uma mudança de planos Nos casos anteriores uma única mudança de um dos planos de projecção resolvia o nosso problema. Existem casos, por exemplo tornar um plano oblíquo de nível, em que o problema só se resolve com duas mudanças de planos. De facto, uma vez que um plano de projecção só pode mudar mantendo-se perpendicular ao outro, não conseguimos rodar nestas condições o plano horizontal e pô-lo paralelo ao plano oblíquo. Podemos resolver o problema se em primeiro lugar transformarmos o plano oblíquo num plano de topo, rodando o plano frontal. Posteriormente rodamos o plano horizontal até ficar paralelo ao plano dado, que é o que pretendemos. Nota: Se o plano for definido por duas rectas concorrentes, ou paralelas, consideramos uma recta de nível do plano, transformámo-la numa recta de topo (mudança de plano frontal) e depois fazemos a mudança do plano horizontal. 5
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA DE BELAS ARTES SISTEMA GEOMÉTRICO DE REPRESENTAÇÃO I PROF. CRISTINA GRAFANASSI TRANJAN
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA DE BELAS ARTES SISTEMA GEOMÉTRICO DE REPRESENTAÇÃO I PROF. CRISTINA GRAFANASSI TRANJAN MÉTODOS DESCRITIVOS Há determinados problemas em Geometria Descritiva
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA DE BELAS ARTES SISTEMA GEOMÉTRICO DE REPRESENTAÇÃO I PROF. CRISTINA GRAFANASSI TRANJAN MÉTODOS DESCRITIVOS Há determinados problemas em Geometria Descritiva
"SISTEMAS DE COTAGEM"
 AULA 6T "SISTEMAS DE COTAGEM" Embora não existam regras fixas de cotagem, a escolha da maneira de dispor as cotas no desenho técnico depende de alguns critérios. A cotagem do desenho técnico deve tornar
AULA 6T "SISTEMAS DE COTAGEM" Embora não existam regras fixas de cotagem, a escolha da maneira de dispor as cotas no desenho técnico depende de alguns critérios. A cotagem do desenho técnico deve tornar
I CAPÍTULO 19 RETA PASSANDO POR UM PONTO DADO
 Matemática Frente I CAPÍTULO 19 RETA PASSANDO POR UM PONTO DADO 1 - RECORDANDO Na última aula, nós vimos duas condições bem importantes: Logo, se uma reta passa por um ponto e tem um coeficiente angular,
Matemática Frente I CAPÍTULO 19 RETA PASSANDO POR UM PONTO DADO 1 - RECORDANDO Na última aula, nós vimos duas condições bem importantes: Logo, se uma reta passa por um ponto e tem um coeficiente angular,
3.8. Problemas métricos
 3.8. Problemas métricos Geometria Descritiva 2006/2007 Tipos de problemas métricos Distância entre dois pontos Distância de um ponto a uma recta Distância de um ponto a um Distância entre duas rectas Ângulo
3.8. Problemas métricos Geometria Descritiva 2006/2007 Tipos de problemas métricos Distância entre dois pontos Distância de um ponto a uma recta Distância de um ponto a um Distância entre duas rectas Ângulo
AV1 - MA 12-2012. (b) Se o comprador preferir efetuar o pagamento à vista, qual deverá ser o valor desse pagamento único? 1 1, 02 1 1 0, 788 1 0, 980
 Questão 1. Uma venda imobiliária envolve o pagamento de 12 prestações mensais iguais a R$ 10.000,00, a primeira no ato da venda, acrescidas de uma parcela final de R$ 100.000,00, 12 meses após a venda.
Questão 1. Uma venda imobiliária envolve o pagamento de 12 prestações mensais iguais a R$ 10.000,00, a primeira no ato da venda, acrescidas de uma parcela final de R$ 100.000,00, 12 meses após a venda.
Prof. Rossini Bezerra Faculdade Boa Viagem
 Sistemas de Coordenadas Polares Prof. Rossini Bezerra Faculdade Boa Viagem Coordenadas Polares Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no
Sistemas de Coordenadas Polares Prof. Rossini Bezerra Faculdade Boa Viagem Coordenadas Polares Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no
PERSPECTIVA LINEAR DEFINIÇÕES E TEOREMAS
 Figura 64. Tapeçaria da sala de actos do Governo Civil de Bragança (800 cm x 800 cm). Luís Canotilho 2000. A geometria é também aplicada ao simbolismo humano. No presente caso as formas geométricas identificam
Figura 64. Tapeçaria da sala de actos do Governo Civil de Bragança (800 cm x 800 cm). Luís Canotilho 2000. A geometria é também aplicada ao simbolismo humano. No presente caso as formas geométricas identificam
CORPOS RÍGIDOS: As forças que actuam num corpo rígido podem ser divididas em dois grupos:
 CORPOS RÍGIDOS: As forças que actuam num corpo rígido podem ser divididas em dois grupos: 1. Forças externas (que representam as acções externas sobre o corpo rígido) 2. Forças internas (que representam
CORPOS RÍGIDOS: As forças que actuam num corpo rígido podem ser divididas em dois grupos: 1. Forças externas (que representam as acções externas sobre o corpo rígido) 2. Forças internas (que representam
Testa os conhecimentos de Geometria Descritiva
 Testa os conhecimentos de Geometria Descritiva Para testar os conhecimentos de Geometria Descritiva, procede da seguinte forma: responde por escrito à questão escolhida; em seguida, clica no Hiperlink
Testa os conhecimentos de Geometria Descritiva Para testar os conhecimentos de Geometria Descritiva, procede da seguinte forma: responde por escrito à questão escolhida; em seguida, clica no Hiperlink
Cotagem de dimensões básicas
 Cotagem de dimensões básicas Introdução Observe as vistas ortográficas a seguir. Com toda certeza, você já sabe interpretar as formas da peça representada neste desenho. E, você já deve ser capaz de imaginar
Cotagem de dimensões básicas Introdução Observe as vistas ortográficas a seguir. Com toda certeza, você já sabe interpretar as formas da peça representada neste desenho. E, você já deve ser capaz de imaginar
Prova Prática de Geometria Descritiva A
 EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/2004, de 26 de Março Prova Prática de Geometria Descritiva A 11.º/ 12.º anos de Escolaridade Prova 708/2.ª Fase 5 Páginas Duração da Prova: 150 minutos.
EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/2004, de 26 de Março Prova Prática de Geometria Descritiva A 11.º/ 12.º anos de Escolaridade Prova 708/2.ª Fase 5 Páginas Duração da Prova: 150 minutos.
Além do Modelo de Bohr
 Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Exercícios Adicionais
 Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Exercícios Adicionais Observação: Estes exercícios são um complemento àqueles apresentados no livro. Eles foram elaborados com o objetivo de oferecer aos alunos exercícios de cunho mais teórico. Nós recomendamos
Um jogo de preencher casas
 Um jogo de preencher casas 12 de Janeiro de 2015 Resumo Objetivos principais da aula de hoje: resolver um jogo com a ajuda de problemas de divisibilidade. Descrevemos nestas notas um jogo que estudamos
Um jogo de preencher casas 12 de Janeiro de 2015 Resumo Objetivos principais da aula de hoje: resolver um jogo com a ajuda de problemas de divisibilidade. Descrevemos nestas notas um jogo que estudamos
Corte composto. abaixo, por apresentarem seus elementos internos fora de alinhamento, precisam de outra maneira de se imaginar o corte.
 A UU L AL A Corte composto Certos tipos de peças, como as representadas abaixo, por apresentarem seus elementos internos fora de alinhamento, precisam de outra maneira de se imaginar o corte. Introdução
A UU L AL A Corte composto Certos tipos de peças, como as representadas abaixo, por apresentarem seus elementos internos fora de alinhamento, precisam de outra maneira de se imaginar o corte. Introdução
É usual dizer que as forças relacionadas pela terceira lei de Newton formam um par ação-reação.
 Terceira Lei de Newton A terceira lei de Newton afirma que a interação entre dois corpos quaisquer A e B é representada por forças mútuas: uma força que o corpo A exerce sobre o corpo B e uma força que
Terceira Lei de Newton A terceira lei de Newton afirma que a interação entre dois corpos quaisquer A e B é representada por forças mútuas: uma força que o corpo A exerce sobre o corpo B e uma força que
ESTUDO DAS PROJEÇÕES NOÇÕES ELEMENTARES 1. DEFINIÇÃO
 Estudo das projeções ESTUDO DAS PROJEÇÕES NOÇÕES ELEMENTARES 1. DEFINIÇÃO Geometria é a ciência que tem por objetivo a medida das linhas, superfícies e dos volumes. Descrever significa representar, contar
Estudo das projeções ESTUDO DAS PROJEÇÕES NOÇÕES ELEMENTARES 1. DEFINIÇÃO Geometria é a ciência que tem por objetivo a medida das linhas, superfícies e dos volumes. Descrever significa representar, contar
PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES
 PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais ordinais Utilizar corretamente os numerais ordinais até centésimo. Contar até um milhão Estender as regras
PLANIFICAÇÃO ANUAL MATEMÁTICA 3 DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais ordinais Utilizar corretamente os numerais ordinais até centésimo. Contar até um milhão Estender as regras
Escalas. Antes de representar objetos, modelos, peças, A U L A. Nossa aula. O que é escala
 Escalas Introdução Antes de representar objetos, modelos, peças, etc. deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas
Escalas Introdução Antes de representar objetos, modelos, peças, etc. deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas
Peça Corte Visualização Representação
 Cortes Prof. Cristiano Arbex 2012 Corte: Em Desenho Técnico tem o significado de secção, separação. É um procedimento imaginário que permite a visualização das partes internas de uma peça, sendo usado
Cortes Prof. Cristiano Arbex 2012 Corte: Em Desenho Técnico tem o significado de secção, separação. É um procedimento imaginário que permite a visualização das partes internas de uma peça, sendo usado
Sistemas de coordenadas e tempo. 1 Sistema de coordenadas horizontal local
 José Laurindo Sobrinho Grupo de Astronomia da Universidade da Madeira Fevereiro 2014 Sistemas de coordenadas e tempo 1 Sistema de coordenadas horizontal local O sistema de coordenadas horizontal local
José Laurindo Sobrinho Grupo de Astronomia da Universidade da Madeira Fevereiro 2014 Sistemas de coordenadas e tempo 1 Sistema de coordenadas horizontal local O sistema de coordenadas horizontal local
INTRODUÇÃO À ENGENHARIA
 INTRODUÇÃO À ENGENHARIA 2014 NOTA AULA PRÁTICA No. 04 VETORES - 20 A 26 DE MARÇO PROF. ANGELO BATTISTINI NOME RA TURMA NOTA Objetivos do experimento: Nesta aula você deverá aprender (ou recordar) a representação
INTRODUÇÃO À ENGENHARIA 2014 NOTA AULA PRÁTICA No. 04 VETORES - 20 A 26 DE MARÇO PROF. ANGELO BATTISTINI NOME RA TURMA NOTA Objetivos do experimento: Nesta aula você deverá aprender (ou recordar) a representação
4Distribuição de. freqüência
 4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
OFICINA DE JOGOS APOSTILA DO PROFESSOR
 OFICINA DE JOGOS APOSTILA DO PROFESSOR APRESENTAÇÃO Olá professor, Essa apostila apresenta jogos matemáticos que foram doados a uma escola de Blumenau como parte de uma ação do Movimento Nós Podemos Blumenau.
OFICINA DE JOGOS APOSTILA DO PROFESSOR APRESENTAÇÃO Olá professor, Essa apostila apresenta jogos matemáticos que foram doados a uma escola de Blumenau como parte de uma ação do Movimento Nós Podemos Blumenau.
INTRODUÇÃO O sistema de coordenadas ao qual estamos acostumados é o sistema de coordenadas
 Encontro de Ensino, Pesquisa e Extensão, Presidente Prudente, 22 a 25 de outubro, 2012 17 ESTUDO DAS CÔNICAS USANDO COORDENADAS POLARES Tiago Santos Arruda 1, Bruno Rogério Locatelli dos Santos, Eugenia
Encontro de Ensino, Pesquisa e Extensão, Presidente Prudente, 22 a 25 de outubro, 2012 17 ESTUDO DAS CÔNICAS USANDO COORDENADAS POLARES Tiago Santos Arruda 1, Bruno Rogério Locatelli dos Santos, Eugenia
Pesquisa Operacional. Função Linear - Introdução. Função do 1 Grau. Função Linear - Exemplos Representação no Plano Cartesiano. Prof.
 Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Basta duplicar o apótema dado e utilizar o problema 1 (pág.: 45).
 Aula 12 Exercício 1: Basta duplicar o apótema dado e utilizar o problema 1 (pág.: 45). Exercício 2: Traçar a diagonal AB, traçar a mediatriz de AB achando M (ponto médio de AB). Com centro em AB M e raio
Aula 12 Exercício 1: Basta duplicar o apótema dado e utilizar o problema 1 (pág.: 45). Exercício 2: Traçar a diagonal AB, traçar a mediatriz de AB achando M (ponto médio de AB). Com centro em AB M e raio
Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru
 Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no plano escrevendo P
Coordenadas Polares Mauri C. Nascimento Dep. De Matemática FC Unesp/Bauru Dado um ponto P do plano, utilizando coordenadas cartesianas (retangulares), descrevemos sua localização no plano escrevendo P
Agrupamento de Escolas Eugénio de Castro 1º Ciclo. Critérios de Avaliação. Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano
 Agrupamento de Escolas Eugénio de Castro 1º Ciclo Critérios de Avaliação Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais
Agrupamento de Escolas Eugénio de Castro 1º Ciclo Critérios de Avaliação Ano Letivo 2015/16 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais
EXERCÍCIO - ROMA : Modelar Capitel de uma Coluna Clássica
 FACULDADE DE ARQUITECTURA UNIVERSIDADE TÉCNICA DE LISBOA SEMESTRE VIII ANO LECTIVO 2012/2013 MODELAÇÃO GEOMÉTRICA PROFESSOR LUÍS MATEUS RAFAELA MEZEIRO 20091261 MIARQ 4ºE EXERCÍCIO - ROMA : Modelar Capitel
FACULDADE DE ARQUITECTURA UNIVERSIDADE TÉCNICA DE LISBOA SEMESTRE VIII ANO LECTIVO 2012/2013 MODELAÇÃO GEOMÉTRICA PROFESSOR LUÍS MATEUS RAFAELA MEZEIRO 20091261 MIARQ 4ºE EXERCÍCIO - ROMA : Modelar Capitel
7 AULA. Curvas Polares LIVRO. META Estudar as curvas planas em coordenadas polares (Curvas Polares).
 1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
Estudo das projeções. Projeções noções elementares.
 COLÉGIO PEDRO II U E EN II 2ª série Ensino Médio Estudo das Projeções Março/ 2011 Aluno(a): N o Turma: Disciplina: DESENHO Coordenação: Prof. Jorge Marcelo Prof.ª: Soraya Izar Apostila extra 1 Estudo das
COLÉGIO PEDRO II U E EN II 2ª série Ensino Médio Estudo das Projeções Março/ 2011 Aluno(a): N o Turma: Disciplina: DESENHO Coordenação: Prof. Jorge Marcelo Prof.ª: Soraya Izar Apostila extra 1 Estudo das
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Projeção ortográfica de modelos com elementos paralelos e oblíquos
 A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
A U L A Projeção ortográfica de modelos com elementos paralelos e oblíquos Introdução Você já sabe que peças da área da Mecânica têm formas e elementos variados. Algumas apresentam rebaixos, outras rasgos,
O Problema da Projecção. Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro
 O Problema da Projecção Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro Introdução Ao longo de séculos, artistas, engenheiros, projectistas e arquitectos tem tentado resolver as dificuldades
O Problema da Projecção Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro Introdução Ao longo de séculos, artistas, engenheiros, projectistas e arquitectos tem tentado resolver as dificuldades
APOSTILA TECNOLOGIA MECANICA
 FACULDADE DE TECNOLOGIA DE POMPEIA CURSO TECNOLOGIA EM MECANIZAÇÃO EM AGRICULTURA DE PRECISÃO APOSTILA TECNOLOGIA MECANICA Autor: Carlos Safreire Daniel Ramos Leandro Ferneta Lorival Panuto Patrícia de
FACULDADE DE TECNOLOGIA DE POMPEIA CURSO TECNOLOGIA EM MECANIZAÇÃO EM AGRICULTURA DE PRECISÃO APOSTILA TECNOLOGIA MECANICA Autor: Carlos Safreire Daniel Ramos Leandro Ferneta Lorival Panuto Patrícia de
Geometria Descritiva
 Geometria Descritiva Revisão: Interseção entre um plano projetante e um plano não projetante INTERSEÇÃO entre DOIS PLANOS NÃO PROJETANTES Interseção entre um plano projetante e um plano não projetante
Geometria Descritiva Revisão: Interseção entre um plano projetante e um plano não projetante INTERSEÇÃO entre DOIS PLANOS NÃO PROJETANTES Interseção entre um plano projetante e um plano não projetante
Mecânica Técnica. Aula 16 Equilíbrio do Corpo Rígido em Duas e Três Dimensões. Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
 Aula 16 Equilíbrio do Corpo Rígido em Duas e Três Dimensões Tópicos Abordados Nesta Aula Equilíbrio do Corpo Rígido em Duas Dimensões. Equilíbrio do Corpo Rígido em Três Dimensões. Equações de Equilíbrio
Aula 16 Equilíbrio do Corpo Rígido em Duas e Três Dimensões Tópicos Abordados Nesta Aula Equilíbrio do Corpo Rígido em Duas Dimensões. Equilíbrio do Corpo Rígido em Três Dimensões. Equações de Equilíbrio
Cap. 7 - Fontes de Campo Magnético
 Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Profa. Dra. Diana Andrade & Prof. Dr. Sergio Pilling Parte 1 - Movimento Retilíneo Coordenada de posição, trajetória,
Dinâmica de um Sistema de Partículas Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Profa. Dra. Diana Andrade & Prof. Dr. Sergio Pilling Parte 1 - Movimento Retilíneo Coordenada de posição, trajetória,
ENERGIA CINÉTICA E TRABALHO
 ENERGIA CINÉTICA E TRABALHO O que é energia? O termo energia é tão amplo que é diícil pensar numa deinição concisa. Teoricamente, a energia é uma grandeza escalar associada ao estado de um ou mais objetos;
ENERGIA CINÉTICA E TRABALHO O que é energia? O termo energia é tão amplo que é diícil pensar numa deinição concisa. Teoricamente, a energia é uma grandeza escalar associada ao estado de um ou mais objetos;
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Introdução À Astronomia e Astrofísica 2010
 CAPÍTULO 1 ESFERA CELESTE E O SISTEMA DE COORDENADAS Esfera Celeste. Sistema de Coordenadas. Coordenadas Astronómicas. Sistema Horizontal. Sistema Equatorial Celeste. Sistema Equatorial Horário. Tempo
CAPÍTULO 1 ESFERA CELESTE E O SISTEMA DE COORDENADAS Esfera Celeste. Sistema de Coordenadas. Coordenadas Astronómicas. Sistema Horizontal. Sistema Equatorial Celeste. Sistema Equatorial Horário. Tempo
CINEMÁTICA VETORIAL. Observe a trajetória a seguir com origem O.Pode-se considerar P a posição de certo ponto material, em um instante t.
 CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
4. Tangentes e normais; orientabilidade
 4. TANGENTES E NORMAIS; ORIENTABILIDADE 91 4. Tangentes e normais; orientabilidade Uma maneira natural de estudar uma superfície S consiste em considerar curvas γ cujas imagens estão contidas em S. Se
4. TANGENTES E NORMAIS; ORIENTABILIDADE 91 4. Tangentes e normais; orientabilidade Uma maneira natural de estudar uma superfície S consiste em considerar curvas γ cujas imagens estão contidas em S. Se
Retas e Planos. Equação Paramétrica da Reta no Espaço
 Retas e lanos Equações de Retas Equação aramétrica da Reta no Espaço Considere o espaço ambiente como o espaço tridimensional Um vetor v = (a, b, c) determina uma direção no espaço Dado um ponto 0 = (x
Retas e lanos Equações de Retas Equação aramétrica da Reta no Espaço Considere o espaço ambiente como o espaço tridimensional Um vetor v = (a, b, c) determina uma direção no espaço Dado um ponto 0 = (x
MECÂNICA GERAL PARA ENGENHEIROS
 MEÂNI GER R ENGENHEIRS apítulo rofª: cilayne Freitas de quino Forças no lano sobre um orpo Rígido R RGID Em mecânica elementar assumimos que a maior parte dos corpos são rígidos, isto é, as deformações
MEÂNI GER R ENGENHEIRS apítulo rofª: cilayne Freitas de quino Forças no lano sobre um orpo Rígido R RGID Em mecânica elementar assumimos que a maior parte dos corpos são rígidos, isto é, as deformações
Apostila Complementar
 Desenho Técnico Apostila Complementar O curso de Desenho técnico mecânico é baseado nas apostilas de Leitura e Interpretação do Desenho Técnico Mecânico do Telecurso 2000 Profissionalizante de Mecânica.
Desenho Técnico Apostila Complementar O curso de Desenho técnico mecânico é baseado nas apostilas de Leitura e Interpretação do Desenho Técnico Mecânico do Telecurso 2000 Profissionalizante de Mecânica.
Projeção ortográfica da figura plana
 A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
MATEMÁTICA GEOMETRIA ANALÍTICA I PROF. Diomedes. E2) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B.
 I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
I- CONCEITOS INICIAIS - Distância entre dois pontos na reta E) Sabendo que a distância entre os pontos A e B é igual a 6, calcule a abscissa m do ponto B. d(a,b) = b a E: Dados os pontos A e B de coordenadas
A Torre de Hanói e o Princípio da Indução Matemática
 A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
A Torre de Hanói e o Princípio da Indução Matemática I. O jogo A Torre de Hanói consiste de uma base com três pinos e um certo número n de discos de diâmetros diferentes, colocados um sobre o outro em
4 Mudança de Coordenadas
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Última atualização: 14 de outubro de 006 4 Mudança de Coordenadas Translação e Rotação de Curvas no R² Introdução O enfoque dos 3 primeiros capítulos
Material by: Caio Guimarães (Equipe Rumoaoita.com) Última atualização: 14 de outubro de 006 4 Mudança de Coordenadas Translação e Rotação de Curvas no R² Introdução O enfoque dos 3 primeiros capítulos
Atividade de Recuperação- Física
 Atividade de Recuperação- Física 3º Ano- 1º Trimestre Prof. Sérgio Faro Orientação: Refazer os exemplos seguintes e resolver os demais exercícios no caderno e anotar eventuais dúvidas para esclarecimento
Atividade de Recuperação- Física 3º Ano- 1º Trimestre Prof. Sérgio Faro Orientação: Refazer os exemplos seguintes e resolver os demais exercícios no caderno e anotar eventuais dúvidas para esclarecimento
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE. Prof. Dr. Daniel Caetano 2012-1
 ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
ARQUITETURA E ORGANIZAÇÃO DE COMPUTADORES SISTEMAS DE NUMERAÇÃO: REPRESENTAÇÃO EM PONTO FLUTUANTE Prof. Dr. Daniel Caetano 2012-1 Objetivos Compreender o que é notação em ponto flutuante Compreender a
INSTRUMENTOS USADOS Lápis e lapiseiras Os lápis médios são os recomendados para uso em desenho técnico, a seleção depende sobretudo de cada usuário.
 INSTRUMENTOS USADOS Lápis e lapiseiras Os lápis médios são os recomendados para uso em desenho técnico, a seleção depende sobretudo de cada usuário. INSTRUMENTOS USADOS Esquadros São usados em pares: um
INSTRUMENTOS USADOS Lápis e lapiseiras Os lápis médios são os recomendados para uso em desenho técnico, a seleção depende sobretudo de cada usuário. INSTRUMENTOS USADOS Esquadros São usados em pares: um
GAAL - 2013/1 - Simulado - 1 Vetores e Produto Escalar
 GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
Usando o do-file editor Automatizando o Stata
 Usando o do-file editor Automatizando o Stata 1 O QUE É O EDITOR DE DO-FILE O Stata vem com um editor de texto integrado, o do-file editor (editor de do-files, em português), que pode ser usado para executar
Usando o do-file editor Automatizando o Stata 1 O QUE É O EDITOR DE DO-FILE O Stata vem com um editor de texto integrado, o do-file editor (editor de do-files, em português), que pode ser usado para executar
Medição tridimensional
 A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
UMC Cotas em desenho técnico (Módulo 2) Componentes gráficos de uma cota: Linha de cota Linha de chamada Setas de cota
 1 UMC Engenharia Mecânica Expressão Gráfica 2 Prof.: Jorge Luis Bazan. Desenho Básico Cotas em desenho técnico (Módulo 2) Em desenho técnico damos o nome de cota ao conjunto de elementos gráficos introduzidos
1 UMC Engenharia Mecânica Expressão Gráfica 2 Prof.: Jorge Luis Bazan. Desenho Básico Cotas em desenho técnico (Módulo 2) Em desenho técnico damos o nome de cota ao conjunto de elementos gráficos introduzidos
Vimos que, conforme as operações que fazem, as máquinas retificadoras podem ser classificadas em planas, cilíndricas universais e center less.
 Retificação plana Vimos que, conforme as operações que fazem, as máquinas retificadoras podem ser classificadas em planas, cilíndricas universais e center less. As retificadoras planas retificam peças
Retificação plana Vimos que, conforme as operações que fazem, as máquinas retificadoras podem ser classificadas em planas, cilíndricas universais e center less. As retificadoras planas retificam peças
GNUPLOT Uma breve introdução
 GNUPLOT Uma breve introdução O GNUPLOT é um programa para traçado de gráficos bi e tridimensionais distribuído livremente na Internet. Ele está disponível para plataformas Linux, Windows e outras do mundo
GNUPLOT Uma breve introdução O GNUPLOT é um programa para traçado de gráficos bi e tridimensionais distribuído livremente na Internet. Ele está disponível para plataformas Linux, Windows e outras do mundo
Aula 17 GRANDEZAS ESCALARES E VETORIAIS. META Apresentar as grandezas vetoriais e seu signifi cado
 GRANDEZAS ESCALARES E VETORIAIS META Apresentar as grandezas vetoriais e seu signifi cado OBJETIVOS Ao fi nal desta aula, o aluno deverá: Diferenciar grandezas escalares e vetoriais; compreender a notação
GRANDEZAS ESCALARES E VETORIAIS META Apresentar as grandezas vetoriais e seu signifi cado OBJETIVOS Ao fi nal desta aula, o aluno deverá: Diferenciar grandezas escalares e vetoriais; compreender a notação
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Desenho de máquinas. Aula 3
 Desenho de máquinas Aula 3 Cotagem A cotagem e a escolhas das vistas que irão compor um desenho, são os dois itens que mais exigem conhecimentos e experiência do engenheiro mecânico na área do Desenho
Desenho de máquinas Aula 3 Cotagem A cotagem e a escolhas das vistas que irão compor um desenho, são os dois itens que mais exigem conhecimentos e experiência do engenheiro mecânico na área do Desenho
Módulo 1: Contextualização
 Módulo 1: Contextualização Este trabalho, tem o objetivo de auxiliar os alunos das disciplinas de Introdução a Programação de Computadores, para cursos de Engenharia e de Automação, em seus estudos e no
Módulo 1: Contextualização Este trabalho, tem o objetivo de auxiliar os alunos das disciplinas de Introdução a Programação de Computadores, para cursos de Engenharia e de Automação, em seus estudos e no
O coeficiente angular
 A UA UL LA O coeficiente angular Introdução O coeficiente angular de uma reta já apareceu na Aula 30. Agora, com os conhecimentos obtidos nas Aulas 40 e 45, vamos explorar mais esse conceito e descobrir
A UA UL LA O coeficiente angular Introdução O coeficiente angular de uma reta já apareceu na Aula 30. Agora, com os conhecimentos obtidos nas Aulas 40 e 45, vamos explorar mais esse conceito e descobrir
(a) a aceleração do sistema. (b) as tensões T 1 e T 2 nos fios ligados a m 1 e m 2. Dado: momento de inércia da polia I = MR / 2
 F128-Lista 11 1) Como parte de uma inspeção de manutenção, a turbina de um motor a jato é posta a girar de acordo com o gráfico mostrado na Fig. 15. Quantas revoluções esta turbina realizou durante o teste?
F128-Lista 11 1) Como parte de uma inspeção de manutenção, a turbina de um motor a jato é posta a girar de acordo com o gráfico mostrado na Fig. 15. Quantas revoluções esta turbina realizou durante o teste?
Como erguer um piano sem fazer força
 A U A UL LA Como erguer um piano sem fazer força Como vimos na aula sobre as leis de Newton, podemos olhar o movimento das coisas sob o ponto de vista da Dinâmica, ou melhor, olhando os motivos que levam
A U A UL LA Como erguer um piano sem fazer força Como vimos na aula sobre as leis de Newton, podemos olhar o movimento das coisas sob o ponto de vista da Dinâmica, ou melhor, olhando os motivos que levam
Dupla Projeção Ortogonal / Método de Monge
 Provas Especialmente Adequadas Destinadas a Avaliar a Capacidade Para a Frequência do Ensino Superior dos Maiores de 23 Anos 2015 Prova de Desenho e Geometria Descritiva - Módulo de Geometria Descritiva
Provas Especialmente Adequadas Destinadas a Avaliar a Capacidade Para a Frequência do Ensino Superior dos Maiores de 23 Anos 2015 Prova de Desenho e Geometria Descritiva - Módulo de Geometria Descritiva
Manual de operação TRUCK LASER EDIÇÃO 2004 MOP 0504
 Manual de operação TRUCK LASER EDIÇÃO 2004 MOP 0504 INTRODUÇÃO O aparelho TRUCK LASER, permite a aferição dos ângulos característicos de todas as rodas e/ou eixos de caminhões, ônibus e camionetes. CONSIDERAÇÕES
Manual de operação TRUCK LASER EDIÇÃO 2004 MOP 0504 INTRODUÇÃO O aparelho TRUCK LASER, permite a aferição dos ângulos característicos de todas as rodas e/ou eixos de caminhões, ônibus e camionetes. CONSIDERAÇÕES
V = 0,30. 0,20. 0,50 (m 3 ) = 0,030m 3. b) A pressão exercida pelo bloco sobre a superfície da mesa é dada por: P 75. 10 p = = (N/m 2 ) A 0,20.
 11 FÍSICA Um bloco de granito com formato de um paralelepípedo retângulo, com altura de 30 cm e base de 20 cm de largura por 50 cm de comprimento, encontra-se em repouso sobre uma superfície plana horizontal.
11 FÍSICA Um bloco de granito com formato de um paralelepípedo retângulo, com altura de 30 cm e base de 20 cm de largura por 50 cm de comprimento, encontra-se em repouso sobre uma superfície plana horizontal.
Realizando cálculos para o aparelho divisor (I)
 Realizando cálculos para o aparelho divisor (I) A UU L AL A Você já estudou como fazer os cálculos para encontrar as principais medidas para a confecção de uma engrenagem cilíndrica de dentes retos. Vamos
Realizando cálculos para o aparelho divisor (I) A UU L AL A Você já estudou como fazer os cálculos para encontrar as principais medidas para a confecção de uma engrenagem cilíndrica de dentes retos. Vamos
Prog A B C A e B A e C B e C A,B e C Nenhum Pref 100 150 200 20 30 40 10 130
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
sendo as componentes dadas em unidades arbitrárias. Determine: a) o vetor vetores, b) o produto escalar e c) o produto vetorial.
 INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
Empurra e puxa. Domingo, Gaspar reúne a família para uma. A força é um vetor
 A U A UL LA Empurra e puxa Domingo, Gaspar reúne a família para uma voltinha de carro. Ele senta ao volante e dá a partida. Nada. Tenta outra vez e nada consegue. Diz então para todos: O carro não quer
A U A UL LA Empurra e puxa Domingo, Gaspar reúne a família para uma voltinha de carro. Ele senta ao volante e dá a partida. Nada. Tenta outra vez e nada consegue. Diz então para todos: O carro não quer
Avaliação 1 - MA12-2015.1 - Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL Avaliação 1 - MA1-015.1 - Gabarito Questão 01 [,00 pts ] Uma escola pretende formar uma comissão de 6 pessoas para organizar uma festa junina. Sabe-se
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL Avaliação 1 - MA1-015.1 - Gabarito Questão 01 [,00 pts ] Uma escola pretende formar uma comissão de 6 pessoas para organizar uma festa junina. Sabe-se
Experimento. Guia do professor. Otimização da cerca. Secretaria de Educação a Distância. Ministério da Ciência e Tecnologia. Ministério da Educação
 Números e funções Guia do professor Experimento Otimização da cerca Objetivos da unidade 1. Resolver um problema de otimização através do estudo de uma função quadrática. 2. Estudar as propriedades de
Números e funções Guia do professor Experimento Otimização da cerca Objetivos da unidade 1. Resolver um problema de otimização através do estudo de uma função quadrática. 2. Estudar as propriedades de
Comunicações. Microfone e Altifalante - Resumindo
 Comunicações { Microfone e Altifalante - Resumindo Microfone Finalidades Altifalante { Instalam-se nos circuitos elétricos para: Microfone transforma vibração mecânica em corrente elétrica alternada de
Comunicações { Microfone e Altifalante - Resumindo Microfone Finalidades Altifalante { Instalam-se nos circuitos elétricos para: Microfone transforma vibração mecânica em corrente elétrica alternada de
C5. Formação e evolução estelar
 AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
AST434: C5-1/68 AST434: Planetas e Estrelas C5. Formação e evolução estelar Mário João P. F. G. Monteiro Mestrado em Desenvolvimento Curricular pela Astronomia Mestrado em Física e Química em Contexto
Tabelas vista de estrutura
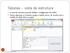 Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Considerando o seguinte eixo de referência:
 FORÇA É uma interacção que se estabelece entre dois corpos capaz de alterar o seu estado de movimento ou de repouso ou de lhes causar deformação. Podem ser interacções à distância ou interacções de contacto.
FORÇA É uma interacção que se estabelece entre dois corpos capaz de alterar o seu estado de movimento ou de repouso ou de lhes causar deformação. Podem ser interacções à distância ou interacções de contacto.
UNESP DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD. Parte 3/5: Prof. Víctor O. Gamarra Rosado
 UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 3/5: 8. Projeções ortogonais 9. Terceira Vista 10. Tipos
UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 3/5: 8. Projeções ortogonais 9. Terceira Vista 10. Tipos
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
Canguru sem fronteiras 2007
 Duração: 1h15mn Destinatários: alunos do 12 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada
Duração: 1h15mn Destinatários: alunos do 12 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Projeção Perspectiva. Desenho Técnico I Profº Msc. Edgar Nogueira Demarqui
 Projeção Perspectiva Desenho Técnico I Profº Msc. Edgar Nogueira Demarqui Definição Quando olhamos para um objeto, temos a sensação de profundidade e relevo; O desenho, para transmitir essa mesma idéia,
Projeção Perspectiva Desenho Técnico I Profº Msc. Edgar Nogueira Demarqui Definição Quando olhamos para um objeto, temos a sensação de profundidade e relevo; O desenho, para transmitir essa mesma idéia,
Objetivos. Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas e
 MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
GDC I AULA TEÓRICA 09
 GDC I AULA TEÓRICA 09 Perspectiva linear de quadro plano: - O perspectógrafo completo (Plano Geometral e a Linha de Terra). - A marcação de pontos por coordenadas. - Determinação dos traços de planos e
GDC I AULA TEÓRICA 09 Perspectiva linear de quadro plano: - O perspectógrafo completo (Plano Geometral e a Linha de Terra). - A marcação de pontos por coordenadas. - Determinação dos traços de planos e
N1Q1 Solução. a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas.
 1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIAS
 MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada.
 Aplicações da lei de Gauss A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada. De maneira genérica, a lei de Gauss diz que: Fluxo elétrico sobre
Aplicações da lei de Gauss A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada. De maneira genérica, a lei de Gauss diz que: Fluxo elétrico sobre
Manual de Montagem REVISÃO 312.20. www.robouno.com.br
 Manual de Montagem REVISÃO 312.20 Manual de Montagem 01 Suporte Roda Caster 01 Roda Caster Parafusos 3x8mm Porcas 11 03 2 Observe a posição dos furos 01 Chassi Lateral 01 Motor Parafusos 3x8mm Porcas 12
Manual de Montagem REVISÃO 312.20 Manual de Montagem 01 Suporte Roda Caster 01 Roda Caster Parafusos 3x8mm Porcas 11 03 2 Observe a posição dos furos 01 Chassi Lateral 01 Motor Parafusos 3x8mm Porcas 12
Circuitos eléctricos
 Um circuito eléctrico µu^u]vz}_ }Œ}v passa a corrente eléctrica. É constituído obrigatoriamente por um gerador e um receptor, podendo-se também intercalar outros componentes como interruptores, motores
Um circuito eléctrico µu^u]vz}_ }Œ}v passa a corrente eléctrica. É constituído obrigatoriamente por um gerador e um receptor, podendo-se também intercalar outros componentes como interruptores, motores
Calculando distâncias sem medir
 alculando distâncias sem medir UUL L No campo ocorrem freqüentemente problemas com medidas que não podemos resolver diretamente com ajuda da trena. Por exemplo: em uma fazenda, como podemos calcular a
alculando distâncias sem medir UUL L No campo ocorrem freqüentemente problemas com medidas que não podemos resolver diretamente com ajuda da trena. Por exemplo: em uma fazenda, como podemos calcular a
Planeamento e Seguimento de Projectos
 Planeamento e Seguimento de Projectos Introdução Uma empresa sem objectivos a atingir é uma empresa desorientada, mas ter objectivos a atingir sem qualquer plano não deixa de ser apenas uma esperança.
Planeamento e Seguimento de Projectos Introdução Uma empresa sem objectivos a atingir é uma empresa desorientada, mas ter objectivos a atingir sem qualquer plano não deixa de ser apenas uma esperança.
