Solução quântica para o poço duplo quadrado unidimensional assimétrico
|
|
|
- Ricardo Gorjão Beltrão
- 5 Há anos
- Visualizações:
Transcrição
1 Revista Brasileira de Ensino de Física, v. 3, n. 4, 4306 (010) Solução quântica para o poço duplo quadrado unidimensional assimétrico (Solution for quantum well double asymmetric square unidimensional) K.H. Paulino 1, E. Drigo Filho 1, A.R. Pulici e R.M. Ricotta 3 1 Departamento de Física, Instituto de Biociências, Letras e Ciências Exatas, Universidade Estadual Paulista, São José do Rio Preto, SP, Brasil Centro Universitário de Votuporanga, Votuporanga, SP, Brasil 3 Faculdade de Tecnologia, São Paulo, SP, Brasil Recebido em 7/7/009; Aceito em 1/01/010; Publicado em 8//011 Poços de potenciais quadrados têm sido bastante explorados, tanto do ponto de vista de aplicação como introdução didática à mecânica quântica. Existem bem poucos potenciais desse tipo que são tratados analiticamente na literatura, embora várias geometrias envolvendo esses poços de potenciais possam ser construídas. Nesse trabalho estudamos o poço duplo quadrado unidimensional assimétrico que possui potencial para uma variedade de aplicações, por exemplo, o aprisionamento atômico devido à diferença de profundidades entre poços vizinhos. As funções de onda e autovalores de energia são determinados explicitamente para um caso ressonante e outro não ressonante. Palavras-chave: poço duplo quadrado unidimensional assimétrico, equação de Schrödinger, autovalores de energia. Square potential wells have been extensively explored, both in terms of application and teaching introduction to quantum mechanics. There are very few such potential who are treated analytically in the literature, although various geometries involving these potential wells study the Double Square Well Asymmetric Unidimensional that has potential for a variety of applications, for example, the atomic trapping due to the difference in depths between neighboring wells. The wave functions and energy eigenvalues are determined explicitly for a resonant case and others not resonant. Keywords: double square well asymmetric unidimensional, Schrödinger equation, energy eigenvalues. 1. Introdução Os poços de potenciais podem ser construídos de várias formas (vide, por exemplo, Refs. 1-10). Devido às suas aplicações 11-13, esses potenciais são bastante estudados em mecânica quântica podendo simular sistemas físicos, químicos e biológicos. A simplicidade matemática desses sistemas permite, em muitos casos, um tratamento formal completo da equação de Schrödinger. Esse tratamento envolve a determinação dos autovalores, em termos de uma fórmula fechada ou através de uma equação transcendental, e das autofunções, escritas em termos de funções elementares. 1 karepaulino@hotmail.com. O poço quadrado mais simples de ser estudado é o poço quadrado infinito, no qual todos os estados estão ligados. Outro tipo de poço, o poço quadrado finito, pode servir como um modelo simples de um elétron confinado em uma placa metálica se deslocando perpendicularmente à superfície. Neste caso o elétron pode se mover livremente no interior do metal, mas terá de escalar uma barreira de potencial para escapar da superfície 1. A equação de Schrödinger para estes poços é facilmente resolvida e suas soluções podem ser encontradas em livros básicos de mecânica quântica 1-6 fazendo parte do conteúdo programático dos cursos iniciais dessa disciplina. As aplicações dos poços de potenciais são diversas, abrangendo vários ramos da física. Classicamente, o enovelamento de proteínas pode ser estudado considerando a difusão unidimensional em um potencial composto de vários poços quadrados, sendo que as barreiras de potencial representam as espécies intermediárias do enovelamento 11. Poços quadrados biestáveis infinitos com assimetria na largura dos poços têm sido explorados na literatura para discutir níveis de energia com curvatura zero 1 e para comparar Copyright by the Sociedade Brasileira de Física. Printed in Brazil.
2 4306- Paulino et al. distribuições de probabilidades clássica e quântica 13. Um aspecto importante a ser destacado é que os poços quadrados, principalmente aqueles envolvendo dois mínimos (biestáveis), permitem cálculos exatos de tempo de tunelamento. O tunelamento é um fenômeno quântico bastante importante que está em conexão com barreiras de energia potencial 7. Ele é usado para explicar o movimento de prótons em ligações de hidrogênio 7, a inversão intramolecular da amônia 7 e a transferência de elétrons em proteínas 8. Poços de potenciais quadráticos biestáveis podem ser classificados como simétricos 9 ou assimétricos. Poços duplos simétricos são aqueles em que os dois poços têm mesma largura, profundidade e barreiras. Nos poços assimétricos, pelo menos um desses parâmetros é diferente. Os casos em que estamos interessados são aqueles em que apenas as profundidades dos dois poços, que formam o poço duplo assimétrico, são diferentes. Esse tipo de poço duplo quadrado assimétrico unidimensional possibilita o aprisionamento de uma partícula, devido à diferença de profundidade dos dois poços. Observando que os resultados encontrados na literatura não contemplam a solução de um poço duplo quadrado e assimétrico com relação à profundidade dos poços, o objetivo deste trabalho é utilizar a equação de Schrödinger independente do tempo para estudar um poço duplo quadrado unidimensional assimétrico, determinando as autofunções e os autovalores. A análise do sistema sugerido permite aprofundar a discussão sobre sistemas quânticos tanto no aspecto formal, uma vez que é possível obter soluções exatas, quanto conceitual, permitindo a introdução do tunelamento quântico, por exemplo. Nesse tipo de problema duas situações distintas podem ocorrer. Em primeiro lugar, considerando os poços individuais, é possível que dois níveis de energia coincidam, esse caso é chamado de ressonante. Por outro lado, os níveis dos poços individuais podem não coincidir, o que leva ao caso não ressonante. Essa distinção é muito útil em estudos de tunelamento 10, sendo que quando os estados são ressonantes a probabilidade de tunelamento é muito maior que aquelas dos casos onde não há ressonância (vide, por exemplo, Ref. 7 para discussão sobre o assunto). Esse trabalho está dividido em seções, sendo que na seção é indicada a solução analítica para o poço duplo quadrado unidimensional simétrico. Essa solução é usada como teste posterior para as soluções do problema assimétrico. Os cálculos envolvidos nessa seção não são apresentados em detalhes uma vez que eles podem ser obtidos na referência 9, por exemplo. Na seção 3 é determinada a solução para o poço assimétrico. Na seção 4, é indicado como obter a solução do problema simétrico partindo da solução encontrada do poço assimétrico. Isso é obtido fazendo a profundidade dos poços convergirem para um mesmo valor. Como exemplo, soluções numéricas, obtidas fixando os parâmetros do potencial, são determinadas na seção 5. Por fim, na seção 6 são colocadas as conclusões do trabalho.. Poço duplo quadrado unidimensional simétrico Um poço duplo quadrado pode ser considerado como a soma de dois poços simples com barreira infinita em um lado e no outro um potencial finito (V 0 ), unidos por este potencial, ficando as barreiras infinitas nos extremos. Caso os poços simples possuam as mesmas alturas e larguras o resultado da junção dos dois consiste em um poço simétrico conforme mostrado na Fig. 1. Nessa figura observamos que a é a largura do cada poço e L a distância entre o centro de cada poço ao outro. O poço duplo quadrado unidimensional simétrico Vs (x) possui cinco diferentes regiões como indicado na Fig. 1. A região III consiste numa barreira de potencial V 0 que separa os poços mais profundos das regiões II e IV, onde o potencial é considerado nulo. Nas regiões I e V, o potencial é infinito. A expressão para o potencial V S pode ser escrita da seguinte forma V s (x) = x < (L a) V s (x) = 0 < x < (L a) (L a) V s (x) = V 0 < x < (L a) V s (x) = 0 < x < V s (x) = x > (I) (II) (III) (IV) (V) (1) Figura 1 - Representação do poço duplo quadrado unidimensional simétrico. Os autovalores de energia para esse caso simétrico são obtidos resolvendo as equações transcendentais que surgem da resolução da equação de Schrödinger independente do tempo aplicando a continuidade da função de onda e da sua derivada em todas as regiões. Dois casos típicos devem ser analisados, a saber: (i) a energia do sistema menor que V 0 e (ii) maior que V 0. Esses resultados são obtidos na Ref. 9 e são apenas indicados aqui para comparação com o caso assimétrico.
3 Solução quântica para o poço duplo quadrado unidimensional assimétrico As equações transcendentais para a energia total menor que a barreira de potencial são tan(ka) = 1 k β tan(ka) = 1 k β tanh β(l a) coth β(l a) () (3) em que k e β são parâmetros relacionados com a energia: k = me e β = m(v0 E). Quando se está interessado em estudar o caso em que a energia total é maior que a barreira de potencial V 0, então as equações transcendentais são ( ) L a k cot ka = β cot β (4) β (L a) β tan = k cot(ka) (5) 3. Poço duplo quadrado unidimensional assimétrico O poço duplo quadrado unidimensional assimétrico pode ser considerado como a junção de dois poços simples com profundidades distintas V 0 e V 1 (V 1 > V 0 ) como indicado na Fig.. Nesta figura existem cinco regiões indicadas, onde a barreira de potencial V 0 está situada à esquerda da região III e a outra de potencial V 1 localizada à direita. Esta região separa os poços da região II e IV. O potencial na região II é V 1 V 0 e na região IV é nulo. Nas regiões I e V o potencial é infinito. sendo que k = me e β = m(e V 0). Resolvendo as equações transcendentais obtidas acima, numérica ou graficamente, é possível obter os autovalores de energia uma vez que a dependência de k e β com a energia é conhecida. Figura - Representação do V as (x) no poço duplo quadrado unidimensional assimétrico. O potencial assimétrico, V as (x), como descrito acima e indicado na Fig., pode ser escrito por V as (x) = x > (I e V) (L a) V as (x) = (V 1 V 0 ) < x < (II) (L a) (L a) V as (x) = V 1 < x < (III) (L a) V as (x) = 0 < x < (IV) Uma vez que a função de onda é zero nas regiões I e V, a equação de Schrödinger independente do tempo é aplicada nas regiões II, III e IV Região II: Região III: Região IV: d m dx Ψ (x) + V 1Ψ (x) V 0 Ψ (x) = EΨ (x), (7) d m dx Ψ (x) + V 1Ψ (x) = EΨ (x), (8) d Ψ (x) = EΨ (x), (9) m dx O processo para obtenção das soluções da equação de Schrödinger para esse potencial é semelhante ao realizado para o poço simétrico (seção ). Assim, os mesmos passos para a obtenção da solução devem ser seguidos. Entretanto, algumas diferenças devem ser ressaltadas, a principal delas é que podemos identificar, dependendo da energia da partícula, três casos distintos para o poço assimétrico. O primeiro ocorre quando a energia é menor que V 1 V 0 0 < E < V 1 V 0, nesse caso há apenas possibilidade de ocorrer níveis de energia no poço mais profundo. O segundo caso ocorre quando o valor da energia total está entre os valores da altura das barreiras (V 1 V 0 ) < E < V 1, nessa situação é possível que a função de onda se distribua nos dois poços. Por fim, quando a energia é maior que V 1 E > V 1 os níveis de energia estarão acima da barreira de potencial interna Energia do sistema abaixo de (V 1 - V 0 ) O primeiro caso estudado refere-se a E < (V 1 V 0 ), no qual o nível de energia está localizado somente no poço de maior profundidade. Nessa situação, a solução da equação de Schrödinger independente do tempo para as cinco regiões do poço duplo quadrado unidimensional assimétrico é dada por (6)
4 Paulino et al. Regiões I e V: Ψ (x) = 0, (10) Região II: Ψ (x) = A 1 e k1x + A e k 1x (11) Região III: Ψ (x) = Be βx + Ce βx (1) Região IV: Ψ (x) = D 1 sen(k x) + D cos(k x), (13) com A 1, A, B, C, D 1, D constantes a serem determinadas pela continuidade da função de onda e sua derivada, além da condição de normalização. Os parâmetros k 1, k e β foram introduzidos para simplificar a notação, para esse caso eles valem k 1 = m (V 1 V 0 ) E, β = m (V 1 E), (14) k = me. Nas regiões I e V a função de onda é nula devido ao potencial ser infinito. Isso significa que, nas fronteiras externas dos poços, Ψ (x) satisfaz: Ψ (L+a) = Ψ = 0. Aplicando esta condição na região II, (L+a) Eq. (11), obtemos a seguinte relação A 1 = A e k 1(L+a) (15) Para satisfazer as condições de contorno na barreira infinita na região IV, Eq. (13), em que a função de onda é zero, foi feita uma aproximação em que o poço é deslocado e a solução da região IV é reduzida da forma Ψ (x) = D 1 senk x. (16) Outra condição a ser usada é a continuidade das funções de onda e suas derivadas nos pontos x = ± (L a). Isso implica para x = (L a) nas Eqs. (11) e (1) que A 1 e k 1 (L a) + A e k 1 (L a) = Be β(l a) + Ce β(l a), (17) A 1 k 1 e k 1 (L a) A k 1 e k 1 (L a) = Bβe β(l a) Cβe β(l a), (18) e para x = (L a) nas Eqs. (1) e (13) que D 1 sen(k a) = Be β(l a) + Ce β(l a), (19) D 1 k cos (k a) = Bβe β(l a) Cβe β(l a). (0) As Eqs. (17) e (19) correspondem à continuidade da função de onda nos pontos indicados e as Eqs. (18) e (0) correspondem à continuidade das derivadas das funções de onda. Para obter uma relação entre essas equações, o primeiro passo é substituir a Eq. (15) na Eq. (17) encontrando uma expressão de A em função das constantes B e C como na equação a seguir Be β(l a) + Ce β(l a) A = ( e k 1(L+a) e k 1 (L a) + k 1 (L a) e ). (1) Outra expressão para A em função das mesmas constantes pode ser encontrada substituindo a Eq. (15) na Eq. (18). β(be β(l a) Ce β(l a) ) A = k 1 (e k 1(L+a) e k 1 (L a) + k 1 (L a) e ). () Igualando a Eq. (1) e a Eq. () é possível obter a seguinte relação B C = (k1 β)e k1(l a) + (k 1 + β)e k1(l+a) e β(l a) ( k1 + β)e k1(l+a) (k 1 + β)e k1(l a). (3) Por outro lado, isolando D 1 da Eq. (19) e substituindo na Eq. (0) chega-se a B C = (β k β(l a) cot(k a)) e. (4) (β + k cot(k a)) e β(l a) Para obter a equação transcendental para o caso em que 0 < E < V 1 V 0 basta igualar a Eq. (3) com a Eq. (4), resultando em (k1 β)e k 1(L a) + (k 1 + β)e k 1(L+a) e β(l a) ( k1 + β)e k 1(L+a) (k 1 + β)e k 1(L a) = β k cot(k a) e β(l a). (5) β + k cot(k a) Com a equação transcendental (5) é possível obter os autovalores de energia contidos em k 1, k e β graficamente, através da intersecção das curvas que representam, uma o lado direito da equação e outra o lado esquerdo, em função da energia.
5 Solução quântica para o poço duplo quadrado unidimensional assimétrico Energia do sistema entre os dois mínimos de potencial Considerando o segundo caso V 1 V 0 < E < V 1, a solução da equação de Schrödinger em cada região é dada por Regiões I e V: Ψ (x) = 0, (6) Região II: Ψ (x) = A 1 sen(k 1 x) + A cos(k 1 x), (7) Região III: Ψ (x) = Be βx + Ce βx, (8) Região IV: Ψ (x) = D 1 sen(k x) + D cos(k x), (9) sendo que A 1, A, B, C, D 1, D são constantes obtidas pela continuidade da função de onda e sua derivada e pela condição de normalização e os números de onda das diferentes regiões são dados por k 1 = m E (V 1 V 0 ), β = m (V 1 E), (30) k = me. Lembrando que nas regiões I e V a função de onda é nula, resultando na condição Ψ (L+a) = Ψ (L+a) = 0. Aplicando esta condição nas soluções da região II e da região IV obtemos as funções de onda, respectivamente Ψ (x) = A 1 senk 1 x +, (31) Ψ (x) = D 1 senk x. (3) Outra condição a ser usada é a continuidade das funções de onda e suas derivadas nos pontos x = ± (L a). Isso implica para x = (L a) que A 1 sen(k 1 a) = Be β(l a) + Ce β(l a), (33) A 1 k 1 cos(k 1 a) = Bβe β(l a) Cβe β(l a), (34) e para x = (L a) que D 1 sen(k a) = Be β(l a) + Ce β(l a), (35) D 1 k cos (k a) = Bβe β(l a) Cβe β(l a). (36) As Eqs. (33) e (35) correspondem à continuidade da função de onda nos pontos indicados e as Eqs. (34) e (36) correspondem à continuidade das derivadas dessas funções de onda. Para obter uma relação entre essas equações, é possível isolar A 1 da Eq. (33) e substituir na Eq. (34) obtendo B C = (β + k β(l a) 1 cot (k 1 a)) e. (37) (β k 1 cot (k 1 a)) e β(l a) Por outro lado, isolando D 1 da Eq. (35) e substituindo na Eq. (36) chega-se a B C = (β k β(l a) cot(k a)) e. (38) (β + k cot(k a)) e β(l a) Finalmente, para obter a equação transcendental para o caso em que (V 1 V 0 ) < E < V 1 basta igualar a Eq. (37) e a Eq. (38), resultando em β + k 1 cot(k 1 a) e β(l a) β k 1 cot(k 1 a) β k cot(k a) e β(l a). (39) β + k cot(k a) = 3.3. Energia acima da barreira de potencial central O terceiro caso para o poço duplo assimétrico é quando a energia é maior que a barreira de potencial V 1 (E > V 1 ). A solução da equação de Schrödinger independente do tempo para as cinco regiões do poço duplo quadrado unidimensional assimétrico, neste caso, é dada por Regiões I e V : Ψ (x) = 0, (40) Região II : Ψ (x) = A 1 sen(k 1 x) + A cos(k 1 x), (41) Região III : Ψ (x) = Bsen(βx) + C cos(βx), (4) Região IV : Ψ (x) = D 1 sen(k x) + D cos(k x). (43)
6 Paulino et al. Novamente, as constantes A 1, A, B, C, D 1, D são obtidas pela continuidade da função de onda e sua derivada e pela constante de normalização. Também foram introduzidos os parâmetros k 1 = m E (V 1 V 0 ), β = m (E V 1), (44) k = me. Seguindo os mesmos passos indicados nos casos anteriores, ou seja, adotando a função de onda igual a zero quando o potencial for infinito e considerando a continuidade na função de onda e na sua derivada em x = ± (L a), tem-se a equação transcendental que permite a determinação dos autovalores de energia para (E > V 1 ) k cot(k a) + β tan β(l a) = β + k tan β(l a) cot(k a) β tan β(l a) + k 1 cot(k 1 a). (45) k 1 tan cot(k 1 a) + β β(l a) Com esse resultado o problema original é completamente resolvido. Particularmente, a energia do sistema é dada pela Eq. (5), Eq. (39) ou Eq. (45), dependendo do caso a ser analisado. 4. Redução da solução obtida para o caso simétrico Usando as soluções conhecidas para a energia do poço simétrico é possível testar a validade da solução encontrada no caso assimétrico. Para que o poço duplo assimétrico se reduza ao poço duplo simétrico basta fazer V 0 = V 1, isso implica em que k = k 1 = k. Usando essas relações na expressão (39), E < V 1, chega-se na (β+k cot(ka)) equação: (β k cot(ka)) = ±e β(l a). Manipulando algebricamente essa relação, reescrevendo-a em termos de funções hiperbólicas, é possível verificar que ela corresponde exatamente as Eqs. () e (3). Por outro lado, para E > V 1, a substituição de k 1 e k por k (lembrando que k = k 1 = k ) na expressão (45) fornece diretamente as Eqs. (4) e (5), como esperado. Esta análise mostra a consistência entre as soluções obtidas para os poços duplos quadrados unidimensionais simétrico e assimétrico. 5. Autovalores de energia para o poço duplo assimétrico Analisando os níveis de energia menores que a barreira de potencial (V 1 ), basicamente, aparecem dois exemplos numéricos típicos, a saber: quando há ressonância entre os níveis de energia dos dois lados do poço e quando não há. No problema do poço duplo simétrico, por construção, todos os níveis de energia são ressonantes. Um efeito dessa situação é o aparecimento de níveis de energia aos pares muito próximos. Isso pode ser observado, no caso geral de potenciais biestáveis, por exemplo, no livro de Landau 10 onde a solução do poço duplo é escrita como uma combinação linear das soluções encontradas para o poço simples. Esse tipo de análise, apesar de ser aproximada, mostra claramente o aparecimento das soluções aos pares. No caso em que não há ressonância, os valores numéricos utilizados como exemplos para as barreiras de potencial são V 0 = 50 ev (8,010 x J) e V 1 = 100 ev (1,60 x J). Para esses valores os níveis de energia dos poços quando analisados separadamente não coincidem. Uma maneira de determinar os autovalores de energia, dados pela equação transcendental correspondente, é através de análise gráfica. Isso é feito desenhando as curvas resultantes das funções escritas nos dois membros da Eq. (39) e observando a intersecção das curvas Fig. 3. Os pontos de intersecção entre as curvas mostradas na Fig. 3 correspondem às soluções da equação transcendental (39), onde k 1, k e β estão definidos na Eq. (30). Nessa condição a função de onda é distribuída nos dois poços. Os valores numéricos utilizados para exemplificar os resultados foram: a = 1 x m e L = x m, que correspondem à largura do poço de um angstron e a distância entre eles de dois angstrons, respectivamente. Outros valores fixados foram m = 9,109 x kg, que corresponde à massa do elétron, e = 1,055 x J.s que corresponde, como usual, à constante de Planck dividida por π. Figura 3 - Curvas das funções obtidas na Eq. (39). O lado esquerdo dessa equação corresponde à linha contínua enquanto a curva tracejada representa a função descrita pelo lado direito, conforme indicado no destaque. As profundidades dos poços correspondem a V 0 = 50 ev e V 1 = 100 ev. A análise gráfica refinada fornece, para esse exemplo, os níveis de energia E = 7,165 ev e E 3 =
7 Solução quântica para o poço duplo quadrado unidimensional assimétrico ,755 ev. O autovalor de energia para estado fundamental é obtido de forma análoga, usando a Eq. (5), e conduz a E 1 = 5,91 ev. Assim, nesse exemplo, existe um nível de energia entre 0 e (V 1 V 0 ) e dois níveis entre (V 1 V 0 ) e V 1. Ajustando a profundidade de um dos poços, como por exemplo, V 0 = 50 ev e V 1 = 130,6 ev (,095 x J), é possível obter a ressonância entre estados provenientes dos dois poços simples. A Fig. 4 mostra os pontos de intersecção das curvas que representam os dois lados da equação transcendental (39) em função da energia. Os níveis de energia obtidos neste caso foram: E 1 = 7,16 ev (obtida da Eq. (5)), E = 101,635 ev e E 3 = 104,089 ev (esses dois últimos valores são obtidos da Eq. (39) analisando o gráfico contido na Fig. 4). Figura 4 - Curvas das funções obtidas na Eq. (39). O lado esquerdo dessa equação corresponde à linha contínua enquanto a curva tracejada representa a função descrita pelo lado direito, conforme indicado no destaque. As profundidades dos poços correspondem a V 0 = 50 ev e V 1 = 130,6 ev. 6. Discussão dos resultados e conclusão Como esperado, os resultados obtidos para o potencial simétrico, Eqs. (), (3), (4) e (5), coincidem com aquele encontrado na literatura 9. No caso do potencial assimétrico sem ressonância, V 0 = 50 ev e V 1 = 100 ev, é possível observar dois níveis de energia (7,165 ev e 94,755 ev) que podem ser interpretados como resultado da interação entre os poços. Dessa maneira é possível observar que cada autovalor de energia no poço simples individual produz dois autovalores distintos de energia no poço duplo assimétrico. Este desdobramento é produzido considerando as funções de onda resultantes do acoplamento de dois poços simples como sendo aproximadamente uma combinação linear simétrica a anti-simétrica das autofunções originais 10. Assim, o potencial biestável pode ser formado por intermédio da junção de dois poços simples. O caso chamado de ressonante foi encontrado para os valores V 0 = 50 ev e V 1 = 130,6 ev. Essa configuração permite uma discussão a respeito do tunelamento; o fato dos níveis de energia dos dois poços individuais (sem interação) estarem à mesma profundidade proporciona uma maior probabilidade de haver tunelamento entre os dois poços. Isso pode ser observado diretamente na fórmula de Rabi usada para descrever a taxa de tunelamento nesse caso. A dedução da fórmula de Rabi envolve algumas aproximações, por exemplo, a suposição de que apenas dois níveis de energia participam do processo. Uma dedução completa dessa expressão, bem como a discussões de algumas aplicações, pode ser encontrada na Ref. 7. Uma característica do poço duplo assimétrico que vale ressaltar é que o estado fundamental está localizado somente no poço de maior profundidade, visto que, pela assimetria do problema não há correspondente no poço de menor profundidade. Nos casos apresentados neste trabalho com V 0 = 50 ev e V 1 = 100 ev, e V 0 = 50 ev e V 1 = 130,6 ev, o estado fundamental foram 5,91 ev e 7,16 ev, respectivamente. Dessa forma, o poço duplo quadrado unidimensional assimétrico fica completamente resolvido com as energias dadas em termos das equações transcendentais, Eqs. (5), (39) e (45) e as autofunções escritas em termos de funções elementares. O caso ressonante aqui estudado não é o único que pode ser encontrado, é possível encontrar outros valores dos parâmetros de potencial (V 0, V 1, L e a) para os quais entre as barreiras de potenciais que conduzam a esta condição. É um e- xercício interessante procurar outras geometrias do potencial assimétrico para as quais há ressonância. Por fim, vale ressaltar que o estudo de poços assimétricos permite ilustrar diversas características de sistemas quânticos sem a exigência de um formalismo matemático muito avançado. Essa característica reforça o seu caráter didático. Referências 1 H.D. Young e R.A. Freedman, Sears e Zemansky, Física IV: Ótica e Física Moderna (Pearson, São Paulo, 004), p R. Eisberg e R.Resnick, Física Quântica: Átomos, Moléculas, Sólidos, Núcleos e Partículas (Editora Campus, Rio de Janeiro, 1979), p D.J. Griffits, Introduction to Quantum Mechanics (Pearson Education, Upper Saddle River, 005). 4 P.A. Tipler, e R.A. Lewellyn, Física Moderna (Editora LTC, Rio de Janeiro, 001), p A. Beiser, Conceptos de Física Moderna (McGraw-Hill, México, D.F. 1981), p ,. 6 L.I. Schiff, Quantum Mechanics (Edition International Student, New York, 1955), p C. Cohen-Tannoudji, C. Diu and B.F. Laloë, Quantum Mechanics (Herman, Paris, 1977), p , v. 1.
8 Paulino et al. 8 D. DeVault, Quantum Mechanical Tunneling in Biological Systems (Cambridge University Press, Cambridge, 1983). 9 W. Greiner, Quantum Mechanics: An Introduction (Springer-Verlag Press, New York, 001), pags L.D. Landau and E.M. Lifshitz, Quantum Mechanics, Non-Relativistic Theory (Pergamon, Oxford, 1977). 11 B. Jun and D.L. Weaver, J. Chem. Phys. 116, 418 (00). 1 L.P. Gilbert, M. Belloni, M.A. Doncheski and R.W. Robinett, Eur. J. Phys. 6, 815 (005). 13 M.A. Doncheski and R.W. Robinett, Eur. J. Phys. 1, 17 (000).
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
Fundamentos de Química Quântica
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Professora: Melissa Soares Caetano Partícula na caixa Sistema ideal
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Professora: Melissa Soares Caetano Partícula na caixa Sistema ideal
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
4 e 6/Maio/2016 Aulas 17 e 18
 9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 12. Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 12 Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico 1 Barreira de potencial Uma barreira de potencial é descrita
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 12 Barreira de potencial, efeito túnel, poço finito, e oscilador harmônico 1 Barreira de potencial Uma barreira de potencial é descrita
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de agosto de 2011 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de agosto de 2011 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
Valores esperados. ψ (x)xψ(x)dx. ψ ψ dx. xp(x)dx P(x)dx. Vimos que: x = = ψ xψ dx. No caso geral de uma função de x: f (x) = f (x) =
 Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
Vimos que: x = + Valores esperados ψ (x)xψ(x)dx xp(x)dx P(x)dx = ψ xψ dx ψ ψ dx No caso geral de uma função de x: f (x) = f (x) = + ψ (x) ˆf (x)ψ(x)dx Para o momento e a energia: ˆp = i x e Ê = i t. 4300375
CONTEÚDO PROGRAMÁTICO EMENTA
 UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
UNIVERSIDADE FEDERAL DO AMAZONAS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. GAL. RODRIGO OTÁVIO JORDÃO RAMOS, 3000 JAPIIM CEP: 69077-000 - MANAUS-AM, FONE/FAX (92) 3305-2829 CONTEÚDO PROGRAMÁTICO
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2009 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2009 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE DE SCHRÖDINGER Primeira Edição junho de 2005 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE DE SCHRÖDINGER Primeira Edição junho de 2005 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 7 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER INDEPENDENTE DO TEMPO Primeira Edição junho de 2005 CAPÍTULO 07 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 7 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER INDEPENDENTE DO TEMPO Primeira Edição junho de 2005 CAPÍTULO 07 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 SOLUÇÕES DA EQUAÇÃO DE SCHORÖDINGER INDEPENDENTE DO TEMPO Edição de junho de 2014 CAPÍTULO 06 SOLUÇÕES DA EQUAÇÃO DE SCRÖDINGER INDEPENDENTE
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 SOLUÇÕES DA EQUAÇÃO DE SCHORÖDINGER INDEPENDENTE DO TEMPO Edição de junho de 2014 CAPÍTULO 06 SOLUÇÕES DA EQUAÇÃO DE SCRÖDINGER INDEPENDENTE
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2010 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de janeiro de 2010 CAPÍTULO 6 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 6.1- Introdução 6.2- Equação
Função de Onda e Equação de Schrödinger
 14/08/013 Função de Onda e Equação de Schrödinger Prof. Alex Fabiano C. Campos, Dr A Função de Onda (ψ) A primeira formulação para esta nova interpretação da Mecânica, a Mecânica Quântica, teoria foi proposta
14/08/013 Função de Onda e Equação de Schrödinger Prof. Alex Fabiano C. Campos, Dr A Função de Onda (ψ) A primeira formulação para esta nova interpretação da Mecânica, a Mecânica Quântica, teoria foi proposta
Instituto de Física USP. Física V - Aula 28. Professora: Mazé Bechara
 nstituto de Física USP Física V - Aula 8 Professora: Mazé Bechara Aula 8 - Estados ligados em movimentos unidimensionais 1. O poço de potencial infinito complementando. Comparação com resultado de de Broglie
nstituto de Física USP Física V - Aula 8 Professora: Mazé Bechara Aula 8 - Estados ligados em movimentos unidimensionais 1. O poço de potencial infinito complementando. Comparação com resultado de de Broglie
RESSALVA. Atendendo solicitação da autora, o texto completo desta tese será disponibilizado somente a partir de 13/03/2016.
 RESSALVA Atendendo solicitação da autora, o texto completo desta tese será disponibilizado somente a partir de 13/03/2016. UNIVERSIDADE ESTADUAL PAULISTA JÚLIO DE MESQUITA FILHO Campus de São José do Rio
RESSALVA Atendendo solicitação da autora, o texto completo desta tese será disponibilizado somente a partir de 13/03/2016. UNIVERSIDADE ESTADUAL PAULISTA JÚLIO DE MESQUITA FILHO Campus de São José do Rio
O poço de potencial quântico infinito: um estudo usando o método de fatorização
 - 1 - Ministério da Educação Brasil Universidade Federal dos Vales do Jequitinhonha e Mucuri UFVJM Minas Gerais Brasil Revista Vozes dos Vales: Publicações Acadêmicas Reg.: 10..095 011 UFVJM ISSN: 38-644
- 1 - Ministério da Educação Brasil Universidade Federal dos Vales do Jequitinhonha e Mucuri UFVJM Minas Gerais Brasil Revista Vozes dos Vales: Publicações Acadêmicas Reg.: 10..095 011 UFVJM ISSN: 38-644
Partícula na Caixa. Química Quântica Prof a. Dr a. Carla Dalmolin
 Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
6. Mecânica Quântica
 6. Mecânica Quântica Sumário A função de onda A equação de Schrödinger Partícula em uma caixa Poço de potencial Barreira de potencial e o efeito túnel Oscilador harmônico A função de onda Ψ descreve uma
6. Mecânica Quântica Sumário A função de onda A equação de Schrödinger Partícula em uma caixa Poço de potencial Barreira de potencial e o efeito túnel Oscilador harmônico A função de onda Ψ descreve uma
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Solução analítica do potencial de Morse em mecânica clássica
 Revista Brasileira de nsino de Física, v. 9, n. 4, p. 543-547, 007) www.sbfisica.org.br Solução analítica do potencial de Morse em mecânica clássica Analytical solution of the Morse potential in classical
Revista Brasileira de nsino de Física, v. 9, n. 4, p. 543-547, 007) www.sbfisica.org.br Solução analítica do potencial de Morse em mecânica clássica Analytical solution of the Morse potential in classical
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Física IV Escola Politécnica P3 7 de dezembro de 2017
 Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Física IV - 4323204 Escola Politécnica - 2017 P3 7 de dezembro de 2017 Questão 1 Uma partícula de massa m que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento angular bem definido
 ÁTOMO DE HIDROGÊNIO Primeiro sistema tratado quanticamente por Schrödinger Modelo de Bohr Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento
ÁTOMO DE HIDROGÊNIO Primeiro sistema tratado quanticamente por Schrödinger Modelo de Bohr Elétrons se movem ao redor do núcleo em órbitas circulares (atração Coulombiana) Cada órbita n possui um momento
Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional
 Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional Caio Vaz Rímoli Resumo: Partículas Livres não relativísticas estão entre os sistemas mais básicos e mais
Evolução temporal de uma Partícula Livre descrita por um Pacote de Onda Gaussiano Unidimensional Caio Vaz Rímoli Resumo: Partículas Livres não relativísticas estão entre os sistemas mais básicos e mais
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 9. Soluções da equação de Schrödinger: partícula numa caixa infinita
 UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Física Moderna II Aula 07
 Universidade de São Paulo Instituto de Física 1 º Semestre de 015 Profa. Márcia de Almeida Rizzutto Oscar Sala sala 0 rizzutto@if.usp.br Física Moderna II Aula 07 Monitor: Gabriel M. de Souza Santos Sala
Universidade de São Paulo Instituto de Física 1 º Semestre de 015 Profa. Márcia de Almeida Rizzutto Oscar Sala sala 0 rizzutto@if.usp.br Física Moderna II Aula 07 Monitor: Gabriel M. de Souza Santos Sala
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FNC376N: Lista de março de ψ r ψ = Eψ. sin θ Y )
 FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
FNC376N: ista 3 31 de março de 5 Tipler - Capítulo 7 7-7 Considere a função de onda ψ = A r a e r/a cos θ, onde A é uma constante e a = /µkze é o raio de Bohr dividido por Z a) Mostre que éla é uma solução
OBTENÇÃO DE EXPRESSÃO SEMI-ANALÍTICA DE FUNÇÃO DE ONDA PARA UM POTENCIAL ÓPTICO.
 OBTENÇÃO DE EXPRESSÃO SEMI-ANALÍTICA DE FUNÇÃO DE ONDA PARA UM POTENCIAL ÓPTICO. Hugo Vieira de Vasconcelos - IC Ricardo Affonso do Rego PQ e-mail: hvieirav@yahoo.com.br e-mail: rego@fis.ita.br Foi estudada
OBTENÇÃO DE EXPRESSÃO SEMI-ANALÍTICA DE FUNÇÃO DE ONDA PARA UM POTENCIAL ÓPTICO. Hugo Vieira de Vasconcelos - IC Ricardo Affonso do Rego PQ e-mail: hvieirav@yahoo.com.br e-mail: rego@fis.ita.br Foi estudada
Aula de Física Atômica e molecular. Operadores em Mecânica Quântica Prof. Vicente
 Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
Aula de Física Atômica e molecular Operadores em Mecânica Quântica Prof. Vicente Definição Seja f uma quantidade física que caracteriza o estado de um sistema quântico. Os valores que uma dada quantidade
Aula-9 Mais Ondas de Matéria I
 Aula-9 Mais Ondas de Matéria I Estados ligados Vimos, até agora, 3 postulados da Mecânica Quântica: a) Toda partícula possui uma função de onda associada a ela. b) A forma e a evolução temporal desta é
Aula-9 Mais Ondas de Matéria I Estados ligados Vimos, até agora, 3 postulados da Mecânica Quântica: a) Toda partícula possui uma função de onda associada a ela. b) A forma e a evolução temporal desta é
Tunelamento em Teoria Quântica de Campos
 Tunelamento em Teoria Quântica de Campos Leonardo Peixoto de Moura Orientador: Prof. Dr Gabriel Flores Hidalgo March 29, 2017 Sumário 1 Introdução 2 N-dimensional 3 T.C. 4 Método de Aproximação 5 Método
Tunelamento em Teoria Quântica de Campos Leonardo Peixoto de Moura Orientador: Prof. Dr Gabriel Flores Hidalgo March 29, 2017 Sumário 1 Introdução 2 N-dimensional 3 T.C. 4 Método de Aproximação 5 Método
Átomos multi-eletrônicos. Indistinguibilidade
 Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Física IV Escola Politécnica GABARITO DA P3 27 de novembro de 2012
 Física IV - 4320402 Escola Politécnica - 2012 GABARITO DA P3 27 de novembro de 2012 Questão 1 Considere uma partícula de massa m e energia E num potencial unidimensional que é nulo na região 0 < x < d
Física IV - 4320402 Escola Politécnica - 2012 GABARITO DA P3 27 de novembro de 2012 Questão 1 Considere uma partícula de massa m e energia E num potencial unidimensional que é nulo na região 0 < x < d
Instituto de Física USP. Física V - Aula 31. Professora: Mazé Bechara
 Instituto de Física USP Física V - Aula 31 Professora: Mazé Bechara Aula 31 - Mecânica quântica de Schroedinger aplicada a estados ligados em movimentos unidimensionais. 1. Estados estacionários na mecânica
Instituto de Física USP Física V - Aula 31 Professora: Mazé Bechara Aula 31 - Mecânica quântica de Schroedinger aplicada a estados ligados em movimentos unidimensionais. 1. Estados estacionários na mecânica
Equação de Schrödinger
 Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
Maria Inês Barbosa de Carvalho Equação de Schrödinger Apontamentos para a disciplina Física dos Estados da Matéria 00/0 Licenciatura em Engenharia Electrotécnica e de Computadores Faculdade de Engenharia
Não serão aceitas respostas sem justificativa:
 Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Potenciais cisalhados em mecânica
 Potenciais cisalhados em mecânica clássica e mecânica quântica Carlos Farina Instituto de Física - UFRJ Mestrado Profissional em Ensino de Física Instituto de Física - UFRJ (16 de abril de 2013) Roteiro
Potenciais cisalhados em mecânica clássica e mecânica quântica Carlos Farina Instituto de Física - UFRJ Mestrado Profissional em Ensino de Física Instituto de Física - UFRJ (16 de abril de 2013) Roteiro
Estrutura Hiperfina e Efeito Zeeman para Muônio e Positrônio
 Estrutura Hiperfina e Efeito Zeeman para Muônio e Positrônio Armando Valter Felicio Zuffi 05 de dezembro de 014 Resumo Neste trabalho, serão exploradas algumas correções da hamiltoniana do átomo de hidrogênio.
Estrutura Hiperfina e Efeito Zeeman para Muônio e Positrônio Armando Valter Felicio Zuffi 05 de dezembro de 014 Resumo Neste trabalho, serão exploradas algumas correções da hamiltoniana do átomo de hidrogênio.
B) [N] é uma constante de normalização indicando que a probabilidade de encontrar o elétron em qualquer lugar do espaço deve ser unitária. R n,l (r) é
![B) [N] é uma constante de normalização indicando que a probabilidade de encontrar o elétron em qualquer lugar do espaço deve ser unitária. R n,l (r) é B) [N] é uma constante de normalização indicando que a probabilidade de encontrar o elétron em qualquer lugar do espaço deve ser unitária. R n,l (r) é](/thumbs/71/66033065.jpg) QUÍMICA I AULA 04: ESTRUTURA ELETRÔNICA DOS ÁTOMOS TÓPICO 05: ORBITAL ATÔMICO 5.1 A EQUAÇÃO DE SCHRODINGER E O ÁTOMO DE HIDROGÊNIO: Como o elétron tem propriedades ondulatórias, ele pode ser descrito como
QUÍMICA I AULA 04: ESTRUTURA ELETRÔNICA DOS ÁTOMOS TÓPICO 05: ORBITAL ATÔMICO 5.1 A EQUAÇÃO DE SCHRODINGER E O ÁTOMO DE HIDROGÊNIO: Como o elétron tem propriedades ondulatórias, ele pode ser descrito como
Dois elétrons num bilhar com paredes suaves
 https://eventos.utfpr.edu.br//sicite/sicite2017/index Dois elétrons num bilhar com paredes suaves Pedro Chebenski Júnior pedroj@alunos.utfpr.edu.br Universidade Tecnológica Federal do Paraná, Ponta Grossa,
https://eventos.utfpr.edu.br//sicite/sicite2017/index Dois elétrons num bilhar com paredes suaves Pedro Chebenski Júnior pedroj@alunos.utfpr.edu.br Universidade Tecnológica Federal do Paraná, Ponta Grossa,
Aula 14 - Ondas de Matéria
 Aula 14 - Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário O Efeito Túnel Capítulo 39 Mais sobre ondas de matéria Introdução Ondas em Cordas e Ondas de Matéria Energia de um Elétron Confinado Funções
Aula 14 - Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário O Efeito Túnel Capítulo 39 Mais sobre ondas de matéria Introdução Ondas em Cordas e Ondas de Matéria Energia de um Elétron Confinado Funções
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 2 elétrons Férmions Hartree-Fock Troca
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
O poço quadrado finito
 O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
O poço quadrado infinito FNC375N: ista 8 5//4. Um próton se encontra num poço infinito de largura. Compute a energia do estado fundamental para (a), nm, o tamanho aproximado de uma molécula, e (b) fm,
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
O oscilador harmônico simples quântico
 1 / 18 O oscilador harmônico simples quântico Prof. Dr. Vicente Pereira de Barros Instituto Federal de Educação Ciência e Tecnologia de São Paulo - Campus Itapetininga 29/05/2014 2 / 18 Introdução Introdução
1 / 18 O oscilador harmônico simples quântico Prof. Dr. Vicente Pereira de Barros Instituto Federal de Educação Ciência e Tecnologia de São Paulo - Campus Itapetininga 29/05/2014 2 / 18 Introdução Introdução
Cap. 39 Mais ondas de matéria
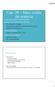 Cap. 39 Mais ondas de matéria Ondas em cordas e ondas de matéria; Energia de um elétron confinado (1D); Mudanças de energia; Função de onda de um elétron confinado (1D); Elétron em poço finito; Outras
Cap. 39 Mais ondas de matéria Ondas em cordas e ondas de matéria; Energia de um elétron confinado (1D); Mudanças de energia; Função de onda de um elétron confinado (1D); Elétron em poço finito; Outras
Aula 15 Mais sobre Ondas de Matéria
 Aula 15 Mais sobre Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário...continuação... Energia de um Elétron Confinado Funções de Onda de um Elétron Confinado Um Elétron em um Poço de Potencial Finito
Aula 15 Mais sobre Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário...continuação... Energia de um Elétron Confinado Funções de Onda de um Elétron Confinado Um Elétron em um Poço de Potencial Finito
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
Denise Caldas Campos. Solução da Equação de Fokker-Planck para o Potencial do Oscilador Harmônico Duplo
 UNIVERSIDADE ESTADUAL PAULISTA JÚLIO DE MESQUITA FILHO Campus de São José do Rio Preto Denise Caldas Campos Solução da Equação de Fokker-Planck para o Potencial do Oscilador Harmônico Duplo São José do
UNIVERSIDADE ESTADUAL PAULISTA JÚLIO DE MESQUITA FILHO Campus de São José do Rio Preto Denise Caldas Campos Solução da Equação de Fokker-Planck para o Potencial do Oscilador Harmônico Duplo São José do
Física Quântica. Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões. Pieter Westera
 Física Quântica Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html
Física Quântica Aula 9: Potenciais Simples III: Tunelamento; Equação de Schrödinger em três Dimensões Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html
O degrau de potencial. Caso I: energia menor que o degrau
 O degrau de potencial. Caso I: energia menor que o degrau A U L A 8 Meta da aula Aplicar o formalismo quântico ao caso de uma partícula quântica que incide sobre um potencial V(x) que tem a forma de um
O degrau de potencial. Caso I: energia menor que o degrau A U L A 8 Meta da aula Aplicar o formalismo quântico ao caso de uma partícula quântica que incide sobre um potencial V(x) que tem a forma de um
Partícula em um Poço de Potencial Infinito e o Método Variacional de Monte Carlo
 Revista Brasileira de Ensino de Física, vol. 25, no. 1, Março, 2003 35 Partícula em um Poço de Potencial Infinito e o Método Variacional de Monte Carlo (Particle in an infinity potential well and the variational
Revista Brasileira de Ensino de Física, vol. 25, no. 1, Março, 2003 35 Partícula em um Poço de Potencial Infinito e o Método Variacional de Monte Carlo (Particle in an infinity potential well and the variational
Mecânica Quântica. Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa
 Mecânica Quântica Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa Limitações do modelo de Bohr A teoria de Bohr não era capaz
Mecânica Quântica Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa Limitações do modelo de Bohr A teoria de Bohr não era capaz
SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO
 FÍSICA IV PROF. DR. DURVAL RODRIGUES JUNIOR SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO Como na Biblioteca do Campus I e do Campus II temos bom número de cópias do Halliday e poucas do Serway, os
FÍSICA IV PROF. DR. DURVAL RODRIGUES JUNIOR SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO Como na Biblioteca do Campus I e do Campus II temos bom número de cópias do Halliday e poucas do Serway, os
Cap. 24. Potencial Elétrico. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 Cap. 24 Potencial Elétrico Copyright 24-1 Potencial Elétrico O potencial elétrico V em um ponto P devido ao campo elétrico produzido por um objeto carregado é dado por Carga de prova q 0 no ponto P onde
Cap. 24 Potencial Elétrico Copyright 24-1 Potencial Elétrico O potencial elétrico V em um ponto P devido ao campo elétrico produzido por um objeto carregado é dado por Carga de prova q 0 no ponto P onde
Física Quântica. Aula 7: Equação de Schrödinger, Potenciais Simples I, Transições. Pieter Westera
 Física Quântica Aula 7: Equação de Schrödinger, Potenciais Simples I, Transições Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html A Equação de Schrödinger
Física Quântica Aula 7: Equação de Schrödinger, Potenciais Simples I, Transições Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html A Equação de Schrödinger
O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana
 Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Física O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana Introdução O Hélio é, depois do Hidrogênio, o átomo mais simples
Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Física O estado fundamental do átomo de Hélio Prof. Ricardo L. Viana Introdução O Hélio é, depois do Hidrogênio, o átomo mais simples
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 8. A equação de Schrödinger
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
Teoria de bandas nos sólidos
 Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
A Densidade Lagrangeana Para Uma Generalização da Equação de Schroedinger e o Berço de píon
 A Densidade Lagrangeana Para Uma Generalização da Equação de Schroedinger e o Berço de píon Edigles Guedes 5 de agosto de 016 Resumo. Nós derivamos a densidade Lagrangeana para uma generalização da equação
A Densidade Lagrangeana Para Uma Generalização da Equação de Schroedinger e o Berço de píon Edigles Guedes 5 de agosto de 016 Resumo. Nós derivamos a densidade Lagrangeana para uma generalização da equação
Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein
 Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein Edigles Guedes e-mail: edigles.guedes@gmail.com 24 de junho de 2012. RESUMO Nós construímos a Teoria da Relatividade
Relatividade Especial Virtual - Uma Generalização da Relatividade Especial de Einstein Edigles Guedes e-mail: edigles.guedes@gmail.com 24 de junho de 2012. RESUMO Nós construímos a Teoria da Relatividade
Oscilador Harmônico. 8 - Oscilador Harmônico. Oscilador Harmônico. Oscilador Harmônico Simples. Oscilador harmônico simples
 Oscilador Harmônico 8 - Oscilador Harmônico Mecânica Quântica Em Física, o oscilador harmônico é qualquer sistema que apresenta movimento oscilatório, de forma harmônica, em torno de um ponto de equilíbrio.
Oscilador Harmônico 8 - Oscilador Harmônico Mecânica Quântica Em Física, o oscilador harmônico é qualquer sistema que apresenta movimento oscilatório, de forma harmônica, em torno de um ponto de equilíbrio.
Física Moderna 2. Aula 9. Moléculas. Tipos de ligações. Íon H2 + Iônica Covalente Outras: ponte de hidrogênio van der Waals
 Física Moderna 2 Aula 9 Moléculas Tipos de ligações Iônica Covalente Outras: Íon H2 + ponte de hidrogênio van der Waals 1 Moléculas Uma molécula é um arranjo estável de dois ou mais átomos. Por estável
Física Moderna 2 Aula 9 Moléculas Tipos de ligações Iônica Covalente Outras: Íon H2 + ponte de hidrogênio van der Waals 1 Moléculas Uma molécula é um arranjo estável de dois ou mais átomos. Por estável
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 11. Soluções da equação de Schrödinger: potencial degrau
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
Aplicação do Método Variacional na Mecânica Quântica:
 Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
SOLUÇÃO ANALÍTICA E NUMÉRICA DA EQUAÇÃO DE LAPLACE
 15 16 SOLUÇÃO ANALÍTICA E NUMÉRICA DA EQUAÇÃO DE LAPLACE 3. Todos os dispositivos elétricos funcionam baseados na ação de campos elétricos, produzidos por cargas elétricas, e campos magnéticos, produzidos
15 16 SOLUÇÃO ANALÍTICA E NUMÉRICA DA EQUAÇÃO DE LAPLACE 3. Todos os dispositivos elétricos funcionam baseados na ação de campos elétricos, produzidos por cargas elétricas, e campos magnéticos, produzidos
Potenciais delta revisitados via transformada de Fourier 1
 arxiv:1210.0204v1 [math-ph] 30 Sep 2012 Potenciais delta revisitados via transformada de Fourier 1 (Delta potentials revisited via Fourier transform) A.S. de Castro 2 Departamento de Física e Química,
arxiv:1210.0204v1 [math-ph] 30 Sep 2012 Potenciais delta revisitados via transformada de Fourier 1 (Delta potentials revisited via Fourier transform) A.S. de Castro 2 Departamento de Física e Química,
A barreira de potencial: casos E < V 0
 A barreira de potencial: casos E < V e E > V A U L A 11 Meta da aula Aplicar o formalismo quântico ao caso de uma partícula que incide sobre uma barreira de potencial, em que a energia potencial tem um
A barreira de potencial: casos E < V e E > V A U L A 11 Meta da aula Aplicar o formalismo quântico ao caso de uma partícula que incide sobre uma barreira de potencial, em que a energia potencial tem um
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das
 Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
Cálculo da taxa de ionização do átomo de hidrogênio em campo elétrico uniforme via método WKB
 Revista Brasileira de Ensino de ísica, v. 32, n. 2, 2306 2010) www.sbfisica.org.br Cálculo da taxa de ionização do átomo de hidrogênio em campo elétrico uniforme via método WKB Semiclassical calculation
Revista Brasileira de Ensino de ísica, v. 32, n. 2, 2306 2010) www.sbfisica.org.br Cálculo da taxa de ionização do átomo de hidrogênio em campo elétrico uniforme via método WKB Semiclassical calculation
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 15 MODELOS NUCLEARES Primeira Edição junho de 2005 CAPÍTULO 15 MODELOS NUCLEARES ÍNDICE 15.1- Introdução 15.2- Composição dos Núcleos
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 15 MODELOS NUCLEARES Primeira Edição junho de 2005 CAPÍTULO 15 MODELOS NUCLEARES ÍNDICE 15.1- Introdução 15.2- Composição dos Núcleos
Gil de Oliveira Neto
 Gil de Oliveira Neto 1. Motivações; 2. Relatividade Geral Quântica; 3. Cosmologia Quântica; 4. Um Modelo para o Início do Universo; 5. Conclusões. 1. Relatividade Geral Clássica; 2. Cosmologia Moderna;
Gil de Oliveira Neto 1. Motivações; 2. Relatividade Geral Quântica; 3. Cosmologia Quântica; 4. Um Modelo para o Início do Universo; 5. Conclusões. 1. Relatividade Geral Clássica; 2. Cosmologia Moderna;
Aula 14 - Ondas de Matéria
 Aula 14 - Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário O Efeito Túnel Capítulo 39 Mais sobre ondas de matéria Introdução Ondas em Cordas e Ondas de Matéria Energia de um Elétron Confinado Funções
Aula 14 - Ondas de Matéria Física 4 Ref. Halliday Volume4 Sumário O Efeito Túnel Capítulo 39 Mais sobre ondas de matéria Introdução Ondas em Cordas e Ondas de Matéria Energia de um Elétron Confinado Funções
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Introdução à Modelagem Molecular
 Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Universidade Tecnológica Federal do Paraná Câmpus Francisco Beltrão
 Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
Universidade de São Paulo em São Carlos Mecânica Quântica Aplicada Prova 1
 Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Universidade de São Paulo em São Carlos 9514 Mecânica Quântica Aplicada Prova 1 Nome: Questão 1: Sistema de dois níveis (3 pontos) Considere um sistema de dois estados 1 e ortonormais H do sistema seja
Átomos e Moléculas. Ligações moleculares. Energia do ion. A molécula de hidrogênio H 2
 Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Instituto de Física USP. Física Moderna. Aula 27. Professora: Mazé Bechara
 nstituto de Física UP Física Moderna Aula 7 Professora: Mazé Bechara Aula 7 A equação de chroedinger para estados estacionários não ligados. Aplicações. 1. Uma barreira de potencial. As posições e energias
nstituto de Física UP Física Moderna Aula 7 Professora: Mazé Bechara Aula 7 A equação de chroedinger para estados estacionários não ligados. Aplicações. 1. Uma barreira de potencial. As posições e energias
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Física IV Escola Politécnica GABARITO DA PS 3 de dezembro de 2015
 1 QUESTÃO 1 Física IV - 4323204 Escola Politécnica - 2015 GABARITO DA PS 3 de dezembro de 2015 Um feixe de elétrons de massa m e velocidade v incide normalmente sobre um anteparo com duas fendas separadas
1 QUESTÃO 1 Física IV - 4323204 Escola Politécnica - 2015 GABARITO DA PS 3 de dezembro de 2015 Um feixe de elétrons de massa m e velocidade v incide normalmente sobre um anteparo com duas fendas separadas
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/2 e de Dois Níveis
 Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
CF100 - Física Moderna II. 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018
 CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
CF100 - Física Moderna II 2º Semestre de 2018 Prof. Ismael André Heisler Aula 10/08/2018 1 Átomos Multieletrônicos 2 Partículas Idênticas 3 Na física quântica, o princípio da incerteza impede a observação
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 1 elétron O princípio variacional Função
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Problema de 1 elétron O princípio variacional Função
Rotor quântico. Quanticamente o rotor é descrito por uma função de onda, tal que: l A função de onda do estado estacionário é dada por:
 Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Decaimento α. Wednesday 12 May 2010 at 3:46 pm. Versão para impressão
 Decaimento α Wednesday 12 May 2010 at 3:46 pm Versão para impressão Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente,
Decaimento α Wednesday 12 May 2010 at 3:46 pm Versão para impressão Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente,
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 10 ÁTOMOS COMPLEXOS Primeira Edição junho de 2005 CAPÍTULO 10 ÁTOMOS COMPLEXOS ÍNDICE 10-1- Introdução 10.2- Átomos com mais de um
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 10 ÁTOMOS COMPLEXOS Primeira Edição junho de 2005 CAPÍTULO 10 ÁTOMOS COMPLEXOS ÍNDICE 10-1- Introdução 10.2- Átomos com mais de um
Mecânica Quântica: uma abordagem (quase) conceitual
 Mecânica Quântica: uma abordagem (quase) conceitual Carlos Eduardo Aguiar Programa de Pós-Graduação em Ensino de Física Instituto de Física - UFRJ IF-UFRJ, fevereiro de 04 Sumário Dificuldades na aprendizagem
Mecânica Quântica: uma abordagem (quase) conceitual Carlos Eduardo Aguiar Programa de Pós-Graduação em Ensino de Física Instituto de Física - UFRJ IF-UFRJ, fevereiro de 04 Sumário Dificuldades na aprendizagem
Física IV - FAP2204 Escola Politécnica GABARITO DA P3 8 de dezembro de 2009
 P3 Física IV - FAP2204 Escola Politécnica - 2009 GABARITO DA P3 8 de dezembro de 2009 Questão 1 Numaexperiência deespalhamentocompton, umelétrondemassam 0 emrepousoespalha um fóton de comprimento de onda
P3 Física IV - FAP2204 Escola Politécnica - 2009 GABARITO DA P3 8 de dezembro de 2009 Questão 1 Numaexperiência deespalhamentocompton, umelétrondemassam 0 emrepousoespalha um fóton de comprimento de onda
Física IV Poli Engenharia Elétrica: 14ª Aula (02/10/2014)
 Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
Física IV Poli Engenharia Elétrica: 14ª Aula (/1/14) Prof Alvaro Vannucci Na última aula vimos: xp / Princípio de Incerteza de Heisenberg: E t / d Equação de Schrödinger: U E mdx Propriedades de : (i)
PGF Mecânica Clássica Prof. Iberê L. Caldas
 PGF 5005 - Mecânica Clássica Prof Iberê L Caldas Quarto Estudo Dirigido o semestre de 08 Os estudos dirigidos podem ser realizados em duplas Apenas os exercícios marcados com asteriscos precisam ser entregues
PGF 5005 - Mecânica Clássica Prof Iberê L Caldas Quarto Estudo Dirigido o semestre de 08 Os estudos dirigidos podem ser realizados em duplas Apenas os exercícios marcados com asteriscos precisam ser entregues
Prof. Dr. Lucas Barboza Sarno da Silva
 Prof. Dr. Lucas Barboza Sarno da Silva Uma outra vez a experiência da dupla fenda 18/11/015 Prof. Dr. Lucas Barboza Sarno da Silva Probabilidade de chegada do elétron, com a fenda fechada: * 1 1 1 * Probabilidade
Prof. Dr. Lucas Barboza Sarno da Silva Uma outra vez a experiência da dupla fenda 18/11/015 Prof. Dr. Lucas Barboza Sarno da Silva Probabilidade de chegada do elétron, com a fenda fechada: * 1 1 1 * Probabilidade
Aspectos Quânticos da Óptica Não Linear
 Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
