c + 1+t 2 (1 + t 2 ) 5/2 dt e 5 2 ln(1+t2 )dt (1 + t 2 ) 5/2 dt (c 5/2 + (1 + t 2 ) 5/2 (1 + t 2 ) 5/2 dt ϕ(t) = (1 + t 2 ) 5/2 (1 + t).
|
|
|
- Luca Paranhos Gil
- 5 Há anos
- Visualizações:
Transcrição
1 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas de valor inicial, indicando os intervalos de existência das respectivas soluções: (a) ϕ = 5tϕ + t 2 + ( + t2 ) 5/2, ϕ(0) = Resoluç ão Cálculo da solução geral pela f ormula da variação das constantes: ϕ(t) = e ˆ 5t +t (c 2 dt + ( e ) 5t +t 2 ( + t 2 ) 5/2 dt ) e 5 2 ln(+t2 )dt ( + t 2 ) 5/2 dt ˆ = e 5 2 ln(+t2 )dt c + ˆ ) = ( + t 2 ) (c 5/2 + ( + t 2 ) 5/2 ( + t 2 ) 5/2 dt = ( + t 2 ) 5/2 (c + t) A condição inicial ϕ(0) = implica c = A solução do problema de valor inicial dado será então ϕ(t) = ( + t 2 ) 5/2 ( + t) Esta função está definida em R, e no seu domínio, é diferenciável e satisfaz a equação diferencial, pelo que é uma solução global Logo, o intervalo máximo de existência é R [,0 val (b) dy dx = x3 e x4 +y, y(0) = 0 Cálculo da solução geral: Resoluç ão dy dx = x3 x4 +y e ˆ e y = y dy e dx = x3 e x4 d dx ( e y ) = x 3 e x4 x 3 e x4 dx = ex4 4 + c y(x) = ln ) ( ex4 4 c A condição inicial y(0) = 0 implica 4 c =, ou seja, c = 5 4 A solução do problema de valor inicial será então ( ) 5 y(x) = ln 4 ex4 4
2 Calculemos o maior intervalo que inclui zero e onde esta expressão está bem definida: 5 4 ex4 4 > 0 ex4 < 5 x 4 ln 5, 4 [ ln 5 e, portanto, este será o intervalo de existência procurado [,0 val 2 (a) Determine a solução geral do sistema [ x 2 4 = 2 2 x Resoluç ão O polinómio característico tem raízes ±2i Considerando λ = 2i, temos que as duas soluções linearmente independentes serão respectivamente a parte real e imaginária da solução complexa z = e 2it v, onde v é um vector próprio associado ao valor próprio 2i O conjunto dos vectores próprios associado a λ = 2i é um espaço linear de dimensão, gerado por exemplo pelo vector [ ( + i) A solução geral do sistema é então dada por x(t) = c [ 2 cos(2t + 5π 4 ) cos(2t) + c 2 [ 2 sen(2t + 5π 4 ) sen(2t), com c, c 2 R [,0 val (b) Determine a solução do problema de valor inicial [ [ x = x , x(0) = Sugestão: Encontre uma solução particular constante Resoluç ão Seguindo a sugestão, procuramos uma solução particular da equação nãohomogénea que seja constante, e, como tal, satisfaça o sistema [ = x + [ 2 4 [ 3
3 A solução é [ 5 x p = 3 Determinamos agora a solução (única) do problema de valor inicial em x = x h + x p, onde x h é uma solução da eq homogénea determinada na alínea anterior Obtemos c = 6 e c 2 = 2, pelo que x(t) = [ cos(2t + 5π 4 ) 2 2 sen(2t + 5π 4 ) cos(2t) 2 sen(2t) [2,0 val 3 Determine a solução geral da equação y 2y + 2y = 4t A equação homogénea pode escrever-se (D 3 2D 2 + 2D)y = 0 D(D i)(d + i)y = 0, e tem portanto como solução geral y(t) = A + Be t cos t + Ce t sen t Por outro lado, qualquer solução da equação não homogénea satisfaz D 3 (D i)(d + i)y = 0, e portanto existe uma solução particular da forma y p (t) = Et 2 + Ft Substituindo na equação obtemos y p (t) = t 2 + 2t, pelo que a solução geral é y(t) = t 2 + 2t + A + Be t cos t + Ce t sen t [,0 val 4 (a) Determine a série Fourier da função f : [ 2π, 2π R dada por { x, 0 x π, f (x) = 2π x, π x 2π, e que satisfaz f ( x) = f (x) 3
4 A função f é ímpar, e portanto a série de Fourier de f é com b n sen n 2 x, n= b n = π = π ˆ 2π 0 ˆ π 0 = 8 πn 2 sen nπ 2 f (x) sen n 2 x dx x sen n 2 x dx + π Portanto a série de Fourier de f é 8 π ( ) n (2n + ) ˆ 2π π 2n + sen x 2 2 (2π x) sen n 2 x [,0 val (b) Resolva o problema de valor inicial com condições na fronteira u t = 2 u sen(x/2), 0 < x < 2π, 0 < t, x 2 u(t, 0) = u(t, 2π) = 0, 0 t, u(0, x) = f (x), 0 x 2π Como a equação diferencial não é homogénea, procuramos uma solução particular estacionária, v = v(x) Obtemos v (x) = sen(x/2), e portanto v(x) = 4 sen x/2 é uma solução particular que satisfaz as condições de fronteira Segue-se que é uma solução do problema se e só se u(t, x) = w(t, x) 4 sen x/2 w t = 2 w 0 < x < 2π, 0 < t, x 2 w(t, 0) = w(t, 2π) = 0, 0 t, w(0, x) = f (x) + 4 sen x/2, 0 x 2π 4
5 Separando variáveis, vemos que w(t, x) = T(t) X(x), satisfaz a equação diferencial e as condições de fronteira se e só se { T X = T X, 0 < x < 2π, 0 < t, T(t) X(0) = T(t) X(2π) = 0, 0 t Segue-se que X + λx = 0, T + λt = 0 com λ constante Para obter soluções não nulas que satisfazem X(0) = X(2π) = 0 devemos escolher λ = n 2 /4 Sobrepondo estas soluções obtemos w(t, x) = b n e n2t/4 sen n 2 x n= Aplicando w(0, x) = f (x) + 4 sen x/2 obtém-se Logo f (x) = 4 sen x/2 + = 8 π u(t, x) = 4(e t/4 ) sen x π ( ) n (2n + ) b n sen n 2 x n= 2n + sen 2 2 x ( ) n (2n + ) 2 e (2n+)2 t/4 sen 2n + x 2 [2,0 val 5 Seja f : R 2 R de classe C, tal que para a : R + R + contínua se tem (t,y) (R + 2, f (t, y) a(t)y ) Para (t 0, y 0 ) (R + ) 2, diga o que pode afirmar quanto à existência e unicidade locais de solução do problema de valor inicial y = f (t, y) arctg y, y(t 0 ) = y 0 Poderá concluir que o intervalo máximo de existência I max contém [t 0, +[? 5
6 (i) A função (t, y) f (t, y) sen y é de classe C em R 2 e, portanto, contínua e localmente Lipschitz relativamente a y, pelo que as hip oteses do teorema de Picard são satisfeitas para qualquer condição inicial (t 0, y 0 ) R 2 e, em particular, para a dada, donde se conclui a existência e unicidade locais de solução para o problema de valor inicial dado (ii) u(t) = 0, para todo o t, é uma solução da equação diferencial Logo, se existisse outra solução que assumisse o valor 0 para algum t, existiria um ponto em que a unicidade local assegurada pelo teorema de Picard seria violada, o que seria absurdo Logo, y(t) será uma função contínua no seu intervalo máximo de existência I max =α, ω[, que satisfaz y(t 0 ) > 0 e y(t) = 0, para todo o t I max Logo, y(t) > 0, para todo o t I max (iii) Pela alínea anterior, y(t) não pode explodir para Mostremos que não explode em tempo finito, ou seja, não pode ocorrer ω < + e y(t) + quando t ω Seja y a a solução do problema de valor inicial ou seja, y a (t) = y 0 e π 2 y a = π 2 a(t)y a, y a (t 0 ) = y 0, t t 0 a(s)ds, definido em todo R + Uma vez que, (t,y) (R + ) 2 f (t, y) arctg y π 2 f (t, y) π 2 a(t)y, e que y(t 0 ) = y a (t 0 ) > 0, por comparação de soluções concluímos que, para todo t [t 0, ω[, 0 < y(t) y a (t) Logo a solução não explode nem para nem para +, pelo que, ω = +, ou seja, [t 0, +[ I max 6
7 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão B MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat Resolva os seguintes problemas de valor inicial, indicando os intervalos de existência das respectivas soluções: [,0 val (a) y = 3xy + x 2 + ( + x2 ) 3/2, y(0) = Resoluç ão y = x + (x 2 + ) 3/2, Logo, o intervalo máximo de existência é R [,0 val (b) dϕ dt = tet2 +ϕ, ϕ() = 0 Resoluç ão φ = log ( ) e t2 + 2 e 2 Logo, o intervalo máximo de existência é log(e 2), [ [,0 val 2 (a) Determine a solução geral do sistema x = [ x Resoluç ão [ cos(2t) sen(2t) sen(2t) x = 2 sen(2t) sen(2t) + cos(2t) [ a b [,0 val (b) Determine a solução do problema de valor inicial x = [ [ 2 x + 6 [ 2, x(0) = 6 Sugestão: Encontre uma solução particular constante
8 [ sen(2t) x = + 5 sen(2t) + 5 cos(2t) [2,0 val 3 Determine a solução geral da equação y 4y + 5y = 0 c + c 2 t + e 2t (c 3 cos t + c 4 sen t) + t 2 [,0 val 4 (a) Determine a série Fourier da função f : [ 2π, 2π R dada por { x, 0 x π f (x) = 2π x, π x 2π e que satisfaz f ( x) = f (x) A função f é par, e portanto a série de Fourier de f é com a 0 = π a n = π ˆ 2π 0 ˆ π a a n cos n 2 x, n= f (x) cos n 2 x dx ˆ 2π = x cos n π 0 2 x dx + (2π x) cos n π π 2 x = 4 [ πn 2 2 cos nπ 2 ( + ( )n ) 2
9 Tem-se a 2n+ = 0, a 4n = 0 e a 4n+2 = 4/π(2n + ) 2 Portanto a série de Fourier de f é π 2 4 cos(2n + )x π (2n + ) 2 [,0 val (b) Resolva o problema de valor inicial com condições na fronteira u t = 2 u + cos x, 0 < x < 2π, 0 < t, x 2 u x (t, 0) = u x (t, 2π) = 0, 0 t, u(0, x) = f (x), 0 x 2π Como a equação diferencial não é homogénea, procuramos uma solução particular estacionária, v = v(x) Obtemos v (x) = cos x, e portanto v(x) = cos x é uma solução particular que satisfaz as condições de fronteira Segue-se que u(t, x) = w(t, x) + cos x é uma solução do problema se e só se w t = 2 w 0 < x < 2π, 0 < t, x 2 w x (t, 0) = w x (t, 2π) = 0, 0 t, w(0, x) = f (x) cos x, 0 x 2π Separando variáveis, vemos que w(t, x) = T(t) X(x), satisfaz a equação diferencial e as condições de fronteira se e só se { T X = T X, 0 < x < 2π, 0 < t, T(t) X (0) = T(t) X (2π) = 0, 0 t Segue-se que X + λx = 0, T + λt = 0 com λ constante Para obter soluções não nulas que satisfazem X (0) = X (2π) = 0 devemos escolher λ = n 2 /4 Sobrepondo estas soluções obtemos w(t, x) = a 0 + a n e n2t/4 cos n 2 x n= 3
10 Aplicando w(0, x) = f (x) cos x obtém-se Logo f (x) = cos x + a 0 + = π 2 4 π u(t, x) = ( e t/4 ) cos x + π 2 4 π a n cos n 2 x n= cos(2n + )x (2n + ) 2 (2n + ) 2 e (2n+)2 t/4 cos(2n + )x [2,0 val 5 Seja f : R 2 R de classe C, tal que para a : R + R + contínua se tem (t,y) (R + 2, f (t, y) a(t)y ) Para (t 0, y 0 ) (R + ) 2, diga o que pode afirmar quanto à existência e unicidade locais de solução do problema de valor inicial y = f (t, y) arctg y, y(t 0 ) = y 0 Poderá concluir que o intervalo máximo de existência I max contém [t 0, +[? (i) A função (t, y) f (t, y) sen y é de classe C em R 2 e, portanto, contínua e localmente Lipschitz relativamente a y, pelo que as hip oteses do teorema de Picard são satisfeitas para qualquer condição inicial (t 0, y 0 ) R 2 e, em particular, para a dada, donde se conclui a existência e unicidade locais de solução para o problema de valor inicial dado (ii) u(t) = 0, para todo o t, é uma solução da equação diferencial Logo, se existisse outra solução que assumisse o valor 0 para algum t, existiria um ponto em que a unicidade local assegurada pelo teorema de Picard seria violada, o que seria absurdo Logo, y(t) será uma função contínua no seu intervalo máximo de existência I max =α, ω[, que satisfaz y(t 0 ) > 0 e y(t) = 0, para todo o t I max Logo, y(t) > 0, para todo o t I max (iii) Pela alínea anterior, y(t) não pode explodir para Mostremos que não explode em tempo finito, ou seja, não pode ocorrer ω < + e y(t) + quando t ω Seja y a a solução do problema de valor inicial y a = π 2 a(t)y a, y a (t 0 ) = y 0, 4
11 ou seja, y a (t) = y 0 e π t 2 t a(s)ds 0, definido em todo R + Uma vez que, (t,y) (R + ) 2 f (t, y) arctg y π 2 f (t, y) π 2 a(t)y, e que y(t 0 ) = y a (t 0 ) > 0, por comparação de soluções concluímos que, para todo t [t 0, ω[, 0 < y(t) y a (t) Logo a solução não explode nem para nem para +, pelo que, ω = +, ou seja, [t 0, +[ I max 5
12 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às :30 Teste 2 versão C MEAmbi, MEBiol, MEEC, MEQ, LEIC [2,0 val Considere o seguinte problema de valor inicial: 2e x y + (e x ye x ) dy = 0 y(0) = /2 dx Mostre que a equação diferencial possui um factor integrante na forma µ = µ(x) e resolva o problema, indicando o intervalo máximo de existência da solução A função µ(x) é um factor integrante daquela equação sse y (µ(x)2ex y) = x (µ(x)(ex ye x )) µ(x)2e x = µ (x)(e x ye x ) + µ(x)(e x + ye x ) µ (x)(e x ye x ) µ(x)(e x ye x ) = 0 µ (x) µ(x) = 0 µ(x) = ce x Um possível factor integrante é então µ(x) = e x e, multiplicando a equação diferencial por este factor obtemos a seguinte equação diferencial equivalente a qual sabemos ser exacta: 2ye 2x + (e 2x y) dy dx = 0 Logo, procuramos uma função Φ(x, y) tal que Φ(x, y) = 2ye 2x x Φ(x, y) = e 2x y y Primitivando a primeira equação obtém-se Φ(x, y) = ye 2x + C(y) Derivando esta expressão em ordem a y e usando a segunda equação, e 2x + C (y) = e 2x y, e, logo, C (y) = y, resultando C(y) = y2 2 + c, onde c é uma constante Portanto, Φ(x, y) = y2 2 + ye2x + c
13 As soluções da equação diferencial são então dadas implicitamente por y 2 2 ye2x c = 0 Usando a condição inicial y(0) = /2, obtemos 8 2 c = 0 c = 3 8 e, portanto, obtemos a forma implícita que define a solução do problema de valor inicial: y 2 2 ye2x = 0 A solução será dada então por y(x) = e 2x e 4x 3 4, onde a escolha da raiz do polinómio do segundo grau em y foi ditada novamente pela condição inicial y(0) = /2 Cálculo do intervalo máximo de existência da solução, I: Logo, e 4x 3 4 > 0 x > 4 ln 3 4, I = ln 4 3 4, +[ [,0 val 2 (a) Determine a solução geral do sistema [ x 2 0 = 0 2 x Resoluç ão A matriz do sistema possui dois valores próprios reais e distintos, respectivamente λ = 2 e λ 2 = 2 Duas soluções linearmente independentes serão e 2t v e e 2t v 2, onde v e v 2 são vectores próprios associados a 2 e 2 respectivamente Podemos tomar v = e e v 2 = e 2 (os vectores da base canónica de R 2 ) 2
14 Então, a solução geral do sistema homogéneo será com c, c 2 R [ e 2t x = c 0 + c 2 [ 0 e 2t, [,0 val (b) Determine a solução do problema de valor inicial x = [ [ 2e 2t x + te 2t [, x(0) = 2 Como Resoluç ão F(t) = [ e 2t 0 0 e 2t é uma matriz fundamental de soluções e se tem que F(0) = I, podemos concluir que F(t) = e At para A = [ Então, ( e At) = e At, e pela fórmula da variação das constantes podemos concluir que a solução do problema de valor inicial é dada por [ e 2t x = 0 [ e 2t + x p, onde x p = = ˆ t 0 ˆ t e A(t s) [ 2e 2s [ 2e 2t 0 se 2t se 2s ds = ds [ 2e 2t s s 2 2 e 2t s=t s=0 = [ 2e 2t t t 2 2 e 2t () [2,0 val 3 Determine a solução geral da equação y + 2y + y = e t 3
15 A equação homogénea pode escrever-se e tem portanto como solução geral (D 3 + 2D 2 + D)y = 0 D(D + ) 2 y = 0, y(t) = A + Be t + Cte t Por outro lado, qualquer solução da equação não homogénea satisfaz D(D + ) 2 (D )y = 0, e portanto existe uma solução particular da forma y p (t) = Ee t Substituindo na equação obtemos y p (t) = 4 et, pelo que a solução geral é y(t) = 4 et + A + Be t + Cte t [,0 val 4 (a) Determine a série Fourier da função f : [π, π R dada por { 0 se π x < 0, f (x) = se 0 x π, estude-a quando à convergência pontual em [ π, π, e calcule ( ) n /(2n + ) A série de Fourier de f (x) é a a n cos nx + b n sen nx n+ 4
16 com a 0 = a n = π = 0 b n = π = π Portanto a série de Fourier de f é π ˆ π 0 ˆ π 0 cos nx dx sen nx dx cos(nπ) n sen(2n + )x 2n + Tem-se sen(2n + )x π 2n + 0 se π < x < 0, = se 0 < x < π, /2 se x = 0 ou x = ±π, e a série é periódica de período 2π Sendo x = π/2 tem-se e portanto π 4 = ( ) n 2n + = π ( ) n 2n +, [,0 val (b) Resolva o problema de valor inicial com condições na fronteira u t 2 u = u, 0 < x < π, 0 < t, x 2 u x (t, 0) = u x (t, π) = 0, 0 t, u(0, x) =, 0 x π Seja u(t, x) = T(t) X(x) A função u satisfaz a equação diferencial e as 5
17 condições de fronteira se e só se { T X T X = T X, 0 < x < π, 0 < t, T(t) X (0) = T(t) X (π) = 0, 0 t Segue-se que X + λx = 0, T + (λ )T = 0 com λ constante Para obter soluções não nulas que satisfazem X (0) = X (π) = 0 devemos escolher λ = n 2 Sobrepondo estas soluções obtemos u(t, x) = a 0 e t + Aplicando u(0, x) = obtém-se = a 0 + a n e ( n2)t cos nx n= a n cos nx n= Logo u(t, x) = e t [2,0 val 5 Seja f : R R contínua não identicamente nula tal que f (0) = 0 Considere o seguinte problema de valor inicial (PVI): dx = f (x), x(0) = 0 dt Dado t > 0, considere o conjunto J(t ) = {y R : existe solução do PVI, x(t), tal que x(t ) = y} Mostre que J(t ) é um intervalo Indique uma condição adicional que garanta que J(t ) = {0} Uma solução do PVI é x(t) = 0, para todo t e, portanto, 0 J(t ) Assim, para mostrar que J(t ) é um intervalo basta mostrar que se existe y = 0 tal que y J(t ), então, dado um qualquer y entre 0 e y, verifica-se y J(t ) Assim, suponhamos que existe y J(t ) \ {0} Pela definição de J(t ), existe uma solução do PVI, digamos φ(t), tal que φ(t ) = y Mas então, para cada c [0, t dado, a função { 0, se 0 t c, x c (t) = φ(t c), se c < t t 6
18 é também uma solução do PVI Como φ(t) é diferenciável e, portanto, contínua, pela continuidade da composta de duas funções contínuas, c φ(t c), ou seja, a correspondência c x c (t ) é contínua Como, x 0 (t ) = y e x t (t ) = 0, pelo teorema de Bolzano, dado qualquer y entre 0 e y, existe c [0, t tal que, x c (t ) = y Logo, y J(t ) Se f é de classe C, o teorema de Picard garante unicidade de solução, e portanto x(t) = 0 é a única solução do PVI Segue-se que com esta condição adicional se tem J(t ) = {0} 7
19 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às :30 Teste 2 versão D MEAmbi, MEBiol, MEEC, MEQ, LEIC [2,0 val Considere o seguinte problema de valor inicial: 3e x y + (ye 2x + e x ) dy dx = 0 y(0) = 3/2 Mostre que a equação diferencial possui um factor integrante na forma µ = µ(x) e resolva o problema, indicando o intervalo máximo de existência da solução [,0 val [,0 val [2,0 val 2 (a) Determine a solução geral do sistema x = [ x (b) Determine a solução do problema de valor inicial x = [ Determine a solução geral da equação [ 3e 3t x + te 3t [ 2, x(0) = 3 y 4y + 4y = e t [,0 val 4 (a) Determine a série Fourier da função f : [π, π R dada por { se x < π/2, f (x) = 0 caso contrário, estude-a quando à convergência pontual em [ π, π, e calcule ( ) n /(2n + ) A função f é par e a série de Fourier de f (x) é a a n cos nx n+
20 com a 0 = ˆ π/2 Portanto a série de Fourier de f é a n = 2 cos nx dx π 0 = 2 sen nπ/2 nπ 0 se n é par, = ( ) m 2 se n = 2m + (2m + )π π n cos(2n + )x ( ) 2n + Tem-se π n cos(2n + )x ( ) 2n + se x < π/2, = /2 se x = ±π/2, 0 caso contrário, e a série é periódica de período 2π Sendo x = 0 tem-se e portanto = π ( ) n 2n +, π 4 = ( ) n 2n + [,0 val (b) Resolva o problema de valor inicial com condições na fronteira 2 u u x 2 t =, 0 < x < π, 0 < t, u(t, 0) = u(t, π) =, 0 t u(0, x) = 2 x2 π 2 x, 0 x π Sugestão: Considere uma solução u(t, x) = v(x) + w(t, x), com d2 v dx 2 = 2
21 Seja u(t, x) = x 2 /2 + Ax + B + w(t, x) A função u é uma solução do problema se e só se 2 w w x 2 t = 0, B + w(t, 0) = π 2 /2 + Aπ + B + w(t, π) =, x 2 /2 + Ax + B + w(0, x) = x 2 /2 πx/2 Escolhendo B = e A = π 2 obtemos Segue-se que w(t, x) = 0, donde 2 w w x 2 t = 0, w(t, 0) = w(t, π) = 0, w(0, x) = 0 u(t, x) = x 2 /2 πx/2 [2,0 val 5 Seja f : R R contínua não identicamente nula tal que f (0) = 0 Considere o seguinte problema de valor inicial (PVI): dx dt Dado t > 0, considere o conjunto = f (x), x(0) = 0 J(t ) = {y R : existe solução do PVI, x(t), tal que x(t ) = y} Mostre que J(t ) é um intervalo Indique uma condição adicional que garanta que J(t ) = {0} 3
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais 2 ō Semestre 2012/2013
 Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec
 Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
d [xy] = x cos x. dx y = sin x + cos x + C, x
![d [xy] = x cos x. dx y = sin x + cos x + C, x d [xy] = x cos x. dx y = sin x + cos x + C, x](/thumbs/66/55981826.jpg) Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
ANÁLISE MATEMÁTICA IV EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN. tet + t
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Introdução às Equações Diferenciais e Ordinárias
 Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
x + 2 > 1 (x 2)(x + 2) x + 2 > e
 Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I 1. Desenhe um campo de direções para a equação diferencial dada. Determine o comportamento de y quando t +. Se esse comportamento depender do valor inicial de
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I 1. Desenhe um campo de direções para a equação diferencial dada. Determine o comportamento de y quando t +. Se esse comportamento depender do valor inicial de
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
d [xy] = x arcsin x. dx + 4x
![d [xy] = x arcsin x. dx + 4x d [xy] = x arcsin x. dx + 4x](/thumbs/65/53462517.jpg) Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
y (n) (x) = dn y dx n(x) y (0) (x) = y(x).
 Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
EDO I. por Abílio Lemos. 16 e 18 de outubro de Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA. MATEMÁTICA APLICADA 1 o SEMESTRE 2016/2017
 3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
8.1-Equação Linear e Homogênea de Coeficientes Constantes
 8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 2017/2 - Mestrado
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 27/2 - Mestrado A prova é composta de 6 (seis) questões, das quais o candidato
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 27/2 - Mestrado A prova é composta de 6 (seis) questões, das quais o candidato
Curso: Engenharia Ambiental. Disciplina: Equações Diferenciais Ordinárias. Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2
 Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))
![GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1)) GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))](/thumbs/97/131760884.jpg) GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
x 2 y 6xy + 10y = 0, x > 0 y(1) = 1, y(2) = 18.
 Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
IST-TAGUS PARQUE-2007/08-2 o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO
 IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
Probabilidades e Estatística
 Departamento de Matemática Probabilidades e Estatística LEAN, LEE, LEGI, LEGM, LEIC-A, LEIC-T, LEMat, LERC, LMAC, MEAer, MEAmbi, MEBiol, MEBiom, MEEC, MEFT, MEMec, MEQ 2 o semestre 2/22 o TESTE (Época
Departamento de Matemática Probabilidades e Estatística LEAN, LEE, LEGI, LEGM, LEIC-A, LEIC-T, LEMat, LERC, LMAC, MEAer, MEAmbi, MEBiol, MEBiom, MEEC, MEFT, MEMec, MEQ 2 o semestre 2/22 o TESTE (Época
SEGUNDA PROVA DE EDB - TURMA M
 SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS
 FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
CÁLCULO III - MAT Encontre as soluções das seguintes equações com condições iniciais:
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0021 7 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0021 7 a Lista de exercícios
Análise Complexa e Equações Diferenciais
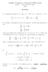 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Questão 1: (2.0 pontos) (a) (1.0 ponto) Obtenha os cinco primeiros termos da série de Taylor da função f(x) = cos x em.
 Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEE, LEIC-T, LEGI e LERC - o semestre - / de Junho de - 9 horas I ( val.). (5, val.) Determine o valor dos integrais: x + (i) x ln x dx (ii) (9 x )( + x ) dx (i) Primitivando
Cálculo Diferencial e Integral I LEE, LEIC-T, LEGI e LERC - o semestre - / de Junho de - 9 horas I ( val.). (5, val.) Determine o valor dos integrais: x + (i) x ln x dx (ii) (9 x )( + x ) dx (i) Primitivando
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
xy + y = 0. (1) Portanto a solução geral de (1) é a família de hipérboles y = C x,
 Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
ORDINÁRIAS. Víctor Arturo Martínez León
 INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
Cálculo Diferencial e Integral I 2 o Exame - (MEMec; MEEC; MEAmb)
 Cálculo Diferencial e Integral I o Exame - MEMec; MEEC; MEAmb) 7 de Julho de - 9 horas I val.). i) Sendo u n n do teorema das sucessões enquadradas, dado que n, tem-se u n. Como a sucessão u n é convergente,
Cálculo Diferencial e Integral I o Exame - MEMec; MEEC; MEAmb) 7 de Julho de - 9 horas I val.). i) Sendo u n n do teorema das sucessões enquadradas, dado que n, tem-se u n. Como a sucessão u n é convergente,
Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / a LISTA DE MAT-32
 1 Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / 2012. 1 a LISTA DE MAT-32 Nos exercícios de 1 a 9, classi car e apresentar, formalmente, solução (ou candidata a solução)
1 Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / 2012. 1 a LISTA DE MAT-32 Nos exercícios de 1 a 9, classi car e apresentar, formalmente, solução (ou candidata a solução)
Cálculo Diferencial e Integral I
 Resolução do exame Cálculo Diferencial e Integral I Versão B Data: 8/ / 8 Grupo I - (a) x 3 + x x = x(x + x ) = x(x + )(x ) Cálculo auxiliar: x + x = x = ± + 8 = ou x + + x + + + + + x + + + + x(x+)(x
Resolução do exame Cálculo Diferencial e Integral I Versão B Data: 8/ / 8 Grupo I - (a) x 3 + x x = x(x + x ) = x(x + )(x ) Cálculo auxiliar: x + x = x = ± + 8 = ou x + + x + + + + + x + + + + x(x+)(x
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Questão 1: (2.5 pontos) f(x) =
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
Análise Complexa e Equações Diferenciais Guia 8 João Pedro Boavida. 16 a 23 de Novembro
 Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
3xy +y 2 +(x 2 +xy) dy dx = 0 (1)
 2. Determine um factor integrante da forma µ(x). 3xy +y 2 +(x 2 +xy) dy (1) 3. Determine a solução da equação que verifica y(1) = 1. Sendo tem-se M(x,y) = 3xy +y 2 e N(x,y) = x 2 +xy M/ y = 3x+2y e N/
2. Determine um factor integrante da forma µ(x). 3xy +y 2 +(x 2 +xy) dy (1) 3. Determine a solução da equação que verifica y(1) = 1. Sendo tem-se M(x,y) = 3xy +y 2 e N(x,y) = x 2 +xy M/ y = 3x+2y e N/
g(s, X n s )ds + t f (s, X s ) 2 ds <, P-q.s. t f (s, X s )db s, t 0.
 CHAPTER 3. INTEGRAIS ESTOCÁSTICOS 88 2. Quais são as propriedades destas soluções? 3. Como podemos resolver uma dada equação? O método usual para provar a existência de uma solução da equação diferencial
CHAPTER 3. INTEGRAIS ESTOCÁSTICOS 88 2. Quais são as propriedades destas soluções? 3. Como podemos resolver uma dada equação? O método usual para provar a existência de uma solução da equação diferencial
1 [20] O problema difusivo
![1 [20] O problema difusivo 1 [20] O problema difusivo](/thumbs/100/145232198.jpg) TEA13 Matemática Aplicada II Curso de Engenharia Ambiental Departamento de Engenharia Ambiental UFPR F 1 Dez 218 Prof. Nelson Luís Dias Declaro que segui o código de ética do Curso de Engenharia Ambiental
TEA13 Matemática Aplicada II Curso de Engenharia Ambiental Departamento de Engenharia Ambiental UFPR F 1 Dez 218 Prof. Nelson Luís Dias Declaro que segui o código de ética do Curso de Engenharia Ambiental
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3]. Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg) Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
36 a Aula AMIV LEAN, LEC Apontamentos
 36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE 2A - 15 DE JUNHO DE DAS 11H. Apresente e justifique todos os cálculos. dy dt = y t t ; y(1) = 1.
 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de 2010
 Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
33 a Aula AMIV LEAN, LEC Apontamentos
 33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Complementos de Análise Matemática
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Ficha prática n o 3 - Equações Diferenciais 1. Determine as equações diferenciais das seguintes famílias de linhas: (a) y = cx (b) y = cx 3
Instituto Politécnico de Viseu Escola Superior de Tecnologia Ficha prática n o 3 - Equações Diferenciais 1. Determine as equações diferenciais das seguintes famílias de linhas: (a) y = cx (b) y = cx 3
Análise Complexa e Equações Diferenciais 1 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS. k + e 1 x, x > 0 f(x) = x cos 1, x > 0
 Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS I. Continuidade de Funções. 1) Considere a função f :
Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS I. Continuidade de Funções. 1) Considere a função f :
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEAmb, LEMat, LQ, MEB, MEEC, MEQ o teste / o eame - 7 de Janeiro de 8 duração: o teste: :3 / o eame: 3: Apresente todos os cálculos e justificações relevantes Para resolver
Cálculo Diferencial e Integral I LEAmb, LEMat, LQ, MEB, MEEC, MEQ o teste / o eame - 7 de Janeiro de 8 duração: o teste: :3 / o eame: 3: Apresente todos os cálculos e justificações relevantes Para resolver
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE
 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE Séries de Fourier (1 Desenvova
Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE Séries de Fourier (1 Desenvova
Lista 1 - Cálculo Numérico - Zeros de funções
 Lista 1 - Cálculo Numérico - Zeros de funções 1.) De acordo com o teorema de Bolzano, se uma função contínua f(x) assume valores de sinais opostos nos pontos extremos do intervalo [a, b], isto é se f(a)
Lista 1 - Cálculo Numérico - Zeros de funções 1.) De acordo com o teorema de Bolzano, se uma função contínua f(x) assume valores de sinais opostos nos pontos extremos do intervalo [a, b], isto é se f(a)
Equações Diferenciais com Derivadas Parciais
 1/13 Equações Diferenciais com Derivadas Parciais Chamam-se equações principais da física matemática às seguintes equações diferenciais com derivadas parciais de segunda ordem: 2/13 2 u t 2 = a 2 2 u x
1/13 Equações Diferenciais com Derivadas Parciais Chamam-se equações principais da física matemática às seguintes equações diferenciais com derivadas parciais de segunda ordem: 2/13 2 u t 2 = a 2 2 u x
Cálculo Diferencial e Integral I 1 o Sem. 2016/17 - LEAN, MEMat, MEQ FICHA 11 - SOLUÇÕES
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
Cálculo Diferencial e Integral II Resolução do Exame/Teste de Recuperação 02 de Julho de 2018, 15:00h - versão 2 Duração: Exame (3h), Teste (1h30)
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II do Exame/Teste de Recuperação 2 de Julho de 218, 15:h - versão 2 Duração: Exame (3h),
TEMPO DE PROVA: 2h30. 1 se 0 x < 1, 0 se 1 x 2. f(x) =
 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Análise Complexa e Equações Diferenciais 1 o Semestre de 2011/ o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2011, 10h,
 Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Análise Matemática II - 1 o Semestre 2001/ o Exame - 25 de Janeiro de h
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
MAT Cálculo Diferencial e Integral para Engenharia IV
 MAT456 - Cálculo Diferencial e Integral para Engenharia IV Parte A: Equações Diferenciais de 1 a Ordem o Semestre de 018-3 a Lista de exercícios 1) Os gráficos de duas soluções de y = x + y podem se cruzar
MAT456 - Cálculo Diferencial e Integral para Engenharia IV Parte A: Equações Diferenciais de 1 a Ordem o Semestre de 018-3 a Lista de exercícios 1) Os gráficos de duas soluções de y = x + y podem se cruzar
1 Definição de uma equação diferencial linear de ordem n
 Equações diferenciais lineares de ordem superior 1 1 Definição de uma equação diferencial linear de ordem n Equação diferencial linear de ordem n é uma equação da forma: a n (x) dn y dx n + a n 1(x) dn
Equações diferenciais lineares de ordem superior 1 1 Definição de uma equação diferencial linear de ordem n Equação diferencial linear de ordem n é uma equação da forma: a n (x) dn y dx n + a n 1(x) dn
Justifique todas as passagens. f v (0,0) = f(0,0) v.
 2 ā Prova de Cálculo II para Oceanográfico - MAT145 27/10/2010 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Justifique todas as passagens Q 1 2 3 4 5 6 7 Total N 1. Dê exemplos
2 ā Prova de Cálculo II para Oceanográfico - MAT145 27/10/2010 Nome : GABARITO N ō USP : Professor : Oswaldo Rio Branco de Oliveira Justifique todas as passagens Q 1 2 3 4 5 6 7 Total N 1. Dê exemplos
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
7.3 Diferenciabilidade
 CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
Lista 1 - Métodos Matemáticos II Respostas
 Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
1. Resolva as equações diferenciais: 2. Resolver os seguintes Problemas dos Valores Iniciais:
 Universidade do Estado de Mato Grosso - Campus de Sinop Cálculo Diferencial e Integral III - FACET Lista 6 Profª Ma. Polyanna Possani da Costa Petry 1. Resolva as equações diferenciais: a) y + 2y = 2e
Universidade do Estado de Mato Grosso - Campus de Sinop Cálculo Diferencial e Integral III - FACET Lista 6 Profª Ma. Polyanna Possani da Costa Petry 1. Resolva as equações diferenciais: a) y + 2y = 2e
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE MAIO DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
Lista 4. Funções de Uma Variável. Derivadas IIII. 3 Encontre y se y = ln(x 2 + y 2 ). 4 Encontre y se y x = x y.
 Lista 4 Funções de Uma Variável Derivadas IIII Encontre y se y = ln(x + y. Derivadas de Ordem Superior Calcule y e y para as seguintes funções: a y = tgh(6x b y = senh(7x c y = cotgh( + x d y = cosh(x
Lista 4 Funções de Uma Variável Derivadas IIII Encontre y se y = ln(x + y. Derivadas de Ordem Superior Calcule y e y para as seguintes funções: a y = tgh(6x b y = senh(7x c y = cotgh( + x d y = cosh(x
Matemática Computacional - 2 o ano LEMat e MEQ
 Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 5 de Fevereiro de - Parte I (h3m). Considere
Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 5 de Fevereiro de - Parte I (h3m). Considere
Módulo III: Processos de Poisson, Gaussiano e Wiener
 Módulo III: Processos de Poisson, Gaussiano e Wiener Wamberto J. L. Queiroz Universidade Federal de Campina Grande-UFCG Departamento de Engenharia Elétrica Processos Estocásticos Campina Grande - PB Módulo
Módulo III: Processos de Poisson, Gaussiano e Wiener Wamberto J. L. Queiroz Universidade Federal de Campina Grande-UFCG Departamento de Engenharia Elétrica Processos Estocásticos Campina Grande - PB Módulo
Equações Diferenciais Ordinárias de Ordem Superior a Um
 Capítulo 2 Equações Diferenciais Ordinárias de Ordem Superior a Um 2.1 EDOs lineares homogéneas de ordem dois. Redução de ordem. Exercício 2.1.1 As seguintes equações diferenciais de 2 a ordem podem ser
Capítulo 2 Equações Diferenciais Ordinárias de Ordem Superior a Um 2.1 EDOs lineares homogéneas de ordem dois. Redução de ordem. Exercício 2.1.1 As seguintes equações diferenciais de 2 a ordem podem ser
t 2 se t 0 Determine a expansão em série de potências para a função F (x) = ( 1) n y2n (2n)!, ( 1) n t4n (2n)! (2n)! ( 1) n t4n 2 dt = ( 1) n t 4n 2 )
 MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
CURSO DE RESOLUÇÃO DE PROVAS de MATEMÁTICA da ANPEC Tudo passo a passo com Teoria e em sequência a resolução da questão! Prof.
 Prof. Chico Vieira MATEMÁTICA da ANPEC Tudo Passo a Passo Teoria e Questões FICHA com LIMITES, DERIVADAS, INTEGRAIS, EDO, SÉRIES Integrais Dupla e Tripla LIMITES ANPEC QUESTÕES JÁ GRAVADAS DERIVADAS ANPEC
Prof. Chico Vieira MATEMÁTICA da ANPEC Tudo Passo a Passo Teoria e Questões FICHA com LIMITES, DERIVADAS, INTEGRAIS, EDO, SÉRIES Integrais Dupla e Tripla LIMITES ANPEC QUESTÕES JÁ GRAVADAS DERIVADAS ANPEC
24 a Aula AMIV LEAN, LEC Apontamentos
 24 a Aula 2004.11.10 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 24.1 Método de Euler na aproximação de EDO s Métodos numéricos para a determinação de soluções de EDO s podem ser analisados
24 a Aula 2004.11.10 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 24.1 Método de Euler na aproximação de EDO s Métodos numéricos para a determinação de soluções de EDO s podem ser analisados
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
32 a Aula AMIV LEAN, LEC Apontamentos
 32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
Exame (1º Teste) de Análise Numérica (LMAC, MEIC, MMA) Instituto Superior Técnico, 11 de Janeiro de 2016, 15h00-16h15 (1º Teste)
 Exame (º Teste) de Análise Numérica (LMAC, MEIC, MMA) Instituto Superior Técnico, de Janeiro de 6, h-6h (º Teste) ) [] a) Determine p, o polinómio de menor grau tal que p() = a, p() = b, p () = p () =
Exame (º Teste) de Análise Numérica (LMAC, MEIC, MMA) Instituto Superior Técnico, de Janeiro de 6, h-6h (º Teste) ) [] a) Determine p, o polinómio de menor grau tal que p() = a, p() = b, p () = p () =
