Redes Neurais e Sistemas Fuzzy
|
|
|
- Terezinha Nobre Salgado
- 7 Há anos
- Visualizações:
Transcrição
1 Redes Neurais e Sistemas Fuzzy Conceitos Básicos da Lógica Fuzzy. Raciocínio aproximado Raciocínio aproximado é a forma mais conhecida de lógica fuzzy, cobrindo várias regras de inferência cujas premissas contêm proposições fuzzy. Uma proposição fuzzy é uma representação simbólica para uma expressão em linguagem natural, envolvendo variáveis lingüísticas. As regras de inferência são expressas como declarações Se - Então. Existem dois métodos diretos importantes de raciocínio fuzzy: o método direto de Mamdani e a modelagem fuzzy de Takagi-Sugeno (T-S). O método de Mamdani é o mais popular baseado numa estrutura simples de operações min-max, envolvendo regras de inferência do tipo: Se x é A e y é B Então z é C onde A, B e C são conjuntos fuzzy O método de T-S modela o consequente da regra como uma equação linear Se x é A e y é B Então z = ax + by + c Neste caso, devemos aplicar técnicas de modelagem usando dados de entrada-saída para obter as regras. 2
2 Exemplo de raciocínio aproximado Considere a regra abaixo: Se a temperatura da sala é pouco alta E a umidade é alta Então ajuste o seletor do ar-condicionado para alto. Neste caso temos a correspondência para a regra de produção (RP) como: Se x é A e y é B Então z é C com x: temperatura da sala; y: umidade; z: seletor do ar-condicionado; e A: pouco alta; B: alta; C: alto µ pouco alta µ alta µ alto 25 T[ C] 80 U[%] A regra equivalente para o método T-S seria: Se x é A e y é B Então z = 0,2x + 0,05y 9 S 3 2 Mecanismos de raciocínio fuzzy O raciocínio fuzzy pode ser visto como uma generalização do raciocínio da lógica binária, que é baseado nos mecanismos complementares modus ponens MP e modus tollens MT. Estes mecanismos são utilizados para raciocinar com regras de produção (RP) baseadas na implicação : Se A, então B ou A B. No MP, se a regra A B for válida e se A for verdadeiro, então nós podemos deduzir que B também é verdadeiro. premissa : A B Se x é A Então y é B premissa 2: A x é A conseqüência: B y é B No MT, se a regra A B for válida e se B for falso, então A é falso. premissa : A B Se x é A Então y é B premissa 2: não B y é não B conseqüência: não A x é não A 4
3 Exemplo de MP Considere o seguinte exemplo de MP em forma de regra P : Se temperatura é menor que 0 C Então aumente o aquecedor P 2 : Temperatura é 5 C C: Aumente o aquecedor A premissa 2 satisfaz completamente a condição da premissa e assim concluimos aumente o aquecedor. O raciocínio fuzzy é baseado no modus ponens generalizado MPG: P : Se x é A Então y é B P 2 : x é A C: y é B onde A, A, B e B são conjuntos fuzzy, sendo A e A conjuntos diferentes, assim como B e B são também diferentes. 5 Exemplo de MPG No MPG A e A são conjuntos fuzzy diferentes mas, apesar disso, podemos inferir a conclusão y é B da premissa y é B, com base na sua similaridade. Por causa disso o raciocínio fuzzy é algumas vezes chamado de raciocínio aproximado. Na lógica binária, A e A nas premissas e 2 devem ser exatamente iguais. O raciocínio humano é parecido com o raciocínio fuzzy. Se, por exemplo, aplicarmos o MPG ao exemplo anterior obteríamos: P : Se temperatura é baixa Então aumente o aquecedor P 2 : Temperatura é muito baixa C: Aumente muito o aquecedor O raciocínio fuzzy é particularmente flexível quando está baseado em múltiplas regras. Neste caso, a adequação do antecedente de cada regra é usada para estabelecer a conclusão de cada regra. Finalmente, as conclusões individuais devem ser agregadas obtendo-se uma conclusão global. 6
4 3. Implicação fuzzy A declaração condicional Se - Então representa uma regra de produção (RP) envolvendo predicados imprecisos. Uma regra de produção é expressa por uma relação fuzzy representando uma implicação fuzzy (IF). A escolha da função IF reflete critérios intuitivos e o efeito do conectivo também utilizado para conectar as diversas regras da base de conhecimento. As características básicas desejáveis de uma função IF são: suavidade, inferência irrestrita, simetria do MPG (Modus Ponens Generalizado) e do MTG (Modus Tollens Generalizado), medida de propagação da incerteza. Uma determinada IF satisfaz um conjunto de critérios relacionados às regras de inferência para raciocínio qualitativo e alguns modificadores lingüísticos: MPG MTG P : x é A P : y é B P 2 : Se x é A então y é B P 2 : Se x é A então y é B C: y é B C: x é A sendo A e B obtidos pelos modificadores: muito, mais ou menos, não. 7 Relação entre antecedentes e conseqüentes na IF Critérios intuitivos relacionando P e C para um P 2 do MPG Crit. : x é A y é B Crit. 2-: x é muito A y é muito B Crit. 2-2: x é muito A y é B Crit. 3-: x é mais ou menos A y é mais ou menos B Crit. 3-2: x é mais ou menos A y é B Crit. 4-: x é não A y é desconhecido Crit. 4-2: x é não A y é não B Critérios intuitivos relacionando P e C para um P 2 do MTG Crit. 5: y é não B xé não A Crit. 6: y é não muito B x é não muito A Crit. 7: y é não mais ou menos B x é não mais ou menos A Crit. 8-: y é B xé desconhecido Crit. 8-2: y é B xé A 8
5 Exemplo de modificadores Os modificadores lingüísticos são implementados por funções algébricas aplicadas sobre o conjunto fuzzy que expressa o conceito original. Considere um conjunto fuzzy A representado por A (x). Os principais modificadores utilizados são: muito A : muito A (x) = ( A (x)) 2 mais ou menos A: mais ou menos A (x) = ( A (x)) /2 Considere que o valor lingüístico alto seja representada pelo conjunto fuzzy A = 0,2/60 + 0,5/70 + /80. Determine os conjuntos fuzzy relativos ao conceito muito alto: muito A (x) = ( A (x)) 2 = 0,04/60 + 0,25/70 + /80 mais ou menos alto 0,5 0,2 50 alto ,25 0,04 50 muito alto ,7 0, Implicação de Mamdani: regra do mínimo Baseada no cálculo proposicional: A B = ( A) (AB) A B A B F F V F V V V F F V V V A AB A AB V F V V F V F F F F V V Os graus de pertinência desta relação de implicação R c : A(x) B(y) são calculados pela conjunção, ou o mínimo, dos conjuntos fuzzy A(x) e B(y). R c = A B = X Y A (x) B (y) / (x, y) µ Rc (x,y) = min(µ A (x), µ B (y)) O conjunto B que representa a conseqüência da aplicação do MPG é calculado pela regra de inferência composicional, considerando a composição do conjunto A de P com a relação R c de P 2. B = A o R c 0
6 Interpretação de uma Base de Regras Uma base de regras envolvendo a implicação (completa) é interpretada como a interseção (produto) das regras individuais, por exemplo: BR: R R 2 R 3 R 4 com: R : A B ; R 2 : A 2 B 2 ; R 3 : A 3 B 3 ; R 4 : A 4 B 4 ; Como cada regra se aplica apenas a uma região da partição (A A 2 A 3 A 4 ), apenas uma regra estará ativa, enquanto as outras fornecem o valor que é o valor neutro do produto. Exemplo: Se A = A 2 Então B: B 2 = B 2 Uma base de regras envolvendo a implicação incompleta (apenas o ) deve ser interpretada como a união (soma) das regras individuais, por exemplo: BR: R R 2 R 3 R 4 com: R : A B ; R 2 : A 2 B 2 ; R 3 : A 3 B 3 ; R 4 : A 4 B 4 ; Como cada regra se aplica apenas a uma região da partição, apenas uma regra estará ativa, enquanto as outras fornecem o valor 0 que é o valor neutro da soma. Exemplo: Se A = A 2 Então B: 0 B = B 2 Representação de um conjunto de regras x x 2 SIF y x 2 y C 2 R R 2 R = A B C 2 R 2 = A B 2 C 2 B 2 A B 2 A 2 B 2 C R 3 = A 2 B C R 4 = A 2 B 2 C A B = ( A) (AB) B A B A A 2 B A 2 x A A B = AB A 2 x R 3 R 4 B B 2 x 2 x x 2 R R 2 R 3 R 4 R i A B C 2 V V V C 2 A B 2 V C 2 V V C 2 A 2 B V V C V C A 2 B 2 V V V C C x x 2 R R 2 R 3 R 4 R i A B C 2 F F F C 2 A B 2 F C 2 F F C 2 A 2 B F F C F C A 2 B 2 F F F C C 2
7 Exemplo de determinação da relação R c Dados os universos X: {30, 50, 80}, correspondente à variável lingüística Peso e Y: {50, 60, 70, 80} correspondente à variável lingüística Altura; Sendo A(x) o conjunto fuzzy correspondente ao valor lingüístico da variável Peso: pouco_pesado A(x) =/30 + 0,6/50 + 0,2/80 e B(y) o conjunto fuzzy correspondente ao valor lingüistico da variável Altura: altura_média B(y) = 0,8/50 + /60 + 0,7/70 + 0,/80 Podemos definir a relação de implicação A(x) B(y), Se peso é pouco_pesado, então altura é altura_média, pela regra do mínimo como: A(x) B(y) = A(x) B(y) R c (x,y) = ec(a) ec(b) A(x) B(y) : R c = A B x y 0,8 0,7 0, ,8 0,7 0, 0,6 50 0,6 0,6 0,6 0, 0,2 80 0,2 0,2 0,2 0, 3 Exemplo de inferência com a relação R c Considerando a relação R c calculada anteriormente, determine quais são os critérios que são satisfeitos para o MPG. pouco_pesado A(x) =/30 + 0,6/50 + 0,2/80 muito pouco_pesado A + (x) =/30 + 0,36/50 + 0,04/80 mais ou menos pouco_pesado A (x) =/30 + 0,77/50 + 0,45/80 0,8 0,7 0, A(x) B(y) : R c = 0,6 0,6 0,6 0, 0,2 0,2 0,2 0, O MPG é calculado pela regra de inferência composicional: B = A R c (a) B = A R c =? (c) B = A R c =? (b) B = A + R c =? 4
8 Implicação de Larsen: regra do produto Baseada no cálculo proposicional: AB = (não A) + A B Os graus de pertinência desta relação de implicação R p : A(x) B(y) são calculados pelo produto dos graus de pertinência dos conjuntos fuzzy A(x) e B(y) A (x) B (y) / (x, y) R p = A B = X Y µ Rp (x,y) = µ A (x) µ B (y) 5 4. Base de Regras A representação genérica típica do conhecimento se dá através de um conjunto de regras de múltiplas entradas e múltiplas saídas (MIMO, multiple input - multiple output), denominado base de regras (BR) onde R i MIMO representa a regra: BR = {R MIMO, R 2 MIMO,, R n MIMO} Se (x é A i e e y é B i ) então (z é C i,, z q é D i ) O antecedente de R i forma um conjunto fuzzy A i B i no espaço do produto cartesiano X Y. O conseqüente é a união de q ações independentes. Assim, a i-ésima regra R i é representada pela implicação: R i MIMO : (A i B i ) (z + + z q ) 6
9 A base de regras pode ser escrita como as regras individuais agregadas pelo conectivo também: R MIMO : Se (x é A e e y é B ) então (z é C,, z q é D ) também R 2 MIMO : Se (x é A 2 e e y é B 2 ) então (z é C 2,, z q é D 2 ) também : : : : R i MIMO : Se (x é A i e e y é B i ) então (z é C i,, z q é D i ) também : : : : R n MIMO : Se (x é A n e e y é B n ) então (z é C n,, z q é D n ) também Cada regra individual é disparada de acordo com a adequação dos valores físicos (x 0,..., y 0 ) apresentados na entrada do sistema (instância) com os conjuntos fuzzy componentes da regra, gerando conseqüentes proporcionais à força de disparo de cada regra. Uma instância é tratada como um singleton no espaço X Y. A conseqüência global do conjunto de regras é dada pela agregação através do operador também dos resultados individuais do disparo de cada regra 7 Propriedades de um conjunto de regras A partir da definição de R i : R i MIMO : (A i B i ) (z + + z q ) verifica-se que o conjunto de regras BR pode ser representado pela união das regras individuais: BR = { n i= R i MIMO} = { n i= [(A i B i ) (z + + z q )]} Como o conseqüente de cada regra é a agregação de q ações independentes, BR pode ser agrupado em q conjuntos de regras de múltiplas entradas - única saída (MISO, multiple input - single output) representados por BR MISO : BR = { n i= [(A i B i ) z ],, n i= [(A i B i ) z q )]} = { q k= n i= [(A i B i ) z k ]} = {BR MISO, BR 2 MISO,, BR q MISO} com BR k MISO = n i= [Se (x é A i e e y é B i ) então (z k é C i ) ] 8
10 Forma geral de um conjunto de regras MISO R : Se x é A e y é B então z é C R 2 : Se x é A 2 e y é B 2 então z é C 2 : : : R n : Se x é A n e y é B n então z é C n Uma regra i é representada pela relação fuzzy R i µ Ri (x,y,z) = [µ Ai (x) µ Bi (y)] µ Ci (z) Para a implicação Mamdani, R c, por exemplo, os graus de pertinência da implicação são calculados pelo operador mínimo: µ Rc (x,y,z) = µ A (x) µ B (y) µ C (z) Para a implicação R c, e considerando as premissas do MPG como sendo A e B, o resultado da inferência é calculado como a composição maxmin do antecedente com o grau de pertinência da relação: µ C (z)= { [µ A (x) µ B (y)] µ Rc (x,y,z) } X Y 9 5. Raciocínio com instâncias Quando as premissas do MPG, são instâncias do domínio físico, ou seja, os valores crisp x 0 e y 0, os conjuntos fuzzy correspondentes aos antecedentes são pontuais, ou seja, os singletons A (x 0 ) / x 0 e B (y 0 ) / y 0. Com isso, a agregação dos antecedentes de uma regra, resulta num ponto, a chamada força de disparo da regra,, calculada como: = A (x 0 ) B (y 0 ) Entrando com os singletons na expressão para o cálculo do conseqüente, e explicitando-se os termos da relação de implicação Mamdani, obtemos : µ C (z)= { [ A (x 0 ) B (y 0 )] [µ A (x) µ B (y) µ C (z)] } X X Y Como o mínimo é uma operação associativa e comutativa, pode-se separar os termos da projeção em X daqueles da projeção em Y, obtendo: µ C (z)= { [ A (x 0 ) µ A (x) µ C (z)] [ B (y 0 ) µ B (y) µ C (z)] } O resultado da projeção (maxmin) produz, um conjunto cortado na saída: µ C (z)= A (x 0 ) B (y 0 ) µ C (z) = µ C (z) z Z Y 20
11 6. Resumo do método direto de Mamdani Para efeitos de apresentação, considere o conjunto de duas regras: R : Se x é A e y é B, então z é C R 2 : Se x é A 2 e y é B 2, então z é C 2 onde A, A 2, B, B 2, C e C 2 são conjuntos fuzzy. Suponha que x 0 e y 0 sejam as medidas físicas das entradas relativas às variáveis x e y das regras, respectivamente. Determine a força de disparo de cada regra, i pelas expressões: = A (x 0) B (y 0) 2 = A 2 (x 0) B 2 (y 0) 2 6. Resumo do método direto de Mamdani Para efeitos de apresentação, considere o conjunto de duas regras: R : Se x é A e y é B, então z é C R 2 : Se x é A 2 e y é B 2, então z é C 2 onde A, A 2, B, B 2, C e C 2 são conjuntos fuzzy. Suponha que x 0 e y 0 sejam as medidas físicas das entradas relativas às variáveis x e y das regras, respectivamente. Determine a força de disparo de cada regra, i pelas expressões: = A (x 0) B (y 0) 2 = A 2 (x 0) B 2 (y 0) Determine a conclusão de cada regra R i como o conjunto cortado C i : C (z) = C (z) z Z C 2 (z) = 2 C 2 (z) z Z Obtenha a conclusão global do conjunto de regras pela união das conclusões individuais: C (z) = C (z) C2 (z) z Z 22
12 Exemplo do raciocínio pelo método direto de Mamdani R : Se x é A e y é B, então z é C = A (x 0) B (y 0) R 2 : Se x é A 2 e y é B 2, então z é C 2 2 = A 2 (x 0) B 2 (y 0) 0 A x 0 B y 0 C C z A 2 B 2 C 2 C x 0 x 0 y 0 y 0 z C (z) = C (z) z Z C 2 (z) = 2 C 2 (z) z Z C (z) = C (z) C2 (z) z Z 0 C 2 C C z 0 z Defuzzificação Um conjunto fuzzy resultante do MPG pode ser defuzzificado para gerar um único valor de saída. Método de defuzzificação pelas alturas Constrói a média ponderada do valor de pico dos conjuntos originais. Sendo f k a altura do conjunto k cortado, c(k) o valor de pico do conjunto k original, e m o número de conjuntos fuzzy do domínio do conseqüente, o valor crisp z 0 induzido pelas entradas é calculado por: z 0 = m k = m k = c(k) f k Repare que no método direto de Mamdani, f k = k : f k f 2 f 0 C C 2 C c() z 0 c(2) z z 0 = c()f + c(2)f 2 f + f 2 24
13 Método de defuzzificação pelo centro de gravidade ou centróide O valor do conseqüente é calculado como o centro de área da figura resultante da união dos conjuntos fuzzy cortados no domínio da saída. Exemplo: z 0 = C z 0 = Z Z C i (z). z C i (z) (z z 5 + z 4 ) + 2 (z z 3 ) z z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 0 z z 2 z 3 z 4 z 0 Calcule z 0 do exemplo, considerando z i = i, = 0,2 e 2 = 0,4 25 Outros métodos de raciocínio fuzzy Método de Larsens: regra do produto como implicação (R p ) A regra R i : Se x é A i e y é B i, então z é C i, com x X, y Y, z Z, produz a seguinte conseqüência: C i (z) = i. C i (z). A função de pertinência da conseqüência inferida C do conjunto de regras é calculada como: C (z) = C (z) C2 (z) = [. C (z)] [ 2. C 2 (z)] Método de Takagi e Sugeno: A conseqüência de uma regra é uma função das variáveis de entrada f i : R i : Se x é A i e y é B i, então z é f i (x,y) Em cada regra, o valor inferido pelas entradas x 0 e y 0 é i. f i (x 0,y 0 ). O valor inferido pelo conjunto de duas regras, z 0, é dado por: z 0 =. f (x 0,y 0 ) + 2. f 2 (x 0,y 0 )
14 8. Arquitetura de um Sistema Fuzzy Ai (x ) A A 2 A 3 X X 2 B B 2 B 3 A2 (x * ) A R R 2 R 3 A3 (x * ) A 2 R 4 R 5 R 6 x * x * 2 Bi (x 2 ) x * x Fuzzificação A (x * ) A2 (x * ) A3 (x * ) B (x 2* ) B2 (x 2* ) B3 (x 2* ) A 3 R 7 R 8 R 9 Inferência Cc (y) C2c (y) C3c (y) Ci (y) Defuzzificação B B 2 B 3 B (x 2* ) B2 (x 2* ) x 2 * x 2 R 4 : Se X é A 2 e X 2 é B, então Y é C R 5 : Se X é A 2 e X 2 é B 2, então Y é C 2 R 7 : Se X é A 3 e X 2 é B, então Y é C 2 R 8 : Se X é A 3 e X 2 é B 2, então Y é C 3 Cc (y) C2c (y) C3c (y) C c C2c C 3c y * y 27 Exemplo de Aplicação: Truck Backer Upper (TBU) Problema: estacionar um carro de ré em um local especificado Variável de controle: ângulo das rodas dianteiras () Estado do carro: Posição central da traseira (x,y) Ângulo do carro em relação ao eixo dos y () Estado final: (x f, y f, f ) x(n) (n) Controlador Fuzzy z n Carro x(n+) y(n+) (n+) (x,y) 2d z 28
15 Diagrama geométrico é positivo para rotações no sentido horário do volante é positivo no sentido anti-horário em relação à vertical x é positivo à direita da origem. Origem é (x f, y f ) ( 00,0) (0,0) (00,0) (x f,y f ) x 00 (x,y) 2d ( 00,200) (00,200) 29 Modelo do deslocamento do carro Modelo cinemático incremental (t + ) = (t) + (t) x(t + ) = x(t) d.sen(t + ) y(t + ) = y(t) d.cos(t + ) (t + ) = (t) + (t) x(t + ) = x(t) d.sen(t + ) y(t + ) = y(t) d. cos(t + ) t) x(t),y(t) (t + ) x(t +),y(t +) d t) 30
16 Conjuntos fuzzy NB NS ZE PS PB NB NS ZE PS PB x NB NS ZE PS PB R i : Se x é A i e é B i então é C i Base de Regras Considera-se o sistema independente de y. A solução para o problema é posicionar o carro verticalmente, com a ré apontando para o alvo, independentemente da distância vertical (x = ZE, = ZE) e com as rodas paralelas ao carro ( = ZE). Regra central: (ZE, ZE) ZE A dinâmica do problema leva o carro então até o alvo. A cada estado do carro, as regras devem direcionar o carro para o estado central. x CF x = 0 (ZE) = 0 (ZE) = 0 (ZE) 32
17 Base de Regras Considera-se o sistema independente de y: x CF x < 0 (NB, NS) >> 0 (PB) << 0 (NB, NB) x < 0 (NB, NS) > 0 (PS) x < 0 (NB, NS) = 0 (ZE) < 0 (NB, NS) < 0 (NS, NS) x < 0 (NB, NS) << 0 (NB) x < 0 (NB, NS) < 0 (NS) > 0 (PS, PS) < 0 (NS, ZE) 33 Base de Regras (PB, PS) x > 0 = 0 (PB, PS) x > 0 (NS) < 0 (PB, PS) x > 0 (NB) << 0 (PB, PB) >> 0 (PS, PS) > 0 (PB, PS) > 0 (PB, PS) x > 0 (PS) > 0 (PB, PS) x > 0 (PB) >> 0 (NS, NS) < 0 (PS, ZE) > 0 34
18 Matriz Associativa Fuzzy (FAM) NB NS ZE PS PB x NB NS ZE PS PB PS NS NS NB NB PS ZE NS NS NB PB PS ZE NS NB PB PS PS ZE NS PB PB PS PS NS 35
Sistema de Inferência Fuzzy baseado em Redes Adaptativas (ANFIS) Sistema de Inferência Fuzzy
 Redes Neurais Sistema de Inferência Fuzzy baseado em Redes Adaptativas (ANFIS) Sistema de Inferência Fuzzy Um Sistema de Inferência Fuzzy (SIF) é um tipo especial de Sistema Baseado em Conhecimento (SBC).
Redes Neurais Sistema de Inferência Fuzzy baseado em Redes Adaptativas (ANFIS) Sistema de Inferência Fuzzy Um Sistema de Inferência Fuzzy (SIF) é um tipo especial de Sistema Baseado em Conhecimento (SBC).
Conteúdo: Sistemas Fuzzy Fuzzifier Inferência Regras Máquina de Inferência Defuzzifier
 Conteúdo: Sistemas Fuzzy Fuzzifier Inferência Regras Máquina de Inferência Defuzzifier Sistemas fuzzy A inferência fuzzy é um paradigma computacional baseado na Teoria de conjuntos fuzzy, regras de inferência
Conteúdo: Sistemas Fuzzy Fuzzifier Inferência Regras Máquina de Inferência Defuzzifier Sistemas fuzzy A inferência fuzzy é um paradigma computacional baseado na Teoria de conjuntos fuzzy, regras de inferência
Modelos Evolucionários e Tratamento de Incertezas
 Ciência da Computação Modelos Evolucionários e Tratamento de Incertezas Aula 07 Inferência Difusa Sistemas de Controle Difuso Max Pereira Regras difusas SE ENTÃO Antecedente:
Ciência da Computação Modelos Evolucionários e Tratamento de Incertezas Aula 07 Inferência Difusa Sistemas de Controle Difuso Max Pereira Regras difusas SE ENTÃO Antecedente:
Sistemas especialistas Fuzzy
 Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
CONTEÚDO LÓGICA FUZZY LÓGICA FUZZY LÓGICA FUZZY. Um dos componentes mais importantes de um sistema fuzzy é o Módulo de Regras.
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
2 Lógica Fuzzy. 2 Lógica Fuzzy. Sintaxe da linguagem
 2 Lógica Fuzzy 2.1 Cálculo proposicional (lógica proposicional) 2.2 Lógica de Predicados 2.3 Lógica de múltiplos valores 2.4 Lógica Fuzzy Proposições fuzzy Inferência a partir de proposições fuzzy condicionais
2 Lógica Fuzzy 2.1 Cálculo proposicional (lógica proposicional) 2.2 Lógica de Predicados 2.3 Lógica de múltiplos valores 2.4 Lógica Fuzzy Proposições fuzzy Inferência a partir de proposições fuzzy condicionais
Métodos de Inferência Fuzzy
 Métodos de Inferência Fuzzy Prof. Paulo Cesar F. De Oliveira, BSc, PhD 16/10/14 Paulo C F de Oliveira 2007 1 Seção 1.1 Método de Mamdani 16/10/14 Paulo C F de Oliveira 2007 2 Professor Ebrahim Mamdani
Métodos de Inferência Fuzzy Prof. Paulo Cesar F. De Oliveira, BSc, PhD 16/10/14 Paulo C F de Oliveira 2007 1 Seção 1.1 Método de Mamdani 16/10/14 Paulo C F de Oliveira 2007 2 Professor Ebrahim Mamdani
CONTEÚDO LÓGICA FUZZY LÓGICA FUZZY. Proposições Fuzzy. Regras são implicações lógicas. Introdução Introdução, Objetivo e Histórico
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzz Propriedades, Formas de Representação e Operações Relações, Composições,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos ásicos Definição, Características e Formas de Imprecisão Conjuntos Fuzz Propriedades, Formas de Representação e Operações Relações, Composições,
Lógica Fuzzy: Introdução a Lógica Fuzzy, exemplo da Gorjeta e ANFIS
 Lógica Fuzzy: Introdução a Lógica Fuzzy, exemplo da Gorjeta e ANFIS 24 de outubro de 2013 Sumário I 1 Introdução 2 Propriedades 3 Variáveis linguísticas 4 Regras Fuzzy 5 Arquitetura 6 Exemplo Exemplo 1
Lógica Fuzzy: Introdução a Lógica Fuzzy, exemplo da Gorjeta e ANFIS 24 de outubro de 2013 Sumário I 1 Introdução 2 Propriedades 3 Variáveis linguísticas 4 Regras Fuzzy 5 Arquitetura 6 Exemplo Exemplo 1
Prof. Doutor Paulo Salgado UTAD. Doutoramento em Engª Electrotécnica e de Computadores - Prof. Paulo Salgado
 Introdução à LÓGICA DIFUSA Prof. Doutor Paulo Salgado UTAD [email protected] Tópicos do Curso Introdução à LÓGICA DIFUSA (Fuzzy Logic). Operações Lógicas e Inferência difusa Técnicas automáticas de geração
Introdução à LÓGICA DIFUSA Prof. Doutor Paulo Salgado UTAD [email protected] Tópicos do Curso Introdução à LÓGICA DIFUSA (Fuzzy Logic). Operações Lógicas e Inferência difusa Técnicas automáticas de geração
lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy)
 lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy) Sumário Introdução Fundamentos Operações básicas Representação do Conhecimento Modelo de Inferência Passos de Projeto de um Sistema Nebuloso
lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy) Sumário Introdução Fundamentos Operações básicas Representação do Conhecimento Modelo de Inferência Passos de Projeto de um Sistema Nebuloso
lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy)
 lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy) Sumário Introdução Fundamentos Operações básicas Representação do Conhecimento Modelo de Inferência Passos de Projeto de um Sistema Nebuloso
lnteligência Artificial Introdução a Lógica Nebulosa (Fuzzy) Sumário Introdução Fundamentos Operações básicas Representação do Conhecimento Modelo de Inferência Passos de Projeto de um Sistema Nebuloso
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação. Inteligência Artificial. Lógica Fuzzy Aula II
 Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação Inteligência Artificial Lógica Fuzzy Aula II Introdução a Lógica Fuzzy Retomada Função de pertinência Variáveis linguísticas
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação Inteligência Artificial Lógica Fuzzy Aula II Introdução a Lógica Fuzzy Retomada Função de pertinência Variáveis linguísticas
TEORIA DOS CONJUNTOS FUZZY
 TEORIA DOS CONJUNTOS FUZZY TEORIA DOS CONJUNTOS FUZZY A Lógica Fuzzy ébaseada na teoria dos Conjuntos Fuzzy. A teoria dos Conjuntos Fuzzy diz que dado um determinado elemento que pertence a um domínio,
TEORIA DOS CONJUNTOS FUZZY TEORIA DOS CONJUNTOS FUZZY A Lógica Fuzzy ébaseada na teoria dos Conjuntos Fuzzy. A teoria dos Conjuntos Fuzzy diz que dado um determinado elemento que pertence a um domínio,
Lógica Fuzzy. Conectivos e Inferência. Professor: Mário Benevides. Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias
 Lógica Fuzzy Conectivos e Inferência Professor: Mário Benevides Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias Conectivos O que são conectivos? São operadores que conectam
Lógica Fuzzy Conectivos e Inferência Professor: Mário Benevides Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias Conectivos O que são conectivos? São operadores que conectam
Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy
 Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy Profa. Dra. Sarajane M. Peres e Prof. Dr. Clodoaldo A. M. Lima EACH USP http://each.uspnet.usp.br/sarajane/ } Baseado em: Dimensão Topológica
Sistemas Fuzzy Lógica Fuzzy e Sistemas Baseados em Regras Fuzzy Profa. Dra. Sarajane M. Peres e Prof. Dr. Clodoaldo A. M. Lima EACH USP http://each.uspnet.usp.br/sarajane/ } Baseado em: Dimensão Topológica
Logica Difusa (Fuzzy( Fuzzy)
 Logica Difusa (Fuzzy( Fuzzy) Patricia Tedesco e Germano Vasconcelos {pcart, gcv}@cin.ufpe.br Horários: 2 as e 4 as 14 às 16 Sala: D001 e D226 Página da Disciplina: www.cin.ufpe.br/~îf684/ec/2010-1/ 1 Introdução
Logica Difusa (Fuzzy( Fuzzy) Patricia Tedesco e Germano Vasconcelos {pcart, gcv}@cin.ufpe.br Horários: 2 as e 4 as 14 às 16 Sala: D001 e D226 Página da Disciplina: www.cin.ufpe.br/~îf684/ec/2010-1/ 1 Introdução
Conjuntos Fuzzy e Lógica Fuzzy
 1 Introdução Conjuntos Fuzzy e Lógica Fuzzy users.femanet.com.br/~fabri/fuzzy.htm Os Conjuntos Fuzzy e a Lógica Fuzzy provêm a base para geração de técnicas poderosas para a solução de problemas, com uma
1 Introdução Conjuntos Fuzzy e Lógica Fuzzy users.femanet.com.br/~fabri/fuzzy.htm Os Conjuntos Fuzzy e a Lógica Fuzzy provêm a base para geração de técnicas poderosas para a solução de problemas, com uma
Objetivos da aula. Introdução. Teoria da Probabilidade Lógica Nebulosa. Introdução 21/02/17. PCS 5869 lnteligência Ar9ficial
 2/2/7 PCS 5869 lnteligência Ar9ficial Prof. Dr. Jaime Simão Sichman Prof. Dra. Anna Helena Reali Costa Material com contribuições de: Prof. Marco Tulio C. Andrade, PCS/EPUSP Objetivos da aula Fornecer
2/2/7 PCS 5869 lnteligência Ar9ficial Prof. Dr. Jaime Simão Sichman Prof. Dra. Anna Helena Reali Costa Material com contribuições de: Prof. Marco Tulio C. Andrade, PCS/EPUSP Objetivos da aula Fornecer
Lógica Nebulosa. Lógica Fuzzy
 Lógica Nebulosa Ou Lógica Fuzzy Lógicas Bivalente e Polivalente Na logica clássica ou aristotélica: Dois valores verdade possíveis: Proposições verdadeiras;ou Proposições falsas. São sistemas chamados
Lógica Nebulosa Ou Lógica Fuzzy Lógicas Bivalente e Polivalente Na logica clássica ou aristotélica: Dois valores verdade possíveis: Proposições verdadeiras;ou Proposições falsas. São sistemas chamados
Lógica Nebulosa (Fuzzy)
 Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Lógica Nebulosa (Fuzzy) Inteligência Artificial Site: http://jeiks.net E-mail: [email protected]
Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Lógica Nebulosa (Fuzzy) Inteligência Artificial Site: http://jeiks.net E-mail: [email protected]
27/8/2011. Princípios, Conceitos e Metodologia de Gestão 2o semestre de 2011 Professores: Alexandre Mota / Lia Mota Agosto/2011
 Tomada de Decisão e Regras Nebulosas Princípios, Conceitos e Metodologia de Gestão 2o semestre de 2011 Professores: Alexandre Mota / Lia Mota Agosto/2011 Representação Matemática de Incertezas Padrões
Tomada de Decisão e Regras Nebulosas Princípios, Conceitos e Metodologia de Gestão 2o semestre de 2011 Professores: Alexandre Mota / Lia Mota Agosto/2011 Representação Matemática de Incertezas Padrões
Lógica Fuzzy. Profs. João Alberto Fabro André Schneider de Oliveira. Sistemas Autônomos Inteligentes
 Sistemas Autônomos Inteligentes Lógica Fuzzy Profs. João Alberto Fabro André Schneider de Oliveira Adaptado de material dos profs. Mauro Roisenberg e Luciana Rech - UFSC Introdução A Lógica Fuzzy é baseada
Sistemas Autônomos Inteligentes Lógica Fuzzy Profs. João Alberto Fabro André Schneider de Oliveira Adaptado de material dos profs. Mauro Roisenberg e Luciana Rech - UFSC Introdução A Lógica Fuzzy é baseada
Sistema de Inferência Fuzzy. Prof. Juan Mauricio Villanueva
 Sistema de Inferência Fuzzy Prof. Juan Mauricio Villanueva [email protected] http://app.cear.ufpb.br/~juan/ 1 Introdução Lógica Fuzzy É uma ferramenta que permite capturar informações imprecisas,
Sistema de Inferência Fuzzy Prof. Juan Mauricio Villanueva [email protected] http://app.cear.ufpb.br/~juan/ 1 Introdução Lógica Fuzzy É uma ferramenta que permite capturar informações imprecisas,
Paulo Eduardo Maciel de Almeida Alexandre Gonçalves Evsukoff
 CAPÍTULO 7 Sistemas Fuzzy Paulo Eduardo Maciel de Almeida Alexandre Gonçalves Evsukoff My crystal ball is Fuzzy Lotfi Zadeh (quando perguntado sobre o futuro após a criação da lógica fuzzy) O termo em
CAPÍTULO 7 Sistemas Fuzzy Paulo Eduardo Maciel de Almeida Alexandre Gonçalves Evsukoff My crystal ball is Fuzzy Lotfi Zadeh (quando perguntado sobre o futuro após a criação da lógica fuzzy) O termo em
Introdução. Lógica Fuzzy (Lógica Nebulosa) Introdução. Conceito
 Lógica Nebulosa Introdução Lógica Fuzzy (Lógica Nebulosa) Adaptado de material da profa. Luciana Rech Lógica Difusa ou Lógica Fuzzy extensão da lógica boolena um valor lógico difuso é um valor qualquer
Lógica Nebulosa Introdução Lógica Fuzzy (Lógica Nebulosa) Adaptado de material da profa. Luciana Rech Lógica Difusa ou Lógica Fuzzy extensão da lógica boolena um valor lógico difuso é um valor qualquer
1. Conjuntos Fuzzy - Fundamentos. Sistemas Nebulosos
 Sistemas Nebulosos Heloisa de Arruda Camargo. Conjuntos Fuzzy - Fundamentos. Conceitos básicos de conjuntos fuzzy.2 Operações em conjuntos fuzzy.3 Relações fuzzy.4 Aritmética fuzzy.5 Variáveis linguísticas
Sistemas Nebulosos Heloisa de Arruda Camargo. Conjuntos Fuzzy - Fundamentos. Conceitos básicos de conjuntos fuzzy.2 Operações em conjuntos fuzzy.3 Relações fuzzy.4 Aritmética fuzzy.5 Variáveis linguísticas
Dedução Natural e Sistema Axiomático Pa(Capítulo 6)
 Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Lógica Difusa (Fuzzy)
 Lógica Difusa (Fuzzy) Prof. Josiane M. Pinheiro Ferreira Outubro/2007 Lógica tradicional x Lógica difusa Lógica tradicional (Aristóteles) Uma proposição = dois estados possíveis (V ou F) Pode ser insuficiente
Lógica Difusa (Fuzzy) Prof. Josiane M. Pinheiro Ferreira Outubro/2007 Lógica tradicional x Lógica difusa Lógica tradicional (Aristóteles) Uma proposição = dois estados possíveis (V ou F) Pode ser insuficiente
Redes Neurais e Sistemas Fuzzy
 1. Inteligência Computacional Redes Neurais e Sistemas Fuzzy Apresentação da disciplina Conceitos básicos A chamada Inteligência Computacional (IC) reúne uma série de abordagens e técnicas que tentam modelar
1. Inteligência Computacional Redes Neurais e Sistemas Fuzzy Apresentação da disciplina Conceitos básicos A chamada Inteligência Computacional (IC) reúne uma série de abordagens e técnicas que tentam modelar
Inteligência Artificial
 DSC/CCT/UFC Universidade Federal de Campina Grande Departamento de Sistemas e Computação Pós-Graduação em Ciência da Computação Inteligência Artificial Representação do Conhecimento (Lógica Fuzzy) Prof.
DSC/CCT/UFC Universidade Federal de Campina Grande Departamento de Sistemas e Computação Pós-Graduação em Ciência da Computação Inteligência Artificial Representação do Conhecimento (Lógica Fuzzy) Prof.
Lógica Fuzzy. Plano de aula. Motivação Fundamentação Teórica Sistemas Difusos (aplicações) Estudo de Caso Considerações Finais
 LÓGICA FUZZY 1 Plano de aula Motivação Fundamentação Teórica Sistemas Difusos (aplicações) Estudo de Caso Considerações Finais 2 Motivação: Grau de Crença vs. Grau de Verdade Grau de crença: População
LÓGICA FUZZY 1 Plano de aula Motivação Fundamentação Teórica Sistemas Difusos (aplicações) Estudo de Caso Considerações Finais 2 Motivação: Grau de Crença vs. Grau de Verdade Grau de crença: População
SISTEMAS NEURO-FUZZY NEURAL-FUZZY SYSTEMS
 SISTEMAS NEURO-FUZZY NEURAL-FUZZY SYSTEMS Stéphanie Lucchesi, Sandra Regina Monteiro Masalskiene Roveda Campus Experimental de Sorocaba Engenharia Ambiental [email protected], ISB. Palavras chave: fuzzy,
SISTEMAS NEURO-FUZZY NEURAL-FUZZY SYSTEMS Stéphanie Lucchesi, Sandra Regina Monteiro Masalskiene Roveda Campus Experimental de Sorocaba Engenharia Ambiental [email protected], ISB. Palavras chave: fuzzy,
Sistemas difusos (Fuzzy Systems)
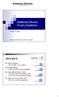 Sistemas difusos (Fuzzy Systems) Victor Lobo Mestrado em Estatística e Gestão de Informação Ideia geral Conjunto das pessoas altas h Lógica clássica Sim ou Não: ou é, ou não é Probabilidades Sim, com uma
Sistemas difusos (Fuzzy Systems) Victor Lobo Mestrado em Estatística e Gestão de Informação Ideia geral Conjunto das pessoas altas h Lógica clássica Sim ou Não: ou é, ou não é Probabilidades Sim, com uma
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
Lógica Computacional
 Lógica Computacional Modus Ponens e Raciocínio Hipotético Introdução e eliminação da Implicação e da Equivalência Completude e Coerência do Sistema de Dedução Natural 24 Outubro 2016 Lógica Computacional
Lógica Computacional Modus Ponens e Raciocínio Hipotético Introdução e eliminação da Implicação e da Equivalência Completude e Coerência do Sistema de Dedução Natural 24 Outubro 2016 Lógica Computacional
Introdução. Sistemas Nebulosos (Fuzzy) Benefícios da Lógica Nebulosa. Introdução. Probabilidade e Possibilidade. Complexidade e Compreensão
 (Fuzzy) Introdução Benefícios da Lógica Nebulosa Conjuntos Nebulosos Variáveis Lingüísticas Operadores (Fuzzy) Raciocínio Etapas Conclusão Introdução Surgiu com Lofti Zadeh em 965. O boom foi nos anos
(Fuzzy) Introdução Benefícios da Lógica Nebulosa Conjuntos Nebulosos Variáveis Lingüísticas Operadores (Fuzzy) Raciocínio Etapas Conclusão Introdução Surgiu com Lofti Zadeh em 965. O boom foi nos anos
Teoria da Decisão. Modelagem de Preferência. Prof. Lucas S. Batista. lusoba
 Teoria da Decisão Modelagem de Preferência Prof. Lucas S. Batista [email protected] www.ppgee.ufmg.br/ lusoba Universidade Federal de Minas Gerais Escola de Engenharia Graduação em Engenharia de Sistemas
Teoria da Decisão Modelagem de Preferência Prof. Lucas S. Batista [email protected] www.ppgee.ufmg.br/ lusoba Universidade Federal de Minas Gerais Escola de Engenharia Graduação em Engenharia de Sistemas
Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos
 Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos Conjuntos Crisp x Fuzzy Conjuntos crisp ou Conjuntos clássicos: cada entidade ou objeto de um dado universo pode pertencer
Conteúdo: Conjuntos crisp x Conjuntos fuzzy Representação Propriedades Formatos Conjuntos Crisp x Fuzzy Conjuntos crisp ou Conjuntos clássicos: cada entidade ou objeto de um dado universo pode pertencer
Universidade Estadual Paulista Campus de Ilha Solteira. Palestra: Carlos Roberto Minussi DEE FEIS UNESP
 Universidade Estadual Paulista Campus de Ilha Solteira Palestra: Lógica Fuzzy (Nebulosa) Carlos Roberto Minussi DEE FEIS UNESP História e Motivação Lógiica Fuzzy Computação com Pallavras Zadeh [1965] desenvolveu
Universidade Estadual Paulista Campus de Ilha Solteira Palestra: Lógica Fuzzy (Nebulosa) Carlos Roberto Minussi DEE FEIS UNESP História e Motivação Lógiica Fuzzy Computação com Pallavras Zadeh [1965] desenvolveu
Lógica. Cálculo Proposicional. Introdução
 Lógica Cálculo Proposicional Introdução Lógica - Definição Formalização de alguma linguagem Sintaxe Especificação precisa das expressões legais Semântica Significado das expressões Dedução Provê regras
Lógica Cálculo Proposicional Introdução Lógica - Definição Formalização de alguma linguagem Sintaxe Especificação precisa das expressões legais Semântica Significado das expressões Dedução Provê regras
Resultantes de um sistema de forças
 Resultantes de um sistema de forças Objetivos da aula Discutir o conceito do momento de uma força e mostrar como calculá-lo em duas e três dimensões. Fornecer um método para determinação do momento de
Resultantes de um sistema de forças Objetivos da aula Discutir o conceito do momento de uma força e mostrar como calculá-lo em duas e três dimensões. Fornecer um método para determinação do momento de
Raciocínio lógico matemático
 Raciocínio lógico matemático Unidade 3: Dedução Seção 3.3 - Contrapositiva 1 Lembrando Modus pones p q, p q Se Pedro guarda dinheiro, então ele não fica negativado. Pedro guardou dinheiro. Dessa forma
Raciocínio lógico matemático Unidade 3: Dedução Seção 3.3 - Contrapositiva 1 Lembrando Modus pones p q, p q Se Pedro guarda dinheiro, então ele não fica negativado. Pedro guardou dinheiro. Dessa forma
Introdução à Lógica Nebulosa
 Distancia Angulo Gerador de Sinal Controlador Nebuloso Osciloscópio 2.141e-016 Display Introdução à Lógica Nebulosa Álvaro Guarda Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade
Distancia Angulo Gerador de Sinal Controlador Nebuloso Osciloscópio 2.141e-016 Display Introdução à Lógica Nebulosa Álvaro Guarda Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade
4. Curvas Paramétricas e Transformações 2D
 4. Curvas Paramétricas e Transformações 2D Curvas Paramétricas (fonte: Wikipédia) Em matemática, uma equação paramétrica é uma forma de representar uma curva (ou, em geral, uma superfície) como a imagem
4. Curvas Paramétricas e Transformações 2D Curvas Paramétricas (fonte: Wikipédia) Em matemática, uma equação paramétrica é uma forma de representar uma curva (ou, em geral, uma superfície) como a imagem
SISTEMAS FUZZY CONTEÚDO CONJUNTOS FUZZY. CONJUNTOS CRISP x FUZZY
 SISTEMAS FUZZY A maioria dos fenômenos com os quais nos deparamos são imprecisos Exemplo: dia QUENTE (40, 35, 30, 29,5?) Imprecisão Intrínseca ajuda na compreensão do problema. Fuzziness é independente
SISTEMAS FUZZY A maioria dos fenômenos com os quais nos deparamos são imprecisos Exemplo: dia QUENTE (40, 35, 30, 29,5?) Imprecisão Intrínseca ajuda na compreensão do problema. Fuzziness é independente
Universidade de São Paulo
 Universidade de São Paulo Uma volta no carrossel Instituto de Física da USP Física I para a Escola Politécnica 2016 Uma criança de 25 kg, em um playground, corre com uma velocidade escalar inicial de 2,
Universidade de São Paulo Uma volta no carrossel Instituto de Física da USP Física I para a Escola Politécnica 2016 Uma criança de 25 kg, em um playground, corre com uma velocidade escalar inicial de 2,
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Cap.04 1 Resultantes de um sistema de forças Prof. Antonio Dias Antonio Dias / Cap.04 2 Objetivo Discutir o conceito do momento de uma força
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Cap.04 1 Resultantes de um sistema de forças Prof. Antonio Dias Antonio Dias / Cap.04 2 Objetivo Discutir o conceito do momento de uma força
Lógica predicados. Lógica predicados (continuação)
 Lógica predicados (continuação) Uma formula está na forma normal conjuntiva (FNC) se é uma conjunção de cláusulas. Qualquer fórmula bem formada pode ser convertida para uma FNC, ou seja, normalizada, seguindo
Lógica predicados (continuação) Uma formula está na forma normal conjuntiva (FNC) se é uma conjunção de cláusulas. Qualquer fórmula bem formada pode ser convertida para uma FNC, ou seja, normalizada, seguindo
Lógica. Fernando Fontes. Universidade do Minho. Fernando Fontes (Universidade do Minho) Lógica 1 / 65
 Lógica Fernando Fontes Universidade do Minho Fernando Fontes (Universidade do Minho) Lógica 1 / 65 Outline 1 Introdução 2 Implicações e Equivalências Lógicas 3 Mapas de Karnaugh 4 Lógica de Predicados
Lógica Fernando Fontes Universidade do Minho Fernando Fontes (Universidade do Minho) Lógica 1 / 65 Outline 1 Introdução 2 Implicações e Equivalências Lógicas 3 Mapas de Karnaugh 4 Lógica de Predicados
Lógica Proposicional Parte II. Raquel de Souza Francisco Bravo 25 de outubro de 2016
 Lógica Proposicional Parte II e-mail: [email protected] 25 de outubro de 2016 Argumento Válido Um argumento simbólica como: pode ser ser representado em forma P 1 P 2 P 3 P n Q Onde P 1, P 2,,P n são proposições
Lógica Proposicional Parte II e-mail: [email protected] 25 de outubro de 2016 Argumento Válido Um argumento simbólica como: pode ser ser representado em forma P 1 P 2 P 3 P n Q Onde P 1, P 2,,P n são proposições
Lógica Proposicional Parte 2
 Lógica Proposicional Parte 2 Como vimos na aula passada, podemos usar os operadores lógicos para combinar afirmações criando, assim, novas afirmações. Com o que vimos, já podemos combinar afirmações conhecidas
Lógica Proposicional Parte 2 Como vimos na aula passada, podemos usar os operadores lógicos para combinar afirmações criando, assim, novas afirmações. Com o que vimos, já podemos combinar afirmações conhecidas
Lógica Proposicional e Dedução Natural 1/48. Douglas O. Cardoso docardoso.github.io
 Lógica Proposicional e Dedução Natural [email protected] docardoso.github.io Lógica Proposicional e Dedução Natural 1/48 Roteiro 1 Uma Introdução Intuitiva 2 Proposições 3 DN: regras básicas
Lógica Proposicional e Dedução Natural [email protected] docardoso.github.io Lógica Proposicional e Dedução Natural 1/48 Roteiro 1 Uma Introdução Intuitiva 2 Proposições 3 DN: regras básicas
Redes Neurais e Sistemas Fuzzy
 Redes Neurais e Sistemas Fuzzy Redes de uma única camada O Perceptron elementar Classificação de padrões por um perceptron A tarefa de classificação consiste em aprender a atribuir rótulos a dados que
Redes Neurais e Sistemas Fuzzy Redes de uma única camada O Perceptron elementar Classificação de padrões por um perceptron A tarefa de classificação consiste em aprender a atribuir rótulos a dados que
Identificando a necessidade de um sistema Fuzzy
 Identificando a necessidade de um sistema Fuzzy Sempre que ocorrem ajustes em máquinas com o objetivo de redução de perdas e de matéria prima, como função de julgamento de um operador é interessante a
Identificando a necessidade de um sistema Fuzzy Sempre que ocorrem ajustes em máquinas com o objetivo de redução de perdas e de matéria prima, como função de julgamento de um operador é interessante a
CONJUNTOS FUZZY CONTEÚDO. CONJUNTOS CRISP x FUZZY. Conjuntos Crisp x Fuzzy Definição Representação Propriedades Formatos Operações Hedges
 CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
CONTEÚDO Introdução Introdução, Objetivo e Histórico Conceitos Básicos Definição, Características e Formas de Imprecisão Conjuntos Fuzzy Propriedades, Formas de Representação e Operações Lógica Fuzzy Relações,
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes [email protected] DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes [email protected] DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
Fundamentos de Lógica Matemática
 Webconferência 3-01/03/2012 Inferência Lógica Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Objetivos Análise
Webconferência 3-01/03/2012 Inferência Lógica Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Objetivos Análise
3.3 Cálculo proposicional clássico
 81 3.3 Cálculo proposicional clássico 3.3.1 Estrutura dedutiva Neste parágrafo serão apresentados, sem preocupação com excesso de rigor e com riqueza de detalhes, alguns conceitos importantes relativos
81 3.3 Cálculo proposicional clássico 3.3.1 Estrutura dedutiva Neste parágrafo serão apresentados, sem preocupação com excesso de rigor e com riqueza de detalhes, alguns conceitos importantes relativos
Lógica para Computação
 Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Sistemas Dedutivos Um Sistema Dedutivo (SD) tem por objetivo obter, a partir de um conjunto
Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Sistemas Dedutivos Um Sistema Dedutivo (SD) tem por objetivo obter, a partir de um conjunto
Geometria Analítica. Prof Marcelo Maraschin de Souza
 Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Geometria Analítica Prof Marcelo Maraschin de Souza Vetor Definido por dois pontos Seja o vetor AB de origem no ponto A(x 1, y 1 ) e extremidade no ponto B(x 2, y 2 ). Qual é a expressão algébrica que
Resumo de Filosofia. Preposição frase declarativa com um certo valor de verdade
 Resumo de Filosofia Capítulo I Argumentação e Lógica Formal Validade e Verdade O que é um argumento? Um argumento é um conjunto de proposições em que se pretende justificar ou defender uma delas, a conclusão,
Resumo de Filosofia Capítulo I Argumentação e Lógica Formal Validade e Verdade O que é um argumento? Um argumento é um conjunto de proposições em que se pretende justificar ou defender uma delas, a conclusão,
Apresentaremos as equações do plano: Equação vetorial e Equação geral do. = AB e v. C A u B. ) não-colineares do plano.
 CAPÍTULO VIII PLANO Consideremos em V 3 o sistema de referência (O, i, j, k ), onde E = ( i, j, k ) é base ortonormal positiva e O(0, 0, 0). 8.1. EQUAÇÕES DO PLANO plano. Apresentaremos as equações do
CAPÍTULO VIII PLANO Consideremos em V 3 o sistema de referência (O, i, j, k ), onde E = ( i, j, k ) é base ortonormal positiva e O(0, 0, 0). 8.1. EQUAÇÕES DO PLANO plano. Apresentaremos as equações do
Lógica Matemática UNIDADE II. Professora: M. Sc. Juciara do Nascimento César
 Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
LÓGICA I ANDRÉ PONTES
 LÓGICA I ANDRÉ PONTES 4. Lógica Proposicional A Linguagem da Lógica Proposicional Letras Proposicionais: P, Q, R, S, T,... Conectivos Lógicos: Símbolos auxiliares: (, ), = Conectivo Leitura Símbolo Símbolos
LÓGICA I ANDRÉ PONTES 4. Lógica Proposicional A Linguagem da Lógica Proposicional Letras Proposicionais: P, Q, R, S, T,... Conectivos Lógicos: Símbolos auxiliares: (, ), = Conectivo Leitura Símbolo Símbolos
Lógica Formal. Matemática Discreta. Prof Marcelo Maraschin de Souza
 Lógica Formal Matemática Discreta Prof Marcelo Maraschin de Souza Implicação As proposições podem ser combinadas na forma se proposição 1, então proposição 2 Essa proposição composta é denotada por Seja
Lógica Formal Matemática Discreta Prof Marcelo Maraschin de Souza Implicação As proposições podem ser combinadas na forma se proposição 1, então proposição 2 Essa proposição composta é denotada por Seja
Vetores no plano Cartesiano
 Vetores no plano Cartesiano 1) Definição de vetor Um vetor (geométrico) no plano R² é uma classe de objetos matemáticos (segmentos) com a mesma direção, mesmo sentido e mesmo módulo (intensidade). 1. A
Vetores no plano Cartesiano 1) Definição de vetor Um vetor (geométrico) no plano R² é uma classe de objetos matemáticos (segmentos) com a mesma direção, mesmo sentido e mesmo módulo (intensidade). 1. A
LOGICA FUZZY. Adão de Melo Neto
 LOGICA FUZZY Adão de Melo Neto SUMÁRIO INTRODUÇÃO PRINCÍPIOS CLÁSSICA x DIFUSA CONJUNTOS FUZZY OPERAÇÕES EM CONJUNTO FUZZY MODIFICADORES Introdução "A logica difusa (fuzzy) tem por objetivo modelar modos
LOGICA FUZZY Adão de Melo Neto SUMÁRIO INTRODUÇÃO PRINCÍPIOS CLÁSSICA x DIFUSA CONJUNTOS FUZZY OPERAÇÕES EM CONJUNTO FUZZY MODIFICADORES Introdução "A logica difusa (fuzzy) tem por objetivo modelar modos
