Figura 1: Esquema das pontes de Königsberg
|
|
|
- Giovana Sanches de Lacerda
- 6 Há anos
- Visualizações:
Transcrição
1 Universidade do Algarve - 0/0 Conteúdo Introdução De nições e conceitos básicos Matrizes de grafos Graus dos vértices Sucessores e antecessores Caminhos e conectividade Circuitos e caminhos de Euler Algoritmo de Fleury Grafos e relações binárias Relações de equivalência e componentes fortemente conexas Relações de ordem e grafos Grafos completos Grafos bipartidos Grafos complementares Árvores Árvores de suporte Árvore de suporte nínima Planaridade Caminhos mais curtos i
2 Universidade do Algarve - 0/ Introdução Era uma vez uma cidade no reino da Prússia. A cidade chamava-se Königsberg e espraiava- -se por ambas as margens de um rio e por duas ilhas bem no meio do rio. Estávamos no início do século XVIII. Não havia telenovelas, nem futebol, nem telemóveis nem se mandavam s nem SMS. Ao Domingo, quando fazia bom tempo, as famílias, depois de saírem da igreja, passeavam nos seus melhores trajes. A cidade não era muito grande, mas tinha a particularidade interessante de ter sete pontes a ligar as margens do rio e as duas ilhas como se mostra esquematicamente na gura 1. Figura 1: Esquema das pontes de Königsberg Havia uma espécie de jogo com que as famílias se divertiam, que consistia em sair de uma zona da cidade (A, B, C ou D) e tentar regressar ao mesmo sítio depois de ter atravessado todas as sete pontes uma única vez. Depois de muitos Domingos e de muitos passeios nunca nenhuma família tinha conseguido esse objectivo e começava-se a pensar na cidade se tal seria de facto possível. 1
3 Universidade do Algarve - 0/0 Só alguns anos mais tarde é que Leonard Euler demonstrou que efectivamente tal passeio era impossível. A demonstração apareceu num artigo de 13 chamado Solutio problematis ad geometriam situs pertinentis, o que quer dizer qualquer coisa como: "Solução de um problema relacionado com a geometria da posição". Este artigo apareceu no número 8 dos Commentarii Academiæ Scientiarum Imperialis Petropolitanæ. A linguagem utilizada não era a actualmente empregue quando se fala de grafos, mas as ideias estavam todas lá. Na simbologia actualmente utilizada, pode-se representar este problema esquematicamente, fazendo corresponder a cada região da cidade um ponto e a cada ponte entre essas regiões um segmento, recto ou curvo como der mais jeito ao desenho, unindo os pontos correspondentes às regiões ligadas pelas pontes que os segmentos representam. Deste modo, obtém-se o esquema da gura. Figura : Esquema de Euler A cada ponto chamamos vértice e a cada segmento chamamos aresta. E o que acabou de se representar é um grafo. A ideia da demonstração de que o passeio pretendido é impossível é muito simples: Sempre que se atravessa para uma parte da cidade é preciso sair de lá. Isto é, sempre que se chega a um vértice do grafo usando uma aresta é preciso que haja outra aresta para sair de lá, ou seja, o número de arestas que chegam a cada vértice tem que ser par. Portanto, como no grafo que representa a cidade há vértices onde chega um número impar de arestas, tal passeio não é possível. Mas os grafos não têm utilidade só para encontrar a solução de jogos. Problemas desde a colocação de sinais de sentido proibido e o estabelecimento de percursos alternativos, a regulação da temporização dos semáforos nos cruzamentos, a sequência de ruas que
4 Universidade do Algarve - 0/0 um carteiro deve percorrer para entregar a correspondência, os percursos a efectuar pelos carros que lavam as ruas das cidades, as rondas dos polícias e muitos outros podem ter uma solução mais e ciente usando conceitos de grafos. Até as agências de casamentos teriam muito a ganhar em e ciência se tivessem especialistas em grafos no seu pessoal. Antes de de nirmos com todo o rigor matemático o que é um grafo, vejamos mais o seguinte exemplo: Cinco turistas de diferentes nacionalidades encontram-se num aeroporto onde passam longas horas à espera de um avião de ligação que os levará para um destino comum. O conhecimento de línguas destes cinco personagens é grande, mas não há uma língua que todos falem, pelo que a conversa não se generaliza. Na tabela seguinte listam-se os idiomas falados pelas cinco pessoas: Turista Língua Inglês Alemão Francês Espanhol p * * * - q - * - * r * - - * s - * * - t * - * * Quem é que fala com quem? Vamos representar cada turista por um vértice. Unimos dois vértices por uma aresta sempre que esses dois turistas tenham uma língua em comum: Por uma simples observação do grafo concluímos que só os turistas r e s não conseguem falar um com outro, visto não haver nenhuma aresta entre estes dois vértices, todos os outros estão ligados directamente, pelo que todos podem falar entre si. Repare-se que se quiséssemos saber quem é que fala com quem e em quantas línguas, teríamos que usar uma aresta para cada língua, obtendo-se o grafo da gura 4. A representação grá ca começa a car muito complicada e é já óbvio que é necessário encontrar um processo mais e ciente de fazer a representação das interligações existentes entre os vértices. 3
5 Universidade do Algarve - 0/0 Figura 3: Quem fala com quem? Figura 4: Em quantas línguas? Além do mais, se o tratamento tiver que ser feito informaticamente, o que será inevitável a partir de certo número de vértices e/ou arestas, o desenho não é a forma mais conveniente. Surgiu assim a ideia de se representar as ligações entre os vértices usando uma matriz quadrada, de dimensão igual ao número de vértices. Cada linha/coluna corresponde a um vértice. A entrada da matriz na linha i e coluna j representa o número de arestas que unem os vértices i e j. Repare-se que nos exemplos até agora apresentados a matriz correspondente é simétrica, mas não é difícil encontrar exemplos em que a matriz não seja simétrica. Pensemos por exemplo num mapa representando as ruas de uma cidade. Neste caso, os vértices representam cruzamentos ou rotundas e as arestas representam as ruas entre esses cruzamentos e essas rotundas. Como é inevitável que numa cidade haja ruas de sentido único, temos aqui um exemplo em que a matriz não é simétrica, pois se há uma rua de sentido único entre os vértices i e j, não há aresta ligando directamente j a i. Um problema interessante (e útil) é saber qual a forma de ir de j para i, uma vez que não se pode circular em ruas no sentido proibido. Para representar no grafo situações em que 4
6 Universidade do Algarve - 0/0 uma aresta só pode ser percorrida num determinado sentido usa-se uma seta para indicar qual o sentido de circulação sobre a aresta, que, neste caso se passa a chamar arco. Se todos os arcos puderem ser percorridos em ambos os sentidos dizemos que temos um grafo não orientado e não há necessidade de usar qualquer seta sobre as arestas. Desde que pelo menos um dos arcos possa ser percorrido num único sentido é necessário indicar qual recorrendo a setas e dizemos que temos um grafo orientado. Vejamos qual o aspecto das matrizes correspondentes aos grafos representados nas guras 3 e 4 respectivamente: Vejamos agora uma representação esquemática das ruas da baixa de uma cidade. Os vértices representam cruzamentos e os arcos representam ruas entre esses cruzamentos. Nesta cidade todas as ruas são de sentido único: Figura 5: Baixa de uma cidade A matriz associada a este grafo é obviamente não simétrica: 5
7 Universidade do Algarve - 0/ Quando se trata de ruas de sentido único, um problema premente é o de saber se cada cruzamento pode ser alcançado a partir de todos os outros. A este problema chama-se conexidade do grafo. Antes de o resolver é porém necessário saber mais alguma coisa sobre grafos. 1. De nições e conceitos básicos Agora que já sabemos representar grafos de duas maneiras diferentes e que já falámos em dois tipos diferentes de grafos, está na altura de de nirmos rigorosamente o que é um grafo. De nição 1 Chama-se grafo orientado a um par ordenado G = (X; ), em que X é um conjunto e X X. A X chama-se conjunto de vértices e a chama-se conjunto de arcos. Se G for um conjunto de subconjuntos de X com elementos (isto é, pares não ordenados) o grafo diz-se não orientado. Neste caso aos elementos de G chamam-se arestas. A m de melhor estudar certos fenómenos que se passam num grafo é, muitas vezes, vantajoso estudar o que se passa em partes desse mesmo grafo. Surgem assim as seguintes de nições: De nição Seja G = (X; ) um grafo e seja G Y = (Y; Y ) outro grafo tal que Y X e Y = \ (Y Y ). A G Y chama-se um subgrafo de G. De nição 3 Seja G = (X; ) um grafo e seja G = (X; ) outro grafo tal que. A G chama-se um grafo parcial de G. Repare-se na diferença destes dois conceitos. Enquanto que num subgrafo se escolhe um subconjunto do conjunto de vértices e se mantêm todas as arestas que existiam entre eles,
8 Universidade do Algarve - 0/0 Figura : Exemplo de subgrafo num grafo parcial mantêm-se todos os vértices e suprimem-se algumas arestas. Vejamos um exemplo: Na gura o grafo da direita resulta do grafo da esquerda por supressão do vértice E e de todas as arestas que partem dele. De acordo com a de nição o grafo da direita é um subgrafo do grafo da esquerda. Figura : Exemplo de grafo parcial Na gura no grafo da direita mantiveram-se os mesmos vértices do grafo da esquerda mas retiraram-se algumas arestas. De acordo com a de nição, dizemos que o grafo da direita é um grafo parcial do grafo da esquerda. Repare-se que os grafos não orientados podem ser transformados em grafos orientados se cada aresta não orientada for substituída por dois arcos de sentidos opostos.
9 Universidade do Algarve - 0/0 1.3 Matrizes de grafos De nição 4 Seja G = (X; uma matriz M n n, tal que ) um grafo, tal que #X = n. A matriz de adjacência de G é 8 >< m ij = 1 se (x i ; x j ) >: m ij = 0 se (x i ; x j ) = (Estamos a designar os elementos de X por x i ; i = 1; :::; n) Já se viram atrás alguns exemplos de matrizes de adjacência. Repare-se que as de nições até agora dadas não mencionam o facto de poder haver mais do que uma aresta ou arco entre dois vértices. Se houver mais do que uma aresta ou arco entre dois vértices, isso signi ca que se admite que o conjunto G possa ter elementos repetidos. Nesse caso, a entrada correspondente na matriz de adjacência em vez de ser 1 será igual ao número de vezes que essa aresta ou arco aparece repetido, como também já se viu atrás. Quando esta situação acontece dizemos que temos arestas múltiplas. Também pode acontecer haver um arco a ligar um vértice a si próprio, o que corresponde a haver em um par da forma (x i ; x i ). A um tal arco chama-se laço. De nição 5 Um grafo sem laços e sem arestas múltiplas chama-se simples. Em termos computacionais, a representação de um grafo depende da situação que se está a modelar e, muitas vezes, do algoritmo que se pretende utilizar. Uma outra representação matricial também muito utilizada é a chamada matriz de incidência. De nição Seja G = (X; ) um grafo, tal que #X = n e # = m. A matriz de incidência de G é uma matriz M n m, tal que 8 >< >: m ij = 1 m ij = 1 m ij = 0 se 9k : u j = (x i ; x k ) se 9k : u j = (x k ; x i ) nos outros casos ; x i = x k ; x i = x k 9 >= ; >; i = 1; : : : ; n j = 1; : : : ; m Vejamos como funciona esta matriz com o grafo da gura 5. Primeiro é preciso começar por ordenar os arcos. A numeração mais usual é a lexicográ ca, isto é, começa-se com os arcos que começam no primeiro vértice e numeram-se por ordem do segundo vértice, depois faz-se a mesma coisa para o segundo vértice e assim por diante. Temos então: 8
10 Universidade do Algarve - 0/0 8 >< u 1 = (A; B) u = (B; C) u 3 = (B; E) u 4 = (C; A) u 5 = (C; D) u = (D; B) e M = >: u = (E; D) Repare-se que em cada coluna há um único elemento igual a 1 e um único igual a -1, sendo todos os outros nulos. O número de elementos iguais a 1 numa linha dá o número de arcos que sai do vértice correspondente a essa linha, enquanto que o número de elementos iguais a -1 dá o número de arcos que chegam ao vértice correspondente a essa linha. 1.4 Graus dos vértices De nição Chama-se semigrau exterior do vértice x i (gr + (x i )) ao número de arcos que saem de x i. Chama-se semigrau interior do vértice x i (gr (x i )) ao número de arcos que chegam a x i. Se o grafo for não orientado, estes dois valores são iguais e designam-se simplesmente por grau de x i (gr(x i )). A partir da de nição de grau de um vértice num grafo não orientado conclui-se facilmente que: Lema 1 A soma dos graus dos vértices num grafo não orientado é um número par que é igual ao dobro do número de arestas. Com efeito, cada aresta é contada duas vezes no cômputo da soma dos graus: uma vez para cada um dos vértices nos seus extremos. Corolário 1 Num grafo não orientado o número de vértices com grau impar é par. Não é difícil estabelecer um resultado análogo para grafos orientados, agora somando os semigraus exteriores e os semigraus interiores de todos os vértices. 9
11 Universidade do Algarve - 0/0 Tendo a representação do grafo pela matriz de adjacência, o semigrau exterior de um vértice é igual ao número de elementos iguais a 1 na linha correspondente a esse vértice, enquanto que o semigrau interior é o número de elementos iguais a 1 na coluna correspondente a esse vértice. Se o grafo for não orientado, a matriz é simétrica e esses dois valores são iguais. Tendo a representação do grafo pela matriz de incidência, o semigrau exterior de um vértice é igual ao número de elementos iguais a 1 na linha correspondente a esse vértice, enquanto que o semigrau interior é igual ao número de elementos iguais a 1 nessa mesma linha. É claro que se o grafo for não orientado estes dois valores são iguais. De nição 8 Um grafo não orientado em que todos os vértices têm o mesmo grau diz-se regular. De nição 9 Um grafo orientado diz-se pseudo-simétrico se para todos os vértices x i se veri ca gr + (x i ) = gr (x i ). 1.5 Sucessores e antecessores A representação por matriz de adjacência é das mais simples, mas, para grafos de grandes dimensões é pouco prática, pois ocupa muito espaço e os programas tornam-se muito demorados. A representação por matriz de incidência, normalmente ainda ocupa mais espaço, só sendo por isso utilizada em certos algoritmos que tiram partido da sua estrutura. Um processo mais económico (em termos de espaço) de representar grafos computacionalmente é o das chamadas listas de sucessores e/ou antecessores. De nição 10 Um vértice x i diz-se sucessor do vértice x j se existir o arco (x j ; x i ). Neste caso o vértice x j diz-se antecessor de x i. Vamos representar o grafo da gura 1.5 por meio de uma lista de sucessores: x A B C D E + (x) B C A; D B A; B; D De modo análogo se pode de nir uma lista de antecessores: 10
12 Universidade do Algarve - 0/0 x A B C D E (x) C; E A; C; D B C; E? Num computador estas listas podem ser representadas de modo muito mais económico, por meio de apontadores, do que através de qualquer uma das matrizes anteriormente de nidas. A noção de sucessor (antecessor) de um vértice pode ser estendida para um conjunto de vértices, como sendo o conjunto de todos os vértices que são sucessores (antecessores) dos vértices do conjunto. Assim, por exemplo, pode-se escrever + (fb; Cg) = fa; C; Dg e (fb; Cg) = fa; B; C; Dg E agora podemos de nir o conjunto sucessor (antecessor) dos sucessores (antecessores) de um conjunto: + (fb; Cg) = + (fa; C; Dg) = fa; B; C; Dg e (fb; Cgg = (fa; B; C; Dg) = fa; B; C; D; Eg Continuando a procurar os sucessores dos sucessores e os antecessores dos antecessores, podemos de nir recursivamente o conjunto de sucessores e de antecessores de ordem n de um vértice ou de um conjunto de vértices: +n (fx i g) = ( +(n 1) (fx i g) e n (fx i gg = ( (n 1) (fx i g)) Fazendo a reunião dos conjuntos de sucessores que se obtêm sucessivamente é possível saber a quais vértices é que se pode chegar partindo de um determinado vértice. Do mesmo modo, 11
13 Universidade do Algarve - 0/0 fazendo a reunião dos conjuntos de antecessores que se obtêm sucessivamente é possível saber de que vértices é que se pode partir para chegar a um determinado vértice. 1. Caminhos e conectividade De nição 11 Dados dois vértices distintos x i e x j chama-se caminho entre x i e x j a uma sucessão de arcos tais que cada arco começa onde o anterior acaba, o primeiro arco da sucessão começa em x i e o último termina em x j. Ao número de arcos desse caminho chama-se comprimento do caminho. Se o caminho começar e acabar no mesmo vértice chama-se circuito. Para se saber se existe ou não um caminho entre dois vértice é preciso analisar os sucessivos conjuntos de sucessores do vértice x i. De nição 1 Chama-se fecho transitivo do vértice x i ao conjunto dos vértices para os quais existe um caminho, de qualquer comprimento a partir, de x i. Este conjunto pode ser determinado por b+ (fx i g) = fx i g [ + (fx i g) [ + (fx i g) [ ::: [ +n (fx i g) [ ::: De nição 13 De ne-se fecho transitivo inverso do vértice x i como o conjunto dos vértices a partir dos quais existe um caminho, de qualquer comprimento, que chega a x i. e determina-se através de b (fxi g) = fx i g [ (fx i g) [ (fx i g) [ ::: [ n (fx i g) [ ::: Vamos exempli car estes conceitos utilizando o grafo da gura 8. Comecemos por determinar o fecho transitivo do vértice x 1. + (fx 1 g) = fx ; x g + (fx 1 g) = + (fx ; x g) = fx 1 ; x 3 ; x 4 ; x 5 g +3 (fx 1 g) = + (fx 1 ; x 3 ; x 4 ; x 5 g) = fx 1 ; x ; x 3 ; x 4 ; x g +4 (fx 1 g) = + (fx 1 ; x ; x 3 ; x 4 ; x g) = fx 1 ; x ; x 3 ; x 4 ; x 5 ; x g Como já chegamos a um conjunto que tem todos os vértices do grafo, não é necessário continuar à procura de sucessores. Temos então: b+ (fx 1 g) = fx 1 ; x ; x 3 ; x 4 ; x 5 ; x g. Vejamos agora qual é o fecho transitivo inverso do mesmo vértice: (fx 1 g) = fx ; x 5 ; x g 1
14 Universidade do Algarve - 0/0 Figura 8: Determinação de caminhos (fx 1 g) = (fx ; x 5 ; x g) = fx 1 ; x ; x 5 g 3 (fx 1 g) = (fx 1 ; x ; x 5 g) = fx ; x 5 ; x g Também, neste caso, não é preciso continuar à procura de antecessores uma vez que os conjuntos fx ; x 5 ; x g e fx 1 ; x ; x 5 g vão alternar e não se vai obter mais nenhum vértice. Temos assim: b (fx 1 g) = fx 1 ; x ; x 5 ; x g. Se zermos a intersecção dos dois conjuntos b+ (fx 1 g) e b (fx 1 g) obtemos o conjunto de todos os vértices que estão ligados a x 1 por um caminho de ida e de volta. De nição 14 Chama-se componente fortemente conexa de x i e representa-se por C(fx i g), ao conjunto de todos os vértices que estão ligados a x i por um caminho de ida e volta. Ou seja, C(fx i g) = : b+ (fx 1 g) \ b (fx 1 g) É claro que determinando a componente fortemente conexa de qualquer outro vértice de C(fx 1 g) se obtém exactamente o mesmo conjunto: C(fx 1 g) = fx 1 ; x ; x 5 ; x g. Os vértices x 3 e x 4 caram de fora desta componente. Vamos agora determinar C(fx 3 g). Começa-se por determinar o fecho transitivo de x 3 : + (fx3g) = fx4g + (fx 3 g) = + (fx 4 g) = fx 3 g E não é preciso procurar mais sucessores. Temos assim: b+ (fx 3 g) = fx 3 ; x 4 g. Vejamos agora qual é o fecho transitivo inverso do mesmo vértice: (fx 3 g) = fx 4 ; x g (fx 3 g) = (fx 4 ; x g) = fx ; x 3 ; x 5 g 3 (fx 3 g) = (fx ; x 3 ; x 5 g) = fx 1 ; x ; x 4 ; x g 13
15 Universidade do Algarve - 0/0 E não é preciso procurar mais antecessores: b (fx 1 g) = fx 1 ; x ; x 3 ; x 4 ; x 5 ; x g. Fazendo agora a intersecção de : b+ (fx 1 g) e b (fx 1 g) obtém-se C(fx 3 g) = fx 3 ; x 4 g. Conclui-se assim que este grafo tem duas componentes fortemente conexas. Vamos seguidamente estudar o processo de determinar as componentes fortemente conexas de um grafo utilizando a sua matriz de adjacência. Vamo-nos socorrer do grafo da gura 8. Escreve-se, em primeiro lugar, a sua matriz de adjacência: M = Comecemos por determinar o fecho transitivo do vértice x1. Na primeira linha da matriz encontramos elementos iguais a 1 nas posições e, isso signi ca que existe um arco entre o vértice x1 e os vértices x e x. Seguidamente inspeccionam-se as linhas correspondentes a x e x à procura de elementos iguais a 1. Esses elementos dão-nos a informação dos vértices para aos quais se pode chegar partindo do vértice x1 usando caminhos de comprimento dois. Prossegue-se inspeccionando as linhas correspondentes a estes novos vértices e assim por diante até que aconteça uma de duas situações: ou já temos todos os vértices, ou já se inspeccionaram todas as linhas e não se juntaram mais vértices ao conjunto. Para simpli car começamos por de nir um vector que colocamos à frente da matriz e onde vamos marcando os vértices que se podem alcançar com um número igual 14
16 Universidade do Algarve - 0/0 ao comprimento do menor caminho utilizado. Assim, começamos por: M = isto é, pode-se ir de x 1 para x e para x usando um caminho de comprimento 1 e para os restantes vértices usando um caminho comprimento (é claro que de x 1 para ele próprio o comprimento do caminho é 0. Concluímos que b+ (fx 1 g) = fx 1 ; x ; x 3 ; x 4 ; x 5 ; x g. Passemos agora à determinação do fecho transitivo inverso. O processo é semelhante, só que, em vez de inspeccionarmos as linhas, vamos inspeccionar as colunas da matriz de adjacência. Usamos como auxiliar um vector linha que colocamos por debaixo da matriz e que construímos usando a mesma lógica: M = Repare-se que agora inspeccionando as colunas assinaladas com 1 não se conseguem marcar mais colunas, pelo que temos b (fx 1 g) = fx 1 ; x ; x 5 ; x g: Após a determinação da componente fortemente conexa que contém x 1, vamos determinar as componentes fortemente conexas dos vértices que caram de fora desta componente. 15
17 Universidade do Algarve - 0/0 Como é C(fx 1 g) = fx 1 ; x ; x 5 ; x g, podemos optar por x 3 ou por x 4. Como já se viu, se formos estudar a componente de qualquer outro vértice já incluído em C(fx 1 g) obter-seá exactamente o mesmo conjunto. Também se percebe facilmente que as componentes conexas dos vértices que caram de fora não vão incluir qualquer dos vértices de C(fx 1 g). Vamos, portanto, estudar só os sucessores e antecessores no subgrafo em que o conjunto de vértices é fx 1 ; x ; x 3 ; x 4 ; x 5 ; x g C(fx 1 g), ou seja, toma-se para conjunto de vértices do subgrafo fx 3 ; x 4 g. A matriz de adjacência só tem as linhas e colunas correspondentes a estes vértices e o processo é repetido: Conclui-se assim que C(fx 3 g) = fx 3 ; x 4 g Repare-se que cada componente conexa pode ser de nida através de uma relação no conjunto dos vértices: x i e x j pertencem à mesma componente fortemente conexa se e só se existe uma caminho de ida e volta entre os dois vértices. É fácil veri car que se trata de uma relação de equivalência e que, portanto, as componentes fortemente conexas são, na realidade classes de equivalência que fazem uma partição no conjunto dos vértices. De nição 15 Um grafo orientado em que haja uma só componente fortemente conexa diz-se fortemente conexo. Nalguns casos é su ciente que haja uma ligação entre os vértices independentemente do sentido. Nesse caso admite-se a construção de caminhos que utilizem arestas em "sentido proibido". Na prática o processo decorre como se todos os arcos se transformassem em arestas. As componentes obtidas deste modo chamam-se componentes conexas. De nição 1 Um grafo orientado em que haja uma só componente conexa diz-se conexo. De nição 1 Num grafo conexo a uma aresta cuja retirada transforma o grafo num grafo desconexo chama-se um istmo. A determinação das componentes conexas é bastante mais simples, pois, neste caso, o conjunto dos sucessores e dos antecessores é o mesmo. Só é necessário construir, a partir 1 3 5
18 Universidade do Algarve - 0/0 da matriz de adjacência, uma matriz auxiliar, correspondente ao grafo não orientado que se obtém quando se transformam os arcos em arestas. simétrica e obtém-se do seguinte modo: 8 9 >< 0 se m ij = m ji = 0 >= i = 1; : : : ; n a ij = >: 1 se nos outros casos >; j = 1; : : : n Esta nova matriz é obviamente No exemplo anteriormente tratado, correspondente ao grafo da gura 8, querendo determinar as componentes conexas, começa-se por construir a matriz auxiliar A como foi descrito e fazer a determinação das componentes sobre a matriz auxiliar. Assim: M = ! A = Conclui-se assim que o grafo da gura 8 é conexo, pois tem uma única componente conexa. Num grafo não orientado não faz sentido em falar em componentes fortemente conexas, pois os conceitos de conexo e fortemente conexo correspondem à mesma realidade. A determinação das componentes fortemente conexas permite identi car todos os pares de vértices entre os quais existem caminhos, mas não nos fornece informação completa sobre o número e o comprimento dos caminhos existentes. Vejamos no grafo da gura 9 como determinar todos os caminhos entre os vértices A e E que não passem mais do que uma vez pelo mesmo vértice. Como o grafo é de muito reduzida dimensão é relativamente fácil, por simples inspecção, determinar todos os caminhos pretendidos: 1
19 Universidade do Algarve - 0/0 Figura 9: Determinação de caminhos A! C! E; A! D! E; A! B! D! E; A! D! C! E; A! B! D! C! E Este grafo só tem 5 vértices e pretendem-se caminhos que não repitam vértices, por isso não se vai além dos caminhos de comprimento 4. Vejamos um processo de encontrar estes caminhos sem ser por observação do grafo. Comecemos por escrever a matriz de adjacência deste grafo: M = O elemento m 15 é nulo, este facto informa-nos que não existe qualquer caminho de comprimento 1 entre os vértices A e E. Calculando M obtém-se informação sobre os caminhos com dois arcos. Com efeito, se há um caminho de comprimento entre os vértices x i e x j, isso signi ca que existe um vértice x k tal que há um arco entre x i e x k e outro entre x k e x j, ou seja m ik = 1 e 18
20 Universidade do Algarve - 0/0 m kj = 1. Como m () ij = n P k=1 m ik m kj, facilmente se percebe que este valor dá informação sobre o número de caminhos de comprimento entre os vértices xi e xj M = = Temos m () 15 =, sabemos assim que há dois caminhos de comprimento entre A e E. Para saber quais são esses caminhos é preciso averiguar quais os produtos que deram origem aquele : m () 15 = m 13 m 35 + m 14 m 45. Temos assim os caminhos: A! C! E e A! D! E. De modo análogo, a matriz M 3 dá informação sobre o número de caminhos de comprimento 3: M 3 = MM = = m (3) 15 = m 1 m () 5 + m 14 m () 45 = m 1 m 4 m 45 + m 14 m 43 m 35. Temos assim os caminhos A! B! D! E e A! D! C! E. Continuando:
21 Universidade do Algarve - 0/0 M 4 = MM 3 = = m (4) 15 = m 1 m (3) 5 +m 13 m (3) 35 = m 1 m 4 m 43 m 35 +m 13 m 31 m 13 m 35 +m 13 m 31 m 14 m 45. Temos assim os caminhos A! B! D! C! E, A! C! A! C! E e A! C! A! D! E. Como o objectivo era encontrar caminhos que não repetissem vértices, só o primeiro destes caminhos cumpre esse objectivo. O problema de, num dado grafo, determinar caminhos que não repitam arestas ou não repitam vértices tem inúmeras aplicações práticas, como veremos. Na maior parte dessas aplicações, trabalha-se com grafos não orientados e o objectivo é encontrar um circuito que contenha todos os vértices ou todas as arestas sem repetição. De nição 18 Um caminho ou circuito diz-se elementar se todos os vértices por onde passa são distintos. Um circuito elementar que contenha todos os vértices de um grafo não orientado diz-se circuito de Hamilton. e E. No exemplo anterior procuravam-se todos os caminhos elementares entre os vértices A 1. Circuitos e caminhos de Euler De nição 19 Um caminho ou circuito diz-se simples se todos os arcos ou arestas que o constituem são distintas. Um circuito simples que contenha todas as arestas de um grafo não orientado diz-se circuito de Euler. O problema das pontes de Königsberg é na realidade o problema de encontrar um circuito de Euler, que já sabemos não existir para aquele grafo. Teorema 1 Num grafo não orientado conexo existe um circuito de Euler se e só se todos os vértices tiverem grau par. 0
22 Universidade do Algarve - 0/0 Demonstração. Existe circuito de Euler =) todos os vértices têm grau par. Se existe um circuito de Euler, então sempre que se chega a um vértice é preciso sair e, por isso, as arestas incidentes em cada vértice têm que ser em número par. Todos os vértices têm grau par =) existe circuito de Euler Se todos os vértices têm grau par o grafo deve conter pelo menos um circuito. Com efeito, considere-se um grafo G com m arestas e todos os vértices com grau par. Seja C o caminho de maior comprimento que se pode ter em G. Sejam os vértices desse caminho x 1 x ::::x p 1 x p. Como x p tem grau par então ele não pode estar ligado só a x p 1, mas como C é o caminho de maior comprimento em G, então a outra aresta deve ligar a um dos outros vértices deste caminho, obtendo-se assim o circuito desejado. Para demonstrar a existência de um circuito de Euler procede-se por indução matemática sobre o número de arestas do grafo. m = 0 O único grafo conexo com 0 arestas é um grafo só com um vértice de grau zero, onde claramente há um circuito de Euler. Por hipótese de indução, considere-se que todos os grafos conexos com número de arestas inferior a m e em que todos os vértices têm grau par possuem um circuito de Euler. Seja agora G um grafo conexo com m arestas e em que todos os vértices têm grau par. G tem um circuito. Seja C esse circuito. Num circuito cada vértice está ligado ao vértice anterior e ao seguinte. Se retirarmos de G as arestas de C, o grafo resultante G 0 continua a ter todos os vértices com grau par. O grafo G 0 pode não ser conexo. Cada uma das suas componentes conexas obedece à hipótese de indução e, por isso, possui um circuito de Euler. Estamos em condições de construir um circuito de Euler para G, começando no circuito C, usando cada circuito de Euler das componentes conexas de G 0 sempre que um vértice de C pertencer a uma dessas componentes, regressando a C exactamente a esse vértice e continuando até voltar ao ponto de partida. Esta demonstração fornece um processo muito pouco prático de encontrar um circuito de Euler. Descreve-se a seguir o algoritmo de Fleury para obtenção de circuitos de Euler. Este é um algoritmo fácil de utilizar em cálculos à mão e também de fácil implementação em computador Algoritmo de Fleury 1. Escolher um vértice qualquer para iniciar. 1
23 Universidade do Algarve - 0/0. Escolher qualquer aresta que saia desse vértice só escolhendo uma aresta que seja um istmo se não houver mais nenhuma. 3. Destruir a aresta utilizada 4. Repetir e 3 até chegar ao vértice inicial. 5. Se não há mais arestas o circuito de Euler está encontrado. Caso ainda haja arestas, recomeçar o circuito a partir de um dos vértices do circuito onde ainda haja arestas incidentes. Exemplo 1 Encontrar um circuito de Euler no grafo representado na gura 10. Figura 10: Circuito de Euler É preciso começar por constatar que realmente existe um tal circuito. Com efeito o grafo é conexo e os graus dos vértices são:, 4, 4, 4, 4,. Começa-se com um vértice qualquer, por exemplo o vértice 1, escolhe-se uma aresta que sai de 1, por exemplo (1, ). Retira-se essa aresta. Escolhe-se uma aresta que sai de, por exemplo (, 3). Retira-se essa aresta. Escolhe-se uma aresta que sai de 3, por exemplo (3, 4). Retira-se essa aresta. Escolhe-se uma aresta que sai de 4, por exemplo (4, 5). Retira-se essa aresta. Neste momento o caminho já construído é 1!! 3! 4! 5 e o grafo está com o aspecto que se mostra na gura 11 Continuando o processo, escolhe-se agora uma aresta a sair de 5, por exemplo (5, ), retira-se a aresta. E repetindo o processo até acabar as arestas obtinha-se o circuito: 1!! 3! 4! 5!! 4!! 5! 3! 1
24 Universidade do Algarve - 0/0 Figura 11: Aplicação do algoritmo de Fleury Este algoritmo é também de fácil programação em computador, a partir da matriz de adjacência. Vejamos com este mesmo exemplo como poderia funcionar um programa de computador. A matriz de adjacência correspondente ao grafo da gura 10 é A = Um programa de computador tem que fazer uma escolha sistemática. Suponhamos que o programa é construído de modo a que a aresta escolhida em cada passo é a correspondente à primeira entrada não nula da linha correspondente ao vértice que está a ser considerado no momento. Note-se que retirar a aresta do vértice i para o vértice j corresponde a anular as entradas a ij e a ji da matriz. Começando no vértice 1, inspecciona-se a primeira linha e encontra-se a primeira entrada não nula correspondente à aresta (1; ). Faz-se a 1 = a 1 = 0. Agora inspecciona-se a segunda linha. A primeira entrada não nula é a 3 correspondente à aresta (; 3). Faz-se a 3 = a 3 = 0. Inspecciona-se agora a terceira linha. A primeira entrada não nula corresponde à aresta (3; 1). Faz-se a 31 = a 13 = 0. Neste momento a matriz de adjacência 3
25 Universidade do Algarve - 0/0 modi cada está com o aspecto: A 0 = e o circuito já construído é 1!! 3! 1. Mas agora a primeira linha já não tem nenhuma entrada não nula. Observa-se o circuito construído e procura-se o primeiro vértice que corresponda a uma linha que ainda tenha alguma entrada não nula. Veri ca-se que a segunda linha está nessas condições. Rescreve-se o circuito a acabar no vértice :! 3! 1! e continua-se com o processo. Agora a primeira entrada não nula da linha corresponde à aresta (; 4). Faz-se a 4 = a 4 = 0. Na linha 4 a primeira entrada não nula corresponde à aresta (4; 3). Faz-se a 43 = a 34 = 0. Na linha 3 a primeira entrada não nula corresponde à aresta (3; 5). Faz-se a 35 = a 53 = 0. Na linha 5 a primeira entrada não nula corresponde à aresta (5; ). Faz-se a 5 = a 5 = 0. Neste momento a matriz de adjacência modi cada está com o aspecto: A 00 = e o circuito construído até ao momento é! 3! 1!! 4! 3! 5!. Agora a linha correspondente ao vértice já não tem nenhuma entrada não nula. Como se fez antes, percorre-se o circuito de modo a terminar num vértice correspondente a uma 4
26 Universidade do Algarve - 0/0 linha que ainda tenha elementos não nulos: 4! 3! 5!! 3! 1!! 4. Continuando o processo, escolhia-se agora a aresta (4; 5), depois a (5; ) e, nalmente a (; 4), obtendo-se o circuito de Euler 4! 3! 5!! 3! 1!! 4! 5!! 4. De notar que no m do processo a matriz A ca nula. Suponhamos agora que os habitantes de Königsberg não se importavam de começar e acabar o seu passeio em partes diferentes da cidade, desde que atravessassem todas as pontes sem repetição. Isto é, por outras palavras, será possível encontrar no grafo da gura 10 um caminho (já não um circuito) que use todas as arestas sem repetição? A resposta mais uma vez é negativa. Teorema Num grafo conexo não orientado existe um caminho de Euler se e só se houver exactamente duas arestas com grau impar. Demonstração. Unindo os dois vértices de grau impar por uma aresta teremos um grafo conexo em que todas as arestas têm grau par. Estamos, assim, em condições de encontrar um circuito de Euler. Basta escrever o circuito de tal modo que a aresta introduzida seja a primeira ou a última e depois retirá-la para obter um caminho de Euler, que vai começar e acabar nos dois vértices de grau impar. Também é possível formular resultados sobre a existência de circuitos e caminhos de Euler em grafos orientados. Teorema 3 Num grafo orientado fortemente conexo existe um circuito de Euler se e só se o grafo for pseudo-simétrico. Teorema 4 Num grafo orientado fortemente conexo existe um caminho de Euler se e só se existirem dois vértices x p e x f tais que gr + (x p ) gr (x p ) = 1 e gr (x f ) gr + (x f ) = 1 e para todos os outros vértices x j com j = p e j = f for gr + (x j ) = gr (x j ). A demonstração destes teoremas é semelhante à já apresentada para o caso não orientado. Vejamos o exemplo da gura 1: 5
27 Universidade do Algarve - 0/0 Figura 1: Circuito de Euler gr + (1) = gr (1) = 1 9 gr + () = gr () = gr + (3) = gr (3) = gr + (4) = gr (4) = gr + (5) = gr (5) = >= Então o grafo é pseudo-simétrico. gr + () = gr () = 1 >; Também não é difícil constatar que o grafo é fortemente conexo. Basta determinar a componente fortemente conexa de um dos seus vértices, para concluir que o grafo tem uma única componente fortemente conexa
28 Universidade do Algarve - 0/0 O processo para encontrar um circuito de Euler é semelhante ao descrito para o caso não orientado. Uma possível solução é o circuito 4!! 5!! 1! 3! 4!! 3! 5! Grafos e relações binárias Um grafo orientado sem arestas múltiplas está associado a uma relação binária de nida no conjunto dos seus vértices. As propriedades da relação traduzem-se em propriedades do grafo. Uma relação binária de nida no conjunto X é identi cada com um subconjunto do produto cartesiano X X. As relações binárias podem ter ou não alguma das seguintes propriedades: 1. re exiva! 8x X; (x; x). simétrica! 8x; y X; (x; y) =) (y; x) 3. anti-simétrica! 8x; y X; (x; y) =) (y; x) = 4. anti-simétrica em sentido lato! 8x; y X; (x; y) ^ (y; x) =) x = y 5. transitiva! 8x; y; z X; (x; y) ^ (y; z) =) (x; z) A uma relação re exiva corresponde um grafo em que todos os vértices têm laços. A uma relação simétrica corresponde um grafo não orientado Numa relação anti-simétrica só há arcos de um único sentido e não há laços. Se a relação for anti-simétrica em sentido lato pode ou não haver laços Relações de equivalência e componentes fortemente conexas Uma relação de equivalência satisfaz as propriedades1, e 5. As classes de equivalência dessa relação vão corresponder às componentes conexas do grafo. Exemplo Considere-se a relação binária de nida no conjunto X = f1; ; 3; 4; 5; ; g através de XX dado por = f(1; 1); (1; ); (1; 3); (1; 4); (; 1); (; ); (; 3); (; 4); (3; 1); (3; ); (3; 3); (3; 4); (4; 1); (4; ); (4; 3); (4; 4); (5; 5); (5; ); (; 5); (; ); (; )g. O grafo correspondente a esta relação está representado na gura 13.
29 Universidade do Algarve - 0/0 Figura 13: Relação de equivalência Como todos os vértices têm laços e todos os arcos de ida têm um correspondente arco de volta, convenciona-se representar grafos deste tipo sem os laços e usando arestas em vez de arcos, isto é, usando um grafo não orientado sem laços, como se mostra na gura 14. Figura 14: Relação de equivalência O grafo é formado por componentes conexas, correspondentes às classes de equivalência da relação. Dentro de cada componente cada vértice é adjacente a todos os outros. Quando tal acontece as componentes têm o nome de cliques Relações de ordem e grafos Uma relação de ordem lata satisfaz as propriedades 1, 4 e 5, enquanto uma relação de ordem estrita satisfaz as propriedades 3 e 5. Quando se representa uma relação de ordem através de um grafo, para simpli car 8
30 Universidade do Algarve - 0/0 as notações, convenciona-se que a orientação dos arco é de baixo para cima e não se representam as arestas que decorrem da transitividade. Exemplo 3 Considere-se o grafo de nido por: X = fa; b; c; d; e; fg e = f(a; b); (a; c); (a; d); (a; e); (a; f); (b; d); (b; f); (c; e); (c; f); (d; f)g Como o vértice a está relacionado com todos os outros deve ser o que ca colocado na parte inferior do desenho. Repare-se que a existência dos pares (a; b) e (b; d), num relação transitiva, obriga à existência do par (a; d). Então, para simpli car notações, omite-se o arco correspondente a este último arco, estando subentendida a sua existência. Com estas convenções, o grafo desenha-se como se mostra na gura 15. Figura 15: Relação de ordem Como a orientação dos arcos é de baixo para cima, pode-se dizer que um vértice está relacionado com outro sempre que houver um caminho entre os dois, composto exclusivamente de arcos dirigidos de baixo para cima. Assim, pode-se concluir que existe o par (a; e) mas não existe o par (b; e). Se o grafo de uma relação de ordem é tal que 8x; y X; (x; y) _ (y; x) _ x = y; isto é, se todos os elementos estão relacionados, a relação diz-se de ordem total. É fácil ver que o grafo correspondente é uma cadeia de baixo para cima. 9
31 Universidade do Algarve - 0/0 Diz-se que um conjunto onde está de nida uma relação de ordem parcial tem um elemento mínimo z se 8x X; (z; x). De modo semelhante diz-se que o conjunto tem um elemento máximo w se 8x X; (x; w). No grafo da gura 15 há um elemento mínimo a; mas não há elemento máximo. 1.9 Grafos completos De nição 0 Seja G = (X; ) um grafo orientado. Se 8x; y X; (x; y) = =) (y; x), o grafo diz-se completo. Não se deve confundir este conceito com o de relação anti-simétrica. Num grafo orientado completo a não existência de um arco entre dois vértices implica a existência do arco simétrico desse, enquanto que nas relações anti-simétricas a existência de um arco impede a existência do arco simétrico, mas pode não haver qualquer arco entre dois vértices, quer num sentido quer noutro. A gura 1 apresenta um exemplo de um grafo orientado completo. Figura 1: Grafo orientado completo No caso dos grafos não orientados, os grafos completos são chamados cliques como já se viu. Para cada número de vértices n existe uma única clique que se representa por K n. A determinação de subgrafos de um grafo que formem cliques é um problema de grande interesse teórico e que tem inúmeras de aplicações como veremos mais tarde. n = 5. Na gura 1 apresenta-se os grafos completos correspondentes a n = ; n = 3; n = 4 e De notar que um grafo não orientado completo é regular, isto é, todos os vértices têm n (n 1) o mesmo grau. É, assim, imediato concluir que K n tem n vértices e arestas. 30
32 Universidade do Algarve - 0/0 Figura 1: Alguns grafos completos 1.10 Grafos bipartidos De nição 1 Se num grafo não orientado for possível encontrar uma partição do conjunto dos vértices X = Y [Z; (Y \Z =?) tal que cada aresta do grafo une um vértice do conjunto Y a um vértice do conjunto Z e não há arestas entre os vértices de Y, nem há arestas entre os vértices de Z, diz-se que o grafo é bipartido. Se todos os vértices de Y estiverem ligadas a todos os vértices de Z o grafo diz-se bipartido completo. Os grafos bipartidos completos são completamente determinados pelo número de vértices nos dois conjuntos de índices. Designa-se por K r;s o grafo bipartido completo em que um dos conjuntos de vértices tem r elementos e o outro tem s. Nas guras 18 e 19 apresentam-se alguns exemplos de grafos bipartidos completos para diferentes valores de r e de s. Para melhor compreensão os vértices de um conjunto são pretos e os do outro conjunto são brancos. Na gura 18 representa-se K ;4 de duas maneiras diferentes. O grafo é o mesmo, o que mudou foi a posição relativa dos vértices. Na gura 19 apresentam-se representações de K 1;3 ; K ; e K 3;3. Figura 18: Duas representações de K ;4 31
33 Universidade do Algarve - 0/0 Figura 19: Representações de K 1;3 ; K ; ; K 3;3 O grafo K r;s tem r + s vértices e r s arestas. Cada um dos r vértices do primeiro conjunto tem grau s e cada um dos s vértices do segundo conjunto tem grau r. Note-se também que os grafos K r;s e K s;r são iguais. Por convenção escreve-se sempre primeiro o menor dos valores de s e r. De modo análogo se pode de nir grafo tripartido e grafo tripartido completo, usando agora três conjuntos disjuntos de vértices em lugar de dois. De nição Se num grafo não orientado for possível encontrar uma partição do conjunto dos vértices X = Y [ Z [ W; (Y \ Z =?; Y \ W =?; W \ Z =?) tal que cada aresta do grafo une um vértice de um dos conjuntos Y; Z ou W a um vértice de outro conjunto e não há arestas entre os vértices de um mesmo conjunto, diz-se que o grafo é tripartido. Se todos os vértices de cada conjunto estiverem ligadas a todos os vértices dos outros conjuntos, o grafo diz-se tripartido completo. Os grafos tripartidos completos, tal como os bipartidos completos, são completamente determinados pelo número de vértices nos dois conjuntos de índices. Designa-se por K r;s;t o grafo tripartido completo em que um dos conjuntos de vértices tem r elementos, outro tem s elementos e o terceiro tem t elementos. Na gura 0 apresenta-se, a título de exemplo o grafo tripartido completo K ;; Grafos complementares Quando uma grafo não é completo é muitas vezes interessante conhecer o grafo que tem as arestas que lhe faltam para ser completo. Surge assim o conceito de grafo complementar. De nição 3 Dado o grafo G = (X; ), chama-se grafo complementar de G e representase por G o grafo que tem X como conjunto de vértices e X X como conjunto de arestas. 3
34 Universidade do Algarve - 0/0 Figura 0: Grafo K ;; Exemplo 4 Na gura 1 representa-se um grafo e o seu complementar. Figura 1: Grafos complementares Facilmente se constata que o complementar de um grafo completo não tem arestas (todos os vértices têm grau zero) e que o complementar do grafo bipartido completo K r;s é o grafo desconexo composto de duas componentes conexas K r e K s. 1.1 Árvores Um outro tipo de grafos que tem muitas aplicações é conhecido por árvore. De nição 4 Uma árvore é um grafo não orientado conexo sem circuitos De nição 5 Uma oresta é um grafo não orientado cujas componentes conexas são árvores. As árvores têm várias propriedades sendo as mais importantes resumidas no seguinte teorema: 33
35 Universidade do Algarve - 0/0 Teorema 5 Seja G = (X; ) uma árvore com n > vértices. As seguintes proposições são equivalentes: a) G é conexo e não tem circuitos. b) G não tem circuitos e tem n 1 arestas. c) G é conexo e tem n 1 arestas. d) G não tem circuitos e acrescentando uma aresta cria-se um único circuito. e) G é conexo e a supressão de uma única aresta torna-o desconexo. f) Qualquer que seja o par de vértices de X há um único caminho simples que os une. Demonstração. a) =) b) Sendo G conexo e sem circuitos, retirando uma aresta ca não conexo e terá duas componentes conexas. Continuando a retirar arestas, por cada aresta retirada cria-se mais uma componente conexa. Quando se tiverem retirado n 1 arestas obtiveram-se n componentes conexas. Como o grafo tem n vértices, cada componente conexa corresponde a um único vértice e o grafo cou sem arestas. Então o grafo tinha exactamente n 1 arestas. b) =) c) Por absurdo suponha-se que o grafo não era conexo. Existem dois vértices em G tais que não existe nenhum caminho entre eles. Unem-se esses vértices por uma aresta. O novo grafo continua a não ter circuitos, porque se se tivesse criado um circuito era porque havia um caminho entre os dois vértices. Se o grafo continua a não ser conexo repete-se o processo de adicionar arestas até que o grafo que conexo e continuará sem circuitos. Suponhamos que o processo tinha sido repetido k vezes. Então o novo grafo é conexo e sem circuitos e terá (n 1 + k) arestas. Mas para não haver circuitos o grafo tem que ter n 1 arestas. Então tem que ser k = 0, concluindo-se assim que o grafo original já era conexo. c) =) d) Por absurdo, supor que o grafo possui pelo menos um circuito. Retirando uma aresta desse circuito obtém-se um grafo com n arestas, que, como tem n vértices, não poderá ser conexo. Sendo o grafo conexo e sem circuitos, há um caminho entre cada par de vértices, acrescentando uma aresta entre um determinado par de vértices cria-se um circuito formado pelo caminho que já existia e por essa nova aresta. d) =) e) 34
36 Universidade do Algarve - 0/0 Por absurdo supor que o grafo não é conexo. Então, há pelo menos um par de vértices entre os quais não existe qualquer caminho. Acrescentando ao grafo a aresta entre esses dois vértices cria-se um circuito. Mas isso signi ca que os dois vértices estavam ligados por um caminho. Então o grafo tem que ser conexo. e) =) f) Por absurdo, suponha-se que há um par de vértices unidos por mais do que um caminho simples. Então o grafo tem pelo menos um circuito. Suprimindo uma aresta desse circuito o grafo continua a ser conexo, o que contraria o facto de o grafo deixar de ser conexo quando uma aresta é suprimida. f) =) a) Se cada par de vértices está unido por um caminho o grafo é conexo. Além disso, como esse caminho é único não pode haver circuitos Teorema Numa árvore há sempre pelo menos dois vértices de grau 1. Demonstração. Seja G um grafo com n vértices e m arestas que é uma árvore. Então m = n 1. Como a soma dos graus dos vértices é o dobro do número de arestas, essa soma é n. Se todos os vértices tivessem grau igual ou superior a, essa soma seria igual ou superior a n. Então, pelo menos um dos vértices deve ter grau 1. Se somente um dos vértices tivesse grau 1 e todos os outros grau ou mais, a soma dos graus seria igual ou superior a n 1. Por isso tem que haver pelo menos dois vértices com grau Árvores de suporte Um problema muito comum é o de tentar chegar a todos os vértices de um grafo usando o menor número de arestas possível. Ora, para se chegar a todos os vértices de um grafo será necessário usar um grafo parcial conexo e querendo usar o menor número possível de arestas não se deverá ter nenhum circuito, pois haveria aí pelo menos uma aresta desnecessária. Ou seja, deve-se encontrar um grafo parcial do grafo original que seja uma árvore. De nição Seja G um grafo. Uma árvore de suporte de G é um grafo parcial de G que é uma árvore. Teorema Um grafo G admite uma árvore de suporte se e só se G é conexo. Demonstração. G admite uma árvore de suporte =) G conexo 35
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 10: Introdução aos Grafos
 Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
MATEMÁTICA DISCRETA. Patrícia Ribeiro 2018/2019. Departamento de Matemática, ESTSetúbal 1 / 47
 1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz. EST Setúbal / IPS. 28 Maio - 3 Junho 2012
 MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz EST Setúbal / IPS 28 Maio - 3 Junho 2012 Carlos Luz (EST Setúbal / IPS) Grafos (1/4) 28 Maio - 3 Junho 2012 1 / 34 Noção de Grafo De nição Um grafo não orientado
MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz EST Setúbal / IPS 28 Maio - 3 Junho 2012 Carlos Luz (EST Setúbal / IPS) Grafos (1/4) 28 Maio - 3 Junho 2012 1 / 34 Noção de Grafo De nição Um grafo não orientado
PERCURSOS. André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré
 PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
Definição 1.1 : Uma árvore é um grafo simples conexo e sem ciclos.
 1 Árvores Definição 1.1 : Uma árvore é um grafo simples conexo e sem ciclos. Um grafo simples sem ciclos mas não conexo (em que cada componente conexa é portanto uma árvore) chama-se uma floresta. Numa
1 Árvores Definição 1.1 : Uma árvore é um grafo simples conexo e sem ciclos. Um grafo simples sem ciclos mas não conexo (em que cada componente conexa é portanto uma árvore) chama-se uma floresta. Numa
ALGA - Eng. Civil e Eng. Topográ ca - ISE / Geometria Analítica 89. Geometria Analítica
 ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Geometria Analítica 9 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste
ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Geometria Analítica 9 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste
Grafos Orientados (digrafos)
 Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Cap. 2 Conceitos Básicos em Teoria dos Grafos
 Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
As Pontes de Königsberg
 As Pontes de Königsberg Anderson Freitas Ferreira e Lívia Minami Borges 13 de junho de 2015 Resumo A teoria de grafos teve seu início em 1736, quando Euler utilizou uma estrutura para resolver o Problema
As Pontes de Königsberg Anderson Freitas Ferreira e Lívia Minami Borges 13 de junho de 2015 Resumo A teoria de grafos teve seu início em 1736, quando Euler utilizou uma estrutura para resolver o Problema
Matemática Discreta - Exercícios de Grafos
 UALG - 0/0 1. Seja G o grafo cuja matriz de adjacência é: 1 8 9 1 8 9 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
UALG - 0/0 1. Seja G o grafo cuja matriz de adjacência é: 1 8 9 1 8 9 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
x y Grafo Euleriano Figura 1
 Grafo Euleriano Um caminho simples ou um circuito simples é dito euleriano se ele contém todas as arestas de um grafo. Um grafo que contém um circuito euleriano é um grafo euleriano. Um grafo que não contém
Grafo Euleriano Um caminho simples ou um circuito simples é dito euleriano se ele contém todas as arestas de um grafo. Um grafo que contém um circuito euleriano é um grafo euleriano. Um grafo que não contém
GRAFOS: UMA INTRODUÇÃO
 GRAFOS: UMA INTRODUÇÃO Vilmar Trevisan -Instituto de Matemática - UFRGS Junho de 2006 Grafos: uma introdução Informalmente, um grafo é um conjunto de pontos no plano ligados entre por flechas ou por segmentos
GRAFOS: UMA INTRODUÇÃO Vilmar Trevisan -Instituto de Matemática - UFRGS Junho de 2006 Grafos: uma introdução Informalmente, um grafo é um conjunto de pontos no plano ligados entre por flechas ou por segmentos
Problemas de Fluxo em Redes
 CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
Capítulo 2- Modelos de grafos.
 Capítulo 2- Modelos de grafos. 2.1- Introdução (pág. 8) [Vídeo 24] Grafo- é um esquema constituído por pontos (ou vértices) e por segmentos (ou arestas). (8) Exemplo 1(pág.8) Um grafo diz-se conexo se
Capítulo 2- Modelos de grafos. 2.1- Introdução (pág. 8) [Vídeo 24] Grafo- é um esquema constituído por pontos (ou vértices) e por segmentos (ou arestas). (8) Exemplo 1(pág.8) Um grafo diz-se conexo se
Matemática II /06 - Matrizes 1. Matrizes
 Matemática II - 00/0 - Matrizes Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma função A : f; ; :::; mg f; ; :::; ng R: (i; j) A (i; j)
Matemática II - 00/0 - Matrizes Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma função A : f; ; :::; mg f; ; :::; ng R: (i; j) A (i; j)
2. Desenhe o grafo orientado G = (X, Γ) para: 3. Em cada alínea dois grafos são iguais. Identifique-os. (a) (b) (c)
 1. Desenhe o grafo não orientado G = (X, Γ) para: (a) X = {a, b, c, d} e Γ = {{a, b}, {b, c}, {c, d}}. (b) X = {a, b, c, d} e Γ = φ. (c) X = {1, 2, 3, 4, 5, 6, 7, 8} e Γ = {{1, 2}, {2, 2}, {2, 3}, {3,
1. Desenhe o grafo não orientado G = (X, Γ) para: (a) X = {a, b, c, d} e Γ = {{a, b}, {b, c}, {c, d}}. (b) X = {a, b, c, d} e Γ = φ. (c) X = {1, 2, 3, 4, 5, 6, 7, 8} e Γ = {{1, 2}, {2, 2}, {2, 3}, {3,
Alguns probleminhas...
 Introdução Vários problemas da computação, com aplicações em diversos problemas importantes, nasceram de jogos ou brincadeiras. Hoje veremos uma pequana amostra deste fato. Alguns probleminhas... Problema
Introdução Vários problemas da computação, com aplicações em diversos problemas importantes, nasceram de jogos ou brincadeiras. Hoje veremos uma pequana amostra deste fato. Alguns probleminhas... Problema
ALGA - Eng. Civil e Eng. Topográ ca - ISE / Matrizes 1. Matrizes
 ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Matrizes 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma aplicação A : f1; ; :::;
ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Matrizes 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma aplicação A : f1; ; :::;
C 3 C 3. De acordo com o teorema de Euler, um grafo não orientado admite um ciclo de Euler se e só for conexo e não tiver vértices de grau ímpar.
 rafos ircuito e iclo de uler X. ircuito e iclo de uler Um grafo orientado diz-se euleriano se há um circuito que contenha todos os seus arcos uma e só uma vez (circuito euleriano ).O grafo da figura é
rafos ircuito e iclo de uler X. ircuito e iclo de uler Um grafo orientado diz-se euleriano se há um circuito que contenha todos os seus arcos uma e só uma vez (circuito euleriano ).O grafo da figura é
Noções da Teoria dos Grafos. André Arbex Hallack
 Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 1.1 Introdução histórica..................................... 1 1.2 Passeios
Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 1.1 Introdução histórica..................................... 1 1.2 Passeios
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Grafos Eulerianos Preparado a partir do texto: Rangel, Socorro.
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Grafos Eulerianos Preparado a partir do texto: Rangel, Socorro.
Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17)
 Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17) Professor: Pedro Nóia Livro adotado: Matemática Aplicada às Ciências Sociais- 11º ano Elisabete Longo e Isabel
Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17) Professor: Pedro Nóia Livro adotado: Matemática Aplicada às Ciências Sociais- 11º ano Elisabete Longo e Isabel
Noções da Teoria dos Grafos
 Noções da Teoria dos Grafos André Arbex Hallack Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 7 3 Árvores 11 4 Emparelhamento em grafos 15 5 Grafos planares: Colorindo
Noções da Teoria dos Grafos André Arbex Hallack Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 7 3 Árvores 11 4 Emparelhamento em grafos 15 5 Grafos planares: Colorindo
Noções da Teoria dos Grafos. André Arbex Hallack
 Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 5 3 Árvores 7 4 Emparelhamento em grafos 11 5 Grafos planares:
Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 5 3 Árvores 7 4 Emparelhamento em grafos 11 5 Grafos planares:
Teoria dos Grafos. Edson Prestes
 Edson Prestes Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 2001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications, 1993; Kaufmann,
Edson Prestes Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 2001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications, 1993; Kaufmann,
Pesquisa Operacional II. Professor João Soares de Mello
 Pesquisa Operacional II Professor João Soares de Mello http://www.uff.br/decisao/notas.htm Ementa Teoria dos grafos (pré-requisitos: PO I, Álgebra Linear) Programação não linear (pré-requisitos: PO I,
Pesquisa Operacional II Professor João Soares de Mello http://www.uff.br/decisao/notas.htm Ementa Teoria dos grafos (pré-requisitos: PO I, Álgebra Linear) Programação não linear (pré-requisitos: PO I,
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 09: Representação de Grafos Preparado a partir do texto: Rangel, Socorro. Teoria
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 09: Representação de Grafos Preparado a partir do texto: Rangel, Socorro. Teoria
Disciplina: Matemática Discreta Agostinho Iaqchan Ryokiti Homa
 Disciplina: Matemática Discreta Agostinho Iaqchan Ryokiti Homa Aula -Grafos Uma figura vale por mil palavras A representação de dados e ou informações utilizando de recursos visuais é, em muitos casos,
Disciplina: Matemática Discreta Agostinho Iaqchan Ryokiti Homa Aula -Grafos Uma figura vale por mil palavras A representação de dados e ou informações utilizando de recursos visuais é, em muitos casos,
Prof. Marco Antonio M. Carvalho
 Prof. Marco Antonio M. Carvalho Lembretes! Lista de discussão! Endereço:! programaacao@googlegroups.com! Solicitem acesso:! http://groups.google.com/group/programaacao! Página com material dos treinamentos!
Prof. Marco Antonio M. Carvalho Lembretes! Lista de discussão! Endereço:! programaacao@googlegroups.com! Solicitem acesso:! http://groups.google.com/group/programaacao! Página com material dos treinamentos!
Teoria dos Grafos. Árvores
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br Preparado a partir
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br Preparado a partir
Investigação Operacional
 nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II
 01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II Prof. Moacir Ponti Jr. www.icmc.usp.br/~moacir Instituto de Ciências Matemáticas e de Computação USP 2011/1 Moacir Ponti Jr. (ICMCUSP) 01
01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II Prof. Moacir Ponti Jr. www.icmc.usp.br/~moacir Instituto de Ciências Matemáticas e de Computação USP 2011/1 Moacir Ponti Jr. (ICMCUSP) 01
O grau de saída d + (v) de um vértice v é o número de arcos que tem
 Grafos Direcionados Definição (Grau de Entrada) O grau de entrada d (v) de um vértice v é o número de arcos que tem v como cabeça. Definição (Grau de Saída) O grau de saída d + (v) de um vértice v é o
Grafos Direcionados Definição (Grau de Entrada) O grau de entrada d (v) de um vértice v é o número de arcos que tem v como cabeça. Definição (Grau de Saída) O grau de saída d + (v) de um vértice v é o
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Espaços vectoriais reais
 Espaços Vectoriais - Matemática II - 2004/05 40 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o
Espaços Vectoriais - Matemática II - 2004/05 40 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o
Helena Alves Rafael Sousa Rui Pedro Soares. MACS - Helena, Rafael, Rui Pedro 1
 Helena Alves Rafael Sousa Rui Pedro Soares MACS - Helena, Rafael, Rui Pedro 1 Disciplina bienal de componente de formação específica com carga horária distribuída por 3 aulas de 90 minutos cada. MACS -
Helena Alves Rafael Sousa Rui Pedro Soares MACS - Helena, Rafael, Rui Pedro 1 Disciplina bienal de componente de formação específica com carga horária distribuída por 3 aulas de 90 minutos cada. MACS -
Capítulo 1 Conceitos e Resultados Básicos
 Introdução à Teoria dos Grafos (MAC-5770) IME-USP Depto CC Profa. Yoshiko Capítulo 1 Conceitos e Resultados Básicos Um grafo é um par ordenado (V, A), onde V e A são conjuntos disjuntos, e cada elemento
Introdução à Teoria dos Grafos (MAC-5770) IME-USP Depto CC Profa. Yoshiko Capítulo 1 Conceitos e Resultados Básicos Um grafo é um par ordenado (V, A), onde V e A são conjuntos disjuntos, e cada elemento
Conteúdo. Histórico. Notas. Teoria dos Grafos BCC204. Notas. Notas. 1736: Euler e as Pontes de Königsberg
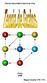
 Teoria dos Grafos BCC204 Haroldo Gambini Santos Universidade Federal de Ouro Preto - UFOP 15 de março de 2011 1 / 31 Conteúdo 1 Introdução 2 Exemplos 3 4 Representação 2 / 31 Histórico 1736: Euler e as
Teoria dos Grafos BCC204 Haroldo Gambini Santos Universidade Federal de Ouro Preto - UFOP 15 de março de 2011 1 / 31 Conteúdo 1 Introdução 2 Exemplos 3 4 Representação 2 / 31 Histórico 1736: Euler e as
Conceito Básicos da Teoria de Grafos
 1 Conceito Básicos da Teoria de Grafos GRAFO Um grafo G(V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w),
1 Conceito Básicos da Teoria de Grafos GRAFO Um grafo G(V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w),
Teoria dos Grafos AULA 1
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA 1 Introdução, Conceitos Iniciais, Isomorfismo Preparado
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA 1 Introdução, Conceitos Iniciais, Isomorfismo Preparado
GRAFOS. Introdução Conceitos Fundamentais
 GRAFOS Introdução Conceitos Fundamentais Uma aplicação do produto de matrizes Agora é a sua vez... Considere o diagrama seguinte Determine, o número de formas diferentes de ir de a 1 até e 2 e de a 2
GRAFOS Introdução Conceitos Fundamentais Uma aplicação do produto de matrizes Agora é a sua vez... Considere o diagrama seguinte Determine, o número de formas diferentes de ir de a 1 até e 2 e de a 2
Curso: Ciência da Computação Turma: 6ª Série. Teoria da Computação. Aula 2. Conceitos Básicos da Teoria da Computação
 Curso: Ciência da Computação Turma: 6ª Série Aula 2 Conceitos Básicos da Computação pode ser definida como a solução de um problema ou, formalmente, o cálculo de uma função, através de um algoritmo. A
Curso: Ciência da Computação Turma: 6ª Série Aula 2 Conceitos Básicos da Computação pode ser definida como a solução de um problema ou, formalmente, o cálculo de uma função, através de um algoritmo. A
TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS
 TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS O conjunto dos números reais,, que possui as seguintes propriedades:, possui uma relação menor ou igual, denotada por O1: Propriedade Reflexiva:
TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS O conjunto dos números reais,, que possui as seguintes propriedades:, possui uma relação menor ou igual, denotada por O1: Propriedade Reflexiva:
Programa. 1 Parte 1 - Conjuntos e Aplicações. 1 Conjuntos. 4 Indução Matemática e Divisibilidade. 5 Congruências Lineares
 Programa Matemática Discreta 2008/09 Jorge Manuel L. André FCT/UNL 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução Matemática e Divisibilidade 5 Congruências Lineares
Programa Matemática Discreta 2008/09 Jorge Manuel L. André FCT/UNL 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução Matemática e Divisibilidade 5 Congruências Lineares
UNIP - Ciência da Computação e Sistemas de Informação. Estrutura de Dados. AULA 8 Grafos. Estrutura de Dados 1
 UNIP - Ciência da Computação e Sistemas de Informação Estrutura de Dados AULA 8 Grafos Estrutura de Dados 1 Grafos - Motivação Muitas aplicações em computação necessitam considerar conjunto de conexões
UNIP - Ciência da Computação e Sistemas de Informação Estrutura de Dados AULA 8 Grafos Estrutura de Dados 1 Grafos - Motivação Muitas aplicações em computação necessitam considerar conjunto de conexões
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
Teoria dos Grafos AULA 1
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br AULA 1 Introdução,
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br AULA 1 Introdução,
Escola Secundária Garcia de Orta
 Escola Secundária Garcia de Orta Porto 2008 Miguel Duarte nº19 11ºA Índice Introdução...pág.3 O que é um Grafo?...pág.4 Classificação de arcos e adjacência de vértices...pág.5 Grafos não-orientados, circuitos
Escola Secundária Garcia de Orta Porto 2008 Miguel Duarte nº19 11ºA Índice Introdução...pág.3 O que é um Grafo?...pág.4 Classificação de arcos e adjacência de vértices...pág.5 Grafos não-orientados, circuitos
Teorema de Gerschgorin...
 Texto da palestra Teorema de Gerschgorin... ou será Ger sgorin? ou ainda Gerŝhgorin? Gersgorin? Geršgorin? Gershgorin? Gerŝgorin? Jaime Gaspar 2004/09/19 1 Introdução 1 Vamos falar um pouco sobre o Teorema
Texto da palestra Teorema de Gerschgorin... ou será Ger sgorin? ou ainda Gerŝhgorin? Gersgorin? Geršgorin? Gershgorin? Gerŝgorin? Jaime Gaspar 2004/09/19 1 Introdução 1 Vamos falar um pouco sobre o Teorema
Estruturas de Dados Grafos
 Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Escola Básica e Secundária Mouzinho da Silveira. MACS 11.º Ano Problema do Caixeiro Viajante
 Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
Teoria dos Grafos Introdu c ao
 Teoria dos Grafos Introdução Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications,
Teoria dos Grafos Introdução Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications,
CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:
![CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo: CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:](/thumbs/54/34072329.jpg) Matemática Discreta ESTiG\IPB Cap4. Elementos da Teoria de Grafos pg 1 CAP4. ELEMENTOS DA TEORIA DE GRAFOS Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E), sendo: Exemplos
Matemática Discreta ESTiG\IPB Cap4. Elementos da Teoria de Grafos pg 1 CAP4. ELEMENTOS DA TEORIA DE GRAFOS Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E), sendo: Exemplos
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Representação de Relações Definição: Uma relação binária de um conjunto A num conjunto
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Representação de Relações Definição: Uma relação binária de um conjunto A num conjunto
Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree
 Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Teoria dos Grafos AULA 3
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA 3 Trajetos, Caminhos, Circuitos, Grafos Conexos Preparado
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br AULA 3 Trajetos, Caminhos, Circuitos, Grafos Conexos Preparado
INE Fundamentos de Matemática Discreta para a Computação
 INE543 - Fundamentos de Matemática Discreta para a Computação 5) Relações 5.) Relações e Dígrafos 5.2) Propriedades de Relações 5.3) Relações de Equivalência 5.4) Manipulação de Relações 5.5) Fecho de
INE543 - Fundamentos de Matemática Discreta para a Computação 5) Relações 5.) Relações e Dígrafos 5.2) Propriedades de Relações 5.3) Relações de Equivalência 5.4) Manipulação de Relações 5.5) Fecho de
ALGA /09 - Geometria Analítica 78. Geometria Analítica
 ALGA - 00/09 - Geometria Analítica 7 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste capítulo faz-se um revisão desses conceitos
ALGA - 00/09 - Geometria Analítica 7 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste capítulo faz-se um revisão desses conceitos
Circuitos Hamiltorianos
 Circuitos Hamiltorianos Vimos que o teorema de euler resolve o problema de caracterizar grafos que tenham um circuito em que cada aresta apareça exatamente uma vez. Vamos estudar aqui uma questão relacionada.
Circuitos Hamiltorianos Vimos que o teorema de euler resolve o problema de caracterizar grafos que tenham um circuito em que cada aresta apareça exatamente uma vez. Vamos estudar aqui uma questão relacionada.
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 27 de abril de 2016 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 27 de abril de 2016 Marco Antonio M. Carvalho
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Grafos Eulerianos e o Problema do Carteiro Chinês
 Prof. Ademir A. Constantino DIN - UEM 1 Grafos Eulerianos e o Problema do Carteiro Chinês Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Prof. Ademir A. Constantino
Prof. Ademir A. Constantino DIN - UEM 1 Grafos Eulerianos e o Problema do Carteiro Chinês Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Prof. Ademir A. Constantino
Matemática II /06 - Determinantes 25. Determinantes
 Matemática II - 00/0 - Determinantes Permutações Determinantes Seja n N. Uma permutação p (p ; p ; : : : ; p n ) do conjunto f; ; ; ng é um arranjo dos n números em alguma ordem, sem repetições ou omissões.
Matemática II - 00/0 - Determinantes Permutações Determinantes Seja n N. Uma permutação p (p ; p ; : : : ; p n ) do conjunto f; ; ; ng é um arranjo dos n números em alguma ordem, sem repetições ou omissões.
GRAFOS. Prof. André Backes. Como representar um conjunto de objetos e as suas relações?
 8/0/06 GRAFOS Prof. André Backes Definição Como representar um conjunto de objetos e as suas relações? Diversos tipos de aplicações necessitam disso Um grafo é um modelo matemático que representa as relações
8/0/06 GRAFOS Prof. André Backes Definição Como representar um conjunto de objetos e as suas relações? Diversos tipos de aplicações necessitam disso Um grafo é um modelo matemático que representa as relações
Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular
 Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular Consideremos uma EDO linear de segunda ordem com a forma
Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular Consideremos uma EDO linear de segunda ordem com a forma
Método de eliminação de Gauss
 Matrizes - Matemática II - 00/0 Método de eliminação de Gauss Seja A = [a ij ] uma matriz de tipo m n. a FASE - ELIMINAÇÃO DESCENDENTE Esta fase permite obter uma matriz em forma de escada a partir da
Matrizes - Matemática II - 00/0 Método de eliminação de Gauss Seja A = [a ij ] uma matriz de tipo m n. a FASE - ELIMINAÇÃO DESCENDENTE Esta fase permite obter uma matriz em forma de escada a partir da
Parte B Teoria dos Grafos
 45 Parte B Teoria dos Grafos B. Grafos e Subgrafos Um grafo G é uma tripla ordenada (V(G), E(G), ), constituindo de um conjunto não vazio V(G) de vértices, um conjunto disjunto E(G) das arestas e uma função
45 Parte B Teoria dos Grafos B. Grafos e Subgrafos Um grafo G é uma tripla ordenada (V(G), E(G), ), constituindo de um conjunto não vazio V(G) de vértices, um conjunto disjunto E(G) das arestas e uma função
Percursos em um grafo
 Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Departamento de Engenharia de Produção UFPR 57
 Departamento de Engenharia de Produção UFPR 57 Introdução a Grafos Muitos problemas de otimização podem ser analisados utilizando-se uma estrutura denominada grafo ou rede. Problemas em redes aparecem
Departamento de Engenharia de Produção UFPR 57 Introdução a Grafos Muitos problemas de otimização podem ser analisados utilizando-se uma estrutura denominada grafo ou rede. Problemas em redes aparecem
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO. 5 a Lista de Exercícios
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO MATEMÁTICA COMBINATÓRIA 5 a Lista de Exercícios 1. O grafo de intersecção de uma coleção de conjuntos A 1,..., A n é o grafo
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO MATEMÁTICA COMBINATÓRIA 5 a Lista de Exercícios 1. O grafo de intersecção de uma coleção de conjuntos A 1,..., A n é o grafo
Comunicação e redes. Aula 2: Teoria dos Grafos Conceitos básicos. Professor: Guilherme Oliveira Mota.
 Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota g.mota@ufabc.edu.br Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota g.mota@ufabc.edu.br Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
Grafos - Motivação. Grafos - Motivação. Algoritmos e Estruturas de Dados II Introdução a Grafos
 Algoritmos e Estruturas de Dados II Introdução a Profa. M. Cristina/ Profa. Rosane (2010) Material de aula original: Profa. Josiane M. Bueno - Motivação : conceito introduzido por Euler, em 1736 Problema
Algoritmos e Estruturas de Dados II Introdução a Profa. M. Cristina/ Profa. Rosane (2010) Material de aula original: Profa. Josiane M. Bueno - Motivação : conceito introduzido por Euler, em 1736 Problema
1 Introdução à Teoria dos Grafos
 1 Introdução à Teoria dos Grafos Informalmente, designamos por grafo um diagrama, que podemos representar graficamente no plano, de pontos e linhas com extremos nesses pontos. Nessa representação gráfica
1 Introdução à Teoria dos Grafos Informalmente, designamos por grafo um diagrama, que podemos representar graficamente no plano, de pontos e linhas com extremos nesses pontos. Nessa representação gráfica
ALGA - Eng.Civil e Eng.Topográ ca-ise-2011/2012- Determinantes 32. Determinantes
 ALGA - Eng.Civil e Eng.Topográ ca-ise-0/0- Determinantes Permutações Determinantes Seja n N. Uma permutação p (p ; p ; : : : ; p n ) dos elementos do conjunto f; ; ; ng é um arranjo dos n números em alguma
ALGA - Eng.Civil e Eng.Topográ ca-ise-0/0- Determinantes Permutações Determinantes Seja n N. Uma permutação p (p ; p ; : : : ; p n ) dos elementos do conjunto f; ; ; ng é um arranjo dos n números em alguma
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/29 5 - RELAÇÕES 5.1) Relações e Dígrafos 5.2) Propriedades
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/29 5 - RELAÇÕES 5.1) Relações e Dígrafos 5.2) Propriedades
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Capítulo 5: Grafos Conexos. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 5: Grafos Conexos Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 5: Grafos Conexos Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005. Cálculo I. Caderno de Exercícios 1
 Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005 Cálculo I Caderno de Exercícios 1 Noções básicas de Lógica e Teoria dos Conjuntos Nota: Os problemas não resolvidos nas aulas constituem
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005 Cálculo I Caderno de Exercícios 1 Noções básicas de Lógica e Teoria dos Conjuntos Nota: Os problemas não resolvidos nas aulas constituem
Conceitos Básicos da Teoria de Grafos
 Conceitos Básicos da Teoria de Grafos Universidade Federal do Pampa - UNIPAMPA Engenharia da Computação Estrutura de Dados Profª Sandra Piovesan Grafos Uma noção simples, abstrata e intuitiva. Representa
Conceitos Básicos da Teoria de Grafos Universidade Federal do Pampa - UNIPAMPA Engenharia da Computação Estrutura de Dados Profª Sandra Piovesan Grafos Uma noção simples, abstrata e intuitiva. Representa
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Capítulo 16: Grafos Planares. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 16: Grafos Planares Preparado a partir do texto: Rangel, Socorro. Teoria do
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 16: Grafos Planares Preparado a partir do texto: Rangel, Socorro. Teoria do
Definições Básicas para Grafos
 Definições Básicas para rafos RAFO Um grafo (V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w), v e w V:
Definições Básicas para rafos RAFO Um grafo (V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w), v e w V:
4.1 Preliminares. No exemplo acima: Dom(R 1 ) = e Im(R 1 ) = Dom(R 2 ) = e Im(R 2 ) = Dom(R 3 ) = e Im(R 3 ) = Diagrama de Venn
 4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
Instituto de Computação Universidade Federal Fluminense. Notas de Aula de Teoria dos Grafos. Prof. Fábio Protti Niterói, agosto de 2015.
 Instituto de Computação Universidade Federal Fluminense Notas de Aula de Teoria dos Grafos Niterói, agosto de 2015. Conteúdo 1 Conceitos Básicos 5 1.1 Grafos, vértices, arestas..................... 5 1.2
Instituto de Computação Universidade Federal Fluminense Notas de Aula de Teoria dos Grafos Niterói, agosto de 2015. Conteúdo 1 Conceitos Básicos 5 1.1 Grafos, vértices, arestas..................... 5 1.2
Matemática /09 - Produto Interno 32. Produto Interno
 Matemática - 2008/09 - Produto Interno 32 Produto Interno A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass. Neste capítulo
Matemática - 2008/09 - Produto Interno 32 Produto Interno A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass. Neste capítulo
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Campus Pato Branco ENGENHARIA DE COMPUTAÇÃO. Prova Parcial 1 Matemática Discreta para Computação
 Prova Parcial 1 2011-2 Aluno(a): Data: 08/09/2011 1. (3p) Usando regras de inferência, prove que os argumentos são válidos. Use os símbolos proposicionais indicados: a. A Rússia era uma potência superior,
Prova Parcial 1 2011-2 Aluno(a): Data: 08/09/2011 1. (3p) Usando regras de inferência, prove que os argumentos são válidos. Use os símbolos proposicionais indicados: a. A Rússia era uma potência superior,
Teoria dos Grafos. Aula 5 - Estruturas de Dados para Grafos. Profª. Alessandra Martins Coelho. março/2013
 Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA
 UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: Torre de Hanói e Triângulo de Sierpinski AUTOR: André Brito (estagiário da BOM) ORIENTADOR: Dr. Professor
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: Torre de Hanói e Triângulo de Sierpinski AUTOR: André Brito (estagiário da BOM) ORIENTADOR: Dr. Professor
Introdução à Teoria dos Grafos
 Capítulo 1 Introdução à Teoria dos Grafos 1.1 História O primeiro problema cuja solução envolveu conceitos do que viria a ser teoria dos grafos, denominado "problema das pontes de Königsberg", foi resolvido
Capítulo 1 Introdução à Teoria dos Grafos 1.1 História O primeiro problema cuja solução envolveu conceitos do que viria a ser teoria dos grafos, denominado "problema das pontes de Königsberg", foi resolvido
ESTRUTURAS DE DADOS. prof. Alexandre César Muniz de Oliveira. 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8.
 ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Planaridade UFES. Teoria dos Grafos (INF 5037)
 Planaridade Planaridade Ideia intimamente ligada à noção de mapa, ou seja, uma representação de um conjunto de elementos (usualmente geográficos) dispostos sobre o plano A planaridade é um conceito associado
Planaridade Planaridade Ideia intimamente ligada à noção de mapa, ou seja, uma representação de um conjunto de elementos (usualmente geográficos) dispostos sobre o plano A planaridade é um conceito associado
Sistemas de equações lineares
 Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Teoria dos Grafos. Edson Prestes
 Edson Prestes As arestas possuem a função de indicar o relacionamento(espacial, comportamental, temporal) entre os elementos de um grafo. Em diversas situações esta relação não é simétrica, ou seja, par
Edson Prestes As arestas possuem a função de indicar o relacionamento(espacial, comportamental, temporal) entre os elementos de um grafo. Em diversas situações esta relação não é simétrica, ou seja, par
Matemática Discreta Capítulo 3 Versão preliminar
 Matemática Discreta Capítulo 3 Versão preliminar Henri Anciaux e Derek Hacon October 25, 2007 1 Generalidades sobre grafos Um grafo G é simplesmente um par de dois conjuntos V e A, o segundo sendo constituído
Matemática Discreta Capítulo 3 Versão preliminar Henri Anciaux e Derek Hacon October 25, 2007 1 Generalidades sobre grafos Um grafo G é simplesmente um par de dois conjuntos V e A, o segundo sendo constituído
1 Trajeto Euleriano. > Trajeto Euleriano 0/20
 Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
